Elastoplastic constitutive model considering the filling and cementation effects for gas hydrate-bearing sediments: development and finite element implementation

Dynamic evolution of hydrate filling and cementation effects significantly affects the mechanical behavior of gas hydrate-bearing sediments (GHBS). To analyze the strength and deformation characteristics of GHBS under varying effective confining pressures and hydrate saturations, we use the unified hardening model for clays and sands (CSUH model) as a framework. A compressive hardening parameter is introduced to describe the isotropic compression behavior. Additionally, cementation strength is incorporated to adjust the yield function, while state parameters are used to modify the potential strength. An elastoplastic constitutive model is developed to capture the strength, stiffness, dilatancy, and softening of GHBS. Based on the user-defined subroutine interface provided by ABAQUS and the modified Euler integral algorithm with error control, the user-defined subroutine (UMAT) is embedded in ABAQUS to implement the finite element model. Numerical solutions are obtained, and the accuracy of the model is verified by comparing theoretical solutions with experimental data, showing good agreement. The results demonstrate that the model accurately represents the stress-strain relations and shear dilatancy characteristics of GHBS under various conditions. Furthermore, the model effectively evaluates the mechanical responses of GHBS with different hydrate formation behaviors under various environmental loads. These findings provide a foundation for further engineering applications.

1 Introduction

Natural gas hydrates are extensively distributed in terrestrial permafrost regions, oceanic bottoms near continental margins, and deep-sea plains (Borowski et al., 1999). These hydrates are an important source of clean, efficient, and low-carbon fossil energy with vast reserves and high calorific value (Davidson et al., 1987). Marine gas hydrates that account for more than 95% of total hydrate resources (Ruppel and Kessler, 2017) have enormous development potential and economic value. Trial production of hydrates has been carried out in countries such as the United States, Canada, Japan, and China, achieving several milestones in the industrialization process (Ye et al., 2020). The monitoring results show that short-term trial production does not cause significant deformation of seabed strata (Yamamoto et al., 2017; Chen et al., 2018), but long-term production requires further examination of the potential destructiveness of reservoir deformation (Handwerger et al., 2017; Yan et al., 2020). Therefore, fully clarifying the mechanism of soil deformation induced by hydrate decomposition and elucidating the deformation characteristics of gas hydrate-bearing sediments (GHBS) are of significant importance for the long-term safe and efficient exploitation of natural gas hydrates.

GHBS occurs in unsaturated, underconsolidated marine soils, exhibiting characteristics similar to loose soils or loose sand. It shares certain mechanical properties with conventional soils, such as high sensitivity (Hong et al., 2013), high compressibility (Zeng et al., 2015), and high liquid and plastic limits (Bian et al., 2021). However, the distinct phase transition properties of hydrates result in physical and mechanical characteristics of GHBS that differ from those of conventional soils, remolded soils, and conventional oil and gas reservoirs. Extensive research on the physical and mechanical properties of GHBS has been conducted through microscopic and macroscopic tests. It is indicated that hydrates tend to form in coarser sediment fractures (Winters et al., 2000) and gradually surround soil particles with increasing hydrate saturation (S_h) (Hyodo et al., 2013). During depressurization, hydrates first decompose in sandy large pores, and the generated water moves to clay small pores and is converted to clay-bound water, causing changes in pore structure due to clay hydration expansion (Ren et al., 2022). Hydrates affect the macroscopic mechanical properties of sediments primarily through filling and cementation effects. Depending on the geological environment, hydrates occur in various modes, such as pore-filling, grain-coating, and cementation (Uchida et al., 2012). The influence mechanisms of different hydrate occurrence modes on the macroscopic mechanical properties of sediments are not entirely identical (Zhao et al., 2023a). However, the fundamental mechanism lies in the fact that the impact of hydrates on the macroscopic mechanical properties of sediments is primarily based on the individual effects of filling and cementation. The filling effect alters the compactness and interparticle friction properties of sediments (Fang et al., 2022; Xu et al., 2023), affecting compressive hardening (Zhao et al., 2023a) and dilatancy (Yang et al., 2024), while the cementation effect directly influences the strength and stiffness of sediments (Wu et al., 2020). The classical constitutive models incorporate parameters like progressive damage (Zhang et al., 2022) and strength degradation (Zhao et al., 2024) to describe these features, leading to the development of various constitutive models for hydrate sediments, including non-linear elastic models (Dong et al., 2024), critical state models (Zhao et al., 2024), and damage statistical models (Li et al., 2016; Wang et al., 2021). Additionally, due to the influence of hydrate formation and decomposition on the sediment pore connectivity and fluid distribution, multi-field coupling models such as the temperature-seepage-stress-saturation model (Zhao et al., 2023b), the temperature-seepage-stress-saturation multi-field coupling model (Yan et al., 2023), and the temperature-seepage-stress-chemical model (Samala and Chaudhuri, 2022; Qiu et al., 2023) have been established. These models provide a vital theoretical foundation for comprehensively understanding the complex characteristics of GHBS.

The established constitutive models enable the prediction of GHBS response characteristics under various conditions. Scholars have employed software such as TOUGH+Hydrate (Li et al., 2024), COMSOL (Sun et al., 2018; Huang et al., 2021), TOUGH+MIXHYD (Liao et al., 2024), and ABAQUS (Jiang et al., 2018) to simulate processes such as depressurization mining, wellbore shear deformation, and hydraulic fracturing, which offers new theoretical insights into the optimization of hydrate extraction techniques and risk management. However, current studies often oversimplify the description of hydrate filling and cementation effects, face challenges in parameter determination, and involve complex computations with limited application in major commercial software.

In this paper, an elastoplastic constitutive model for GHBS is established to provide a more accurate theoretical foundation and computational results for the safe extraction of natural gas hydrates. First, the cementation strength is introduced into the unified hardening model for clay and sand (CSUH model) framework to describe its evolution law. State parameters are used to reflect the hydrate filling effect, adjusting the hardening behavior of GHBS, while cohesion strength is incorporated to describe the cementation effect, forming the basis of the elastoplastic constitutive model. Subsequently, the numerical integration algorithm of the model is developed, and a user-defined subroutine (UMAT) is implemented to integrate the model into the commercial finite element software ABAQUS. The accuracy and applicability of the model are validated by comparing theoretical solutions with experimental data. Finally, the comparison with experimental data confirms that the model effectively captures the hardening, softening, dilatancy, and contraction behaviors of GHBS, demonstrating its advantages in providing a more accurate theoretical basis for the safe extraction of natural gas hydrates.

2 Establishment of the constitutive model

2.1 Hardening of GHBS

The compressive hardening is the property of soil modulus to change with pressure during compression, which is essentially due to friction, sliding, and subsequent structural collapse between solid particles (Onitsuka et al., 1995). For soils containing exogenous components, significant changes in specific surface area and pore structure lead to variations in compressibility (Bian et al., 2024). These microstructural changes further influence the compressibility of the soil, resulting in more complex mechanical responses. In the case of GHBS, during compression, the crushing and rearrangement of GHBS particles (Bai et al., 2023; Bai et al., 2025) induce changes in the pore structure of the soil skeleton and specific surface area (Bian et al., 2024). These microstructural alterations modify the compressibility of GHBS, causing its compression line in e-lnp space to deviate from an ideal linear form and exhibit a more complex curved characteristic, resembling the behavior of sand under specific conditions. The unified hardening model for clays and sands (CSUH model) introduced by Yao et al. (2019) incorporates a compressive hardening parameter, which is denoted as p_s, to accurately depict the isotropic compression behavior of sands, clays, and structured soils. This model can also be used to characterize the compressive properties of GHBS (Lin et al., 2020).

Based on these foundational studies, to comprehensively reflect the manifestation of micro-mechanisms in macroscopic compressibility, this study elucidates the normal consolidation line (NCL) expression for GHBS as expressed in Equations 1:

$e=Z-\lambda \ln \left(\frac{p+p_{\mathrm{s}}}{1+p_{\mathrm{s}}}\right)(1)$

where Z is the void ratio at an average normal stress of 1 kPa on the NCL, determining the NCL’s position in the e-lnp space; λ is the slope of the NCL’s asymptote; p_s is the introduced compressive hardening parameter, indicating the curvature. When p_s = 0, Equation 1 reverts to the conventional NCL expression for normally consolidated clay.

Hydrates alter the cementation degree and pore structure of sediments, thereby affecting the hardening property of GHBS (Hou et al., 2022). The extent to which hydrates influence the hardening property of GHBS is closely related to the S_h. Depending on the storage form of hydrates (such as pore-filling, particle-coating, and cementing), p_s can be expressed as a linear function of S_h (Yang et al., 2023) and an exponential relationship (Uchida et al., 2012; Lijith et al., 2019), etc. To uniformly describe the compressibility of GHBS, this study assumes that p_s and S_h satisfy a functional relationship:

$p_{\mathrm{s}}=p_{\mathrm{s}0}+A_{\mathrm{s}}{S}_{\mathrm{h}}^{B_{\mathrm{s}}}(2)$

where p_s0 is the compressibility parameter of sediments without hydrates; A_s and B_s reflect the degree of hydrate contribution to compressibility, which depend on hydrate morphology and are determined based on experimental data.

As the hydrostatic pressure increases from p_x0 to p_x, and by combining Equation 2 with the rebound properties of geotechnical materials, the expression for p_x is derived as:

$p_x=\left(p_{x0}+p_{\mathrm{s}}\right)\exp \left(\frac{{\epsilon }_{\mathrm{v}}^{\mathrm{p}}}{c_{\mathrm{p}}}\right)-p_{\mathrm{s}}(3)$

where ${\epsilon }_{\mathrm{v}}^{\mathrm{p}}$ is the plastic volume strain; c_p= (λ-κ)/ (1 + e₀), with κ being the slope of the overconsolidation compression line (OCL) in e-lnp space, and e₀ is the initial void ratio.

2.2 Cementation characteristics of GHBS

Sandy soil exhibits a distinct critical state line (CSL). Given that the distance between the NCL and CSL is affected by the yield equation, the CSUH model employs the same yield surface equation as the modified Cambridge model, albeit with a modified expression for p_x. The yield equation is formulated as:

$f=q^2+M^{2}p\left(p-p_x\right)(4)$

Laboratory experiments on GHBS indicate that its cementation strength should not be neglected (Bai et al., 2025; Yao et al., 2019). Thus, this paper extends Equation 4 as:

$f=q^2+M^2\left(p+p_{\mathrm{t}}\right)\left(p-p_x\right)(5)$

where p_t represents the cementation strength of GHBS.

The cementation strength of GHBS is gradually decaying during the deformation process, accompanied by the rotation and slippage of skeleton particles and destruction of soil skeleton structure. With reference to the review of experimental test results of GHBS by Lijith et al. (2019), the initial cementation strength p_t0 is formulated as an exponential relationship in Equations 6:

$p_{\mathrm{t}0}=A_{\mathrm{t}}{S}_{\mathrm{h}}^{B_{\mathrm{t}}}(6)$

where A_t and B_t are material constants characterizing cementation strength, describing the contribution of hydrates to the cementation strength of sediments, and are determined based on experimental data.

Referring to the research of Lijith et al. (2019), Fang et al. (2020), and Iwai et al. (2022), it is assumed that the cementation strength p_t decreases with increasing plastic shear strain, the p_t and its increment dp_t during shearing are given by:

$\left.\begin{array}{r}{p}_{\mathrm{t}}=p_{\mathrm{t}0}\exp \left(-a{\epsilon }_{\mathrm{s}}^{\mathrm{p}}\right)\hspace{0.33em}\\ \mathrm{d}{p}_{\mathrm{t}}=-a{p}_{\mathrm{t}}\mathrm{d}{\epsilon }_{\mathrm{s}}^{\mathrm{p}}\end{array}\right\}(7)$

where a denotes the decay rate of cementation strength.

Substituting Equations 3, 7 into Equation 5 and employing ${\epsilon }_{\mathrm{v}}^{\mathrm{p}}$ as the compressive hardening parameter for yield surface. Within the CSUH model framework, the compressive hardening parameter is substituted with the unified hardening parameter H to characterize various soil properties. Consequently, the yield surface equation for the GHBS model is formulated in Equations 8:

$f=\ln \left(\frac{p+p_{\mathrm{s}}}{p+p_{\mathrm{t}}}+\frac{q^2}{M^2{\left(p+p_{\mathrm{t}}\right)}^2}\right)+\ln \left(\frac{p+p_{\mathrm{t}}}{p_{x0}+p_{\mathrm{s}}}\right)-\frac{1}{c_{\mathrm{p}}}H(8)$

2.3 Constitutive model of GHBS

The stress ratio η considering the dynamic cementation strength of GHBS is expressed in Equations 9:

$\eta =\frac{q}{p+p_{\mathrm{t}}}(9)$

The unified hardening parameter H is defined in Equations 10 based on Yao et al. (2019):

$H=\int \frac{M_{\mathrm{f}}^4-{\eta }^4}{M^4-{\eta }^4}\mathrm{d}{\epsilon }_{\mathrm{v}}^{\mathrm{p}}(10)$

where M_f denotes the potential strength, indicating the strength variation of GHBS,

$M_{\mathrm{f}}=M\exp \left(m\xi \right)(11)$

where m represents the strength parameter; and ξ is the densification state parameter.

As illustrated in Figure 1, ξ represents the distance between the anisotropic compression line (ACL) and the critical state line (CSL), which is described in Equations 12:

$\xi =Z-\lambda \ln \left(\frac{p+p_{\mathrm{s}}}{1+p_{\mathrm{s}}}\right)-\left(\lambda -\kappa \right)\ln \left(\frac{p+p_{\mathrm{s}}}{p+p_{\mathrm{t}}}+\frac{q^2}{M^2{\left(p+p_{\mathrm{t}}\right)}^2}\right)-e(12)$

Figure 1

Figure 1. State parameter ξ.

The associated flow rule is adopted, and the dilation equation is expressed as:

$d=\frac{M^2-{\eta }^2}{2\eta }(13)$

2.4 Elastoplastic matrix

Based on elastoplastic theory, the elastoplastic matrix for GHBS is deduced in Equations 14:

$\left\{\begin{array}{c}\mathrm{d}p\\ \mathrm{d}q\end{array}\right\}=\left[\begin{array}{cc}{D}_{\text{pp}}& D_{\text{pq}}\\ D_{\text{qp}}& D_{\text{qq}}\end{array}\right]\left\{\begin{array}{c}\mathrm{d}{\epsilon }_{\mathrm{v}}\\ \mathrm{d}{\epsilon }_{\mathrm{s}}\end{array}\right\}(14)$

Where the components are expressed as Equations 15:

$\left\{\begin{array}{l}{D}_{\text{pp}}=K-\frac{K^{2}d}{N}\frac{\partial f}{\partial p}\\ D_{\text{pq}}=-\frac{3KGd}{N}\frac{\partial f}{\partial q}\\ D_{\text{qp}}=-\frac{3KG}{N}\frac{\partial f}{\partial p}\\ D_{\text{qq}}=3G-\frac{9G^2}{N}\frac{\partial f}{\partial q}\end{array}\right.(15)$

with N in Equations 15 defined by Equations 16:

$N=K_{\mathrm{p}}+Kd\frac{\partial f}{\partial p}+3G\frac{\partial f}{\partial q}(16)$

where d corresponds to the dilation equation depicted in Equation 13; K and G are the bulk modulus and shear modulus, respectively, with K = E/[3 (1−2μ)] and G = E/[2 (1+μ)]; μ denotes poisson’s ratio; and K_p is the hardening modulus, which is expressed as:

$K_{\mathrm{p}}=\frac{d}{c_{\mathrm{p}}}\frac{M_{\mathrm{f}}^4-{\eta }^4}{M^4-{\eta }^4}+a{p}_{\mathrm{t}}\frac{\partial f}{\partial p_{\mathrm{t}}}(17)$

3 Development and validation of the constitutive model

3.1 Modified euler integration algorithm process

The numerical integration algorithm for constitutive model primarily consists of explicit and implicit integration methods. The explicit method is straightforward but lacks accuracy and computational efficiency. The implicit method performs better in terms of numerical stability, but requires the solution of implicit equations and has only first-order accuracy. To address these limitations, Sloan et al. (2001) introduced an enhanced Euler integration algorithm. This approach initially calculates an estimated value using the explicit Euler method, then calculates a corrected value using the implicit Euler method, and finally takes the average of two values as the final approximation. The difference between the estimated and corrected values is used to evaluate the error. If the error exceeds a predefined threshold, the step size is reduced; otherwise, it is increased. This strategy combines the simplicity of the explicit method with the stability of the implicit method. The UMAT subroutine for the constitutive model of GHBS is developed using modified Euler integration algorithm with error control. The computational procedure is as follows (see Figure 2):

(1) Assume time T = 0 and time increment ΔT = 1, and determine the initial elastic stiffness matrix [D^e] based on the current stress under elastic loading.

(2) Determine the sub-step strain increment {Δε_s} = ΔT{Δε}, perform the first stress increment estimation {Δσ₁} = [D^ep ({σ}, H)]{Δε_s}, and calculate the plastic strain increment {Δε^p} and the hardening parameter increment {ΔH}.

(3) Update the stiffness matrix [D^ep ({σ+Δσ₁}, H+ΔH)] based on the first estimated stress {σ+Δσ₁}, and then calculate the second stress increment estimation {Δσ₂} = [D^ep ({σ+Δσ₁}, H+ΔH)]{Δε_s}.

(4) Calculate the average stress increment {Δσ} = ({Δσ₁}+{Δσ₂})/2.

(5) Calculate the error R = ||({Δσ₁}+{Δσ₂})/2||/||{σ+Δσ}||. If R > sstol, then reduce ΔT_new according to ΔT_new = 0.8 [sstol/R]^(1/2)ΔT and return to step (2). If R ≤ sstol, proceed to the next step.

(6) Update the stress {σ} = {σ}+{Δσ}, plastic strain increment {ε^p}, and hardening parameter {H}.

(7) Set T = T+ΔT. The time increment ΔT_new takes 0.8 [sstol/R]^ (1/2)ΔT. If T+ΔT_new > 1, then take ΔT_new = 1-T and return to step (2).

(8) When T = 1, the computation is completed, and the stiffness matrix, i.e., the Jacobian matrix, is updated.

Figure 2

Figure 2. Flowchart of the modified Euler integration algorithm.

3.2 Validation of the constitutive model

3.2.1 Parameter determination

The model constructed in this study includes 12 parameters, which can be categorized into two types, as follows:

(1) The first category consists of fundamental physical parameters, including λ, κ, Z, μ, M, and e₀. Among them, λ and κ are fundamental parameters determined through isotropic compression (NCL) and unloading (OCL) tests; μ is the Poisson’s ratio; M is the critical state stress ratio; and e₀ is the initial void ratio. These parameters are determined using the same method as the Modified Cam Clay model (MCC model).

(2) The second category includes characteristic parameters, where the hardening parameters p_s0, A_s, and B_s are inverted based on Equation 2. The cementation parameters A_t and B_t can be calibrated by referring to the cohesion determination method of the Mohr-Coulomb model. The strength parameter m is determined according to Equation 11 by obtaining the state parameter at peak strength and deriving the mathematical relationship for m. For the cementation degradation rate a, since the cohesion degradation rate of GHBS under the same hydrate occurrence mode and shear rate is identical, only a single experimental result that closely matches the predicted results is required to determine the parameter a.

3.2.2 Model prediction

To validate the applicability of the model established in this paper, the analytical solution of the model and the numerical solution of a single element are compared with the laboratory experimental data of GHBS.

Miyazaki et al. (2012) prepared GHBS samples with different S_h (S_h = 0, 27%–34%, 41%–45%) using Toyoura sand, with an initial porosity of 37.8% (corresponding to an initial void ratio of 0.6077). Triaxial shear tests were conducted at various effective confining pressures (σ₃) of 0.5 MPa, 1 MPa, 2 MPa, and 3 MPa. The model developed in this paper is used for comparison, and the values of the model validation parameters are presented in Table 1.

Table 1

Table 1. Model parameters.

Figure 3 presents a comparison of experimental data, analytical solutions, and numerical solutions for sediments without hydrate (S_h = 0) under σ₃ = 2 MPa. The analytical solutions are in good agreement with numerical solutions and agree well with the experimental data, indicating that the model accurately captures the strain hardening and softening behavior of sediments. This preliminary validation suggests that the model’s algorithm and programming are correctly implemented.

Figure 3

Figure 3. Comparison with Miyazaki et al. (S_h = 0, σ₃ = 2 MPa).

In the experiments on GHBS conducted by Miyazaki et al., the S_h of the samples ranged from 27% to 34% and from 41% to 45%. For simplicity, this study uses the average values of S_h = 30.5% and S_h = 43% for prediction and comparison. Figure 4 shows the comparison between experimental data (S_h = 27%–34%) and predicted data (S_h = 30.5%) at the same σ₃ (2 MPa). The agreement between the analytical and numerical solutions further confirms the accuracy of UMAT subroutine. Compared with Figures 3, 4 exhibits more pronounced strain softening behavior, which is due to the fact that the hydrate changes the internal pore structure of sample and enhance the cementation strength of soil skeleton. This cementation strength decreases during shearing, resulting in more evident strain softening in GHBS.

Figure 4

Figure 4. Comparison with Miyazaki et al. (S_h = 30.5%, σ₃ = 2 MPa).

As observed in Figure 5, when the σ₃ is fixed at 2 MPa, an increase in S_h further enhances the stiffness and strength of the GHBS. Both the initial stiffness and peak strength experience noticeable increases. Figure 5 also presents the analytical and numerical solutions, which are in high agreement but differ from the experimental data. This discrepancy is due to the fact that the actual experimental S_h values are between 41% and 45%, whereas the predictions use a fixed average value of S_h = 43%.

Figure 5

Figure 5. Comparison with Miyazaki et al. (S_h = 43%, σ₃ = 2 MPa).

Figure 3–5 compare the experimental data, analytical solutions, and numerical solutions for GHBS with different S_h values under the same σ₃ of 2 MPa. For sediments with the same S_h = 43%, the comparison curves of the results with effective confining pressures of 0.5 MPa, 1 MPa, and 3 MPa are illustrated in Figure 6–8, respectively.

Figure 6

Figure 6. Data comparison with Miyazaki et al. (S_h = 43%, σ₃ = 0.5 MPa).

Figure 7

Figure 7. Data comparison with Miyazaki et al. (S_h = 43%, σ₃ = 1 MPa).

Figure 8

Figure 8. Data comparison with Miyazaki et al. (S_h = 43%, σ₃ = 3 MPa).

Figure 6 presents a comparison of the data at S_h = 43%. In the case of a lower σ₃ of 0.5 MPa, the frictional strength between the particles is relatively small, the sample reaches the peak strength at smaller strains and experiences a rapid decline in strength. As depicted in Figure 7, as the σ₃ increases to 1 MPa, the particle contact becomes denser, leading to an increase in the peak strength and its corresponding strain. As shown in Figure 8, the stress-strain curve becomes smoother as the σ₃ further increase to 2 MPa, indicating that the larger the σ₃, the more obvious the filling and cementation effects of hydrates. Figure 6–8 demonstrate that the analytical and numerical solutions are in agreement, and they exhibit good consistency with the experimental data, suggesting that the modified Euler integration algorithm with error control provides accurate and stable calculation results, validating the precision of the model and its algorithm.

To further validate the model’s applicability, comparisons are made with the laboratory experiments conducted by Hyodo et al. (2013). They firstly prepared Toyoura sand samples with an initial void ratio of 0.67, and then produced samples with different S_h values. The shear test data for σ₃ of 5 MPa and S_h values of 0, 24.2%, 35.1%, and 53.1% are presented in Figures 9, 10, respectively. The values of λ, κ, and M are given in a study by Hyodo et al. (2016). Table 1 lists the parameters required for the model predictions in this study.

Figure 9

Figure 9. Comparisons of predicting stress-strain curves and experimental results with Hyodo et al.

Figure 10

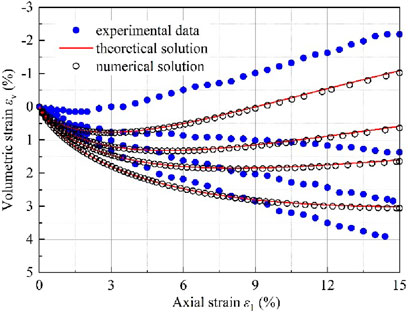
Figure 10. Comparisons of predicting volumetric strain curves and experimental results with Hyodo et al.

Observation of the experimental data, analytical solutions, and numerical solutions presented in Figure 9 reveals that the model accurately captures the stress-strain behaviors under varying S_h. As S_h increases, the peak deviatoric stress gradually increases while its corresponding strain decreases. The model accurately captures the key features of the experimental data, demonstrating its reliability and effectiveness in describing the mechanical behavior of GHBS.

Figure 10 illustrates the prediction results of volume strain by the model, which match well with the experimental data, indicating a good match in the overall trend, despite some deviations. Furthermore, the model still demonstrates commendable computational accuracy and effectively captures characterize the deformation properties of GHBS at high S_h.

4 Conclusion

The application of the GHBS constitutive model in large commercial software is limited. This paper develops and establishes the GHBS constitutive model, investigating the mechanical characteristics of GHBS under varying hydrate saturations and confining pressures. The main work and conclusions are as follows:

(1) Using the CSUH model as a framework, an elastoplastic constitutive model for GHBS is developed. To account for the hydrate filling effect, a hardening parameter is introduced. Cementation strength is introduced to represent the cementation effect of hydrates. Additionally, state parameters are used to adjust potential strength, resulting in an elastoplastic constitutive model that considers both the hydrate filling and cementation effects.

(2) A modified Euler integration algorithm with error control is employed to program the UMAT subroutine for elastoplastic constitutive model. The subroutine is embedded in ABAQUS to compute numerical solutions for shear tests under various confining pressures and hydrate saturations.

(3) A comparative analysis of numerical simulations, experimental data, and theoretical solutions demonstrates that our model more comprehensively captures the effects of hydrate filling and cementation on sediment mechanical behavior. It also better accounts for complex mechanical properties, such as strength, stiffness, shear dilation, and softening.

For future research, we suggest optimizing algorithms and using hardware acceleration to reduce computational costs and improve the model’s practicality. Additionally, multi-field coupling effects (e.g., temperature-permeability-stress coupling) on GHBS should be considered, with further validation through field-scale experiments. These steps will enhance the application of the model in more complex geological conditions. Based on our current findings, these directions will contribute to a deeper understanding of GHBS.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

QY: Data curation, Software, Validation, Visualization, Writing–original draft. QL: Conceptualization, Funding acquisition, Methodology, Project administration, Writing–original draft, Writing–review and editing. JL: Formal Analysis, Methodology, Project administration, Writing–review and editing. ZW: Data curation, Software, Writing–original draft. LY: Data curation, Software, Writing–original draft. XW: Software, Validation, Writing–review and editing. BG: Validation, Visualization, Writing–review and editing. YD: Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was financially supported by the Guangdong Major Project of Basic and Applied Basic Research (No. 2023B0303000021), Director’s research fund of the Guangzhou Marine Geological Survey (No. 2023GMGSJZJJ00002), and the Marine Geological Survey Program of China Geological Survey (No. DD20221706; No. DD20230065). The support is gratefully acknowledged with thanks.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Zhang, B., Chen, H., and Chen, P. (2025). A novel thermodynamic constitutive model of coarse-grained soils considering the particle breakage. Transp. Geotech. 50, 101462. doi:10.1016/j.trgeo.2024.101462

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Yang, G., Zou, W., and Yuan, W. (2023). The constitutive behavior and dissociation effect of hydrate-bearing sediment within a granular thermodynamic framework. Ocean. Eng. 268, 113408. doi:10.1016/j.oceaneng.2022.113408

CrossRef Full Text | Google Scholar

Bian, X., Ren, Z., Zeng, L., Zhao, F., Yao, Y., and Li, X. (2024). Effects of biochar on the compressibility of soil with high water content. J. Clean. Prod. 434, 140032. doi:10.1016/j.jclepro.2023.140032

CrossRef Full Text | Google Scholar

Bian, X., Zeng, L.-L., Li, X.-Z., Li, X.-Z., and Hong, J. T. (2021). Deformation modulus of reconstituted and naturally sedimented clays. Eng. Geol., 295, 106450. doi:10.1016/j.enggeo.2021.106450

CrossRef Full Text | Google Scholar

Borowski, W. S., Paull, C. K., and Ussler Iii, W. (1999). Global and local variations of interstitial sulfate gradients in deep-water, continental margin sediments: sensitivity to underlying methane and gas hydrates. Mar. Geol. 159 (1-4), 131–154. doi:10.1016/s0025-3227(99)00004-3

CrossRef Full Text | Google Scholar

Chen, L., Feng, Y. C., Okajima, J., Komiya, A., and Maruyama, S. (2018). Production behavior and numerical analysis for 2017 methane hydrate extraction test of Shenhu, South China Sea. J. Nat. Gas Sci. Eng. 53, 55–66. doi:10.1016/j.jngse.2018.02.029

CrossRef Full Text | Google Scholar

Davidson, D. W., Desando, M. A., Gough, S. R., Handa, Y. P., Ratcliffe, C. I., Ripmeester, J. A., et al. (1987). A Clathrate hydrate of carbon-Monoxide. Nature 328 (6129), 418–419. doi:10.1038/328418a0

CrossRef Full Text | Google Scholar

Dong, L., Li, Y., Zhang, Y., Hu, G., Liao, H., Chen, Q., et al. (2024). Deformation characteristics of hydrate-bearing sediments. J. Ocean Univ. China 23 (1), 149–156. doi:10.1007/s11802-024-5551-y

CrossRef Full Text | Google Scholar

Fang, H., Shi, K., and Yu, Y. (2020). Geomechanical constitutive modelling of gas hydrate-bearing sediments by a state-dependent multishear bounding surface model. J. Nat. Gas Sci. Eng. 75, 103119. doi:10.1016/j.jngse.2019.103119

CrossRef Full Text | Google Scholar

Fang, H., Shi, K., and Yu, Y. (2022). A state-dependent subloading constitutive model with unified hardening function for gas hydrate-bearing sediments. Int. J. Hydrogen Energy 47 (7), 4441–4471. doi:10.1016/j.ijhydene.2021.11.104

CrossRef Full Text | Google Scholar

Handwerger, A. L., Rempel, A. W., and Skarbek, R. M. (2017). Submarine landslides triggered by destabilization of high-saturation hydrate anomalies. Geochem. Geophys. Geosystems 18 (7), 2429–2445. doi:10.1002/2016gc006706

CrossRef Full Text | Google Scholar

Hong, Z. S., Bian, X., Cui, Y. J., Gao, Y. F., and Zeng, L. L. (2013). Effect of initial water content on undrained shear behaviour of reconstituted clays. Géotechnique 63 (6), 441–450. doi:10.1680/geot.11.p.114

CrossRef Full Text | Google Scholar

Hou, X., Qi, S., Huang, X., Guo, S., Zou, Y., Ma, L., et al. (2022). Hydrate morphology and mechanical behavior of hydrate-bearing sediments: a critical review. Geomechanics Geophys. Geo-Energy Geo-Resources 8 (5), 161–236. doi:10.1007/s40948-022-00461-8

CrossRef Full Text | Google Scholar

Huang, L., Xu, C., Xu, J., Zhang, X., and Xia, F. (2021). The depressurization of natural gas hydrate in the multi-physics coupling simulation based on a new developed constitutive model. J. Nat. Gas Sci. Eng. 95, 103963. doi:10.1016/j.jngse.2021.103963

CrossRef Full Text | Google Scholar

Hyodo, M., Nakata, Y., and Yoshimoto, N. (2016). Challenge for methane hydrate production by geotechnical engineering. Jpn. Geotech. Soc. Spec. Publ. 2 (1), 62–75. doi:10.3208/jgssp.kl-6

CrossRef Full Text | Google Scholar

Hyodo, M., Yoneda, J., Yoshimoto, N., and Nakata, Y. (2013). Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed. Soils Found. 53 (2), 299–314. doi:10.1016/j.sandf.2013.02.010

CrossRef Full Text | Google Scholar

Iwai, H., Kawasaki, T., and Zhang, F. (2022). Constitutive model for gas hydrate-bearing soils considering different types of hydrate morphology and prediction of strength-band. Soils Found. 62 (1), 101103. doi:10.1016/j.sandf.2021.101103

CrossRef Full Text | Google Scholar

Jiang, M., Liu, J., and Shen, Z. (2018). Investigating the shear band of methane hydrate-bearing sediments by FEM with an elasto-plastic constitutive model. Bull. Eng. Geol. Environ. 77 (2018), 1015–1025. doi:10.1007/s10064-017-1109-1

CrossRef Full Text | Google Scholar

Li, S., Liu, L., Wu, D., Zhang, N., and Guo, Y. (2024). Numerical simulation on gas production from hydrate-bearing sediments by depressurization considering time-varying reservoir compressibility. Gas Sci. Eng. 121, 205180. doi:10.1016/j.jgsce.2023.205180

CrossRef Full Text | Google Scholar

Li, Y., Liu, C., and Liu, L. (2016). Damage statistic constitutive model of hydrate-bearing sediments and the determination method of parameters. Acta Pet. Sin. 37 (10), 1273. doi:10.7623/syxb201610007

CrossRef Full Text | Google Scholar

Liao, T., Yuan, L., Li, W., Kan, J., Luo, W., Xiong, X., et al. (2024). One-dimensional numerical simulation on removal of CO2 hydrate blockage around wellbore by N2 injection. Processes 12 (1), 204. doi:10.3390/pr12010204

CrossRef Full Text | Google Scholar

Lijith, K. P., Malagar, B. R. C., and Singh, D. N. (2019). A comprehensive review on the geomechanical properties of gas hydrate bearing sediments. Mar. Petroleum Geol. 104, 270–285. doi:10.1016/j.marpetgeo.2019.03.024

CrossRef Full Text | Google Scholar

Lin, L., Yangping, Y., and Xuhui, Z. (2020). An elastoplastic constitutive model for gas hydrate-bearing sediments. Chin. J. Theor. Appl. Mech. 52 (2), 556–566. doi:10.6052/0459-1879-19-184

CrossRef Full Text | Google Scholar

Miyazaki, K., Tenma, N., Aoki, K., and Yamaguchi, T. (2012). A nonlinear elastic model for triaxial compressive properties of artificial methane-hydrate-bearing sediment samples. Energies 5 (10), 4057–4075. doi:10.3390/en5104057

CrossRef Full Text | Google Scholar

Onitsuka, K., Hong, Z., Hara, Y., and Yoshitake, S. (1995). Interpretation of oedometer test data for natural clays. Soils Found. 35 (3), 61–70. doi:10.3208/sandf.35.61

CrossRef Full Text | Google Scholar

Qiu, Y., Wang, X., Wang, Z., Liang, W., and Zhao, T. (2023). THMC fully coupled model of natural gas hydrate under damage effect and parameter sensitivity analysis. J. Mar. Sci. Eng. 11 (3), 612. doi:10.3390/jmse11030612

CrossRef Full Text | Google Scholar

Ren, J., Yin, Z., Li, Q., Wu, F., Chen, D., and Li, S. (2022). Pore-Scale investigation of CH4 hydrate kinetics in clayey-silty sediments by low-field NMR. Energy Fuels 36 (24), 14874–14887. doi:10.1021/acs.energyfuels.2c03255

CrossRef Full Text | Google Scholar

Ruppel, C. D., and Kessler, J. D. (2017). The interaction of climate change and methane hydrates. Rev. Geophys. 55 (1), 126–168. doi:10.1002/2016rg000534

CrossRef Full Text | Google Scholar

Samala, R., and Chaudhuri, A. (2022). Coupled THMC modeling of dissociation induced deformation of gas hydrate bearing media. Comput. Geosciences 166, 105162. doi:10.1016/j.cageo.2022.105162

CrossRef Full Text | Google Scholar

Sloan, S. W., Abbo, A. J., and Sheng, D. C. (2001). Refined explicit integration of elastoplastic models with automatic error control. Eng. Comput. 18 (1-2), 121–194. doi:10.1108/02644400110365842

CrossRef Full Text | Google Scholar

Sun, X., Luo, H., and Soga, K. (2018). A coupled thermal–hydraulic–mechanical–chemical (THMC) model for methane hydrate bearing sediments using COMSOL Multiphysics. J. Zhejiang University-Science A 19 (8), 600–623. doi:10.1631/jzus.a1700464

CrossRef Full Text | Google Scholar

Uchida, S., Soga, K., and Yamamoto, K. (2012). Critical state soil constitutive model for methane hydrate soil. J. Geophys. Res. Solid Earth 117, B03209. doi:10.1029/2011jb008661

CrossRef Full Text | Google Scholar

Wang, F., Wang, Z., Zhang, D., and Wang, Z. (2021). Statistical damage constitutive model based on self-consistent Eshelby method for natural gas hydrate sediments. Energy Sci. and Eng. 9 (11), 2079–2098. doi:10.1002/ese3.968

CrossRef Full Text | Google Scholar

Winters, W. J., Wilcox-Cline, R. W., Long, P., Dewri, S. K., Kumar, P., Stern, L., et al. (2000). Comparison of the physical and geotechnical properties of gas-hydrate-bearing sediments from offshore India and other gas-hydrate-reservoir systems. Mar. Petroleum Geol. 2014, 1–29. doi:10.1016/j.marpetgeo.2014.07.024

CrossRef Full Text | Google Scholar

Wu, P., Li, Y., Liu, W., Sun, X., Kong, X., and Song, Y. (2020). Cementation failure behavior of consolidated gas hydrate-bearing sand. J. Geophys. Research-Solid Earth 125 (1), e2019JB018623. doi:10.1029/2019jb018623

CrossRef Full Text | Google Scholar

Xu, J., Wang, R., Xu, C., Wang, Y., and Zhang, J. (2023). Application and improvement of a stress partition framework-based methane hydrate-bearing sediment constitutive model for wide range confining stress. Comput. Geotechnics 159, 105463. doi:10.1016/j.compgeo.2023.105463

CrossRef Full Text | Google Scholar

Yamamoto, K., Kanno, T., Wang, X. X., Tamaki, M., Fujii, T., Chee, S. S., et al. (2017). Thermal responses of a gas hydrate-bearing sediment to a depressurization operation. Rsc Adv. 7 (10), 5554–5577. doi:10.1039/c6ra26487e

CrossRef Full Text | Google Scholar

Yan, C., Dong, L., Ren, X., and Cheng, Y. (2023). Stability of submarine slopes during replacement of methane in natural gas hydrates with carbon dioxide. J. Clean. Prod. 383, 135440. doi:10.1016/j.jclepro.2022.135440

CrossRef Full Text | Google Scholar

Yan, C., Ren, X., Cheng, Y., Song, B., Li, Y., and Tian, W. (2020). Geomechanical issues in the exploitation of natural gas hydrate. Gondwana Res. 81, 403–422. doi:10.1016/j.gr.2019.11.014

CrossRef Full Text | Google Scholar

Yang, D., Yan, R., Yan, M., Lu, D., and Wei, C. (2023). Geomechanical properties of artificial methane hydrate-bearing fine-grained sediments. Gas Sci. Eng. 109, 104852. doi:10.1016/j.jngse.2022.104852

CrossRef Full Text | Google Scholar

Yang, F., Li, C., Wei, N., Jia, W., He, J., Song, S., et al. (2024). Mechanical properties and constitutive model of high-abundance methane hydrates containing clayey–silt sediments. Ocean. Eng. 298, 117245. doi:10.1016/j.oceaneng.2024.117245

CrossRef Full Text | Google Scholar

Yao, Y., Liu, L., Luo, T., Tian, Y., and Zhang, J. M. (2019). Unified hardening (UH) model for clays and sands. Comput. Geotechnics 110, 326–343. doi:10.1016/j.compgeo.2019.02.024

CrossRef Full Text | Google Scholar

Ye, J., Qin, X., Xie, W., Lu, H. L., Ma, B. J., Qiu, H. J., et al. (2020). The second natural gas hydrate production test in the South China Sea. China Geol. 3 (2), 197–209. doi:10.31035/cg2020043

CrossRef Full Text | Google Scholar

Zeng, L.-L., Hong, Z.-S., and Cui, Y.-J. (2015). Determining the virgin compression lines of reconstituted clays at different initial water contents. Can. Geotechnical J. 52 (9), 1408–1415. doi:10.1139/cgj-2014-0172

CrossRef Full Text | Google Scholar

Zhang, N., Wang, H., and Jiang, M. (2022). A mesoelastic-plastic damage model for hydrate-bearing sediments with various hydrate-growth patterns. Ocean. Eng. 266, 112919. doi:10.1016/j.oceaneng.2022.112919

CrossRef Full Text | Google Scholar

Zhao, Y., Kong, L., Liu, J., Sang, S., Zeng, Z., Wang, N., et al. (2023a). Permeability properties of natural gas hydrate-bearing sediments considering dynamic stress coupling: a comprehensive experimental investigation. Energy 283, 129214. doi:10.1016/j.energy.2023.129214

CrossRef Full Text | Google Scholar

Zhao, Y., Kong, L., Liu, L., Hu, G., Ji, Y., Bu, Q., et al. (2024). Mechanical behaviors of natural gas hydrate-bearing clayey-silty sediments: experiments and constitutive modeling. Ocean. Eng. 294, 116791. doi:10.1016/j.oceaneng.2024.116791

CrossRef Full Text | Google Scholar

Zhao, Y., Liu, J., Sang, S., Hua, L., Kong, L., Zeng, Z., et al. (2023b). Experimental investigation on the permeability characteristics of methane hydrate-bearing clayey-silty sediments considering various factors. Energy 269, 126811. doi:10.1016/j.energy.2023.126811

CrossRef Full Text | Google Scholar