Gaussian beam migration in exploration seismology: methods, advantages and implementation

Migration methods are fundamental to seismic imaging. Generally, seismic migration imaging methods can be categorized in pre-stack and post-stack techniques that are based on either wave-equation or ray-theory principles. Key methods include Kirchhoff Migration, a ray-theory-based approach; wave-equation-based techniques such as Reverse Time Migration (RTM); and Gaussian Beam Migration (GBM), which combines the flexibility of ray theory with the accuracy of wave-equation methods and is getting more attention recently. The GBM methods include two implementations: the frequency domain and the space-time domain. In the construction of the reverse wavefield, the frequency-domain GBM employs ray-tracing methodology to compute the wavefield; by utilizing the kinematic characteristics of the seismic wavefield, it discretizes the computational domain into equal angular segments, thereby reducing computational iterations for imaging points located at greater offsets from the virtual source (receiver point). In contrast, the space-time-domain GBM incorporates the wavefield extrapolation approach derived from RTM, accounting for the dynamic characteristics of the seismic wavefield; it enhances the imaging accuracy of migration results through direct computation of the wavefield information at each imaging point, albeit at the cost of increased computational time. This review firstly traces the development of GBM methods, which progresses from acoustic to viscous, elastic and anisotropic media, and from simple horizontal surface to complex geological structures. It also explores the evolution from Gaussian beam to focused beam and Fresnel beam. A complex multi-layer model is then used to display the imaging differences between the frequency-domain and space-time-domain GBM methods. To enhance readers’ comprehension, a vertical transversely isotropic field dataset is employed to demonstrate the application of GBM methods to real-world datasets, highlighting the advantage of incorporating the actual mechanical properties of subsurface media. Finally, we quantitatively compare the computational efficiency of different methods under three classic scenarios, and accordingly provide application-oriented concrete recommendations.

1 Introduction

The advancement of the petroleum industry has heightened the demand for high-precision imaging techniques in seismic exploration. Seismic migration, like taking a photograph of underground structures, resolves geometric distortions and noise interference in raw seismic data. As an indispensable technique in seismic exploration, its essence is to image through the convergence points of the forward wavefield and the reverse wavefield, providing reliable foundations for geological interpretation. It primarily includes Kirchhoff Migration (KM), Reverse Time Migration (RTM) and Gaussian Beam Migration (GBM). KM, characterized by its computational efficiency and operational flexibility, serves as a widely adopted tool in seismic imaging. Particularly effective for rapidly delineating medium-complexity geological structures, this method fundamentally employs ray-theoretical approximations and integral stacking methods, constituting a speed-for-accuracy compromise strategy. In contrast, RTM utilizes two-way wave equation solutions to achieve high-fidelity subsurface imaging. By synthesizing forward source wavefield with back receiver wavefield through imaging conditions, it demonstrates superior performance in resolving intricate geological features. As a high-frequency asymptotic solution to the wave equation, GBM satisfies both regularity and concentration conditions, achieving imaging accuracy comparable to RTM. Developed from ray theory, GBM combines high flexibility with computational efficiency. Additionally, it adheres to the regularity condition, avoiding amplitude singularities and thus eliminating imaging issues associated with caustics and shadow regions. Due to these unique advantages, GBM has been the subject of extensive research and is increasingly being implemented in practical applications.

The Gaussian beam method has undergone systematic theoretical evolution in seismic wavefield simulation and imaging applications since its inception. The foundational work was established by Červený et al. (1982), who pioneered the application of Gaussian beam superposition theory to seismic wavefield modeling, laying the theoretical groundwork for subsequent developments in Gaussian beam forward modeling and migration. Building upon this framework, Hill (1990) and Hill (2001) made significant advancements by developing the first frequency-domain GBM (FGBM) imaging system and introducing the concept of pre-stack depth migration. His work demonstrated that it maintains the computational advantages of ray-based migration while exhibiting superior adaptability to complex wave phenomena, including wavefront dispersion and shadow zone effects. To address inherent limitations in pre-stack FGBM implementations, Gray (2005) proposed an optimized common shot domain FGBM approach. This innovation not only enhanced azimuthal data processing capabilities but also provided more effective solutions for near-surface seismic challenges. Subsequent technical refinements emerged through the work of Hu and Stoffa (2009), who derived a slowness-driven FGBM formulation incorporating horizontal surface slowness parameters. Their methodology achieved natural integration of Fresnel weighting with beam superposition, effectively suppressing artifacts caused by incomplete superposition and thereby improving migration fidelity. Yang and Zhu (2018a) developed a data-driven optimization strategy to mitigate offset artifacts prevalent in low signal-to-noise ratio datasets, significantly enhancing interpretability. Through systematic analysis of crust-mantle structures, Han et al. (2022) quantitatively validated FGBM as a high-precision pre-stack depth migration method for deep reflection seismic data, establishing critical theoretical benchmarks for practical implementations. Recently, Yu et al. (2022) extended the method’s applicability through vertical seismic profile implementations, introducing a free-surface multiple FGBM technique that effectively compensates for shallow structural imaging energy loss in far-offset acquisitions.

The application of GBM in complex topographic environments has undergone significant methodological advancements to address surface-related imaging challenges. Initial breakthroughs emerged from the work of Yue et al. (2010) and Yue et al. (2012), who developed the amplitude-preserved FGBM formulation for rugged terrains through fundamental modifications to the tilt-stacking operator. By explicitly incorporating surface elevation parameters into the plane-wave synthesis algorithm, their method achieved enhanced accuracy in local wavefield reconstruction under complex surface geometries. Subsequent field applications demonstrated the method’s practical value in mountainous regions. Cao et al. (2013) successfully implemented this amplitude-preserved FGBM algorithm in piedmont zone environments, providing the systematic validation of its adaptability to fields with complex topographic structures. Building upon these topographic adaptations, Huang et al. (2015a) introduced a FGBM framework specifically designed for dual-complexity scenarios involving both irregular surface geometries and heterogeneous subsurface media. They maintained computational efficiency while handling multi-scale wave propagation effects. Recently, Han et al. (2020) extended the FGBM framework of Huang et al. (2015a) to anisotropic elastic media through rigorous incorporation of Thomsen anisotropy parameters. Their anisotropic elastic FGBM formulation not only preserved the method’s inherent advantages in handling surface complexity but also enabled more physically accurate imaging in stratified media with directional velocity variations.

The extension of GBM to complex media has driven critical methodological innovations to address wave propagation complexity in realistic subsurface environments. Initial theoretical breakthroughs emerged from Alkhalifah’s (1995) FGBM formulation for transversely isotropic (TI) media, which introduced anisotropic ray-tracing modifications but required precise estimation of Thomsen parameters. To overcome this limitation, Zhu et al. (2007) rederived the ray-tracing system using phase velocity parametrization, establishing a generalized TI media framework with reduced parameter sensitivity. Building upon these foundations, Han et al. (2014) systematically quantified P/SV-wave propagation in 2D TI media through kinematic/dynamic ray tracing, coupled with PS-wave common-shot imaging conditions, thereby enabling converted-wave pre-stack depth migration in anisotropic media. Bai et al. (2016) derived viscoacoustic Green’s functions via Gaussian beam superposition, incorporating Q-compensation mechanisms to address the attenuation effects. Concurrently, Li and Mao (2016) resolved 3D polarity reversals in elastic wavefield by developing cross-correlation imaging conditions integrated with beam-based wavefield extrapolation. Subsequent refinements by Li et al. (2018) introduced converted-wave ray tracing in vertical transversely isotropic (VTI) media, while Xu and Mao (2018) enhanced computational efficiency through multilayer anisotropic ray tracing with complex initial conditions, explicitly accounting for multipath effects through rigorous model validation. Some other researches have focused on multi-physics integration and practical optimization. Yang et al. (2018b) achieved simultaneous P/S-wavefield extrapolation via Kirchhoff-Helmholtz decomposition, paired with an enhanced dot-product imaging condition to improve PS-wave resolution. Qin (2020) further streamlined anisotropic implementations through GBM formulations with optimized ray-tracing coefficients. Recently, Shi et al. (2023) addressed sparse ocean-bottom node imaging challenges by developing a 4-component elastic FGBM framework based on elastic reciprocity theory, demonstrating robust performance in low-coverage acquisition scenarios.

The continuous refinement of GBM has driven systematic improvements in imaging precision through beam optimization strategies. Initial progress was marked by Nowack’s (2008) and Nowack’s (2011) dynamic focused beam migration framework, which introduced spatial control of beam geometry by concentrating the narrowest beam segment within predefined target zones, thereby establishing the foundational principle of beam focusing for resolution enhancement. Building upon this foundation, Yang et al. (2015a) developed an amplitude-preserved adaptive focusing beam method that synergistically integrated multiple focusing operators with velocity-dependent beam waist adjustments, which is like a camera focusing, thus improving the imaging accuracy of the target area. Concurrently, Huang et al. (2015b) proposed a paradigm shift through Fresnel beam migration, constraining beam geometry via Fresnel zone width limitations rather than conventional Gaussian beam. Their methodology achieved superior wavefield reconstruction accuracy, particularly in complex near-surface environments, while expanding applicability to cross-well seismic configurations through optimized beam superposition criteria (Yang et al., 2022). Recent advancements have extended these beam optimizations to complex media. Liu et al. (2022a) extended the focused beam migration algorithm to anisotropic media, and used anisotropic ray tracing equations with optimized coefficients to obtain the beam information, and proposed an anisotropic dynamic focused beam migration method. Similarly, focused beam migration is also applied to viscoacoustic media (Zhang et al., 2024).

In order to further optimize the results of migration imaging, many scholars have carried out the Least Square GBM (LSGBM) method. Hu et al. (2016) first proposed the concept, compared with the traditional GBM method, the resolution and amplitude fidelity of the migration results can be further improved through continuous iterative optimization. Based on the Born approximation theory of isotropic acoustic wave equation, Yang et al. (2018c) derived a time-domain linear Gaussian beam modeling operator, and proposed a time-domain LSGBM method, which greatly reduced the computational cost. Since then, the LSGBM method has gradually considered the influence of elasticity and viscosity of the medium (Yue et al., 2019; Yue et al., 2021; Mao et al., 2022).

Space-time-domain GBM (STGBM) is a higher precision seismic imaging method well developed in recent years compared to FGBM. STGBM utilizes Gaussian beams to model the propagation of seismic wave in the space-time domain, enabling the construction of both forward and reverse seismic wavefield for migration imaging. This method primarily encompasses two techniques: Gaussian Envelope Migration and Gaussian Beam Reverse Time Migration (GBRTM). The foundational work in this field was conducted by Žáček (2006), who first realized Gaussian Envelope Migration by deriving a series of space-time-domain wavefield formulas based on Gaussian envelope superposition. Building on this, Popov et al. (2010) developed a GBRTM method using Kirchhoff integral-based reverse time extrapolation, laying the theoretical groundwork for STGBM. A significant advancement was made by Yang et al. (2015b), who implemented wavefield back-propagation using Gaussian beams and employed Gabor transform for sparse decomposition of seismic wavefield. This STGBM approach demonstrated superior performance with reduced migration artifacts compared to FGBM. Further developments in STGBM have addressed various complexities in seismic imaging. Huang et al. (2017) extended the method to account for elastic media characteristics by applying Gaussian beam superposition to RTM imaging. Lv et al. (2019) enhanced the method’s performance in structures with sharp lateral velocity variations through the introduction of dynamic focusing theory. The method’s applicability to elastic media was further improved by Hu et al. (2020), who incorporated wavefield separation of pure P and S waves in elastic STGBM. Recent advancements have focused on computational efficiency and practical applications. Zhang et al. (2022a) and Zhang et al. (2022b) developed a fast STGBM method using dominant frequency approximation and ray optimization strategies, significantly improving computational efficiency while maintaining accuracy in VTI media. Recently, Liu et al. (2022b) proposed an optimized STGBM method for TI media through enhanced ray tracing techniques.

When the field is dealing with the deep exploration data in the large work area, especially the 3D massive data, it is optimal to use GBM. Therefore, it is very important for engineers and researchers to study GBM methods and applications. In this paper, we will first introduce in detail the FGBM and STGBM methods in acoustic media, so as to enable readers to have a good understanding of the principles and implementation methods of the two GBM methods, and then demonstrate the imaging differences between the two types of methods using simulated data. Furthermore, we will use two STGBM methods respectively in acoustic and VTI media to image the actual oil field data, aiming to help engineers and researchers better understand the application of GBM and the necessity of taking into account the real mechanical properties of the media. Finally, we will present the calculation times of different methods under three classic scenario conditions, and based on these results, we will provide specific suggestions for selecting different imaging methods.

2 FGBM in acoustic media

In this chapter, we mainly present the implementation of the FGBM and some important formulas. The detailed derivations are from the paper (Červený et al., 1982). In 2D ray-centered coordinate system (Figure 1), the travel time along a ray path can be expressed as:

$\tau \left(s\right)={\displaystyle \underset{0}{\overset{s}{\int }}}\frac{1}{v\left(s\right)}ds(1)$

where $\tau \left(s\right)$ is the travel time along the central ray, $s$ is the arc length along the central ray, and $v\left(s\right)$ is the velocity of the seismic wave.

Figure 1

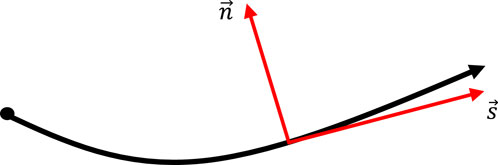
Figure 1. The 2D ray-centered coordinate system. $\overrightarrow{s}$ and $\overrightarrow{n}$ are the tangential and normal vectors, respectively.

In acoustic media, consider the following scalar wave equation in 2D Cartesian coordinate system:

$\mathbf{\Delta }U\left(x,z,\omega \right)+\frac{{\omega }^2}{V{\left(x,z\right)}^2}U\left(x,z,\omega \right)=0(2)$

where $\left(x,z\right)$ represents the coordinates of a 2D space point, $\omega$ is the angular frequency of the seismic wave, $U\left(x,z,\omega \right)$ represents the displacement of the seismic wavefield related to space and frequency, $V\left(x,z\right)$ is the velocity at $\left(x,z\right)$, and $\mathbf{\Delta }$ is Laplacian operator, which can be written in the following form within 2D Cartesian coordinate system:

$\mathbf{\Delta }={\nabla }^2={\left(\frac{\mathbf{\partial }}{\mathbf{\partial }x}\right)}^2+{\left(\frac{\mathbf{\partial }}{\mathbf{\partial }z}\right)}^2(3)$

Numerous methods exist for solving wave equations, including ray tracing, finite difference method, finite element method, and spectral element method. Among these, ray tracing offers an efficient kinematic and dynamic description of the wavefield, circumventing the computational expense of full wave equation solvers while effectively capturing wave propagation in complex media. Building upon the ray-centered coordinate system, Červený et al. (1982) formulated Equation 2 and derived the ray tracing system of equations and the high-frequency asymptotic solution to the wavefield through high-frequency approximations and variable substitutions, establishing the theoretical framework for Gaussian beam forward modeling. Extending this work, Hill (1990) developed a migration theory based on Gaussian beam superposition, employing different notation to reexpress the same forward modeling equations as those presented by Červený et al. (1982).

In 2D problems, the wave equation for ray tracing is given by:

$\left\{\begin{array}{l}\frac{dQ\left(s\right)}{ds}=v\left(s\right)P\left(s\right)\\ \frac{dP\left(s\right)}{ds}=-\frac{1}{v^2\left(s\right)}\frac{\mathbf{\partial }V\left(s,n\right)}{\mathbf{\partial }{n}^2}Q\left(s\right)\end{array}\right.(4)$

where $v\left(s\right)=V\left[x\left(s\right),z\left(s\right)\right]$, $P\left(s\right)$ and $Q\left(s\right)$ are complex solutions of the ray tracing equations. Specifically, $P\left(s\right)$ characterizes the dynamic properties of the beam, including amplitude attenuation and phase variation, while $Q\left(s\right)$ describes the geometric attributes such as beam width and curvature.

The solution to Equation 4, corresponding to the Gaussian beam expression, is given by:

$u_{\text{GB}}\left(s,n,\omega \right)=\sqrt{\frac{v\left(s\right)}{Q\left(s\right)}}\exp \left[\mathrm{i}\omega \tau \left(s\right)+\frac{1}{2}\mathrm{i}\omega \frac{P\left(s\right)}{Q\left(s\right)}{n}^2\right](5)$

Figure 2A shows the ray field in a simple two-layer model. The ray field is calculated using Equation 4, and the two-layer model is discretized into a 201 × 201 grid, with a sampling interval of 10 m in both horizontal and vertical directions. It is easy to see that the directions of the rays change when they hit the interface. Figure 2B is the Gaussian beam of the two-layer model at the reference frequency of 20 Hz.

Figure 2

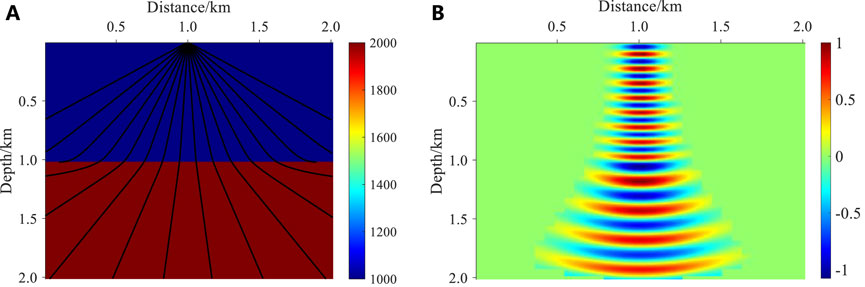
Figure 2. A two-layer model. (A) 2D ray field. (B) Gaussian beam at the reference frequency of 20 Hz. The black lines represent the ray paths in different directions generated by the seismic source at (1 km, 0). The model is relatively simple, with velocities of 1,000 m/s and 2000 m/s in the first and second layers, respectively.

Meanwhile, the seismic receiver wavefield $U\left(\mathbf{r},\omega \right)$ can be expressed via the integral relationship between the seismic source wavefield $U\left({\mathbf{r}}^{\prime },\omega \right)$ and the complex conjugate of the Green’s function $G^{*}\left(\mathbf{r},{\mathbf{r}}^{\prime },\omega \right)$:

$U\left(\mathbf{r},\omega \right)=-\frac{1}{2\mathrm{\pi }}\iint d{x}^{\prime }\frac{\mathbf{\partial }{G}^{*}\left(\mathbf{r},{\mathbf{r}}^{\prime },\omega \right)}{\mathbf{\partial }{z}^{\prime }}U\left({\mathbf{r}}^{\prime },\omega \right)(6)$

where $\mathbf{r}=\left(x,z\right)$ and ${\mathbf{r}}^{\prime }=\left(x^{\prime },z^{\prime }\right)$ represent the coordinates of the receiver and shot points, respectively. $G$ is the Green’s function and $G^{*}$ represents its complex conjugate. The Green’s function can be expressed as the superposition of a series of Gaussian beams (Hill, 2001):

$G\left(\mathbf{r},{\mathbf{r}}^{\prime };\omega \right)\approx \frac{\mathrm{i}}{2\mathrm{\pi }}\omega \iint \frac{d{p_x}^{\prime }}{{p_z}^{\prime }}{u}_{\text{GB}}\left(\mathbf{r};{\mathbf{r}}^{\prime },{\mathbf{p}}^{\prime };\omega \right)(7)$

where ${\mathbf{p}}^{\prime }=\left({p_x}^{\prime },{p_z}^{\prime }\right)$ is the slowness of the shot point.

According to the imaging principle, the formula of the FGBM can be derived from the cross-correlation between the seismic receiver wavefield $U\left(\mathbf{r},\omega \right)$ and the seismic source wavefield $U\left({\mathbf{r}}^{\prime },\omega \right)$:

$I_{\text{FGBM}}=\int d\omega U\left(\mathbf{r},\omega \right)U\left({\mathbf{r}}^{\prime },\omega \right)(8)$

3 STGBM in acoustic media

STGBM employs a hybrid strategy integrating wave equation approximations with ray-tracing techniques to enhance imaging accuracy at the expense of increased computational overhead. This methodology establishes an accuracy-complexity equilibrium, positioning itself as a balance between FGBM and RTM. In the space-time domain, the expression of the Gaussian beam can be written in the following form (Popov et al., 2010):

$U\left({\mathbf{x}}_0,t;{\mathbf{x}}_{\mathrm{s}}\right)=-\frac{\mathrm{i}}{4\mathrm{\pi }}\int d\omega \sqrt{\frac{{\epsilon }_{GB}\left(s_0\right)v\left(s\right)}{v\left(s_0\right)Q\left(s\right)}}\exp \left[\mathrm{i}\omega \left(-\left(t-\tau \right)+\frac{1}{2}\frac{P\left(s\right)}{Q\left(s\right)}{n}^2\right)\right](9)$

where ${\mathbf{x}}_{\mathbf{0}}=\left(x_0,z_0\right)$ and ${\mathbf{x}}_{\mathrm{s}}=\left(x_{\mathrm{s}},0\right)$ represent the locations of the imaging and shot points, respectively, and ${\epsilon }_{GB}$ is the initial Gaussian beam parameter.

According to the Gaussian beam forward modeling theory (Červený et al., 1982), the forward wavefield can be represented by a series of Gaussian beams emitted in different angles:

$W^{\left(1\right)}=-\frac{\mathrm{i}}{4\mathrm{\pi }}{\int }_0^{2\mathrm{\pi }}d\phi \int d\omega \sqrt{\frac{{\epsilon }_{GB}\left(s_0\right)v\left(s\right)}{v\left(s_0\right)Q\left(s\right)}}\exp \left[\mathrm{i}\omega \left(-\left(t-\tau \right)+\frac{1}{2}\frac{P\left(s\right)}{Q\left(s\right)}{n}^2\right)\right](10)$

where $\phi$ is the angle at which the Gaussian beam emerges from the surface.

The back propagation process of the recorded wavefield from the receiver point to the imaging point can be realized by the Kirchhoff integral (Popov et al., 2010). In other words, the up-going ray tracing strategy is used to construct the reverse wavefield, as shown in Figure 3:

$W^{\left(2\right)}=-2{\int }_0^{\mathrm{T}}dt\int d{\mathbf{x}}_{\mathbf{r}}{P}_{\mathrm{U}}\left({\mathbf{x}}_{\mathbf{r}},t\right)\frac{\mathrm{\partial }}{\mathrm{\partial }z}G\left({\mathbf{x}}_{\mathbf{r}},t-t_0;{\mathbf{x}}_{\mathbf{0}}\right)(11)$

where $P_{\mathrm{U}}\left({\mathbf{x}}_{\mathbf{r}},t\right)$ is the recorded wavefield, which is used as the input in the migration algorithm; $G\left({\mathbf{x}}_{\mathbf{r}},t;{\mathbf{x}}_{\mathbf{0}},t_0\right)$ is Green’s function, which can be expressed in the following form:

$G\left({\mathbf{x}}_{\mathbf{r}},t-t_0;{\mathbf{x}}_{\mathbf{0}}\right)=-\frac{\mathrm{i}}{4\mathrm{\pi }}{\int }_0^{2\mathrm{\pi }}d\phi \int d\omega \sqrt{\frac{{\epsilon }_{GB}\left(s_0\right)v\left(s\right)}{v\left(s_0\right)Q\left(s\right)}}\exp \left[\mathrm{i}\omega \left(-\left(t-t_0\right)+\frac{1}{2}\frac{P\left(s\right)}{Q\left(s\right)}{n}^2\right)\right](12)$

Figure 3

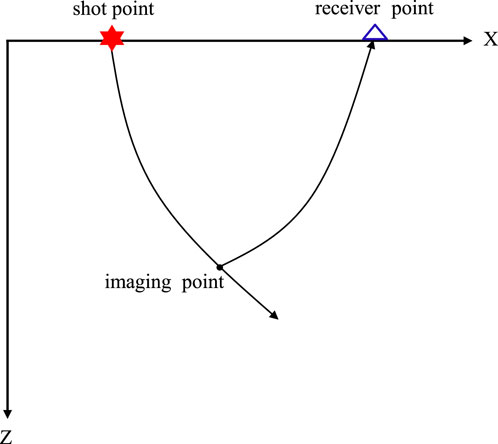
Figure 3. Illustration of the up-going ray tracing strategy. It simply describes the relationship between the shot point, the imaging point and the receiver point.

In the migration algorithm, the imaging condition is very important, which can directly affect the final image quality. In the time window $t\in \left[t_1,t_2\right]$, when the wavelet phases of the forward wavefield $W^{\left(1\right)}$ and the reverse wavefield $W^{\left(2\right)}$ are the same, the cross-correlation of the two reaches the maximum value, the formula of the STGBM method in acoustic media can be obtained:

$I_{\text{STGBM}}={\int }_{t_1}^{t_2}\mathrm{d}t{W}^{\left(1\right)}{W}^{\left(2\right)}(13)$

We construct a multi-layer model to verify the above two GBM methods, as shown in Figure 4. Figure 4A is the realistic velocity model, and Figure 4B is its smoothed version. In the forward modeling process, an observation system with middle excitation and two sides receiving is adopted. A total of 201 shots are set up with a spacing of 30 m, the position coordinate of the first shot is (2 km, 0), and the position coordinate of the last shot is (8 km, 0). The dominant frequency of the wavelets is 20 Hz. Figure 5 shows the results of the first 1,200 traces of the shot records.

Figure 4

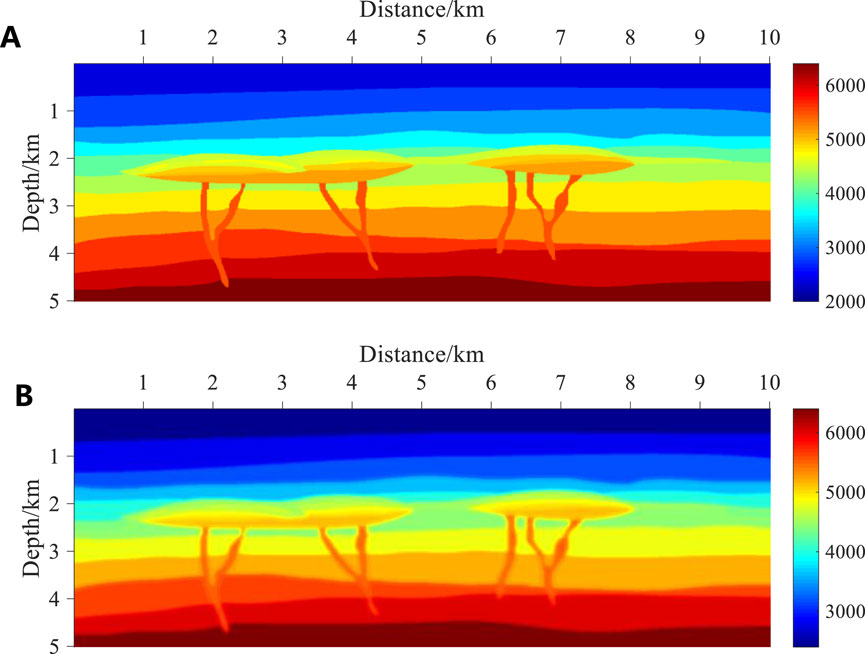
Figure 4. A multi-layer model. (A) Realistic velocity model. (B) Smoothed version of the model in (A). The model is discretized into a 1,001 × 501 grid, with a sampling interval of 10 m in both horizontal and vertical directions.

Figure 5

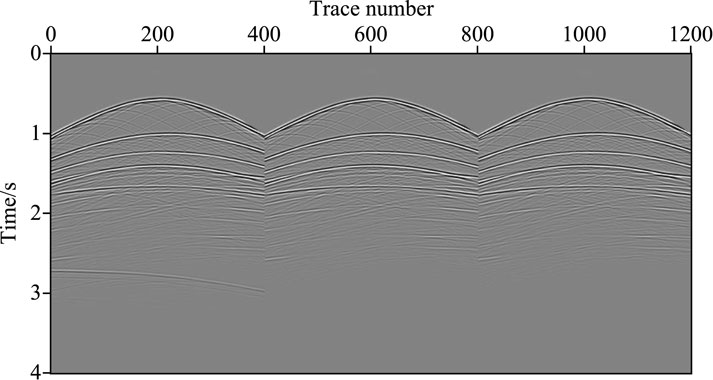
Figure 5. First 1,200 traces of the shot records in the multi-layer model. Each shot has 401 traces, with a trace spacing of 10 m. The time sampling interval is 4 ms, and the total time is 4 s.

Figure 6 shows the imaging results using the above two GBM methods. Both methods can produce relatively clear migration results and image the karst cave structures in the middle layer, which verifies the effectiveness of the above two GBM methods. As shown by the red arrows in Figure 6, the FGBM method (Hill, 1990; Hill, 2001; Gray, 2005) produces some migration artifacts near the shallow layer, while the STGBM method (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a) is clearer and sharper. We extract the longitudinal single-trace results of the two in the shallow layer when the transverse distance is 4 km, it can be obviously found that the STGBM results have higher resolution in the shallow part (Figure 6C). This is because the STGBM computes more beam information at the same time, which improves the imaging accuracy of the migration results at a higher computational cost.

Figure 6

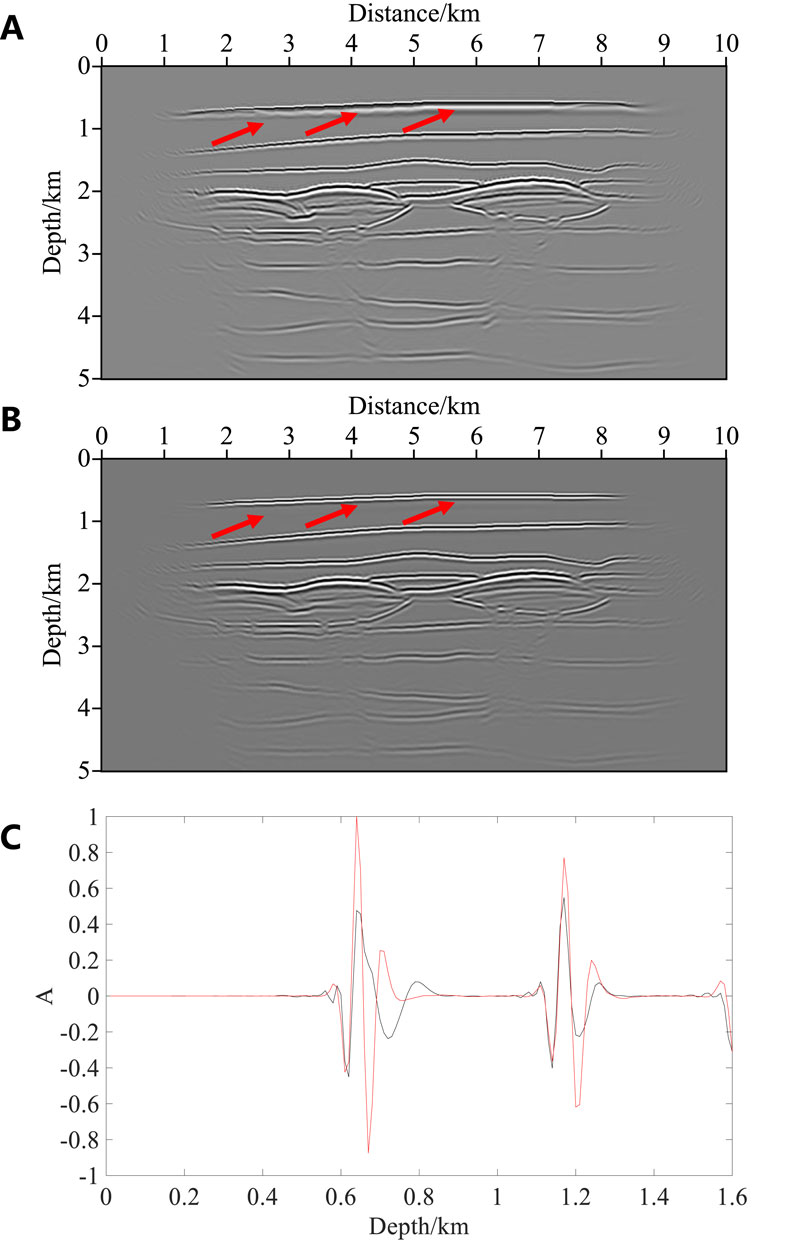
Figure 6. GBM imaging results for the multi-layer model. (A) FGBM (Hill, 1990, 2001; Gray, 2005). (B) STGBM (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a). The red arrow highlights the difference in the accuracy of the two shallow images. (C) When the transverse distance is 4 km, the longitudinal single-trace results of the two in shallow layer, where the black line represents A and the red line represents B.

4 Migration results of a VTI field data

In seismic exploration, subsurface media are often complex. The VTI model is representative for most sedimentary basins with relatively low parameter complexity. In terms of elastic parameters, there are three parameters for acoustic VTI media: Vp (vertical P-wave velocity), ε (the difference between horizontal and vertical P-wave velocities), and δ (the curvature of the P-wave velocity variation with the angle). For elastic VTI media, there are five parameters in total, with the addition of Vs (vertical S-wave velocity) and γ (the difference between horizontal and vertical S-wave velocities). Due to these characteristics of the VTI model, we will mainly introduce the principle and implementation of the GBM in VTI media, and compare the imaging differences between the VTI STGBM and acoustic STGBM.

In VTI media, the implementation of GBM mainly modifies the ray tracing parameters. Hanyga (1986) presented the dynamic ray-tracing equations in VTI media:

$\left\{\begin{array}{l}\frac{\mathrm{d}Q\left(s\right)}{\mathrm{d}\tau }=WQ\left(s\right)+VP\left(s\right)\\ \frac{\mathrm{d}P\left(s\right)}{\mathrm{d}\tau }=-HQ\left(s\right)-VP\left(s\right)\end{array}\right.(14)$

where W, V and H are coefficient matrices related to the elastic properties.

The Gaussian beam propagation equation, reverse wavefield construction and migration are similar to the GBM methods in acoustic media.

Next, we present results using the actual data from an oil field to verify the STGBM method in VTI media. Figure 7A shows the velocity field, and the anisotropic parameters ε and δ are shown in Figures 7B, C, respectively. In the process of seismic data acquisition, the observation mode of unilateral reception is adopted. A total of 204 shots are set up, each shot has 60 traces, the position coordinate of the first shot is (3 km, 0), and the position coordinate of the last shot is (13.2 km, 0); both shot spacing and trace spacing are 50 m. The first 300 traces of the shot records for the actual data are shown in Figure 8.

Figure 7

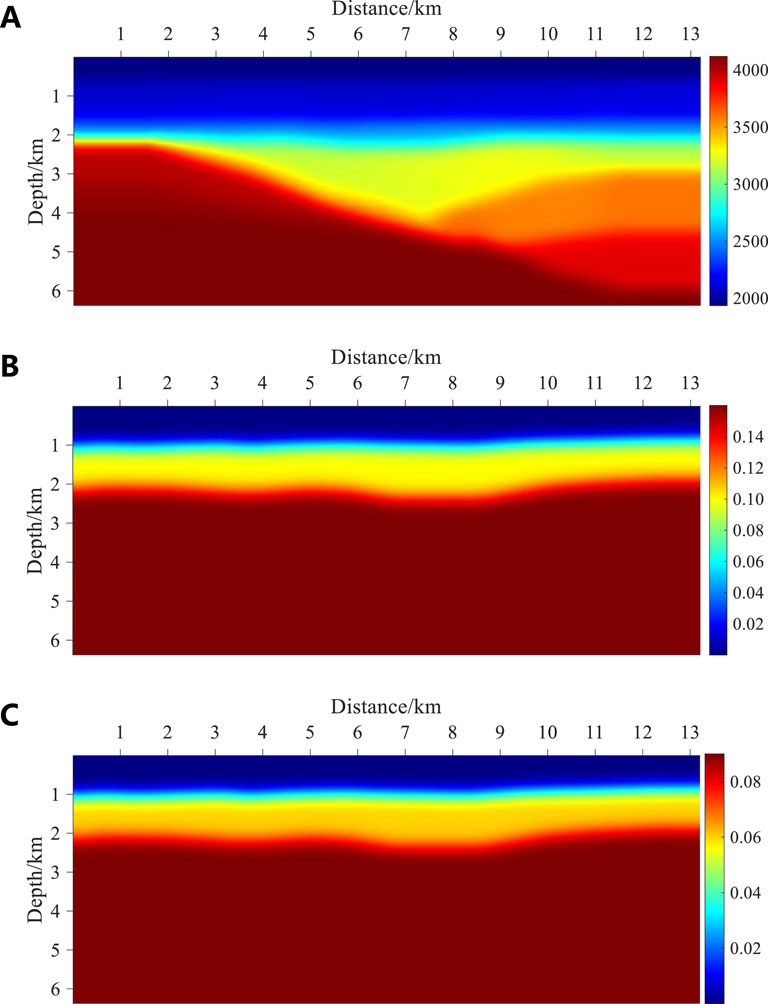
Figure 7. The actual data. (A) Velocity field. (B) Parameter ε. (C) Parameter δ. It is discretized into a 1,056 × 510 grid with an interval of 12.5 m in both horizontal and vertical directions.

Figure 8

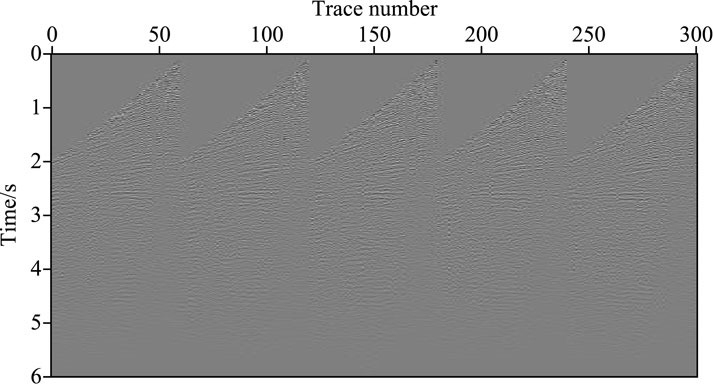
Figure 8. First 300 traces of the shot records for the actual data. The time sampling interval is 1 ms, and the total time of the shot records is 6 s.

Figure 9 shows two imaging results obtained by the acoustic STGBM (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a) and the VTI STGBM (Zhang et al., 2022b; Liu et al., 2022b), and Figures 10, 11 are the magnified views of the red and blue boxes in Figure 9, respectively. Compared with the blue ellipse, it can be seen that the migration results generated by the GBM method in VTI media exhibit relatively clear fault characteristics, which provides a more favourable condition for the subsequent oil reservoir interpretation. This is because the VTI GBM method considers the influence of the anisotropy, and more accurately calculates the travel time and amplitude of the seismic beam, so that the reflected wave of the offset result is correctly located.

Figure 9

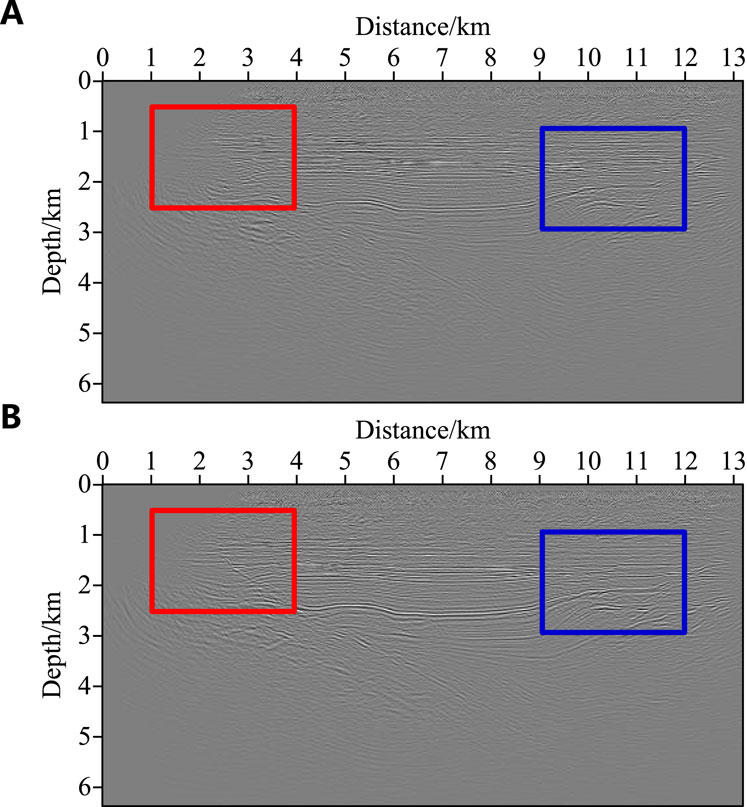
Figure 9. STGBM imaging results for the actual data. (A) Isotropic media (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a). (B) VTI media (Zhang et al., 2022b; Liu et al., 2022b). The red and blue boxes are the main areas of contrast.

Figure 10

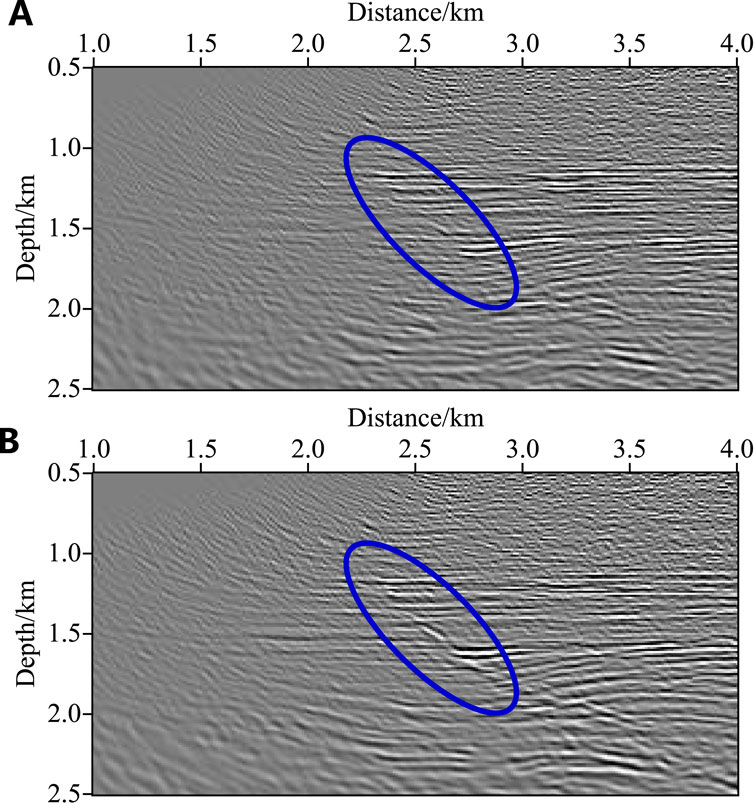
Figure 10. Magnified view of the STGBM images for the area indicated by the red rectangle in Figure 9. (A) Isotropic media (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a). (B) VTI media (Zhang et al., 2022b; Liu et al., 2022b). It can be seen that Figure B has more obvious and continuous fault characteristics.

Figure 11

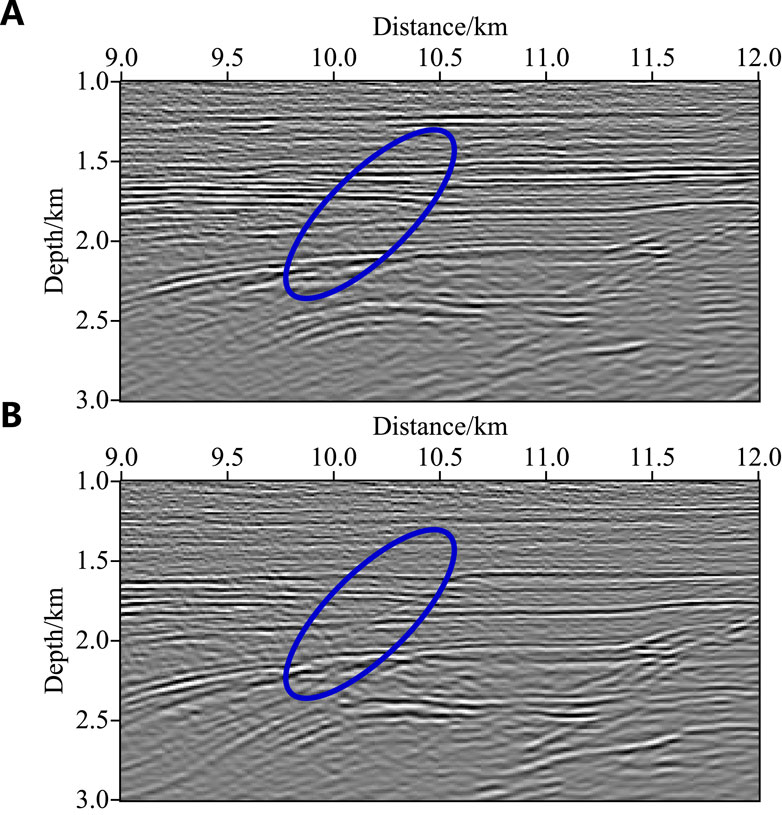
Figure 11. Magnified view of the STGBM images for the area indicated by the blue rectangle in Figure 9. (A) Isotropic media (Yang et al., 2015b; Lv et al., 2019; Zhang et al., 2022a). (B) VTI media (Zhang et al., 2022b; Liu et al., 2022b). The faults in Figure B are more continuous.

5 Conclusion and discussion

We systematically introduce GBM methods from the perspectives of media properties and computational domains, supplemented by examples utilized three GBM methods. A multi-layer model is employed to show the effectiveness of the GBM, demonstrating that both FGBM and STGBM can effectively image complex structures; however, the STGBM exhibits reduced noise in shallow regions compared to the FGBM. Then, we separately apply acoustic and VTI STGBM to process a field dataset; the results indicate that the VTI GBM method provides superior fault image clarity compared to the acoustic GBM method.

In this study, we demonstrate the time consumption of FGBM and STGBM through the calculation of a multi-layer model. The FGBM demonstrates computational efficiency, with processing times per shot on a single-core CPU on the order of 10^–2 ∼ 10^–1 h for an array with dimensions of 401 (traces) × 1,001 (time sampling points); in contrast, the STGBM requires longer computational durations, typically on the order of 10^–1 ∼ 10⁰ h. The oilfield sector currently encounters significant challenges in processing ultra-large-scale work area datasets. As shown in Table 1, we present the order of magnitude of computation time per shot for the FGBM, STGBM, and RTM methods under different classic scenarios on a single-core CPU. In these scenarios, RTM incurs prohibitively high computational costs, where GBM presents itself as the optimal solution, striking an effective balance between computational efficiency and imaging accuracy. During the process of selecting the GBM, it is advisable to prioritize the application of the FGBM for its computational efficiency. However, in scenarios where substantial computational resources are accessible, including the utilization of supercomputing facilities, the adoption of the STGBM is recommended to achieve enhanced accuracy. When addressing diverse and complex work area data, it is essential to approach the problem by considering medium properties, such as anisotropy, elasticity, and viscosity, to progressively enhance the imaging quality of migration results (Alkhalifah, 1995; Bai et al., 2016; Shi et al., 2023). Furthermore, in cases where sufficient computational resources are available, the LSGBM (Hu et al., 2016; Yang et al., 2018c; Yue et al., 2019, 2021; Mao et al., 2022) can be employed to achieve higher resolution and improved fidelity in the migration results.

Table 1

Table 1. The order of magnitude of computation time per shot on a single-core CPU (Calculation parameters: Time = 8 s, Sampling time interval = 4 ms, Trace spacing = 20 m).

The GBM represents a versatile imaging tool that not only preserves the advantages of traditional ray-based migration but also achieves imaging accuracy comparable to wave-equation migration. As such, it serves as a highly effective approach for seismic data processing. We propose that its future development will primarily focus on the following directions:

1) Research on GBM methods in more complex media for deep structure areas;

2) Expansion of GBM methods in 3D for more real situation;

3) Research on GBM methods based on variable grid for saving calculation costs.

Author contributions

DZ: Data curation, Methodology, Writing–original draft, Writing–review and editing. TZ: Funding acquisition, Writing–original draft, Writing–review and editing. JY: Writing–review and editing. JN: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the “Basic Research Cooperation Project in Strategic Cooperation Agreement of China National Petroleum Corporation and Peking University.” The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

We would like to thank Professor Zhao Li of Peking University for his comments on the manuscript. Many thanks to the reviewers and editors for their valuable suggestions for the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alkhalifah, T. (1995). Gaussian beam depth migration for anisotropic media. Geophysics 60 (5), 1474–1484. doi:10.1190/1.1443881

CrossRef Full Text | Google Scholar

Bai, M., Chen, X., Wu, J., Liu, G., Chen, Y., Chen, H., et al. (2016). Q-compensated migration by Gaussian beam summation method. J. Geophys. Eng. 13 (1), 35–48. doi:10.1088/1742-2132/13/1/35

CrossRef Full Text | Google Scholar

Cao, W., Wang, H., Li, Z., and Yue, Y. (2013). Application of complex topographic Gaussian beam amplitude-preserved pre-stack depth migration in piedmont zone. Prog. Geophys. 28 (6), 3086–3091. doi:10.6038/pg20130633

CrossRef Full Text | Google Scholar

Červený, V., Popov, M., and Pšenčík, I. (1982). Computation of wave fields in inhomogeneous media—Gaussian beam approach. Geophys. J. Int. 70 (1), 109–128. doi:10.1111/j.1365-246X.1982.tb06394.x

CrossRef Full Text | Google Scholar

Gray, S. (2005). Gaussian beam migration of common-shot records. Geophysics 70 (4), S71–S77. doi:10.1190/1.1988186

CrossRef Full Text | Google Scholar

Han, J., Lv, Q., Gu, B., and Xing, Z. (2022). Gaussian beam summation migration of deep reflection seismic data: numerical examples. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2022.3224211

CrossRef Full Text | Google Scholar

Han, J., Lv, Q., Gu, B., Yan, J., and Zhang, H. (2020). 2D anisotropic multicomponent Gaussian-beam migration under complex surface conditions. Geophysics 85 (2), S89–S102. doi:10.1190/geo2018-0841.1

CrossRef Full Text | Google Scholar

Han, J., Wang, Y., Xing, Z., and Lu, J. (2014). Gaussian beam prestack depth migration of converted wave in TI media. J. Appl. Geophys. 109, 7–14. doi:10.1016/j.jappgeo.2014.07.008

CrossRef Full Text | Google Scholar

Hanyga, A. (1986). Gaussian beams in anisotropic elastic media. Geophys. J. Int. 85 (3), 473–504. doi:10.1111/j.1365-246X.1986.tb04528.x

CrossRef Full Text | Google Scholar

Hill, N. (1990). Gaussian beam migration. Geophysics 55 (11), 1416–1428. doi:10.1190/1.1442788

CrossRef Full Text | Google Scholar

Hill, N. (2001). Prestack Gaussian-beam depth migration. Geophysics 66 (4), 1240–1250. doi:10.1190/1.1487071

CrossRef Full Text | Google Scholar

Hu, C., and Stoffa, P. (2009). Slowness-driven Gaussian-beam prestack depth migration for low-fold seismic data. Geophysics 74 (6), WCA35–WCA45. doi:10.1190/1.3250268

CrossRef Full Text | Google Scholar

Hu, H., Liu, Y., Zheng, Y., Liu, X., and Lu, H. (2016). Least-squares Gaussian beam migration. Geophysics 81 (3), S87–S100. doi:10.1190/geo2015-0328.1

CrossRef Full Text | Google Scholar

Hu, Z., Lv, Q., Han, L., Liu, W., Huang, J., Yang, J., et al. (2020). Elastic space-time Gaussian beam method for seismic depth imaging. Chin. J. Geophys. 63 (2), 652–665. doi:10.6038/cjg2020M0542

CrossRef Full Text | Google Scholar

Huang, J., Yuan, M., Li, Z., and Yue, Y. (2015a). The accurate beam migration method without slant stack under dual-complexity conditions and its application (I): acoustic equation. Chin. J. Geophys. 58(1), 267–276. doi:10.6038/cjg20150124

CrossRef Full Text | Google Scholar

Huang, J., Yang, J., Liao, W., Wang, X., and Li, Z. (2015b). Common-shot Fresnel beam migration based on wave-field approximation in effective vicinity under complex topographic conditions. Geophys. Prospect. 64 (3), 554–570. doi:10.1111/1365-2478.12276

CrossRef Full Text | Google Scholar

Huang, J., Yuan, M., Zhang, Q., Jia, L., Li, Z., Li, J., et al. (2017). Reverse time migration with elastodynamic Gaussian beams. J. Earth Sci. 28, 695–702. doi:10.1007/s12583-015-0609-9

CrossRef Full Text | Google Scholar

Li, X., and Mao, W. (2016). Multimode and multicomponent Gaussian beam prestack depth migration. Chin. J. Geophys. 59 (8), 2989–3005. doi:10.6038/cjg20160822

CrossRef Full Text | Google Scholar

Li, Z., Liu, Q., Han, W., Zhang, M., Wang, T., Xiao, J., and Wu, J.(2018). Angle domain converted wave Gaussian beam migration in VTI media. Chin. J. Geophys. 61(4), 1471–1481. doi:10.6038/cjg2018K0455

CrossRef Full Text | Google Scholar

Liu, Q., Li, Z., Zhang, K., Yue, Y., Xiao, J., Zhang, M., et al. (2022a). Two dimensional dynamically focused beam migration in weakly anisotropic media. J. Appl. Geophys. 202, 104644. doi:10.1016/j.jappgeo.2022.104644

CrossRef Full Text | Google Scholar

Liu, Q., Li, Z., Xiao, J., and Xu, X.(2022b). Reverse time migration with Gaussian beams using optimized ray tracing systems in transversely isotropic media. Geophys. Prospect. 70(1), 95–107. doi:10.1111/1365-2478.13154

CrossRef Full Text | Google Scholar

Lv, Q., Huang, J., Yang, J., and Guan, Z. (2019). An optimized space-time Gaussian beam migration method with dynamic parameter control. J. Appl. Geophys. 160, 47–56. doi:10.1016/j.jappgeo.2018.11.006

CrossRef Full Text | Google Scholar

Mao, W., Duan, W., Sun, C., and Shi, X. (2022). Elastic least-squares Gaussian beam imaging with point spread functions. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2022.3173303

CrossRef Full Text | Google Scholar

Nowack, R. (2008). Focused Gaussian beams for seismic imaging. SEG Int. Expo. Annu. Meet., 2376–2380. doi:10.1190/1.3059356

CrossRef Full Text | Google Scholar

Nowack, R. (2011). Dynamically focused Gaussian beams for seismic imaging. Int. J. Geophys. 2011 (1), 316581–316588. doi:10.1155/2011/316581

CrossRef Full Text | Google Scholar

Popov, M., Semtchenok, N., Popov, P., and Verdel, A. (2010). Depth migration by the Gaussian beam summation method. Geophysics 75 (2), S81–S93. doi:10.1190/1.3361651

CrossRef Full Text | Google Scholar

Qin, N. (2020). Time-domain Gaussian beam prestack depth migration for acoustic anisotropic media. Oil Geophys. Prospect. 55 (4), 813–820. doi:10.13810/j.cnki.issn.1000-7210.2020.04.013

CrossRef Full Text | Google Scholar

Shi, X., Mao, W., Li, X., Yue, Y., and Sun, H. (2023). Elastic common-receiver Gaussian beam migration of 4C ocean-bottom node data. Geophysics 88 (3), S115–S130. doi:10.1190/geo2021-0681.1

CrossRef Full Text | Google Scholar

Xu, Q., and Mao, W. (2018). An efficient ray-tracing method and its application to Gaussian beam migration in complex multilayered anisotropic media. Geophysics 83 (5), T281–T289. doi:10.1190/geo2017-0402.1

CrossRef Full Text | Google Scholar

Yang, F., Ren, G., Yao, F., and Zhao, C. (2022). The inverse Fresnel beam XSP-CDP stack imaging in crosswell seismic. Front. Earth Sci. 10, 851379. doi:10.3389/feart.2022.851379

CrossRef Full Text | Google Scholar

Yang, J., Huang, J., Wang, X., and Li, Z. (2015a). An amplitude-preserved adaptive focused beam seismic migration method. Pet. Sci. 12, 417–427. doi:10.1007/s12182-015-0044-7

CrossRef Full Text | Google Scholar

Yang, J., Huang, J., Wang, X., and Li, Z. (2015b). Prestack depth migration method using the time-space Gaussian beam. Seg. Tech. Program Expand. Abstr. 2015, 4303–4307. doi:10.1190/segam2015-5749505.1

CrossRef Full Text | Google Scholar

Yang, J., and Zhu, H. (2018a). A practical data-driven optimization strategy for Gaussian beam migration. Geophysics 83 (1), S81–S92. doi:10.1190/geo2017-0314.1

CrossRef Full Text | Google Scholar

Yang, J., Zhu, H., Huang, J., and Li, Z. (2018b). 2D isotropic elastic Gaussian-beam migration for common-shot multicomponent records. Geophysics 83 (2), S127–S140. doi:10.1190/geo2017-0078.1

CrossRef Full Text | Google Scholar

Yang, J., Zhu, H., McMechan, G., and Yue, Y. (2018c). Time-domain least-squares migration using the Gaussian beam summation method. Geophys. J. Int. 214 (1), 548–572. doi:10.1093/gji/ggy142

CrossRef Full Text | Google Scholar

Yu, D., Yang, F., Wen, B., Wang, Y., Huang, D., and Zhao, C. (2022). Gaussian beam migration for free-surface multiples in VSP. Front. Earth Sci. 10, 851206. doi:10.3389/feart.2022.851206

CrossRef Full Text | Google Scholar

Yue, Y., Li, Z., Qian, Z., Zhang, J., Sun, P., and Ma, G. (2012). Amplitude-preserved Gaussian beam migration under complex topographic conditions. Chin. J. Geophys. 55 (4), 1376–1383. doi:10.6038/j.issn.0001-5733.2012.04.033

CrossRef Full Text | Google Scholar

Yue, Y., Li, Z., Zhang, P., Zhou, X., and Qin, N. (2010). Prestack Gaussian beam depth migration under complex surface conditions. Appl. Geophys. 7 (2), 143–148. doi:10.1007/s11770-010-0238-0

CrossRef Full Text | Google Scholar

Yue, Y., Liu, Y., Li, Y., and Shi, Y. (2021). Least-squares Gaussian beam migration in viscoacoustic media. Geophysics 86 (1), S17–S28. doi:10.1190/geo2020-0129.1

CrossRef Full Text | Google Scholar

Yue, Y., Sava, P., Qian, Z., Yang, J., and Zou, Z. (2019). Least-squares Gaussian beam migration in elastic media. Geophysics 84 (4), S329–S340. doi:10.1190/geo2018-0391.1

CrossRef Full Text | Google Scholar

Žáček, K. (2006). Decomposition of the wave field into optimized Gaussian packets. Stud. Geophys. Geod. 50 (3), 367–380. doi:10.1007/s11200-006-0023-y

CrossRef Full Text | Google Scholar

Zhang, D., Huang, J., Yang, J., Li, Z., Zhuang, S., and Li, Q. (2022a). A fast space-time-domain Gaussian beam migration approach using the dominant frequency approximation. Pet. Sci. 19 (4), 1555–1565. doi:10.1016/j.petsci.2022.03.008

CrossRef Full Text | Google Scholar

Zhang, D., Huang, J., Yang, J., Zhou, B., Zhang, J., and Li, Q. (2022b). Space-time-domain Gaussian beam migration in VTI media based on the upward ray tracing and its application in land field data. J. Seism. Explor. 31 (6), 545–562.

Google Scholar

Zhang, K., Pan, Y., Sang, Y., Xu, X., and Meng, F. (2024). Adaptive focus beam migration method in visco-acoustic media. J. Geophys. Eng. 21 (1), 1–14. doi:10.1093/jge/gxad086

CrossRef Full Text | Google Scholar

Zhu, T., Gray, S., and Wang, D. (2007). Prestack Gaussian-beam depth migration in anisotropic media. Geophysics 72 (3), S133–S138. doi:10.1190/1.2711423

CrossRef Full Text | Google Scholar