Numerical modelling of erosional landforms driven by offshore groundwater flow on siliciclastic continental margins: a conceptual approach

Offshore freshened groundwater (OFG) has long been hypothesised to be a key factor shaping continental margins worldwide. Field observations from siliciclastic margins suggest strong causal links between sub-seafloor OFG flow and seafloor depressions, canyons and landslide scars. These links have been hard to validate due to a paucity of appropriate field data and difficulty in simulating the subsurface flow and geomorphic processes in the laboratory. Here we present a numerical study that simulates the geomorphic action of sub-seafloor OFG seepage in an idealised 3D continental margin. Analysis of the coupling conditions highlights the multiplicative nature of the primary driving mechanisms (seepage-induced erosion and slope instability), suggesting a continuous transition between flow- and stress-controlled landforms. We find that OFG can create landforms in siliciclastic margins when buried flow pathways exist. Shelf-break depth determines landform type and timing. Shelf-breaks deeper than the sea-level lowstand lead to shallow circular depressions in the mid-shelf region, while those shallower than the lowstand yield V-shaped and theatre-headed valleys in the outer shelf to upper slope. Landforms emerge during falling sea-levels, starting as pockmark trains along the edges of the buried channels. Sensitivity studies show that: (1) channel width and depth affect only landform size, not type, and (2) OFG-related landforms are mainly erosion-driven and can evolve into slope failures in coarse-grained sediments with low cohesive strength. Our model aligns with field observations of pockmarks, canyons, and landslides in various continental margin settings.

1 Introduction

Offshore freshened groundwater (OFG) is groundwater stored in sub-seafloor sediments/rocks with a total dissolved solid concentration below that of seawater. First reported in the 1960s (Kohout, 1964), OFG has now been documented in continental margins worldwide in water depths down to 3,000 m and is estimated to have a global volume of ${10}^5-{10}^6$ km³ (Zamrsky et al., 2022; Micallef et al., 2021; Post et al., 2013). The majority of this OFG is thought to predominantly occur in passive siliciclastic margins, and to have been emplaced by meteoric recharge during sea-level lowstands as a result of continental shelf exposure and an increase in hydraulic heads (Cohen et al., 2010; Kooi and Groen, 2001; Micallef et al., 2021; 2020). Key factors influencing OFG distribution are topography-driven flow, salinization via haline convection, permeability contrasts, and the continuity/connectivity of permeable and confining strata (Micallef et al., 2020). Considering that sea-level has been lower than today for 80% of the Quaternary period (Bintanja et al., 2005), OFG systems are likely to have been more extensive, and associated with higher groundwater fluxes, for the majority of the last 2.6 Ma (Cohen et al., 2010; Faure et al., 2002; Morrissey et al., 2010).

OFG has long been hypothesised to be a key factor shaping continental margins (Johnson, 1939; Stetson, 1936). Field observations, primarily from siliciclastic shelves and slopes, have been used to infer that sub-seafloor OFG flow can deform sediment or trigger slope failures by generating excess pore pressure and lowering effective stress (Kopf et al., 2016; Paull et al., 2021; Stegmann et al., 2011). Depressions, and potentially blind canyons, are thought to have formed where OFG actively discharges at the seafloor (Goff, 2019; Green and Uken, 2008; Gwiazda et al., 2018; Virtasalo et al., 2019). A comprehensive list of seafloor landforms associated with OFG is found in Micallef et al. (2023). Most of these inferences are speculative, although recent 2D models have demonstrated that OFG flow during sea-level lowstands can generate the pore pressures required to trigger mechanical instabilities in the outer shelf to upper slope of passive (or divergent, or rifted), non-glaciated margins (Micallef et al., 2023). Such a phenomenon has been shown to be more likely in carbonate margins, although it may occur in siliciclastic margins under specific conditions, e.g., where preferential flow pathways cross the shelf. Precise understanding of how subsurface flow of OFG impacts the morphodynamics of the surface/seafloor remains elusive. This is primarily because of (1) limited understanding of OFG characteristics (e.g., distribution, flow rate, pressure/chemical characteristics): due to a paucity of field measurements, (2) difficulties with observing/measuring OFG-driven seafloor processes and simulating them in the laboratory, and (3) challenges in isolating the effects of groundwater from those of the other processes occurring in the vicinity of the seafloor. Establishing a diagnostic link between OFG and seafloor landforms is important because it can support models that reconstruct or predict the geomorphic evolution of continental margins, refine hazard assessments, and identify topographic signatures of OFG flow/seepage.

The objective of this study is to determine whether groundwater processes can independently initiate and drive landform evolution on the seafloor. If so, it seeks to identify the types of landforms that may develop and the specific conditions under which they occur. This study focuses solely on exploring the mechanistic relationship between groundwater flow and seafloor landforms, without attempting to assess the relative significance of groundwater action compared to other known drivers of landform evolution. We use a “reduced order modelling” approach to delineate the characteristics of seafloor landforms generated by OFG flow and seepage in a passive siliciclastic margin with a buried channel across the shelf, and to identify their key controls. We focus on passive siliciclastic margins because they are the major host of OFG globally (Micallef et al., 2021), where most landforms associated to OFG are located (Micallef et al., 2023). Buried channels are a common feature of siliciclastic margins, e.g., northwest European shelf (Lericolais et al., 2003; Chaumillon et al., 2010; Menier et al., 2010; 2016; Traini et al., 2013), north-eastern Australian shelf (Fielding et al., 2003), New Jersey shelf (Nordfjord et al., 2005; Nordfjord, 2006), Huanghai shelf (Kong et al., 2011), South African shelf (Green, 2009), Sunda shelf in south-east Asia (Hanebuth et al., 2009), Gulf of Mexico (Anderson and Fillon, 2004). We consider sea-level fluctuations during a late Quaternary glacial cycle to account for the widest range of OFG velocities and associated pore pressures. We develop a conceptual 3D groundwater and landscape evolution model that reduces the physical processes to narrowly focus on the interactions of OFG with seafloor landscapes under ideal conditions. A particular highlight of this model is that it provides a generalised mathematical framework to analyse the coupling conditions between fluid flow field and its associated stress field. The presented model is ‘complex’ as it preserves the coupled transient dynamics of flow-induced landscape evolution, but within the context of this study, it is `reduced’ as it resolves only the flow fields associated with fluid seepage while ignoring those that arise from the density gradients due to the freshening process. Analysis of the model parameters and comparison with documented landforms attributed to OFG show that the solutions of our model can provide useful qualitative and quantitative insights regarding the OFG-driven seafloor processes.

2 Methodology

2.1 Mathematical model

To model the impact of OFG on the evolution of continental margins, we assume that the representative elementary volume on the continuum scale is composed of two distinct phases: (s) ediment and pore-(w) ater. The governing equations are derived by considering the mass balance of each phase. Sea-level changes and meteoric recharge drive groundwater recharge and flow. The resulting hydro-mechanical forces impact the mechanical stability of the sediment.

A partial poro-mechanical coupling is considered. Elastic deformations (up-to the limit of the yield surface) induced by pore-pressure changes are used for the evaluation of stress states, which determine the erosional processes. The back-coupling of the elastic deformation on the pore pressure is ignored. The poro-elastic responses of sediment unloading are described through coupling between sediment mass loss and the momentum balance.

For simplicity, salinity effects on the erosional dynamics have been ignored (i.e., the mechanical properties of the sediments as well as the erosion rate parameters are assumed to be independent of salinity). Tidal loading is also ignored as it is not directly relevant for testing the hypothesis.

The following set of governing equations is solved in a 3D computational domain:

${\mathbf{\partial }}_{\mathit{t}}\left[\mathbf{\varphi }{\mathit{C}}_{\mathit{w}}+\left(\mathbf{1}-\mathbf{\varphi }\right){\mathit{C}}_{\mathit{s}}\right]\mathit{P}+\nabla \cdot {\mathit{v}}_{\mathit{w}}+\nabla \cdot {\mathit{v}}_{\mathit{b}}=\mathbf{0}(1)$

${\mathrm{\partial }}_t\left(1-\mathrm{\varphi }\right)C_{s}P-{\mathrm{\partial }}_t\mathrm{\varphi }+\nabla \cdot \left(1-\mathrm{\varphi }\right){\mathit{v}}_b=Q(2)$

$\nabla \cdot \mathbf{\sigma }+\nabla P=\left[\mathrm{\varphi }{\mathrm{\rho }}_w+\left(1-\mathrm{\varphi }\right){\mathrm{\rho }}_s\right]\mathit{g}(3)$

where, Equation 1 corresponds to total mass balance of water and sediment phases, Equation 2 to mass balance of sediment phase, and Equation 3 to quasi-steady-state momentum balance of sediment matrix.

The variable $\mathbf{\varphi }\left(\mathbf{x},\mathbf{t}\right)$ is the sediment porosity and $\mathbf{P}\left(\mathbf{x},\mathbf{t}\right)$ the pore-water pressure, with $\mathbf{t}\ge \mathbf{0}$ as time and $\mathbf{x}≔{\left[\mathbf{x},\mathbf{y},\mathbf{z}\right]}^{\mathbf{T}}$ as the spatial coordinates. Furthermore, ${\mathbf{\rho }}_{\mathbf{w}},{\mathbf{\rho }}_{\mathbf{s}}\left(\mathbf{x},\mathbf{t}\right)$ are water and sediment phase densities, such that:

${\mathrm{\rho }}_{\mathrm{\beta }}=\frac{1}{C_{\mathrm{\beta }}}\frac{\mathrm{\partial }{\mathrm{\rho }}_{\mathrm{\beta }}}{\mathrm{\partial }P}\forall \mathrm{\beta }=\left\{w,s\right\}(4)$

with ${\mathbf{C}}_{\mathbf{w}},{\mathbf{C}}_{\mathbf{s}}$ as the water and sediment phase compressibilities, respectively (Equation 4). The variable ${\mathit{v}}_{\mathit{w}}$ is the Darcy seepage velocity of the water phase, such that:

${\mathit{v}}_w\left(\mathit{x},t\right)≔-\frac{\mathit{K}}{{\mathrm{\mu }}_w}\left(\nabla P+{\mathrm{\rho }}_w\mathit{g}\right)(5)$

with permeability $\mathit{K}\left(\mathit{x},\mathit{t}\right)$, dynamic viscosity of water ${\mathbf{\mu }}_{\mathit{w}}$, and acceleration due to gravity $\mathit{g}$ (Equation 5). To reflect the changes in the permeability field due to changes in porosity, we parameterize the $\mathit{K}-$ relationship using an exponential model (e.g., Hommel et al., 2018; Rutqvist et al., 2002), such that:

$\mathbf{K}≔{\mathit{K}}_0\exp \left[\mathrm{\lambda }\left(\frac{\mathrm{\varphi }-{\mathrm{\varphi }}_0}{1-{\mathrm{\varphi }}_0}\right)\right](6)$

where, ${\mathbf{\varphi }}_{\mathbf{0}}$ and ${\mathit{K}}_{\mathbf{0}}$ are the reference porosity and permeability distributions, and $\mathbf{\lambda }$ is a model parameter. The variable ${\mathit{v}}_{\mathit{b}}≔{\left[{\mathit{v}}_{\mathit{b}\mathit{x}},{\mathit{v}}_{\mathit{b}\mathit{y}},{\mathit{v}}_{\mathit{b}\mathit{z}}\right]}^{\mathit{T}}$ is the sediment burial velocity that accounts for the sediment aggradation, such that:

$v_{bx}=v_{by}=0\text{\hspace{0.5em}and\hspace{0.5em}}{v}_{bz}=\left(\frac{1-{\mathrm{\varphi }}_0}{1-\mathrm{\varphi }}\right)v_{b0}(7)$

where ${\mathit{v}}_{\mathit{b}\mathbf{0}}$ is the effective burial rate measured at the seafloor (Equation 7). For simplicity, we assume that the burial rate remains the same throughout the glacial cycle (i.e., invariant over time). The variable $\mathbf{\sigma }\left(\mathit{x},\mathit{t}\right)$ is the effective Cauchy stress tensor, resolved using an elastic constitutive law in the limit of infinitesimal strains, such that:

$\mathbf{\sigma }≔\mathbf{2}\mathbf{\Gamma }\mathbf{ϵ}+\mathbf{\Lambda } \mathit{t}\mathit{r}\left(\mathbf{ϵ}\right)\mathit{I}(8)$

where, the $\mathbf{ϵ}≔\frac{\mathbf{1}}{\mathbf{2}}\left(\nabla \mathit{u}+{\nabla }^{\mathit{T}}\mathit{u}\right)$ is the infinitesimal strain tensor evaluated based on the gradient of sediment displacement $\mathit{u}$ (Equation 8). Here, $\mathbf{\Gamma }$ and $\mathbf{\Lambda }$ are the Lamé parameters of the sediment material, and are related to the elastic properties, Young’s modulus $\mathit{E}$ and Poisson’s ratio $\mathbf{\nu }$, as Equation 9,

$\mathrm{\Gamma }=\frac{E}{2\left(1+\mathrm{\nu }\right)}\text{\hspace{0.17em}and\hspace{0.17em}}\mathrm{\Lambda }=\frac{E\mathrm{\nu }}{\left(1+\mathrm{\nu }\right)\left(1-2\mathrm{\nu }\right)}(9)$

Finally, $\mathit{Q}\left(\mathit{x},\mathit{t}\right)$ denotes the rate of sediment mass-removal, parameterized as:

$Q=\left\{\begin{array}{ll}\left.-e_0 {\mathcal{F}}^{\mathcal{n}}\left|v_w\right.\right|& \text{if\hspace{0.17em}}\mathcal{F}>0\\ 0& \text{if\hspace{0.17em}}\mathcal{F}\le 0\end{array}\right.(10)$

where, the stress-state $\mathcal{F}$ measures the potential for a mechanical instability to occur in the sediment matrix, such that the states $\mathcal{F}<\mathbf{0}$ are considered stable and $\mathcal{F}\ge \mathbf{0}$ are considered unstable. In our model, the stress-state is estimated using a Drucker-Prager failure-envelope (also called the yield-surface):

$\mathcal{F}\left(\mathbf{\sigma }\right)≔\mathit{q}\left(\mathbf{\sigma }\right)+\mathbf{\alpha } \mathit{p}\left(\mathbf{\sigma }\right)-\mathit{c}(11)$

with mean stress $\mathit{p}≔\frac{\mathbf{1}}{\mathbf{2}} \mathit{t}\mathit{r}\left(\mathbf{\sigma }\right)$ shear stress $\mathit{q}≔\frac{\mathbf{1}}{\mathbf{2}}\mathbf{\sigma }:\mathbf{\sigma }$, and yield parameters $\mathbf{\alpha }$ (frictional resistance) and $\mathit{c}$ (cohesion).

The landscape evolves by removal of sediment mass due to sediment-groundwater interactions. In this study, we only consider the slope failure and seepage-induced erosion mechanisms of sediment-mass removal. The functional form of the sediment-mass removal rate in Equation 10 is central to our model of landscape evolution, where $\mathit{Q}$ can be seen as a multiplicative decomposition of the principal drivers of the mass-removal mechanisms, such that, $\mathit{Q}\propto {\mathit{Q}}_{\mathit{s}}\cdot {\mathit{Q}}_{\mathit{f}}$, where ${\mathit{Q}}_{\mathit{s}}≔{\mathcal{F}}^{\mathcal{n}}$ is the stress-controlled mass-removal term and $\left.{\mathit{Q}}_{\mathit{f}}≔\left|{\mathit{v}}_{\mathit{w}}\right.\right|$ is the flow-controlled (or seepage-controlled) mass-removal term.

The assumption of multiplicative decomposition of the source term $Q$ can be justified with the following argument:

a) First, we consider the conditions for slope-stability. A sediment slope remains intact if the stress-states remain within the failure envelope. Conversely, the slope becomes mechanically unstable if the stress-states lie outside the failure envelope. Assuming perfect plasticity (which is a strong constraint), we can express this in the following mathematical form:

$q_{sf}^{*}=0\text{\hspace{0.17em}if\hspace{0.17em}}\mathcal{F}<0\text{\hspace{0.5em}and\hspace{0.5em}}{q}_{sf}^{*}<0\text{\hspace{0.17em}if\hspace{0.17em}}\mathcal{F}=0\Rightarrow q_{sf}^{*}\mathcal{F}=0(12)$

which is essentially a type of Kharush-Kuhn-Tucker (KKT) constraint (Equation 12). Here, $q_{sf}^{*}$ is some arbitrary slope-failure related sink term. If we weaken the assumption of perfect plasticity and consider a rate-based sediment-mass removal due to slope failure, then we can express this mathematically as,

$q_{sf}^{*}<0\text{\hspace{0.17em}if\hspace{0.17em}}\mathcal{F}>0\text{\hspace{0.5em}and\hspace{0.5em}}{q}_{sf}^{*}=r_0{\mathcal{F}}^{\mathcal{n}}(13)$

for some rate constant $r_0>0$ and exponent $n>0$. Equation 13 means that the sediment-mass removal due to slope-failure can occur only when the stress-state is unstable (i.e., $\mathcal{F}$ lies outside the failure-envelope) and the mass loss is proportional to the magnitude of the stress-state (i.e., higher stress $\Rightarrow$ higher $\left|q_{sf}^{*}\right|$).

b) Next, based on the typical parametric forms (Rahmati et al., 2013 and references therein) for the seepage-induced erosion rate, we can consider some arbitrary erosion-related sink term $q_{er}^{*}$, as,

$q_{er}^{*}=e_0{\mathcal{F}}^{\mathcal{m}}\left(\left|{\mathit{v}}_w\right.|-v_{cr}\left(\mathcal{F}\right)\right)(14)$

For some rate constant ${ϵ}_0>0$, exponent $m>0$, and stress-dependent threshold seepage rate $v_{cr}\ge 0$. Equation 14 implies that the mass loss is proportional to the magnitude of the seepage velocity [Howard and McLane (1988); Howard (1988)] and the intrinsic erosion rate $ϵ≔{ϵ}_0{\mathcal{F}}^{\mathcal{m}}$, which depends on the strength of the sediment matrix, is proportional to the stress-state of the sediment.

c) Adding the two sink terms in Equations 13, 14 leads to the total sediment mass removal rate as,

$Q=-q_{sf}^{*}-q_{er}^{*}=-e_0{\mathcal{F}}^{\mathcal{n}}\left(\frac{\left.\left|{\mathit{v}}_w\right.\right|}{v^{*}}+{\tau }^{*}\right)(15)$

with $v*={\mathcal{F}}^{\left(\mathcal{n}-\mathcal{m}\right)}$ and $\tau *=\frac{r_0}{e_0}\left(1-\frac{e_{0{\mathcal{F}}^{\mathcal{m}}}}{r_{0{\mathcal{F}}^{\mathcal{n}}}}{v}_{cr}\right)$. In this modeling study, we consider a special case of Equation 15 with $v_{cr}≔\frac{r_{0{\mathcal{F}}^{\mathcal{n}}}}{e_{0{\mathcal{F}}^{\mathcal{m}}}}$ and $n=m$, which leads to $v^{*}=1$ and ${\tau }^{*}=0$, reducing Equation 15 to Equation 10.

Mechanistically, this model offers a strong conceptual advantage because, although the system of Equations 1–3 describing the landscape evolution is highly nonlinear, the parameterisation of the sediment removal rate in Equation 10 allows us to lump the contributions of each underlying mechanism into components of the principal driving forces (i.e., stress-states and seepage flow-field), providing a unified framework for analysing the process-couplings. An important property of this model is that the individual mechanisms of landscape evolution are not independent. Rather, there is a continuous bi-directional feedback loop leading to rich time-dependent dynamics between the emergence of erosional morphological features like pockmark-clusters, channels, canyons, and landslide scars. Depending on the relative magnitudes of ${\mathit{Q}}_{\mathit{s}}$ and ${\mathit{Q}}_{\mathit{f}}$, the dominant control for the landscape evolution can be either slope failure or seepage-induced erosion. Moreover, it is possible that landscape evolution starts with one dominant control, but transitions towards the other, depending on how the stress-states and flow-field evolve over time. We shall refer to such landscapes as transitional. It is also possible that ${\mathit{Q}}_{\mathit{s}}$ and ${\mathit{Q}}_{\mathit{f}}$ are locally dominant in different regions of the same landscape due to intrinsic heterogeneity in the sediment sub-structure (e.g., variations in sediment compaction or permeability). Additionally, extrinsic factors, such as the evolving topography of the landscape, may create regional variations in erosional patterns. For instance, erosion could expose weaker or more permeable layers, potentially altering fluid flow and sediment transport in specific areas.

Finally, instead of assuming a shallow-transport approximation for groundwater and sediment flow, this model resolves the full 3D structure of the sediment subsurface. Therefore, the simulation results are presented in terms of the relative loss in the sediment volume, i.e., $\mathit{s}≔\left[\mathbf{1}-\frac{\left(\mathbf{1}-\mathbf{\varphi }\right)}{\left(\mathbf{1}-{\mathbf{\varphi }}_{\mathbf{0}}\right)}\right]$, where the morphological features are identified based on the distribution of s such that $\mathit{s}>\mathbf{0}$ implies a local loss in sediment (i.e., depression-features), and $\mathit{s}<\mathbf{0}$ implies a local gain in sediment (i.e., elevation-features).

2.2 Numerical scheme

The mathematical model has three main governing equations: Equations 1–3. We chose the following primary variables for our numerical model: P, $\varphi$, and $\mathit{u}$.

The governing equations are discretized spatially using a standard Galerkin finite elements method and temporally using an implicit Euler finite difference approximation. At each time-step, the numerical solution of the coupled problem is obtained using a Newton-based nonlinear solver. The resulting numerical scheme is implemented within C++ based DUNE-PDELab framework (Sander, 2020), and uses in-built matrix assembler, linearization algorithm (Newton method with numerical Jacobian), and linear solver (parallel Algebraic Multi-Grid (AMG) solver with stabilized bi-CG preconditioner).

2.3 Test setting and scenarios

We consider a narrow section $\left(W_D=4\text{\hspace{0.17em}km}\right)$ of an idealized continental margin with a shelf of length $L_m=60$ km, and a 4° continental slope $\left(L_s=14\text{\hspace{0.17em}km},H_s=1\text{\hspace{0.17em}km}\right)$ (Figures 1A, B). The chosen margin characteristics are representative of the global continental margins, based on mean global measurements of shelf length and continental slope-gradient (Harris et al., 2014; Kennet, 1982). The depth of the shelf-break is variable $\left(H_{sb}\in \left\{60,120,240\right\}m\right)$, based on minimum and intermediate values of mean global shelf-break depth, as well as a hypothetically very shallow shelf-break (Harris and Macmillan-Lawler, 2016).

Figure 1

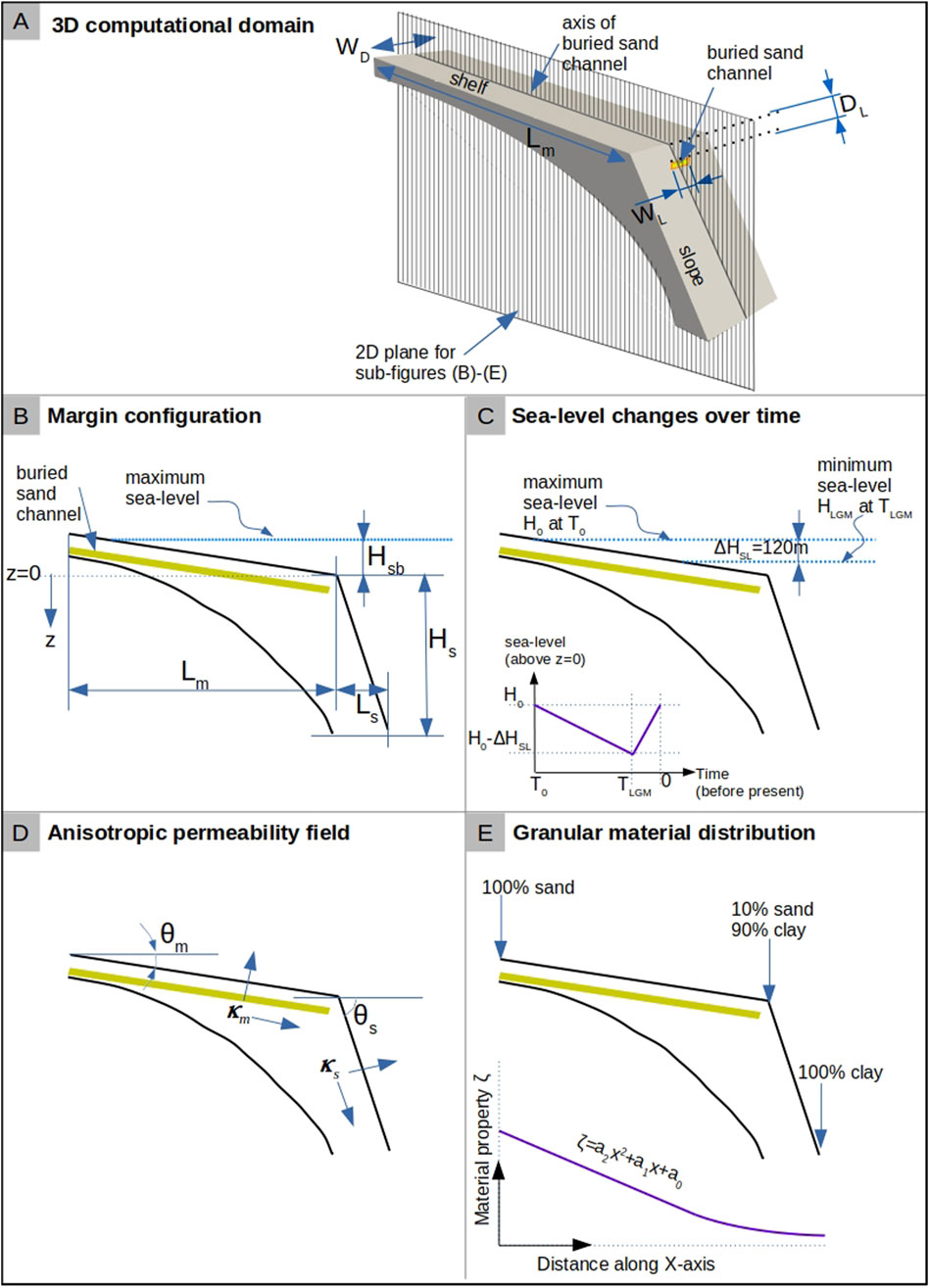
Figure 1. Computational domain and test-setting. In (A), the 3D computational domain for the idealised continental margin is shown. The margin domain contains a buried sand channel of width $W_L$ and thickness ${\Delta }_L=20$ m, located at a depth of $D_L$ below the seafloor. In (B), $L_m=60$ km is the length of the shelf, $L_s=14$ km the length of the slope, and $H_{sb}\in \left\{60,120,240\right\}$ m the depth of the shelf-break measured with respect to the maximum sea-level. The datum for depth $z$ (i.e., $z=0$) is chosen to coincide with the depth of the shelf-break. In (C), $\Delta H_{SL}=120$ m is the total change in sea-level over one glacial cycle, starting at time $T_0=120$ ka before present where the sea-level was the highest at $H_0$, decreasing to a level $H_0-\Delta H_{SL}$ at $T_{LGM}=20$ ka before present, and finally increasing back to $H_0$ in modern time. The sea-level changes are modelled as a linear ramp function over time. In (D), ${\mathrm{\theta }}_m$ and $K_m$ denote the angle of rotation and permeability tensor for the shelf, and ${\mathrm{\theta }}_s$ and $K_s$ denote the same for the slope. In (E), the heterogeneity in the sediment properties $\mathrm{\zeta }$ due to the sand-to-clay distribution of granular material from coast to offshore are modelled as a quadratic mapping (Equation 16). The sediment properties only vary along the shelf (i.e., from coast to sea) but not across the shelf. The buried sand layer is composed of sand only.

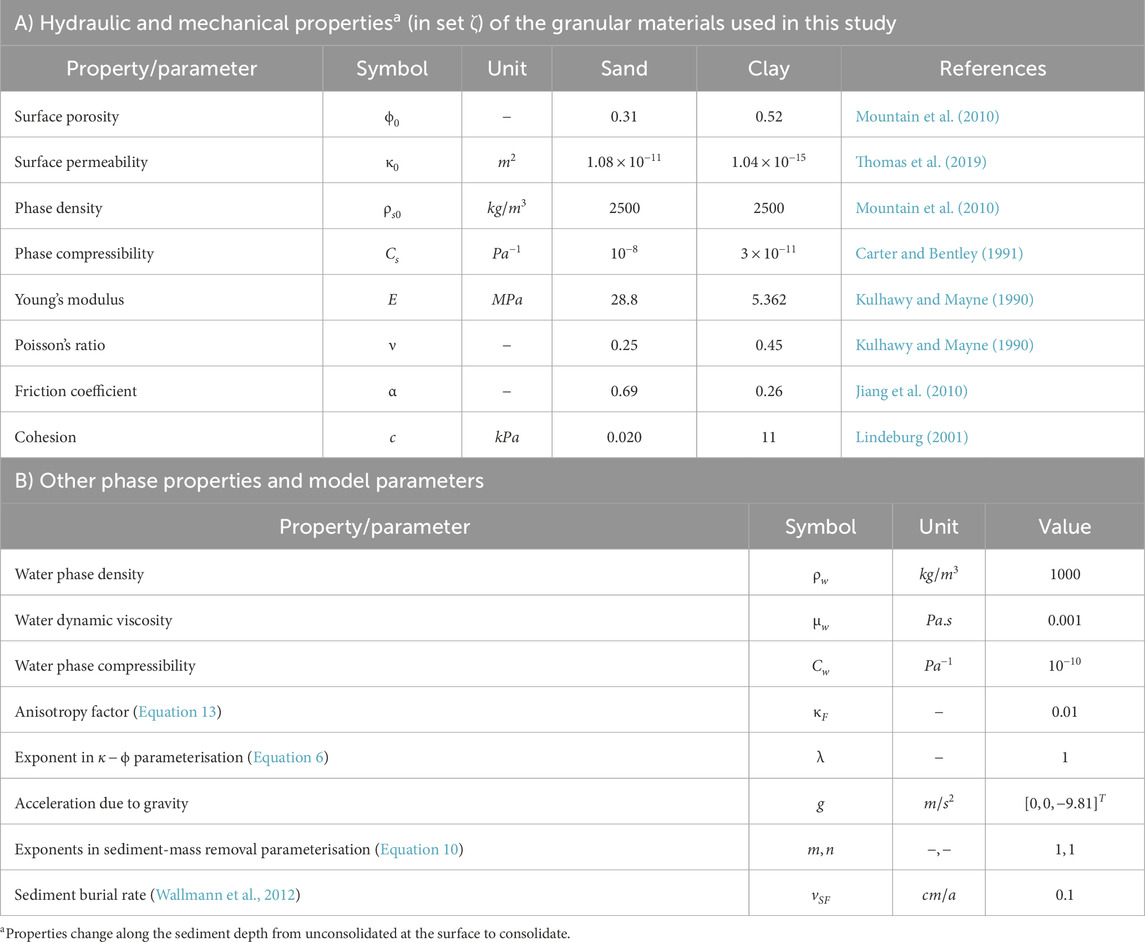
The margin consists of sediment with a graded granular structure, with sand coastwards, smoothly transitioning to clay seawards (Figure 1E). The heterogeneity in the corresponding hydraulic and mechanical properties $\mathrm{\zeta }$ $\in$ $\left\{{\mathrm{\varphi }}_0,K_0,{\mathrm{\rho }}_{s0},C_s,\mathrm{\Gamma },\mathrm{\Lambda },\mathrm{\alpha },c,e_0\right\}$ is described using the following mapping (shown schematically in Figure 1E):

$\mathrm{\zeta }\left(x\right)≔a_2{x}^2+a_{1}x+a_0(16)$

with,

$a_2=\frac{{\left.\mathrm{\zeta }\right|}_{x=L_T}-{\left.\mathrm{\zeta }\right|}_{x=0}}{L_T\left(L_T-L_m\right)}-\frac{{\left.\mathrm{\zeta }\right|}_{x=L_m}-{\left.\mathrm{\zeta }\right|}_{x=0}}{L_m\left(L_T-L_m\right)}$

$a_1=\frac{{\left.\mathrm{\zeta }\right|}_{x=L_T}-{\left.\mathrm{\zeta }\right|}_{x=0}}{L_T}-L_T{a}_2$

${\mathit{a}}_{\mathbf{0}}={\left.\mathbf{\zeta }\right|}_{\mathit{x}={\mathit{L}}_{\mathit{T}}}-{\mathit{L}}_{\mathit{T}}^{\mathbf{2}} {\mathit{a}}_{\mathbf{2}}-{\mathit{L}}_{\mathit{T}} {\mathit{a}}_{\mathbf{1}}$

The effects of steady-state compaction on the sediment properties $\mathrm{\zeta }$ is also accounted for by assuming that the properties vary along the depth exponentially, smoothly changing from unconsolidated at the seafloor to fully consolidated 200 m below seafloor. Furthermore, as the margin forms over time through continuous deposition and burial, we consider an anisotropic permeability distribution, rotated along the topography as shown in Figure 1D, to reflect the layered stratigraphy of a typical margin in the ideal limit of continuous burial of identically graded material at a constant rate:

${\mathit{K}}_0≔\left[\begin{array}{ccc}{\mathrm{\kappa }}_0\mathit{cos}\left(\mathrm{\theta }\left(x\right)\right)& 0& {\mathrm{\kappa }}_0{\mathrm{\kappa }}_F\mathit{sin}\left(\mathrm{\theta }\left(x\right)\right)\\ 0& {\mathrm{\kappa }}_0& 0\\ -{\mathrm{\kappa }}_0\mathit{sin}\left(\mathrm{\theta }\left(x\right)\right)& 0& {\mathrm{\kappa }}_0{\mathrm{\kappa }}_F\mathit{cos}\left(\mathrm{\theta }\left(x\right)\right)\end{array}\right](17)$

where, ${\mathrm{\kappa }}_0$ is the scalar permeability of the sediment, ${\mathrm{\kappa }}_F\ge 1$ reflects the degree of flow anisotropy, and $\mathrm{\theta }\left(x\right)$ is the angle of rotation (relative to the X-axis) of the margin topography. Specifically, in Figure 1D, ${\mathrm{\theta }}_m$ and $K_m$ denote the angle of rotation and permeability tensor for the shelf respectively, and ${\mathrm{\theta }}_s$ and $K_s$ denote the same for the slope.

We consider the continental margin described here as representative of global continental margins as it preserves the following necessary features during idealization: 1) Simplified geometry has distinct shelf, shelf-break, and slope based on mean global measurements as described above; and 2) sediment properties reflect the lithological complexity through variation from coarse-grained (i.e., higher sand volume) onshore to fine-grained (i.e., higher clay volume) offshore, unconsolidated on seafloor to fully-consolidated at depth, and anisotropic permeability distribution to mimic the sediment layering during deposition and burial processes.

A buried high-permeability (sand) channel (Figures 1A, B) acts as a preferential flow pathway for groundwater flow. The thickness of this channel is assumed to be fixed (${\Delta }_L=20$ m) and its depth below the seafloor ($D_L\in \left\{50,100,200\right\}$ m) and lateral width ($W_L\in \left\{200,400,800\right\}$ m) are varied.

The sea-level fluctuations during the last glacial cycle are approximated as an asymmetric hat function (Bintanja et al., 2005), shown in Figure 1C. This function is imposed on the surface (seafloor) of this continental margin with a time-period of $T_0=120$ ka, such that the total sea-level change is $\Delta H_{SL}=120$ m and the minimum sea-level occurs at $T_{LGM}=20$ ka BP [Last Glacial Maximum (LGM)].

Annual rainfall (R) of 100 cm is assumed to act on the exposed shelf as the sea-level drops, and the meteoric recharge flux is assumed to be 25% of R based on the global mean annual rainfall and recharge rates (Moeck et al., 2020). A 2D modelling study by Micallef et al. (2023) showed that these values for annual rainfall and recharge can trigger mechanical instabilities. Sea-level changes and the meteoric recharge fluxes induce transient groundwater flow offshore. Although seasonal variations in rainfall are expected to cause local perturbations over short time scales, these perturbations will average out over a period of several thousand years. Furthermore, the groundwater recharge rates are hard to quantify as they vary substantially depending upon the geological environment, ranging from 40% in shallow aquifers of Quaternary sands to 13% and 4% in deeper aquifers of Miocene-Pliocene sandstone and weathered crystalline rocks, respectively (Kotchoni et al., 2018). Since the focus of this study is purely mechanistic, the assumption of continuous average rainfall at a moderate recharge rate is reasonable.

Table 1A lists the values of parameters in $\mathrm{\zeta }$ for the reference sand and clay used in this study, derived from published values from New Jersey, and Table 1B lists the remaining model parameters. The erosion rate in this study was chosen based on Dronkers and van den Berg (2024) where the typical intrinsic erosion rate constant of coastal sediments is estimated to be in the order of 1e-1 Pa⁻¹ m^-1.

Table 1

Table 1. Material properties and model parameters.

The modelling study by Micallef et al. (2023) has shown that the permeability contrast, rather than the absolute permeability, affects mechanical stability. Therefore, within the scope of this study, testing the effect of permeability is not directly relevant to the mechanistic understanding of the relationship between OFG and evolution of landforms.

In our model, the evolution of the landscape strongly depends on the ‘relative’ magnitudes of $Q_f$ and $Q_s$. To test the sensitivity of the simulated landscapes, we adjust the magnitude of $Q_s$ by varying the values of the sediment cohesive strength $c$. Micallef et al. (2023) showed that the mechanical stability of the margin depends on the heterogeneity in the sediment material. Therefore, we consider a range of cohesive strengths of the clayey offshore sediments ($c_{clay}\in \left\{1100,11,0.11\right\}$ kPa), which represents a wide range of heterogeneity.

In total, two sets of scenarios were simulated. The first set includes nine scenarios without the buried channel for all combinations of $H_{sb}$ and $c_{clay}$, and the second set includes eighty-one scenarios with the buried channel for all combinations of $H_{sb}$, $W_L$, $D_L$ and $c_{clay}$.

3 Results

In scenarios without a buried sand channel, OFG flow and seepage only generate landforms in the margin configurations with shallow shelf-break ($H_{sb}=60$ m) and very low cohesion ($c_{clay}=0.11$ kPa) (Figures 2Aii, iii). These landforms are predominantly stress-controlled, with slope failure scars occurring in the upper slope and outer shelf regions. This outcome confirms that, in siliciclastic margins with shelf-breaks at 120 m or deeper, and without a buried sand channel, OFG flow and seepage do not form landforms in the outer shelf to upper slope, in agreement with Micallef et al. (2023).

Figure 2

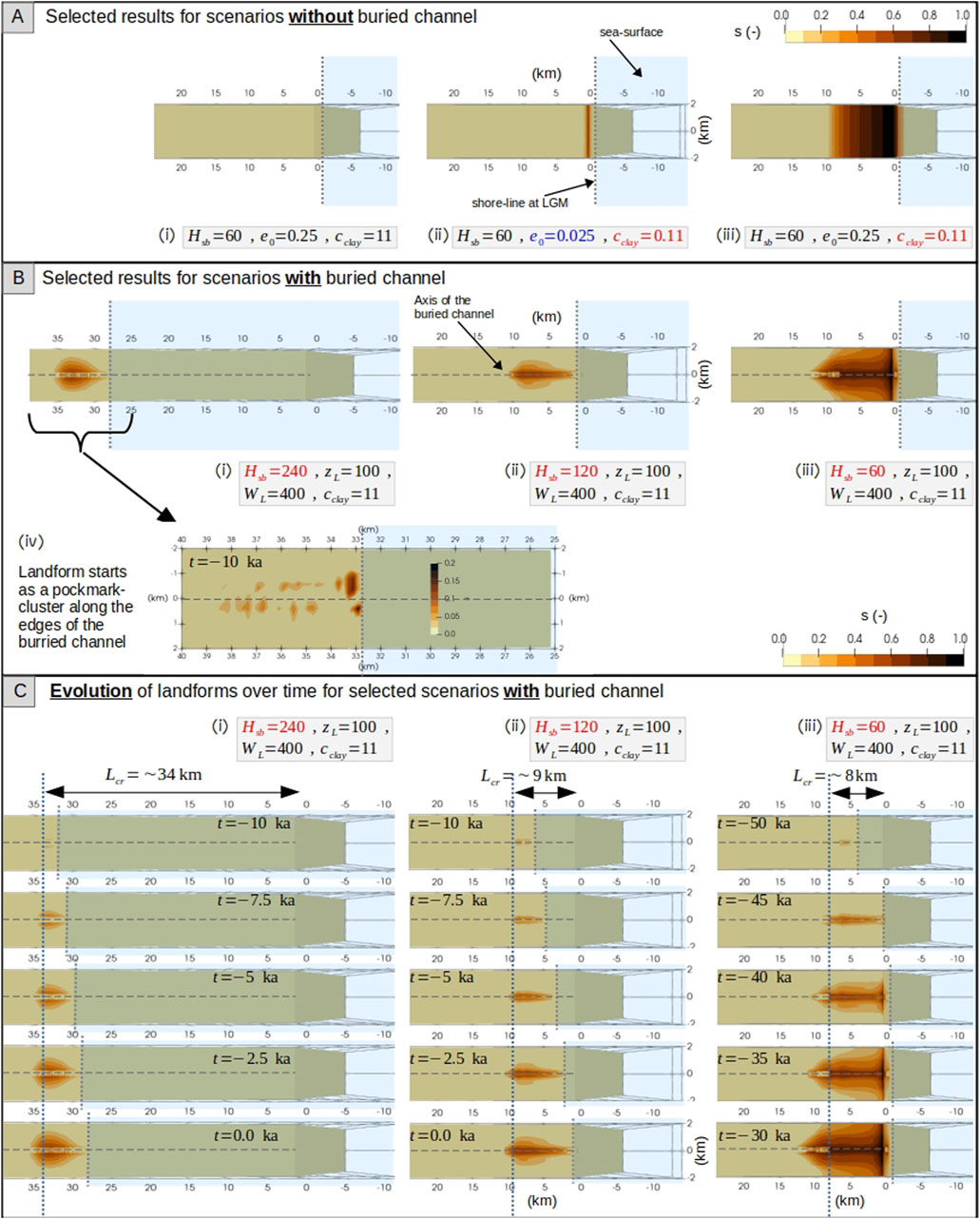
Figure 2. (A) Distribution of relative sediment volume loss $\left(s≔\left(\mathrm{\varphi }-{\mathrm{\varphi }}_0\right)/\left(1-{\mathrm{\varphi }}_0\right)\right)$ for selected scenarios without buried sand channel plotted at time $t=T_{LGM}$, corresponding to sea-level lowstand. OFG flow generated landforms only in the margin configurations with shallow shelf-break ($H_{sb}=60$ m) and very low cohesion ($c_{clay}=0.11$ kPa). These landforms are predominantly stress-controlled, with slope failure scars occurring in the upper slope and outer shelf regions. (B) Distribution of $s$ for selected scenarios with a buried sand channel, plotted at sea-level lowstand. Depth of the shelf-break emerged as the dominant control for the type, location, and timing of the landform formation. Shelf-break deeper than the sea-level lowstand ($H_{sb}=240$ m) led to shallow sub-circular depressions in the mid-shelf region, while shallower shelf-breaks ($H_{sb}=60,120$ m) led to V-shaped and theatre-headed valleys in the outer shelf to upper slope region. All simulated landforms initiated as pockmark clusters along the edges of the buried channel. (C) Time-evolution of the landforms shown in B (i-iii). All simulated landforms started to develop during sea-level fall, either close to $T_{LGM}$ (as for $H_{sb}=120$ m or 240 m) or earlier (as for $H_{sb}=60$ m).

In scenarios with a buried sand channel, the depth of the shelf-break ($H_{sb}$) plays the most dominant role in controlling the type, location, and timing of the landforms that develop as a result of OFG flow and seepage. Margin configurations with shallower shelf-breaks ($H_{sb}=\left\{60,120\right\}$ m) give rise to seepage-controlled erosional features similar to theatre-headed valleys ($H_{sb}=120$ m, Figure 2Bii) or V-shaped valleys ($H_{sb}=60$ m, Figure 2Biii) that originate at the shelf-break. In the case of the shallowest shelf-break, which is shallower than the sea-level lowstand, the upper slope region may also experience slope failure (Figure 2Biii), similar to the scenarios without buried channels. The deepest shelf-break ($H_{sb}=240$ m), in contrast, promotes the development of sub-circular regions of seepage-controlled erosional landforms in the mid-shelf region, originating at the intersection of lowest sea-level with the shelf (Figure 2Bi). Moreover, high resolution simulations show that all landforms originate as pockmark clusters along the edges of the buried channel that, due to continuous erosion, subsequently evolve into channels and valleys; this corroborates the hypothesis of Pilcher and Argent (2007) based on field observations. An example of this behaviour is shown in Figure 2Biv, corresponding to the early stage of the mid-shelf landform evolution shown in Figure 2Bi. In terms of timing, all simulated landforms start to develop during sea-level fall, either close to $T_{LGM}$ (as for $H_{sb}=120$ m or 240 m (see Figures 2Ci, ii) or earlier (as for $H_{sb}=60$ m (see Figure 2Ciii)).

The size (i.e., length, width, and volume) of the landforms is controlled by the characteristics of the buried sand channel (e.g., its width $W_L$ and depth $D_L$ below the seafloor) and the volume of clay in the surface sediments, whereas the mechanical properties of the sediments exert a strong control on the landform evolution, as described below:

a. Impact of the buried sand channel characteristics: The buried sand channel modulates the groundwater flow field by providing a preferential flow path and thus enhances the erosion-driven sediment removal. Wider channels ($W_L$, Figure 3A) located at shallower sub-seafloor depths ($D_L$, Figure 3B) tend to lead to the formation of wider valleys, and vice versa. Moreover, the largest volume of sediment removal occurs along the edges of the channel due to the anisotropic flow-fields in the subsurface, such that groundwater seeps faster into the sand channel from the edges rather than from top. A similar phenomenon has been reported in the field by Mulligan et al. (2007).

b. Impact of clay content in surface sediments: A landform can only evolve where the stress-state is unstable (i.e., $\mathcal{F}>0$, see Equation 10). Therefore, the exact location ($L_{cr}$) where the landforms first begin to evolve depends on where the clay content is just high enough to perturb the sediment stability but remains low enough so that the cohesive strength of clay does not restabilise the sediment. For margin configurations with $H_{sb}=\left\{60,120\right\}$ m, $L_{cr}$ lies roughly 10 km upslope from the shelf-break, and for configurations with $H_{sb}=240$ m, $L_{cr}$ lies $\sim 35$ km upslope from the shelf-break (see Figure 2C). The total extent of the landform is, therefore, the length between $L_{LGM}$ and $L_{cr}$. Due to the small topographic gradient of the continental shelf (${0.05}^o$ to ${0.25}^o$, derived from the chosen margin geometries in the simulated scenarios), the stress-states remain below 0 upslope, and greater than, but very close to, 0 downslope from $L_{cr}$. The topographic gradient of the continental slope is, in comparison, an order of magnitude steeper ($\sim 4^o$), and therefore, experiences much larger stresses. Consequently, all landforms on the mid- and outer shelf regions begin to form at $L_{cr}$ as seepage-controlled features and evolve with competing seepage and stress controls in the wake of the receding shoreline (Figures 2i–iii). When the sea-level drops below the shelf-break (i.e., for $H_{sb}=60$ m), additional stress-controlled slope failure occurs along the continental slope. The length of the emerging landforms is, therefore, controlled by $L_{cr}$ (and, thus, the volume of clay along the margin length).

c. Impact of cohesive strength of clay-rich sediment: The cohesion parameter controls the boundary of the failure envelope $\mathcal{F}$ (see Equation 11). The landforms evolve in mid- and outer shelf regions, where sediment is mostly clay rich. A high $c_{clay}$ (1100 kPa) implies smaller $\mathcal{F}$, and therefore higher stability, while low $c_{clay}$ (0.11 kPa) implies larger $\mathcal{F}$, and therefore, lower stability. High $c_{clay}$ implies that the landforms on the mid- and outer shelf remain flow-controlled, while low $c_{clay}$ implies that stress-component may exceed the flow-component, such that the erosional landforms on the mid- and outer-shelf evolve into translational slope failures (Figure 3Ciii).

Figure 3

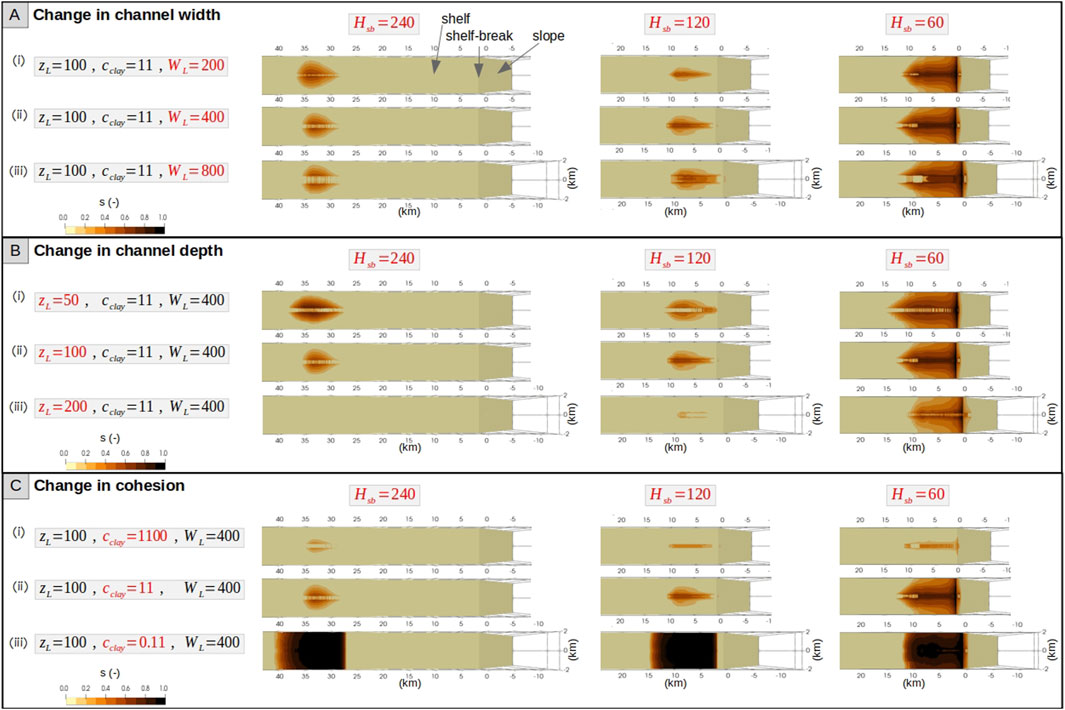
Figure 3. Snapshots of the distribution of relative sediment volume loss $\left(s≔\left(\mathrm{\varphi }-{\mathrm{\varphi }}_0\right)/\left(1-{\mathrm{\varphi }}_0\right)\right)$ for the margin configurations with $H_{sb}=\left\{240,120,60\right\}$ m showing sensitivity of the landforms to the (A) width ($W_L$) and (B) depth ($D_L$) of the buried channel, and (C) the cohesive strength ($c_{clay}$) of the sediment. Wider channels located at shallower sub-seafloor depths lead to the formation of wider erosional features, and vice versa. High $c_{clay}$ leads to predominantly erosional landforms, while low $c_{clay}$ promotes translational slope failures.

4 Discussion

The depth of the shelf-break ($H_{sb}$) emerged as the dominant control as it modulates the rate of exposure of the shelf area during sea-level change (and, therefore, the extent of meteoric recharge) (Figure 4). This impacts the groundwater flow rate and, in turn, the dynamics of landform evolution by regulating the flow-field dependent $Q_f$ component of the sediment removal rate. To that effect, we can generalize that low exposure rates (i.e., deep shelf-break) lead to shallow elliptical depressions, whereas high exposure rates (i.e., shallow shelf-break) lead to valleys. Moreover, for a given shelf gradient, the shelf-break depth also determines where the lowest sea-level intersects with the margin ($L_{LGM}$). The deeper the shelf-break, the farther from the shelf-break the landform develops. Furthermore, the correlation between the location where the landform initiates ($L_{cr}$) and the depth of the shelf-break further reinforces the dominant role of shelf-break depth in controlling the landform characteristics.

Figure 4

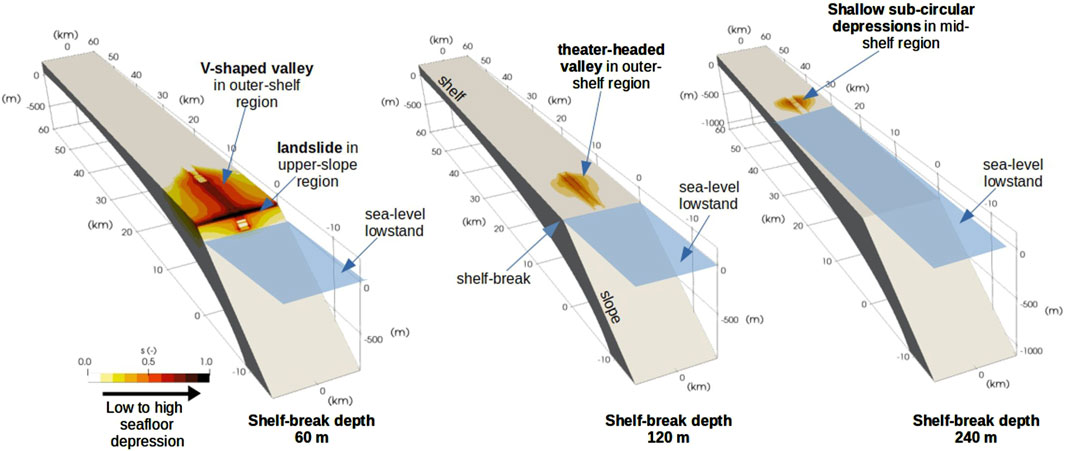
Figure 4. Schematic representation summarising the key morphological features formed by sub-seafloor OFG seepage observed across varying shelf-break depths (60 m, 120 m, and 240 m) during sea-level lowstand conditions.

4.1 Comparison with field data

We compare our simulation results with examples of mapped seafloor landforms that have been attributed to OFG activity (see Table 2 for a summary of the seafloor landform characteristics). Note that the scope of this study is limited to synthetic scenarios with a clear focus on analysing the process controls, rather than simulating the specific geological scenario for each field-analogue. Therefore, the purpose of this comparison is not to simulate the details of the particular geological settings, but to show that many field analogues support our main results vis-à-vis the role of ${\mathit{H}}_{\mathit{s}\mathit{b}}$ in controlling the characteristics of the landforms.

a. Pockmarks in the New England Mud Patch (USA) (Goff, 2019): The New England margin has a shelf gradient of ${0.05}^o$, a 160 km wide shelf, and a shelf-break depth of 140 m, which is deeper than the LGM sea-level lowstand. Geophysical investigations and numerical modelling suggest that the OFG system here extends 90 km from the coast (Gustafson et al., 2019) and that it was primarily emplaced by subglacial recharge from Pleistocene ice sheets (Person et al., 2003; Siegel et al., 2014). The reported pockmark field is located between 50 and 60 km upslope from the shelf-break. For margins with shelf-breaks deeper than the LGM sea-level lowstand, our model predicts a shallow sub-circular erosion dominated landscape (with pockmark clusters along the channel edges similar to Figure 2Biv). Since the landforms originate at the intersection of lowest sea-level with the shelf, based on a simple geometric calculation, the location of the pockmark field at $\sim 50$ km from the shelf-break is in agreement with the sea-level drop of 120 m and the margin characteristics (i.e., shelf-gradient of ${0.05}^o$ and $H_{sb}=140$ m). Furthermore, according to our model, the reported 10 km downslope extent of the pockmark field correlates well with a shallow buried channel ($〈50$ m deep), similar to Figure 3Bi. Seismic reflection data from across the New England shelf show both buried channels (McMaster and Ashraf, 1973) and pipe structures indicative of focused fluid flow (Goff, 2019).

b. Shelf-indenting canyons with retrogressive slope failure at the head in Northern KwaZulu-Natal (South Africa) (Green and Uken, 2008): The KwaZulu-Natal margin has a shelf-break depth of 120 m, which corresponds to the LGM sea-level lowstand, and buried channels (Green and Garlick, 2011; Green, 2009). No clear evidence of OFG has been published for this margin, although the hydraulic head from the adjacent coastal groundwater table is thought to drive freshwater seepage offshore (Meyer et al., 2001; Green and Uken, 2008). For such a margin, our model predicts the formation of a V-shaped canyon originating at the shelf-break (e.g., Figure 2Bii and 3A,B with $H_{sb}=120$ m). Additionally, our model predicts that slope failure can occur at the head of the canyon if the sand content of the sediment is high and, consequently, its cohesive strength is low. This is in agreement with interpretations of seismic reflection data (Sydow, 1988), which suggest that canyons likely incise loosely consolidated silty sandstones.

c. Slope failure at the shelf-break offshore Nice (France) (Kopf et al., 2016; Stegmann et al., 2011): The Nice margin has a shelf-break depth of 100 m, which is shallower than the LGM sea-level lowstand. A sandy layer is present at shallower depth (Steiner et al., 2015). Moreover, Kopf et al. (2016) suggest that coarse-grained sediments may be located close to the shelf-break. This is consistent with our model prediction of slope failures in the upper slope and shelf-break region for margins with shallow $H_{sb}$ and low-cohesion sediments. Based on our model runs, the reported extent of slope failure on the Nice margin is consistent with a buried channel depth of 50–100 m (e.g., Figure 3Ciii).

d. Slope failure in the upper continental slope of the Canadian Beaufort Sea (Canada) (Paull et al., 2021): The margin of the Beaufort Sea has a shelf-break depth of 110 m (slightly shallower than LGM). Here, permafrost extends to the outer continental shelf (Grob et al., 2023), and a large-scale submarine groundwater flow system is thought to be present (Frederick and Buffett, 2015). The shelf consists of a series of banks and infilled cross-shelf troughs/channels (Blasco et al., 2013). The reported slope failure in the upper slope region is consistent with our model predictions for margins with shallow $H_{sb}$ and low-cohesion sediments (Blasco et al., 2013). Furthermore, our model suggests that the deeper the buried channel, the lower the impact of OFG on the outer shelf, i.e., the slope-failure occurs primarily on the upper slope, with a limit extent onto the outer-shelf. Therefore, the limited impact of OFG observed on the outer shelf of the Beaufort Sea margin suggests that the buried channel (or other preferential groundwater flow pathways) may be located at large depths (deeper than $200$ m). This is in agreement with the inferred depths where relict Pleistocene permafrost is predicted to have thawed with consequent movement of liberated groundwater (Paull et al., 2021).

e. New Jersey margin (USA) (Brothers et al., 2014): There is extensive evidence for OFG across this margin, which was derived from drilling campaigns (Hathaway et al., 1979; Lofi et al., 2013; Mountain et al., 2010), geophysical surveys (Gustafson et al., 2019; Key, 2016) and numerical modelling (Thomas et al., 2019). The OFG system extends 90 km from the coast and is thought to have been emplaced by meteoric recharge either in modern times or at a time when climatic and hydrologic conditions were similar (Mottl and Hayashi, 2009; van Geldern et al., 2013). The New Jersey shelf has a slope gradient of ${0.03}^o$, and a shelf-break depth of 140 m. The middle-outer shelf hosts shallowly buried incised-valley fills (Nordfjord et al., 2005; Nordfjord, 2006). The slope features canyons and pockmarks in the upper slope ($150-600$ m), which have been attributed to the combined effect of pore fluid over-pressure induced by sediment loading and gas hydrate dissociation (Brothers et al., 2014). Our model suggests that these landforms may also be associated to OFG. Since the shelf-break is deeper than the sea-level lowstand, the landforms are expected to have started forming already before LGM, and would extend from outer shelf to the upper slope, depending on the buried channel system.

Table 2

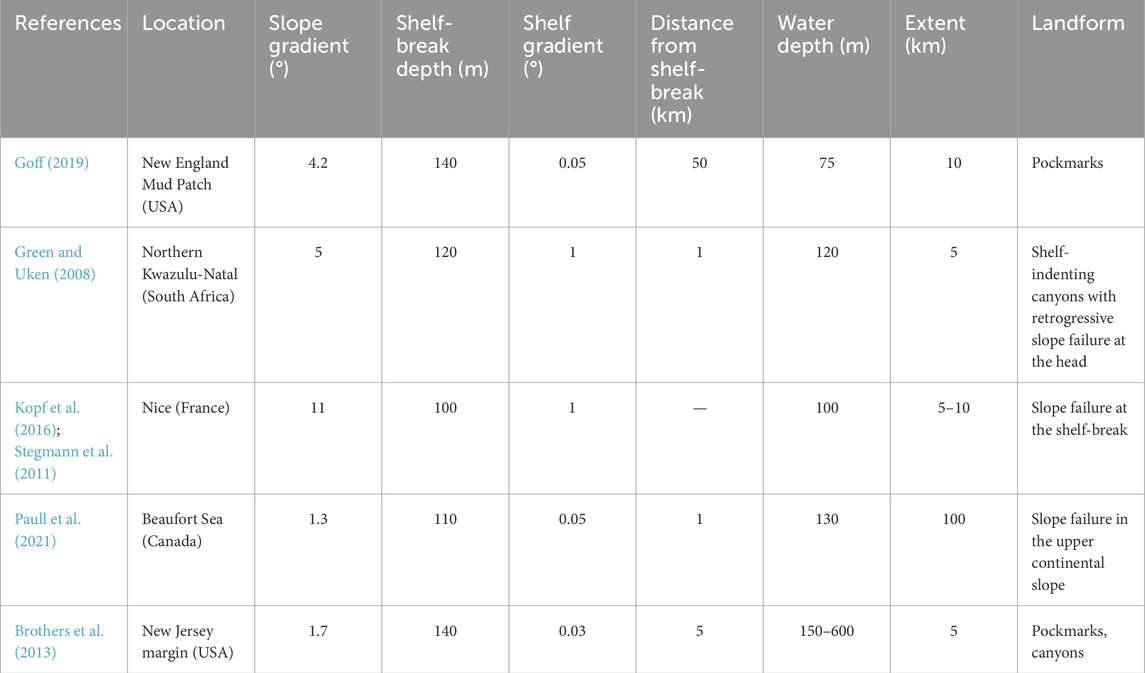
Table 2. Published examples of seafloor landforms attributed to OFG flow/seepage. The location of the landforms, their characteristics (extent, water depth, distance from shelf break) and the characteristics of the margin where they are located (shelf gradient, shelf break depth) are provided.

The available field observations, thus, support our model results in terms of the influence of the depth of the shelf-break ($H_{sb}$) on the type and the location of the landforms. The influence of buried channel characteristics and sediment cohesive strength is harder to elucidate due to lack of data, but qualitative correlations do appear.

It is important to recognize that various processes influencing continental margins can also contribute to the formation of the landforms described. For instance, pockmarks can result from the expulsion of different fluids, including methane, carbon dioxide, and hydrothermal fluids (Hovland et al., 2002). Slope failure may be preconditioned by factors such as rapid sediment accumulation, weak sedimentary layers, seafloor erosion, and tectonic activities. Common triggers for these failures include earthquakes, cyclic loading, and human activities (Masson et al., 2006). The development of submarine canyons is largely driven by erosion from turbidity currents, slope failures, tectonic forces, and hydrodynamic processes (Amblas et al., 2018).

4.2 Implications and limitations

In view of the above, and as long as there is a contrast between the sediment in the buried channel and the surrounding material, we expect the outcomes of our numerical simulations to be applicable to the geomorphic evolution of numerous siliciclastic passive margins globally in the last 1 Ma. We expect the applicability to extend to convergent margins, although additional factors (e.g., margin deformation, thrust faulting, overpressure generation) are likely to distort the interrelation between groundwater processes and seafloor form described here. We would expect similar types of landforms to emerge with similar controls in carbonate margins, considering that dissolution, a key process operating in such settings, is also seepage driven.

In this study, our primary focus is on understanding the basic mechanistic links between subsurface flow fields and their surface manifestations on seafloor morphology. While our motivation stems from observations in freshened groundwater systems, the broader and more fundamental question we address concerns the impact of subsurface flows—arising from meteoric and sea-level perturbations—on landform evolution at the seafloor. To explore this, we employed a simplified modelling approach that does not include solute transport or account for the effects of variable density flow. This decision was based on our objective to isolate and analyse the hydro-mechanical interactions that are most critical to the genesis of erosional features under idealized conditions. By abstracting away the complexities associated with chemical and density-driven processes, our model elucidates the primary dynamics of flow-induced erosion and its potential to drive significant geomorphic changes. This approach allows us to provide a clear demonstration of how groundwater flow, even in its simplest form, can be an independent (and possibly primary) driver of morphological evolution, thereby setting the stage for future studies to incorporate more complex interactions, including those involving solute transport and variable density flows. Our model also overlooks chemical processes (e.g., leaching, dissolution), which are likely to enhance the erosive action of OFG (e.g., Saadatkhah et al., 2023), and stratigraphic structures (e.g., clinoforms), which are known to provide heterogeneous conduits systems for groundwater flow (e.g., Gustafson et al., 2019). The model employs a simplified approach to permeability, idealizing the spatial, lithological and anisotropic variations. The model does not incorporate varying rainfall scenarios with distinct spatial and temporal characteristics. During some stages of lowstand, erosion is expected on the shelf, which we do not account for. We also do not account for the influence of rivers and the onshore drainage basin. The model for the sediment mass removal rate in Equation 10 is a special case of the more general form (Equation 15). This reduced form is helpful in characterising the qualitative features of the evolving landforms but, quantitatively, we expect the actual timing of the initiation of the landform formation and the magnitude of mass removal to be sensitive to the parameterisation of the general form. The landforms are shown in terms of relative volume loss of the sediments. While there exists a positive correlation between the sediment volume fraction (i.e., volume of sediment contained in a unit elemental volume) and height of the landform, it is not straightforward to extract this correlation due to the inherent complexity of the subsurface domain. Finally, while we could qualitatively show how the characteristics of seafloor landforms like pockmarks, canyons, and slope failures associated to OFG flow/seepage align with our model predictions, a case-by-case modelling study of these analogues will be beneficial to better constrain the model parameters and improve the understanding of additional environmental controls.

5 Conclusion

We presented a numerical study simulating the geomorphic action of OFG in an idealised 3D passive siliciclastic margin to delineate the characteristics of the resulting landforms and their main controls.

Our main findings are the following:

a. OFG can generate seafloor landforms in the presence of buried, high permeability channels.

b. These landforms are primarily erosion-controlled features that may evolve into translational slope failures in sediments with low cohesive strength.

c. Depth of the shelf-break controls the type, location, and timing of landform formation. Shelf-breaks deeper than the sea-level lowstand lead to shallow sub-circular depressions in the mid-shelf region, while shallower shelf-breaks lead to V-shaped and theatre-headed valleys in the outer shelf to upper slope region. These landforms develop during sea-level fall and initiate as pockmark clusters along the edges of the buried channel.

d. The width and depth of the buried channel affect the size of the landform, but not the type. Wider channels located at shallow depths lead to larger landforms.

e. Volume of clay in the sediments also exerts an important control. Since clay is more cohesive than sands, but has less frictional strength, it alters the failure envelope and therefore controls the location of initial failure. The higher the clay content, the farther coastwards the landform will extend.

f. Finally, we showed how the characteristics of field examples of seafloor landforms like pockmarks, canyons, and slope failures that have been associated with OFG flow/seepage align well with our model predictions.

This study establishes a clear mechanistic link between the subsurface flow of groundwater and its surface manifestations as various seafloor landforms. Our analysis also shows that the landforms are inherently transitional, i.e., they change from one type to another dynamically. By showing that the source/sink term that drives the landform evolution can be decomposed into a stress-controlled mechanical part and a flow-controlled hydraulic part, we provide a general analytical framework with which the dynamic transition of landforms can be analyzed.

Data availability statement

The source code for the model and test scenarios presented in this manuscript are archived and can be accessed as https://doi.org/10.5281/zenodo.7554639.

Author contributions

SG: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft. AM: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program [grant agreement No 677898 (MARCAN)]. SG acknowledges the additional support from MSCA Postdoctoral ERA Fellowships 2021 action, under the Horizon Europe program, project `WarmArctic’ number 101090338. AM was supported by the David and Lucile Packard Foundation. The work was carried out in the framework of COST (European Cooperation in Science and Technology) Action CA21112 - Offshore freshened groundwater: An unconventional water resource in coastal regions? – OFF-SOURCE.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amblas, D., Ceramicola, S., Gerber, T. P., Canals, M., Chiocci, F. L., Dowdeswell, J. A., et al. (2018). “Submarine canyons and gullies,” in Submarine geomorphology. Editors A. Micallef, S. Krastel, and A. Savini (Springer), 251–272.

Google Scholar

Anderson, J. B., and Fillon, R. H. (2004). Late Quaternary stratigraphic evolution of the northern Gulf of Mexico margin.

Google Scholar

Bintanja, R., Van de Wal, R., and Oerlemans, J. (2005). Modelled atmospheric temperatures and global sea levels over the past million years. Nature 437, 125–128. doi:10.1038/nature03975

PubMed Abstract | CrossRef Full Text | Google Scholar

Blasco, S., Bennett, R., Brent, T., Burton, M., Campbell, P., Carr, E., et al. (2013). 2010 state of knowledge: beaufort Sea seabed geohazards associated with offshore hydrocarbon development. Geol. Surv. Can. Offshore Geoscience Program 6989, 340. doi:10.4095/292616516

CrossRef Full Text | Google Scholar

Brothers, D., Ruppel, C., Kluesner, J. W., Ten Brink, U., Chaytor, J., Andrews, B., et al. (2014). Seabed fluid expulsion along the upper slope and outer shelf of the U.S. Atlantic continental margin. Geophys. Res. Lett. 41, 96–101. doi:10.1002/2013gl058048

CrossRef Full Text | Google Scholar

Brothers, L. L., Van Dover, C. L., German, C. R., Kaiser, C. L., Yoerger, D., Ruppel, C., et al. (2013). Evidence for extensive methane venting on the southeastern U.S. Atlantic margin. Geology 41, 807–810. doi:10.1130/G34217.1

CrossRef Full Text | Google Scholar

Carter, M., and Bentley, S. (1991). Correlations of soil properties. London: Penetech Press Publishers.

Google Scholar

Chaumillon, E., Tessier, B., and Reynaud, J. (2010). Stratigraphic records and variability of incised valleys and estuaries along French coasts. Bull. la Soc. Geol. Fr. 181 (2), 75–85. doi:10.2113/gssgfbull.181.2.75

CrossRef Full Text | Google Scholar

Cohen, D., Person, M., Wang, P., Gable, C., Hutchinson, D., Marksamer, A., et al. (2010). Origin and extent of fresh paleowaters on the atlantic continental shelf, USA. Groundwater 48, 143–158. doi:10.1111/j.1745-6584.2009.00627.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Dronkers, J., and van den Berg, J. (2024). Coastal and marine sediments. Coast. Wiki. Available at: http://www.coastalwiki.org/wiki/Coastal_and_marine_sediments (Accessed March 15, 2024).

Google Scholar

Faure, H., Walter, R., and Grant, D. (2002). The coastal oasis: ice age springs on emerged continental shelves. Glob. Planet. Change 33, 47–56. doi:10.1016/s0921-8181(02)00060-7

CrossRef Full Text | Google Scholar

Fielding, C., Trueman, J., Dickens, G., and Page, M. (2003). Anatomy of the buried Burdekin River channel across the Great Barrier Reef shelf: how does a major river operate on a tropical mixed siliciclastic/carbonate margin during sea level lowstand? Sediment. Geol. 157, 291–301. doi:10.1016/s0037-0738(02)00238-5

CrossRef Full Text | Google Scholar

Frederick, J., and Buffett, B. (2015). Effects of submarine groundwater discharge on the present-day extent of relict submarine permafrost and gas hydrate stability on the beaufort sea continental shelf. J. Geophys. Res. Earth Surf. 120 (3), 417–432. doi:10.1002/2014jf003349

CrossRef Full Text | Google Scholar

Goff, J. (2019). Modern and fossil pockmarks in the New England Mud Patch: implications for submarine groundwater discharge on the middle shelf. Geophys. Res. Lett. 46, 12213–12220. doi:10.1029/2019gl084881

CrossRef Full Text | Google Scholar

Green, A. (2009). Palaeo-drainage, incised valley fills and transgressive systems tract sedimentation of the northern Kwazulu-Natal continental shelf, South Africa, SW Indian ocean. Mar. Geol. 263 (1), 46–63. doi:10.1016/j.margeo.2009.03.017

CrossRef Full Text | Google Scholar

Green, A., and Garlick, G. (2011). A sequence stratigraphic framework for a narrow, current-swept continental shelf: the Durban bight, central Kwazulu-Natal, South Africa. J. Afr. Earth Sci. 60, 303–314. doi:10.1016/j.jafrearsci.2011.03.007

CrossRef Full Text | Google Scholar

Green, A., and Uken, R. (2008). Submarine landsliding and canyon evolution on the northern KwaZulu-Natal continental shelf, South Africa, SW Indian Ocean. Mar. Geol. 254, 152–170. doi:10.1016/j.margeo.2008.06.001

CrossRef Full Text | Google Scholar

Grob, H., Riedel, M., Duchesne, M., Krastel, S., Bustamante, J., Fabien-Ouellet, G., et al. (2023). Revealing the extent of submarine permafrost and gas hydrates in the Canadian Arctic Beaufort Sea using seismic reflection indicators. Geochem. Geophys. Geosystems 24 (5), e2023GC010884. doi:10.1029/2023gc010884

CrossRef Full Text | Google Scholar

Gustafson, C., Key, K., and Evans, R. (2019). Aquifer systems extending far offshore on the U.S. Atlantic margin. Sci. Rep. 9, 8709. doi:10.1038/s41598-019-44611-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Gwiazda, R., Paull, C., Dallimore, S., Melling, H., Jin, Y., Hong, J., et al. (2018). Freshwater seepage into sediments of the shelf, shelf edge, and continental slope of the Canadian Beaufort Sea. Geochem. Geophys. Geosystems 19, 3039–3055. doi:10.1029/2018gc007623

CrossRef Full Text | Google Scholar

Hanebuth, T., Stattegger, K., and Bojanowski, A. (2009). Termination of the last glacial maximum sea-level lowstand: the sunda-shelf data revisited. Glob. Planet. Change 66, 76–84. doi:10.1016/j.gloplacha.2008.03.011

CrossRef Full Text | Google Scholar

Harris, P., and Macmillan-Lawler, M. (2016). “Global overview of continental shelf geomorphology based on the SRTM30 PLUS 30-Arc second database,” in Seafloor mapping along continental shelves: research and techniques for visualizing benthic environments. Editors C. Finkl, and C. Makowski (Cham: Springer International Publishing), 169–190.

CrossRef Full Text | Google Scholar

Harris, P., Macmillan-Lawler, M., Rupp, J., and Baker, E. (2014). Geomorphology of the oceans. Mar. Geol. 352, 4–24. doi:10.1016/j.margeo.2014.01.011

CrossRef Full Text | Google Scholar

Hathaway, J., Poag, C., Valentine, P., Manheim, F., Kohout, F., Bothner, M., et al. (1979). U.S. geological survey core drilling on the Atlantic shelf. Science 206, 515–527. doi:10.1126/science.206.4418.515

PubMed Abstract | CrossRef Full Text | Google Scholar

Hommel, J., Coltman, E., and Class, H. (2018). Porosity–permeability relations for evolving pore space: a review with a focus on (bio-)geochemically altered porous media. Transp. Porous Media 124, 589–629. doi:10.1007/s11242-018-1086-2

CrossRef Full Text | Google Scholar

Hovland, M., Gardner, J. V., and Judd, A. G. (2002). The significance of pockmarks to understanding fluid flow processes and geohazards. Geofluids 2, 127–136. doi:10.1046/j.1468-8123.2002.00028.x

CrossRef Full Text | Google Scholar

Howard, A. D. (1988). “Groundwater sapping on Earth and Mars,” in Sapping Features of the Colorado Plateau. Editors A. D. Howard, R. C. Kochel, and H. R. Holt (NASA), 1–4.

Google Scholar

Howard, A. D., and McLane, C. F. (1988). Erosion of cohesionless sediment by groundwater seepage. Water Resour. Res. 24 (10), 1659–1674. doi:10.1029/WR024i010p01659

CrossRef Full Text | Google Scholar

Jiang, X.-W., Wang, X.-S., and Wan, L. (2010). Semi-empirical equations for the systematic decrease in permeability with depth in porous and fractured media. Hydrogeology J. 18, 839–850. doi:10.1007/s10040-010-0575-3

CrossRef Full Text | Google Scholar

Johnson, D. (1939). The origin of submarine canyons: a critical review of hypotheses. New York: Columbia University Press.

CrossRef Full Text | Google Scholar

Kennet, J. (1982). Marine geology. Upper Saddle River: Prentice-Hall.

Google Scholar

Key, K. (2016). MARE2DEM: a 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 207 (1), 571–588. doi:10.1093/gji/ggw290

CrossRef Full Text | Google Scholar

Kohout, F. (1964). “The flow of fresh water and salt water in the Biscayne aquifer of the Miami area, Florida,” in Sea water in coastal aquifers: relation of salt water to fresh groundwater. Editors H. Cooper, K. F. A., H. Henry, and R. Glover (Reston, VA: USGS Water supply), C12–C33.

Google Scholar

Kong, X., Liu, J., Du, Y., Wen, C., and Xu, G. (2011). Seismic geomorphology of buried channel systems in the western South Huanghai sea: retrodiction for paleo-environments. Acta Oceanol. Sin. 30 (1), 47–58. doi:10.1007/s13131-011-0090-y

CrossRef Full Text | Google Scholar

Kooi, H., and Groen, K. (2001). Offshore continuation of coastal groundwater systems; predictions using sharp-interface approximations and variable-density flow modelling. J. Hydrology 246, 19–35. doi:10.1016/s0022-1694(01)00354-7

CrossRef Full Text | Google Scholar

Kopf, A., Stegmann, S., Garziglia, S., Henry, P., Dennielou, B., Haas, S., et al. (2016). Soft sediment deformation in the shallow submarine slope off Nice (France) as a result of a variably charged Pliocene aquifer and mass wasting processes. Sediment. Geol. 344, 290–309. doi:10.1016/j.sedgeo.2016.05.014

CrossRef Full Text | Google Scholar

Kotchoni, D. O. V., Vouillamoz, J. M., Lawson, F. M. A., Adjomayi, P. A., Boukari, M., and Taylor, R. G. (2018). Relationships between rainfall and groundwater recharge in seasonally humid Benin: a comparative analysis of long-term hydrographs in sedimentary and crystalline aquifers. Hydrogeology J. 27, 447–457. doi:10.1007/s10040-018-1806-2

CrossRef Full Text | Google Scholar

Kulhawy, F., and Mayne, P. (1990). Manual on estimating soil properties for foundation design. Palo Alto, California: Electric Power Research Institute.

Google Scholar

Lericolais, G., Auffret, J.-P., and Bourillet, J.-F. (2003). The Quaternary channel river: seismic stratigraphy of its palaeo-valleys and deeps. J. Quat. Sci. 18, 245–260. doi:10.1002/jqs.759

CrossRef Full Text | Google Scholar

Lindeburg, M. (2001). Civil engineering reference manual for the PE exam. Belmont, California: Professional Publications.

Google Scholar

Lofi, J., Inwood, J., Proust, J., Monteverde, D., Loggia, D., Basile, C., et al. (2013). Fresh-water and salt-water distribution in passive margin sediments: insights from integrated ocean drilling program expedition 313 on the New Jersey margin. Geosphere 9 (4), 1009–1024. doi:10.1130/ges00855.1

CrossRef Full Text | Google Scholar

Masson, D. G., Harbitz, C. B., Wynn, R. B., Pedersen, G., and Løvholt, F. (2006). Submarine landslides: processes, triggers and hazard prediction. Philosophical Transaction R. Soc. 364, 2009–2039. doi:10.1098/rsta.2006.1810

PubMed Abstract | CrossRef Full Text | Google Scholar

McMaster, R., and Ashraf, A. (1973). Drowned and buried valleys on the southern New England continental shelf. Mar. Geol. 15 (4), 249–268. doi:10.1016/0025-3227(73)90073-x

CrossRef Full Text | Google Scholar

Menier, D., Estourn`es, G., Mathew, M., Ramkumar, M., Briend, C., Siddiqui, N., et al. (2016). Relict geomorphological and structural control on the coastal sediment partitioning, north of Bay of Biscay. Z. F. ̈ur Geomorphol. 60 (1), 67–74. doi:10.1127/zfg/2016/0267

CrossRef Full Text | Google Scholar

Menier, D., Tessier, B., Proust, J., Baltzer, A., Sorrel, P., and Traini, C. (2010). The Holocene transgression as recorded by incised-valley infilling in a rocky coast context with low sediment supply (southern Brittany, western France). Bull. la Soc. Geol. Fr. 181, 115–128. doi:10.2113/gssgfbull.181.2.115

CrossRef Full Text | Google Scholar

Meyer, R., Talma, A., Duvenhage, A., Eglington, B., Taljaard, J., Botha, J., et al. (2001). Geohydrological investigation and evaluation of the Zululand coastal aquifer. Water Res. Comm. 51.

Google Scholar

Micallef, A., Person, M., Berndt, C., Bertoni, C., Cohen, D., Dugan, B., et al. (2021). Offshore freshened groundwater in continental margins. Rev. Geophys. 59, e2020RG000706. doi:10.1029/2020rg000706

CrossRef Full Text | Google Scholar

Micallef, A., Person, M., Gupta, S., Saadatkhah, N., Camille, A., and Gratacós, Ò. (2023). Can offshore meteoric groundwater generate mechanical instabilities in passive continental margins? Geophysical Research. Earth Surf. 128. doi:10.1029/2022JF006954

CrossRef Full Text | Google Scholar

Micallef, A., Person, M., Haroon, A., Weymer, B., Jegen, M., Schwalenberg, K., et al. (2020). 3D characterisation and quantification of an offshore freshened groundwater system in the Canterbury Bight. Nat. Commun. 11, 1372. doi:10.1038/s41467-020-14770-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Moeck, C., Grech-Cumbo, N., Podgorski, J., Bretzler, A., Gurdak, J. J., Berg, M., et al. (2020). A global-scale dataset of direct natural groundwater recharge rates: a review of variables, processes and relationships. Sci. Total Environ. 717, 137042. doi:10.1016/j.scitotenv.2020.137042

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrissey, S., Clark, J., Bennett, M., Richardson, E., and Stute, M. (2010). Groundwater reorganization in the Floridan aquifer following Holocene sea-level rise. Nat. Geosci. 3, 683–687. doi:10.1038/ngeo956

CrossRef Full Text | Google Scholar

Mottl, M., and Hayashi, T. (2009). Fresh and salty: chemistry of sediment pore water from the New Jersey shallow shelf: IODP Exp 313. San Francisco: AGU Fall Meeting.

Google Scholar

Mountain, G., Proust, J., McInroy, D., and Cotterill, C. (2010). “Expedition 313 scientists,” in Proceedings of the integrated ocean drilling program.

Google Scholar

Mulligan, A. E., Evans, R. L., and Lizarralde, D. (2007). The role of paleochannels in groundwater/seawater exchange. J. Hydrology 335, 313–329. doi:10.1016/j.jhydrol.2006.11.025

CrossRef Full Text | Google Scholar

Nordfjord, S., Goff, J., Austin, Jr. J., Gulick, S., and Galloway, W. (2006). Seismic facies of incised-valley fills, New Jersey continental shelf: implications for erosion and preservation processes acting during latest pleistocene-holocene transgression. J. Sediment. Res. 76, 1284–1303. doi:10.2110/jsr.2006.108

CrossRef Full Text | Google Scholar

Nordfjord, S., Goff, J., Austin, Jr. J., and Sommerfield, C. (2005). Seismic geomorphology of buried channel systems on the New Jersey outer shelf: assessing past environmental conditions. Mar. Geol. 214, 339–364. doi:10.1016/j.margeo.2004.10.035

CrossRef Full Text | Google Scholar

Paull, C., Dallimore, S., Caress, D., Gwiazda, R., Lundsten, E., Anderson, K., et al. (2021). A 100-km wide slump along the upper slope of the Canadian Arctic was likely preconditioned for failure by brackish pore water flushing. Mar. Geol. 435, 106453. doi:10.1016/j.margeo.2021.106453

CrossRef Full Text | Google Scholar

Person, M., Dugan, B., Swenson, J., Urbano, L., Stott, C., Taylor, J., et al. (2003). Pleistocene hydrogeology of the atlantic continental shelf, New England. Geol. Soc. Am. Bull. 115, 1324–1343. doi:10.1130/b25285.1

CrossRef Full Text | Google Scholar

Pilcher, R., and Argent, J. (2007). Mega-pockmarks and linear pockmark trains on the West African continental margin. J. Petroleum Eng. 244 (1–4), 15–32. doi:10.1016/j.margeo.2007.05.002

CrossRef Full Text | Google Scholar

Post, V., Groen, J., Kooi, H., Person, M., Ge, S., and Edmunds, W. (2013). Offshore fresh groundwater reserves as a global phenomenon. Nature 504, 71–78. doi:10.1038/nature12858

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahmati, H., Jafarpour, M., Azadbakht, S., Nouri, A., Vaziri, H., and Chan, D. (2013). Review of sand production pediction models. J. Pet. Eng. 2013, 864981.

Google Scholar

Rutqvist, J., Wu, Y.-S., Tsang, C.-F., and Bodvarsson, G. (2002). A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 39 (4), 429–442. doi:10.1016/S1365-1609(02)00022-9

CrossRef Full Text | Google Scholar

Saadatkhah, N., Kassim, A., Siat, Q. A., and Micallef, A. (2023). Salt leaching by freshwater and its impact on seafloor stability: an experimental investigation. Mar. Geol. 455, 106959. doi:10.1016/j.margeo.2022.106959

CrossRef Full Text | Google Scholar

Sander, O. (2020). DUNE — The Distributed and Unified Numerics Environment. Switzerland: Springer Nature, 616.

Google Scholar

Siegel, J., Person, M., Dugan, B., Cohen, D., Lizarralde, D., and Gable, C. (2014). Influence of late Pleistocene glaciations on the hydrogeology of the continental shelf offshore Massachusetts, USA. Geochem. Geophys. Geosystems 15, 4651–4670. doi:10.1002/2014gc005569

CrossRef Full Text | Google Scholar

Stegmann, S., Sultan, N., Kopf, A., Apprioual, R., and Pelleau, P. (2011). Hydrogeology and its effect on slope stability along the coastal aquifer of Nice, France. Mar. Geol. 280, 168–181. doi:10.1016/j.margeo.2010.12.009

CrossRef Full Text | Google Scholar

Steiner, A., Kopf, A. J., Henry, P., Stegmann, S., Apprioual, R., and Pelleau, P. (2015). Cone penetration testing to assess slope stability in the 1979 Nice landslide area (Ligurian Margin, SE France). Mar. Geol. 369, 162–181. doi:10.1016/j.margeo.2015.08.008

CrossRef Full Text | Google Scholar

Stetson, H. (1936). Part I. Geology. Geol. Soc. Am. Bull. 47, 339–366. doi:10.1130/gsab-47-339

CrossRef Full Text | Google Scholar

Sydow, C. (1988). “Stratigraphic control of slumping and canyon development on the continental margin, east coast, South Africa,”, 55. Cape Town: Department of Geological Sciences, University of Cape Town.

Google Scholar

Thomas, A., Reiche, S., Riedel, M., and Clauser, C. (2019). The fate of submarine fresh groundwater reservoirs at the New Jersey shelf, USA. Hydrogeology J. 27, 2673–2694. doi:10.1007/s10040-019-01997-y

CrossRef Full Text | Google Scholar

Traini, C., Menier, D., Proust, J., and Sorrel, P. (2013). Transgressive systems tract of a ria-type estuary: the Late Holocene Vilaine River drowned valley (France). Mar. Geol. 337, 140–155. doi:10.1016/j.margeo.2013.02.005

CrossRef Full Text | Google Scholar

van Geldern, R., Hayashi, T., Bottcher, M., Mottl, M., Barth, J., and Stadler, S. (2013). Stable isotope geochemistry of pore waters and marine sediments from the New Jersey shelf: methane formation and fluid origin. Geosphere 9 (1), 96–112. doi:10.1130/GES00859.1

CrossRef Full Text | Google Scholar

Virtasalo, J., Schr ̈oder, J., Luoma, S., Majaniemi, J., Mursu, J., and Scholten, J. (2019). Submarine groundwater discharge site in the First Salpausselk ̈a ice-marginal formation, south Finland. Hydrology Earth Syst. Sci. 10, 405–423. doi:10.5194/hess-2018-507

CrossRef Full Text | Google Scholar

Wallmann, K., Pinero, E., Burwicz, E., Haeckel, M., Hensen, C., Dale, A., et al. (2012). The global inventory of methane hydrate in marine sediments: a theoretical approach. Energies 5 (7), 2449–2498. doi:10.3390/en5072449

CrossRef Full Text | Google Scholar

Zamrsky, D., Oude Essink, G. H. P., Sutanudjaja, E. H., van Beek, L. H. P., and Bierkens, M. F. P. (2022). Offshore fresh groundwater in coastal unconsolidated sediment systems as a potential fresh water source in the 21st century. Environ. Res. Lett. 17, 014021. doi:10.1088/1748-9326/ac4073

CrossRef Full Text | Google Scholar