- 1College of Mining Engineering, Taiyuan University of Technology, Taiyuan, China
- 2Shanxi Transportation Technology Research and Development Co., Ltd., Taiyuan, China
- 3China Railway 12th Bureau Group Co., Ltd., Taiyuan, China
- 4School of Earth Sciences and Engineering, Hohai University, Nanjing, China
Because of its non-viscosity, sand layer is easy to cause rock instability, which is always a difficult problem in tunnel excavation.This study employs an integrated approach of numerical simulation and theoretical analysis to investigate the phenomenon of shield tunnel faces blow-out in shallowly buried sandy soil strata. The research study the effects of burial depth to diameter ratio and the angle of internal friction on the ultimate support pressure and the shape of the failure zone. According to the simulation results, an analytical model for the blow-out of tunnel faces has been developed. The study reveals a linear relationship between the passive ultimate support pressure and the burial depth ratio, as well as the tangent of the friction angle. Upon tunnel passive failure, the failure zone is composed of a rigid core in the form of a lower wedge shape and an upper passive zone in the form of an inclined cylinder. Furthermore, using the wedge shape and inclined cylinder model and applying the theory of limit analysis, the corresponding formula for the ultimate support pressure has been derived. Compared to existing numerical models and classical analytical models, the analytical solution proposed in this paper is more accurate. The research on the failure zone found that an increase in the friction angle causes an enlargement of the failure zone and an increase in the dissipated power at the boundary, resulting in an exponential growth of the limit support pressure. The cohesion has a minimal effect on the shape and area of the failure zone, primarily manifesting as an increase in the dissipated power at the failure zone boundary. Additionally, the burial depth ratio has an insignificant effect on the lower failure zone, but as the cover ratio increases, the area of the upper failure zone gradually expands. At a smaller cover ratio, the weight of the soil plays a dominant role, whereas at a larger cover ratio, the effects of frictional force and cohesion at the failure zone boundary become more pronounced.
1 Introduction
In recent years, the shield construction method has become the primary technique for the construction of tunnels beneath rivers and lakes. The rational determination of the excavation face supporting pressure is crucial for shield construction. If the support pressure is set too low, it can easily lead to tunnel face collapse, also known as active failure. On the contrary, excessively high support pressure may readily induce ground uplift, which is referred to as passive failure (blow-out), particularly in the case of shallowly buried tunnels (Chen et al., 2013). Currently, shield construction often faces challenges such as shallow overburden at the launch, and navigating through riverbed scour zones. Excessive support pressure can lead to engineering incidents such as surface heave and riverbed blowouts, as exemplified by the Heinenroord Second Tunnel in the Netherlands, where an overly high setting of face support pressure resulted in passive failure at the tunnel face, causing a 6-month delay in the project schedule (Bezuijen and Brassinga, 2020). Therefore, the study of passive instability at the tunnel face during shield tunneling possesses significant engineering importance (Li et al., 2022).
In the quest to ascertain the failure modes of tunnel excavation faces, Researchers have utilized both laboratory testing and computational modeling to delve into this matter. Research conducted by Chambon and Corte (1994), Kamata and Mashimo (2003) Kirsch (2010), Ahmed and Iskander (2012) and Qiang et al. (2023) using centrifuge tests, large-scale model experiments, and numerical simulations has revealed that in sandy soil strata, when shield tunneling faces experience active failure, the failure zone takes on a wedge-like contour in front of the tunnel, with a cylindrical shape extending almost vertically to the surface. On the other hand, studies on cohesive soil strata by Schofield (1980), Juneja et al. (2010), Zhang et al. (2015) and Li W. et al. (2019), also utilizing centrifuge tests, large-scale model experiments, and numerical simulations, have found that due to the presence of cohesion, the zone of influence of the sliding area is larger, with the sliding zone exhibiting an arc-shaped sliding surface, and a basin-shaped failure pattern in the area ahead of the tunnel face. Comparative studies by Mair et al. (1993) on the failure modes of tunnel faces in sandy and cohesive soil have highlighted significant differences in the area and shape of the failure zones between the two types of soil.
Scholars, based on the instability patterns of the tunnel face, have abstracted and generalized analytical models for tunnel face instability to reveal the mechanisms behind the tunnel face instability. Horn (1961) introduced the silo-wedge model and derived the limiting support force using the theory of limit equilibrium. Broere (2002) improved upon the wedge model by proposing the prism-wedge model, which was applied to the stability analysis of tunnel faces in layered soil strata. Anagnostou and Kovári (1996) considered the horizontal soil arching effect, modified the prism-wedge model, and employed the slice method to obtain an expression for the support pressure at the tunnel face. Additionally, scholars have refined the model to account for vertical soil arching effects, seepage, and bolt reinforcement, among other factors. The upper bound limit analysis method constructs a kinematically admissible velocity field and derives the limiting support pressure for tunnel face collapse from an energetic perspective. Leca and Dormieux (1990) established models for a single rigid cone and a double rigid cone and used the upper bound limit analysis method to deduce the limiting support pressure at the tunnel face. Proposed a multi-cone model based on the double cone model, which offers higher accuracy compared to single and double cone models; however, the accuracy improvement becomes insignificant when the number of cones exceeds five. Mollon et al. (2010) and Mollon et al. (2011) employed a spatial discretization technique to establish a tunnel face instability model through a point generation method, further enhancing computational precision. Han et al. (2016) and Li et al. (2020) considered the soil arching effect above the tunnel face and developed a combined failure mode with a multi-cone model and a collapse arch. Li P. et al. (2019), through numerical simulation, identified partial failure phenomena at the tunnel face during passive instability and made corrections to the model proposed by Soubra and others. Zhu et al. (2024a); Zhu et al. (2024b) conducted shear experiments on rough rock joints to study the instability mechanism of rock joints induced by stress. Wu et al. (2022); Wu et al. (2024); Wu et al. (2020) studied the influence of mechanical properties and microstructure of cement through particle size distribution.
A review of the literature has revealed that current research predominantly focuses on the active instability of tunnel faces, with comparatively fewer studies addressing passive instability. The applicability of the models proposed for passive instability remains to be validated (Li et al., 2022). In this paper, an integrated approach combining Computational simulation and theoretic analysis has been employed to investigate the phenomenon of passive instability at the excavation face. Consequently, an analytical model for the blow-out of the tunnel face has been proposed. Utilizing this analytical model, the underlying mechanisms of passive failure at the excavation face have been explored.
2 Numerical simulation
2.1 Numerical models
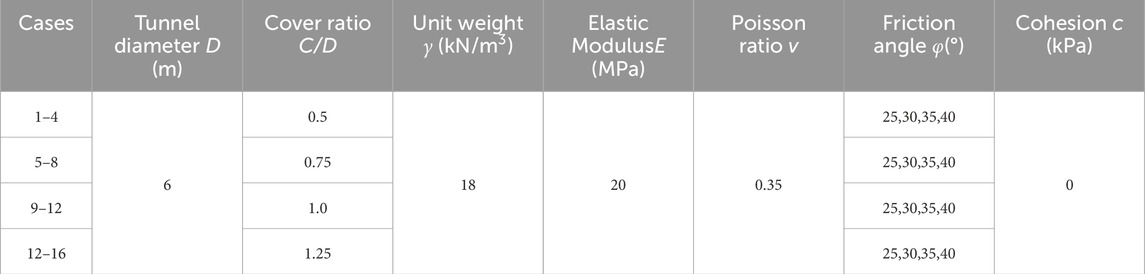
In this section, numerical simulation is primarily utilized to explore the effect of the burial depth to diameter ratio (C/D) and the friction angle (φ) on tunnel face stability in cohesionless soils. The variation in the limit support pressure (PS) at the tunnel excavation face are studied as C/D is adjusted from 0.5 to 1.25, and the φ is modified from 25° to 40°. For this study, a total of 16 cases have been designed, with the details provided in Table 1.
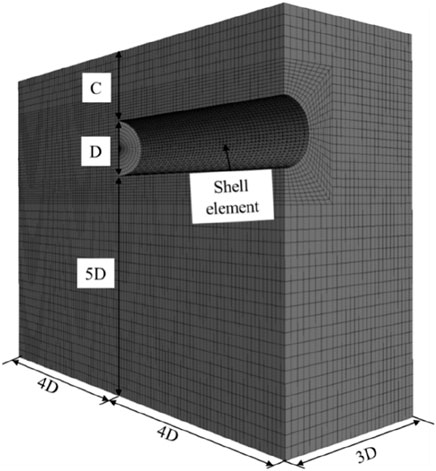
As depicted in Figure 1, a half-model was employed for the sake of computational efficiency. The dimensions of the model were configured with a width of 3 times the tunnel radius (3D), an extended length of 8 times the radius (8D), and the excavation depth progressed to 4 times the radius (4D), while the model’s height was maintained at 6D plus the burial depth (C), with D being the tunnel radius and C representing the depth of burial. The boundary conditions were established as follows: the base was immobilized, normal displacements were restricted on the four lateral sides, and the upper boundary was left unrestricted. The soil was represented using solid elements, under the assumption of adherence to the Mohr-Coulomb failure criterion. The parameters assigned to the soil were as follows: unit weight γ of 18 kN/m³, elastic modulus E of 20 MPa, Poisson’s ratio v of 0.35, and cohesion c set to 0 kPa. The tunnel lining was modeled using 'shell’ elements, characterized by an elastic modulus of 20 GPa, Poisson’s ratio of 0.17, and a thickness of 0.35 m.”
The sequence of the simulation procedure is delineated as follows:
(1) A model of the geological formation is constructed, and an initial state of stress equilibrium is attained.
(2) For the purpose of streamlining the simulation process, the excavation proceeds to a depth of 4D in a single step, with 'shell’ elements utilized to represent the tunnel lining components.
(3) A support pressure (PT) is exerted on the tunnel face, corresponding to the horizontal stress at the midpoint of the tunnel face.
(4) This support pressure is incrementally enhanced, and the horizontal displacement at the midpoint of the tunnel face, under the influence of the support pressure, is documented.
(5) Upon reaching a critical threshold, a precipitous escalation in the horizontal displacement at the tunnel face’s midpoint is detected. At this juncture, the applied support pressure is deemed to have reached the critical support pressure (PS).
2.2 Numerical results
2.2.1 Limit support pressure
Figure 2A to Figure 2B depict the support pressure (PT)-horizontal displacement (dh) curves at the midpoint of the tunnel face for various friction angles, corresponding to burial depth ratios of 0.5, 0.75, 1.0, and 2.5. It is evident from the figures that when the support pressure (PT) is relatively low, there is a linear correlation between the PT and the dh at the midpoint of the tunnel face. As the PT increases, the soil transitions into a plastic state, and the support pressure-displacement curve assumes a curved profile. Upon reaching the critical support pressure, the soil enters a state of plastic flow, at which point the support pressure-displacement curve becomes approximately horizontal. Zhang et al. (2015) identified the PT at the point of abrupt change in the curve as the passive limiting support pressure (PS) and introduced the double secant method to ascertain the magnitude of this limiting support pressure.
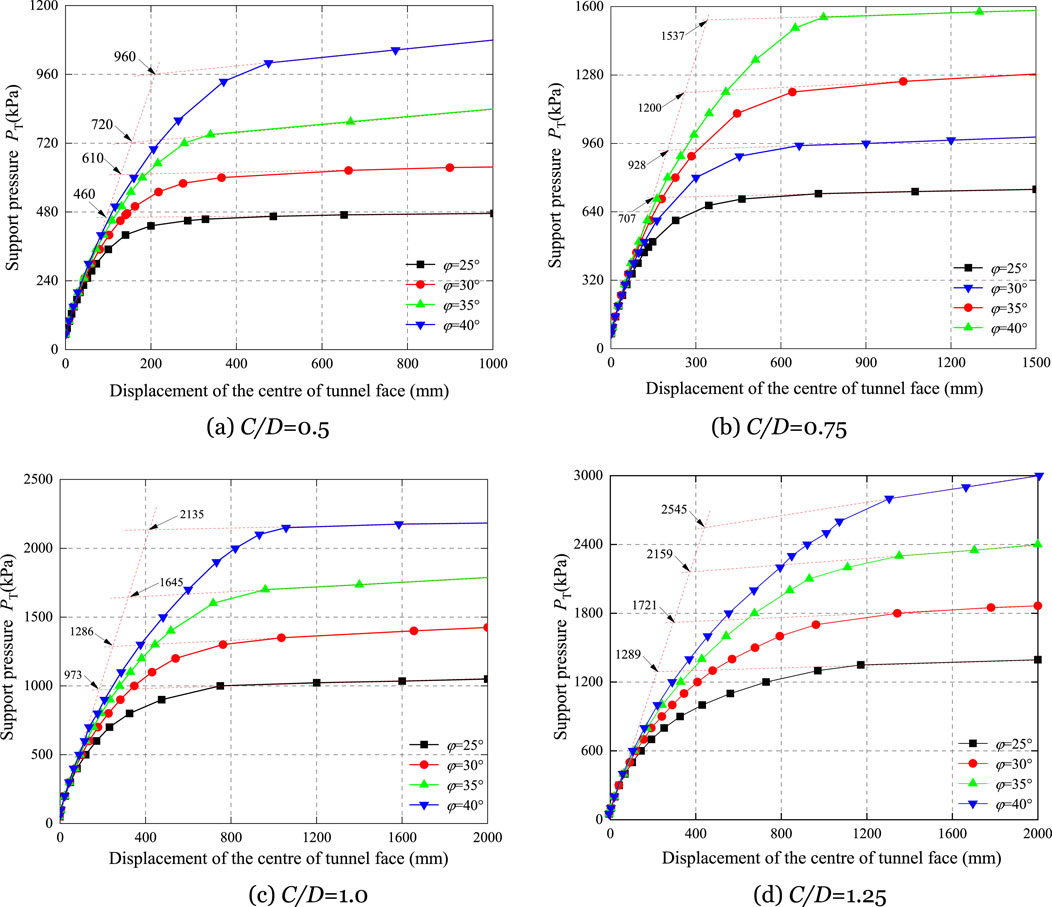
Figure 2. Support pressure-displacement curve of tunnel face. (A) C/D=0.5. (B) C/D=0.75. (C) C/D=1.0. (D) C/D=1.25.
From Figure 2A, it can be observed that under the condition of a C/D of 0.5, the PS increases progressively with the friction angle, rising from 460 kPa to 960 kPa as the angle increments from 25° to 40°. Figure 2B further illustrates the variation in the PS under a C/D of 0.75 for different friction angles. Under these conditions, the calculated
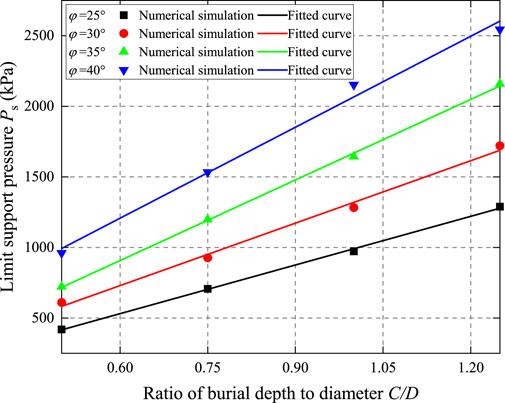
To elucidate the effect of the C/D on the PS, Figure 3 is constructed with the C/D as the horizontal axis and the PS as the vertical axis, plotting the curves of l PS against C/D under various friction angle conditions. Upon examination of Figure 3, it is apparent that in the event of passive instability at the tunnel face, the PS increases linearly with the C/D, a pattern that holds true for all friction angles. However, there is a notable difference in the slope of the curves corresponding to different friction angles, with those having higher friction angles exhibiting steeper slopes. Specifically, when the friction angle φ is 25°, 30°, 35°, and 40°, the respective slopes (k) are 1,149, 1,474, 1902, and 2,418. This indicates that the larger the friction angle, the more sensitive the PS is to changes in the C/D. This observation suggests a synergistic interaction between the φ and the C/D in their influence on the PS.
Figure 4 illustrates the variation in PS with the tangent of the friction angle. It is observable from the figure that under different conditions of burial depth ratios of 0.5, 0.75, 1.0, and 1.25, the PS exhibits a linear increase with the augmentation of the tangent of the φ. Furthermore, the slopes of the lines corresponding to different burial depth ratios vary within the graph. As the C/D increases from 0.5 to 1.25, the slope of the line increases significantly from 1,398 to 3,375. This variation indicates that the sensitivity of the PS to the friction angle intensifies with an increase in the C/D. The observations from Figure 4 further confirm a significant synergistic effect between the φ and the C/D on the passive PS.
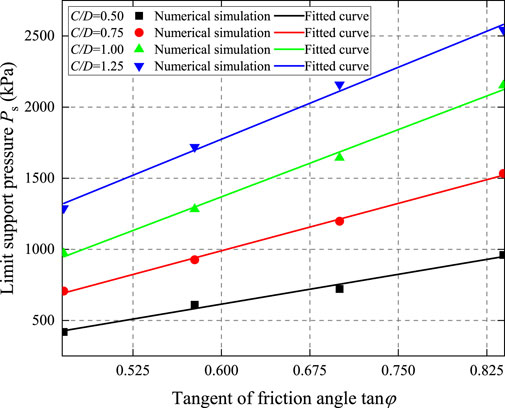
Figure 4. Comparison diagram of the relation curve between ultimate abutment pressure and friction Angle.
2.2.2 Failure zone
Figure 5 presents the displacement cloud diagrams of the damage zone when the tunnel excavation face undergoes passive failure at a C/D of 1.0, under various friction angles. A red curve traces the boundary of the failure zone, indicated by an abrupt displacement gradient change. In instances of passive failure, the failure zone is divisible into a sliding zone in front of the tunnel face and a passive failure zone above the tunnel face, taking on the shape of a truncated inclined cylinder. By comparing Figure 5A to Figure 5D, it is evident that as φ increases, the sliding failure zone in front of the tunnel face becomes flatter, and the inclination angle of the upper passive zone becomes larger. Measurements reveal that the axis of the upper truncated inclined cylinder forms an angle of approximately φ with the vertical.
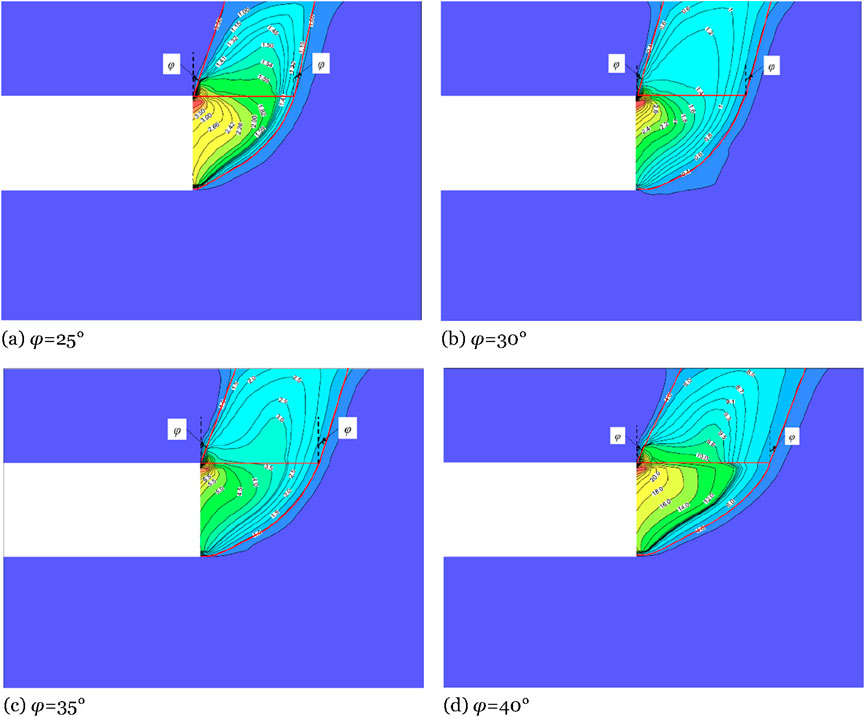
Figure 5. Displacement cloud map of damage area under different friction angles (unit: dm). (A)
3 Analytical model
3.1 Failure mechanism
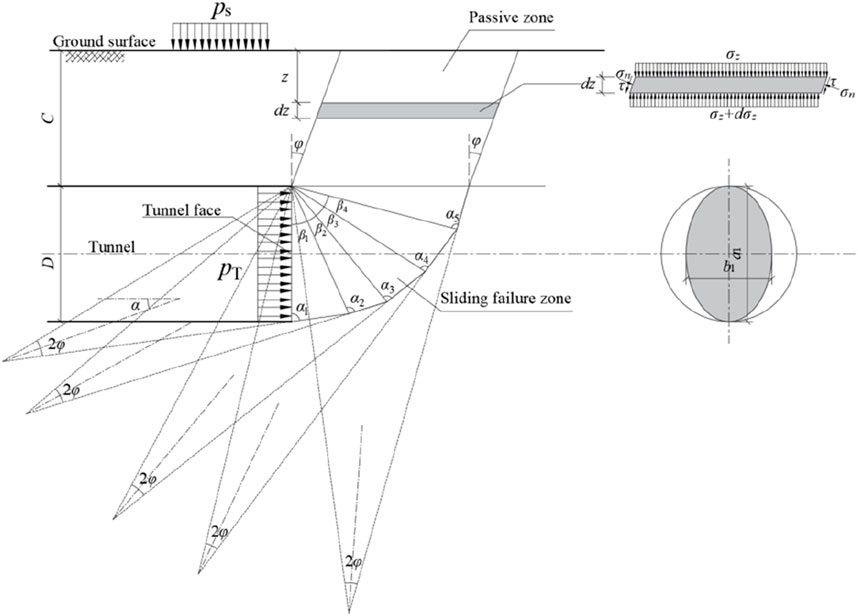
According to the outcomes of the numerical simulation, an analytical model has been proposed for the passive instability of the tunnel face in shallowly buried shield tunnel within sandy soil strata. As depicted in Figure 6, the tunnel has a diameter of D and a burial depth of C, with the support pressure PT uniformly applied to the tunnel face. The failure zone is composed of two distinct parts: the lower part is a sliding failure zone, generated by mirroring five truncated cones; the upper part is a passive zone, shaped as an inclined truncated cylinder, with the axis of the inclined cylinder making an angle of φ with the vertical axis. The impact of the upper failure zone on the limiting support force is considered through the vertical soil pressure σv. It is assumed that upon failure, each truncated cone translates along its axis at a velocity vi.
3.2 Derivation of geometric relationships
This is shown by the geometric relation (Equations 1–5):
Geometric analysis reveals that the intersecting surfaces between the individual truncated cones are elliptical in shape. The major axis of the ellipse, denoted as ai (i=0–5) can be calculated using Equations 6, 7.
The areas of the ellipses, Ai denoted as can be computed using Equation 8 to Equation 9.
In Equation 9, the angle θi is determined by Equations 10–12.
The heights of the individual truncated cones, denoted as hi can be calculated using Equations 13, 14.
The volumes of the individual sliding blocks can be calculated using Equation 15.
The lateral surface areas of the sliding blocks can be calculated using Equations 16, 17.
3.3 Derivation of the velocity relation
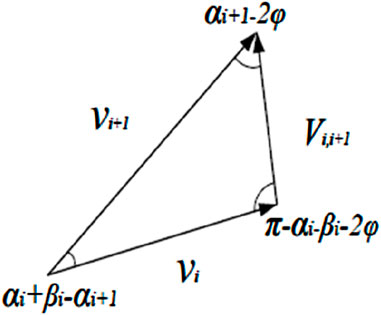
When employing the limit analysis method to solve for the limiting support pressure, it is necessary to postulate a permissible velocity field for the rigid bodies within the failure region. Assuming that each truncated cone translates along its axis, the velocity vector is depicted in Figure 7. Through geometric relationships, the relationship between the velocity of the i+1st truncated cone and the velocity of the ith truncated cone can be deduced (Equation 18):
The velocity of the i+1st truncated cone relative to the i truncated cone is shown in Equation 19:
3.4 Limit support pressure
3.4.1 Limit analysis method
The upper-bound method within the limit analysis theory is extensively applied for determining the limit support pressure required. Based on the upper-bound method, for a tunnel face to remain stable, it must adhere to Equation 20:
Where We represents the power of external forces and Wv represents the dissipated power in the failure zone.
In the context of limit analysis, the virtual power of external forces, denoted as We, is comprised of three components: the power due to the support pressure at the tunnel face WPT, the virtual power due to the load in the passive zone Wσv, and the virtual power due to gravity WG. This can be expressed as Equation 21:
The power due to the support pressure at the excavation face, denoted as WPT, can be calculated using Equation 22:
The virtual power of the vertical load in the passive zone, denoted as Wσv, can be calculated using Equation 23:
In the equation, σv represents the soil pressure transmitted by the passive zone above.
The virtual power due to the weight of the failure zone, denoted as WG, can be calculated using Equation 24:
In the equations, ψi represents the angle between the velocity vi and the vertical direction, which can be calculated using Equations 25, 26:
The internal dissipated power in the failure region can be calculated from Equation 27:
3.4.2 Upper earth pressure solving
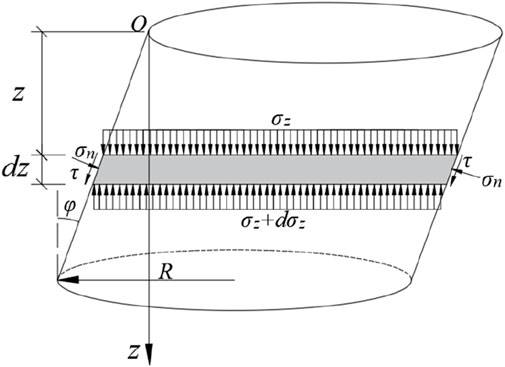
To determine the vertical soil pressure σv, the calculation schematic depicted in Figure 8. In this model, the upper failure zone is assumed to form an inclined cylindrical body with a base that is a circle of radius R. The mechanical behavior of the soil follows the Mohr-Coulomb failure criterion, where the axis of the inclined cylinder makes an angle φ with the vertical.
An Oz coordinate system is established, and a micro-element with a thickness of dz is taken at position z. By applying the equilibrium equation to this micro-element, Equation 28 is obtained:
Where k0 denotes the coefficient of lateral earth pressure; S represents the perimeter of the cylindrical cross-section; A signifies the area of the cylindrical cross-section; c is the cohesion of the soil.
Solving the differential Equation 28 and substituting the conditions at z=0, σz=0, yields
Additionally, by substituting z=C into Equation 29, σv can derive Equation 30:
4 Comparison and analysis
The validity and adaptability of the proposed model were confirmed through a comparison with existing numerical models, classical analytical solutions (Mollon et al., 2010; Li P. et al., 2019), and test results (Qian et al., 2023a).
4.1 Comparing with numerical simulation results and existing models
Figure 9A–D respectively illustrate the variation of the PS calculated by different models as the C/D changes, for the φ of 20°, 25°, 30°, and 35°. It can be observed that when the C/D is less than or equal to 1.25, PS predicted by the models increases approximately linearly with the increase in burial ratio. In terms of the magnitude of support force, the results obtained by Mollon et al. (2010) and Li P. et al. (2019) are significantly higher than those predicted by numerical simulations; the analytical solution presented in this study is more consistent with the numerical results. A detailed comparison reveals the following: when the φ is 20°, the maximum differences between the analytical models proposed by Mollon et al. (2010), Li P. et al. (2019) and the present model with the numerical solution are 35%, 23%, and 8%, respectively; when φ is 25°, these differences are 45%, 39%, and 9%, respectively; when φ is 30°, the maximum differences are 39%, 32%, and 8.7%, respectively; when φ is 35°, they are 60%, 52%, and 10%, respectively. It is particularly noteworthy that for the excavation face in a passive instability, a lower support pressure is more advantageous for engineering design.
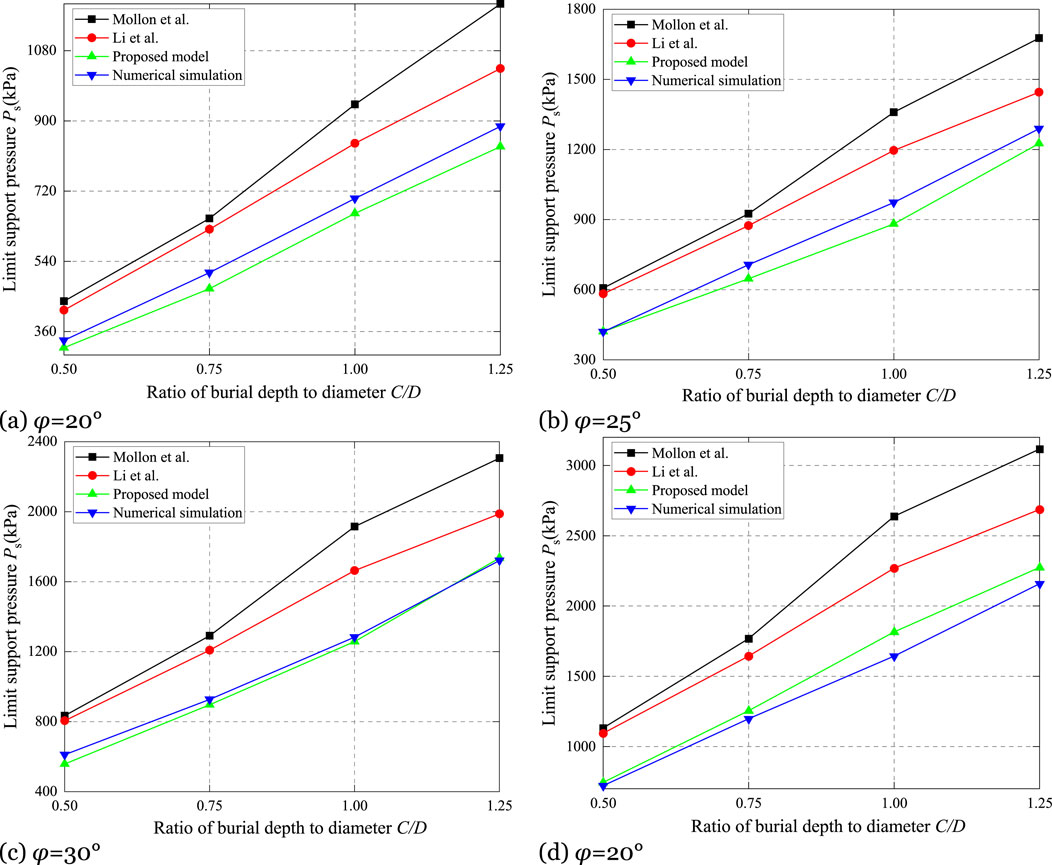
Figure 9. Comparison of proposed model with other models under different C/D. (A)
Figure 10 presents the variation of the PS predicted by different models with respect to the friction angle at various C/D=0.5,0.75,1.0, and 1.25. It can be observed that the PS calculated by all models increases approximately exponentially with the increase of the internal friction angle. The analytical models proposed by Mollon et al. (2010) and Li P. et al. (2019) exhibit more pronounced trends of change, while the analytical model presented in this study aligns more closely with the numerical model. Numerically, the analytical models by Mollon et al. (2010) and Li P. et al. (2019) significantly exceed the predictions of the numerical model, whereas the analytical model of this study is more in agreement with the numerical model. Specifically, when C/D=0.5, the maximum differences between the analytical models proposed by Mollon et al. (2010), Li P. et al. (2019), and the numerical solution presented in this study are 44%, 39%, and 9%, respectively; when C/D=0.75, these differences are 39%, 37%, and 8.5%, respectively; when C/D=1.0, the maximum differences are 60%, 38%, and 9.4%, respectively; when C/D=1.25, the maximum differences are 44%, 17%, and 6%, respectively.
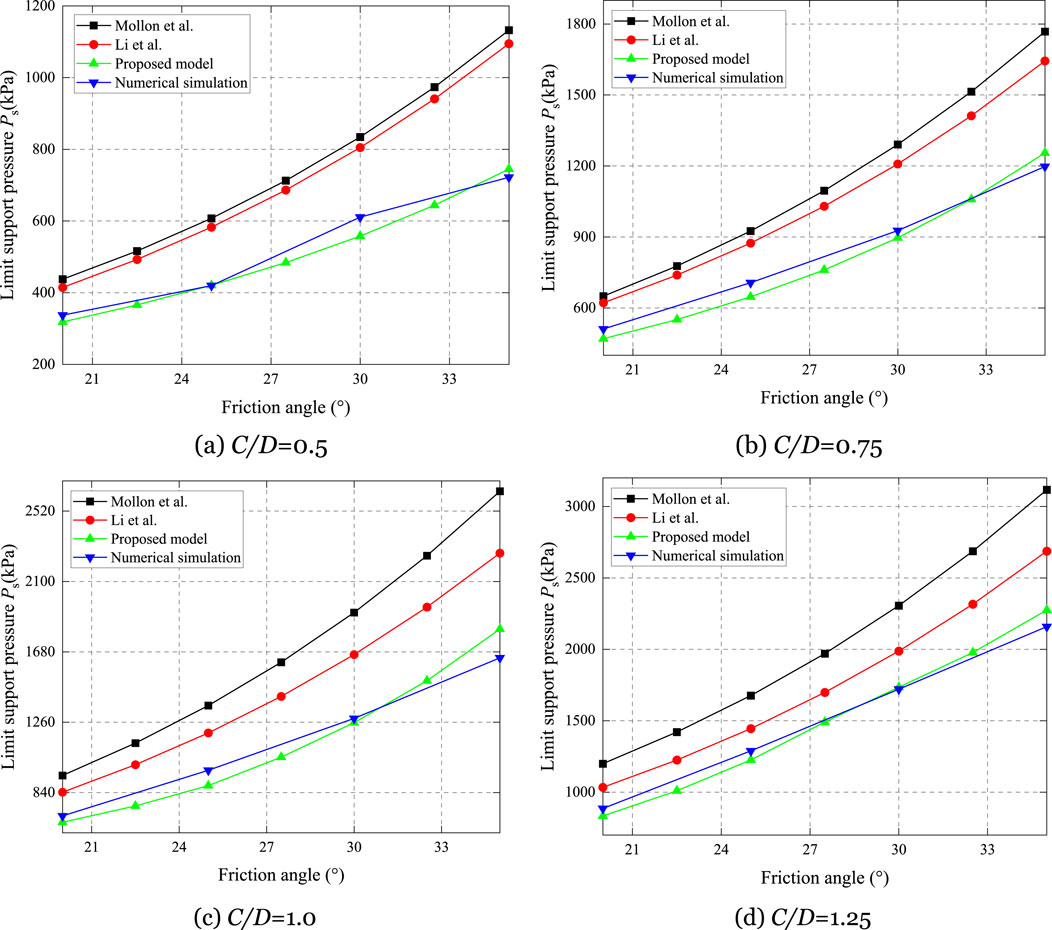
Figure 10. Comparison between the proposed model and the existing model under different φ. (A) C/D=0.5. (B) C/D=0.75. (C) C/D=1.0. (D) C/D=1.25.
In engineering, sandy soil layers often contain fine particles such as clay, which confer a certain degree of cohesion to the soil. Typically, the cohesion of sandy soil layers ranges from 0 to 5 kPa. Figure 11 shows the trend of PS with cohesion derived from various models. It can be observed that the limit support pressure predicted by all models increases linearly with cohesion, and the slopes of the trends are similar across models. The model proposed by Li P. et al. (2019) accounts for the phenomenon of partial instability, and as cohesion increases, the mode of tunnel instability transitions from local to global instability. Consequently, the models proposed by Mollon et al. (2010) and Li P. et al. (2019) exhibit intersecting trends with increasing cohesion. In terms of numerical values, the values of the limit support pressure is as follows: the analytical solution by Mollon et al. (2010) > the analytical solution by Li P. et al. (2019) > the numerical solution > the analytical solution presented in this study. For passive instability, the proposed model is more favorable for ensuring engineering safety.
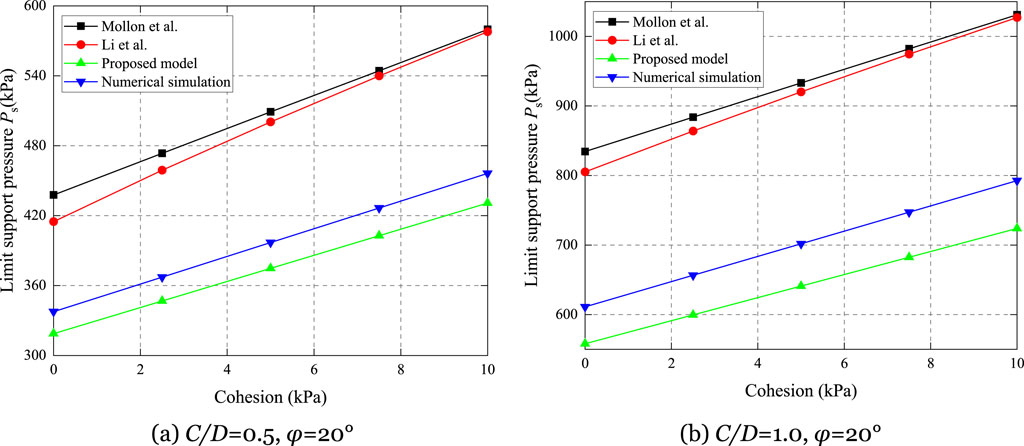
Figure 11. Comparison between the proposed model and the existing model under different cohesion c. (A) C/D=0.5,
4.2 Comparison with model test results
Table 2 presents a comparison between the analytical solution proposed in this study and the results of model tests (Qian et al., 2023b). The material used in the model tests was sandy soil with an internal friction angle of φ = 34∘ and cohesion c = 0 kPa. For ease of comparison, the support pressure was non-dimensionalized using the support pressure ratio PT/γD. It can be observed that under Case 1, the analytical solution presented in this study is approximately 18% less than the experimental results; under Case 2, the analytical solution is very close to the experimental results, with a difference of only 2.4%. Upon comparison, it is found that the limit support pressure predicted by the model proposed in this study is smaller than that of the model test results, which is more advantageous for engineering construction.
In summary, through comparison with existing classical and numerical models, it has been found that the analytical solution proposed in this paper is more consistent with the numerical model results and significantly lower than the predictions of other analytical models, providing greater safety for engineering applications. Additionally, it has been observed that when the φ and the C/D are relatively large, the upper failure zones predicted by the analytical models proposed by Mollon et al. (2010) and Li P. et al. (2019) are significantly larger than the actual failure zones, leading to an overestimation of the PS. In contrast, the analytical model presented in this paper overcomes this drawback and more accurately describes the phenomenon of passive failure zones in shallowly buried sandy strata.
5 Failure zone
The geometry and scope of the failure zone clearly visualize the instability mechanism of the excavation face. This section primarily analyzes the effect of the φ, the c, and the C/D on the failure zone, and elucidates their influence on the blow-out of the excavation face.
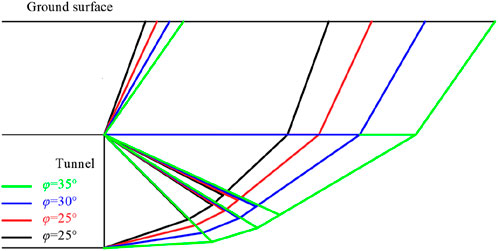
5.1 Effect of friction angle on the failure zone
Figure 12 clearly demonstrates the influence of the φ on the area of the damage zone. The observations indicate that the lower part of the failure zone consists of a sliding mass composed of three truncated cones, while the upper part takes the shape of a truncated cylinder. As the φ increases, the failure zone becomes flatter, expanding its range of influence and consequently enlarging the upper part of the failure zone. According to the theory of limit analysis, the internal friction angle significantly affects the internal dissipated work. For an equivalent volume of the failure zone, the greater the φ, the larger the amount of work dissipated, and thus the greater the required support force. In summary, the φ influences the PS in two ways: firstly, an increase in the φ leads to an expansion of the failure zone; secondly, an increase in the internal friction angle results in a greater dissipated power along the boundary of the failure zone. Therefore, the ultimate support force exhibits exponential growth with the increase of the φ.
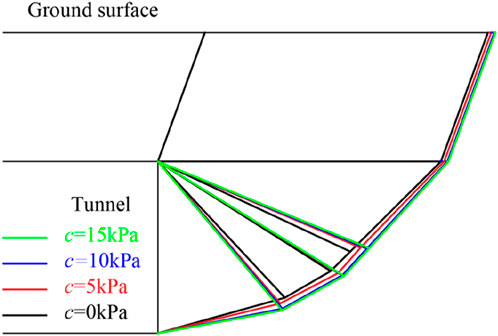
5.2 Effect of cohesion on the failure zone
Figure 13 clearly illustrates the shape of the failure zone under conditions of cohesion of 0 kPa, 5 kPa, 10 kPa, and 15 kPa. It can be observed that the magnitude of cohesion has a negligible effect on the geometry and scope of the failure zone, with the boundaries of the four cases nearly overlapping. Analysis of Equation 26 reveals that the dissipated energy due to cohesion primarily occurs along the boundaries of the failure zone. When the geometry and scope of the failure zone are consistent, the limit support pressure is directly proportional to the magnitude of cohesion. This explanation also accounts for the phenomenon observed in Figure 11, where the ultimate support pressure increases linearly with cohesion under otherwise identical conditions.
5.3 Effect of C/D on the failure zone
Figure 14 demonstrates the impact of the C/D on the failure zone. Observations indicate that the C/D has a negligible effect on the geometry and scope of the failure zone’s lower section. However, as the C increases, the scope of the upper failure zone gradually expands. The expansion of the upper region of failure results in an increased requirement to perform work against gravity, and concurrently, the internal dissipated work along the boundaries of the failure zone also increases. As shown in Figure 9, when the C/D ≤ 1.25, the support pressure increases approximately linearly with the increase in the cover-to-depth ratio. In this scenario, due to the relatively small C/D, the gravitational force of the soil plays a dominant role. As the C/D increases further, the effects of frictional force and cohesion along the boundaries of the failure zone become increasingly pronounced. Consequently, the limit support pressure exhibits a nonlinear increase with the increase in the C/D.
6 Engineering application
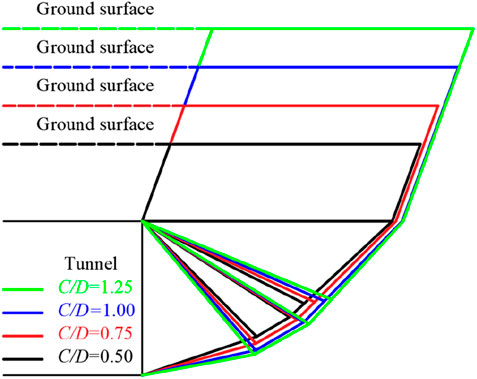
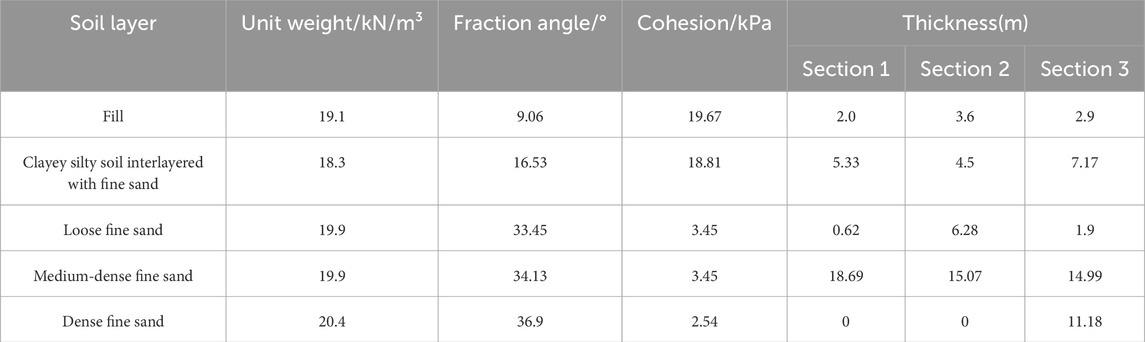
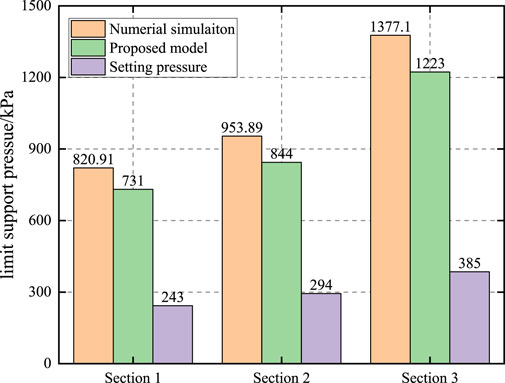
The river-crossing tunnel, spanning 2,350 m in length, is constructed using the shield tunneling method with a tunnel diameter of 15 m. During the initial phase, the depth of burial is relatively shallow, with the minimum depth reaching only 0.76 times the diameter (D). An excessively high setting of the slurry chamber pressure could easily trigger ground uplift. To safeguard the project’s safety, this model and numerical simulation techniques have been employed to calculate the corresponding passive limit support pressure, serving as an early warning value. Table 3 presents the burial depth, soil layer parameters, and other relevant data for three typical cross-sections selected for analysis.
For computational convenience, the stratified soil is treated as equivalent homogeneous soil layers. The equivalent unit weights for Sections 1–3 are 19.52 kN/m³, 19.56 kN/m³, and 19.68 kN/m³, respectively; the equivalent friction angles are 28.71°, 28.23°, and 29.69°; and the equivalent cohesion are 7.74 kPa, 7.78 kPa, and 7.3 kPa, respectively. These values are substituted into the analytical model to obtain the limit support pressure for the three sections: 731 kPa, 844 kPa, and 1,223 kPa. Figure 15 presents a comparison between the analytical solutions, numerical solutions, and actual tunnel pressure settings for the three sections. It is observed that the numerical solutions for Sections 1–3 are approximately 12.3%, 13.02%, and 12.6% higher than the analytical solutions, respectively. For passive instability conditions, a lower passive limit support pressure is more favorable for the project. The minimum value of 731 kPa from the three sections is taken as the upper limit for the support pressure.
7 Conclusion
This paper presents a study on the passive failure of the tunnel face during shield tunneling in shallow, cohesionless soil layers by integrating numerical simulation, theoretical analysis. The main conclusions drawn from the study are as follows:
(1) Simulation results indicate that the Ps required at the tunnel face during shield tunneling in shallow soil is linearly related to the C/D and the tangent of friction angle. Upon passive instability at the excavation face, the failure zone can be delineated into a lower rigid wedge-shaped core and an upper truncated cylindrical passive zone. The area of the failure zone is closely related to the soil’s internal friction angle, with larger angles corresponding to larger failure zones.
(2) Based on the numerical simulation findings, this study proposes a wedge-shaped + truncated cylindrical tunnel face passive instability model and derives the corresponding PS using the theory of limit analysis method. The reliability and accuracy of the model proposed in this paper are verified by comparing it with numerical models and classical analytical models.
(3) Compared with existing classical and numerical models, the analytical solution presented in this paper is more consistent with numerical models and significantly lower than other analytical models, providing greater safety assurance for engineering applications. It is also found that the analytical models proposed by Mollon et al. and Li et al. predict an upper failure zone that significantly exceeds the actual failure area when the φ and C/D are large, leading to an overestimation of the PS. The proposed analytical model overcomes this deficiency and more accurately describes the phenomenon of passive failure zones in shallow sandy strata.
(4) Further research on the failure zone reveals that the φ affects the failure zone in two main ways: firstly, an increase in the φ leads to an increase in the scope of the failure zone; secondly, as the internal friction angle increases, the dissipated power along the boundary of the failure zone also increases. Consequently, the PS increases exponentially with the φ. Additionally, the cohesion has little effect on the geometry and scope of the failure zone. However, when the geometry and scope of the failure zone are the same, the Ps is directly proportional to the value of the cohesion. The C/D has little effect on the geometry and scope of the lower failure zone, but as the depth of burial increases, the scope of the upper failure zone gradually enlarges. When the C/D is small, the gravitational force of the soil plays a dominant role. As the C/D increases, the effects of frictional force and cohesion along the boundary of the failure zone become more pronounced.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.
Author contributions
Y-XS: Conceptualization, Writing–original draft. B-PX: Data curation, Writing–review and editing. Q-GD: Formal Analysis, Writing–review and editing. F-NW: Investigation, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the National Natural Science Foundation of China (No. 51874207), National Natural Science Foundation of China—Railway Fundamental Research Joint Fund Project (U2468219), Shanxi Basic Research Program (202303021212371), the Natural Science Foundation of Shanxi Province (Nos 202303021211042, 202303011222006, and 202303021212371) and China Railway 12th Bureau Group Co., Ltd. Technology Research and Development Plan Project (2024-01).
Conflict of interest
Authors Y-XS and F-NW were employed by Shanxi Transportation Technology Research and Development Co., Ltd. Author Q-GD was employed by China Railway 12th Bureau Group Co., Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, M., and Iskander, M. (2012). Evaluation of tunnel face stability by transparent soil models. J. Tunn. Undergr. Sp. Tech. 27 (1), 101–110. doi:10.1016/j.tust.2011.08.001
Anagnostou, G., and Kovári, K. (1996). Face stability conditions with earth-pressure-balanced shields. J. Tunn. Undergr. Sp. Tech. 11 (2), 165–173. doi:10.1016/0886-7798(96)00017-x
Bezuijen, A., and Brassinga, H. E. (2020). Blow-out pressures measured in a centrifuge model and in the field. Boca Raton, US: CRC Press.
Broere, W. (2002). Tunnel face stability and new CPT applications. Delft, Netherlands: Delft University Press.
Chambon, P., and Corte, J. F. (1994). Shallow tunnels in cohesionless soil: stability of tunnel face. J. J. Geotech. Eng. 120 (7), 1148–1165. doi:10.1061/(asce)0733-9410(1994)120:7(1148)
Chen, R. P., Li, J., Kong, L. G., and Tang, L. J. (2013). Experimental study on face instability of shield tunnel in sand. J. Tunn. Undergr. Sp. Tech. 33, 12–21. doi:10.1016/j.tust.2012.08.001
Han, K., Zhang, C., Li, W., and Guo, C. (2016). Face stability analysis of shield tunnels in homogeneous soil overlaid by multilayered cohesive-frictional soils. J. Math. Probl. Eng. 2016, 1–9. doi:10.1155/2016/1378274
Horn, N. (1961). “Horizontal earth pressure on the vertical surfaces of the tunnel tubes,” in National conference of the Hungarian civil engineering industry. Budapest, 7–16.
Juneja, A., Hegde, A., Lee, F., and Yeo, C. (2010). Centrifuge modelling of tunnel face reinforcement using forepoling. J. Tunn. Undergr. Sp. Tech. 25 (4), 377–381. doi:10.1016/j.tust.2010.01.013
Kamata, H., and Mashimo, H. (2003). Centrifuge model test of tunnel face reinforcement by bolting. J. Tunn. Undergr. Sp. Tech. 18 (3), 205–212. doi:10.1016/s0886-7798(03)00029-4
Kirsch, A. (2010). Experimental investigation of the face stability of shallow tunnels in sand. J. Acta Geotech. 5, 43–62. doi:10.1007/s11440-010-0110-7
Leca, E., and Dormieux, L. (1990). Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. J. Géotechnique 40 (4), 581–606. doi:10.1680/geot.1990.40.4.581
Li, P., Chen, K., Wang, F., and Li, Z. (2019a). An upper-bound analytical model of blow-out for a shallow tunnel in sand considering the partial failure within the face. J. Tunn. Undergr. Sp. Tech. 91, 102989. doi:10.1016/j.tust.2019.05.019
Li, P., Wei, Y., Zhang, M., Huang, Q., and Wang, F. (2022). Influence of non-associated flow rule on passive face instability for shallow shield tunnels. J. Tunn. Undergr. Sp. Tech. 119, 104202. doi:10.1016/j.tust.2021.104202
Li, P., Zou, H., Wang, F., and Xiong, H. (2020). An analytical mechanism of limit support pressure on cutting face for deep tunnels in the sand. J. Comput. Geotech. 119, 103372. doi:10.1016/j.compgeo.2019.103372
Li, W., Zhang, C., Zhu, W., and Zhang, D. (2019b). Upper-bound solutions for the face stability of a non-circular NATM tunnel in clays with a linearly increasing undrained shear strength with depth. J. Comput. Geotech. 114, 103136. doi:10.1016/j.compgeo.2019.103136
Mair, R., Taylor, R., and Bracegirdle, A. (1993). Subsurface settlement profiles above tunnels in clays. Geotechnique 43 (2), 315–320. doi:10.1680/geot.1993.43.2.315
Mollon, G., Dias, D., and Soubra, A. H. (2010). Face stability analysis of circular tunnels driven by a pressurized shield. J. J. Geotech. Geoenviron 136 (1), 215–229. doi:10.1061/(asce)gt.1943-5606.0000194
Mollon, G., Dias, D., and Soubra, A. H. (2011). Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. J. Int. J. Numer. Anal. Methods Geomech. 35 (12), 1363–1388. doi:10.1002/nag.962
Qian, Y., Nie, X., Wu, J., Wang, Q., Bian, K., and Jing, H. (2023b). Experimental study on unloading induced shear performances of 3D saw-tooth rock fractures. Int. J. Min. Sci. Technol. 33 (4), 463–479. doi:10.1016/j.ijmst.2023.02.002
Qian, Y., Zhu, C., Wu, J., Pu, H., Wang, Q., Zhang, Y., et al. (2023a). Shear sliding of rough-walled fracture surfaces under unloading normal stress. J. Rock Mech. Geotechnical Eng. 15 (10), 2658–2675. doi:10.1016/j.jrmge.2023.02.005
Qiang, S., Zhao, L., Wang, X., Li, X., and Wang, F. (2023). Analysis of face stability for shallow shield tunnels in sand. J. Front. Earth Sci. 11, 1287151. doi:10.3389/feart.2023.1287151
Schofield, A. N. (1980). Cambridge geotechnical centrifuge operations. J. Geotech. 30 (3), 227–268. doi:10.1680/geot.1980.30.3.227
Wu, J. Y., Jing, H. W., Yin, Q., Yu, L., Meng, B., and Li, S. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189
Wu, J. Y., Wong, H. S., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345
Wu, J. Y., Wu, H. W., Gao, Y., Meng, Q., Yin, Q., and Du, Y. (2022). Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. Concr. Compos. 127, 104408. doi:10.1016/j.cemconcomp.2022.104408
Zhang, C., Han, K., and Zhang, D. (2015). Face stability analysis of shallow circular tunnels in cohesive–frictional soils. J. Tunn. Undergr. Sp. Tech. 50, 345–357. doi:10.1016/j.tust.2015.08.007
Zhu, Q., Yin, Q., and Tao, Z. (2024b). “The role of cyclic normal loading conditions on shear mechanical characteristics and instability mechanisms of rough rock joints,” in Journal of rock mechanics and geotechnical engineering, 2024, qi L (2012) study on blow-out face pressure of shield tunnels in sand. Hangzhou, China: Zhejiang University.
Keywords: shallow shield tunnel, sandy stratum, blow-out of tunnel face, limit analysis method, explode
Citation: Shi Y-X, Xi B-P, Di Q-G and Wang F-N (2025) Research on blow-out of shield tunnel in sandy soil with shallow burial. Front. Earth Sci. 12:1522374. doi: 10.3389/feart.2024.1522374
Received: 04 November 2024; Accepted: 27 December 2024;
Published: 23 January 2025.
Edited by:
Jiangyu Wu, China University of Mining and Technology, ChinaReviewed by:
Jian Cao, Inner Mongolia University of Science and Technology, ChinaXinxin Guo, Chengdu University of Technology, China
Copyright © 2025 Shi, Xi, Di and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Feng-Nian Wang, MTA0Mzc5NDYyQHFxLmNvbQ==
 Yong-Xiang Shi
Yong-Xiang Shi Bao-Ping Xi
Bao-Ping Xi Qi-Guang Di
Qi-Guang Di Feng-Nian Wang
Feng-Nian Wang