Envelope and intelligent prediction of horizontal bearing capacity for offshore wind monopiles in sandy seabed under HM combined loading

This study presents a practical finite element model for evaluating laterally loaded monopiles embedded in sandy seabed, verified through comparison with field test data from the PISA project. The classical Mohr-Coulomb model, used for soil plasticity in this study, provides reliable predictions and required parameters that are straightforward to determine, enhancing its utility in engineering practice. The numerical model, combines with an artificial neural network (ANN), provides a feasible approach to predict the bearing capacity of monopiles in offshore wind applications, even under different seabed conditions and combined horizontal (H) and moment (M) loads. Results reveal that the horizontal bearing capacity significantly varies depending on slope direction, with increased capacity in the slope upward direction and decreased capacity in the slope downward direction. An elliptical equation is developed to represent the horizontal bearing capacity envelope in the HM plane, accurately predicting ultimate horizontal force (H_u) and bending moment (M_u) across different length-to-diameter (L/D) ratios and seabed slopes. To further enhance predictive capability, an ANN surrogate model is developed, trained on 288 scenarios. Using L/D ratio, seabed slope, horizontal displacement and rotation angle at the monopile head as inputs, the ANN successfully predicts the horizontal bearing capacity with error margins within ±10%. This research offers a practical, validated finite element and ANN-based approach for modeling and predicting the lateral bearing capacities of monopiles in complex offshore environments, making it a valuable tool for the construction and measurement of offshore wind turbine foundations under HM loading conditions.

1 Introduction

In the fields of geotechnical and offshore engineering, monopiles are favored for their advantages, including simple installation, cost-effectiveness, stability, and high strength and stiffness. These qualities make them particularly effective in withstanding horizontal loads (Xu et al., 2013; Xu et al., 2017a; Xu et al., 2017b). However, in complex offshore environments, under the excitation of wind and earthquake, monopiles are often subjected to combined loads, among which the most common is the combined action of horizontal force H and bending moment M (Raj et al., 2019; Xu et al., 2023a; Xu et al., 2023b; Xu et al., 2023c). The horizontal bearing capacity of monopiles refers to the boundary curve that represents the relation of the maximum lateral loads and bending moments that the monopile can withstand under certain conditions. This boundary reflects the safe bearing limit that a pile foundation can achieve when subjected to horizontal forces. Studying the horizontal bearing capacity envelope of monopile foundations for wind turbines is of great significance. By plotting the envelope, the safe bearing range of the pile under various working conditions can be clearly defined, providing scientific guidance for the design of wind turbine tower foundations.

Rigid piles are widely used for offshore winds. In recent years, scholars in this field have conducted many valuable studies on the horizontal bearing capacity of monopiles. Sawant and Shukla (2012) developed a procedure for evaluating the response of piles to horizontal forces in inclined sites based on the analysis of 3D finite element software. Keawsawasvong and Ukritchon (2020) used finite element method to perform three-dimensional analysis and conducted a comprehensive study and discussion on the effect on cover stress on the bearing capacity of monopiles under undrained conditions under the combined action of lateral load and bending moment load. Shao et al. (2024) discussed the failure envelope of offshore rigid monopiles in undrained clay under lateral and moment loads. Many scholars have also studied the failure envelope of monopiles under the combined action of horizontal force (H), vertical force(V) and bending moment(M). Graine et al. (2021) developed a generalized failure criterion monopiles installed in cohesive soil under combined H-M-V load. Li et al. (2014) conducted numerical simulations using radial displacement method and sliding tests, determined the envelope of failure under H-M-V action, and presented analytical equations that were consistent with the 3D analysis results, which can be used to design and simplify finite element models. Zhao et al. (2024) studied monopile body parameters, load parameters and horizontal bearing capacity of rigid pile groups under the combined action of H-M-V load. For the horizontal bearing capacity of monopiles on slopes. Muthukkumaran (2014) conducted extensive indoor model tests to investigate the effects of slope and load direction on the horizontal bearing capacity and p-y curve of monopiles in non-cohesive soil (Muthukkumaran and Almas Begum, 2015). Jiang et al. (2020) conducted an analysis of the monopiles on non-cohesive soil slopes under composite of loads and derived the balance equation of the pile-soil system based on the moment balance theory Lin et al. (2022) put forward a method to calculate the nonlinear lateral response of monopiles in the sandy seabed under slope effects. From the above research, it can be seen that significant progress has been made in studying the horizontal bearing capacity and bearing capacity envelopes of rigid piles. However, according to present situation, most of these studies focused on the impact of flat ground or slope effects on the lateral response of monopiles, while there are relatively few studies on the influence of micro-inclination in sandy seabed on the horizontal bearing capacity envelope of monopiles.

With the growing maturity of machine learning and AI algorithms, their application in geotechnical engineering is also expanding. In recent years, AI algorithms have rapidly developed in the prediction of pile bearing capacity. Das and Basudhar (2006) applied an ANN model to predict the horizontal bearing capacity of monopiles in clay. Muduli et al. (2013) compared the applicability of different AI algorithms in predicting the horizontal bearing capacity of monopiles in clay. Benbouras et al. (2021) demonstrated the effectiveness of deep neural networks in predicting the bearing capacity of driven monopiles. Wang and Heo (2022) studied artificial neural networks (ANNs) using a comprehensive database and found their applicability for alternative modeling. They developed a multilevel neural network with multiple output variables to accurately capture the lateral displacement and moment responses of offshore wind turbine monopiles under different hazardous conditions such as earthquakes, wind, and waves. Taherkhani et al. (2023) established a surrogate model based on a hybrid neural network for predicting the horizontal bearing capacity of monopiles in sandy soil. It can be seen that AI algorithms have broad prospects, but their training requires a large amount of data. This paper will further extend the application of AI algorithms to predict the horizontal bearing capacity of monopiles in the slightly inclined sandy seabed.

In this study, a practical finite element model for a laterally loaded monopile in sand is proposed, requiring fewer input parameters while maintaining accuracy. The soil is modeled using the Mohr-Coulomb constitutive model, which allows for easy determination of soil parameters. The numerical model is validated using field test results from the Pile Soil Analysis (PISA) project, confirming its applicability for monopiles at different embedment depths. The effect of seabed slope angle and length-to-diameter ratio on the load-displacement curve, equivalent plastic strain around the pile, and bearing capacity envelope is analyzed. Finally, an artificial neural network (ANN)-based surrogate model is developed to predict the ultimate horizontal load and bending moment of monopiles. The surrogate model is trained and validated using 288 cases. For small datasets like this, ANNs can automatically identify and learn key features in the data and construct reliable predictive models. This significantly reduces workload and saves time in marine geotechnical engineering.

2 Finite element model

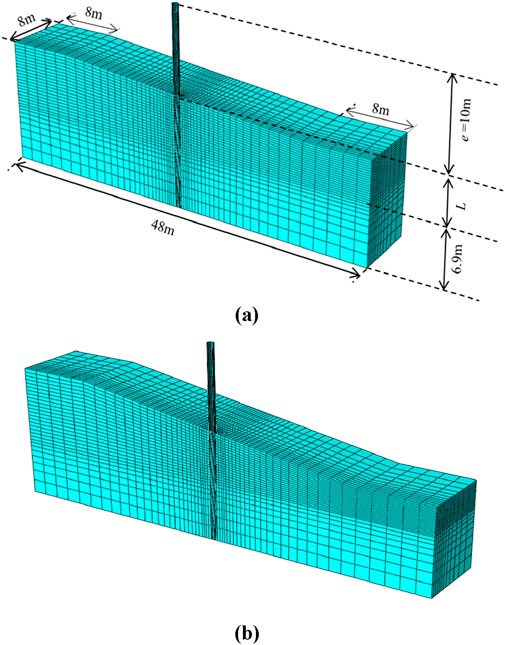
In this study, the finite element model is developed based on the field test in the Pile–Soil Analysis (PISA) project. Figure 1A presents a schematic diagram of the monopile model under horizontal loading from the PISA project (Zdravković et al., 2020). The PISA project focused on the evaluation and improvement of monopile foundations for offshore wind turbines by developing advanced methods to predict pile-soil interactions under lateral load. The project is primarily divided into three components: 1) Conducting field tests on a scaled-down monopile, 2) Developing a novel design method for single piles, and 3) Creating a three-dimensional finite element model to simulate the behavior of each monopile configuration. The monopile is a hollow steel pipe pile, and its geometric properties are shown in Table 1. Since this study uses a symmetric model, the load applied at the top of the monopile is half of the total load. Numerical simulations were conducted on monopiles subjected to horizontal loading in sandy soil, with three working conditions in total, where the length-to-diameter ratios (L/D) vary across different conditions (see Table 1).

Figure 1

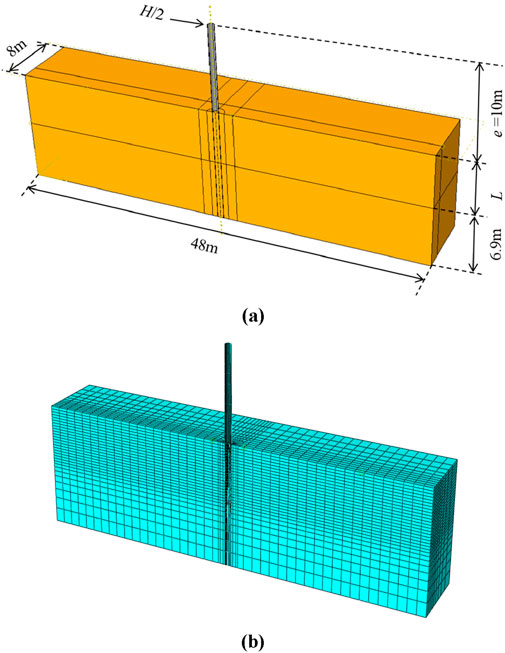
Figure 1. Finite element model for laterally loaded piles: (A) Configuration of the test and (B) Typical finite-element mesh for L/D = 8.

Table 1

Table 1. Geometric characteristics of piles.

Figure 1B shows the 3D finite element model of pile-soil interaction created using Abaqus software (Dassault Systèmes, 2014), with the monopile and soil modeled using C3D8 elements. The monopile is assumed to be a purely elastic material, the pile and soil are in frictional contact, and the elastic-plastic behavior of the sand is described by the modified Mohr-Coulomb model. The lateral boundary is horizontally constrained, while the bottom boundary is fixed. The upper boundary is entirely free, and the displacement loading is applied to the monopile at a height of 10 m above the ground. As reported by Xu et al. (2023b), Xu et al. (2023c), the mesh size around the monopile was refined to 0.1 times its diameter. Furthermore, when the finite element mesh size was halved and the simulation was repeated, the results deviated by less than 3% from those of the original model, confirming that the mesh size adopted in this study ensures adequate calculation accuracy.

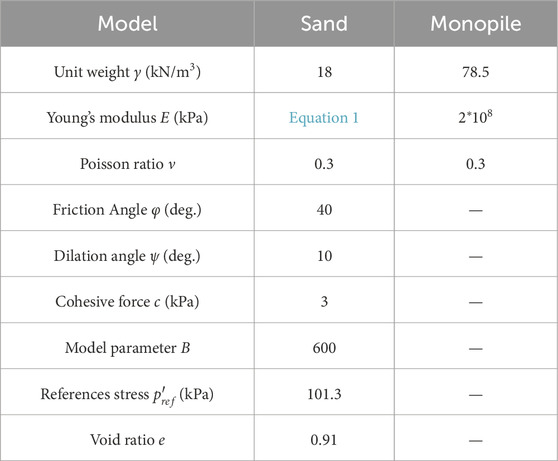
The input parameters of monopiles and soil are shown in Table 2. According to the triaxial compression experiment of sand, the friction angle (φ) is 40°, and the shear expansion angle ($\psi$) is estimated according to the formula $\psi =\phi -30°$ (Tatsuoka, 1993). Young’s modulus (E) is derived from Equations 1, 2.

$E=2\left(1+2\nu \right)G_0(1)$

where $\nu$ is Poisson’s ratio and $G_0$ is the shear modulus (Hardin and Black, 1968)

$G_0=\frac{B{p}_{ref}^{\prime }}{0.3+0.7e^2}\sqrt{\frac{p^{\prime }}{p_{ref}^{\prime }}}(2)$

where B is the model parameter.

Table 2

Table 2. Parameters of the pile–soil system.

Figure 2 compares the simulated the horizontal force (H) -ground-level horizontal displacement (y₀) curves with the measured data from the PISA project. Analysis shows that under the condition of different L/D, simulation curves are in good agreement with the experimental results. Taborda et al. (2020) used an advanced constitutive model based on sand state to simulate the load-displacement curves of monopiles at different embedment depths. Figure 2 also compares the simulation results with those of Taborda et al. (2020), showing that the difference between the simulations and those predicted by Taborda et al. (2020) was minimal for L/D = 8 and L/D = 5.25. However, for L/D = 3, the simulation results in this study were closer to the experimental data than those of Taborda et al. (2020). This indicates that the 3D finite element model established in this study has sufficient accuracy to evaluate the effects of different pile embedment lengths. Furthermore, this study utilizes a finite element model based on the Mohr-Coulomb constitutive model, which simplifies the acquisition of soil parameters and offers greater benefits for practical engineering applications. As a result, the model is referred to as a practical finite element model.

Figure 2

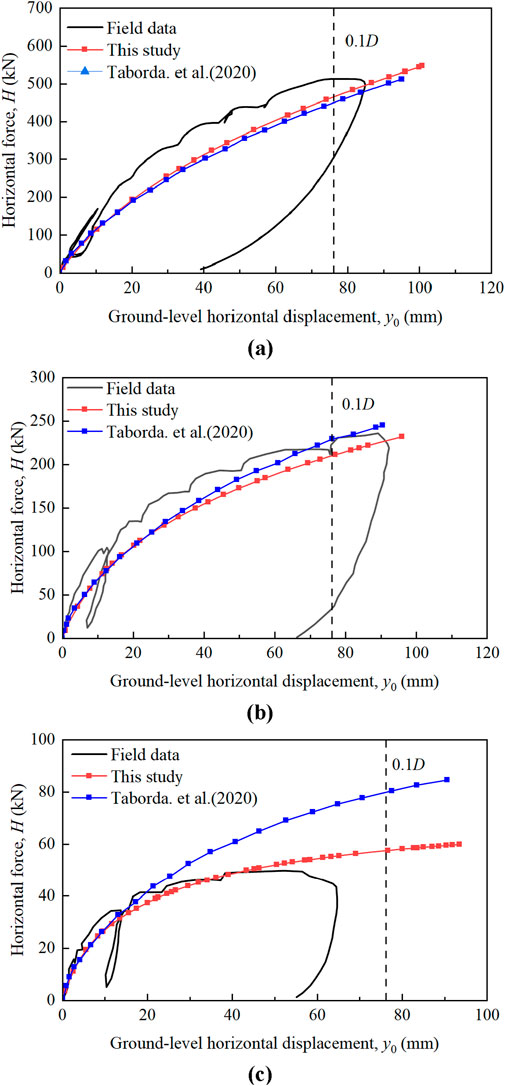
Figure 2. Comparison of horizonal force-displacement curves of monopile measured and simulated by finite element method (A) L/D = 8; (B) L/D = 5.25; and (C) L/D = 3.

3 Discussions on various influential factors

This section explores the influence of L/D and seabed slope angle (α) on the H-y₀ curve of OWT monopiles, equivalent plastic strain around the pile, and the bearing capacity envelope. In this study, the L/D of monopiles was taken as 3, 5.25, and 8, as designed from the PISA project. The seabed was assumed to have a slight incline, with slope angles of 5° and 10°. The seabed slope angle was altered based on the flat seabed in the test of the PISA project. Figures 3A, B show the finite element mesh for α = 5° and α = 10°, respectively.

Figure 3

Figure 3. Finite element mesh with different slope angles: (A) 5° and (B) 10° (L/D = 8).

3.1 Effect of slope angle (α) of the seabed

The change in slope angle also impacts the bearing capacity of the monopile, which is analyzed in this study. Figure 4 shows the effect of α on the H-y₀ relationship. In the slope downward direction. Note that only H was applied at the mudline in Figure 4. The ultimate horizonal force (H_u) decreased as the slope angle increased, primarily because of the reduction in effective stress in the soil downstream of the monopile as the slope angle increases, where H_u was defined when the monopile’s horizontal displacement at the mudline reaches 0.1D. When α rose from 0° to 5° and 10°, the H_u of the monopile decreased by1% and 6%, respectively. However, in the slope upward direction, the horizontal bearing capacity increased with increasing slope angle. When α increased from 0° to 5° and 10°, the horizontal bearing capacity increased by 17% and 35%, respectively. This demonstrates that the slope angle had a greater impact on the horizontal bearing capacity in the slope upward direction compared to the slope downward direction.

Figure 4

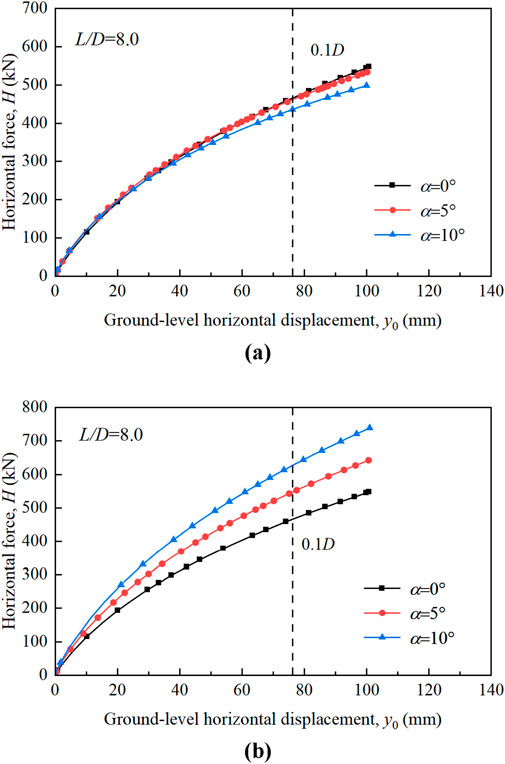
Figure 4. Effect of slope angle on the H-y₀ curve of monopiles: (A) slope downward direction; (B) slope upward direction (L/D = 8).

To provide a more intuitive comparison of the effects of slope angles, Figure 5 illustrates the effect of slope angle on the equivalent plastic strain around the monopile when the horizontal displacement of monopile at the mudline is 0.1D. Overall, the equivalent plastic strain (ε_p) was localized primarily in the shallow layers of the seabed. Noticeable ε_p also occurred at the monopile tip, mainly due to the monopile rotation under lateral loading. Additionally, in the slope downward direction, the slope angle had little effect on the distribution of the ε_p around the monopile. However, in the slope upward direction, the distribution of ε_p around the monopile decreased as α increased.

Figure 5

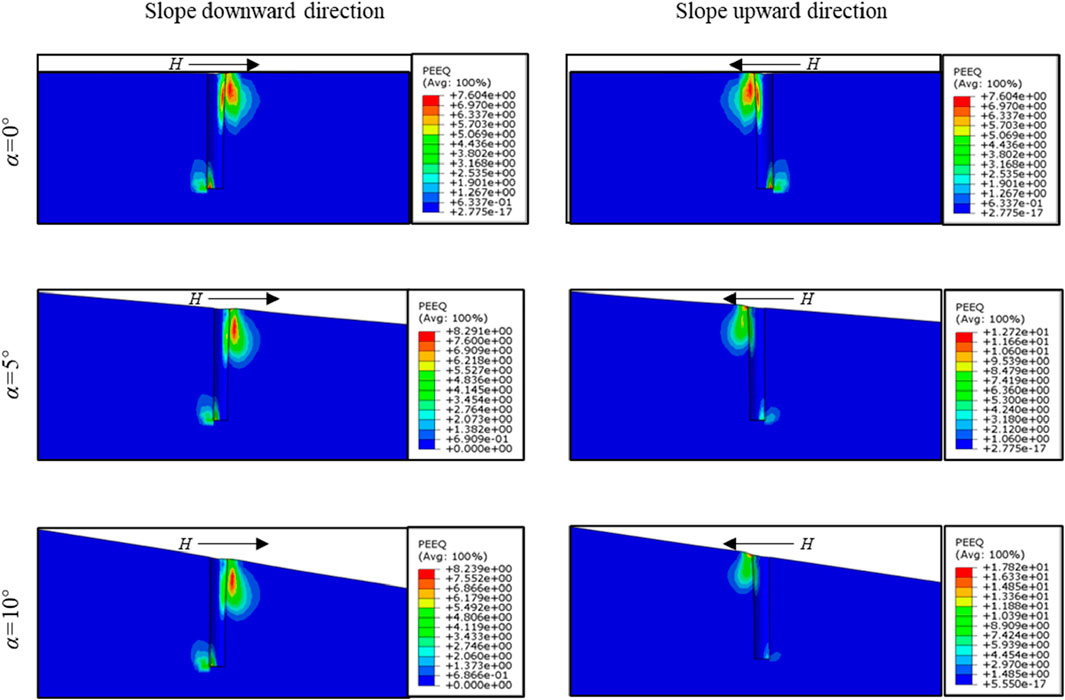
Figure 5. Effect of slope angle on the equivalent plastic strain surrounding the monopiles at the slope downward and slope upward directions (L/D = 8).

3.2 Effect of L/D

Figure 6 illustrates the effect of the L/D on the H-y₀ curves of monopiles in the gently sloping sandy seabed. It can be seen that, in both the slope downward direction and the slope upward direction, H_u increased as L/D increased. When L/D increases from 3 to 5.25 and 8, H_u increases by 2.7 and 7.2 times in the downslope direction, respectively, and by 2.7 and 6.5 times in the upslope direction, respectively. This is primarily because the increased pile length restricted the rotation at the monopile tip. Additionally, the increase in the H_u is more pronounced in the slope upward direction.

Figure 6

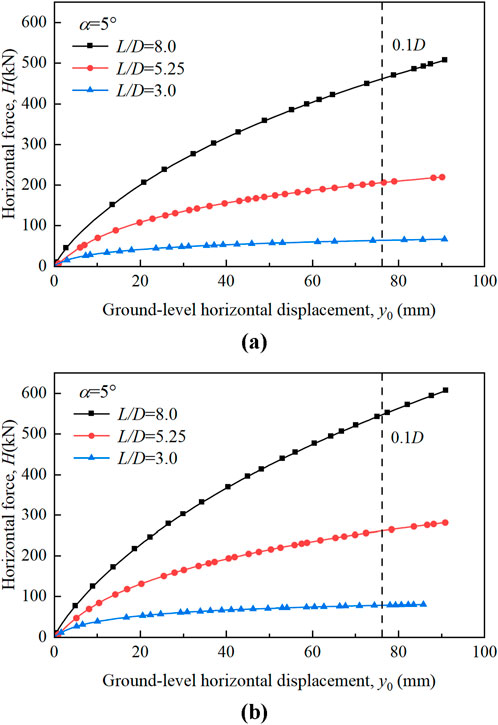
Figure 6. Effect of L/D on the H-y₀ curve of monopiles: (A) slope downward direction; (B) slope upward direction (α = 5°).

Similarly, to directly demonstrate the influence of L/D, Figure 7 illustrates the effect of the L/D ratio on the ε_p around the monopile when the horizontal displacement of monopile at the mudline is 0.1D. Generally, the ε_p around the monopile increased as the L/D decreased, primarily because the monopile’s rotation angle grew with decreasing the L/D.

Figure 7

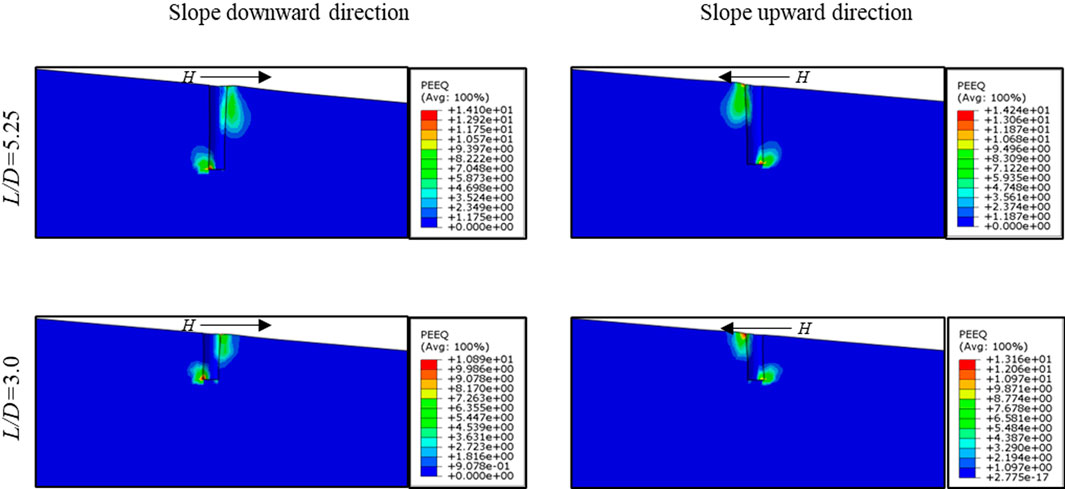
Figure 7. Effect of L/D on the equivalent plastic strain surrounding the monopiles at the slope downward and slope upward directions (α = 5°; see L/D = 8 in Figure 5).

3.3 Horizontal bearing capacity envelope of monopiles in the HM plane

Offshore wind monopiles are mainly subjected to combined HM loading caused by wind and waves. Horizontal bearing capacity envelope provide an efficient tool of the design of monopiles and is therefore investigated in HM plane in this study. Figure 8 defines the positive direction for H and M acting on the monopile in both flat and sloping seabed. The H applied in the slope downward direction (positive X-axis) is considered positive, as is the M that moves the monopile head in the same direction.

Figure 8

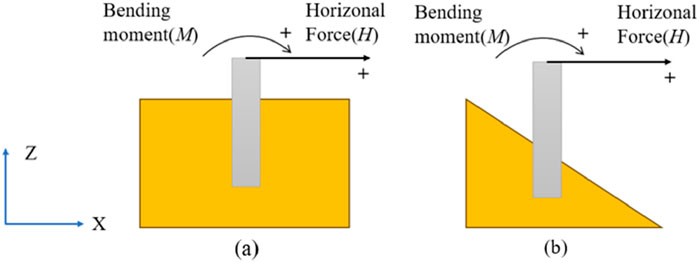
Figure 8. Sign definition for H and M force applied to the monopile: (A) flat seabed and (B) sloping seabed.

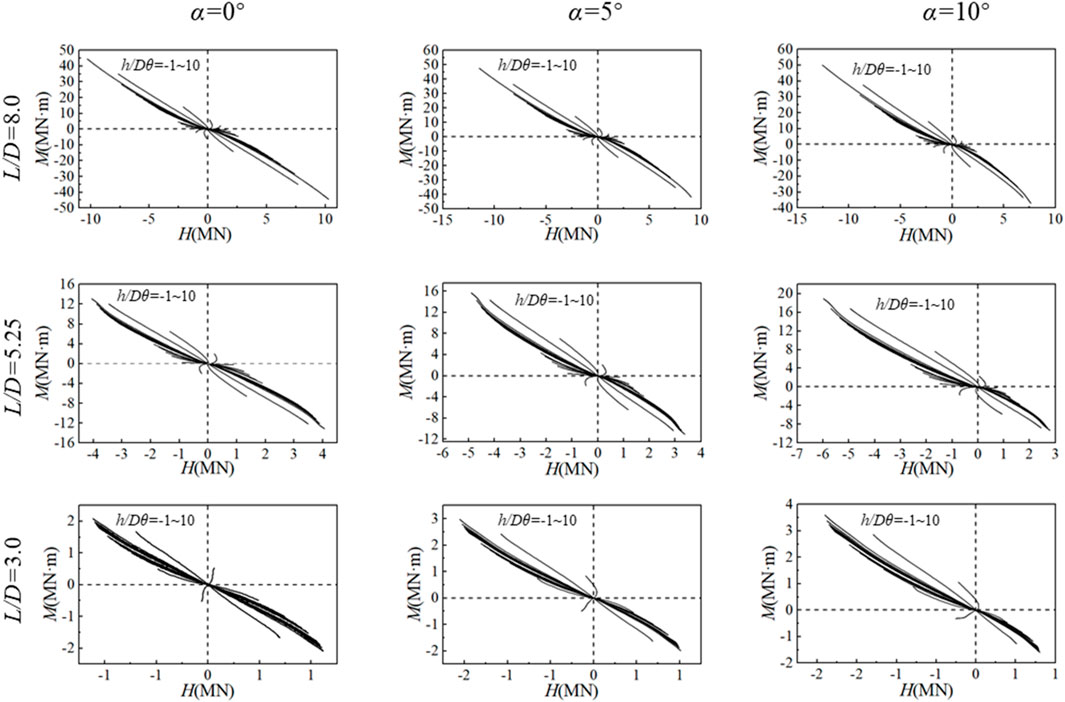
In this study, the horizontal bearing capacity, including the ultimate lateral load (H_u) and ultimate bending moment (M_u), was determined by applying both horizontal displacement (h) and rotation (θ) at the mudline. During the loading process, the ratio h/Dθ remains constant, and by adjusting this ratio, the horizontal bearing capacity under different H-M load combinations was obtained, enabling the construction of a horizontal bearing capacity envelope.

Figure 9 presents the load path for monopiles under various L/D and slope angle (α) combinations, with nine sets of conditions. Each set covers a range of h/Dθ values from −1 to 10, resulting in 32 load cases per set and 288 total cases. For the flat seabed (α = 0°), the load paths under different H-M combinations exhibited central symmetry. Additionally, as L/D increased, the rise in M_u was more pronounced than the increase in the H_u. In contrast, monopile load paths on the gently sloping seabed lost this symmetry due to the difference in the horizontal bearing capacity between the slope downward direction and the slope upward direction (refer to Figures 4, 6). As the slope increased, it is observed that the H_u and M_u increased in the second quadrant, while they gradually decreased in the fourth quadrant. This is because, in the second quadrant, the horizontal displacement was generally applied in the upward slope direction, whereas in the fourth quadrant, it was applied in the downward slope direction. This result was also confirmed in Figure 5.

Figure 9

Figure 9. Loading paths of laterally loaded monopiles for varying L/D and α.

3.4 Theoretical analysis of the horizontal bearing capacity envelope of monopiles in the HM plane

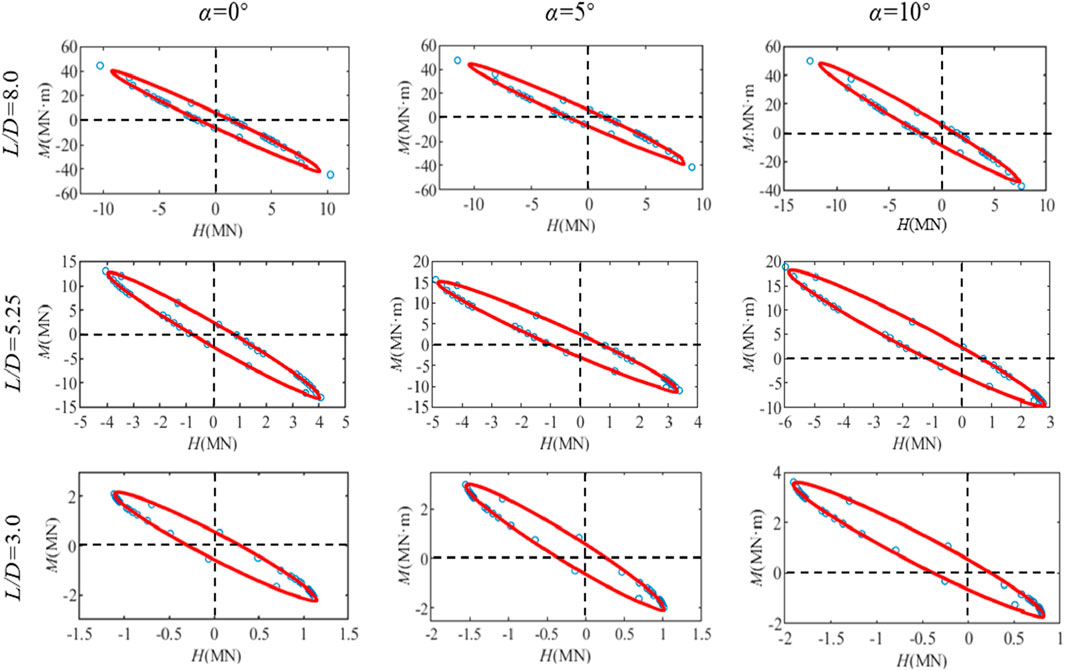
Figure 10 shows that the envelope of the monopile’s horizontal bearing capacity forms an inclined elliptical shape. To confirm this observation, we used a general elliptical equation (i.e., Equation 3) to fit various H_u - M_u data points:

$C_1{H}_{\mathrm{u}}^2+C_2{H}_{\mathrm{u}}{M}_{\mathrm{u}}+C_3{M}_{\mathrm{u}}^2+C_4{H}_{\mathrm{u}}+C_5{M}_{\mathrm{u}}+1=0(3)$

where C₁, C₂, C₃, C₄, and C₅ are constants controlling the shape of the ellipse. These five constants help define the coordinates of the ellipse’s center (H₀, M₀), with R₁ and R₂ representing the lengths of the ellipse’s major and minor axes, respectively, and ψ representing the rotation angle of the major axis. H₀, M₀, R₁, R₂, and ψ were given in Equation 4:

$\left\{\begin{array}{l}{H}_0=\frac{C_2{C}_5-2C_3{C}_4}{4C_1{C}_3-C_2^2}\\ M_0=\frac{C_2{C}_4-2C_1{C}_5}{4C_1{C}_3-C_2^2}\\ R_1=\sqrt{\frac{2\left(C_1{H}_0^2+C_3{M}_0^2+C_2{H}_0{M}_0-1\right)}{C_1+C_3+\sqrt{{\left(C_1-C_3\right)}^2+C_2^2}}}\\ R_2=\sqrt{\frac{2\left(C_1{H}_0^2+C_3{M}_0^2+C_2{H}_0{M}_0-1\right)}{C_1+C_3-\sqrt{{\left(C_1-C_3\right)}^2+C_2^2}}}\\ \psi =\frac{1}{2}\arctan \left(\frac{C_2}{C_1-C_3}\right)\end{array}\right.(4)$

Figure 10

Figure 10. Failure envelope of lateral bearing capacities of monopiles.

Figure 10 shows that the elliptical equation effectively described the relationship between H_u and M_u of laterally loaded piles under varying L/D, slope angle α, and h/Dθ. Figures 11A–C further illustrate the effect of L/D and α on R₁, R₂, and ψ, respectively. It can be seen that as L/D increased, both R₁ and R₂ increased. This is because the H_u and M_u increased with L/D. Additionally, the α had little effect on the R₁ likely because the increase in the horizontal bearing capacity in the second quadrant was nearly equal to the decrease in the fourth quadrant for the sloping seabed. However, the seabed slope angle had a more significant impact on R₂. This can be attributed to the fact that when H is applied in the slope upward direction, the increase in H_u was greater than the increase in M_u, causing the fitted ellipse to expand outward. This trend became more pronounced as α and L/D increased, indicating that under this load combination, the slope angle had a larger impact on the ultimate horizontal load than on the ultimate moment.

Figure 11

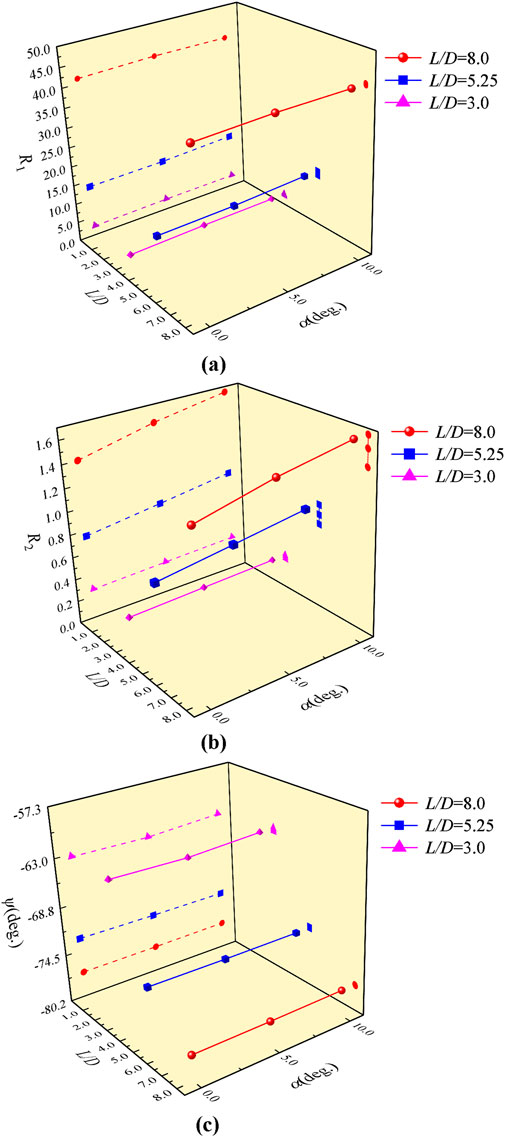
Figure 11. Effect of L/D and α on the dominating parameters of the ellipse of lateral bearing capacities of monopiles: (A) the length of the major axis (R₁), (B) the length of the minor axis (R₂), and (C) the rotation angle of the major axis (ψ).

4 Intelligent prediction of the horizontal bearing capacity of monopiles

This paper introduces an artificial neural network (ANN) as a surrogate model to predict the ultimate horizontal load and ultimate moment of monopiles. Inspired by biological neural systems, ANNs are computational models commonly used for complex tasks such as data classification, regression, and prediction. These models simulate how information is transmitted between neurons in the brain, with adaptive learning abilities that enable them to adjust internal parameters during training to match input data. For a simple feedforward neural network, as illustrated in Figure 12, the output of the ith hidden neuron h_i is described by Equation 5:

$h_i=\sigma \left({\displaystyle \sum _j^m}{w}_j\cdot x_j+b\right)(5)$

where w_j represents the regression coefficient for the jth node in the previous layer (e.g., input node x_j in Figure 12), m is the number of nodes in pervious layer, b is the bias term, and σ is the activation function that introduces nonlinearity into the network. ReLU was taken as the activation function in this study. Neural network modeling fundamentally involves calculating the regression coefficients and bias terms between layers. The coefficients were determined using stochastic gradient descent (Amari, 1993) by minimizing the loss function within a certain tolerance. In this study, Mean Squared Error (MSE) was used as the loss function in Equation 6:

$MS{E}^{\left(s\right)}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(y_i^{\left(s\right)}-{\widehat{y}}_i^{\left(s\right)}\right)}^2(6)$

where $y_i^{\left(s\right)}$ and ${\widehat{y}}_i^{\left(s\right)}$ are the observed and predicted values, respectively, with i representing the ith data point in a total of n data points. For neural networks with multiple output nodes, the overall loss function is the sum of ${MSE}^{\left(s\right)}$ across all outputs.

Figure 12

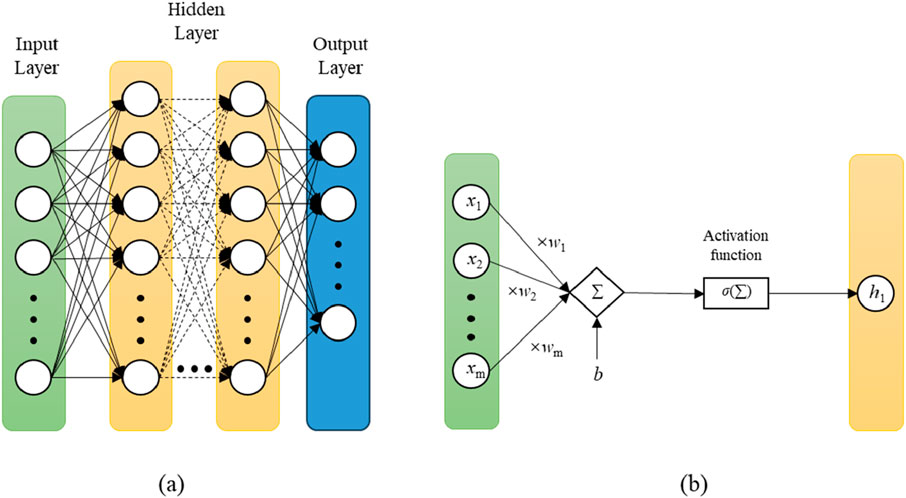
Figure 12. Schematic illustration of artificial neural network with multiple input and multiple output variables: (A) the entire artificial neural network (B) computing a hidden neuron.

In this study, 288 scenarios were used, with 70% (201 cases) chosen as the training set and the remaining 30% (87 cases) as the test set This process involved random sampling, where a certain proportion of samples were randomly selected to create a test set while retaining the original data distribution, with the remaining samples used as the training set. The inputs to the ANN model included four parameters: L/D, α, the horizontal displacement of the pile at the seabed h, and rotational load θ, as listed in Table 3, while the outputs were the ultimate horizontal load H_u and ultimate moment M_u.

Table 3

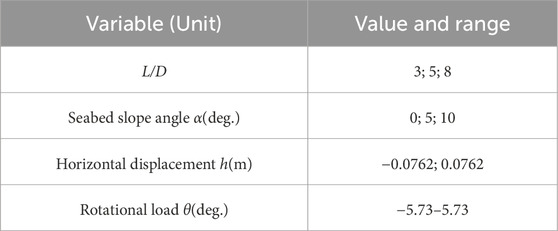
Table 3. Data limits of input variables associated with ultimate horizontal load and ultimate moment.

Based on Wang and Heo (2022), the neural network was designed with two hidden layers, each containing 12 neurons. Figure 13 shows the comparison between the predicted and measured H_u and M_u for the 87 test scenarios, demonstrating a small error margin. Specifically, most errors between predicted and observed values remain within ±10% for the H_u and M_u responses. Certainly, some data bias is also observed in the predictions of the test set, which is primarily related to the MSE values and the limited number of data points. In this study, the MSE for the training and test sets are 0.24 and 0.26, respectively. As the number of iterations increases, the training set MSE decreases by an order of magnitude. However, the MSE for the test set reaches its minimum and no longer changes, indicating the occurrence of overfitting. Therefore, increasing the amount of data in the training set can further reduce the MSE and the bias of some data points. Nevertheless, these results demonstrate the effectiveness of the multi-layer neural network as a surrogate model for predicting the horizontal bearing capacity envelope of offshore wind turbine monopiles under various HM loading combinations.

Figure 13

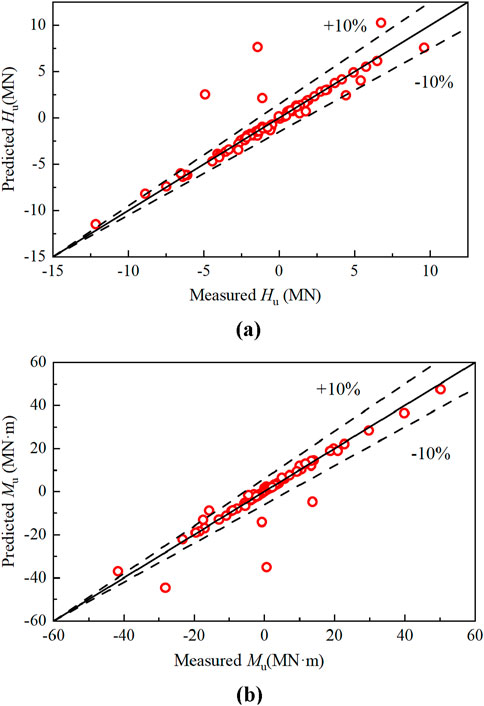
Figure 13. Comparison of output parameters of test sets: (A) Ultimate horizonal force (H_u) and (B) Ultimate bending moment (M_u).

5 Conclusion

A practical finite element model was developed and validated against the PISA project’s field test data for monopiles under lateral loads in sandy soils. The classical Mohr-Coulomb model, used for soil plasticity in this study, provided reliable predictions and required parameters that are straightforward to determine, enhancing its utility in engineering practice. The model’s effectiveness was confirmed for various L/D ratios, proving its applicability in complex offshore scenarios. Based on the numerical investigations, some conclusions were summarized:

(1) In the slope upward direction, the horizontal bearing capacity increased significantly with greater slope angle, while the opposite effect was observed in the slope downward direction. The slope angle (α) of the sloping seabed had a greater impact on the ultimate lateral load in the slope upward direction compared to the slope downward direction.

(2) For the flat seabed, the load paths under different HM combinations exhibited central symmetry; however, the load paths on the gently sloping seabed lost this symmetry due to the difference in the horizontal bearing capacity between the slope downward direction and the slope upward direction.

(3) The horizontal bearing capacity envelope of monopiles in the HM plane exhibited an elliptical shape for both the flat seabed and sloping seabed. This elliptical equation proved to be accurate in describing load capacity under different L/D ratios and seabed slope angles. Both the short-axis (R₂) and long-axis (R₁) lengths increased as L/D increased. The slope angle had little effect on the R₁, but it had a more significant impact on R₂.

(4) An artificial neural network (ANN) surrogate model was developed to predict ultimate horizontal load and bending moment, with training and testing on 288 scenarios. With L/D ratio, α, and the horizontal displacement h and rotation angle θ at the monopile head as inputs, the ANN effectively predicted the horizontal bearing capacity, with most errors remaining within ±10% across the test dataset.

(5) The numerical model, along with the surrogate ANN, offers a viable approach for predicting the horizontal bearing capacity of monopiles in offshore wind applications, even under varying seabed conditions and loading scenarios.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

X-YY: Writing–review and editing. S-YQ: Conceptualization, Software, Validation, Writing–original draft. BL: Conceptualization, Writing–original draft. JW: Supervision, Writing–review and editing. L-YX: Methodology, Supervision, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the project of Nanjing Urban Construction Tunnel and Bridge Intelligent Management Co., Ltd. (Name: Impact Assessment of Huimin Avenue Comprehensive Renovation Project on 220 kV Xiamao Line 1# and 2# Steel Poles).

Conflict of interest

Author X-YY was employed by Nanjing Urban Construction Tunnel and Bridge Intelligent Management Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from Nanjing Urban Construction Tunnel and Bridge Intelligent Management Co., Ltd. The funder had the following involvement in the study: interpretation of data and analysis.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amari, S. I. (1993). Backpropagation and stochastic gradient descent method. Neurocomputing 5 (4-5), 185–196. doi:10.1016/0925-2312(93)90006-O

CrossRef Full Text | Google Scholar

Benbouras, M. A., Petrişor, A. I., Zedira, H., Ghelani, L., and Lefilef, L. (2021). Forecasting the bearing capacity of the driven piles using advanced machine-learning techniques. Appl. Sci. 11 (22), 10908. doi:10.3390/app112210908

CrossRef Full Text | Google Scholar

Das, S. K., and Basudhar, P. K. (2006). Undrained lateral load capacity of piles in clay using artificial neural network. Comput. Geotech. 33 (8), 454–459. doi:10.1016/j.compgeo.2006.08.006

CrossRef Full Text | Google Scholar

Dassault Systèmes (2014). Abaqus analysis users' manual. Providence, RI, USA: Simula Corp.

Google Scholar

Graine, N., Hjiaj, M., and Krabbenhoft, K. (2021). 3D failure envelope of a rigid pile embedded in a cohesive soil using finite element limit analysis. Int. J. Numer. Anal. Methods Geomech. 45 (2), 265–290. doi:10.1002/nag.3152

CrossRef Full Text | Google Scholar

Hardin, B. O., and Black, W. L. (1968). Vibration modulus of normally consolidated clay. J. Soil Mechs. Founds. Engg. Div. 94 (2), 353–369. doi:10.1061/JSFEAQ.0001100

CrossRef Full Text | Google Scholar

Jiang, C., Zhang, Z., and He, J. (2020). Nonlinear analysis of combined loaded rigid piles in cohesionless soil slope. Comput. Geotech. 117, 103225. doi:10.1016/j.compgeo.2019.103225

CrossRef Full Text | Google Scholar

Keawsawasvong, S., and Ukritchon, B. (2020). Failure modes of laterally loaded piles under combined horizontal load and moment considering overburden stress factors. Geotech. Geol. Eng. 38, 4253–4267. doi:10.1007/s10706-020-01293-7

CrossRef Full Text | Google Scholar

Li, Z., Kotronis, P., and Escoffier, S. (2014). Numerical study of the 3D failure envelope of a single pile in sand. Comput. Geotech. 62, 11–26. doi:10.1016/j.compgeo.2014.06.004

CrossRef Full Text | Google Scholar

Lin, M., Jiang, C., Chen, Z., Liu, P., and Pang, L. (2022). A method for calculating lateral response of offshore rigid monopile in sand under slope effect. Ocean. Eng. 259, 111812. doi:10.1016/j.oceaneng.2022.111812

CrossRef Full Text | Google Scholar

Muduli, P. K., Das, S. K., and Das, M. R. (2013). Prediction of lateral load capacity of piles using extreme learning machine. Int. J. Geotech. Eng. 7 (4), 388–394. doi:10.1179/1938636213Z.00000000041

CrossRef Full Text | Google Scholar

Muthukkumaran, and K. (2014). Effect of slope and loading direction on laterally loaded piles in cohesionless soil. Int. J. Geomech. 14 (1), 1–7. doi:10.1061/(ASCE)GM.1943-5622.0000293

CrossRef Full Text | Google Scholar

Muthukkumaran, K., and Almas Begum, N. (2015). Experimental investigation of single model pile subjected to lateral load in sloping ground. Geotech. Geol. Eng. 33, 935–946. doi:10.1007/s10706-015-9875-7

CrossRef Full Text | Google Scholar

Raj, D., Singh, Y., and Kaynia, A. M. (2019). V–H–M seismic capacity envelopes of strip foundations on slopes for capacity design of structure-foundation system. Bull. Earthq. Eng. 17, 2963–2987. doi:10.1007/s10518-019-00577-5

CrossRef Full Text | Google Scholar

Sawant, V., and Shukla, S. (2012). Finite element analysis for laterally loaded piles in sloping ground. Coupled Syst. Mech. 1 (1), 59–78. doi:10.12989/csm.2012.1.1.059

CrossRef Full Text | Google Scholar

Shao, X., Jiang, C., Fu, Y., Yao, J., and Pang, L. (2024). Failure envelope for offshore rigid piles under combined horizontal-moment loading in clay with linearly increasing undrained shear strength. Ocean. Eng. 307, 118168. doi:10.1016/j.oceaneng.2024.118168

CrossRef Full Text | Google Scholar

Taborda, D. M., Zdravković, L., Potts, D. M., Burd, H. J., Byrne, B. W., Gavin, K. G., et al. (2020). Finite-element modelling of laterally loaded piles in a dense marine sand at Dunkirk. Géotechnique 70 (11), 1014–1029. doi:10.1680/jgeot.18.PISA.006

CrossRef Full Text | Google Scholar

Taherkhani, A. H., Mei, Q., and Han, F. (2023). Capacity prediction and design optimization for laterally loaded monopiles in sandy soil using hybrid neural network and sequential quadratic programming. Comput. Geotech. 163, 105745. doi:10.1016/j.compgeo.2023.105745

CrossRef Full Text | Google Scholar

Tatsuoka, F. (1993). Relationships between stress and strain increments. Intr. Strength Soils Fail. Ground, 57–81.

Google Scholar

Wang, X., and Heo, Y. (2022). “Artificial neural network surrogate modeling for offshore wind turbines under multi-hazards,” in ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering. Volume 2: Structures, Safety, and Reliability, USA, June 10, 2022. doi:10.1115/OMAE2022-81048

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., and Chen, G. X. (2017a). Nonlinear analysis of single laterally loaded piles in clays using modified strain wedge model. Int. J. Civ. Eng. 15, 895–906. doi:10.1007/s40999-016-0072-8

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., Chen, G. X., and Li, Y. Y. (2017b). Nonlinear analysis of single reinforced concrete piles subjected to lateral loading. KSCE J. Civ. Eng. 21, 2622–2633. doi:10.1007/s12205-017-1010-2

CrossRef Full Text | Google Scholar

Xu, L. Y., Cai, F., Wang, G. X., and Ugai, K. (2013). Nonlinear analysis of laterally loaded single piles in sand using modified strain wedge model. Comput. Geotech. 51, 60–71. doi:10.1016/j.compgeo.2013.01.003

CrossRef Full Text | Google Scholar

Xu, L. Y., Chen, W. Y., Cai, F., Song, Z., Pan, J. M., and Chen, G. X. (2023a). Response of soil–pile–superstructure–quay wall system to lateral displacement under horizontal and vertical earthquake excitations. Bull. Earthq. Eng. 21, 1173–1202. doi:10.1007/s10518-022-01572-z

CrossRef Full Text | Google Scholar

Xu, L. Y., Liu, L., Cai, F., Chen, W. Y., and Chen, G. X. (2023b). A practical framework for assessing the effect of cyclic softening of clays on the lateral response of single piles. Ocean. Eng. 288, 115933. doi:10.1016/j.oceaneng.2023.115933

CrossRef Full Text | Google Scholar

Xu, L. Y., Song, C. X., Cai, F., Chen, W. Y., Xue, Y. Y., and Chen, G. X. (2023c). An integrated model for offshore wind turbine monopile in porous seabed under multi-directional seismic excitations. Ocean. Eng. 285, 115250. doi:10.1016/j.oceaneng.2023.115250

CrossRef Full Text | Google Scholar

Zdravković, L., Jardine, R. J., Taborda, D. M., Abadias, D., Burd, H. J., Byrne, B. W., et al. (2020). Ground characterisation for PISA pile testing and analysis. Géotechnique 70 (11), 945–960. doi:10.1680/jgeot.18.PISA.001

CrossRef Full Text | Google Scholar

Zhao, Z., Zhang, H., Shiau, J., Du, W., Ke, L., Wu, F., et al. (2024). Failure envelopes of rigid tripod pile foundation under combined vertical-horizontal-moment loadings in clay. Appl. Ocean. Res. 150, 104131. doi:10.1016/j.apor.2024.104131

CrossRef Full Text | Google Scholar