Determination of the fracture closure pressure in fractural-cavity carbonate reservoirs using a failure criterion based on asperity behavior

As fluid flow paths in fractural-cavity carbonate reservoirs, fractures have a significant impact on the production performance of carbonate reservoirs. In particular, well production depends on the apertures of the fractures, which vary with the effective stress acting on the fractures. Thus, predicting the fracture closure pressure is crucial for carbonate reservoir development. In our research, fracture closure pressures are derived using the Zienkiewicz–Pande failure criterion, which defines the pressure at which most asperities come into contact. The results reveal that fracture closure is influenced by the geo-stress field, rock mechanics, and spatial location of the fracture. Ultimately, the fracture closure pressure of typical wells located in different tectonic zones in the Shunbei Oilfield is calculated, and the results indicate that the fracture closure pressure in the Shunbei Oilfield is significantly affected by the dip of fractures and the angle between the fracture strike and maximum principal stress. To demonstrate the accuracy of the estimated fracture closure pressure, production performance corresponding to fracture closure was evaluated. It reveals that the flowing bottom pressure decreases rapidly and the recoverable oil reserves reduce when the pressure approaches the fracture closure pressure. This observation verifies that the fracture closure pressure determined using our formula is a feasible predictor of the production performance of fractural-cavity carbonate reservoirs.

1 Introduction

Carbonate reservoirs are the major oil- and gas-producing sources in many parts of the world, including the Middle East, Central Asia, West Texas, and South America (Chang, 2022). Oil and gas in carbonate reservoirs are mainly stored in caves, vugs, and fractures, which are different in size and have a complex distribution. It is estimated that more than 60% of the world’s proven oil reserves and 40% of the world’s gas resources are in carbonate rocks (Burchette, 2012; Zeng et al., 2021). This means that abundant remaining oil and gas reserves exist in carbonate reservoirs (Sheng, 2013). It is clear that the relative importance of carbonate reservoirs, compared with other types of reserves, will increase dramatically in the coming decades.

Carbonate reservoirs, known for their extremely strong heterogeneity, are usually classified as cave, vuggy, and fractured reservoirs; among these, fractural-cavity reservoirs are dominant in carbonate reservoirs in northwest China (Jiang et al., 2019; Li et al., 2023). Fractures are the most important paths for the fluid flow in carbonate reservoirs, and it is of utmost importance to understand and study fracture characteristics, patterns, and factors that influence fracture aperture or length to optimize hydrocarbon production and reduce exploitation risk (Zahedi et al., 2019; Awdal et al., 2016; Li et al., 2024). In carbonate reservoirs, opening-mode fractures (extension fractures, veins, and joints) and faults commonly strongly influence production (Nelson, 1985) because fracture apertures are significantly greater than typical matrix pore throat sizes, and they contribute the major portion of the fluid flow in rocks and, consequently, are an important factor in production performance (Tiab and Donaldson, 2016).

Once production starts, the formation pore pressure decreases obviously, and the fracture aperture decreases (Dong et al., 2021). As the fluid is further extracted from the formation, the reservoir pressure will continue to decrease, and the effective overburden load on the reservoir rock will increase (Bin Tajul Amar et al., 1995). Decreasing reservoir pressure leads to stress variations, which further alter the apertures of fractures and even vugs, ultimately changing the transmissivity of reservoirs (Ruistuen et al., 1999; Wang et al., 2015; Rashid et al., 2023). Nevertheless, rough fracture surfaces preserve channels during stress variations, and the roughness of asperities in the fracture surface is a noteworthy influencing factor for the stress sensitivity of fractures (Cardona et al., 2021).

Fracture closure characteristics are commonly depicted by the stress sensitivity of the permeability and apertures of fractures. The stress sensitivity of permeability is usually evaluated by experimental methods to determine the relationship between permeability and effective stress (Xie et al., 2011). Current research studies reveal that the impact of stress-sensitive permeability on productivity increases with increasing permeability modulus and decreasing flowing bottom-hole pressure, and the higher the reservoir pressure, the greater the influence of stress-sensitive permeability on production (He et al., 2022). Normal stress increments cause contact yield, fracture closure, and changes in the fracture void space (Cardona et al., 2021).

The conductivity of a rock fracture is governed by the geometry of the void space between the two fracture surfaces (Hakami et al., 1995; Rashid et al., 2021). Fracture conductivity is defined as fracture width multiplied by fracture permeability (Yu and Sepehrnoori, 2018). The influence of fracture width on permeability was investigated by numerical methods, and the results revealed that the overall permeability of the fracture network was controlled by large fractures with higher assigned apertures (de Dreuzy et al., 2004; Baghbanan and Jing, 2007). The reduction in the pressure of oil reservoirs results in the closure of open fractures (Cao and Sharma, 2023; Martyushev et al., 2024). Specifically, when fracture apertures are very small, wall roughness and tortuosity can significantly affect the fluid flow (Fanchi, 2018).

In our research, the failure criterion was involved in the closure pressure of fracture research. After establishing the function of closure pressure, parameter sensitivity analysis was performed to illustrate the influence of various parameters and determine their optimum value. Finally, the closure pressure of fractures in the Shunbei Oilfield, located in the Tarim Basin, Northwest China, was calculated, and corresponding production performance was evaluated to clarify the influences of fracture closure.

2 Methods

2.1 Fracture model

In fractured and cavity carbonate reservoirs, fractures form complex networks with multi-scale features, which include macro- and micro-fractures. It is notable that the fractures that significantly affect the fluid flow are those that connect caves because fault-related fractures have very high permeability potentials. Thus, fracture closure analysis focuses on fractures at this scale because of their important role in the conductivity of fractural and cavity carbonate reservoirs.

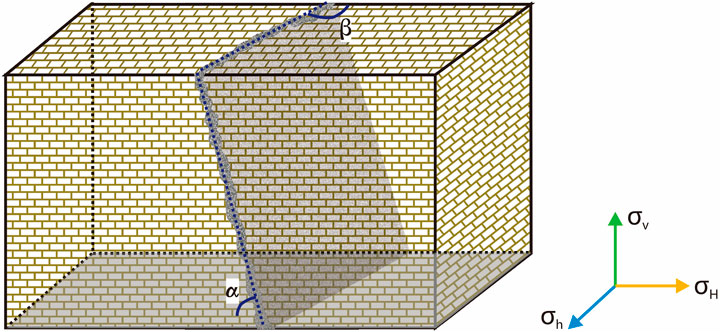
To clarify the calculation of the fracture closure pressure, the fracture is assumed to be a plate in the rock matrix, making the geo-stress field anisotropic. In detail, $\alpha$ is the dip angle of the fracture, and $\beta$ is the angle between the strike of the fracture and the direction of maximum horizontal principal stress (Figure 1). Hence, the geo-stress field is a significant factor that affects the force analysis of the fracture plane. On the scale of the fracture surface, asperities are assumed to be hemispheroids with different radii and consistent spacing across the otherwise smooth and rigid surfaces. In particular, the asperities are independent, meaning that the deformation of a single asperity does not influence others even when the load increases until asperities on two opposite surfaces of the fracture come into contact.

Figure 1

Figure 1. Spatial location of the fracture in the geo-stress field.

With these assumptions, fracture closure occurs when opposing asperities come into contact under load, simultaneously causing variability in the fracture conductivity. As the load is applied, the distance between the asperities on the two plates decreases (Figure 2A), and the conductivity of the fracture depends on the fracture width only until the asperities on the two plates are in contact (Figure 2B). In these two stages, fractures still maintain considerable conductivity, so fracture closure slightly affects the production performance. After that, asperities become deformed, and the uncontacted fracture area is crucial for fracture conductivity (Figure 2C). In this situation, appropriate measures such as water injection are effective for preventing fractures from getting closer. Under a small load, asperities deform elastically, and the effective flow path decreases with the increasing load. When the load reaches a critical point at which the asperities yield, plastic deformation occurs along the fracture, and the fracture conductivity reaches the lowest value when the fracture closes completely (Figure 2D).

Figure 2

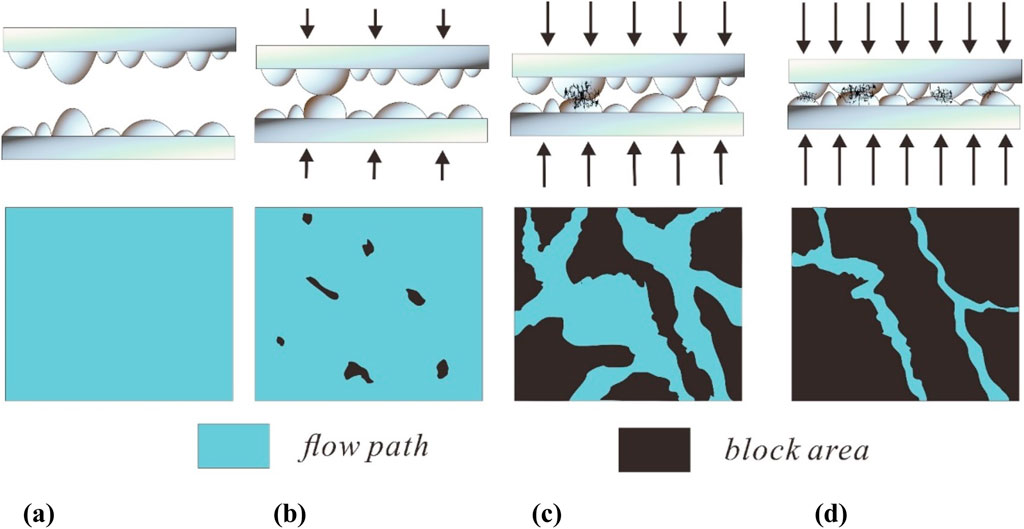
Figure 2. Asperity contact and corresponding flow path along the fracture: (A) entirely open; (B) asperities initially come into contact; (C) asperities come into contact and plastic deformation occurs; and (D) most asperities come into contact and deform.

2.2 Yield criterion for asperities

The onset of plastic deformation in materials is predicted by the yield criteria. Yield criteria are also called theories of yielding. Several yield criteria have been developed for ductile and brittle materials to predict the yielding behavior in simple ductile materials, and the Drucker–Prager failure criterion and Zienkiewicz–Pande failure criterion are fit for the material properties that may apply to fracture closure pressure calculation.

The theoretical differences between the Drucker–Prager failure criterion and the Zienkiewicz–Pande failure criterion lies in the mechanisms of yielding, which are caused by the hydrostatic pressure and strength differential effect. For the carbonate reservoir in the Shunbei Oilfield, the depth of the reservoir is approximately 8 km, and asperities on the fracture surface are significantly loaded by hydrostatic pressure, which means that the yielding caused by hydrostatic pressure is not negligible. In addition, the tensile strength of the rock is very low, approximately 0.1 times the compressive strength. Thus, rock materials are more likely to fail in tension than in compression (Aadnøy and Looyeh, 2019). This reveals that the strength differential effect is also important for fracture closure pressure estimation via the failure criterion. In contrast, the Zienkiewicz–Pande failure criterion is more suitable for fracture closure pressure estimation due to the yielding being caused by hydrostatic pressure and the strength differential effect.

The Zienkiewicz–Pande failure criterion was proposed based on a model for rocks and rock-like materials with multiple planes of weakness. The behavior of the assembly applies tensile and Mohr‒Coulomb shear limits on each such plane with possible strain dependence of the frictional properties. The model is applicable to the stability analysis of rock slopes. It is expressed as follows (Zienkiewicz and Pande, 1977; Li et al., 2017):

$f\left(I_1,J_2\right)=\frac{m}{9}{I}_1^2+\frac{n}{3}{I}_1-k+\frac{J_2}{g^2\left({\theta }_{\sigma }\right)}=0,(1)$

where $g\left({\theta }_{\sigma }\right)$ is the function of the stress Lode angle ${\theta }_{\sigma }$ and is simply expressed as follows:

$g\left({\theta }_{\sigma }\right)=\frac{2K^{\prime }}{\left(1+K^{\prime }\right)-\left(1-K^{\prime }\right)\sin 3{\theta }_{\sigma }}.(2)$

Parameters $m$, $n$, $k$, and $K^{\prime }$ are all functions of the internal friction angle ${\varphi }_0$, which are expressed as follows:

$m=-{\tan }^2{\varphi }_0,(3)$

$n=2\overline{c}\tan {\varphi }_0,(4)$

$k={\overline{c}}^2-a^2\tan {\varphi }_0,(5)$

$K^{\prime }=\frac{3-\sin {\varphi }_0}{3+\sin {\varphi }_0}.(6)$

Here, $a$ and $\overline{c}$ are defined as follows:

$\overline{c}=\frac{6c\cos {\varphi }_0}{\sqrt{3}\left(3-\sin {\varphi }_0\right)},(7)$

$a=\frac{\overline{c}}{24\tan {\varphi }_0}.(8)$

3 Results

Fracture closure analysis is considered because the load on the fluid in the fracture varies. Thus, force analysis of the fluid in fractures is fundamental to fracture closure. Then, the closure pressure of the fracture is determined by both force analysis of the fluid and the yield criterion for the asperities.

3.1 Force analysis of fluids in fractures

As mentioned above, since fracture aperture is sensitive to effective load, force analysis of fluids in fractures is fundamental to studying fracture closure via stress variation. In our research, the geo-stress field and fluid pressure are introduced in the force analysis.

Derived from the fracture model we built in Figure 1, the effective normal stress on fracture ${\sigma }_{ne}$ is as follows:

${\sigma }_{ne}={\sigma }_v\cos \alpha +\sin \alpha \left({\sigma }_H\sin \beta +{\sigma }_h\cos \beta \right)-P_f,(9)$

where ${\sigma }_v$ is the gravity of the overlying rock, which is determined by the density of the overlying rock and its depth. ${\sigma }_h$ and ${\sigma }_H$ are the minimum horizontal principal stress and the maximum horizontal principal stress, respectively, and these two stresses depend on the tectonic stress and horizontal stress derived from the vertical principal stress. $P_f$ is the fluid pressure, which is the force on the fluid in the fracture.

The limit of yielding is assumed to be equal to the effective normal stress and vertical principal stress:

${\sigma }_s={\sigma }_{ne}={\sigma }_z.(10)$

3.2 Closure pressure based on failure criteria

In subsurface formations that are not subjected to significant tectonic forces, ${\sigma }_1$ is in the vertical direction due to the lithostatic pressure of the overburden, but significant compressional forces can result in ${\sigma }_1$ being oriented in or close to the horizontal plane. In our case, ${\sigma }_v={\sigma }_1$, ${\sigma }_H={\sigma }_2$, and ${\sigma }_h={\sigma }_3$ (Rackley, 2017).

Additionally, triaxial stresses are expressed as follows:

${\sigma }_x={\sigma }_y=\frac{\mu }{1-\mu }{\sigma }_z,(11)$

where $\mu$ is the Poisson’s ratio.

Then, the Zienkiewicz–Pande failure criterion is used in closure pressure analysis. From Equations 1–11, the closure pressure of the fracture derived from the Zienkiewicz–Pande failure criterion is expressed as follows:

$P_f={\sigma }_v\cos \alpha +\sin \alpha \left({\sigma }_H\sin \beta +{\sigma }_h\cos \beta \right)-\frac{\sqrt{N^2-4MK}-N}{2M},(12)$

Parameters M, N and K in Equation 11 are expressed as Equations 12–15.

$M=\frac{4}{3}\frac{{\sin }^2{\varphi }_0}{{\left(3-\sin {\varphi }_0\right)}^2}{\left(\frac{1+\mu }{1-\mu }\right)}^2+\left(\frac{2\mu -1}{1-\mu }\right)\left(\frac{36-34\sin {\varphi }_0{\sin }^{2}3{\theta }_{\sigma }-4{\sin }^2{\varphi }_0{\sin }^{2}3{\theta }_{\sigma }}{96+12{\cos }^2{\varphi }_0}\right),(13)$

$N=\frac{8c\sin {\varphi }_0\cos {\varphi }_0}{{\left(3-\sin {\varphi }_0\right)}^2},(14)$

and

$K=\frac{12c^2{\cos }^2{\varphi }_0\left(1-576\tan {\varphi }_0\right)}{576\tan {\varphi }_0{\left(3-\sin {\varphi }_0\right)}^2}.(15)$

4 Discussion

For a fractured carbonate reservoir, the closure pressure is affected by the geo-stress field, rock mechanics parameters, and the spatial position of the fractures, such as their orientation and depth. For this reason, a parameter sensitivity analysis is performed to illustrate the relationship between different parameters, and then, based on a reasonable range of parameter values, the fracture closure pressure is determined by the Zienkiewicz–Pande failure criterion.

4.1 Factors that influence the fracture closure pressure

Based on the fracture closure pressure equation, the pressure is determined by three groups of parameters: the geo-stress field parameters, which include the gravity of the overlying rock, the minimum horizontal principal stress, and the maximum horizontal principal stress; the rock mechanics parameters, which involve Poisson’s ratio, the internal friction angle, and rock cohesion; and the fracture parameters, such as the dip angle of fracture and the angle between the fracture strike and the maximum principal stress. Higher geo-stress values result in higher fracture closure pressure; thus, we focus on the influence analysis of rock mechanics and fracture parameters.

4.1.1 Rock mechanics parameters

Regarding the rock mechanics parameters, the Poisson’s ratio of a rock depends on its lithology and porosity and is a critical rock property related to closure stress. It serves as a necessary constant for determining the stress and deflection properties of materials in engineering analysis (Rosato and Rosato, 2003; Hoss Belyadi, 2019; Zhang, 2019).

Moreover, cohesion is the most crucial rock shear strength parameter (Chen et al., 2020). Rock cohesion is a key parameter for the deformation degree of fractures in a fractured formation. Low cohesion facilitates rapid deformation involving the undeformed parts in the models, while high cohesion leads to a relatively low transfer rate (Meng and Hodgetts, 2019).

It is well-known that the internal friction angle is a physical property of petroleum rock, and it represents the slope of a linear representation of the shear strength of the formation matrix (Keaton, 2017). The size and hardness of sedimentary particles give rise to different shear behaviors of sediments, thus significantly affecting the internal friction angle (Kim and Ha, 2014).

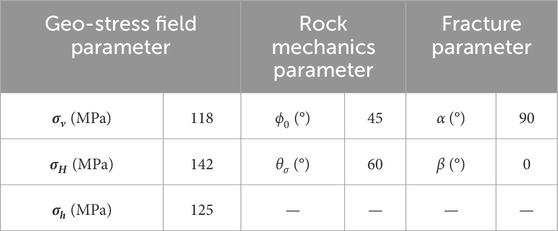
Considering the stable component of the carbonate matrix, only Poisson’s ratio and rock cohesion are discussed in this section. Regarding the fracture closure pressure, to illustrate the influence exerted by Poisson’s ratio and rock cohesion, other parameters are fixed, as shown in Table 1.

Table 1

Table 1. Parameter values for the sensitivity analysis of rock mechanics parameters.

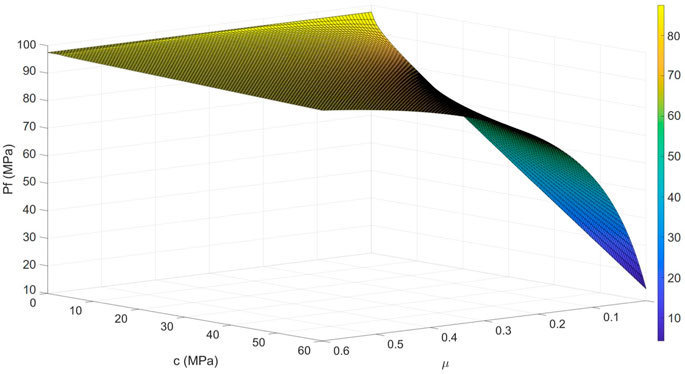
The fracture closure pressure was evaluated with respect to various Poisson’s ratios and rock cohesions and is exhibited in Figure 3. It is evident that Poisson’s ratio impacts the closure pressure as the closure pressure monotonically increases with Poisson’s ratio for any given rock cohesion value. A disparity exists in the relationship between the closure pressure and rock cohesion since the fracture closure pressure tends to become smaller with higher rock cohesion. It is remarkable that the rate of increase or decrease in the pressure depends on both Poisson’s ratio and rock cohesion. When the rock cohesion is very close to 0, the pressure shows a slight increment as the Poisson’s ratio varies. Correspondingly, the value of Poisson’s ratio also determines the variation in the fracture closure pressure with different rock cohesions. As the Poisson’s ratio becomes higher, the pressure appears to be less sensitive to changes in rock cohesion.

Figure 3

Figure 3. Graph of the fracture closure pressure versus Poison’s ratio and rock cohesion.

4.1.2 Fracture parameters

The dip angle of a fracture is defined as the angle between the fracture and horizontal planes. With increasing depth, the vertical and horizontal stresses change significantly, which has a substantial impact on the fracture opening. Therefore, the fracture dip angle and its three-dimensional stress state are the main factors influencing the fluid flow in the fractures within the surrounding reservoirs (Zhu et al., 2022).

Due to the influence of stress on the dip angle, the aperture and permeability of the fracture are related to the dip angle (Fatehi et al., 2012; Wei et al., 2021). For fractured reservoirs, the dip angles of the fractures also affect the production performance, especially during water injection exploitation. In addition to the weight stress caused by the gravity of the overlying strata, the tectonic stress, represented by the maximum and minimum principal stresses, is also crucial for fracture closure behavior. Thus, the spatial position of a fracture in the stress field is one of the essential factors for closure pressure (Kang et al., 2010; Meng et al., 2011; Chen et al., 2018). Consequently, the influences of the dip angle of the fracture and the angle between the fracture strike and the maximum principal stress were evaluated regarding the effect of fracture parameters on the fracture closure pressure.

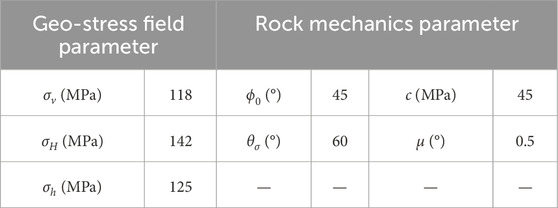
Similar to the analysis of influencing factors in rock mechanics, the parameters related to the sensitivity analysis of fracture parameters are also considered constant values, as shown in Table 2.

Table 2

Table 2. Parameter values for the sensitivity analysis of fracture parameters.

The fracture closure pressure varies in a convex manner as the dip angle of the fracture and the angle between the fracture strike and the maximum principal stress range from 0°–90° (Figure 4). The fracture closure pressure forms a parabola with different angles between the fracture strike and the maximum principal stress when the dip angle of the fracture is fixed. Similarly, the fracture closure pressure first increases and then decreases with various dip angles of the fracture and a given angle between the fracture strike and the maximum principal stress. It is particularly worth noting that when the fractures tend to be parallel to the maximum principal stress, a change in the dip angle of the fracture results in almost the same pressure.

Figure 4

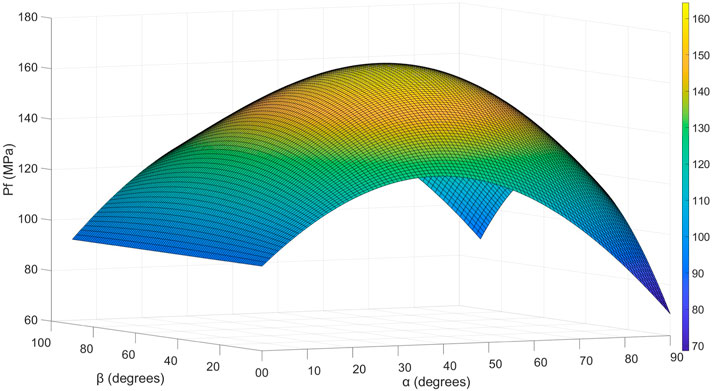
Figure 4. Graph of the fracture closure pressure versus the dip angle of fracture and the angle between the fracture strike and the maximum principal stress.

4.2 Fracture closure pressure for typical wells

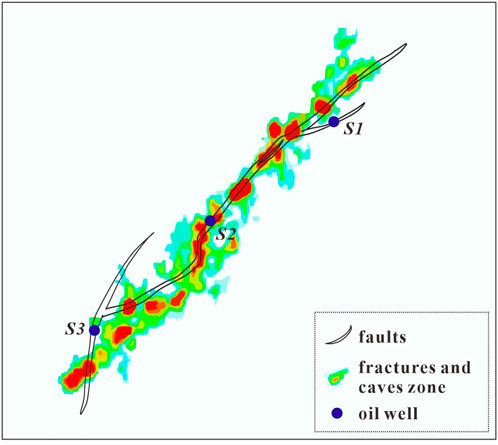
For the oil production wells in the fractured-cavity reservoir, fractures are the dominant factor in production performance, and the aperture of the fracture determines its conductivity from the reservoir to the wellbore. In our research, oil production wells located in the same fault and exploitation unit were selected as typical wells to evaluate the fracture closure pressure (Figure 5).

Figure 5

Figure 5. Locations of typical wells S1–S3.

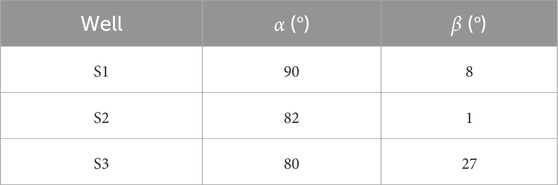
From geophysical data, ${\sigma }_H$, ${\sigma }_h$, and ${\sigma }_v$ are 180 MPa, 130 MPa, and 150 MPa, respectively, for the Ordovician carbonate reservoir in the Shunbei Oilfield, and the direction of maximum principal stress is N54°E about the fault zone. Rock mechanics parameters were obtained by experiments and sonic log interpretation. The dip and strike of fractures were derived from well log and seismic interpretation images. The values of fracture parameters for fracture closure pressure are listed in Table 3.

Table 3

Table 3. Values of fracture parameters for wells S1–S3.

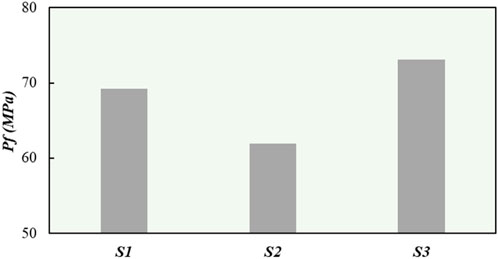
Finally, we obtained the fracture closure pressures for these three wells, which are 69.28 MPa, 61.91 MPa, and 73.11 MPa for wells S1, S2, and S3, respectively (Figure 6). It is observed that the fracture closure pressure of S3 is the highest. The reason, inferred from the analysis of the influencing factors, is that the fractures of well S3 have the largest angle between the fracture strike and the maximum principal stress. From the perspective of tectonic genesis, this may be caused by the stress transition zone. Correspondingly, the fracture closure pressures of wells S1 and S2 are lower due to smaller angles. The evaluation of the influencing factors reveals that a large dip angle leads to a lower closure pressure. However, for well S3, although the dip angle of the fracture is the smallest, the fracture closure pressure is not as high as that of other wells. This is because the strike of the fractures is almost parallel to the direction of the maximum principal stress. Based on the pressure calculation, the difference in fracture closure pressure among the wells located in this fault in the Shunbei Oilfield is mainly determined by the strike of the fractures.

Figure 6

Figure 6. Comparison of the fracture closure pressure of wells S1–S3.

4.3 Production performance behavior under fracture closure

Since we estimated the closure pressure for the Shunbei Oilfield based on the Zienkiewicz–Pande failure criterion, stress field parameters, and rock mechanics parameters of the Shunbei Oilfield, the production performance of the oil wells after fracture closure was also discussed to verify the closure pressure estimate.

4.3.1 Oil production rate variation

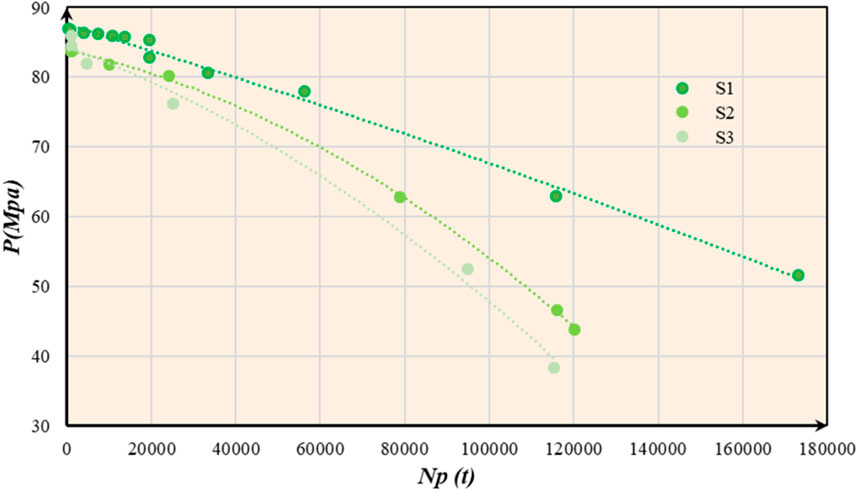
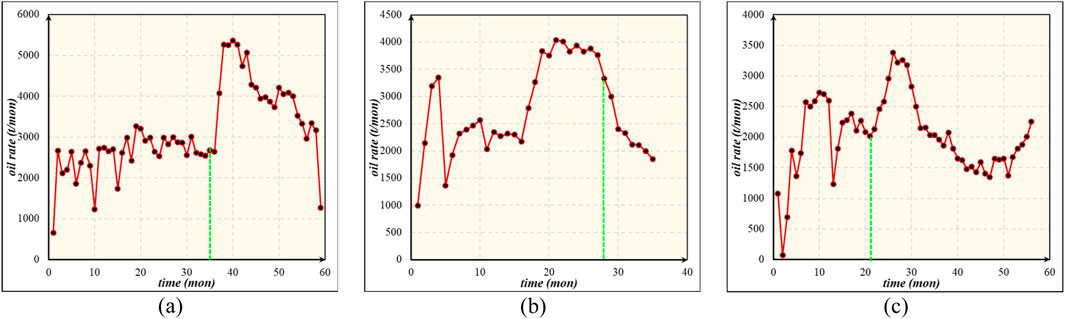
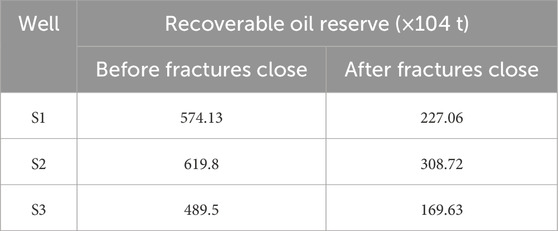
The reservoir pressure test provides the oil-bearing formation pressure of wells S1–S3 at different production times. Due to the scarcity of pressure data, the cumulative oil production amount and formation pressure data were plotted to obtain a data series of pressure versus cumulative oil production amount (Figure 7). As the fracture closure pressure values have been calculated by Equation 12, accumulative oil production amounts before fracture closure were clarified as 8.78×10⁴ t, 8.21×10⁴ t, and 4.08×10⁴ t for wells S1, S2, and S3, respectively.

Figure 7

Figure 7. Oil-bearing formation pressure of wells S1–S3.

As the fracture and cave structures of the carbonate reservoir are complex, fracture closure indicates that some flow paths are blocked rather than every fracture being closed, and it mostly means that the main flow path is closed. It should be emphasized that the water cut of wells S1–S3 has always been below 1% so far. Therefore, only the oil rate is considered in this section although the effect of fracture closure affects not only oil seepage but also water flow in the reservoir. With the oil production profile, the oil rate is very stable before the fracture closes for S1 and S3 (Figures 8A, C). When the fracture closure pressure is almost reached, the main task of exploitation is to maintain an appropriate reservoir pressure to ensure sustainable oil production. Unfortunately, the choke size of wells S1 and S3 was enlarged at months 35 and 21 when the pressure reached the fracture closure pressure. This led to a rapid increase in the oil production rate due to the inherent strong energy of the oil-bearing formations, but the oil rate profile shows a significant downward trend after that. Different from wells S1 and S3, the oil rate of well S2 decreased notably after month 28 when the pressure was the same as the fracture closure pressure (Figure 8B). Before that, a larger choke size caused a high oil rate, and this situation lasted for 9 months.

Figure 8

Figure 8. Oil production rate curve of wells S1–S3.

Based on the analysis of the oil production rate, we can note that fracture closure does not always result in an immediate decrease in the oil rate. This is attributed to the diverse fractured-cavity structures and changing oil production plans. This is also the reason why fracture closure is much more difficult to identify based solely on oil rate profiles.

4.3.2 Flowing bottom-hole pressure variation

In addition to the fluid flow, fracture closure also causes a variation in the flowing bottom-hole pressure. Moreover, the flowing bottom-hole pressure is crucial for oil reserve estimation based on the material balance law. To clarify this, we introduced the material balance equation for the fractured-cavity carbonate reservoir to evaluate the production performance change caused by fracture closure. To compare the recoverable oil reserves affected by fracture closure, we assumed that the drive mechanism of the reservoir is elastic drive. Meanwhile, the water phase is ignored since the water cut of these three wells is all below 5% in our research. Thus, the material balance equation for the fractured-cavity carbonate reservoir was established as follows:

$N_p=\frac{N{B}_{oi}{C}_t}{B_o}\cdot \left(P_i-P\right),(16)$

where $N_p$ is the accumulative oil production in ${10}^4{m}^3$, $N$ is the oil in place in ${10}^4{m}^3$, $P_i$ is the initial formation pressure in $MPa$, $P$ is the formation pressure in $MPa$, $B_o$ is the oil volume factor (dimensionless), $B_{oi}$ is the initial oil volume factor (dimensionless), and $C_t$ is the total compressibility coefficient.

The fluid flow in fractures is considered the plate laminar flow, which obeys the cubic law:

$q_o=\frac{a^3}{12\mu }\cdot \frac{P-P_{wf}}{L},(17)$

where $q_o$ is the oil production rate in $m^3$, $a$ is the width of the fracture in $m$, $\mu$ is the oil velocity in $mPa\cdot s$, $L$ is the length of the fracture in $m$, and $P_{wf}$ is the flowing bottom-hole pressure in $MPa$.

Combining Equations 16, 17, flowing bottom-hole pressure is expressed as follows:

$P_{wf}=P_i-\frac{12\mu L}{a^3}{q}_o-\frac{B_o}{N{B}_{oi}{C}_i}\cdot N_p.(18)$

Using Equation 18, we plotted flowing bottom-hole pressure curves for three oil wells, as shown in Figure 9. Considering the slight density fluctuation of oil in the Shunbei Oilfield during exploitation, we ignored the volume deviation of unit oil by weight and metered oil production in tons instead of cubic meters.

Figure 9

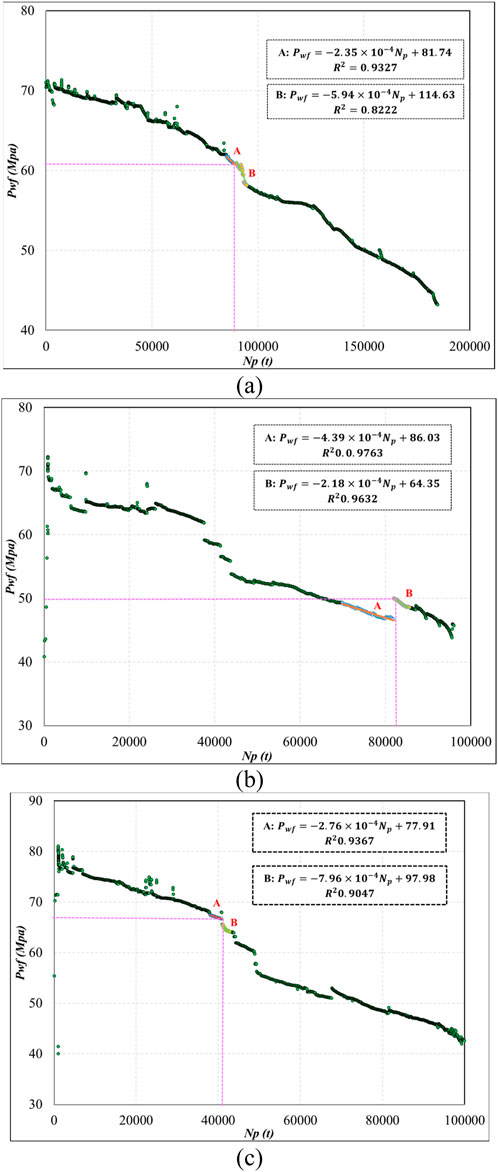
Figure 9. Plot of flowing bottom-hole pressure versus accumulative oil production amount (wells S1–S3).

In general, the flowing bottom-hole pressure of these three wells decreases with increasing cumulative oil production. Before the fractures close, the rate of pressure decrease is relatively low, and the flowing bottom-hole pressure curve decreases gently. Comparatively, the drawdown of the flowing bottom-hole pressure seems to be quite rapid after the fractures close. This indicates that the blocking of flow paths accelerates the decreases in the flowing bottom-hole pressure in the fractured-cavity carbonate reservoir.

To clarify the influence of fracture closure on oil production, relevant oils in place were evaluated as the recoverable oil reserves. The parameters involved in the process were fixed as follows: $B_{oi}$ is 1.0752, $B_o$ is 1.0433, and $C_t$ is 7.19×10⁻⁴ $Mp{a}^{-1}$. As shown in Table 4, once fractures closed, recoverable oil reserves varied with a 50% reduction. This verified the fractures’ closure status determined by the fracture closure pressure and interpreted the significant influence of fracture closure.

Table 4

Table 4. Recoverable oil reserve comparison of wells S1–S3.

5 Conclusion

Fracture closure is one of the crucial factors in the oilfield exploitation of facture-rich reservoirs because it causes a dramatic decrease in the production rate. Fracture closure in fractural and cavity carbonate reservoirs with rough surfaces is the process of aperture decrease, asperity contact, and asperity deformation through both elastic and plastic deformation. Thus, the asperity failure criterion is one of the main tasks in fracture closure analysis. Considering the influence of hydrostatic pressure and principal stress, the fracture closure pressure equation was built based on the Zienkiewicz–Pande failure criteria in our research. In addition, fracture closure pressure estimation was verified by applying it to typical wells in the Shunbei Oilfield, which represent different tectonic settings. On the whole, our research is concluded as follows:

1. Fracture closure pressure for fractural carbonate reservoirs is determined by the geo-stress field, rock mechanics, and the spatial characteristics of the fracture, such as the dip angle of the fracture, the angle between the fracture strike and the maximum principal stress, and the asperity yield criterion.

2. Fracture closure pressure estimation for the Shunbei Oilfield reveals that fracture closure behavior is influenced more by the dip of fractures and the angle between the fracture strike and the maximum principal stress for fault-controlled carbonate reservoirs. Fractures with large angles between the fracture strike and the maximum principal stress or those with small strikes result in large fracture closure pressure.

3. Comparing the production performance before and after fracture closure, it is verified that fracture closure behavior may not immediately affect oil production rates, but it has a significant effect on recoverable oil reserves, which is reflected by flowing bottom pressure variation. Once fractures are closed, the recoverable oil reserve varies with more than a 50% reduction.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YT: data curation, investigation, methodology, writing–original draft, and writing–review and editing. QC: conceptualization, data curation, formal analysis, project administration, writing–original draft, and writing–review and editing. JW: data curation, investigation, and writing–original draft. KL: data curation, methodology, and writing–original draft. CY: project administration, supervision, and writing–original draft. YH: investigation and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors declare that this study received funding from Key Laboratory of Marine Oil and Gas Reservoirs Production, Sinopec (Grant nunmber: 33550000-22-ZC0613-0013). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author YH was employed by Sichuan Jiayuan Natural Gas Co. LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aadnøy, B. S., and Looyeh, R. (2019). “Chapter 9 - rock strength and rock failure,” in Petroleum rock mechanics. Second Edition (Boston: Gulf Professional Publishing), 145–163.

Google Scholar

Awdal, A., Healy, D., and Alsop, G. I. (2016). Fracture patterns and petrophysical properties of carbonates undergoing regional folding: a case study from Kurdistan, N Iraq. Mar. Petroleum Geol. 71, 149–167. doi:10.1016/j.marpetgeo.2015.12.017

CrossRef Full Text | Google Scholar

Baghbanan, A., and Jing, L. (2007). Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 44 (5), 704–719. doi:10.1016/j.ijrmms.2006.11.001

CrossRef Full Text | Google Scholar

Bin Tajul Amar, Z. H., Altunbay, M., and Barr, D. (1995). “Stress sensitivity in the dulang field - how it is related to productivity,” in SPE European formation damage conference.

Google Scholar

Burchette, T. (2012). “Carbonate rocks and petroleum reservoirs: a geological perspective from the industry,” 370. Bath: Geological Society of London Special Publications, 17–37. doi:10.1144/sp370.14

CrossRef Full Text | Google Scholar

Cao, M., and Sharma, M. M. (2023). A computationally efficient model for fracture propagation and fluid flow in naturally fractured reservoirs. J. Petroleum Sci. Eng. 220, 111249. doi:10.1016/j.petrol.2022.111249

CrossRef Full Text | Google Scholar

Cardona, A., Finkbeiner, T., and Santamarina, J. C. (2021). Natural rock fractures: from aperture to fluid flow. Rock Mech. Rock Eng. 54 (11), 5827–5844. doi:10.1007/s00603-021-02565-1

CrossRef Full Text | Google Scholar

Chang, F. F. (2022). “Chapter 10 - acid fracturing stimulation,” in Fluid chemistry, drilling and completion. Editors Q. Wang, and Q. Wang (Boston: Gulf Professional Publishing), 387–419.

Google Scholar

Chen, S., Tang, D., Tao, S., Xu, H., Zhao, J., Fu, H., et al. (2018). In-situ stress, stress-dependent permeability, pore pressure and gas-bearing system in multiple coal seams in the Panguan area, western Guizhou, China. J. Nat. Gas Sci. Eng. 49, 110–122. doi:10.1016/j.jngse.2017.10.009

CrossRef Full Text | Google Scholar

Chen, W., Khandelwal, M., Murlidhar, B. R., Bui, D. T., Tahir, M. M., and Katebi, J. (2020). Assessing cohesion of the rocks proposing a new intelligent technique namely group method of data handling. Eng. Comput. 36 (2), 783–793. doi:10.1007/s00366-019-00731-2

CrossRef Full Text | Google Scholar

de Dreuzy, J., Darcel, C., Davy, P., and Bour, O. (2004). Influence of spatial correlation of fracture centers on the permeability of two-dimensional fracture networks following a power law length distribution. Water Resour. Res. 40, 1–11. doi:10.1029/2003wr002260

CrossRef Full Text | Google Scholar

Dong, L., Wang, D., Li, F., Fu, X., and Wang, M. (2021). Investigation of fracture width change under closure pressure in unconventional reservoir based on the hertz contact theory. Geofluids 2021, 1–6. doi:10.1155/2021/1268352

CrossRef Full Text | Google Scholar

Fanchi, J. R. (2018). “Chapter 13 - fracture and shale systems,” in Principles of applied reservoir simulation. Fourth Edition (Boston: Gulf Professional Publishing), 241–256.

Google Scholar

Fatehi, M., Pashapour, A., and Gholamnejad, J. (2012). Relationship between fracture dip angle, aperture and fluid flow in the fractured rock masses. J. Min. Environ. 2 (2), 136–145.

Google Scholar

Hakami, E., Einstein, H. H., Gentier, S., and Iwano, M. (1995). “Characterisation of fracture apertures - methods and parameters,” in 8th ISRM congress.

Google Scholar

He, C., Zhao, L., Song, H., and Fan, Z. (2022). Productivity prediction with consideration of stress-sensitive permeability in naturally fractured carbonate reservoir. Energy Explor. and Exploitation. 40(5):1426-1441. doi:10.1177/01445987211064675

CrossRef Full Text | Google Scholar

Hoss Belyadi, E. F. F. B. (2019). Hydraulic fracturing in unconventional reservoirs. 2nd Edition, 215–231.

Google Scholar

Jiang, T., Sun, H., and Deng, X. (2019). “Chapter 1 - typical characteristics of fractured vuggy carbonate gas reservoirs,” in Dynamic description technology of fractured vuggy carbonate gas reservoirs. Editors T. Jiang, H. Sun, X. Deng, T. Jiang, H. Sun, and X. Deng (Boston: Gulf Professional Publishing), 1–29.

Google Scholar

Jiao, C., He, S., Xie, Q., Gu, D., Zhu, H., Sun, L., et al. (2011). An experimental study on stress-dependent sensitivity of ultra-low permeability sandstone reservoirs. Acta Petrol. Sin. 32 (3), 489–494.

Google Scholar

Kang, H., Zhang, X., Si, L., Wu, Y., and Gao, F. (2010). In-situ stress measurements and stress distribution characteristics in underground coal mines in China. Eng. Geol. 116 (3), 333–345. doi:10.1016/j.enggeo.2010.09.015

CrossRef Full Text | Google Scholar

Keaton, J. R. (2017). “Angle of internal friction,” in Encyclopedia of engineering geology. Editors P. T. Bobrowsky, B. Marker, P. T. Bobrowsky, and B. Marker (Cham: Springer International Publishing), 1–2.

CrossRef Full Text | Google Scholar

Kim, D., and Ha, S. (2014). Effects of particle size on the shear behavior of coarse grained soils reinforced with geogrid. Materials 7, 963–979. doi:10.3390/ma7020963

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, D., Yang, X., and Chen, J. (2017). A study of Triaxial creep test and yield criterion of artificial frozen soil under unloading stress paths. Cold Regions Sci. Technol. 141, 163–170. doi:10.1016/j.coldregions.2017.06.009

CrossRef Full Text | Google Scholar

Li, Q., Li, Q., Wang, F., Wu, J., and Wang, Y. (2024). The carrying behavior of water-based fracturing fluid in shale reservoir fractures and molecular dynamics of sand-carrying mechanism. Processes 12 (9), 2051. doi:10.3390/pr12092051

CrossRef Full Text | Google Scholar

Li, Y., Wang, J., Li, C., Xie, J., and Wu, R. (2023). Fracture modeling of carbonate rocks via radial basis interpolation and discrete fracture network. Carbonates Evaporites 38 (4), 85. doi:10.1007/s13146-023-00904-7

CrossRef Full Text | Google Scholar

Martyushev, D. A., Ponomareva, I. N., Davoodi, S., and Kadkhodaie, A. (2024). Interporosity flow between matrix and fractures in carbonates: a study of its impact on oil production. Arabian J. Sci. Eng. doi:10.1007/s13369-024-09533-1

CrossRef Full Text | Google Scholar

Meng, Q., and Hodgetts, D. (2019). Combined control of décollement layer thickness and cover rock cohesion on structural styles and evolution of fold belts: a discrete element modelling study. Tectonophysics 757, 58–67. doi:10.1016/j.tecto.2019.03.004

CrossRef Full Text | Google Scholar

Meng, Z., Zhang, J., and Wang, R. (2011). In-situ stress, pore pressure and stress-dependent permeability in the Southern Qinshui Basin. Int. J. Rock Mech. Min. Sci. 48 (1), 122–131. doi:10.1016/j.ijrmms.2010.10.003

CrossRef Full Text | Google Scholar

Nelson, R. A. (1985). Geologic analysis of naturally fractured reservoirs. Houston, TX: Gulf Publishing Company.

Google Scholar

Rackley, S. A. (2017). “Preface to the second edition,” in Carbon capture and storage. Second Edition (Boston: Butterworth-Heinemann).

Google Scholar

Rashid, F., Hussein, D., Lawrence, J. A., and Ahmed, Z. (2021). Fluid flow and permeability analysis of tight gas carbonate reservoir rocks using fractures and dynamic data. J. Nat. Gas Sci. Eng. 90, 103894. doi:10.1016/j.jngse.2021.103894

CrossRef Full Text | Google Scholar

Rashid, F., Hussein, D., Lorinczi, P., and Glover, P. W. J. (2023). The effect of fracturing on permeability in carbonate reservoir rocks. Mar. Petroleum Geol. 152, 106240. doi:10.1016/j.marpetgeo.2023.106240

CrossRef Full Text | Google Scholar

Rosato, D., and Rosato, D. (2003). “6 - PLASTIC PERFORMANCE,” in Plastics engineered product design. Editors D. Rosato, D. Rosato, D. Rosato, and D. Rosato (Amsterdam: Elsevier Science), 381–438.

CrossRef Full Text | Google Scholar

Ruistuen, H., Teufel, L. W., and Rhett, D. (1999). Influence of reservoir stress path on deformation and permeability of weakly cemented sandstone reservoirs. SPE Reserv. Eval. and Eng. 2 (03), 266–272. doi:10.2118/56989-pa

CrossRef Full Text | Google Scholar

Sheng, J. J. (2013). “Chapter 12 - surfactant enhanced oil recovery in carbonate reservoirs,” in Enhanced oil recovery field case studies. Editors J. J. Sheng, and J. J. Sheng (Boston: Gulf Professional Publishing), 281–299.

Google Scholar

Tiab, D., and Donaldson, E. (2016). Petrophysics: theory and practice of measuring reservoir rock and fluid transport properties. Second Edition. Boston: Gulf Professional Publishing, 1008.

Google Scholar

Wang, S., Ma, M., Ding, W., Lin, M., and Chen, S. (2015). Approximate analytical-pressure studies on dual-porosity reservoirs with stress-sensitive permeability. SPE Reserv. Eval. and Eng. 18 (04), 523–533. doi:10.2118/174299-pa

CrossRef Full Text | Google Scholar

Wei, Z., Yang, K., Chi, X., Liu, W., and Zhao, X. (2021). Dip angle effect on the main roof first fracture and instability in a fully-mechanized workface of steeply dipping coal seams. Shock Vib. 2021, 5557107. doi:10.1155/2021/5557107

CrossRef Full Text | Google Scholar

Yu, W., and Sepehrnoori, K. (2018). “Chapter 2 - numerical model for shale gas and tight oil simulation,” in Shale gas and tight oil reservoir simulation. Editors W. Yu, K. Sepehrnoori, W. Yu, and K. Sepehrnoori (Boston: Gulf Professional Publishing), 11–70.

Google Scholar

Zahedi, S. A., Kodsi, C., and Berto, F. (2019). Numerical predictions of U-notched sample failure based on a discrete energy argument. Theor. Appl. Fract. Mech. 100, 298–306. doi:10.1016/j.tafmec.2018.12.014

CrossRef Full Text | Google Scholar

Zeng, J., Guo, J., Ren, J., Zeng, F., Gou, B., and Liu, Y. (2021). “Well performance evaluation of carbonate reservoirs after a novel hybrid volume stimulation treatment,” in SPE/IATMI Asia pacific oil and gas conference and exhibition, D031S030R003.doi:10.2118/205538-MS

CrossRef Full Text | Google Scholar

Zhang, J. J. (2019). “Chapter 2 - rock physical and mechanical properties,” in Applied Petroleum Geomechanics. Editor J. J. Zhang (Boston: Gulf Professional Publishing), 29–83.

Google Scholar

Zhu, H., Han, L., Meng, L., Dong, W., and Yan, S. (2022). True triaxial experimental study on fluid flow in single fracture with different dip angles under three-dimensional stress at different depths. J. Petroleum Sci. Eng. 211, 110193. doi:10.1016/j.petrol.2022.110193

CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., and Pande, G. N. (1977). Time-dependent multilaminate model of rocks—a numerical study of deformation and failure of rock masses. Int. J. Numer. Anal. Methods Geomechanics 1, 219–247. doi:10.1002/nag.1610010302

CrossRef Full Text | Google Scholar