
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 13 December 2024
Sec. Geohazards and Georisks
Volume 12 - 2024 | https://doi.org/10.3389/feart.2024.1515670
This article is part of the Research TopicFailure Analysis and Risk Assessment of Natural Disasters Through Machine Learning and Numerical Simulation: Volume IVView all 22 articles
This study investigates the effects of interface shape and bonding conditions on the side friction resistance of the cast-in-place pile in coral reef limestone stratum of the China-Maldives Friendship Bridge area. Large-scale direct shear tests are performed on the coral reef limestone-concrete interface to investigate the exertion mechanism of interfacial strength. A finite-discrete element coupling method (FDEM) is employed to develop a constitutive model for coral reef limestone. A numerical calculation method for the side friction resistance capacity of pile foundations in coral reef limestone strata is proposed based on the bearing characteristics of side friction resistance in pile-coral reef limestone interactions. The shear tests on seven shapes of pile-rock interfaces indicate that bonding condition is the primary factor influencing interface strength, while interface shape has a minimal impact. The cement slurry fills the pores to form an interface reinforcement that possesses a strength greater than that of the coral reef limestone. The computational results from the constitutive model of coral reef limestone match well with the laboratory test results, demonstrating that the FDEM can effectively simulate the effects of high porosity and bonding strength on the mechanical properties of coral reef limestone. The FDEM-based numerical results for the interface strength between cast-in-place pile and coral reef limestone exhibit good consistency with the laboratory shear test results, which validates the effectiveness and accuracy of the numerical calculation method for side friction resistance of cast-in-place pile in coral reef limestone strata. These findings can provide valuable reference for the design and construction of pile foundations in marine island and reef projects.
Coral reefs are geological structures formed from the remnants of reef-building coral colonies after their death over a long geological period (Cortés, 1997). The Great Barrier Reef in Australia (Scoffin and Tudhope, 1985) and the Maldives (Agassiz, 1903) are prominent examples of such formations (Sun and Huang, 1999). Different from the high-temperature and high-pressure diagenesis of land-sourced rocks (Dorobek, 1984), coral reef limestone is formed through biochemical cementation, compaction, and cold metamorphic (Nohl and Munnecke, 2019), and thus coral reef rocks are characterized by high porosity (Armstrong et al., 1980), low strength (Burton et al., 2001), and brittleness (Madin, 2005; Clark and Walker, 1977).
Research on the engineering mechanical properties of coral reef sediments and the load-bearing characteristics of pile foundations in these strata began internationally in the 1970s (Ghazali et al., 1990). Areas involved in the design and construction of offshore platform pile foundations include Australia (Nyland, 1988), South Africa (Ebelhar et al., 2021), the Bass Strait (Angemeer et al., 1973), the Philippines (Dutt et al., 1985), the Suez Bay (Dutt and Cheng, 1984), the Red Sea (Hagenaar, 2021; Ghazali et al., 1988), and Cuba (Puech et al., 1990). Researchers have investigated the vertical load-bearing capacity of pile foundations in coral reef strata and have proposed load-bearing capacity parameters as well as design and construction methods for piles. Falney and Jewell (1988) and Ghazali et al. (1988); Ghazali et al. (1987) conducted field comparative tests on driven piles and bored cast-in-place post-grouting piles based on the NRA platform area of the northwest Australian continental shelf and the coral reef strata offshore the Red Sea, respectively. Their findings indicated that the load-bearing capacity of driven piles in coral reef strata is significantly lower than that of bored cast-in-place post-grouting piles (Zhang et al., 2022a). To ascertain the vertical load-bearing capacity of piles, numerous researchers have examined the mechanical properties of the pile-coral reef limestone interface. Ooi and Carter (1987) performed direct shear tests on coral reef limestone under constant normal stiffness conditions and suggested that the shear strength of the concrete-coral reef limestone is related to its interface shape. Indraratna et al. (Indraratna et al., 1998) demonstrated that the interface dilation angle under constant normal stress condition was greater than that under constant normal stiffness condition, while the peak shear stress was lower under constant normal stiffness condition. Liu et al. (Liu et al., 2021)and Li et al. (Li et al., 2022) analyzed the mechanisms behind the high strength at the coral reef limestone interface from a microstructural perspective. They stated that due to the high porosity of coral reef limestone, the cement slurry diffuses extensively within it, leading to the formation of embedded occlusal and strongly cemented reinforcement at the concrete-coral reef limestone interface. Wan (WAN et al., 2021) confirmed through static load tests on end post-grouting piles that the pressure grout can fill the voids and cavities in the rock mass, thereby improving weak areas within the coral reef limestone strata. Existing research indicates that pile foundations in coral reef limestone strata exhibit high side friction resistance capacity (Fan et al., 2023a); however, the load-bearing mechanisms of these piles are not well understood (Fan et al., 2022), and there is a lack of theoretical and computational methods for assessing the side friction resistance capacity of pile foundations in coral reef limestone strata (Fan et al., 2023b).
The combined finite discrete element method (FDEM) is an efficient method for simulating the entire process of rock materials from fracture to failure. Since its proposal by Munjiza et al. (1995), this method has been widely applied in the field of geotechnical engineering. FDEM is not limited by the number of cracks and can simulate the entire process of rock materials in indoor tests such as uniaxial compression and direct shear (Liu et al., 2024). FDEM has demonstrated strong numerical simulation capabilities in predicting crack propagation in rock materials. Zheng et al. (2023) proposed an improved joint element constitutive model for finite discrete element method (FDEM). The revised model addresses the stress on both sides of the crack by considering the aperture of the fracture joint element rather than the contact. Hu et al. (2024) used a combination of finite element and discrete element methods (FDEM) to study the mechanical properties of rockfill materials and developed an improved constitutive model that can effectively capture their hysteresis behavior. At present, there are no FDEM program development cases for the constitutive model of reef limestone. Reef limestone is a porous cemented rock and soil material, and its instability and disintegration process belongs to a large deformation discontinuous mechanical phenomenon. FDEM can accurately and efficiently describe the failure process of reef limestone.
This study firstly performs large-scale direct shear tests on cast-in-place pile-coral reef limestone and analyzes the failure mechanism of the cast-in-place pile-coral reef limestone interface. Subsequently, based on the mechanical properties of coral reef limestone, the FDEM is used to develop a constitutive model for coral reef limestone, which is then validated against results from laboratory uniaxial compression tests. Finally, based on the bearing characteristics of side friction resistance in pile-coral reef limestone interactions, a numerical method for calculating the side friction resistance capacity of pile foundations in coral reef limestone strata is proposed.
Coral reef limestone is brittle and porous, which makes it prone to forming jagged interfaces during grouting and hole formation. Based on the field scan results from the China-Maldives Friendship Bridge, as shown in Figures 1A, B, the interface shapes are classified into seven types: vertical pile, sloped jagged, stepped jagged, outer arc jagged, outer V-shaped jagged, inner arc jagged, and inner V-shaped jagged. Shear tests are conducted for each type. To ensure sampling quality, coral reef limestone with lower porosity is selected. Fine processing of coral reef limestone, partially prepared into blocks with dimensions of 100 mm × 100 mm × 50 mm, and partially made into irregular rock samples based on the actual dimensions of each working condition. C30 concrete with standard dimensions of 150×150×50 mm is used to simulate the pile foundation and modify the shape of the concrete according to the corresponding irregular rock sample. Three sets of tests are conducted for each interface shape under normal stresses of 100, 200, and 400 kPa. Concrete is cast on coral reef limestone with different interface shapes. The sample sizes and molding effects are illustrated in Table 1. Loading is performed using a DZJ-15 direct shear apparatus (Li et al., 2023). Considering the effect of loading rate on shear test results (Tang and Wong, 2016), the preloading rate for normal stress is set at 0.1 kN/s, and the shear rate is 0.002 mm/s.
Various failure modes from the interface shear tests are displayed in Figure 2. Figures 2A–D show the results of interface failure under normal pressures of Vertical pile, Sloped jagged, Outer arc jagged, and Outer V-shaped jagged, respectively. Due to the high porosity of coral reef limestone, the cement slurry fills the pores to form an interface reinforcement with strength greater than the coral reef limestone. Most failure surfaces are located within the coral reef limestone, which indicates that the bearing mechanism of the pile side friction resistance in coral reef limestone strata is rock failure rather than interface friction (Zhao et al., 2020).

Figure 2. Failure modes of each interface shape. (A) Vertical pile; (B) Sloped jagged; (C) Outer arc jagged; (D) Outer V-shaped jagged.
The shear stress-shear displacement curve for the vertical pile interface is displayed in Figure 3A. The shear stress-shear displacement curve for the sloped jagged interface is displayed in Figure 3B. The shear stress-shear displacement curve for the stepped jagged interface is illustrated in Figure 3C. The shear stress-shear displacement curve for the outer arc jagged interface is depicted in Figure 3D. The shear stress-shear displacement curve for the outer V jagged interface is shown in Figure 3E. The shear stress-shear displacement curve for the inner arc jagged interface is shown in Figure 3F. The shear stress-shear displacement curve for the inner V jagged interface is presented in Figure 3G. The peak cohesion and friction angle of the interface shear test are summarized in Table 2.(Zhao and Liu, 2012).
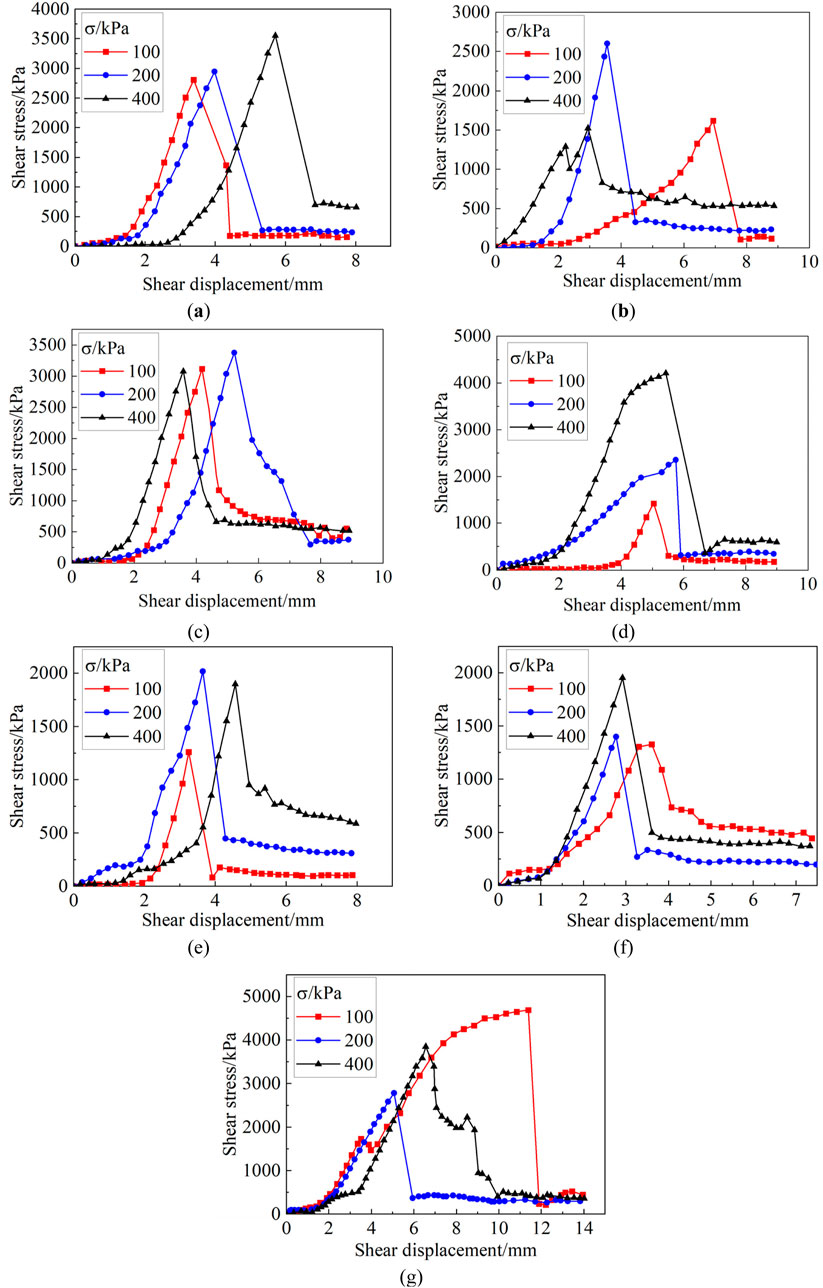
Figure 3. Shear stress and displacement curve of interface shear test. (A) vertical pile interface.; (B) sloped jagged interface; (C) stepped jagged interface; (D) jagged interface; (E) V-shaped jagged interface; (F) inner arc jagged interface; (G) inner V-shaped jagged interface.
In Figures 3B, C, E, G, there are some cases where the confining pressure is high but the peak strength of the rock is low. This is because coral reef limestone is a porous bonding material with high brittleness and fragility. Therefore, when the confining pressure is high, the reef limestone may undergo local fragmentation, leading to lower peak strength.
During concrete casting, the shear stress-shear displacement curve is given in Figure 4. Figures 4A–C show the results corresponding to vertical pressures of 100kPa, 200kPa, and 400kPa, respectively. The shear displacement initially increases rapidly with shear stress, then drops sharply and stabilizes (Zhao et al., 2019). The residual shear strength is about 5%–10% of the interface shear strength, and the failure strain is about 2%–4%.
The influence of normal stress on the shear strength of cast samples is presented in Figure 5. For the same interface shape, normal stress has little effect on interface shear strength (Zuo et al., 2024). For the same normal stress, there is no significant relationship between interface shape and shear strength. Overall, the bonding condition of the interface has a greater impact on shear strength than the interface shape.
Regarding the degree of interface bonding, the shear strengths of jagged and vertical pile interfaces under different normal stresses are displayed in Figure 6. Both have similar bonding strengths of about 2.6 MPa. The saturated uniaxial compressive strength ranges from 6.0 MPa to 7.6 MPa, and the ratio of interface bonding strength to uniaxial compressive strength is about 0.34–0.43.
According to the typical shear stress-shear displacement curve shown in Figure 7, the exertion of interface shear strength can be divided into five stages: initial stage, compaction stage, bearing stage (elastic deformation stage), failure stage, and friction stage. The characteristics of each stage are presented in Figure 8.
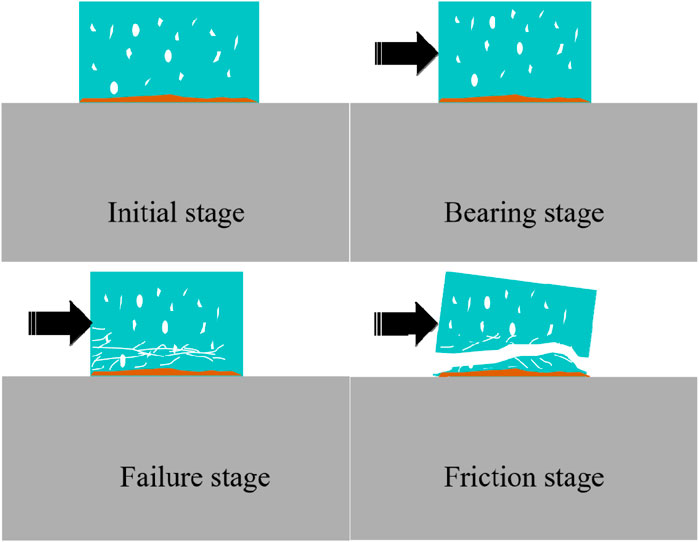
Figure 8. Mechanism diagram of interface interaction between cast-in-place pile and coral reef limestone.
Initial Stage: The high-porosity coral reef limestone bonds with the concrete interface. The cement slurry fills the pores of the coral reef limestone near the interface to form an interface reinforcement with strength greater than that of the coral reef limestone.
Bearing stage: At the beginning of loading, the pores of the coral reef limestone near the interface reinforcement are compacted, and the shear stress increases non-linearly with shear displacement. As shear displacement increases, the compaction of the pores near the interface reinforcement is completed, and shear stress increases linearly at a rate higher than that in the compaction stage. The rock sample, interface reinforcement, and concrete are in an elastic state, in which the bonded elements of the rock sample bear the load.
Failure stage: As loading progresses, cracks start to develop in the weaker areas near the lower part of the loading point. The bonded elements begin to transform into frictional elements, while the coral reef limestone farther from the loading point remains undamaged. This asynchronous damage generates an uneven sliding surface with an upward trend. As shear displacement further increases, the interface strength is gradually controlled by the tensile strength of the coral reef limestone. Once interface strength exceeds the tensile strength, the cracks penetrate, and the shear stress drops rapidly.
Friction stage: As shear displacement continues to increase, the rock sample slid along the penetrated cracks, and the shear stress remains unchanged. At this stage, the frictional elements of the rock sample bear the load (Huang et al., 2024).
In summary, the majority of the failure zone at the pile-coral reef limestone interface was located within the coral reef limestone. Initially, the interface strength was controlled by the shear strength of the coral reef limestone, resulting in the formation of an uneven sliding surface. Later, it was controlled by the tensile strength of the coral reef limestone, leading to the penetrative failure. Overall, the interface strength of the pile-coral reef limestone is the result of the combined effects of the tensile and shear strengths of the coral reef limestone.
Figure 9A shows the physical image of cement slurry filling the pores of reef limestone (Wang et al., 2024). It can be clearly seen from the figure that the gray cement slurry penetrates into the pores of the reef limestone, filling the pores and forming a denser interface. Figure 9B shows the microscopic interface image of the bond between the reef limestone and concrete (Cheng et al., 2022). From the image, it can be seen that the concrete fills the pores of the reef limestone, forming a more tightly embedded interface reinforcement at the interface between the two. Compared with the original porous state, this interface reinforcement significantly improves the stress characteristics of the interface between the reef limestone and concrete. Therefore, most shear failure surfaces do not occur at the interface and are located inside the reef limestone with more pores (Cheng et al., 2024).

Figure 9. Macroscopic and microscopic images of the bonding interface between reef limestone and concrete. (A)Physical picture of cement slurry filling the pores of reef limestone; (B) Microscopic image of the interface between reef limestone and concrete after bonding.
The understanding of the strength exertion mechanism of the pile-coral reef limestone interface discussed in the previous section reveals that developing a constitutive model suitable for coral reef limestone is crucial for the analysis of vertical load-bearing of piles. Assuming that the damage to coral limestone follows a Weibull distribution, a combined macro-micro approach is used to propose an elastoplastic damage constitutive model considering the bonding properties and porosity of coral reef limestone (Chen et al., 2023; Zhang et al., 2022b). This model reveals the strength exertion mechanism and evolution law of coral reef limestone. During the programming of the elastoplastic constitutive model for coral reef limestone, problems such as non-convergence of strain-softening integration and difficulty in determining the post-softening modulus generally arise, which makes secondary development based on large finite element programs challenging. This study focuses on the calculation of the vertical load-bearing capacity of piles in coral reef limestone strata and the engineering practice, with emphasis on the stage from the onset of strength exertion to peak strength. The programming procedure for the proposed constitutive model of coral reef limestone is as follows. The coral reef limestone at the early stage of loading is a bonded continuous medium, which can be simulated by the finite element method with high computational efficiency. In the middle and later stages of loading, the bonded material of the coral reef limestone gradually fails and disintegrates, while the load mainly carried by friction between particles, which can be simulated by the discrete element method. Throughout the process, joint elements are used to identify and store the transition from bonded elements to frictional elements.
The finite-discrete element coupling method (FDEM) that integrates the finite element method based on constitutive relationships and the discrete element method based on contact rules allows for detailed analysis of the whole failure process (Gibson, 1997).
Before loading, the foundation or structure is divided into variable triangular elements. Joint elements, which have no thickness, are embedded between the triangular elements to connect them. After loading, the triangular elements are calculated according to the principles of the finite element method to obtain their stresses and displacements. When the stress state of certain elements reaches the failure criterion, the elements break at the joints and become rigid triangles. The movement, collision, and friction of the rigid bodies are computed with the rigid body dynamics to achieve continuous to discrete computations. Locally broken triangular rigid bodies transmit forces and displacements through nodes at the contact points of the original continuous medium (Amiri et al., 2024).
Each discrete element in the FDEM model corresponds to an independent mesh, which determines the shape, boundary, and contact relationships between discrete elements. The interaction between discrete elements can cause the elements to fracture and break, so as to generate more elements and contact interactions. Special treatments of element contacts are required to avoid overlapping between elements during calculations and to accurately analyze each contact relationship. The contact interaction algorithm can simulate the interactions after discrete elements come into contact. It searches among numerous discrete elements and once contact is detected between a group of elements, it computes the interaction force between the two elements. The interactions between discrete bodies in FDEM can be calculated using a potential function, where the discrete bodies at the contact points can penetrate each other to form distributed contact forces, as illustrated in Figure 10.
The FDEM model employs triangular elements to describe two-dimensional problems (Figure 11), with element division directly following the meshing rules of the finite element method. The discrete fracture model is crucial for the transition from continuous to discontinuous behavior in FDEM. This model introduces a joint cohesion element, which has no thickness, connects adjacent triangles, and contacts the four endpoints of the neighboring edges, between two triangular elements. This joint element, which has no thickness but possesses a certain strength, does not exist in reality, and it becomes active only when the joint or triangular elements break.
The joint element has two failure modes: 1) Tension failure mode, where adjacent elements experience relative motion perpendicular to their shared edge, and tensile strength determines the peak strength prior to cracking. 2) Shear failure mode, where adjacent elements undergo relative motion parallel to their shared edge, and frictional force that is governed by the Mohr-Coulomb criterion determines the peak strength before cracking. Once the fracture energy of the material is fully released, the joint cohesion element ruptures, leading to the formation of real joints corresponding to the cracks generated by the joint element. The damaged joint elements are simultaneously removed from the continuous calculation cycle, thus completing the transition from continuous to discontinuous behavior. The constitutive form of the fracture unit is shown in Figure 12.
Changes, damage, yielding, or failure of the microscopic structural elements is the root cause of the eventual fracture of the material. Given the potential defects and stress concentration within the material, the fracture model in the program needs to be modified. The FDEM employs a strain-based cohesive crack model that integrates single crack and dispersed crack models, and its computational process is illustrated in Figure 13.(Li et al., 2024)
First, the finite element program computes the stress and strain fields of coral reef limestone in the elastic stage, after which the data are imported into a discrete element program to analyze the process from crack propagation to rock failure. The detailed steps are as follows.
① Use preprocessing software to output the ELIST.lis (element information file), NLIST.lis (node information file), and DLIST.lis (load information file).
② Employ an existing format conversion program to convert the three files into formats recognizable by the computational program, i.e., n.y (node file) and e.y (element file).
③ Input the determined parameters into the *.y files according to the specified format.
④ Use the computational program to compute the set file information.
⑤ The LS-PrePost post-processing software visualizes the generation, development, and penetration of cracks in the sample, as well as the disintegration, rolling, and collision of elements. It also simultaneously outputs the shear force-displacement curves.
The parameters required for analyzing the mechanical properties of coral reef limestone using FDEM are divided into two main categories: 1) structural element parameters, and 2) joint element parameters. Structural element parameters primarily include Lamé constants λ and μ, density, viscous damping, friction coefficient, normal contact penalty function factor, and tangential contact penalty function factor. Joint element parameters include tensile strength, maximum fracture energy, cohesion, friction coefficient, and fracture penalty function factor. The Lamé constants can be derived from the elastic modulus and Poisson’s ratio. In conjunction with the constitutive model for coral reef limestone, the expression of elastic modulus considering mesoscale parameters is shown in Equation 1, where parameter a is the expression of elastic modulus and shear modulus, as shown in Equation 2, the expression of shear modulus is shown in Equation 3, and the expression of Lame constant is shown in Equation 4.
This study adopts the viscous damping formula proposed by Munjiza (Munjiza and Latham, 2004), where the viscous damping is ks=2.9 × 107. The values of the normal and tangential penalty function factors are related to computational time and accuracy (Mahabadi, 2012).
The mechanical analysis program for coral reef limestone is developed based on the constitutive model of coral reef limestone. Firstly, it is necessary to clarify the constitutive model of coral reef limestone and obtain relevant parameter values through relevant experiments. Among them, the porosity is determined as
To demonstrate the reliability of the rock constitutive model, the stress-strain curves of reef limestone under uniaxial compression were compared and verified with the calculated results of the model, as shown in Figure 15. The calculation parameters are as follows: the porosity of samples I, II, and III is 0.17, 0.20, and 0.18, respectively; The values of
To validate the reliability of the FDEM-based mechanical analysis method for coral reef limestone (Zhang et al., 2024a), a numerical model is established, as displayed in Figure 14. The model parameters are taken from corresponding test values of coral reef limestone. For the main structural element parameters, the density, friction coefficient, as well as tangential and normal penalty factors are set at 2,150 kg/m³, 0.55, 45 MPa, and 450 MPa, respectively. For the joint element parameters, the tensile strength, fracture energy, cohesion, internal friction coefficient, and fracture penalty factor are at 2.30 MPa, 25 g/s2, 130 kPa, 0.65, and 3.5 GPa, respectively. The viscous damping ks is set at 2.9 × 107 kg/(m.s) (Wang et al., 2023; Meng et al., 2024).
The stress-strain relationships at different porosities and bonding strengths are depicted in Figure 15. Figures 15A–C correspond to the results of Sample I, Sample II, and Sample III, respectively. In the early stage of loading, the stress gradually increases and peaks with occurrence of strain softening. In contrast to the measured values and the elastoplastic model for coral reef limestone that accounts for porosity and bonding characteristics, the strain-softening phenomenon is more pronounced in the FDEM-based numerical simulation. The main reason is that the FDEM does not account for the connections between macro and micro scales and suffers from certain defects in describing the prevalent joint load-bearing behavior of bonded and frictional elements. In summary, the FDEM can effectively simulate the effects of high porosity and bonding strength on the mechanical properties of coral reef limestone.
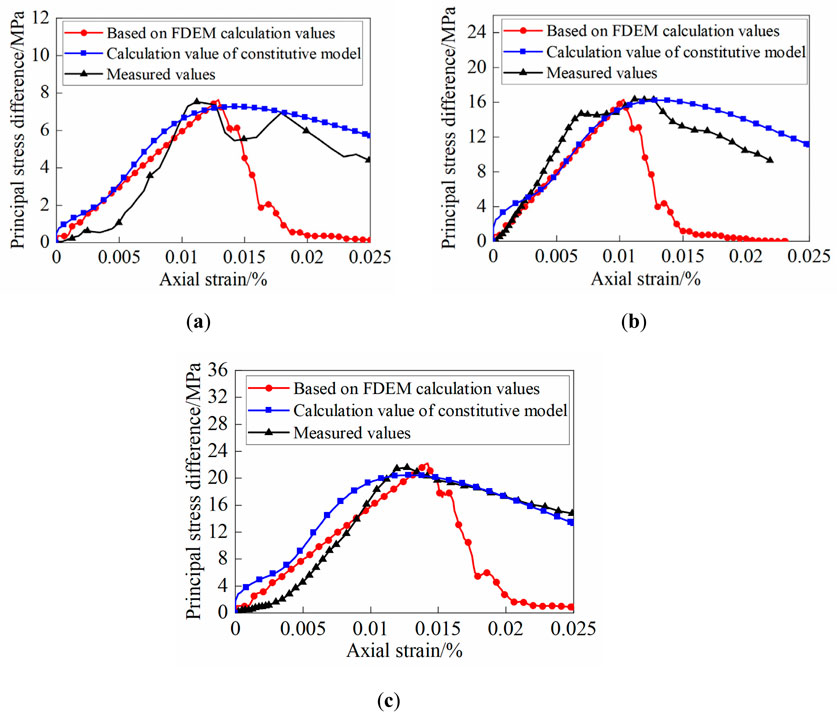
Figure 15. Comparison between calculated values of coral reef limestone (based on FDEM calculation and constitutive model calculation) and measured values. (A) Sample I; (B) Sample II; (C) Sample III.
Shear tests on the pile-coral reef limestone interface indicate that the cement slurry fills the pores of the coral reef limestone to an interface reinforcement. This results in most failure surfaces being located within the coral reef limestone, while the interface shape has minimal impact on the side friction resistance. The pile-coral reef limestone interface characteristics can be simulated using either shared nodes or interface reinforcement. Since the latter approach requires consideration of factors such as porosity and the range of the reinforcement, this study employs the shared node approach.
The FDEM for assessing the side friction resistance capacity of the pile in coral reef limestone strata requires determining three key parameters: 1) structural element parameters; 2) joint element parameters; and 3) loading block parameters. Structural and joint element parameters are obtained from laboratory test data of the coral reef limestone. The stiffness of the loading block should be maximized within permissible limits, with Lamé constants set at λ = 4.8 × 1012 and μ = 8.5 × 1012, and a friction coefficient of 0.1 to avoid dispersion of the computational domain. Since the loading block is not meshed, parameters such as viscous damping, normal penalty function factor, and tangential penalty function factor are not meaningful and can be selected based on the rules of the structural block. Considering factors such as peak material strength, elastic modulus, Poisson’s ratio, and time step, the fracture penalty function factor is set at five times the elastic modulus, i.e., 10 × 1010, while the maximum fracture energy is set at 20 g/s2. The chosen parameters for various elements are detailed in Table 4.
The numerical simulations are compared with experimental results to verify the reliability of the simulation approach. The interface shear strength tests can be simplified into a two-dimensional problem, and then a two-dimensional model can be established, as presented in Figure 16. The concrete part is 150 mm long and 50 mm high (blue part), while the coral reef limestone measures 100 mm in length and 50 mm in height (green part), with a large stiffness loading block on the left side (red part). The meshing is performed using the meshing tool in the computational program based on solid-4 node 182 elements, with a minimum mesh size of 2 mm.
Through repeated trial calculations, the time step and loading block velocity are determined to be 5 × 10−6 s and 0.25 m/s, respectively. The analysis focuses on a shear test with a vertical load of 100 kPa to examine the interface failure process during loading. At loading time t = 0 m, the failure status of the model is illustrated in Figure 17, where the joint elements between the structural and concrete elements are undamaged, with no cracks present.
At loading time t = 30 m, the failure status of the model is depicted in Figure 18. In the early loading stage, the stress field of the elements connecting the structural and loading blocks is disturbed, while the joint elements begin to fail (green), but the cracks are not fully developed. The cracks appear, extend, and widen within the joint elements between the structural block and the concrete. The fracture surface begins to penetrate, forming long and narrow gaps that eventually propagate along the contact surface.
At the loading time t=50 m, the failure state of the model is shown in Figure 19. As the loading continues, the stress field of the components connecting the structure and the loading block is disturbed, causing the connecting components to fail and cracks to fully develop. Cracks appear, extend, and widen within the joint elements between structural blocks and concrete. The fracture surface begins to penetrate, forming narrow gaps and eventually propagating along the contact surface.The shape of the crack shows a slight upward trend, indicating that the failure location of the fracture is located inside the reef limestone.
Figure 20 compares the simulation results under various vertical stresses with the shear test results of planar concrete and coral reef limestone. Figures 20A–C correspond to the results of vertical pressures of 100kPa, 200kPa, and 400kPa, respectively. As shear displacement increases, the shear force first increases, then decreases, and finally stabilizes, and the peak shear force rises gradually as vertical stress increases. The reasons for this phenomenon are as follows. As horizontal shear displacement increases, the shear force gradually rises to a peak. However, the generation and propagation of cracks on the contact surface leads to a decrease in shear strength. With increasing vertical stress, the interlocking and embedding effects occur between contact surface elements, causing an increase in friction, which consequently enhances the shear strength. The experimental and simulation curves exhibit similar trends under various vertical stresses, suggesting that the FDEM effectively simulates the side friction resistance characteristics of the concrete-coral reef limestone interface.
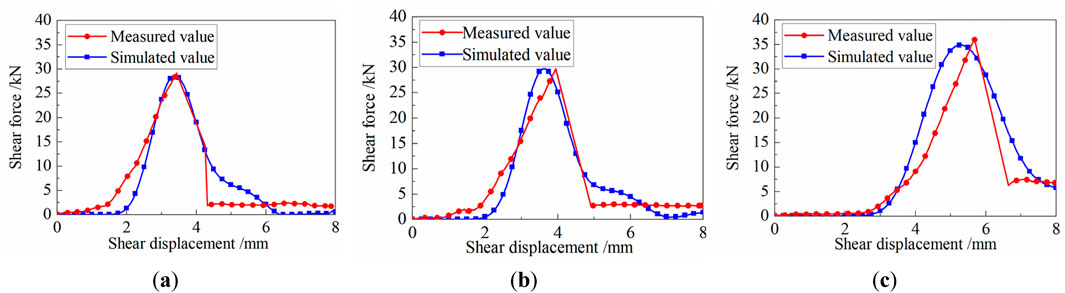
Figure 20. Comparison of simulated and measured shear force vs. shear displacement. (A) 100kPa; (B) 200kPa; (C) 400 kPa.
The calculation Formula 5 for the allowable axial compressive bearing capacity of single rock socketed drilled piles in the “Code for Design of Highway Bridge and Culvert Foundation”.
In the formula:
After studying the mechanism of lateral resistance in the injection section of coral reef limestone, combined with the FDEM calculation method of coral reef limestone, it is recommended to revise the value of the lateral resistance coefficient
In the light of the high efficiency of side friction resistance exertion of cast-in-place piles in coral reef limestone strata (Pitchumani et al., 2024), this study firstly examines the mechanical properties of the pile-coral reef limestone interface (Zhang et al., 2024b). After that, a computational program for the constitutive model of coral reef limestone is developed, which is validated through laboratory uniaxial compression tests. Finally, a numerical method for calculating pile side friction resistance applicable to coral reef limestone strata is proposed based on the exertion characteristics of side friction resistance in pile-coral reef limestone interactions. The following conclusions are drawn.
(1) The interface between coral reef limestone and case-in-place pile can be categorized into seven types: vertical pile, sloped jagged, stepped jagged, outer arc jagged, outer V-shaped jagged, inner arc jagged, and inner V-shaped jagged. The bonding strength has a significant impact on the interface strength, while the interface shape has a relatively small impact on it.
(2) The shear process at the pile-coral reef limestone interface consists of initial stage, compaction stage, bearing stage, failure stage, and friction stage. Most shear failure surfaces are located within the coral reef limestone, which is primarily due to its high porosity. The cement slurry fills these pores to form an interface enhancement with strength greater than that of the coral reef limestone. Under shear stress, the internal pores of the coral reef limestone become the relatively weak points that fail first.
(3) Based on the unique phenomenon of the prevalent coexistence of bonding and damage in coral reef limestone, a finite-discrete element coupling method, in which the undamaged and damaged coral reef limestones are simulated by finite and discrete elements, respectively, and the damage process is judged by joint elements, is proposed to realize the programming development of the constitutive model for coral reef limestone. Based on the exertion mechanism of the pile-coral reef limestone interface strength, a shared node interface treatment method is proposed to consider porosity and interface reinforcement, which addresses the computational issues at the interface between case-in-place pile and coral reef limestone. Finally, a numerical method for calculating side friction resistance of the case-in-place pile in coral reef limestone strata is proposed.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
YZ: Conceptualization, Funding acquisition, Methodology, Writing–review and editing. RZ: Formal Analysis, Software, Validation, Visualization, Writing–original draft. PC: Data curation, Writing–review and editing. FJ: Resources, Writing–review and editing. HL: Investigation, Writing–review and editing. EL: Project administration, Supervision, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Natural Science Foundation of Hubei Province of China (Grant No.2023AFB508) and Open Research Fund of State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences (Grant No. SKLGME022032).
Authors YZ, RZ, PC, FJ and HL were employed by CCCC Second Harbour Engineering Company Ltd.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declare that no Generative AI was used in the creation of this manuscript.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Amiri, F., Bahrani, N., Lisjak, A., Mahabadi, O., Ha, J., and Li, Y. (2024). Influence of unloading-induced brittle damage on laboratory properties and behavior of hard rocks: insights from the hybrid Finite-Discrete Element Method (FDEM). Comput. Geotechnics 176, 106766. doi:10.1016/j.compgeo.2024.106766
Angemeer, J., Carlson, E. G., and Klick, J. H. (1973). Techniques and results of offshore pile load testing in calcareous soils. Offshore Technol. Conf. doi:10.4043/1894-MS
Armstrong, A. K., Snavely, P. D., and Addicott, W. O. (1980). Porosity evolution of upper Miocene reefs, Almeria Province, southern Spain. AAPG Bull. 64, 188–208. doi:10.1306/2f918950-16ce-11d7-8645000102c1865d
Burton, C., Waltham, A., and Mclaren, S. (2001). Strength variation in young reef limestones. Geotechnique 51, 887–889. doi:10.1680/geot.2001.51.10.887
Cheng, Y., Song, Z., Xu, Z., Yang, T., and Tian, X. (2024). Failure mechanism and infrared radiation characteristic of hard siltstone induced by stratification effect. J. Mt. Sci. 21, 1058–1074. doi:10.1007/s11629-023-8444-4
Cheng, Y., Song, Z., Yang, T., Han, J., Wang, B., and Zhang, Z. (2022). Investigating the aging damage evolution characteristics of layered hard sandstone using digital image correlation. Constr. Build. Mater. 353, 128838. doi:10.1016/j.conbuildmat.2022.128838
Chen, Y., Liu, E., Yu, Y., Luo, H., and Chen, P. (2023). A binary-medium-based constitutive model for porous rocks. Int. J. Rock Mech. Min. Sci. 164, 105345. doi:10.1016/j.ijrmms.2023.105345
Clark, A., and Walker, B. (1977). A proposed scheme for the classification and nomemclature for use in the engineering description on Middle Eastern sedimentary rocks. Geotechnique 27, 93–99. doi:10.1680/geot.1977.27.1.93
CortéS, J. (1997). Biology and geology of eastern Pacific coral reefs. Coral Reefs 16, S39–S46. doi:10.1007/s003380050240
Dorobek, S. L. (1984). Stratigraphy, sedimentology, and diagenetic history of the siluro-devonian helderberg group, central appalachians(carbonate sedimentology, diagenesis). Virginia Polytechnic Institute and State University.
Dutt, R., and Cheng, A. (1984). Frictional response of piles in calcareous deposits. Offshore Technol. Conf. doi:10.4043/4838-MS
Dutt, R., Moore, J., Mudd, R., and Rees, T. (1985). Behavior of piles in granular carbonate sediments from offshore Philippines. Offshore Technol. Conf. doi:10.4043/4849-MS
Ebelhar, R. J., Young, A. G., and Stieben, G. P. (2021). Cone penetrometer and conductor pullout tests in carbonate soils offshore Africa. Eng. Calcareous Sediments Vol. 1. doi:10.1201/9781003211433
Falney, M., and Jewell, R. (1988) “Model piles tests in calcarenite,” in International conference on calcareous sediments, 555–564.
Fan, K.-F., Cai, Z.-Y., Zhu, X., and Li, W.-X. (2023a). Investigation of natural frequency of wide-shallow composite bucket supported offshore wind turbine: application to real data. Ocean. Eng. 286, 115640. doi:10.1016/j.oceaneng.2023.115640
Fan, K.-F., Guan, Y.-F., Zhu, X., Li, W.-X., Tang, Y., and Chen, Y.-Y. (2023b). Investigation of composite bucket foundation bearing characteristics in various soil properties. Mar. Georesources and Geotechnol. 41, 1175–1186. doi:10.1080/1064119x.2022.2126338
Fan, K.-F., Li, W.-X., and Wang, Q.-Q. (2022). Horizontal bearing capacity of composite bucket foundation in clay: a case study. Eng. Fail. Anal. 140, 106572. doi:10.1016/j.engfailanal.2022.106572
Ghazali, F. M., Baghdadi, Z., and Mansur, O. (1990). A comparative study of pile foundations in coral formations and calcareous sediments. Eng. Sci. 2, 3–17. doi:10.4197/eng.2-1.1
Ghazali, F. M., Sotiropoulos, E., and Mansour, O. A. (1988). Large-diameter bored and grouted piles in marine sediments of the Red Sea. Can. Geotechnical J. 25, 826–831. doi:10.1139/t88-090
Gilchrist, J. M. (1985). Load tests on tubular piles in coralline strata. J. Geotechnical Eng. 111, 641–655. doi:10.1061/(asce)0733-9410(1985)111:5(641)
Hagenaar, J. (2021) “The use and interpretation of SPT results for the determination of axial bearing capacities of piles driven into carbonate soils and coral,” in Penetration testing (London, United Kingdom), Vol. 1. 51–55. doi:10.1201/9780203743959-8
Huang, J., Li, J., Li, M., Pan, Y., and Zong, Z. (2024). Dynamic response and failure mechanism of ocean coral reef limestone under high strain rate loading. Ocean. Eng. 299, 117370. doi:10.1016/j.oceaneng.2024.117370
Hu, J., Ma, G., Wang, J., Mei, J., Xiong, K., Zhou, W., et al. (2024). Leveraging FDEM simulations of rockfill materials for an improved constitutive model considering hysteretic behavior. Comput. Geotechnics 174, 106662. doi:10.1016/j.compgeo.2024.106662
Indraratna, B., Haque, A., and Aziz, N. (1998). Laboratory modelling of shear behaviour of soft joints under constant normal stiffness conditions. Geotechnical and Geol. Eng. 16, 17–44. doi:10.1023/a:1008880112926
Li, D.-J., Shi, C., Ruan, H.-N., Li, B.-Y., Li, W.-Y., and Yao, X.-C. (2022). Study on shear behavior of coral reef limestone–concrete interface. Mar. Georesources and Geotechnol. 40, 438–447. doi:10.1080/1064119x.2021.1906365
Liu, H., Zhu, C., Wang, R., Cui, X., and Wang, T. (2021). Characterization of the interface between concrete pile and coral reef calcarenite using constant normal stiffness direct shear test. Bull. Eng. Geol. Environ. 80, 1757–1765. doi:10.1007/s10064-020-02039-8
Liu, P., Liu, Q., Deng, P., Pan, Y., Lei, Y., DU, C., et al. (2024). Anisotropic shearing mechanism of Kangding slate: experimental investigation and numerical analysis. J. Rock Mech. Geotechnical Eng. 16, 1487–1504. doi:10.1016/j.jrmge.2023.08.002
Li, X., Zhang, R., Yang, Z., Chen, P., Ji, F., and Wen, B. (2023). Mechanical behavior analysis and bearing capacity calculation of CFG pile composite foundation on coral sand site. Front. Earth Sci. 11, 1204989. doi:10.3389/feart.2023.1204989
Li, Y., Zhang, Q., and Jiang, B. (2024). Numerical investigation on the fracture and mechanical behaviors of marble containing two parallel fissures under triaxial compression conditions using FDEM. Theor. Appl. Fract. Mech. 131, 104408. doi:10.1016/j.tafmec.2024.104408
Madin, J. S. (2005). Mechanical limitations of reef corals during hydrodynamic disturbances. Coral Reefs 24, 630–635. doi:10.1007/s00338-005-0042-0
Mahabadi, O. K. (2012). Investigating the influence of micro-scale heterogeneity and microstructure on the failure and mechanical behaviour of geomaterials. University of Toronto Canada.
Meng, Q., Wu, K., Zhao, Y., Luo, L., Li, X., Wang, C., et al. (2024). Dynamic compressive properties and self-similarity characteristics of deep coral reef limestone subjected to high loading rates. J. Build. Eng. 86, 108853. doi:10.1016/j.jobe.2024.108853
Munjiza, A., and Latham, J. P. (2004). Some computational and algorithmic developments in computational mechanics of discontinua. Philosophical Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 362, 1817–1833. doi:10.1098/rsta.2004.1418
Munjiza, A., Owen, D., and Bicanic, N. (1995). A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 12, 145–174. doi:10.1108/02644409510799532
Nohl, T., and Munnecke, A. (2019). Reconstructing time and diagenesis of limestone-marl alternations from the selective compaction of colonies of the tabulate coral Halysites. Bull. Geosciences 94, 279–298. doi:10.3140/bull.geosci.1752
Nyland, G. (1988) “Detailed engineering geological investigation of north rankin a platform site,” in International conference on calcareous sediments, 503–512.
Ooi, L. H., and Carter, J. P. (1987). A constant normal stiffness direct shear device for static and cyclic loading. Geotechnical Test. J. 10, 3–12. doi:10.1520/gtj10132j
Gibson, A. D. (1997). Physical scale modeling of geotechnical structures at one-G. Pasadena, CA, United States: California Institute of Technology.
Pitchumani, N. K., Giovanny, A., and Khatavkar, A. S. (2024). Challenges in large-diameter bored piling in coralline rock formations. Indian Geotechnical J. 54, 1767–1778. doi:10.1007/s40098-024-00927-4
Puech, A., Bustamante, M., and Auperin, L. (1990). Foundation problems in coral soils: a case history-The oil terminal of Matanzas, Cuba. Offshore Technol. Conf. doi:10.4043/6238-MS
Scoffin, T. P., and Tudhope, A. W. (1985). Sedimentary environments of the central region of the great barrier reef of Australia. Coral Reefs 4, 81–93. doi:10.1007/bf00300866
Sun, Z., and Huang, D. (1999). Research progresses on coral reef engineering geology. Adv. Earth Sci. 14 (6), 577. doi:10.11867/j.issn.1001-8166.1999.06.0577
Tang, Z. C., and Wong, L. N. Y. (2016). Influences of normal loading rate and shear velocity on the shear behavior of artificial rock joints. Rock Mech. Rock Eng. 49, 2165–2172. doi:10.1007/s00603-015-0822-y
Wan, Z.-H., Dai, G.-L., Gao, L.-C., and Gong, W.-M. (2021). A practical method of calculation of bearing capacity and settlement of large-diameter post-grouting piles. Rock Soil Mech. 41, 9. doi:10.16285/j.rsm.2019.7026
Wang, J., Huang, X., Xu, J., Wang, S., Jin, G., and Zhang, Z. (2024). Identifying the pore structure and permeability anisotropy of coral reef limestone based on CT image analysis. Mar. Georesources and Geotechnol. 42, 993–1010. doi:10.1080/1064119x.2023.2243270
Wang, Q., Cai, Z., and Liu, E. (2024) “Numerical simulation of shear characteristics of reef limestone-concrete interface,” in Liu, T., Liu, E. (eds). Proceedings of the 2nd International Conference on Advanced Civil Engineering and Smart Structures. ACESS 2023. Lecture Notes in Civil Engineering. Singapore: Springer, 474. doi:10.1007/978-981-97-1514-5_9
Zhang, B.-N., Han, B., He, B., and Guo, J. (2024a). FDEM analysis of deep rock mass failure and its impact on horizontal bearing capacity in offshore wind turbine piles. Ocean. Eng. 302, 117638. doi:10.1016/j.oceaneng.2024.117638
Zhang, S., Sang, D., Feng, G., and Su, S. (2024b). Experimental study on the friction characteristics of the interface between piles and coral reef rock. J. Phys. Conf. Ser. 2808, 012048. doi:10.1088/1742-6596/2808/1/012048
Zhang, Y., Deng, Z., Chen, P., Luo, H., Zhang, R., Yu, C., et al. (2022a). Experimental and numerical analysis of pile–rock interaction characteristics of steel pipe piles penetrating into coral reef limestone. Sustainability 14, 13761. doi:10.3390/su142113761
Zhang, Y., Liu, W., Liu, Y., Ding, J., Chen, P., Luo, H., et al. (2024c). Study on bearing characteristics of bored piles in coral reef. Geotechnical Geol. Eng. 42, 501–521. doi:10.1007/s10706-023-02585-4
Zhang, Y., Luo, H., Chen, P., Liu, E., and Chen, Y. (2022b). Mechanical properties and binary-medium-based constitutive model for coral-reef limestone samples subjected to uniaxial loading. Sustainability 14, 12193. doi:10.3390/su141912193
Zhao, Y., He, P., Zhang, Y., and Wang, C. (2019). A new criterion for a toughness-dominated hydraulic fracture crossing a natural frictional interface. Rock Mech. Rock Eng. 52, 2617–2629. doi:10.1007/s00603-018-1683-y
Zhao, Y., and Liu, H.-H. (2012). An elastic stress–strain relationship for porous rock under anisotropic stress conditions. Rock Mech. rock Eng. 45, 389–399. doi:10.1007/s00603-011-0193-y
Zhao, Y., Wang, C., and Bi, J. (2020). Analysis of fractured rock permeability evolution under unloading conditions by the model of elastoplastic contact between rough surfaces. Rock Mech. Rock Eng. 53, 5795–5808. doi:10.1007/s00603-020-02224-x
Zheng, Y., Yan, C., and Zheng, H. (2023). Modified joint element constitutive model for FDEM to simulate the nonlinear mechanical behavior of rocks. Comput. Geotechnics 164, 105831. doi:10.1016/j.compgeo.2023.105831
Keywords: coral reef limestone, cast-in-place pile, interface shear, side friction resistance, elastoplastic damage constitutive model, numerical computational method
Citation: Zhang Y, Zhang R, Chen P, Ji F, Luo H and Liu E (2024) Study on lateral friction resistance of concrete pouring structure in coral reef limestone formation. Front. Earth Sci. 12:1515670. doi: 10.3389/feart.2024.1515670
Received: 23 October 2024; Accepted: 25 November 2024;
Published: 13 December 2024.
Edited by:
Faming Huang, Nanchang University, ChinaReviewed by:
Zhanping Song, Xi’an University of Architecture and Technology, ChinaCopyright © 2024 Zhang, Zhang, Chen, Ji, Luo and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ruiyuan Zhang, MTM1NTQwODIxNTBAMTYzLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.