One-dimensional consolidation analysis of layered foundations with continuous drainage boundaries considering soil structure and physical properties

Introduction: Many theories of consolidation for soils have been proposed in the past, but most of them have ignored the structural characteristics of clay, yet the natural layered soils are widely distributed around the world.

Methods: A theoretical model is established to analyze the one-dimensional consolidation behavior of layered soils, in which a time-dependent drainage boundary and the structural characteristics of the soil are taken into account. Using the integral transform and characteristic function methods, the analytical solution is derived, the effectiveness of which is evaluated against the degradation of solutions and the numerical results calculated using the finite element method.

Results and discussion: Finally, the influences of interface parameter, soil permeability coefficient and soil compressibility on consolidation behaviors are discussed. Results show that in structured soils, early dissipation of excess pore water pressure and consolidation rates are predominantly influenced by interface parameters, permeability, and volume compression coefficients. Higher values of these parameters accelerate early stages of consolidation, which is especially evident in the upper soil layers. Over time, the distinct effects of interface and permeability coefficients on consolidation diminish. Higher volume compression coefficients, while initially beneficial, eventually slow down the consolidation process, indicating an interaction with the ongoing soil structural changes.

1 Introduction

Natural saturated soft clay, affected by its depositional history and formation condition, often has low permeability and high compressibility, thus typically showing long consolidation time, large deformation, and low bearing capacity in engineering projects (Burland, 1990; Poskitt, 1969). In addition, many laboratory and field tests indicate that soft soil exhibits significant structural characteristics and yielding phenomenon upon loading, and structural failure occurs only when the effective stress exceeds the structural yield stress (Leroueil and Vaughan, 1990; Shen, 1998; Zhang, 1983).

In the exploration of structured soil mechanics, significant efforts have been made through the development of analytical models that delineate the relationship between effective stress and key soil properties, i.e., the permeability and compression coefficients (Tang et al., 2007; Wang and Chen, 2003; Wang et al., 2004). These models are broadly categorized into linear segmented and nonlinear types, each stemming from rigorous experimental research. Linear models clarified the consolidation behavior of soils in simple and complex formation, providing a sound theoretical basis for practical applications (An et al., 2012; Xie et al., 2016a; Xie et al., 2016b). Furthermore, nonlinear models helped to advance the understanding of soil responses under variable loading conditions. These formulations integrated the nonlinearities of soil properties, and can be solved by machine learning (Li et al., 2024) and robust numerical techniques, such as the Crank-Nicolson method (Cao et al., 2006; Hu et al., 2018). The advancements in semi-analytical solutions, which account for the peculiarities of soil structure and loading variabilities, have enriched the theoretical framework and enhanced the predictive accuracy, especially through the integration of one-dimensional nonlinear large deformation consolidation analysis (Cui et al., 2018; Hu et al., 2020). Additionally, these models’ applicability to marine environments has been substantiated by explorations using the finite difference method, specifically examining the large deformation consolidation behavior of marine soft clay, and thereby offering valuable insights into marine soil mechanics (Li et al., 2020).

The consolidation theory, pioneered by Terzaghi, is based on the effective stress principle (Terzaghi, 1925), and provides the crucial theoretical framework underpinning the response of soil deformation. This theory incorporates a set of governing equations along with specific initial and boundary conditions. Traditional approaches often depict the boundary conditions as either entirely drained or undrained, which is inconsistent with the reality. Subsequently, Gray (1945) introduced a semi-permeable drainage boundary to bridge this gap, merging the features of both permeable and impermeable types, but significant complexities were introduced in derivation due to the lack of straightforward solutions. Alternatively, Mei et al. (2011) proposed the continuous drainage boundary that can capture the exponential decay of excess pore water pressure at the boundary. The continuous drainage boundary was further improved in subsequent research, enabling it to accurately describe the dissipation process of excess pore water pressure during loading (Feng et al., 2019a).

The exploration of consolidation research with continuous drainage boundaries also includes linear and nonlinear analyses. Techniques, such as the Laplace transformation and finite Fourier transform, have facilitated the development of linear analytical models, addressing the effects of various factors, such as soil’s self-weight (Feng et al., 2019b), loading conditions (Liu and Lei, 2013) and soil stratification (Yang et al., 2024). In the realm of nonlinear consolidation, studies have focused on material behaviors and large deformation impacts, with notable models addressing one-dimensional consolidation of viscoelastic soil under dynamic loads (Chen et al., 2021; Feng et al., 2023; Zong et al., 2022; Zong et al., 2023). However, the role of soil structural properties in the consolidation responses under continuous drainage boundaries remains unclear, presenting an opportunity for further research. Feng et al. (2024) derived a semi-analytical solution of consolidation for single-layer structured soil with continuous drainage boundaries. However, the consolidation theory of layered structured soil with continuous drainage boundaries has not yet been reported in the literature.

In this study, a mathematical model for one-dimensional consolidation under continuous drainage boundaries considering soil structural properties and soil stratification is established. Then, the corresponding analytical solutions of the model are derived, and the correctness of the proposed solutions is evaluated by comparing with the results of boundary condition degradation and numerical calculation using the finite element method. Subsequently, the influences of interface parameters and soil structural properties on the consolidation process of layered foundation are discussed through numerical analyses.

2 Model description

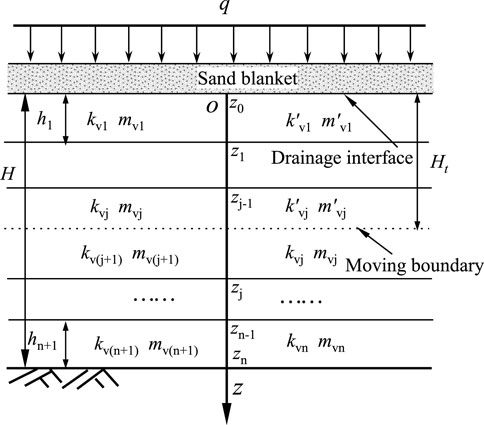
The settlement rate of clay soils is controlled by two consolidation processes (Cosenza and Korošak, 2014; Liu et al., 2018). However, this paper mainly considers the primary consolidation and does not consider secondary consolidation issues, as secondary consolidation does not involve the process of excess pore water pressure dissipation. As illustrated in Figure 1, the continuous drainage boundaries of the calculation model for layered soft soil foundation are characterized by an interface parameter $\alpha$ and an impermeable bottom surface. It is worth noting that although the permeability of the upper and lower soil layers is different (Ng et al., 2024a; Ng et al., 2024b), the perched water table at the interface of two-layered soil was not considered in this paper. The imposed load on the foundation surface is kept constant at $q_u$. The primary assumptions are as follows: (1) The foundation soil is normally consolidated, saturated, and consists of layered homogeneous soft clay; (2) Both soil particles and pore water are incompressible; (3) The seepage process within the soil adheres to the Darcy’s law; (4) Soil deformation occurs only in the vertical direction, i.e., the deformation of foundation can be considered as one-dimensional consolidation. However, it should be noted that the permeability coefficient and compression modulus of the soil is changing during the consolidation process, and the model described in this study is valid under the classic Terzaghi hypothesis.

Figure 1

Figure 1. Schematic of the one-dimensional consolidation model applied to layered soils.

Within the interval $0<t\le t_0$, the effective stress at the boundary of the soil does not exceed the structural yield stress, indicating that the soil structure is in an undamaged state. The associated consolidation problem during this phase is characterized as a one-dimensional consolidation problem for a layered foundation under continuous drainage boundary.

During the interval $t_0<t\le t_1$, the effective stress at the soil boundary exceeds the structural yield stress, triggering the onset of soil structure failure. At this stage, foundation deformation is analyzed as a one-dimensional consolidation problem for an $n+1$ layered soil with an initial non-uniform excess pore water pressure distribution ${\left.u_1^i\left(t,z\right)\right|}_{t=t_0}$, under continuous drainage boundary. Figure 2 depicts the division of soil layers. It is postulated that the structural failure surface forms within a specific layer, located at $H_t$ $\left(z_{j-1}<H_t<z_j\right)$, dividing the $jth$ soil layer into two parts with distinct consolidation parameters and thicknesses $H_t-z_{j-1}$ and $z_j-H_t$. This transition expands the soil from $n$ to $n+1$ layers, with the consolidation characteristics of the soil above the failure surface changing to those of remolded soil, whereas those below remain consistent. The layer number above the failure surface remains unchanged, while the layer below transits from $j+k\left(k=1,2,\cdots \right)$ to $j+k+1$.

Figure 2

Figure 2. Assessment of the proposed solution by degenerated analyses.

Once $t$ exceeds $t_1$, the effective stress at the soil’s lower boundary exceeds the structural yield stress, resulting in complete failure of the soil structure. This phase is identified as the stage of absolute soil structure failure. In the calculation, one can obtain $t^{″}=t-t_1$, where $t^{″}$ is the time coordinate. Currently, the consolidation problem is addressed as a one-dimensional consolidation of an n-layer foundation with a non-uniformly distributed initial pore pressure ${\left.u_2^i\left(t^{\prime },z\right)\right|}_{t^{\prime }=t_1-t_0}$ under continuous drainage boundary.

3 Solving procedures

3.1 Undamaged stage

During the period where the soil structure remains undamaged, namely, $0<t\le t_0$, the soil deformation is governed by the one-dimensional consolidation theory of layered foundations (n layers) with continuous drainage boundary conditions. The governing equation and its boundary conditions are presented as follows:

Governing equation:

$\frac{\mathrm{\partial }{u}_1^i}{\mathrm{\partial }t}=c_{\mathrm{v}i}\frac{{\mathrm{\partial }}^2{u}_1^i}{\mathrm{\partial }{z}^2}\left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n\right)(1)$

Boundary conditions:

${\left.u_1^1\right|}_{z=0}=q{\mathrm{e}}^{-bt},{\left.\frac{\mathrm{\partial }{u}_1^n}{\mathrm{\partial }z}\right|}_{z=H}=0(2)$

$\begin{array}{l}{\left.u_1^i\right|}_{z=z_i}={\left.u_1^{i+1}\right|}_{z=z_i},{\left.k_{vi}\frac{\mathrm{\partial }{u}_1^i}{\mathrm{\partial }z}\right|}_{z=z_i}={\left.k_{v\left(i+1\right)}\frac{\mathrm{\partial }{u}_1^{i+1}}{\mathrm{\partial }z}\right|}_{z=z_i}\\ \left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n-1\right)\end{array}(3)$

Initial conditions:

${\left.u_1^i\right|}_{t=0}=q(4)$

Initially, the non-homogeneous boundary is homogenized, i.e.,

$u_1^i=v_i+q{\mathrm{e}}^{-bt}(5)$

Substituting Equation 5 into the governing equation of Equation 1 and solving conditions of Equations 2–5, one can get Equations 6–9

$\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }t}=c_{\mathrm{v}i}\frac{{\mathrm{\partial }}^2{v}_i}{\mathrm{\partial }{z}^2}+R_1\left(t\right)\left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n\right)(6)$

where $R_1\left(t\right)=bq{\mathrm{e}}^{-bt}$.

${\left.v_1\right|}_{z=0}=0,{\left.\frac{\mathrm{\partial }{v}_n}{\mathrm{\partial }z}\right|}_{z=H}=0(7)$

$\begin{array}{l}{\left.v_i\right|}_{z=z_i}={\left.v_{i+1}\right|}_{z=z_i},{\left.k_{vi}\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }z}\right|}_{z=z_i}={\left.k_{v\left(i+1\right)}\frac{\mathrm{\partial }{v}_{i+1}}{\mathrm{\partial }z}\right|}_{z=z_i}\\ \left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n-1\right)\end{array}(8)$

${\left.v\right|}_{t=0}=0(9)$

The following dimensionless parameters are taken into account in the analysis, i.e., Equation 10,

$\begin{array}{l}{\kappa }_i=k_{vi}/k_{v1},{\eta }_i=m_{vi}/m_{v1},{\rho }_i=h_i/H,{\mu }_i\\ =\sqrt{\frac{c_{\mathrm{v}1}}{c_{\mathrm{v}i}}}=\sqrt{\frac{{\kappa }_i}{{\eta }_i}}i=1,2,\cdots ,n\end{array}(10)$

The formulation for excess pore water pressure is assumed to follow the form of Equation 11, namely,

$v_i={\displaystyle \sum _{m=1}^{\infty }}{C}_m{g}_{mi}\left(z\right){\mathrm{e}}^{-{\beta }_{m}t}{\int }_0^t\frac{\mathrm{d}{R}_1}{\mathrm{d}t}{\mathrm{e}}^{{\beta }_{m}t}\mathrm{d}t\left(i=1,2,\cdots ,n\right)(11)$

where ${\beta }_m={{\lambda }_m}^2{c}_{v1}/H^2$, and $g_{mi}\left(z\right)=A_{mi}\sin \left({\mu }_i{\lambda }_m\frac{z}{H}\right)+B_{mi}\cos \left({\mu }_i{\lambda }_m\frac{H-z}{H}\right)$.

The coefficients $A_{mi}$ and $B_{mi}$ in parameter $g_{mi}\left(z\right)$ can be calculated by the following recursive formula, i.e., Equation 12,

$\left\{\begin{array}{l}{\left[\begin{array}{cc}{A}_{m1}& B_{m1}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cc}1& 0\end{array}\right]}^{\mathrm{T}}\\ {\left[\begin{array}{cc}{A}_{mi}& B_{mi}\end{array}\right]}^{\mathrm{T}}=S_i{\left[\begin{array}{cc}{A}_{m\left(i-1\right)}& B_{m\left(i-1\right)}\end{array}\right]}^{\mathrm{T}}i=2,3,\cdots ,n\end{array}\right.(12)$

Parameter $S_i$ can be derived by the following equation, i.e., Equation 13,

${\mathrm{S}}_i=\left[\begin{array}{cc}{A}_i{B}_i+d_i{C}_i{D}_i& A_i{D}_i-d_i{C}_i{B}_i\\ C_i{B}_i+d_i{A}_i{D}_i& C_i{D}_i-d_i{A}_i{B}_i\end{array}\right]i=2,3,\cdots ,n(13)$

where the calculation formulas for the coefficients $A_i,B_i,C_i,D_i$ and $d_i$ in the matrix are as follows, i.e., Equation 14,

$\begin{array}{l}{A}_i=\sin \left({\mu }_i{\lambda }_m\frac{z_{i-1}}{H}\right),B_i=\sin \left({\mu }_{i-1}{\lambda }_m\frac{z_{i-1}}{H}\right),C_i=\cos \left({\mu }_i{\lambda }_m\frac{z_{i-1}}{H}\right),\\ D_i=\cos \left({\mu }_{i-1}{\lambda }_m\frac{z_{i-1}}{H}\right),d_i=\frac{k_{\mathrm{v}\left(i-1\right)}}{k_{\mathrm{v}i}}\sqrt{\frac{c_{\mathrm{v}i}}{c_{\mathrm{v}\left(i-1\right)}}}=\sqrt{\frac{{\kappa }_{i-1}{\eta }_{i-1}}{{\kappa }_i{\eta }_i}}\end{array}(14)$

Parameter ${\lambda }_m$ is the positive root of the following transcendental equation, i.e., Equation 15,

${\mathrm{S}}_{n+1}\cdot {\mathrm{S}}_n\cdot {\mathrm{S}}_{n-1}\cdots {\mathrm{S}}_2\cdot {\mathrm{S}}_1=0(15)$

where ${\mathrm{S}}_1={\left[\begin{array}{cc}1& 0\end{array}\right]}^{\mathrm{T}}$, ${\mathrm{S}}_{n+1}=\left[\begin{array}{cc}\cos \left({\mu }_n{\lambda }_m\right)& -\sin \left({\mu }_n{\lambda }_m\right)\end{array}\right]$.

The undetermined coefficients $C_m$ can be determined by the following integral equations, i.e., Equation 16,

$C_m=\frac{{\displaystyle \sum _{i=1}^n}{\eta }_i{\int }_{z_{i-1}}^{z_i}{g}_{mi}\left(z\right)\mathrm{d}z}{{\displaystyle \sum _{i=1}^n}{\eta }_i{\int }_{z_{i-1}}^{z_i}{g_{mi}}^2\left(z\right)\mathrm{d}z}(16)$

Finally, the solution of excess pore water pressure can be expressed as Equation 17:

$u_1^i={\displaystyle \sum _{m=1}^{\infty }}{C}_m{g}_{mi}\left(z\right){\mathrm{e}}^{-{\beta }_{m}t}{\int }_0^t\frac{\mathrm{d}{R}_1}{\mathrm{d}t}{\mathrm{e}}^{{\beta }_{m}t}\mathrm{d}t+q_1\left(t\right){\mathrm{e}}^{-bt}(17)$

where ${\beta }_m=\frac{c_{\mathrm{v}1}{{\lambda }_m}^2}{H^2}$, and $c_{\mathrm{v}1}$ is the consolidation coefficient of the first layer of soil before structural failure.

3.2 Failure stage

During the structural failure stage of the soil, specifically when $t_0<t\le t_1$, the soil structure commences failure, transiting from an $n$-layer foundation to an $\left(n+1\right)$-layer foundation. Adopting $t^{\prime }$ as the time coordinate, the problem evolves into the consolidation of an $\left(n+1\right)$-layer foundation under continuous drainage boundary, with the initial excess pore water pressure denoted by $u_1^i\left(t_0,z\right)$.

Governing equation:

$\frac{\mathrm{\partial }{u}_2^i}{\mathrm{\partial }{t}^{\prime }}=c_{\mathrm{v}i}\frac{{\mathrm{\partial }}^2{u}_2^i}{\mathrm{\partial }{z}^2}\left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n+1\right)(18)$

Boundary conditions:

${\left.u_2^1\right|}_{z=0}=q_2{\mathrm{e}}^{-b{t}^{\prime }},{\left.\frac{\mathrm{\partial }{u}_2^n}{\mathrm{\partial }z}\right|}_{z=H}=0(19)$

where $q_2=q{\mathrm{e}}^{-b{t}_0}$.

${\left.u_2^i\right|}_{z=z_i}={\left.u_2^{i+1}\right|}_{z=z_i},{\left.k_{\mathrm{v}i}\frac{\mathrm{\partial }{u}_2^i}{\mathrm{\partial }z}\right|}_{z=z_i}={\left.k_{\mathrm{v}\left(i+1\right)}\frac{\mathrm{\partial }{u}_2^{i+1}}{\mathrm{\partial }z}\right|}_{z=z_i}(20)$

Initial conditions:

${\left.u_2^i\right|}_{t^{\prime }=0}={\sigma }_2\left(z\right)={\left.u_1^i\right|}_{t=t_0}(21)$

First, the non-homogeneous boundary is homogenized by setting

$u_2^i=v_i+q_2{\mathrm{e}}^{-b{t}^{\prime }}(22)$

Substituting Equation 22 into the governing equation of Equation 18 and solving conditions of Equation 19 - Equation 21, one can get Equations 23–26

$\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }{t}^{\prime }}=c_{\mathrm{v}i}\frac{{\mathrm{\partial }}^2{v}_i}{\mathrm{\partial }{z}^2}+R_2\left(t^{\prime }\right)\left(z_{i-1}\le z\le z_i,i=1,2,\cdots ,n+1\right)(23)$

where $R\left(t^{\prime }\right)=b{q}_2{\mathrm{e}}^{-b{t}^{\prime }}$.

${\left.v_1\right|}_{z=0}=0,{\left.\frac{\mathrm{\partial }{v}_n}{\mathrm{\partial }z}\right|}_{z=H}=0(24)$

$\left\{\begin{array}{l}{\left.v_i\right|}_{z=z_i}={\left.v_{i+1}\right|}_{z=z_i}\\ {\left.k_{\mathrm{v}i}\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }z}\right|}_{z=z_i}={\left.k_{\mathrm{v}\left(i+1\right)}\frac{\mathrm{\partial }{v}_{i+1}}{\mathrm{\partial }z}\right|}_{z=z_i}\end{array}\right.(25)$

${\left.v\right|}_{t=0}={\sigma }_2\left(z\right)-q_2={\sigma }_2^{\prime }\left(z\right)(26)$

Assuming the solution satisfies the above equation, one can derive Equation 27:

$v_i={\displaystyle \sum _{m=1}^{\infty }}{g}_{mi}\left(z\right){\mathrm{e}}^{-{\beta }_m{t}^{\prime }}\left(B_m+C_m{\int }_0^{t^{\prime }}\frac{\mathrm{d}{R}_2}{\mathrm{d}{t}^{\prime }}{\mathrm{e}}^{{\beta }_m\tau }\mathrm{d}\tau \right)i=1,2,\cdots ,n+1(27)$

where $g_{mi}\left(z\right)=A_{mi}\sin \left({\mu }_i{\lambda }_m\frac{z}{H}\right)+B_{mi}\cos \left({\mu }_i{\lambda }_m\frac{z}{H}\right)$, ${\beta }_m=\frac{{c_{\mathrm{v}1}}^{\prime }{{\lambda }_m}^2}{H^2}$, ${c_{\mathrm{v}1}}^{\prime }$ is the consolidation coefficient of the first soil layer after the soil structure is damaged.

The coefficients $A_{mi}$ and $B_{mi}$ in $g_{mi}\left(z\right)$ are calculated using the following recursive formula, i.e., Equation 28,

$\left\{\begin{array}{l}{\left[\begin{array}{cc}{A}_{m1}& B_{m1}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cc}1& 0\end{array}\right]}^{\mathrm{T}}\\ {\left[\begin{array}{cc}{A}_{mi}& B_{mi}\end{array}\right]}^{\mathrm{T}}=S_i{\left[\begin{array}{cc}{A}_{m\left(i-1\right)}& B_{m\left(i-1\right)}\end{array}\right]}^{\mathrm{T}}i=2,3,\cdots ,n+1\end{array}\right.(28)$

The matrix ${\mathrm{S}}_i$ can be calculated using the Equation 29:

${\mathrm{S}}_i=\left[\begin{array}{cc}{A}_i{B}_i+d_i{C}_i{D}_i& A_i{D}_i-d_i{C}_i{B}_i\\ C_i{B}_i-d_i{C}_i{D}_i& C_i{D}_i+d_i{A}_i{B}_i\end{array}\right]i=2,3,\cdots ,n+1(29)$

where $A_i=\sin \left({\mu }_i{\lambda }_m\frac{z_{i-1}}{H}\right)$, $B_i=\sin \left({\mu }_{i-1}{\lambda }_m\frac{z_{i-1}}{H}\right)$, $C_i=\cos \left({\mu }_i{\lambda }_m\frac{z_{i-1}}{H}\right)$, $D_i=\cos \left({\mu }_{i-1}{\lambda }_m\frac{z_{i-1}}{H}\right)$, $d_i=\sqrt{\frac{{\kappa }_{i-1}{\eta }_{i-1}}{{\kappa }_i{\eta }_i}}$, and ${\lambda }_m$ is the positive root of the following transcendental equation, i.e., Equation 30,

${\mathrm{S}}_{n+2}\cdot {\mathrm{S}}_{n+1}\cdots {\mathrm{S}}_2\cdot {\mathrm{S}}_1=0(30)$

Where ${\mathrm{S}}_1={\left[\begin{array}{cc}1& 0\end{array}\right]}^{\mathrm{T}},{\mathrm{S}}_{n+2}={\left[\begin{array}{cc}{D}_{n+2}& -B_{n+2}\end{array}\right]}^{\mathrm{T}}$.

$B_m$ and $C_m$ are determined by the integral formulas of Equation 31:

$B_m=\frac{{\displaystyle \sum _1^{n+1}}{\eta }_i{\int }_{z_{i-1}}^{z_i}{\sigma }_2^{\prime }\left(z\right)g_{mi}\left(z\right)\mathrm{d}z}{{\displaystyle \sum _1^{n+1}}{\eta }_i{\int }_{z_{i-1}}^{z_{i-1}}{g}_{mi}^2\left(z\right)\mathrm{d}z},C_m=\frac{{\displaystyle \sum _1^{n+1}}{\eta }_i{\int }_{z_{i-1}}^{z_i}{g}_{mi}\left(z\right)\mathrm{d}z}{{\displaystyle \sum _1^{n+1}}{\eta }_i{\int }_{z_{i-1}}^{z_{i-1}}{g}_{mi}^2\left(z\right)\mathrm{d}z}(31)$

On this basis, the solution of excess pore water pressure in the failure stage can be expressed as Equation 32

$u_2^i={\displaystyle \sum _{m=1}^{\infty }}{g}_{mi}\left(z\right){\mathrm{e}}^{-{\beta }_m{t}^{\prime }}\left(B_m+C_m{\int }_0^{t^{\prime }}\frac{\mathrm{d}{R}_2}{\mathrm{d}t}{\mathrm{e}}^{{\beta }_m\tau }\mathrm{d}\tau \right)+q_2{\mathrm{e}}^{-b{t}^{\prime }}i=1,2,\cdots ,n+1(32)$

In the aforementioned expressions, $H_t$ is an unknown variable associated with $t^{\prime }$, and its interrelation can be derived by setting the effective stress at $H_t$ equal to the structural yield stress at the base of the jth layer.

If $z=H_t$, then ${\sigma }_j^{\prime }=q_2-u_j\left(z\right)={\sigma }_{\mathrm{p}j}^{\prime }$, namely,:

${\displaystyle \sum _{m=1}^{\infty }}{g}_{mj}\left(H_t\right){\mathrm{e}}^{-{\beta }_m{t}^{\prime }}\left(\frac{B_m}{q_u}+\frac{C_m}{q_u}{\int }_0^{t^{\prime }}\frac{\mathrm{d}R}{\mathrm{d}t}{\mathrm{e}}^{{\beta }_m\tau }\mathrm{d}\tau \right)+Q_j-Q^{\prime }=0(33)$

where $Q_j=\frac{{\sigma }_{\mathrm{p}j}^{\prime }}{q_{\mathrm{u}}},Q^{\prime }=\frac{q\left(1-{\mathrm{e}}^{-b{t}^{\prime }}\right)}{q_{\mathrm{u}}}$.

The above Equation 33 represents the corresponding relationship between $H_t$ and $t^{\prime }$. Given any moment $t^{\prime }$, the depth $H_t$ of the corresponding moving boundary can be determined using the iterative method.

3.3 Complete failure stage

In the phase of complete soil structural failure (occurring when $t>t_1$), it is assumed that $t^{″}=t-t_1$ and $t^{″}$ is the time coordinate. The structure then shifts from an $\left(n+1\right)$-layer configuration back to $n$ layers. The consolidation challenge changes from dealing with an $\left(n+1\right)$-layered foundation under continuous drainage boundary to solving a one-dimensional consolidation problem for an $n$-layered foundation. The initial excess pore water pressure is calculated as ${\sigma }_3\left(z\right)={\left.u_2^i\left(t^{\prime },z\right)\right|}_{t^{\prime }=t_1-t_0}$. Based on the solving process previously described, the excess pore water pressure at the stage of complete soil structural failure can be determined as Equation 34

$u_3^i={\displaystyle \sum _{m=1}^{\infty }}{g}_{mi}\left(z\right){\mathrm{e}}^{-{\beta }_m{t}^{″}}\left(B_m^{\prime }+C_m{\int }_0^{t^{″}}\frac{\mathrm{d}{R}_3}{\mathrm{d}t}{\mathrm{e}}^{{\beta }_m\tau }\mathrm{d}\tau \right)+q_3{\mathrm{e}}^{-b{t}^{″}}i=1,2,\cdots ,n(34)$

where $q_3=q{\mathrm{e}}^{-b{t}_1},{\sigma }_3^{\prime }\left(z\right)={\sigma }_3\left(z\right)-q_3$, $B_m^{\prime }=\frac{{\displaystyle \sum _1^n}{\eta }_i{\int }_{z_{i-1}}^{z_i}{\sigma }_3^{\prime }\left(z\right)g_{mi}\left(z\right)\mathrm{d}z}{{\displaystyle \sum _1^n}{\eta }_i{\int }_{z_{i-1}}^{z_{i-1}}{g}_{mi}^2\left(z\right)\mathrm{d}z}$, and $C_m=\frac{{\displaystyle \sum _1^n}{\eta }_i{\int }_{z_{i-1}}^{z_i}{g}_{mi}\left(z\right)\mathrm{d}z}{{\displaystyle \sum _1^n}{\eta }_i{\int }_{z_{i-1}}^{z_{i-1}}{g}_{mi}^2\left(z\right)\mathrm{d}z}$.

The average consolidation degree defined by excess pore water pressure can be expressed as Equation Equation 35

$U=\left\{\begin{array}{l}1-\frac{{\overline{u}}_1}{q_u},0<t\le t_0\\ 1-\frac{{\displaystyle \sum _{i=1}^{n+1}}{\rho }_i{\overline{u}}_2^i}{q_u},t_0<t\le t_1\\ 1-\frac{{\overline{u}}_3}{q_u},t_1<t\end{array}\right.(35)$

where ${\overline{u}}_2^i=\frac{{\int }_{z_{i-1}}^{z_i}{u}_2^i\mathrm{d}z}{h_i},i=1,2,\cdots ,n+1$.

3.4 Evaluation of the proposed solution

3.4.1 Comparison against degenerated cases

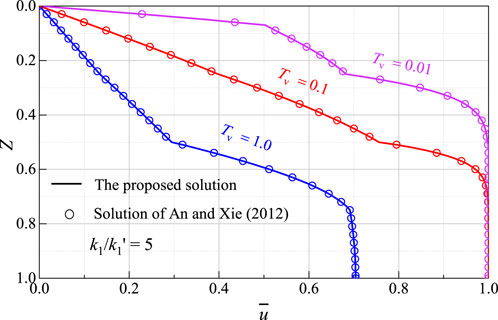
An et al. (2012) provided an analytical solution for the consolidation of layered structured soil, where the upper boundary condition is considered as a completely permeable boundary. In order to evaluate the correctness of the solutions proposed in this study, the proposed solution is degenerated when the interface parameter $\alpha$ takes 1,000. On this basis, a numerical analysis of four-layer soil system is employed to compare the consistency between the proposed solution and the solution provided by An et al. (2012). The parameter values required for calculation are specified as follows: (1) the thickness of each soil layer is 5 m; (2) the ratios of consolidation coefficients before and after soil structure failure for each soil layer are given by $c_{\mathrm{v}i}/c_{\mathrm{v}i}^{\prime }=1,1,5,1$, respectively; (3) the magnitude of the imposed load on the foundation surface is 100 kPa; (4) the structural yield stress of the soil is 50 kPa. The solutions obtained from the two methods are depicted in Figure 2. It can be found that the degenerated results of the proposed solution shows a good agreement with the solution calculated by An et al. (2012), which preliminarily demonstrates the correctness of the present solution.

3.4.2 Comparison against numerical calculations

To further assess the correctness of the proposed analytical solutions, numerical analyses are conducted using the finite element method for comparison. The computational model consists of four soil layers, and the parameter values of each soil layer are as follows: (1) the permeability coefficients for each soil layer are $1.5\times {10}^{-8}$ m/s, $1.2\times {10}^{-8}$ m/s, $3\times {10}^{-9}$ m/s, and $7.5\times {10}^{-8}$ m/s, respectively; (2) the bulk moduli for each soil layer are $6\times {10}^{-7}$ 1/Pa, $7.5\times {10}^{-7}$ 1/Pa, $3\times {10}^{-6}$ 1/Pa, and $6\times {10}^{-7}$ 1/Pa, respectively; (3) the ratios of the bulk moduli before and after soil structure failure for each soil layer are 1, and the ratios of the permeability coefficients before and after soil structure failure for each soil layer are 1, 1, 5, 1, respectively; (4) the interface parameter $\alpha$ is set to 10 and the other parameters are consistent with those mentioned above. In addition, as shown in Figure 3A, the computational region was discretized with equal spacing computational units when performing the finite element numerical calculations, where n is the node number, e is the unit number. there are a total of N nodes and E units, and N=E+1. The time step is $\Delta t^j$, where the superscript j represents the variation of time step. Figure 3B depicts the distribution of excess pore water pressure with depth of a layered structured soil foundation with continuous drainage boundary at different times, comparing the proposed analytical solutions with the numerical solutions obtained using the finite element method. It can be seen that there is high consistency between the analytical solutions and the numerical results, thus demonstrating the correctness and reliability of the proposed solutions.

Figure 3

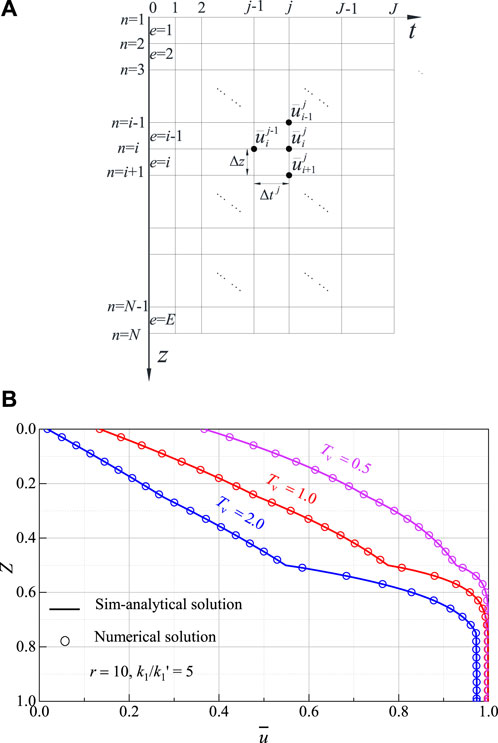
Figure 3. (A)Schematic diagram of numerical model and unit discretization. (B) Comparison of calculated results using the presented solution and the numerical approach.

4 Results and discussions

In this section, a four-layer structured soil with continuous drainage boundary is taken as a case study to analyze the impact of interface parameter, permeability, and compressibility of the soil on the soil consolidation characteristics. The calculation parameters for remolded soil are shown in Table 1.

Table 1

Table 1. Calculating parameters of remolded soil for a four-layer structured soil foundation.

4.1 Influence of interface parameter

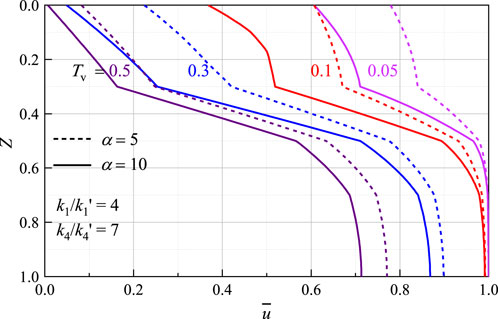
Figure 4 illustrates the impact of interface parameter on the vertical distribution of excess pore water pressure in the foundation soil, in which the parameters vary from $k_1/k_1^{\prime }=4$, $k_4/k_4^{\prime }=7$, to $k_2/k_2^{\prime }=k_3/k_3^{\prime }=1$. It can be seen that the greater the interface parameter, the faster the dissipation of excess pore water pressure. The differences in excess pore water pressure at the upper part of the soil decrease over time, while those at the lower part increase. This is because in the early stages of consolidation, the soil structure is not damaged, and thus the rate of excess pore water pressure dissipation is only related to the interface parameters. However, as the consolidation progresses, different interface parameters result in different structural damages. The larger the interface parameter, the earlier the structural damage. This leads to a decrease in permeability coefficient and an increase in compressibility coefficient at the upper part of the soil, thus slowing down the dissipation of excess pore water pressure and gradually reducing the differences in dissipation of excess pore water pressure across different interface parameters.

Figure 4

Figure 4. Influence of interface parameter on the profile of excess pore water pressure with depth.

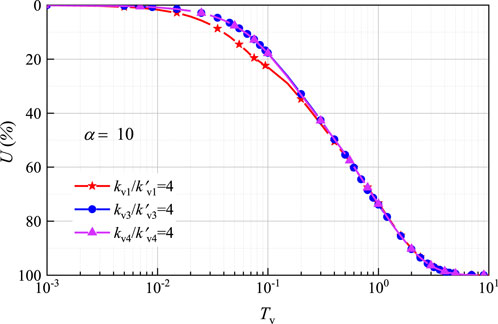
The effect of interface parameters on the consolidation degree of layered structured soil is shown in Figure 5. It can be seen that the greater the interface parameter, the faster the consolidation rate, and the larger the early differences in consolidation. In the later stages of consolidation, the differences in consolidation degree between different interface parameters gradually decrease. This indicates that the impact of interface parameters on the average consolidation degree of structured soils is significant in the early stages of consolidation.

Figure 5

Figure 5. Influence of interface parameter on average degree of consolidation.

4.2 Influence of soil permeability coefficient

Figure 6 illustrates the effects of soil permeability coefficient on the vertical distribution of excess pore water pressures in layered structured soil, in which the parameters are $\alpha =10$, and $k_i/k_i^{\prime }=4$. Figure 6 reveals that at different time factors, such as T_v = 0.05 and T_v = 0.1, there are significant differences in excess pore water pressure at the upper part of the foundation, showing a faster dissipation rate with the parameter $k_1/k_1^{\prime }=4$ compared to the case of $k_4/k_4^{\prime }=4$. However, these differences diminish at later times (e.g., T_v = 0.3 and T_v = 0.5), and at the bottom of the foundation, where the excess pore water pressure dissipation at $k_1/k_1^{\prime }=4$ is slower than that at $k_4/k_4^{\prime }=4$. This is because, during the phase when the soil structure is intact, a higher permeability coefficient leads to faster dissipation of excess pore water pressure, as seen in the early stages of consolidation where the upper part of the soil at $k_1/k_1^{\prime }=4$ dissipates faster. During the structural damage and complete destruction phases, the differences in the upper pore pressure at $k_4/k_4^{\prime }=4$ decrease, and lower pore pressure dissipates more rapidly.

Figure 6

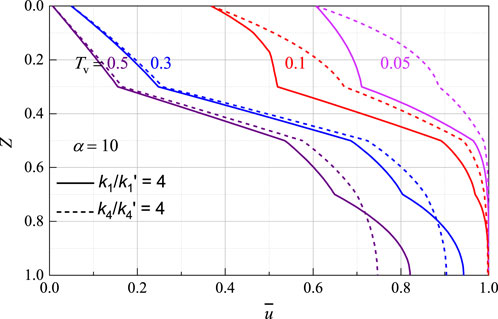
Figure 6. Influence of permeability coefficient on the profile of excess pore water pressure with depth.

The impact of permeability coefficient on consolidation is shown in Figure 7, which indicates that different permeability ratios have little effect on the later stages of consolidation. In the early stages, the ratio of $k_{\mathrm{v}1}/k_{\mathrm{v}1}^{\prime }$ has the greatest impact on consolidation, resulting in higher initial consolidation degrees. This is because, in the early stages of consolidation, the soil structure is undamaged, and the average consolidation is mostly influenced by the upper soil layer (shorter drainage path). The higher the permeability of the upper soil layer, the higher the consolidation degree; while in the later stages, as the soil structure is damaged, the pore pressure in the lower soil dissipates quickly, reducing the differences in average consolidation.

Figure 7

Figure 7. Influence of permeability coefficient on the average degree of consolidation.

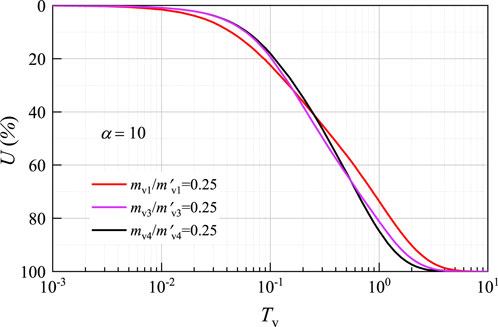
4.3 Influence of soil compressibility

Figure 8 shows the impact of volume compression coefficient on the distribution of excess pore water pressure in layered structured soil, in which the parameters are $\alpha =10$, and $m_{\mathrm{v}i}/m_{\mathrm{v}i}^{\prime }=0.25$, respectively. It indicates that at $m_1/m_1^{\prime }=0.25$ and $m_4/m_4^{\prime }=0.25$, the spatial variation in excess pore water pressure across different time factors resembles the impact of permeability coefficient: at smaller consolidation time factors (such as T_v = 0.05 and T_v = 0.1), there is a significant difference in excess pore water pressure in the upper part of the soil, with faster dissipation for $m_1/m_1^{\prime }=0.25$ compared to $m_4/m_4^{\prime }=0.25$. As time progresses, this difference diminishes (as seen at T_v = 0.3 and T_v = 0.5), and at $m_1/m_1^{\prime }=0.25$, the dissipation of pore pressure at the base of the soil is slower than at $m_4/m_4^{\prime }=0.25$.

Figure 8

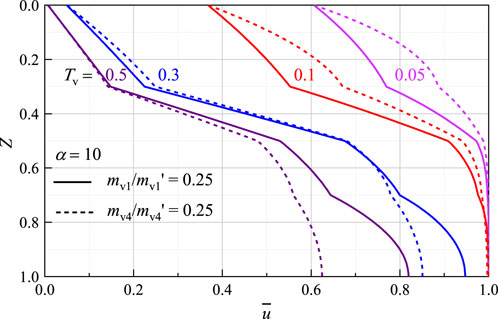
Figure 8. Influence of compression coefficient on the profile of excess porewater pressure with depth.

Figure 9 shows the impact of volume compression coefficient on the consolidation of layered structured soil with continuous drainage boundary, in which the interface parameter is $\alpha =10$. It is observed that at $m_1/m_1^{\prime }=0.25$, the consolidation curve exhibits the fastest consolidation rate in the early stages, having the most significant impact, but the slowest rate in the later stages. Conversely, at $m_4/m_4^{\prime }=0.25$, the consolidation curve is the slowest in the early stages but the fastest in the later stages, with an increasing impact. The consolidation curve for $m_3/m_3^{\prime }=0.25$ falls between these two trends. This is because, in the early stages of consolidation, the soil structure remains undamaged, indicating that the volume compression coefficient at the bottom has a greater impact on the average consolidation degree of structured soil.

Figure 9

Figure 9. Influence of compression coefficient on the consolidation degree.

5 Conclusion

To fill the knowledge gap in consolidation solutions for layered structured soil foundation with continuous drainage boundary, an analytical solution is then proposed by using integral transform methods. The effectiveness of the proposed solution is discussed by comparing against a degenerated case and the numerical results calculated using the finite element method. Parametric analysis is carried out to study the influence of interface parameter, soil permeability coefficient and soil compressibility on consolidation behaviors of foundation soils. The main conclusions in this study are summarized as follows:

(1) Initial soil consolidation is markedly affected by the permeability coefficient, with higher values accelerating excess pore water pressure dissipation in the upper layers. As the consolidation progresses, these effects become less pronounced, indicating that higher permeability leads to more rapid initial consolidation stage, but it has minimal impact in later stages.

(2) The volume compression coefficient markedly influences the early dissipation of excess pore water pressure in structured soil, with pronounced effects in upper layers that diminish over time.

(3) Higher interface parameters significantly accelerate the dissipation of excess pore water pressure and enhance the initial consolidation rate in structured soil. However, the differences in consolidation due to varying interface parameters diminish over time.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JF: Conceptualization, Data curation, Investigation, Methodology, Writing–original draft, Writing–review and editing. XD: Conceptualization, Data curation, Methodology, Writing–review and editing. RL: Conceptualization, Data curation, Methodology, Writing–review and editing. LoW: Data curation, Writing–review and editing. LiW: Validation, Software and Writing–review and editing. GM: Conceptualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52008124, 52268054 and 52208345), the China Postdoctoral Science Foundation (2020M683210), and the Natural Science Foundation of Guizhou Minzu University (GZMUZK[2023]CXTD04).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, R., Xie, K., Deng, Y., and Wang, K. (2012). Approximate solution for one-dimensional consolidation of structured soils under time-dependent loading. Rock Soil Mech. 33 (10), 3194–3200. doi:10.16285/j.rsm.2012.10.021

CrossRef Full Text | Google Scholar

Burland, J. B. (1990). On the compressibility and shear strength of natural clays. Geotechnique 40 (3), 329–378. doi:10.1680/geot.1990.40.3.329

CrossRef Full Text | Google Scholar

Cao, Y., Chen, Y., and Huang, M. (2006). One-dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading. Chin. J. Geotechnical Eng. 28 (5), 569–574.

Google Scholar

Chen, P., Li, J., Huang, M., and Li, D. (2021). Consolidation of viscoelastic soil with vertical drains for continuous drainage boundary conditions incorporating a fractional derivative model. Front. Mater. 8, 670150. doi:10.3389/fmats.2021.670150

CrossRef Full Text | Google Scholar

Cosenza, P., and Korošak, D. (2014). Secondary consolidation of clay as an anomalous diffusion process. Int. J. Numer. Anal. Methods Geomechanics 38 (12), 1231–1246. doi:10.1002/nag.2256

CrossRef Full Text | Google Scholar

Cui, J., Xie, K., Xia, C., Hu, A., and Zhou, Y. (2018). One-dimensional nonlinear consolidation analysis of double layered structured soils under time-dependent loading. J. Central South Univ. Technol. 49 (7), 1710–1717. doi:10.11817/j.issn.1672-7207.2018.07.018

CrossRef Full Text | Google Scholar

Feng, J., Chen, Z., Li, Y., and Mei, G. (2019a). Analytical solution for one-dimensional consolidation of soft clayey soil with a continuous drainage boundary under linear loading. Eng. Mech. 36 (6), 219–226.

Google Scholar

Feng, J., Ma, X., Liu, X., Wang, L., Wu, Z., and Mei, G. (2024). Analytical solution for one-dimensional consolidation of structured soft soils with continuous drainage boundary. Rev. Int. 40 (1), 1–14. doi:10.23967/j.rimni.2024.01.007

CrossRef Full Text | Google Scholar

Feng, J., Ni, P., and Mei, G. (2019b). One-dimensional self-weight consolidation with continuous drainage boundary conditions: solution and application to clay-drain reclamation. Int. J. Numer. Anal. Methods Geomechanics 43 (8), 1634–1652. doi:10.1002/nag.2928

CrossRef Full Text | Google Scholar

Feng, X., Zong, M., Tian, Y., Mei, G., and Wu, W. (2023). Approximate solution for one-dimensional nonlinear consolidation theory of soil considering the time effect of boundary drainage. Eng. Mech. 40 (1), 100–110.

Google Scholar

Gray, H. (1945). Simultaneous consolidation of contiguous layers of unlike compressive soils. Am. Soc. Civ. Eng. 110, 1327–1356.

CrossRef Full Text | Google Scholar

Hu, A., Xia, C., Cui, J., Li, C., and Xie, K. (2018). Nonlinear consolidation analysis of natural structured clays under time-dependent loading. Int. J. Geomechanics 18 (2), 04017140. doi:10.1061/(asce)gm.1943-5622.0001059

CrossRef Full Text | Google Scholar

Hu, A., Zhou, Y., Chen, Y., Xia, C., and Xie, K. (2020). Semi-analytical solutions for one-dimensional nonlinear large strain consolidation of structured soft clay. Rock Soil Mech. 41 (8), 2583–2591. doi:10.16285/j.rsm.2018.2047

CrossRef Full Text | Google Scholar

Leroueil, S., and Vaughan, P. R. (1990). The general and congruent effects of structure in natural soils and weak rocks. Geotechnique 40 (3), 467–488. doi:10.1680/geot.1990.40.3.467

CrossRef Full Text | Google Scholar

Li, C., Wang, L., Li, J., and Chen, Y. (2024). Application of multi-algorithm ensemble methods in high-dimensional and small-sample data of geotechnical engineering: a case study of swelling pressure of expansive soils. J. Rock Mech. Geotechnical Eng. 16 (5), 1896–1917. doi:10.1016/j.jrmge.2023.10.015

CrossRef Full Text | Google Scholar

Li, C., Xiao, J., Wu, W., Mei, G., Ni, P., and Leo, C. (2020). Analysis of 1D large strain consolidation of structured marine soft clays. J. Zhejiang Univ-Sc A 21 (1), 29–43. doi:10.1631/jzus.a1900268

CrossRef Full Text | Google Scholar

Liu, J., and Lei, G. (2013). One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries. Comput. Geotechnics 54 (10), 202–209. doi:10.1016/j.compgeo.2013.07.009

CrossRef Full Text | Google Scholar

Liu, Q., Deng, Y. B., and Wang, T. Y. (2018). One-dimensional nonlinear consolidation theory for soft ground considering secondary consolidation and the thermal effect. Comput. and Geotechnics 104 (DEC.), 22–28. doi:10.1016/j.compgeo.2018.08.007

CrossRef Full Text | Google Scholar

Mei, G., Xia, J., and Mei, L. (2011). Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary. Chin. J. Geotech. Eng. 33 (1), 28–31.

Google Scholar

Ng, C. W. W., Guo, H., Ni, J., Chen, R., Xue, Q., Zhang, Y., et al. (2024a). Long-term field performance of non-vegetated and vegetated three-layer landfill cover systems using construction waste without geomembrane. Géotechnique. 74 (2), 155–173. doi:10.1680/jgeot.21.00238

CrossRef Full Text | Google Scholar

Ng, C. W. W., Zhang, Q., Zhang, S., Lau, S. Y., Guo, H., and Li, Z. (2024b). A new state-dependent constitutive model for cyclic thermo-mechanical behaviour of unsaturated vegetated soil. Can. Geotechnical J. 61 (10), 2155–2179. doi:10.1139/cgj-2023-0268

CrossRef Full Text | Google Scholar

Poskitt, T. J. (1969). The consolidation of saturated clay with variable permeability and compressibility. Géotechnique. 19 (2), 234–252. doi:10.1680/geot.1969.19.2.234

CrossRef Full Text | Google Scholar

Shen, Z. (1998). Engineering properties of soft soils and design of soft ground. Chin. J. Geotechnical Eng. 20 (1), 100–111.

Google Scholar

Tang, Y., Zhou, M., and Jiang, L. (2007). One dimensional nonlinear semi-analytical solution for structured soft soils. Chin. J. Undergr. Space Eng. 3 (4), 605–608. doi:10.3969/j.issn.1673-0836.2007.04.005

CrossRef Full Text | Google Scholar

Terzaghi, K. (1925). Erdbaumechanik and bodenphysikalischer grundlage. wien: fanz deuticke.

Google Scholar

Wang, J., and Chen, Y. (2003). Analytical solution to 1-D consolidation of uniform structured soft foundation. J. Hydraulic Eng. 34 (3), 19–24.

Google Scholar

Wang, L., Ding, L., Chen, Y., and Li, L. (2004). Study on compressibility of structured soft soil. China Civ. Eng. J. 37 (4), 46–53. doi:10.15951/j.tmgcxb.2004.04.010

CrossRef Full Text | Google Scholar

Xie, K., Xia, C., An, R., Hu, A., and Zhang, W. P. (2016a). A study on the one-dimensional consolidation of double-layered structured soils. Comput. Geotechnics 73 (1), 189–198. doi:10.1016/j.compgeo.2015.12.007

CrossRef Full Text | Google Scholar

Xie, K., Xia, C., An, R., Ying, H., and Wu, H. (2016b). A study on one-dimensional consolidation of layered structured soils. Int. J. Numer. Anal. Methods Geomechanics 40 (7), 1081–1098. doi:10.1002/nag.2477

CrossRef Full Text | Google Scholar

Yang, W., Qiu, C., Duan, Y., Feng, J., and Mei, G. (2024). One-dimensional consolidation analysis of layered foundations subjected to arbitrary loads under a continuous drainage boundary. Int. J. Geomechanics 24 (6), 04024091. doi:10.1061/ijgnai.gmeng-9317

CrossRef Full Text | Google Scholar

Zhang, C. (1983). Geotechnical characteristics of two structure clays. J. Nanjing Hydraulic Res. Inst. 4, 65–71.

Google Scholar

Zong, M., Tian, Y., Liang, R., Wu, W., Xu, M., and Mei, G. (2022). One-dimensional nonlinear consolidation analysis of soil with continuous drainage boundary. J. Cent. South Univ. 29 (1), 270–281. doi:10.1007/s11771-022-4916-x

CrossRef Full Text | Google Scholar

Zong, M., Wu, W., El Naggar, M. H., Mei, G., Ni, P., and Xu, M. (2023). Analytical solution for one-dimensional nonlinear consolidation of double-layered soil with improved continuous drainage boundary. Eur. J. Environ. Civ. Eng. 27 (8), 2746–2767. doi:10.1080/19648189.2020.1813207

CrossRef Full Text | Google Scholar