- 1School of Geological Engineering and Geomatics, Chang’an University, Xi’an, China
- 2International College, Northwestern Polytechnical University, Xi’an, China
Introduction: Young’s modulus and shear modulus are essential mechanical parameters for evaluating subsurface rocks, playing a pivotal role in the exploration and development of unconventional resources. Young’s modulus indicates the brittleness of the reservoir, while shear modulus determines the ease of fracturing rock layers.
Methods: Traditional methods estimate these moduli through indirect calculations and approximate expressions, which are prone to cumulative errors and rely on multiple assumptions, reducing inversion accuracy. This paper presents a direct inversion method for acquiring of Young’s modulus and shear modulus using the exact Zoeppritz equations, integrated within a Bayesian framework for pre-stack inversion. The quantum particle swarm optimization (QPSO) algorithm is introduced to achieve a nonlinear solution to the objective function.
Results: Tests on synthetic and actual field data demonstrate the feasibility and effectiveness of the proposed method, yielding more accurate inversion results compared to traditional methods.
Discussion: These findings provide valuable insights for predicting reservoir brittleness and characterizing reservoirs in unconventional shale gas exploration and development.
1 Introduction
As exploration advances, unconventional resources have become the primary focus in contemporary oil and gas exploration (Zong et al., 2018; Wang et al., 2022; Zhou et al., 2022). The exploration and development of unconventional oil and gas are essential for ensuring sustainable and stable economic growth. In this context, accurately evaluating the brittleness of reservoir rocks is a crucial step in identifying shale oil and gas reservoirs. Parameters such as Young’s modulus and shear modulus reflect the fracture characteristics of rocks, which are vital for assessing reservoir rock brittleness and estimating the extent of fracturing (Li et al., 2023; Liu et al., 2023; Zhou et al., 2023). Therefore, extracting these elastic modulus parameters from seismic data is key to identifying shale oil and gas reservoirs.
The acquisition of elastic parameters such as Young’s modulus and shear modulus has evolved from indirect calculation to direct inversion (Zheng et al., 2024). After obtaining elastic parameters such as P-wave and S-wave velocities and density, the rock physics relationships among these elastic parameters are used to calculate Young’s modulus and shear modulus profiles (Liu et al., 2022; Chen et al., 2023). Indirect calculation methods are prone to introducing cumulative errors, which reduce the accuracy of the inversion. To address the drawbacks of indirect inversion methods, many researchers have derived reflection coefficient equations involving Young’s modulus to establish direct inversion procedures. For example, Zong et al. (2013) derived the linear relationship between the P-wave reflection coefficient and Young’s modulus, Poisson’s ratio, and density (YPD equation) from the Aki–Richards approximation of Zoeppritz equations. ZHANG et al. (2014) proposed that the product of Young’s modulus and density (Eρ) has good hydrocarbon indication effects. They derived approximate equations for the P-wave reflection coefficient and converted the wave reflection coefficient based on Eρ, Poisson’s ratio, and density and tested the approach in shale reservoirs.
Amplitude Variations with Offset (AVO) is a technique that obtains subsurface lithology information by studying the relationship between seismic amplitude and offset, playing an important theoretical role in pre-stack seismic inversion (Buland and Omre, 2003; Liu and Grana, 2018; Zhou et al., 2020; Cheng et al., 2022). Through pre-stack AVO inversion, fluid information and elastic parameters in reservoir rocks can be extracted from seismic data. Pre-stack AVO inversion requires the Zoeppritz equations as the forward modeling foundation. Aki–Richards introduced approximations to the Zoeppritz equations for small incidence angles and low contrast, allowing rapid development of the AVO technology (Aki and Richards, 2009). Many scholars proposed various approximations to the Zoeppritz equations (Shuey, 1985; Fatti et al., 1994; Gray et al., 1999). The introduction of these approximations made the pre-stack AVO technology based on the Zoeppritz equations feasible, contributing significantly to the oil and gas industry (Grana et al., 2022; Zhou et al., 2023). However, with the increasing demands for refined exploration, inversion based on approximation formulas shows low resolution when applied to complex oil and gas reservoirs, big offsets, and large incident angles. With the development of inversion algorithms, the pre-stack AVO technology based on exact Zoeppritz equations has been developed and applied. Chen et al. (2023) derived the PP-wave equation from the exact Zoeppritz equations in a form that includes Young’s modulus and proposed a nonlinear inversion method, which performed well in practical field applications. Song et al. (2023) conducted similar derivations and applied them in sandstone reservoirs. Zhou et al. (2021) re-derived the exact Zoeppritz equations in terms of fluid factors and shear modulus, achieving simultaneous inversion of the elastic modulus and fluid factors. This paper will derive reflection coefficient equations based on Young’s modulus and shear modulus from the exact solutions of the Zoeppritz equations and apply them to pre-stack AVO inversion.
Constructing the inversion objective function within the Bayesian framework allows for the targeted introduction of prior distributions, reducing the uncertainty of geophysical inverse problems (Zong and Ji, 2021). By using Bayesian theory, the correlation of elastic parameters can be effectively introduced into the objective function as a regularization constraint, thus enhancing the well-posedness of the inversion. In the study of prior distributions, Alemie and Sacchi (2011) proposed a pre-stack AVO inversion process by introducing the trivariate Cauchy distribution. Zhou et al. (2017) believed that a prior model based on the Laplace distribution can better characterize reservoir boundaries. They introduced and tested the Laplace distribution in their inversion. The modified trivariate Cauchy distribution can highlight weak reflection information, balance the enhancement of strong reflection boundaries, improve the signal-to-noise ratio, and suppress weak reflections (Pan et al., 2019). This approach has been adopted by many scholars in addressing geophysical inverse problems.
Inversion based on the exact Zoeppritz equations is a highly intensive nonlinear problem. Traditional quasi-linear iterative algorithms have difficulty handling such problems. Moreover, linear solution methods heavily rely on the initial model (Pan et al., 2017). If the initial model deviates significantly from the true value, the iterative results are prone to getting trapped in local minima. In areas with few drillings, it is difficult to provide an accurate initial model, affecting the accuracy of the inversion results. Using fully nonlinear algorithms to directly map nonlinear problems from data space to model space can achieve global optimization of the solution area, such as genetic algorithms, Monte Carlo methods, simulated annealing, and particle swarm optimization (PSO) (Liu et al., 2022). Fully nonlinear algorithms can achieve the global optimization process by establishing appropriate search strategies. Compared with linear algorithms, these algorithms have higher computational accuracy. PSO, a global intelligent optimization algorithm, is widely applied in various engineering problems due to its iterative stability and fast solving speed (Kennedy and Eberhart, 1995). However, PSO also has limitations, such as a tendency to get trapped in local minima and complex parameter settings. Sun et al. introduced the concept of quantum bits, enabling particles to exhibit quantum behavior, and proposed a quantum particle swarm optimization (QPSO) algorithm (Sun et al., 2005, Sun et al., 2012). In the QPSO algorithm, each particle’s position is no longer a definite value but a probability distribution, which enhances the global search capability of the particles and allows for greater exploration within the search space (Xu et al., 2016).
Therefore, this paper first introduces the exact solution to the exact Zoeppritz equation and rederives it into a form that includes Young’s modulus, shear modulus, and density. An exact PP-wave reflection coefficient expression based on Young’s modulus, shear modulus, and density was obtained. Then, within the Bayesian inversion framework, the modified trivariate Cauchy distribution was introduced to construct the objective function for the direct inversion of Young’s modulus, shear modulus, and density. The inversion objective function was solved using the quantum particle swarm optimization algorithm. The proposed algorithm was validated using synthetic data and real-field data.
2 Materials and methods
2.1 Derivation of the exact Zoeppritz equation based on Young’s modulus, shear modulus, and density
When a P-wave is incident, the geological properties on both sides of the interface do not vary significantly, and the incident angle is small, approximate formulas can be used as forward operators. However, for complex reservoirs, these approximate formulas no longer satisfy inversion requirements, necessitating the use of the exact Zoeppritz equation as the forward operator. The Zoeppritz equation can be expressed as follows (Equation 1):
In the above equation, RPP, RPS, TPP, and TPS represent the reflection and transmission coefficients of P-waves and converted S-waves, respectively. The subscripts 1 and 2 in parameters such as VP, VS, and ρ represent the medium parameters on the upper and lower sides of the interface, respectively.
In the abovementioned formula,
Next, it is necessary to derive the relationship between Young’s modulus, shear modulus, and wave velocity based on rock physics relationships. According to rock physics relationships, the bulk modulus K can be expressed in terms of Young’s modulus E and Poisson’s ratio
The relationship between shear modulus and P-wave and S-wave velocities can be expressed as Equations 4, 5.
The relationship between Poisson’s ratio and P-wave and S-wave velocities is
By solving Equations 3 and 6 simultaneously, the relationship between Young’s modulus E, shear modulus
By substituting Equations 7, 8 into Equation 3, a new form of the reflection coefficient equation in terms of Young’s modulus E, shear modulus
The specific form of the equation is provided in Appendix A.
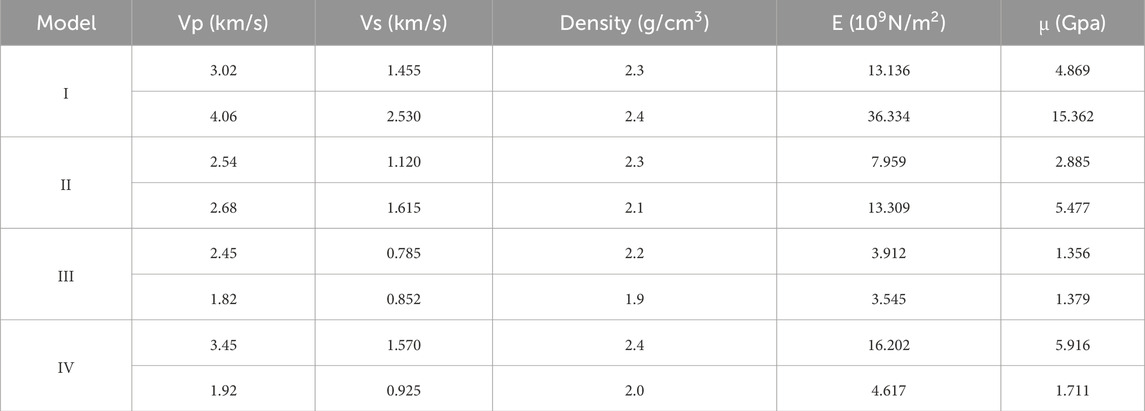
To compare the accuracy of the newly derived PP-wave reflection coefficient (EGD-Zoeppritz) with that of the traditional exact Zoeppritz reflection coefficient, we tested four types of AVO models. Table 1 lists the parameters of the four AVO models. Figure 1 shows the reflection coefficients of the exact Zoeppritz equation, Aki–Richards approximation, Fatti approximation, and EGD-Zoeppritz equation under different AVO models. The reflection coefficient accuracy of the EGD-Zoeppritz equation is the same as that of the exact Zoeppritz equation and better than that of the approximate equations. When the incident angle exceeds 30°, the reflection coefficients calculated by the approximate equations start to deviate from the exact reflection coefficients. This deviation is caused by the small-angle assumption inherent in the approximate equations. However, the EGD–Zoeppritz equation can consistently fit the exact reflection coefficient equation with high accuracy. Figure 1 demonstrates the correctness of the reflection coefficient equation derived in this paper.
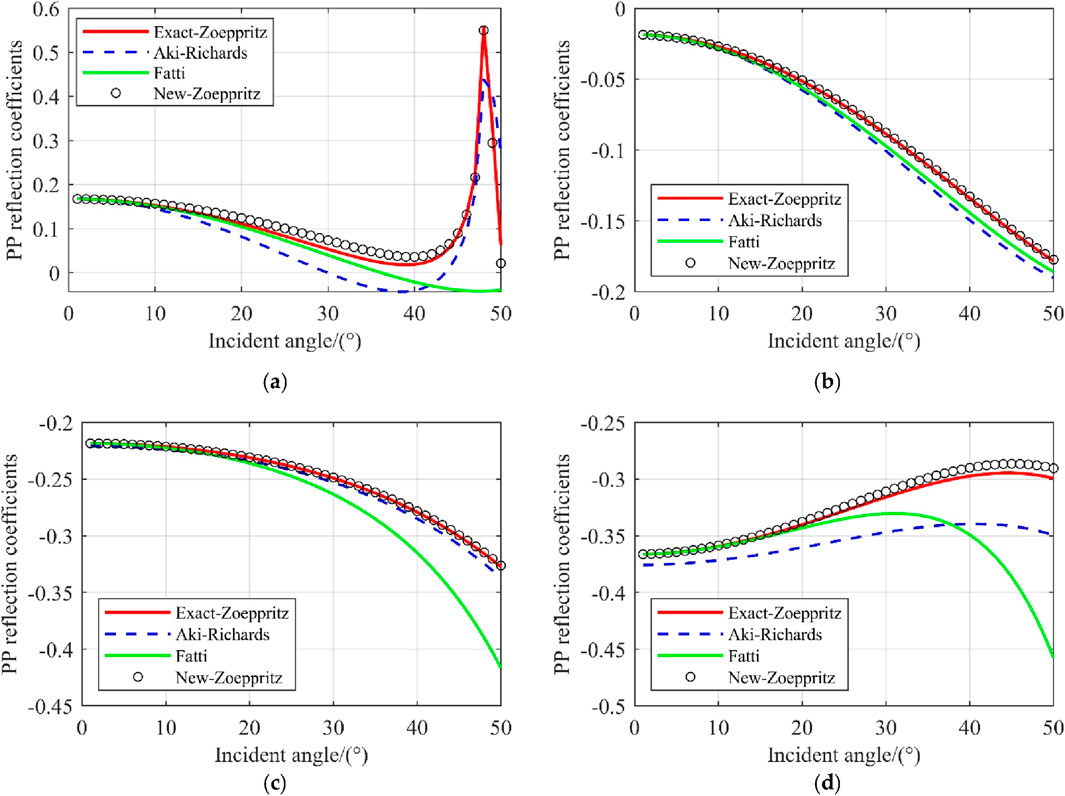
Figure 1. Comparison of PP-wave reflection coefficients for four AVO models. (A) Model I; (B) Model II; (C) Model III; and (D) Model IV.
2.2 Construction of the inversion objective function
In seismic exploration, seismic records can be obtained by convolving reflection coefficients with seismic wavelets, and the relationship between seismic observation data and model parameters can be expressed as Equation 10.
Here, d represents seismic records, m represents model parameters, G represents the forward operator, and n represents added noise data. In geophysical inverse problems, the physical properties of the subsurface medium are inferred from observed data, which are often ill-posed, exhibiting non-uniqueness, nonlinearity, and other issues. Bayesian inversion is a probabilistic inversion method that can effectively address various problems encountered in geophysical inversion.
In the above equation,
Here, nd represents the data dimension, Σe represents the noise covariance matrix, and m is the model parameter to be inverted.
The advantage of the Bayesian method is that it can introduce prior information in a targeted manner during the inversion process, thus improving the accuracy of the inversion results. The modified trivariate Cauchy distribution has heavy tails, which can enhance the resolution of inversion results, while reducing the suppression of weak reflection information and highlighting strong reflection boundaries, effectively recovering thin layers and weak reflection strata (Wang et al., 2023). Assuming that the model parameters follow a modified trivariate Cauchy distribution, we obtain
Here, χ is a 3×3 covariance matrix that includes the statistical correlations between model parameters, ω is the average value of model parameters obtained from prior information, and
Substituting the prior model distribution probability (Equation 13) and the likelihood distribution probability (Equation 12) into Equation 11, the expression for the posterior probability distribution function is obtained as Equation 15.
Taking the natural logarithm of both sides of Equation 11 and multiplying by −1 transform the maximization of the posterior probability distribution function
where
2.3 Introduction of the quantum particle swarm optimization algorithm
Inspired by the regularity of bird foraging behavior, Kennedy and Eberhart (1995) proposed the traditional PSO algorithm. The conventional PSO algorithm is characterized by its simplicity, ease of implementation, and fast convergence speed. However, it also has drawbacks such as requiring numerous parameter settings, poor global optimization capability, and a tendency to get trapped in local minima. To address these issues, Sun et al. (2012) introduced the concept of quantum bits, allowing particles to exhibit quantum behavior, and proposed the QPSO algorithm. In the QPSO algorithm, the position of each particle is no longer a fixed value but rather a probability distribution, enhancing the particle’s global search capability and allowing for greater exploration within the search space.
The core of the QPSO algorithm lies in transforming the deterministic description of a particle’s position and velocity into a probabilistic description, achieved by simulating the behavior of quantum particles. Unlike classical particles, quantum particles do not have a definite trajectory; their position is represented as a probability cloud or probability density function. In the QPSO algorithm, particles do not possess a velocity vector. Therefore, in the tth iteration, the particle’s update can be expressed as follows:
where
Here, mBest represents the mean best position of the particle swarm, defined as the average of the best positions of all particles (the global best position). PBest refers to the best position of each particle at the current iteration (individual best position). N denotes the number of particles in the swarm. In the QPSO algorithm, Pi is the local attractor, determined jointly by the individual and global best positions. The term φ is a random number between 0 and 1. In Equation 17 and Equation 18, both k and u are also random numbers within the range of (0, 1). The parameter β is the only constant that needs to be manually specified in the QPSO algorithm, known as the contraction–expansion coefficient, which controls the convergence speed of the algorithm. The β value plays a crucial role in the algorithm, where a larger β promotes global exploration in the early stages, while a smaller β is suitable for local optimization in the later stages. In this study, we set β to decrease linearly within the range of [1, 0.5] according to Equation 19.
3 Synthetic seismic data testing
In this section, synthetic angle-gathered seismic records are used to test the effectiveness and reliability of the Young’s modulus inversion based on the exact Zoeppritz equation (EGD-Zoeppritz). Based on real well-logging data, Young’s modulus and shear modulus curves are constructed as the model parameters to be estimated, as shown in Figure 2. The incident angle range of the synthetic multi-wave seismic data is 1°–40°. The PP wave reflection coefficients at different incident angles are calculated using the rederived exact reflection coefficient equation and convolved with a 30 Hz Ricker wavelet to obtain the synthetic seismic records, as shown in Figure 3A. Next, to test the noise resistance of the proposed algorithm, Gaussian random noise with signal-to-noise ratios (SNR) of 5 and 2 is added to the noise-free synthetic seismic records to obtain the noisy synthetic seismic records, as shown in Figures 3B, C. The QPSO algorithm is introduced to solve the inversion task. In this experiment, we set the QPSO search range to fluctuate within ±50% of the well log curve values. The population size is set to 400, and the number of iterations is set to 800.
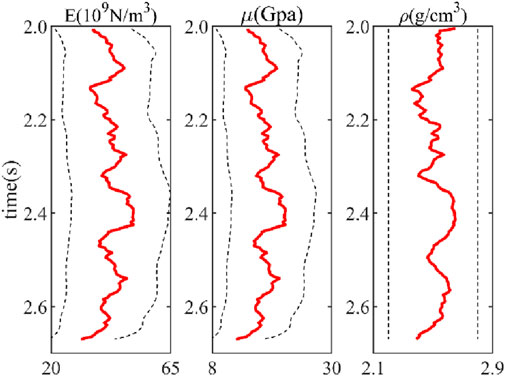
Figure 2. Single-well model; the red line represents the true value, and the black dashed line represents the search range.
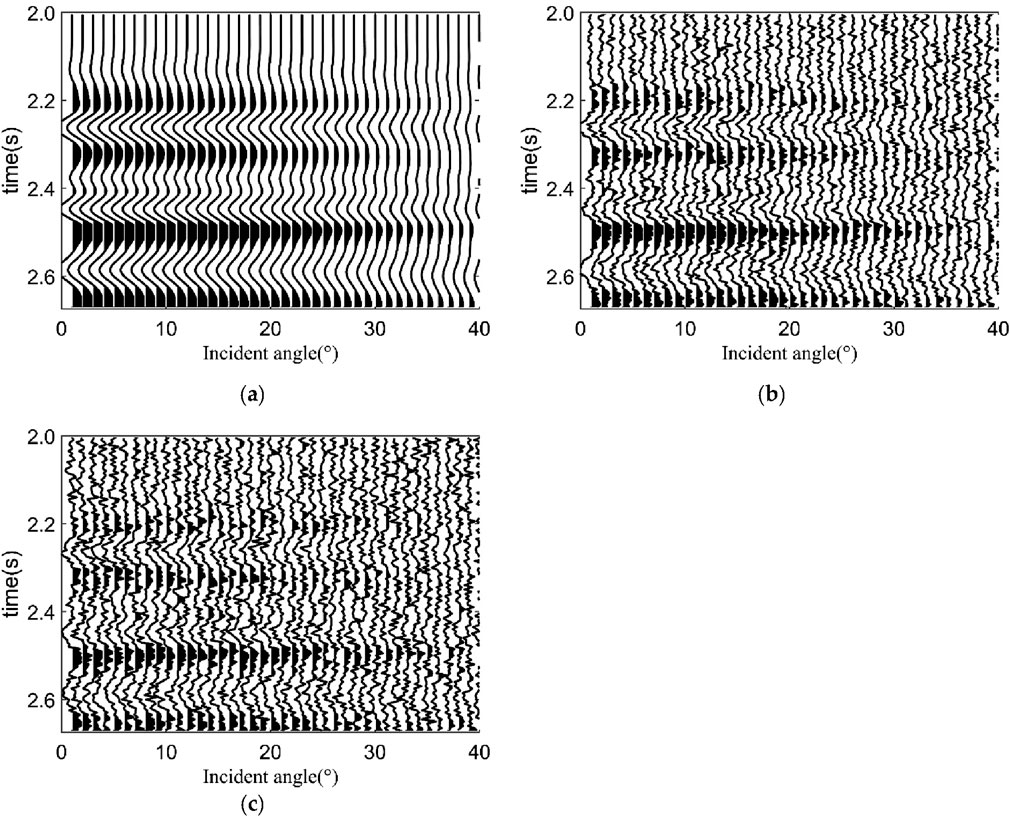
Figure 3. Synthetic angle-gathered seismic records. (A) Noise-free synthetic seismic record; (B) S/N=5 synthetic seismic records; (C) S/N=2 synthetic seismic records.
Comparing Figures 4A–C, it can be seen that the method proposed in this paper can reasonably and effectively estimate the values of Young’s modulus, shear modulus, and density of the strata. When the synthetic seismic data are noise-free, the inversion results can almost accurately fit the pseudo-well curves. As the noise increases, the precision of the inversion results gradually decreases, but the overall shape of the curves can still be fitted. Specifically, when the noise level is raised to a high noise state with a signal-to-noise ratio of 2, the fit of the inversion results to Young’s modulus remains stable. However, the inversion accuracy of the density term decreases due to its insensitivity in the Zoeppritz equation. Figure 5 shows the inversion results using the Aki–Richards approximation. By comparing Figures 4A–C, 5A–C, it can be seen that the inversion results based on the exact Zoeppritz equation are significantly better than those based on the approximate equations.
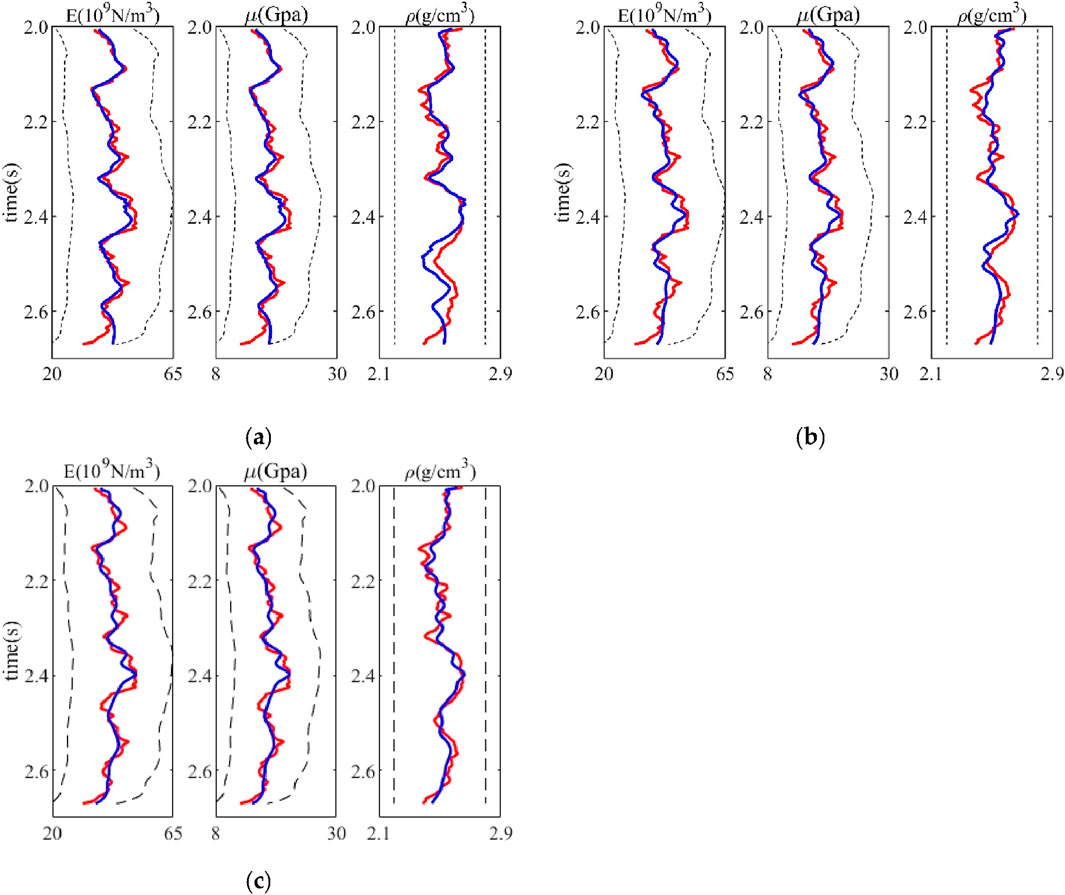
Figure 4. Nonlinear inversion results based on the EGD-Zoeppritz equation: the red line represents the model values, the blue line represents the inversion results, and the black dashed line represents the search boundaries. (A) Inversion results without noise; (B) inversion results with noise S/N=5; and (C) inversion results with noise S/N=2.
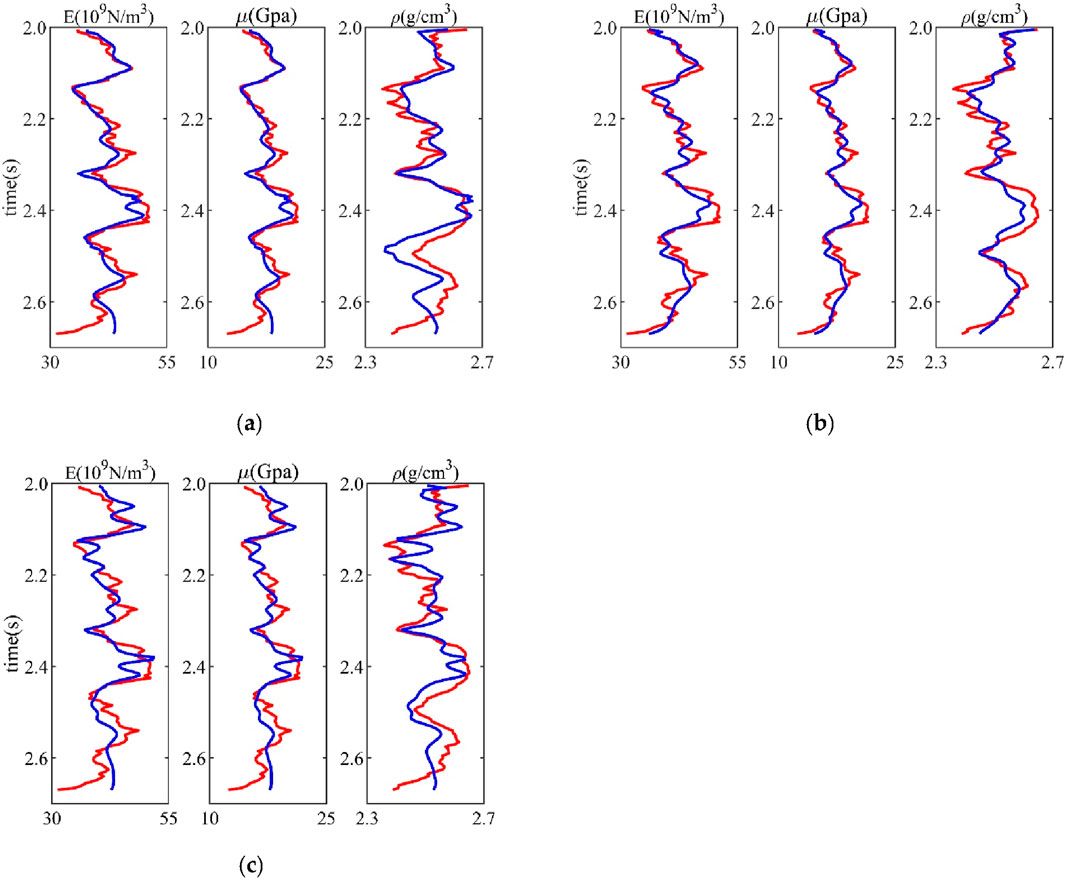
Figure 5. Inversion results based on the Aki–Richards equation: the red line represents the model values, and the blue line represents the inversion results. (A) Inversion results without noise; (B) inversion results with noise S/N=5; and (C) inversion results with noise S/N=2.
4 Actual production data testing
To verify the practical application of the method proposed in this paper for estimating formation Young’s modulus based on the exact Zoeppritz equation, seismic data from an actual field are selected for testing in this section. The actual data used for testing come from an exploration area in western China. This area is located in the transitional zone where the Tianhuan syncline’s western edge fault-fold belt converges with the western margin of the Ordos Basin. The faults in this region play a controlling role in hydrocarbon accumulation, and source rocks are relatively well-developed within the study area. The target reservoir is mainly distributed in the central part of the exploration area, predominantly controlled by two large distributary channel sand bodies. The reservoir has a considerable thickness, with an average of 25 m and a maximum of 40 m. The reservoir properties are favorable, with an average porosity of 12% and a maximum of 15%. The data were processed with amplitude compensation and correction, deconvolution, noise suppression, and pre-stack time migration, extracting pre-stack seismic records for angles of 3°, 9°, 15°, 21°, and 27°. The seismic sampling rate is 4 ms, and the angle-gathered seismic profiles are shown in Figures 6A–E, with the black line indicating the well location. The phase-carrying seismic wavelet was extracted from the well for inversion testing. Pseudo-logging curves of Young’s modulus and shear modulus were calculated from conventional logging curves from the well.
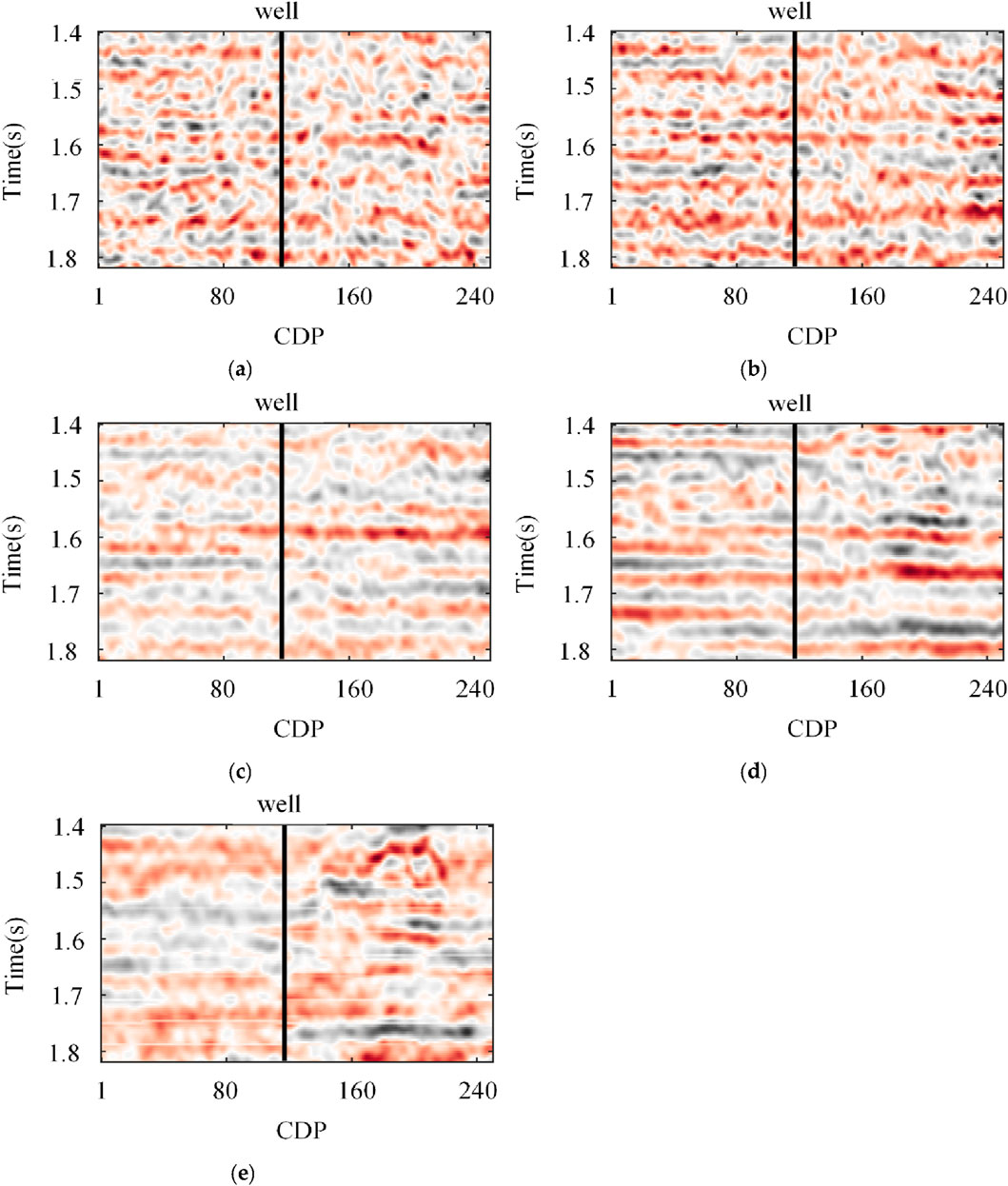
Figure 6. Seismic records of PP waves at different angles in the X area, with the black line indicating the well location. (A) Seismic record at 3° incidence angle. (B) Seismic record at 9° incidence angle. (C) Seismic record at 15° incidence angle. (D) Seismic record at 21° incidence angle. (E) Seismic record at 27° incidence angle.
When applying intelligent optimization algorithms to solve practical problems, it is often challenging to accurately define the search range. Typically, hard constraints (fixed values) are set, or the search range is determined based on well log curves. In this study, since the strata in the working area are relatively gentle, we set the search range to fluctuate within ±50% of the well log curve values. The population size was set to 400, and the number of iterations was set to 800. To reduce the computational time, we also implemented multi-core parallel computing using the CPU.
The inversion results for Young’s modulus, shear modulus, and density using the method proposed in this paper are shown in Figure 7, with the blue line indicating the magnitude of the logging curve. From the inversion profile, it can be seen that the inversion results match the logging curve well. Simultaneously, we applied the approximate formula to invert this area, as depicted in Figure 8. Comparing Figures 7, 8, it is clear that the method proposed in this paper performs well on actual data, with the inversion results having a higher resolution than those obtained using the approximate formula. We extracted the seismic trace at the well location and compared it with the logging curve, as shown in Figure 9, and the inversion results align with the trend of the logging curve. Thus, the actual application results validate the reliability of the proposed direct inversion method in field data applications, with the estimation accuracy meeting the requirements for brittleness calculation and sweet spot favorable area planning.
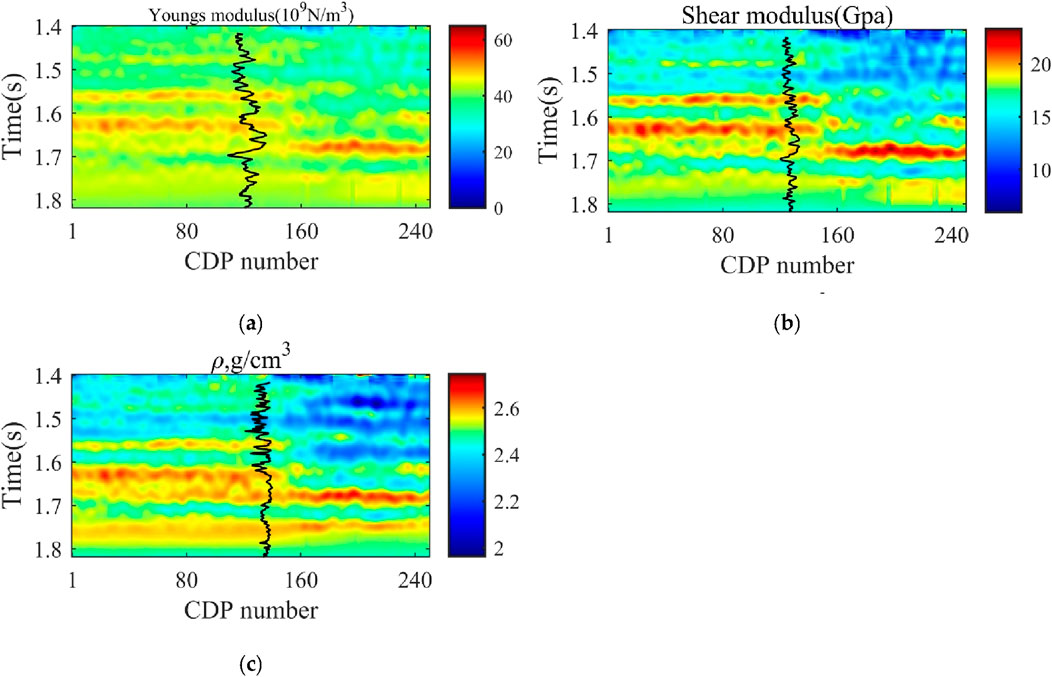
Figure 7. Inversion results using the method proposed in this paper. (A) Young’s modulus. (B) Shear modulus. (C) Density.

Figure 8. Inversion results based on the Aki–Richards equation. (A) Young’s modulus. (B) Shear modulus. (C) Density.
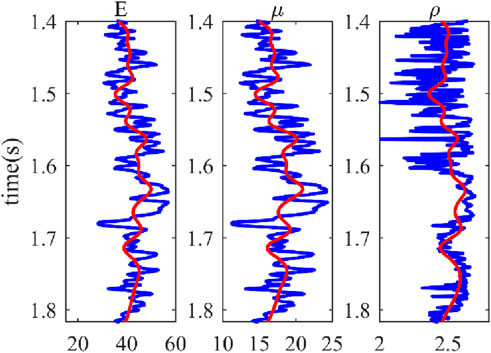
Figure 9. Comparison of inversion results using the proposed method beside the well track. The red solid line represents the smoothed curve of the inversion results, and the blue solid line represents the logging curve.
5 Conclusion
Due to the approximate expressions and indirect calculations associated with the Zoeppritz equation, it cannot meet the requirement of high-precision inversion results for Young’s modulus, shear modulus, and density. The paper deduced a new form of the exact Zoeppritz equation for reflection coefficients based on the Young’s modulus, shear modulus, and density. Subsequently, a direct synchronous AVO inversion method for Young’s modulus, shear modulus, and density is proposed based on the new Zoeppritz expression of PP wave reflection coefficients. Then, under the Bayesian inversion framework, an inversion objective function that can simultaneously invert Young’s modulus, shear modulus, and density is constructed in this paper. The quantum particle swarm algorithm is introduced into the inversion method to address ill-posed inverse problems. The applications of synthetic data and field seismic data show that the proposed inversion method based on the new Zoeppritz expression can directly and reliably predict Young’s modulus, shear modulus, and density simultaneously. The method proposed in this paper provides some ideas for predicting reservoir brittleness and characterizing reservoirs in unconventional shale gas exploration and development.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YC: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, supervision, validation, visualization, writing–original draft, and writing–review and editing. SS: conceptualization, data curation, funding acquisition, methodology, validation, visualization, and writing–review and editing. DL: supervision and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Natural Science Basic Research Program of Shaanxi (No. 2024JC-YBMS-199) the Fundamental Research Funds for the Central Universities, CHD (Ref. 300102262205)..
Acknowledgments
The authors would like to thank the Yellow River Research Institute of Chang’an University and Shaanxi Yellow River Science Research Institute. In addition, they thank the reviewers and the editors for their valuable comments, which improved the quality of this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aki, K., and Richards, P. G. (2009). Quantitative seismology. 2. edition. Mill Valley, California New York: University Science Books. corrected printing.
Alemie, W., and Sacchi, M. D. (2011). High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution. GEOPHYSICS 76, R43–R55. doi:10.1190/1.3554627
Buland, A., and Omre, H. (2003). Bayesian linearized AVO inversion. GEOPHYSICS 68, 185–198. doi:10.1190/1.1543206
Chen, X., Zong, Z., and Zuo, Y. (2023). Direct exact nonlinear broadband seismic amplitude variations with offset inversion for young’s modulus. IEEE Trans. Geosci. Remote Sens. 61, 1–16. doi:10.1109/TGRS.2022.3231594
Cheng, J.-W., Zhang, F., and Li, X.-Y. (2022). Nonlinear amplitude inversion using a hybrid quantum genetic algorithm and the exact zoeppritz equation. Pet. Sci. 19, 1048–1064. doi:10.1016/j.petsci.2021.12.014
Fatti, J. L., Smith, G. C., Vail, P. J., Strauss, P. J., and Levitt, P. R. (1994). Detection of gas in sandstone reservoirs using AVO analysis: a 3-D seismic case history using the Geostack technique. GEOPHYSICS 59, 1362–1376. doi:10.1190/1.1443695
Grana, D., Figueiredo, L. D., and Mosegaard, K. (2022). Markov chain Monte Carlo for petrophysical inversion. GEOPHYSICS 87, M13–M24. doi:10.1190/geo2021-0177.1
Gray, D., Goodway, B., and Chen, T. (1999). “Bridging the gap: using AVO to detect changes in fundamental elastic constants,” in SEG technical Program expanded abstracts 1999 (Society of Exploration Geophysicists), 852–855. doi:10.1190/1.1821163
Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN'95 - International Conference on Neural Networks (Houston, Texas: IEEE), 1942–1948.
Li, X., Wei, W., Xia, Y., Wang, L., and Cai, J. (2023). Modeling and petrophysical properties of digital rock models with various pore structure types: an improved workflow. Int. J. Coal Sci. Technol. 10, 61. doi:10.1007/s40789-023-00627-z
Liu, M., and Grana, D. (2018). “Ensemble-based joint inversion of PP and PS seismic data using full Zoeppritz equations,” in SEG International Exposition and Annual Meeting, (SEG), 511–515. SEG-2018-2993625. doi:10.1190/segam2018-2993625.136
Liu, X., Chen, X., Cheng, J., Zhou, L., Chen, L., Li, C., et al. (2023). Simulation of complex geological architectures based on multistage generative adversarial networks integrating with attention mechanism and spectral normalization. IEEE Trans. Geosci. Remote Sens. 61, 1–15. doi:10.1109/TGRS.2023.3294493
Liu, X., Shao, G., Liu, Y., Liu, X., Li, J., Chen, X., et al. (2022). Deep classified autoencoder for lithofacies identification. IEEE Trans. Geosci. Remote Sens. 60, 1–14. doi:10.1109/TGRS.2021.3139931
Pan, X., Zhang, G., Chen, H., and Yin, X. (2017). McMC-based AVAZ direct inversion for fracture weaknesses. J. Appl. Geophys. 138, 50–61. doi:10.1016/j.jappgeo.2017.01.015
Pan, X., Zhang, G., and Yin, X. (2019). Amplitude variation with offset and azimuth inversion for fluid indicator and fracture weaknesses in an oil-bearing fractured reservoir. GEOPHYSICS 84, N41–N53. doi:10.1190/geo2018-0554.1
Shuey, R. T. (1985). A simplification of the Zoeppritz equations. GEOPHYSICS 50, 609–614. doi:10.1190/1.1441936
Song, B., Li, X.-Y., Ding, P., Chen, S., and Cai, J. (2023). Direct pre-stack inversion of elastic modulus using the exact Zoeppritz equation and the application in shale reservoir. Front. Earth Sci. 11. doi:10.3389/feart.2023.1107068
Sun, J., Fang, W., Wu, X., Palade, V., and Xu, W. (2012). Quantum-Behaved particle swarm optimization: analysis of individual particle behavior and parameter selection. Evol. Comput. 20, 349–393. doi:10.1162/EVCO_a_00049
Sun, J., Xu, W., and Feng, B. (2005). “A global search strategy of quantum-behaved particle swarm optimization,” in IEEE Conference on Cybernetics and Intelligent Systems, 2004 (Singapore: IEEE), 111–116. doi:10.1109/ICCIS.2004.1460396
Wang, H., Zhou, L., Chen, Q., Gao, J., Chen, K., Liu, B., et al. (2022). Deep carbonate reservoir and gas prediction based on multicomponent seismic amplitude attributes — a case study. Interpretation 10, T759–T774. doi:10.1190/INT-2021-0050.1
Wang, P.-Q., Liu, X.-Y., Li, Q.-C., Zhou, X.-W., and Feng, Y.-F. (2023). Nonlinear inversion method of russell’s fluid factor based on exact-zoeppritz equation. IEEE Trans. Geosci. Remote Sens. 61, 1–14. doi:10.1109/TGRS.2023.3294501
Xu, X., Shan, D., Wang, G., and Jiang, X. (2016). Multimodal medical image fusion using PCNN optimized by the QPSO algorithm. Appl. Soft Comput. 46, 588–595. doi:10.1016/j.asoc.2016.03.028
Yin, X.-Y., Cheng, G.-S., and Zong, Z.-Y. (2018). Non-linear AVO inversion based on a novel exact PP reflection coefficient. J. Appl. Geophys. 159, 408–417. doi:10.1016/j.jappgeo.2018.09.019
Zhang, G.-Z., Du, B.-Y., Li, H.-S., Chen, H.-Z., Li, Z.-Z., and Yin, X.-Y. (2014). The method of joint pre-stack inversion of PP and P-SV waves in shale gas reservoirs. Chin. J. Geophys. 57, 4141–4149. doi:10.6038/cjg20141225
Zheng, X., Zong, Z., and Wang, M. (2024). Prediction of calcareous sandstone based on simultaneous broadband nonlinear inversion of young’s modulus, Poisson’s ratio and S-wave modulus. J. Appl. Geophys. 229, 105477. doi:10.1016/j.jappgeo.2024.105477
Zhou, L., Li, J., Chen, X., Liu, X., and Chen, L. (2017). Prestack amplitude versus angle inversion for Young’s modulus and Poisson’s ratio based on the exact Zoeppritz equations. Geophys. Prospect. 65, 1462–1476. doi:10.1111/1365-2478.12493
Zhou, L., Li, J., Yuan, C., Liao, J., Chen, X., Liu, Y., et al. (2022). Bayesian deterministic inversion based on the exact reflection coefficients equations of transversely isotropic media with a vertical symmetry Axis. IEEE Trans. Geosci. Remote Sens. 60, 1–15. doi:10.1109/TGRS.2022.3176628
Zhou, L., Liao, J., Li, J., Chen, X., Yang, T., and Hursthouse, A. (2020). Bayesian time-lapse difference inversion based on the exact Zoeppritz equations with blockiness constraint. J. Environ. Eng. Geophys. 25, 89–100. doi:10.2113/jeeg19-045
Zhou, L., Liao, J.-P., Liu, X.-Y., Wang, P., Guo, Y.-N., and Li, J.-Y. (2023). A high resolution inversion method for fluid factor with dynamic dry-rock VP/VS ratio squared. Pet. Sci. 20, 2822–2834. doi:10.1016/j.petsci.2023.09.015
Zhou, L., Liu, X., Li, J., and Liao, J. (2021). Robust AVO inversion for the fluid factor and shear modulus. GEOPHYSICS 86, R471–R483. doi:10.1190/geo2020-0234.1
Zong, Z., and Ji, L. (2021). Model parameterization and amplitude variation with angle and azimuthal inversion in orthotropic media. GEOPHYSICS 86, R1–R14. doi:10.1190/geo2018-0778.1
Zong, Z., Wang, Y., Li, K., and Yin, X. (2018). Broadband seismic inversion for low-frequency component of the model parameter. IEEE Trans. Geosci. Remote Sens. 56, 5177–5184. doi:10.1109/TGRS.2018.2810845
Zong, Z., Yin, X., and Wu, G. (2013). Elastic impedance parameterization and inversion with young’s modulus and Poisson’s ratio. GEOPHYSICS 78, N35–N42. doi:10.1190/geo2012-0529.1
Appendix A
Keywords: exact Zoeppritz equations, Young’s modulus, shear modulus, pre-stack inversion, Bayesian framework, shale gas exploration, quantum particle swarm optimization
Citation: Cheng Y, Song S and Li D (2024) A nonlinear inversion method for Young’s modulus and shear modulus based on the exact Zoeppritz equations. Front. Earth Sci. 12:1493749. doi: 10.3389/feart.2024.1493749
Received: 09 September 2024; Accepted: 08 October 2024;
Published: 23 October 2024.
Edited by:
Xingye Liu, Chengdu University of Technology, ChinaReviewed by:
Qin Li, Xi’an University of Science and Technology, ChinaTao Liu, Tongji University, China
Copyright © 2024 Cheng, Song and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sha Song, c2hhc29uZ0BjaGQuZWR1LmNu
 Yao Cheng
Yao Cheng Sha Song
Sha Song Dan Li2
Dan Li2