Study on its application and unstable risk subarea estimation method of mountainous traffic engineering’s spoil ground

Residues disposal areas with different quantities and scales are produced with the traffic engineering construction in mountainous areas construction, whose environment security threats need to be termly estimated. Countermeasures are adopted by estimated results, and safety risk management and control of waste dump engineering are realized. Based on field research and data access, stage characteristics of the process is summarized. Then force equilibrium and moving balance equation of waste dump sliding body at different stages are formed. So, risk grades and subarea labeled by red, yellow and green colors based on different moving distances are established. Finally, traditional way and the failure risk subarea assessment method are compared in practice, which proves feasibility of the method. Main conclusions are as following. 1) Fail process of mountainous highway waste slag slope is divided into initial limit equilibrium stage, speed-up downslide stage on slipping surface in which the sliding friction coefficient continues to decrease with acceleration, and speed-down downside stage on ground surface in which the sliding friction coefficient continues to increase with the deceleration. 2) Force balance equation at initial stage, downslide force formula at speed-up downslide stage and anti-slide force formula at speed-down downslide stage are presented by sliding body mechanical model on slipping surface and ground surface. Maximum moving velocity formula at the toe of the slope is established. And moving distance of waste dump sliding body is induced by energy balance equation. 3) Minimum and maximum of moving distance are computed under maximum and minimum of sliding friction coefficient conditions. According to these distances, safety threats of fail waste dump are classified into three grades: red region being high risk locates, yellow region being middle risk locates, green region being low risk. Relying on practical residues disposal area, disadvantage and advantage of the method and traditional method are compared. Found that mechanical mechanism of the method is simple, forces and parameters are all unified in balance equations, which meets to practical waste dump fail process. And the method does good to guiding mountainous residues disposal area unstable risk assessment.

1 Introduction

The choice of dump disposal sites in mountain traffic projects is limited by geographical location, project cost and other aspects. Some dump disposal sites are set in villages, roads and upstream of other projects, while some dump disposal sites are surrounded by farmland, roads, forest lands and so on. The environment is complex. As time goes by, the natural environment deteriorates and the slope of dump disposal sites becomes unstable and occurs landslides, which will cause disasters to the downstream. How to evaluate the safety and stability of the existing slag dump is an important engineering problem (GB51018-2014, 2014, T/CWHID 0018-2021).

At present, it is a common practice to use the potential energy to kinetic energy relationship formula of different hypothesis conditions and the instability motion distance of slag slope to evaluate the safety threat brought by the instability of mountain road slag slope from far to near under different motion modes (Liu et al., 2022; Ge et al., 2019; Hu et al., 2019; Wu et al., 2011; Li and Han, 2015; Wu et al., 2015; Fan et al., 2012; Zhang et al., 2017; Wang et al., 2003; Zeng et al., 2014; Wang et al., 2023). The safety risk scope assessment based on moving distance is a combination of slope instability moving distance and rolling stone moving distance. The difference of failure mechanism, balance equation, parameters and other factors have great influence on the accuracy of evaluation, which is not in line with the actual engineering motion mechanism. There are evaluation errors in the formula, which does not reflect the difference between static friction properties and sliding friction properties of soil-rock slag.

The research on rate effect of slag discarding materials is insufficient to support the relevant calculation, and most of them are empirical values. The error superposition of parameters and formulas results in a large gap between the evaluation of relevant formulas and the actual situation. The partition is a little arbitrary, not a standard obtained under the same formula system, belongs to combined partitioning, and is not standardized. Therefore, it is necessary to propose a subarea estimation method and index system for the instability risk assessment of soil-rock mixed slag slope. The related work is standardized and quantified under the same method to improve the instability risk assessment efficiency of dump abandonment projects under complex surrounding environment.

The research in this field mainly focuses on the following aspects: dynamic energy dissipation mechanism and quantitative evaluation of sliding body (Liu et al., 2022; Ge et al., 2019; Hu et al., 2019; Wu et al., 2011); evaluation of the movement mechanism and distance of the sliding body (Li and Han, 2015; Wu et al., 2015; Fan et al., 2012, Zhang et al., 2017; Wang et al., 2003; Zeng et al., 2014); Slope instability risk assessment considering potential energy kinetic energy conversion equation and motion distance (Liu et al., 2015, Xiao et al., 2013; Sun et al., 2019; Wang, 2019; Yang et al., 2018; Wang et al., 2022; Olemskoi and Yushchenko, 2003; Popov et al., 2021). Most of them use statistical fitting of moving distance and initial starting height to form regional empirical relationship, or simply use large deformation numerical simulation to evaluate moving distance, which does not involve the relationship between basic material properties and movement of dispersed materials, and the physical and mechanical mechanism of establishing the formula is not perfect. Through analyzing the instability motion characteristics of the slope formed by particulate materials, it is found that the sliding distance is related to the action which is between the particulate materials and the sliding surface, rather than the general characteristics calculated by a large number of landslide data. These deficiencies point out the direction for follow-up research, and extensive engineering needs provide the possibility for research breakthroughs.

Based on the instability risk assessment of mountain highway slag dump, the characteristics of slag slope instability movement were summarized, the evolution mechanism of static and dynamic friction performance during slag dump movement was discussed, and the sliding motion equation of mountain highway slag slope considering the frictional energy rate effect was constructed. This is a key feature of the relationship between the distance and the sliding surface after the slip of the slope, which is the result of the relative motion between the granular material and the slip surface.

Using the motion equation is used to derive the formula for the movement distance of slope instability, and the regional rating method and index system of the instability risk of the waste dump area are constructed, which can provide guidance for the instability risk assessment of the abandoned slag slope in the mountainous area.

2 Analysis of instability process of highway slag slope in mountainous area

Through site investigation and existing data reference, combined with the analysis of the instability process of the actual slag slope, it can be considered that the instability process of the slag slope has typical stage characteristics:

(1) The limit stage is reached along the initial sliding surface

The actual slope failure generally develops multistage sliding surface, which is caused by the constant velocity shear of rock and soil mass failure. Under the full action of deformation, the dominant fracture surface is generated, the overall sliding is formed, and the sliding starts. The slope body along the sliding surface is in the ultimate equilibrium state, and the sliding force is equal to the anti-sliding force. At this time, the static friction property of slag is dominant.

(2) The phase of accelerating motion in which potential energy is converted into kinetic energy

Once the limit state is reached, a small disturbance deteriorates, most of which are caused by rainfall entering the slope body along the slope cracks and accumulating at the sliding surface, which further causes the deterioration of the strength characteristics of the material, the sliding force is greater than the anti-sliding force, and the sliding body accelerates along the sliding surface until all the potential energy is converted into kinetic energy. In this accelerating process, the sliding friction performance of slag is dominant, because the sliding friction performance is negatively correlated with the speed. So it keeps decreasing, and the speed keeps increasing, until it reaches its maximum speed at the foot of the slope.

(3) The phase of deceleration in which kinetic energy is exhausted by friction

Once the sliding body breaks away from the parent body and reaches the toe, the accumulation rate of the ground relative to the slope is relatively slow. The sliding force is much less than the friction resistance. As the sliding body moves away from the toe, it gradually slows down until the accumulation is stable again. The sliding friction performance of the dump is dominant in this deceleration process, and it has been increasing, because the speed has been decreasing.

3 Unstable risk subarea estimation method of mountain dump slop

3.1 Equilibrium equation of motion process

3.1.1 The limit stage is reached along the initial sliding surface

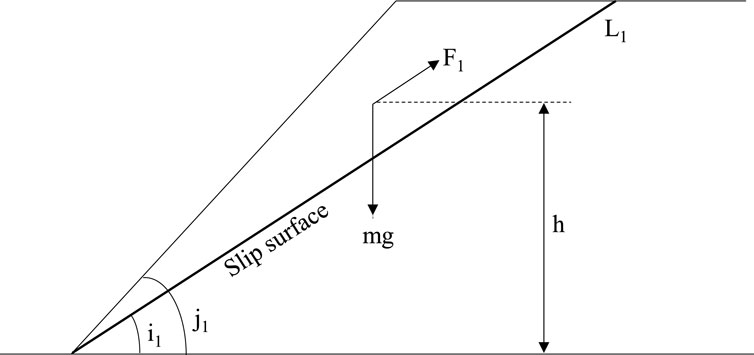
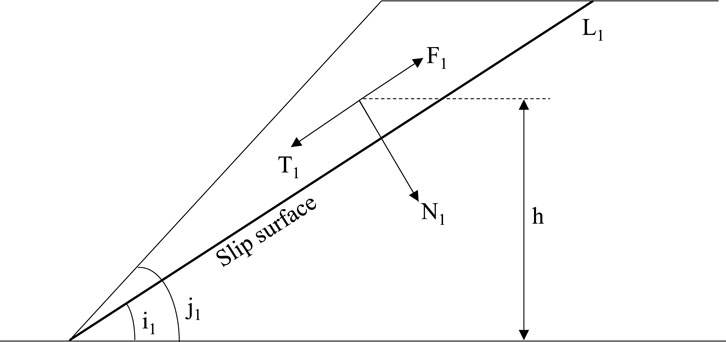
It is assumed that the destruction of the slag slope is similar to that of non-viscous sandy soil, and the destruction is along the active fracture surface. The relationship between the movement mode and force is shown in Figures 1, 2.

Figure 1

Figure 1. Landslide force diagram.

Figure 2

Figure 2. Moving and forces on slip surface.

According to Figure 2, the force balance relationship along the initial limit equilibrium stage of the sliding surface is established, and the Formulas 1–4 for calculating the static friction coefficient of the sliding surface is as follows:

$T_0=F_0(1)$

$T_0=mg\sin i_1(2)$

$N_0=mg\cos i_1(3)$

$F_0=c{L}_1+mg\cos i_1{\mu }_1\left(0\right)(4)$

Where, F₀ is the static ultimate friction resistance under the action of the normal component N₀ of gravity along the sliding surface; T₀ is the tangential component of the middle gravity along the sliding surface towards the toe; μ₁ (0) is the static friction coefficient of sliding surface; G is gravity; c is cohesion; L₁ is the length of the sliding surface; i₁ is the angle between the sliding plane and the horizontal plane.

3.1.2 The phase of accelerating motion in which potential energy is converted into kinetic energy

According to Figure 2, the force balance relationship of accelerating slide with sliding force greater than anti-sliding force is established. At this time, the sliding body moves along the sliding surface, and the friction coefficient is the sliding friction coefficient, which is generally less than the static friction coefficient. The calculation Formulas 5, 6 is as follows:

$R_1=T_1-F_1(5)$

$F_1=mg\cos i_1{\mu }_1\left(v\right)(6)$

Where, R₁ is the remaining sliding force along the sliding surface; T₁ is the tangential component of gravity along the sliding surface towards the toe; F₁ gravity sliding friction resistance along the sliding surface normal force N₁; μ₁(v) is the sliding friction coefficient when the sliding velocity of the sliding body along the sliding surface is v, and μ₁ is negatively correlated with the velocity v; i₁ is the angle between the sliding plane and the horizontal plane.

$v_1=at(7)$

$R_1=ma(8)$

$a=g\sin i_1-g\cos i_1{\mu }_1\left(v\right)(9)$

$\frac{h}{\sin i_1}=\frac{1}{2}a{t}^2(10)$

Combining the above Formulas 7–10, Formula 11 is obtained.

$v_1=\sqrt{2gh\left(1-\frac{{\mu }_1\left(v_1\right)}{\tan i_1}\right)}(11)$

Where, a is the acceleration of the sliding body under the action of the remaining sliding force; t is the time to move to the toe; v₁ is the maximum speed of sliding body moving to the toe; h is the heart height of sliding body; g is the gravitational acceleration; m is the mass of the sliding body.

3.1.3 The phase of deceleration in which kinetic energy is exhausted by friction

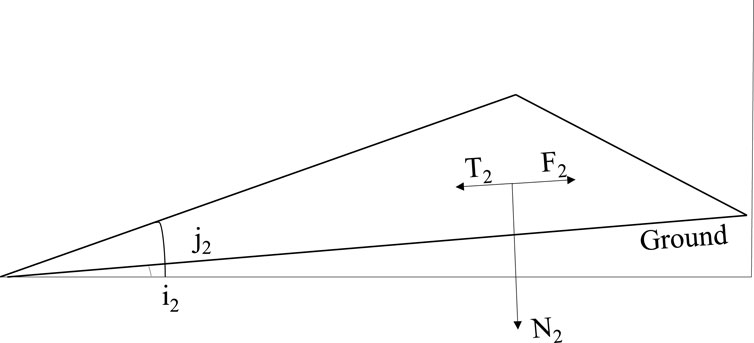
After the sliding body reaches the toe, it moves along the ground. At this time, the relationship between the motion mode and the force is shown in Figure 3.

Figure 3

Figure 3. Sliding and forces on the ground.

According to Figure 3, the force balance relationship of decelerating sliding along the ground where the friction resistance is greater than the sliding force is established. At this time, the sliding surface is the sliding friction coefficient, and the formula is as follows:

$R_2=F_2-T_2(12)$

$T_2=G\sin j_2(13)$

$N_2=G\cos j_2(14)$

$F_2=G\cos j_2{\mu }_2\left(v\right)(15)$

Where, R₂ is the residual friction resistance along the ground; F₂ is the friction resistance generated by the normal component of the sliding weight force along the ground; T₂ is the sliding force generated by tangential component of sliding weight force along the ground; N₂ is the normal component of sliding weight force along the ground; μ₂(v) is the sliding friction coefficient between the sliding body and the ground; v is the speed at which the sliding body slides along the ground; j₂ is the inclination of the ground.

3.2 Motion distance calculation formula

On the basis of the motion equation established in Section 2.1, the maximum velocity formula of toe position can be derived. The formula of kinetic energy equal to friction energy is established with the force balance relationship in deceleration stage. The motion distance formula is derived as follows:

$\frac{1}{2}m{v_1}^2=R_2{L}_2(16)$

By substituting Formulas 12–15 into Formula 16, we get:

$L_2=\frac{h\left(\tan j_1-{\mu }_1\left(v_1\right)\right)}{\tan j_1\left(\cos j_2{\mu }_2\left(v_1\right)-\sin j_2\right)}(17)$

Where, μ₂ is the ground sliding friction coefficient, and μ₂ is negatively correlated with velocity v; L₂ is the ground sliding distance.

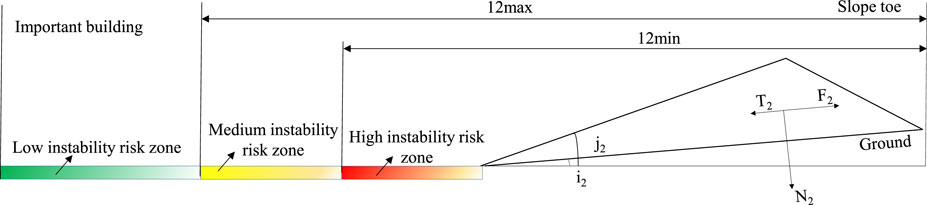
3.3 Red, yellow and green 3 colors 3 level risk zones

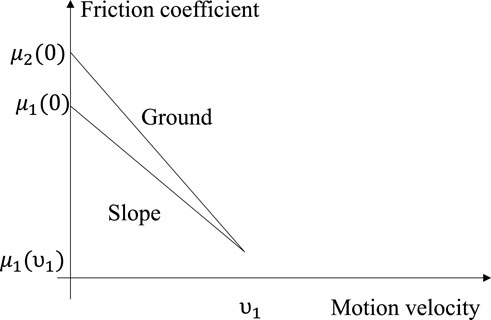
According to the evolution law of the static and dynamic friction properties of the slag dump particles, the friction properties of the slag dump are negatively correlated with the velocity, that is, the larger the velocity, the smaller the sliding friction coefficient; the smaller the velocity, the larger the sliding friction coefficient, and the largest static friction coefficient. The relationship between specific friction coefficient and velocity is shown in Figure 4.

Figure 4

Figure 4. Curve of friction coefficient and velocity on waste dump.

It is generally believed that the sliding friction coefficient curve of the sliding surface and the sliding friction coefficient of the ground are different, but they can also be considered the same. Because the sliding body is same, the sliding body crushing and other energy dissipation are not considered during sliding, and the friction energy dominates the whole process.

Formula 17 is used to assume that the sliding friction coefficient of the sliding body is consistent with that of the sliding surface or ground, and L₂ is the minimum motion distance if the maximum value is taken; L₂ is the maximum motion distance if the minimum value is taken. Using minimum and maximum motion distance, the instability risk threat is divided into: High risk, red zone, 0 - L_2min; Medium risk, yellow zone, L_2min - L_2max; Low risk, green zone, > L_2max, as shown in Figure 5.

Figure 5

Figure 5. Sliding and forces on the ground.

4 Engineering application and inspection

4.1 Brief introduction of an expressway dump

The dump site is located above an existing expressway and an operating secondary highway. There are 5 slag slopes, the first slope height is 20.6 m, the total height is 95 m, and the total amount of abandoned square is 2.0 × 10⁵ cubic meters. The dump wall is 47.0 m away from the toe, and the bridge pile is 127.0 m away from the toe. As shown in Figure 6 for details about the dump site and its surroundings.

Figure 6

Figure 6. Typical mountainous highway residues disposal area. (A) Total landform (B) principal section.

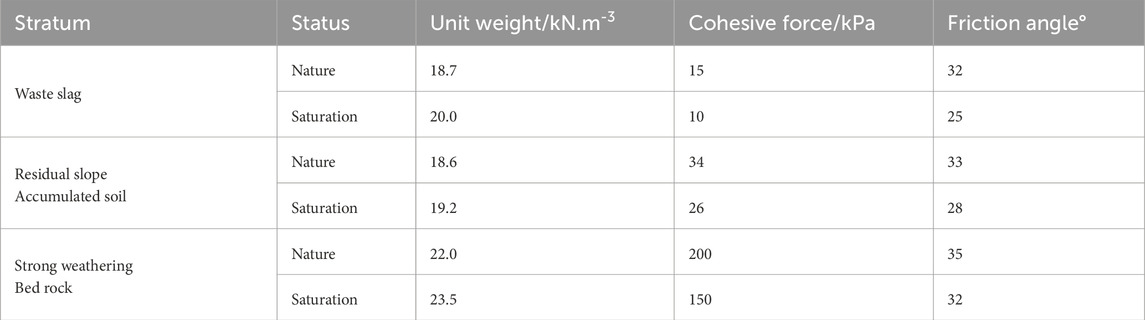
According to the field test, engineering analogy and parameter reverse analysis, the calculation parameters of the main rock and soil layers of the slag dump are listed in Table 1.

Table 1

Table 1. Computing parameters of rock and soil in the typical residue disposal area.

4.2 Orthodox method

Energy equation method is used to calculate the rolling distance of falling body in slag dump, which is often used in engineering. The specific Formulas 18, 19 are, as follows:

$mgh=\frac{1}{2}m{v}^2+mghx(18)$

$v=\sqrt{2\left(1-x\right)gh}(19)$

Where, m is the mass of the falling body; g is the gravitational acceleration; h is the sliding height; v is the speed of the falling body reaching the toe; x is the coefficient of kinetic energy loss after rolling, generally 0.35.

$L=\frac{v^2}{2\epsilon g}(20)$

Where, L is the motion distance of the falling body; $\epsilon$ is the friction coefficient of motion, generally 0.50.

By substituting the grade 1 slope height of 20.6 m into Formula 19, the velocity to the toe can be calculated as 16.2 m/s; By substituting the velocity result into Formula 20, the motion distance of 26.6 m can be obtained. By substituting the total height of grade 5 slope 95.0 m into Formula 19, the velocity of movement to the toe 34.8 m/s can be obtained; By substituting the velocity result into Formula 20, the moving distance of 123.5 m can be obtained. Grade 1 slope sliding, the motion distance is 20.6 m, the dump wall is 47.0 m from the toe, which can not threaten the safety of the dump wall; The bridge pile is 127.0 m away from the toe, which does not threaten the bridge pile and the secondary highway. Grade 5 slope sliding, the motion distance is 123.5 m, the dump wall is 47.0 m from the toe, which can threaten the safety of the dump wall; The bridge pile is 127.0 m away from the toe, which does not threaten the bridge pile and the secondary highway.

4.3 Textual method

It can be seen from Table 1 that the static friction coefficient of slag abandonment can refer to the parameter value of natural state μ₁ (0)=0.62, and the maximum sliding friction coefficient can refer to the parameter value of saturated water μ₁ (v₁)=0.47; The sliding surface refers to the active rupture angle of slag abandonment, considering that most of the operating conditions of slag abandonment are natural or close to nature, j₁ is 45°–32°/2, which is about 29°; By substituting the grade 1 slope height of 20.6 m into Formula 11, the velocity of motion to the toe can be obtained by 7.8 m/s; By substituting the speed result, ground slope j₂ about 10°, into Formula 17, the motion distance of 10.8 m can be obtained. By substituting the total height of grade 5 slope 95.0 m into Formula 11, the velocity of motion to the toe 16.8 m/s can be obtained. By substituting the velocity result into Formula 17, the motion distance of 49.8 m can be obtained. Grade 1 slope sliding, the motion distance is 10.8 m, the dump wall is 47.0 m from the toe, which can not threaten the safety of the dump wall; The bridge pile is 127.0 m away from the foot of the slope, which does not threaten the bridge pile and the secondary road. Grade 5 slope sliding, the movement distance is 49.8 m, the dump wall is 47.0 m from the toe, which can threaten the safety of the dump wall; The bridge pile is 127.0 m away from the toe, which does not threaten the bridge pile and the secondary highway. The above calculation results are L_2min values under sliding conditions of different scales.

Considering that the sliding friction coefficient of slag after sliding to the ground is closely related to the water saturation property and dynamic friction angle of this kind of soil-rock mixed soil, the formula is as follows:

$\mu =\left(1-{\gamma }_u\right)\tan \delta (21)$

Where, μ is the sliding friction coefficient between the sliding mass and the sliding surface or the ground; ${\gamma }_u$ is the pore water pressure ratio, generally 0.1–0.5 for coarse grained soil. δ is the dynamic friction angle. Considering the actual slag damage, the sliding surface is generally not saturated with water, but the ground is saturated with water. The sliding friction coefficient μ₂ is calculated according to Formula 21. The calculation results of L_2max with different values of μ between 0.1 and 0.5 are organized into curves, as shown in Figure 6.

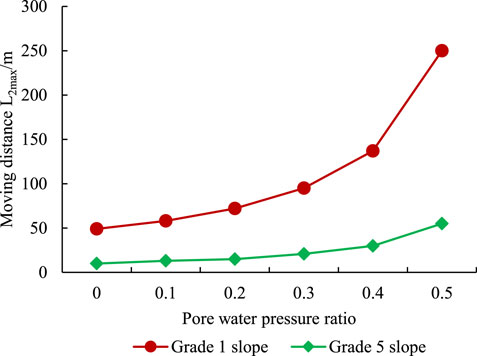
Figure 7 shows that when the ratio of pore water pressure ratio ${\gamma }_u$ is 0.48, the motion distance of grade 1 slope slip is 46.5 m, which is close to the threatening dump barrier wall (47.0 m from the toe), but not threatening the bridge pile and secondary highway (127 m from the toe). Grade 5 slope slip motion, when the pore water pressure ratio ${\gamma }_u$ is 0.38, the motion distance is 127.0 m, threatening the dump wall (47.0 m from the toe), close to the threatening bridge pile and secondary highway (127 m from the toe).

Figure 7

Figure 7. Curve of pore water pressure ratio and moving distance L_2max.

In conclusion, considering the existing terrain and rainfall conditions, the pore water pressure ratio ${\gamma }_u$ is 0 and 0.3, and the maximum and minimum sliding friction coefficient of μ₂ on the ground are determined to be 0.47 and 0.33, respectively. The slippage motion distance of slag is different, and the L_2min and L_2max of grade 1 slope slippage are 10.8 m and 20.8 m respectively. Dump wall, bridge pile and secondary road are located in the green zone. Grade 5 slope slip motion, L_2min is 49.8 m, L_2max is 95.7 m, dump wall (from the toe 47.0 m) in the red zone, bridge pile and secondary highway (from the toe 127.0 m) in the green zone.

4.4 Comparative analysis

According to the instability mechanism and instability stage characteristics of the waste slag slope, the force balance relationship and motion equation of the waste slag sliding body along the sliding surface and the ground are established, and the evaluation method and index system of the spoil instability zoning of the mountain highway based on the maximum and minimum motion distance are formed. The conclusions are as follows.

(1) The proposed regional evaluation method and index system of slag dump instability risk in mountain traffic engineering are more consistent with the physical and mechanical mechanism of slag instability, and the sliding surface is determined by the active rupture angle. The stage division is more consistent with several stages of the actual slag slope instability process, namely, starting (limit equilibrium) and accelerating sliding stage (friction performance decreases with the increase of speed until the maximum speed of the toe reaches the minimum value). The motion from starting to sliding is accelerated under the action of the residual sliding force generated on the sliding surface. After reaching the ground, the ground slope slows down, the sliding force is less than the friction resistance, and the friction performance gradually slows down (the friction performance gradually increases as the speed decreases) until the motion stops. The minimum motion distance is estimated according to the maximum sliding friction coefficient, and the maximum motion distance is estimated according to the minimum sliding friction coefficient. The risk ranges defined by the two extremes have conservative characteristics. Different color partitions, in line with the national standard for the use of color, that is, red danger level (high risk) > yellow (medium risk) > green (low risk). The method is simple and easy from calculation to partition, and has strong operability. The relevant parameters can be obtained through designated experimental tests, and the evaluation results are feasible for the safety control of actual projects.

(2) The regional assessment of the instability risk of the slag dump in mountain traffic engineering under the same motion equation and energy equation is different from the combination calculation of the existing methods, that is, different distances are obtained by different equations to form the regional standard. At present, there is no uniform color labeling and partition standard for different partition results, which is somewhat arbitrary, which is not conducive to the authority and comparison of evaluation conclusions.

(3) The proposed regional evaluation method and index system of the instability risk of the slag dump in the mountain traffic engineering are supported by the characteristic curves of the evolution law of the material static and sliding friction properties, which can be used to estimate the maximum and minimum value, and can also be used to obtain more accurate moving distance through the integration of dynamic parameters. It has a limited range of versatility. Tracking evaluation and parameter accumulation are conducive to the formation of regional big data, and relevant regional experience values are more guiding to the instability risk assessment of regional slag abandonment projects.

5 Conclusion

According to the instability motion mechanism of slag slope and the stage characteristics of slag slope instability, the force balance relationship and motion equation of dump sliding mass along the sliding surface and the ground are established, and a subarea evaluation method and index system of dump instability on mountain road based on the maximum and minimum motion distance are formed. The conclusions are as follows:

(1) The instability stage of the slag slope in the mountain traffic engineering mainly includes: reaching the starting stage of the static limit equilibrium, the accelerating sliding stage of the sliding force being greater than the friction force along the sliding surface, and the decelerating stage until the static stage of the friction being greater than the sliding force along the ground. Starting stage and static friction coefficient dominate; The sliding friction coefficient along the sliding surface is dominant in the accelerated sliding stage and has been decreasing. When the toe reaches the maximum speed, the sliding friction coefficient along the sliding surface reaches the minimum value; The sliding friction coefficient along the ground is dominant in the deceleration glide stage and has been increasing. When the motion stops the sliding friction coefficient along the ground reaches the maximum value, which is the mechanical mechanism of the slag slope instability.

(2) Based on the analysis of the mechanical mechanism of the slag slope instability stage characteristic, the force balance and energy conservation equations of the above three stages are established, the maximum velocity formula and the motion distance formula are derived, and the subarea method and index system based on the moving distance are constructed. The sliding friction coefficient along the sliding surface does not consider the water saturation factor of the coarse-grained soil and the sliding friction coefficient along the ground does not consider the ratio of pore water pressure of the coarse-grained soil, estimating the minimum motion distance L_2min; The sliding friction coefficient along the sliding surface does not consider the water-saturated factor of the coarse-grained soil and the sliding friction coefficient along the ground considers the ratio of pore water pressure of the coarse-grained soil, estimating the maximum motion distance L_2min. The danger range defined by the two factors has certain conservative characteristics. Different colored are designed to comply with national standards for color usage, which classify risks as follows: danger level (high risk, ≤L_2min), yellow (medium risk, > L_2min and ≤L_2max), and green (low risk, > L_2max).

(3) The traditional instability risk estimation is only related to the height of the slag slope, and the motion friction coefficient is the statistical experience value; The subarea evaluation method of slag slope instability risk in this paper is not only related to height, but also to sliding surface slope, ground slope, sliding friction coefficient along the sliding surface, sliding friction coefficient along the ground and other factors. It is more consistent with the mechanical mechanism, stage characteristics and motion characteristics of slag instability, and the subarea has some conservative characteristics and strong operability.

(4) There are many researches on the rate effect of rock, but few on the rate effect of soil. The exploration and accumulation of these basic mechanical properties of rock and soil materials is the key to the maturity and accuracy of the method. Further exploration in this area will be carried out in the later stage.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JZ: Resources, Project administration, Writing–original draft. ZD: Resources, Project administration, Writing–original draft. XY: Methodology, Formal analysis, Resources, Writing–original draft. MY: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Loess Soil Mechanics and Engineering Key Laboratory of Shaanxi Province Foundation (13JS073) and the Natural Science Foundation of Shaanxi Province (2017JM5059).

Conflict of interest

Authors JZ and ZD were employed by Xi’an Engineering Investigation and Design Research Institute of China National Metals Industry Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fan, X., Qiao, J., Han, M., and Zeng, Y. (2012). Volumes and movement distances of earthquake and rainfall-induced catastrophic landslides. Rock Soil Mech. 33 (10), 3051–3055. doi:10.16285/j.rsm.2012.10.016

CrossRef Full Text | Google Scholar

GB51018-2014, (2014). Ministry of housing and urban-rural development of the people’s republic of China. Code for design of soil and water conservation engineering. Beijing: China Architecture and Building Press.

Google Scholar

Ge, Y., Zhou, T., Huo, S., Xia, D., Hu, Y., Zhong, P., et al. (2019). Energy transfer mechanism during movement and accumulation of rockslide avalanche. Earth Sci. 44 (11), 3939–3949. doi:10.3799/dqkx.2017.589

CrossRef Full Text | Google Scholar

Hu, X., Fan, X., and Ma, X. (2019). Energy consumption evaluation of high-speed and long-distance landslide in accelerated motion. Yangtze River 50 (2), 191–196. doi:10.16232/j.cnki.1001-4179.2019.02.034

CrossRef Full Text | Google Scholar

Liu, H., Hu, Y., Cao, Z., and Zheng, L. (2015). Study on highway slope stability zoning based on fuzzy clustering theory. J. Highw. Transp. Res. Dev. 32 (05), 49–55. doi:10.3969/j.issn.1002-0268.2015.05.009

CrossRef Full Text | Google Scholar

Liu, Y., Chen, J., Gao, C., Song, K., and Xuan, TANG (2022). Energy conversion of the high-speed landslide movement process based on a sliding surface partition mechanical model. Bull. Geol. Sci. Technol. 41 (2), 139–146. doi:10.19509/j.cnki.dzkq.2022.0061

CrossRef Full Text | Google Scholar

Li, L., and Han, J. (2015). Discussion on the hazard distance of landslide-debris flow triggered by wenchuan earthquake. Geol. Sci. Technol. Inf. 34 (5), 219–224.

Google Scholar

Olemskoi, A. I., and Yushchenko, O. V. (2003). Transition of a loose medium to the fluid state: a phenomenological theory. Tech. Phys. 48, 1233–1237. doi:10.1134/1.1620113

CrossRef Full Text | Google Scholar

Popov, V. L., Li, Q., Lyashenko, I. A., and Pohrt, R. (2021). Adhesion and friction in hard and soft contacts: theory and experiment. Friction 9, 1688–1706. doi:10.1007/s40544-020-0482-0

CrossRef Full Text | Google Scholar

Sun, C., Chen, C., Yun, ZHENG, Lu, Z., and Deng, Y. (2019). Discussion on slope stability analysis method of abandoned dreg site based on spatial effect. J.54 (01), 97–105. doi:10.3969/j.issn.0258-2724.20170607

CrossRef Full Text | Google Scholar

T/CWHID 0018-2021 “China water conservancy and hydropower investigation and design association,” in Stability and safety assessment specification on residues disposal area for water conservancy and hydropower engineering. Beijing: China Water and Power Press.

Google Scholar

Wang, C., Rui, YONG, Luo, Z., Shigui, D. U., Karakus, M., and Huang, C. (2023). A novel method for determining the three-dimensional roughness of rock joints based on profile slices. Rock Mech. Rock Eng. 56, 4303–4327. doi:10.1007/s00603-023-03274-7

CrossRef Full Text | Google Scholar

Wang, J. (2019). Study on stability of freeway slag waste site in mountainous area under different compaction conditions. Chongqing: Chongqing jiaotong university.

Google Scholar

Wang, N., Zhang, D., and Wang, J. (2003). Forecasting method of sliding distance on typical loess landslides. J. Northwest Univ. Nat. Sci. Ed. 33 (1), 111–114. doi:10.16152/j.cnki.xdxbzr.2003.01.030

CrossRef Full Text | Google Scholar

Wang, S., Zeng, P., Tianbin, L. I., and Sun, X. (2022). Initiation, movement and impact simulation of soil landslide using material point method. J. Eng. Geol. 30 (4), 1362–1370. doi:10.13544/j.cnki.jeg.2020-155

CrossRef Full Text | Google Scholar

Wu, Y., Liu, D., and Li, M. (2011). Landslide model experimental of energy dissipation principle in the sliding and impact process. Chin. J. Rock Mech. Eng. 30 (4), 693–701.

Google Scholar

Wu, Y., Liu, D., and Zhou, Z. (2015). Mobility assessment model for landslide mass considering disintegration energy consumption in slipping process. Chin. J. Geotechnical Eng. 37 (01), 35–46. doi:10.11779/CJGE201501003

CrossRef Full Text | Google Scholar

Xiao, R., Wang, S., He, X., Zhang, X., Rao, X., and Luo, B. (2013). Safety zonation of large-scale slopes based on local strength reduction method. Chin. J. Rock Mech. Eng. 32 (S2), 3928–3937.

Google Scholar

Yang, W., Dong, YANG, and Xie, Q. (2018). Study on slope risk assessment method based on cloud model and its application. J. Huazhong Univ. Sci. and Tech. Nat. Sci. Ed. 46 (04), 30–34. doi:10.13245/j.hust.180406

CrossRef Full Text | Google Scholar

Zeng, Y., Fan, X., and Duan, X. (2014). Deceleration mechanism of slope foot site to landslide movement. Bull. Soil Water Conservation 34 (04), 193–196. doi:10.13961/j.cnki.stbctb.2014.04.052

CrossRef Full Text | Google Scholar

Zhang, Y., Yao, H., Jiang, N., Xiang, Y., Sun, Y., and Wei, Y. (2017). A model for influencing distance prediction of landslide clastic flow in slag site based on empirical statistics. Yangtze River 48 (12), 65–69. doi:10.16232/j.cnki.1001-4179.2017.12.018

CrossRef Full Text | Google Scholar