- Department of Road and Bridge Engineering, Guizhou Communications Polytechnic University, Guizhou, China
Modern bays and lakes typically develop shallow deltas dominated by rivers, with lake levels playing a significant role in their formation. However, the precise effects of lake level height on the scale and growth dynamics of these deltas remain unclear. To address this, this study employs the sedimentary numerical simulation software Delft3D to model delta development under high, medium, and low lake levels. By analyzing flow velocity distribution, sediment accumulation, and sediment thickness, the study quantitatively assesses the impact of varying lake levels on shallow deltas. The results indicate that: (1) the areal extent of the delta is inversely related to the lake level, whereas sediment thickness is directly proportional to it; (2) within the same simulation period, higher lake levels tend to produce fewer breach distributary channels, while lower levels are more conducive to forming numerous breach distributary channels; however, the impact of lake level on active distributary channels is minimal; (3) deltas consist of multiple complexes. Under high lake levels, a single complex typically exhibits a bird-foot shape, characterized by active distributary channels and mouth bars, with sediment thickness decreasing from the source. In contrast, under low lake levels, a single complex tends to have a flower shape, with active distributary channels, mouth bars, and multiple breach distributary channels, resulting in a more evenly distributed sediment thickness. This research result can provide new ideas for the comparative evolution of deltas under different lake level water levels.
1 Introduction
Shallow delta is a type of lake basin delta, developed in shallow water, with relatively stable structure, flat terrain, and slow overall sedimentation (Fisk et al., 1954; Donaldson, 1974; Paola et al., 2011). In modern sedimentation, shallow deltas usually attract billions of people to settle with their continuous fertile land and are beneficial to the ecosystem (Woodroffe et al., 2006; Syvitski and Saito, 2007). In ancient sediments, shallow delta deposits have been discovered in China, such as the Songliao Basin (Zhu et al., 2012; Wu et al., 2021), the Ordos Basin (Qiu et al., 2016; Feng et al., 2021; Cao et al., 2024), the Nile Delta, the Mississippi Delta and the Mekong Delta (Stanley and Warne, 1993; Zeydan, 2005; Paola et al., 2011; Törnqvist et al., 2020; Loc et al., 2021; Park, 2024), etc., and their rich geological reserves of oil and gas are increasingly attracting the attention of petroleum geologists.
Previous studies on the factors affecting delta formation have focused on factors such as waves, tide and discharge, and only some scholars have noticed the impact of water level changes on river control of deltas (Penland et al., 1988; McLennan, 1993; Törnqvist et al., 2004; Lesser et al., 2004; Hillen et al., 2014; Jalowska et al., 2015; Nienhuis et al., 2023; Abdelwahhab et al., 2023; Kulp et al., 2024). Compared with the stability of sea level, due to the relatively small area of lakes, the water level varies greatly due to factors such as seasons and climate, and the water level plays a vital role in the formation of lake deltas. Studies have shown that the height of the lake will lead to differences in the longitudinal sequence and distribution range of the delta. When the lake level is high, the river action of the branch channel retreats to the erosion zone, and the delta front estuary bar and prodelta sediments are deposited on the river channel sediments, making its longitudinal sequence present a sedimentary body with positive cyclic characteristics that gradually tapers upward, thus forming an inland shoal (He, 1986; Penland et al., 1988; Wright et al., 2005; Luo, 2015). Similarly, water level changes will also affect the lateral and vertical connectivity of the delta. When the lake level is low, the delta is in an overcompensated state. Under the influence of the river, the delta is mainly deep in the vertical direction and continuous in the horizontal direction. When the lake level is high, the delta is in an undercompensated state, the river channel has almost no cutting ability, the vertical direction is mainly separated strips, and the horizontal direction is mainly isolated strips (Zhipeng et al., 2012; Wang et al., 2012; Anthony, 2015).
However, despite the accumulation of a large amount of data from groundwater reservoir records, outcrop analysis and modern sedimentary environments, most current studies still focus on describing sedimentary phenomena. This practice relies on inferring sedimentary processes from sedimentary results, which brings uncertainty to the reconstruction of the evolution of shallow deltas under different lake conditions. In addition, for different regions, the scale and sedimentary characteristics of deltas that have been stable at high, medium and low water levels for a long time are very different. The geometric scale, growth and development process, and river sedimentary characteristics of deltas under different lake levels still need to be relatively accurately described. Therefore, it is particularly important to systematically and clearly understand the spatial distribution, sedimentary thickness and dynamic evolution of deltas under different lake levels.
In recent years, the three-dimensional hydrodynamic field sedimentation simulation technology using Delft3D software has been successfully applied to delta and river sedimentology research and has been widely recognized by scholars at home and abroad (Edmonds and Slingerland, 2010; Burpee et al., 2015; Schuurman and Kleinhans, 2011; Li et al., 2023). Previous studies have focused on the influence of major controlling factors such as sediment composition (Caldwell and Edmonds, 2014; Burpee et al., 2015), water depth (Geleynse, 2007), river (Edmonds and Slingerland, 2010), wave (Geleynse et al., 2011; Nardin and Fagherazzi, 2012; Nienhuis et al., 2013) and tide (Geleynse et al., 2011) on the sedimentation process and geomorphology of shallow deltas, and have achieved a series of excellent results. In this paper, the lake water level will be changed in Delft3D software, and other conditions will be kept unchanged, focusing on the numerical simulation of the formation process of shallow deltas under three different lake surface conditions of high, medium and low for a long time.
2 Research methods and sedimentation simulation
In this paper, Delft3D, a sedimentary numerical simulation software that continuously solves three-dimensional hydrodynamic fields, is used to simulate the sedimentary processes of shallow deltas at various lake levels, generating sedimentary landform evolution sequence data. Based on this data, the differences in scale characteristics and evolution processes of shallow deltas under high, medium, and low lake levels are analyzed through landform evolution studies.
2.1 Delft 3D model introduction
Delf3D is a three-dimensional simulation software package developed by the Deltares Institute in the Netherlands. It is based on the Navier-Stokes equations (N-S equations) that describe hydrodynamics. It uses the finite difference method to solve the N-S equations, combined with the material balance equations that describe the state of sediments, to achieve sediment transport and sedimentary landform evolution. In the horizontal direction, Delf3D provides three types of coordinates: Cartesian coordinates (intuitively represent the distribution of objects); orthogonal coordinates (reduce the discrete error of some curved edge parts); while in the vertical direction, Delf3D mainly provides two differential vertical grid systems: α coordinate system and Cartesian coordinate system, both of which are used to characterize undulating terrain and moving free surfaces.
Horizontal coordinate system.
1) Cartesian coordinate system (rectangular coordinate system)
(xi, yi) are the coordinates of any point. The distance formula d between two points, such as A (x1, y1) and B (x2, y2) is as described above.
2) Polar coordinate system (a two-dimensional orthogonal coordinate system)
Any point P in the plane is represented by the polar radius r and the polar angle
Vertical coordinate system:
z is the vertical coordinate in physical space;
The key components of Delft3D include: Hydrodynamics: The model calculates the flow field through simplified Navier-Stokes equations, assuming that vertical acceleration is neglected and the pressure distribution is hydrostatic. The model can handle water flows caused by tides, currents and wind. Sediment transport: Delft3D simulates the transport process of cohesive sediments (such as clay) and non-cohesive sediments (such as sand). It takes into account bed load and suspended load transport, and uses Van Rijn and other formulas to describe the erosion and deposition process of sediment. Landform evolution: The model calculates the change of riverbed elevation based on sediment transport and simulates erosion and deposition rates. These changes affect the hydrodynamics, forming a feedback loop between flow, sediment transport and geomorphic changes. Meshing: Delft3D uses structured curved or rectilinear grids to represent the physical domain. The accuracy of the results depends on the resolution of the grid. The finer the grid, the more accurate the simulation results, but the calculation time will also increase. Numerical solver: The model uses iterative solvers such as Newton’s method to solve nonlinear equations. The convergence and accuracy of the solution depend on the time step, grid resolution and solver settings. Error and stability: Numerical dispersion and truncation errors are important considerations that affect the reliability of the simulation. The stability of the simulation is ensured by appropriate time steps and CFL condition checks.
This study mainly uses the Flow module in Delf3D. The Flow module is mainly used to solve two-dimensional (depth average) and three-dimensional unsteady shallow water equations. Taking into account the effects of water flow and meteorology, the software adopts a curve grid discrete format with good boundary fitting and reasonable structure. The resolution of a single grid is set by the simulator. The curve grid can be used to calculate unsteady flow and material transport phenomena, and is particularly suitable for simulating the sediment deposition process of rivers. The simulation process follows the law of conservation of fluid momentum and the law of conservation of mass. The completed simulation mainly includes four steps: (a) Solve the Navier-Stokes equation (N-Sequations) to obtain the flow state of the water body in the simulation grid; (b) Calculate sediment transport, deposition and erosion; (c) Obtain relevant parameters such as sedimentary landforms based on the results of steps (a) and (b); (d) Save the results and update the simulation data. The Flow module realizes continuous dynamic simulation of the sediment deposition process through iterative calculations of steps (a) to (d). In order to accurately simulate the transport, deposition and erosion of muddy and sandy sediments in rivers and lakes, the Engelund-Hansen formula is used for sediment transport calculation. The main calculation formulas 1–8 is as follows:
1) Flow field calculation:
Wherein, x is the coordinate in the downstream direction; y is the coordinate in the direction across the water flow; z is the vertical coordinate; Zw is the water level; u is the flow velocity in the x direction, m/s; v is the flow velocity in the y direction, m/s; w is the flow velocity in the z direction, m/s; h is the water depth; C is the Chezy roughness, m1/2/s; g is the acceleration of gravity, m/s2; Vh is the horizontal eddy viscosity coefficient, m2/s; Vv is the vertical eddy viscosity coefficient, m2/s.
2) Suspended sediment transport and deposition calculations:
Where: c(l) is the concentration of sediment component (l), kg/m3; u, v, w are the flow velocities in the x, y, z directions, m/s; Ꜫs,x(l), Ꜫs,y(l), Ꜫs,z(l)) are the eddy diffusion rates of sediment component (l); ws(l) is the settling velocity of the obstructed sediment component (l), m/s.
3) Non-cohesive material deposition and erosion equation:
Where:
4) Sediment settling velocity equation:
Where:
5) Depth average kinetic energy calculation:
Wherein,
2.2 Overview of poyang lake and ganjiang river delta
Poyang Lake, situated in Jiangxi Province (28°24′–29°46′N, 115°49′–116°46′E), extends 110 km from north to south and 50–70 km from east to west, narrowing to just 5–8 km in the northern region. Covering a total area of 3,210 km2, it is characterized by relatively flat terrain and is recognized as the largest freshwater lake in China. The lake features well-developed delta plains, delta fronts, and prodeltas. The upper and lower delta plains are expansive and widely distributed, whereas the delta front is relatively narrow, with a clear distinction between the upper and lower delta plains (Figure 1) (Li et al., 1990; Jin et al., 2014).

Figure 1. Geographic location and sedimentary microfacies of Poyang Lake Delta. (A) Latitude and longitude coordinates of Poyang Lake Delta; (B) Sedimentary microfacies of Poyang Lake Delta.
The hydrological system of Poyang Lake is extensively developed and primarily fed by five major rivers: the Ganjiang, Xiuhe, Xinhe, Raohe, and the Jiangxi River. Among these, the Ganjiang River has the most complex and well-established water system. Hydrological data from the Ganjiang River, recorded by a station located in its upper reaches since the establishment of the People’s Republic of China, indicate an annual average flow ranging from 1,000 to 1,800 m³/s, a sediment concentration of approximately 0.15 kg/m³, and a flow velocity between one and 2.5 m/s (Wang, 2002). Additionally, Poyang Lake is hydraulically connected to the Yangtze River in its northern region. During the flood season, water from Poyang Lake flows into the Yangtze River, while in the dry season, there is a possibility of backflow from the Yangtze into the lake. Consequently, Poyang Lake is classified as a typical shallow lake with river connectivity (Jin et al., 2014).
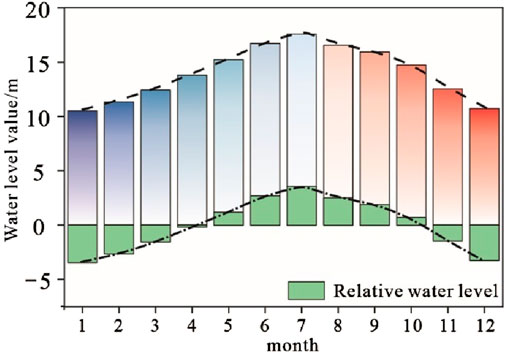
The annual water level of Poyang Lake exhibits significant variability. Data from the Duchang hydrological station, which recorded the average monthly water levels from 1953 to 1992, reveal a seasonal difference of up to 7 m between the wet and dry seasons. During the summer wet season (May–October), the lake’s water level is notably higher, with specific values illustrated in Figure 2. Conversely, in the autumn and winter dry season (December–March), the water level decreases substantially, reducing the lake’s surface area to less than 1,000 km2. During this period, the delta sedimentary area advances northward and retreats southward by approximately 30–50 km annually (Liu et al., 2016; Zhang et al., 2016; Gao et al., 2016).
2.3 Simulation experiment design
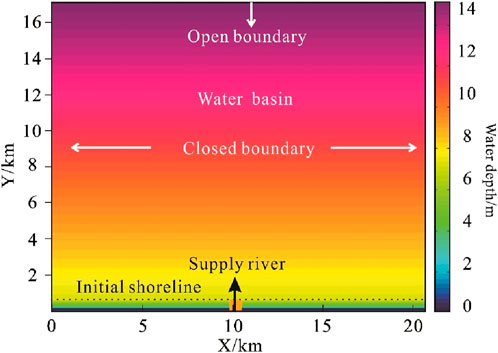
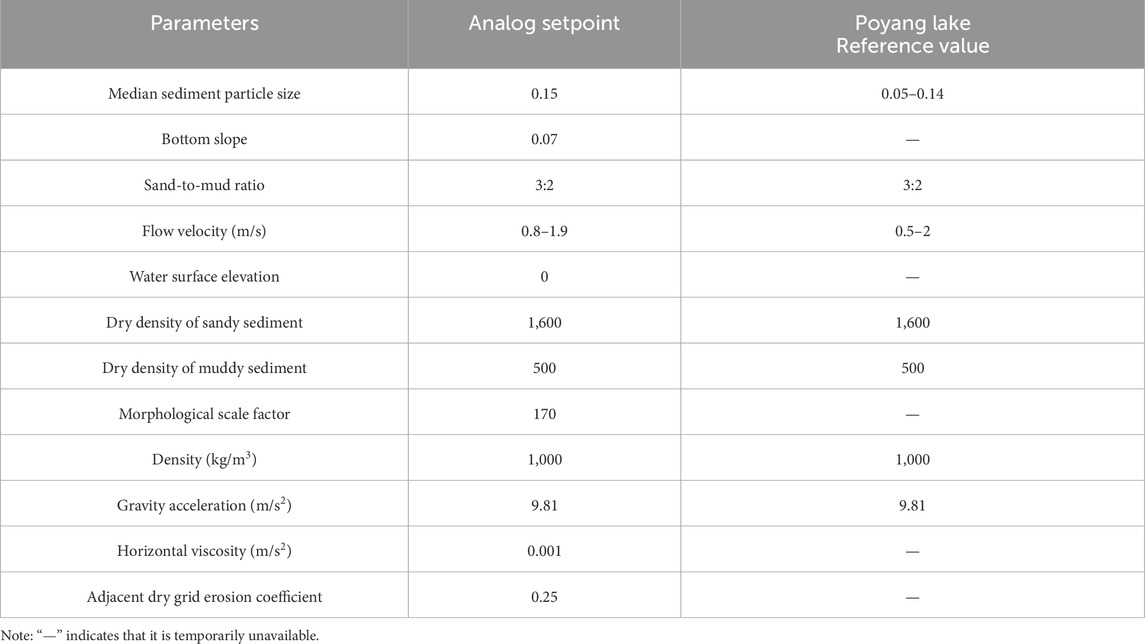
The boundary conditions of the simulation are crucial to ensure the accuracy of the calculation and the reliability of the results. In this study, the setting of the experimental work area scale is mainly based on the modern Poyang Lake sedimentary area in China. There are many typical shallow water delta deposits in this area. The study takes a delta in the middle reaches of the Ganjiang River as an example (Blue frame line), and its sedimentary area is about 20 km * 20 km by measuring (Figure 1 blue area). Based on this, the size of the simulated work area in this study is set to 21 km long and 17.5 km wide (Figure 3). This configure provides sufficient space for the dynamic evolution of the delta under different lake levels. At the same time, the initial sedimentary bed slope was set to 0.07° (Table 1). In order to accurately capture the geometry of the delta, the grid size used in the simulation was defined as 70 m × 70 m, which minimized the error of the delta geometry and ensured that each diversion channel occupied at least one to three grid cells. Previous studies have shown that grid sizes ranging from 25 m to 100 m produce the best simulation results.
Regarding boundary conditions, the left and right boundaries of the simulation domain were designated as closed boundaries, while the upper boundary was set as an open boundary. Additionally, a water supply port was included at the bottom of the domain to maintain a constant total flow.
For the sediment dynamics parameters, settings were based on sediment dynamics data from the Ganjiang Delta of Poyang Lake and similar simulation studies (Edmonds and Slingerland, 2010; Caldwell and Edmonds, 2014; Xu et al., 2017). The simulation included both sandy (non-cohesive) sediments and muddy (cohesive) sediments. The sandy sediments had median particle sizes of 300 mm, 150 mm, and 80 mm. The sand-to-mud ratio was set at 3:2, with a river supply rate of 1,500 m³/s and a flow velocity range of 0.8–2.0 m/s, consistent with the hydrological and sediment data of the Ganjiang Delta (Table 2).
To compare and analyze the scale characteristics and sedimentation processes of shallow deltas under varying lake levels, this study conducted three simulation experiments, designated as A1, A2, and A3. These simulations were based on real lake level data from Poyang Lake, with lake levels set at minimum, average, and maximum values. Specifically, the lowest lake level of A1 was set to −1 m to simulate delta sedimentation under low lake conditions. The highest lake level of A3 was set to 6 m to simulate delta evolution under high lake conditions. Experiment A2 represented a transitional lake level, reflecting average conditions to examine the growth and development of shallow deltas under intermediate lake levels. In all three experiments, only the lake level values were varied, while the remaining simulation parameters were kept constant.
To ensure the accuracy of the simulation experiments, the time step was set to 0.4 min. To expedite the simulation process, previous research has demonstrated that incorporating a morphological scale factor can be effective. Specifically, when the morphological scale factor is less than 200, it does not adversely impact the simulation results (Caldwell and Edmonds, 2014). Consequently, this study set the morphological scale factor to 150, resulting in a 150-fold acceleration of the simulation. Additional parameters are detailed in Table 2.
3 Parameter standard description
Since Delft3D cannot perform sediment increment difference analysis and diversion channel characterization in different time series, this study used MATLAB software to independently develop a set of codes to achieve the following multiple purposes: (1) Obtain sediment thickness and flow velocity in each time series, and calculate the sediment increment distribution in different time series to characterize the sedimentation process and differences of the delta under different lake levels; (2) Obtain the flow velocity during all simulation times to characterize the diversion channels and breach distributary channels developed in the delta under different lake levels. (3) Batch obtain the length, width, surface value, and shoreline of the delta under different time series to characterize the differences in the scale characteristics of shallow water deltas under different lake levels.
3.1 Delta parameter
Delta Length (L): This parameter represents the maximum distance the delta extends along the coastline, as described by Caldwell and Edmonds (2014) and Xu et al. (2021). It indicates the delta’s capacity to prograde into the basin. A specific schematic diagram illustrating delta length is shown in Figure 4A.
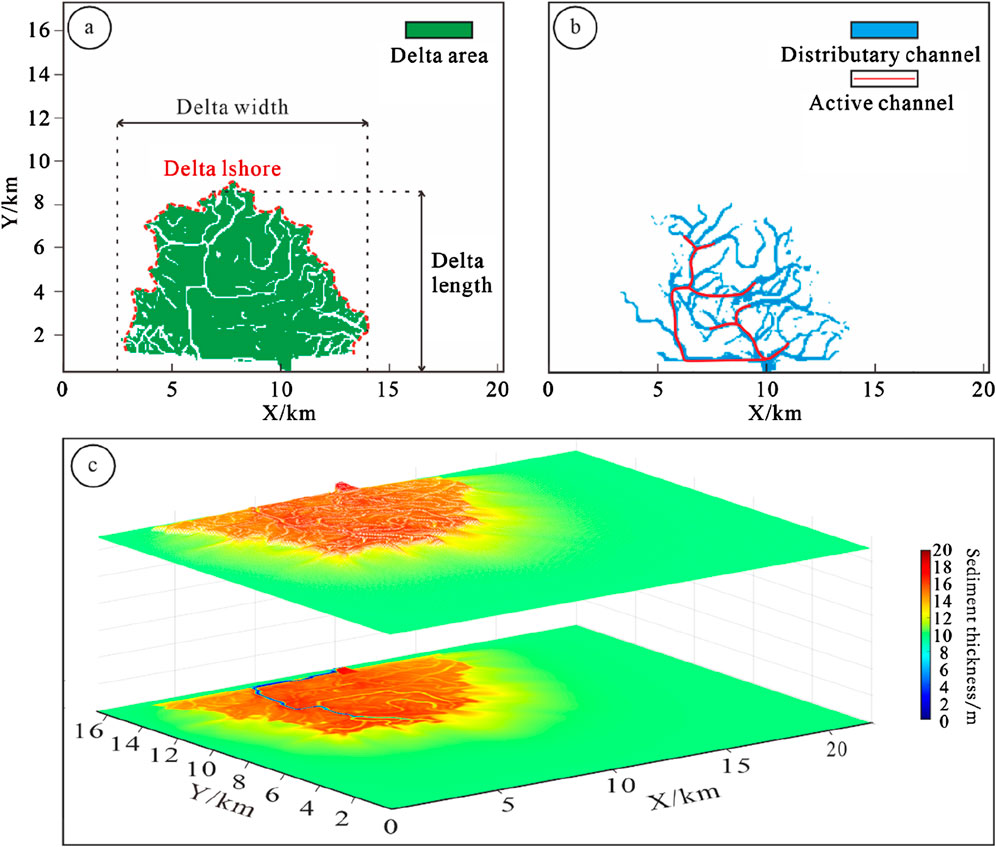
Figure 4. Schematic diagram of delta parameters. (A) Delta length, width, shoreline, and land area; (B) Active distributary channels and breach distributary channels; (C) 3D and plane diagrams of delta thickness.
Delta Width (W): Defined as the maximum span of the delta perpendicular to its length, this metric reflects the delta’s spreading capability (Caldwell and Edmonds, 2014). Figure 4A provides a schematic representation of delta width.
Delta Area (A): This parameter is determined by accumulating and summing the two-dimensional plane data of sediments over the simulation period. By binarizing the simulation results based on the two-dimensional water depth data and corresponding lake surface values, the area of the shallow water delta can be accurately measured. A plane schematic diagram of the delta area is presented in Figure 4A.
Delta Shoreline (SH): The shoreline length, representing the outer boundary of the delta front, serves as a key parameter for characterizing delta shoreline morphology. A longer shoreline suggests a more complex delta morphology with increased branching and frequent flow velocity changes, whereas a shorter shoreline indicates a simpler and more stable delta form. The specific schematic diagram is shown in Figure 4A.
Delta Thickness (SE): The sediment thickness distribution reflects the topographic variations of the delta. This study extracts two-dimensional sediment thickness data from different time series and analyzes it using MATLAB software. By calculating the standard deviation of sediment thickness through custom code, the variability in terrain thickness is quantified. A larger standard deviation indicates greater topographic variation. The plane and 3D schematic diagrams of delta thickness are shown in Figure 4C.
Depth-averaged velocities: in Delft3D numerical simulation, the two-dimensional depth-averaged velocities of each time series on a certain grid is saved. This study counted the depth-averaged velocities of each grid in the work area under all simulation time series conditions and averaged them to obtain a two-dimensional plane distribution map of the depth-averaged velocities in the simulation area.
3.2 Delta geomorphic parameters
Delta Land Area: In this study, the delta sedimentary area is defined as the land portion of the delta where the water depth is less than 0.5 m. Figure 4A presents a schematic diagram of the delta area, from which the land area of the delta is measured.
Distributary Channel: The classification of distributary channels is based on flow velocity. Two-dimensional plane diagrams of flow velocity for various time series in the simulated sections are analyzed. Channels with an average flow rate greater than 1 m/s are classified as active distributary channels. These channels are characterized by higher flow velocities, indicating a longer survival time, a greater sediment and water transport capacity, and a significant influence on delta growth and development. Channels with flow velocities ranging from 0 m/s to 1 m/s are classified as breach distributary channels, indicating shorter survival times and quick abandonment after formation. Active distributary channels are depicted in red, while breach distributary channels are shown in blue in Figure 4B.
4 Result
This study takes the simulation experiments of shallow deltas under high, medium and low lake levels (A1 and A3) as an example to investigate the differences in shallow delta scale characteristics, number of distributary channels and delta land area under different lake levels.
4.1 Delta plane geometry differences
As illustrated in Figure 5, the scale of the delta exhibits considerable variation across different lake levels. Within the same simulation period, the length, width, and area of the delta are inversely related to the lake level. At the maximum lake level of 6 m and a simulation duration of 100 h, the delta attains its smallest dimensions, with a length of 2.09 km, a width of 1.79 km, and an area of 1.28 km2, assuming a flower-like shape. At an intermediate lake level of 2.5 m, the delta’s dimensions increase slightly, reaching a length of 2.26 km, a width of 4.41 km, and an area of 6.99 km2. Conversely, at the minimum lake level of −1 m, the delta reaches its largest scale, with a length of 4.43 km, a width of 12.56 km, and an area of 30.87 km2.

Figure 5. Changes in delta size under different lake levels. (A–C) Show the evolution process of a delta under low lake level (-1 m); (D–F) Show the evolution process of a delta under medium lake level (2.5 m); (G–I) Show the evolution process of a delta under high lake level (6 m).
As simulation time progresses, the scale of deltas under varying lake levels generally increases, although deltas at higher lake levels remain the smallest. In comparison to other lake levels, deltas under lower lake levels exhibit a pronounced growth. After 500 h of simulation, the rate of increase in length, width, and area of deltas under high lake levels is slower compared to those under medium and low lake levels. As illustrated in Figure 6A, the growth rate of delta length, width, and area at high lake levels is the least pronounced, with dimensions of 4.12 km in length, 7.58 km in width, and an area of 22.82 km2. Conversely, deltas at medium and low lake levels grow at a faster rate. The disparity in scale between deltas at medium and low lake levels and those at high lake levels becomes more pronounced over time. At the 500-h mark, deltas under medium lake levels measure 5.46 km in length, 11.76 km in width, and cover an area of 45.12 km2, while deltas under low lake levels reach 8.49 km in length, 18.39 km in width, and encompass an area of 100.97 km2.
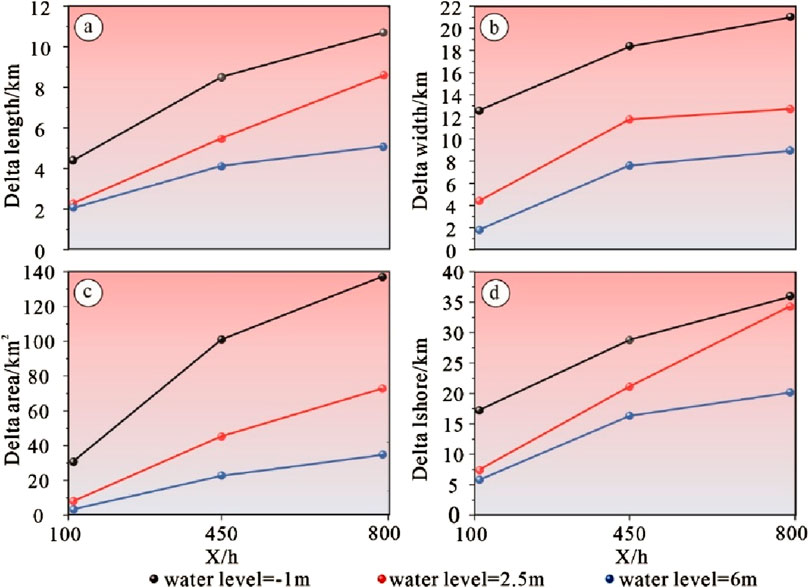
Figure 6. Differences in delta scale parameters under different lake levels. (A) Delta length difference; (B) Delta width difference; (C) Delta area difference; (D) Delta lshore difference.
As the delta scale continues to expand, the growth rate of the delta’s dimensions gradually diminishes, leading to the maximum disparity in scale between deltas at different lake levels. After 800 h of simulation, the delta at a low lake level achieved dimensions of 10.64 km in length, 21.03 km in width, and 139.79 km2 in area. These measurements are approximately twice the length and width and four times the area of the delta observed at high lake levels, highlighting a substantial scale difference.
Further analysis of the delta shoreline values provides additional insights into the morphological changes under varying lake levels over time. The study reveals significant differences in delta morphology across lake levels. The shoreline length of the delta exhibits a gradual increase over time, with the growth rate being slower at high lake levels compared to low lake levels. Shoreline measurements taken at 100, 500, and 800 h indicate that at low lake levels, the delta shoreline extends to 17.22 km, 28.75 km, and 36.02 km, respectively. In contrast, at high lake levels, the shoreline values are substantially lower, measuring 5.80 km, 16.33 km, and 18.69 km. This data underscores that lower lake levels significantly promote the expansion of the delta shoreline.
4.2 Delta thickness difference
The MATLAB code developed for this study measures the thickness of the delta at various lake levels. As illustrated in Figure 7, there is considerable variation in delta thickness across different lake levels. Specifically, the average thickness of the delta increases with rising lake levels. Correspondingly, the standard deviation of delta thickness also increases, indicating that higher lake levels lead to more pronounced topographic variations and a more rugged surface terrain.
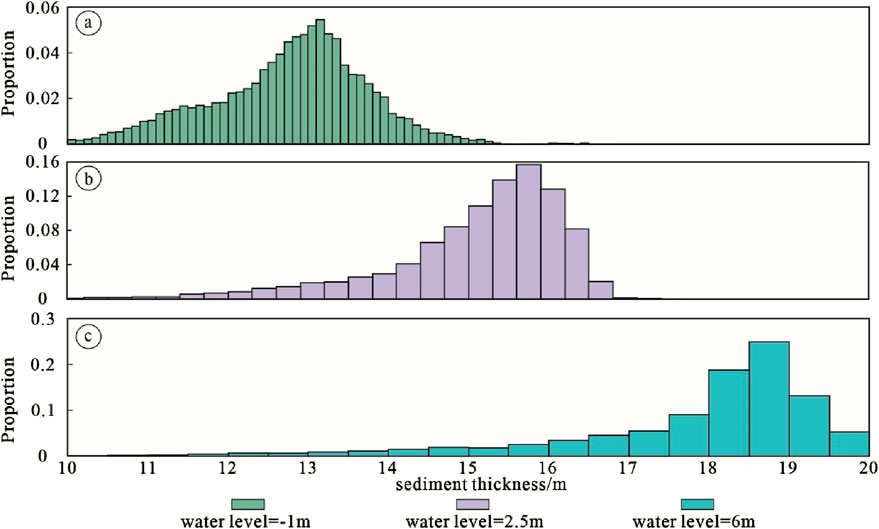
Figure 7. Delta thickness runderio under different lake levels. (A) Proportion of delta thickness values under low lake level (-1 m); (B) Proportion of delta thickness values under medium lake level (2.5 m); (C) Proportion of delta thickness values under high lake level (6 m).
At a low lake level (lake level = -1m), the distribution of delta thickness is relatively uniform, with sediment thickness predominantly ranging between 10 and 15 m. The most common sediment thickness is approximately 13 m, which constitutes the largest proportion at 5.7%. As shown in Table3, at this low lake level, the average delta thickness is the smallest, approximately 12.66 m, and the maximum thickness is also relatively modest, around 16.73 m. The delta exhibits minimal topographic variation at this level, as evidenced by the smallest standard deviation of thickness, which is approximately 1.22 m.
At a high lake level (lake level = 6m), the delta thickness predominantly ranges between 15 and 20 m. The most common sediment thickness is approximately 18.5 m, accounting for 25% of the measurements. As indicated in Table3, at this high lake level, the average delta thickness is the greatest, around 18.03 m, with a maximum thickness reaching up to 21.03 m. However, the distribution of delta thickness is uneven, as evidenced by a relatively high standard deviation of approximately 2.5 m.
At a medium lake level (lake level = 2.5 m), the delta thickness primarily falls between 14 and 17 m, with a maximum thickness of 18.03 m and an average thickness of 14.84 m. This average thickness is intermediate between the values observed at low and high lake levels. The standard deviation of delta thickness at this level is 2.03 m, which is slightly lower than the standard deviation observed at high lake levels.
4.3 Differences in distributary channels
As illustrated in Figure 8, the characteristics of the delta distributary channels vary significantly across different lake levels. Specifically, the number of distributary channels is inversely proportional to the lake level height. At low lake levels, the number of distributary channels is the highest, followed by medium lake levels, with the fewest distributary channels observed at high lake levels. Conversely, the number of active distributary channels remains relatively constant regardless of the lake level height. This observation suggests that variations in lake level have a more pronounced effect on breach distributary channels than on active distributary channels.
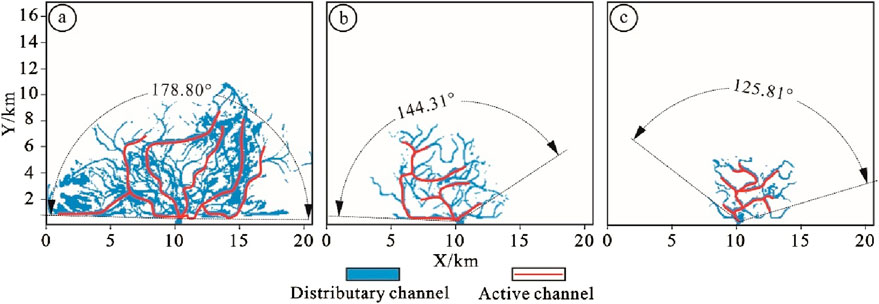
Figure 8. Delta distributary channels under different lake levels. (A) Delta distributary channels under low lake level (-1 m); (B) Delta distributary channels under medium lake level (2.5 m); (C) Delta distributary channels under high lake level (6 m).
Similarly, the distribution range of distributary channels is inversely proportional to lake level height. This study uses the distribution angle of active distributary channels as a parameter to quantify the distribution range. At low lake levels, the development angle of active distributary channels is approximately 178.8°, covering nearly the entire lake basin. At medium lake levels, the development angle decreases to 144.31°, with reduced development observed on the right side of the lake basin. At high lake levels, the distribution angle of active distributary channels reaches a minimum of 125.81°, with active distributary channels primarily concentrated near the river mouth. Consequently, higher lake levels correspond to a narrower distribution range of distributary channels and a more restricted riverine function.
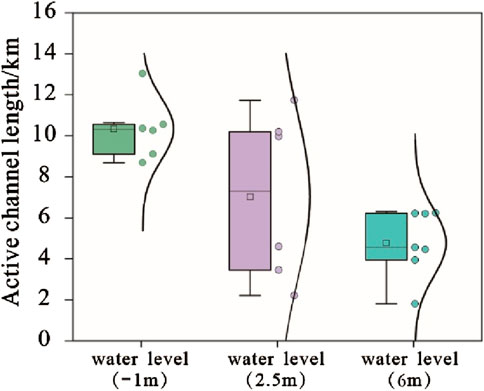
This study also assessed the length of active distributary channels across different lake levels. As depicted in Figure 9, the length of active distributary channels is inversely related to lake level height. At low lake levels, the average length of active distributary channels is approximately 10.33 km, with channels remaining distinct and separated by significant distances. At medium lake levels, the average length decreases to 7.02 km, with multiple active distributary channels becoming more compact. At high lake levels, the average length of active distributary channels is reduced to 4.52 km, with channels closely distributed in the direction of the river source.
4.4 Differences in delta evolution under different lake levels
Under different lake levels, the growth and development process of the delta determines the differences in its scale. Numerical simulation reproduces the complete development process of the river-controlled delta from early to middle to late. This time, we will take low and high lake levels as examples to compare and analyze the differences in its evolution process.
4.4.1 Delta evolution process under low lake level
In a low lake level environment, during the initial phase of delta formation, a substantial amount of sediment rapidly accumulates in the estuarine area as the river flows into the lake. This accumulation forms a semicircular mouth bar characterized by a relatively gentle shape and low curvature. During this stage, the effect of channelization by the distributary channels is not yet pronounced, and deposition in the mouth bar predominantly constitutes the initial sediment overlay (Figures 10, 11A–C).
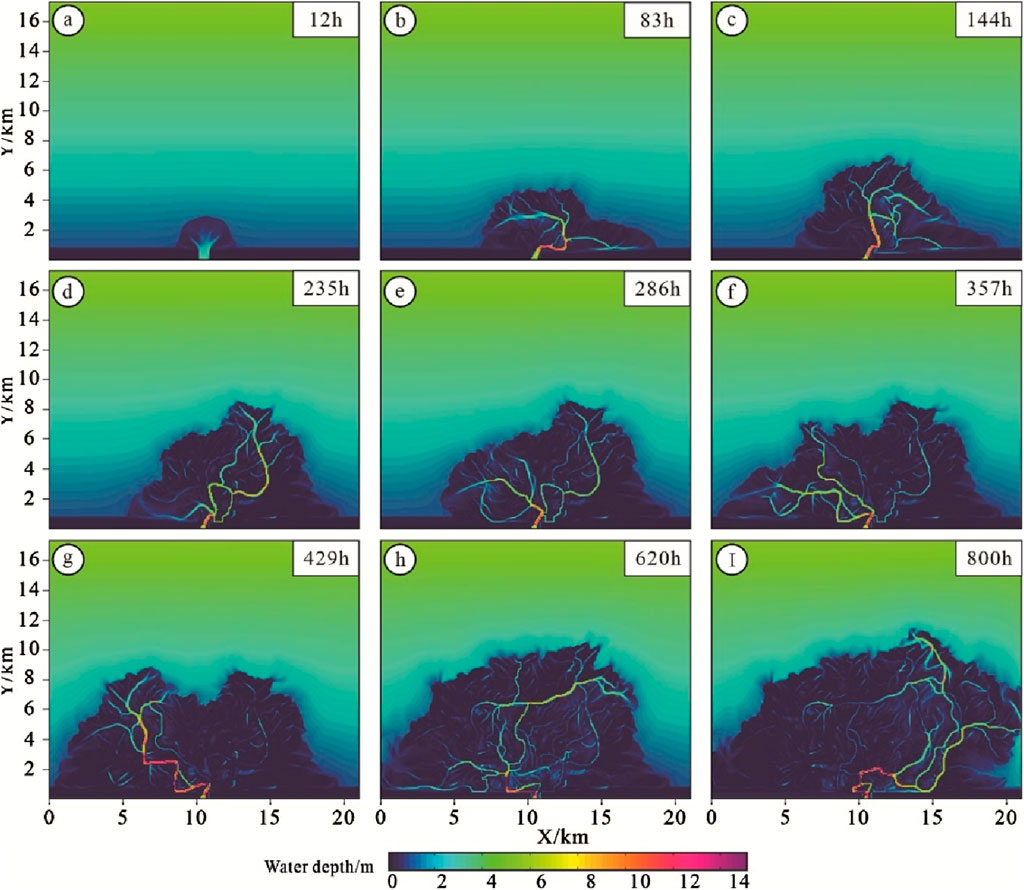
Figure 10. Evolution of delta water depth under low lake level. (A–I) Shows the evolution process of a delta under low lake level (-1 m) at different simulation times.
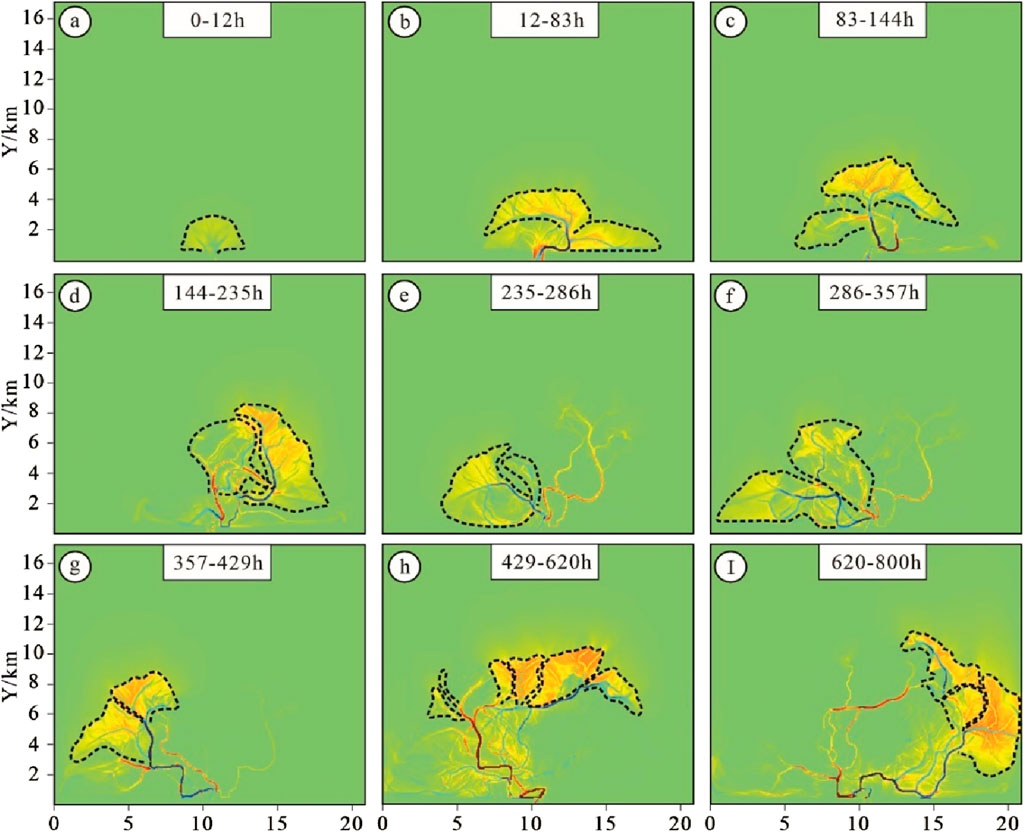
Figure 11. Delta sediment increment map under low lake level. (A–I) shows the sediment increment process of a delta under low lake level (-1 m) during different simulation time periods.
Between 12 and 357 h of simulation, the mouth bar undergoes continuous vertical accretion. As its thickness approaches the lake level and with the river basin maintaining a relatively low water level, the dynamic effect of the river is enhanced. This change causes significant divergence of the distributary channels, resulting in the formation of multiple new distributary channels in front of and on either side of the main channel. These new distributary channels advance sediment further, creating a new overlay comprised of breach distributary channels and mouth bars at their respective new estuary locations. Compared to the initial stage, these new formations exhibit a more complex and irregular bouquet shape on the plane, evolving from a scattered distribution to a more closely arranged conFigureuration (Figures 10, 11B–F).
During the simulation period of 357–800 h, the distributary channels in the delta showed a clear migration trajectory, gradually advancing from the left to the middle and even to the right. At the same time, the distribution pattern of sediment increment also followed this migration law, and the distance between multiple complex was significantly reduced, and finally multiple complex was completely closely arranged (Figures 10, 11H).
4.4.2 Delta evolution process under high lake level
At the commencement of the simulation, the delta was in its nascent stage. Due to the elevated lake level, the sediments transported by the supplying river were dispersed and deposited to form initial mouth bar deposits. At this stage, sediment thickness was greatest at the river supply location and decreased as one moved towards the center of the lake basin. The degree of channelization of the distributary channels was minimal, with negligible erosion observed (Figures 12, 13A).
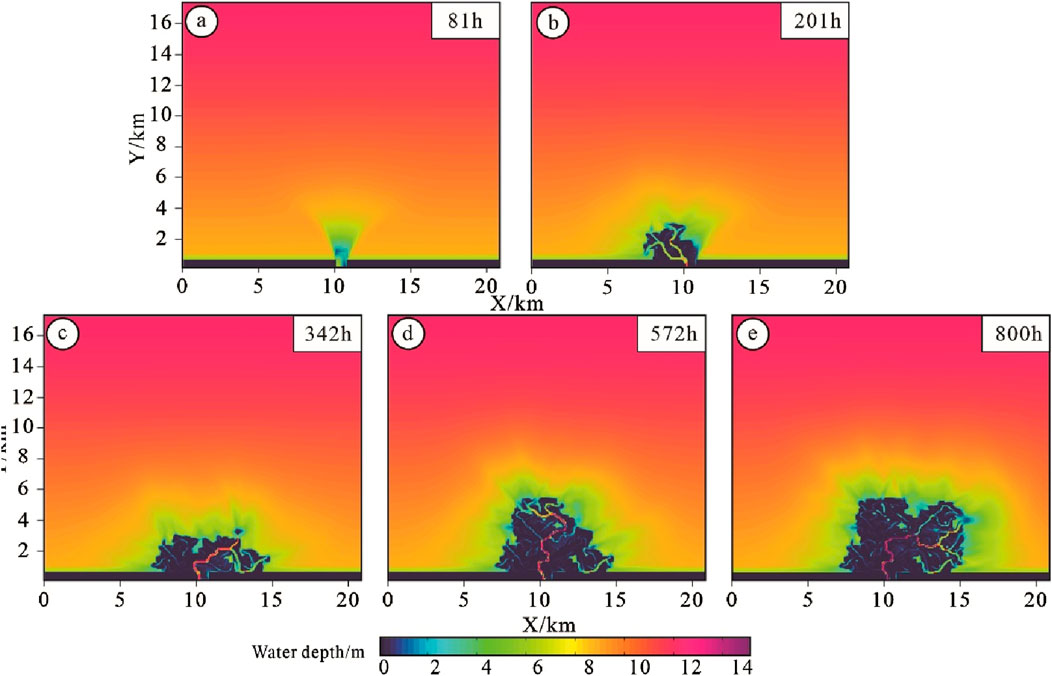
Figure 12. Delta water depth evolution under high lake level. (A–E) Shows the evolution process of a delta under high lake level (-1 m) under different simulation times.
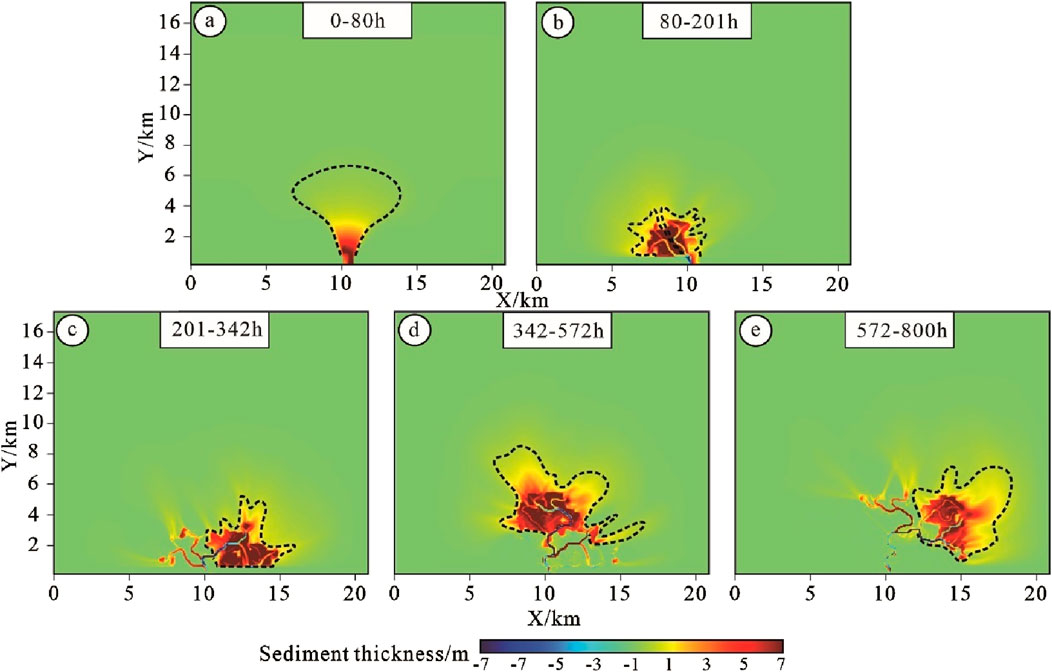
Figure 13. Delta sediment increment map under high lake level. (A–E) Shows the sediment increment process of a delta under high lake level (6 m) during different simulation time periods.
Between 80 and 342 h of simulation, the sediment distribution predominantly exhibited a bird-foot shape, and the channelization of the distributary channels increased. As illustrated in Figures 12, 13B, the sedimentary body primarily consisted of one to two distributary channels with weak bifurcation, and secondary distributary channels were virtually absent. The sedimentary complex was largely composed of distributary channels and mouth bars. From 342 to 800 h of simulation, with a constant river flow and increasing distance from the source, the supply energy to the distributary channels gradually diminished, while the supporting effect of the lake level became more pronounced, leading to an expansion of the sediment deposition range. The increased sediment area during this period primarily comprises the sediment edge area, mostly submerged underwater, while the area of the main sediment increment zone remained nearly unchanged compared to the previous simulation period (Figures 12, 13D).
By comparing and analyzing the evolution of deltas under different lake levels, the study shows that deltas under low lake levels are mainly composed of flower-shaped complex, and multiple complex is closely arranged. The thickness of a single overburden is relatively uniform, and mouth bars, distributary channels, and breach distributary channels are mainly developed in the complex. Deltas under high lake levels are mainly composed of bird-foot-shaped complex, which are scattered. Distributary channels and mouth bars are mainly developed in a single complex, and breach distributary channels are almost not developed. The thickness of the complex varies greatly, among which the area with thicker sediments is smaller and mainly distributed in the direction close to the source, while the area with thinner sediments is closer to the center of the lake basin and has a larger area.
5 Discussion
5.1 The influence mechanism of different lake level values on delta scale and sediment thickness
Previous researchers believed that the supply of river materials was the key factor affecting the scale of river-controlled deltas. Previous studies were based on bird-foot deltas, such as the modern Mississippi River Delta and the Yellow River Delta, whose sediment ratios were 11.2 and 2.8, respectively; while typical tongue-shaped deltas, such as the Wax Lake Delta and the Mossy Delta in the United States, had sediment ratios less than 1 (Edmonds and Slingerland, 2010). This confirmed that the supply of fine-grained, highly viscous sediments can promote the accumulation of natural levees, enhance the cohesion of natural levees, and be conducive to the formation of bird-foot deltas. Such deltas have a smaller geometric scale and a larger sediment thickness; while coarse-grained, low-viscosity sediments lead to the rapid deposition of estuary bars and the diversion of distributary channels, promoting the formation of tongue-shaped deltas with distributary sand bars as the main source. Mainly, this type of delta has a larger geometric scale and a relatively smaller sediment thickness than that of a bird-foot delta (Edmonds and Slingerland, 2007; Caldwell and Edmonds, 2014; Burpee et al., 2015; Orton and Reading, 1993).
In addition to supplying river materials, river discharge is also an important factor affecting the formation of delta scale. Based on numerical simulation of sedimentation, Xu et al. (2021) found that under high river discharge, river-controlled deltas are prone to develop diversion and breach and form large and thin tongue-shaped deltas; under low discharge, the diversion channel in the river-controlled delta is relatively stable, and it is easy to form a small and thick bird-foot-shaped delta, and pointed out that the discharge value of 1,000 m3/s is a key threshold.
However, based on the numerical simulation method, this paper found that the height of the lake level also has a great influence on the scale of the delta by comparing three different lake level values: high, medium and low. When the lake level is high, the delta is bird-foot-shaped, with a small plane scale but a large sediment thickness (Figures 5G, H, L; Figures 6A–D); when the water level is low, the delta is tongue-shaped, with a large plane scale but a thin sediment thickness; when the water level is between the two, the scale of the delta is also between the two.
The size of the delta reflects the strength of the river’s energy supply. The larger the delta, the stronger the river’s energy supply (Galloway, 1975; Olariu, 2014). When the lake level is low, the delta is large, indicating that the lake basin has low energy, and the corresponding supply river has relatively high energy. When the lake level is low, the limited accommodation space and the smaller A/S ratio lead to the supply river being mainly erosive, and the sediments can be transported farther. As the supply river’s ability to carry sediments gradually weakens with the increase of the extension distance, the coarser sand bodies are deposited first because they are less affected by the support of the top of the lake surface; the finer sand bodies are more affected by the support of the top of the lake surface, and expand outward to form a larger delta plane. On the contrary, when the lake level is high, the accommodation space is larger, resulting in a larger A/S ratio, and the downcutting ability of the supply river is weakened, mainly vertical accumulation, resulting in a thicker delta and a smaller scale at high lake levels. The study characterized the water velocity data corresponding to the delta plane at different lake level values under a simulation time of 506h (Figures 14A–C). As can be seen from Figure 14, at high lake level water levels, the water flow rate is slow and the flow range is small. Most sediments are deposited quickly and it is difficult to migrate further. At low water levels, there is flow to varying degrees in all parts of the delta front (i.e., the underwater delta part), which leads to the continuous transportation of sediments and their rapid diffusion to the surrounding areas, resulting in a large and rapid increase in the size of the delta.
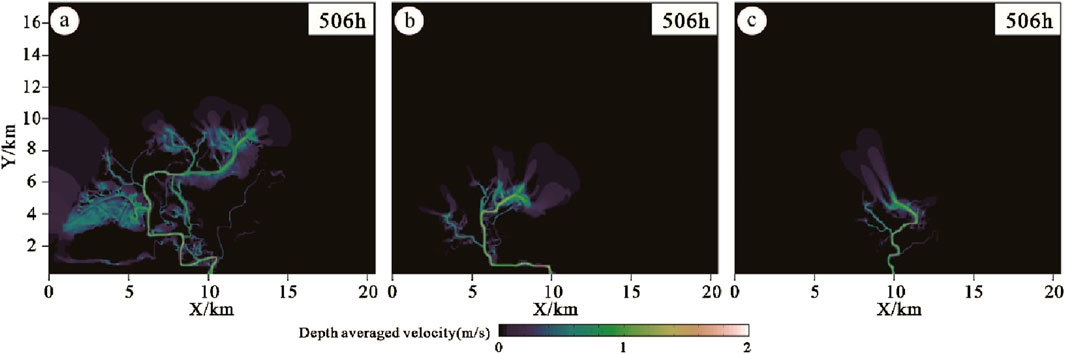
Figure 14. Plane distribution of instantaneous flow velocity in the lake basin at 506 h of simulation time under different lake levels. (A): distribution map of flow velocity in the delta under low lake level (-1 m) at 506 h; (B) distribution map of flow velocity in the delta under medium lake level (2.5 m) at 506 h; (C) distribution map of flow velocity in the delta under high lake level (6 m) at 506 h.
5.2 The impact mechanism of different lake level values on the number of delta distributary channels
Consistent with delta size, the number of distributary channels is also affected by multiple factors, including the flow and sediment characteristics of the source river and the depth of the lake basin. Edmonds et al. (2009) demonstrated through numerical simulation of sediment that changes in river flow affect the stability of shallow deltas. Specifically, a decrease in river flow leads to a proportion of existing distributary channels being abandoned, resulting in a decrease in their number. Conversely, a 60% increase in river flow may lead to the formation of new distributary channels. In addition, sediments with high viscosity, low sand-mud ratio and fine grain texture generally lead to fewer distributary channels, while sediments with low viscosity, high sand-mud ratio and coarse grains are associated with more distributary channels (Burpee et al., 2015).
This study also found that different water level values also have a great influence on the number of distributary channels in the delta, but the impact of water level on distributary channels is mainly concentrated in breach distributary channels, while it has little effect on active distributary channels (Figure 8). At low lake levels, the supply capacity of the river is relatively strong, resulting in the formation and dispersion of distributary channels. This condition increases the likelihood of breach distributary channels. In contrast, during high lake levels, the lake supports the feeding rivers, concentrating the flow at the front of the feeding channels. As a result, these channels tend to migrate laterally, which reduces breaching and the likelihood of breach distributary channels.
6 Conclusion
The study conducted a simulation experiment to investigate the evolution of deltas under varying lake levels, comparing and analyzing the differences in their scale characteristics and growth processes. The findings are summarized as follows:
The plane scale of the delta is directly proportional to the lake level. Under low lake levels, the delta exhibits larger dimensions in terms of length, width, area, and distribution angle, but its thickness is relatively small. In contrast, under high lake levels, the delta’s length, width, area, and distribution angle are smaller, while its thickness is more pronounced.
The length of active distributary channels and the number of breach distributary channels are inversely proportional to the lake level. However, the number of active distributary channels remains relatively constant regardless of lake level. During the same simulation period, deltas under different lake levels show nearly the same number of active distributary channels. Nonetheless, at low lake levels, these channels are longer, and there are numerous breach distributary channels that form an intricate network. At high lake levels, the active distributary channels are shorter, with fewer and more dispersed breach distributary channels.
The delta comprises multiple complexes. Under high lake levels, the sedimentary structures are predominantly bird-foot-shaped, with considerable thickness near the source and reduced thickness towards the lake basin’s center. These complexes mainly consist of active distributary channels and mouth bars. Conversely, under low lake levels, the sedimentary structures are tongue-shaped with relatively uniform thickness throughout, and include active distributary channels, mouth bars, and breach distributary channels.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
JL: Writing–original draft, Writing–review and editing. DZ: Conceptualization, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funded Projects: (1) Guizhou Sci-Tech Cooperation Platform Talent-CXTD [2021]008; (2) Study on risk zoning and early warning of geological hazards on highway slopes in mountainous areas of Guizhou under rainfall-No. 2023-122-035.
Acknowledgments
This experiment used Delft3d sedimentary numerical simulation software developed in collaboration between Delft University in the Netherlands and deltaes, with version number 4.04.01.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelwahhab, M. A., Abdelhafez, N. A., and Embabi, A. M. (2023). Machine learning-supported seismic stratigraphy of the Paleozoic Nubia Formation (SW Gulf of Suez-rift): implications for paleoenvironment− petroleum geology of a lacustrine-fan delta. Petroleum 9 (2), 301–315. doi:10.1016/j.petlm.2022.01.004
Anthony, E. J. (2015). Wave influence in the construction, shaping and destruction of river deltas: a review. Mar. Geol. 361, 53–78. doi:10.1016/j.margeo.2014.12.004
Burpee, A. P., Slingerland, R. L., Edmonds, D. A., Parsons, D., Best, J., Cederberg, J., et al. (2015). Grain-size controls on the morphology and internal geometry of river-dominated deltas. J. Sediment. Res. 85 (6), 699–714. doi:10.2110/jsr.2015.39
Caldwell, R. L., and Edmonds, D. A. (2014). The effects of sediment properties on deltaic processes and morphologies: a numerical modeling study. J. Geophys. Res. Earth Surf. 119 (5), 961–982. doi:10.1002/2013jf002965
Cao, J., Qiao, X., and He, Y. (2024). Experimental study on sedimentary simulation of shallow meandering river delta in the second segment of Shanxi Formation in Yan'an area, Ordos Basin. Acta Sedimentol. Sin., 1–18. doi:10.14027/j.issn.1000-0550.2022.121
Donaldson, A. C. (1974). Pennsylvanian sedimentation of central Appalachians. J. Sediment. Res., 47–78. doi:10.1130/spe148-p47
Edmonds, D. A., Hoyal, D. C. J. D., Sheets, B. A., and Slingerland, R. L. (2009). Predicting delta avulsions: implications for coastal wetland restoration. Geology 37 (8), 759–762. doi:10.1130/g25743a.1
Edmonds, D. A., and Slingerland, R. L. (2007). Mechanics of river mouth bar formation: implications for the morphodynamics of delta distributary networks. J. Geophys. Res. Earth Surf. 112 (F2). doi:10.1029/2006jf000574
Edmonds, D. A., and Slingerland, R. L. (2010). Significant effect of sediment cohesion on delta morphology. Nat. Geosci. 3 (2), 105–109. doi:10.1038/ngeo730
Feng, X., Gao, S., and Liu, Y. (2021). Characteristics of the progradational structure of the delta front of the yanchang formation in longdong area, Ordos Basin. Lithol. Reserv. 33 (06), 48–58. doi:10.12108/yxyqc.20210606
Fisk, H. N., Kolb, C. R., McFarlan, E., and Wilbert, L. J. (1954). Sedimentary framework of the modern Mississippi delta [Louisiana]. J. Sediment. Res. 24 (2), 76–99. doi:10.1306/d4269661-2b26-11d7-8648000102c1865d
Galloway, W. E. (1975). Process framework for describing the morphologic and stratigraphic evolution of deltaic depositional systems.
Gao, Z., Zhou, C., and Dong, W. (2016). Dynamic growth process model of shallow water delta and distribution of favorable sand bodies: a case study of the Poyang Lake Ganjiang Delta. Mod. Geol. 30 (02), 341–352. doi:10.3969/j.issn.1000-8527.2016.02.009
Geleynse, N. (2007). Modelling cyclic bar behaviour: a bottom-up modelling approach with Delft3D. Z4099.
Geleynse, N., Storms, J. E. A., Walstra, D. J. R., Jagers, H. A., Wang, Z. B., and Stive, M. J. (2011). Controls on river delta formation; insights from numerical modelling. Earth Planet. Sci. Lett. 302 (1-2), 217–226. doi:10.1016/j.epsl.2010.12.013
He, Z. (1986). Preliminary discussion on the classification of lake basin deltas. Petroleum & Nat. Gas Geol. (04), 395–403. doi:10.11743/ogg19860410
Hillen, M., Geleynse, N., Storms, J., Walstra, D., and Groenenberg, R. (2014). “Morphodynamic modelling of wave reworking of an alluvial delta and application of results in the standard reservoir modelling workflow,” in From depositional systems to sedimentary successions on the Norwegian continental margin, 167–185.
Jalowska, A. M., Rodriguez, A. B., and McKee, B. A. (2015). Responses of the Roanoke Bayhead Delta to variations in sea level rise and sediment supply during the Holocene and Anthropocene. Anthropocene 9, 41–55. doi:10.1016/j.ancene.2015.05.002
Jin, Z., Li, Y., and Gao, B. (2014). Sedimentation model of modern gentle slope delta: a case study of the Ganjiang Delta in Poyang Lake. Acta Sedimentol. Sin. 32 (04), 710–723. doi:10.14027/j.cnki.cjxb.2014.04.011
Kulp, M. A., Miner, M. D., and FitzGerald, D. M. (2024). Subsurface controls on transgressive tidal inlet retreat pathways, Mississippi River Delta Plain, USA. J. Coast. Res. 50 (sp1), 816–820. doi:10.2112/jcr-si50-152.1
Lesser, G. R., Roelvink, J. A., van Kester, J. A. T. M., and Stelling, G. (2004). Development and validation of a three-dimensional morphological model. Coast. Eng. 51 (8-9), 883–915. doi:10.1016/j.coastaleng.2004.07.014
Li, S., Yang, S., and Xie, X. (1990). Evolution of the lake delta sedimentary system of the Yan'an Formation in Ordos and comparative sedimentological study of this system and the Ganjiang Delta. Geol. Sci. Transl. Ser. (01), 92–93. doi:10.15964/j.cnki.027jgg.1990.01.025
Li, W., Colombera, L., Yue, D., and Mountney, N. P. (2023). Controls on the morphology of braided rivers and braid bars: an empirical characterization of numerical models. Sedimentology 70 (1), 259–279. doi:10.1111/sed.13040
Liu, L., Zeng, F., and Fu, Z. (2016). Analysis of the 62-year variation pattern of water level at xingzi station of Poyang Lake. Yangtze River J. 47 (03), 30–32+66. doi:10.16232/j.cnki.1001-4179.2016.03.008
Loc, H. H., Lixian, M. L., and Park, E. (2021). How the saline water intrusion has reshaped the agricultural landscape of the Vietnamese Mekong Delta: a review. Sci. Total Environ. 794, 148651. doi:10.1016/j.scitotenv.2021.148651
Luo, Q. (2015). On the transgressive delta: on the genesis of the thick sand layers of the Xujiahe Formation in the Sichuan Basin. Acta Sedimentol. Sin. 33 (05), 845–854. doi:10.14027/j.cnki.cjxb.2015.05.001
McLennan, S. M. (1993). Weathering and global denudation. J. Geol. 101 (2), 295–303. doi:10.1086/648222
Nardin, W., and Fagherazzi, S. (2012). The effect of wind waves on the development of river mouth bars. Geophys. Res. Lett. 39 (12). doi:10.1029/2012gl051788
Nienhuis, J. H., Ashton, A. D., Roos, P. C., Hulscher, S. J. M. H., and Giosan, L. (2013). Wave reworking of abandoned deltas. Geophys. Res. Lett. 40 (22), 5899–5903. doi:10.1002/2013gl058231
Nienhuis, J. H., Kim, W., Milne, G. A., Quock, M., Slangen, A. B., and Törnqvist, T. E. (2023). River deltas and sea-level rise. Annu. Rev. Earth Planet. Sci. 51 (1), 79–104. doi:10.1146/annurev-earth-031621-093732
Olariu, C. (2014). “Autogenic process change in modern deltas: lessons for the ancient,” in From depositional systems to sedimentary successions on the Norwegian continental margin, 149–166. doi:10.1002/9781118920435.ch7
Orton, G. J., and Reading, H. G. (1993). Variability of deltaic processes in terms of sediment supply, with particular emphasis on grain size. Sedimentology 40 (3), 475–512. doi:10.1111/j.1365-3091.1993.tb01347.x
Paola, C., Twilley, R. R., Edmonds, D. A., Kim, W., Mohrig, D., Parker, G., et al. (2011). Natural processes in delta restoration: application to the Mississippi Delta. Annu. Rev. Mar. Sci. 3 (1), 67–91. doi:10.1146/annurev-marine-120709-142856
Park, E. (2024). Sand mining in the Mekong delta: extent and compounded impacts. Sci. Total Environ. 924, 171620. doi:10.1016/j.scitotenv.2024.171620
Penland, S., Boyd, R., and Suter, J. R. (1988). Transgressive depositional systems of the Mississippi Delta plain; a model for barrier shoreline and shelf sand development. J. Sediment. Res. 58 (6), 932–949. doi:10.1306/212F8EC2-2B24-11D7-8648000102C1865D
Qiu, L., Yang, B., and Zhang, Y. (2016). Effect of lake water level on the main sand body types in the delta front: a case study of the Jurassic Yan'an Formation section in Shenmu area, Ordos Basin. J. Palaeogeogr. 18 (06), 939–950. doi:10.7605/gdlxb.2016.06.071
Schuurman, F., and Kleinhans, M. G. (2011). “Self-formed braided bar pattern in a numerical model,” in Proceedings of the 7th IAHR conference on river, estuarine and coastal morphodynamics (Beijing, China), 1647–1657.
Stanley, D. J., and Warne, A. G. (1993). Nile Delta: recent geological evolution and human impact. Science 260 (5108), 628–634. doi:10.1126/science.260.5108.628
Syvitski, J. P. M., and Saito, Y. (2007). Morphodynamics of deltas under the influence of humans. Glob. Planet. Change 57 (3-4), 261–282. doi:10.1016/j.gloplacha.2006.12.001
Törnqvist, T. E., Jankowski, K. L., Li, Y. X., and González, J. L. (2020). Tipping points of Mississippi Delta marshes due to accelerated sea-level rise. Sci. Adv. 6 (21), eaaz5512. doi:10.1126/sciadv.aaz5512
Törnqvist, T. E., González, J. L., Newsom, L. A., van der Borg, K., de Jong, A. F., and Kurnik, C. W. (2004). Deciphering holocene sea-level history on the us gulf coast: a high-resolution record from the Mississippi delta. Geol. Soc. Am. Bull. 116 (7-8), 1026–1039. doi:10.1130/b2525478.1
Wang, J., Chen, H., Jiang, T., Tang, Z., Zhao, B., and Xu, D. (2012). Structural anatomy of the sand body of the underwater distributary channel in the shallow delta of Xinli area in Songliao Basin. Earth Sci. J. China Univ. Geosciences 37 (03), 556–564. doi:10.3799/dqkx.2012.062
Wang, S. (2002). Study on the network river system in the delta where Ganjiang River flows into the lake. Geogr. Sci. (02), 202–207. doi:10.3969/j.issn.1000-0690.2002.02.013
Woodroffe, C. D., Nicholls, R. J., Saito, Y., Chen, Z., and Goodbred, S. L. (2006). “Landscape variability and the response of Asian megadeltas to environmental change,” in Global change and integrated coastal management: the Asia-Pacific region, 277–314. doi:10.1007/1-4020-3628-0_10
Wright, E. E., Hine, A. C., Goodbred, S. L., and Locker, S. D. (2005). The effect of sea-level and climate change on the development of a mixed siliciclastic–carbonate, deltaic coastline: suwannee River, Florida, USA. J. Sediment. Res. 75 (4), 621–635. doi:10.2110/jsr.2005.051
Wu, S., Yue, D., Feng, W., Zhang, J., and Xu, Z. (2021). Some progress in the study of clastic rock sedimentary architecture. J. Palaeogeogr. 23 (02), 245–262. doi:10.7605/gdlxb.2021.02.018
Xu, Z., Wu, S., Yue, D., Zhao, J., Deng, M., Liu, Z., et al. (2017). Effects of upstream conditions on digitate shallow-water delta morphology. Mar. Petroleum Geol. 134, 105333. doi:10.1016/j.marpetgeo.2021.105333
Xu, Z. H., Wu, S. H., Liu, M. C., Zhao, J. S., Chen, Z. H., Zhang, K., et al. (2021). Effects of water discharge on river-dominated delta growth. Petroleum Sci. 18 (6), 1630–1649. doi:10.1016/j.petsci.2021.09.027
Zeydan, B. A. (2005) “The Nile Delta in a global vision,” in Proceedings of the ninth international water technology conference, 31–40.
Zhang, Y., Qiu, L., and Yang, B. (2016). Sedimentary characteristics of river-controlled delta mouth bars and the influence of water level changes during their formation. Nat. Gas. Geosci. 27 (05), 809–819.
Zhipeng, L., Lin, C., Dong, B., and Xiali, B. (2012). Internal architectural structure model of sand bodies in underwater distributary channels of river-controlled deltas. Acta Pet. Sin. 33 (01), 101–105. doi:10.7623/syxb201201013
Keywords: shallow delta, lake level, scale size, growth process, distributary channel
Citation: Liu J and Zhou D (2024) Scale characteristics and growth process of shallow water delta under different lake levels— based on Delft3D numerical simulation research. Front. Earth Sci. 12:1489238. doi: 10.3389/feart.2024.1489238
Received: 31 August 2024; Accepted: 13 November 2024;
Published: 10 December 2024.
Edited by:
Uwe Jenchen, Autonomous University of Nuevo León, MexicoReviewed by:
Carlos G. Aguilar-Madera, Autonomous University of Nuevo León, MexicoErik César Herrera-Hernández, Autonomous University of San Luis Potosí, Mexico
Copyright © 2024 Liu and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianning Liu, NzY3OTgzMTU5QHFxLmNvbQ==
 Jianning Liu
Jianning Liu Dejun Zhou
Dejun Zhou