Study on rock damage mechanics in the sustainable development of the red sandstone area in China: Taking Zhongjiang County as an example

There are many hilly areas dominated by red sandstone in western China. At the same time, China is also rapidly advancing the modernization of sustainable development in the abovementioned areas. Therefore, in order to ensure the safety and sustainable advancement of modernization, it has become an urgent task for the local government to explore the mechanical properties of red sandstone in relevant areas. Zhongjiang County, Sichuan Province, China, is mainly dominated by red sandstone, and the study of red sandstone in this area is very rare. Therefore, this paper takes the red sandstone in Zhongjiang County as the research object and studies the damage evolution characteristics of red sandstone under the uniaxial compression load using the acoustic emission monitoring technology. The results show that when the axial stress of red sandstone shows a V-shaped evolution phenomenon and the acoustic emission ringing count enters a relatively quiet period, it indicates that the red sandstone will undergo instability failure. By exploring the evolution law of Ф (AF (ringing count/duration)/RA (rise time/amplitude)), the evolution characteristics of fracture types of red sandstone in the process of damage were found. Based on Weibull function and continuum damage mechanics, the damage evolution model and stress–strain constitutive model are derived. Based on the evolution law of damage variables, the damage evolution characteristics of red sandstone are quantitatively characterized. The research findings provide the government of Zhongjiang County with a reference basis for formulating sustainable construction plans.

1 Introduction

China is a multi-topography country with rich rock types. Therefore, many scholars have done a lot of research on various types of rocks. However, the same rocks in different regions also have great differences in properties. This difference increases the difficulty of infrastructure construction in related areas. Under the premise of lacking the standard of rock mechanical properties in the region, it is very dangerous to carry out infrastructure construction, which is prone to major accidents, and may affect the sustainable development of the region and pose a potential threat to people‘s lives and property. Therefore, many research workers have conducted a lot of research on rocks in different regions to help the government make accurate decisions.

The exploration of rock mechanics by human beings is mainly divided into the following: the initial stage (the end of the 19th century and the beginning of the 20th century), the empirical theory stage (the beginning of the 20th century and the 1930s), the classical theory stage (the 1930s and the 1960s), and the modern development stage (the 1960s and now). Since Christian Otto Mohr proposed the Mohr–Coulomb strength theory in 1900, rock mechanics has made great progress. With the development of science and technology, nondestructive testing technology (Du et al., 2024; Ge et al., 2020; Sun et al., 2020; Xiong et al., 2022; Xu et al., 2020; Xu et al., 2022; Zhang et al., 2019; Zhao et al., 2021; Zhou et al., 2019) has become the mainstream method to explore the law of rock damage. Su G. et al. (2024) showed that the acoustic emission (AE) signal on the eve of brittle failure of hard rock usually indicates a quiet period, during which the number of AE signals is significantly reduced. Dong et al. (2021) studied the qualitative relationship between the precursor of rock instability and the direction of principal stress through the wave velocity in the rock AE experiment (Liu et al., 2022). According to the relationship among mechanical parameters, acoustic emission parameters, and the energy dissipation rate (EDR) in the process of rock failure, the energy evolution law in the process of rock failure is analyzed, and a new index for evaluating the precursor of rock failure is proposed based on the EDR. Su et al. (2020) used a true triaxial test system to study the AE precursors of coarse-grained hard rock instability. Bi et al. (2024) obtained the mechanical and acoustic emission information of the whole process of rock damage and fracture through the uniaxial compression test, Brazilian splitting test, and improved shear test on marble, granite, limestone, and sandstone. He et al. (2022) proposed an early warning method based on the “quiet period” phenomenon of AE and EMR during fracture.

The tensile strength (Park, 2023; Sun et al., 2023) and shear strength (Cui, 2019; Fathipour-Azar, 2022) are important mechanical properties of rocks. Therefore, many scholars have also conducted extensive research on the types of rock failure. In order to realize the efficient and accurate identification of tensile or shear fracture modes in the process of rock failure, Qin et al. (2023) proposed an intelligent identification method based on the characteristics of Wigner–Ville distribution (WVD) spectrum of AE signals. A series of rock tests such as the Brazilian indirect tensile test (BITT), three-point bending test (TPBT), modified shear test (MST), and uniaxial compression test (UCT) were carried out by Du et al. (2020a), and the AE characteristics and crack classification in the process of rock fracture were also studied. In order to study the classification of fracture modes of rocks in the process of cracking, Niu et al. (2020) carried out uniaxial compression tests on intact and defective red sandstone samples, and used AE and digital image correlation (DIC) techniques for real-time monitoring and recording. Based on the newly introduced quantitative analysis of the AE waveform, Zhang et al. (2022) conducted a microscopic analysis of direct tensile failure of rocks.

The evolution mechanism of rocks (Bi et al., 2016; Chen et al., 2018; Li et al., 2019; Lu et al., 2024; Wang et al., 2018; Wang et al., 2016; Zhao et al., 2020) is an important research point to explore their essential properties. Damage mechanics is one of the main theories to explore the evolution mechanism of rocks (Chen et al., 2019; Ge et al., 2022; Li et al., 2023; Meng et al., 2020). In 1958, Kachanov was the first to introduce the concept of damage in the study of metal creep. Rabotnov generalized the concept of Kachanov and introduced the damage variable 10 years later. Until now, with the rapid development of acoustic emission technology, many rock research workers have introduced acoustic emission into damage mechanics and carried out a lot of research. Wu et al. (2021) proposed a quantitative measurement method for crack damage stress of rock materials based on AE signal detection. Lyu et al. (2024) used AE characteristic parameters to establish a damage constitutive model, which revealed that the damage evolution of salt rock showed an exponential growth trend during creep. Tian et al. (2021) used the cumulative acoustic emission energy method to obtain the damage parameter curve of rock samples during loading and analyzed the development trend of the curve in combination with the concepts of crack initiation stress and crack damage stress. Li et al. (2024) studied the anisotropic damage characteristics of Gosford sandstone samples under triaxial compression tests using various monitoring techniques such as ultrasonic velocity measurement, active acoustic emission positioning, and passive acoustic emission tomography. Cao et al. (2019) carried out uniaxial compression tests of rock samples at different loading rates and systematically analyzed the influence of strain rate on rock mechanical properties, acoustic emission parameter responses, and damage evolution law.

In summary, a large number of studies have been carried out to explore the AE precursor characteristics, failure types, and damage evolution mechanism of a certain rock. However, there is a lack of special research on rocks in a certain area. Zhongjiang County, Sichuan Province, China, is a typical hilly area, mainly dominated by red sandstone. Moreover, the research on red sandstone in Zhongjiang County is relatively rare. Therefore, this paper takes the red sandstone in Zhongjiang County, Sichuan Province, China, as the research object to explore the mechanical properties of red sandstone in Zhongjiang County. Based on the current research results, this paper explores the instability precursor information and failure types of red sandstone through acoustic emission technology. At the same time, based on the Weibull function and continuous damage mechanics, the damage evolution mechanism of red sandstone is explored. This provides a great reference for Zhongjiang County in sustainable construction planning.

2 Overview of the study area and experimental methods

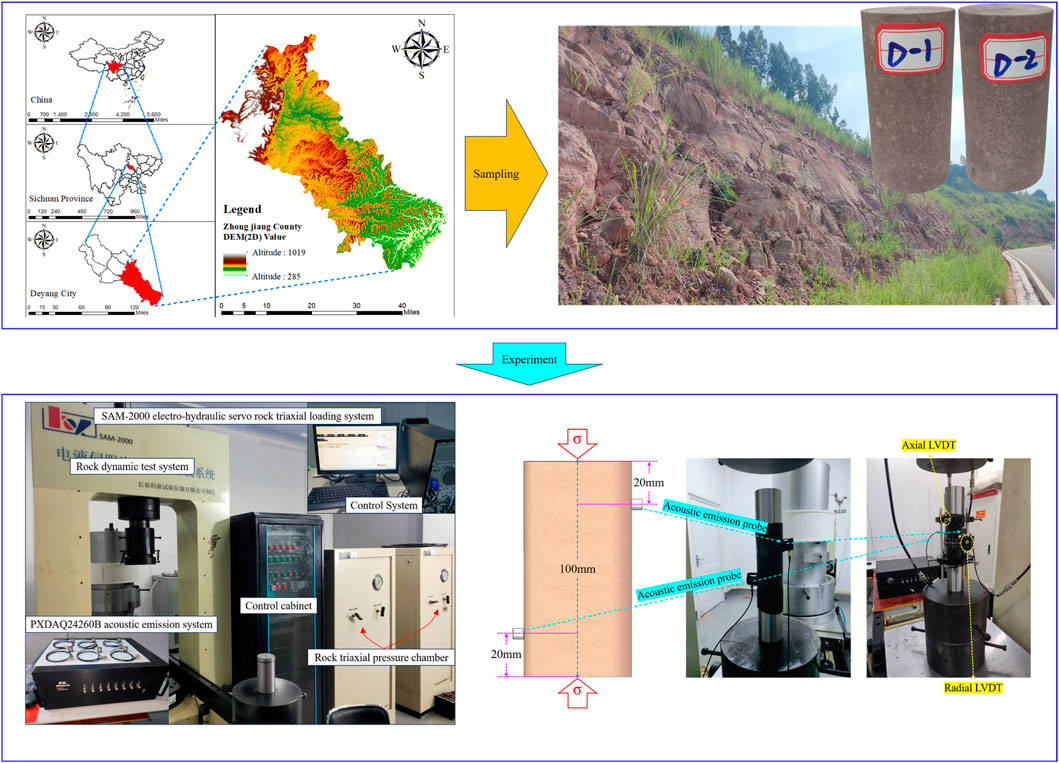
Zhongjiang County is located in the hilly area of central Sichuan Province. The geographical coordinates are 104° 26′ to 105° 15′ east longitude and 30° 31′ to 31° 17′ north latitude. The terrain in Zhongjiang County is high in the northwest and low in the southeast, with most areas consisting of hills. The altitude is generally 500–600 m, and the rest are flat dams and low mountains. Zhongjiang County is located in the subtropical monsoon humid climate zone. The average annual temperature is 16.7°C and the average annual rainfall is 882.5 mm. The county covers an area of 2,200 square kilometers, with 30 townships, 436 administrative villages, 86 communities, and a permanent population of 948,000. In terms of water conservancy projects, there are 18,842 water storage projects in Zhongjiang County, with a total water storage of 203 million cubic meters. Among them, there are 5 medium-sized reservoirs, 62 small reservoirs, 14,503 Shanpingtang, 1,331 Shihe Weir, and 2,941 water storage tank. The mineral resources that have been explored in Zhongjiang County mainly include natural gas, oil, salt, mineral water, copper mine, shale, and clay. The data on natural conditions such as topography and climate in the above study area are derived from the Geospatial Data Cloud (Geospatial Data Cloud, 2024) and the China Meteorological Administration (China Meteorological Administration, 2024).

In this paper, the red sandstone in Zhongjiang County is used as the experimental object. The red sandstone specimen is a standard cylinder specimen specified by the International Society of Rock Mechanics. Its height is 100 mm, and its diameter is 50 mm. The length error of all samples is less than 2 mm. The unevenness of the two ends after grinding is ±0.05 mm. The end face is perpendicular to the axis, and the maximum deviation is not more than 0.25°. The equipment used in the mechanical experiment is the SAM-2000 electro-hydraulic servo rock triaxial loading system and PXDAQ24260 B acoustic emission system. The sample numbers of the uniaxial compression experiment are D-1 and D-2. The loading method of the experiment is displacement control, and the loading rate is 0.05 mm/min. During uniaxial compression, damage monitoring is performed by an acoustic emission system (Li et al., 2022). By monitoring the environmental noise, the maximum environmental noise in the laboratory is 35 db. Therefore, in order to improve the accuracy of acoustic emission monitoring, the threshold value is set to 45 db. The sampling rate is set to 1.25 M. The peak definition time (PDT) was set to 50 μs The end definition time (HDT) was set to 100 μs The system locking time (HLT) was set to 300 μs The maximum duration of the waveform was set to 100 ms. Two acoustic emission probes were used in the acoustic emission experiment, and the probes were fixed using the insulating tape. The coupling agent between the probe and the sample is lithium grease. The details are shown in Figure 1.

Figure 1

Figure 1. Study area and experimental overview.

3 Results and discussion

3.1 AE precursor characteristics of red sandstone failure instability

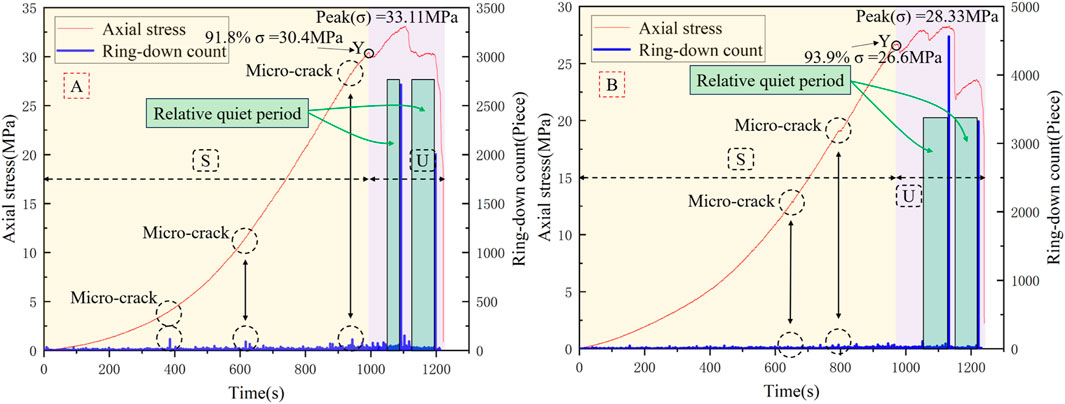
The evolution law of stress and acoustic emission ringing count of red sandstone under the uniaxial compression load is shown in Figure 2. It can be observed from Figure 2 that the damage stage of red sandstone can be divided into two parts: damage stable development stage (S) and damage unstable development stage (U). The two parts take the Y point as the dividing point. After the Y point, the stress appears as a V-shaped evolution phenomenon. This shows that the damage evolution process of red sandstone enters the unstable stage from the stable stage. When the red sandstone reaches its peak strength, the ringing count appears at the peak point. In addition, near the peak intensity, the ringing count is relatively low, and this response characteristic is called the relative quiet period phenomenon (Su G. S. et al., 2024). In the post-peak residual stage, the ringing count also showed a significant relative quiet period before the sample was completely destroyed. This is the AE precursor information of the instability failure of red sandstone. Before the Y point, the fluctuation range of the ringing count is small, the red sandstone is mainly elastic deformation, and the phenomenon of micro-crack development is not obvious. This shows that before the Y point, red sandstone will contain a significant amount of elastic energy. When the red sandstone reaches the ultimate bearing capacity, the elastic energy will be released sharply in a short time, and the brittle fracture failure characteristics will appear. The ratio of axial stress to peak stress at the Y point of red sandstone is equal to 92.9%, as calculated by the mean calculation method. Therefore, when the axial stress reaches 92.9% of the peak strength of red sandstone, the damage stage changes from the stable development stage (S) to the unstable development stage (U).

Figure 2

Figure 2. Time-stress-ringing count evolution characteristics: (A) D-1 and (B) D-2.

3.2 Evolution characteristics of red sandstone failure types

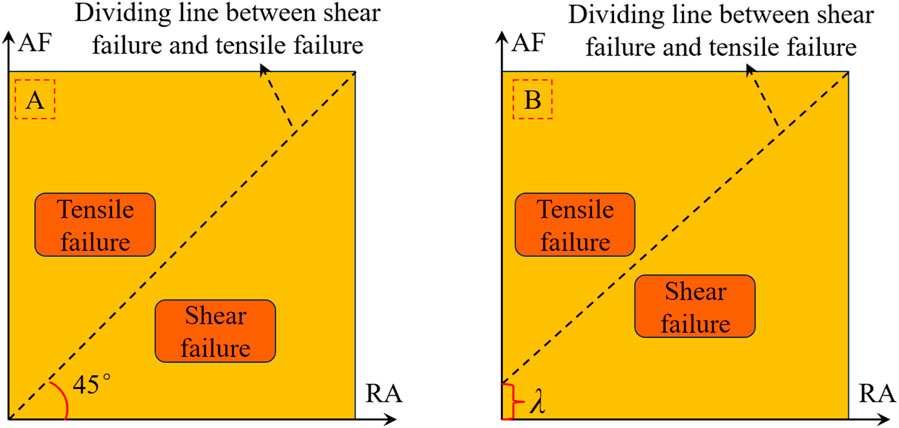
In Section 3.1, the damage stages of red sandstone are divided based on the evolution law of the stress–strain curve. In this section, we will conduct a more detailed exploration of the damage stage and failure type of red sandstone through acoustic emission characteristics. Figure 3 shows the macroscopic failure characteristics of red sandstone samples. It is very important to understand the evolution characteristics of failure types of red sandstone in the process of damage evolution. In this section, the damage type of red sandstone is explored by the acoustic emission parameter Ф (AF (ringing count/duration)/RA (rise time/amplitude) ). At present, there are two main methods to classify rock failure types using the RA-AF diagram (Du et al., 2020b), as shown in Table 1.

Figure 3

Figure 3. Macroscopic rupture characteristics: (A) D-1 and (B) D-2.

Table 1

Table 1. Classification method of rock failure types.

Figure 4

Figure 4. Classification method of rock failure type: (A) first method and (B) second method.

The abovementioned two methods define the area larger than Ф as tensile failure and the area smaller than Ф as shear failure. In this paper, the first method is adopted, and the 45° inclined line is taken as the dividing line. The region with Ф > 1 is defined as tensile failure, and the region with Ф < 1 is defined as shear failure.

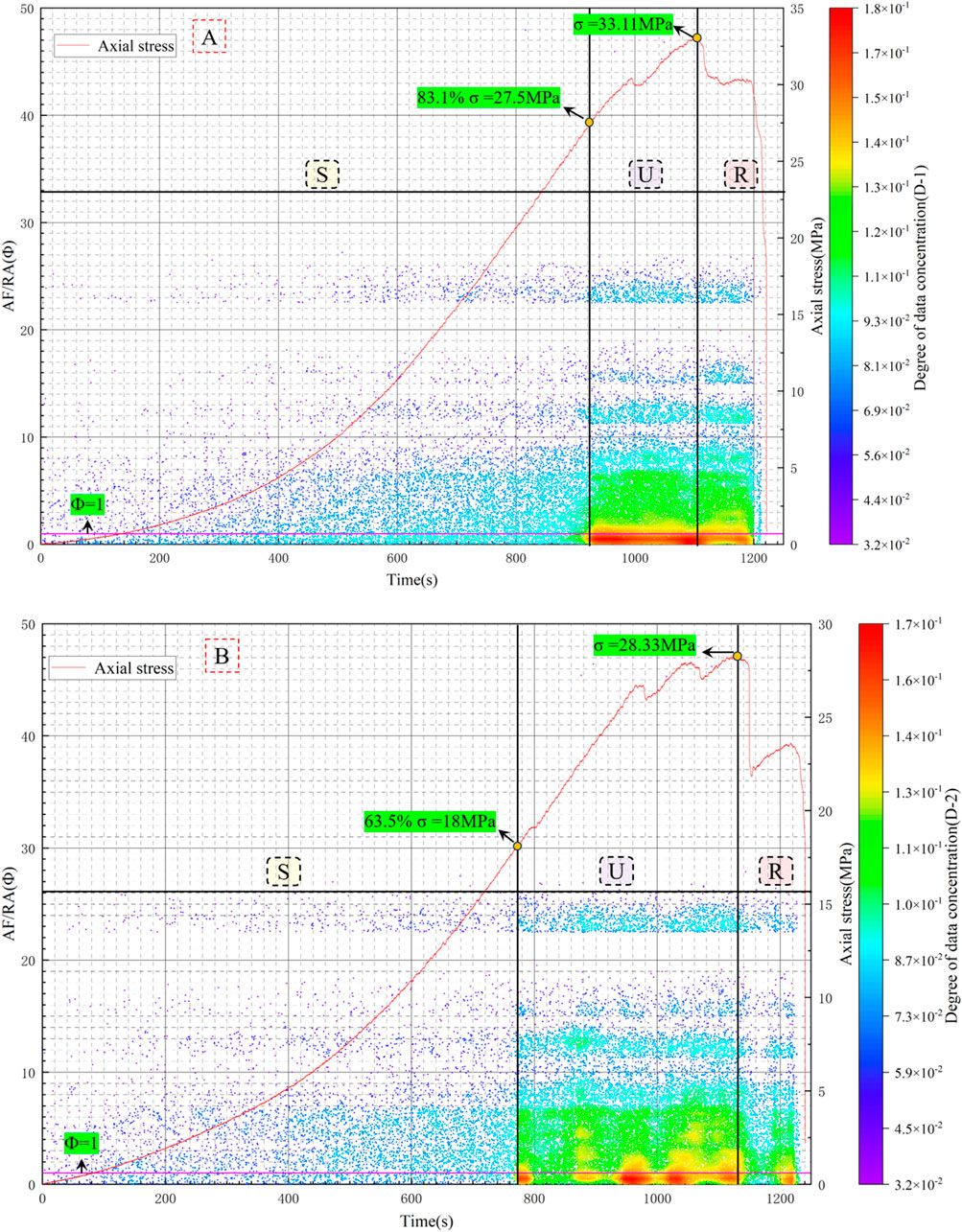
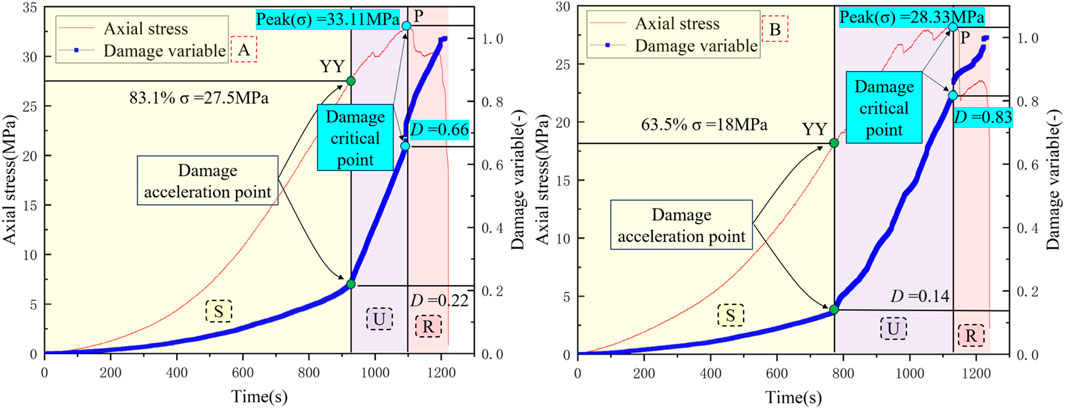
It can be observed from Figure 5 that the damage stage of red sandstone can be divided into the following: the damage stable development stage (S), the damage unstable development stage (U), and the damage rapid development stage (R) according to the evolution process of data distribution degree of Ф value. By exploring D-1, it can be observed that when the axial stress reaches 83.1% of the peak strength, the damage stage changes from the damage stable development stage (S) to the damage unstable development stage (U). When the axial stress reaches the peak strength, the damage stage changes from the damage unstable development stage (U) to the damage rapid development stage (R). By exploring D-2, it can be observed that when the axial stress reaches 63.5% of the peak strength, the damage stage changes from the damage stable development stage (S) to the damage unstable development stage (U). When the axial stress reaches the peak strength, the damage stage changes from the damage unstable development stage (U) to the damage rapid development stage (R). According to the mean value method, the boundary point between the S and U stages is 73.3% of the peak stress of red sandstone, and the boundary point between the U and R stages is the peak stress of red sandstone. In the damage stable development stage (S), there is no high concentration of data in the Ф value, and the damage development stage is relatively stable. In the unstable damage development stage (U), there is a high concentration of data in the Ф < 1 region. This shows that the red sandstone is dominated by shear failure at this stage. In the rapid damage development stage (R), the data in the Ф < 1 region are still highly concentrated, but the degree of data concentration is generally lower than that in the U stage. This shows that the red sandstone is still dominated by shear failure at this stage, but the extent of shear failure is decreasing.

Figure 5

Figure 5. Distribution characteristics of failure types: (A) D-1 and (B) D-2.

It can be observed from Figures 4, 5 that in the U and R stages, when the integrity of the data concentration phenomenon in the Ф < 1 region is good, the macroscopic fracture characteristics of the red sandstone sample show a single penetrating crack. When the integrity of the data concentration phenomenon in the Ф < 1 region is poor, the macroscopic fracture characteristics of the red sandstone sample show a serrated penetrating crack. It can be observed from Figure 5 that the samples are in a composite fracture state during the whole experiment. This shows that red sandstone is a highly heterogeneous material with micro-cracks. When red sandstone is subjected to compression, the propagation and interaction of micro-cracks result in a composite fracture pattern in the final fracture morphology (see Figure 4).

3.3 Damage evolution model of red sandstone

Constructing a mathematical model of rock damage evolution law is an important method for quantitatively evaluating rock instability and failure. The core of constructing the mathematical model is how to define the damage variable. At present, the definition of damage variable mainly includes dissipation energy/total energy, damage area/apparent area, and elastic modulus/initial elastic modulus. Regardless of the method used to define the damage variable, it is necessary to follow the following assumptions: the rock is a homogeneous, isotropic continuum; the damage deformation of rock is a continuous failure, and the assumption is suitable for all mesoscopic units. The distribution of rock structural units conforms to the distribution law of the Weibull function. The Weibull distribution function is as follows:

$F\left(x;k,m\right)=\left\{\begin{array}{l}\frac{m}{k}{\left(\frac{x}{k}\right)}^{m-1}\mathit{exp}\left[-{\left(x/k\right)}^m\right]x>0\\ 0x\le 0\end{array}\right..(1)$

In Formula 1, $x$ is the red sandstone strain, $k$ is the proportional parameter, and $m$ is the Weibull modulus.

It is assumed that the rock is composed of several identical mesoscopic units. A mesoscopic unit rupture corresponds to a ringing count. Therefore, when the rock strain reaches $x$, the number of ruptures of the mesoscopic unit can be expressed by the cumulative ringing count ($N_{AE}\left(x\right)$). The number of meso-unit ruptures during rock failure can be expressed by the cumulative ringing count ($N_{AE}$). Therefore, based on continuous damage mechanics, the damage variable can be expressed as follows:

$D=\frac{N_{AE}\left(x\right)}{N_{AE}}.(2)$

The continuity factor ($\phi$) can be expressed as follows:

$\phi =1-D.(3)$

When the strain of rocks changes from 0 to $x$, the fracture number of rock meso-units can be expressed as follows:

$\begin{array}{l}{N}_{AE}\left(x\right)=N_{AE}{\int }_0^{x}F\left(x;k,m\right)dx\\ =N_{AE}\left\{1-\mathit{exp}\left[-{\left(x/k\right)}^m\right]\right\}\end{array}.(4)$

Combining Formulas 2–4, the expression of damage variable D is obtained as follows:

$D=1-\mathit{exp}\left[-{\left(x/k\right)}^m\right].(5)$

It is assumed that the mechanical properties of rock materials satisfy Hooke‘s law under the uniaxial compression load. The axial stress–strain relationship of rock materials can be expressed as follows:

$\sigma =E\left(1-D\right)\epsilon .(6)$

In Formula 6, $\sigma$ is the axial stress, $\epsilon$ is the axial strain, and $E$ is the initial elastic modulus.

Combining Formulas 5, 6, the following expression of axial stress–strain of the rock material under the uniaxial compression load is obtained:

$\sigma =E\left(\mathit{exp}\left[-{\left(x/k\right)}^m\right]\right)\epsilon .(7)$

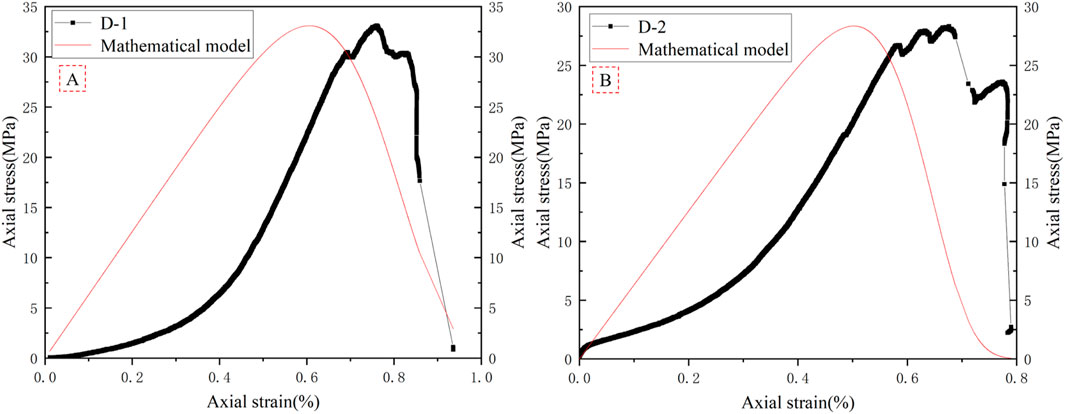
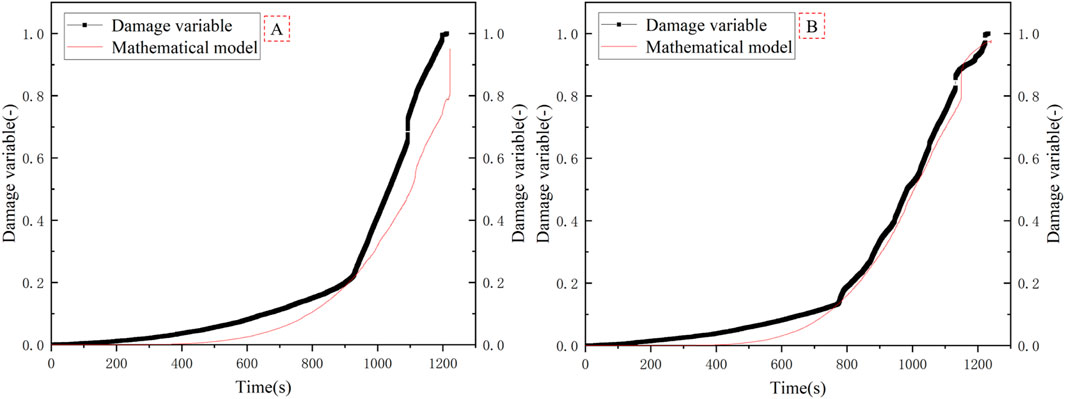
Based on the ringing counting parameters, the damage evolution characteristics of red sandstone are obtained. The practical application results of Formula 7 are obtained (see Figure 8). In the mathematical calculation, the initial elastic modulus calculated by the secant method is 6.3 GPa. Based on Figure 6, the damage variable value of the red sandstone damage boundary point is calculated by the mean value calculation method. When D < 0.18, the red sandstone is in the damage stable development stage (S). When 0.18 < D < 0.75, the red sandstone is in the damage unstable development stage (U). When 0.75 < D < 1.0, the red sandstone is in the damage rapid development stage (R). Therefore, the point D = 0.18 is defined as the damage acceleration point (YY). The point D = 0.75 is defined as the damage critical point (P). At this time, the average value of the axial stress ratio corresponding to the YY point is 73.3%, and the axial stress corresponding to the P point is the peak stress. The abovementioned results are the same as those obtained in Section 3.2. This shows that the abovementioned damage variables can well-characterize the damage evolution characteristics of red sandstone. Compared with the damage stage described in Section 3.1, the damage stage divided by acoustic emission characteristic parameters is more detailed. Moreover, the axial stress value of the YY point is lower than that of the Y point, which provides more decision-making time for predicting the instability and failure of red sandstone in advance. Furthermore, it can be observed from Figure 7 that the abovementioned damage model can better characterize the damage evolution process of red sandstone.

Figure 8

Figure 8. Evolution results of stress–strain model: (A) D-1 and (B) D-2.

Figure 6

Figure 6. Damage evolution characteristics: (A) D-1 and (B) D-2.

Figure 7

Figure 7. Damage model evolution results: (A) D-1 and (B) D-2.

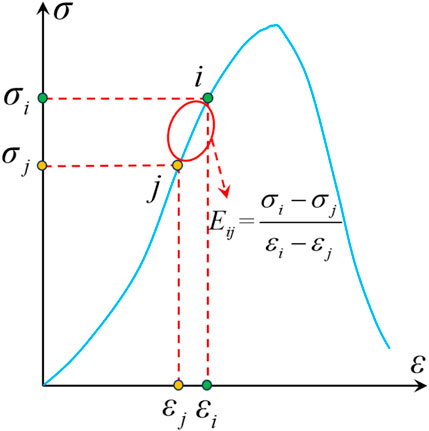
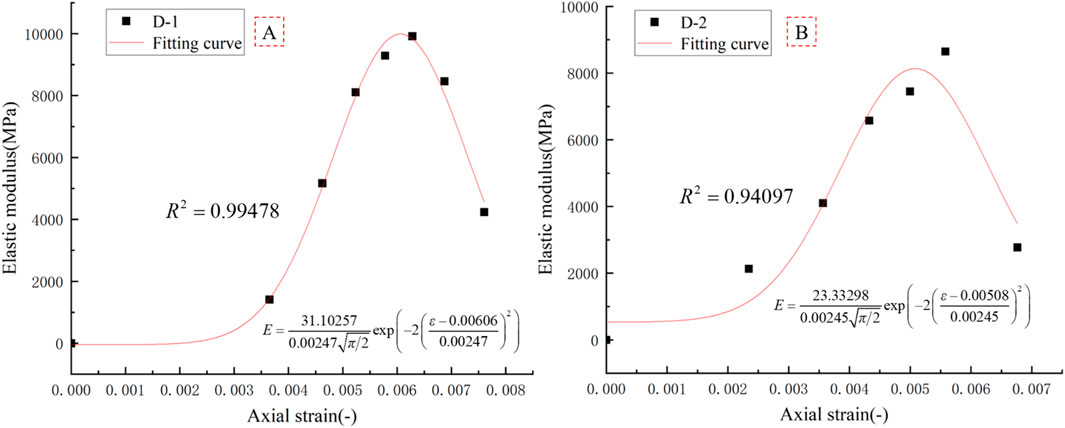
It can be observed from Figure 8 that when the value of E is the initial elastic modulus of red sandstone, the linear evolution law appears in the initial stage of the mathematical model calculation results. This is obviously inconsistent with the actual evolution law of red sandstone. This is mainly due to the fact that the E value of red sandstone is constantly changing during the stress process. However, in the calculation, E is usually set to a fixed value, which is the main factor leading to a large deviation in the calculation results. In order to explore the variation law of the E value, in this paper, we use the piecewise calculation method to calculate the E value of red sandstone (see Figure 9). The calculation method is shown in Formula 8. Using Formula 8, the evolution law of the E value of D-1 and D-2 is obtained, as shown in Figure 10.

$E_{ij}=\frac{{\sigma }_i-{\sigma }_j}{{\epsilon }_i-{\epsilon }_j}.(8)$

In Formula 8, $E_{ij}$ is the elastic modulus between i and j, ${\sigma }_i$ is the axial stress at i, ${\sigma }_j$ is the axial stress at j, ${\epsilon }_i$ is the axial strain at i, and ${\epsilon }_j$ is the axial strain at j.

Figure 9

Figure 9. Segmented calculation method.

Figure 10

Figure 10. Fitting results: (A) D-1 and (B) D-2.

It can be observed from Figure 10 that the evolution law of the E value of red sandstone samples conforms to the distribution law of the Gauss function. The expression is as follows:

$E=\frac{A}{W\sqrt{\pi /2}}\mathit{exp}\left(-2{\left(\frac{\epsilon -\chi }{W}\right)}^2\right).(9)$

Substituting Formula 9 into Formula 7, the expression of axial stress–strain of red sandstone can be obtained.

$\sigma =\frac{A}{W\sqrt{\pi /2}}\mathit{exp}\left(-2{\left(\frac{\epsilon -\chi }{W}\right)}^2\right)\left(\mathit{exp}\left[-{\left(x/k\right)}^m\right]\right)\epsilon .(10)$

In this formula, $A$, $W$, and $\chi$ are the fitting parameters.

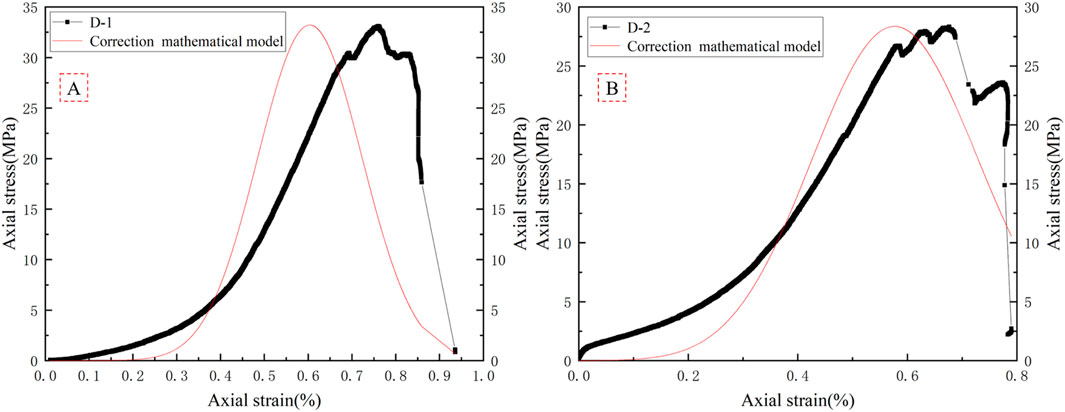
Formula 10 is applied in the actual application, and the modified stress–strain evolution process is obtained (see Figure 11). It can be observed from Figure 11 that the calculation results of the modified mathematical model change from a linear evolution law to a nonlinear evolution law, aligning more closely with the deformation behavior of red sandstone. This shows that Gauss function combined with the Weibull distribution function and Hooke‘s law can better represent the stress–strain behavior of red sandstone.

Figure 11

Figure 11. Evolution results of the modified stress–strain model: (A) D-1 and (B) D-2.

4 Conclusion

In this paper, the damage evolution characteristics of red sandstone in Zhongjiang County under the uniaxial compression load are explored by the acoustic emission monitoring system. The main results are as follows:

1. Through the stress–strain evolution law, the damage stage of red sandstone is divided into two parts: damage stable development stage (S) and damage unstable development stage (U). Furthermore, the Y point (axial stress = 92.9% σ) is the demarcation point. After the Y point, the stress appears as a V-shaped evolution phenomenon. This shows that the damage evolution process of red sandstone enters the unstable stage from the stable stage. When the red sandstone reaches its peak strength, the ringing count appears at the peak point. In addition, near the peak intensity, the ringing count appears as a relatively quiet period phenomenon. This is the precursor information of red sandstone instability failure.

2. According to the evolution process of the data distribution degree of the Ф value, the damage stage of the red sandstone is divided into the damage stable development stage (S), the damage unstable development stage (U), and the damage rapid development stage (R). The boundary point between the S and U stages is 73.3% of the peak stress of red sandstone, and the boundary point between the U and R stages is the peak stress of red sandstone. In the S stage, the damage development is relatively stable. In the U stage, the red sandstone is dominated by shear failure. In the R stage, the red sandstone is still dominated by shear failure, but the extent of shear failure is decreasing. In the U and R stages, when the integrity of the data concentration phenomenon in the Ф < 1 region is good, the macroscopic fracture characteristics of the red sandstone sample show a single penetrating crack. When the integrity of the data concentration phenomenon in the Ф < 1 region is poor, the macroscopic fracture characteristics of the red sandstone sample show a serrated penetrating crack.

3. The damage variable is characterized by the acoustic emission parameter ringing count. Based on the Weibull function and continuous damage mechanics, the damage mathematical model and stress–strain mathematical model of red sandstone are derived. The stress–strain mathematical model of red sandstone in Zhongjiang County was modified by introducing the Gauss function. Based on the evolution law of damage variables, the damage evolution characteristics of red sandstone are quantitatively characterized. When D < 0.18, the red sandstone is in the damage stable development stage (S). When 0.18 < D < 0.75, the red sandstone is in the damage unstable development stage (U). When 0.75 < D < 1.0, the red sandstone is in the damage rapid development stage (R). The point D = 0.18 is defined as the damage acceleration point (YY). The point D = 0.75 is defined as the damage critical point (P). At this time, the average value of the axial stress ratio corresponding to the YY point is 73.3% and the axial stress corresponding to the P point is the peak stress.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

AL: Writing–review and editing. WZ: Writing–original draft. CY: Writing–review and editing. XZ: Writing–review and editing. TL: Writing–review and editing. ZF: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Key Project of Xihua University [grant number Z201036], the Chengdu Agricultural College-Level Scientific Research Project [grant numbers 22zr213 and 22zr113], the Sichuan Province Key Laboratory of Higher Education Institutions for Comprehensive Development and Utilization of Industrial Solid Waste in Civil Engineering [grant number SC_FQWLY-2021-Y-11], the Key Laboratory of Intelligent Emergency Management [grant number 2024ZHYJGL-15], and the Japan Emergency Management Research Center of China [grant no. 2024RBYJGL-9].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1484633/full#supplementary-material

References

Bi, J., Zhao, Y., Wu, Z. J., Li, J. S., and Wang, C. L. (2024). Research on crack classification method and failure precursor index based on RA-AF value of brittle rock. Theor. Appl. Fract. Mec. 129, 104179. doi:10.1016/j.tafmec.2023.104179

CrossRef Full Text | Google Scholar

Bi, J., Zhou, X. P., and Qian, Q. H. (2016). The 3D numerical simulation for the propagation process of multiple pre-existing flaws in rock-like materials subjected to biaxial compressive loads. Rock Mech. Rock Eng. 49, 1611–1627. doi:10.1007/s00603-015-0867-y

CrossRef Full Text | Google Scholar

Cao, A., Jing, G., Ding, Y. L., and Liu, S. (2019). Mining-induced static and dynamic loading rate effect on rock damage and acoustic emission characteristic under uniaxial compression. Saf. Sci. 116, 86–96. doi:10.1016/j.ssci.2019.03.003

CrossRef Full Text | Google Scholar

Chen, S., Qiao, C., Ye, Q., and Khan, M. U. (2018). Comparative study on three-dimensional statistical damage constitutive modified model of rock based on power function and Weibull distribution. Environ. Earth Sci. 77, 108. doi:10.1007/s12665-018-7297-6

CrossRef Full Text | Google Scholar

Chen, Z., He, C., Ma, G., Xu, G., and Ma, C. (2019). Energy damage evolution mechanism of rock and its application to brittleness evaluation. Rock Mech. Rock Eng. 52, 1265–1274. doi:10.1007/s00603-018-1681-0

CrossRef Full Text | Google Scholar

China Meteorological Administration (2024). China meteorological administration. Available at: https://weather.cma.cn/ (Accessed August 18, 2024).

Google Scholar

Cui, Y. (2019). Effect of joint type on the shear behavior of synthetic rock. Bull. Eng. Geol. Environ. 78, 3395–3412. doi:10.1007/s10064-018-1325-3

CrossRef Full Text | Google Scholar

Dong, L. J., Chen, Y. C., Sun, D. Y., and Zhang, Y. H. (2021). Implications for rock instability precursors and principal stress direction from rock acoustic experiments. Int. J. Min. Sci. Techno 31, 789–798. doi:10.1016/j.ijmst.2021.06.006

CrossRef Full Text | Google Scholar

Du, K., Li, X., Tao, M., and Wang, S. (2020a). Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock Mech. Min. 133, 104411. doi:10.1016/j.ijrmms.2020.104411

CrossRef Full Text | Google Scholar

Du, K., Li, X. F., Tao, M., and Wang, S. F. (2020b). Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock Mech. Min. 133, 104411. doi:10.1016/j.ijrmms.2020.104411

CrossRef Full Text | Google Scholar

Du, K., Luo, X., Liu, M., Liu, X., and Zhou, J. (2024). Understanding the evolution mechanism and classification criteria of tensile -shear cracks in rock failure process from acoustic emission (AE) characteristics. Eng. Fract. Mech. 296, 109864. doi:10.1016/j.engfracmech.2024.109864

CrossRef Full Text | Google Scholar

Fathipour-Azar, H. (2022). New interpretable shear strength criterion for rock joints. Acta Geotech. 17, 1327–1341. doi:10.1007/s11440-021-01442-z

CrossRef Full Text | Google Scholar

Ge, X., Xiao, Y., Fan, Y., Liu, J., and Zhang, Y. (2020). Laboratory investigation of the relationship between static rock elastic parameters and low field nuclear magnetic resonance data. Int. J. Rock Mech. Min. 127, 104207. doi:10.1016/j.ijrmms.2019.104207

CrossRef Full Text | Google Scholar

Ge, Y., Zhang, C., Ren, G., and Zhang, L. (2022). Experimental investigation of the mechanical behavior and damage evolution mechanism of oil-impregnated gypsum rock. Sustainability 14, 11172. doi:10.3390/su141811172

CrossRef Full Text | Google Scholar

Geospatial Data Cloud (2024). Geospatial data Cloud. Available at: https://www.gscloud.cn/ (Accessed August 18, 2024).

Google Scholar

He, S. Q., Qin, M. L., Qiu, L. M., Song, D. Z., and Zhang, X. F. (2022). Early warning of coal dynamic disaster by precursor of AE and EMR quiet period. Int. J. Coal Sci. Techn 9, 46. doi:10.1007/s40789-022-00514-z

CrossRef Full Text | Google Scholar

Li, G., Sun, Q., Ma, F., Guo, J., Zhao, H., and Wu, Y. (2023). Damage evolution mechanism and deformation failure properties of a roadway in deep inclined rock strata. Eng. Fail Anal. 143, 106820. doi:10.1016/j.engfailanal.2022.106820

CrossRef Full Text | Google Scholar

Li, H., Yang, J., Han, Y., Yang, C., Daemen, J. J. K., and Li, P. (2019). Weibull grain-based model (W-GBM) for simulating heterogeneous mechanical characteristics of salt rock. Eng. Analysis Bound. Elem. 108, 227–243. doi:10.1016/j.enganabound.2019.09.001

CrossRef Full Text | Google Scholar

Li, T., Zhang, X., Shu, Z., and Zhong, W. (2022). Modified model of sound velocity with different saturation in fractured sandstone. Sci. Adv. Mater. 14, 985–1000. doi:10.1166/sam.2022.4281

CrossRef Full Text | Google Scholar

Li, X., Si, G., Cao, A., Wang, C., Oh, J., Zhang, Z., et al. (2024). Rock anisotropic damage characterisation and its evolution model by integrating acoustic emission tomography and ultrasonic monitoring. Int. J. Rock Mech. Min. 180, 105817. doi:10.1016/j.ijrmms.2024.105817

CrossRef Full Text | Google Scholar

Liu, X. H., Xue, Y., Zheng, Y., and Li, H. Y. (2022). Research on failure precursor based on characteristics of energy dissipation rate for rock. Front. Earth Sc-Switz 9. doi:10.3389/feart.2021.812438

CrossRef Full Text | Google Scholar

Lu, T., Wu, H., Yin, S., and Xu, X. (2024). Study of rock damage constitutive model considering temperature effect based on Weibull distribution. Appl. Sciences-Basel 14, 3766. doi:10.3390/app14093766

CrossRef Full Text | Google Scholar

Lyu, C., Ma, C., Dai, H., Zhou, P., Xu, D., Liang, C., et al. (2024). A creep model for salt rock considering damage during creep. Mech. Time-Dependent Mater. 28, 255–272. doi:10.1007/s11043-023-09648-2

CrossRef Full Text | Google Scholar

Meng, N., Bai, J., Chen, Y., Wang, X., Wu, W., Wu, B., et al. (2020). Damage evolution mechanisms of rock induced by blasting with the aid of empty-hole effect. Energies 13, 756. doi:10.3390/en13030756

CrossRef Full Text | Google Scholar

Niu, Y., Zhou, X. P., and Berto, F. (2020). Evaluation of fracture mode classification in flawed red sandstone under uniaxial compression. Theor. Appl. Fract. Mec. 107, 102528. doi:10.1016/j.tafmec.2020.102528

CrossRef Full Text | Google Scholar

Park, D. (2023). Influence of the Hoek-Brown failure criterion with tensile strength cut-off on the roof stability in deep rock tunnels. Tunn. Undergr. Space Technol. 136, 105016. doi:10.1016/j.tust.2023.105016

CrossRef Full Text | Google Scholar

Qin, Z. X., Chen, X. J., Yan, Y. F., Liu, Z. H., and Wang, Z. F. (2023). A SVM-based method for identifying fracture modes of rock using WVD spectrogram features of AE signals. Front. Earth Sc-Switz 11. doi:10.3389/feart.2023.1206269

CrossRef Full Text | Google Scholar

Su, G., Huang, L., Qin, Y., and Yan, X. (2024a). Experimental study of the “AE quiet period” on the eve of brittle failure in hard rock. Eng. Fail Anal. 162, 108391. doi:10.1016/j.engfailanal.2024.108391

CrossRef Full Text | Google Scholar

Su, G. S., Gan, W., Zhai, S. B., and Zhao, G. F. (2020). Acoustic emission precursors of static and dynamic instability for coarse-grained hard rock. J. Cent. South Univ. 27, 2883–2898. doi:10.1007/s11771-020-4516-6

CrossRef Full Text | Google Scholar

Su, G. S., Huang, L., Qin, Y. Z., and Yan, X. Y. (2024b). Experimental study of the AE quiet period on the eve of brittle failure in hard rock. Eng. Fail Anal. 162, 108391. doi:10.1016/j.engfailanal.2024.108391

CrossRef Full Text | Google Scholar

Sun, X., Li, X., Zheng, B., He, J., and Mao, T. (2020). Study on the progressive fracturing in soil and rock mixture under uniaxial compression conditions by CT scanning. Eng. Geol. 279, 105884. doi:10.1016/j.enggeo.2020.105884

CrossRef Full Text | Google Scholar

Sun, Z., Wang, B., Li, Y., Xu, J., and Ji, J. (2023). 3D limit analysis of rock slopes based on equivalent linear failure criterion with tension cut-off. J. Rock Mech. Geotechnical Eng. 15, 3118–3130. doi:10.1016/j.jrmge.2023.02.009

CrossRef Full Text | Google Scholar

Tian, Y., Yu, R., Zhang, Y., and Zhao, X. (2021). Research on damage evolution of deep formation rock based on acoustic emission test. Int. J. Damage Mech. 30, 145–159. doi:10.1177/1056789520957381

CrossRef Full Text | Google Scholar

Wang, Y., Zhou, X., Wang, Y., and Shou, Y. (2018). A 3-D conjugated bond-pair-based peridynamic formulation for initiation and propagation of cracks in brittle solids. Int. J. Solids Struct. 134, 89–115. doi:10.1016/j.ijsolstr.2017.10.022

CrossRef Full Text | Google Scholar

Wang, Y., Zhou, X., and Xu, X. (2016). Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics. Eng. Fract. Mech. 163, 248–273. doi:10.1016/j.engfracmech.2016.06.013

CrossRef Full Text | Google Scholar

Wu, C., Gong, F., and Luo, Y. (2021). A new quantitative method to identify the crack damage stress of rock using AE detection parameters. Bull. Eng. Geol. Environ. 80, 519–531. doi:10.1007/s10064-020-01932-6

CrossRef Full Text | Google Scholar

Xiong, Q., Lin, Q., Gao, Y., and Hampton, J. C. (2022). Fundamental physics distinguishes the initial stage acoustic emission (AE) behavior between compressive and fracture toughness tests in rock. Eng. Fract. Mech. 275, 108829. doi:10.1016/j.engfracmech.2022.108829

CrossRef Full Text | Google Scholar

Xu, J., Haque, A., Gong, W., Gamage, R. P., Dai, G., Zhang, Q., et al. (2020). Experimental study on the bearing mechanisms of rock-socketed piles in soft rock based on micro X-ray CT analysis. Rock Mech. Rock Eng. 53, 3395–3416. doi:10.1007/s00603-020-02121-3

CrossRef Full Text | Google Scholar

Xu, Y., Li, X., Wu, X., Zheng, W., Zhou, B., and Tong, J. (2022). Experimental study on pore fluid characteristics of fractured sandstone based on nuclear magnetic resonance technology. J. Petroleum Sci. Eng. 214, 110408. doi:10.1016/j.petrol.2022.110408

CrossRef Full Text | Google Scholar

Zhang, J.-Z., Zhou, X.-P., Zhou, L.-S., and Berto, F. (2019). Progressive failure of brittle rocks with non-isometric flaws: insights from acousto-optic-mechanical (AOM) data. Fatigue and Fract. Eng. Mater. and Struct. 42, 1787–1802. doi:10.1111/ffe.13019

CrossRef Full Text | Google Scholar

Zhang, Z., Ma, K., Li, H., and He, Z. (2022). Microscopic investigation of rock direct tensile failure based on statistical analysis of acoustic emission waveforms. Rock Mech. Rock Eng. 55, 2445–2458. doi:10.1007/s00603-022-02788-w

CrossRef Full Text | Google Scholar

Zhao, Y., Bi, J., Wang, C., and Liu, P. (2021). Effect of unloading rate on the mechanical behavior and fracture characteristics of sandstones under complex triaxial stress conditions. Rock Mech. Rock Eng. 54, 4851–4866. doi:10.1007/s00603-021-02515-x

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, C. L., and Bi, J. (2020). Analysis of fractured rock permeability evolution under unloading conditions by the model of elastoplastic contact between rough surfaces. Rock Mech. Rock Eng. 53, 5795–5808. doi:10.1007/s00603-020-02224-x

CrossRef Full Text | Google Scholar

Zhou, X.-P., Wang, Y.-T., Zhang, J.-Z., and Liu, F.-N. (2019). Fracturing behavior study of three-flawed specimens by uniaxial compression and 3D digital image correlation: sensitivity to brittleness. Rock Mech. Rock Eng. 52, 691–718. doi:10.1007/s00603-018-1600-4

CrossRef Full Text | Google Scholar