A method for calculating saturation in tight sandstone reservoirs based on the dual porosity model

Introduction: With the continuous development of exploration and development, tight sandstone reservoirs have become an essential field of oil and gas exploration. The tight sandstone reservoirs are characterized by complex lithology, poor pore structure, and strong heterogeneity, which bring great difficulties to formation evaluation by well logs. Especially, the accuracy of the Archie formula for calculating the water saturation of tight sandstone reservoirs containing fractures is not high, saturation evaluation faces greater challenges. Therefore, how to calculate the saturation of tight sandstone reservoirs more accurately is an urgent problem to be solved.

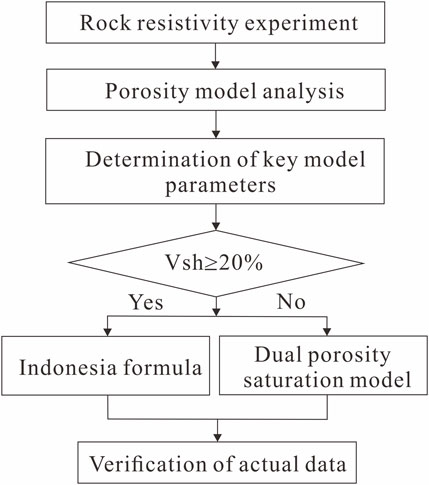
Methods: In this paper, the tight sandstone reservoirs of the Jurassic Ahe Formation in the Tarim Basin were taken as the research area. A saturation model that combines the effects of shale and fractures was proposed. Specifically, if the shale content is more than 20%, the Indonesian formula is used to calculate the saturation. If the shale content is less than 20%, the dual porosity model is adopted. Based on the rock resistivity and nuclear magnetic resonance (NMR) experiment results, the porosity and T₂ logarithmic mean values are selected as influencing factors to calculate the key parameters of the dual porosity model.

Results and Discussion: The saturation of tight sandstone reservoirs in the Jurassic Ahe Formation of the Tarim Basin is calculated through the method proposed in this paper. The case study shows that the accuracy of the proposed method is higher than that of the Archie model. The method proposed in this paper demonstrates excellent adaptability in the quantitative evaluation of saturation for tight sandstone reservoirs.

1 Introduction

Tight sandstones generally refer to sandstones with a permeability of less than 0.1 mD and a porosity of less than 10% (Gao and Li, 2016). With the continuous development of exploration and development, tight sandstone reservoirs have become an essential field of oil and gas exploration (Dai et al., 2012; Zou et al., 2012). Tight sandstone reservoirs are characterized by tight lithology, complex pore structure and firm heterogeneity (Rezaee et al., 2012; Desbbois et al., 2011; Lai et al., 2015). As a result, the accuracy of the Archie formula for calculating the water saturation of tight sandstone reservoirs is not high (Li et al., 2020; Hu et al., 2017; Feng et al., 2023). In addition, the Archie formula is not applicable to formations with high shale content (Zhang et al., 2023; Zhao et al., 2023; Vincent and wladyslaw, 2015). Therefore, how to calculate the saturation of tight sandstone reservoirs more accurately is an urgent problem to be solved.

Shale has a significant influence on the reservoir performance of tight sandstone reservoirs. When the reservoirs contain shale, the reservoirs’ resistivity will be reduced, and the accuracy of the traditional method for calculating saturation will also decrease (Feng et al., 2021). There are many saturation models involving the influence of shale. The Simandoux formula (Simandoux, 1963) and the Indonesia formula (Leveaux and Poupon, 1971) apply to shale sandstones. With the development of the dual layer theory, the W-S model (Waxman and Smits, 1968) was developed for shaly sandstones or low-resistivity reservoirs. Clavier et al. (1984) proposed that clay water and free water in argillaceous sandstone conduct electricity in parallel, and they proposed the D-W model. Silva and Bassiouni (1986) investigated the influence of matrix and pore structure on shaly sandstone and proposed the S-B model. Given the internal sedimentary structure characteristics of thin interbedded sandstone and mudstone, Zhang et al. (2015) regarded the reservoir as a layered medium, and established a saturation calculation model of thin interbedded sandstone and mudstone.

The matrix porosity and permeability of tight sandstone reservoirs are low, and fractures are good channels and reservoir spaces for oil and gas migration (Luo, 2010; Zeng et al., 2013). Fractures affect the accurate calculation of tight sandstone saturation (Liu et al., 2018; Liao et al., 2024). The reservoir space of tight sandstone includes matrix pores and fractures. Aguilera and Aguilera (2003) considered the effects of matrix pores, fractures, and caves on the electrical conductivity of carbonate rocks and proposed the triple porosity model. Zhang (2010) established the saturation calculation model for fractured reservoirs based on the triple porosity model. Tang et al. (2018) calculated the saturation of Dabie Area, specifically when the fracture porosity is less than 0.055%, the equation based on conductive pore water is used for calculation. When the fracture porosity is more than 0.055%, the equation based on the theory of dual porosity media is deployed. Wang et al. (2022) established the tight sandstone saturation model using the fracture and matrix pore parallel conductivity model and digital core.

Additionally, the selection of the Archie parameters m and n is essential for saturation calculation. Many scholars have improved the accuracy of the Archie formula by adjusting the values of m and n. (Zhang and Shi, 2005; Yan et al., 2015; Xiao et al., 2013; Luo et al., 2014; Jiang, 2018; Li et al., 2020; Li et al., 2012; Wang et al., 2005; Zhang et al., 2006). In previous studies, there is a lack of a more comprehensive saturation model that combines the effects of shale and fractures. Additionally, the model parameters of tight sandstone are affected by pore structure (Li et al., 2020), and accurate calculation methods of the key parameters are difficult to establish. Therefore, the saturation calculation of tight sandstone needs to be further studied.

In this paper, the tight sandstone reservoirs of the Jurassic Ahe Formation in Tarim Basin were taken as the research area. This paper proposed a saturation model that combines the effects of shale and fractures. Specifically, when the shale content is more than 20%, the Indonesian formula is used to calculate the saturation. When the shale content is less than 20%, the dual porosity model of the matrix pore and fracture pore is adopted. The application to the tight sandstone reservoirs in Tarim Oilfield shows that the saturation calculation method proposed in this paper has less minor interpretation errors than the traditional calculation method. The saturation calculation method proposed in this paper improves the accuracy of saturation evaluation.

2 Geological setting

Kuqa Depression is a geological formation located in the northern Tarim Basin, which is adjacent to the Tianshan fold belt in the north. Tectonic units and location of Dibei gas field in Kuqa Depression are shown in Figure 1. Kuqa Depression is classified as a Mesozoic-Cenozoic foreland basin and is comprised of four thrust belts and three sags. The Northern Monocline, Kela, Yiqikelike, and Qiulitage thrust belts make up the four structural belts. The Baicheng, Yangxin, and Wushi sags are the main negative tectonic units (Zhao et al., 2022). The study area of this research is situated in the middle of the Yiqikelike thrust belt, specifically focusing on the DB 5 well as the primary research object.

The primary gas-bearing interval in the Dibei gas field is the Lower Jurassic Ahe Formation (Shi et al., 2018; Shi et al., 2024), which consists of braided river delta plain surface deposits characterized by low compositional maturity. The lithology of the Ahe Formation primarily comprises gravel, coarse sandstone, and medium sandstone. The sandstone reservoirs in this formation have an average thickness between 250 and 300 m. Dibei gas field is a typical tight sandstone gas reservoir, with the porosity of the Ahe Formation between 3.0% and 9.0%, with an average porosity of 5.94%. The permeability is between 0.1mD and 5.0mD, with an average air permeability of 0.818mD. According to the data from the drilling core, micro casting thin section, and scanning electron microscope, the tight sandstone reservoirs of Jurassic Ahe Formation in Tarim Basin are mainly pore-type reservoirs and pore-fracture-type reservoirs. The main reservoir space of pore reservoirs is matrix pores, such as argillaceous micropores and intergranular dissolved pores (see Figure 2).

Figure 1

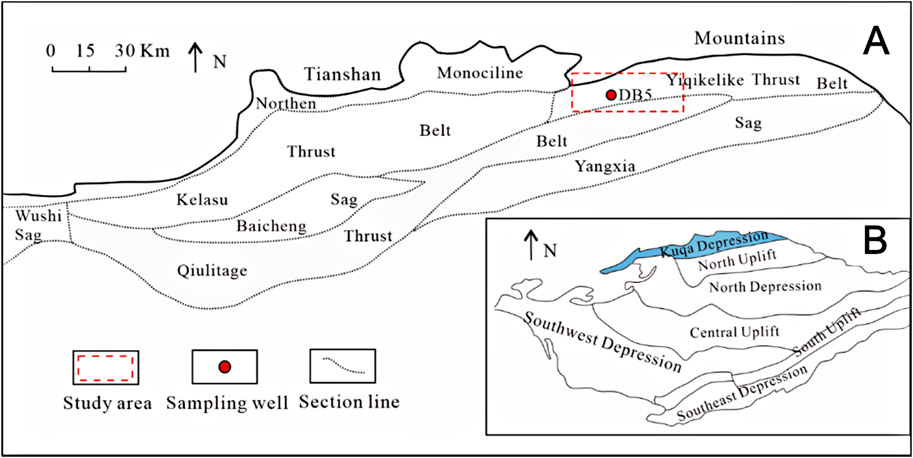
Figure 1. Tectonic units and location of Dibei gas field in Kuqa Depression. (A) Location of Kuqa Depression. (B) Sample well and structural outline of Dibei gas field in Kuqa Depression. (modified from Zhao et al., 2022).

Figure 2

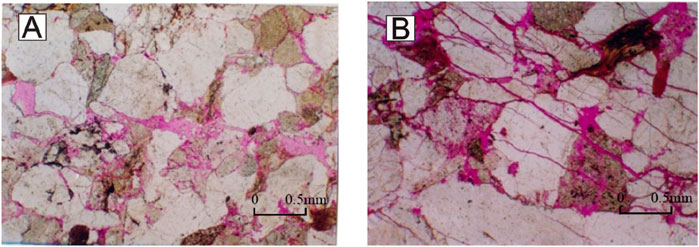
Figure 2. Reservoir space types of Jurassic Ahe Formation in Dibei area. (A) Shale micropores, a small amount of intragranular dissolved pores. (B) Structural fractures, potassium feldspar intragranular dissolved pores, matrix micropores.

The core observation results show that the fractures in the Ahe Formation are generally developed which are mainly high-angle structural fractures in the open or semi-closed state (Figure 3). Silicon and carbonate minerals can be seen in some fractures and corrosion traces of fillers can also be seen. The main reservoir space of a fracture-pore reservoir is matrix pore, and matrix rock is cut by various fractures with different occurrences. While providing part of the reservoir space, fractures mainly play the role of connecting matrix rocks and improving reservoir permeability.

Figure 3

Figure 3. Characteristics of core fractures of Jurassic Ahe Formation in the Dibei area.

3 Method for calculating saturation in tight sandstones

3.1 Dual porosity model

Aguilera and Aguilera (2003) published rigorous equations for dual porosity systems that were shown to be valid for all combinations of matrix and fractures or matrix and nonconnected pores. The model used in this paper is a combination of matrix and fractures, the model is composed of a rock skeleton, matrix pores, and fractures. The pore structure of rock determines the conductive path of rock, suppose the additional shale conductivity is not considered (core experiments of reservoirs in multiple research blocks show that the cation exchange capacity is minimal and can be ignored). In that case, the conductivity of matrix pores and fractured water is the same, but the conductive paths are different. Therefore, the rock is conductive in parallel through the matrix pore network and the fracture network. The model of the dual porosity reservoirs is shown in Figure 4, the matrix pores and fractures constitute a very complex fracture-pore system. Matrix porosity is the ratio of matrix pore volume to total volume which is calcuiated using Equation 1.

${\varphi }_b=\frac{V_b}{V}(1)$

where ϕ_b is the matrix porosity (%); V_b is the volume of matrix pores (cm³); V is the total volume of the composite system (cm³).

Figure 4

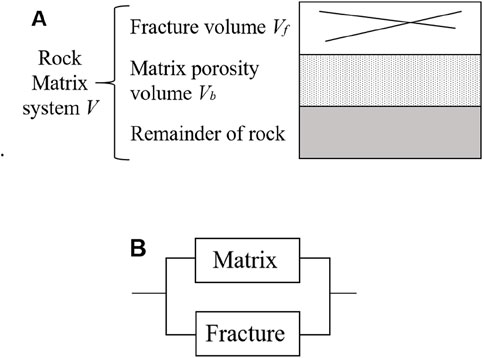
Figure 4. Schematic display of dual-porosity model. (A) Structure of rock dual porosity model. (B) Conductive path of rock dual porosity model (modified from Aguilera and Aguilera, 2004).

Rock fracture porosity is the ratio of matrix pore volume to total volume which is calculated using Equation 2.

${\varphi }_f=\frac{V_f}{V}(2)$

where ϕ_f is the fracture porosity (%); V_f is the volume of fracture (cm³).

Total porosity of rock is calculated by Equation 3.

$\varphi =\frac{V_f+V_b}{V}(3)$

where ϕ is the total porosity (%).

3.2 Calculation method of saturation

According to the theory of dual porosity medium, the pore space of a tight sandstone reservoir is divided into matrix pore space and fracture pore space. According to the definition of water saturation, the total water saturation can be expressed as Equation 4.

$S_w=\frac{{\varphi }_b{S}_{wb}+{\varphi }_f{S}_{wf}}{{\varphi }_b+{\varphi }_f}(4)$

where ϕ_b is the matrix porosity (%); S_wb is the matrix water saturation (%); ϕ_f is fracture porosity (%); S_wf is fracture water saturation (%).

Under the background of fractures and non-connected pores, the physical properties of the matrix of the reservoir are relatively uniform. Therefore, when calculating the matrix pore saturation, we use the classical Archie formula (Archie, 1942), and the Archie formula is shown in Equation 5.

$S_{w\mathrm{b}}=\sqrt[nb]{\frac{ab{R}_w}{{\varphi }_b^{mb}{R}_t}}(5)$

where R_w is the formation water resistivity ($\mathrm{\Omega }\cdot \mathrm{m}$); R_t is the formation resistivity ($\mathrm{\Omega }\cdot \mathrm{m}$); a, b, m_b, n_b are the rock electrical parameters of the matrix, which are determined by rock resistivity experiments. The rock samples contain virtually no fractures, so the m and n obtained from the rock resistivity experiment are regarded as the m_b and n_b of the rock matrix in this paper. Subsequently, this paper will enhance the calculation approach of rock electrical parameters in accordance with the actual circumstances of the reservoir, thereby enabling the saturation calculation to be more rational and precise.

According to the permeability characteristics of the dual porosity, Tang et al. (2018) and Wang (2020) calculated the water saturation of fracture using Equation 6.

$S_{wf}=\sqrt[n_f]{\frac{1/R_t-1/R_{xo}+\left(1/R_{mf}\right){\varphi }_f^{m_f}}{\left(1/R_w\right){\varphi }_f^{m_f}}}(6)$

where R_xo is the resistivity of the flushing zone ($\mathrm{\Omega }\cdot \mathrm{m}$); R_mf is the resistivity of mud filtrate ($\mathrm{\Omega }\cdot \mathrm{m}$); m_f and n_f are the electrical parameters of fractures.

Shale is dispersedly filled in the intergranular pore space of sandstone, which is conductive in parallel with the water of formation. When the reservoir contains shale, the resistivity of the reservoir will decrease, and the accuracy of the traditional method for calculating saturation will also decrease. There are many saturation models involving the influence of shale. The Indonesian formula is a famous formula in formation evaluation by well logs, as shown in Equation 7.

$\frac{1}{S_w^n}={\left(\frac{V_{sh}^{cc}}{R_{sh}}+\frac{\varphi }{\sqrt{a{R}_w}}\right)}^2{R}_t(7)$

where V_sh is the shale content (%); R_sh is the resistivity of the shale ($\mathrm{\Omega }\cdot \mathrm{m}$); cc = 1-V_sh/2. This formula is suitable for low-formation water salinity and shaly sandstone with V_sh less than 50%. This formula better solves the saturation calculation of shaly sandstone formation.

The research area belongs to fractured tight sandstone reservoirs. Fractures developed in rocks enhance the productivity of oil and gas reservoirs but also complicate the evaluation of oil and gas saturation. When calculating the oil and gas saturation of fractured tight sandstone reservoirs, factors such as physical properties, fractures, and lithology should be considered. For such reservoirs, this paper proposes a saturation evaluation method considering pore types and shale content (Figure 5). Specifically, when the shale content exceeds 20%, the Indonesian formula is used to calculate saturation. If the shale content is less than 20%, the dual porosity model is used to calculate saturation.

Figure 5

Figure 5. The calculation process of saturation.

4 Parameters of the dual porosity model

4.1 Porosity

Usually, intersection processing of multiple well logging methods is used to obtain accurate total porosity of the reservoirs. Compared with other well-logging methods, density and compensated neutron log responses are less affected by the heterogeneity of fractured reservoirs (Yong and Zhang, 1986). Therefore, we use the intersection of density and neutron logs to obtain the total porosity of the reservoir. The specific method is shown in Equations 8–10.

$\varphi =\sqrt{\frac{pords{c}^2+porns{c}^2}{2}}(8)$

$pordsc=\frac{{\rho }_b-{\rho }_{ma}}{{\rho }_f-{\rho }_{ma}}-V_{sh}\frac{{\rho }_{sh}-{\rho }_{ma}}{{\rho }_f-{\rho }_{ma}}(9)$

$pornsc=\frac{{\varphi }_N-{\varphi }_{ma}}{{\varphi }_{Nf}-{\varphi }_{ma}}-V_{sh}\frac{{\varphi }_{Nsh}-{\varphi }_{ma}}{{\varphi }_{Nf}-{\varphi }_{ma}}(10)$

where ${\rho }_{sh}$, ${\rho }_{ma}$, ${\rho }_f$ are the density logging values of mud, skeleton, and fluid, respectively (g/cm³); ${\varphi }_{sh}$, ${\varphi }_{ma}$, ${\varphi }_f$ are the neutron logging values of shale, rock matrix, and pore fluid, respectively (%).

Acoustic logging data basically do not reflect the fracture porosity but mainly reflect the matrix porosity of the rocks. The matrix porosity of the reservoirs is calculated by the acoustic volume model. The calculation formula is shown in Equation 11.

${\varphi }_b=\frac{\Delta t-\Delta t_{ma}}{\Delta t_f-\Delta t_{ma}}-V_{sh}\frac{\Delta t_{sh}-\Delta t_{ma}}{\Delta t_f-\Delta t_{ma}}(11)$

where $\Delta t_{sh}$, $\Delta t_{ma}$, $\Delta t_f$ are the acoustic time difference logging values of shale, rock matrix, and pore fluid, respectively (μs/ft).

In reservoir evaluation, imaging logging, and dual lateral logging data are usually used to calculate fracture porosity (Zhao et al., 2012). In this paper, the fractures are picked manually based on the intuitive interpretation of FMI (Formation Micro Scanner Image), and the electrical imaging data are calibrated using the optical scanning imaging data of the cores. Finally, the fracture parameters, such as fracture porosity, were calculated (Chen and Tan, 2003; Lai et al., 2015).

4.2 Determination of model parameters

Accurate model parameters m_b and n_b are the key to the quantitative evaluation of saturation. The porosity and the microscopic pore structure of the reservoirs affect the parameters of models (Ding et al., 2017). Capillary pressure measurement and nuclear magnetic resonance (NMR) measurement are the main methods to describe the microscopic pore structure of the reservoirs. In this paper, the standard NMR T₂ spectrum is selected to characterize the microscopic pore structure. Rock electrical and nuclear magnetic resonance experiments were carried out on 10 tight sandstone samples from Ahe Formation. The m_b value and n_b value of each core are obtained by rock electricity experiment, and the NMR T₂ spectrum of each core is obtained by the nuclear magnetic resonance experiment. Figure 6 shows the standard T₂ spectra of six tight sandstone samples. Six rock samples are saturated with NaCl solution, and the resistivity of NaCl solution is 0.138 $\mathrm{\Omega }\cdot \mathrm{m}$. The position and shape of the T₂ spectrum of the three rock samples are basically the same (Figure 6A), which indicates that the microscopic pore distributions of the three rock samples are similar. The amplitude and envelope area of the T₂ spectra of the three rock samples are different, which indicates that the porosity of the three rock samples is different. Under the condition that the formation water resistivity and micro-pore structure are basically the same, the parameters m_b and n_b are different when the porosity of the three rock samples is different. The results show that the change of porosity will lead to the change of m_b and n_b values. The position and shape of the T₂ spectra of the three rock samples are different, but the envelope area is the same (Figure 6B), indicating that the porosity of the three rock samples is the same, but the microscopic pore structure is different. Under the condition that formation water resistivity and porosity are basically the same, the parameters m_b and n_b are different if the microscopic pore structure of the three rock samples is different. The results show that the microscopic pore structure affects the values of m_b and n_b.

Figure 6

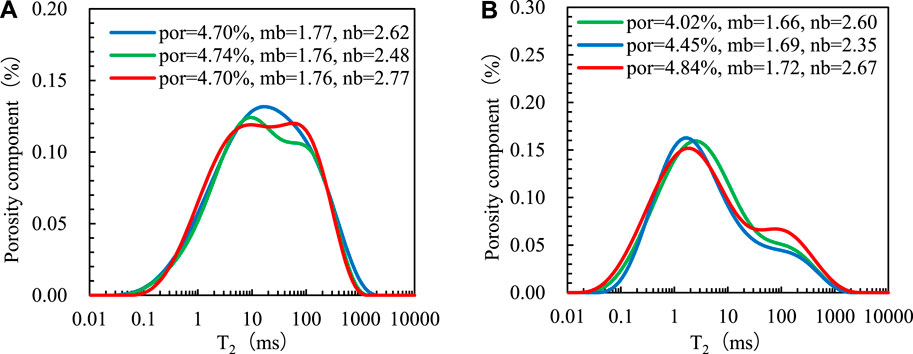
Figure 6. Standard T₂ distribution of different rock samples. (A) The effect of pore structure on model parameters. (B) The effect of porosity on model parameters.

On the basis of determining the factors affecting the electrical properties of tight sandstone, it is necessary to determine the response relationship between the parameters and pore structure so as to provide a basis for the accurate calculation of saturation. Through the above analysis, it can be concluded that porosity and pore structure have a significant influence on the model parameters of rocks. The logarithmic mean of the NMR T₂ spectrum is usually used to describe the variation in the reservoir’s microscopic pore structure (Zhang and Shi, 2005; Guo et al., 2022). The larger the logarithmic mean value of T₂ (T_2lm), the larger the pore size of the reservoirs. And the smaller the T_2lm, the smaller the pore size of the reservoirs. Figure 7A shows the relationship between mb value and porosity ϕ of core analysis. It can be seen from the Figure that the m_b value and the porosity present a power function relationship, and the m_b value increases with the increases of porosity ϕ. Figure 7B shows the relationship between the m_b value of the core analysis and the T_2lm values. The statistical results show that the m_b value first increases with the increase of the T_2lm value, and then the m_b value decreases with the increase of the T_2lm value.

Figure 7

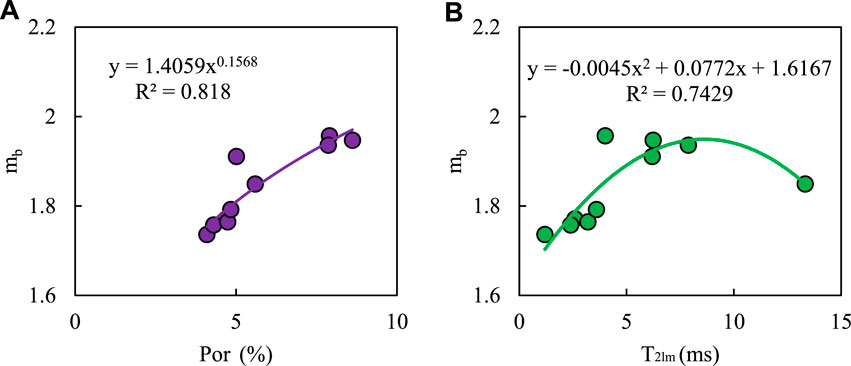
Figure 7. Analysis of influencing factors of m_b values. (A) Relationship between mb value and porosity. (B) Relationship between m_b value and T2 logarithmic mean value.

Figure 8A shows the relationship between the n_b value of core analysis and porosity ϕ. The value of n_b increases with the increase of the porosity ϕ and presents a power function relationship. Figure 8B shows the relationship between the n_b value of the core analysis and the T_2lm value. The statistical results show that as the T_2lm value increases, the n_b value decreases firstly, and then increases.

Figure 8

Figure 8. Analysis of influencing factors of n_b value. (A) The relationship between the value of n_b value and porosity. (B) The relationship between the value of nb and the T₂ logarithmic mean value.

The experimental results show that the correlation between model parameters and any single factor is not particularly high. To reduce the error of single actor regression calculation, m_b and n_b values are calculated using the multi-factor fitting regression method. Multifactor regression considers the complex interaction between multiple parameters and reflects the actual properties of rocks more accurately. According to the results of the rock resistivity and nuclear magnetic resonance (NMR) experiment, porosity and T₂ logarithmic mean value are selected as influencing factors, and the calculation model of m_b value and n_b value is established by using multiple regression methods. The model is shown in Equations 12, 13.

$m_b=1.401{{\varphi }_b}^{0.1524}-0.0004826{T_{2lm}}^2+0.004525T_{2lm}(12)$

$n_b=4.447{{\varphi }_b}^{-0.3701}+0.0002246{T_{2lm}}^2-0.01689T_{2lm}(13)$

where m_b and n_b are the rock electrical parameters of the matrix; ϕ_b is the porosity of the matrix (%); T_2lm is the logarithmic mean of T₂ (ms).

Figure 9 shows the calculation results of the model. The m_b and n_b values calculated by the multiple linear regression method have a reasonable correlation with the m and n values measured by the experiment. The coefficient of determination for the m_b value is 0.8377, and for the n_b value is 0.7041, indicating that the calculation accuracy of this method is high, and porosity and pore structure are important factors affecting the model parameters of rocks.

Figure 9

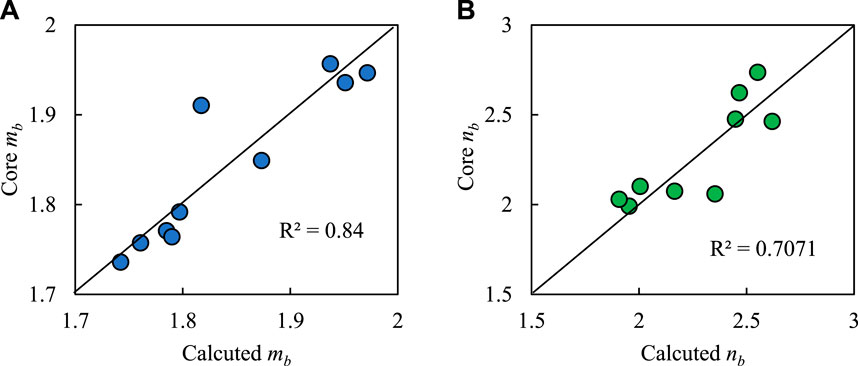
Figure 9. Cross plots of measured rock electrical parameter values and calculated rock electrical parameter values. (A) Cross plots of core analysis m_b and calculated m_b value. (B) Cross plots of core analysis n_b and calculated n_b values.

In order to obtain electrical parameters for fractures, Tang et al. (2018) and Wang (2020) assume that the rock is a regular hexahedron with side length l, a diagonal fracture with angle β and width d_f passes through the rock, and a regular hexahedron hole with side length c develops inside the rock. According to the theory, the formula for calculating the parameters of fractured rock is shown in Equation 14.

$m_f=-\frac{\log \left[l\left(\frac{1}{c+d_f}+\frac{l-c\cos \beta }{l\cos \beta d_f}+\frac{c}{\left(l-c\right)d_f}\right)\right]}{\log \left\{\left[\left(\frac{l^2}{\cos \beta }-c^2\right)d_f+c^3\right]/l^3\right\}}(14)$

where d_f is the fracture width (mm); β is the fracture angle (dega). Substituted into Equations 5, 6, the matrix saturation and fracture saturation are calculated, and the total water saturation of the reservoir is calculated by Equation 4.

For the n_f, there is still no method to determine it. We assume it is equal to n_b in this paper.

5 Results of saturation calculation

The saturation calculation method proposed in this paper was used to quantitatively evaluate the reservoir saturation of the Jurassic Ahe Formation in Tarim Basin. The reservoir space types in the study area are mainly muddy micropores, intra-granular dissolved pores, intergranular dissolved pores, and micro-fractures, and the development degree of primary pores is low. Taking well DB5 as an example, the average core porosity is 5.67%, and the permeability is 0.52 × 10⁻³ μm². The Ahe Formation is a typical tight sandstone reservoir. Figures 10, 11 show the saturation calculation results. The sixth track is the processing result of the imaging logging. The seventh track is the fracture characteristic curves, which were calculated by using the imaging logging data. Fracture characteristic curves include fracture width, fracture length, and fracture porosity. The eighth track is the m_b value of multi-factor regression calculation and the m_b value of core analysis, and the ninth track is the n_b value of multi-factor regression calculation and the n_b value of core analysis. The m_b and n_b calculated by this method agree well with the m_b and n_b obtained by core analysis. The 10th track is the water saturation calculated by the Archie model, and the 11th track is the saturation calculated by the tight sandstone saturation calculation method proposed in this paper. As can be seen from Figures 10, 11, the water saturation calculated by the traditional Archie formula and the method proposed in this paper is in good agreement with the core analysis value.

Figure 10

Figure 10. Saturation calculation results of the upper section of Ahe Formation in DB 5 Well, Dibei Gas Reservoir, Tarim Basin.

Figure 11

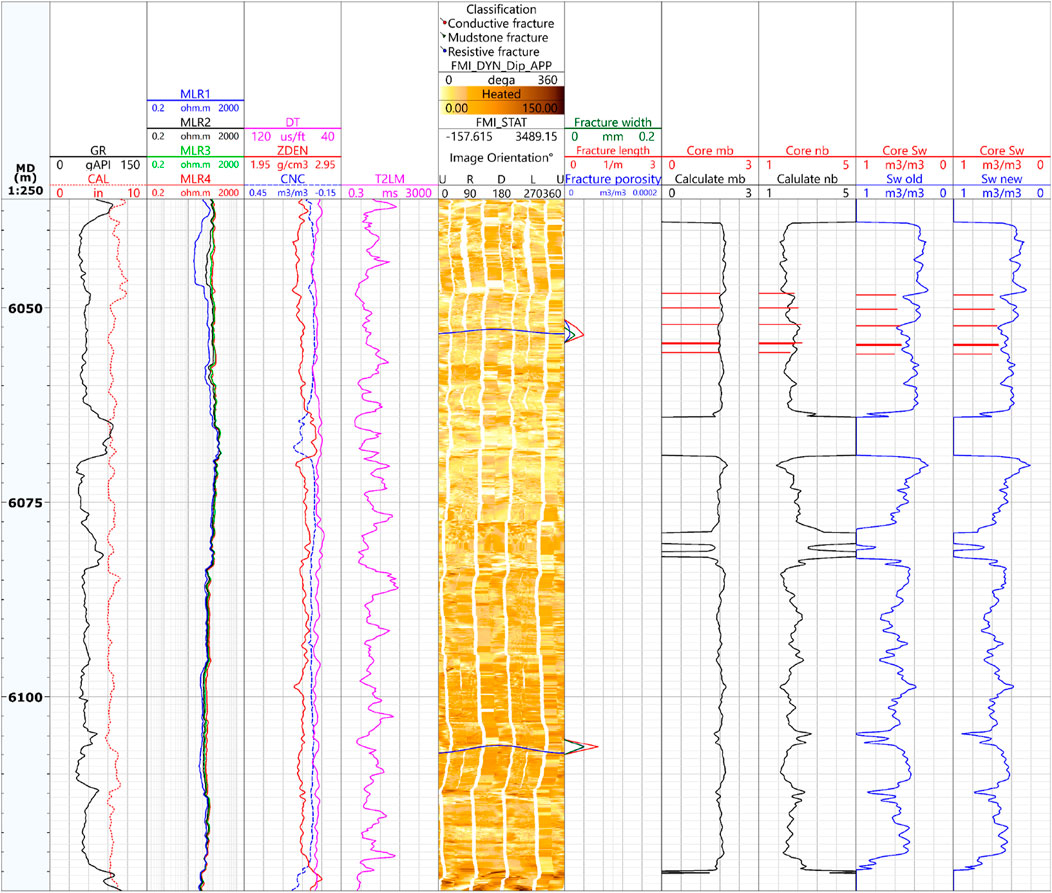
Figure 11. Saturation calculation results of the lower section of Ahe Formation in DB 5 Well, Dibei Gas Reservoir, Tarim Basin.

In order to test the accuracy of the saturation calculation method more intuitively, we evaluate the accuracy of the saturation calculation by calculating the absolute error and the relative error. As can be seen from Table 1, the average relative error of saturation calculated by the traditional Archie formula is 5.88%. In comparison, the average relative error of the saturation calculation method proposed in this paper is 3.55%, which reduces the average relative error by 2.33%. Similarly, the average absolute error calculated by the traditional Archie formula is 9.87%. The average absolute error of the saturation calculation method proposed in this paper is only 6.11%, and the accuracy is improved by 3.76%. The results show that the saturation calculation method proposed in this paper meets the error requirement of reserve calculation and has higher accuracy than the traditional method.

Table 1

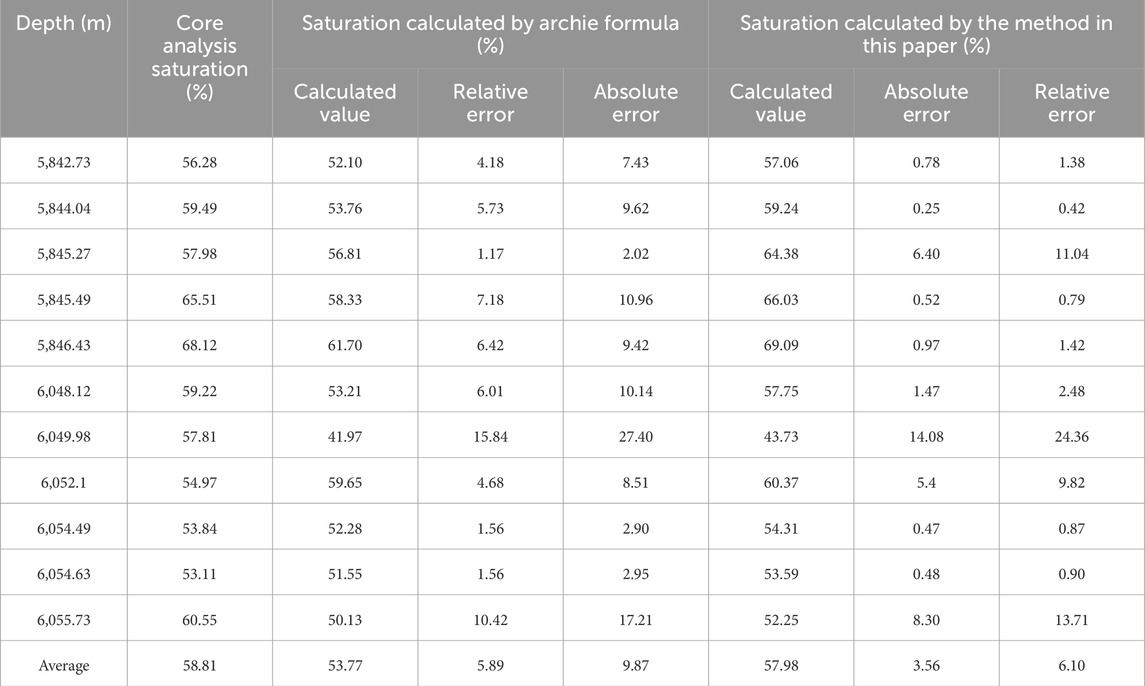
Table 1. Comparative analysis table of saturation calculation error of Well Dibei 5 in Dibei Gas reservoir, Tarim Basin.

6 Discussion

Tight sandstone reservoirs are characterized by complex pore structure, high shale content, and developed fractures, but the Archie formula is applicable to pure sandstone reservoirs with favorable physical properties, and the accuracy of the Archie formula for calculating the water saturation of tight sandstone reservoirs is not high (Feng et al., 2023; Zhou et al., 2019). Different from the Archie formula, this paper adopts the dual porosity model for saturation calculation. The properties of the reservoir are influenced by its pore structure, and a precise understanding of the pore structure of the rock is the prerequisite for obtaining accurate saturation (Zhang, 2010). The fracture-matrix dual porosity model divides the rock pore system into two components: fracture porosity and matrix porosity. The fracture-matrix dual porosity model can independently consider the contribution of fracture and matrix porosity to the saturation, thus its calculation accuracy is high. In this paper, the precise parameters of the saturation model are determined by conducting the rock electricity and NMR experiments, further enhancing the calculation accuracy of the saturation model. The saturation calculation method proposed in this paper takes into account the multiple influences of lithology, physical properties, pore structure, and fractures on electrical properties. However, the Archie model merely considers the effects of physical properties and oil content on electrical properties (Hu et al., 2017). Therefore, the saturation calculated by this method is highly consistent with that of coring analysis and has high accuracy in the quantitative evaluation of hydrocarbon properties of tight sandstone reservoirs. Finally, when applying the saturation calculation method, it is necessary to carry out matching rock electricity and NMR measurement experiments to establish accurate model parameters.

7 Conclusion

(1) Tight sandstone reservoirs are characterized by complex pore structure, high shale content, and developed fractures, which render the evaluation of saturation challenging. To address this issue, a method for calculating saturation in tight sandstone reservoirs is developed, comprehensively taking into account the influence of fractures, lithology, and other factors. If the shale content exceeds 20%, saturation is calculated using the Indonesian formula. Otherwise, the saturation is calculated using the double porosity model.

(2) The pore structure of rock constitutes one of the most crucial factors influencing the parameters of the saturation model. Based on the results of the rock resistivity and NMR experiments, porosity and the logarithmic mean value of T2 are chosen as input factors for calculating model parameters. Finally, the calculation model of m_b value and n_b value is established by the multiple regression method.

(3) The processing outcomes of logging data for tight sandstone reveal that the saturation calculation method proposed in this paper exhibits high precision in the saturation assessment of tight sandstone reservoirs. In contrast to the Archie model, this method considers the influences of lithology, pore structure, and fractures. Hence, the saturation evaluation results are more in line with the actual conditions of the reservoirs. The method proposed in this paper demonstrates excellent adaptability in the quantitative evaluation of saturation for tight sandstone reservoirs, and the saturation model suitable for other reservoirs will be further studied in the future.

Data availability statement

The datasets presented in this article are not readily available because exploratory research. Requests to access the datasets should be directed to PZ, pqzhao@cup.edu.cn.

Author contributions

YX: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft, Writing–review and editing. WD: Data curation, Formal Analysis, Methodology, Software, Validation, Writing–original draft, Writing–review and editing. CH: Validation, Writing–review and editing. KB: Validation, Writing–review and editing. XZ: Validation, Writing–review and editing. YA: Validation, Writing–review and editing. PZ: Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors wish to appreciate the support provided by Tarim Oilfield Company and Beijing Key Laboratory of Earth Prospecting and Information Technology. The authors would also like to ackonwlege the editorial department and the reviewers for their comments on this paper.

Conflict of interest

Authors YX, CH, KB, XZ, and YA were employed by Tarim Oilfield Company and China National Petroleum Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguilera, M. S., and Aguilera, R. (2003). Improved models for petrophysical analysis of dual porosity reservoirs. Petrophysics - SPWLA J. Form. Eval. Reserv. Descr. 44 (January), 21–35.

Google Scholar

Aguilera, R. F., and Aguilera, R. (2004). A triple porosity model for petrophysical analysis of naturally fractured reservoirs. Petrophysics - SPWLA J. Form. Eval. Reserv. Descr. 45 (March), 157–166.

Google Scholar

Archie, G. E. (1942). The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. Aime 146 (01), 54–62. doi:10.2118/942054-G

CrossRef Full Text | Google Scholar

Chen, Y., and Tan, M. J. (2003). Fracture detection and identification dsing logging techniques. Well logging Technol. 27 (S1), 11–14. doi:10.16489/j.issn.1004-1338.2003.s1.004

CrossRef Full Text | Google Scholar

Clavier, C., Coates, G., and Dumanoir, J. (1984). Theoretical and experimental bases for the dual-water model for interpretation of shaly sands. Soc. Petroleum Eng. J. 24 (02), 153–168. doi:10.2118/6859-pa

CrossRef Full Text | Google Scholar

Dai, J., Ni, Y., and Wu, X. (2012). Tight gas in China and its significance in exploration and exploitation. Petroleum Explor. Dev. 39 (3), 277–284. doi:10.1016/s1876-3804(12)60043-3

CrossRef Full Text | Google Scholar

Desbois, G., Urai, J. L., Kukla, P. A., Konstanty, J., and Baerle, C. (2011). High-resolution 3D fabric and porosity model in a tight gas sandstone reservoir: a new approach to investigate microstructures from mm-to nm-scale combining argon beam cross-sectioning and SEM imaging. J. Petroleum Sci. Eng. 78, 243–257. doi:10.1016/j.petrol.2011.06.004

CrossRef Full Text | Google Scholar

Ding, Y. J., Chai, X. Y., Shao, W. Z., Li, J. G., Han, Y., and Li, Q. H. (2017). Key parameters of water saturation based on concentration of T, spectrum distribution. Well Logging Technol. 41 (04), 405–411. doi:10.16489/j.issn.1004-1338.2017.04.005

CrossRef Full Text | Google Scholar

Feng, S., Xie, R., Radwan, A. E., Wang, Y., Zhou, W., and Cai, W. (2023). Accurate determination of water saturation in tight sandstone gas reservoirs based on optimized Gaussian process regression. Mar. Petroleum Geol. 150, 106149. doi:10.1016/j.marpetgeo.2023.106149

CrossRef Full Text | Google Scholar

Feng, S., Xie, R., Zhou, W., Yin, S., Chen, J., Zhang, M., et al. (2021). The new interpretation of the geological origin about differentiation phenomenon of resistivity in the tight sandstone reservoir. Arabian J. Geosciences 14 (20), 2074. doi:10.1007/s12517-021-08451-y

CrossRef Full Text | Google Scholar

Gao, H., and Li, H. A. (2016). Pore structure characterization, permeability evaluation and enhanced gas recovery techniques of tight gas sandstones. J. Nat. Gas Sci. Eng. 28, 536–547. doi:10.1016/j.jngse.2015.12.018

CrossRef Full Text | Google Scholar

Guo, Y., Pan, B., Zhang, L., Lei, J., Fan, Y., Ruhan, A., et al. (2022). A study on water saturation predictions in igneous reservoirs based on the relationship between the transverse relaxation time and the resistivity index. J. Petroleum Sci. Eng. 208, 109519. doi:10.1016/j.petrol.2021.109519

CrossRef Full Text | Google Scholar

Hu, S. F., Zhou, C. C., Li, X., Li, C. L., and Zhang, S. Q. (2017). A tight sandstone trapezoidal pore oil saturation model. Petroleum Explor. Dev. 44 (5), 876–886. doi:10.1016/s1876-3804(17)30099-x

CrossRef Full Text | Google Scholar

Jiang, H. (2018). Experimental study of the conductivity model for tight oil rock in the Jurassic Systen of Sichuan Basin. Beijing: China University of Petroleum. [dissertation/master's thesis]. [China (Beijing)].

Google Scholar

Lai, J., Wang, G. W., Sun, S. M., Jiang, C., Zhou, L., Zheng, X. H., et al. (2015). Research advances in logging recognition and evaluation method of fractures in tight sandstone reservoirs. Prog. Geophys. (in Chinese) 30 (4), 1712–1724. doi:10.6038/pg20150426

CrossRef Full Text | Google Scholar

Leveaux, J., and Poupon, A. (1971). Evaluation of water saturation in shaly formations. The Log Analyst 12 (04), 3–8.

Google Scholar

Li, X., Li, C. L., Li, B., Liu, X. F., and Yuan, C. (2020). Response laws of electrical property and saturation evaluation method of tight sandstone. Petroleum Exploration and Development 47 (1), 202–212. doi:10.11698/PED.2020.01.20

CrossRef Full Text | Google Scholar

Li, X., Zhao, W. Z., Zhou, C. C., Wang, T. S., and Li, C. L. (2012). Dual-porosity saturation model of low-porosity and low-permeability clastic reservoirs. Petroleum Exploration and Development 39 (01), 88–98. doi:10.1016/s1876-3804(12)60019-6

CrossRef Full Text | Google Scholar

Liao, Q. Z., Wang, B., Chen, X., and Tan, P. (2024). Reservoir stimulation for unconventional oil and gas resources: recent advances and future perspectives. Advances in Geo-Energy Research 13 (1), 7–9. doi:10.46690/ager.2024.07.02

CrossRef Full Text | Google Scholar

Liu, Z. Y., Zhang, C. G., Tang, J., and Xiao, C. G. (2018). Influence of fracture on rock resistivity and its application in saturation calculation. Lithologic Reservoirs 30 (02), 120–128. doi:10.12108/yxyqc.20180213

CrossRef Full Text | Google Scholar

Luo, Q. (2010). Core observation and description of tight sandstone fractured reservoir an example from Wen ming zhai tight sandstone. Xinjiang Petroleum Geology (in Chinese) 31 (3), 229–231. doi:10.3724/SP.J.1077.2010.01195

CrossRef Full Text | Google Scholar

Luo, S. C., Cheng, Z. G., Zhou, J. Y., Xi, H., and Wang, C. S. (2014). Research on saturation index n of tight sandstone reservoir. Journal of Southwest Petroleum University Science and Technology Edition 36 (04), 116–122. doi:10.11885/j.issn.1674-5086.2013.10.10.01.html

CrossRef Full Text | Google Scholar

Rezaee, R., Saeedi, A., and Clennell, B. (2012). Tight gas sands permeability estimation from mercury injection capillary pressure and nuclear magnetic resonance data. Journal of Petroleum Science and Engineering 88–89, 92–99. doi:10.1016/j.petrol.2011.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, H., Luo, X. R., Lei, G. L., Wei, H. X., Zhang, L. Q., Zhang, L. K., et al. (2018). Effects of early oil emplacement on reservoir quality and gas migration in the Lower Jurassic tight sand reservoirs of Dibei gas field, Kuqa Depression, western China. Journal of Natural Gas Science and Engineering 50, 250–258. doi:10.1016/j.jngse.2017.12.004

CrossRef Full Text | Google Scholar

Shi, P. Y., Shi, P. D., Bie, K., Han, C., Ni, X. W., Mao, Z. Q., et al. (2024). Prediction of permeability in a tight sandstone reservoir using a gated network stacking model driven by data and physical models. Frontiers in Earth Science 12. doi:10.3389/feart.2024.1364515

CrossRef Full Text | Google Scholar

Silva, P. L., and Bassiouni, Z. (1986). Statistical evaluation of the S-b conductivity model for water-bearing shaly formations. The log analyst 27 (3), 9–19.

Google Scholar

Simandoux, P. (1963). Dielectric measurements on porous media, application to the measurements of water saturation: study of behavior of argillaceous formations. Revue de L’ Institut Francais du Petrole. 18 (S1), 193–215.

Google Scholar

Tang, J., Xin, Y., Cai, D. Y., and Zhang, C. G. (2018). A method of calculating saturation for tight sandstone reservoirs: a case of tight sandstone reservoir in Dabie area of Kuqa depression in Tarim Basin of NW China. Open Journal of Yangtze Oil and Gas 03, 21–35. doi:10.4236/ojogas.2018.31003

CrossRef Full Text | Google Scholar

Vincent, M., and Wladyslaw, A. (2015). Calculation of water saturation in low resistivity gas reservoirs and pay-zones of the Cretaceous Grudja Formation, onshore Mozambique basin. Marine and Petroleum Geology 67 (11), 249–261. doi:10.1016/j.marpetgeo.2015.05.016

CrossRef Full Text | Google Scholar

Wang, L., Sun, B. D., Shen, A. X., and Wan, J. B. (2005). On application of rock electricity parameters of shaly sand reservoir with low-porosity and permeability, permeability, × field. Well Logging Technology 29 (02), 91–94+184. doi:10.16489/j.issn.1004-1338.2005.02.001

CrossRef Full Text | Google Scholar

Wang, Q. (2020). Study on saturation model and water cut evaluation method of tight sandstone. China University of Geosciences. [dissertation/master's thesis]. [China(Beijing)].

Google Scholar

Wang, Q., Tan, M. J., Xiao, C. W., Wang, S. Y., Han, C., and Zhang, L. T. (2022). Pore-scale electrical numerical simulation and new saturation model of fractured tight sandstone. AAPG Bulletin 106 (7), 1479–1497. doi:10.1306/04132220165

CrossRef Full Text | Google Scholar

Waxman, M. H., and Smits, L. J. M. (1968). Electrical conductivities in oil-bearing shaly sands. Society of Petroleum Engineers Journal 8 (02), 107–122. doi:10.2118/1863-A

CrossRef Full Text | Google Scholar

Xiao, L., Zou, C. C., Mao, Z. Q., Shi, Y. J., Liu, X. P., Jin, Y., et al. (2013). Estimation of water saturation from nuclear magnetic resonance (NMR) and conventional logs in low permeability sandstone reservoirs. Journal of Petroleum Science and Engineering 108 (August), 40–51. doi:10.1016/j.petrol.2013.05.009

CrossRef Full Text | Google Scholar

Yan, J. P., Wen, D. N., Li, Z. Z., Gen, B., Liang, Q., and He, X. (2015). The influence of low permeable sandstone pore structure on rock electrical parameters and its applications. Natural Gas Geoscience 26 (12), 2227–2233. doi:10.11764/j.issn.1672-1926.2015.12.2227

CrossRef Full Text | Google Scholar

Yong, S. H., and Zhang, C. M. (1986). Logging data processing and comprehensive interpretation. Beijing: China University of Petroleum Press.

Google Scholar

Zeng, L. B., Su, H., Tang, X. M., Peng, Y. M., and Lei, G. (2013). Fractured tight sandstone oil and gas reservoirs: a new play type in the Dongpu depression. Bohai Bay basin, China. AAPG Bulletin 97 (3), 363–377. doi:10.1306/09121212057

CrossRef Full Text | Google Scholar

Zhang, H. M. (2010). Saturation interpretation model study on fractured reservoirs. East China: China University of Petroleum. [dissertation/master's thesis]. [China(Qingdao)].

Google Scholar

Zhang, J. Y., Liu, H. H., Liu, W., J. Sun, M., and Zhao, J. P. (2015). Thin sand and mudstone interbed saturation model based on a dual mudstone indicator. Petroleum Drilling Techniques 43 (02), 59–62. doi:10.11911/syztjs.201502011

CrossRef Full Text | Google Scholar

Zhang, L. H., Zhou, C. C., Liu, G. Q., Xiu, L. J., Li, C. X., and Liu, Z. H. (2006). Influence of pore structures on electric properties and well logging evaluation in low porosity and permeability reservoirs. Petroleum Exploration and Development 33 (06), 671–676. doi:10.3321/j.issn:1000-0747.2006.06.006

CrossRef Full Text | Google Scholar

Zhang, M. L., and Shi, Y. J. (2005). On archie’s electrical parameters of sandstone reservoir with complicated pore structures. Well Logging Technology 29 (01), 21-23+28–12. doi:10.16489/j.issn.1004-1338.2005.05.016

CrossRef Full Text | Google Scholar

Zhang, X., Li, Q. P., Li, L. X., Fan, Q., and Geng, J. H. (2023). Combination of sonic wave velocity, density and electrical resistivity for joint estimation of gas-hydrate reservoir parameters and their uncertainties. Advances in Geo-Energy Research 10 (2), 133–140. doi:10.46690/ager.2023.11.07

CrossRef Full Text | Google Scholar

Zhao, G. J., Li, X. Q., Liu, M. C., Dong, C. Y., Chen, D. Y., and Zhang, J. (2022). Reservoir characteristics of tight sandstone and sweet spot prediction of Dibei gas field in eastern Kuqa depression, northwest China. Energies 15 (9), 3135. doi:10.3390/en15093135

CrossRef Full Text | Google Scholar

Zhao, H., Shi, X., and SiMa, L. Q. (2012). Study on porosity exponent, saturation and fracture porosity for fractured reservoirs. Progress in Geophysics. (in Chinese) 27 (6), 2639–2645. doi:10.6038/j.issn.1004-2903.2012.06.043

CrossRef Full Text | Google Scholar

Zhao, P. Q., Wang, Y. T., Li, G. R., Hu, C., Xie, J. R., Duan, W., et al. (2023). Joint inversion of saturation and qv in low-permeability sandstones using spontaneous potential and resistivity logs. Petrophysics 64, 741–752. doi:10.30632/PJV64N5-2023a8

CrossRef Full Text | Google Scholar

Zhou, X. Q., Zhang, C., Zhang, Z. S., Zhang, R. F., Zhu, L. Q., and Zhang, C. M. (2019). A saturation evaluation method in tight gas sandstones based on diagenetic facies. Marine and Petroleum Geology 107, 310–325. doi:10.1016/j.marpetgeo.2019.05.022

CrossRef Full Text | Google Scholar

Zou, C. N., Zhu, R. X., Liu, K. Y., Su, L., Bai, B. J., Zhang, X. X., et al. (2012). Tight gas sandstone reservoirs in China: characteristics and recognition criteria. Journal of Petroleum Science and Engineering 88 (89), 82–91. doi:10.1016/j.petrol.2012.02.001

CrossRef Full Text | Google Scholar