Validation of atmospheric evaporation duct in the eastern Indian Ocean

An atmospheric duct is an anomalous atmospheric structural phenomenon that causes trap refraction in the troposphere to change the propagation paths and ranges of electromagnetic waves, thereby increasing the detection distances of radar and other communications. Atmospheric ducts include evaporation, surface, and elevated ducts. Evaporation ducts are commonly found near the sea surface and can impact electromagnetic wave propagation, radar communication, and livelihood applications at low altitudes. The meteorological environment of the Indian Ocean is complex, and the characteristics of its evaporation duct are still poorly understood. We validate four select atmospheric duct models using the observed evaporation duct height (EDH) in the Indian Ocean and present their spatial as well as temporal characterizations in spring using in situ meteorological variables. The results show that the EDH derived using the Babin model has the lowest bias with the observed value; thus, the Babin model can be used by researchers in the future to study changes to the EDHs in sea areas with similar seasonal conditions. The EDH in the Indian Ocean has diurnal variations, with higher (lower) values during the daytime (nighttime). The EDH has a negative correlation with the relative humidity, and the standard deviation of the EDH is largest when the relative humidity is 90%. The EDH has the maximum value when the wind speed is in the range of 8–14 m/s and when the air–sea temperature difference is zero, i.e., $∆T=T_{air}-T_{sea}=0$. This study validates four different EDH models in the Indian Ocean, thus broadening our knowledge on the tropical atmospheric boundary layer.

1 Introduction

Atmospheric ducts are refractive layers occurring in the troposphere that affect the propagation of electromagnetic waves and greatly disturb radar detection (Mosczkowicz et al., 1994; Mesnard and Sauvageot, 2010). Hence, they have been important subjects of study since World War II (Kerr, 1951; Kirby and Sofaer, 1966; Vilar et al., 1993; Adel et al., 1996; Heemskerk and Boekema, 1993; Sarma, 1993). Atmospheric ducts are associated with inverse temperatures or sharp decreases in the water vapor content (Yang et al., 2023). Atmospheric ducts include evaporation, surface, and elevated ducts. The evaporation duct is formed as a result of evaporation near the sea surface, where the water content decreases with increasing height (Yang et al., 2023); this duct type usually has a height of less than 40 m, with an offshore occurrence probability of up to 80% at low latitudes (Liu et al., 1996). Moreover, meteorological variables can influence the evaporation duct, such as the sea surface evaporation rate, high-pressure subsidence, frontal processes, nocturnal radiation inversion, and advection. Zhu et al. (2022) categorized the surface duct type into temperature-induced (T-type) and humidity-induced (H-type) ducts.

Direct measurement of the evaporation duct height (EDH) is difficult, so several models have been proposed by researchers based on meteorological variables, such as the structural model based on Monin–Obukhov similarity theory (Jeske, 1973), Fairall model based on the flux coefficient algorithm (Fairall et al., 1978), P-J model proposed by Paulus (1985), MGB model proposed by Météo France based on the mesoscale forecasting system using the analytical method (Musson-Genon et al., 1992), refractivity from clutter (RFC) atmospheric duct inversion technique (Tabrikian et al., 1999), NPS model proposed by the U.S. Naval Postgraduate School (Babin and Dockery, 2002), RSHMU model proposed by the Russian State Hydrometeorological University (Dinc and Akan, 2015), and parabolic model (Zhu et al., 2018). The pseudorefractive index model for the evaporation duct was proposed by Liu et al. (2001) based on the Monin–Obukhov similarity theory. Some other advanced models have also been developed using optimal methods (Gerstoft et al., 2004). The accuracy of the EDH is important for characterizing the strength of the duct and is a key factor in determining the degree of influence on the observations of radar and other electronic devices (Cai et al., 2020); hence, we aim to examine the accuracies of traditional EDH evaluation models using in situ observations.

The EDH observations are mainly obtained from methods such as low-altitude sounding balloon detection, meteorological gradient tower detection, and microwave refractometer detection (Liu, 2002; Zhao et al., 2013). Low-altitude sounding balloon detection can be used to collect and store real-time and parametric measurements, but it suffers from inaccuracies due to hysteresis and calculation formula errors (Lin, 2002); although microwave refractometer detection is capable of detecting the atmospheric refractive index values at different altitudes for evaporation duct detection, it is more difficult to build towers at sea (Fan, 2015). Both the sounding balloon and microwave refractometer detection methods are suitable for single-point detection. Although meteorological gradient tower detection can provide time-series information of the EDH, the vertical resolution of its sampling points is low and tends to produce large errors. Evaporation duct prediction is helpful for radar detection. Liao et al. (2023) reported that accurate EDH prediction can be achieved using the deep forest method. Other scientists have used a new non-linear prediction algorithm called the Darwinian evolutionary algorithm (DEA) to realize short-term prediction of the EDH (Mai et al., 2020). Therefore, real-time observations of the EDH are necessary to compensate for the limitations of single-point detection methods when predicting the EDH.

The Indian Ocean has a unique geographical location and is surrounded by land on three sides. The Indian Ocean is a typical monsoon region owing to sea–land interactions; in contrast to the equatorial Pacific and Atlantic Oceans, the annual mean surface winds over the Indian Ocean are westerlies (Chen et al., 2015a). The tropical Indian Ocean circulation system includes equatorial and near-equatorial circulations, marginal sea circulation, and eddies. The Indian Ocean is a typical monsoon region with complex marine meteorological activities and multiscale oceanic motions, such as the Indian Ocean dipole (IOD) that is capable of influencing and potentially varying the seasonal climate phenomena like rainfall in the vicinity through sea–air interactions (Saji et al., 1999; Abram et al., 2008). The Madden–Julian oscillation (MJO) affects various types of weather and weather systems (Zhang, 2005). These meteorological variations and oceanic motions result in complex EDH characteristics. The accuracies of EDH models and spatial variations of the EDH are still unclear for the Indian Ocean.

In this study, we used ship-based equipment to derive the real-time EDH. The accuracies of several EDH models and the spatial distribution of the EDH in the Indian Ocean were also investigated based on a domestic evaporation duct system installed on the ship to achieve real-time detection. The data collection procedures and methods are outlined in Section 2. The characteristics and mechanisms of the EDH are discussed in Section 3 and Section 4. The conclusions of this study are presented in Section 5.

2 Data and methodology

2.1 Data

The “Shiyan 1” Research Vessel undertook a cruise from 10 March 2021 to 4 May 2021. The evaporation duct system in the vessel detects hydrometeorological elements automatically, including the sea surface skin temperature, sea surface temperature, barometric pressure, relative humidity, wind speed, wind direction, and EDH data, with a time resolution of 5 min. The real-time EDH was designed based on the Babin model. The specific sailing routes and experimental zones are shown in Figure 1. Four zones (i.e., E1, E2, E3, and E4) were chosen to investigate the spatial variations of the EDH, and these were individually investigated from Mar. 22–25, Mar. 29–Apr. 1, Apr. 3–6, and Apr. 20–23, respectively. To detect the temporal variations of the EDH, two replicate transects R1 and R2 were selected in the E1 zone.

Figure 1

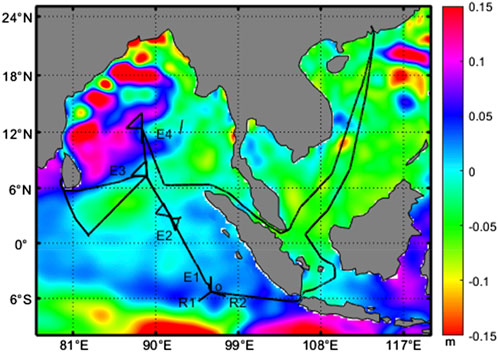
Figure 1. Background field data showing the mean sea level height anomalies for the time period from 10 March 2021 to 4 May 2021, where the specific navigation routes are shown in black line segments. The red boxes are the study zones E1, E2, E3, and E4. The repeat sections R1 and R2 are located in the E1 experimental area. The starting point of the repeated sections is point O, and the ending points are point 1 and point 2.

2.2 Methods

2.2.1 Evaporation duct refractive index profile calculation

The in situ EDH is based on the atmospheric refractivity distribution obtained from the air pressure, temperature, and humidity profiles (Babin and Rowland, 1992; Babin, 1996; Brooks et al., 1999; Mentes and Kaymaz, 2007; Cheng et al., 2015). The atmospheric refractive index $N$ is given by Equation 1

$N=\frac{a_1}{T_a}p+\frac{a_2}{{T_a}^2}\frac{pq}{0.622\left(1+0.608q\right)},(1)$

where p is the pressure, q is the specific humidity, and ${\text{a}}_1=77.6\times {10}^{-2}$ and ${\text{a}}_2=3.73\times {10}^3$ are the corresponding coefficients. To remove the influences of the Earth’s surface, the atmospheric corrected refractive index was obtained as $M=N+0.157h$, where h is the height from the sea surface, such that the EDH is obtained as the minimum value of $\mathrm{M}$.

2.2.2 Four models for EDH

2.2.2.1 P-J model

The P-J model was proposed by Paulus (1985), and the EDH according to this model is dependent on the air temperature, relative humidity, and wind speed.

The Monin–Obukhov length L is obtained as $\frac{1}{L}=\frac{R_i}{10z\mathit{\Gamma }}$ . The Richardson number is given by $R_i=\frac{g\left[T_a-T_s\right]z}{0.1\times T_a{u}^2}$, where $T_a,T_s,z,\text{and\hspace{0.17em}}u$ are the air temperature immediately above the sea surface, sea surface temperature, measurement height, and wind speed, respectively. The function $\mathit{\Gamma }$ is calculated from the value of $R_i$ as Equation 2:

$\mathrm{\Gamma }=\left\{\begin{array}{l}0.05if{R}_i\le -3.7\\ 0.065+0.004\times R_{i}if-3.75<R_i\le -0.12\\ 0.109+0.367\times R_{i}if-0.12<R_i\le 0.14\\ 0.155+0.021\times R_{i}if0.14\le R_i\end{array}\right..(2)$

The refractive index $∆N$ is calculated from the difference between the refractive index of air just above the sea surface $N_a$ and the refractive index of the water at the sea surface $N_s$ as Equation 3:

$∆N=N_a-N_s.(3)$

The refractive index of the air just above the sea surface $N_a$ and the related vapor pressure $\text{e}$ are expressed as Equations 4, 5:

$N_a=\frac{77.6}{T_a\left[1000+4810\frac{e}{T_a}\right]},(4)$

$e=\frac{h_m}{100}\left[6.105\times \mathit{exp}\left[25.22〈\frac{T_a-273.2}{T_a}〉-5.31\mathit{ln}〈\frac{T_a}{273.2}〉\right]\right],(5)$

where h_m is the humidity.

The refractive index of the water at the sea surface ${\mathrm{N}}_{\mathrm{s}}$ and the sea surface vapor pressure ${\text{e}}_{\text{s}}$ are derived as Equations 6, 7:

$N_s=\frac{77.6}{T_s\left[1000+4810\frac{e_s}{T_s}\right]},(6)$

$e_{\mathrm{s}}=6.105\times \exp \left[25.22〈\frac{T_s-273.2}{T_s}〉-5.31\mathit{ln}〈\frac{T_s}{273.2}〉\right].(7)$

The stability of the ocean–atmosphere interface is related to the value of the Richardson number. The steady state is represented by $0\le R_i\le 1$, and the unstable state is given by $R_i<0$. The calculation formula for the EDH, i.e., $Z_d$, is given by Equation 8

$Z_d=\left\{\begin{array}{ll}0& ∆N\ge 0\\ \frac{∆N}{-0.125\left(\mathit{ln}\frac{z}{z_0}+5.2\frac{z}{L}\right)-5.2\frac{∆N}{L}}& ∆N<0\end{array}\right.,0\le R_i\le 1,(\mathrm{8a})$

where $z_0=0.00015\mathrm{m}$; thus,

$Z_d=\frac{1}{4\sqrt{{\mathrm{A}}^4-18\frac{{\mathrm{A}}^3}{\mathrm{L}}}},R_i<0,(\mathrm{8b})$

where $A=-0.125\frac{B}{∆N},\text{and\hspace{0.17em}}B=\mathit{ln}\left(\frac{z}{z_0}\right)-\phi$.

2.2.2.2 Babin model

The tropical ocean global atmosphere coupled ocean–atmosphere response experiment (TOGA COARE) model was used to solve for the characteristic scale parameters, Monin–Obukhov length $\mathit{L}$, as well as the universal functions of humidity, wind speed, and potential temperature (Kang et al., 2014).

$T\left(z\right)=T_s+\frac{{\theta }_{*}}{\kappa }\left[\mathit{ln}\frac{z}{z_{\theta }^0}-\psi h\left(\frac{z}{L}\right)\right],(\mathrm{9a})$

$q\left(z\right)=q_s+\frac{q_{*}}{\kappa }\left(\mathit{ln}\frac{z}{z_{\theta }^0}-\psi q\left(\frac{z}{L}\right)\right),(\mathrm{9b})$

$U\left(z\right)=\frac{U_{*}}{\kappa }\left(\mathit{ln}\frac{z}{z_q^0}-\psi u\left(\frac{z}{L}\right)\right),(\mathrm{9c})$

In Equation 9 $T\left(z\right),q\left(z\right),\text{and\hspace{0.17em}}U\left(z\right)$ are the dimensionless universal contour equations for the air temperature, specific humidity, and wind speed at height z, respectively; ${\theta }_{*},q_{*},\text{and\hspace{0.17em}}{U}_{*}$ are the Monin–Obukhov scaling parameters; q_s is the specific humidity of the sea surface; $z_{\theta }^0\text{\hspace{0.17em}and\hspace{0.17em}}{z}_q^0$ are the temperature roughness and humidity roughness, respectively; $\psi h\left(\frac{z}{L}\right),\psi q\left(\frac{z}{L}\right),\text{and\hspace{0.17em}}\psi u\left(\frac{z}{L}\right)$ are the temperature, specific humidity, and wind speed advection functions.

From Equation 1, Equation 10 can be derived,

$\left\{\begin{array}{l}\frac{\partial N}{\partial z}=b_1+b_2\frac{\partial T_a}{\partial z}+b_3\frac{\partial q}{\partial z}\\ \begin{array}{l}{b}_1=\frac{\partial N}{\partial p}·\frac{\partial p}{\partial z}=\left[\frac{a_1}{T_a}+\frac{a_2}{{T_a}^2}\times \frac{q}{0.622\left(1+0.608q\right)}\right]\left(-\rho g\right)\\ b_2=\frac{\partial N}{\partial T}=\frac{a_2}{{T_a}^2}\times \frac{q}{{0.622\left(1+0.608q\right)}^2}\\ b_3=\frac{\partial N}{\partial q}·\frac{\partial p}{\partial z}=\frac{a_2}{{T_a}^2}\times \frac{p}{{0.622\left(1+0.608q\right)}^2}.\end{array}\end{array}\right.(10)$

From the relationship between the potential temperature and temperature, we have

$\left\{\begin{array}{l}\frac{\partial N}{\partial z}=c_1+c_2\frac{\partial \theta }{\partial z}+c_3\frac{\partial q}{\partial z}\\ c_1=b_1-\frac{b_2\mathrm{g}}{\text{Cpa}\left(1+0.608\mathrm{q}\right)}\\ c_2=b_2{\left(\frac{\mathrm{p}}{{10}^5}\right)}^{\frac{\text{Ra}}{\text{Cpa}}}\\ 3\\ c_3=b_3\end{array}\right.,(11)$

In Equation 11 Cpa is the specific heat of dry air, Ra is the gas constant of dry air, $\rho$ is the air density, and g is the gravitational acceleration.

Babin used the salinity revision proposed by Sverdrup et al. (1943) to calculate the specific humidity of saturation at the sea surface $q_s$ as Equation 12:

$q_s=0.98q_{sat}\left(T_s\right),(\mathrm{12a})$

$q_{sat}\left(T_s\right)=\frac{0.622e_{sat}\left(T_s\right)}{p-0.378e_{sat}\left(T_s\right)}.(\mathrm{12b})$

The saturated water vapor pressure at the sea surface $q_{sat}$ is a function of the saturated water vapor pressure $e_{sat}$ (Buck, 1981) given by Equation 13

$e_{sat}\left(T_s\right)=6.1121\left(1.0007+3.46\times {10}^{-6}p\right)\mathit{exp}\left[\frac{17.502\left(T_s-273.16\right)}{240.97+\left(T_s-273.16\right)}\right].(13)$

Under stable and neutral conditions, the EDH $Z_d$ is defined as Equation 14

$Z_d=-\frac{c_2{\theta }_{*}+c_3{q}_{*}}{k\left(c_1+0.157\right)+\frac{5}{L}\left(c_2{\theta }_{*}+c_3{q}_{*}\right)}.(14)$

Under unstable lamination conditions, the EDH $Z_d$ is defined as Equation 15

$Z_d=\frac{c_2{\mathrm{\theta }}_{*}+c_3{\mathrm{q}}_{*}}{\mathrm{k}\left(-0.157-c_1\right)}{\mathrm{\phi }}_{\mathrm{\theta }}\left(\frac{\mathrm{d}}{\mathrm{L}}\right).(15)$

2.2.2.3 NPS model

The NPS model also uses the TOGA COARE model and Monin–Obukhov length:

$T\left(z\right)=T_s+\frac{{\theta }_{*}}{\kappa }\left[\mathit{ln}\frac{z}{z_{\theta }^0}-\psi h\left(\frac{z}{L}\right)\right]-\mathit{\Gamma }z,(16)$

In Equation 16 $\mathit{\Gamma }=0.00976K/m$.

The dimensional and roughness parameters of the sea surface were calculated using the COARE 3.0 algorithm, and the stability correction function ${\psi }_h$ applied to the wind speed and temperature under steady conditions is calculated as Equation 17:

${\psi }_h=-\frac{5\sqrt{5}}{4}\mathit{ln}\left(1+3\xi +{\xi }^2\right)\times \left(\mathit{ln}\frac{2\xi +3\sqrt{5}}{2\xi +5.24}+1.93\right),(17)$

where $\xi =z/L$.

In this model, the air pressure is expressed as Equation 18

$p\left(z_1\right)=p\left(z_0\right)\times \exp \left(\frac{1.2\times \left({\mathrm{z}}_0-{\mathrm{z}}_1\right)}{{\mathrm{T}}_{\mathrm{m}}}\right),(18)$

where $p\left(z_1\right)$ and $p\left(z_0\right)$ are the air pressures at measurement heights ${\text{z}}_1\text{\hspace{0.17em}and\hspace{0.17em}}{z}_0$, respectively, and ${\text{T}}_{\text{m}}$ is the mean value of the virtual potential temperatures at heights $z_1\text{\hspace{0.17em}and\hspace{0.17em}}{z}_0$.

$e=\frac{qP}{\epsilon +\left(1-\epsilon \right)q},(19)$

In Equation 19 ε is the ratio of the dry-air gas constant to the water vapor constant (0.622).

2.2.2.4 RSHMU model

In this model, the wind speed and temperature profile stability functions are expressed as Equation 20:

${\psi }_u\left(\xi \right)=\left\{\begin{array}{ll}\frac{3}{2}\mathit{ln}\frac{1+x_1+x_1^2}{3}-\sqrt{3}\mathit{arctan}\left(\frac{2x_1+1}{\sqrt{3}}+\frac{\pi }{\sqrt{3}}\right)& \xi \le 0\\ -{\gamma }_1\xi & \xi >0\end{array}\right.,(\mathrm{20a})$

${\psi }_h\left(\xi \right)=\left\{\begin{array}{l}1.5\mathit{ln}\left(1+{\beta }_1{\xi }^2\right)+\\ 0.7({\frac{3}{2}\mathit{ln}\frac{1+y_1+y_1^2}{3}-\sqrt{3}\mathit{arctan}\left(\frac{2x_1+1}{\sqrt{3}}+\frac{\pi }{\sqrt{3}}\right)}^{-1/3}& \xi \le 0,\\ -{\gamma }_2\xi & \xi >0\end{array}\right.(\mathrm{20b})$

where $x_1={\left(1-{\beta }_1\xi \right)}^{1/3}$ and $y_1={\left(1-{\beta }_2\xi \right)}^{1/3}$, with ${\beta }_1=8$, ${\beta }_2=$ 35, and constant values of ${\gamma }_1=8$ and ${\gamma }_2=6$.

3 Results

3.1 Temporal variation in the EDH

Figure 2 shows the diurnal variations of the in situ EDH values from 0:00 UTC on April 5 to 0:00 UTC on April 9 as measured using the evaporation duct system. It is noted that the EDH value is greater during daytime and lower at night. The EDH first increases and then decreases, with mean values of 15.1 m and 14.8 m during the daytime and nighttime, respectively. There is an obvious opposite trend between the EDH and relative humidity.

Figure 2

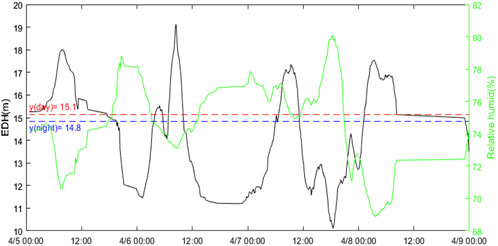
Figure 2. Diurnal variations in the EDH (black) and relative humidity (green). The red dashed line is the mean EDH during daytime (LT 6:00–18:00), and the blue dashed line is the mean EDH at night (LT 18:00–6:00).

Figure 3 shows the in situ EDH variations at two repeated cross sections R1 and R2 having different observation times; these durations are divided into t1 (from 2:35 on March 22 to 01:30 on March 23) and t2 (from 01:30 to 13:10 on March 23) for the R1 transection as well as t3 (from 13:10 to 22:15 on March 23) and t4 (22:15 on March 23 to 13:40 on March 24) for the R2 transection. In the R1 area, the EDH increased from south to north during both t1 and t2. Excluding the spatial trends, the oscillation of EDH during t1 is more significant than that during t2, which may be induced by the high temporal interval during t1. There is no obvious trend from 5.8° S to 5.5° S at the R2 transection, which may be attributed to the limited zonal area. In the R2 area, the EDH is greater during t3 than t4.

Figure 3

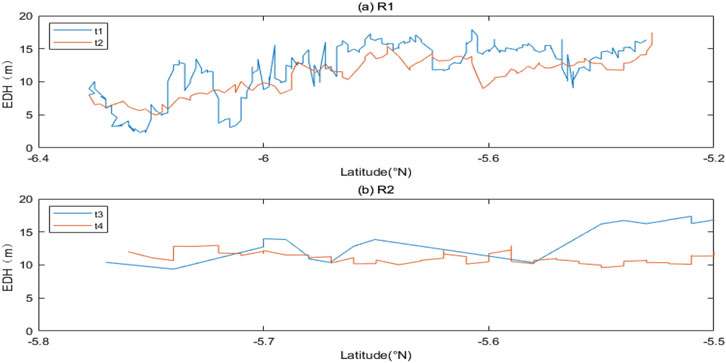
Figure 3. EDH variations at the (A) R1 and (B) R2 transections. The blue and red lines indicate the t1 (t3) and t2 (t4) periods, respectively.

3.2 Spatial variation in the EDH

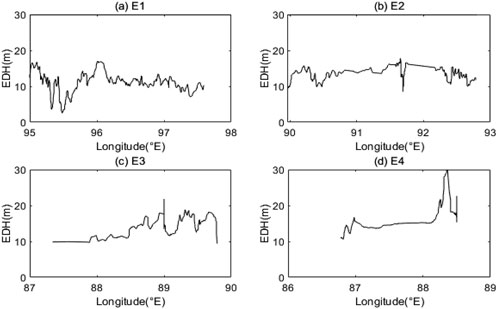
The variations of the EDH in the different zones are shown in Figure 4. E1 has the lowest EDH value of 5 m, while E4 has the largest EDH value of 30 m. The EDH in the entire experimental area of E2 does not have obvious variations; this may be induced by the oceanic motions below the atmosphere. Note that a low sea level anomaly zone with low temperature develops to the east of the E4 zone (Figure 1), which could increase the EDH owing to the low evaporation rate.

Figure 4

Figure 4. Spatial variations in the EDH at (A) E1, (B) E2, (C) E3, and (D) E4.

3.3 Validation of the modeled EDH

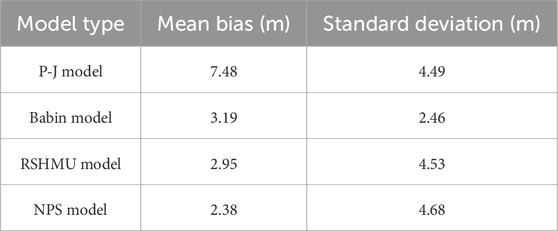
Figure 5 shows the EDH variations from the four models along with the in situ value measured using the evaporation duct system. It is observed that the Babin model curve is the best fit for the actual curve. Compared to the in situ value, the mean biases and standard deviations (in parentheses) of the P-J, Babin, RSHMU, and NPS models are 7.48 (4.49), 3.19 (2.46), 2.95 (4.53), and 2.38 (4.68) m, respectively (Table 1). Therefore, the accuracy of the Babin model is the highest among the four models and can be used by researchers to study the EDH in the corresponding sea area. However, it remains to be seen whether this model is applicable to other sea areas and times, which would need to be validated in future studies.

Figure 5

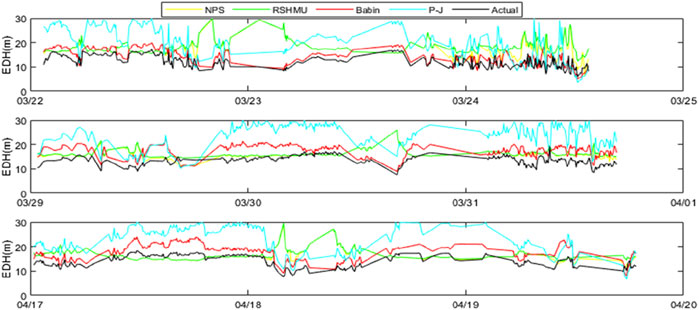
Figure 5. EDH variations for March 22–25, March 29 to April 1, and April 17–20 during the study period. The black, red, green, blue, and yellow lines are the EDH values from the in situ, Babin, RSHMU, P-J, and NPS measurements, respectively.

Table 1

Table 1. Mean biases and standard deviations of the EDH between the four models and in situ value.

4 Discussion

There are obvious spatial and temporal differences in the EDH. In addition to the basic conditions of the ocean, meteorological variables like wind speed, humidity, and atmospheric temperature may influence the EDH (Ding et al., 2015). We used the EDH measurement obtained using an evaporation duct system to study the relationship of the actual EDH to the meteorological variables.

The scatter plots between the EDH and meteorological variables are shown in Figure 6. As the relative humidity increases, the EDH decreases gradually, which is consistent with the conclusions of Twigg (2007). When the relative humidity is 90%, the standard deviation of the EDH is maximum, which could be attributed to the sparse samples. The EDH has the maximum value when the wind speed is in the range of 8–14 m/s, which could be explained by the stability of the atmospheric boundary layer; when the wind speed exceeds 14 m/s, the relative humidity is reduced. Ding et al. (2015) found that the EDH increases as the wind speed increases from 0–10 m/s, and they attributed this to the developing mechanical turbulence. Meanwhile, the mixing effect of the wind speed can change the air temperature, relative humidity, and vapor pressure, further affecting the EDH. The air–sea temperature difference $∆T=T_a-T_s$ directs the stability of the atmosphere; that is, when the difference $∆T>0$, the atmosphere is stable; when $∆T=0$, the atmosphere is under a neutral condition; when $∆T<0$, the atmosphere is considered to be unstable. Figure 6C shows that when the air–sea temperature difference is zero, the EDH has the maximum value. Paulus (1985) also suggested that the EDH is maximum when the atmosphere is under a neutral condition.

Figure 6

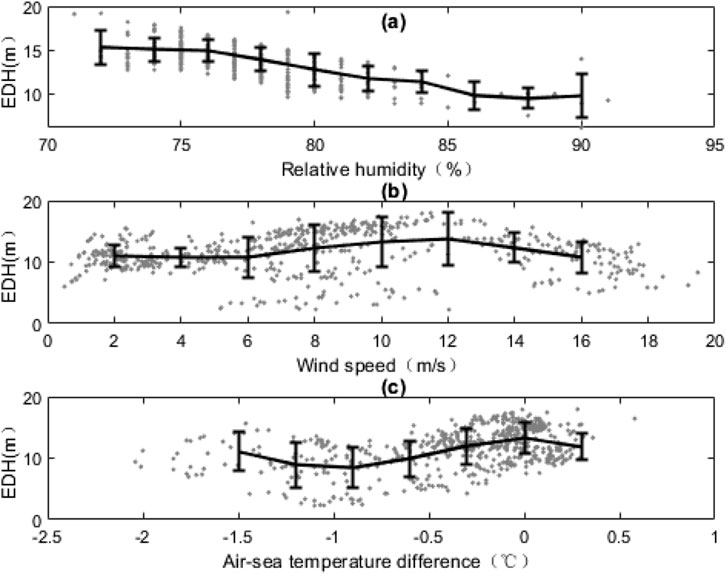
Figure 6. Scatter plots between the meteorological variables and EDH: (A) relative humidity, (B) wind speed, and (C) air–sea temperature difference. The error bars represent the standard deviations of the EDH for every 2% change in relative humidity, 2 m/s change in wind speed, and 0.3°C difference in air–sea temperature.

5 Conclusion

Using the observations obtained with an evaporation duct system onboard a research vessel, we present the spatial and temporal variations in the EDH and its possible mechanisms based on evaluations using four EDH models. The findings of this work are as follows:

(1) Based on the in situ EDH measurement in the Indian Ocean, we validated four models of EDH, namely the Babin, P-J, RSHMU, and NPS models. We found that the Babin model has the smallest standard deviation compared to the obtained measurements.

(2) The EDH has a significant diurnal variation, with higher values during the daytime. Spatially, the EDH has a minimum value of 5 m in the south (E1 zone) and a maximum value of 30 m in the north (E4 zone).

(3) The EDH is closely related to meteorological variables like the relative humidity, wind speed, and air–sea temperature difference. The relative humidity is negatively correlated with the EDH, and the standard deviation of EDH value is largest when the relative humidity is 90%. Greater values of the EDH correspond to wind speeds of 8–14 m/s, which may be attributed to the stability of the atmospheric boundary layer. Larger EDH values may also be observed under neutral conditions (when $∆T=0$).

Based on a new real-time observation system, we measured the EDH to provide a reliable value and determine the most suitable model applicable to the evaporation duct in the Indian Ocean. Moreover, we provide viable data to predict the EDH. This study not only broadens our knowledge of the marine atmospheric boundary layer but also supports research efforts on marine radar, electromagnetic wave propagation, and marine combat.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

ZQ: conceptualization, investigation, methodology, software, supervision, writing–original draft, and writing–review and editing. HM: funding acquisition, resources, and writing–review and editing. CQ: writing–review and editing, conceptualization, and methodology. YQ: conceptualization, software, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This study was suported by the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant No. XDC0190101, the National Key R&D Plan of China, Grant Nos. 2021YFC2803104, 2021YFC3101301, and 2022YFC3104403, the National Natural Science Foundation of China, Grant No. 42276193.

Acknowledgments

The authors thank the crew of the research vessel “Shiyan 1,” as well as other scientists and technicians available during the cruise. The authors also acknowledge the scholars and organizations who helped with this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abram, N., Gagan, M., Cole, J., Hantoro, W. S., and Mudelsee, M. (2008). Recent intensification of tropical climate variability in the Indian Ocean. Nat. Geosci. 1, 849–853. doi:10.1038/ngeo357

CrossRef Full Text | Google Scholar

Adel, A. S., Abo, S., and Samila, T. (1996). Transient electromagnetic field of a vertical electric dipole above an atmospheric surface duct. Radio Sci. 31 (4), 833–840. doi:10.1029/96rs00283

CrossRef Full Text | Google Scholar

Babin, S. M. (1996). Surface duct height distributions for Wallops Island, Virginia, 1985-1994[J]. Appl. Meteorology 35 (1), 86–93. doi:10.1175/1520-0450

CrossRef Full Text | Google Scholar

Babin, S. M., and Dockery, G. D. (2002). LKB-based evaporation duct model comparison with buoy data[J]. Appl. Meteor.Climatol. 41, 434–446. doi:10.1175/1520-0450(2002)041<0434:lbedmc>2.0.co;2

CrossRef Full Text | Google Scholar

Babin, S. M., and Rowland, J. R. (1992). Observation of a strong surface radar duct using helicopter acquired fine-scale radio refractivity measurements. Geophys. Res. Lett. 19 (9), 917–920. doi:10.1029/92GL00562

CrossRef Full Text | Google Scholar

Brooks, I. M., Goroch, A. K., and Rogers, D. P. (1999). Observations of strong surface radar ducts over the Persian Gulf[J]. Appl. Meteorology 38 (9), 1293–1310. doi:10.1175/1520-0450(1999)038<1293:oossrd>2.0.co;2

CrossRef Full Text | Google Scholar

Buck, A. L. (1981). New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorology Climatol. 20 (12), 1527–1532. doi:10.1175/1520-0450(1981)020<1527:nefcvp>2.0.co;2

CrossRef Full Text | Google Scholar

Cai, X., Wang, J., He, X., Zhang, S., Zhu, Q., and Hu, J. (2020). Research on change features of evaporation duct over the East China Sea. Chin. J. radio Sci. 35 (3), 372–376. doi:10.13443/j.cjors.2019111901

CrossRef Full Text | Google Scholar

Chen, G., Han, W., Li, Y., Wang, D., and McPhaden, M. (2015a). Seasonal-to-interannual time-scale dynamics of the equatorial undercurrent in the Indian ocean. J. Phys. Oceanogr. 45, 1532–1553. doi:10.1175/JPO-D-14-0225.1

CrossRef Full Text | Google Scholar

Cheng, Y., Zhou, S., Wang, D., Lu, Y., and Yao, J. (2015). Statistical characteristics of the surface ducts over the South China Sea from GPS radiosonde data. Acta Oceanol. Sin. 34 (11), 63–70. doi:10.1007/s13131-015-0749-x

CrossRef Full Text | Google Scholar

Dinc, E., and Akan, O. B. (2015). Channel model for the surface ducts: large-scale path-loss, delay spread, and AOA. IEEE Trans. Antennas Propag. 63 (6), 2728–2738. doi:10.1109/TAP.2015.2418788

CrossRef Full Text | Google Scholar

Ding, J., Fei, J., Huang, X., Cheng, X., Hu, X., and Ji, L. (2015). Development and validation of an evaporation duct model. Part I: model establishment and sensitivity experiments. J. Meteorol. Res. 29, 467–481. doi:10.1007/s13351-015-3238-4

CrossRef Full Text | Google Scholar

Fairall, C. W., Houlihan, T. M., Davidson, K. L., and Schacher, G. E. Evaporation duct height measurements in the mid-atlantic[J]. prepared for naval oceanographic office, 1978.

Google Scholar

Fan, J. (2015). Study on the method of detecting atmospheric duct[D]. Ocean University of China.

Google Scholar

Gerstoft, P., Hodgkiss, W., Rogers, L., and Jablecki, M. (2004). Probability distribution of low altitude propagation loss from radar sea-clutter data. Radio Sci. 39, 1–9. doi:10.1029/2004RS003077

CrossRef Full Text | Google Scholar

Heemskerk, H. J. M., and Boekema, R. B. (1993) “The influence of evaporation duct on the propagation of electromagnetic waves low above the sea surface at 3-94 GHz[C]//Antennas and Propagation,” in Eighth international conference on. IET. doi:10.1007/s00606-006-0489-7

CrossRef Full Text | Google Scholar

Jeske, H. (1973) State and limits of prediction methods of radar wave propagation conditions over sea, 36. Netherlands: Springer, 130–148.

Google Scholar

Kang, S., Zhag, Y., and Wang, H. (2014). Atmospheric duct in troposphere environment. 1st ed. Beijing, China: Science Press, 85–86.

Google Scholar

Kerr, D. E. (1951). Propagation of short radio waves. New York: MIT Radiation Laboratory Series, 1–22. doi:10.1126/science.114.2964.425

CrossRef Full Text | Google Scholar

Kirby, R. S., and Sofaer, E. (1966) “Radiowaves: Tropospheric Radiowave Propagation beyond the Horizon. François du Castel,”. New York: tr. Pergamon, 183–184. Science155. doi:10.1126/science.155.3759.183.b

CrossRef Full Text | Google Scholar

Liao, Q., Mai, Y., Sheng, Z., Wang, Y., Ni, Q., and Zhou, S. (2023). The comparison of long short-term memory neural network and deep forest for the evaporation duct height prediction. IEEE Trans. Antennas Propag. 71 (5), 4444–4450. doi:10.1109/TAP.2023.3254201

CrossRef Full Text | Google Scholar

Lin, F. (2002). The measurements of atmospheric duct near sea surface and its comparison with other study results. Chin[J]. Radio Sci. doi:10.1007/s11769-002-0041-9

CrossRef Full Text | Google Scholar

Liu, C., Pan, Z., and Guo, L. (1996) Statistical analysis of occurrence and characteristics of atmospheric ducts in China. Chin[J]. Radio Sci., 11(2):60–66.

Google Scholar

Liu, C.-G. (2002). The occurrence of tropospheric ducts over the south-eastern coast of China. Chin[J]. Radio Sci.

Google Scholar

Liu, C.-G., Huang, J., Jiang, C., and Lin, F. (2001). Modeling evaporation duct over sea with pseudo-refractivity and similarity theory[J]. Acta Electron. Sin. 29(7): 970–972.

Google Scholar

Mai, Y., Sheng, Z., Shi, H., Li, C., Liao, Q., and Bao, J. (2020). A new short-term prediction method for estimation of the evaporation duct height. IEEE Access 8, 136036–136045. doi:10.1109/ACCESS.2020.3011995

CrossRef Full Text | Google Scholar

Mentes, S. S., and Kaymaz, Z. (2007). Investigation of surface duct conditions over Istanbul, Turkey [J]. Appl. Meteorology Climatol. 46 (3), 318–337. doi:10.1175/JAM2452.1

CrossRef Full Text | Google Scholar

Mesnard, F., and Sauvageot, H. (2010). Climatology of anomalous propagation radar echoes in a coastal area [J]. Appl. Meteorology Climatol. 49 (11), 2285–2300. doi:10.1175/2010JAMC2440.1

CrossRef Full Text | Google Scholar

Mosczkowicz, S., Ciach, G. J., and Krajewski, W. F. (1994). Statistical detection of anomalous propagation in radar reflectivity patterns [J]. Atmos. Ocean. Technol. 11 (4), 1026–1034. doi:10.1175/1520-0426(1994)011<1026:sdoapi>2.0.co;2

CrossRef Full Text | Google Scholar

Musson-Genon, L., Gauthier, S., and Bruth, E. (1992). A simple method to determine evaporation duct height in the sea surface boundary layer. Radio Sci. 27 (5), 635–644. doi:10.1029/92rs00926

CrossRef Full Text | Google Scholar

Paulus, R. A. (1985). Practical application of an evaporation duct model. Radio Sci. 20 (4), 887–896. doi:10.1029/rs020i004p00887

CrossRef Full Text | Google Scholar

Saji, N., Goswami, B., Vinayachandran, P., and Yamagata, T. (1999). A dipole mode in the tropical Indian Ocean. Nature 401, 360–363. doi:10.1038/43854

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarma, S. B. S. S. (1993). Airborne microwave refractometer studies over the Indian subcontinent for exploiting electromagnetic propagation effects[J].

Google Scholar

Sverdrup, H. U., Johnson, M. W., and Fleming, R. H. (1943). The oceans: their physics, chemistry, and general biology. Copeia 1943, 261. doi:10.2307/1438154

CrossRef Full Text | Google Scholar

Tabrikian, J., Krolik, J., and Vasudevan, S. (1999). “Estimating tropospheric refractivity parameters from radar sea clutter,” in Proceedings of the IEEE signal processing workshop on caesarea (Israel), 345–348.

Google Scholar

Twigg, K. (2007). “A smart climatology of evaporation duct height and surface radar propagation,” in The Indian ocean.

Google Scholar

Vilar, E., Austin, J., and Tawfik, A. N. (1993) Narrow and wide band transhorizon propagation studies at X B and [C].

Google Scholar

Yang, N., Su, D., and Wang, T. (2023). Atmospheric ducts and their electromagnetic propagation characteristics in the northwestern south China sea. Remote Sens. 15, 3317. doi:10.3390/rs15133317

CrossRef Full Text | Google Scholar

Zhang, C. (2005). Madden-julian oscillation. Rev. Geophys. 43 (2), RG2003. doi:10.1029/2004RG000158

CrossRef Full Text | Google Scholar

Zhao, X., Wang, D., Huang, S., Huang, K., and Chen, J. (2013). Statistical estimations of atmospheric duct over the South China Sea and the tropical eastern Indian Ocean. Chin. Sci. Bull. 58, 2794–2797. doi:10.1007/s11434-013-5942-8

CrossRef Full Text | Google Scholar

Zhu, J., Zou, H., Kong, L., Zhou, L., Li, P., Cheng, W., et al. (2022). Surface atmospheric duct over Svalbard, Arctic, related to atmospheric and ocean conditions in winter. Arct. Antarct. Alp. Res. 54 (1), 264–273. doi:10.1080/15230430.2022.2072052

CrossRef Full Text | Google Scholar

Zhu, X., Li, J., Zhu, M., Jiang, Z., and Li, Y. (2018). An evaporation duct height prediction method based on deep learning. IEEE Geoscience Remote Sens. Lett. 15, 1307–1311. doi:10.1109/lgrs.2018.2842235

CrossRef Full Text | Google Scholar