Kinematic GNSS inversion of the large afterslip (Mw 6.4) following the 2019 Mw 6.2 Hualien earthquake (Taiwan)

The postseismic deformation following the April 2019 Mw 6.2 Hualien earthquake presents an unique opportunity to investigate the mechanisms by which the northern section of the Longitudinal Valley accommodates lithospheric deformation. We apply a variational Bayesian independent component analysis approach to displacement time-series to infer a 6-month long afterslip. Kinematic inversion shows that displacements are well explained by widespread afterslip (∼60 km in the along-strike direction) with limited slip (≤0.1 m) surrounding the coseismic slip area. The total geodetic moment relieved by afterslip (M0 ∼ 4.6 × 10¹⁸ Nm, i. e., Mw ∼ 6.4) is twice as large as the mainshock seismic moment, which represents a rare exception of a moderate magnitude event for which the afterslip moment exceeds that of the seismic moment. Then, combining geodetic and seismological analysis, we infer that afterslip is the dominant mechanism of near-to intermediate-field postseismic deformation and also likely represents the driving force that controls aftershock productivity and the spatiotemporal migration of seismicity. Besides, the fault zone frictional stability parameter a-b of rate-and-state dependent friction (a-b ∼ 0.0067–0.02) is comparable with previous estimates in the Longitudinal Valley. Finally, the study demonstrates that the northern Longitudinal Valley region hosts complex seismogenic structures that display a variety of slip behaviors.

1 Introduction

Geodetic measurements have revealed that earthquakes are generally followed by a phase of postseismic relaxation gradually decaying with time. Postseismic deformation, which represents the Earth’s response to coseismic stress perturbations, can last hours to years following an earthquake (Fukuda and Johnson, 2021; Zhao et al., 2022). Several mechanisms are commonly involved in postseismic deformation, including afterslip on fault portions surrounding the coseismic rupture (Marone et al., 1991) or on nearby faults (Tang et al., 2023), viscoelastic flow in the lower crust and/or upper mantle (Bürgmann and Dresen, 2008; Fukuda and Johnson, 2021) and poroelastic fluid flow in the shallow crust (Peltzer et al., 1996; McCormack et al., 2020). Postseismic deformation usually contributes significantly more to earthquake moment release than aftershocks (Gualandi et al., 2020) and afterslip is often considered as the primary force that drives aftershocks (Perfettini and Avouac, 2004; Canitano et al., 2018).

Located at the collisional boundary between the Eurasian plate (EP) and the Philippine Sea plate (PSP), Taiwan is a highly active seismic and tectonic zone. In eastern Taiwan, the Longitudinal Valley (LV) represents the suture of the collision (Barrier and Angelier, 1986), accounting for a third of tectonic plate convergence (Yu and Kuo, 2001). A major part of the oblique plate convergence (geodetic rate $\sim$ 40 mm${\mathrm{y}\mathrm{r}}^{-1}$) is accommodated by the Longitudinal Valley fault (LVF) (Thomas et al., 2014), which bounds the eastern flank of the LV, and represents the main active fault in eastern Taiwan (Yu and Kuo, 2001). The Central Range fault (CRF) dips westward beneath the western flank of the LV, contributing to the rapid uplift (geological rate of 3–10 mm${\mathrm{y}\mathrm{r}}^{-1}$) of the Central Range (Shyu et al., 2006). The Hualian region in the northern LV is located in a complex post-collisional environment (Shyu et al., 2016; Lin et al., 2023a) characterized by the transition from the Ryukyu subduction to the collision between the Luzon arc and the Chinese continental margin (Rau et al., 2008) (Figure 1). This complex tectonic setting creates various seismogenic structures associated with destructive earthquakes [e.g., 1951 $M_L$ 7.3 Hualien-Taitung sequence (Chen et al., 2008), 2018 $M_w$ 6.4 Hualien earthquake (Huang and Huang, 2018) or the 2024 $M_w$ 7.4 event (Chang et al., 2024)] and also with frequent seismic swarms (Rau and Liang, 2022; Huang and Wang, 2022).

Figure 1

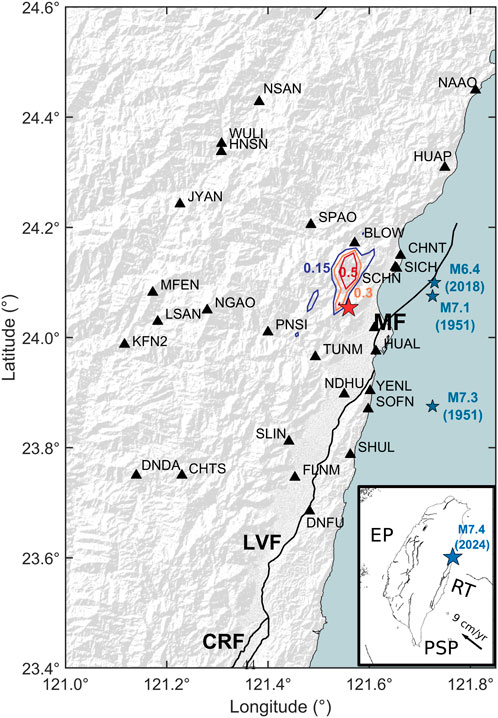
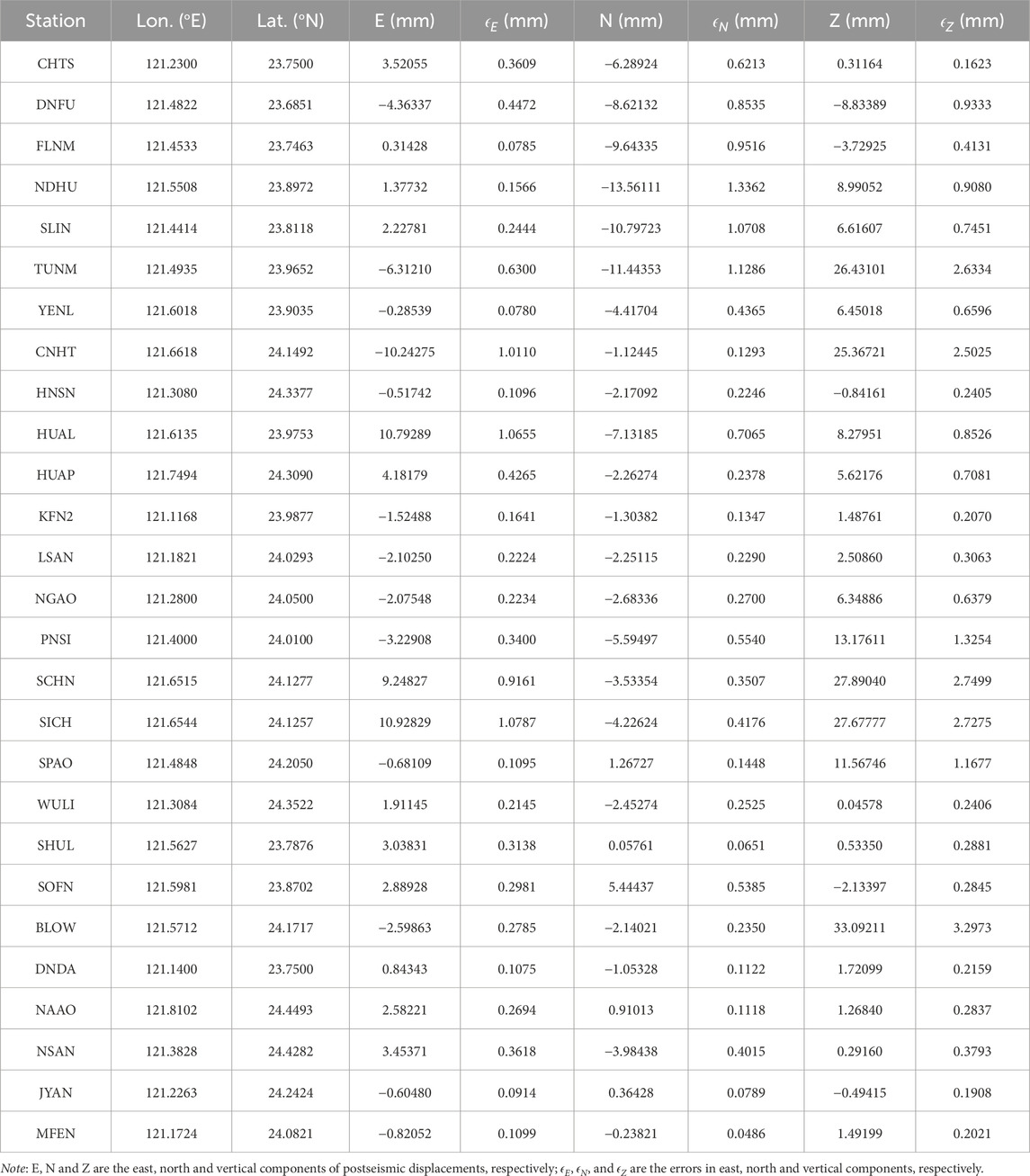
Figure 1. Map of eastern Taiwan. The red star shows the epicenter of the 2019 Hualien earthquake and colored contours outline the coseismic slip distribution (with 0.15, 0.30 and 0.50-m intervals) of the Lee et al. (2020) finite-fault source. The blue stars show the epicenters of the large earthquakes ($M_w\ge$ 6.4) occurring in the Hualien region from 1951 to 2024. The black triangles represent the GNSS stations used in this study (Inset) Geodynamic framework of Taiwan. The black arrow indicates the relative motion between the Philippine Sea plate (PSP) and the Eurasian plate (EP); (RT): Ryukyu Trench. LVF: Longitudinal Valley fault; CRF: Central Range fault; MF: Milun fault.

The 18 April 2019 $M_w$ 6.2 earthquake ruptured a compact asperity (about 15 km $\times$ 10 km) located on the intermediate to deep section of a west-dipping blind fault (15–25 km depth) (Jian and Wang, 2022) with maximum coseismic slip of 0.8 m (Lee et al., 2020). Huang and Wang (2022) proposed that this blind fault may represent the northern extension of the CRF, albeit further observations are needed to better characterizing the complex seismotectonics of the northern LV. However, the rare occurrence of a moderately large earthquake in the area presents an unique opportunity to investigate the mechanisms by which the northern LV region accommodates lithospheric deformation. In this study, we invert GNSS displacement time-series to derive a kinematic model for the 6-month long afterslip following the 2019 Hualien event. We then analyze the seismicity and its possible interactions with aseismic fault motion throughout the earthquake postseismic period.

2 Instrumentation and data processing

2.1 GNSS displacements

We use the GAMIT10.42/GLOBK5.16 software packages (Herring et al., 2010) to process the 3-D displacement time-series from 2018 to 2021 for 27 Global Navigation Satellite System (GNSS) stations deployed in the Hualien region (Figure 1). We obtain daily solutions in the ITRF2014 reference frame (Altamini et al., 2016) by utilizing double-differenced carrier phase measurements, and we enhance the regional deformation pattern for Taiwan by incorporating additional stations, including 362 from Taiwan, 8 from the Ryukyu islands and 17 International GNSS Service sites in the Asia-Pacific region. We utilize the following model equation to parametrize the time-dependent displacements (Lin et al., 2023b):

$\begin{array}{l}x\left(t\right)=x_0+vt+{\displaystyle \sum _{i=1}^{n_{eq}}}H\left(t-t_{eq}^{\left(i\right)}\right)A_{eq}^{\left(i\right)}+{\displaystyle \sum _{j=1}^{n_{\mathit{off}}}}H\left(t-t_{\mathit{off}}^{\left(j\right)}\right)A_{\mathit{off}}^{\left(j\right)}\hfill \\ +A_{yr}\sin \left(2\pi t\right)+B_{yr}\cos \left(2\pi t\right)+A_{\mathit{hfyr}}\sin \left(4\pi t\right)\hfill \\ +B_{\mathit{hfyr}}\cos \left(4\pi t\right)+{\displaystyle \sum _{i=1}^{n_{eq}}}H\left(t-t_{eq}^{\left(i\right)}\right)A_{\mathit{post}}^{\left(i\right)}\times \left(1-e^{-\frac{t-t_{eq}^{\left(i\right)}}{{\tau }_{\mathit{post}}^{\left(i\right)}}}\right)\hfill \end{array}$

where $x_0+vt$ is the secular velocity, $A_{eq}^{(i)}$ and $A_{\mathit{off}}^{(j)}$ are the coseismic steps and instrumental offsets starting at time $t_{eq}^{(i)}$ and $t_{\mathit{off}}^{(j)}$ respectively, $n_{eq}$ and $n_{\mathit{off}}$ are the number of detected earthquakes and offsets, $A_{yr}$ and $B_{yr}$ are sine and cosine terms to represent the annual seasonal motion, $A_{\mathit{hfyr}}$ and $B_{\mathit{hfyr}}$ are sine and cosine terms to represent the semi-annual cycle, $A_{\mathit{post}}^{(i)}$ is the maximum amplitude of the postseismic displacement with relaxation time ${\tau }_{\mathit{post}}^{(i)}$, and $H$ is the Heaviside step function. The $H$ function aims to correct offsets that inevitably contaminate GNSS time-series. Offsets can be categorized into actual crustal motions such as earthquakes, or artificial events (e.g., equipment malfunction and change, environmental perturbations) (Williams, 2003). In particular, changes of antennas at GNSS reference stations frequently produce discontinuities in the coordinate time series that are mainly caused by changes of carrier-phase multipath effects and different errors in the antenna phase center corrections (Wanninger, 2009).

To isolate the signals related to postseismic deformation, we input the GNSS time-series detrended and cleaned for tectonic and non-tectonic offsets into a variational Bayesian independent component analysis (vbICA) algorithm (Choudrey and Roberts, 2003) modified to study complex geodetic signals (Gualandi et al., 2016). This method assumes that observations are a combination of a limited number of statistically independent sources, which can be extracted and characterized using their multimodal probability density functions. We extract four independent components (IC) determined by the Automatic Relevance Determination method (Gualandi et al., 2016). The postseismic deformation signal from the 2019 earthquake is mapped in the first independent component IC1 (Figure 2) and explains approximately 60% of the total GNSS data variance. IC2 component denotes the postseismic signal associated with the 2018 $M_w$ 6.4 Hualien event (Zhao et al., 2020) (early to mid-2018), explaining about 20%–25% of the signal variance. Finally, annual (IC3) and multi-annual (IC4) hydrological perturbations (Hsu et al., 2020; Lin et al., 2023b) represent less than 10% of the total GNSS data variance. Figure 3 shows an example of vbICA approach over the 3-year period (2018–2021) that shows the extraction of the 6-month long postseismic displacements (IC1).

Figure 2

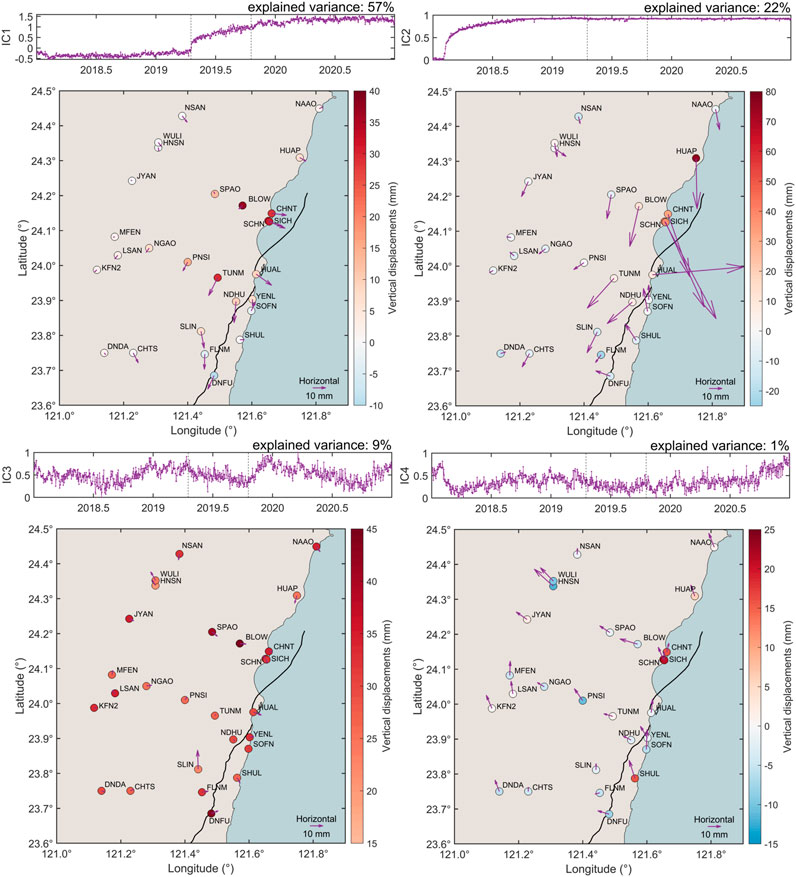
Figure 2. Temporal evolution of the four independent components (ICs) over a 3-year period (2018–2021) and related 3-D displacements. The vertical dashed lines denote the occurrence of the 2019 Hualien earthquake and the duration of postseismic deformation (about 6 months), respectively. The afterslip following the 2019 Hualien earthquake is mapped in IC1 component.

Figure 3

Figure 3. Example of analysis in independent component (ICA) over a 3-year period (2018–2021) showing the extraction of the 6-month long postseismic displacements (IC1) (black box) related to the 2019 Hualien earthquake. The black curve denotes the GNSS time-series corrected for a linear trend and large coseismic and instrumental offsets and the red curve shows the IC1 component, respectively.

2.2 Seismicity

We analyze the seismicity collected by the Central Weather Administration (CWA) of Taiwan during the first 6 months following the mainshock (until 15 October 2019). We select all events located between the depth of 0–30 km in the region defined by $121.4°$E−$121.7°$E and $23.8°$N-$24.3°$N (2,504 events). We estimate the magnitude of completeness $M_c$ of the aftershock sequence using the maximum curvature approach in the ZMAP software (Wiemer, 2001) with a correction factor of 0.1 (Schorlemmer et al., 2005). We find $M_c$ = 1.1 $\pm$ 0.1 and estimate parameters $a$ = 4.20 and $b$ = 0.86 $\pm$ 0.01 in the Gutenberg-Richter law (Gutenberg and Richter, 1944) through a maximum-likelihood approach (Supplementary Figure S1). We observe that the $b$-value is slightly larger than previous estimates inferred for the LV ($b$ $\sim$ 0.70–0.80) (Wu et al., 2018).

We observe mainly two patterns of seismicity during the 6 months following the mainshock (Figure 4). First, the main earthquake cluster is concentrated at mid-crustal depth ($\sim$ 13–25 km) and events fall both within and at the edge of the regions of moderate to large coseismic slip (0.15–0.5 m). The temporal evolution of seismicity is well explained by an Omori-like decay (Utsu et al., 1995) with parameters: $p$ = 0.67, $k$ = 44.6, and $c$ = 0.01 days. Second, several events (about 30%) are also located at shallow depth ($\le \sim$12 km). A first cluster, which is possibly activated during the entire postseismic period, is located in the NE Hualien region (between $24.2°$N to $24.3°$N) at the depth of about 2–8 km. The second cluster is located on the eastern side of the rupture region at the depth of 8–12 km and coincides with the activity of a NW-dipping structure in September-October 2019 (cluster C1) (Jian and Wang, 2022). Overall, the cumulative seismicity at shallow depth shows a succession of low earthquake activity followed by impulsive seismic episodes, which is likely characteristic of earthquake swarm activity (Hainzl, 2004).

Figure 4

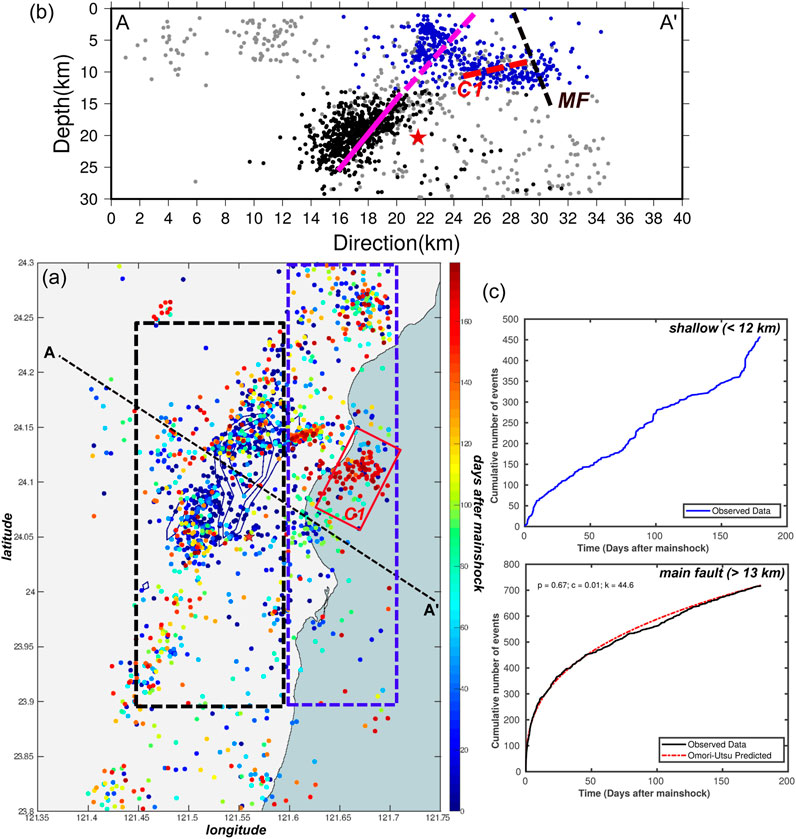
Figure 4. (A) Surface projection of the spatiotemporal evolution of the seismicity (with $M_L\ge$ 1.1) during the first 6 months following the 2019 Hualien mainshock. The blue contours outline the coseismic slip distribution (see Figure 1). The black dashed line denotes the cross-section in (B). The black and blue dashed boxes represent the events retained to analyze the seismicity in (B) and (C). The red plane outlines the west-dipping fault plane C1 associated with earthquake swarms in September-October 2019 [adapted from Jian and Wang (2022)]. The red star shows the mainshock epicenter. (B) Cross-section perpendicular to the mainshock fault plane. The black and blue dots show the events that occurred on the mainshock fault plane (depth $\ge$ 13 km) and at shallower depth (depth $<$ 12 km), respectively. Gray dots are events not used in (C). The black dashed line denotes the MF, the purple line is the mainshock fault plane with its possible extension towards the surface denoted as a purple dashed line and the red dashed line denotes C1, respectively. (C) Cumulative seismicity (with $M_L\ge$ 1.1) calculated for each region over a 6-month period following the mainshock. Cumulative number of events $(N)$ in the mainshock region are approximated with the cumulative Omori-Utsu law ($N(t)=K(c^{1-p}-{(t+c)}^{1-p})/(p-1)$, where $K$, $c$ and $p$ are constants and $t$ is time).

3 Analysis of the postseismic deformation process

3.1 Forward models of postseismic deformation

In a first step, we perform a forward modeling to approximate the 3-D surface displacements generated by viscoelastic relaxation in the lower crust and by poroelastic rebound. We use the finite-fault coseismic model from Lee et al. (2020) as the initial stress perturbation. Although being usually the dominant mechanism of deformation in the long run (Bürgmann and Dresen, 2008), viscoelastic deformation can also accompany moderate-magnitude events (typically $M_w\sim$ 6.0–6.5) (Bruhat et al., 2011; Mandler et al., 2021). We utilize the Relax software (Barbot and Fialko, 2010a; Barbot and Fialko 2010b) to estimate the contribution of viscoelastic relaxation to postseismic deformation signals. We use a Maxwell model with an effective viscosity of ${10}^{18}$ Pa.s and a rigidity of 30 GPa to characterize the viscoelastic behavior of the lower crust below the CR at depths greater than 20 km (Huang et al., 2015; Tang et al., 2019) during the first 6 months following the mainshock. We model poroelastic flow by subtracting the elastic coseismic solution for the undrained condition (Poisson ratio of 0.25) to the solution for the drained condition (Poisson ratio of 0.31) (Freed et al., 2017; Li et al., 2021). We observe that poroelastic rebound and viscoelastic relaxation make very little contribution to the postseismic deformation (maximum horizontal displacements $\le$1 mm) (Figure 5), therefore we assume that afterslip represents the dominant mechanism of postseismic slip following the Hualien event. Consequently, we do not correct the GNSS displacements for viscoelastic and poroelastic deformation for the kinematic afterslip inversion (Table 1).

Figure 5

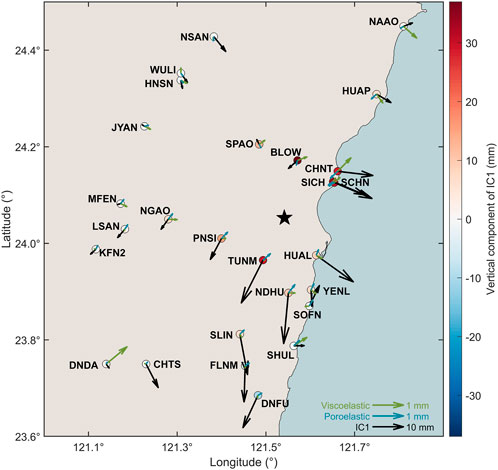
Figure 5. Forward modeling approximating the surface displacements generated by viscoelastic relaxation in the lower crust (green vector) and by poroelastic rebound (blue vector) during the first 6 months following the mainshock. The black vectors show the displacements related to IC1 component (Figure 2) and the black star denotes the mainshock epicenter. Viscoelastic relaxation and poroelastic rebound show no appreciable contribution to postseismic deformation (maximum displacements $\le$1 mm).

Table 1

Table 1. GNSS displacements analyzed for the kinematic afterslip inversion.

3.2 Kinematic afterslip inversion

To obtain a realistic afterslip model, we discretize the mainshock fault plane into 240 subfaults with dimensions of 5 km $\times$ 4 km. We fix the fault geometry (strike = $205°$, dip = $56°$) following the Lee et al. (2020) model but we allow for a variable rake on each subfault to account for possible slip complexity. We perform a weighted linear slip inversion incorporating a smoothness constraint and zero-slip boundary conditions (Lin et al., 2023b) in which we add a zero-slip asperity constraint (Zhao et al., 2022). The latter condition precludes that velocity-weakening regions that exhibit the largest coseismic slip ($\ge$0.5 m) would continue to rapidly slide throughout the postseismic period (Johnson et al., 2012). We solve for the slip on each subfault by minimizing the following cost function $\varphi (s)$:

$\varphi \left(s\right)=\Vert \underset{d}{\overset{-1/2}{\mathrm{\Sigma }}}\left(d-Gs\right){\Vert }^2+\alpha \Vert Bs{\Vert }^2+\beta \Vert Ls{\Vert }^2+\gamma \Vert A{W}_{s}s{\Vert }^2$

where ${\mathrm{\Sigma }}_d$ is the data covariance matrix, $d$ is the matrix of GNSS displacements (Table 1), $G$ is the Green’s function following Okada (1992), $s$ is the slip vector on each subfault, $B$ represents the zero slip boundary condition, and $L$ is the 9-point stencil finite difference Laplacian. $\alpha$ and $\beta$ are the weighting factors for boundary and smoothing constraints, respectively, $A$ represents the zero slip asperity condition with weight $W_s$ proportional to the amount of coseismic slip on each subfault and $\gamma$ is the related weighting factor. We define the weighted misfit $m_G$ between the corrected GNSS displacements and the modeled afterslip displacements following Lin et al. (2023b):

$m_G=\sqrt{\frac{r^{T}Wr}{Tr\left(W\right)/3}}$

where $r$ is the vector of residual displacements between GNSS observations and models, $W$ is the weight matrix, and $Tr(.)$ is the matrix trace. We estimate the optimal smoothing factor ($\beta$ = 181) by minimizing the leave-one-out cross-validation mean squared error (Matthews and Segall, 1993) (Supplementary Figure S2A).

Our preferred model ($m_G$ = 6.0 mm, see Supplementary Figure S2B) exhibits a dominant thrust-faulting mechanism with a left-lateral component, which is compatible with the coseismic slip direction of the mainshock (Lee et al., 2020) (Figure 6A). The afterslip spreads around the coseismic slip region with relatively limited slip ($\le$ 0.1 m) and extends about 60 km in the along-strike direction and 40 km in the along-dip direction. The two main peaks of afterslip ($\sim$ 0.07–0.09 m) are located at the NE and SW edges of the coseismic slip within a similar depth range as the latter. We also observe afterslip ($\sim$0.05–0.07 m) that extends toward the surface in the region located right above the main asperity. We infer a total geodetic moment of 4.6$\times 10^{18}$ N.m, which represents an equivalent moment magnitude of about 6.4. Then, we assess the effect of coseismic slip and associated stress changes on the occurrence and on the spatial distribution of afterslip by resolving the coseismic shear stress changes onto the mainshock fault plane (Figure 6B). The regions with moderate afterslip (0.04–0.06 m) that surround the coseismic rupture are associated with maximum coseismic shear changes (0.04–0.05 MPa) while the areas with peak afterslip are associated with shear changes of about 0.03 MPa. We observe an overall coherent spatial correlation between afterslip distribution and positive coseismic shear changes, which suggests that coseismic shear stress changes may have played a role in controlling the spatial distribution of afterslip (Zhao et al., 2020; Fukuda and Johnson, 2021).

Figure 6

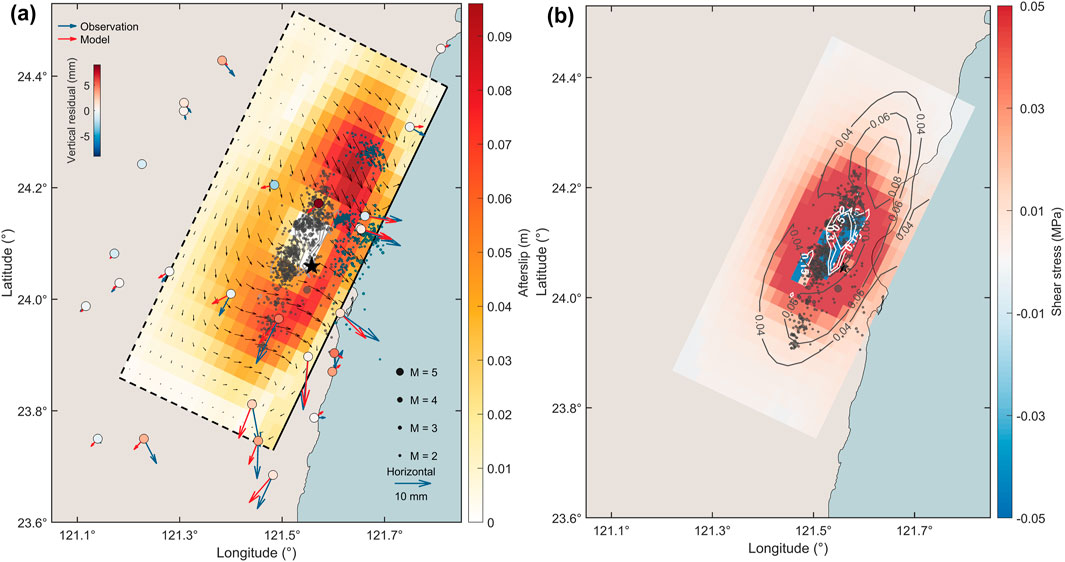
Figure 6. (A) Kinematic afterslip distribution over a 6-month period following the 2019 Hualien earthquake resolved on 5 km $\times$ 4 km subfaults ($\beta$ = 181). The black and blue circles show the aftershocks in the mainshock and shallow regions sized by magnitude, respectively (see Figure 4 for detail). The gray contours outline the coseismic slip distribution and the black star denotes the mainshock epicenter. The thick black line depicts the top edge of the fault plane and the dashed lines show its surface projection. (B) Coseismic shear stress changes resolved onto the mainshock fault plane. The gray contours outline the afterslip distribution in (A) and the white contours denote the coseismic slip distribution.

4 Dynamics of the aftershock sequence in the mainshock region

We investigate a possible link between aftershock activity in the mainshock region and afterslip by comparing the cumulative seismicity with the afterslip temporal function mapped in the IC1 component. We find that the cumulative number of aftershocks and afterslip follow a similar temporal decay that is relatively well-explained with $p$-value $\sim$0.67 (Figure 7). To investigate a possible gradual expansion of the aftershock front on the fault plane, as often observed during aftershock migration driven by afterslip (Frank et al., 2017; Perfettini et al., 2018), we consider a rate-strengthening rheology (Dieterich, 1994), and assume that an aftershock is triggered when afterslip reaches a critical level on a nearby creeping patch (Perfettini et al., 2018). The bilateral expansion of the aftershock zone $\mathrm{\Delta }{A}^{+/-}$ along-strike and along-dip since the onset time $t_i$ of the first aftershock can be expressed as (Perfettini et al., 2018; Perfettini et al., 2019):

$\mathrm{\Delta }{A}^{+/-}=\zeta \left(a-b\right)\sigma \frac{A^{+/-}}{\mathrm{\Delta }\sigma }\log \left(\frac{t}{t_i}\right)(1)$

where $\zeta$ is a constant of order unity (Frank et al., 2017), $(a-b)\sigma$ is a constitutive parameter, $\mathrm{\Delta }\sigma$ is the earthquake stress drop and $A^{+/-}$ are characteristic dimensions of the coseismic rupture ($W^{+/-}$ and $L^{+/-}$ in Figure 7).

Figure 7

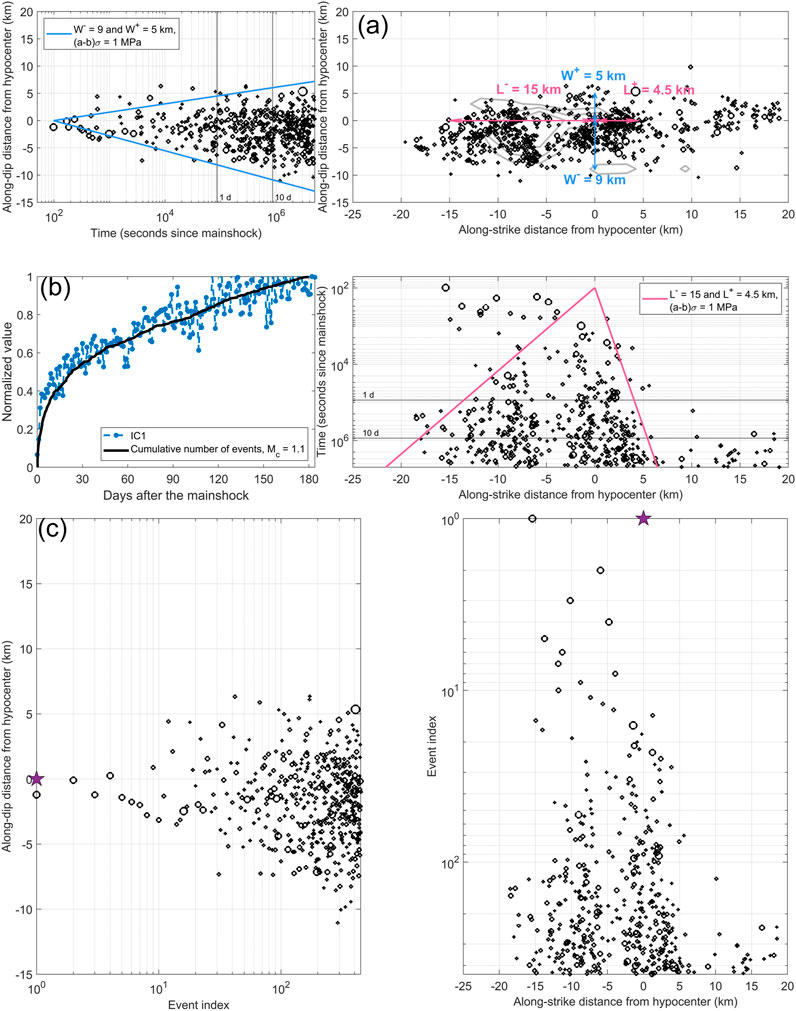
Figure 7. (A) Spatiotemporal evolution of the aftershocks along the mainshock fault plane (see Figure 4, black cluster) during the first 6 months following the Hualien earthquake. The pink and blue arrows represent the characteristic dimensions retained for modeling the expansion of the seismicity front along-strike ($L^{+}$ = 4.5 km, $L^{-}$ = 15 km) and along-dip ($W^{+}$ = 5 km, $W^{-}$ = 9 km) away from the centroid (purple star), respectively. The gray contours outline the coseismic slip distribution. The blue and pink lines denote the semilogarithmic bilateral expansion of the aftershock front Equation 1 along dip (left) and along strike (bottom) on the fault plane, respectively. (B) Comparison between the cumulative seismicity (with $M_L\ge$ 1.1) (black curve) and the temporal evolution of afterslip (IC1 component) (blue dotted dashed line) over a 6-month period. Signals are normalized by their maximum amplitude after 6 months (C) Event-index plots computed for the along-dip and along-strike directions away from the hypocenter.

We assume $\mathrm{\Delta }\sigma$ = 3.3 MPa (Lee et al., 2020), $t_i$ = 98 s and inferred $(a-b)\sigma$ = 1 MPa that best fit our data. This value is consistent with typical values observed for afterslip on continental faults (Perfettini and Avouac, 2004). We observe that the first order features of the bilateral aftershock migration along-strike and along-dip on the fault plane during the first 6 months following the mainshock are well captured by our simple model. We find aftershock migration away from the epicenter with apparent velocity of approximately 5–10 km. day⁻¹, which is in good agreement with estimates typically observed in the case of seismicity driven by aseismic slip (Lohman and McGuire, 2007). Further, we also find an overall coherent spreading of seismicity through the analysis of the event-index (i.e., the order of the occurrence of events) plots for along-strike and along-dip directions, suggesting that subsequent aftershock ruptures are mainly facilitated by aseismic slip rather than by the coseismic slip itself (Fischer and Hainzl, 2021; Cabrera et al., 2022).

Finally, we estimate the effective stress drop $\mathrm{\Delta }{\sigma }_{\mathit{eff}}$ of the aftershock sequence in the mainshock region following Fischer and Hainzl (2017):

$\mathrm{\Delta }{\sigma }_{\mathit{eff}}=\frac{7}{16}\frac{M_0^{\mathit{aft}}}{R^3}$

where $R$ is the characteristic radius of the aftershock activated area and $M_0^{\mathit{aft}}$ represents the total seismic moment of the aftershock sequence ($M_0^{\mathit{aft}}$ = 1.25$\times 10^{16}$ N.m for events with $M_L\ge$ 1.1). We infer $\mathrm{\Delta }{\sigma }_{\mathit{eff}}$ varying from 0.0016 MPa to 0.044 MPa for $R$ ranging from 5 km to 15 km. In general, $\mathrm{\Delta }{\sigma }_{\mathit{eff}}<\sim$0.1 MPa is indicative of a low density of asperities with respect to the area covered by the seismicity (Cabrera et al., 2022). Therefore, the relatively low estimated values further support the idea that afterslip represents the dominant mechanism that drives aftershock activity rather than stress transfer in-between sparse asperities (Essing and Poli, 2024).

5 Discussion and conclusions

We analyze GNSS and seismological data to constrain the spatiotemporal evolution of crustal deformation and seismicity throughout the postseismic phase of the 2019 Hualien earthquake. Afterslip often represents the dominant deformation mechanism in the early postseismic phase (Gualandi et al., 2020; Lin et al., 2023b) and we demonstrate that near-source GNSS displacements during the 6 months following the 2019 Hualien earthquake are well explained by widespread afterslip located on the mainshock fault plane. While the existence of velocity-strengthening regions, that can sustain afterslip for months or years, were previously evidenced on the southern section of the LVF (Thomas et al., 2014; Canitano et al., 2018) and on the southern and central sections of the CRF (Lin et al., 2023b; Tang et al., 2023), the 2019 Hualien earthquake reveals unambiguously the presence of a large velocity-strengthening zone at shallow to mid-crustal depth in the Hualien region. The afterslip distribution shows a relatively good spatial coherence with coseismic shear stress changes, which suggests that the latter may have helped to promote afterslip (Fukuda and Johnson, 2021). We infer that mid-crustal aftershocks (15–20 km depth) are mainly located in areas of moderate afterslip ($\sim$0.03–0.05 m) that directly surround the rupture zone. Besides, the presence of the velocity-strengthening region with moderate afterslip ($\sim$0.05–0.07 m) right above the coseismic zone may be compatible with the gap of aftershocks observed at the depth of 10–15 km (see Figure 4). We assess the fault zone frictional stability parameter $a-b$ in the mainshock region based on the relationship between afterslip and aftershock migration in a rate-and-state regime (Section 4). Considering an effective normal stress at the depth of 20 km ranging from about 50 to 150 MPa in eastern Taiwan (Thomas et al., 2017), we infer $a-b\sim$ 0.0067–0.02 that are comparable to estimates in the LV (Thomas et al., 2017) and to laboratory measurements (Marone et al., 1991).

The analysis of seismicity during the first 6 months following the mainshock exhibits two distinct features (Figure 4). The main aftershock cluster is located at mid-crustal depth ($\sim$ 13–25 km) in regions associated with moderate to large afterslip ($\ge$ 0.04 m) (Figure 6). We show evidence that the first order features of the bilateral aftershock migration along-strike and along-dip on the fault plane are well captured by a simple model of afterslip migration built on rate-and-state rheology (Perfettini et al., 2019) (Figure 7). Besides, the temporal evolution of seismicity and afterslip are likely correlated, which may further suggest that afterslip represents the driving force behind aftershock productivity (Perfettini and Avouac, 2004; Canitano et al., 2018; Gualandi et al., 2020). We found that the cumulative seismic moment released by aftershocks is only an infinitesimal percent $(\le 0.03\%)$ of the total geodetic moment relieved by afterslip. Consequently, afterslip represents the prominant driving mechanism of near-to intermediate-field postseismic deformation following the 2019 Hualien event; a pattern typically observed in active regions (Gualandi et al., 2020; Lin et al., 2023b). Nonetheless, Omori-like decays (Utsu et al., 1995) of seismicity and afterslip are well explained with $p$-value $\sim$0.67, which is slightly lower than the typical estimates ($p$ = 0.80–1.04) (Ingleby and Wright, 2017). The Omori-like decay of afterslip with $p$ $<$ 1 suggests that additional post-earthquake processes may have contributed to GNSS surface displacements (Morikami and Mitsui, 2020). For instance, Periollat et al. (2022) proposed that early postseismic deformation (minutes to months) with $p$ $<$ 1 can result from a transient brittle creep mechanism within an unruptured fault section and its surroundings; a mechanism that is not accounted for in our kinematic model.

We also observe clustered seismic activity at shallow depth (depth $\le$ 10 km). The cumulative seismicity pattern shows a succession of low earthquake activity followed by impulsive seismic episodes (Figure 4) that is likely characteristic of earthquake swarm activity (Hainzl, 2004). These events are part of the intense seismic swarm activity in the northern LV that strenghtened following the 2018 $M_w$ 6.4 Hualien earthquake (Jian and Wang, 2022; Huang and Wang, 2022). Here, we infer a first cluster located in the NE Hualien region (between $24.2°$N to $24.3°$N) at the depth of about 2–8 km. The cluster, which coincides with the region of maximum afterslip (Figure 6A), is activated during the entire postseismic period, likely through sustained aseismic slip at shallow depth. A second cluster, located on the eastern side of the rupture region at the depth of 8–12 km (cluster C1, Figure 4) (Jian and Wang, 2022), is activated in September-October 2019. This cluster, which likely occurred near the end of the postseismic period, coincides with the activity of a NW-dipping structure. Therefore, the afterslip had likely little to no impact on the activation of cluster C1. Overall, the impact of afterslip on shallow seismicity is difficult to assess because of the episodic nature of earthquakes swarms (Soares et al., 2023). The analysis of the interplay between aseismic transient slip and the occurrence of seismic swarms would require further seismological [e.g., repeating earthquakes (Peng et al., 2021)] and geodetic observations [e.g., borehole strainmeter data (Canitano et al., 2021)] and is thus beyond the scope of this study.

Finally, we observe that the geodetic moment of the afterslip ($M_w\sim$ 6.4) exceeds that of the seismic moment ($M_w$ 6.2). In general, the afterslip moment of $M_w\ge$ 6.0 events rarely exceeds that of the seismic moment (Churchill et al., 2022), with rare exceptions of the 2004 $M_w$ 6.0 Parkfield earthquake (Bruhat et al., 2011) or the 2008 $M_w$ 6.8 Methoni earthquake sequence (Greece) (Howell et al., 2017). However, Hawthorne et al. (2016) suggested that compact ruptures have the potential to generate higher afterslip rates compared to larger, more elongated ruptures because of the relatively larger size of the velocity-strengthening region surrounding the coseismic region that can experience afterslip. For instance, the 2013 $M_w$ 6.3 Ruisui earthquake, which has a rupture elongation about twice larger than the 2019 Hualien event, has generated afterslip with moment that did not exceed 30% of the seismic moment (Lin et al., 2023b). Besides, the unusually large regional ground shaking ($>$ 4 m s⁻²) for a mainshock of the size of the 2019 earthquake (Lee et al., 2020) may have induced a transient perturbation of the elastic and frictional properties of the fault zone material (Cruz-Atienza et al., 2021) that could have contributed to enhance afterlip. Finally, since high afterslip rates often correlate with fault regions associated with a high level of fluid pressure (Moreno et al., 2014), the elevated pore-fluid pressure observed in the source regions of the 2019 and 2018 Hualien earthquakes (Toyokuni et al., 2021) may have contributed to induce abundant afterslip. Nonetheless, the afterslip moment of the 2018 Hualien earthquake is only a fraction of the seismic moment (about 25%) (Zhao et al., 2020), which further suggests that several factors likely influence afterlip rates in active regions (Churchill et al., 2022).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

H-FL: Conceptualization, Formal Analysis, Investigation, Software, Visualization, Writing–original draft. AC: Conceptualization, Funding acquisition, Project administration, Supervision, Validation, Writing–original draft. Y-JH: Conceptualization, Formal Analysis, Investigation, Software, Visualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by the Ministry of Science and Technology grant NSTC 113-2116-M-001-009.

Acknowledgments

We are grateful to IES colleagues for collecting and processing the GNSS data. We are thankful to Shiann-Jong Lee for providing the coseismic slip model and Wen-Tzong Liang for insightful comments. Figures were created by using the Generic Mapping Tools (GMT) (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/) (Wessel and Smith, 1998). We are thankful to the Associate Editor Fuqiong Huang and two reviewers for their constructive suggestions and comments allowing to improve the manuscript. This is the contribution of the Institute of Earth Sciences, Academia Sinica, IESAS2423.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1457240/full#supplementary-material

References

Altamini, Z., Rebischung, P., Metivier, L., and Collilieux, X. (2016). ITRF2014: a new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 121, 6109–6131. doi:10.1002/2016jb013098

CrossRef Full Text | Google Scholar

Barbot, S., and Fialko, Y. (2010a). Fourier-domain Green’s function for an elastic semi-infinite solid under gravity, with applications to earthquake and volcano deformation. Geophys. J. Int. 182 (2), 568–582. doi:10.1111/j.1365-246x.2010.04655.x

CrossRef Full Text | Google Scholar

Barbot, S., and Fialko, Y. (2010b). A unified continuum representation of postseismic relaxation mechanisms: semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophys. J. Int. 182 (3), 1124–1140. doi:10.1111/j.1365-246x.2010.04678.x

CrossRef Full Text | Google Scholar

Barrier, E., and Angelier, J. (1986). Active collision in eastern taiwan: the coastal range. Tectonophysics 125, 39–72. doi:10.1016/0040-1951(86)90006-5

CrossRef Full Text | Google Scholar

Bruhat, L., Barbot, S., and Avouac, J. P. (2011). Evidence for postseismic deformation of the lower crust following the 2004 M_w6.0 Parkfield earthquake. J. Geophys. Res. 116, B08401. doi:10.1029/2010JB008073

CrossRef Full Text | Google Scholar

Bürgmann, R., and Dresen, G. (2008). Rheology of the lower crust and upper mantle: evidence from rock mechanics, geodesy, and field observations. Annu. Rev. Earth Planet. Sci. 36, 531–567. doi:10.1146/annurev.earth.36.031207.124326

CrossRef Full Text | Google Scholar

Cabrera, L., Poli, P., and Frank, W. B. (2022). Tracking the spatio-temporal evolution of foreshocks preceding the M_w6.1 2009 L’Aquila earthquake. J. Geophys. Res. Solid Earth 127. doi:10.1029/2021JB023888

CrossRef Full Text | Google Scholar

Canitano, A., Godano, M., Hsu, Y. J., Lee, H. M., Linde, A. T., and Sacks, S. (2018). Seismicity controlled by a frictional afterslip during a small magnitude seismic sequence (ML < 5) on the Chihshang Fault, Taiwan. J. Geophys. Res. Solid Earth 123 (2), 2003–2018. doi:10.1002/2017jb015128

CrossRef Full Text | Google Scholar

Canitano, A., Godano, M., and Thomas, M. Y. (2021). Inherited state of stress as a key factor controlling slip and slip mode: inference from the study of a slow slip event in the Longitudinal Valley, Taiwan. Geophys. Res. Lett. 48 (3). doi:10.1029/2020GL090278

CrossRef Full Text | Google Scholar

Chang, J. M., Chao, W. A., Yang, C. M., and Huang, M. W. (2024). Coseismic and subsequent landslides of the 2024 hualien earthquake (M7.2) on April 3 in taiwan. Landlides 21, 2591–2595. doi:10.1007/s10346-024-02312-x

CrossRef Full Text | Google Scholar

Chen, K. H., Toda, S., and Rau, R. J. (2008). A leaping, triggered sequence along a segmented fault: the 1951 M_L 7.3 Hualien-Taitung earthquake sequence in eastern Taiwan. J. Geophys. Res. 113. doi:10.1029/2007JB005048

CrossRef Full Text | Google Scholar

Choudrey, R. A., and Roberts, S. J. (2003). Variational mixture of Bayesian independent component analyzers. Neural comput 15 (1), 213–252. doi:10.1162/089976603321043766

PubMed Abstract | CrossRef Full Text | Google Scholar

Churchill, R. M., Werner, M. J., Biggs, J., and Fagereng, A. (2022). Afterslip moment scaling and variability from a global compilation of estimates. J. Geophys. Res. Solid Earth 127, e2021JB023897. doi:10.1029/2021JB023897

PubMed Abstract | CrossRef Full Text | Google Scholar

Cruz-Atienza, V. M., Tago, J., Villafuerte, C., Wei, M., Garza-Girón, R., Dominguez, L. A., et al. (2021). Short-term interaction between silent and devastating earthquakes in Mexico. Nat. Commun. 12, 2171. doi:10.1038/s41467-021-22326-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Dieterich, J. H. (1994). A constitutive law for rate of earthquake production and its application to earthquake clustering. J. Geophys. Res. 99, 2601–2618. doi:10.1029/93jb02581

CrossRef Full Text | Google Scholar

Essing, D., and Poli, P. (2024). Unraveling earthquake clusters composing the 2014 Alto Tiberina earthquake swarm via unsupervised learning. J. Geophys. Res. Solid Earth 129. doi:10.1029/2022JB026237

CrossRef Full Text | Google Scholar

Fischer, T., and Hainzl, S. (2017). Effective stress drop of earthquake clusters. Bull. Seismol. Soc. Am. 107, 2247–2257. doi:10.1785/0120170035

CrossRef Full Text | Google Scholar

Fischer, T., and Hainzl, S. (2021). The growth of earthquake clusters. Front. Earth Sci. 9. doi:10.3389/feart.2021.638336

CrossRef Full Text | Google Scholar

Frank, W. B., Poli, P., and Perfettini, H. (2017). Mapping the rheology of the Central Chile subduction zone with aftershocks. Geophys. Res. Lett. 44, 5374–5382. doi:10.1002/2016gl072288

CrossRef Full Text | Google Scholar

Freed, A. M., Hashima, A., Becker, T. W., Okaya, D. A., Sato, H., and Hatanaka, Y. (2017). Resolving depth-dependent subduction zone viscosity and afterslip from postseismic displacements following the 2011 Tohoku-oki, Japan earthquake. Earth Planet. Sci. Lett. 459, 279–290. doi:10.1016/j.epsl.2016.11.040

CrossRef Full Text | Google Scholar

Fukuda, J., and Johnson, K. M. (2021). Bayesian inversion for a stress-driven model of afterslip and viscoelastic relaxation: method and application to postseismic deformation following the 2011 M_w 9.0 Tohoku-Oki earthquake. J. Geophys. Res. Solid Earth 126. doi:10.1029/2020JB021620

CrossRef Full Text | Google Scholar

Gualandi, A., Liu, Z., and Rollins, C. (2020). Post-large earthquake seismic activities mediated by aseismic deformation processes. Earth Planet. Sci. Lett. 530, 115870. doi:10.1016/j.epsl.2019.115870

CrossRef Full Text | Google Scholar

Gualandi, A., Serpelloni, E., and Belardinelli, M. E. (2016). Blind source separation problem in GPS time series. J. Geod. 90, 323–341. doi:10.1007/s00190-015-0875-4

CrossRef Full Text | Google Scholar

Gutenberg, R., and Richter, C. F. (1944). Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 185–188. doi:10.1785/bssa0340040185

CrossRef Full Text | Google Scholar

Hainzl, S. (2004). Seismicity patterns of earthquake swarms due to fluid intrusion and stress triggering. Geophys. J. Int. 159, 1090–1096. doi:10.1111/j.1365-246x.2004.02463.x

CrossRef Full Text | Google Scholar

Hawthorne, J. C., Simons, M., and Ampuero, J.-P. (2016). Estimates of aseismic slip associated with small earthquakes near San Juan Bautista, CA. J. Geophys. Res. Solid Earth 121, 8254–8275. doi:10.1002/2016jb013120

CrossRef Full Text | Google Scholar

Herring, T., King, W., and McCluskey, S. M. (2010). Introduction to GAMIT/GLOBK release 10.4. Cambridge: Mass. Inst. of Technol.

Google Scholar

Howell, A., Palamartchouk, K., Papanikolaou, X., Paradissis, D., Raptakis, C., Copley, A., et al. (2017). The 2008 Methoni earthquake sequence: the relationship between the earthquake cycle on the subduction interface and coastal uplift in SW Greece. Geophys. J. Int. 208, 1592–1610. doi:10.1093/gji/ggw462

CrossRef Full Text | Google Scholar

Hsu, Y. J., Fu, Y., Bürgmann, R., Hsu, S. Y., Lin, C. C., Tang, C. H., et al. (2020). Assessing seasonal and interannual water storage variations in Taiwan using geodetic and hydrological data. Earth Planet. Sci. Lett. 550, 116532. doi:10.1016/j.epsl.2020.116532

CrossRef Full Text | Google Scholar

Huang, H. H., and Wang, Y. (2022). Seismogenic structure beneath the northern Longitudinal Valley revealed by the 2018-2021 Hualien earthquake sequences and 3-D velocity model. Terr. Atmos. Ocean. Sci. 33, 17. doi:10.1007/s44195-022-00017-z

CrossRef Full Text | Google Scholar

Huang, M. H., and Huang, H. H. (2018). The complexity of the 2018 M_w6.4 Hualien earthquake in east Taiwan. Geophys. Res. Lett. 45 (13), 249–313. doi:10.1029/2018gl080821

CrossRef Full Text | Google Scholar

Huang, T. Y., Gung, Y., Kuo, B. Y., Chiao, L. Y., and Chen, Y. N. (2015). Layered deformation in the Taiwan orogen. Science 349, 720–723. doi:10.1126/science.aab1879

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingleby, T., and Wright, T. (2017). Omori-like decay of postseismic velocities following continental earthquakes. Geophys. Res. Lett. 44, 3119–3130. doi:10.1002/2017gl072865

CrossRef Full Text | Google Scholar

Jian, P. R., and Wang, Y. (2022). Applying unsupervised machine-learning algorithms and MUSIC back-projection to characterize 2018-2022 Hualien earthquake sequence. Terr. Atmos. Ocean. Sci. 33, 28. doi:10.1007/s44195-022-00026-y

CrossRef Full Text | Google Scholar

Johnson, K. M., Fukuda, J., and Segall, P. (2012). Challenging the rate-state asperity model: afterslip following the 2011 M9 Tohoku-oki, Japan, earthquake. Geophys. Res. Lett. 39. doi:10.1029/2012GL052901

CrossRef Full Text | Google Scholar

Lee, S. J., Wong, T. P., Liu, T. Y., Lin, T. C., and Chen, C. T. (2020). Strong ground motion over a large area in northern Taiwan caused by the northward rupture directivity of the 2019 Hualien earthquake. J. Asian Earth Sci. 192, 104095. doi:10.1016/j.jseaes.2019.104095

CrossRef Full Text | Google Scholar

Li, S., Tao, T., Chen, Y., He, P., Gao, F., Qu, X., et al. (2021). Geodetic observation and modeling of the coseismic and postseismic deformation associated with the 2020 M_w6.5 Monte Cristo earthquake. Earth Space Sci. 8. doi:10.1029/2021EA001696

CrossRef Full Text | Google Scholar

Lin, H. F., Gualandi, A., Hsu, Y. F., Hsu, Y. J., Huang, H. H., Lee, H. M., et al. (2023b). Interplay between seismic and aseismic deformation on the central Range fault during the 2013 M_w6.3 Ruisui earthquake (taiwan). J. Geophys. Res. Solid Earth 128 (9). doi:10.1029/2023JB026861

CrossRef Full Text | Google Scholar

Lin, H. F., Hsu, Y. F., and Canitano, A. (2023a). Source modeling of the 2009 Fengpin-Hualien earthquake sequence, Taiwan, inferred from static strain measurements. Pure Appl. Geophys. 180, 715–733. doi:10.1007/s00024-022-03068-y

CrossRef Full Text | Google Scholar

Lohman, R. B., and McGuire, J. J. (2007). Earthquake swarms driven by aseismic creep in the Salton Trough, California. J. Geophys. Res. 112, B04405. doi:10.1029/2006JB004596

CrossRef Full Text | Google Scholar

Mandler, E., Pintori, F., Gualandi, A., Anderlini, L., Serpelloni, E., and Belardinelli, M. E. (2021). Post-seismic deformation related to the 2016 Central Italy seismic sequence from GPS displacement time-series. J. Geophys. Res. Solid Earth 126, e2021JB022200. doi:10.1029/2021JB022200

PubMed Abstract | CrossRef Full Text | Google Scholar

Marone, C. J., Scholz, C. H., and Bilham, R. (1991). On the mechanics of earthquake afterslip. J. Geophys. Res. 96, 8441–8452. doi:10.1029/91jb00275

CrossRef Full Text | Google Scholar

Matthews, M. V., and Segall, P. (1993). Estimation of depth-dependent fault slip from measured surface deformation with application to the 1906 San Francisco earthquake. J. Geophys. Res. 98 (12), 12153–12163. doi:10.1029/93jb00440

CrossRef Full Text | Google Scholar

McCormack, K., Hesse, M. A., Dixon, T., and Malservisi, R. (2020). Modeling the contribution of poroelastic deformation to postseismic geodetic signals. Geophys. Res. Lett. 47. doi:10.1029/2020GL086945

CrossRef Full Text | Google Scholar

Moreno, M., Haberland, C., Oncken, O., Rietbrock, A., Angiboust, S., and Heidbach, O. (2014). Locking of the Chile subduction zone controlled by fluid pressure before the 2010 earthquake. Nat. Geosci. 7, 292–296. doi:10.1038/NGEO2102

CrossRef Full Text | Google Scholar

Morikami, S., and Mitsui, Y. (2020). Omori-like slow decay (p < 1) of postseismic displacement rates following the 2011 Tohoku megathrust earthquake. Earth Planets Space 72, 37. doi:10.1186/s40623-020-01162-w

CrossRef Full Text | Google Scholar

Okada, Y. (1992). Internal deformation due to shear and tensile faults in a half-space. Bull. Seism. Soc. Am. 82 (2), 1018–1040. doi:10.1785/bssa0820021018

CrossRef Full Text | Google Scholar

Peltzer, G., Rosen, P., Rogez, F., and Hudnut, K. (1996). Postseismic rebound in fault step-overs caused by pore fluid flow. Science 273 (5279), 1202–1204. doi:10.1126/science.273.5279.1202

CrossRef Full Text | Google Scholar

Peng, W., Marsan, D., Chen, K. H., and Pathier, E. (2021). Earthquake swarms in Taiwan: a composite declustering method for detection and their spatial characteristics. Earth Planet. Sci. Lett. 574, 117160. doi:10.1016/j.epsl.2021.117160

CrossRef Full Text | Google Scholar

Perfettini, H., and Avouac, J. P. (2004). Postseismic relaxation driven by brittle creep: a possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. 109. doi:10.1029/2003JB002488

CrossRef Full Text | Google Scholar

Perfettini, H., Frank, W. B., Marsan, D., and Bouchon, M. (2018). A model of aftershock migration driven by afterslip. Geophys. Res. Lett. 45, 2283–2293. doi:10.1002/2017gl076287

CrossRef Full Text | Google Scholar

Perfettini, H., Frank, W. B., Marsan, D., and Bouchon, M. (2019). Updip and along-strike aftershock migration model driven by afterslip: application to the 2011 Tohoku-Oki aftershock sequence. J. Geophys. Res. Solid Earth 124 (3), 2653–2669. doi:10.1029/2018jb016490

CrossRef Full Text | Google Scholar

Periollat, A., Radiguet, M., Weiss, J., Twardzik, C., Amitrano, D., Cotte, N., et al. (2022). Transient brittle creep mechanism explains early postseismic phase of the 2011 Tohoku-Oki megathrust earthquake: observations by high-rate GPS solutions. J. Geophys. Res. Solid Earth. 127. doi:10.1029/2022JB024005

CrossRef Full Text | Google Scholar

Rau, R. J., Ching, K. E., Hu, J. C., and Lee, J.-C. (2008). Crustal deformation and block kinematics in transition from collision to subduction: global positioning system measurements in northern Taiwan, 1995–2005. J. Geophys. Res. 113, B09404. doi:10.1029/2007jb005414

CrossRef Full Text | Google Scholar

Rau, R. J., and Liang, W. T. (2022). Introduction to the special issue on the Hualien earthquake swarms. Terr. Atmos. Ocean. Sci. 33, 27. doi:10.1007/s44195-022-00028-w

CrossRef Full Text | Google Scholar

Schorlemmer, D., Wiemer, S., and Wyss, M. (2005). Variations in earthquake-size distribution across different stress regimes. Nature 437, 539–542. doi:10.1038/nature04094

PubMed Abstract | CrossRef Full Text | Google Scholar

Shyu, J. B. H., Chen, C. F., and Wu, Y. M. (2016). Seismotectonic characteristics of the northernmost Longitudinal Valley, eastern Taiwan: structural development of a vanishing suture. Tectonophysics 692, 295–308. doi:10.1016/j.tecto.2015.12.026

CrossRef Full Text | Google Scholar

Shyu, J. B. H., Sieh, K., Chen, Y. G., and Chung, L. H. (2006). Geomorphic analysis of the Central Range fault, the second major active structure of the Longitudinal Valley suture, eastern Taiwan. Geol. Soc. Am. Bull. 118, 1447–1462. doi:10.1130/b25905.1

CrossRef Full Text | Google Scholar

Soares, A., Custodio, S., Cesca, S., Silva, R., Vuan, A., and Mendes, V. B. (2023). The february 2018 seismic swarm in sao miguel, azores. Front. Earth Sci. 11. doi:10.3389/feart.2023.1144151

CrossRef Full Text | Google Scholar

Tang, C. H., Hsu, Y. J., Barbot, S., Moore, J. D. P., and Chang, W. L. (2019). Lower-crustal rheology and thermal gradient in the Taiwan orogenic belt illuminated by the 1999 Chi-Chi earthquake. Sci. Adv. 5 (2), eaav3287. doi:10.1126/sciadv.aav3287

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, C. H., Lin, Y., Tung, H., Wang, Y., Lee, S. J., Hsu, Y. J., et al. (2023). Nearby fault interaction within the double-vergence suture in eastern Taiwan during the 2022 Chihshang earthquake sequence. Commun. Earth Environ. 4, 333. doi:10.1038/s43247-023-00994-0

CrossRef Full Text | Google Scholar

Thomas, M. Y., Avouac, J. P., Champenois, J., Lee, J. C., and Kuo, L. C. (2014). Spatiotemporal evolution of seismic and aseismic slip on the Longitudinal Valley fault, taiwan. J. Geophys. Res. 119 (6), 5114–5139. doi:10.1002/2013jb010603

CrossRef Full Text | Google Scholar

Thomas, M. Y., Avouac, J. P., and Lapusta, N. (2017). Rate-and-state friction properties of the Longitudinal Valley Fault from kinematic and dynamic modeling of seismic and aseismic slip. J. Geophys. Res. 122 (4), 3115–3137. doi:10.1002/2016jb013615

CrossRef Full Text | Google Scholar

Toyokuni, G., Zhao, D., and Chen, K. H. (2021). Structural control on the 2018 and 2019 hualien earthquakes in taiwan. Phys. Earth Planet. Inter. 312, 106673. doi:10.1016/j.pepi.2021.106673

CrossRef Full Text | Google Scholar

Utsu, T., Ogata, Y., Matsu’ura, R. S., and Matsu'ura, (1995). The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 43, 1–33. doi:10.4294/jpe1952.43.1

CrossRef Full Text | Google Scholar

Wanninger, L. (2009). Correction of apparent position shifts caused by GNSS antenna changes. GPS Solutions 13, 133–139. doi:10.1007/s10291-008-0106-z

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1998). New, improved version of generic mapping tools released. Eos Trans. AGU 79, 579. doi:10.1029/98EO00426

CrossRef Full Text | Google Scholar

Wiemer, S. (2001). A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 72 (3), 373–382. doi:10.1785/gssrl.72.3.373

CrossRef Full Text | Google Scholar

Williams, S. D. P. (2003). Offsets in global positioning system time series. J. Geophys. Res. 108. doi:10.1029/2002JB002156

CrossRef Full Text | Google Scholar

Wu, Y. M., Chen, S. K., Huang, T. C., Huang, H. H., Chao, W. A., and Koulakov, I. (2018). Relationship between earthquake b-values and crustal stresses in a young orogenic belt. Geophys. Res. Lett. 45, 1832–1837. doi:10.1002/2017gl076694

CrossRef Full Text | Google Scholar

Yu, S. B., and Kuo, L. C. (2001). Present-day crustal motion along the Longitudinal Valley fault, eastern taiwan. Tectonophysics 333, 199–217. doi:10.1016/s0040-1951(00)00275-4

CrossRef Full Text | Google Scholar

Zhao, B., Bürgmann, R., Wang, D., Zhang, J., Yu, J., and Li, Q. (2022). Aseismic slip and recent ruptures of persistent asperities along the Alaska-Aleutian subduction zone. Nat. Comm. 13, 3098. doi:10.1038/s41467-022-30883-7

CrossRef Full Text | Google Scholar

Zhao, D., Qu, C., Shan, X., Bürgmann, R., Gong, W., Tung, H., et al. (2020). Multifault complex rupture and afterslip associated with the 2018M_w6.4 Hualien earthquake in northeastern Taiwan. Geophys. J. Int. 224, 416–434. doi:10.1093/gji/ggaa474

CrossRef Full Text | Google Scholar