
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 02 September 2024
Sec. Geohazards and Georisks
Volume 12 - 2024 | https://doi.org/10.3389/feart.2024.1456186
This article is part of the Research Topic Failure Analysis and Risk Assessment of Natural Disasters Through Machine Learning and Numerical Simulation: Volume IV View all 20 articles
Geological parameters of soil exhibit spatial variability. Inverse analysis allows the acquisition of accurate spatial distributions of key geological parameters, which is crucial for structural safety assessment. In this study, an ensemble Kalman filter (EnKF) is employed in the context of data assimilation. Random fields are used as the initial input ensembles for the algorithm. The present study effectively integrates the ensemble Kalman filter with the numerical simulation software ABAQUS, enabling the inversion of parameter fields under various operating conditions. An in-house Python code script is developed to control ABAQUS for finite element computations and to obtain observations at target points. During the stepwise computation process, the algorithm can utilize newly acquired observations to accelerate the convergence of the parameter field to the true field. The effectiveness of the algorithm is validated, and the method is applied to a case study of double-tunnel excavation and a stepwise excavation analysis of a three-layered slope. The impact of the number of ensemble members and the ratio of the horizontal correlation scale to the vertical correlation scale of random fields on the effectiveness of updating the parameter field have also been investigated.
The stratigraphy of natural environments is formed through prolonged sedimentation, resulting in soil exhibiting heterogeneity. Many scholars regard soil as a complex heterogeneous substance and have demonstrated that soil parameters constitute a spatial stochastic variable (Lumb, 1966), implying that soil parameters possess different values at different locations. Due to the inability to access all material parameters possessed by soil within a given area, rock and soil material parameters are typically treated as stochastic variables. Vanmarcke Erik (1977) presented stochastic models using random fields, achieving more accurate spatial simulations of geological parameters. Building upon the concepts of Vanmarcke’s random field theory, Griffiths and Fenton Gordon (2004) proposed a more rigorous probabilistic analysis method known as the random finite element method (RFEM), which incorporates considerations of spatial correlation length. In RFEM, Monte Carlo methods and random field theory are employed to address the challenge of simulating spatial variability in soil parameters. To tackle the issue of spatial variability in soil parameters, Li X. et al.(2015) focused on the role of conditional random fields. Li et al. (Li et al., 2013; Li Y. J. et al., 2015; Li et al., 2016) concentrated on the domain of three-dimensional slope stability. Furthermore, Li (2017) utilized RFEM to investigate three-dimensional spatial variability in slope stability analysis and conducted performance comparisons with other methods.
Inaccuracies often arise in computational simulations compared to actual engineering scenarios when a crucial geological parameter of the model is crudely defined as a single value. Numerical simulation and monitoring are very important for geohazard and geohazard mitigation (Fang et al., 2023; Fang et al., 2024; Yuan et al., 2024). To address the challenge of obtaining precise soil parameters, the methods of inverse analysis have garnered significant attention in the field of geotechnical engineering. Cividini et al. (1983) employed both the least squares method and Bayesian method to inversely compute Young’s modulus of foundation soil layers based on foundation displacements. Honjo et al. (1994) extended the Bayesian method, while Lee and Kim (1999) applied this approach in tunnel engineering, inversely computing four parameters. Ledesma et al. (1996) provided a brief overview and comparison of four commonly used inverse analysis methods: the least squares method, maximum likelihood method, Bayesian method, and Kalman filtering (KF). Other inverse analysis methods include the Markov Chain Monte Carlo method (MCMC) (Zhang et al., 2010) and the Hamiltonian Monte Carlo method (HMC) (Koch et al., 2020). While inverse analysis methods have shown great potential in geotechnical engineering, they face several challenges, i.e., the bayesian method require numerous forward simulations, which can be computationally expensive for complex geotechnical models. Moreover, traditional methods often struggle to properly account for uncertainties in both measurements and model parameters.
The Kalman filter, particularly the ensemble Kalman filter (Evensen, 1994; Evensen, 2006), and particle filter (Doucet et al., 2000), among other nonlinear methods, have gradually evolved into data assimilation techniques when combined with finite element methods. Among these, EnKF has stood out due to its excellent computational efficiency and has found widespread application. The EnKF has the following advantages over the traditional methods, for example, it provides a probabilistic framework that can handle multiple possible solutions, allowing for sequential updating, which is particularly suited for time-evolving geotechnical problems and it is more computationally efficient. Data assimilation techniques, particularly the Ensemble Kalman Filter (EnKF), have gained significant traction in geotechnical engineering over the past decade. EnKF, originally developed for weather forecasting, has proven to be a powerful tool for integrating observations with numerical models in geotechnical applications. For instance, Chen and Zhang (2006) employed EnKF to update permeability coefficients and pressure heads. Vardon et al. (2016) utilized EnKF to reduce spatial variability in permeability coefficients.
In the context of slope stability, recent studies have shown the potential of data assimilation methods to improve predictions and reduce uncertainties. Liu et al. (2018) proposed a data assimilation framework based on EnKF, utilizing measurements of pore water pressure to improve estimates of hydraulic parameters and consequently predict slope stability. Caballero Perez et al. (2018) enhanced the prediction accuracy of coupled fluid and geomechanical sequential methods at a lower computational cost using EnKF. Li and Liu (2019) combined conditional random fields with EnKF, effectively improving estimates of parameter spatial distributions. Tao et al. (2020) utilized EnKF to investigate key issues in geotechnical and geological domains, such as surface subsidence, and compared simulation results with actual data. Mohsan et al. (2021) combined the EnKF with PLAXIS to investigate the influence of the Mohr-Coulomb model and the Hardening Soil model on the inversion of key parameters in coupled hydro-mechanical slope. Ren et al. (2022) estimated the spatial distribution of the Young’s modulus of an earth-fill dam using EnKF by assimilating arrival times of surface waves.
The use of EnKF for inverse analysis within data assimilation methods requires a forward solver, which in geotechnical engineering is often a custom code script rather than a standardised implementation. In this paper, EnKF is integrated with the numerical simulation software ABAQUS, taking advantage of ABAQUS’ robust problem-solving capabilities. This approach provides a versatile and flexible method for inverse data assimilation analysis, significantly reducing the learning curve associated with this technique.
The main objective of this paper is to achieve parameter updates through EnKF, a data assimilation algorithm. In this process, random fields of critical parameters are generated as the initial input ensemble for filtering. A Python script is employed to control ABAQUS and its subroutines for finite element computations, obtaining observations at each step. This enables the stepwise updating of the parameter field, progressively reducing uncertainties inherent in structural stability analysis. While our work builds upon the foundation laid by Li and Liu (2019), we introduce several innovative aspects. By integrating EnKF with ABAQUS, we extend the applicability of the method to a wider range of complex geotechnical scenarios. Our approach offers enhanced flexibility in problem formulation, improved computational efficiency through optimized scripting, and the ability to handle multi-stage analyses effectively. Furthermore, we provide a comprehensive sensitivity analysis, offering insights into the method’s performance under varying conditions.
The paper is organized into several sections: Section 2 delves into the primary implementation methods of EnKF. A detailed description of the implementation steps and key aspects of the inverse analysis method is provided in Section 3. Section 4 presents a simplified four-step excavation case for comparative analysis and validation of the method’s effectiveness. Section 5 discusses the analysis of a double-tunnel excavation case, focusing on the impact of ensemble size and the ratio of horizontal to vertical fluctuation scales in the random fields on the update results. An analysis of a slope excavation case involving three steps is included in Section 6. The final section is the conclusion of the paper.
Under normal circumstances, the outcomes of observations come from the observation space. This can be mathematically expressed as follows in Equations 1, 2:
In which,
in this context,
Utilizing the algorithm proposed by Evensen (2003), we generate a set of ensembles
In Equation 4, the average value of the set of ensembles of state variables is given by:
let
The covariance matrix of the predicted errors in the state variables can be obtained in Equation 6 as follows:
The calculation formula for error statistics in the Kalman Filter is defined as follows in Equations 7, 8:
where
Monte Carlo sampling of random numbers is employed to simulate Gaussian white noise with a mean of 0 and a standard deviation equal to the observation multiplied by a noise scaling factor. In this scenario, the displacement vector of measurement points constitutes a set of observations with added perturbations, where the
where the statistical characteristics of
In Equation 12 the Kalman gain matrix is given by:
where
The primary computational burden of the Kalman filter lies in the calculation of the covariance matrix. In EnKF process, it is evident that the observation operator
Finally, update the state variables by:
In Equation 14 the optimal estimate is obtained by taking the mean of
The initial value of the state variable are random fields of key geological parameters, which will be updated through EnKF. Upon completion of all iterations, the ensembles’ mean can be regarded as the optimal estimate.
ABAQUS, recognized as a robust finite element analysis software, possesses the capability to simulate a diverse range of mechanical problems and intricate engineering scenarios. It has found widespread application in numerical simulations and engineering computations. Notably, the functionality of ABAQUS subroutines is highly potent. By leveraging these subroutines and connecting them within the ABAQUS framework, various functionalities can be achieved through the utilization of customized Python or Fortran code script. This study specifically employs ABAQUS and its subroutines to assign distinct material parameters to all nodes in the model and to extract displacement values for selected nodes. The flexibility afforded by subroutines ensures the theoretical problem-solving capacity of ABAQUS, rendering it’s theoretically capablity of addressing a spectrum of problems through corresponding inverse analyses.
Accurately predicting the stability of a structure through existing observations is crucial for structural maintenance and safety assessments. The main objective of this paper is to achieve parameter updates through EnKF, a data assimilation algorithm. In this process, random fields of critical parameters are generated as the initial input ensemble for filtering. Customized Python code script is employed to control ABAQUS and its subroutines for finite element computations, obtaining displacement values of the observation points at each step. This enables the stepwise updating of the parameter field, progressively reducing uncertainties inherent in structural stability analysis.
This study utilizes random fields of key geological parameters as the initial ensembles for EnKF. The displacements or stresses at measurement points in the corresponding finite element model are considered as observations. ABAQUS and its subroutines are employed as the computational tools for the model, ultimately achieving the update and inversion of the parameter field.
The general steps of the parameter field inversion method using EnKF with ABAQUS are as follows:
1. Initialization: Generate initial ensemble members using random fields of key parameters. Obtain key parameters such as mean, variance, and spatial correlation from soil data. Use a local averaging subdivision method to generate unconditional random fields of geological parameters to be inverted.
2. Forward Simulation: For each ensemble member, use ABAQUS to simulate the system response. Map the parameters of the random fields to the Abaqus finite element mesh perform finite element analysis.
3. Observation Simulation: Extract simulated observations from ABAQUS output corresponding to measurement locations.
4. EnKF Update: Apply the EnKF update equation to adjust parameter fields based on the difference between simulated and actual observations. The EnKF update equation is given by Equation 13.
5. Use the updated parameter fields for the next round of finite element calculations. Repeat for a specified number of iterations. Upon completion of all iterations, consider the ensembles’ mean as the optimal estimate of the parameter field to be inverted.
The integration with ABAQUS is achieved through custom Python scripts that control the ABAQUS simulations, extract relevant outputs, and feed them into the EnKF algorithm. This approach allows for seamless coupling between the finite element simulations and the data assimilation process. The detailed flowchart of the parameter field inversion method achieved by coupling EnKF with ABAQUS is illustrated in Figure 1.
In the section on stochastic finite element analysis, an in-house Python code script is employed to map the input parameter field onto the mesh nodes of the computational model. The size of the input parameter field is
To validate the proposed Abaqus Enkf framework in geotechnical engineering applications, a simplified excavation is considered in this section. Li and Liu (2019) investigated the influence of unconditional and conditional random fields on the inversion of parameter fields. They conducted a computational case study involving the inversion of Young’s modulus for a simplified four-step excavation, as shown in Figure 2. Measurement points were strategically placed within the model, which can obtain observations after each excavation step. These observations were then utilized to update the parameter field. The updated parameter fields were subsequently employed in the next excavation step.
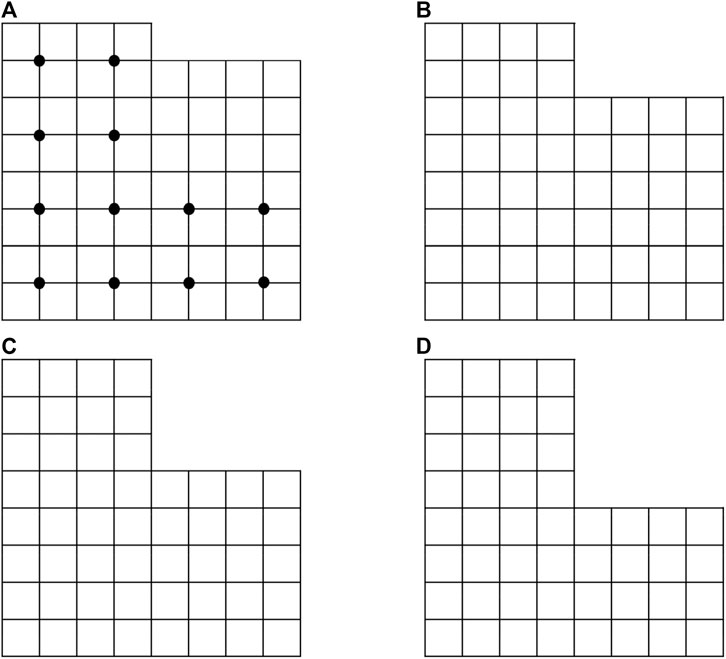
Figure 2. Four-step excavation case: first layer excavation (A) second layer excavation (B) third layer excavation (C) and fourth layer excavation (D) (dots indicate 12 displacement measurement locations).
In this paper, the feasibility of the parameter field inversion method using EnKF with ABAQUS was validated by a reference case study. Li and Liu (2019) used the Enkf with an in-house Fortran finite element code for this case study. The excavation problem assumed in this case had a dimension of
When generating unconditional random fields as the initial ensembles, an additional reference field was generated specifically for the current parameter field inversion. To facilitate a better comparison of the two methods in parameter field inversion, both methods utilized the same reference field.
The results of the inversion of Young’s modulus field after the first three excavation steps using Fortran code and the parameter field inversion method using EnKF with ABAQUS are illustrated in Figures 3, 4, respectively. In the plots, cells closer to red indicate higher values, while those closer to blue indicate lower values. For better numerical comparison, the maximum and minimum values in the legend of the plots for each step of both methods are kept identical. Additionally, root mean square error (RMSE) is introduced to better evaluate the results of the parameter field inversion:
here,
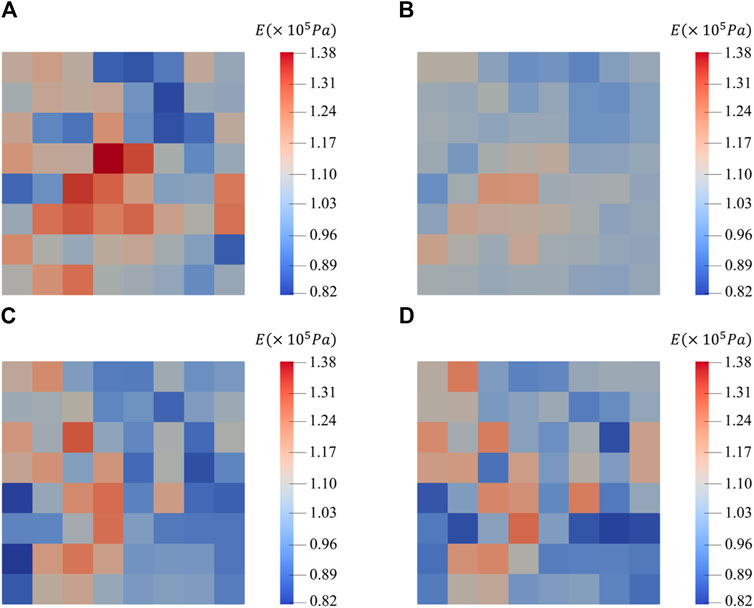
Figure 3. Young’s modulus field using Fortran of: reference field (A) first layer excavation and update (B) second layer excavation and update (C) and third layer excavation and update (D).
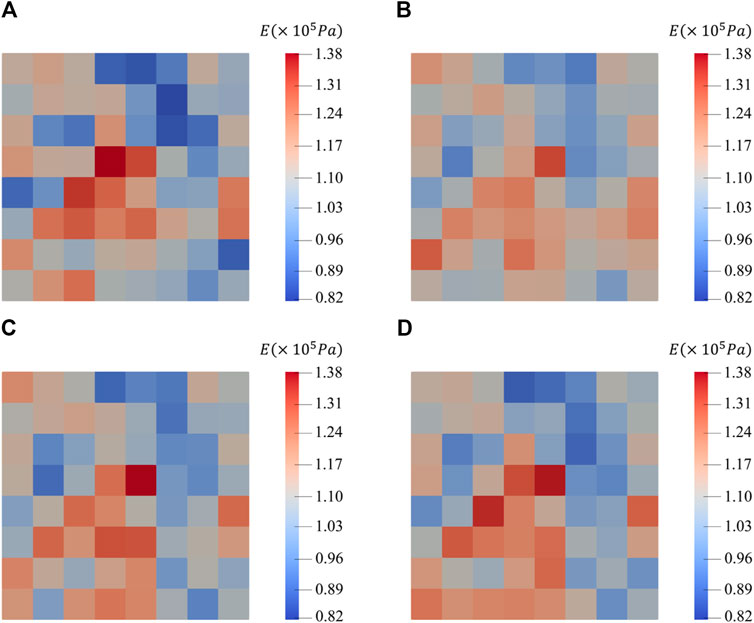
Figure 4. Young’s modulus field using ABAQUS of: reference field (A) first layer excavation and update (B) second layer excavation and update (C) and third layer excavation and update (D).
Following the first update, the distribution of larger and smaller values in the parameter field is already essentially consistent with the reference field, reflecting the spatial variability of the parameters. However, there is still a significant numerical deviation. This issue sees substantial improvement after the second update, and by the third update, the parameter field is nearly identical to the reference field. As seen in Figure 5, the RMSE values of the parameter fields obtained by the two methods continue to decrease, indicating that the uncertainty of the parameter field decreases continuously under the updating of the algorithm, and the updated parameter field converges to the reference field continuously.
Thus, through the comparison with the results of the four-step excavation case studied by Li and Liu, the feasibility and effectiveness of the parameter field inversion method using EnKF with ABAQUS has been demonstrated.
In the previous section, the feasibility and effectiveness of the parameter field inversion method using EnKF with ABAQUS was validated using a simplified four-step excavation case. In this section, a more complex and realistic two-dimensional double-tunnel excavation case is introduced. The double-tunnel excavation case is selected to demonstrate the applicability of our method to complex, multi-stage geotechnical problems. This case presents challenges in capturing the spatial variability of soil properties and their evolution during sequential excavations, which are common in urban tunneling projects. By applying our EnKF-ABAQUS integration to this scenario, we aim to show how the method can improve parameter field estimations in realistic engineering contexts.
The schematic diagram of the model is shown in Figure 6, with a length of
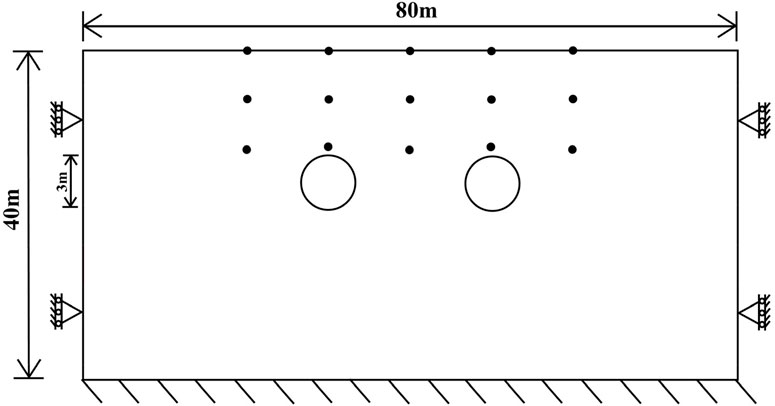
Figure 6. Size and boundary conditions of double-tunnel excavation (dots indicate 15 displacement target points).
According to the parameter sensitivity analysis by Wang et al. (2022), under the Mohr-Coulomb criterion, the sensitivity of displacement values to Young’s modulus is much higher than other parameters. Additionally, since not all elements enter the plastic stage during the simulated excavation process, parameters such as cohesion and friction angle only affect displacement in a few elements. Therefore, in this case, Young’s modulus field is chosen as the parameter field for inversion. To simulate geological stratification and make the inversion results clearer, the reference field is set to have four distinct layers, as shown in Figure 7. Young’s modulus values from top to bottom are:
A customized Fortran code was used to generate an unconditional random field of Young’s modulus as the initial ensembles for EnKF. The ensemble size as well as the number of random fields were set to 500. The mean of Young’s modulus was
After the first excavation, the updated parameters were used for the second excavation. The mean of the parameter fields from the 500 ensembles after the two excavations can be considered the best estimate for the parameter field.
The distribution of the parameter field after two excavations is shown in Figure 8. In this Figure, regions closer to red represent higher values, while those closer to blue represent lower values. From Figure 8, it is evident that after the first excavation and update, the distribution of Young’s modulus field already exhibits a clear four-layer pattern, although the boundaries are not well-defined, and there are mixed regions between every two layers. The inversion results for Young’s modulus field in the left edge and right edge regions of the model are not as pronounced. After the second excavation and update, the four-layer pattern, especially in the central region, has clearer boundaries. Young’s modulus field in the left and right regions of the model is now consistent with the reference field, and the distinguishability of Young’s modulus values between the four layers is higher and closer to the corresponding values in the reference field. The trend of RMSE (Equation 15) values for the random fields and the updated fields after two excavations, as shown in Figure 9, also indicates that the inversion of the parameter field has been quite effective after the two-step excavations.
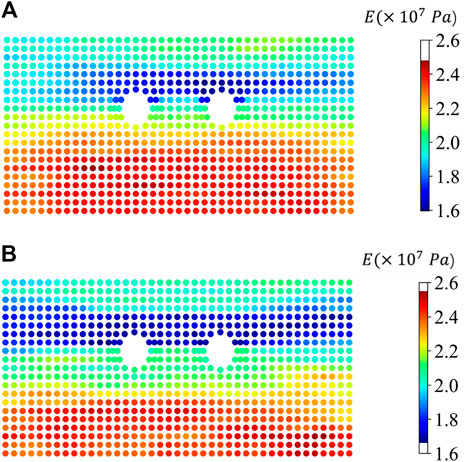
Figure 8. Young’s modulus field of: first tunnel excavation and update (A) second tunnel excavation and update (B).
The primary focus is to investigate the influence of the ensemble size and the ratio of the horizontal fluctuation scale to the vertical fluctuation scale
In the first part of the investigation into the impact of ensemble size on the results of the parameter field inversion, while keeping other parameters constant, the ratio of the horizontal fluctuation scale to the vertical fluctuation scale is set to
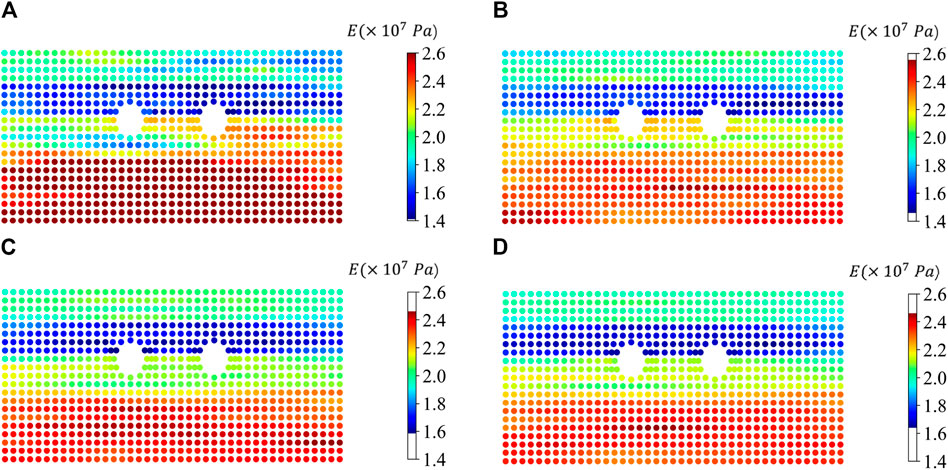
Figure 10. Young’s modulus field of double-tunnel excavation after one update using: 200 ensembles (A) 300 ensembles (B) 500 ensembles (C) 1,000 ensembles (D).
In this Figure, regions closer to red indicate higher Young’s modulus values, while those closer to blue indicate lower values. When the ensemble size is 200, the four-layer stratification in the distribution of the parameter field after one update is almost invisible, with unclear layer boundaries and even mixing between different layers. This outcome is nearly unusable. However, with an increase in the ensemble size, this situation is significantly improved. After one update, the parameter field already exhibits a more distinct four-layer stratigraphic distribution. When the ensemble size is increased to 500, the stratigraphic distribution becomes more apparent, and the contours between each layer are clearer, with no mixing at the layer edges. Increasing the ensemble size to 1,000 does not show a significant improvement compared to an ensemble size of 500, as the results are already fairly close to the reference field. Meanwhile, the RMSE values of the parameter fields for the four ensemble sizes after one update are shown in Figure 11. From this Figure, it can be seen that the curve converges when the ensemble size reaches 500, and further increasing the ensemble size does not lead to a noticeable improvement. It is essential to note that an increase in ensemble size implies a proportional increase in computational cost (i.e. increase the ensemble size from 500 to 1,000 will double the computational cost), as each ensemble’s parameter field undergoes finite element calculation at least once. Considering these factors, an ensemble size of 500 appears to be a reasonable choice for this case.
Figure 12 presents the probability density distributions of parameter field values for four ensemble sizes after one update, as part of the investigation into the impact of ensemble size on the results of the parameter field inversion. When the ensemble size is 200, the data distribution is extensive, and the four values corresponding to the reference field (
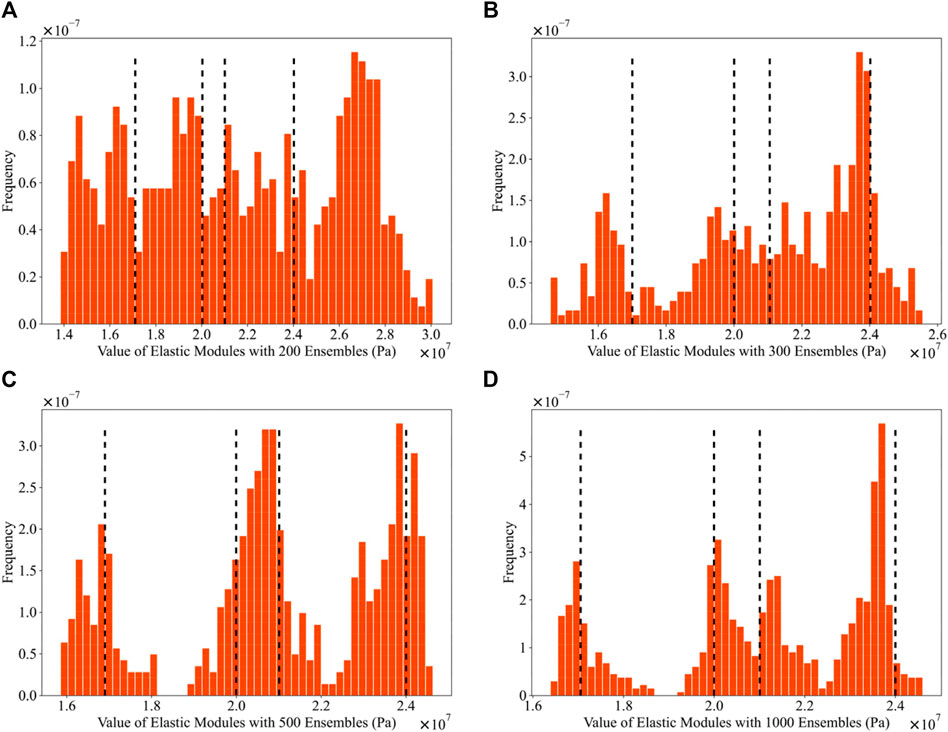
Figure 12. Probability density distributions of Young’s modulus field values after one update using: 200 ensembles (A) 300 ensembles (B) 500 ensembles (C) 1,000 ensembles (D) (The dashed lines in the illustration denote the parameter values of the reference field).
In the second part, the focus is primarily on exploring the impact of the ratio of horizontal to vertical fluctuation scales, denoted as
Figure 13 presents the distributions of the reference field and the parameter field after one update for aniso values of 2, 4, 8, 12, 16, and 20. In this Figure, regions closer to red indicate higher values of Young’s modulus, while regions closer to blue indicate lower values. When aniso is set to 2, the parameter field distribution shows almost no discernible four-layer stratification, and the boundaries between layers are relatively unclear, with different layers even exhibiting mixing, making it nearly unusable.
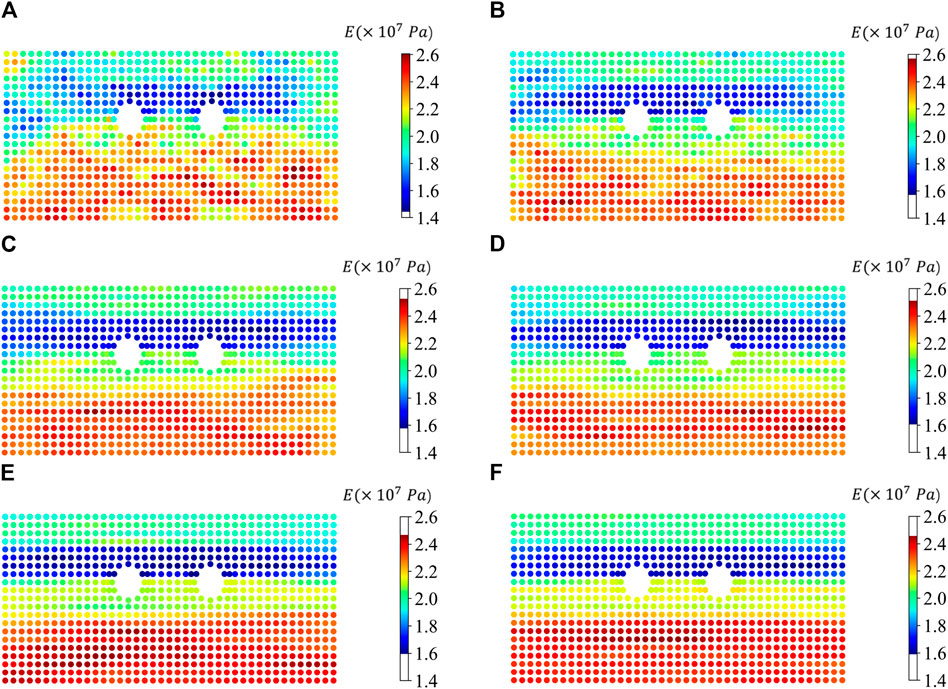
Figure 13. Young’s modulus field of double-tunnel excavation after one update using:
However, when aniso is set to 4 and 8, this situation improves significantly. After one update, the parameter field already exhibits a more apparent stratified distribution, although the contours of the layers are still not very clear, and there are still mixed regions along the edges. When the value of aniso increases to 12, the layer distribution becomes more distinct, with clearer contours between each layer, and the edges of the layers no longer exhibit mixing. When aniso is set to 16 or higher, the parameter field after one update is essentially indistinguishable from the reference field, showing a very clear stratification, and the contours of the layers are highly distinct. Simultaneously, the RMSE values of the parameter field after one update for six values of aniso are shown in Figure 14. From this Figure, it is evident that increasing the value of aniso from 2 to 4 results in a significant improvement in the inversion effectiveness. However, subsequent increases in aniso have a relatively less pronounced impact on the inversion effectiveness. The results depicted in the two Figures can be explained by considering that when the value of aniso is excessively large, the horizontal fluctuation scale approaches the width of the model. As a result, the two-dimensional spatial variability tends to become one-dimensional along the vertical axis, making the inversion much less challenging for one-dimensional data compared to two-dimensional data. In practical geological distributions, layers are unlikely to be so regular and uniformly distributed, rendering excessively large values of aniso meaningless in realistic scenarios.
Figure 15 presents the probability density distributions of parameter field values after one update for six values of aniso when investigating the influence of the ratio of horizontal to vertical fluctuation scales, denoted as
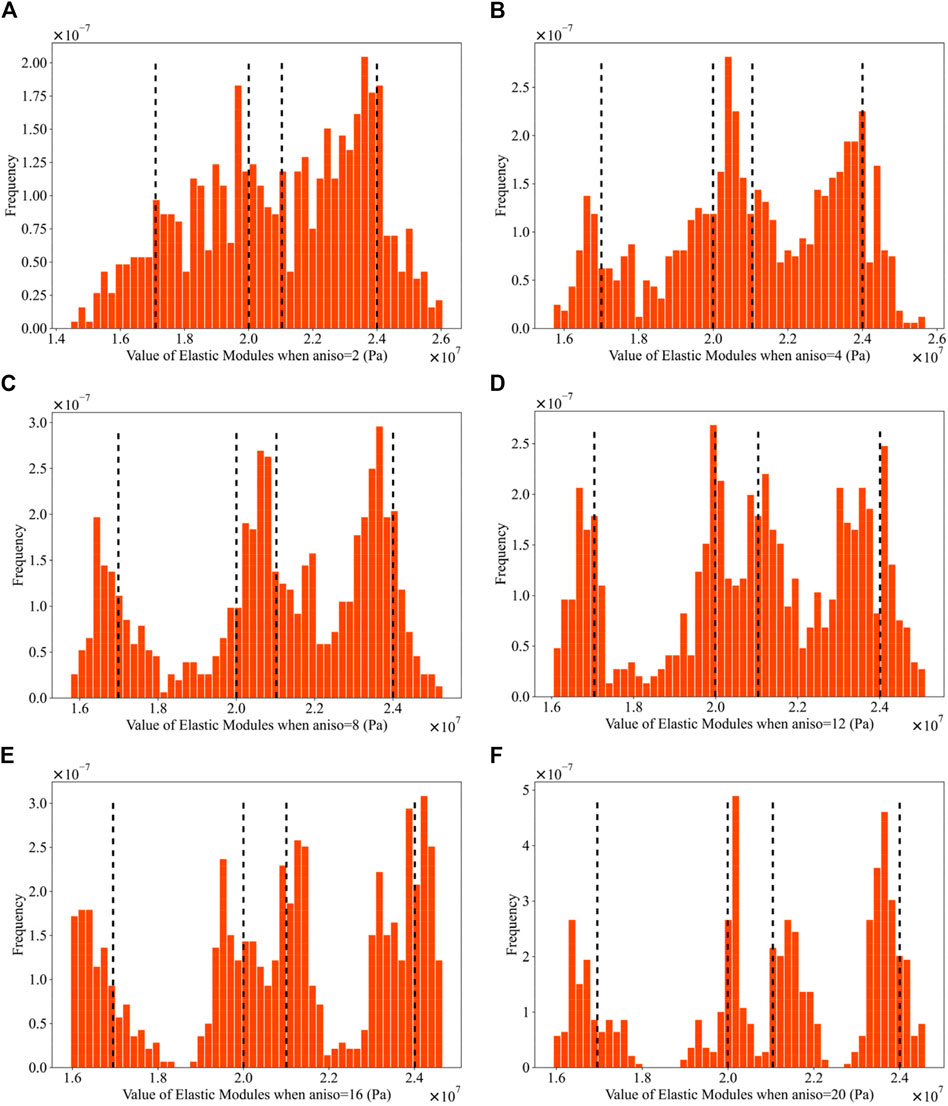
Figure 15. Probability density distributions of Young’s modulus field values after one update using:
In the previous section, we employed a two-dimensional case of a double-tunnel excavation to validate the accuracy of the algorithm and conducted an analysis of relevant parameters. Building upon that foundation, this section will introduce a simplified two-dimensional layered slope with a three-step excavation case for additional validation. The three-layered slope excavation case was chosen to further validate our method in a different geotechnical context and to explore its performance in capturing distinct stratigraphic features. Slope stability analysis is a critical aspect of geotechnical engineering, and accurate estimation of soil parameters in layered slopes is essential for reliable stability assessments. This case study allows us to demonstrate the method’s capability in handling varying spatial correlations and its effectiveness in updating parameter fields across different geological layers.
The schematic diagram of the model is shown in Figure 16, with a length of 240 m, height of 120 m. The three-step excavation is carried out from top to bottom as indicated in the diagram. Excavation sequence is as follows:
1) Initial state: Full slope profile;
2) First excavation: Remove top 20 m from the slope face, part (a) in Figure 16;
3) Second excavation: Remove additional 20 m from the slope face, part (b) in Figure 16
4) Third excavation: Remove final 20 m to achieve the target slope profile, part (3) in Figure 16
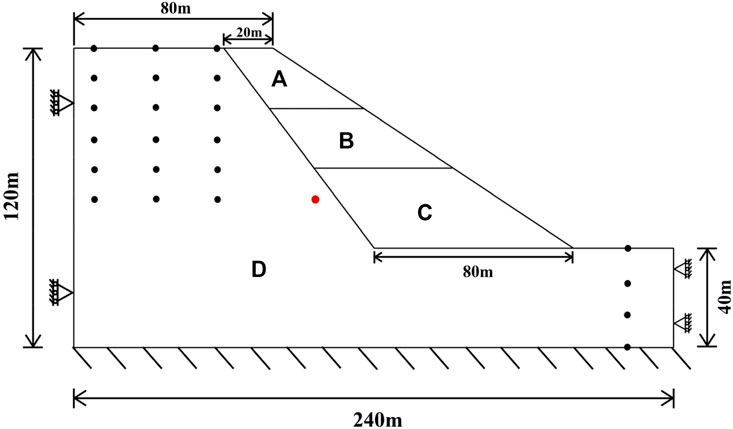
Figure 16. Excavation sequence: first layer excavation (A) second layer excavation (B) third layer excavation (C). (D) Represents the regions involved in the inverse analysis (Black dots indicate displacement measurement locations and the red dot indicates the target point).
Each excavation stage is followed by an EnKF update of the parameter field.
The boundary conditions of the model involve constraining horizontal displacements at both ends, while the bottom is fixed. The model employs the Mohr-Coulomb failure criterion, and detailed material parameters are provided in Table 2.
Consistent with the double-tunnel excavation case, a parameter inversion will be conducted for Young’s modulus field. In order to simulate geological stratification and enhance the clarity of the parameter inversion results, a reference field is set with an apparent three-layer stratification, as illustrated in Figure 17. Young’s modulus values are assigned from top to bottom as
A Fortran code was employed to generate random fields of Young’s modulus for the initial ensembles in EnKF. The ensemble size and the number of random fields remained at 500. The mean of Young’s modulus
The distribution of the parameter field after the three-step excavation update is depicted in Figure 18. In this Figure, regions closer to red indicate higher values, while regions closer to blue signify lower values. From Figure 18, it is obvious that after the first excavation and update, Young’s modulus field distribution has clearly exhibited a three-layer pattern, with distinct edges. Notably, there is no evident lack of inversion effectiveness for Young’s modulus field in the regions at the left and right ends of the model. The results after the first update are superior to the double-tunnel excavation case, primarily due to the increased value of the anisotropy factor (aniso).
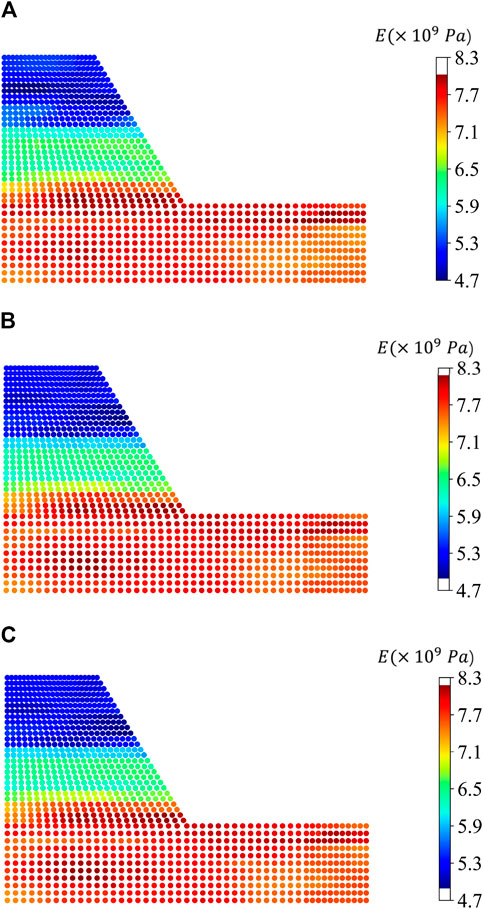
Figure 18. Youngs modulus field of: first excavation and update (A) second excavation and update (B) third excavation and update (C).
In the second and third excavations and updates, the boundary lines of the three-layered region become more distinct. Young’s modulus field at the left and right ends of the model also aligns closely with the reference field, and the discriminability of Young’s modulus values in the three layers is higher, numerically approaching the reference field. The RMSE values for the updated fields of the three-step excavation are shown in Figure 19. After the first excavation and update, the inversion of the parameter field is already quite effective.
As depicted in Figure 16, the red dots therein represent the selected target point. The displacement distribution of this point in both the horizontal and vertical directions under the reference field, as well as within the three successive updating fields, is illustrated in Figure 20. The histograms in the figure depict the distribution of displacements in the horizontal and vertical directions for the target point. The blue curve represents the fitted curve, while the black dashed line signifies the displacements in the horizontal and vertical directions under the reference field for the selected point in the three excavation scenarios. Following each update, the displacement distributions under the parameter fields approximate a normal distribution. Simultaneously, with an increasing number of steps, the mean values of the displacements under the parameter fields converge towards those under the reference field. Additionally, the standard deviation of the displacement distribution progressively decreases. After the three excavation and updating steps, the mean values of the displacements in the horizontal and vertical directions under the updated parameter fields closely resemble those under the reference field, indicating the effectiveness of the parameter field updates.
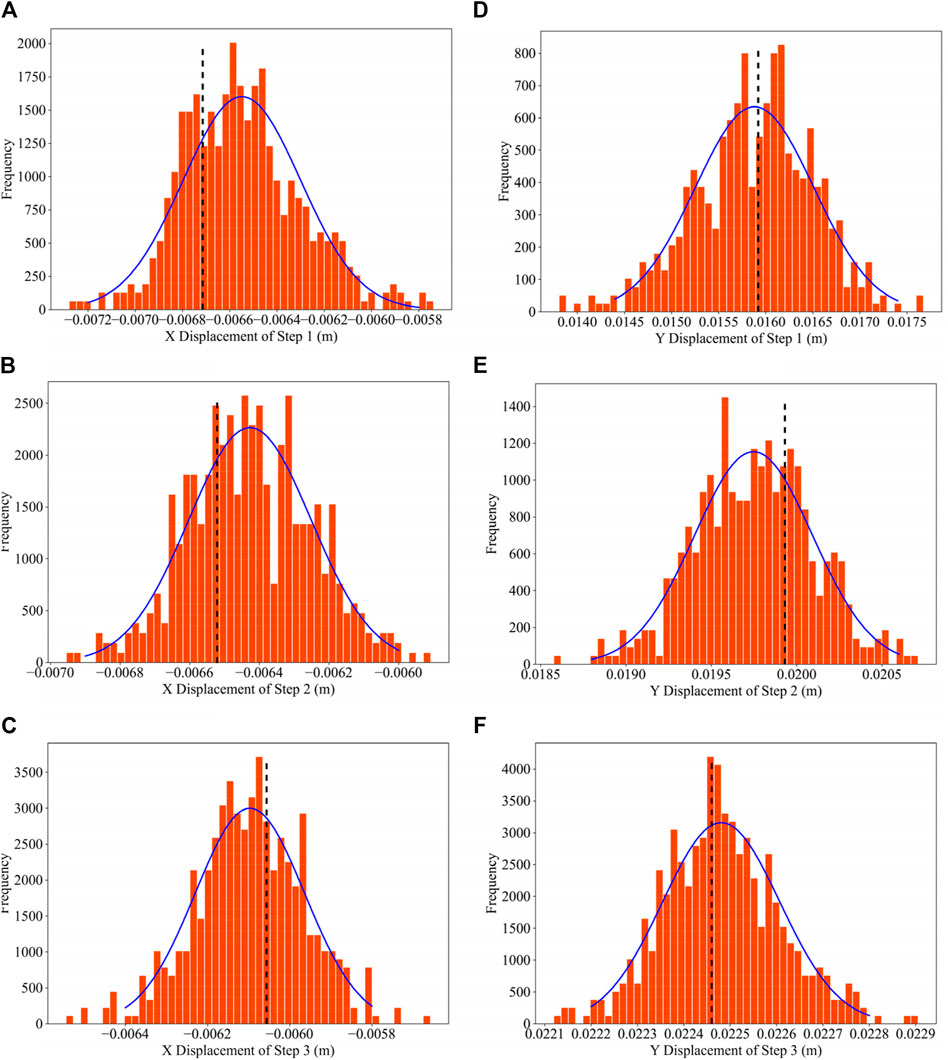
Figure 20. Probability density distributions of target point’s displacement values: in X direction after step 1 (A) in X direction after step 2 (B) in X direction after step 3 (C) in Y direction after step 1 (D) in Y direction after step 2 (E) in Y direction after step 3 (F) (The dashed lines in the illustration denote the target point’s displacement values of three steps under the reference field).
This paper presents a parameter field inversion method based on a data assimilation method named EnKF with a finite element analysis tool called ABAQUS. The method employs an ABAQUS subroutine to assign material parameters to nodes, and a customized in-house Python code script is used to control ABAQUS for computations and to read observation points data, which is subsequently utilized for EnKF updates. The method can be applied to various scenarios, including double-tunnel excavation and slope excavation. By using random fields of key parameters as the initial input ensembles for EnKF and utilizing displacement data from observation points, precise inversion of the parameter field can be achieved.
For geological formations characterized by stratified distribution, the ratio of horizontal to vertical fluctuation scales in the random fields, denoted as aniso, significantly influences the results of parameter updates. Similarly, the ensemble size is also a major factor affecting the updating outcomes. In general, a larger ensemble size tends to yield better updating effects. However, a larger ensemble size also implies a greater computational burden. For a specific problem, once the ensemble size reaches a certain value, the improvement in updating results becomes limited.
The results indicate that, owing to higher precision of ABAQUS in finite element computations, this method provides more accurate updates for the parameter field. For multi-step engineering or practical problems, new observations are generated after each step, and these can be utilized for updating the parameter field. Consequently, the parameter field gradually converges to the true values. This characteristic can be beneficial in guiding realistic engineering applications.
The integration with ABAQUS allows for the use of high-performance computing resources to handle more complex and finely discretized models. Future work will focus on optimizing the method for large-scale applications, potentially incorporating techniques such as localization or model reduction to manage computational costs effectively.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
DW: Conceptualization, Formal Analysis, Methodology, Writing–original draft. CW: Formal Analysis, Investigation, Methodology, Software, Writing–original draft. XP: Supervision, Validation, Writing–review and editing. HS: Methodology, Resources, Validation, Writing–review and editing. JW: Data curation, Investigation, Validation, Writing–review and editing. ZC: Project administration, Resources, Software, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research is supported by the Hunan Provincial Transportation Technology Project (No. 202316).
Authors DW, HS, JW, and ZC were employed by Hunan Provincial Water Transportation Construction and Investment Group Co.,Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer LG declared a shared affiliation with the authors DW, CW to the handling editor at time of review.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1456186/full#supplementary-material
Burgers, G. J. H., Leeuwen, P. J. v., and Evensen, G. (1998). Analysis scheme in the ensemble kalman filter. Mon. Weather Rev. 126, 1719–1724. doi:10.1175/1520-0493(1998)126<1719:asitek>2.0.co;2
Caballero Perez, E. F., Rochinha, F., Borges, M., and Murad, M. (2018). An enhanced ensemble Kalman filter scheme incorporating model error in sequential coupling between flow and geomechanics. Int. J. Numer. Anal. Methods Geomechanics 43, 482–500. doi:10.1002/nag.2872
Chen, Y., and Zhang, D. (2006). Data assimilation for transient flow in geologic formations via Ensemble Kalman Filter. Adv. Water Resour. 29, 1107–1122. doi:10.1016/j.advwatres.2005.09.007
Cividini, A., Maier, G., and Nappi, A. (1983). Parameter estimation of a static geotechnical model using a Bayes' approach. Int. J. Rock Mech. Min. Sci. & Geomechanics Abstr. 20 (5), 215–226. doi:10.1016/0148-9062(83)90002-5
Doucet, A., Godsill, S., and Andrieu, C. (2000). On sequential Monte Carlo sampling methods for Bayesian filtering. Statistics Comput. 10 (3), 197–208. doi:10.1023/A:1008935410038
Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 99 (C5), 10143–10162. doi:10.1029/94JC00572
Evensen, G. (2003). The Ensemble Kalman Filter: theoretical formulation and practical implementation. Ocean. Dyn. 53 (4), 343–367. doi:10.1007/s10236-003-0036-9
Evensen, G. (2006). Data assimilation: the ensemble kalman filter. Berlin, Heidelberg: Springer-Verlag.
Fang, K., Dong, A., Tang, H., An, P., Wang, Q., Jia, S., et al. (2024). Development of an easy-assembly and low-cost multismartphone photogrammetric monitoring system for rock slope hazards. Int. J. Rock Mech. Min. Sci. 174, 105655. doi:10.1016/j.ijrmms.2024.105655
Fang, K., Tang, H., Li, C., Su, X., An, P., and Sun, S. (2023). Centrifuge modelling of landslides and landslide hazard mitigation: a review. Geosci. Front. 14 (1), 101493. doi:10.1016/j.gsf.2022.101493
Griffiths, D. V., and Fenton Gordon, A. (2004). Probabilistic slope stability analysis by finite elements. J. Geotechnical Geoenvironmental Eng. 130 (5), 507–518. doi:10.1061/(ASCE)1090-0241(2004)130:5(507)
Honjo, Y., Wen-Tsung, L., and Guha, S. (1994). Inverse analysis of an embankment on soft clay by extended Bayesian method. Int. J. Numer. Anal. Methods Geomechanics 18 (10), 709–734. doi:10.1002/nag.1610181004
Koch, M. C., Fujisawa, K., and Murakami, A. (2020). Adjoint Hamiltonian Monte Carlo algorithm for the estimation of elastic modulus through the inversion of elastic wave propagation data. Int. J. Numer. Methods Eng. 121 (6), 1037–1067. doi:10.1002/nme.6256
Ledesma, A., Gens, A., and Alonso, E. E. (1996). Parameter and variance estimation in geotechnical backanalysis using prior information. Int. J. Numer. Anal. Methods Geomechanics 20 (2), 119–141. doi:10.1002/(SICI)1096-9853(199602)20:2<119::AID-NAG810>3.0.CO;2-L
Lee, I.-M., and Kim, D.-H. (1999). Parameter estimation using extended Bayesian method in tunnelling. Comput. Geotechnics 24 (2), 109–124. doi:10.1016/S0266-352X(98)00031-7
Li, X., Zhang, L., and Li, J. L. (2015a). Using conditioned random field to characterize the variability of geologic profiles. J. Geotechnical Geoenvironmental Eng. 142, 04015096. doi:10.1061/(ASCE)GT.1943-5606.0001428
Li, Y. (2017). Reliability of long heterogeneous slopes in 3D: model performance and conditional simulation. PhD thesis. Delft University of Technology.
Li, Y., Hicks, M. A., and Nuttall, J. (2013) “Probabilistic analysis of a benchmark problem for slope stability in 3D,” in Proceedings of the 3rd international symposium on computational geomechanics (COMGEO III). Krakow, Poland.
Li, Y., and Liu, K. (2019). Updating soil spatial variability and reducing uncertainty in soil excavations by kriging and ensemble kalman filter. Adv. Civ. Eng. 2019, 1–14. doi:10.1155/2019/8518792
Li, Y. J., Hicks, M. A., and Nuttall, J. D. (2015b). Comparative analyses of slope reliability in 3D. Eng. Geol. 196, 12–23. doi:10.1016/j.enggeo.2015.06.012
Li, Y. J., Hicks, M. A., and Vardon, P. J. (2016). Uncertainty reduction and sampling efficiency in slope designs using 3D conditional random fields. Comput. Geotechnics 79, 159–172. doi:10.1016/j.compgeo.2016.05.027
Liu, K., Vardon, P. J., and Hicks, M. A. (2018). Sequential reduction of slope stability uncertainty based on temporal hydraulic measurements via the ensemble Kalman filter. Comput. Geotechnics 95, 147–161. doi:10.1016/j.compgeo.2017.09.019
Lumb, P. (1966). The variability of natural soils. Can. Geotechnical J. 3 (2), 74–97. doi:10.1139/t66-009
Mohsan, M., Vardon, P. J., and Vossepoel, F. C. (2021). On the use of different constitutive models in data assimilation for slope stability. Comput. Geotechnics 138, 104332. doi:10.1016/j.compgeo.2021.104332
Ren, Y., Nishimura, S., Shibata, T., and Shuku, T. (2022). Data assimilation for surface wave method by ensemble Kalman filter with random field modeling. Int. J. Numer. Anal. Methods Geomechanics 46 (15), 2944–2961. doi:10.1002/nag.3435
Tao, Y., Sun, H., and Cai, Y. (2020). Predicting soil settlement with quantified uncertainties by using ensemble Kalman filtering. Eng. Geol. 276, 105753. doi:10.1016/j.enggeo.2020.105753
Vanmarcke Erik, H. (1977). Probabilistic modeling of soil profiles. J. Geotechnical Eng. Div. 103 (11), 1227–1246. doi:10.1061/AJGEB6.0000517
Vardon, P. J., Liu, K., and Hicks, M. A. (2016). Reduction of slope stability uncertainty based on hydraulic measurement via inverse analysis. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 10 (3), 223–240. doi:10.1080/17499518.2016.1180400
Wang, C., Wang, K., Tang, D., Hu, B., and Kelata, Y. (2022). Spatial random fields-based Bayesian method for calibrating geotechnical parameters with ground surface settlements induced by shield tunneling. Acta Geotech. 17 (4), 1503–1519. doi:10.1007/s11440-021-01407-2
Yuan, W.-H., Liu, M., Dai, B.-B., Wang, Y., Chan, A., Zhang, W. *, Zheng, X.-C., and Wang, Y. (2024). Stabilizing nodal integration in dynamic smoothed particle finite element method: a simple and efficient algorithm. Comput. Geotechnics 169, 106208. doi:10.1016/j.compgeo.2024.106208
Keywords: geomechanical parameter, spatial variability, data assimilation, EnKF, inverse analysis
Citation: Wang D, Wang C, Pu X, Song H, Wan J and Cao Z (2024) Data assimilation by combining ABAQUS with ensemble Kalman filter and its application to geotechnical engineering. Front. Earth Sci. 12:1456186. doi: 10.3389/feart.2024.1456186
Received: 28 June 2024; Accepted: 06 August 2024;
Published: 02 September 2024.
Edited by:
Faming Huang, Nanchang University, ChinaReviewed by:
Lei Gao, Hohai University, ChinaCopyright © 2024 Wang, Wang, Pu, Song, Wan and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaogang Pu, eGlhb2dhbmdwdTIwMjRAMTYzLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.