- 1School of Soil and Water Conservation, Beijing Forestry University, Beijing, China
- 2National Disaster Reduction Center of China, Ministry of Emergency Management, Beijing, China
Earthquake-induced landslides (EQIL) are one of the most catastrophic geological hazards. Immediate and swift evaluation of EQIL hazard in the aftermath of an earthquake is critically important and of substantial practical value for disaster reduction. The selection of influencing factor layers is crucial when using machine learning methods to predict EQIL hazard. As important input factors for EQIL hazard models, lithology and precipitation are extensively employed in forecasting EQIL hazard. However, few work explored whether these layers can improve the accuracy of EQIL hazard predictions. With Random Forest (RF) models, we employed a traditional and a state-of-the-art sampling strategy to assess EQIL modelling with and without lithology and precipitation data for the 2022 Luding earthquake in China. First, by excluding both factors, we used eight other influencing factors (land use, slope aspect, slope, elevation, distance to faults, distance to rivers, NDVI, and peak ground acceleration) to generate a landslide hazard map. Second, lithology and precipitation were separately added to the original EQIL hazard models. The results indicate that neither lithology nor precipitation have positive effects on the prediction of EQIL for both sampling strategies. The high-risk areas (or low-risk areas) tend to cluster within certain lithology types or precipitation ranges, which significantly affects the accuracy of the hazard map. Additionally, the model with the state-of-the-art sampling strategy deteriorates more than the model with the traditional sampling strategy. We believe this is very likely due to the strong spatial clustering of negative sample points caused by the latest sampling strategy. Our findings will contribute to the assessment of post-earthquake landslide hazards and the advancement of emergency disaster mitigation efforts.
1 Introduction
Earthquake-induced landslides pose significant threats to human life and property. EQIL hazard maps, indicating the likelihood of landslides in areas affected post-earthquake, are critical for enabling decision-makers to implement emergency responses. Thus, accurately predicting and mapping the hazard of earthquake-induced landslides is indispensable (Jibson et al., 2000; Marano et al., 2010; Raspini et al., 2017). Despite considerable research efforts, the accuracy of EQIL hazard maps frequently falls short, leading to a substantial number of areas being misjudged or their risk levels exaggerated (Dreyfus et al., 2013; Allstadt et al., 2018). This situation hampers decision-makers’ ability to devise accurate emergency response strategies, thus making the creation of high-quality EQIL hazard maps a particularly challenging task.
Machine learning methods are currently the mainstream approach for creating EQIL hazard maps (Shao and Xu, 2022). In machine learning approaches, selecting the influencing factors for co-seismic landslides is a critical step that directly impacts the outcomes of predictions. During the selection of influencing factors, lithology factors and mean annual precipitation are widely used by researchers (Shao et al., 2022; Aditian et al., 2018; Pyakurel et al., 2024; Li et al., 2024; Khaliq et al., 2023; Nefeslioglu et al., 2008). Especially, lithology factors are recognized as one of the landslide-triggering factors considered in any landslide susceptibility assessment using data-driven methods, a fact well acknowledged in the field (Guzzetti et al., 1996; Van Westen et al., 2006; Blahut et al., 2010). But whether these factors positively impact the precision of EQIL hazard prediction results has seldom been explored.
The classification of lithology is usually conducted through stratigraphic ages, with rocks from various epochs exhibiting distinct physical properties (Gallen et al., 2015). These differences contribute to varying levels of landslide susceptibility. Although there is a strong correlation between lithology and EQIL hazard, lithology layers come in a wide variety and often have lower resolution, with significant differences in lithology across different regions. Therefore, lithology factors may not always play a beneficial role in predicting EQIL hazards. Precipitation increases pore water pressure and reduces the shear resistance of soil and rock layers, thereby leading to landslides (Aditian et al., 2018). Precipitation data (such as mean annual precipitation) is also a significant factor affecting landslide occurrence. However, the resolution of mean annual precipitation layers is coarse, at 0.1°, and regional differences are significant. Whether using mean annual precipitation layers can effectively enhance the accuracy of EQIL predictions merits further investigation.
To address these issues, this study utilized high-quality landslide inventories from eight earthquake events in China to create two sets of positive and negative sample points datasets for machine learning, employing both traditional and contemporary non-landslide point sampling strategies. Utilizing the Random Forest model, eight influencing factors were selected: “land use,” “slope aspect,” “slope,” “elevation,” “distance to fault lines,” “distance to rivers,” “NDVI,” and “peak ground acceleration.” These were used to predict the EQIL hazard for the VII degree area affected by the 2022 Luding earthquake. The prediction results were validated against the interpreted landslide inventory for this earthquake, exploring the accuracy of the prediction outcomes from the two sampling strategies. Subsequently, lithology factors and mean annual precipitation were added to the aforementioned eight influencing factors, while keeping the machine learning model and sample datasets unchanged. This allowed for an exploration of how the inclusion of lithology or precipitation factors affects the differences in prediction outcomes. The novelty of this study lies in its demonstration of how lithology and mean annual precipitation impact the accuracy of EQIL hazard predictions. It shows that both factors have a significant effect on prediction accuracy. Avoiding these factors can notably enhance the precision of EQIL hazard forecasts.
2 Study area
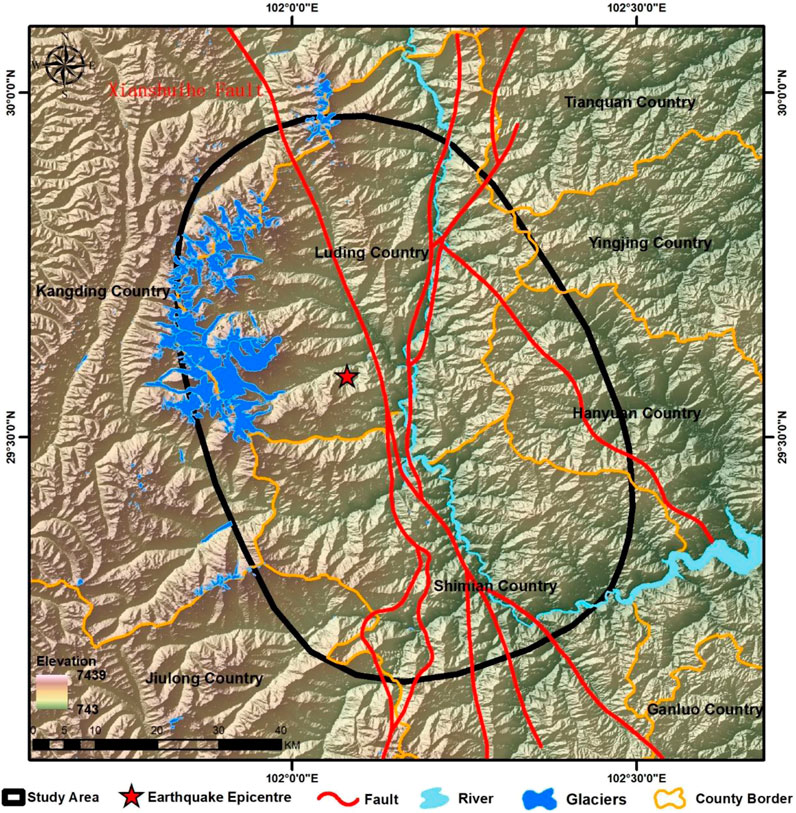
The study area selected for this research encompasses the VII degree zone affected by the 6.8 magnitude Luding earthquake in 2022 (Figure 1), situated at the southeastern edge of the Tibetan Plateau, covering the southern part of Luding County and the northern part of Shimian County in Ganzi Prefecture. The earthquake’s epicenter was located near the Moxi Fault, close to the Gongga Mountain Hailuogou Glacier Forest Park, along the southeastern edge of the Tibetan Plateau within the Xianshuihe fault zone. The Xianshuihe fault zone is one of the highly active and large-scale boundary strike-slip fault zones, positioned at the eastern edge of the Tibetan Plateau, where the Bayan Har block meets the Sichuan-Yunnan block. It intersects with the Longmenshan Fault Zone and the Anning River Fault Zone, forming the famous “Y-shaped” fault zone in western Sichuan (Wang et al., 2015).
This earthquake triggered at least 5,007 landslides, with preliminary spatial distribution analysis indicating that the landslides were concentrated in areas of VIII and IX earthquake intensity. There is a clear connection between the coseismic fault and the distribution of landslides, with the landslides primarily clustered around both sides of the causative fault. Notably, there are more landslides on the northeast side compared to the southwest side (Huang et al., 2023).
3 Materials and methods
3.1 Landslide inventories
We obtained open access lists of high-quality earthquake landslides from publicly available research, as follows: the 2008 Wenchuan earthquake (Xu et al., 2014a), the 2010 Yushu earthquake (Xu et al., 2013), the 2013 Lushan earthquake (Xu et al., 2015), the 2013 Minxian earthquake (Xu et al., 2014b), the 2014 Ludian earthquake (Wu et al., 2020), the 2017 Jiuzhaigou earthquake (Xu et al., 2018), the 2017 Milin earthquake (Hu et al., 2019), the 2022 Lushan earthquake (Shao et al., 2022), and the 2022 Luding earthquake (Huang et al., 2023). High-quality landslide inventories from the first eight earthquakes were used to create the training samples. The landslide inventory from the 2022 Luding earthquake was used to validate the EQIL hazard prediction results for the Luding study area.
3.2 Identifying influencing factors for EQIL
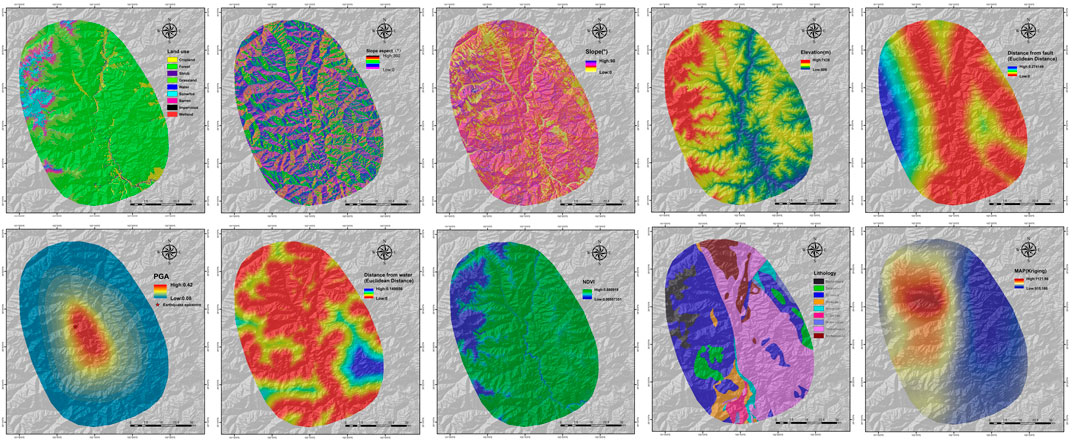
The occurrence of landslides is influenced by a variety of factors, and scientifically selecting these factors is crucial for conducting studies on regional landslide risk assessment. To investigate the impact of lithology and mean annual precipitation on the precision of EQIL hazard prediction, we selected ten potential factors that could cause landslides. This selection was made after a comprehensive process that included field observations, collection of available data, review of relevant literature, and numerous tests (Fan et al., 2021; Chen et al., 2017; Pham et al., 2017; Tien et al., 2016; Youssef et al., 2016). The factors are elevation, slope aspect, slope, land use, mean annual precipitation (MAP), lithology, distance to faults, distance to rivers, NDVI, and peak ground acceleration (PGA) during earthquakes. The data sources for these factors can be seen in Table 1.
It is noteworthy that, in the case of the 2022 Luding earthquake event, there was some discrepancy between the epicenter location and peak ground acceleration provided by the USGS and the results of field investigations. Therefore, we estimated and mapped the peak ground acceleration raster for the study area based on intensity zones provided by the China Earthquake Administration. Examples of influencing factor layers focused on the study area are shown in Figure 2.
3.3 Creation of machine learning training sample points
3.3.1 Creation of positive sample points
In this study, the landslide inventories from the eight selected earthquake events are all represented as landslide polygon layers. Centroids of the landslide polygons were generated using ArcMap version 10.8. Given that many landslide polygons are of irregular shapes, some centroids did not fall within their respective polygons (Qiu et al., 2024). Therefore, using ArcMap, all centroids located within the landslide polygons were selected to serve as landslide points (positive sample points).
3.3.2 Creation of negative sample points
In traditional landslide hazard assessments, the sampling ratio of positive (landslide) to negative (non-landslide) sample points is 1:1 (Hong et al., 2020). Zhu et al. (2017) proposed a method in areas with landslide polygons where every seismic zone is filled with a sampling grid at 100 m intervals. If a grid cell contains a landslide point, or if 30% of the grid cell is covered by landslide polygons, that cell is marked as a landslide grid. Then, non-landslide points are randomly selected from areas not marked as landslide grids. In seismic zones where the landslide inventory consists of point data, non-landslide points are generated using the range of point buffers, ultimately balancing the total number of landslide and non-landslide points at a one-to-one ratio. M. A. Nowicki Jessee also utilized this method for global sampling of positive and negative sample points for EQIL (Nowicki et al., 2018). Huang and colleagues concluded that an unequal number of positive and negative sample points affects model performance and adopted a 1:1 ratio for sampling positive and negative sample points (Huang and Zhao, 2018; Tien et al., 2012). Currently, in studies concerning landslide hazard, traditional methods predominantly utilize a sampling ratio of 1:1 for positive and negative samples.
However, some studies have proposed alternative negative sample sampling strategies that achieved results superior to the traditional approach. Shao and colleagues argued that the conventional 1:1 sampling method might exaggerate the proportion of landslide samples in the study area, thereby diminishing model performance. They introduced logistic regression models constructed with different sampling intensities and non-landslide/landslide sampling ratios, applying their method to the Lushan earthquake (Shao et al., 2020). Yang H. et al., (2023) predicted landslide susceptibility using an uncertain positive/negative sample ratio method, while Pourghasemi and colleagues explored three different ratios to identify the most suitable ratio for model training, finding that a 1:2 ratio of positive to negative samples yielded the best results (Pourghasemi et al., 2020). After multiple trials of different ratios of positive to negative samples, Sun and colleagues opted for a 1:5 ratio, randomly selecting negative sample points within the study area (Sun et al., 2023). These studies suggest that the 1:1 sampling strategy might not be the most appropriate choice for selecting negative sample points.
Regarding the scope of negative sample point sampling, traditional methods often lack detailed descriptions. He and others suggested randomly sampling negative sample points within the range provided by the USGS ShakeMap (He et al., 2021). Many references simply state “selection within the study area,” where the study area is usually a range delineated by the authors or the boundaries of a province, city, or county (Wu et al., 2023; Heo et al., 2023; Hu et al., 2021).
In the absence of a clear standard for the range of negative sample point sampling and the ratio of positive to negative sample points, Yang H. et al., (2023) proposed a heterogeneous negative sample sampling strategy, which achieved commendable results in the inversion of the Wenchuan earthquake. It significantly reduced the areas overestimated for EQIL hazard, though this study was not applied to predictions in areas without historical EQIL landslide inventories. In order to fully consider the characteristic differences between the landslide surface in the historical landslide inventory and its surrounding non-landslide surface, we improved the negative sample point sampling strategy of Yang et al., in order to generate more high-quality negative sample points around the landslide surface, and put them into the EQIL hazard prediction in areas without historical earthquake landslide inventory.
3.3.2.1 Creation of negative sample points using the improved heterogeneous sampling strategy
Using ArcGIS, a 2 km*2 km grid (fishnet) is generated for the landslide inventory, retaining grids that contain positive sample points. Within each grid, the landslide area (a), non-landslide area (b), and the number of landslide points (c) are calculated. The number of negative sample points to be sampled in each grid (d) is then calculated using the formula
3.3.2.2 Creation of negative sample points using the traditional strategy
To conduct comparative studies and investigate the impact of lithology and mean annual precipitation on the accuracy of the traditional negative sample point sampling strategy, we also need to create negative sample points generated by the traditional strategy. In the traditional approach, the ratio of positive to negative sample points is set at 1:1. Thus, within the aforementioned grid (fishing net) scope, we generate a number of negative sample points equal to the number of positive sample points. Other than the difference in the number of negative sample points, all other rules remain the same.
3.4 Random forest model
Random Forest is a powerful machine learning model known for its exceptional performance in several areas. First, it excels in handling large datasets. Thanks to the parallel nature of Random Forest, it can efficiently process data containing millions of samples without leading to overfitting. This makes it highly advantageous for applications in big data environments. Secondly, Random Forest boasts remarkable robustness. It tolerates outliers and noisy data well due to its foundation on ensemble learning from multiple decision trees. By aggregating the outcomes of various trees, Random Forest minimizes the impact of individual tree errors on the overall model, thereby enhancing the model’s robustness. Furthermore, Random Forest can effectively assess the importance of features. This capability is incredibly useful as it aids in identifying which features play critical roles in prediction. This contributes to feature selection, simplifying the model and improving its interpretability. Increasingly, studies have demonstrated the efficacy of Random Forest models in landslide susceptibility research.
4 Results
4.1 Results of positive and negative sample point creation
Sample points were created for the historical earthquake events using both the traditional strategy and the improved heterogeneous sampling strategy. The numbers of positive sample points and negative sample points created by the two strategies are presented in Table 2. Figure 3 illustrates the sample point creation results using the 2017 Jiuzhaigou EQIL inventory as an example. Figure 3A shows the landslide polygon inventory, Figure 3B displays the positive sample points, Figure 3C represents the negative sample points generated by the traditional strategy (Strategy 1), and Figure 3D depicts the negative sample points generated by the improved heterogeneous sampling strategy (Strategy 2).
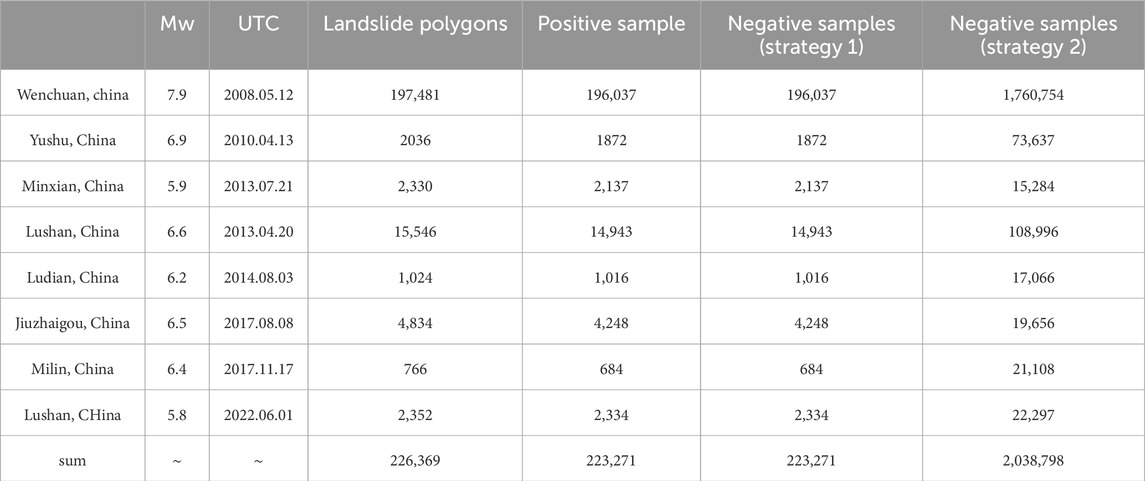
Table 2. Number of landslide inventories, positive samples, and negative samples for eight historical earthquake events.
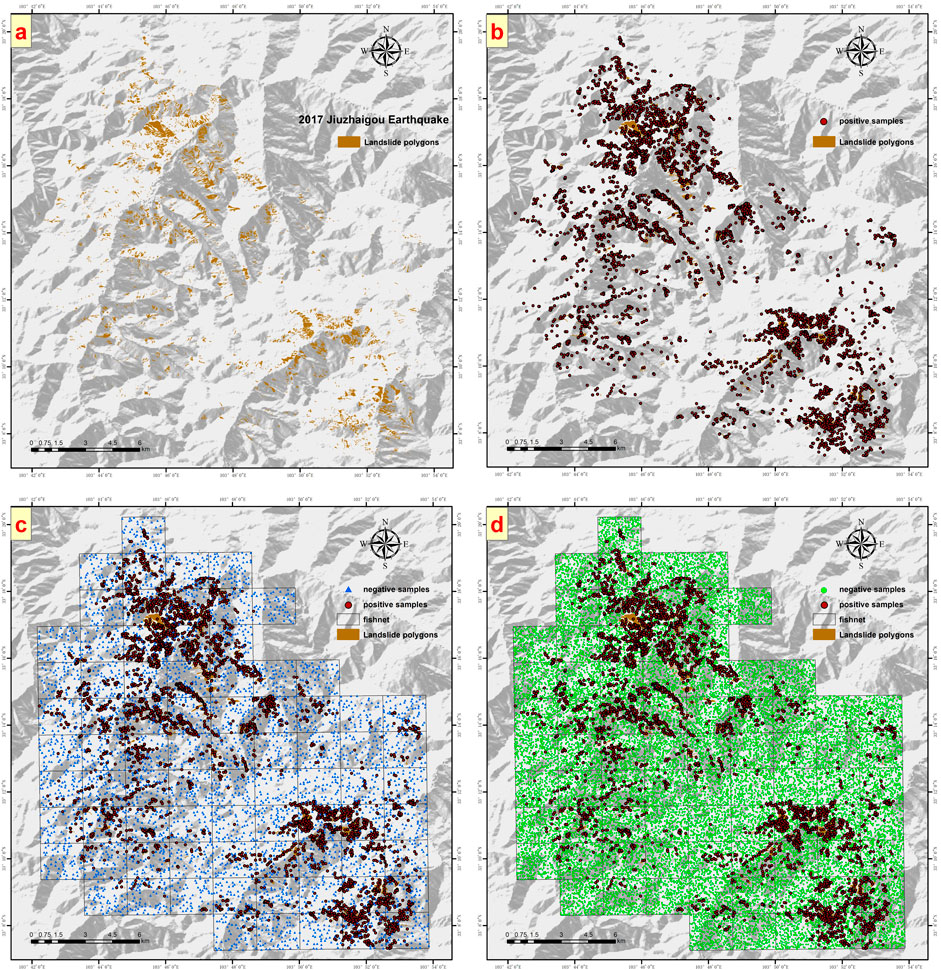
Figure 3. Using the 2017 Jiuzhaigou Earthquake Landslide Inventory as an Example, (A) shows the landslide inventory polygons, (B) displays the created positive sample points, (C) illustrates the negative sample points generated by Strategy 1, and (D) shows the negative sample points generated by Strategy 2.
4.2 EQIL hazard prediction using eight influencing factors under two sampling strategies
This section utilizes two sampling strategies and employs eight influencing factors: “land use,” “slope aspect,” “slope,” “elevation,” “distance to faults,” “distance to rivers,” “NDVI,” and “peak ground acceleration.” These are used for predicting the EQIL hazard in the VII degree area affected by the 2022 Luding earthquake. The accuracy and precision of the prediction results are validated using the interpreted landslide inventory from this earthquake event.
4.2.1 Modeling results of the two sampling strategies
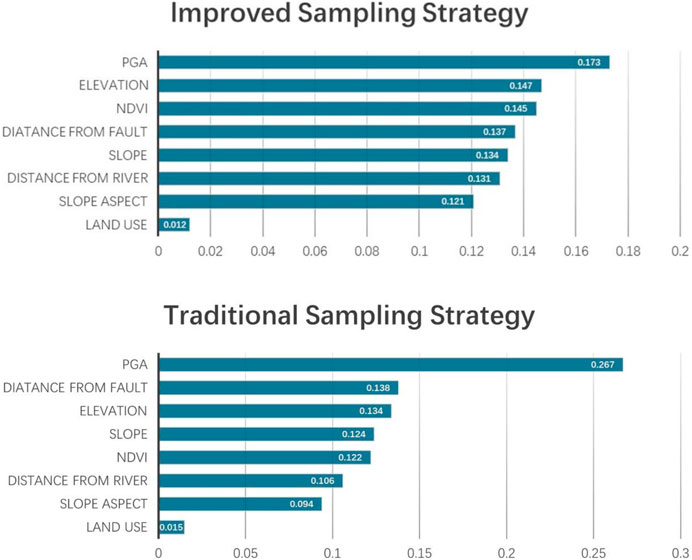
The Random Forest model can directly output the contribution of influencing factors. The contributions of the eight influencing factors under the two sampling strategies are presented in Figure 4.
The EQIL hazard prediction results under the two sampling strategies are shown in Figure 5.
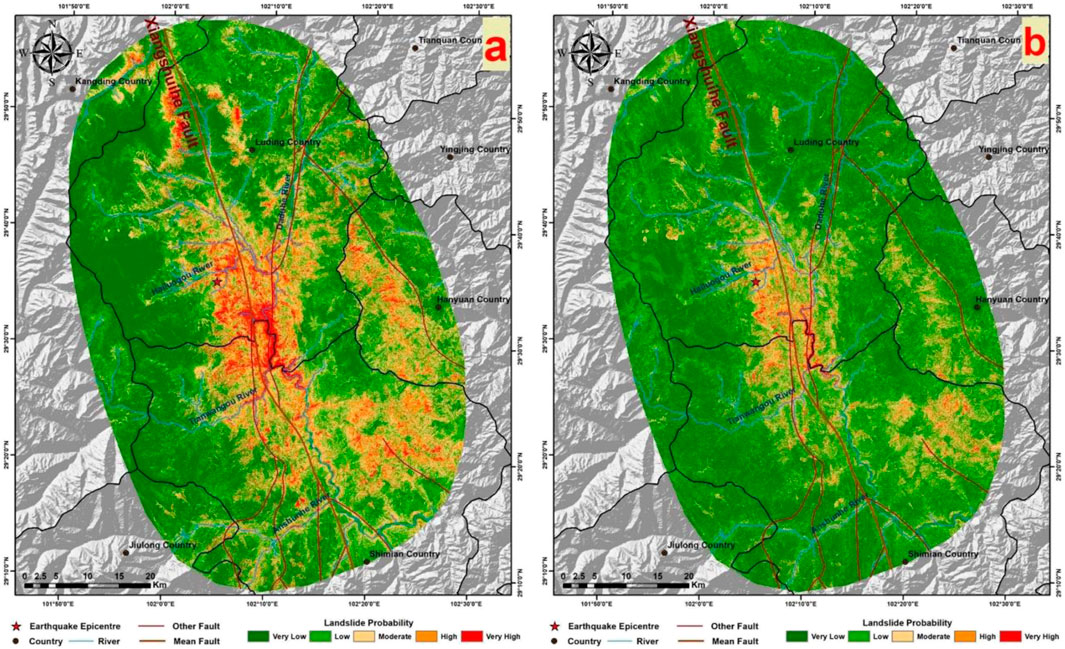
Figure 5. (A) shows the prediction results using the traditional strategy, and (B) displays the prediction results using the improved heterogeneous strategy.
4.2.2 Validation of prediction results
4.2.2.1 ROC curve
The ROC curve and AUC value are utilized to assess the performance of the models. The samples were randomly divided into two subsets, with 70% serving as the training data and the remaining 30% used for validation. The Random Forest models were then applied to their respective validation datasets to estimate the probability of landslides. These predicted probabilities of landslides were compared against their known labels to determine the predictive capability of the models. The Area Under the Curve (AUC) was calculated for this purpose. As shown in Figure 6, both strategies achieved high AUC values. The traditional strategy’s AUC (0.8909) was slightly higher than that of the improved heterogeneous strategy (0.8816), indicating that the models constructed from datasets prepared by both strategies performed well.
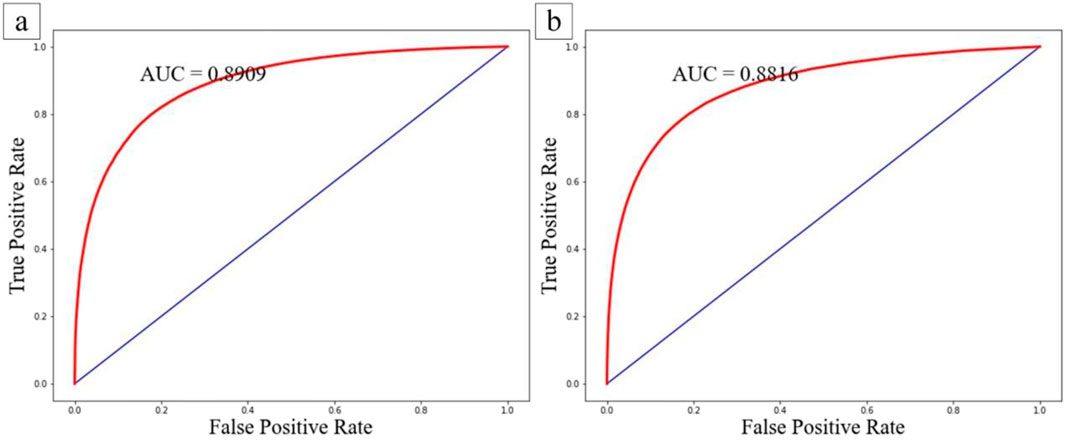
Figure 6. ROC Curves for the Training Sets of the Two Strategies. (A) Shows the ROC curve for the traditional strategy, and (B) displays the ROC curve for the improved heterogeneous sampling strategy.
4.2.2.2 Validation against the interpreted landslide inventory
Earthquake-induced landslides are universally acknowledged as stochastic events (36), making it impossible for EQIL landslide hazard predictions to achieve 100% accuracy. As illustrated in Figure 7, by selecting areas near the epicenter with a dense concentration of landslide inventories for comparison, it is clear that the spatial distribution of medium to high hazard levels in both prediction results closely matches the spatial distribution of the interpreted landslide inventory. The vast majority of landslide areas fall within the regions predicted to have medium or higher hazard levels, demonstrating the reliability of both prediction outcomes.
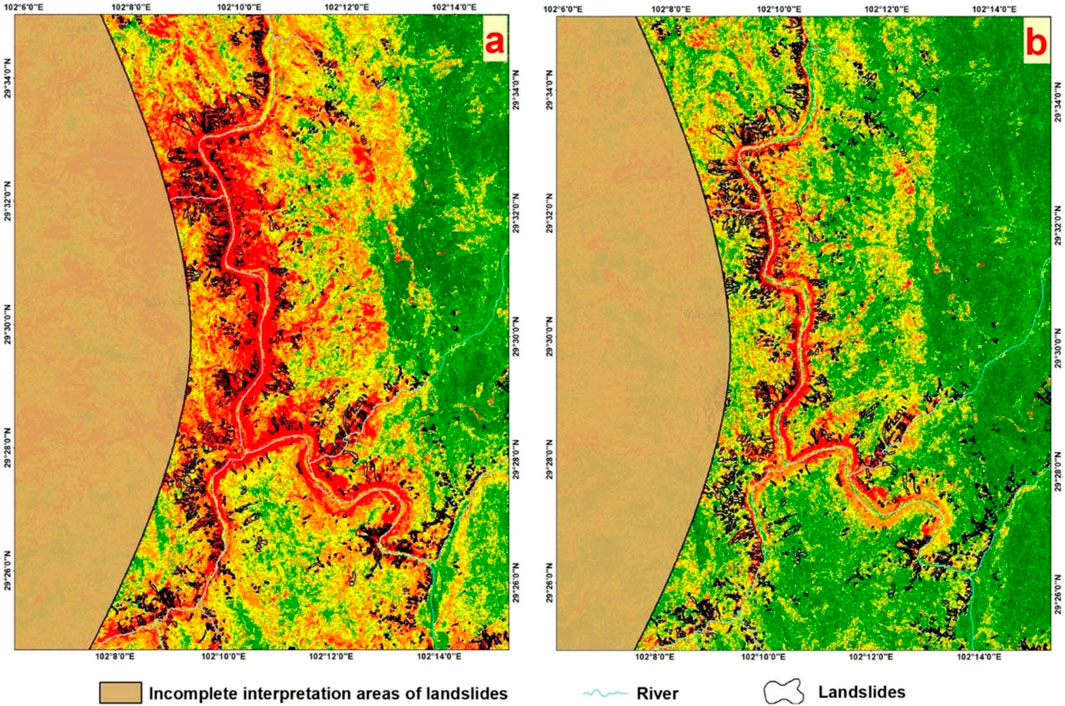
Figure 7. Epicentral Area and Interpreted Landslide Inventory Maps for the Two Prediction Outcomes. (A) Represents the epicentral area using the traditional strategy, and (B) shows the epicentral area with the improved heterogeneous sampling strategy.
We selected six densely landslide-populated areas, each measuring 4 km by 6 km (as shown in Figure 8), for a closer comparison of the two prediction results. This comparison clearly reveals that all landslide areas fall within the predicted regions of medium or higher risk. However, in both sets of results, there are sections within the medium to high hazard areas where no landslides occurred. Therefore, we quantified the number of non-landslide grid cells within the areas classified as medium or higher hazard for each region, with the results presented in Table 3.

Figure 8. Selected six area locations and comparison of results for each area using the two strategies.
It is evident that the improved heterogeneous sampling strategy (Strategy 2) resulted in fewer areas classified as medium or higher hazard on non-landslide surfaces compared to the traditional sampling strategy (Strategy 1). This demonstrates that the actual predictive performance of the improved negative sample point heterogeneous sampling strategy surpasses that of the traditional negative sample point sampling strategy, with a performance improvement of approximately 30% in areas prone to landslides.
4.3 EQIL hazard prediction with the addition of lithology factors
In this section, the set of influencing factors is expanded. Building upon the previously utilized eight influencing factors, lithology factors are added, making a total of nine influencing factors. The lithology layer is categorized into 14 classes based on stratigraphic age. This section explores the EQIL hazard prediction results under the two strategies with the inclusion of lithology factors, comparing the differences with predictions made without using lithology factors.
4.3.1 Prediction results after adding lithology factors using the traditional sampling strategy
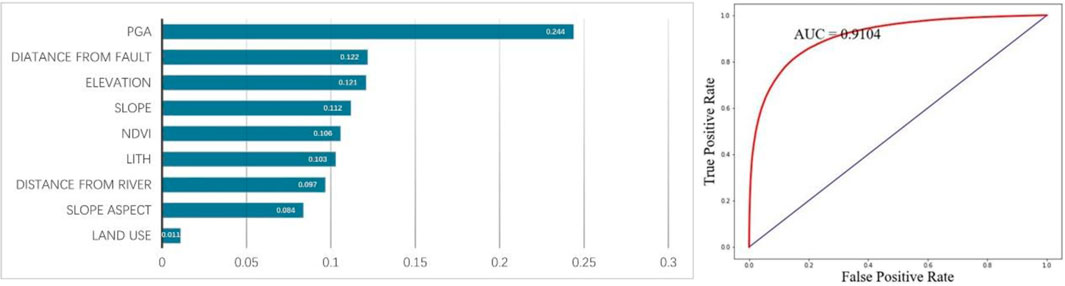
The contributions of the nine influencing factors and the ROC curve of the model are presented in Figure 9. It can be seen from the contribution table that the contribution of lithology factors is about 10%. The trends in contributions from other factors remain essentially consistent with those observed when lithology factors were not included. This indicates that the addition of lithology factors does have a certain impact on the prediction results. The ROC curve reveals that the AUC value of the model constructed with lithology factors is 0.9104, slightly higher than the AUC value of 0.8909 when lithology factors were not used. Based solely on the ROC curve, the modeling results incorporating lithology factors appear superior. However, this conclusion is drawn purely from the model construction perspective and requires further comparative analysis with actual prediction effectiveness.
Figure 10 sequentially presents the results without using lithology factors from earlier sections, the current prediction results, and the lithology factor layer. Overall, a significant segmentation phenomenon in the current prediction results is clearly visible. By comparing with the lithology factor layer, it is observed that the boundaries of the apparent segmented blocks in these results align with the boundaries of different lithology classifications within the lithology layer. This demonstrates that, despite lithology factors contributing only about 10%, they have a significant impact on the actual prediction effectiveness. We selected areas where the differences between the two sets of results are most pronounced, marked with blue boxes. Within these blue-boxed areas, regions classified as “Archaeozoic” exhibit a wide range of relatively higher hazard levels compared to the results without lithology factors. We zoom into these blue-boxed areas for a closer comparison with the landslide inventory from this earthquake to explore whether the addition of these medium to high hazard regions is justified, as shown in Figure 11.
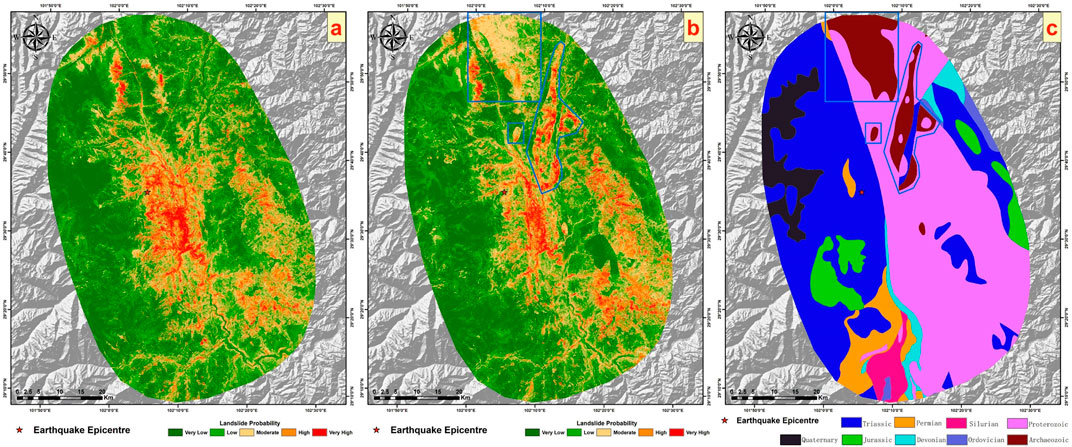
Figure 10. (A) shows the results using the eight factors from earlier sections, (B) displays the current results, and (C) illustrates the lithology factor layer.
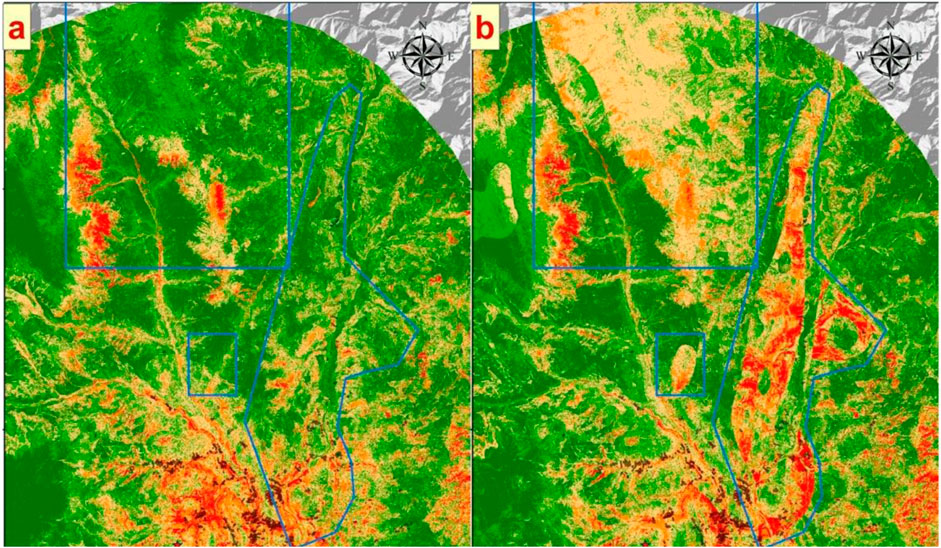
Figure 11. Enlarged comparison of the blue areas in Figure 10. (A) Figure 10A's detail view, and (B) Figure 10B's detail view.
It is evident that in both images, landslide areas are located within regions classified as medium or higher hazard. However, the prediction results utilizing lithology factors contain more mistakenly predicted medium to high hazard areas compared to those without lithology factors. Therefore, we can conclude that under the traditional sampling strategy, employing lithology factors does not enhance the precision of predictions. On the contrary, it affects the original prediction outcomes, resulting in a significant number of incorrectly predicted areas.
4.3.2 EQIL hazard prediction results with the addition of lithology factors under the improved heterogeneous sampling strategy
The contributions of the nine influencing factors and the ROC curve of the model are presented in Figure 12.
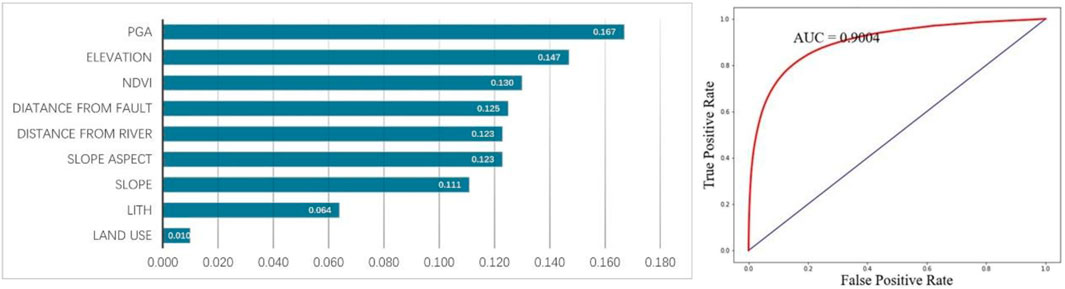
Figure 12. Contributions of various factors and ROC curve with the addition of lithology factors using the improved heterogeneous strategy.
The contribution table shows that under the improved sampling strategy, the contribution of lithology factors is lower than that under the traditional strategy (about 10%), accounting for only about 6%. The ROC curve indicates that incorporating lithology factors under the improved strategy results in a higher AUC value compared to not using them. Similar to the traditional sampling strategy, the inclusion of lithology factors improves the model’s simulation effect. Moving on to an analysis of the actual prediction results, Figure 13 compares the outcomes without using lithology factors under the improved strategy, the current results, and the outcomes with lithology factors under the traditional strategy. Under the improved heterogeneous sampling strategy, the overall prediction results exhibit a more pronounced difference compared to the results obtained without incorporating lithology factors. As previously demonstrated, the improved heterogeneous sampling strategy enhances prediction accuracy, reduces areas of medium to high hazard, and increases the proportion of low hazard areas predicted. Therefore, after adding lithology factors, the segmentation phenomenon becomes more marked compared to using the strategy without lithology factor. Within the blue-boxed areas in Figure 13, regions classified as “Archaeozoic” lithology also show a significant number of areas where the hazard level has been mistakenly overestimated, compared to predictions made without lithology factors.
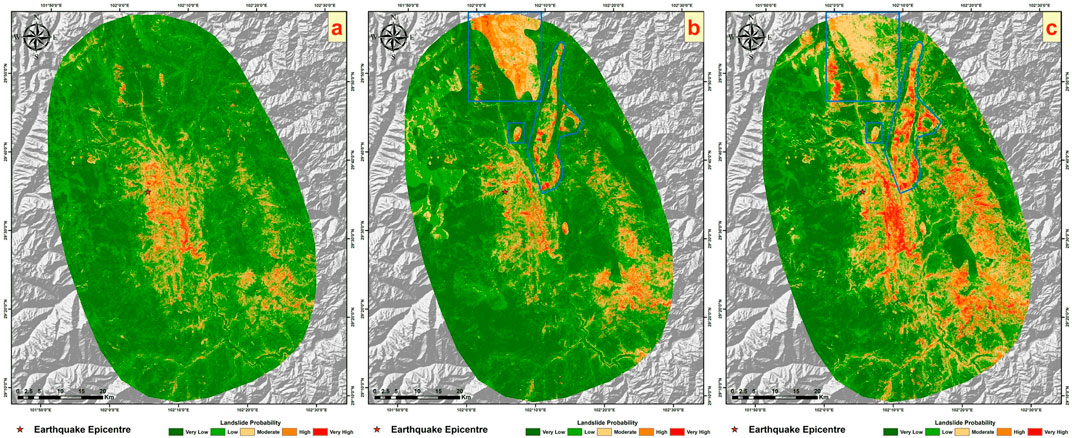
Figure 13. (A) shows the results of the eight factors using the improved heterogeneous strategy from earlier sections, (B) displays the current results, and (C) illustrates the results of adding lithological factors using the traditional strategy from earlier sections.
As the previous article verified, the prediction results without lithology factors under the two sampling strategies are reliable. However, the two sets of results with lithology factors added in this chapter have large errors. The use of lithology factors will lead to excessively high hazard levels in some lithology areas in the study area. From this, we can conclude that lithology has a negative effect on the prediction of EQIL hazard. On the contrary, not using lithology factors will have a better prediction effect.
4.4 EQIL hazard prediction including precipitation factors
Having explored the EQIL hazard prediction with the addition of lithology factors previously, this section investigates the EQIL hazard prediction incorporating precipitation factors. Similarly, the analysis employs the eight influencing factors plus the mean annual precipitation, making a total of nine factors. The hazard predictions are conducted using the two sampling strategies, with a comparative validation to verify the accuracy of the prediction results.
4.4.1 Prediction results after adding precipitation factors using the traditional sampling strategy
The contributions of the nine factors, the ROC curve, and the prediction results are shown in Figure 14, and the prediction results are illustrated in Figure 15.
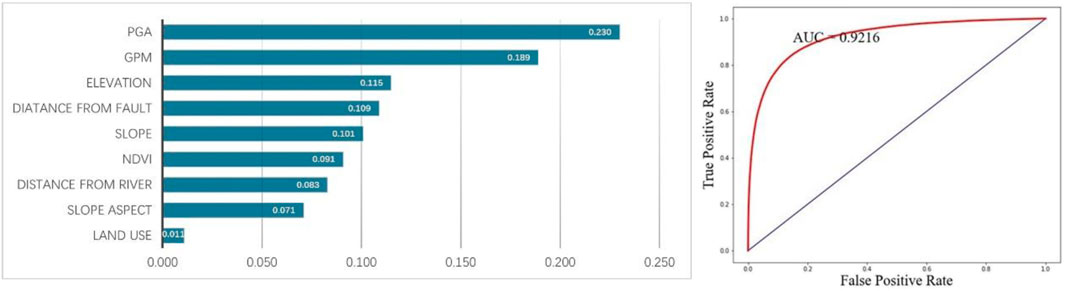
Figure 14. Contributions of various factors and ROC curve with the addition of mean annual precipitation using the traditional strategy.
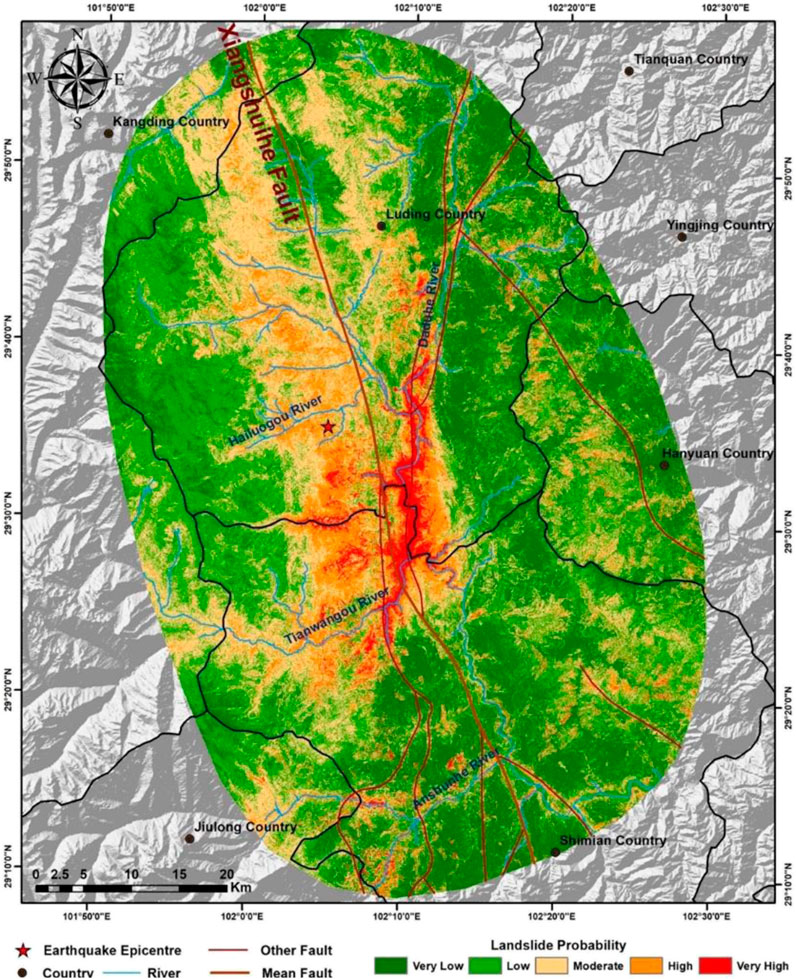
Figure 15. Result map with the addition of mean annual precipitation using the traditional strategy.
From the contribution table, it is noticeable that the contribution of the mean annual precipitation factor is second only to peak ground acceleration, with a contribution significantly higher than other influencing factors, at about 19%. This indicates that the mean annual precipitation factor has a substantial impact on predicting landslide hazard. The ROC curve reveals a higher AUC value (0.9216) after incorporating the mean annual precipitation factor, but the actual prediction performance requires further comparative research. The comparison and validation against the landslide inventory are shown in Figure 16. Sequentially, Figure 16 presents the prediction results using the eight factors under the traditional sampling strategy, the current prediction results, and the mean annual precipitation layer. Given the high contribution of mean annual precipitation, there’s a strong consistency between the prediction effect graph and the distribution trend of mean annual precipitation. Compared to the results without using precipitation factors, the lower part of the map shows lower hazard levels, while the upper part shows higher hazard levels. Considering the landslide inventory for this earthquake event, many landslide areas in the lower part of the current prediction results are underestimated in terms of hazard level, whereas the upper part has many medium to high hazard areas without landslides occurring, leading to severe underestimation and overestimation of hazard levels. Under the traditional sampling strategy, despite the superior AUC value with precipitation factors, the prediction results were poorer, failing to enhance prediction accuracy and resulting in numerous incorrectly predicted areas.
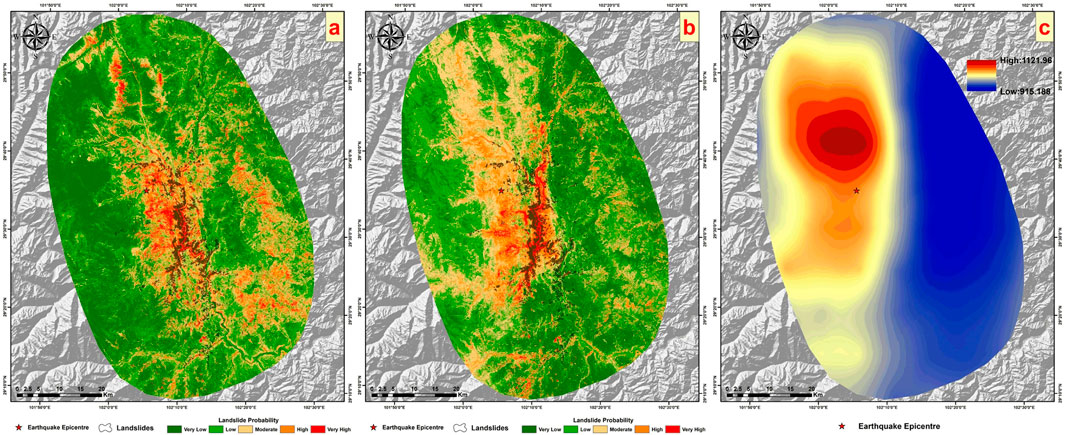
Figure 16. Comparison using the landslide inventory. (A) Shows the results of the eight factors under the traditional strategy from earlier sections, (B) displays the current results, and (C) illustrates the Mean Annual Precipitation layer.
4.4.2 Prediction results after adding precipitation factors under the improved heterogeneous sampling strategy
The contributions of the nine influencing factors and the ROC curve of the model are presented in Figure 17, and the results are illustrated in Figure 18. Under the heterogeneous sampling strategy, the mean annual precipitation contributes more significantly than the peak ground acceleration, approximately 20% compared to about 14% for the latter. This indicates an unrealistic dominant role of mean annual precipitation, given that our study focuses on landslides triggered by earthquakes, where seismic factors (peak ground acceleration) should logically have the highest contribution. Despite a higher AUC value with the inclusion of precipitation factors, the actual outcomes, as shown in Figure 19, present some concerns. Comparing previous results without precipitation factors and the current prediction outcomes, the current results exhibit a more pronounced segmentation phenomenon. In the prediction map, lower hazard levels are assigned to landslide areas in the lower part of the layer, while higher hazard levels are attributed to non-landslide areas in the upper part. This leads to a more distinct regional segmentation than seen with the traditional sampling strategy predictions, aligning closely with the mean annual precipitation layer. It is evident from the map that areas with higher annual precipitation generally have higher EQIL hazard levels, and areas with lower annual precipitation have lower EQIL hazard levels, which is unreasonable.
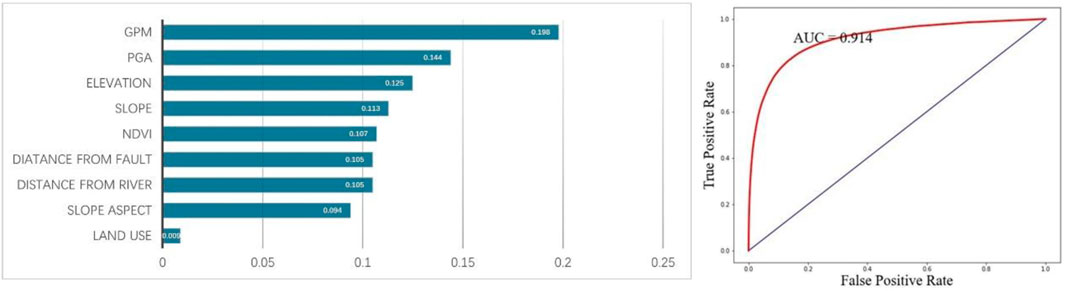
Figure 17. Contributions of various factors and ROC curve with the addition of mean annual precipitation using the improved heterogeneous strategy.
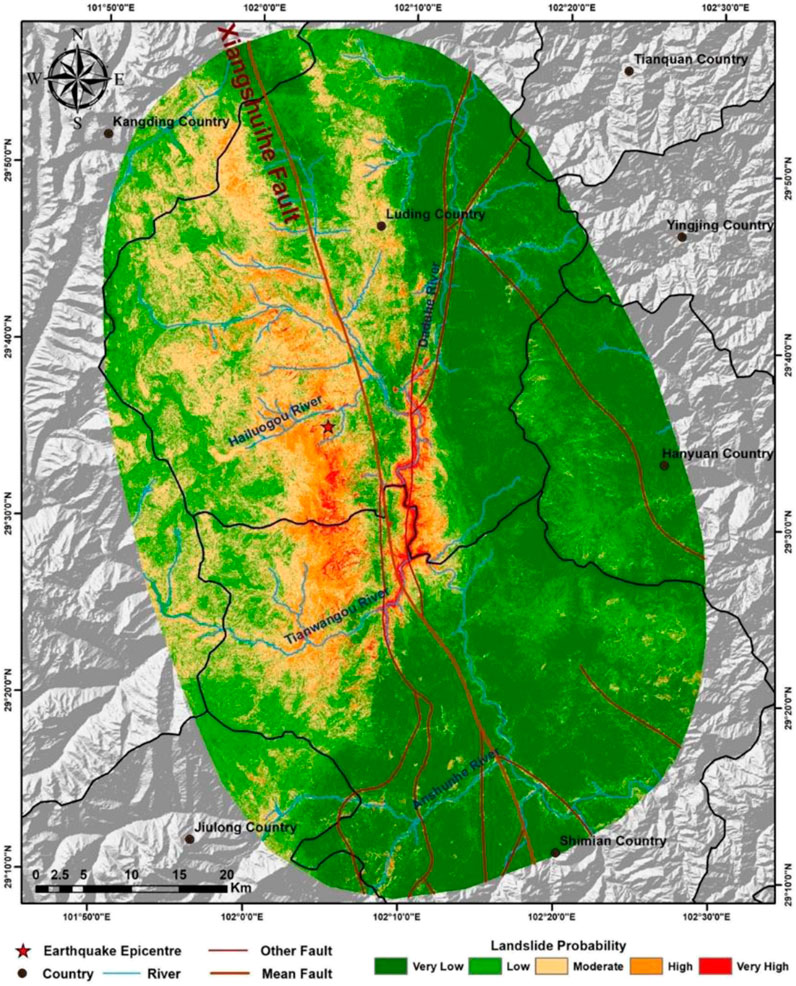
Figure 18. Result map with the addition of mean annual precipitation using the improved heterogeneous strategy.
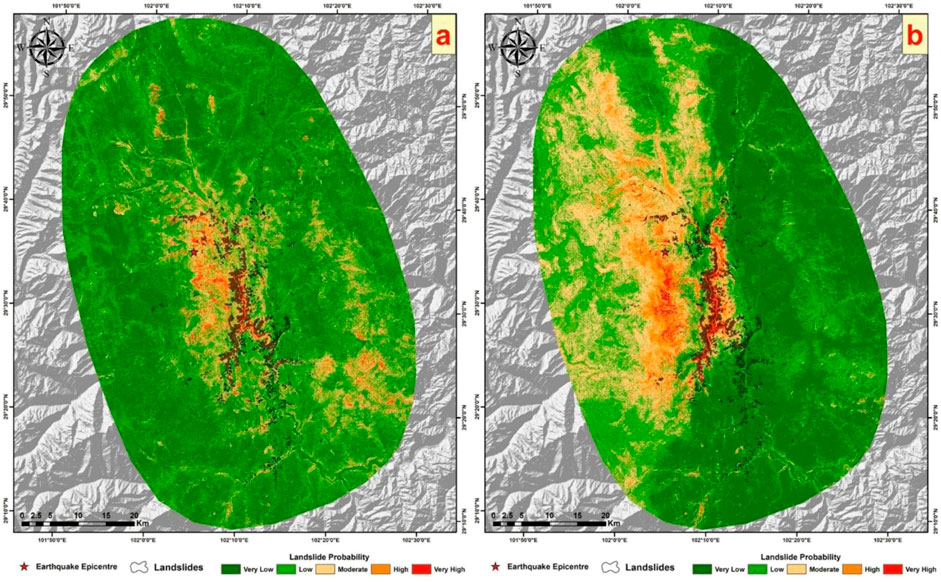
Figure 19. (A) shows the result map using eight factors with the improved heterogeneous strategy from earlier sections, and (B) displays the current result map.
Based on the prediction results using mean annual precipitation factors under both the traditional sampling strategy and the improved heterogeneous sampling strategy, we can conclude that using the annual average precipitation factor will have a significant negative effect on the prediction results, not favorably for enhancing the precision of earthquake-induced landslide hazard predictions.
5 Discussion
In landslide susceptibility mapping, the quality of input data decisively influences the quality of landslide susceptibility assessment (Pradhan, 2013; Pradhan et al., 2014; Kalantar et al., 2018). Hence, the sampling of training sample points and the selection of influencing factors are critical steps that determine the quality of input data. During the process of negative sample sampling, the improved heterogeneous sampling strategy can generate a large number of non-landslide points around landslide areas. There are fewer non-landslide points in densely landslide-affected areas and more in sparsely affected areas. This strategy enables a focused differentiation between the characteristics of historical co-seismic landslide areas and surrounding non-landslide areas. In existing studies, nearly all EQIL hazard maps overestimate the hazard level of the seismic area, especially giving excessively high hazard ratings to the epicentral region (Dreyfus et al., 2013; Allstadt et al., 2018). This study demonstrates that the improved heterogeneous sampling strategy can more accurately predict the spatial location of EQIL occurrences, reducing the overestimated hazard areas around the epicenter. This proves the strategy to be reasonable and advanced, making the investigation into the effectiveness of using lithology and precipitation factors under this strategy and the traditional strategy highly persuasive.
Lithology factors and mean annual precipitation are important influencing factors for the occurrence of EQIL (Duman et al., 2006; Yalcin, 2008; Ercanoglu and Temiz, 2011; Nefeslioglu et al., 2012; Das et al., 2013; Nefeslioglu et al., 2008). However, the results of this study indicate that under both sampling strategies, the use of lithology and mean annual precipitation factors has an adverse impact on EQIL hazard prediction. We believe this is closely related to the model training sample dataset. Initially, the training samples for EQIL hazard prediction following an earthquake event should be created using the historical EQIL inventory from the location of that earthquake. However, in reality, historical landslide inventories from the same location area are scarce. To address this issue, we considered creating a large sample dataset using high-quality landslide inventories from eight historical earthquake events in China, aiming to identify the patterns of EQIL occurrence through machine learning and then apply these insights to EQIL hazard prediction after an earthquake event. These eight historical earthquake landslide inventories are distributed across different regions in Southwest China, where there is a significant variation in lithology and mean annual precipitation across regions. This variation is likely a reason for the poor performance of lithology and mean annual precipitation factors. It is possible that certain lithologies or ranges of annual precipitation have a large number of historical earthquake landslide samples (or non-landslide samples), leading to a higher (or lower) hazard level being predicted for these lithologies or precipitation ranges in the prediction area, thus resulting in poor performance when using lithology and mean annual precipitation factors.
Secondly, the resolution of lithology and mean annual precipitation layers is relatively low, resulting in significant segmentation. The scale of lithology data is 1:2,500,000, which corresponds to a spatial resolution of approximately 660 m. After classifying lithology by geological age, the segmentation phenomenon becomes pronounced. If mispredictions occur, it can easily lead to hazard levels being generally overestimated or underestimated within certain lithology regions. In such cases, the segmentation phenomenon in prediction results is inevitable unless higher precision lithology data are used, a more detailed lithology classification method is applied, or lithology factors are not utilized at all. The resolution of mean annual precipitation is 0.1°, and even after interpolation to a 30 m resolution grid, the variability between different regions remains significant. The impact of layer resolution differences on lithology and mean annual precipitation factors cannot be overlooked.
Furthermore, the two sampling strategies used in this study generate non-landslide sample points in areas near landslide samples, emphasizing the differences in characteristics between landslide and surrounding non-landslide areas, thereby achieving better prediction results. However, this approach also results in a strong clustering of non-landslide sample points, especially with the improved heterogeneous sampling strategy, which produces ten times as many negative sample points as the traditional strategy, leading to even greater clustering. This could explain why, in the experiments described earlier, the use of lithology or precipitation factors led to a more pronounced segmentation phenomenon with the heterogeneous sampling strategy compared to the traditional strategy. Coupled with the regional differences and lower resolution of lithology and mean annual precipitation factors, this might cause negative sample points to cluster around certain lithology types and precipitation ranges, resulting in these areas being assigned lower hazard levels and affecting the accuracy of the prediction results.
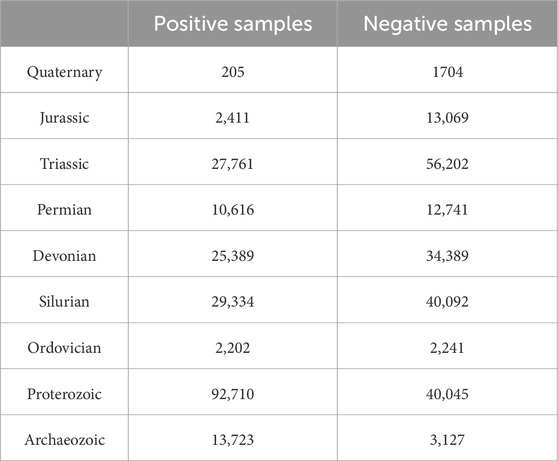
To verify this hypothesis, we analyzed the number of positive and negative sample points located within each lithology classification in the study area under the traditional sampling strategy, as shown in Table 4.
It was observed that the number of landslide sample points in the “Archaeozoic” lithology category is about three times the number of non-landslide sample points. This disproportion could lead to the “Archaeozoic” lithology areas in the study region generally being assigned a higher EQIL hazard level, resulting in erroneous predictions.
Finally, although lithology and precipitation factors are important, why are the results without using these two factors so reliable? We believe that the other influencing factors used may have a certain degree of correlation with these two factors. Topography can influence precipitation distribution patterns through its impact on large-scale weather systems, atmospheric flows, and the microphysics of clouds (Wu et al., 2005; Beniston, 2006; Liu et al., 2024; Yang, D. et al., 2023). Elevation, slope aspect, and slope gradient have been shown to have strong correlations with precipitation (Liu et al., 2018; Zhang et al., 2014). Distance to rivers and proximity to seas also share a strong correlation with precipitation levels (Zheng et al., 2017). The Normalized Difference Vegetation (NDVI) is used to assess the condition of surface vegetation. The relationship between precipitation and NDVI is dynamic, influenced by various factors, including geographical location, season, soil type, and vegetation type. To a certain extent, there is a strong correlation between NDVI and precipitation (Ding et al., 2007; Kawabata et al., 2001). The link between landslides and lithology considers the geological strength index and cohesion of rocks (Gallen et al., 2015). Although rocks from different geological ages can have significant differences in shear strength, but the actual strength of rock is affected by many factors (Gallen et al., 2015; Li et al., 2020; Schmidt and Montgomery, 1995; Hoek and Brown, 1980; Ye et al., 2024). It is difficult to characterize shear strength on global and regional scales (Dreyfus et al., 2013). However, environmental factors are very likely to affect the strength of near-surface rocks (Gallen et al., 2015), and there is a certain correlation between environmental factors and lithology. Factors such as slope aspect, slope gradient, elevation, land use, distance to rivers, and the NDVI all affect environmental conditions to some extent, thereby affecting rock strength. In summary, although lithology and precipitation factors were not directly used, employing other factors may have indirectly considered these two factors as well.
6 Uncertainties and prospects
This study employs traditional and novel negative sample sampling strategies to create sample points from historical earthquake-induced landslides and investigates the impact of lithology factors and mean annual precipitation on the accuracy of earthquake-induced landslide hazard predictions. This is of significant importance for future research on the influencing factors and precision of earthquake-induced landslide hazard predictions. However, there are still some limitations that need to be further improved and explored.
We improved the latest EQIL negative sample point sampling strategy proposed by Yang, H. et al., (2023). However, the 2 km × 2 km grid for negative sample points may not be suitable for all EQIL inventories used in this study. Therefore, in the future, grids of appropriate sizes can be customized for each earthquake event’s landslide inventory, considering factors such as the range of the landslide inventory and the area of landslide polygons. Moreover, the approach is not limited to grids; methods such as buffer zones can also be used to define the sampling range for non-landslide points.
This study found a significant discrepancy between the ROC curves of machine learning methods and the actual prediction outcomes, indicating that ROC curves can be misleading. A higher AUC value does not necessarily equate to better prediction results. Future efforts should focus on evaluating models based on actual outcomes or developing more sophisticated methods to assess model quality.
Lithology and precipitation factors are considered significant influencing factors for EQIL. However, this study found that their impact on the accuracy of actual predictions was poor. Future research should explore how to improve these two factors to make them more effectively applicable to EQIL prediction, such as enhancing the precision of lithology and mean annual precipitation layers or using alternative layers that can represent lithology and precipitation more accurately.
This study utilized sample points created from eight historical EQIL inventories. In the future, more high-quality EQIL lists can be added to improve the sample point data, allowing for the selection of influencing factors that are more suitable for the dataset to construct the model. The broader the coverage of sample points, the wider the prediction range can be, leading to higher prediction accuracy. The more appropriate the influencing factors, the better the prediction outcomes will be.
This study exclusively employed the Random Forest model for modeling and did not engage in a series of studies with other machine learning models. Therefore, the effectiveness of the methodologies and datasets used in this research when applied to other machine learning models remains uncertain.
7 Conclusion
This study exploring the impact of lithology factors, classified by geological age, and mean annual precipitation on the accuracy of earthquake-induced landslide hazard predictions. The use of lithology and mean annual precipitation factors was found to reduce the accuracy of the predictions. Without these two factors, both strategies demonstrated good predictive performance, with the improved heterogeneous sampling strategy showing an approximate 30% improvement in predictive performance in the epicentral region compared to the traditional strategy. In summary, lithology factors classified by geological age and mean annual precipitation factors have a significant negative impact on EQIL hazard predictions. They are not suitable for EQIL hazard prediction. This research holds significant implications for the selection of influencing factors and the precision of future earthquake-induced landslide hazard predictions.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
HW: Data curation, Formal Analysis, Investigation, Methodology, Software, Writing–original draft, Writing–review and editing. WW: Resources, Supervision, Visualization, Writing–review and editing. WY: Supervision, Writing–review and editing. ML: Resources, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project is funded by the National Key R&D Program “Design and Development Technology of Multi-Agency Multi-Hazard Comprehensive Risk Prevention Service Product System” (Project No. 2018YFC1508901).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aditian, A., Kubota, T., and Shinohara, Y. (2018). Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 318, 101–111. doi:10.1016/j.geomorph.2018.06.006
Allstadt, K. E., Jibson, R. W., Thompson, E. M., Massey, C. I., Wald, D. J., Godt, J. W., et al. (2018). Improving near-real-time coseismic landslide models: lessons learned from the 2016 Kaikōura, New Zealand, earthquake. Bull. Seismol. Soc. Am. 108 (3B), 1649–1664. doi:10.1785/0120170297
Beniston, M. (2006). Mountain weather and climate: a general overview and a focus on climatic change in the Alps. Hydrobiologia 562, 3–16. doi:10.1007/s10750-005-1802-0
Blahut, J., Van Westen, C. J., and Sterlacchini, S. (2010). Analysis of landslide inventories for accurate prediction of debris-flow source areas. Geomorphology 119 (1-2), 36–51. doi:10.1016/j.geomorph.2010.02.017
Chen, W., Panahi, M., and Pourghasemi, H. R. (2017). Performance evaluation of GIS-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. Catena 157, 310–324. doi:10.1016/j.catena.2017.05.034
Das, H. O., Sonmez, H., Gokceoglu, C., and Nefeslioglu, H. A. (2013). Influence of seismic acceleration on landslide susceptibility maps: a case study from NE Turkey (the Kelkit Valley). Landslides 10, 433–454. doi:10.1007/s10346-012-0342-8
Ding, M., Zhang, Y., Liu, L., Zhang, W., Wang, Z., and Bai, W. (2007). The relationship between NDVI and precipitation on the Tibetan Plateau. J. Geogr. Sci. 17, 259–268. doi:10.1007/s11442-007-0259-7
Dreyfus, D., Rathje, E. M., and Jibson, R. W. (2013). The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake. Eng. Geol. 163, 41–54. doi:10.1016/j.enggeo.2013.05.015
Duman, T. Y., Can, T., Gokceoglu, C., Nefeslioglu, H. A., and Sonmez, H. (2006). Application of logistic regression for landslide susceptibility zoning of Cekmece Area, Istanbul, Turkey. Environ. Geol. 51, 241–256. doi:10.1007/s00254-006-0322-1
Ercanoglu, M., and Temiz, F. A. (2011). Application of logistic regression and fuzzy operators to landslide susceptibility assessment in Azdavay (Kastamonu, Turkey). Environ. Earth Sci. 64, 949–964. doi:10.1007/s12665-011-0912-4
Fan, X., Yunus, A. P., Scaringi, G., Catani, F., Siva Subramanian, S., Xu, Q., et al. (2021). Rapidly evolving controls of landslides after a strong earthquake and implications for hazard assessments. Geophys. Res. Lett. 48 (1), e2020GL090509. doi:10.1029/2020gl090509
Gallen, S. F., Clark, M. K., and Godt, J. W. (2015). Coseismic landslides reveal near-surface rock strength in a high-relief, tectonically active setting. Geology 43 (1), 11–14. doi:10.1130/g36080.1
Guzzetti, F., Cardinali, M., and Reichenbach, P. (1996). The influence of structural setting and lithology on landslide type and pattern. Environ. and Eng. Geoscience 2 (4), 531–555. doi:10.2113/gseegeosci.ii.4.531
He, Q., Wang, M., and Liu, K. (2021). Rapidly assessing earthquake-induced landslide susceptibility on a global scale using random forest. Geomorphology 391, 107889. doi:10.1016/j.geomorph.2021.107889
Heo, S., Park, S., and Lee, D. K. (2023). Multi-hazard exposure mapping under climate crisis using random forest algorithm for the Kalimantan Islands, Indonesia. Sci. Rep. 13 (1), 13472. doi:10.1038/s41598-023-40106-8
Hoek, E., and Brown, E. T. (1980). Empirical strength criterion for rock masses. J. geotechnical Eng. Div. 106 (9), 1013–1035. doi:10.1061/ajgeb6.0001029
Hong, H., Tsangaratos, P., Ilia, I., Loupasakis, C., and Wang, Y. (2020). Introducing a novel multi-layer perceptron network based on stochastic gradient descent optimized by a meta-heuristic algorithm for landslide susceptibility mapping. Sci. total Environ. 742, 140549. doi:10.1016/j.scitotenv.2020.140549
Hu, K., Zhang, X., You, Y., Hu, X., Liu, W., and Li, Y. (2019). Landslides and dammed lakes triggered by the 2017 Ms6. 9 Milin earthquake in the Tsangpo gorge. Landslides 16, 993–1001. doi:10.1007/s10346-019-01168-w
Hu, X., Mei, H., Zhang, H., Li, Y., and Li, M. (2021). Performance evaluation of ensemble learning techniques for landslide susceptibility mapping at the Jinping county, Southwest China. Nat. Hazards 105, 1663–1689. doi:10.1007/s11069-020-04371-4
Huang, Y., Xie, C., Li, T., Xu, C., He, X., Shao, X., et al. (2023). An open-accessed inventory of landslides triggered by the MS 6.8 Luding earthquake, China on September 5, 2022. Earthq. Res. Adv. 3 (1), 100181. doi:10.1016/j.eqrea.2022.100181
Huang, Y., and Zhao, L. (2018). Review on landslide susceptibility mapping using support vector machines. Catena 165, 520–529. doi:10.1016/j.catena.2018.03.003
Jibson, R. W., Harp, E. L., and Michael, J. A. (2000). A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 58 (3-4), 271–289. doi:10.1016/s0013-7952(00)00039-9
Kalantar, B., Pradhan, B., Naghibi, S. A., Motevalli, A., and Mansor, S. (2018). Assessment of the effects of training data selection on the landslide susceptibility mapping: a comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomatics, Nat. Hazards Risk 9 (1), 49–69. doi:10.1080/19475705.2017.1407368
Kawabata, A., Ichii, K., and Yamaguchi, Y. (2001). Global monitoring of interannual changes in vegetation activities using NDVI and its relationships to temperature and precipitation. Int. J. remote Sens. 22 (7), 1377–1382. doi:10.1080/01431160119381
Khaliq, A. H., Basharat, M., Riaz, M. T., Tayyib Riaz, M., Wani, S., Al-Ansari, N., et al. (2023). Spatiotemporal landslide susceptibility mapping using machine learning models: a case study from district Hattian Bala, NW Himalaya, Pakistan. Ain Shams Eng. J. 14 (3), 101907. doi:10.1016/j.asej.2022.101907
Li, B., Ye, X., Dou, Z., Zhao, Z., Li, Y., and Yang, Q. (2020). Shear strength of rock fractures under dry, surface wet and saturated conditions. Rock Mech. Rock Eng. 53, 2605–2622. doi:10.1007/s00603-020-02061-y
Li, Y., Ming, D., Zhang, L., Niu, Y., and Chen, Y. (2024). Seismic landslide susceptibility assessment using newmark displacement based on a dual-channel convolutional neural network. Remote Sens. 16 (3), 566. doi:10.3390/rs16030566
Liu, W., Zhang, Q., Fu, Z., Chen, X., and Li, H. (2018). Analysis and estimation of geographical and topographic influencing factors for precipitation distribution over complex terrains: a case of the Northeast slope of the Qinghai–Tibet plateau. Atmosphere 9 (9), 349. doi:10.3390/atmos9090349
Liu, Y., Qiu, H., Kamp, U., Wang, N., Wang, J., Huang, C., et al. (2024). Higher temperature sensitivity of retrogressive thaw slump activity in the Arctic compared to the Third Pole. Sci. Total Environ. 914, 170007. doi:10.1016/j.scitotenv.2024.170007
Marano, K. D., Wald, D. J., and Allen, T. I. (2010). Global earthquake casualties due to secondary effects: a quantitative analysis for improving rapid loss analyses. Nat. hazards 52, 319–328. doi:10.1007/s11069-009-9372-5
Nefeslioglu, H. A., Duman, T. Y., and Durmaz, S. (2008). Landslide susceptibility mapping for a part of tectonic kelkit valley (eastern black sea region of Turkey). Geomorphology 94 (3-4), 401–418. doi:10.1016/j.geomorph.2006.10.036
Nefeslioglu, H. A., San, B. T., Gokceoglu, C., and Duman, T. (2012). An assessment on the use of Terra ASTER L3A data in landslide susceptibility mapping. Int. J. Appl. earth observation geoinformation 14 (1), 40–60. doi:10.1016/j.jag.2011.08.005
Nowicki Jessee, M. A., Hamburger, M. W., Allstadt, K., Wald, D. J., Robeson, S. M., Tanyas, H., et al. (2018). A global empirical model for near-real-time assessment of seismically induced landslides. J. Geophys. Res. Earth Surf. 123 (8), 1835–1859. doi:10.1029/2017jf004494
Pham, B. T., Tien Bui, D., Pourghasemi, H. R., Indra, P., and Dholakia, M. B. (2017). Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: a comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 128, 255–273. doi:10.1007/s00704-015-1702-9
Pourghasemi, H. R., Kornejady, A., Kerle, N., and Shabani, F. (2020). Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. Catena 187, 104364. doi:10.1016/j.catena.2019.104364
Pradhan, B. (2013). A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. and Geosciences 51, 350–365. doi:10.1016/j.cageo.2012.08.023
Pradhan, B., Abokharima, M. H., Jebur, M. N., and Tehrany, M. S. (2014). Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS. Nat. hazards 73, 1019–1042. doi:10.1007/s11069-014-1128-1
Pyakurel, A., Kc, D., and Dahal, B. K. (2024). Enhancing co-seismic landslide susceptibility, building exposure, and risk analysis through machine learning. Sci. Rep. 14 (1), 5902. doi:10.1038/s41598-024-54898-w
Qiu, H., Su, L., Tang, B., Yang, D., Ullah, M., Zhu, Y., et al. (2024). The effect of location and geometric properties of landslides caused by rainstorms and earthquakes. Earth Surf. Process. Landforms 49 (7), 2067–2079. doi:10.1002/esp.5816
Raspini, F., Bardi, F., Bianchini, S., Ciampalini, A., Del Ventisette, C., Farina, P., et al. (2017). The contribution of satellite SAR-derived displacement measurements in landslide risk management practices. Nat. hazards 86, 327–351. doi:10.1007/s11069-016-2691-4
Schmidt, K. M., and Montgomery, D. R. (1995). Limits to relief. Science 270 (5236), 617–620. doi:10.1126/science.270.5236.617
Shao, X., Ma, S., Xu, C., and Zhou, Q. (2020). Effects of sampling intensity and non-slide/slide sample ratio on the occurrence probability of coseismic landslides. Geomorphology 363, 107222. doi:10.1016/j.geomorph.2020.107222
Shao, X., and Xu, C. (2022). Earthquake-induced landslides susceptibility assessment: a review of the state-of-the-art. Nat. Hazards Res. 2 (3), 172–182. doi:10.1016/j.nhres.2022.03.002
Shao, X., Xu, C., and Ma, S. (2022). Preliminary analysis of coseismic landslides induced by the 1 June 2022 Ms 6.1 Lushan Earthquake, China. Sustainability 14 (24), 16554. doi:10.3390/su142416554
Sun, D., Gu, Q., Wen, H., Xu, J., Zhang, Y., Shi, S., et al. (2023). Assessment of landslide susceptibility along mountain highways based on different machine learning algorithms and mapping units by hybrid factors screening and sample optimization. Gondwana Res. 123, 89–106. doi:10.1016/j.gr.2022.07.013
Tien Bui, D., Pradhan, B., Lofman, O., and Revhaug, I. (2012). Landslide susceptibility assessment in vietnam using support vector machines, decision tree, and Naive Bayes Models. Math. problems Eng. 2012 (1), 974638. doi:10.1155/2012/974638
Tien Bui, D., Tuan, T. A., Klempe, H., Pradhan, B., and Revhaug, I. (2016). Spatial prediction models for shallow landslide hazards: a comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 13, 361–378. doi:10.1007/s10346-015-0557-6
Van Westen, C. J., Van Asch, T. W. J., and Soeters, R. (2006). Landslide hazard and risk zonation—why is it still so difficult? Bull. Eng. Geol. Environ. 65, 167–184. doi:10.1007/s10064-005-0023-0
Wang, M. J., Li, T. B., Meng, L. B., and Tang, H. (2015). Back analysis of stress field in the intersection region of Y shaped fault, Sichuan. J. Railw. Sci. Eng. 12 (5), 1088–1095. doi:10.19713/j.cnki.43-1423/u.2015.05.016
Wu, G. X., Wang, J., and Liu, X. (2005). Numerical modeling of the influence of Eurasian orography on the atmospheric circulation in different seasons. Acta Meteorol. Sin. 63 (5), 603–612.
Wu, W., Guo, S., and Shao, Z. (2023). Landslide risk evaluation and its causative factors in typical mountain environment of China: a case study of Yunfu City. Ecol. Indic. 154, 110821. doi:10.1016/j.ecolind.2023.110821
Wu, W., Xu, C., Wang, X., Tian, Y., and Deng, F. (2020). Landslides triggered by the 3 August 2014 Ludian (China) M w 6.2 earthquake: an updated inventory and analysis of their spatial distribution. J. Earth Sci. 31, 853–866. doi:10.1007/s12583-020-1297-7
Xu, C., Wang, S. Y., Xu, X. W., Zhang, H., Tian, Y. Y., Ma, S. Y., et al. (2018). A panorama of landslides triggered by the 8 August 2017 Jiuzhaigou, Sichuan M S 7.0 earthquake. Seismol. Geol. 40 (1), 232–260. doi:10.3969/j.issn.0253-4967.2018.01.010
Xu, C., Xu, X., and Shyu, J. B. H. (2015). Database and spatial distribution of landslides triggered by the Lushan, China Mw 6.6 earthquake of 20 April 2013. Geomorphology 248, 77–92. doi:10.1016/j.geomorph.2015.07.002
Xu, C., Xu, X., Shyu, J. B. H., Zheng, W., and Min, W. (2014b). Landslides triggered by the 22 July 2013 Minxian–Zhangxian, China, Mw 5.9 earthquake: inventory compiling and spatial distribution analysis. J. Asian Earth Sci. 92, 125–142. doi:10.1016/j.jseaes.2014.06.014
Xu, C., Xu, X., Yao, X., and Dai, F. (2014a). Three (nearly) complete inventories of landslides triggered by the May 12, 2008 Wenchuan Mw 7.9 earthquake of China and their spatial distribution statistical analysis. Landslides 11, 441–461. doi:10.1007/s10346-013-0404-6
Xu, C., Xu, X., and Yu, G. (2013). Landslides triggered by slipping-fault-generated earthquake on a plateau: an example of the 14 April 2010, Ms 7.1, Yushu, China earthquake. Landslides 10, 421–431. doi:10.1007/s10346-012-0340-x
Yalcin, A. (2008). GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): comparisons of results and confirmations. catena 72 (1), 1–12. doi:10.1016/j.catena.2007.01.003
Yang, C., Liu, L. L., Huang, F., and Wang, X. M. (2023). Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 123, 198–216. doi:10.1016/j.gr.2022.05.012
Yang, D., Qiu, H., Ye, B., Liu, Y., Zhang, J., and Zhu, Y. (2023). Distribution and recurrence of warming-induced retrogressive thaw slumps on the Central Qinghai-Tibet plateau. J. Geophys. Res. Earth Surf. 128 (8), e2022JF007047. doi:10.1029/2022jf007047
Yang, H., Shi, P., Quincey, D., Qi, W., and Yang, W. (2023). A heterogeneous sampling strategy to model earthquake-triggered landslides. Int. J. Disaster Risk Sci. 14 (4), 636–648. doi:10.1007/s13753-023-00489-8
Ye, B., Qiu, H., Tang, B., Liu, Y., Liu, Z., Jiang, X., et al. (2024). Creep deformation monitoring of landslides in a reservoir area. J. Hydrology 632, 130905. doi:10.1016/j.jhydrol.2024.130905
Youssef, A. M., Pourghasemi, H. R., El-Haddad, B. A., and Dhahry, B. K. (2016). Landslide susceptibility maps using different probabilistic and bivariate statistical models and comparison of their performance at Wadi Itwad Basin, Asir Region, Saudi Arabia. Bull. Eng. Geol. Environ. 75, 63–87. doi:10.1007/s10064-015-0734-9
Zhang, K., Pan, S., Cao, L., Wang, Y., Zhao, Y., and Zhang, W. (2014). Spatial distribution and temporal trends in precipitation extremes over the Hengduan Mountains region, China, from 1961 to 2012. Quat. Int. 349, 346–356. doi:10.1016/j.quaint.2014.04.050
Zheng, Y., He, Y., and Chen, X. (2017). Spatiotemporal pattern of precipitation concentration and its possible causes in the Pearl River basin, China. J. Clean. Prod. 161, 1020–1031. doi:10.1016/j.jclepro.2017.06.156
Keywords: earthquake-induced landslide, hazard prediction, lithology, precipitation, luding
Citation: Wang H, Wu W, Yang W and Liu M (2024) Examining the contribution of lithology and precipitation to the performance of earthquake-induced landslide hazard prediction. Front. Earth Sci. 12:1431203. doi: 10.3389/feart.2024.1431203
Received: 11 May 2024; Accepted: 18 September 2024;
Published: 28 October 2024.
Edited by:
Hans-Balder Havenith, University of Liège, BelgiumReviewed by:
Haijun Qiu, Northwest University, ChinaJian Fang, Central China Normal University, China
Yajun Li, Lanzhou University, China
Copyright © 2024 Wang, Wu, Yang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wentao Yang, eWFuZ193ZW50YW9AYmpmdS5lZHUuY24=
†These authors share first authorship
 Hui Wang
Hui Wang Wei Wu2†
Wei Wu2† Wentao Yang
Wentao Yang