Numerical simulations on effects of turbulence on the size spectrum of sinking particles in ocean surface boundary layer

Sinking particles in the ocean play a crucial role in the climate system by transporting materials, such as carbon, deep into the ocean. The amount of this transport is influenced by the net sinking speed of the particles and the amount of material attached to them, both of which are determined by the size spectrum of the particles. The spectrum is shaped by aggregation and disaggregation processes, which are typically most active in the ocean surface boundary layer (OSBL), where intense turbulent flows can enhance both particle collision (aggregation) and particle fragmentation (disaggregation). This study aims to reveal the mechanism by which turbulence transforms the size spectrum through these competing processes and to determine whether turbulence alters the downward material transport from the OSBL. To achieve this, we performed large-eddy simulations to reproduce wind- and wave-induced turbulent flows, employing a Lagrangian particle model to track passive particles in the flow and simulate their aggregation and disaggregation. The model tracked groups of particles rather than individual ones. The results revealed that the shape of the simulated size spectrum was characterized by two length scales, the compensation radius (characterizing the particle floatability) and the Kolmogorov scale, which define the shear range where the turbulent shear shapes the spectrum, the sinking range where the gravitational sinking of particles shapes the spectrum, and the transition range between them. The findings revealed that turbulence tends to increase the terminal velocity and decrease the specific surface area of sinking particles when turbulent aggregation dominates over disaggregation, and vice versa. Although these results may be influenced by uncertain parameterizations (e.g., disaggregation parameterization), the study demonstrates the effectiveness of the numerical approach in investigating the fundamental processes governing particle sinking in turbulent flows.

1 Introduction

Biogenic particles in the ocean, such as phytoplankton, transport and sink with various materials contained in their bodies and/or attached to their body surfaces into the ocean. For example, phytoplankton utilizes the carbon dioxide from the surrounding water in the euphotic zone, and upon dying, transports the carbon deep into the ocean as it sinks. This process, called the biological pump, plays a vital role in the global carbon cycle, contributing to approximately one-fourth of annual anthropogenic carbon emissions from the atmosphere to the deep ocean (Gruber et al., 2019). In addition, these particles transport various metal ions on their surfaces, particularly $\text{Fe}$ ions, which are critical to the carbon cycle as it promotes primary production in high-nutrient, low-chlorophyll (HNLC) regions (Tsuda et al., 2003). Several studies (Lam et al., 2006; Misumi et al., 2021) have suggested that the particulate $\text{Fe}$ from continental shelf regions to HNLC regions can stimulate phytoplankton blooms in the region. High sinking speeds of particles enhance the vertical transport of $\text{Fe}$ near source regions, while diminishing its horizontal transport toward HNLC regions. Thus, particle sinking has some impact on phytoplankton blooming in HNLC regions and should be accurately represented in numerical models in a qualitative manner (e.g., Tagliabue et al., 2023). Therefore, quantifying the material transported by sinking particles is essential for a more precise evaluation of the global carbon cycle.

The characteristics of sinking biogenic particles and their material transport are governed by several biological, chemical, and physical factors. The processes controlling these biological, chemical and physical factors are complicated and are not fully understood. To clarify these complicated processes, this study focuses on the kinematics of particle sinking and investigates the physical processes involved. By assuming that sinking particles are small (i.e., non-inertial) spheres with constant density, their vertical velocity $W$ (upward positive) can be divided into the vertical velocity of the surrounding flow $w$ and the gravitational sinking speed, or terminal velocity, $W_T$ in still water (e.g., Monroy et al., 2017).

$W=w-W_T.$

As $W_T(r)(>0)$ increases with particle radius $r$, the vertical material transport $T$ by sinking particles depends on their size distribution. Based on the size spectrum $n(r)$ (the probability density function of particle numbers per unit water volume as a function of particle radius), $T$ can be expressed as

$T={\int }_0^{\infty }A\left(r\right)W\left(r\right)n\left(r\right)\mathrm{d}r=cw-{\int }_0^{\infty }A\left(r\right)W_T\left(r\right)n\left(r\right)\mathrm{d}r,(1)$

where $A(r)$ denotes the material (e.g., carbon or $\text{Fe}$) contained within or attached to a single particle of radius $r$, and $c=\int An\mathrm{d}r$ represents the concentration of the material. For example, $T$ is the downward flux of the molecule of $\text{Fe}$ attached to the sinking particles [µmol m s⁻¹], if $A$ is the number of $\text{Fe}$ molecules per particle [µmol pcs⁻¹]. If $c$ is known, the first (advection) term can be evaluated independently of the particle size spectrum $n(r)$. However, the second (sinking) term requires knowledge of $W_T(r)$, which complicates its evaluation. Moreover, even if the material concentration $c$ is identical between two water volumes, the vertical transport $T$ may vary depending on the particle size spectrum. Thus, the size spectrum $n(r)$ is a key parameter for material transport (Buesseler et al., 2007).

In general, the size spectrum is often approximated using an exponential function (Sheldon et al., 1972; Kostadinov et al., 2009),

$n\left(r\right)\propto r^{-\zeta }.$

This approximation facilitates analytical investigations into the spectral shape (spectral slope $\zeta$) in a given surrounding environment. However, the actual spectral shapes in the OSBL cannot be represented by a single exponential function: observed size spectra exhibit significant spatial and temporal variability (e.g., Alldredge and Gotschalk, 1988; Jackson et al., 1995; Kostadinov et al., 2009; Cael and White, 2020) owing to the simultaneous occurrence of multiple processes. In particular, flow-induced aggregation and disaggregation processes alter the size spectrum of sinking particles $n(r)$ and influence the vertical transport $T$. More specifically, these processes are most active in the OSBL, where intense flow shear due to turbulence enhances particle collision rates (Saffman and Turner, 1956; Ayala et al., 2008) while also breaks particles into smaller fragments (Dyer, 1989; Takeuchi et al., 2019). Nonetheless, the net effect of these competing processes on material transport remains unclear. To quantitatively estimate the global carbon cycle, understanding flow-induced particulate processes in the OSBL is essential because increased (decreased) downward carbon transport from the OSBL reduces (increases) the ${\text{pCO}}_2$ in this layer, thereby enhancing (reducing) the adsorption of carbon dioxide from the atmosphere.

Numerical simulations are valuable tools for investigating aggregation and disaggregation processes in the OSBL. One such approach uses a spectral model (Gelbard et al., 1980) that numerically solves the Smoluchowski equation, a temporal evolution equation for the size spectrum (Smoluchowski, 1918; Spielman, 1985). Previous studies (Li et al., 2004; Burd and Jackson, 2002) have applied this approach, incorporating disaggregation into the original Smoluchowski equation, and examined variations in spectral shape under realistic conditions. However, this model is essentially zero-dimensional, limiting its ability to capture turbulent-induced variations with homogeneous statistics. To extend the discussion to the actual OSBL, where turbulence statistics vary mostly in the vertical direction, Jackson (1990) and Jouandet et al. (2014) applied a stacked-layer approach, dividing the OSBL into several thin homogeneous layers and applied the spectral model to each layer. Nevertheless, this approach requires turbulence statistics to be defined a priori.

Another approach simulates both the turbulent flows and the Lagrangian motions of sinking particles within the flow. By simulating a sufficiently large number of particles and appropriately modeling particle aggregation and disaggregation processes, the evolution of the size spectrum can be estimated without the need to specify the turbulent statistics beforehand. Recently, this method has been adopted to simulate cloud droplet evolution in the atmosphere: Riechelmann et al. (2012) used the Lagrangian-cloud model (LCM) to trace groups of particles in a Lagrangian framework, where their radii were altered by parameterized aggregation processes. This approach is advantageous because it allows spatial and temporal variability in turbulence to be more accurately considered.

To better quantify the effects of turbulence in the OSBL on vertical material transport, this study numerically simulated the transformation of size spectra for sinking particles in the OSBL. In particular, we employed large-eddy simulations (LES) to compute the flow and adopted an LCM to model particulate processes. We simulated the sinking of particles in wind- or wave-induced turbulent flows in an unstratified turbulent mixing layer above a calm layer, with or without stratification, to investigate the influence of mixing-layer turbulence on the particle size spectrum. The procedures and configurations of these numerical experiments are described in Section 2. The simulation results are presented in Section 3. The effects of the turbulence intensity, initial particle radius, and the vertical structure of the turbulent flow on particle spectrum were investigated, with a specific focus on the shapes of the simulated particle size spectra (Section 3.1) and the amount of material transport (Section 3.2). Finally, concluding remarks and the implications for material transport in the actual OSBL are summarized in Section 4.

2 Methods

We considered a laterally periodic cubic ocean with dimension $L$ in all directions. The model ocean is unstratified everywhere or stratified below the surface unstratified layer in the stratification experiments (described later). The turbulent flows in the model ocean were forced by uniform and steady wind stress (and wave forcing in the wave experiments) at the top surface of the domain. The sinking passive particles released at the top surface were tracked. The numerical methods simulating the turbulent flows (LES) and particle motions (LCM) are described in the following subsections.

2.1 Flow model: LES

This study used the same LES settings as that used in Ushijima and Yoshikawa (2019), except for the wave forcing and boundary/initial conditions described later. The governing equations included the momentum equation, the continuity equation, and the advection-diffusion equation of temperature under incompressible, Boussinesq, and $f$-plane approximations. The seawater density $\rho$ is connected to the water temperature $T$ by the linear equation of state, $\rho ={\rho }_0[1-a(T-T_0)]$, with ${\rho }_0$ (the reference density) = 1,000 kg m⁻³, $a$ (the thermal expansion coefficient of sea water) = 2$\times$10^–4°C ⁻¹, and $T_0$ (the reference sea water temperature) = 20°C.

The Cartesian coordinates $x,y$, and $z$ (or $x_1,x_2$, and $x_3$) are directed eastward, northward, and upward, respectively, with the origin $(x,y,z)=(\mathrm{0,0,0})$ located at the southwest corner on the top surface. The other constants include the gravitational acceleration $g$ (=9.8 m s⁻²) and the Coriolis parameter $f$ (=10^–4 s⁻¹). The eddy diffusivity and the eddy viscosity were parameterized according to Deardorff (1980).

In certain experiments, the vortex force (Craik and Leibovich, 1976) representing the rectified effects of vortex tilting, stretching, and shrinking by surface waves (Fujiwara et al., 2018) was added to the momentum equations to evaluate the effects of turbulence caused by the Langmuir circulations (Langmuir turbulence). The force ${\mathit{F}}_w$ was expressed as

${\left({\mathit{F}}_w\right)}_i=-{ϵ}_{\mathit{ijk}}{\left({\mathit{u}}_{\text{st}}\right)}_j\left({\delta }_{k3}f+{\omega }_k\right),(2)$

where ${\omega }_i=\partial u_j/\partial x_k-\partial u_k/\partial x_j$ denotes the relative vorticity in the $i$ direction, ${\mathit{u}}_{\text{st}}$ denotes the Stokes drift velocity associated with the surface waves, and ${ϵ}_{\mathit{ijk}}$ and ${\delta }_{ij}$ indicate the Levi-Civita epsilon and the Kronecker delta, respectively. Herein, we assumed a monochromatic surface wave and set ${\mathit{u}}_{\text{st}}$ as

${\left({\mathit{u}}_{\text{st}}\right)}_i={\delta }_{i1}\left(\frac{\pi H_w^2{\sigma }_w}{2{\lambda }_w}\right)\exp \left(4\pi z/{\lambda }_w\right),(3)$

where $H_w$, ${\sigma }_w$, and ${\lambda }_w$ denote the wave height, wave angular frequency, and wavelength, respectively. Furthermore, we assumed fully developed windseas in the open ocean and related these wave parameters to the imposed wind, as follows (Pierson and Moskowitz, 1964):

$H_w=0.22\times \frac{U_{10}^2}{g},{\sigma }_w=0.82\times \frac{g}{U_{10}},{\lambda }_w=2\pi \times \frac{g}{{\sigma }_w^2},(4)$

where $U_{10}$ denotes the wind speed at 10 m above the sea surface.

At the top surface of the model domain, we imposed momentum flux and subgrid-scale kinetic energy flux induced by wave breaking through the friction velocity $U_{*}$ of the imposed wind:

${\nu }_E\frac{\partial u}{\partial z}=U_{\ast }^2,$

$2{\nu }_E\frac{\partial e}{\partial z}=m{U}_{\ast }^3,(5)$

where $u$ denotes the velocity component of the flow in the surface wind direction (defined as a positive $x$ direction), $e$ indicates the subgrid-scale kinetic energy, and ${\nu }_E$ is the eddy viscosity. The friction velocity $U_{*}$ was set proportional to $U_{10}$:

$U_{*}=\sqrt{C_{AO}{\rho }_a/{\rho }_0}{U}_{10},$

where ${\rho }_a$ = 1.2 kg m⁻³ represents the air density, and $C_{AO}=1.14\times 10^{-3}$ denotes the drag coefficient at the ocean surface. The coefficient $m$ in Equation 5 was set to 100 (Craig and Banner, 1994). Considering that the wind-driven turbulence can penetrate down to the turbulent Ekman layer depth $\sim U_{\ast }/f$ (Zikanov et al., 2003), we set the domain size $L$ to $1.5U_{*}/f$ resulting in $L$ ranging from 160 to 640 m, depending on $U_{*}$, to minimize distortion effects from the rigid bottom boundary. At the bottom, free-slip and no-normal flow conditions were imposed.

The model domain was segmented equally into $64\times 64\times 64$ grids. Our previous study (Ushijima and Yoshikawa, 2022) verified that this grid resolution is adequate for accurately simulating the turbulent flows in the OSBL. The simulated vertical profiles of the wind-induced flows and turbulence statistics in the present model were overall consistent with those reported by Zikanov et al. (2003) and Yoshikawa (2019), validating the flow simulations at this grid resolution. The governing equations and boundary conditions were approximated using the second-order central difference method with the Arakawa-C grid for spatial discretization and the second-order Runge–Kutta scheme for time integration.

2.2 Particle model: LCM

The LCM, employed as the particle model in this study, was initially developed to investigate microscale cloud physics (Shima et al., 2009; Andrejczuk et al., 2010; Riechelmann et al., 2012; Oh and Noh, 2022) and was recently applied in oceanic contexts (Matsumura and Ohshima, 2015; Noh et al., 2021).

Conventional Lagrange-type particle model tracks the movement of each particle in a three-dimensional flow field while considering characteristics such as particle radius, density, and/or stickiness. Nonetheless, tracking all particles in the OSBL is computationally prohibitive, as a unit volume of water may contain up to $10^{10}$ particles (Kostadinov et al., 2009). To reduce the numerical cost, we used the LCM, which tracks groups of particles (referred to as parcels) and simulates particle interactions, including aggregation and disaggregation processes, between these parcels. A single parcel represents a group of particles with the same characteristics (e.g., radius, density, and stickiness) within a certain volume of water. Motions of the particles within a single parcel are assumed to be represented by two quantities of the parcel: position and velocity. The full set of variables for the $i$-th parcel includes the position ${\mathit{X}}_i$ and velocity ${\mathit{U}}_i$ of the parcel, the number of particles $C_i$ in the parcel, and the radius of particles $r_i$ in the parcel. The first two are three-dimensional vectors, whereas the others are scalar quantities. The number of particles $C_i$ was treated as a non-integer to conserve the total particle volume after the aggregation and disaggregation processes.

Assuming a sphere shape for the particles, the particle radius $r_i$, the particle density ${\rho }_p$, and the particle stickiness $\alpha$ are key parameters. The particle radius affects the aggregation/disaggregation processes (described later), while the particle density ${\rho }_p$ (=1,200 kg m⁻³) and the stickiness $\alpha$ $(=1)$ were set as constants for simplicity. In particular, setting $\alpha =1$ (assuming every colliding particle attaches together) may overestimate the aggregation frequency in the actual OSBL, but it does not qualitatively alter the effects of turbulence on sinking particles. The parcel volume $V_p$, representing the water volume occupied by a single parcel, remains unchanged and is defined by interaction distance $L_p$ (described later).

$V_p\equiv L_p^3.(6)$

Hereinafter, “small/large parcel” refers to parcels containing small-/large-sized particles.

2.2.1 Advection and sinking

Assuming that the particles in the parcels have sufficiently small radii and excess densities, their inertia can be neglected, and their motion can be approximated as a linear combination of advection and sinking (Monroy et al., 2017). This assumption holds for the particles in the current experiments, as their inertial response time ($\simeq 10^{-4}\mathrm{s}$) was much smaller than the smallest value of the simulated turbulence time scale ($>10^{-2}\mathrm{s}$), where the turbulence time scale was estimated as the Kolmogorov time scale $\sqrt{\nu /\epsilon }$ with the kinematic molecular viscosity of water ($\nu =10^{-6}{\mathrm{m}}^2{\mathrm{s}}^{-1}$) and the simulated kinetic energy dissipation rate ($\epsilon <1\times 10^{-4}10^{-6}{\mathrm{m}}^2{\mathrm{s}}^{-3}$ as shown later). Additionally, we assumed that the average advection velocity of the particles (within a single parcel) equals the flow velocity $\mathit{u}$ at the average position of the particles ${\mathit{X}}_i$. Under these assumptions, the parcel velocity can be expressed as

$\frac{\mathrm{d}{\mathit{X}}_i}{\mathrm{d}t}={\mathit{U}}_i=\mathit{u}\left({\mathit{X}}_i\right)-{\left(\mathrm{0,0},W_T\left(r_i\right)\right)}^T,$

where the terminal velocity $W_T(>0)$ is defined as (Haller and Sapsis, 2008)

$\begin{array}{ll}\hfill & W_T=\frac{1}{2}\left(1-\beta \right)g{\tau }_p,\hfill \\ \hfill & \beta \equiv \frac{3{\rho }_0}{2{\rho }_p+{\rho }_0},{\tau }_p\equiv \frac{2r_i^2}{3\beta \nu }.\hfill \end{array}(7)$

In this calculation, the kinematic viscosity of water was set to $\nu$ = 10^–6 m² s⁻¹, resulting in $W_T\ge$4$\times$10^–5 m s⁻¹, as depicted in Figure 1. The flow velocity $\mathit{u}$ at the parcel position ${\mathit{X}}_i$, was determined through linear interpolation of the flow velocities simulated at the LES grid points.

Figure 1

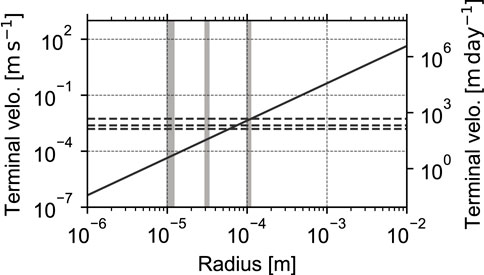
Figure 1. The terminal velocity of the particle used in the current simulations as a function of the particle radius (Equation 7). The gray-shaded areas correspond to the radius ranges of the initial particles in the S, M, and L experiments from left to the right, respectively. Horizontal-dashed lines indicate the root mean square of the vertical velocities of the simulated turbulence calculated over the entire domain in the experiment with $U_{10}=9$ (bottom), 18 (middle), 37 m s⁻¹ (top), respectively.

2.2.2 Aggregation

The aggregation procedure used in this study primarily followed the approach outlined in Riechelmann et al. (2012). In this method, aggregation was represented by changes in parcel characteristics ($C_i$ and $r_i$), caused by the exchange of particulate volume between colliding parcels. When two parcels ($i$-th and $j$-th parcels) are located within the interaction distance $(L_p)$, they aggregate such that the smaller $i$-th parcel loses a certain number of particles and the larger $j$-th parcel receives the volume of these particles. During this aggregation process, the particle radius $r_i$ in the smaller parcel and the particle number $C_j$ in the larger parcel are assumed to remain constant. Instead, the particle number $C_i$ in the smaller parcel decreases, while the particle radius $r_j$ in the larger parcel increases.

$C_i^{\text{new}}=C_i^{\text{old}}-\frac{\mathrm{\Delta }{V}_{ij}}{{\left(r_i^{\text{old}}\right)}^3},$

$r_j^{\text{new}}={\left({\left(r_j^{\text{old}}\right)}^3+\frac{\mathrm{\Delta }{V}_{ij}}{C_j^{\text{old}}}\right)}^{1/3},$

where the superscripts “old/new” represent the states before and after aggregation, respectively, and $\mathrm{\Delta }{V}_{ij}$ denotes the exchanged particulate volume from the $i$-th to the $j$-th parcels. In this procedure, no new parcels were created, and the resulting aggregates were also assumed to be spherical.

The exchanged volume $\mathrm{\Delta }{V}_{ij}$ was determined as follows. In Riechelmann et al. (2012), $\mathrm{\Delta }{V}_{ij}$ was originally evaluated as

$\mathrm{\Delta }{V}_{ij}=\alpha \frac{K\left(r_i^{\text{old}},r_j^{\text{old}}\right)C_i^{\text{old}}{C}_j^{\text{old}}{\left(r_i^{\text{old}}\right)}^3}{V_p}\mathrm{\Delta }t,(8)$

where $\mathrm{\Delta }t$ denotes the time integration interval, $K\left(r_i,r_j\right)$ indicates the coagulation kernel (to be described later), and $V_p$ is the parcel volume (Equation 6).

We found that Equation 8 becomes numerically unstable under conditions of intensive aggregation involving a substantial number of particles. To prevent this instability, we slightly modified the evaluation method. Note that $C_i^{\text{old}}{(r_i^{\text{old}})}^3=V(t)$ denotes the total particle volume in the $i$-th parcel at time $t$ and $\mathrm{d}V/\mathrm{d}t\sim -\mathrm{\Delta }{V}_{ij}/\mathrm{\Delta }t$, allowing Equation 8 to be expressed as follows:

$\frac{\mathrm{d}V}{\mathrm{d}t}=-\frac{1}{V_p}\alpha K\left(r_i^{\text{old}},r_j^{\text{old}}\right)C_j^{\text{old}}V.$

Assuming $\alpha K{C}_j^{\text{old}}/V_p$ remains constant during the time integration from $t=t_0$ to $t=t_0+\mathrm{\Delta }t$, this equation yields the following solution.

$V=V\left(t_0\right)\exp \left[-\alpha \frac{K\left(r_i^{\text{old}},r_j^{\text{old}}\right)C_j^{\text{old}}}{V_p}\left(t-t_0\right)\right].$

Based on this solution, the exchanged volume $\mathrm{\Delta }{V}_{ij}=V(t_0)-V(t_0+\mathrm{\Delta }t)$ can be expressed as

$\mathrm{\Delta }{V}_{ij}=C_i^{\text{old}}{\left(r_i^{\text{old}}\right)}^3\left[1-\exp \left(-\alpha \frac{K\left(r_i^{\text{old}},r_j^{\text{old}}\right)C_j^{\text{old}}}{V_p}\mathrm{\Delta }t\right)\right].(9)$

We used Equation 9 in place of Equation 8, as this finite difference form is numerically more stable. Since the particle number $C_i$ in the parcel never reaches zero due to the definition of the exchanged volume (Equation 9), parcels with $C_i$ below the minimum threshold $(=10.0)$ were removed from the numerical domain.

The coagulation kernel $K(r_i,r_j)$, representing the volume of water occupied by the $i$-th particles (particles in the $i$-th parcel) colliding with the $j$-th particles per unit time, can be considered a linear combination of the Brownian, flow shear, and gravitational kernels (Burd and Jackson, 2009),

$K_{\text{Brown}}\left(r_i,r_j\right)=\frac{2}{3}\frac{kT}{{\rho }_0\nu }\frac{{\left(r_i+r_j\right)}^2}{r_i{r}_j},(10)$

$K_{\text{shear}}\left(r_i,r_j\right)=\frac{4}{3}\gamma {\left(r_i+r_j\right)}^3,(11)$

$K_{\text{grav.}}\left(r_i,r_j\right)=\pi {\left(r_i+r_j\right)}^2\left|W_T\left(r_i\right)-W_T\left(r_j\right)\right|,(12)$

where $r_i,r_j$ represents the radii of the colliding particles, $k$ is the Boltzmann constant, $T$ denotes the absolute temperature, and $\gamma$ symbolizes the mean flow shear, approximated as

$\gamma \approx \frac{\left|\mathit{u}\left({\mathit{X}}_i\right)-\mathit{u}\left({\mathit{X}}_j\right)\right|}{\left|{\mathit{X}}_i-{\mathit{X}}_j\right|},$

where the absolute bracket $|◯|$ denotes the length of the vector, allowing $\gamma$ here to be evaluated as a scalar.

To effectively identify pairs of parcels for aggregation, we followed the approach developed by Matsumura and Ohshima (2015), where two parcels were assumed to aggregate if they were located within the same parcel grid box. Aggregation of more than two parcels is implicitly represented through sequential aggregation between all possible pairs of parcels within a single time step. Herein, we considered a cubic parcel grid box with a dimension of $L_p$.

2.2.3 Disaggregation

The disaggregation process was modeled based on an empirical relationship between the radius of sinking particles and the Kolmogorov scale. Previous studies conducted in a laboratory tank and in the actual OSBL (e.g., Akers et al., 1987; Fugate and Friedrichs, 2003; Braithwaite et al., 2012; Takeuchi et al., 2019) reported that the average or maximum radius of sinking particles is linearly related to the Kolmogorov scale. Accordingly, we assumed that particle would disintegrate into smaller particles if the radius $r_i$ of a particle in the $i$-th parcel at ${\mathit{X}}_i$ exceeded the Kolmogorov scale $\eta$ at ${\mathit{X}}_i$. The disintegrated daughter particles may have various smaller sizes than $\eta$. Among other possible modelings, we chose η as the representative size of daughter particles and set the new radius of the smaller particles to η:

$r_i^{\text{new}}=\eta \left({\mathit{X}}_i\right),(13)$

$C_i^{\text{new}}=C_i^{\text{old}}{\left(\frac{r_i^{\text{old}}}{r_i^{\text{new}}}\right)}^3.(14)$

This modeling assumption might be strong but we believe it is one of reasonable assumptions. Note that Equation 14 represents the conservation of the total volume of particles in a parcel $(4\pi C_i{r}_i^3/3)$. The Kolmogorov scale $\eta$ is defined as

$\eta ={\left(\frac{{\nu }^3}{\epsilon \left({\mathit{X}}_i\right)}\right)}^{1/4},$

where the kinetic energy dissipation rate, $\epsilon$, was calculated in the LES using the subgrid parameterization scheme (Deardorff, 1980). Disaggregation can occur when a large parcel moved into a highly turbulent (small $\eta$) region or when turbulence intensified within a region of large parcels.

2.2.4 Numerical configurations

Parcels were continuously released at the top surface of the model domain with randomly assigned horizontal positions. By controlling the particle number in each released parcel $(C_i)$ within the range of $8\times 10^{11}\text{\hspace{0.17em}–\hspace{0.17em}}5\times 10^{14}$ and the number of released parcels per unit time within the range of $0.2\text{\hspace{0.17em}–\hspace{0.17em}}$0.8 s⁻¹, we maintained constant particle number density in parcels and a constant particle flux at the top surface for all experiments (1$\times$10⁸ m⁻³ and 6$\times$10⁶ m⁻² s⁻¹, respectively). The latter configuration aligns with the constant phytoplankton growth rate in the OSBL. These values were chosen to ensure that the resulting particle number density beneath the surface boundary of the model domain remained close to the actual range, $10^7\text{\hspace{0.17em}–\hspace{0.17em}}10^{10}$ (Kostadinov et al., 2009). Parcels reaching the domain bottom were removed immediately.

The second-order Runge–Kutta scheme was used to integrate the parcel’s motion equation (Equation 10). For numerical convenience, the integration time interval was set to the same value as that of the flow field integration. To ensure the accuracy of particle position calculations, a Courant-Friedrichs-Lewy (CFL) condition was applied: parcels moving distances exceeding half the flow grid spacing over $\mathrm{\Delta }t$ were eliminated from the domain. The number of such parcels was negligible in these experiments. The dimension of the parcel grid box $L_p$ was set to $L/16$ (10–40 m). In some additional tests (not shown), we confirmed that results obtained at twice the resolution $(L/32)$ were almost identical to those of the original resolution $(L/16)$.

2.3 Experimental cases

The first set of experiments was conducted using various paired values of wind speed (U₁₀ = 9, 18, 37 m s⁻¹) and initial particle radius $\left(r_{\text{in}}=10\text{\hspace{0.17em}–\hspace{0.17em}}\mathrm{12,30}\text{\hspace{0.17em}–\hspace{0.17em}}\mathrm{33,100}\text{–}\right.$110 µm), assuming a uniform water density (temperature = 20°C) throughout the model domain. This assumption makes linkage between the particle kinematics in turbulent flow and the shape of the size spectrum clear with minimal physical variables. Hereafter, this set of experiments is referred to as wind experiments, while each initial radius range is referred to as small (10–12 µm), medium (30–33 µm), and large (100–110 µm). The experiments for each initial particle radius were labeled as the S, M, and L experiments, respectively. For instance, the experiment with small particles and a wind speed of 18 m s⁻¹ is referred to as S18 (Table 1). In addition to the wind experiments, two other sets of experiments were conducted to explore additional physical aspects. One aspect concerns the characteristics of the turbulent flow. Wind-induced turbulence is local and decays with depth, whereas wave-induced or convective turbulence is non-local and hence is energetic at greater depths. To quantify this effect, wave experiments were conducted, incorporating wave-related terms (the vortex force) (Equations 2–4) for small and medium particles. These experiments were labeled as “w” (e.g., S18w). The second aspect involves pre-existing stratification, which can result in a shallower mixing layer (ML). A shallow ML reduces the residence time of sinking particles in the turbulent layer where aggregation and disaggregation occur, potentially altering particulate processes. Pre-existing stratification may also change the vertical profiles of turbulent flow, as a transition layer (Johnston and Rudnick, 2009) often formed just below the ML, where shear-driven turbulence is generated due to the large vertical shear of the surrounding flow. To examine this, stratification experiments were conducted with temperature stratification below the ML for small particles. Detailed configurations of the stratification are described in Section 3.1.3. These experiments were labeled as “s” (e.g., S18s). To evaluate the effects of particle disaggregation, all experiments were accompanied by additional runs where the disaggregation process was disabled.

Table 1

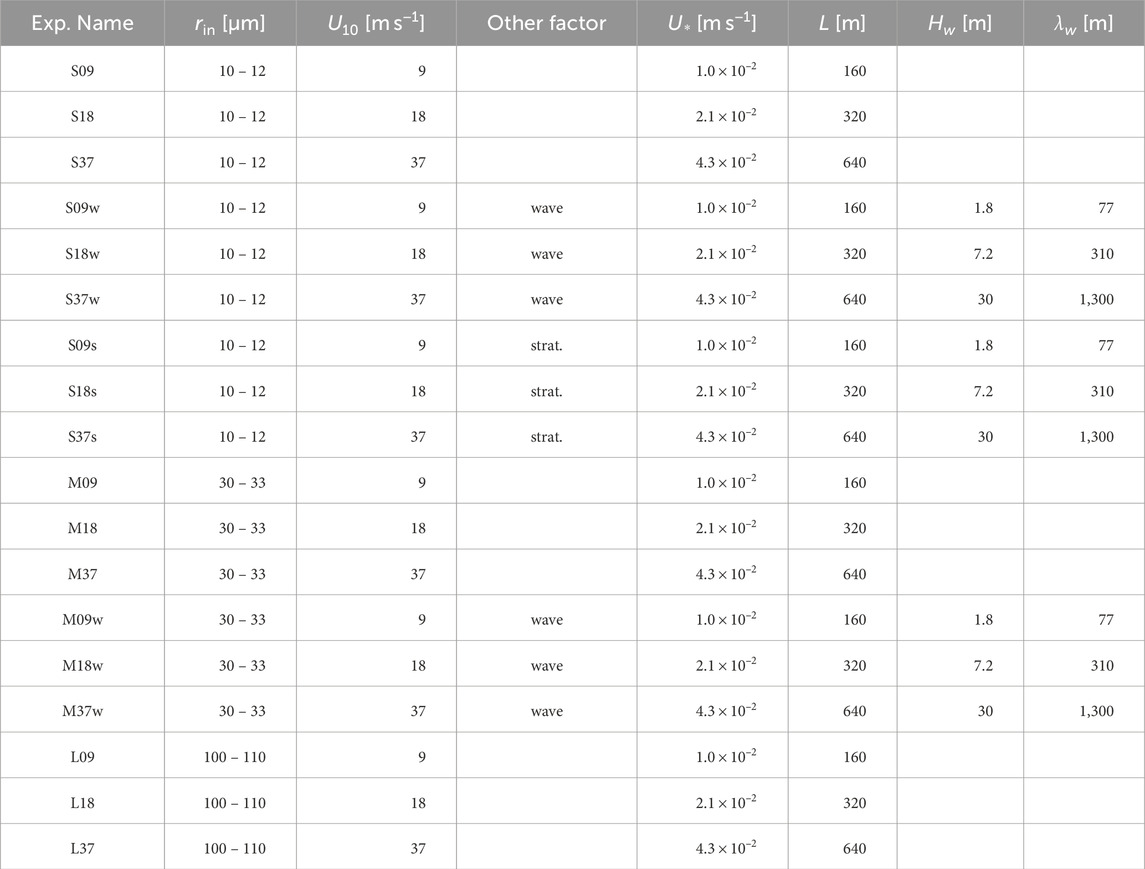
Table 1. Parameters set in experiments. “strat.” is short for “stratification.” Parameters on the right is determined from $U_{10}$.

Initially, the water was at rest and contained no parcel. Water temperature was uniform (20°C) except in the stratification experiments, where the initial temperature profiles are described in Section 3.1.3. To generate turbulence, small random perturbations were introduced into vertical component of the momentum equation. Time integrations were performed over 13 inertial periods $\left(T_f\equiv 2\pi /f\sim \right.$ 0.73  days), during which the simulated turbulence reached statistical equilibrium. At the point when a statistically steady state was reached, we set $t=0$ and initiated the release of the parcels from the top surface of the model domain. The time integration was continued till $t=20T_f$, and all data used in the subsequent analyses were acquired from 15 to $20T_f$, during which statistically steady states were realized in both the parcel (and particle) distributions.

3 Results

3.1 Particulate processes and spectral shapes in turbulent flows

3.1.1 Wind-induced turbulence case

The simulated vertical velocity field of the turbulent flow at $t=20T_f$ in the S09 experiment is presented in Figure 2. As observed, the wind stress imposed on the top surface (z = 0 m) induced three-dimensional turbulence with a vertical velocity of approximately 0.02 m s⁻¹ in magnitude. The horizontally averaged turbulent kinetic energy (TKE) $=\overline{u^{\prime 2}+{\nu }^{\prime 2}+w^{\prime 2}}/2$ was highest near the top surface and decayed almost exponentially with depth (Figure 3). Here, $\overline{◯}$ and ${◯}^{\prime }$ denote horizontal ($x$–$y$) 2D average and the anomaly from the 2D average, respectively. The wind-induced energetic flow formed a turbulent layer beneath the top surface. For the following discussions, we define the mixing-layer depth (MLD) using the TKE profile, where MLD is the depth at which TKE is 5% of the surface value (maximum TKE). This ratio was selected to ensure the defined MLD corresponds with the depth of the buoyancy frequency maximum in the stratification experiments described in Section 3.1.3.

Figure 2

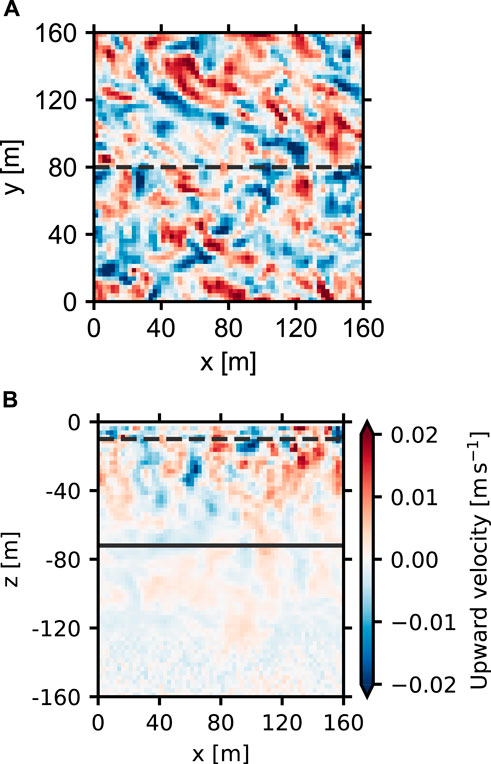
Figure 2. Snapshots of the simulated vertical velocity field of the turbulent flow in the S09 experiment: (A) Horizontal (z = −10 m) and (B) vertical ($y$ = 80 m) sections of the upward velocity $(w)$ at $t=20T_f$. The black-dashed line in the panel A (the panel B) denotes the section location presented in the panel B (the panel A). The black-solid horizontal line in the panel B denotes the MLD in this experiment. This flow field is identical to the flow fields in the M09 and L09 experiments.

Figure 3

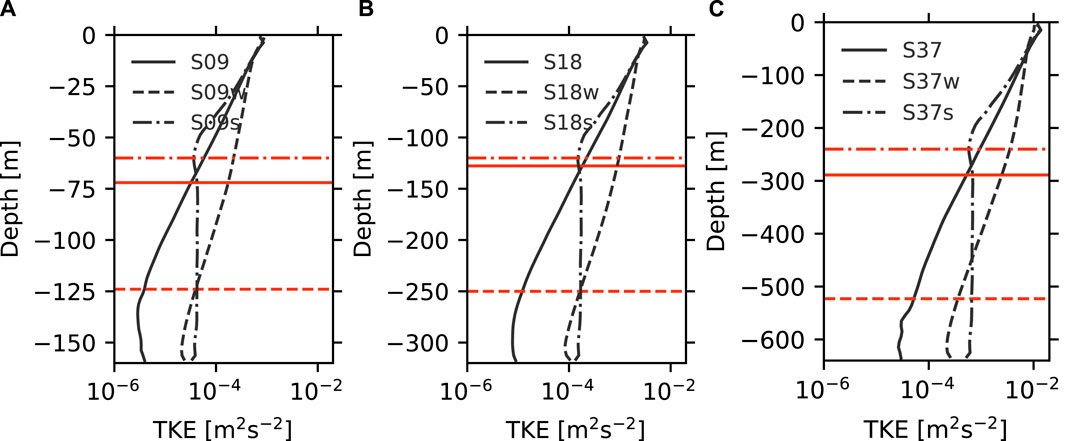
Figure 3. Vertical profiles of horizontally averaged TKE in steady-states in the S experiments (solid), the Sw experiments (dashed), and the Ss experiments (dash dotted) with the wind speeds of (A) 9 m s⁻¹, (B) 18 m s⁻¹, and (C) 37 m s⁻¹. Red horizontal lines denote the MLD in each experiment.

The simulated parcel distribution in the S09 experiment is presented in Figure 4. Upon entering the model domain from the top surface, the small parcels sank under the influence of gravity and were advected by the surrounding turbulence, interacting (aggregating) with each other. In this experiment, the parcels rarely disaggregated. As the depth increased, the radius of the parcels increased, while the number of sinking parcels decreased. The time series of the particle number density (number of particles per unit water volume) and the particle volume density (volume of particles per unit water volume) in this experiment are illustrated in Figure 5. Both densities increased linearly at first due to the continuous input of particles at the top surface but later began to decrease $(t\sim 0.5T_f)$ before reaching a steady state. The reduction in the particle number density was driven by aggregation, whereas the removal of the particles reaching the bottom of the model ocean reduced the volume density. After $t\sim 0.5T_f$, a balance was achieved between parcel release from the top surface, aggregation, and parcel output at the bottom boundary, resulting in statistically steady particle number density and volume densities. Statistically steady states were obtained in all other experiments, although these states were reached later in experiments with higher wind speeds (because of larger model domains) and earlier in those with larger initial particles (because of rapid sinking and faster aggregation, Equations 7, 10–12). For all experiments, we confirmed that the steady states were accomplished within the time range of the subsequent analyses ($t=15$ to $20T_f$).

Figure 4

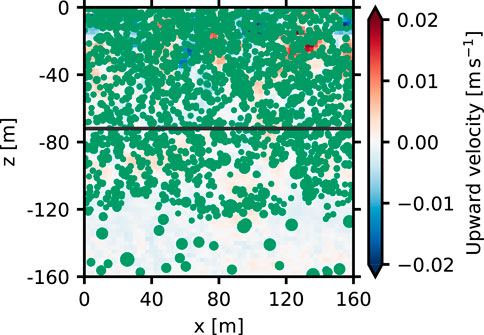
Figure 4. A snapshot of the sinking parcels (green circles) in the S09 experiment. The size of the circle is proportional to the particle radius. Background colors are the same as those in Figure 2B, and the black-solid horizontal line denotes the MLD in this experiment.

Figure 5

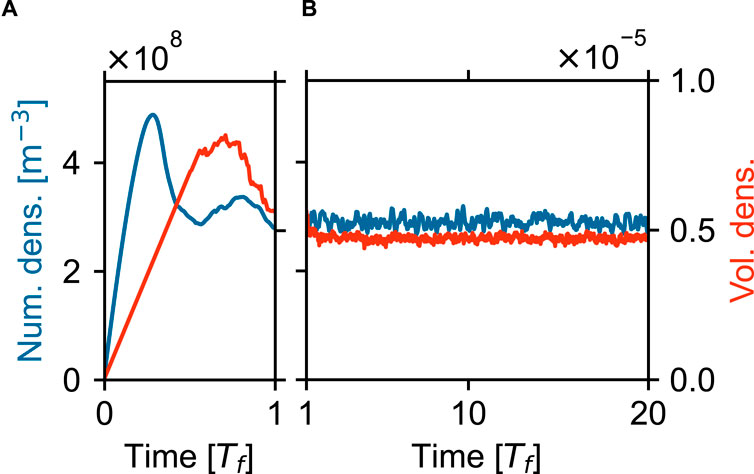
Figure 5. The time series of particle number density (blue line, vertical axis on the left) and particle volume density (red line, vertical axis on the right) in the S09 experiment during (A) $0\text{\hspace{0.17em}–\hspace{0.17em}}1T_f$ and (B) $1\text{\hspace{0.17em}–\hspace{0.17em}}20T_f$.

The steady-state size spectra are illustrated in Figure 6, including the S (Figure 6A) and L (Figure 6B) experiments for $U_{10}=\mathrm{9,18}$ and 37 m s⁻¹. These spectra were obtained from all the particles in the model domain. In all figures illustrating the size spectra, including Figure 6, spectral data are not displayed when the cumulative parcel count in the radial bin over the last $5T_f$ was less than 10, due to the instability of such data. In all experiments, the spectral peak was observed near the smallest radius (i.e., initial radius), and the spectral density decreased as the radius increased. These trends are consistent with the fact that particle number decreases as particle radius increases due to aggregation. Notably, the spectrum was composed of two straight lines connected at a certain radius $(r_c)$, where the spectral slope $(\zeta )$ abruptly transforms from being gentle at $r<r_c$ to steep at $r>r_c$. The physical interpretation of this critical radius will be discussed later in this section. As shown in Figure 6, the slopes at $r>r_c$ were similar throughout all the experiments, but $r_c$ varied with the imposed wind speed. These results demonstrate the influence of turbulence intensity on the spectral shape.

Figure 6

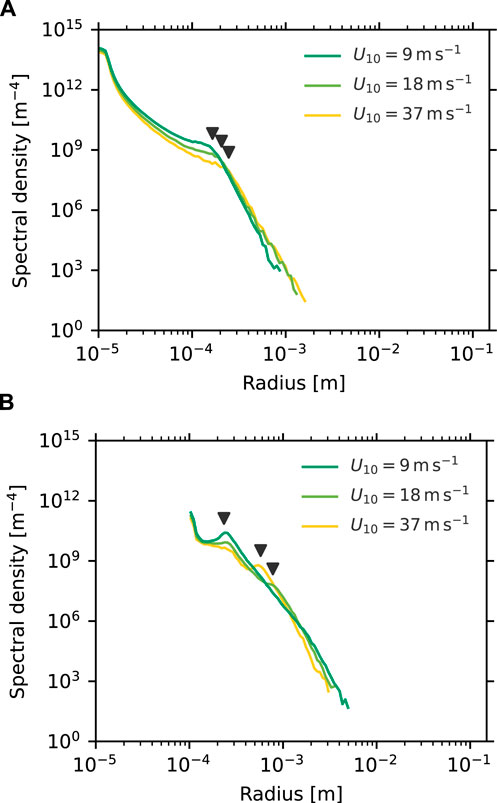
Figure 6. The steady-state size spectra averaged over the whole domains in (A) S and (B) L experiments. Black triangles indicate $r_c$.

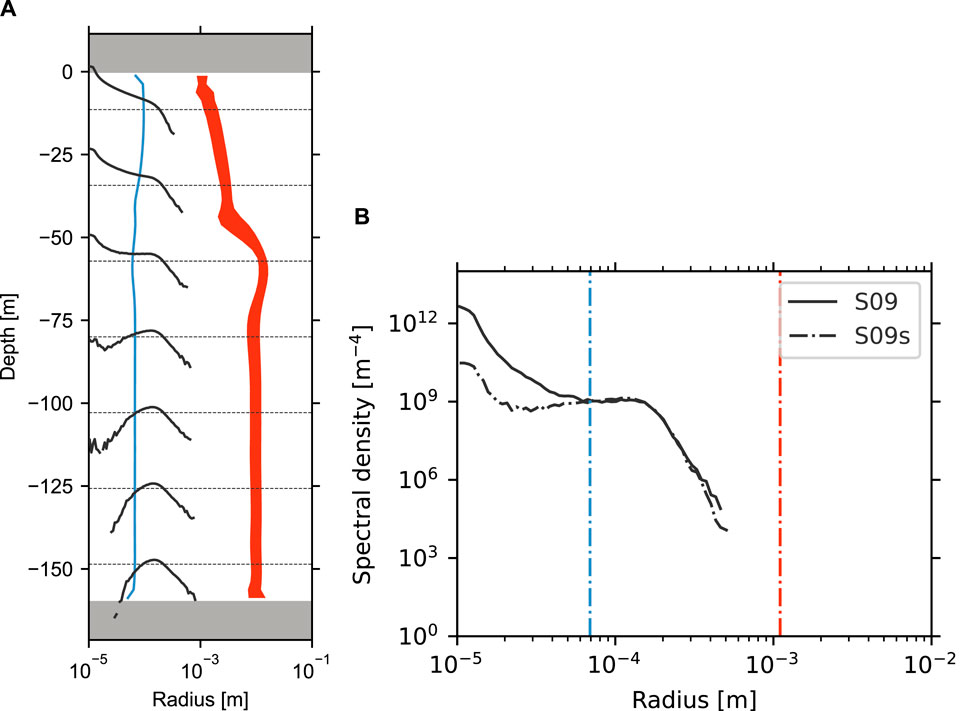
To better understand the variations in spectral shape caused by turbulence, the model domain was divided into seven horizontal layers, and the size spectra in each layer were examined. The spectra from the S09 experiment are presented in Figure 7. The spectral shape in the uppermost layer (Figure 7B) was similar to the one averaged across the entire domain (Figure 6A), but, as shown in Figure 7A, it differed evidently in the deeper layers. At $r<r_c$, the spectra in the deeper layers exhibited a downward convexity. In contrast, at $r>r_c$, the spectral slopes varied less, whereas the spectrum gradually extended to larger radius.

Figure 7

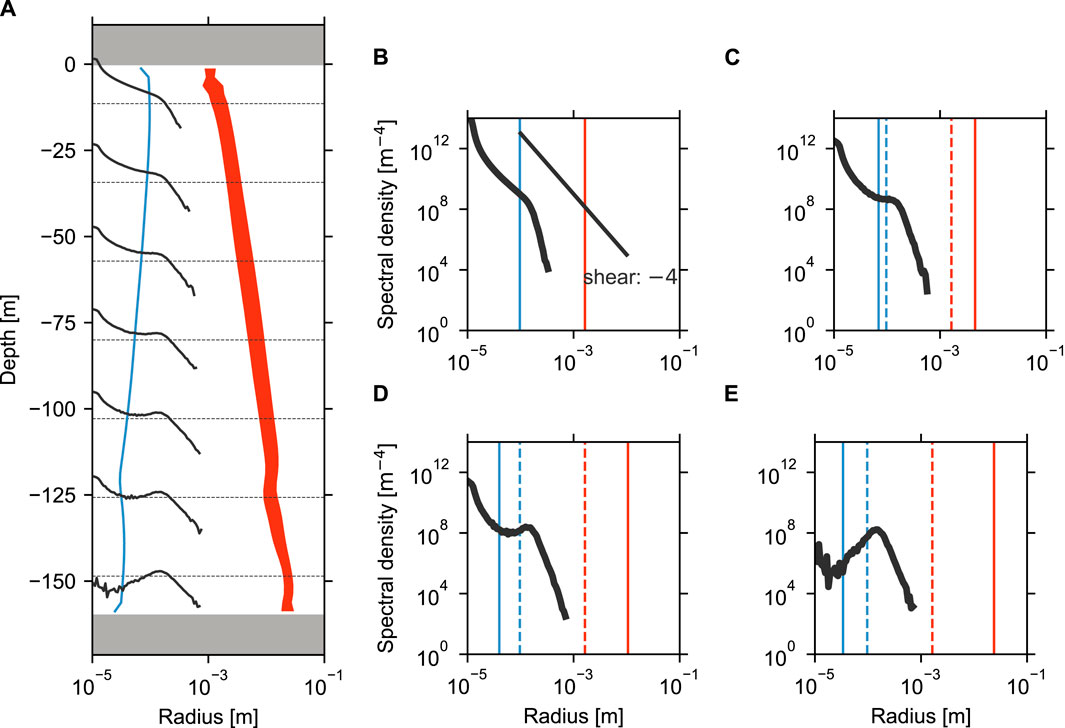
Figure 7. (A) Steady-state size spectra in seven horizontal layers (black lines) and vertical profiles of the compensation radius (blue line) and the Kolmogorov scale (red shading represents the horizontal mean $\pm$ one standard deviation) in the S09 experiment. Each spectrum was evaluated at the depth of the horizontal-dashed line. (B–E) Size spectrum at (B) the top (first), (C) the 3rd,(D) the 5th, and (E) the bottom (7th) layers. Thin black-dashed line represents the spectrum in the experiments without the disaggregation process, but it is almost overlapped by those with disaggregation process in this experiment. Blue-solid (dashed) line denotes the compensation radius at that depth (top), whereas the red-solid (dashed) line represents the Kolmogorov scale at that depth (top). The theoretical slope of the shear aggregation (McCave, 1984) is visualized in panel (B).

To explain these vertical changes in the spectrum and clarify the dominant particulate processes responsible for the variations, we introduced a length scale, $r_w(z)$, defined as

$W_T\left(r_w\left(z\right)\right)=w_{\text{rms}}\left(z\right),$

where $w_{\text{rms}}(z)$ is the root-mean-square of the turbulent vertical velocity (averaged over horizontal directions), while $W_T(r)$ is the terminal velocity of the sinking particle (Equation 7). This scale, referred to as the compensation radius, is related to the relative floatability of a particle in its surrounding flow: particles with radii smaller than $r_w$ are more influenced by advection, while those larger than $r_w$ are more strongly affected by gravitational sinking. The compensation radius at the top surface $r_{w0}$ mostly corresponds to $r_c$, where the spectral slopes abruptly changes in Figure 6.

The compensation radius at each layer is also plotted in Figure 7. The two nearly straight lines forming the spectrum in the shallowest layer intersected around the compensation radius in this layer $(r_{w0})$. Since particles with $r<r_{w0}$ are more influenced by turbulent flow, they grow primarily through aggregation driven by turbulent shear. The spectral slope of $-4$ in this radius range aligns with the theoretical slope for shear aggregation (McCave, 1984), and this range is hereinafter referred to as the “shear range”. Moreover, the spectrum in the range $r>r_{w0}$ is predominantly affected by gravitational aggregation, referred to as the “sinking range”. Notably, the spectral slope in the sinking range was approximately $-10$, which is far steeper than the theoretical value of $-4.5$ derived by McCave (1984). This discrepancy can be explained by the finite thickness of the layer in the current experiments, where sinking particles undergo aggregation over a limited period, unlike the theory assumes an infinitely thick layer with uniformly and steadily coexisting particles.

In the deeper layers, weaker turbulence reduced the compensation radius although the spectral slopes in the shear range $(r<r_w)$ showed little variation (Figure 7A). In comparison, the sinking range expanded in the deeper layers due to the rightward extension of the size spectrum under aggregation, whereas the smaller end and slope of the sinking range remained relatively unchanged. This led to the emergence of a transition range $(r_w<r<r_{w0})$ in the deeper layers. In this radius range, particles were influenced by both flow shear aggregation in the shallower layers and gravitational aggregation in the deeper layers. In the bottom few layers, the spectral density in the shear range gradually decreased because wind-driven turbulence could not effectively transport smaller particles to these depths. This is supported by the fact that the MLD did not reach these depths (Figure 3). As a consequence, the spectral shape in the shear range of the bottom layer is unclear due to the narrow size range and lower particle number density (Figure 7E).

The Kolmogorov scale, another important length scale, is also displayed in Figure 7. This scale is important for particle disaggregation, as particles are assumed to disintegrate at this scale in our model. The Kolmogorov scale was smaller in the shallower layers due to more energetic turbulence in those regions, and it increased monotonically with depth. In the S09 experiment, the smallest Kolmogorov scale was about 1$\times$10^–3 m, which was larger than the largest particle radius in the shallowest layer. In deeper layers, both the Kolmogorov scale and the largest particle radius increased, but the Kolmogorov scale grew faster. Consequently, disaggregation did not occur in the S09 experiment. In particular, no significant differences were observed between the spectra with and without the disaggregation process in the S09 experiment (Figures 7B–E).

The results of the S37 experiment are presented in Figure 8. Although the overall spectral shapes—shear, sinking, transition ranges, and their slopes—were nearly identical to those in the S09 experiment, the stronger turbulence in the S37 experiment, due to higher wind speeds, increased the compensation radius $r_w$ in the shallowest layer, where the shear range transitions into the sinking range. Simultaneously, stronger turbulence diminished the Kolmogorov scale $\eta$ throughout the domain. However, the Kolmogorov scale was comparable to the largest particle radius in the top layer and was larger than the largest particle radius in the deeper layers (Figure 8A). Therefore, disaggregation occurred rarely in the S37 experiment. It is important to note that the Kolmogorov scale, which was defined based on the local TKE dissipation rate $(\epsilon )$, was not horizontally uniform. Therefore, in the top layer, large particles in regions of locally stronger turbulence (with locally smaller Kolmogorov scale) were broken apart. However, the size spectra from experiments with and without disaggregation (bold solid lines and thin dashed lines in Figures 8B–E) were almost identical across all layers. This indicates that disaggregation in the shallow layers had no net effect on the size spectrum in the deeper layers, even in this experiment.

Figure 8

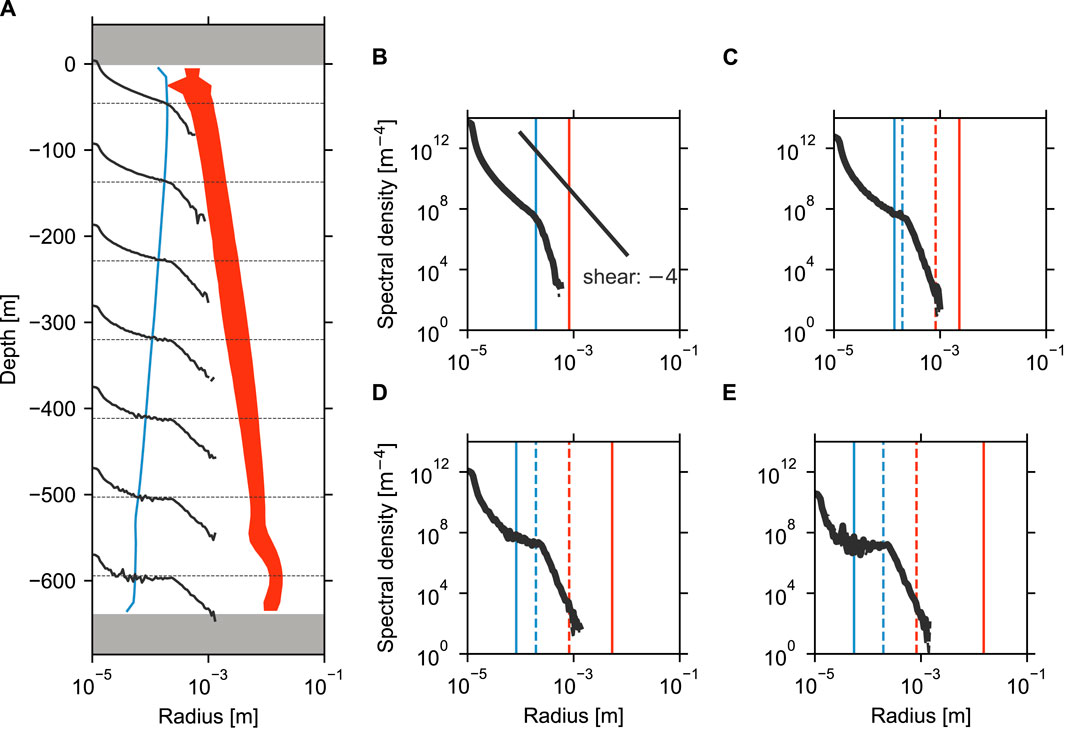
Figure 8. Similar to Figure 7 but for the S37 experiment.

In contrast, the particulate processes and resulting spectral shapes varied significantly in experiments with large initial particles. The spectra from the L37 experiment are visualized in Figure 9. In this experiment, the initial particle radius was close to the compensation radius in the shallowest layer $(r_{w0})$, meaning the size spectrum consisted primarily of the sinking range. Since larger particles grow faster through aggregation (Equations 10–12), the particle radius in the L37 experiment increased to the Kolmogorov scale, and disaggregation occurred in all but the bottommost layers. Disaggregation was most active in the shallowest layer, leading to an upward convexity in the size spectrum around the Kolmogorov scale at the layer $\left({\eta }_0\sim \right.$ 1$\times$10^–3 m), with the rightward segment of the spectrum $(r>{\eta }_0)$ showing a steeper slope than the sinking range. Although the Kolmogorov scale increased faster with depth than the particle radius, the convexity persisted into deeper layers (e.g., Figure 9E). This indicates that disaggregation effects reached greater depths in this experiment. In fact, the spectral shapes differed between the experiments with and without disaggregation; for example, the spectrum with disaggregation was limited to $r<$ 2$\times$10^–3 m, while the spectrum without disaggregation extended to larger radii (Figure 9E). Thus, in this experiment, disaggregation affected the size spectrum across all layers. The spectral distortion caused by disaggregation was not observed in the bottom layer of the L09, M09, and M18 experiments but was evident in the M37, L18, and L37 experiments. Thus, disaggregation is crucial in experiments with larger initial particles and higher wind speeds (i.e., $\ge$ 37 m s⁻¹).

Figure 9

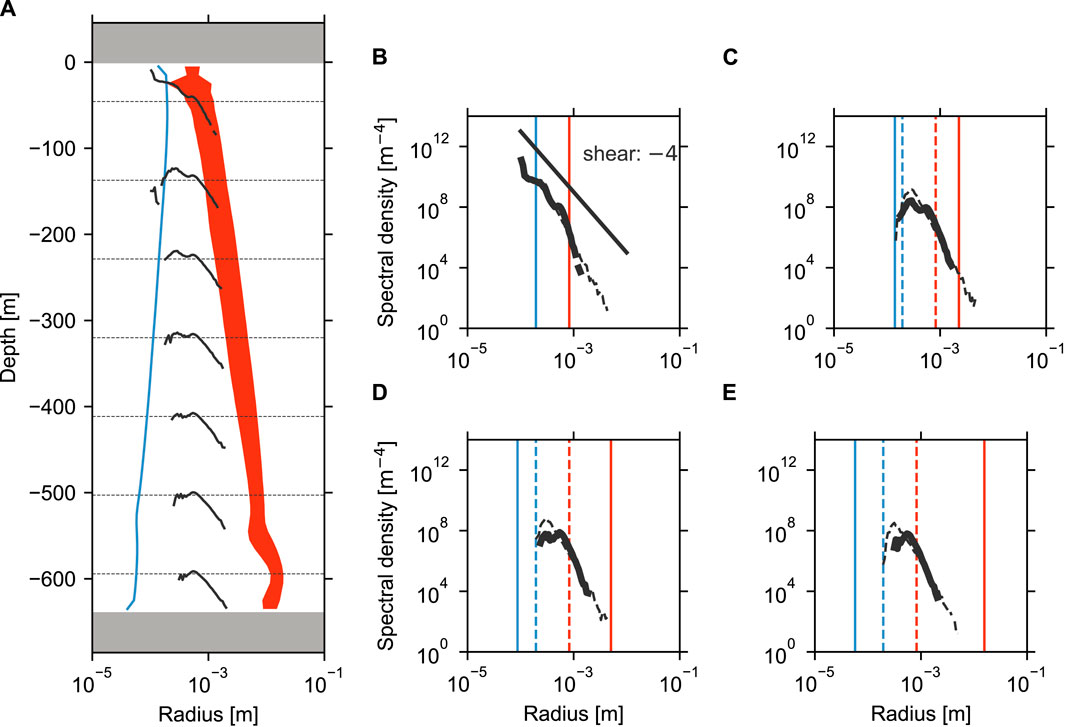
Figure 9. Similar to Figure 7 but for the L37 experiment.

3.1.2 Wave-induced turbulence case

The wind-induced turbulence discussed above is local and decays relatively quickly with depth. In contrast, convective and wave-induced turbulence, such as Langmuir turbulence, is non-local and penetrates to greater depths than wind-induced turbulence. Thus, the Kolmogorov scales associated with these types of turbulence are expected to be smaller in deeper layers and thus more likely to influence the spectral shapes. To examine the effects of such non-local turbulence, this subsection discusses the results of the experiments with wave forces (vortex forcing) that induce turbulence owing to Langmuir circulation—a secondary circulation generated by the interaction between wave- and wind-driven turbulence.

The vertical profiles of horizontally averaged TKE in the wave experiments are shown in Figure 3. As observed, the TKE near the top surface in the wave experiments was almost identical to that in the corresponding wind experiments, but the wave forces in the wave experiments caused the turbulence to penetrate to greater depths. As a consequence, the MLDs in the wave experiments were greater than in the wind experiments.

By normalizing the vertical coordinates by the ML thickness $L_{\text{ML}}$, we can directly compare the particle distributions between the experiments. The size spectrum at the MLD $(z=-L_{\text{ML}})$ in the S09w experiment is illustrated in Figure 10. Similar to the S experiments, the shear, transition, and sinking ranges were observed in the Sw experiments. Notably, the spectral shapes are similar, indicating that the primary effect of the non-local penetrating turbulence is to deepen the ML. However, the spectral density in the shear range is slightly higher in the S09w experiment compared to the S09 experiment. This is because the coherent vortices generated by the Langmuir circulation effectively transported smaller particles to deeper layers, where particle numbers were relatively lower, and thus, aggregation was less active. This affects $W_T$ and, consequently, the downward particulate transport, as described later (Section 3.2).

Figure 10

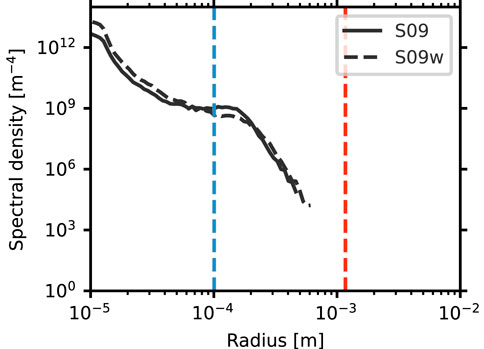
Figure 10. Steady-state size spectra at $z={-L}_{\text{ML}}$ in the S09 experiments (solid) and the S09w experiment (dashed) (These spectra were evaluated in the layer of $0.1L$ thickness centered at $z={-L}_{\text{ML}}$.). The blue (red) vertical line represents the compensation radius (the Kolmogorov scale) at the depth in the S09w experiment.

3.1.3 Effects of pre-existing stratification

The ocean is typically stratified at low- and mid-latitudes beneath the surface ML. Pre-existing stratification makes the MLD shallower compared to that in the unstratified regions. The shorter residence time of sinking particles in the thinner ML may alter the turbulent effects on particulate processes discussed earlier. Stratification also induces the formation of a transition layer beneath the ML, where large vertical shear in the horizontal flow generates shear-driven turbulence (Johnston and Rudnick, 2009). This turbulence at the ML base may further modify the effects of turbulence on particle processes. To explore these effects and the resulting spectral shapes of sinking particles, we conducted additional stratification experiments, where the model ocean was stratified below the ML. The stratification intensity below the ML was set to $N^2=$2.5$\times$10^–5 s⁻¹, corresponding to a water temperature gradient of −1.25$\times$10^–2°C  m⁻¹. The MLD above the stratified layer can be scaled with $U_{*}/\sqrt{Nf}\equiv L_P$ (Pollard et al., 1973). It is important to note that the MLD continues to increase with time, even if the imposed wind stress remains steady. Ushijima and Yoshikawa (2019) showed that the wind-induced MLD reaches approximately $1.8L_P$, $1.9L_P$ and $2.3L_P$ at $1.0T_f$, $1.5T_f$ and $5.0T_f$ after the onset of wind, respectively, and no steady state is achieved. To investigate the particulate processes of sinking particles in statistically steady turbulent flows, we set the initial MLD to $2L_P$ and relaxed the simulated temperature back to the initial temperature with a relaxation time of $T_f/4$.

The vertical profiles of horizontally averaged TKE in the stratification experiments are displayed in Figure 3. Wind forcing at the top surface generated turbulence as intense as the wind experiments, but the pre-existing stratification limited its penetration to greater depths. The MLDs (defined as corresponding to the depths of maximum stratification) in the stratification experiments were shallower than those in the wind experiments. Below this depth, the decaying turbulence appeared more vertically homogeneous compared to the other two groups of experiments. This vertical distribution clearly indicates a two-layer flow field: a top turbulent ML and a subsequent calm layer.

The vertical transformation of the steady-state size spectrum in the S09s experiment is illustrated in Figure 11A. Similar to the S09 experiment (Figure 7A), intense turbulence scattered small particles throughout the ML. The shear, transition, and sinking ranges were also present in the ML (about $>$ −60 m), though the transition range was less apparent because $r_w$ and $\eta$ did not differ significantly in this shallow layer. Shear-driven turbulence near the ML base (z $\sim$ −50 m) slightly reduced the Kolmogorov scale, but this length scale remained much larger than the largest particle size at that depth. Thus, as in the S experiments, disaggregation did not occur in the Ss experiments. In the calm layer below (z $<$ −60 m), spectral densities in the shear range were dramatically reduced due to the lack of downward transport of smaller particles by turbulent flows. As a result, a relatively narrow unimodal spectrum formed in the deeper layers, where particles gradually grew, mainly through gravitational aggregation.

Figure 11

Figure 11. Similar to (A) Figure 7A and (B) Figure 10 but for the S09s experiment.

Figure 11B displays the size spectra at the MLD $(z={-L}_{\text{ML}})$ in the S09 and S09s experiments. The two spectra had similar slopes in the larger radius range (r $>$ 1$\times$10^–4 m); however, the spectral density in the smaller radius range was significantly lower in the S09s experiment compared to the S09 experiment. It is worth noting that the spectra at $z=-0.5L_{\text{ML}}$ in both experiments were nearly identical (not shown). These facts indicate that the number of smaller particles was rapidly decreasing near the MLD, where the vertical turbulent velocity was suppressed by the stratification preventing small particles from being advected to this depth. In contrast, larger particles in the sinking range, having sufficiently high terminal velocities, were hardly affected by the turbulent velocity or the stratification.

3.2 Material transports by particles sinking in turbulent flows

In this subsection, we examined the effects of turbulence on material transport by particles sinking from the surface ML. As shown in Equation 1, the downward flux $T_V$ of materials contained within the sinking particles and the flux $T_S$ of materials attached to the surface of sinking particles can be expressed as follows:

$T_V=A_V{\int }_0^{\infty }{\nu }_p{W}_T{n}_{\text{MLD}}\mathrm{d}r,(15)$

$T_S=A_S{\int }_0^{\infty }{s}_p{W}_T{n}_{\text{MLD}}\mathrm{d}r,(16)$

where $A_V$ and $A_S$ denote the amount of material per unit particle volume and per unit surface area, respectively, while ${\nu }_p(r)$ and $s_p(r)$ indicate the volume and surface area of a particle with radius $r$, respectively. For simplicity, $A_V$ and $A_S$ were assumed to be constants, although they may vary depending on particle types (e.g., phytoplankton species) and the physicochemical environment of the surrounding water in the real ocean. To evaluate the material flux through the bottom of the ML, the size spectrum $n$ was evaluated at the MLD $(z=-L_{\text{ML}})$, and this spectrum is denoted as $n_{\text{MLD}}$. It is important to note that the vertical component of the turbulent flow velocity was assumed to be zero, and flow-related transport was omitted in Equations 15, 16. In our experimental setup, $T_V$ was equal to the particle volume flux at the top surface in the steady state. The volume flux at the top surface was set constant across all experiments and depended only on the initial particle radius (Section 2.2.4). Thus, in the steady state, the value of $T_V$ does not change for experiments with the same initial radius (Figure 12A).

Figure 12

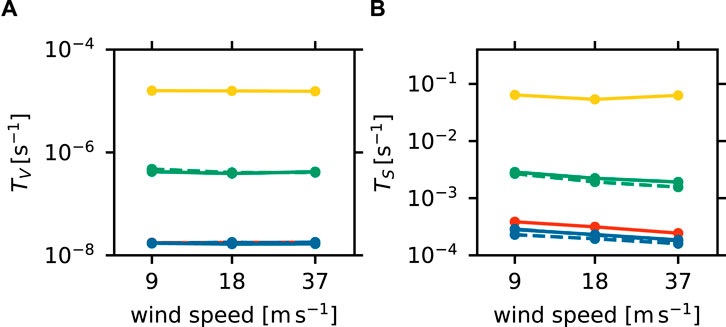
Figure 12. Wind speed dependencies of (A) $T_V$ and (B) $T_S$ in the S (blue solid), Sw (blue dashed), Ss (blue dash dotted), M (green solid), Mw (green dashed), L (yellow), and N (red) experiments.

Here, we investigated the surface flux $T_S$ (Figure 12B), which can be influenced by turbulence. In the S experiments (solid-blue line), $T_S$ decreased with increasing wind speed. To understand this dependency, we analyzed how wind speed altered the spectral shape weighted by surface area and terminal velocity, or the integrand in Equation 16 $(s_p{W}_T{n}_{\text{MLD}})$. Figure 13A reveals two peaks in the weighted spectra of the S experiments. The smaller peak consisted of input particles advected from the top surface, while the larger peak, around the compensation radius (Figures 7E, 8E), shifted rightward and downward (with a decreased peak value) as wind speed increased. This shift corresponds to a decrease in the integral of the weighted spectrum (downward flux $T_S$) with higher wind speeds. This transformation in the weighted spectrum can be attributed to variations in the spectral shape discussed in previous subsections. Wind-induced turbulence in the S experiments promoted aggregation, causing the spectral shape to be largely characterized by the compensation radius. As wind intensity increased, so did the compensation radius, extending the shear region rightward and increasing the size of sinking particles. The shift in the larger peak potentially contributes to an increase in $T_S$ through both $s_p$ and $W_T$, which are increasing functions of $r$. Conversely, the enlarged particle size reduces the particle number (the spectral density of $n_{\text{MLD}}$) and the specific surface area under the constant particles’ volume. Consequently, the peak density decreases as wind intensifies. It is noteworthy that enhanced aggregation with higher wind speeds partially resulted from the longer MLDs ($\propto U_{*}/f$ in the S experiments), allowing for greater aggregation opportunities. To quantify these effects, we performed additional experiments (the N experiments) in which particles sank in still water, without turbulent motion, with their radii increasing only due to Brownian and gravitational aggregation. In these additional experiments, the same model configuration was used as in the corresponding S experiments, except for fluid motion. A similar variation in $T_S$ was observed in the N experiments (red line), but the differences between the S and N experiments indicate that the turbulence in the S experiments reduces $T_S$ by approximately 25%.

Figure 13

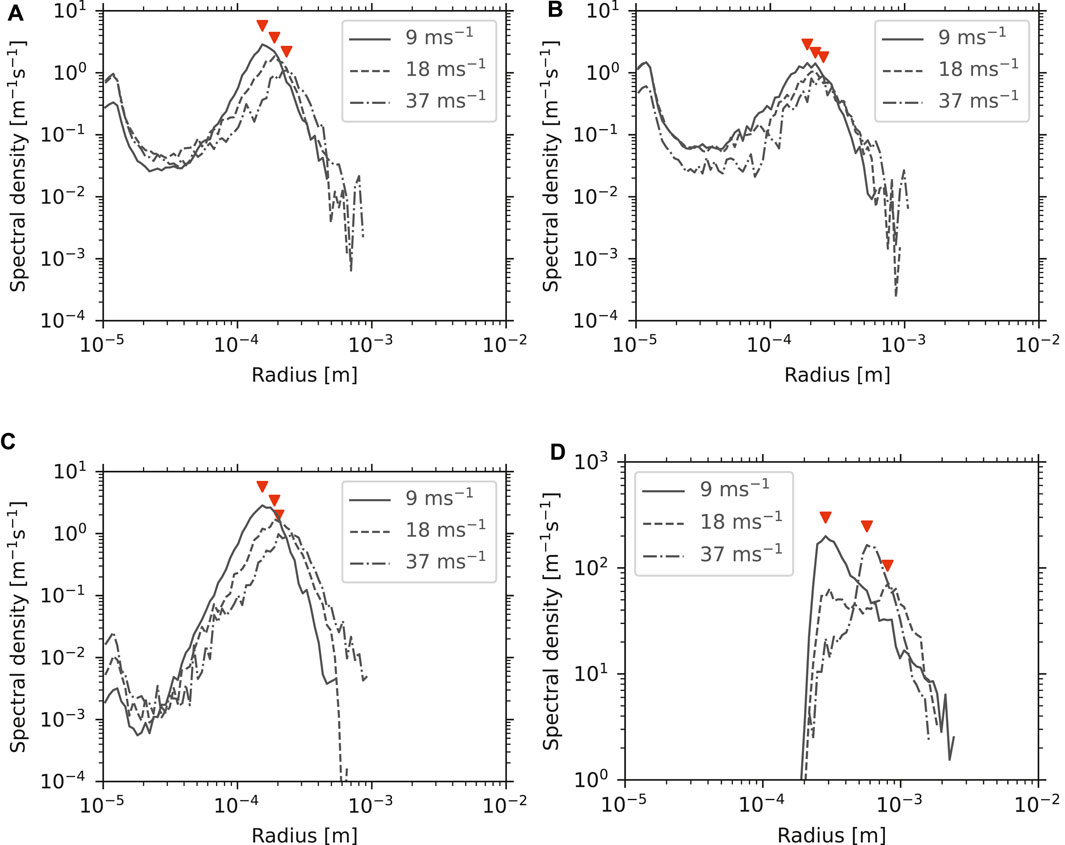
Figure 13. The size spectra weighted by the surface area and the terminal velocity (the integrand of Equation 16) in (A) the S experiments, (B) the Sw experiments, (C) the Ss experiments and (D) the L experiments. Red triangles denote spectral peaks at larger radius than 10^–4 m.

The surface area flux in the Sw experiments (dashed blue line) and Ss experiments (dash-dotted blue line) were approximately the same as in the S experiments. The slight decreases in the Sw experiments were due to larger spectral densities in the shear region (Section 3.1.2). The weighted spectra’s shapes—bimodal and the peak shifts—were also similar to those in the S experiments, except for the more unimodal shapes in the Ss experiments, caused by the suppressed advection of smaller particles from the top boundary due to stratification.

In the L experiments (yellow line), turbulence enhanced aggregation at lower wind speeds but caused disaggregation at higher wind speeds. In the weighted spectra (Figure 13D), the peak radius decreased from 1$\times$10^–3 m to 5$\times$10^–4 m as wind speed increased from 18 m s⁻¹ to 37 m s⁻¹. This led to an increase in peak densities and, ultimately, an increase in $T_S$, due to the opposite mechanism observed in the S experiments. The results of the M experiments were similar to those of the S experiments.

4 Conclusions and discussion

This study examined the transformations of the size spectrum of sinking particles under turbulent flows in the OSBL and investigated their impact on material transport through numerical simulations. Turbulence generated by winds and waves (Langmuir circulations) was simulated through LES, while particle motions and aggregation/disaggregation processes in the temporally and spatially varying turbulent flow fields were modeled with the LCM. Initially developed for atmospheric cloud particles (Riechelmann et al., 2012), the LCM was adapted in this study to simulate oceanic biogenic particles. Aggregation was parameterized with coagulation kernels (Burd and Jackson, 2009), while disaggregation was modeled based on the Kolmogorov scale according to recent observations (e.g., Takeuchi et al., 2019).

The results revealed that the simulated size spectrum in the OSBL was characterized by two key length scales: the compensation radius $(r_w)$ and the Kolmogorov scale $(\eta )$. The compensation radius reflects the floatability of sinking particles in the surrounding turbulence, while the Kolmogorov scale represents the smallest turbulent eddies. Based on these scales, the size spectrum can be divided into three distinct ranges: the shear range $(r<r_w)$, the sinking range ($r_{w0}<r<\eta$, where $r_{w0}$ denotes $r_w$ near the ocean surface), and the transition range between them. In the shear range, the spectral shape is primarily determined by turbulent shear, while in the sinking range, it is influenced by particles sinking due to gravity. Turbulence extends the shear range by increasing the compensation radius, but it limits the maximum particle radius through disaggregation at the Kolmogorov scale. Different turbulence fields result in distinct spectral shapes, but all spectral transformations can be understood in terms of the compensation radius and the Kolmogorov scale.

The influence of turbulence on material transport was assessed through the surface area flux of particles. Turbulence generally caused particles to grow in size and sink more rapidly but reduced the specific surface area when aggregation was more prominent than disaggregation, and vice versa. Overall, when aggregation dominated, turbulence reduced the downward surface area flux of particles.

Key factors shaping the particle size spectrum included the initial radius, the intensity of turbulent flow (i.e., the compensation radius), and the turbulent kinetic energy dissipation rate (i.e., the Kolmogorov scale). The particle number density, which determines the aggregation frequency, was another important factor, although it was not controlled in these experiments. Figure 14 provides an illustration of the parameters in our numerical experiments and the parameters in the actual OSBL in typical open-ocean environments. Phytoplankton sizes in the OSBL range widely with respect to seas and species from pico-phytoplankton ($<$ 2 µm), nano-phytoplankton (2–20 µm) to micro-phytoplankton (20–200 µm) (Sieburth et al., 1978). Diatom, a typical sinking algae, fall into the nano- or micro-phytoplankton categories (Vidussi et al., 2001; Finkel et al., 2010), with OSBL water typically containing approximately $10^5$ – $10^{10}$ nano-phytoplankton or $10^4$ – $10^7$ micro-phytoplankton per unit volume (Kostadinov et al., 2009). Turbulent kinetic energy dissipation rates $\epsilon$ in the OSBL typically range from 10^–9 m² s⁻³ to 10^–5 m² s⁻³, and $\epsilon$ of 10^–5 m² s⁻³ is not rare in the OSBL especially under Langmuir turbulence (Yoshikawa et al., 2018). Although wind speeds in the ocean can exceed 37 m s⁻¹, such high winds are usually brief. Considering a typical wind speed of 9 m s⁻¹, we infer that turbulence in the OSBL accelerated the aggregation of pico- and nano-phytoplankton, while disaggregation is more significant for micro-phytoplankton under strong turbulent conditions. Although stratification below the ML affects the size spectrum and downward transport of sinking particles, it does not significantly alter the tendency to aggregate/disaggregate within the parameter range investigated in this study.

Figure 14

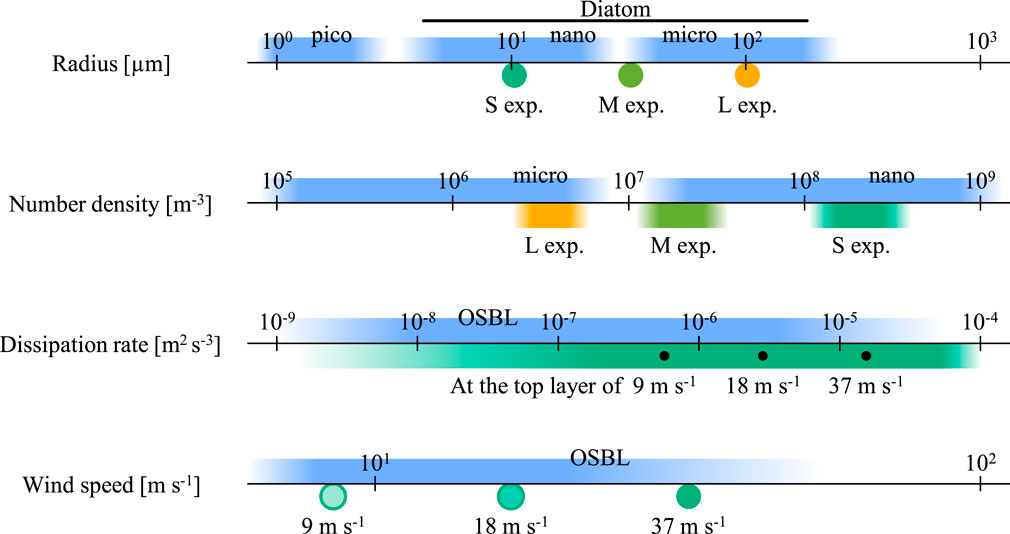
Figure 14. Parameters affecting particle sinking in current numerical simulations and in the actual OSBL.

Nonetheless, the current model stands on several assumptions, simplifications, and parameterizations that may limit its ability to quantitatively compare its results with those observed in the real ocean. For example, the fractal dimension (related to the structure or porosity of particle aggregates) and the particle density influence sinking behavior, particularly the sinking speed. A more realistic (smaller) stickiness would likely result in a slower particle growth rate, leading to a higher concentration of smaller particles in and below the ML. This would likely decrease the average radius of sinking particles exiting the ML, but the presence of numerous smaller particles could ultimately produce larger particles by extending their residence time in the ML. Therefore, the net effect of these physical parameters remains uncertain, and future studies will need to compare results from various perspectives to fully understand these dynamics. Moreover, phytoplankton in the real ocean have ability to move actively by changing their buoyancy (Qiu et al., 2022; Mashayekhpour et al., 2019; Marchioli et al., 2019). This factor might cause the spatial distribution of sinking phytoplankton in the real ocean differ from that in our numerical experiments. Among the uncertainties, we consider the disaggregation parameterization to be the least reliable. While we modeled disaggregation based on observations that the largest particle size corresponds to the local Kolmogorov scale (Equation 13), other numerical studies have used alternative models grounded in mechanical principles. Babler et al. (2015) and Marchioli and Soldati (2015) tracked individual particles in turbulence fields reproduced by direct numerical simulations, and in their models, particles disaggregated when the turbulent shear stress at their locations exceeded a critical threshold. In such models, the breakup rate is linked to the kinetic energy dissipation rate. Additionally, there are different approaches in modeling the size distribution of the daughter particles other than our approach (setting the daughter particle size to the Kolmogorov scale η). Burd and Jackson (2002) modeled the disaggregation by redistributing the parent particle mass uniformly across smaller particle bins, which resulted in selective mass accumulation in a specific size bin and a bimodal spectrum in the steady state. Li et al. (2004), on the other hand, modeled disaggregation as the disintegration of a parent particle into two daughter particles of equal size, which led to a steep spectral slope beyond a certain radius. The spectral shape, and potentially the vertical fluxes in the current experiments, will vary with the adoption of these disaggregation models. Further research into disaggregation processes is necessary to better quantify the impact of turbulence on material transport. Nevertheless, we believe that the current approach (LES + LCM) provides a powerful tool for understanding the fundamental processes governing particle sinking in turbulent flows. This study represents an initial step toward quantifying the particle-sinking processes and the related material transport in the OSBL, which should be further improved in future research.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KN: Conceptualization, Funding acquisition, Investigation, Methodology, Resources, Validation, Visualization, Writing–original draft, Writing–review and editing. YY: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Validation, Writing–original draft, Writing–review and editing.

Funding

The authors declare that financial supports were received for the research, authorship, and/or publication of this article. This work was partially supported by the Environmental Radioactivity Network Center, Japan (Grant no. Y-23-27, Y-24-18 to KN), and by the Japan Society for the Promotion of Science, KAKENHI (Grant no. 21H05305 to YY).

Acknowledgments

We are sincere grateful to Yoshimasa Matsumura for his technical comments on the developed particle tracking method and Hidekatsu Yamazaki for his advice on the current disaggregation modeling. We appreciate the insightful discussions with Kazunori Akitomo and Masanori Konda on the direction of this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akers, R. J., Rushton, A. G., and Stenhouse, J. I. T. (1987). Floc breakage: the dynamic response of the particle size distribution in a flocculated suspension to a step change in turbulent energy dissipation. Chem. Eng. Sci. 42, 787–798. doi:10.1016/0009-2509(87)80038-6

CrossRef Full Text | Google Scholar

Alldredge, A. L., and Gotschalk, C. (1988). In situ settling behavior of marine snow. Limnol. Oceanogr. 33, 339–351. doi:10.4319/lo.1988.33.3.0339

CrossRef Full Text | Google Scholar

Andrejczuk, M., Grabowski, W. W., Reisner, J., and Gadian, A. (2010). Cloud-aerosol interactions for boundary layer stratocumulus in the Lagrangian Cloud Model. J. Geophys. Res. Atmos. 115. doi:10.1029/2010JD014248

CrossRef Full Text | Google Scholar

Ayala, O., Rosa, B., and Wang, L.-P. (2008). Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10, 075016. doi:10.1088/1367-2630/10/7/075016

CrossRef Full Text | Google Scholar

Babler, M. U., Biferale, L., Brandt, L., Feudel, U., Guseva, K., Lanotte, A. S., et al. (2015). Numerical simulations of aggregate breakup in bounded and unbounded turbulent flows. J. Fluid Mech. 766, 104–128. doi:10.1017/jfm.2015.13

CrossRef Full Text | Google Scholar

Braithwaite, K. M., Bowers, D. G., Nimmo Smith, W. a. M., and Graham, G. W. (2012). Controls on floc growth in an energetic tidal channel. J. Geophys. Res. Oceans 117. doi:10.1029/2011JC007094

CrossRef Full Text | Google Scholar

Buesseler, K. O., Antia, A. N., Chen, M., Fowler, S. W., Gardner, W. D., Gustafsson, O., et al. (2007). An assessment of the use of sediment traps for estimating upper ocean particle fluxes. J. Mar. Res. 65, 345–416. doi:10.1357/002224007781567621

CrossRef Full Text | Google Scholar

Burd, A. B., and Jackson, G. A. (2002). Modeling steady-state particle size spectra. Environ. Sci. and Technol. 36, 323–327. doi:10.1021/es010982n

PubMed Abstract | CrossRef Full Text | Google Scholar

Burd, A. B., and Jackson, G. A. (2009). Particle aggregation. Annu. Rev. Mar. Sci. 1, 65–90. doi:10.1146/annurev.marine.010908.163904

PubMed Abstract | CrossRef Full Text | Google Scholar

Cael, B. B., and White, A. E. (2020). Sinking versus suspended particle size distributions in the north pacific subtropical gyre. Geophys. Res. Lett. 47, e2020GL087825. doi:10.1029/2020GL087825

CrossRef Full Text | Google Scholar

Craig, P. D., and Banner, M. L. (1994). Modeling wave-enhanced turbulence in the ocean surface layer. J. Phys. Oceanogr. 24, 2546–2559. doi:10.1175/1520-0485(1994)024⟨2546:MWETIT⟩2.0.CO;2

CrossRef Full Text | Google Scholar

Craik, A. D. D., and Leibovich, S. (1976). A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426. doi:10.1017/S0022112076001420

CrossRef Full Text | Google Scholar

Deardorff, J. W. (1980). Stratocumulus-capped mixed layers derived from a three-dimensional model. Boundary-Layer Meteorol. 18, 495–527. doi:10.1007/BF00119502

CrossRef Full Text | Google Scholar

Dyer, K. R. (1989). Sediment processes in estuaries: future research requirements. J. Geophys. Res. Oceans 94, 14327–14339. doi:10.1029/JC094iC10p14327

CrossRef Full Text | Google Scholar

Finkel, Z. V., Beardall, J., Flynn, K. J., Quigg, A., Rees, T. A. V., and Raven, J. A. (2010). Phytoplankton in a changing world: cell size and elemental stoichiometry. J. Plankton Res. 32, 119–137. doi:10.1093/plankt/fbp098

CrossRef Full Text | Google Scholar

Fugate, D. C., and Friedrichs, C. T. (2003). Controls on suspended aggregate size in partially mixed estuaries. Estuar. Coast. Shelf Sci. 58, 389–404. doi:10.1016/S0272-7714(03)00107-0

CrossRef Full Text | Google Scholar

Fujiwara, Y., Yoshikawa, Y., and Matsumura, Y. (2018). A wave-resolving simulation of Langmuir circulations with a nonhydrostatic free-surface model: comparison with craik–leibovich theory and an alternative eulerian view of the driving mechanism. J. Phys. Oceanogr. 48, 1691–1708. doi:10.1175/JPO-D-17-0199.1

CrossRef Full Text | Google Scholar

Gelbard, F., Tambour, Y., and Seinfeld, J. H. (1980). Sectional representations for simulating aerosol dynamics. J. Colloid Interface Sci. 76, 541–556. doi:10.1016/0021-9797(80)90394-X

CrossRef Full Text | Google Scholar

Gruber, N., Landschützer, P., and Lovenduski, N. S. (2019). The variable southern ocean carbon sink. Annu. Rev. Mar. Sci. 11, 159–186. doi:10.1146/annurev-marine-121916-063407

PubMed Abstract | CrossRef Full Text | Google Scholar

Haller, G., and Sapsis, T. (2008). Where do inertial particles go in fluid flows? Phys. D. Nonlinear Phenom. 237, 573–583. doi:10.1016/j.physd.2007.09.027

CrossRef Full Text | Google Scholar

Jackson, G. A. (1990). A model of the formation of marine algal flocs by physical coagulation processes. Deep Sea Res. Part A. Oceanogr. Res. Pap. 37, 1197–1211. doi:10.1016/0198-0149(90)90038-W

CrossRef Full Text | Google Scholar

Jackson, G. A., Logan, B. E., Alldredge, A. L., and Dam, H. G. (1995). Combining particle size spectra from a mesocosm experiment measured using photographic and aperture impedance (Coulter and Elzone) techniques. Deep Sea Res. Part II Top. Stud. Oceanogr. 42, 139–157. doi:10.1016/0967-0645(95)00009-F

CrossRef Full Text | Google Scholar

Johnston, T. M. S., and Rudnick, D. L. (2009). Observations of the transition layer. J. Phys. Oceanogr. 39, 780–797. doi:10.1175/2008JPO3824.1

CrossRef Full Text | Google Scholar

Jouandet, M.-P., Jackson, G. A., Carlotti, F., Picheral, M., Stemmann, L., and Blain, S. (2014). Rapid formation of large aggregates during the spring bloom of Kerguelen Island: observations and model comparisons. Biogeosciences 11, 4393–4406. doi:10.5194/bg-11-4393-2014

CrossRef Full Text | Google Scholar

Kostadinov, T. S., Siegel, D. A., and Maritorena, S. (2009). Retrieval of the particle size distribution from satellite ocean color observations. J. Geophys. Res. Oceans 114. doi:10.1029/2009JC005303

CrossRef Full Text | Google Scholar

Lam, P. J., Bishop, J. K. B., Henning, C. C., Marcus, M. A., Waychunas, G. A., and Fung, I. Y. (2006). Wintertime phytoplankton bloom in the subarctic Pacific supported by continental margin iron. Glob. Biogeochem. Cycles 20. doi:10.1029/2005GB002557

CrossRef Full Text | Google Scholar

Li, X.-y., Zhang, J.-j., and Lee, J. H. W. (2004). Modelling particle size distribution dynamics in marine waters. Water Res. 38, 1305–1317. doi:10.1016/j.watres.2003.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchioli, C., and Soldati, A. (2015). Turbulent breakage of ductile aggregates. Phys. Rev. E 91, 053003. doi:10.1103/PhysRevE.91.053003

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchioli, C., Bhatia, H., Sardina, G., Brandt, L., and Soldati, A. (2019). Role of large-scale advection and small-scale turbulence on vertical migration of gyrotactic swimmers. Phys. Rev. Fluids. 4, 124304. doi:10.1103/PhysRevFluids.4.124304

CrossRef Full Text | Google Scholar

Mashayekhpour, M., Marchioli, C., Lovecchio, S., Lay, E. N., and Soldati, A. (2019). Wind effect on gyrotactic micro-organism surfacing in free-surface turbulence. Advan. Water. Resou. 129(0309-1708), 328–337. doi:10.1016/j.advwatres.2017.09.001

CrossRef Full Text | Google Scholar

Matsumura, Y., and Ohshima, K. I. (2015). Lagrangian modelling of frazil ice in the ocean. Ann. Glaciol. 56, 373–382. doi:10.3189/2015AoG69A657

CrossRef Full Text | Google Scholar

McCave, I. N. (1984). Size spectra and aggregation of suspended particles in the deep ocean. Deep Sea Res. Part A. Oceanogr. Res. Pap. 31, 329–352. doi:10.1016/0198-0149(84)90088-8

CrossRef Full Text | Google Scholar

Misumi, K., Nishioka, J., Obata, H., Tsumune, D., Tsubono, T., Long, M. C., et al. (2021). Slowly sinking particles underlie dissolved iron transport across the pacific ocean. Glob. Biogeochem. Cycles 35, e2020GB006823. doi:10.1029/2020GB006823

CrossRef Full Text | Google Scholar

Monroy, P., Hernández-García, E., Rossi, V., and López, C. (2017). Modeling the dynamical sinking of biogenic particles in oceanic flow. Nonlinear Process. Geophys. 24, 293–305. doi:10.5194/npg-24-293-2017

CrossRef Full Text | Google Scholar

Noh, K. M., Noh, Y., Brereton, A., and Kug, J.-S. (2021). The route to spring phytoplankton blooms simulated by a Lagrangian plankton model. J. Geophys. Res. Oceans 126, e2020JC016753. doi:10.1029/2020JC016753

CrossRef Full Text | Google Scholar

Oh, D., and Noh, Y. (2022). Roles of drop size distribution and turbulence in autoconversion based on Lagrangian cloud model simulations. J. Geophys. Res. Atmos. 127, e2022JD036495. doi:10.1029/2022JD036495

CrossRef Full Text | Google Scholar

Pierson, W. J., and Moskowitz, L. (1964). A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. (1896-1977) 69, 5181–5190. doi:10.1029/JZ069i024p05181

CrossRef Full Text | Google Scholar

Pollard, R. T., Rhines, P. B., and Thompson, R. O. R. Y. (1973). The deepening of the wind-Mixed layer. Geophys. Fluid Dyn. 4, 381–404. doi:10.1080/03091927208236105

CrossRef Full Text | Google Scholar

Qiu, J., Marchioli, C., and Zhao, L. (2022). A review on gyrotactic swimmers in turbulent flows. Acta Mech. Sin. 38, 722323. doi:10.1007/s10409-022-22323-x

CrossRef Full Text | Google Scholar

Riechelmann, T., Noh, Y., and Raasch, S. (2012). A new method for large-eddy simulations of clouds with Lagrangian droplets including the effects of turbulent collision. New J. Phys. 14, 065008. doi:10.1088/1367-2630/14/6/065008

CrossRef Full Text | Google Scholar

Saffman, P. G., and Turner, J. S. (1956). On the collision of drops in turbulent clouds. J. Fluid Mech. 1, 16–30. doi:10.1017/S0022112056000020

CrossRef Full Text | Google Scholar

Sheldon, R. W., Prakash, A., and Sutcliffe, W. H. (1972). The size distribution of particles in the ocean1. Limnol. Oceanogr. 17, 327–340. doi:10.4319/lo.1972.17.3.0327

CrossRef Full Text | Google Scholar

Shima, S., Kusano, K., Kawano, A., Sugiyama, T., and Kawahara, S. (2009). The super-droplet method for the numerical simulation of clouds and precipitation: a particle-based and probabilistic microphysics model coupled with a non-hydrostatic model. Q. J. R. Meteorological Soc. 135, 1307–1320. doi:10.1002/qj.441

CrossRef Full Text | Google Scholar

Sieburth, J. M., Smetacek, V., and Lenz, J. (1978). Pelagic ecosystem structure: heterotrophic compartments of the plankton and their relationship to plankton size fractions 1. Limnol. Oceanogr. 23, 1256–1263. doi:10.4319/lo.1978.23.6.1256

CrossRef Full Text | Google Scholar

Smoluchowski, M. (1918). Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Z. für Phys. Chem. 92U, 129–168. doi:10.1515/zpch-1918-9209

CrossRef Full Text | Google Scholar

Spielman, L. A. (1985). “Hydrodynamic aspects of flocculation,” in Mathematical models and design methods in solid-liquid separation. Editor A. Rushton (Dordrecht: Springer Netherlands), 207–232. doi:10.1007/978-94-009-5091-7_9

CrossRef Full Text | Google Scholar

Tagliabue, A., Buck, K. N., Sofen, L. E., Twining, B. S., Aumont, O., Boyd, P. W., et al. (2023). Authigenic mineral phases as a driver of the upper-ocean iron cycle. Nature 620, 104–109. doi:10.1038/s41586-023-06210-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeuchi, M., Doubell, M. J., Jackson, G. A., Yukawa, M., Sagara, Y., and Yamazaki, H. (2019). Turbulence mediates marine aggregate formation and destruction in the upper ocean. Sci. Rep. 9, 16280. doi:10.1038/s41598-019-52470-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsuda, A., Takeda, S., Saito, H., Nishioka, J., Nojiri, Y., Kudo, I., et al. (2003). A mesoscale iron enrichment in the western subarctic pacific induces a large centric diatom bloom. Science 300, 958–961. doi:10.1126/science.1082000

PubMed Abstract | CrossRef Full Text | Google Scholar

Ushijima, Y., and Yoshikawa, Y. (2019). Mixed layer depth and sea surface warming under diurnally cycling surface heat flux in the heating season. J. Phys. Oceanogr. 49, 1769–1787. doi:10.1175/JPO-D-18-0230.1

CrossRef Full Text | Google Scholar

Ushijima, Y., and Yoshikawa, Y. (2022). Nonlinearly interacting entrainment due to shear and convection in the surface ocean. Sci. Rep. 12, 9899. doi:10.1038/s41598-022-14098-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidussi, F., Claustre, H., Manca, B. B., Luchetta, A., and Marty, J.-C. (2001). Phytoplankton pigment distribution in relation to upper thermocline circulation in the eastern Mediterranean Sea during winter. J. Geophys. Res. Oceans 106, 19939–19956. doi:10.1029/1999JC000308

CrossRef Full Text | Google Scholar

Yoshikawa, Y. (2019). “Wind-driven mixing under the earth rotation,” in Encyclopedia of ocean sciences (Elsevier), 586–590. doi:10.1016/B978-0-12-409548-9.10954-6

CrossRef Full Text | Google Scholar

Yoshikawa, Y., Baba, Y., Mizutani, H., Kubo, T., and Shimoda, C. (2018). Observed features of Langmuir turbulence forced by misaligned wind and waves under destabilizing buoyancy flux. J. Phys. Oceanogr. 48, 2737–2759. doi:10.1175/JPO-D-18-0038.1

CrossRef Full Text | Google Scholar

Zikanov, O., Slinn, D. N., and Dhanak, M. R. (2003). Large-eddy simulations of the wind-induced turbulent Ekman layer. J. Fluid Mech. 495, 343–368. doi:10.1017/S0022112003006244

CrossRef Full Text | Google Scholar