Simulation research on blasting of an open pit mine slope considering elevation conditions and slope shape factors

This study established a numerical model that considers elevation conditions and slope shape factors by the modified Sadovsky formula to analyze the vibration attenuation law of open-pit slopes under blasting vibration conditions. The blasting excavation of a slope in a certain open-pit mine in Yunfu, Guangdong, is selected as an example. Using a numerical model that considers elevation conditions and slope shape factors by the modified Sadovsky formula, a triangular pulse load was utilized to approximate the time-history characteristics of explosion vibration with FLAC^3D software. The simulation results showed the radiation range of the blasting vibration seismic wave. By comparison with field monitoring data, the numerical model that considers the slope shape factor had a relative error of ∼10%, while the numerical model that disregards the slope shape factor had a relative error of ∼15%. The relative accuracy of the calculation results of the new numerical model is higher and closer to the actual attenuation law of blasting particle vibration speed, providing more reliable results for slope stability assessment. The peak particle velocities obtained from the numerical simulation results were generally higher than the field monitoring data. These discrepancies might be attributed to the use of simplified models that disregard the discontinuous structural planes within the rock mass. This study provides an important reference for the stability assessment of open-pit slopes under blasting vibration conditions, offering guidance for improving slope stability assessment and related engineering practices.

1 Introduction

The blasting of open pit mine slopes can lead to slope deformation and damage, potentially resulting in safety hazards in some nonmining areas that should be kept stable. Blast-induced vibrations are the phenomenon where energy released from explosions causes vibrations in rock mass or slopes, causing instability and alteration of the rock structure. Furthermore, this phenomenon can cause slope instability and rock mass collapse. Inside the rock mass, the discontinuity in the surface rock mass is common and its distribution is complex (Wang et al., 2023; An et al., 2024; Yong et al., 2024), which is one of the important factors affecting the blast vibration velocity. Outside the rock mass, the topography also affects the propagation of the blast vibration velocity. Therefore, in the context of open-pit mining, reliable blasting design is crucial to avoid generating excessive vibrations and shock waves that could cause irreversible damage to slopes and rock masses in some nonmining areas.

The effects of blast vibration on slope stability are classified into three methods: one is to predict the blast vibration rate by field monitoring using the traditional Sadowski correction formula (Singh and Roy, 2008; Dindarloo, 2015); some other scientists use machine learning techniques to predict blast vibration to overcome the limitations of the traditional formula (Nguyen et al., 2019; Bui et al., 2021; Zhang et al., 2021; Xu and Wang, 2023); In recent years, numerical simulation methods have been widely employed in conjunction with vibration attenuation principles to investigate slope stability, providing crucial insights for engineering construction. These studies encompass methods such as the Janbu limit equilibrium method and pseudostatic methods to assess the impact of blasting loads on slope stability (Ma et al., 2016). Based on the monitoring results and the propagation and attenuation patterns of blasting-induced vibrations, these studies offer guidance for mine safety production (Li et al., 2017). The effects of blast vibration velocity on the slope surface, offering practical value for blast vibration prediction and regional protection, are explored (Yan et al., 2022). Certain scholars have employed laboratory methods to calibrate numerical models for the influence of different fault rock structures on rock slope stability (Azarfar et al., 2019; Kang et al., 2020; Dehghan and Khodaei, 2022). The three-dimensional dynamic stability of high slopes due to blast vibrations using a combination of engineering geological surveys, field blasting tests, vibration monitoring, and numerical simulations is explored, providing technical support and theoretical guidance for mining blasts (Li et al., 2022). By comparing the impact of seismic events and blasting on slope stability, scaling seismic acceleration spectra have been proposed to obtain more reliable dynamic slope stability results (Jiang et al., 2018; Shafiei Ganjeh et al., 2019). Through the study of different blasting techniques, predictions of blasting vibration attenuation and propagation patterns have been made, and mathematical models for cumulative rock damage due to blasting have been established (Wang et al., 2021; 2022; Cao et al., 2023). Other researchers have examined the optimization of blasting parameters, vibration effect predictions, and stability analysis of steep slopes under deep bench blasting vibrations and have proposed effective solutions for open-pit mining blasting issues, offering significant references for engineering practice (Soren, 2014; Cao et al., 2018; Yin et al., 2021; Su and Ma, 2022; Yang et al., 2022; Bai et al., 2023). Through experiments and numerical simulations, the damage patterns of slopes due to blasting vibrations have been investigated, leading to the development of slope blasting vibration damage functions and the identification of the most critical areas (Liu et al., 2023).

In summary, extensive research on slope stability is conducted by combining numerical simulation methods with vibration attenuation principles. This research has predominantly focused on factors such as blasting loads, vibration propagation, and geological characteristics but have given relatively limited consideration to the influence of slope geometry factors. Slope geometry factors are critical parameters affecting slope stability and have a significant impact under different blasting conditions. Therefore, we aim to integrate relevant vibration attenuation theories and introduce the Sadowski modified formula, which incorporates elevation conditions and slope geometry factors into numerical simulations. Through a combined approach of field measurements and numerical simulations, this study analyzes the patterns of blasting-induced vibrations and predicts the displacement of slopes under blast conditions. This study also provides an important theoretical basis and technical support for the safe production of the Guangdong Yunfu Sulfur-Iron Mine.

2 Materials and methods

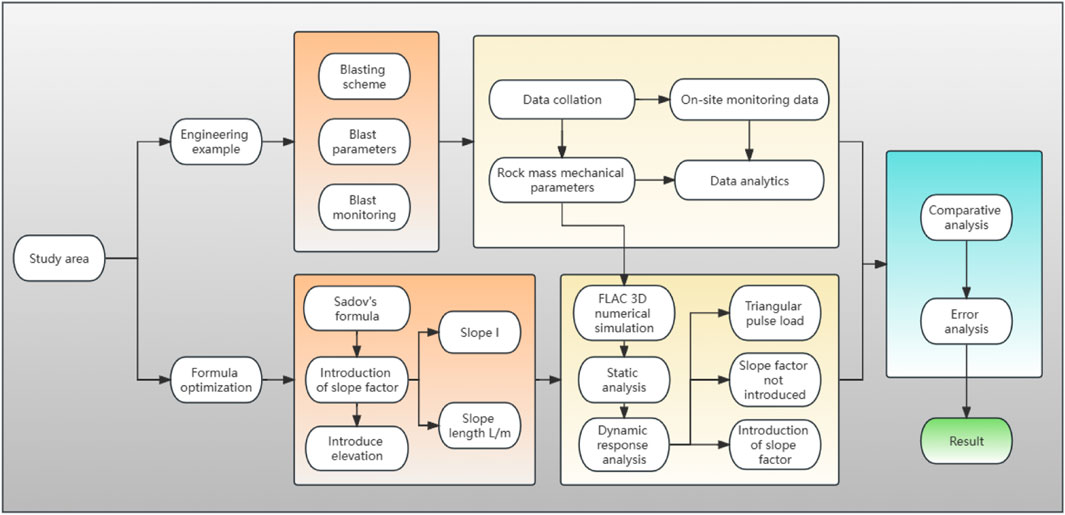
Elevation conditions and the slope shape factor are considered. FLAC^3D software is selected to establish the numerical model of the slope to simulate the blasting vibration propagation process and analyze the vibration velocity attenuation law of rock mass particles inside the slope. By comparing and verifying the measured data and simulation results, the accuracy of the numerical simulation and the reliability of the evaluation results are discussed. An in-depth understanding of the dynamic response characteristics of the slope provides a valuable reference for engineering stability evaluation. The technical route adopted in this paper is shown in Figure 1.

Figure 1

Figure 1. Technology route.

2.1 Elevation conditions and slope shape factor

When an explosive explodes in rock, the generated pressure shock forms a shock stress wave. With an increase in the explosion center distance, the shock wave gradually decays into a stress wave. Presently, an empirical formula proposed by Sadovsky is often utilized to analyze the attenuation law of particle vibration velocity. Regression analysis is carried out according to the Sadovsky formula, which is denoted Formula 1, and then the magnitude of the blasting vibration velocity is predicted based on the Sadovsky formula obtained by regression.

$V=K{\left(\frac{Q^{\frac{1}{3}}}{R}\right)}^{\alpha }(1)$

where K is the coefficient related to rock properties, blasting site conditions and other factors; Q is the maximum amount of explosive charge (kg) in blasting; R is the blasting center distance, that is, the distance (m) from the measuring point to the center of the explosion source; and α is the blasting vibration attenuation coefficient.

However, with an increase in the height difference and topographic complexity of the mine slope, the applicability of the Sadowski formula is limited. The monitoring data show that the peak vibration velocity V of the blasting particle decreases with increasing elevation but that the vibration velocity still increases when it reaches a certain elevation. The formula only considers the influence of the vibration velocity V with the blasting center distance R and has high accuracy under the condition of levelling the terrain. However, the formula does not reflect the influence of elevation. Therefore, some scholars have proposed improved formulas based on this understanding. Li et al. (1997) investigated the amplification effect of blasting vibration on high slopes. Hu and Wu (2004) added a height difference factor on the basis of the Sadovsky formula and modified the vibration velocity formula to Eq. 2:

$V=K{\left(\frac{Q^{\frac{1}{3}}}{R}\right)}^{\alpha }{\left(\frac{R}{S}\right)}^{\beta }(2)$

where S is the horizontal distance (m) between the measuring point and the explosion center and β is the elevation influence coefficient.

Wang and Lu (1994) then enter the dimensionless treatment of the influence coefficient of elevation H on the vibration speed and suggest that the vibration speed has an amplification effect along the elevation. Thus the calculation formula should be Eq. 3:

$V=K{\left(\frac{Q^{\frac{1}{3}}}{R}\right)}^{\alpha }{\left(\frac{Q^{\frac{1}{3}}}{H}\right)}^{\beta }(3)$

where H is the relative height difference between the measuring point and the explosion center.

Chen et al. (2011) suggest that during the blasting process, the open-air multilevel slope will substantially vibrate near the free suspended surface, and some rocks on the open-air slope steps will produce a whiplash effect, resulting in a more obvious rock mass amplification effect of the slope steps. There is an amplification effect in the blasting vibration process of the slope step and introduced elevation parameters, but a slope factor is not introduced to analyze its influence on the amplification effect. Our study introduces elevation conditions and slope factors and establishes a blasting vibration amplification effect formula considering these factors as follows Eq. 4:

$V=K{\left(\frac{Q^{\frac{1}{3}}}{R}\right)}^{\alpha }{\left(\frac{Q^{\frac{1}{3}}}{H}\right)}^{\beta }\frac{cI+d}{eL+f}(4)$

where I is the slope of the stepped slope, L is the slope length of the stepped slope, and c, d, e, and f are the relevant influence coefficients.

In the study, slope I is usually expressed as the percentage value of the tangent function of the foot γ of the slope, while slope length L represents the length from the foot of the slope to the top of the slope. When considering the impact of slope shape on blasting, a larger slope angle results in greater vibration velocity, while increased slope length leads to the gradual attenuation of the vibration wave and a corresponding decrease in velocity. Because the height of each step in the study area is much larger than the width of the step, it is possible to connect the end point of the slope foot of the blasting horizontal plane with the end point of the slope top of the horizontal plane of each step and to construct a new slope as a multilevel slope with different steps.

2.2 Principle of dynamic calculations in FLAC^3D

FLAC^3D uses a linear explicit Lagrangian finite difference method and a mixed discrete technique to solve the motion equations. The specified computational domain is divided into several elements, with nodes connecting these elements. When a load is applied to a particular node, the node’s motion equation is expressed in the form of finite differences over a small time increment. The load applied to a node within a small time step only affects adjacent nodes. Based on the stress state at a given time $t$ and the strain increments over the time step $\Delta t$, the stress state at $t+\Delta t$ is determined. According to Gauss’s law, the strain increment of an element is calculated based on the node’s velocities. Then, the stress‒strain relationship, i.e., the constitutive equations, and the element stresses are computed and integrated to obtain the stress vectors acting on the nodes. By combining the equilibrium equations, the node velocities and displacements are further solved from the node forces. This iterative process continues with a time step advancing throughout the entire computational domain until convergence is achieved, simulating the plastic deformation and flow of rock masses and other materials.

In the dynamic calculations of velocity and displacement, FLAC3D focuses on nodes as the computational entities. Mass and forces are concentrated at the nodes, and the motion equations are solved in the time domain. The node motion equation is expressed as follows Eq. 5:

$\frac{\partial v_i^l}{\partial t}=\frac{F_i^l\left(t\right)}{m^l}(5)$

In the equation, $F_i^l\left(t\right)$ represents the equilibrium force component in the $i$ -direction for node $l$ at time $t$, which can be derived from the principle of virtual work, and $m^l$ is the concentrated mass of node $l$.

By approximating the left side of Eq. 5 using central differencing, the node’s velocity is obtained Eq. 6:

$v_i^l\left(t+\frac{\Delta t}{2}\right)+\frac{F_i^l}{m^l}=v_i^l\left(t-\frac{\Delta t}{2}\right)+\frac{F_i^l\left(t\right)}{m^l}\Delta t(6)$

2.3 Strength reduction

In FLAC^3D, the numerical analysis method that utilizes the strength reduction technique is employed to analyze engineering problems related to slope stability. When performing stability analysis of slopes, the safety factor needs to be redefined. It is assumed that all parameters, with the exception of the shear strength of the rock or soil (comprising cohesion and internal friction angle), remain negligibly unchanged. The shear strength of the rock or soil is continuously reduced until the critical sliding state of the slope is reached. The final reduction factor (ratio of the ultimate shear strength to the initial shear strength) is then considered as the safety factor, which is expressed by the following Eqs 7, 8:

$F_S=\frac{{\displaystyle {\int }_0^l}{\tau }_{f}dl}{{\displaystyle {\int }_0^l}\tau dl}=\frac{{\displaystyle {\int }_0^l}\left(c+\sigma \mathit{tan}\phi \right)dl}{{\displaystyle {\int }_0^l}\tau dl}(7)$

$F_S\frac{{\displaystyle {\int }_0^l}\left(\frac{c}{F_S}+\sigma \frac{\mathit{tan}\phi }{F_S}\right)dl}{{\displaystyle {\int }_0^l}\tau dl}=\frac{{\displaystyle {\int }_0^l}\left(c^{\prime }+\sigma \mathit{tan}{\phi }^{\prime }\right)dl}{{\displaystyle {\int }_0^l}\tau dl}(8)$

Here, $c^{\prime }=c/F_s$ and ${\phi }^{\prime }=\mathit{arctan}\left(\mathit{tan}\phi /F_S\right)$, with $c$, $\phi$, $c^{\prime }$, and ${\phi }^{\prime }$, are used to represent the cohesion coefficient and internal friction angle of the soil, respectively, before and after applying the strength reduction method. $l$ represents the length of the sliding surface.

3 Simulation research

3.1 Introduction of engineering case

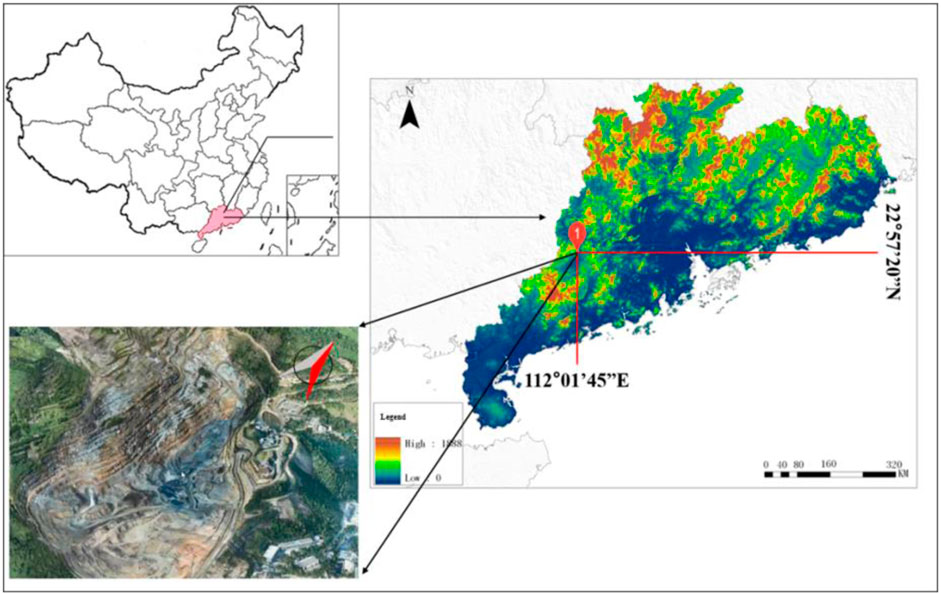
This study case is the Guangdong Yunfu Open-pit Mining Project, which is located in Yunfu City, Guangdong Province. The project involves large-scale blasting operations, and these blasting vibrations can have a significant impact on slope stability in some nonmining areas. Therefore, accurate assessment and prediction of slope stability is essential to ensure the safe operation of the project. The Guangdong Yunfu Pyrite Open-pit is the largest pyrite mine in China, with an annual output of three million tons. The Yunfu pyrite mine started large-scale construction in 1979 and was completed and put into operation in January 1988. The long axis with 1,800 m of the open pit is due north‒south. The short axis is positive east‒west, and the width is approximately 800 m. The geographical location of Yunfu open pit mine is shown in Figure 2.

Figure 2

Figure 2. Geographical location of the Yunfu open-pit mine.

The length of the open stope is approximately 1,800 m from north to south and 800 m wide from east to west. The height of the steps in the mining area is 10 m above 370 m and 12 m below 370 m, and the slope angle of the working steps is 70°. The maximum height of the designed slope exceeds 800 m. Because the mining area is a metamorphic rock area, there are discontinuities that are not conducive to slope stability, and shallow landslides have occurred many times. Therefore, conducting blasting vibration tests and stability research on the open-pit slope of the Yunfu Pyrite Mine is not only essential but also important.

3.2 Blasting scheme

The ore rock of the Yunfu Pyrite Mine is difficult and cannot be directly shoveled by excavators, so the horizontal step mining and stripping method of loose blasting is adopted. To ensure the normal operation of mechanical equipment, detonators are used to realize hole-by-hole initiation, control the blasting scale, and reduce the impact of vibration and flying stones on the surrounding environment. The step height is 12 m, and the minimum working platform width is 40 m. The blasting adopts vertical drilling and a triangular arrangement. The hole spacing is 7–8 m, and the row spacing is 6–7 m. By balancing the blasting scale and adhering to safety requirements through such a blasting scheme, the efficiency and safety of blasting operations are improved.

3.3 Open-pit mine blasting vibration monitoring

3.3.1 Purpose of blasting vibration monitoring

Through blasting vibration monitoring, information on blasting vibration waves, such as vibration speed and frequency, can be obtained, and the blasting attenuation propagation law can be linearly analyzed by regression according to measured blasting vibration data. The accuracy of the numerical simulation is simultaneously verified by comparison with the numerical simulation results and analysis of the measured data. The test results will provide a scientific basis for formulating a reasonable blasting plan, controlling blasting vibration and taking disaster prevention and mitigation measures.

3.3.2 Blasting vibration monitoring

Because the blasting vibration monitoring of open-pit mines is real-time monitoring work, it is necessary to survey the topography and formulate a detailed monitoring plan before monitoring. Sensors are installed before blasting, each sensor is connected to the collector, and the parameters are configured. During the blasting process, if the vibration exceeds the established threshold, the vibrometer starts to record the blasting vibration signal. After blasting, we can obtain data such as vibration speed and frequency. The data are utilized for the K value and α value of the mining area.

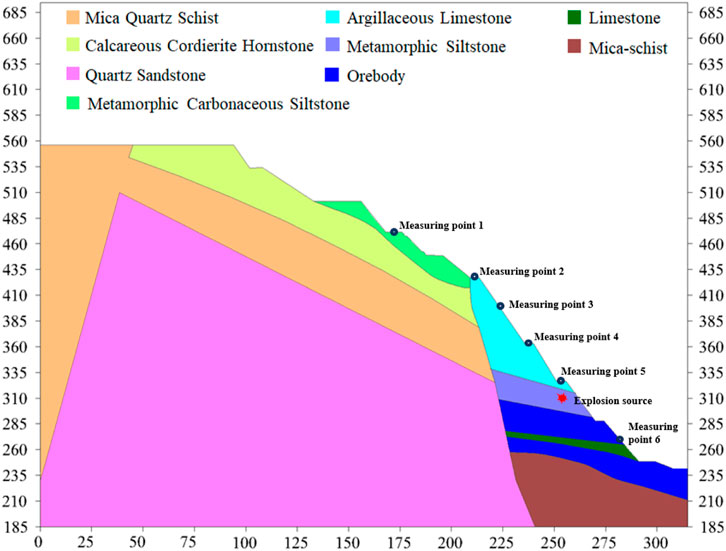
The main factors of the seismic effect of blasting are the blasting charge and blasting center distance. The increase in the charge will cause more energy to be converted to seismic waves, resulting in more violent ground vibration. The farther from the explosion center, the more obvious the vibration attenuation and ground vibration. According to the site conditions, measurement points are arranged at different elevations of the slope measurement line, and TCS-B3 triaxial vibration velocity sensors are arranged at each measurement point to test the blasting vibration speed value of each point of the slope. The slope section and the arrangement of measurement points are shown in Figure 3.

Figure 3

Figure 3. Profile geological generalization model and measurement point arrangement.

In this blasting monitoring, the blasting vibration self-recording instrument TC-4850 is employed for monitoring. The instrument can set various collection parameters on site and can display the waveform, peak value, and frequency in real time. Numerical analysis is performed using the TC-4850 blasting vibration self-recording instrument supporting software and the Vib’SYS numerical vibration signal acquisition and analysis system. To make the blasting vibration data more accurate, the sensor is bonded to the surface with gypsum, and the sensor forms a whole with the surface to facilitate the collection of vibration waves and other data. The layout of the monitoring points for a part of the monitoring site is shown in Figure 4.

Figure 4

Figure 4. Placement of site monitoring points.

3.3.3 Blasting vibration monitoring data

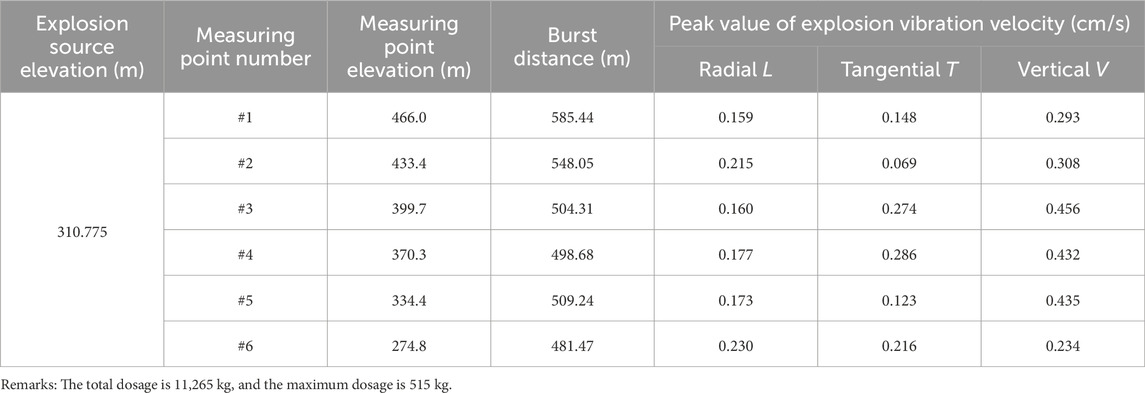
The blasting parameters used in the blasting vibration monitoring were statistically analyzed, and detailed vibration data were obtained. Table 1 shows the blasting monitoring data.

Table 1

Table 1. Blasting monitoring data.

3.4 Numerical simulation

In this study, FLAC^3D numerical analysis and simulation software is selected to numerically simulate the slope of the Guangdong Yunfu open-pit mine under blasting vibration. The numerical analysis and calculation model of this time appropriately simplifies the original project. According to the profile geological generalization model, the geometric shape of the slope is transformed into a three-dimensional, finite difference mesh model via RHINO software and imported into FLAC^3D software to establish a numerical model. The slope shape factor is introduced into the FISH language for numerical calculation and analysis. The results of the numerical model development can be seen in Figure 5.

Figure 5

Figure 5. FLAC^3D numerical analysis mesh model.

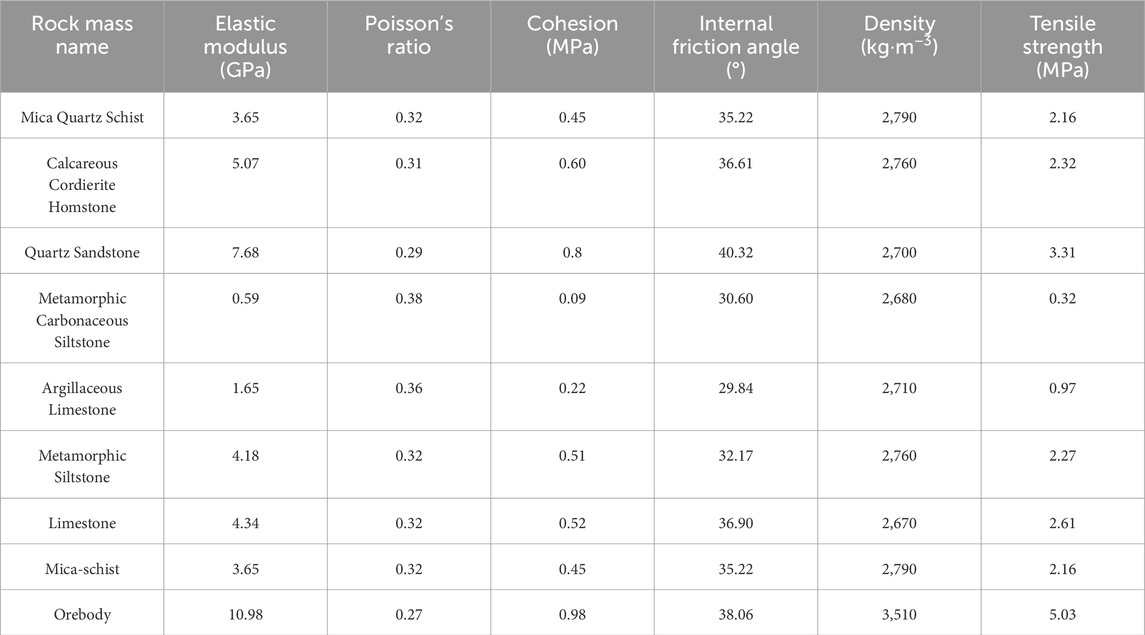
According to the actual geological survey and experimental test data, key parameters such as the elastic modulus, Poisson’s ratio, and strength parameters of the slope material are determined. The physical and mechanical parameters of the rock mass needed in this model are shown in Table 2.

Table 2

Table 2. Rock mass mechanical parameters.

3.4.1 Static analysis of open pit slope

The blasting vibration was simulated by a numerical simulation method and analyzed by comparison with the measured data. The static analysis part is a key step in evaluating the stability of the open-pit slope, and it plays an important role in blasting simulation research. A reliable basis for blasting simulation research is provided by comprehensively considering factors such as geological characteristics, slope geometric parameters and material properties. The static analysis part of this time adopts the Mohr‒Coulomb constitutive model, and the slope model formed from the survey data generates the initial in situ stress field under the action of gravity in Figure 6A. The initial vertical in situ stress is distributed in layers. The maximum value is 8.42 MPa at the bottom of the slope, and the minimum value is 0.52 MPa at the surface of the slope.

Figure 6

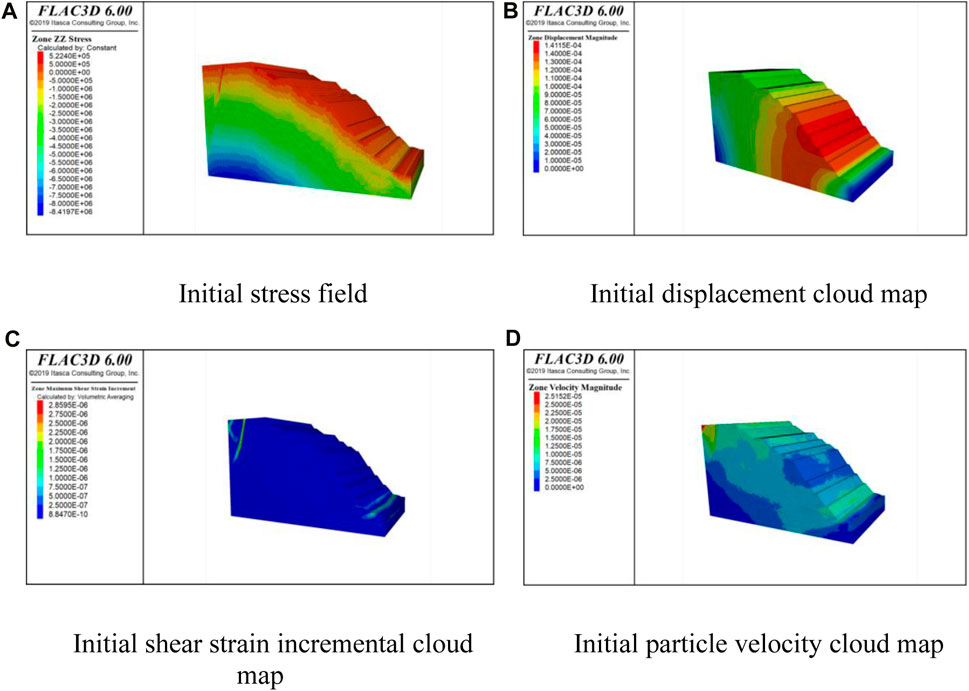
Figure 6. Static analysis of open pit slope. (A) Initial stress field (B) Initial displacement cloud map (C) Initial shear strain incremental cloud map (D) Initial particle velocity cloud map.

After the initial in situ stress field of the slope is generated, the stability of the slope in the preblasting stage is calculated and analyzed. The initial displacement cloud diagram of the slope under static conditions is shown in Figure 6B. The largest area of slope displacement is in the middle of the high and steep slope, and there is no obvious plastic area distribution of the slope. The increment of the slope shear strain is shown in Figure 6C. There is a significant shear strain increment at the top and bottom regions of the slope, while in other areas, the shear strain increment is relatively small, indicating no substantial tensile and shear failures. The particle velocity of the slope is shown in Figure 6D. The slope has no large movement speed, the velocity change area is distributed mainly at the top and bottom, and the overall stability of the slope is good.

3.4.2 Dynamic analysis of an open pit mine slope

Due to the complexity of the explosion process and the limitation of the actual measurement, every detail of the explosion vibration cannot be directly obtained and can only be equivalently treated by an empirical formula. The triangular pulse load is adopted in this study to approximate the time-history characteristics of the explosion vibration. In the numerical simulation, the determined triangular pulse load is applied to the slope model using FLAC^3D software. By defining the load function in FLAC^3D and using it as an external loading condition, the deformation and stress distribution of the slope under the action of explosion vibration are simulated. The determination of the triangular pulse load involves two fundamentals: the load amplitude and load time history (Kuhlemeyer and John, 1973; Moszynski, 1983; Chen et al., 2000; Xia et al., 2005).

The determination of the load amplitude determines the peak compressive stress of the detonation gas generated during the explosion of the explosive on the gun hole wall. According to the C-J theory of detonation waves, the average bombardment pressure of the explosive acting on the gun hole wall is Eq. 9:

$p_j=\frac{{\rho }_e{D}_j^2}{2\left(\gamma +1\right)}(9)$

In the formula, p_j is the average initial detonation pressure of the instantaneous explosive, ρ_e is the explosive density, D_j is the detonation velocity of the explosive, γ is the isentropic coefficient of the explosive, and the value of γ is related to the charge density. Research shows that when ρ_e < 1.2 g/cm³, γ is 2.1, and when ρ_e ≥ 1.2 g/cm³, γ is 3.

Under the condition of coupled charge, the initial explosion pressure P0 after the explosion of the explosive is Eq. 10:

$P_0=P_j(10)$

Under the condition of uncoupled loading, according to the diameter d_b of the blast hole and the diameter d_e of the charge coil, the initial blasting pressure after the modified explosive explosion is Eq. 11

$P_0=n\frac{{\rho }_e{D}_j^2}{2\left(\gamma +1\right)}{\left(\frac{d_b}{d_e}\right)}^{-2\gamma }(11)$

In the formula, n is the pressure increase coefficient when the explosion product expands on the hole wall, n = 8–10, and 10 is used in this study.

The specific blasting peak calculation parameters are shown in Table 3:

Table 3

Table 3. Blasting load peak calculation-related parameters.

During the action time of the blasting load, the shock wave and the pressure of the detonation gas generated by the explosion of the explosive will instantly act on the mine slope or rock formation, resulting in its rupture and fragmentation. Therefore, reasonable control of the action time of the blasting load and the time of pressure rise and fall can effectively control the blasting effect. The action time of the blasting load is very short. In this study, the load rises by 1 ms and falls by 7 ms. The total action time is 8 ms.

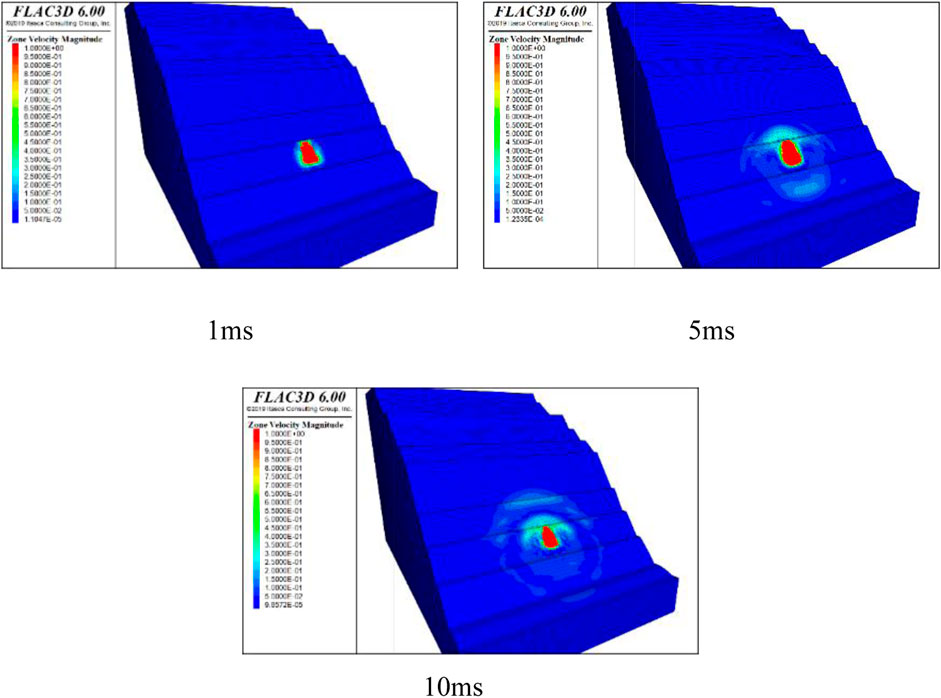
In this blasting simulation calculation, the radiation range of the blasting seismic wave is shown in Figure 6. Because blasting vibration seismic waves exhibit distinct directionality, when blasting occurs on high and steep slopes, although the rock mass below also slightly responds, over time, the propagation direction of the blasting vibration seismic wave is predominantly concentrated on the upper slope where the load is applied. Figure 7 shows the distribution of the model particle velocity between 1, 5, and 10 ms after blasting.

Figure 7

Figure 7. Cloud diagram of the particle vibration velocity at different times after blasting.

4 Analysis of the results

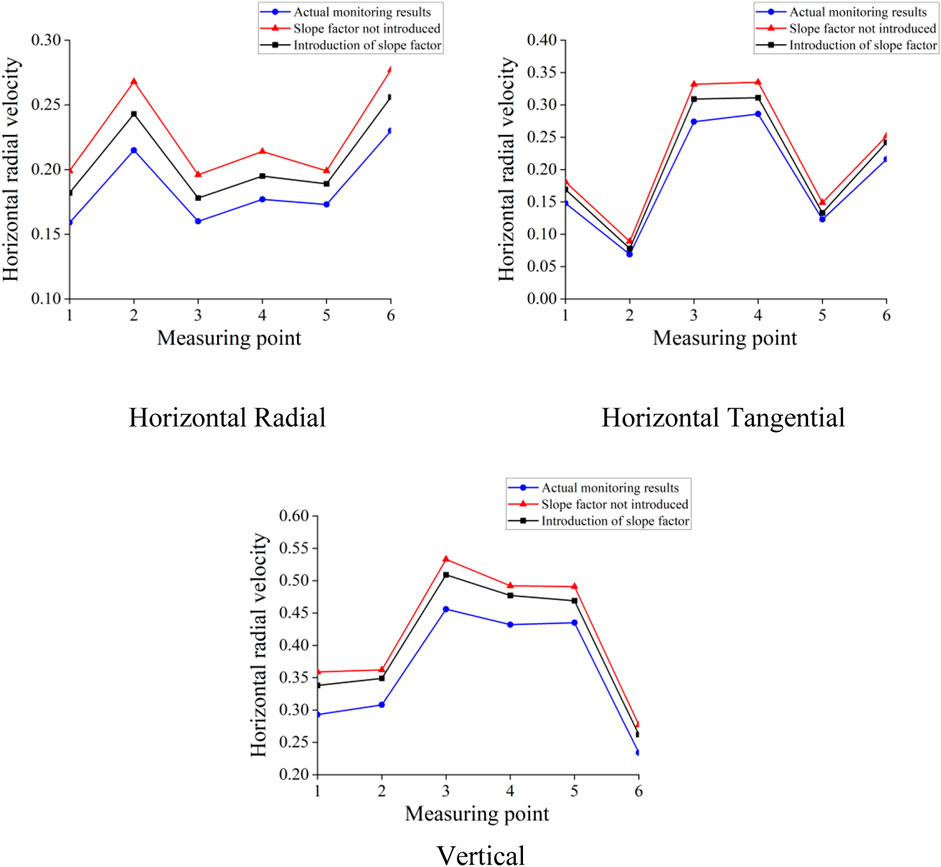
This study establishes pertinent monitoring points and explosive load parameters within the model, ensuring that the imposition of loads in numerical computations closely aligns with monitored outcomes and real-world conditions. The numerical calculation results are improved by introducing elevation conditions and slope factors and compared with the on-site monitoring data in Figure 8.

Figure 8

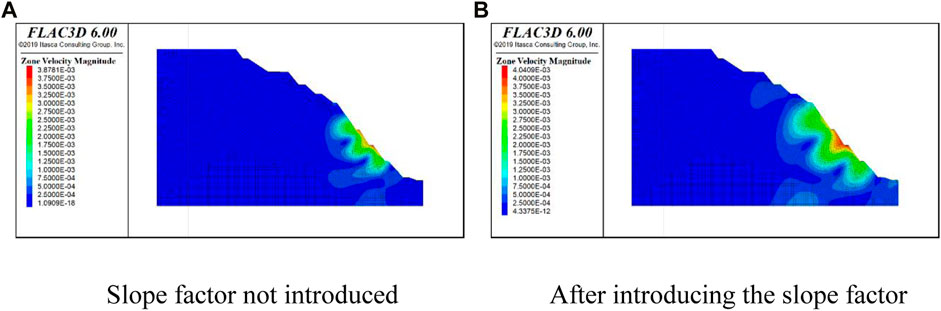
Figure 8. Particle vibration velocity cloud diagram. (A)Slope factor not introduced (B)After introducing the slope factor.

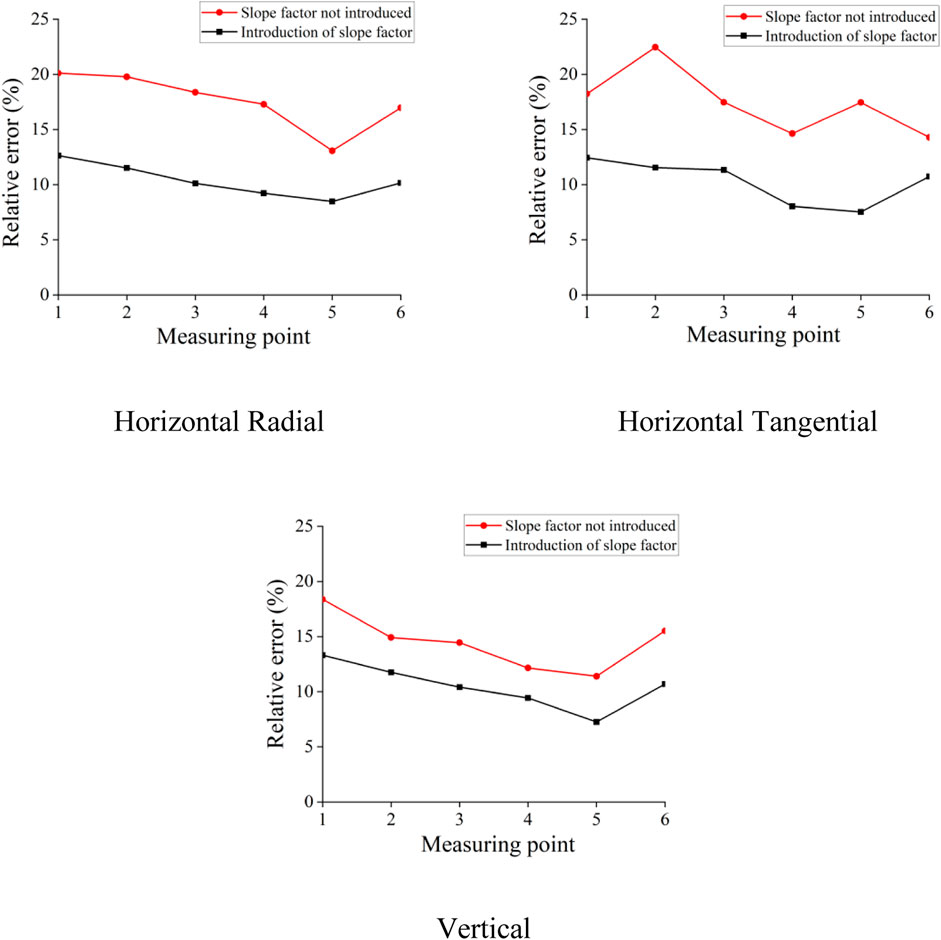
The results with and without the introduction of the slope factor at each measuring point are compared, and the error analysis is carried out in Figure 9. The relative error was calculated according to Eq. 8, which is given in Eq. 12, and the line graph is shown in Figure 9.

$\left|\frac{V_1}{V_2}-1\right|\times 100\%(12)$

In the formula, V₁ is the vibration velocity of the particle monitored on site, and V₂ is the numerical simulation calculation result.

Figure 9

Figure 9. Comparison of monitoring data and calculation results.

When incorporating the slope shape factor into numerical simulations, it is observed that there is a relative error of approximately 10% in the peak vibration velocity compared to the field monitoring data as shown in Figure 10. However, when the slope shape factor is not considered in the numerical simulation, the relative error between the simulation results and field monitoring data for the peak vibration velocity is approximately 15%. For multitiered slopes in the Yunfu open-pit mine in Guangdong, analyzing the slope shape factor leads to an overall velocity attenuation pattern that is closer to the measured data and has a higher accuracy. Notably, the peak vibration velocities from both sets of numerical simulation results are generally higher than the field monitoring data. This discrepancy could be attributed to the simplified model employed in the numerical simulation, where the rock mass is treated as a uniform and continuous medium, disregarding discontinuities such as joints and fractures within the actual rock mass. This simplification may lead to a slightly slower attenuation of the blasting-induced seismic wave, causing differences from real-world engineering scenarios. Despite these deviations, overall, the accuracy of numerical calculation results remains within an acceptable range.

Figure 10

Figure 10. Comparison of relative errors.

Observed by the vibration velocity in all directions, when the value of α is large, the vibration velocity of the particle will rapidly decrease with increasing horizontal distance. In addition, the more negative the value of β is and the smaller the value is, the more obvious the amplification effect. The calculation results show that the improved formula considers the elevation factor and slope factor, and its error is smaller than that of the original model, which is closer to the actual situation. In a multilevel slope, in addition to considering the influence of factors such as rock properties, blast center distance, explosive quantity and elevation on the blasting mining results, the slope shape of different steps would also have a certain degree of influence on the blasting results. Therefore, before blasting mining, we need to more accurately assess the blasting strength of the explosive for a blasting method.

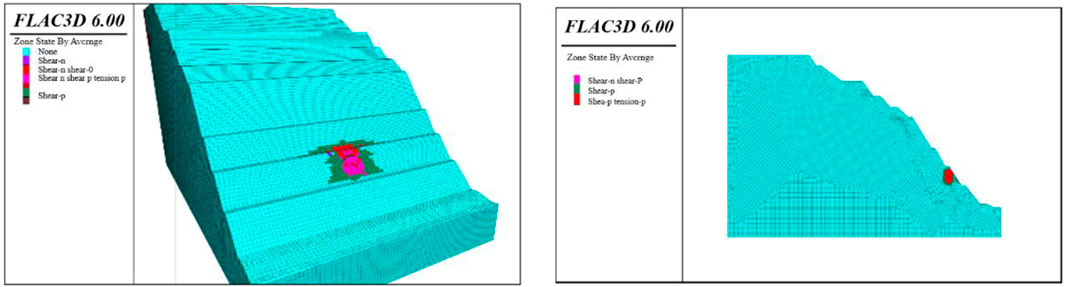
In Figure 11, the numerical simulation results after multiple strength reductions on the model indicate that the surface of the slope exhibits a potential sliding surface in the form of arc-shaped failure. The simulation results are shown in Figure 12, with a safety factor of 1.332, a reduction of approximately 10% compared to the pre-sandblasting period. The reduction in the safety factor signifies a weakening of slope stability. However, the slope’s safety factor remains above 1.2, meeting the needed safety margin. The plastic zone is distributed mainly around the blast source, and no continuous plastic zone appears above the slope. This finding suggests an overall stabilizing trend in the slope’s condition. The numerical simulation results after slope blasting provide crucial insights for assessing slope stability.

Figure 11

Figure 11. Distribution of plastic zones after blasting.

Figure 12

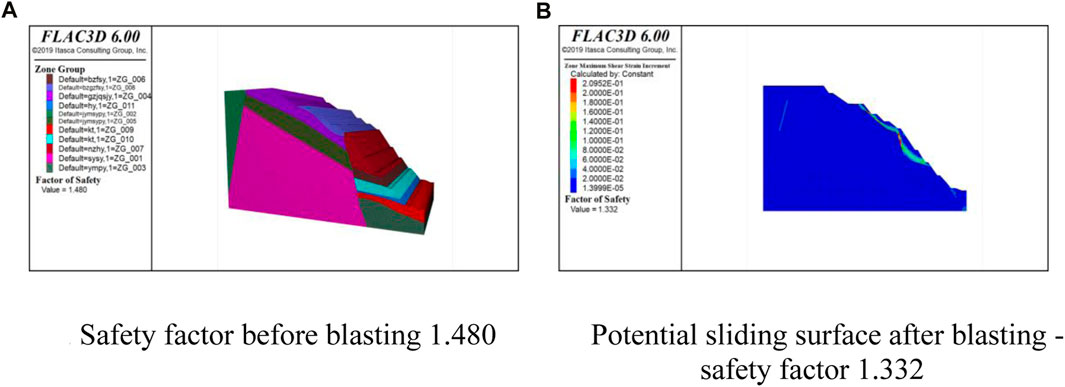
Figure 12. Safety factor before and after blasting. (A)Safety factor before blasting 1.480 (B)Potential sliding surface after blasting—safety factor 1.332.

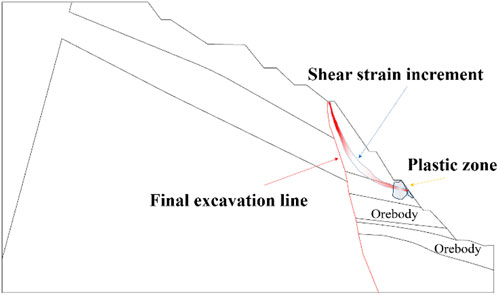
The blasting simulation results indicate the formation of plastic zones and potential sliding surfaces predominantly within the excavation and stripping area needed for this project. In Figure 13, the red solid line represents the final slope excavation line, with ore bodies and other features located to the right of the excavation line, i.e., in the construction-ready area. The distribution of sliding surfaces and plastic zones is centered in the construction-ready area, positively impacting the project plan and suggesting that a moderate level of geological disturbance has occurred in the excavation zone. This phenomenon creates more favorable geological conditions for construction in the subsequent excavation and stripping processes. In contrast, no potential distribution of sliding surfaces and plastic zones has been observed on the left and upper slopes of the excavation line. This result indicates that the geological conditions in these areas are relatively stable, with no signs of moderate disruption, providing a more controlled environment for the project. Overall, the observed moderate geological disturbance in the construction-ready area lays a solid foundation for subsequent construction, ensuring stability during the excavation and stripping processes and contributing to the planning and execution of the subsequent construction phases.

Figure 13

Figure 13. Schematic of the slope state after blasting Additional Requirements.

5 Conclusion

Based on the numerical simulation results and analysis of this study, the following conclusion can be drawn.

1) By introducing the slope influence factor, there is only a relative error of approximately 10% between the calculation results and the peak vibration speed of the on-site monitoring data. Compared with the calculation results without the introduction of the slope influence factor, it is closer to the particle vibration speed attenuation law of the on-site monitoring data.

2) The time-history characteristics of blasting vibration simulated by triangular pulse load can approximate the actual explosion vibration. Numerical simulation results show that the action range of blasting vibration seismic waves is concentrated on the upper slope where the load is applied and has obvious directionality.

3) The numerical simulation results show some deviation from the field monitoring data in terms of peak vibration velocity. However, the overall accuracy still falls within an acceptable range, providing a significant reference for slope stability assessment. The presence of a potential sliding surface in the slope after the blasting simulation is observed. Nevertheless, the safety factor of the slope remains above 1.2, satisfying the safety factor requirement. The plastic zones are concentrated in the excavation and stripping area needed for this project, while no continuous plastic zone is observed above the slope.

In conclusion, the numerical simulation results of this study validate the accuracy of incorporating the slope factor, which is significant for assessing the stability of open pit mine slopes under blasting-induced vibrations. Future research can consider integrating more field monitoring data and complex vibration propagation models, considering the influence of internal joints and fractures in the rock mass, and embedding the discontinuous nature of the rock mass in the numerical simulations, in order to optimise the blast design and ensure the stability of the slope and the safety of the engineering project.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XW: Investigation, Methodology, Writing–original draft, Writing–review and editing. DZ: Writing–review and editing. HL: Data curation, Writing–original draft. LL: Data curation, Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, P., Yong, R., Song, J., Du, S., Wang, C., Xu, H., et al. (2024). Exploring the potential of smartphone photogrammetry for field measurement of joint roughness. Measurement 225, 114055. doi:10.1016/j.measurement.2023.114055

CrossRef Full Text | Google Scholar

Azarfar, B., Ahmadvand, S., Sattarvand, J., and Abbasi, B. (2019). Stability analysis of rock structure in large slopes and open-pit mine: numerical and experimental fault modeling. Rock Mech. Rock Eng. 52, 4889–4905. doi:10.1007/s00603-019-01915-4

CrossRef Full Text | Google Scholar

Bai, R., Zhang, P., Zhang, Z., Sun, X., Fei, H., Bao, S., et al. (2023). Optimization of blasting parameters and prediction of vibration effects in open pit mines based on deep neural networks. Alexandria Eng. J. 70, 261–271. doi:10.1016/j.aej.2023.02.043

CrossRef Full Text | Google Scholar

Bui, X.-N., Nguyen, H., Tran, Q.-H., Nguyen, D.-A., and Bui, H.-B. (2021). Predicting ground vibrations due to mine blasting using a novel artificial neural network-based cuckoo search optimization. Nat. Resour. Res. 30, 2663–2685. doi:10.1007/s11053-021-09823-7

CrossRef Full Text | Google Scholar

Cao, H., Ma, G., Liu, P., Qin, X., Wu, C., and Lu, J. (2023). Multi-factor analysis on the stability of high slopes in open-pit mines. Appl. Sci. 13, 5940. doi:10.3390/app13105940

CrossRef Full Text | Google Scholar

Cao, L., Wang, Z., and Wang, D. (2018). Law of blasting vibration damage and stability analysis to slope in open-pit mine. China Saf. Sci. J. doi:10.16265/j.cnki.issn1003-3033.2018.02.013

CrossRef Full Text | Google Scholar

Chen, M., Lu, W., Li, P., Liu, M., Zhou, C., and Zhao, G. (2011). Elevation amplification effect of blasting vibration velocity in rock slope. Chin. J. Rock Mech. Eng. 30, 2189–2195.

Google Scholar

Chen, S. G., Zhao, J., and Zhou, Y. X. (2000). UDEC modeling of a field explosion test. Fragblast 4, 149–163. doi:10.1076/frag.4.2.149.7451

CrossRef Full Text | Google Scholar

Dehghan, A. N., and Khodaei, M. (2022). Stability analysis and optimal design of ultimate slope of an open pit mine: a case study. Geotechnical Geol. Eng. 40, 1789–1808. doi:10.1007/s10706-021-01993-8

CrossRef Full Text | Google Scholar

Dindarloo, S. R. (2015). Prediction of blast-induced ground vibrations via genetic programming. Int. J. Min. Sci. Technol. 25, 1011–1015. doi:10.1016/j.ijmst.2015.09.020

CrossRef Full Text | Google Scholar

Hu, G., and Wu, Y. (2004). A new method of the control of the earthquake vibration caused by explosive. Coal Technol., 104–106.

Google Scholar

Jiang, N., Zhou, C., Lu, S., and Zhang, Z. (2018). Effect of underground mine blast vibrations on overlaying open pit slopes: a case study for daye iron mine in China. Geotechnical Geol. Eng. 36, 1475–1489. doi:10.1007/s10706-017-0402-x

CrossRef Full Text | Google Scholar

Kang, K., Fomenko, I. K., Wang, J., and Nikolskaya, O. V. (2020). PROBABILISTIC ASSESSMENT OF ROCK SLOPE STABILITY IN OPEN PIT MINE CHAARAT USING THE GENERALIZED HOEK–BROWN CRITERION. J. Min. Sci. 56, 732–740. doi:10.1134/S1062739120057068

CrossRef Full Text | Google Scholar

Kuhlemeyer, R. L., and John, L. (1973). Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 99, 421–427. doi:10.1061/JSFEAQ.0001885

CrossRef Full Text | Google Scholar

Li, X., Hu, H., He, L., and Li, K. (2017). An analytical study of blasting vibration using deep mining and drivage rules. Clust. Comput. 20, 109–120. doi:10.1007/s10586-017-0736-4

CrossRef Full Text | Google Scholar

Li, X., Li, Q., Hu, Y., Chen, Q., Peng, J., Xie, Y., et al. (2022). Study on three-dimensional dynamic stability of open-pit high slope under blasting vibration. Lithosphere 2021, 6426550. doi:10.2113/2022/6426550

CrossRef Full Text | Google Scholar

Li, X., Zhu, R., Zhu, W., Hu, Y., and Li, H. (1997). IN-SITU TESTING STUDY OF PROTECTIVE LAYER FOR BLASTING VIBRATION REDUCTION UNDER COMPLEX ENVIRONM ENT. Chin. J. Rock Mech. Eng., 584–589.

Google Scholar

Liu, C., Wang, F., Ren, Q., Chen, B., Jin, H., Cui, S., et al. (2023). Field test of blasting vibration and adjacent slope stability under the influence of blasting vibration in mining. J. vibroeng. 25, 713–728. doi:10.21595/jve.2022.22826

CrossRef Full Text | Google Scholar

Ma, L., Li, K., Xiao, S., Ding, X., and Chinyanta, S. (2016). Research on effects of blast casting vibration and vibration absorption of presplitting blasting in open cast mine. Shock Vib. 2016, 1–9. doi:10.1155/2016/4091732

CrossRef Full Text | Google Scholar

Moszynski, J. R. (1983). The dynamics of explosion and its use. Nucl. Technol. 60, 167. doi:10.13182/NT83-A33116

CrossRef Full Text | Google Scholar

Nguyen, H., Bui, X.-N., Tran, Q.-H., and Moayedi, H. (2019). Predicting blast-induced peak particle velocity using BGAMs, ANN and SVM: a case study at the Nui Beo open-pit coal mine in Vietnam. Environ. Earth Sci. 78, 479. doi:10.1007/s12665-019-8491-x

CrossRef Full Text | Google Scholar

Shafiei Ganjeh, R., Memarian, H., Khosravi, M. H., and Mojarab, M. (2019). A comparison between effects of earthquake and blasting on stability of mine slopes: a case study of Chadormalu open-pit mine. J. Min. Environ. 10, 223–240. doi:10.22044/jme.2019.7535.1607

CrossRef Full Text | Google Scholar

Singh, P. K., and Roy, M. P. (2008). Damage to surface structures due to underground coal mine blasting: apprehension or real cause? Environ. Geol. 53, 1201–1211. doi:10.1007/s00254-007-0709-7

CrossRef Full Text | Google Scholar

Soren, K. (2014). STABILITY ANALYSIS OF OPEN PIT SLOPE BY FINITE DIFFERENCE METHOD. Int. J. Res. Eng. Technol. 03, 326–334. doi:10.15623/ijret.2014.0305062

CrossRef Full Text | Google Scholar

Su, H., and Ma, S. (2022). Study on the stability of high and steep slopes under deep bench blasting vibration in open-pit mines. Front. Earth Sci. 10. doi:10.3389/feart.2022.990012

CrossRef Full Text | Google Scholar

Wang, C., Yong, R., Luo, Z., Du, S., Karakus, M., and Huang, C. (2023). A novel method for determining the three-dimensional roughness of rock joints based on profile slices. Rock Mech. Rock Eng. 56, 4303–4327. doi:10.1007/s00603-023-03274-7

CrossRef Full Text | Google Scholar

Wang, M., Li, X., Li, Q., Hu, Y., Chen, Q., and Jiang, S. (2021). Study on blasting Technology for open-pit layering of complex mine adjacent to high and steep slope. Front. Earth Sci. 9. doi:10.3389/feart.2021.773872

CrossRef Full Text | Google Scholar

Wang, Z., and Lu, W. (1994). Vibration propagation law and quality control of high slope blasting excavation. Blasting, 1–4.

Google Scholar

Wang, Z., Wu, G., and Zhou, L. (2022). Optimization of pre-splitting blasting hole network parameters and engineering applications in open pit mine. Appl. Sci. 12, 4930. doi:10.3390/app12104930

CrossRef Full Text | Google Scholar

Xia, X., Li, J., Li, H., Liu, Y., and Zhou, Q. (2005). Udec modeling of vibration characteristics of jointed rock mass under explosion. Rock Soil Mech., 50–56. doi:10.16285/j.rsm.2005.01.012

CrossRef Full Text | Google Scholar

Xu, G., and Wang, X. (2023). Support vector regression optimized by black widow optimization algorithm combining with feature selection by MARS for mining blast vibration prediction. Measurement 218, 113106. doi:10.1016/j.measurement.2023.113106

CrossRef Full Text | Google Scholar

Yan, B., Liu, M., Meng, Q., Li, Y., Deng, S., and Liu, T. (2022). Study on the vibration variation of rock slope based on numerical simulation and fitting analysis. Appl. Sci. 12, 4208. doi:10.3390/app12094208

CrossRef Full Text | Google Scholar

Yang, Y., Ding, X., Zhou, W., Lu, X., Ebelia, M., An, W., et al. (2022). Open-pit mine geological model construction and composite rock blasting optimization research. Shock Vib. 2022, 1–9. doi:10.1155/2022/1468388

CrossRef Full Text | Google Scholar

Yin, Z., Wang, D., Wang, X., Dang, Z., and Li, W. (2021). Optimization and application of spacing parameter for loosening blasting with 24-m-High bench in barun open-pit mine. Shock Vib. 2021, 1–13. doi:10.1155/2021/6670276

CrossRef Full Text | Google Scholar

Yong, R., Wang, C., Barton, N., and Du, S. (2024). A photogrammetric approach for quantifying the evolution of rock joint void geometry under varying contact states. Int. J. Min. Sci. Technol. doi:10.1016/j.ijmst.2024.04.001

CrossRef Full Text | Google Scholar

Zhang, X., Nguyen, H., Choi, Y., Bui, X.-N., and Zhou, J. (2021). Novel extreme learning machine-multi-verse optimization model for predicting peak particle velocity induced by mine blasting. Nat. Resour. Res. 30, 4735–4751. doi:10.1007/s11053-021-09960-z

CrossRef Full Text | Google Scholar