NESZ effects on wind retrievals from Gaofen-3 SAR wave mode data

This study analyzes the effects of noise equivalent sigma zero (NESZ) on wind retrieval accuracy based on the estimated NESZ and wind retrievals from Gaofen-3 (GF3) synthetic aperture radar (SAR) wave mode data. The NESZ was estimated from the normalized radar cross-section (NRCS) bottom envelope from the calm sea (winds <1 m/s). The data used included GF3 SAR wave mode data, collocated NOAA/NCEP Global Forecast System (GFS), Advanced Scatterometer (ASCAT) and National Data Buoy Center (NDBC) buoy wind data. First, the GF3 data were recalibrated using a numerical weather prediction method in which the recalibration coefficients at four polarizations and different incidence angles were estimated. The NESZ trends were then estimated along with the in-orbit time and incidence angles based on the recalibrated GF3 NRCS. NESZ trends show no obvious change with in-orbit time, whereas it shows significant fluctuations with the incidence angle. Moreover, wind speed and direction were retrieved by the CMOD5.N model using the optimal scheme (for co-polarized data, VV, and HH data) and a linear model (for cross-polarized data, VH, and HV data). The wind retrieval accuracy was estimated by comparison with ASCAT and NDBC winds. Finally, the wind retrieval accuracy with the NESZ for different incidence angle bins was analyzed. The root mean square error (RMSE) of the wind speed and direction increase with the NESZ for each polarization. For the NESZ effects, the co-polarized data are more evident than the cross-polarized data for wind speed retrieval, whereas the two co-polarized data are close for wind direction retrieval. When the NESZ increases from −41 dB to −29 dB, there is a wind speed RMSE degradation of 1.5 m/s, 1.2 m/s, 0.7 m/s and 0.5 m/s for VV-, HH-, VH-, and HV-polarized data respectively, while there is a wind direction RMSE degradation of 5^o for co-polarized data. This reveals the necessity of reducing the SAR NESZ to improve wind retrieval accuracy.

1 Introduction

The sea surface wind field is an important dynamic environmental parameter of the ocean that can be measured using multiple radars, such as synthetic aperture radar (SAR) and scatterometers, based on interactions between radar signals and ocean surface capillary waves (Valenzuela, 1978). Owing to the high spatial resolution in an azimuth, SAR can derive fine sea surface wind fields reaching levels up to hundreds of meters. Considerable research has been conducted on SAR wind retrieval. Usually, a geophysical model function (GMF) is used to retrieve the wind field from calibrated SAR data. The GMF relates the wind data to the SAR-measured normalized radar cross-section (NRCS), which can be developed empirically using scattermeters or SAR data and collocated true winds. Here the NRCS is defined as the radar cross-section normalized by a reference area, which allows for the comparison of radar performance across different targets and conditions. For C-band SAR, common GMFs include CMOD4 (Stoffelen and Anderson, 1997), CMOD_IFR2 (Quilfen et al., 1998), CMOD5 (Hersbach et al., 2007), CMOD5.N (Hersbach, 2008), etc. Once the SAR NRCS is determined for a certain sea area, the corresponding wind field can be estimated by solving GMFs.

Methods for improving the accuracy of SAR wind products have long been a research focus in the field of marine microwave remote sensing. Four factors are considered to primarily affect the accuracy of wind field retrieval. The first is radiometric calibration accuracy. The calibration process transfers the radar voltage signal to the NRCS, and the calibration coefficient is generally considered constant for the determined incidence angle, polarization, and system gain. Active transponders and corner reflectors are commonly used for calibration (Chen et al., 2018), and the NWP method has gained increasing attention in recent years owing to its convenience and low cost (Horstmann and Lehner, 2002; Verspeek et al., 2012; Verspeek et al., 2010; Mu and Song, 2014). The second factor is GMF accuracy, which is related to the model structure and accuracy of the data samples. GMFs have been continuously improved in terms of C-band GMF family evolution (Stoffelen and Anderson, 1997; Quilfen et al., 1998; Hersbach et al., 2007; Hersbach, 2008). The third factor is retrieval algorithm effectiveness. The wind direction was determined for the latter experiment. Some methods directly substitute model wind into the GMF to estimate wind speed (Monaldo et al., 2001; Vogelzang et al., 2009; Bergeron et al., 2011; Monaldo, 2000; Beaucage et al., 2007), whereas an optimal algorithm solves for wind speed and direction simultaneously based on a cost function that includes model wind and SAR data (Portabella et al., 2002; Kerbaol, 2007). The fourth factor is the NESZ effect. NESZ is the noise floor of NRCS measurements that can describe noise intensity. Noise characteristics are determined by the radar system design (Vachon and Wolfe, 2011; Scheuchl and Cumming, 2005; Ren et al., 2017; Mouche and Chapron, 2015; Shi et al., 2020). Suppose that noise is a random signal with mean and variance. Here, the mean noise can induce a bias in the original NRCS, whereas the variance can induce a fluctuation. Note that bias can be removed during the calibration process, whereas the effects of fluctuations remain in the final retrievals.

Previous studies on SAR NESZ analyses have employed RADARSAT-2 and ENVISAT SAR quad-polarization products to directly yield NESZ information. Using these data, Vachon et al. (Vachon and Wolfe, 2011) compared the NESZ values for different polarizations. The comparisons show that the NESZ increases with the incidence angle but is independent of the wind speed. Moreover, the NESZ increment with the incidence angle is more obvious for cross-polarization than for co-polarization. Scheuchl et al. (Scheuchl and Cumming, 2005) compared the NESZ of data from different sea ice regions based on ENVISAT SAR dual-polarization data from 31° to 34.5° and analyzed the effect of NESZ changes on sea ice characteristics at different polarizations. It was found that the variation range of NESZ of VV-polarized data is from −18.47 dB to −9.28 dB, while the variation range of NESZ of VH-polarized data is from −23.89 dB to −18.48 dB. The NESZ of the VH-polarized data is significantly smaller than that of the VV-polarized data.

However, some SAR data products cannot provide the NESZ. To account for this, two methods have been proposed to estimate the SAR NESZ. The first method estimates the NESZ using the NRCS at very low winds with respect to Gaofen-3 (GF3) SAR QPSI and QPSII mode data (Ren et al., 2017; Mouche and Chapron, 2015). The bottom envelope of the NRCS was considered the NESZ. This estimate showed that the NESZ at four polarizations (VV, HH, VH, and HV) was approximately −33, −33, −37, and −37 dB. The co-polarized data produced identical NESZ values, and the NESZ for the cross-polarized data was also the same. The second method estimated the NESZ using a reciprocity-based minimum noise envelope estimator with respect to the same-mode GF3 data (Shi et al., 2020). This estimator presumed that the HV and VH polarimetric responses of targets are identical and considers the difference between VH and HV to be NESZ. From the estimated GF3 NESZ, they found that GF3 had a better noise control performance than RADARSAT-2 at most elevation angles. There have been some studies on NESZ estimation and analysis, but studies on the effects of NESZ on wind retrieval are still rare.

GF3, launched on 10 August 2016, was the first Chinese C-band multipolarization civil SAR and has a large coverage, fine scale, multiple modes, and quad-polarization (Sun et al., 2017). In recent years, many studies using GF3 data have been conducted in the field of ocean remote sensing, including wind and wave retrieval (Ren et al., 2019; Wang et al., 2019; Li et al., 2018; Wang et al., 2017; Shao et al., 2017). It is noteworthy that many new data features require further exploration. The primary design task for the GF3 wave mode is to observe global waves, and wave mode data have been found to be suitable for retrieving wind fields. Wang et al. (Wang et al., 2019) recalibrated the GF3 wave mode data with an incidence angle of 40.01° by using the NWP method. The wind speed was then retrieved from the recalibrated HH polarization data. By the recalibration, the bias and root mean square error (RMSE) of the retrieved wind speed decreases by 0.83 m/s and 0.49 m/s, respectively, compared with the collocated HY-2A SCAT wind data. This study revealed the feasibility of using GF3 wave mode data for wind retrieval. However, the data at incidence angles other than 40.01° have not yet been recalibrated. In addition, the NESZ estimation and its effects on GF3 wind retrievals were not considered.

Numerous studies have focused on the first three factors (calibration, GMF, and retrieval algorithms) affecting wind retrieval accuracy. However, the NESZ estimation and analysis of the SAR data requires further supplementation. In particular, studies on the effects of the NESZ on wind retrieval accuracy have rarely been conducted. Therefore, this study aims to analyze the effects of the NESZ on the wind retrieval accuracy for GF3 SAR wave mode data. To achieve this goal, GF3 data were recalibrated to derive an accurate NRCS using the NWP method. Using the recalibrated data, the NESZ was estimated, and the wind speed and direction were retrieved using the corresponding algorithm to provide data for analysis.

2 Data

The data used in this study included GF3 SAR wave mode data (Wang et al., 2019), NOAA/NCEP Global Forecast System (GFS) winds (Ren et al., 2019), Advanced Scatterometer (ASCAT) winds (Yang et al., 2011), National Data Buoy Center (NDBC) buoy winds (Monaldo et al., 2001), and Earth Topography 1 Arc-Minute Global Relief Model (ETOPO1) digital elevation (Amante and Eakins, 2009). Level-1A (L1A) GF3 data were collected from January 2017 to October 2018 and included approximately 18,970 images. The GF3 SAR operates in the C band (approximately 5.3 GHz) and revolves around the Earth at an altitude of 755 km in a sun-collocated orbit, with an orbital repetition period of approximately 29 days. Among the 12 imaging modes of the GF3 sensor, the wave mode provides 5 km × 5 km images at intervals of 50 km along the orbit, with a resolution of about 2.3 m (range) × 5.2 m (azimuth) and a quad-polarization (VV + HH + VH + HV) configuration. To remove the speckle noise, wave mode data were filtered by averaging data in a box of 1 km × 1 km before retrieval processing. The main task of wave mode data is to measure ocean waves. But it can also observe high-resolution NRCS of the sea surface, which make it have the ability of measuring sea surface winds. To directly use the mature GMFs established by previous researchers, this study adopted a recalibration method to remove the bias between data and GMFs. Although the incidence angle of the GF3 wave mode is designed to switch from 20° to 50°, most GF3 wave mode data are located at middle incidence angles. In this study, the incidence angles ranges from 28° to 49°. Figure 1 shows the data location map. The data are mainly geographically distributed in the Pacific Ocean, and small amounts of data are distributed in the Atlantic and Indian Oceans.

Figure 1

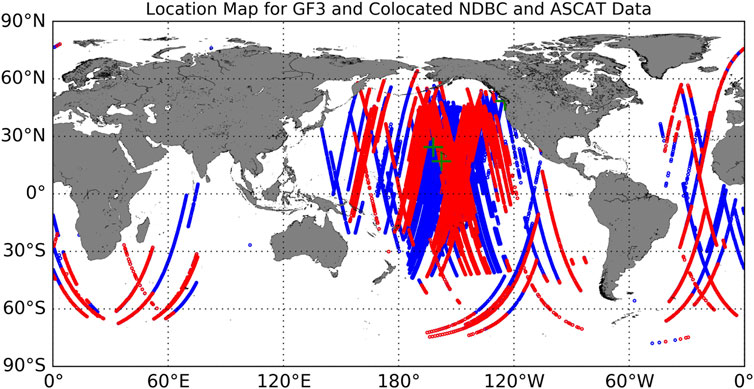
Figure 1. Data location map. The blue circles indicate the GF3 SAR wave mode data, the red circles indicate the collocated ASCAT scatterometer wind data, and the green plus signs indicate the collocated NDBC buoy wind data.

Three types of collocated wind data (GFS, ASCAT and NDBC winds) were used in this study. GFS winds (Ren et al., 2019) are obtained from reanalysis model data and have a spatial resolution of 0.75°×0.75° and a time resolution of 6 h. ASCAT winds are measured using a scatterometer on the Metop A and B satellites with a standard spatial resolution of 25 km × 25 km (Yang et al., 2011). This provides high-quality wind-field products with wide swaths. The NDBC winds are measured in situ by buoy. The GFS wind accuracy is lower than those of the scatterometer and buoy data. However, the GFS wind data are a type of global grid data; thus, they can be matched with the GF3 wave mode data to obtain a large amount of collocated data to determine the true wind field trend. The trend from the GFS wind data was used to recalibrate the NRCS bias in this study. Meanwhile, compared to GFS wind data, the ASCAT and NDBC winds are more accurate, although it has fewer collocations with the GF3 data. For this purpose, ASCAT and NDBC wind data were used to validate the wind retrievals. The time difference for the collocation standard between ASCAT and GF3 is less than 3 h, and the spatial difference of the central locations is less than 12.5 km. For NDBC data, the time and spatial collocation standard is 0.5 h and 10 km respectively. Here the spatial difference was calculated using the latitude and longitude of two locations by the Vincent’s formula (Vincenty, 1975). Moreover, the scatterometer data are not suitable for observation near to the coast. For that, only the data with ETOPO1 water depths less than −50 m were used for avoiding the contamination from land.

3 NESZ estimation

3.1 Recalibration

Radiometric calibration of SAR data is a prerequisite for ensuring the accuracy of the SAR NRCS. GF3 wave mode data are calibrated at the manpower calibration site. The L1A NRCS at different polarization channels can be calibrated using the following formula in Equations 1, 2:

${\mathrm{\sigma }}^0=10{\log }_{10}\text{DN}–\mathrm{K}(1)$

$DN=\left(I^2+Q^2\right)\times {\left(qv/32767\right)}^2(2)$

where σ⁰ is the NRCS in dB, DN represents the intensity, K is the calibration coefficient, I represents the real part of the L1A data, Q represents the imaginary part of the L1A data, qv represents the maximum qualified value stored in the product comment file according to the polarization. Generally, K varies only with the incidence angle and polarization.

However, according to previous studies, there is some calibration bias for the GF3 wave mode data (Wang et al., 2019). Considering that routine calibration activities on land sites usually incur huge costs, this study adopted the NWP method to recalibrate the data, which has been widely used in the calibration of marine microwave remote sensing satellites. This method is briefly described as follows: First, the measured GF3 wave mode NRCS was obtained using the original radiometric calibration method at four polarizations. Second, based on GFS wind data, the simulated NRCS was obtained using the GMF models at different polarizations. Then, the bias between the measured GF3 NRCS and the simulated NRCS was estimated by Equation 3, which is called the recalibration coefficient $K_{recal}$.

$K_{recal}={\sigma }_m^0-{\sigma }_s^0(3)$

where ${\sigma }_m^0$ is the original GF3 NRCS and ${\sigma }_s^0$ is the simulated NRCS based on GMF and GFS winds. Using the recalibration coefficient, the NRCS can be recalibrated in Equation 4 as

${\sigma }_{recal}^0={\sigma }_m^0-K_{recal}(4)$

where ${\sigma }_{recal}^0$ is the recalibrated NRCS.

Figure 2 shows the accuracy of the recalibrated NRCS at 40.5^o incidence angle using the NWP method, which was estimated by comparing the measured GF3 NRCS against the simulated NRCS from the GMF and GFS winds. Here the used GMFs at VV, HH, VH and HV are described in the following text (Section 4.1). Wind speeds greater than 5 m/s were used to ensure a stable wind field and a strong NRCS, thus helping relieve interference from noise. Figures 2A–D show the comparisons before recalibration for the VV, HH, VH, and HV polarizations, while Figures 2E–H show similar comparisons after recalibration.

Figure 2

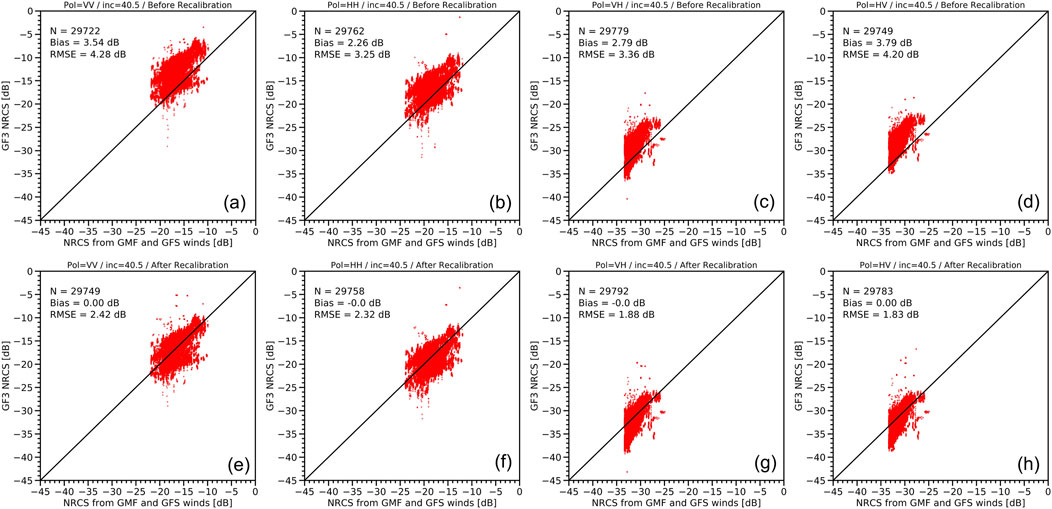
Figure 2. Scatterplots of measured GF3 NRCS against simulated NRCS from GMF and GFS winds at four polarizations. The first line indicates the data before recalibration, while the second line is the data after recalibration. These GF3 NRCS data were measured at the same incidence angle of 40.5° with a bin of 1° for (A) VV polarization and before recalibration, (B) HH polarization and before recalibration, (C) VH polarization and before recalibration, (D) HV polarization and before recalibration, (E) VV polarization and after recalibration, (F) HH polarization and after recalibration, (G) VH polarization and after recalibration, and (H) HV polarization and after recalibration.

Before calibration, the biases of the GF3 NRCS are 3.54, 2.26, 2.79, and 3.79 dB, while the RMSE is 4.28, 3.25, 3.36, and 4.2 dB. After calibration, all biases are less than 0.1 dB, and the RMSE is 2.42, 2.32, 1.88, and 1.83 dB. In contrast, the recalibration process significantly improves the accuracy of GF3 NRCS.

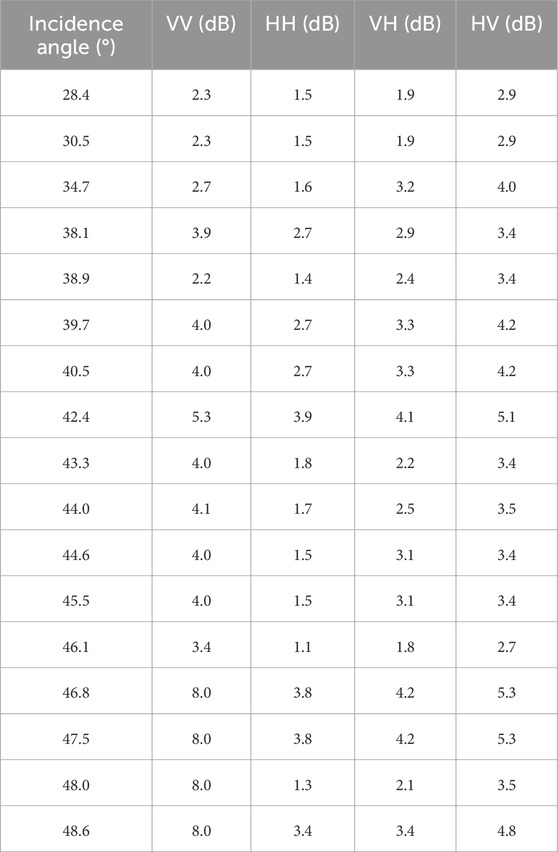
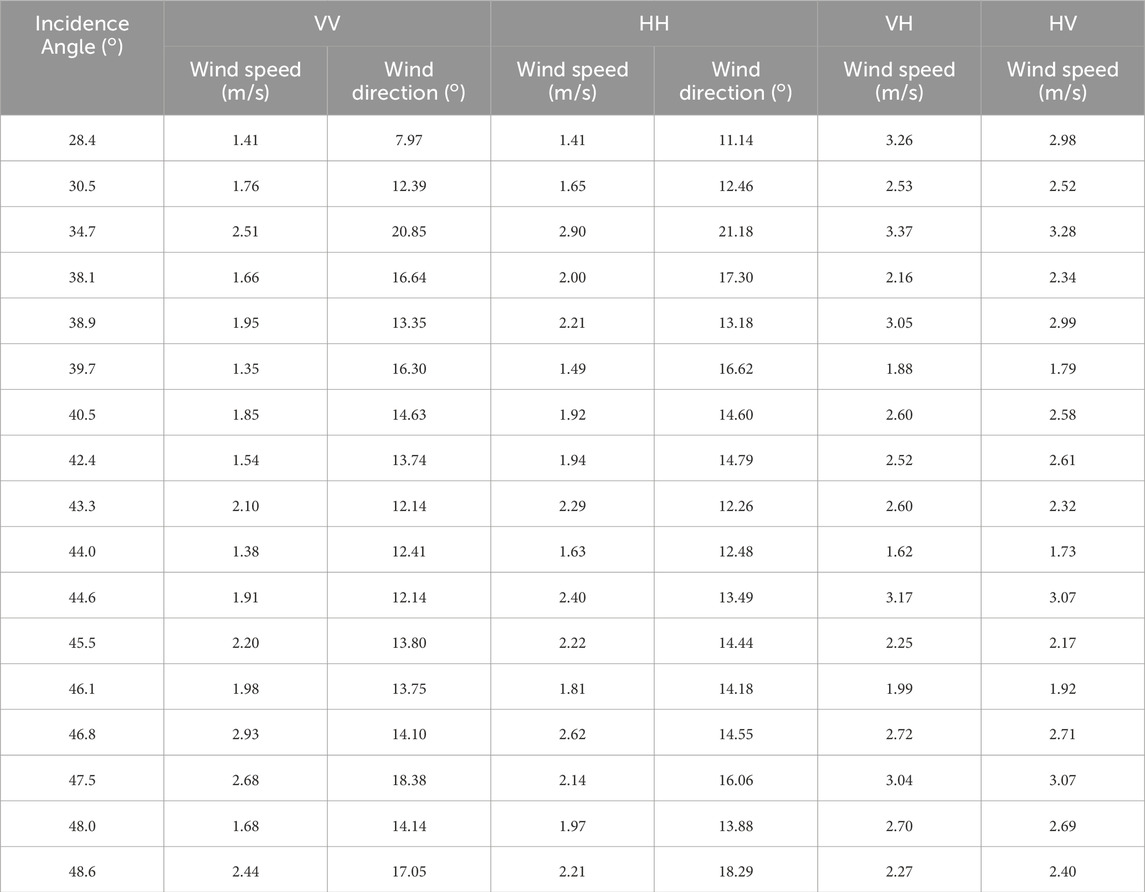
The recalibration coefficients of the GF3 wave mode data at each incidence angle bin were estimated using the same method, as shown in Figure 2. Table 1 presents the estimated coefficients. Considering the actual distribution of the incidence angles, 17 incidence angle bins were chosen intermittently and not continuously. The distribution of incidence angle bins can be found in the Table 1.

Table 1

Table 1. Recalibrated coefficients for GF3 wave mode data.

3.2 Estimating NESZ trend with in-orbit time

Based on the recalibrated GF3 NRCS, we estimated the NESZ using the GF3 NRCS under calm sea conditions (winds <1 m/s). Here we assume that sea surface wind speed is the main trigger of NRCS changes, after averaging the NRCS modulation from ocean waves. When the wind speed on the sea surface is very low, the contribution from wind speed to NRCS will approach zero. So the NRCS in the absence of noise should also approach zero. In this case, the still existing NRCS under calm sea conditions is considered as the NESZ for a certain incidence angle bin. By plotting a large amount of data, the bottom envelope of the measured NRCS, referred to as the NESZ, can be determined. This study aims to analyze the effects of the NESZ on wind retrieval accuracy. The estimated NESZ is expected to change according to the measurement conditions. We considered that the noise of the SAR system likely increased with the in-orbit time of the satellite, owing to the aging of the equipment. However, the NESZ may also vary with the incidence angle, owing to differences in the antenna beam gain. For this purpose, the NESZ with in-orbit time and incidence angle was estimated.

The estimated NESZ trends with in-orbit time (from January 2017 to October 2018) at the four polarizations are plotted in Figure 3. Owing to the discontinuity of the satellite operating time, only the data at 40.5^o can span a long time based on the statistics of the collected data. The nearer date spanned March 2017, whereas the longer date spanned April 2018. Thus, the estimated NESZ at 40.5^o for these two dates was used to analyze the NESZ variation with in-orbit time.

Figure 3

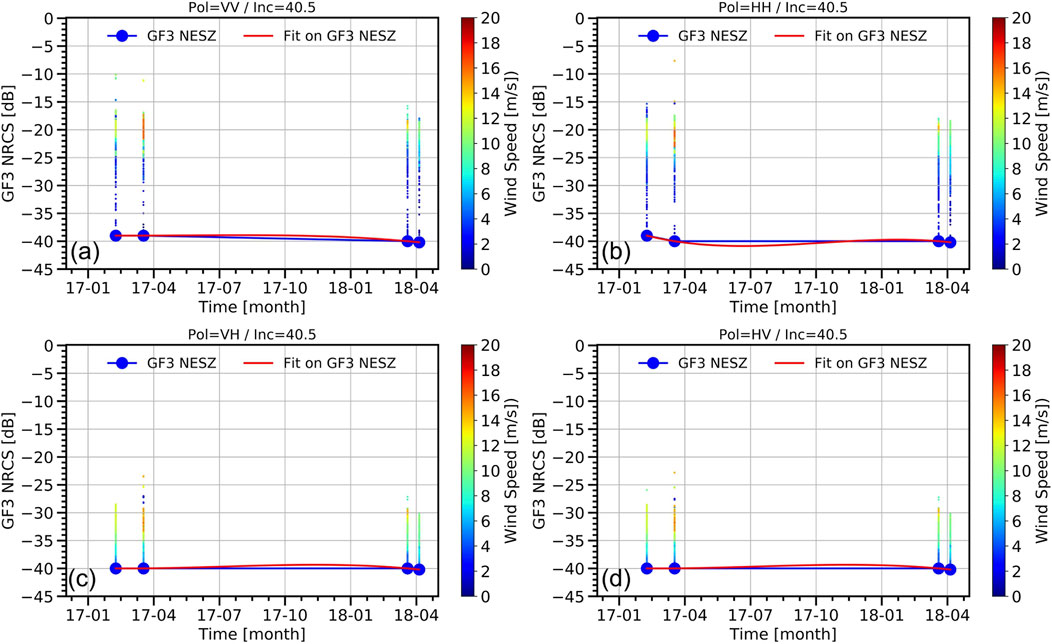
Figure 3. Estimated NESZ trends with in-orbit time for GF3 wave mode data for (A) VV, (B) HH, (C) VH, and (D) HV polarization.

The NESZ trends for the four polarizations show consistent characteristics. First, all NESZ are approximately −40 dB. More importantly, all NESZ remain unchanged for approximately 1 year. The NESZ shows no significant change over the in-orbit time, which may indicate that the quality of the GF3 data is relatively stable. It should be noted that the unchanged NESZ trend with in-orbit time is not sufficient for analyzing its effects on wind retrievals.

3.3 Estimating NESZ trend with incidence angle

Figure 4 shows the estimated NESZ trends with the incidence angles for the four polarizations. The incidence angles used are from 28° to 49° and intermittent rather than continuous, owing to the observation configuration. For each polarization, the NESZ varies with the incidence angle and exhibited a shape close to a sine function. The troughs are located at 28°, 40°, and 48°.

Figure 4

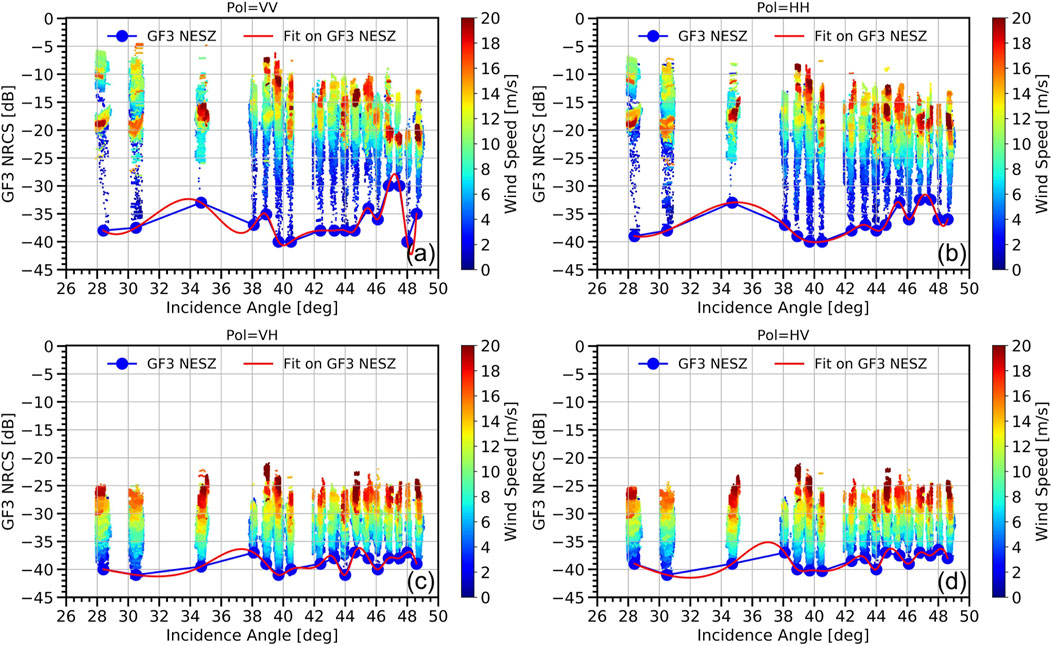
Figure 4. Estimated NESZ trends with incidence angle for GF3 wave mode data for (A) VV, (B) HH, (C) VH, and (D) HV polarization.

Figure 5 compares the differences observed in NESZ trends for four polarizations. The comparisons reveal that the NESZ for the co-polarized NRCS is clearly higher than that for the cross-polarized NRCS for most incidence angles, whereas it is comparable at around 40^o incidence angle. In addition, both the co-polarized (VV and HH) NESZ and the two cross-polarized (VH and HV) NESZ exhibit similar trends. Considering the NESZ variation, its trend with the incidence angle is suitable for analyzing the NESZ effects on wind retrievals.

Figure 5

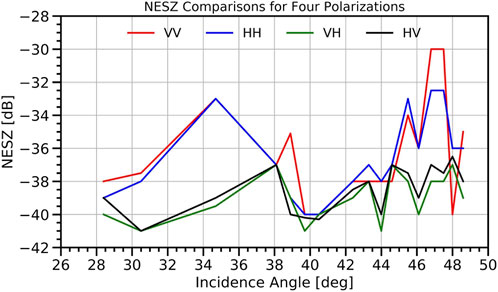
Figure 5. Comparisons of estimated NESZ trends with incidence angles for GF3 wave mode data for four polarizations.

4 Wind retrieval

4.1 GMFs

As mentioned previously, GMFs relate the NRCS measurements to the wind vector. Based on this relationship, GMFs were used to simulate the NRCS from a given GFS wind vector during the recalibration process and, in reverse, to retrieve the wind vector from the measured NRCS. The GMFs used for different polarizations are briefly described below.

For VV-polarized data, the GMF is commonly expressed as nonlinear second-order cosine function in Equation 5 (Stoffelen and Anderson, 1997; Quilfen et al., 1998; Hersbach et al., 2007; Hersbach, 2008):

${\sigma }^0\left(u_{10}\right)=a_0{\left(1+a_1\mathit{cos}\phi +a_2\mathit{cos}2\phi \right)}^p(5)$

where σ⁰ is the NRCS, u₁₀ is the wind speed at 10 m above the sea surface, φ is the wind direction relative to the radar line of sight, the variables a₀, a₁, a₂, and p are the coefficients of the model. For GF3 SAR data, preliminary studies have shown that CMOD5.N can accurately describe quad-polarization mode VV-polarized data (Ren et al., 2017). Therefore, CMOD5.N was also used as the GMF for the GF3 wave mode VV-polarized data.

Some features of the HH-polarized data are very similar to those of the VV-polarized data. Thus, VV data can be converted into HH data using a polarization ratio (PR) model. The HH GMF is usually described as a combination of a PR model and a VV GMF (Thompson et al., 1998; Vachon and Dobson, 2000; Horstmann et al., 2000; Mouche et al., 2005; Zhang et al., 2011; Jagdish et al., 2018). In a previous study, a PR model was developed using GF3 quad-polarization mode data, as described by Equation 6 (Ren et al., 2017). Therefore, a combination of the PR model in Equation 6 and CMOD5.N was used as the GMF of the GF3 wave mode HH-polarized data.

$\mathit{PR}=\frac{{\sigma }_{VV}^0}{{\sigma }_{HH}^0}=\frac{{\left(1+{2\mathit{tan}}^2\theta \right)}^2}{{\left(1+{1.3\mathit{tan}}^2\theta \right)}^2}(6)$

where PR is the polarization ratio, θ is the incidence angle, ${\sigma }_{VV}^0$ and ${\sigma }_{HH}^0$ are the NRCS at VV and HH polarization, respectively.

For cross-polarized data, the NRCS is linearly related to the wind speed. It is different from the relation from co-polarized NRCS data, which presents a nonlinear cosine function. Moreover, the VH-polarized data have characteristics that are very similar to those of the HV-polarized data. This makes the cross-polarized GMF a simple and single linear function (the VH and HV data adopt the same function) (Vachon and Wolfe, 2011; Zhang et al., 2014; Hwang et al., 2015; Jagdish et al., 2020). In a previous study, a cross-polarized GMF was developed using the GF3 quad-polarization data (Equation 7) (Ren et al., 2017), which was also used as the GMF for the GF3 wave mode cross-polarized data in this study.

${\sigma }_{\raisebox{1ex}{$\mathrm{V}\mathrm{H}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{H}\mathrm{V}$}\right.}^0\left(u10\right)=0.592\mathit{u}10–35.6(7)$

where ${\sigma }_{VH/HV}^0$ is the NRCS at VH or HV polarization.

4.2 Retrieval algorithm and accuracy assessment

For co-polarized data, two algorithms are typically used to retrieve SAR wind: classical and optimal algorithms. The former directly institutes the model wind direction into the GMF, and the wind speed is estimated by solving the GMF. The latter institutes the model wind vector and NRCS measurements into a cost-function-related GMF, and the wind vector can then be estimated by minimizing the cost function. In this study, an optimization algorithm was used to retrieve the GF3 wind vector. The cost function J (u, v) is expressed in Equation 8:

$J\left(u,v\right)={\left(\frac{{\sigma }_{\text{GF}3}^0-{\sigma }_{GMF}^0\left(u,v\right)}{\Delta {\sigma }^0}\right)}^2+{\left(\frac{u-u_m}{\Delta u}\right)}^2+{\left(\frac{v-v_m}{\Delta v}\right)}^2(8)$

where ${\sigma }_{GF3}^0$ is the measured GF3 NRCS, ${\sigma }_{GMF}^0$ is the NRCS estimated by substituting wind vector (u, v) into the GMF, ($u_m$, $v_m$) is the GFS wind vector, Δ ${\sigma }_0$ = 0.5 dB, Δu = $\sqrt{3}$ m/s, and Δv = $\sqrt{3}$ m/s (Mouche et al., 2012).

For cross-polarized data, only the wind speed can be retrieved from the measured NRCS. The retrieval process is simple; wind speed can be directly estimated by solving a linear GMF.

In the retrieval process, a look-up table (LUT) technique is employed to address the above equations. The LUT includes wind speed values ranging from 0 to 30 m/s, with increments of 0.1 m/s. Wind direction, relative to the observation direction, spans from 0° to 360° with a 0.1° resolution. The incidence angle is set between 20° and 50°, also with a 0.1° increment. These gridded parameters (wind speed, wind direction, and incidence angle) are then input into the GMF to calculate the corresponding normalized radar cross-section (NRCS). For co-polarized data, initial ambiguous wind vector solutions are generated based on the observed NRCS and incidence angle. The LUT is used to compute cost function values for these ambiguous wind vectors. The wind vector that minimizes the cost function is selected as the final retrieved wind vector. In contrast, for cross-polarized data, the wind speed can be estimated directly from the observed NRCS using the relevant cross-polarized GMF.

After retrieving the winds, the collocated ASCAT winds were used to assess retrieval accuracy. From reference (Monaldo et al., 2004), we think the GMF becomes uncertain at very low wind speeds. In this case, the wind retrievals with low speeds from GF3 and ASCAT data are probably invalid. For that, we masked the wind speeds lower than 2 m/s in the assessment. Figure 6 shows the wind speed retrieval accuracy for the four polarizations. The data were obtained from an incidence angle bin of 40.5^o. Data with errors greater than three times the standard deviation were excluded. The RMSE for the two co-polarized datasets (VV and HH) is approximately 1.9 m/s, whereas the RMSE for the two cross-polarized datasets (VH and HV) is approximately 2.6 m/s. Moreover, the correlation coefficient for the co-polarized data is higher than that for the cross-polarized data.

Figure 6

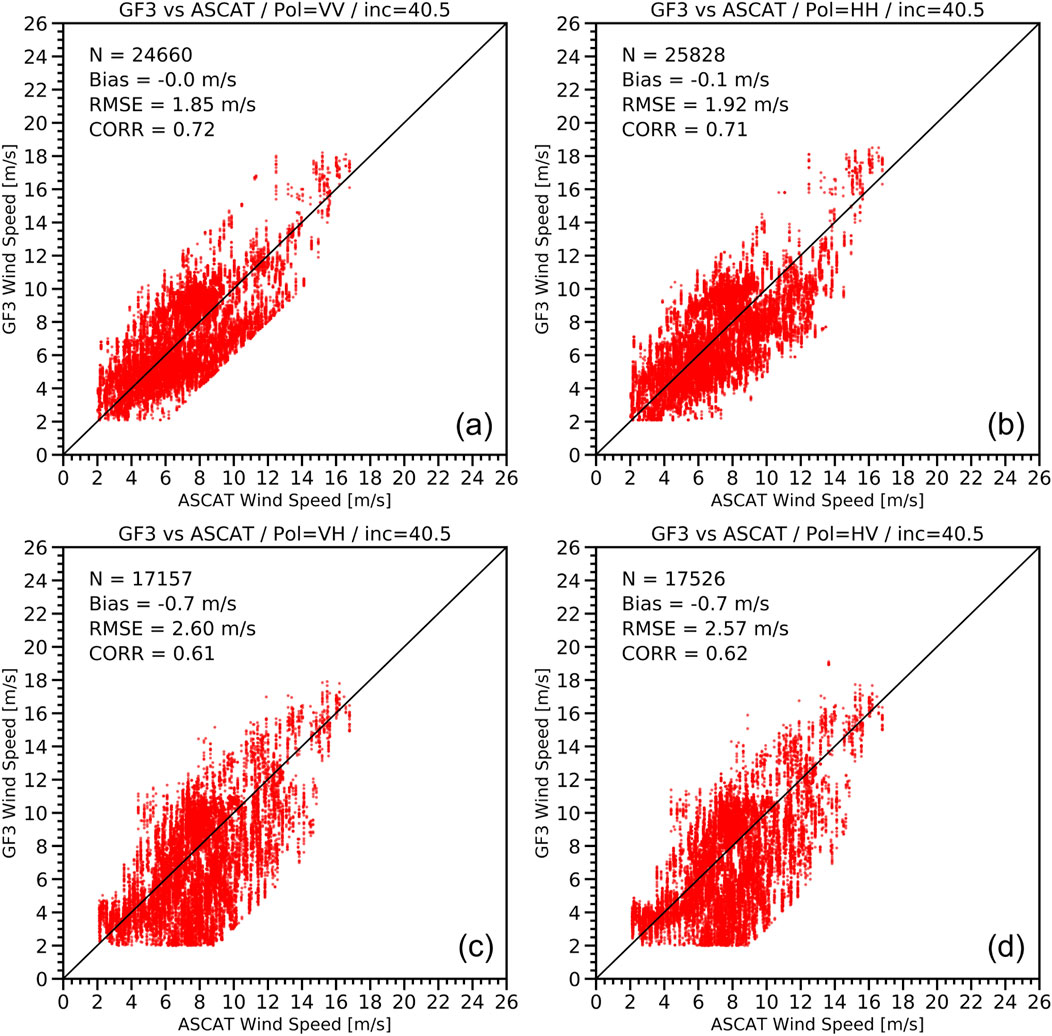
Figure 6. GF3 wind speed retrieval accuracy estimated by comparing with collocated ASCAT wind speed. The used GF3 wave mode data are at (A) VV, (B) HH, (C) VH, and (D) HV polarizations.

As mentioned previously, the wind direction cannot be retrieved from the cross-polarized NRCS; therefore, Figure 7 only shows the wind direction retrieval accuracy for the co-polarized data. The RMSE for the retrieved wind direction from the two co-polarized datasets are all approximately 14.5°. And their correlation coefficient is clearly higher (up to 0.97) than that for wind speed retrieval (around 0.7).

Figure 7

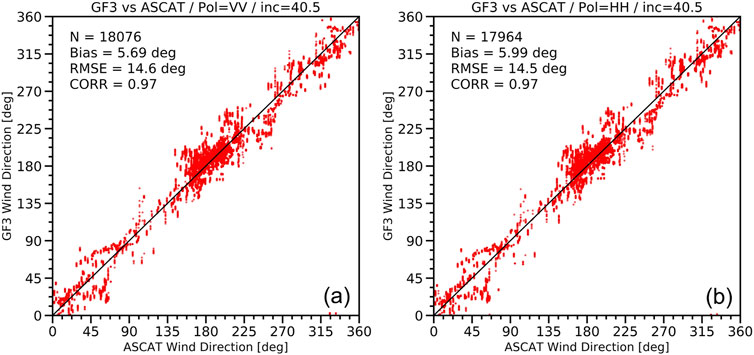
Figure 7. GF3 wind direction retrieval accuracy estimated by comparing with collocated ASCAT wind direction. The used GF3 wave mode data are at (A) VV and (B) HH polarizations. Each circle corresponds to the analysis of the incidence angle bin.

Figures 6, 7 show retrieval accuracy data for an incidence angle bin of 40.5°. Using the same method, assessments at all incidence angle bins were performed. These RMSE in assessments are listed in Table 2 and can also be found in Figures 10, 11 for the NESZ effect analysis. From the table, the medium incidence angle range (around 43°) has the best wind direction RMSE, while there is no clear trend with incidence angle for wind speed RMSE.

Table 2

Table 2. RMSE of wind retrieval accuracy at different polarizations and incidence angle bins.

As a supplement, the NDBC data were also used to assess wind retrieval accuracy. Figure 8 shows the accuracy assessment for wind speed, while Figure 9 is for the wind direction. From these figures, the wind speed RMSE from buoy winds is better than the one from ASCAT winds at four polarizations, while it is close for wind direction RMSE. Moreover, similar to wind speed RMSE from ASCAT winds, the wind speed retrieval accuracy for co-polarized data is significantly better than the one for cross-polarized data. Although buoy wind accuracy is better than the one from ASCAT winds, collocated buoy data volume in this study is less. So, the next NESZ Effect analysis is only based on the estimated retrieval accuracy from ASCAT winds.

Figure 8

Figure 8. GF3 wind speed retrieval accuracy estimated by comparing with collocated NDBC wind speed. The used GF3 wave mode data are at (A) VV, (B) HH, (C) VH, and (D) HV polarizations.

Figure 9

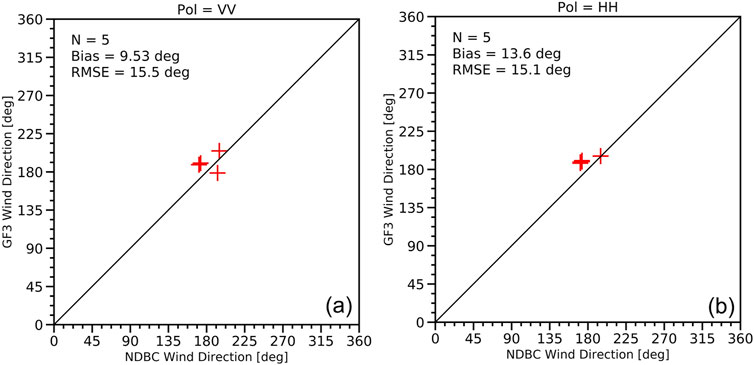
Figure 9. GF3 wind direction retrieval accuracy estimated by comparing with collocated NDBC wind direction. The used GF3 wave mode data are at (A) VV and (B) HH polarizations.

5 NESZ effects on wind retrieval accuracy

The effects of the NESZ on the wind retrieval accuracy were analyzed based on the estimated NESZ and wind retrieval accuracy. Figure 10 shows the wind speed analysis. As shown in the figure, the wind speed retrieval RMSE error increases with NESZ for each polarization. The higher the NESZ, the lower the retrieval accuracy. For VV-polarized data, when the NESZ is −41 dB, the RMSE for wind speed are about 1.4 m/s. When the NESZ increases to −29 dB, the RMSE are about 2.9 m/s. There is a RMSE degradation of 1.5 m/s for 12 dB NESZ increment. Similarly, the RMSE degradation are 1.2 m/s, 0.7 m/s and 0.5 m/s for 12 dB NESZ difference for HH-, VH-, and HV-polarized data respectively. This indicates that the NESZ degrades the wind speed retrieval accuracy. Moreover, the NESZ effects for the co-polarized data are more evident than those for the cross-polarized data.

Figure 10

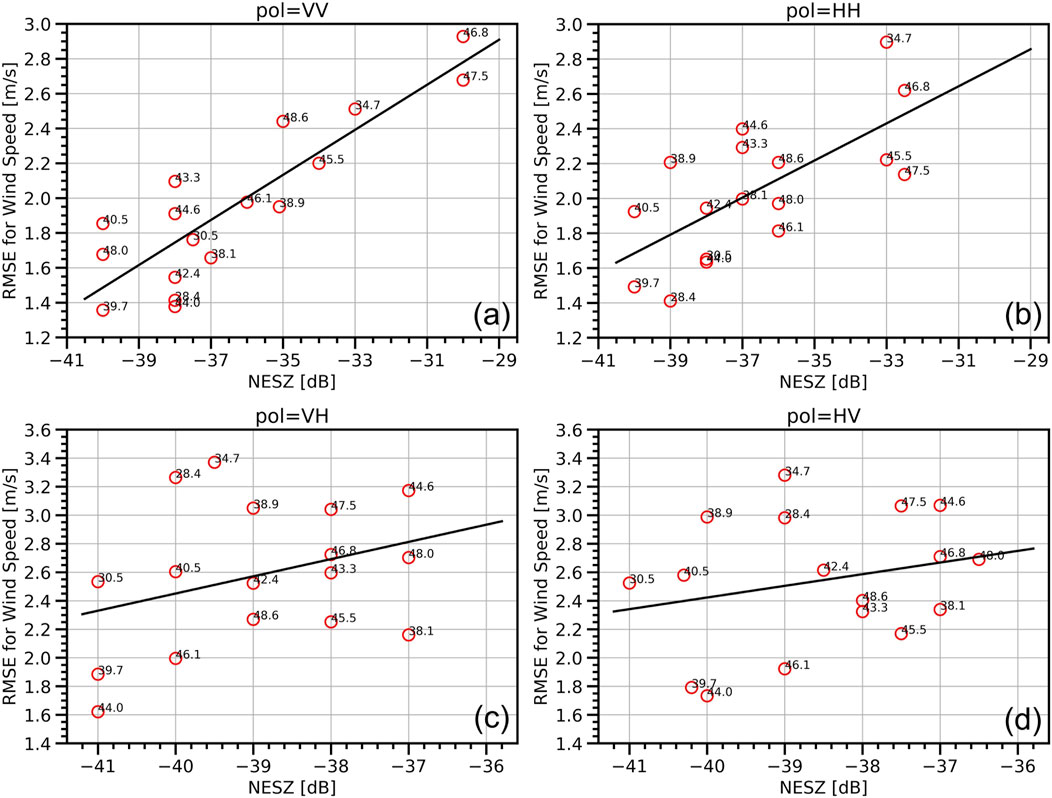
Figure 10. Wind speed RMSE with different NESZ for GF3 wave mode data for (A) VV, (B) HH, (C) VH, and (D) HV polarizations. Each red circle corresponds to a NESZ and a RMSE estimated in an incidence angle bin of 1°, for which the center value of each bin is listed on the edge of red circle. The black line was plotted by fitting all red circles.

Figure 11 shows a similar analysis to Figure 10 but for the retrieved wind direction from the co-polarized data. We also observed degradation of the RMSE due to the NESZ. The degradation for the two co-polarized datasets is closed. When the NESZ is −41 dB, the RMSE is around 13^o. When the NESZ increases to −29 dB, the wind direction RMSE is around 18^o. There is an RMSE degradation of 5^o for a 12 dB NESZ increment. This also means that NESZ degrades the accuracy of wind direction retrieval.

Figure 11

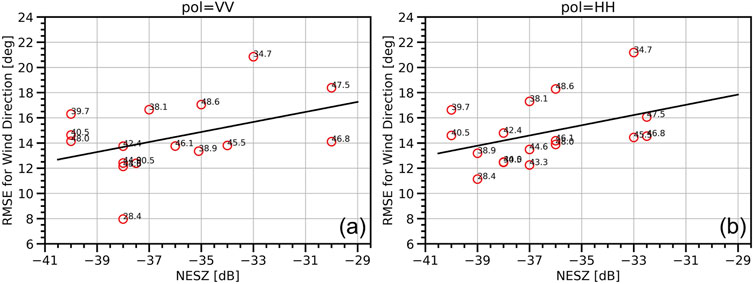
Figure 11. Wind direction RMSE with different NESZ for GF3 wave mode data for (A) VV and (B) HH polarizations. Each red circle corresponds to a NESZ and a RMSE estimated in an incidence angle bin of 1°, for which the center value of each bin is listed on the edge of red circle. The black line was plotted by fitting all red circles.

6 Discussion

This study complements existing recalibration research on GF3 SAR wave mode data. The recalibration coefficients were estimated for different incidence angle bins and four polarizations using the NWP method. The NESZ was then estimated, and the wind vector was retrieved from the recalibrated NRCS. The effects of the NESZ on wind retrieval were analyzed based on the estimated NESZ and wind retrieval accuracy. From the analysis, we found that the RMSE errors of wind speed and direction retrieval increased with NESZ. In particular, for the wind speed retrieval accuracy for co-polarized data, a 12 dB NESZ difference can induce an RMSE difference of 1.5 m/s. This implies that the presence of noise significantly degrades the accuracy of wind retrieval. From another perspective, the performance of the hardware system should be improved to obtain better noise conditions. This method improves the accuracy of SAR wind retrievals in addition to existing methods such as calibration, GMF, and algorithms.

According to the results presented, the accuracies of the wind speed retrievals at the four polarizations vary with the incident angles. The wind speed accuracies are relatively low in certain specific incidence angle ranges, and these differences are probably attributable to the influence of the NESZ. In this case, an NESZ with a relatively low value can help determine which incidence angle range is more suitable for wind retrieval. However, an NESZ with a relatively high value can also prompt us to check for possible problems in terms of satellite hardware.

In addition, noise or NESZ patterns were observed in each antenna beam at the four polarizations in our analysis. Smooth filtering is an effective method for reducing noise. During the retrieval process in this study, the spatial resolution of the wind speed product was set to 1 km to filter noise by averaging data in a box of 1 km × 1 km. This scale was selected on the basis of our previous research but may not be optimal for yielding the best NESZ for the wave mode data. Thus, it is recommended that future studies aim to determine the best scale for obtaining the minimum NESZ.

The NESZ analysis in our study is limited to the wave mode data of the GF3 SAR, which involves 12 modes associated with different observation conditions and spatial resolutions. In this case, the influence of the estimated NESZ on wind retrieval likely differs from that of the other modes. Therefore, it is necessary to explore the NESZ features using data from other modes. It should be noted that the recalibration coefficients must be revised according to the radiometric characteristics of the data of each mode using the NWP method adopted in this study.

Moreover, gaps in both the incidence angle and in-orbit time can affect the integrity of the NESZ analysis. In this study, the incidence angle range used is 28°–49°, and the in-orbit time range is from January 2017 to October 2018. Although abundant data were collected, some discontinuities remain. There are two possible reasons for these discontinuities: satellite operational control and the limited incidence angle range owing to the narrow swath of the wave mode data. In this case, the conclusions of this study are only applicable to specific incidence angle ranges from the GF3 SAR wave mode data used. In this case, we propose an interpolation method for estimating the NESZ of the gap position.

7 Conclusion

Based on the developed GMFs and collocated GFS wind data, the recalibration coefficients of the GF3 wave mode data at four polarizations and different incidence angles were estimated using the NWP method. This recalibration makes the biases of the GF3 NRCS less than 0.1 dB, in comparison with the simulated NRCS. Using the recalibrated NRCS, the NESZ trends with the in-orbit time and incidence angles were estimated. We found that the NESZ trends show no obvious change with in-orbit time, whereas it exhibits significant fluctuations with the incidence angle. Moreover, wind vectors were retrieved and further validated using the collocated ASCAT and NDBC wind data. In this case, the wind retrieval accuracy with the NESZ for different incidence angle bins was analyzed. The analysis shows that the wind retrieval RMSE error increases with NESZ for each polarization. This means that the NESZ degrades the accuracy of the wind vector retrieval. In addition, for the NESZ effects, the co-polarized data are more evident than the cross-polarized data for wind speed retrieval, while the two co-polarized data are close for wind direction retrieval. When the NESZ increases from −41 dB to −29 dB, there is a wind speed RMSE degradation of 1.5 m/s, 1.2 m/s, 0.7 m/s and 0.5 m/s for VV-, HH-, VH-, and HV-polarized data respectively, while there is a wind direction RMSE degradation of 5^o for co-polarized data. In next work, we will continue to improve the GF3 wind retrieval accuracy in terms of NESZ source analysis and correction.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LR: Conceptualization, Funding acquisition, Methodology, Validation, Writing–original draft, Writing–review and editing. JD: Methodology, Validation, Writing–original draft. JY: Conceptualization, Funding acquisition, Writing–original draft. CJ: Methodology, Validation, Writing–review and editing. GZ: Conceptualization, Methodology, Writing–review and editing. PC: Methodology, Validation, Writing–review and editing. XL: Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded in part by the National Key Research and Development Program of China (Grant No. 2022YFC3103101), the Project of Key Laboratory of Space Ocean Remote Sensing and Application, Ministry of Natural Resources (Grant No. 2023CFO009), and the Zhejiang Provincial Natural Science Foundation of China (Grant No. LGF21D060002); Project of the State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources (Grant no. SOEDZZ2205), and Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) (Grant nos. 311021004 and 311021001).

Acknowledgments

The authors would like to thank the China Ocean Satellite Data Service System Gaofen-3 (GF3) SAR wave mode data, the NOAA/NCEP Global Forecast System (GFS) wind data, and the collocated Advanced Scatterometer (ASCAT) wind data. The authors would also like to thank the reviewers for their valuable comments that improved the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amante, C., and Eakins, B. W. (2009). ETOPO1 1 arc-minute global relief model: procedures, data sources and analysis. Psychologist 16 (3), 20–25.

Google Scholar

Beaucage, P., Glazer, A., Choisnard, J., Yu, W., Bernier, M., Benoit, R., et al. (2007). Wind assessment in a coastal environment using synthetic aperture radar satellite imagery and a numerical weather prediction model. Can. J. Remote Sens. 33 (5), 368–377. doi:10.5589/m07-043

CrossRef Full Text | Google Scholar

Bergeron, T., Bernier, M., Chokmani, K., Lessard-Fontaine, A., Lafrance, G., and Beaucage, P. (2011). Wind speed estimation using polarimetric RADARSAT-2 images: finding the best polarization and polarization ratio. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 4 (4), 896–904. doi:10.1109/jstars.2011.2158067

CrossRef Full Text | Google Scholar

Chen, Q., Li, Z., Zhang, P., Tao, H., and Zeng, J. (2018). A preliminary evaluation of the Gaofen-3 SAR radiation characteristics in land surface and compared with radarsat-2 and sentinel-1A. IEEE Geoscience Remote Sens. Lett. 15 (7), 1040–1044. doi:10.1109/lgrs.2018.2821238

CrossRef Full Text | Google Scholar

Hersbach, H. (2008). CMOD5.N: a C-band geophysical model function for equivalent neural wind. ECMWF, 554.

Google Scholar

Hersbach, H., Stoffelen, A., and Haan, S. (2007). An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. 112, C03006. doi:10.1029/2006jc003743

CrossRef Full Text | Google Scholar

Horstmann, J., Koch, W., Lehner, S., and Tonboe, R. (2000). Wind retrieval over the ocean using synthetic aperture radar with C-band HH polarization. IEEE Trans. Geoscience Remote Sens. 38 (5), 2122–2131. doi:10.1109/36.868871

CrossRef Full Text | Google Scholar

Horstmann, J., and Lehner, S. (2002). A new method for radiometric calibration of spaceborne SAR and its global monitoring. IEEE Int. Geosicence Remote Sens. Symposium 1, 620–622. doi:10.1109/igarss.2002.1025124

CrossRef Full Text | Google Scholar

Hwang, P. A., Stoffelen, A., Zadelhoff, G. V., Perrie, W., Zhang, B., Li, H., et al. (2015). Cross-polarization geophysical model function for C-band radar backscattering from the ocean surface and wind speed retrieval. J. Geophys. Res. Oceans 120 (2), 893–909. doi:10.1002/2014jc010439

CrossRef Full Text | Google Scholar

Jagdish, S., Abhisek, C., Bipasha, P., and Raj, K. (2020). Development of wind speed retrieval model using RISAT-1 SAR cross-polarized observations. Curr. Sci. 118 (8), 1282–1286. doi:10.18520/cs/v118/i8/1282-1286

CrossRef Full Text | Google Scholar

Jagdish, S., Abhisek, C., Raj, K., and Kumar, R. (2018). Validation of wind speed retrieval from RISAT-1 SAR images of the North Indian Ocean. Remote Sens. Lett. 9 (5), 421–428. doi:10.1080/2150704x.2018.1430392

CrossRef Full Text | Google Scholar

Kerbaol, V. (2007). The SAR Ocean Wind, Waves and Currents Team, Improved bayesian wind vector retrieval scheme using envisat asar data: principles and validation results. Montreux, Switzerland: Envisat Symposium.

Google Scholar

Li, X., Zhang, T., Huang, B., and Jia, T. (2018). Capabilities of the Chinese GF3 SAR for ocean, coast and polar ice observations. Rome, Italy: SEASAR Workshop.

Google Scholar

Monaldo, F. (2000). The Alaska SAR demonstration and near-real-time synthetic aperture radar winds. Johns Hopkins Apl. Tech. Dig. 21 (1), 75–79.

Google Scholar

Monaldo, F. M., Thompson, D. R., Beal, R. C., Pichel, W. G., and Clemente-Colón, P. (2001). Comparison of SAR-derived wind speed with model predictions and ocean buoy measurements. IEEE Trans. Geoscience Remote Sens. 39 (12), 2587–2600. doi:10.1109/36.974994

CrossRef Full Text | Google Scholar

Monaldo, F. M., Thompson, D. R., Pichel, W. G., and Clemente-Colon, P. (2004). A systematic comparison of QuikSCAT and SAR ocean surface wind speeds. IEEE Trans. Geoscience Remote Sens. 42 (2), 283–291. doi:10.1109/tgrs.2003.817213

CrossRef Full Text | Google Scholar

Mouche, A., and Chapron, B. (2015). Global C-Band Envisat, RADARSAT-2 and Sentinel-1 SAR measurements in co-polarization and cross-polarization. J. Geophys. Res. Oceans 120, 7195–7207. doi:10.1002/2015jc011149

CrossRef Full Text | Google Scholar

Mouche, A., Collard, F., Chapron, B., Dagestad, K., Guitton, G., Johannessen, J. A., et al. (2012). On the use of Doppler shift for sea surface wind retrieval from SAR. IEEE Trans. Geoscience Remote Sens. 50 (7), 2901–2909. doi:10.1109/tgrs.2011.2174998

CrossRef Full Text | Google Scholar

Mouche, A., Hauser, D., Daloze, J. F., and Guerin, C. (2005). Dual-polarization measurements at C-band over the ocean: results from airborne radar observations and comparison with ENVISAT ASAR data. IEEE Trans. Geoscience Remote Sens. 43 (4), 753–769. doi:10.1109/tgrs.2005.843951

CrossRef Full Text | Google Scholar

Mu, B., and Song, Q. (2014). In-orbit radiometric calibration of the HY-2A microwave scatterometer through open ocean measurements. J. Remote Sens. 18 (5), 1072–1086. doi:10.11834/jrs.20143174

CrossRef Full Text | Google Scholar

Portabella, M., Stoffelen, A., and Johannessen, J. A. (2002). Toward an optimal inversion method for synthetic aperture radar wind retrieval. J. Geophys. Res. Oceans 107 (C8)–3086. doi:10.1029/2001jc000925

CrossRef Full Text | Google Scholar

Quilfen, Y., Chapron, B., Elfouhaily, T., Katsaros, K., and Tournadre, J. (1998). Observation of tropical cyclones by high-resolution scatterometry. J. Geophys. Res. 103, 7767–7786. doi:10.1029/97jc01911

CrossRef Full Text | Google Scholar

Ren, L., Yang, J., Mouche, A. A., Wang, H., Chen, P., Wang, J., et al. (2019). Assessments of ocean wind retrieval schemes used for Chinese Gaofen-3 synthetic aperture radar co-polarized data. IEEE Trans. Geoscience Remote Sens. 99, 7075–7085. doi:10.1109/tgrs.2019.2911325

CrossRef Full Text | Google Scholar

Ren, L., Yang, J., Mouche, A. A., Wang, H., Wang, J., Zheng, G., et al. (2017). Preliminary analysis of Chinese GF-3 SAR quad-polarization measurements to extract winds in each polarization. Remote Sens. 9, 1215. doi:10.3390/rs9121215

CrossRef Full Text | Google Scholar

Scheuchl, B., and Cumming, I. (2005). Analysis of the influence of NESZ variations on cross-polarized signatures of sea ice. IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea (South), 29-29 July 2005 (IEEE).

Google Scholar

Shao, W., Sheng, Y., and Sun, J. (2017). Preliminary assessment of wind and wave retrieval from Chinese Gaofen-3 SAR imagery. Sensors 17 (8), 1705. doi:10.3390/s17081705

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, L., Yang, L., Zhao, L., Li, P., Yang, J., and Zhang, L. (2020). NESZ Estimation and calibration for Gaofen-3 polarimetric products by the minimum noise envelope estimator. IEEE Trans. Geoscience Remote Sens. 99, 1–18. doi:10.1109/TGRS.2020.3033534

CrossRef Full Text | Google Scholar

Stoffelen, A., and Anderson, D. (1997). Scatterometer data interpretation: estimation and validation of the transfer function CMOD4. J. Geophys. Res. 102, 5767–5780. doi:10.1029/96jc02860

CrossRef Full Text | Google Scholar

Sun, J., Yu, W., and Deng, Y. (2017). The SAR payload design and performance for the GF-3 mission. Sensors 17, 2419. doi:10.3390/s17102419

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, D. R., Elfouhaily, T. M., and Chapron, B. (1998). Polarization ratio for microwave backscattering from the ocean surface at low to moderate incidence angles. IEEE International Geoscience and Remote Sensing Symposium, Seattle, USA, 06-10 July 1998 (IEEE) 1671–1673 vol.3. doi:10.1109/igarss.1998.692411

CrossRef Full Text | Google Scholar

Vachon, P. W., and Dobson, F. W. (2000). Wind retrieval from RADARSAT SAR images: selection of a suitable C-band HH polarization wind retrieval model. Can. J. Remote Sens. 26 (4), 306–313. doi:10.1080/07038992.2000.10874781

CrossRef Full Text | Google Scholar

Vachon, P. W., and Wolfe, J. (2011). C-band cross-polarization wind speed retrieval. IEEE Geoscience Remote Sens. Lett. 8 (3), 456–459. doi:10.1109/lgrs.2010.2085417

CrossRef Full Text | Google Scholar

Valenzuela, G. R. (1978). Theories for the interaction of electromagnetic and oceanic waves—a review. Boundary-Layer Meteorol. 13, 61–85. doi:10.1007/bf00913863

CrossRef Full Text | Google Scholar

Verspeek, J., Stoffelen, A., Verhoef, A., and Portabella, M. (2012). Improved ASCAT wind retrieval using NWP ocean calibration. IEEE Trans. Geoscience Remote Sens. 50 (7), 2488–2494. doi:10.1109/tgrs.2011.2180730

CrossRef Full Text | Google Scholar

Verspeek, J., Verhoef, A., and Stoffelen, A. (2010). ASCAT-B NWP ocean calibration and validation. Ultrasound Obstetrics Gynecol. 36 (S1), 173–177.

Google Scholar

Vincenty, D. (1975). Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Surv. Rev. 23 (176), 88–93. doi:10.1179/sre.1975.23.176.88

CrossRef Full Text | Google Scholar

Vogelzang, J., Stoffelen, A., Verhoef, A., de Vries, J., and Bonekamp, H. (2009). Validation of two-dimensional variational ambiguity removal on seawinds scatterometer data. J. Atmos. Ocean. Technol. 26, 1229–1245. doi:10.1175/2008jtecha1232.1

CrossRef Full Text | Google Scholar

Wang, H., Li, H., Lin, M., Zhu, J., Wang, J., Li, W., et al. (2019). Calibration of the co-polarized backscattering measurements from Gaofen-3 synthetic aperture radar wave mode imagery. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 99, 1748–1762. doi:10.1109/jstars.2019.2911922

CrossRef Full Text | Google Scholar

Wang, H., Yang, J., Mouche, A., Shao, W., Zhu, J., Ren, L., et al. (2017). GF-3 SAR ocean wind retrieval: the first view and preliminary assessment. Remote Sens. 9, 694. doi:10.3390/rs9070694

CrossRef Full Text | Google Scholar

Yang, X., Li, X., Pichel, W. G., and Li, Z. (2011). Comparison of ocean surface winds from ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model. IEEE Trans. Geoscience Remote Sens. 49 (12), 4743–4750. doi:10.1109/tgrs.2011.2159802

CrossRef Full Text | Google Scholar

Zhang, B., Perrie, W., and He, Y. (2011). Wind speed retrieval from RADARSAT2 quad-polarization images using a new polarization ratio model. J. Geophys. Res. 116, C08008. doi:10.1029/2010jc006522

CrossRef Full Text | Google Scholar

Zhang, B., Perrie, W., Zhang, J. A., Uhlhorn, E. W., and He, Y. (2014). High-resolution hurricane vector winds from C-band dual-polarization SAR observations. J. Atmos. Ocean. Technol. 31 (2), 272–286. doi:10.1175/jtech-d-13-00006.1

CrossRef Full Text | Google Scholar