Estimation of the resonance frequency of rotational and translational signals evoked by mining-induced seismicity

The horizontal-to-vertical (H/V) method is a fundamental fast tool to estimate local site effect parameters by using the registered signals of the translational motion. The spectral ratio is mostly calculated using the Fourier Spectrum Analysis (FSA), which may lead to problems with accurate resonant frequency determination due to evident multi-amplification peaks occurrence on the spectrum. Alternatively the H/V ratio may be estimated by use Response Spectrum Analysis (RSA), where only a general amplification peak is expected. However, the fundamental limitations of the RSA assumption are related to the real impact of the events’ scenario dependence (i.e., magnitude, distance, focal mechanism, etc.). The limitations and advantages of the RSA and FSA are commonly known in the case of the analysis performed for the translational signals. Therefore, the critical question is: should the RSA and FSA methods be used to estimate the H/V ratio of the recorded rotational signals of the events? The article presents horizontal-to-vertical (H/V) spectral ratios calculated for rotational and translational signals registered as an effect of mining-induced seismicity by four independent seismic stations located in Poland's Upper Silesian Coal basin. The spectral ratios of the signals were estimated using the RSA and the FSA method. The studies show that in the case of translational motion, the H/V estimations using the RSA derived clear information of the resonant frequency peak, confirming the method’s usefulness in the case of multi-amplification peaks. The opposite situation was noticed in the case of the rotational motion. The derived H/V spectrum, using the RSA, produced single amplification peaks for the seismic stations, where the sensors were mounted on a small floor at a significant distance from the walls. In cases where the sensors were deployed on the building floor, a decrease in the reliability of the RSA and the FSA method was noticed. The results of the studies suggested that the possibility of the estimations of the H/V spectrum using the RSA and FSA algorithm is strongly limited for rotational motions due to the size of the floor and distance to the building walls where the sensors were mounted. The explanation of that fact is related to the effects of kinematic soil-structure interaction, which may significantly affect rotational measurements due to the tendency to obtain higher frequency content than in the case of the translations. Consequently, the values of the Z- component of the rotational motion may be lovered than in the free-field measurements, decreasing the reliability of the H/V estimations for rotational motion.

1 Introduction

The adverse effects of shaking are significant and well-known problems occurring in seismic areas worldwide. Moreover, these harmful phenomena can be magnified by specific conditions of local geology. If loose near-surface layers are characterized by natural frequency (resonance frequency), which is in accordance with the shaking frequencies, the resonance effect can occur, and horizontal amplitudes amplify many times, resulting in more damage on the surface. Some investigations (e.g., Zhao and Xu, 2013; Stambouli et al., 2017; Zhu et al., 2019) suggested that the site resonance frequency can be used as a primary variable in site–effect model description. The resonance frequency and amplification factor are the site effect parameters that can be obtained directly from the horizontal-to-vertical spectral ratio (HVSR) method, in which the calculated spectra of the horizontal (H) and vertical (V) components of the signals are divided as follows: H/V. Taking into account some pieces of research (e.g., Miura et al., 2019; Zhu et al., 2020), the H/V spectral ratio can be estimated from the Fourier spectrum analysis (FSA) and from the response spectrum analysis (RSA). However using the FSA and RSA interchangeably may be a reason of inaccuracies in resonant frequency determination due to the following facts: (1) the response spectrum at the high frequency has a strong tendency to be scenario dependent (i.e. magnitude, distance, focal mechanism etc.) of the events (Stafford et al., 2017), which however may be reduced by rotation of the horizontal motions axis (Rupakhety and Sigbjörnsson 2013; Pinzón et al., 2019); (2) the Fourier spectral ordinate is not controlled at the similar frequency of the response spectral ordinate at a high oscillator frequency but is determined by Fourier amplitudes in a wide frequency range (Bora et al., 2016); (3) the H/V spectral ratio calculated from the standard Nakamura approach by using the FSA may present more than one significant peak, which fulfills the criteria of the amplification peak reliability and, in consequence, may lead to inconsistent analysis of determining the first or the highest peak as corresponding to the absolute resonance frequency of the site (Albarello, 2001; Zhu et al., 2020). So far, the input data for the calculation of the H/V can come from translational records of the natural earthquake or microtremor (e.g., Stephenson et al., 2009; Stanko et al., 2017; Stanko and Markušić, 2020).

Considering the observation of the rotational motion as an effect of natural (e.g., Lee et al., 2009; Liu et al., 2009; Stupazzini et al., 2009) and induced seismicity (e.g., Kalab et al., 2012; Mutke et al., 2020) leads to the conclusion that the H/V ratio can also be applied to the rotational motion (Sbaa et al., 2017; Ringler et al., 2018; Nawrocki et al., 2021; Nawrocki et al., 2022). However, geometrical planes of registration rotational motion described as rocking (vertical plane) and torsion (horizontal plane) (Zembaty, 2006, 2009) obligated to estimate the rotational H/V curve as a ratio of the torsion-to-rocking components, which directly means the inverse of the translational H/V spectral ratio (Ringler et al., 2018; Nawrocki et al., 2021; Nawrocki et al., 2022) and, in consequence, leads to re-naming the method as a torsion-to-rocking spectral ratio (TRSR).

Taking into account the limitations to the RSA method, the fundamental questions are as follows: (1) can the RSA method be applied to estimate the rotational resonance frequency, producing comparable results obtained from the FSA? (2) Can potential differences between H/V curves obtained from the FSA and RSA be similarly observed for the rotational and translational data? Answers to the above questions motivated us to compare the H/V curves obtained from the FSA and RSA for the rotational and translational registration of the induced seismic events at the sites characterized by different settings of the stations.

2 Data description and study area

The tests of H/V methods were performed using mining-induced seismicity waveforms registered by four seismic stations located in the Upper Silesian Coal Basin (USCB), Poland (Figure 1). The seismic circumstance of the USCB allows us to divide two primary types of events, which are an effect of the mining and the mining–tectonic seismicity (Stec, 2006). Compared to the explosive and compressional components, a relatively small shear component characterized the mining seismicity events. Opposite details occur in the case of mining–tectonic seismicity, where the shear component is dominant, corresponding to the double-couple source mechanism. The occurrence of the peak values of the motion at the S-wave phase of the seismic signals confirmed that the analyzed events were linked to mining–tectonic seismicity.

Figure 1

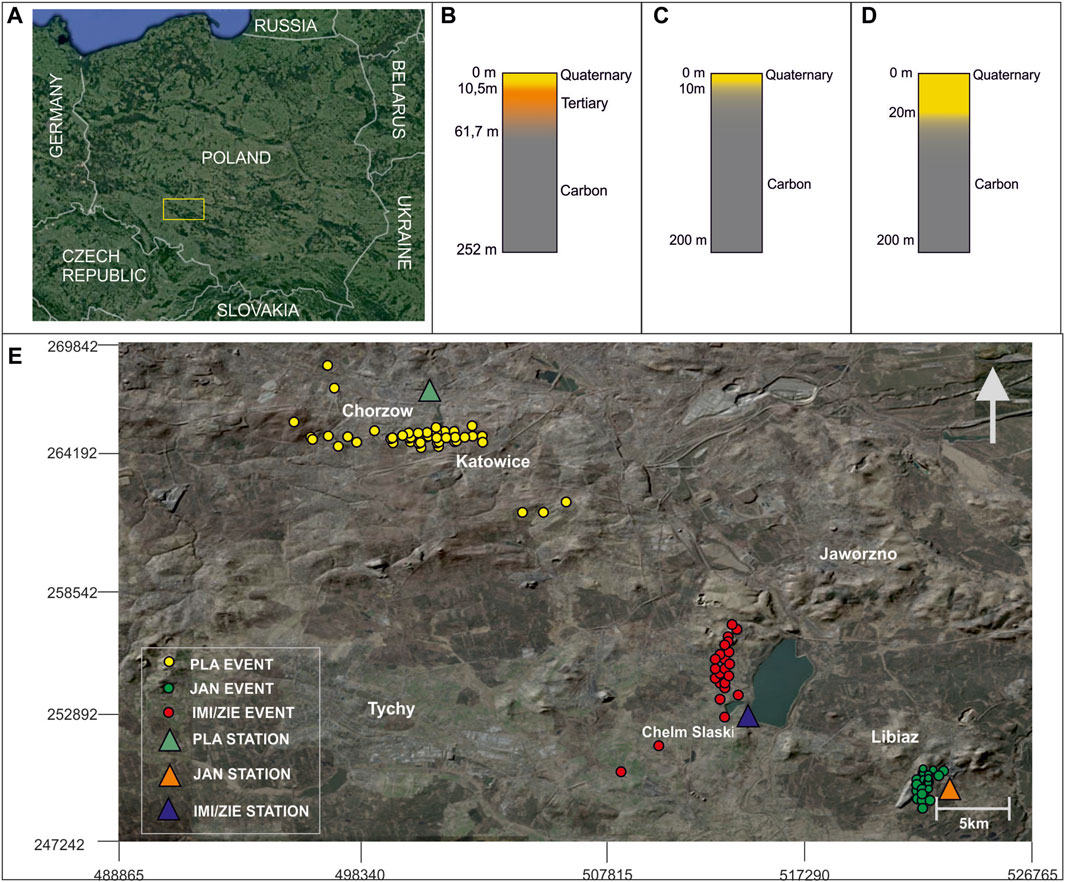
Figure 1. Study area information. Location: (A) Poland; geological profiles: (B) at the IMI and ZIE station sites; (C) at the PLA station site; (D) at the JAN station, and (F) detailed map of registered seismic events.

First, the station, known as the PLA station, registered 60 relatively far-distant events, with epicentral distances ranging from 5 to 20 km and characterized by a local magnitude of 2.4–3.5. The equipment was mounted on the pedestal in the basement of the local planetarium. In the case of the following two stations, IMI and ZIE, the location of the sensors was almost the same, and the distance between them reached almost 5 mm. The measuring set of the IMI station was mounted in the technical venue (Zembaty et al., 2017), while the ZIE station was deployed on the ground floor of the one-story technical building, which did not have a basement. The sensors were mounted in the corner of load-bearing and partition walls. Both registered the close-distant events characterized by local magnitudes of 1.7–2.7 and epicentral distances up to 5 km. Nevertheless, the ZIE station registered 45 events, while in the IMI station, 60 events were recorded. The last of the stations, JAN, was situated in the basement center of the small building closest to the central exploitation. The catalog consists of 45 events, with a magnitude between 2.2 and 3.4, while the distance was between 0.5 and 30.0 km.

The location of the IMI, ZIE, and JAN stations was selected due to the relatively close distance to the potential area of the mining event occurrence. Considering the IMI and ZIE stations, the venue occurrence at the safety area allows for the analysis of the impact on the building on recorded signals. Due to the lack of technical circumstances caused in the case of the JAN station, the sensors were situated only inside the building instead of mounting in the building and the venue. In the case of the PLA, the described pedestal allows us to register events from a relatively far distance. Consequently, the location of the stations allows for the comparison of rotational signals registered from far and close distances. The equipment of the JAN station contains the accelerometer EA-120 and rotational seismometer R-2, but in the case of the remaining stations, the measuring set was composed of the accelerometer EA-120 and rotational seismometer R-1 (e.g., Lin et al., 2009; Liu et al., 2009). Each of the sensors was responsible for measuring the three axes of the movement and was linked to the Eentec recorders. The measured temperature at the stations was stable and lower than 18°C. Therefore, following the studies presented by Bernauer et al., 2012, potential problems with the measurement reliability of the rotational sensors were excluded.

Buła and Kotas (1994) and Jureczka et al. (1995) showed that the seismic stations were situated under similar geological conditions represented by the shallow layer of Quaternary sediments covering the intermediate layer of the Triassic sandstones except for the PLA station, where the rigid basement of Carboniferous formation was directly underneath them. The near-surface loose deposit comprised sands, pebbles, mud, and alluvia material (e.g., Buła and Kotas, 1994; Jureczka et al., 1995). Sandstones, mudstones, and siltstones represented the rigid basement interbedded with hard coal seams, building the Carboniferous formation (e.g., Teper, 2000; Mendecki et al., 2020) (Figures 1 b-d).

3 Site effect

3.1 General description

Generally, the site effect is defined by two parameters: the resonance frequency of the near-surface layer and the corresponding amplification. Considering two-layered geology composed of loose sediments and a rigid basement, the resonance frequency is related to the former layer due to the contrast of the acoustic impedance. The formation of the resonating layer can be a combination of many different geological layers characterized by different elastic properties. However, the resonance frequency as a value depends on its thickness, which works as a bandpass filter enhancing selected frequencies. On the other hand, the amplification coefficient determines the level of increasing the measured amplitudes of the signals and dependence on the acoustic impedance between stiff and loose rocks. The method that allows us to find site effect parameters from empirically registered signals is the HVSR technique. The HVSR amplification curve is formed by the spectral ratio of translation signals recorded for two main directions (Figure 3A): horizontal, H, and vertical, V (Nakamura, 1989; Bard, 2004; Stephenson et al., 2009; Pastén et al., 2015; Stanko et al., 2017; Stanko and Markušić, 2020).

Figure 3

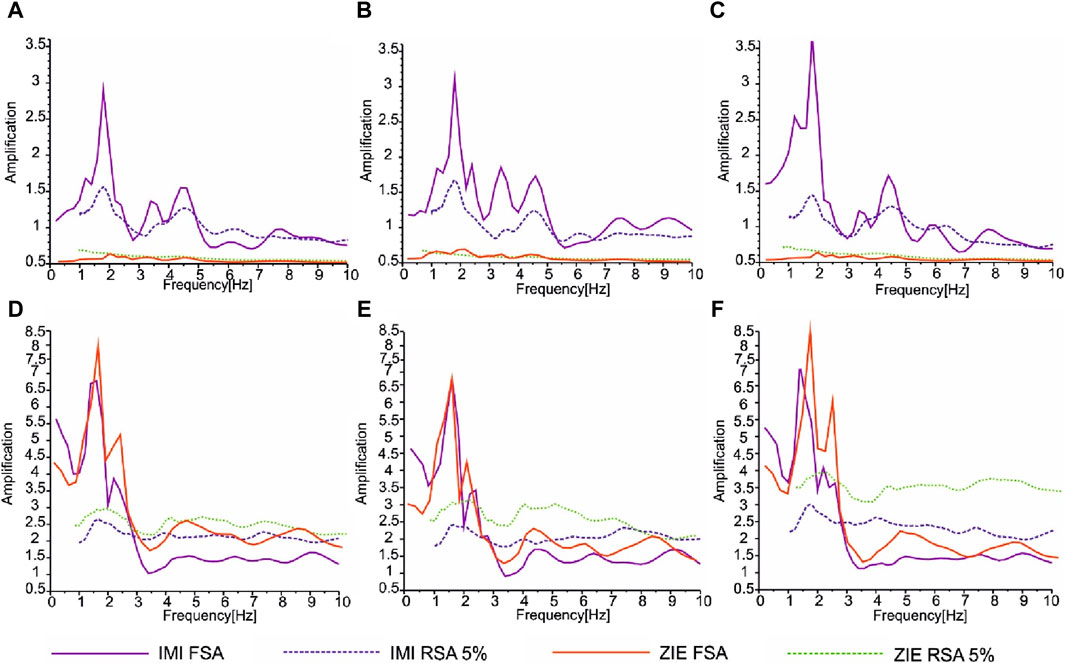
Figure 3. HVSR and TRSR amplification curves obtained for IMI and ZIE station records: (A) average TRSR curve; (B) EW- direction TRSR curve; (C) NS-direction TRSR curve; (D) average HVSR curve; (E) EW-direction HVSR curve; and (F) NS-direction HVSR curve.

The spectral ratio is generally estimated as a ratio of the Fourier amplitude spectrum of the registered signals, which, as was mentioned above, may produce more than one peak of the amplification curve and, therefore, make difficulties with the recognition of the corrected resonance frequency values (Albarello, 2001; Zhu et al., 2020). The multi-amplification peaks, recognized as significant by SESAME criteria (Site EffectS Assessment using Ambient Excitations, 2004), can be a consequence of the industrial origin of the place and the occurrence of geological zones characterized by strong impedance contrast at different scales. However, Zhu et al. (2020) pointed out that the choice of the smoothing technique of the spectrum, such as the type of the smoothing operator or soothing degree, impacts the spectral ratio value and, therefore, the qualification of the significant peak. The FSA may be replaced by the RSA, which allows to determine the resonance frequency too but may underestimate the amplification value due to scenario dependency (Stafford et al., 2017; Rong et al., 2017). However, considering the multiple peak occurrence as a result of applying the FSA, the RSA may indicate the real amplification peaks and, therefore, the approximate resonant frequency value.

3.2 Translational and rotational H/V curve calculations

The HVSR of the ith event is described by the following equation (e.g., Zhu et al., 2020):

${\mathit{log}}_{10}HVS{R}_{AVi}\left(f\right)=0.5\left[lo{g}_{10}\left(S_{Txi}\left(f\right)\right)+lo{g}_{10}\left(S_{Tyi}\left(f\right)\right)\right]-lo{g}_{10}\left(S_{Tzi}\left(f\right)\right),(1)$

where S is the spectrum result of the FSA or RSA obtained from horizontal $T_x$, $T_y$, and vertical $T_z$ components of the translational registration. In the case of the estimation of HVSR, the curve for one of the horizontal components (in that case, along the x-axis of registration), Eq. 1 can be rewritten as follows:

${\mathit{log}}_{10}HVS{R}_{xi}\left(f\right)=\left[lo{g}_{10}\left(S_{Txi}\left(f\right)\right)\right]-lo{g}_{10}\left(S_{Tzi}\left(f\right)\right).(2)$

The torsion-to-rocking spectral ratio is rewritten as the HVSR for the rotational motion under the following assumption: the torsion tilts are in a parallel plane to the horizontal recordings of the translations, while the rocking tilts are in a parallel plane to the vertical recordings of the translations (Sbaa et al., 2017; Ringler et al., 2018; Nawrocki et al., 2022). Therefore, the accurate spectral ratio is the opposite of the basic HVSR. Regarding the planes of the rotational signal (Figure 2), the TRSR of the $i$th event can be described as follows (Nawrocki et al., 2022):

${\mathit{log}}_{10}TRS{R}_{AVi}\left(f\right)=lo{g}_{10}\left(S_{Rzi}\left(f\right)\right)-0.5\left[lo{g}_{10}\left(S_{Rxi}\left(f\right)\right)+lo{g}_{10}\left(S_{Ryi}\left(f\right)\right)\right],(3)$

where S is also the spectrum result of the FSA or RSA obtained from rocking $R_x,R_y$, and torsion $R_z$ components of the rotational registration. The TRSR curve, including the estimation of the amplification for one of the rocking components (also along the x-axis), can be described as follows:

${\mathit{log}}_{10}TRS{R}_{xi}\left(f\right)=lo{g}_{10}\left(S_{Rzi}\left(f\right)\right)-\left[lo{g}_{10}\left(S_{Rxi}\left(f\right)\right)\right].(4)$

Figure 2

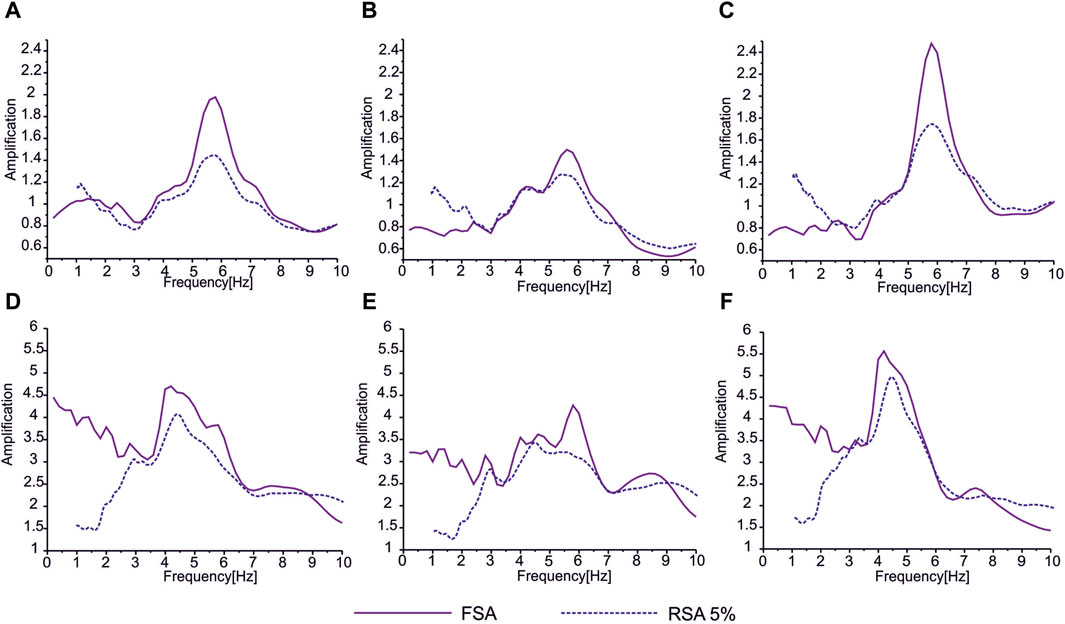
Figure 2. HVSR and TRSR amplification curves obtained for PLA station records: (A) average TRSR curve; (B) EW- direction TRSR curve; (C) NS-direction TRSR curve; (D) average HVSR curve; (E) EW- direction HVSR curve; and (F) NS-direction HVSR curve.

The HVSR/TRSR estimations (Nakamura, 1989; Wang et al., 2019) were carried out for the S-wave phase, which was motivated by the following facts: 1) dominant peak values of the signals were recognized for the S-wave content and 2) double-couple focal mechanism, which is responsible for the generation of torsion as a consequence of SH-wave propagation (Suryanto, 2006), characterized the analyzed events. Therefore, the spectral H/V curves were estimated using the FSA (Nakamura, 1989), also known as the “Nakamura technique,” and separately by using the RSA technique (Zhu et al., 2020). The spectral ratios were calculated for the filtrated signals of rotational velocity and translational acceleration using a Butterworth filter in the frequency range of ca. 1 Hz–20 Hz. The FSA was estimated by using the fast Fourier transform (FFT) method with the Hamming function of windowing. Estimations of the RSA were performed separately, assuming 5% damping for the whole dataset. The response spectrum acceleration was estimated for the translational signals, while in the case of rotation, the response spectrum velocity was obtained. Finally, curves estimated for each event were averaged separately for the FSA and RSA method results, distinguished in the article as H/V-FSA and H/V-RSA for the translations and T/R-FSA and T/R-RSA for the rotations.

4 Results

The results of comparisons obtained from the H/V-FSA and H/V-RSA showed that H/V-averaged spectrum curves distinguished similar resonance frequencies. However, the H/V-RSA presented a lower level of amplification than the H/V-FSA. Nevertheless, in the case of the comparison for the rest of the directions, the obtained resonance frequency values in some cases were divergent and dependent on the method used (see Figures 2–4).

Figure 4

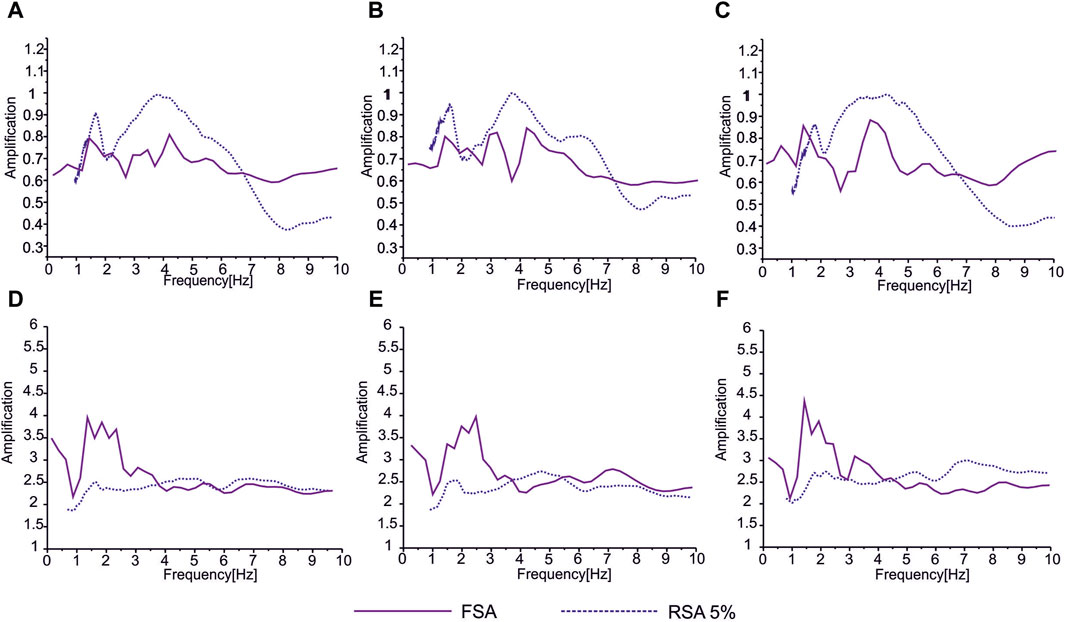
Figure 4. HVSR and TRSR amplification curves obtained for JAN station records: (A) average TRSR curve; (B) EW-direction TRSR curve; (C) NS-direction TRSR curve; (D) average HVSR curve; (E) EW- direction HVSR curve; and (F) NS-direction HVSR curve.

Considering the results of the averaged HVSR estimations for the PLA station, the resonance frequency derived from H/V-FSA and H/V-RSA reached 4.2 Hz and 4.5 Hz, respectively. The H/V-RSA for the horizontal planes showed unchangeable resonance frequency values, the same as for the averaged HVSR. However, the horizontal H/V-FSA showed that the resonance frequency reached 6.0 Hz for the E–W direction, while for the N–S direction, it was 4.2 Hz. Nevertheless, the TRSR results showed consistency in the resonance frequency estimation on analyzed planes. Therefore, T/R-FSA and the T/R-RSA showed that the resonance frequency was 5.8 Hz and 5.7 Hz, respectively.

In the case of the IMI station, the H/V-FSA showed more than one general maximum: at 1.6 Hz (1.4 Hz in the case of the NS direction) and 2.2 Hz (2.4 Hz in the case of the EW direction). Data obtained from the H/V-RSA showed only one amplification maximum at 1.6 Hz despite the analyzed plane. The rotational amplification curve estimated from the T/R-FSA method showed three peaks at 1.8 Hz, 3.4 Hz, and 4.6 Hz, while based on the second method, two amplification peaks were found at 1.8 Hz and 4.6 Hz. The analyzed amplification spectrum of the translations from the ZIE station showed similarity to those estimated from the IMI station. It is worth highlighting that the both the IMI and ZIE stations were located close to each other but mounted on various foundations. The H/V-FSA showed two general maximums, at 1.6 Hz (1.4 Hz in the case of the NS direction) and 2.2 Hz, while the H/V-RSA derived only one maximum at 2.0 Hz (2.4 in the case of the EW direction). The T/R-FSA showed four amplification maximums, i.e., at 1.4 Hz, 2.0 Hz, 3.4 Hz, and 4.6 Hz, but the dominant, characterized by the highest amplification value, was at 2.0 Hz. The T/R-RSA approach distinguished the amplification peaks at 1.1 Hz and 4.4 Hz. The second amplification peak can be distinguished at 1.75 Hz but only during exact comparison to the T/R-FSA results.

Taking into consideration the JAN station, the averaged amplification curves of the translations presented peaks at 1.5 Hz, 2.0 Hz, and 2.4 Hz for the H/V-FSA. The H/V-RSA produced amplification peaks at 1.9 Hz. Considering the EW direction, the resonance frequency was 1.8 Hz for the H/V-RSA, and only the second maximum at 2.4 Hz was distinguishable for the H/V-FSA. On the other hand, the NS direction presented only the first maximum at 1.6 Hz for the H/V-FSA, while in the case of the H/V-RSA, it was impossible to find the resonance frequency. The averaged T/R-RSA allowed us to distinguish the resonance frequency at 1.8 Hz and 4.0 Hz, while for the T/R-FSA, the general maximums were observed at 1.8 Hz and 4.4 Hz. Considering the NS direction, the resonance frequency was 1.8 Hz for the T/R-RSA, and three peaks at 0.8 Hz, 1.8 Hz, and 4.0 Hz were distinguishable for the T/R-FSA. Nevertheless, in the case of the EW plane, the T/R-RSA generated a maximum at 1.8 Hz, while the T/R-FSA produced four distinguishable maximums at 1.0 Hz, 2.0 Hz, 3.2 Hz, and 4.4 Hz. Each of the distinguished amplification peaks fulfilled the SESAME criteria of peak reliability, e.g., the standard deviation ranges of resonant frequency (SESAME; 2004).

5 Discussion

5.1 Comparison of the RSA and FSA results

First, a comparison between H/V curve estimation was presented by using the FSA and the RSA. Generally, as was mentioned by Zhu et al. (2020), the FSA produced more amplification peaks than the RSA. As a consequence, the determination of the site effect parameters may generate disputes. However, estimating the H/V curves using the RSA cannot be treated as a method that specifies the site effect parameters, which confirms the spectrum curve from the JAN and ZIE stations. Considering the results for the JAN station, the translational spectrum curves produced an unreadable peak. On the contrary, in the case of the rotation, apart from the main peak, the second maxim at the main peak was observed for a wide frequency range, which excluded the determination of the resonance frequency. On the other hand, the maximum was clearly defined in the FSA in the respective frequency range. Therefore, in that case, only the results of the geophysical surveys may clearly define the site effect parameters of the JAN station proximity. Completely opposite observations to the JAN situation were obtained at the ZIE station, where the RSA method, in contrast to the FSA, did not produce an amplification peak of the rotational motion. A theoretical explanation of that fact may be that the close distance to the walls, which should avoid the occurrence of the torsion, damped the measuring signals or the position of the sensors was not in the mass center of the building (e.g., Gosar et al., 2010). The above explanation is supported by the PLA station results, where the sensors were mounted on the separated basement postument plinth far from the walls.

However, it could not be ignored that in the case of translational measurements, the RSA and FSA produced comparable general peaks to that obtained from the IMI station. Moreover, the TRSR derived from the FSA also presented a comparable amplification maximum to that obtained from the IMI station. Therefore, the reason for that observation can be treated as an influence on the dimension of the floor on the estimated response spectrum, as discussed by Falamarz-Sheikhabadi and Ghafory-Ashtiany (2015), which affected the torsional spectrum curve and, therefore, affected the whole TRSR (derived a the spectral ratio between the vertical and horizontal components). As was pointed out by Falamarz-Sheikhabadi and Ghafory-Ashtiany (2015), the effects of the kinematic soil–structure interaction may significantly affect the rotational measurement more than translational measurement due to the tendency to obtain higher-frequency content by rotational motion compared to the translations (Trifunac, 1982; Zembaty, 2009). Consequently, the torsion values in the building due to foundation interaction may be lower than those in the case of free-field measurements at the same site.

Nevertheless, the tendency of rotations to obtain higher-frequency content was presented by comparing the central frequency values of the Fourier spectrum between rotations and translations (Zembaty, 2009). Still, that fact was also observed in the response spectrum comparison (Bońkowski et al., 2019) Considering the rest of the analyzed stations, the RSA confirmed the general peaks obtained by the FSA and precisely determined the primary resonance frequency. A separate aspect is connected with the frequency character of the rotational motion.

5.2 The reasons for the difference between the rotational and translational site effect parameters

Recent studies showed that rotational motion is characterized by higher frequency values than those of translational motion (e.g., Trifunac, 1982; Zembaty, 2009; Fuławka et al., 2020). In the case of the amplification spectrum analysis, obtaining high values of the resonant frequency by the rotational motion was observable for all stations apart from the JAN station data analysis. The derived values for the IMI and PLA stations suggested that a shallower geological layer produced rotational resonance than in the case of translations.

A potential explanation of the observation was related to the influence of the compaction level of the geological structures on rotational resonance generation, which means that the fracturing of the geological layers may be responsible for amplifying the registered rotational signal (Nawrocki et al., 2022). The occurrence of the shallow fracturing of the Carboniferous layer below PLA station and Triassic rocks below the IMI station may be responsible for higher resonance frequency values of translations than those of the rotations. However, the results from the JAN station pointed out that deeper layers produced rotational resonance than those in the case of the translations. Considering the assumption of the presented theory, the results suggested strong compaction of the geological material. They excluded the trend invariability to obtain higher resonance frequency values by rotational motion. Taking into account research presented by Singh et al. (2020), the wavefield gradient measurements to which strain and rotations belong are influenced by geological heterogeneities. Altering the signal phase and amplitude is considered an effect of the impact of the heterogeneities on the rotations. Consequently, different geological layers can produce the rotational site effect than the translational rotation.

A separate aspect of the rotational site effect is related to the obtained amplification values compared to translations. In the case of the presented results during that research, rotational amplification tends to obtain lower values than translations. However, considering the research presented by Ringler et al. (2018), the rotational H/V spectrum may produce higher amplification values than translations. Consequently, local site circumstances impact the rotational and translational motion on different levels, and obtaining a lower amplification value by rotational motion cannot be treated as a constant.

5.3 Frequency characteristic of the H/V ratio

It is extremely difficult to ignore the fact that the estimation of the H/V spectrum by using only the RSA method might lead to incorrect data analysis. Considering the frequency character of the used spectral method, it was confirmed that Fourier and response spectral ratios are close at low-frequency ranges, with the first being larger than the latter at higher frequency ranges (Bora et al., 2016).

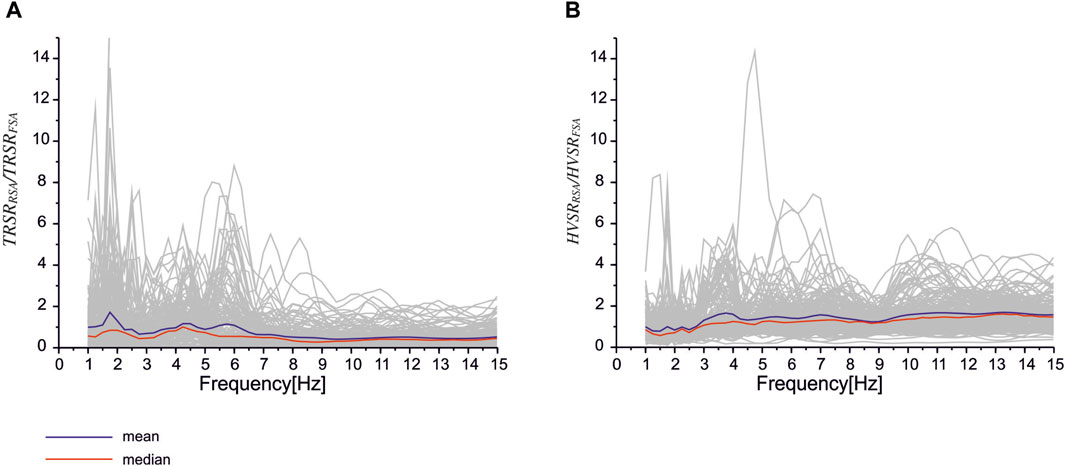
The translational HVSR_RSA/HVSR_FSA derived for the 207 KiK—net sites (Zhu et al., 2019) showed that the ratio was rarely constant in the frequency range between 1 Hz and 8 Hz while rapidly increasing (Zhu et al., 2019). Similar ratios, estimated separately for the rotational (TRSR_RSA/TRSR_FSA) and translational (HVSR_RSA/HVSR_FSA) data, presented different characters of the curve and higher values (Figure 5). The HVSR_RSA/HVSR_FSA in our research increased rapidly from 0.7 to 3.4 in the frequency range between 2.5 Hz and 4.0 Hz. Below 4.0 Hz, fluctuations in the values occurred between 1.2 and 1.5 but under the rarely constant course of the curve. The opposite situation was observed in the case of the TRSR_RSA/TRSR_FSA, where two peaks were generated at 1.74 Hz and 4.24 Hz. Below 4.24 Hz, an increase in the value from 1.0 to 0.4 was observed, while below 7.0 Hz, fluctuations in the values occurred between 0.3 and 0.2 but under a rarely constant course of the curve.

Figure 5

Figure 5. H/V RSA-to-FSA ratio for rotation (A) and translation (B) motions.

The comparisons between rotational and translational ratios of the H/V presented different frequency dependencies between rotational and translational data, which were published by Zhu et al. (2019). The scenario-dependence effect, which affects the results of the response spectrum analysis, may be one of the relevant points in the presented results by us and Zhu et al. (2019). However, a separate aspect is connected with the event type: which was chosen for the analysis—far-field or near-field? Considering the KiK-net database, it is supposed that far-field events were analyzed by Zhu et al. (2019). The near-field events registered up to 20 km (Sharma et al., 2021) are characterized by a shorter duration and higher frequency content than far-field events (Davoodi and Mani, 2015). Moreover, the response spectrum comparison between the records considered as the far-field and near-field shows that far-field events cause a higher-peak response than near-field ones. Considering that the presented results of our studies were performed for the near-field events, it is supposed that the critical issue of the differences in HVSR_RSA/HVSR_FSA curves is connected with the type of analyzed events.

6 Conclusion

The presented study compared the estimated H/V curves between Fourier and response spectrum analysis methods for the rotational and translational motion signals. Generally, the RSA method clarified the amplification peaks in a comparable frequency range to the FSA, except in the case of considering the stations where the sensors were mounted on the document or in the thin value. For the stations where sensors were mounted on the floor, determining site effect parameters from the RSA method was less accurate or impossible. In that situation, the H/V ratio estimated from the FSA method produced a more detailed spectrum curve despite the possibility of multi-peak generation. Considering rotational motion, the size of the floor where the sensors were mounted has a more significant impact on the calculated spectrum than in the case of translational motion analysis.

The H/V ratio estimated from the RSA and the FSA presented different frequency characters in previous studies. Consequently, the critical issue connected with the scenario dependence, which affects the RSA method, should be considered on a divisional basis of near-field and far-field events. Therefore, the estimation of the H/V ratio using the RSA method should be considered an additive tool to verify the prominent amplification peak derived from the classical Nakamura approach but not primary.

Data availability statement

The datasets for this study can be found in the Central Mining Institute Repository (https://grss.gig.eu/repozytorium/). The data can be obtained by contacting the Department of Geology and Geophysics of the Central Mining Institute (Grzegorz MUTKE: Zy5tdXRrZUBnaWcuZXU=). More information on the R-1, EA-120, and DR-4000 instruments is available at www.eentec.com (last accessed on 07 July 2020).

Author contributions

DN: investigation, methodology, resources, visualization, writing–original draft, and writing–review and editing. MM: conceptualization, funding acquisition, investigation, and writing–review and editing. LT: funding acquisition, methodology, supervision, validation, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors thank Professor Grzegorz Mutke from the Central Mining Institute in Katowice for sharing the registered signal of induced seismic events, registered at the Upper Silesian Coal Basin in Poland.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albarello, D. (2001). Detection of spurious maxima in the site amplification characteristics estimated by the HVSR technique. Bull. Seismol. Soc. Am. 91, 718–724. doi:10.1785/0119990172

CrossRef Full Text | Google Scholar

Bard, P. Y. (2004). “The SESAME project: an overview and main results,” in Proceedings, 13th World conference on earthquake engineering, Canada, August 1-6, 2004 (Vancouver). Paper 2207.

Google Scholar

Bernauer, F., Wassermann, J., and Igel, H. (2012). Rotational sensors—a comparison of different sensor types. J. Seismol. 16, 595–602. doi:10.1007/s10950-012-9286-7

CrossRef Full Text | Google Scholar

Bońkowski, P. A., Zembaty, Z., and Minch, M. Y. (2019). Engineering analysis of strong ground rocking and its effect on tall structures. Soil Dyn. Earthq. Eng. 7. doi:10.1016/j.soildyn.2018.10.026

CrossRef Full Text | Google Scholar

Bora, S. S., Scherbaum, F., Kuehn, N., and Stafford, P. (2016). On the relationship between Fourier and Response spectra: implications for the adjustment of empirical ground-motion prediction equations (GMPEs). Bull. Seismol. Soc. Am. 106, 1235–1253. doi:10.1785/0120150129

CrossRef Full Text | Google Scholar

Z. Buła, and A. Kotas (1994). Geological atlas of the upper silesian Coal Basin, part III.Structural-geological maps 1:100 000 (Warszawa: Państwowy Instytut Geologiczny).

Google Scholar

Davoodi, M., and Mani, S. (2015). Assessment of near-field and far-field strong ground motion effects on soil-structure SDOF system. Int. J. Civ. Eng., 153–166. doi:10.22068/IJCE.13.3.153

CrossRef Full Text | Google Scholar

Falamarz-Sheikhabadi, M. R., and Ghafory-Ashtiany, M. (2015). Rotational components in structural loading. Soil Dyn. Earthq. Eng. 75, 220–233. doi:10.1016/j.soildyn.2015.04.012

CrossRef Full Text | Google Scholar

Fuławka, K., Pytel, W., and Pałac-Walko, B. (2020). Near-field measurement of six degrees of freedom mining-induced tremors in lower silesian copper basin. Sensors 20, 6801. doi:10.3390/s20236801

PubMed Abstract | CrossRef Full Text | Google Scholar

Gosar, A., Rošer, J., Šket Motnikar, B., and Zupančič, P. (2010). Microtremor study of site effects and soil-structure resonance in the city of Ljubljana (central Slovenia). Bull. Earthq. Eng. 8, 571–592. doi:10.1007/s10518-009-9113-x

CrossRef Full Text | Google Scholar

Jureczka, J., Aust, J., Buła, Z., Dopita, M., and Zdanowski, A. (1995). Geological map of the upper silesian Coal Basin (carboniferousiferous subcrop) 1:200 000. Państw. Inst. Geol. Warszawa.

Google Scholar

Kalab, Z., Knejzlik, J., and Lednicka, M. (2012). Application of newly developed rotational sensor for monitoring of mining-induced seismic events in the Karvina region. ActaGeodyn. Geomater. 2 (170), 197–205. doi:10.13168/AGG.2013.0020

CrossRef Full Text | Google Scholar

Lee, W. H. K., Huang, B. S., Langston, C. A., Lin, C. J., Liu, C. C., Shin, T. C., et al. (2009). Review: progress in rotational ground motion observations from explosions and local earthquakes in Taiwan. Bull. Seismol. Soc. Am. 99 (2B), 958–967. doi:10.1785/0120080205

CrossRef Full Text | Google Scholar

Lin, C. J., Liu, C. C., and Lee, W. H. (2009). Recording rotational and translational ground motions of two TAIGER explosions in northeastern Taiwan on 4 March 2008. Bull. Seismol. Soc. Am. 99 (2B), 1237–1250. doi:10.1785/0120080176

CrossRef Full Text | Google Scholar

Liu, C. C., Huang, B. S., Lee, W. H. K., and Lin, C.-J. (2009). Observing rotational and translational ground motions at the HGSD station in Taiwan from 2007 to 2008. Bull. Seismol. Soc. Am. 99, 1228–1236. doi:10.1785/0120080156

CrossRef Full Text | Google Scholar

Mendecki, M. J., Szczygieł, J., Lizurek, G., and Teper, L. (2020). Mining-triggered seismicity governed by a fold hinge zone: the Upper Silesian Coal Basin, Poland. Eng. Geol. 274, 105728–728. doi:10.1016/j.enggeo.2020.105728

CrossRef Full Text | Google Scholar

Miura, H., Okamura, T., Matsuoka, M., Leal, M., García, H., and Pulido, N. (2019). Empirical models for surface- and body-wave amplifications of response spectra in the bogotá basin, Colombia. Bull. Seismol. Soc. Am. 109, 987–1004. doi:10.1785/0120180154

CrossRef Full Text | Google Scholar

Mutke, G., Lurka, A., and Zembaty, Z. (2020). Prediction of rotational ground motion for mining-induced seismicity - case study from Upper Silesian Coal Basin, Poland. Eng. Geol. 276, 105767–767. doi:10.1016/j.enggeo.2020.105767

CrossRef Full Text | Google Scholar

Nakamura, Y. (1989). A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. QR RTR 130, 25–33.

Google Scholar

Nawrocki, D., Mendecki, M., and Teper, L. (2021). Rotational-translational scaling relations from induced seismic events – comparison before and after amplification correction. Explor. Geophys. Remote Sens. Environ. 28, 18–28. doi:10.26345/egrse-018-21-202

CrossRef Full Text | Google Scholar

Nawrocki, D., Mendecki, M., and Teper, L. (2022). Estimation of site resonance frequency using HVSR method for rotational and translational signals: result comparison from Fourier and response spectrum methods. Proc. 3^rd ECEES, Buchar. Romania.

Google Scholar

Pastén, C., Sáez, M., Ruiz, S., Leyton, F., Salomón, J., and Poli, P. (2015). Deep characterization of the santiago basin using HVSR and cross-correlation of ambient seismic noise. Eng. Geol. 201, 57–66. doi:10.1016/j.enggeo.2015.12.021

CrossRef Full Text | Google Scholar

Pinzón, L. A., Pujades, L. G., Macau, A., Carreño, E., and Alcalde, J. M. (2019). Seismic site classification from the horizontal-to-vertical response spectral ratios: use of the Spanish strong-motion database. Geosciences 9 (7), 294. doi:10.3390/geosciences9070294

CrossRef Full Text | Google Scholar

Ringler, A., Anthony, R., Holland, A., Wilson, D., and Lin, C. J. (2018). Observations of rotational motions from local earthquakes using two temporary portable sensors in waynoka, Oklahoma. Okla. Bull. Seismol. Soc.Am. 108. doi:10.1785/0120170347

CrossRef Full Text | Google Scholar

Rong, M. L. Y., Fu, Z., Wang, X., Li, N. S., Carpenter, E. W., Lyu, Y., et al. (2017). On the amplitude discrepancy of HVSR and site amplification from strong-motion observations. Bull. Seismol. Soc.Am. 107, 2873–2884. doi:10.1785/0120170118

CrossRef Full Text | Google Scholar

Rupakhety, R., and Sigbjörnsson, R. (2013). Rotation-invariant measures of earthquake response spectra. Bull. Earthq. Eng. 11, 1885–1893. doi:10.1007/s10518-013-9472-1

CrossRef Full Text | Google Scholar

Sbaa, S., Hollender, F., Perron, V., Imtiaz, A., Bard, P.-Y., Mariscal, A., et al. (2017). Analysis of rotation sensor data from the SINAPS@ Kefalonia (Greece) post-seismic experiment—link to surface geology and wavefield characteristics. Earth Planets Space 2017 (69), 124–219. doi:10.1186/s40623-017-0711-6

CrossRef Full Text | Google Scholar

Sharma, V., Shrimali, M. K., Bharti, S. D., and Datta, T. K. (2021). Seismic fragility evaluation of semi-rigid frames subjected to near-field earthquakes. J. Constr. Steel Res. 176, 106384. doi:10.1016/j.jcsr.2020.106384

CrossRef Full Text | Google Scholar

Singh, S., Capdeville, Y., and Igel, H. (2020). Correcting wavefield gradients for the effects of local small-scale heterogeneities. Geophys. J. Int. 220 (2), 996–1011. doi:10.1093/gji/ggz479

CrossRef Full Text | Google Scholar

Site EffectS Assessment using AMbient Excitations (SESAME) (2004). Guidelines for the implementation of the H/V spectralratio technique on ambient vibrations measurements, processing and interpretation. SESAME Eur. Res. Proj. WP12 Deliv. D23.12.

Google Scholar

Stafford, P., Rodriguez-Marek, A., Edwards, B., Kruiver, P., and Bommer, J.(2017). Scenario dependence of linear site-effect factorsfor short-period response spectral ordinates. Bull. Seismol. Soc.Am. 107, 2859–2872. doi:10.1785/0120170084

CrossRef Full Text | Google Scholar

Stambouli, A. B., Zendagui, D., Bard, P. Y., and Derras, B. (2017). Deriving amplification factors from simple site parameters using generalized regression neural networks: implications for relevant site proxies. Earth Planets Space 69, 99. doi:10.1186/s40623-017-0686-3

CrossRef Full Text | Google Scholar

Stanko, D., and Markušić, S. (2020). An empirical relationship between resonance frequency, bedrock depth and VS30 for Croatia based on HVSR forward modelling. Nat. Hazards 103 (3), 3715–3743. doi:10.1007/s11069-020-04152-z

CrossRef Full Text | Google Scholar

Stanko, D., Markušić, S., Strelec, S., and Gazdek, M. (2017). HVSR analysis of seismic site effects and soil-structure resonance in Varaždin city (North Croatia). Soil Dynam Earthq. Eng. 92, 666–677. doi:10.1016/j.soildyn.2016.10.022

CrossRef Full Text | Google Scholar

Stec, K. (2006). Characteristics of seismic activity of the upper silesian Coal Basin in Poland. Geophys. J. Int. 168, 757–768. doi:10.1111/j.1365-246X.2006.03227.x

CrossRef Full Text | Google Scholar

Stephenson, W. J., Hartzell, S., Frankel, A., Asten, M., Carver, D., and Kim, W. (2009). Site characterization for urban seismic hazards in lower Manhattan, New York City, from microtremor array analysis. Geophys Res. Lett. 36. doi:10.1029/2008GL036444

CrossRef Full Text | Google Scholar

Stupazzini, M., de la Puente, J., Smerzini, C., Käser, M., Igel, H., and Castellani, A. (2009). Study of rotational ground motion in the near-field region. Bull. Seismol. Soc. Am. 99 (2B), 1271–1286. doi:10.1785/0120080153

CrossRef Full Text | Google Scholar

Suryanto, W. (2006). Rotational motions in seismology: theory and application. LMU München Fac. Geosciences. Dissertation.

Google Scholar

Teper, L. (2000). “Geometry of fold arrays in the Silesian-Cracovian region of southern Poland,”Forced folds and fractures. Editors J. W. Cosgrove, and M. S. Ameen (London: Geological Society, London, Special Publications).

Google Scholar

Trifunac, M. D. (1982). A note on rotational components of earthquake motions on ground surface for incident body waves. Int. J. Soil Dyn. Earthq. Eng. 1, 11–19. doi:10.1016/0261-7277(82)90009-2

CrossRef Full Text | Google Scholar

Wang, Z., Carpenter, N. S., and Woolery, E. W. (2019). Horizontal-to-Vertical spectral ratio of S-waves and SH-wave transfer functions at the vertical seismic and strong-motion arrays in the Central United States. J. Appl. Geophys. 162, 64–71. doi:10.1016/j.jappgeo.2018.10.017

CrossRef Full Text | Google Scholar

Zembaty, Z. (2006). “Deriving seismic surface rotations for engineering purposes,” in Earthquake source asymmetry, structural media and rotation effects. Editors R. Teisseyre, M. Takeo, and E. Majewski (Berlin, Heidelberg: Springer), 549–568.

Google Scholar

Zembaty, Z. (2009). Tutorial on surface rotations from wave passage effects: stochastic spectral approach. Bull. Seismol. Soc. Am. 99, 1040–1049. doi:10.1785/0120080102

CrossRef Full Text | Google Scholar

Zembaty, Z., Mutke, G., Nawrocki, D., and Bobra, P. (2017). Rotational ground-motion records from induced seismic events. Seismol. Res.Lett. 88 (1), 13–22. doi:10.1785/0220160131

CrossRef Full Text | Google Scholar

Zhao, J. X., and Xu, H. (2013). A comparison ofV_S30and site period as site-effect parameters in response spectral ground-motion prediction equations. Bull. Seismol. Soc. Am. 103, 1–18. doi:10.1785/0120110251

CrossRef Full Text | Google Scholar

Zhu, C., Cotton, F., and Pilz, M. (2019). Testing the depths to 1.0 and 2:5 km=s velocity isosurfaces in a velocity model for Japan and implications for ground motion modelling. Bull. Seismol. Soc. Am. 109, 2710–2721. doi:10.1785/0120190016

CrossRef Full Text | Google Scholar

Zhu, C., Cotton, F., and Pilz, M. (2020). Detecting site resonant frequency using HVSR: fourier versus response spectrum and the first versus the highest peak frequency. Bull. Seism. Am. 110 (2), 427–440. doi:10.1785/0120190186

CrossRef Full Text | Google Scholar