
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 22 May 2024
Sec. Geohazards and Georisks
Volume 12 - 2024 | https://doi.org/10.3389/feart.2024.1402798
This article is part of the Research TopicInvestigation, Monitoring, Stability and Risk Assessment of GeohazardsView all 15 articles
A substantial number of shallow landslides can still occur in areas with high vegetation cover under extreme rainfall. The cause and mechanism of this type of landslide remain unknown, and thus a case study is selected for study in this paper. The extreme rainfall from June 10–13, 2019, caused mass landslides throughout Mibei Village. Most landslides happened in well-vegetated areas, and some even transformed into debris flows. This paper presents detailed field investigations on 31 of them, the result of which were used to perform numerical simulations and ring shear tests. The objective of this study was to investigate the damage cause and mechanism of well-vegetated soil slopes under extreme rainfall. The results indicate that vegetation exerts a dual effect on slope stability. Within the rhizosphere zone, roots significantly enhance the soil shear strength, thereby reducing the likelihood of slope instability. Simultaneously, the rhizosphere zone exhibits enhanced permeability and acts as a relatively impermeable layer at the bottom, which makes the shallow layer of the slopes more easily saturated by rainfall infiltration. The slopes are prone to instability at the soil layer situated below the bottom of the rhizosphere zone, and mostly are translational slides with suddenness. The main triggering factor for the landslide is the presence of positive pore water pressure in the soil, which makes the matrix suction lost and the effective stress reduced. The slip zone soil exhibits negative dilatancy, while the saturated slip soil undergoes liquefaction, which can make landslides conversion into debris flows.
Rainfall is the common exogenous factor contributing to landslide occurrence (Guzzetti et al., 2008; Picarelli et al., 2020). The transformation of groundwater by rainfall and its complex interaction with the geotechnical body has detrimental effect on the stress environment of slopes, which in turn induces landslides (Zeng et al., 2017; Senthilkumar et al., 2018; Tang et al., 2018). Landslide hazards pose a serious threat to ecology, life safety and infrastructure (Garcia-Delgado et al., 2022; Liang et al., 2022). Consequently, the cognition of the cause and mechanism of landslide is of significant value in risk assessment, preventive measures formulation, engineering design, and environment protection, among others (Grima et al., 2020; Ahmed, 2021; Zhang et al., 2024).
Vegetation can effectively prevent slope disasters through the soil reinforcement by roots and the beneficial hydrological effects that they induce (Leung et al., 2015; Giadrossich et al., 2019; Nguyen et al., 2018; Masi et al., 2021). However, with the increasing occurrence of extreme rainfall caused by global warming, the frequency of mass landslides events on vegetated slopes are being reported (Crozier, 2005; Bellprat et al., 2019). Examples include the January 2011 mass landslides in Rio de Janeiro, Brazil; the July 2013 mass landslides in Qinzhou District, Gansu, China; and the September 2019 mass landslides in the Mengdong Town, Yunnan, China. These group-occurring landslides are invariably accompanied by heavy rainfall and tend to occur on slopes with well-developed vegetation (Nielsen et al., 2016; Li et al., 2020; Yang et al., 2020). It is evident that there are significant questions regarding the role of vegetation in extreme rainfall. Vegetation intercepts only a small fraction of rainfall (Keim and Skaugset, 2003; Kim et al., 2013), and the additional cohesion provided by the root system disappears below the area of root development (Xu et al., 2005; McGuire et al., 2016). The beneficial contributions of vegetation will be subject to a certain degree of attenuation during periods of heavy rainfall. Root-soil interstices and decayed root channels are commonly present in vegetated soil (Benegas et al., 2014; Guo et al., 2019). These large pores facilitate the rainfall infiltration (Cui et al., 2022; Li et al., 2023). Preferential flow significantly increases the rate and volume of rainwater infiltration compared to matrix flow, which in turn more significantly reduces the strength of the geotechnical body. The above effect may outweigh the root consolidation effect, at which point vegetation can negatively affect slope stability (Ghestem et al., 2011; Löbmann et al., 2020).
Some studies seek to elucidate the question through field surveys. Guo et al. (2019) and Qin et al. (2022) conducted comparative analysis of the soil properties of the upper and lower layers of the sliding surface. Their findings indicated that the root-soil composite exhibited higher water content and hydraulic conductivity, which may serve as significant contributing factors in the initiation of landslides. In field investigation of the landslide area in northern Shaanxi and eastern Gansu, China, Li et al. (2022) concluded that tree loading is the main factor triggering shallow landslides. Some scholars have constructed vegetated slopes through cultivation for artificial rainfall experiments. Some scholars have constructed vegetated slopes through cultivation for artificial rainfall experiments. Huang et al. (2023) found that Cynodon dactylon can effectively inhibit soil erosion on slopes, and no landslides occurred during the test. Xu et al. (2024) concluded that revegetation in the Chinese Loess Plateau will reduce gully erosion, while simultaneously promoting shallow landslides. Song and Tan (2024) observed distinct patterns of damage for various herb-developed slopes. Additionally, numerical calculations are applied in this study. Świtała and Wu (2018) proposed a numerical model that can be used to simulate rainfall-induced instability of vegetated slopes by considering coupled mechanical-hydrological system. Brunella et al. (2019) calculated the impact of the root system on rainfall infiltration and analyzed the pore water pressure distribution pattern within the soil. Zhuang et al. (2022) calculated the change in the safety factor and analyzed the location of critical slip surface by integrating the effects of typhoons, rainfall, and trees on slopes.
Existing studies have rarely addressed the formation mechanisms of landslides in vegetated areas, especially the scientific issue of the transformation of such landslides into debris flows. In light of the aforementioned issues, this study selected the Mass Landslides in Mibei Village, Longchuan County, Guangdong Province, China, as the subject of its investigation. Field surveys were conducted to establish a well-vegetated geological slope model and to perform landslide numerical simulation using GeoStudio software. The rainfall infiltration law, the safety factor, and the landslide evolution stage were analyzed. Previous studies have not devoted significant attention to the changes in soil properties that occur during the occurrence of landslides. Therefore, the ring shear tests were employed to study the mechanical properties of soil during shear damage. The results of the numerical simulation and ring shear tests were utilized to elucidate the formation mechanisms of landslides in vegetated areas and the transformation of such landslides into debris flows. This study not only enhances the understanding of the mechanisms underlying such landslides, but also provides a theoretical basis for the prevention and mitigation of disasters.
Mibei Village is located in the northern part of Beiling Town, Longchuan County, Guangdong Province, China, with the center coordinates of 115°18′25″E; 24°38′53″N (Figure 1A). The northern part of Mibei Village is characterized by medium and low mountains, the central part is a valley, and the southern part has low mountains and hills. The mountains and hills account for a large proportion, presenting a typical mountainous–hilly landform. The mountains are steep, the peaks are sharp and cone-shaped, and the valley is “V” shaped. The topography of Mibei Village exhibits considerable variation, with a range of relative height differences of 100–200 m and topographic slopes of 40°–45°. The geological condition of the area is simple (Figure 1B). There are no faults that traverse the area, the bedrock is Late Paleozoic mixed granite, and the surface is exposed by a Quaternary residual layer. The stratum consisted of a granite weathered layer and a residual layer, with a clear stratigraphic boundary. The thickness of the residual layer ranged from 4.21 to 11.60 m, with an average thickness of 9.83 m. The residual soil is hard plastic, slightly wet, and yellowish-brown in color. Quartz grains are visible to the naked eye. The particle grading indicates that the soil type is sandy clay (Zhang et al., 1997). The water-richness of the strata is relatively poor, and due to the high topography, the groundwater is deeper, with an average annual water level of 10.0–14.0 m. The vegetation cover of the study area is high, reaching over 90%. It is dominated by Pinus massoniana and Cunninghamia lanceolata, with a few shrubs and herbs.
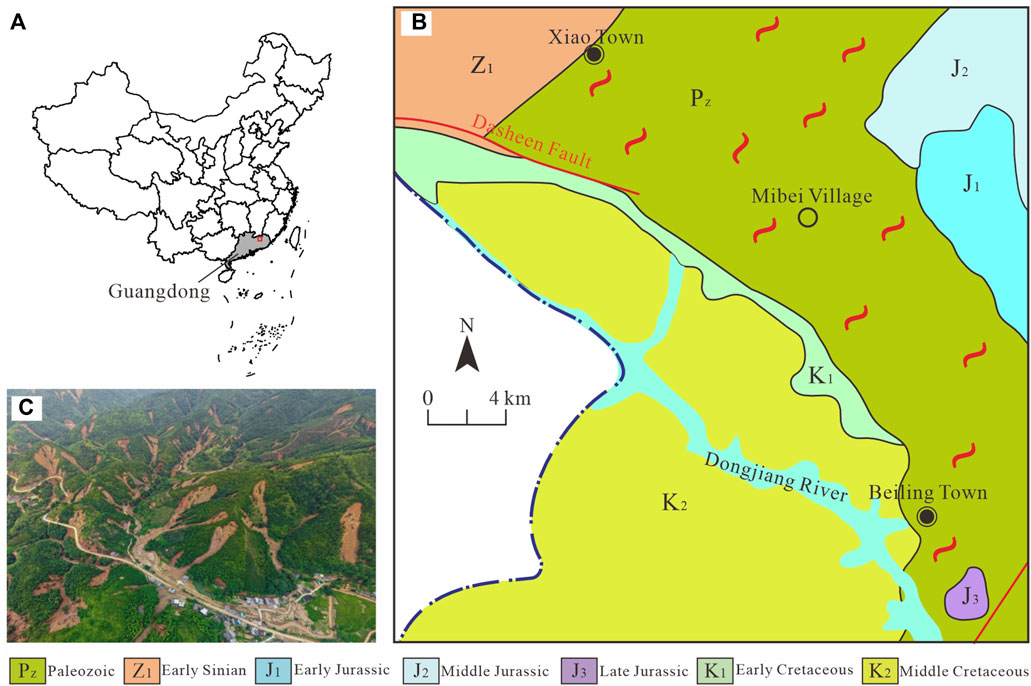
Figure 1. Study area overview map. (A) The study area locality; (B) The geological map of study area; (C) UAV image of Mibei Village mass landslides.
From June 10–13, 2019, a continuous heavy rainfall occurred in Longchuan County, resulting in numerous landslide disasters throughout the county, with Mibei Village being particularly affected. The extreme rainfall (average rainfall intensity 33.15 mm/h) caused the formation of mass landslides in Mibei Village, and the scale affected the entire village (Figure 1C). According to the preliminary investigation, there were nearly 327 landslides of varying sizes and scales occurred in Mibei Village. The landslides were distributed throughout the entire hillside, with no obvious regional concentration. In this event, almost all the landslides occurred on the vegetated slopes, while poorly vegetated hills demonstrated greater stability in the face of heavy rainfall. This distribution pattern prompts consideration of the potential relationship between landslides and vegetation.
Detailed field surveys of 31 landslides were carried out in October 2019 March 2020, respectively (Figure 2). The relative height difference of the landslides was approximately 50–74 m, and the original angle of the landslides was approximately 40°–45°. The maximum thickness of the landslides was 2.5 m, with the majority of landslide body thicknesses were between 1.7 m and 2 m, which were typical shallow soil landslides. Most sliding surfaces were located within the residual layer. Almost all the landslides were translational slides in this event (Figure 3A), showing traction deformation and failure. The top of the trailing edge of the landslide experienced varying degrees of tensile failure, resulting in tension cracks and the overturning deformation of trees (Figure 3B). Some of the landslides transformed into debris flows, with the typical example being landslide No. 11. The landslide lacked an obvious sliding surface and moved towards the slope toe in a fluid form (Figure 3C). The field survey found the presence of a considerable number of large solid particles, with particle sizes ranging from 0.5 to 1 m or even larger. Additionally, poorly rounded particles were observed (Figure 3D), which were formed during the conversion of gravity instability, such as landslides and collapses into debris flows.

Figure 3. Detailed investigation of landslides in the study area. (A) Landslide No. 15 (translational slide); (B) Deformation characteristics; (C) Landslide No. 11 (conversion of landslides into debris flows); (D) Large solid particles.
High vegetation cover is a distinctive feature of this event. The survey found a large number of trees were moved along with the landslide, with the vegetation becoming part of the slide (Figure 4A). The roots were rarely cut off, and the depth of the sliding surface was generally greater than the vertical length of the roots (Figure 4B). In order to investigate the root distribution, the profiles of a depth of 200 cm were excavated at at a distance of 50 cm from the trunk. The number of roots in the root cross-section was quantified using a 20 cm × 20 cm frame, and the diameters of the roots were measured using vernier calipers. Due to the variation in the mean shear strength with root diameter, the average root tensile strength was divided into five different diameter classes, namely, 0.5–1.0 mm, 1.0–2.0 mm, 2.0–5.0 mm, 5.0–10.0 mm, and >10 mm (Ji et al., 2012). This study randomly investigated four groups of roots (Figure 4C). It can be seen that the coarse roots and the high-density area of roots are concentrated at a depth of 1.4–1.6 m below the surface, with the vertical extent of the roots not exceeding 2 m at the longest.
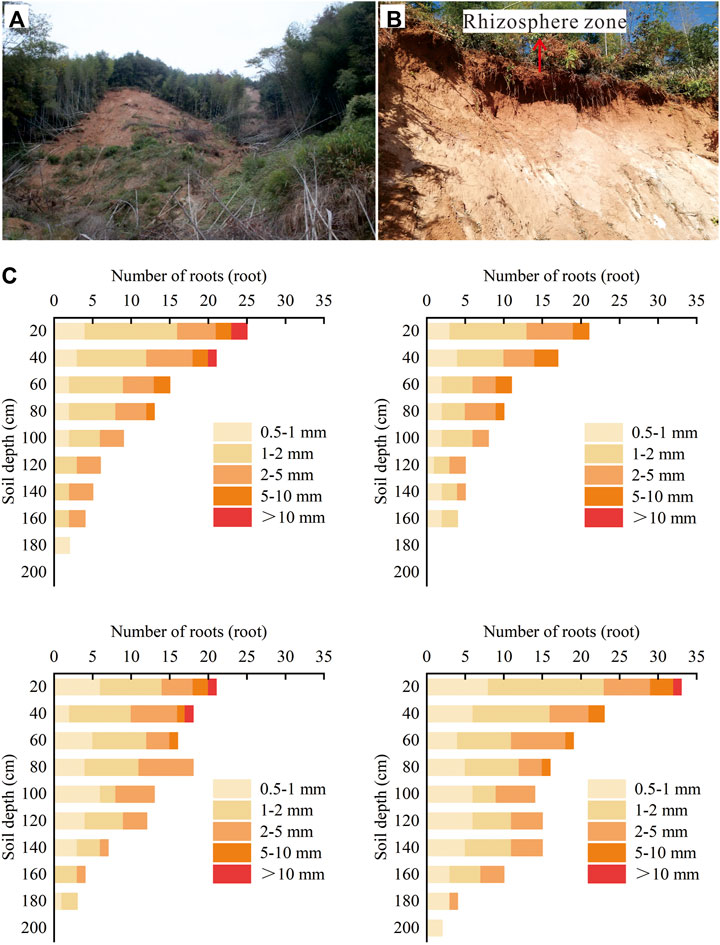
Figure 4. Roots survey in the study area. (A) Plant debris in the slide; (B) Rhizosphere zone at landslide trailing edge; (C) Roots distribution survey.
The impact of vegetation on rainfall-type landslides is mainly manifested in the self-weight above the ground surface, the root mechanical reinforcement and the enhanced permeability in the rhizosphere zone (Vergani et al., 2013; Shao et al., 2015; Reichenbach et al., 2018). This study quantifies these three effects based on field surveys, which mainly provide parameters for numerical simulation, as follows.
This paper converted plant self-weight using uniform load based on the survey of the self-weight of trees within 50 m × 20 m on the slope. The formula is as follows (Zou et al., 2021). The load was calculated using Eq. 1.
The calculation of tree volume was based on the Forest stock volume calculation method. The formula is presented in Eq. 2; (Liu et al., 2017).
Here,
This paper quantifies the root mechanical reinforcement by additional cohesion. The values of additional cohesion were calculated using the corrected Wu–Waldron model, and the results are shown in Figure 5A. The formula is presented in Eq. 3; (Wu, 2013; Zhu et al., 2018).
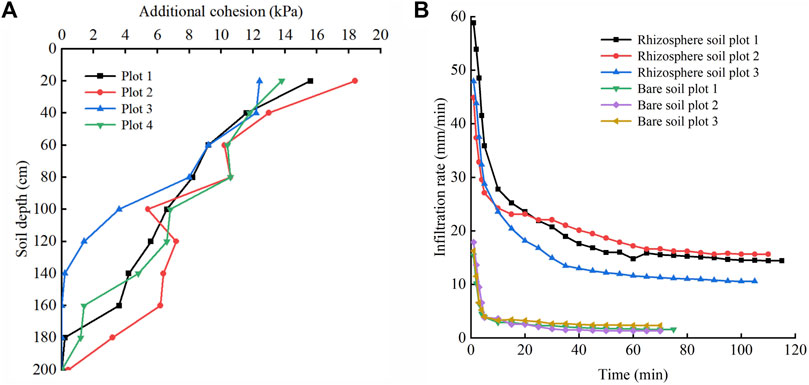
Figure 5. Vegetation effect survey in the study area. (A) Curve of infiltration under different soil conditions; (B) Additional cohesion at different soil depths.
The calculation of the root tensile strength is based on the root tensile strength test. The formula is presented in Eq. 4; (Gong et al., 2021).
Here,
Six plots were randomly selected from the research area to measure the infiltration rate of bare soil and rhizosphere soil using the double-ring method (Figure 5B). The soil saturated permeability coefficient was calculated based on the test result. The formula is presented in Eq. 5; (Chen et al., 2023).
Here,
GeoStudio series analysis software, developed by GEO-SLOPE Canada, is a professional and powerful numerical calculation software. The GeoStido software performs unsaturated seepage-stress analyses by treating each soil layer as a porous medium with internal fluids in accordance with Darcy seepage law. The seepage analysis is independent of the volume change analysis, and the change in pore water pressure obtained from the seepage solution is applied to each loading step of the stress-strain analysis to ensure an effective stress change (GEO-SLOPE International Ltd, 2018a; GEO-SLOPE International Ltd, 2018b). The software has been widely used in studies of rainfall infiltration pattern, landslide mechanism, and landslide early warning (Zhan et al., 2012; Zhang et al., 2020; Li et al., 2023). The GeoStudio software is well-suited for the simulation of soil-type landslide and, thus, is applied in this study. The detailed model is set up and operated as follows.
Pinus massoniana was selected for modeling in this study. This species has well-developed primary roots and sparse lateral roots (Yang et al., 2021). The field survey found that the main root mainly extended to the depth of 1.4–1.6 m, situated at a nearly identical level. The occurrence of the individual rock-soil layers formed by granite weathering is essentially the same and parallel to each other. On this basis, a generalized well-vegetated geological slope model was created (Figure 6). The following simplifications were used in the modeling process. 1) The soil at the depth of the main influence of the roots was defined as the rhizosphere layer. 2) The slope profile was divided into three layers, from top to bottom, the rhizosphere layer (1.5 m thick), the residual layer (8.5 m thick), and the bedrock, respectively. 3) Each geotechnical layer of the slope model was parallel to the slope surface. A monitoring line extending 3 m vertically was set up in the middle of the slope model to study the changes of volumetric water content, pore water pressure, and displacement in the area. The hydrological and physicomechanical parameters of each soil layer applied in the model are shown in Table 1. The weight (γ) and saturated water content (θs) were quantified through conventional soil tests. The saturated permeability coefficient (Ks) was measured by double-ring infiltrometer. The shear strength index was determined by direct shear apparatus. The VG model parameter were measured by pressure plate instrument. The friction angle associated with matrix suction (φb) and residual water content (θr) were taken as empirical values (Tang et al., 2008; Zhan et al., 2012).
The boundary conditions were set as follows. 1) The steady seepage boundary condition. The annual mean groundwater level was set to the constant head boundary on both sides for steady-state analysis. Concurrently, flow boundary with very small value was applied to the slope. This is due to the fact that the maximum negative pore water pressure is not solely contingent upon the height of capillary rise; it is also influenced by the soil permeability coefficient and rainfall infiltration rate. This approach ensures that the initial hydraulic state is more realistic. 2) The transient seepage boundary condition. The zero-flow boundary was set above the initial groundwater, and the slope surface was set as the rainfall infiltration boundary and the potential seepage surface is checked. In the event that the rainfall intensity is less than the soil saturated infiltration coefficient, the rainfall infiltration boundary is calculated based on flow infiltration. Conversely, when the rainfall intensity is greater than the soil saturated infiltration coefficient, the rain infiltration boundary is calculated based on the head. This is in line with the reality. 3) The slope deformation boundary condition: both sides of the model were set to constrain the horizontal displacement boundary, and the bottom of the model was set to constrain the horizontal and vertical displacement boundary. Because this work focuses on a shallow soil landslide, these boundary conditions are reasonable (Gasmo et al., 2000). The model was meshed using a nodal quadrilateral cell with a side length of 1 m. The numbers of nodes and cells in the mesh were 4,197 and 4,058, respectively.
Based on the real-time rainfall of this event, this simulation set up rainfall scenarios with a rain intensity of 33.15 mm/h, and a rainfall duration of 24 h. The specific simulation calculation steps were as follows. 1) The initial volumetric water content distribution in the slope was obtained by applying the SEEP/W module for steady seepage analysis. 2) Based on the initial condition, a transient seepage analysis was carried out by applying rainfall scenarios to obtain the volumetric water content and pore water pressure distribution at different rainfall duration. 3) The SIGMA/W module was applied to couple stress and pore water pressure to obtain the displacement at different rainfall duration, where the stress was obtained from SIGMA/W in situ analysis, and the pore water pressure was obtained from SEEP/W transient analysis. 4) The potential sliding surface was predefined, and the SIGMA/W STRESS analysis type in the SLOPE/W module was applied to calculate the safety factor at different soil depths. The formulas are presented in Eqs 6–8; (GEO-SLOPE International Ltd, 2008).
Here,
An understanding of the mechanical behavior of soil during shear damage contributes to the understanding of landslide mechanisms. The ring shear test can simulate long-distance shear, which is closer to the sliding situation after slope destabilization in the natural state. This approach is designed to restore the alterations in the physical and mechanical properties of the soil. This test used the fully automatic static ring shear instrument produced by Wille Geotechnik company in Germany. The parameters of the test apparatus are as follows: the shear ring has a size of 100 mm × 50 mm × 20 mm (outer ring × inner ring × height), the consolidation pressure ranges from 0 to 1,000 kPa, and the shear rate varies from 0.00001° to 180°/min. The test soil were taken from the soil near the sliding surface at the scarp at the front edge of landslide No. 11, this part of soil can represent the material composition and grain size distribution of the soil near the sliding surface before the landslide occurred. The basic physical property of the soil are shown in Table 2.
Under real conditions, the actual movement of the slide is fast, the pore water pressure in the soil is difficult to discharge timely, so the consolidation un-drained shear was adopted. The steps of the test are as follows. 1) The test soil was dried and configured with four water content soil samples of 22.58% (natural state), 29.63%, 36.69% and 43.74% (saturated state). 2) Based on the slide thickness, the vertical load was calculated to be about 100 kPa. The samples were subjected to a vertical load of 100 kPa for drainage consolidation. 3) The samples were sheared at a constant shear rate of 3 mm/min. The test was stopped when the shear displacement reached 1,000 mm and the shear stress, pore water pressure, shear displacement and vertical displacement during the test were recorded.
Figure 7 shows the pore water pressure and volumetric water content at different soil depth with rainfall duration. The infiltration of rainwater into the slope at the onset of rainfall led to an increase in the volumetric water content and pore water pressure of the soil within a depth of 1.2 m of the rhizosphere layer. This increase was observed to decrease in magnitude with increasing soil depth. Following 4 h of rainfall, the volumetric water content of the rhizosphere soil at the soil interface exhibited a rapid increase. This rate of increase accelerated as the rainfall continued, resulting in the rhizosphere soil near the soil interface reaching saturation after 10 h. Following 12 h of rainfall, the pore water pressure of the rhizosphere soil reached a positive value and increased with increasing soil depth, indicating that the soil layer had reached saturation. Concurrently, the volumetric water content and pore water pressure of the residual soil in the vicinity of near the soil interface also increased slowly, with the rate of increase decreasing with soil depth.
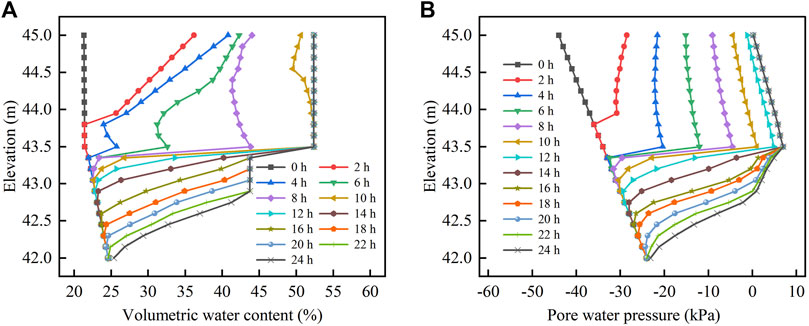
Figure 7. Slope seepage characteristics at monitoring line. (A) Variation of volume water content with elevation; (B) Variation of pore water pressure with elevation.
Figure 8 reflects the evolution of the saturated stagnant water on the slope during rainfall. Following 4 h of rainfall, the transient saturated zone was first formed on the surface of the residual layer at the foot of the slope, which was small in extent and very thin in thickness (Figure 8A). As the rainfall continued, the transient saturated zone gradually moved upward along the interface (Figure 8B). After 10 h of rainfall, the transient saturated zone gradually evolved to be approximately parallel to the interface and located between the upper and lower soil layers (Figure 8C). After 12 h of rainfall, the transient saturated zone almost filled the entire residual layer by diffusion (Figure 8D). As the rainfall continued, the infiltration of the lower residual soil resulted in the gradual downward migration of the transient saturated zone, ultimately reaching a depth of 2.02–3.05 m below the slope (Figure 8E). The presence of the slope resulted in the continuous seepage of rainwater from the upper portion, which in turn caused the transient saturated zone at the slope toe to remain the thickest throughout the whole process. Simultaneously, the rate of rainwater infiltration in the residual layer was controlled by its own permeability, thereby resulting in the expansion rate of the saturated zone was slow within the residual layer.
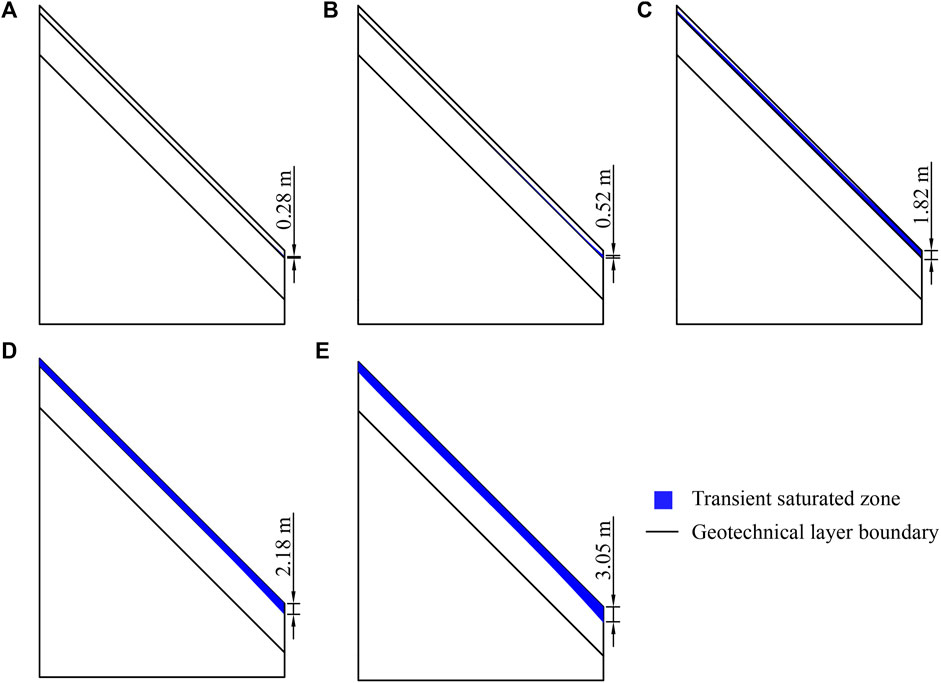
Figure 8. Schematic of the evolution of saturated stagnant water area of slope. (A) Rainfall duration 4 h; (B) rainfall duration 5 h; (C) Rainfall duration 10 h; (D) Rainfall duration 14 h; (E) Rainfall duration 24 h.
The results indicate that rainfall infiltration does not directly recharge groundwater. Instead, a certain thickness of transient saturation zone is formed. The formation of this phenomenon can be attributed to the enhancement of the permeability of the rhizosphere layer by the vegetation macropore. When rainfall infiltrates to the bottom of the rhizosphere layer, the poor permeability of the lower soil results in a significant reduction in the rainwater infiltration rate. Rainwater from the upper soil is unable to dissipate in a short period of time, resulting in the formation of a temporary groundwater table on the soil interface. This, in turn, causes a significant rise in the volumetric water content and pore water pressure. As the rainfall continues, the water table at the soil interface gradually rises, resulting in a faster increase in volumetric water content of the rhizosphere soil in the vicinity of the interface. Due to the stagnation effect, the transient saturated zone initially spreads upward from the soil interface, so that the rhizosphere layer is the first to saturate. Subsequently, the surface infiltration flow rate is greater than the outflow rate of the wetting front, resulting in the gradual accumulation of uninfiltrated rainwater above the wetting front. This causes a larger area of soil saturation, which demonstrates that the area of the transient saturated zone continues to expand to the residual layer as the rainfall infiltration continues.
Figure 9A shows the safety factor with rainfall duration at different soil depths. 1) During the rainfall, the safety factor at a depth of 1.5 m was consistently greater than 1.2, indicating that the slope is unlikely to slide at the soil interface. This result differs from the traditional view. Previous studies have concluded that when the permeability of the upper soil layer is higher than that of the lower layer, the infiltrated rainwater gathers at the soil interface to form stagnant water, which generates positive pore water pressure and poses a threat to slope stability. This results in the potential sliding surface to appear at the soil interface (Zhan and Ng, 2004; Han and Huang, 2012). The phenomenon observed in well-vegetated slopes can be attributed to the significant shear strength provided by roots, which results in an initial slope stability coefficient at the soil interface that is 34.4%–46.8% higher than that of the lower residual layer. This makes it difficult for the slope to slide even even if the rhizosphere layer is filled with water. 2) When rainwater infiltrated into the residual layer, the root mechanical reinforcement disappeared and the slope was more likely to slide in the residual layer. Additionally, there were also significant differences in the slope stability at different soil depths within the residual layer. During the rainfall, the safety factor at the soil depths of 1.7 m, 1.9 m, 2.1 m, and 2.3 m was reduced to less than 1, indicating potential for landslide occurrence in this depth range. This is because the transient saturated zone spreads downward, saturating or nearly saturating the soil in this depth range, which in turn reduces the soil shear strength and causes the slope to be prone to instability. 3) Following the cessation of rainfall, the safety factor at 2.5 m and 2.7 m remained greater than 1, indicating that the likelihood of a landslide occurring in this depth range was low. This is because the soil is still unsaturated at this depth until the end of rainfall, and the soil still maintains good shear strength. Simultaneously, the soil layer is thin, and the sliding force generated by it is insufficient to make the slope slide at this soil depth. This analysis shows that the potential sliding surface of the slope is more likely to be within the saturated or nearly saturated soil layers of the residual layer.
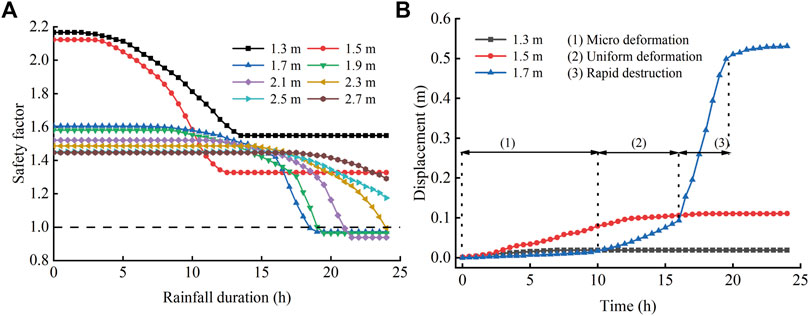
Figure 9. Deformation characteristics of slope. (A) Curve of safety factor at different soil depths changing with rainfall time; (B) Curve of monitoring point displacement changing with rainfall time.
Figure 9B shows the displacements of the monitoring points at different depths with rainfall duration. The displacements of the monitoring points at 1.3 m depth and 1.5 m depth were minimal, with maximum displacements of 0.02 m and 0.09 m, respectively. The displacement of the monitoring point at a depth of 1.7 m exhibited an overall increasing trend, with a maximum displacement of 0.54 m. The preceding analysis indicates that the slope tends to slide at a depth of 1.7 m. Consequently, the displacement curve of the monitoring point at this depth is more realistic in reflecting the process of the landslide evolution. The landslide evolution process was summarized in three stages according to the displacement change characteristics. The initial stage, the micro-deformation phase, is characterized by an extremely slow increase in displacement, with a change of only 0.01 m. The curve remained relatively stable throughout this phase. The second stage, the uniform deformation phase, is distinguished by a uniform increase in displacement of 0.08 m, with a relatively constant gradient of the curve. The final stage, the rapid destruction phase, is marked by a dramatic increase in displacement, reaching 0.41 m in a short period of time. The curve exhibits a nonlinear growth during this phase, indicating that the landslide was sudden in nature.
Figure 10 shows the variation of shear stress, pore water pressure and vertical displacement with shear displacement for samples with different water contents. 1) As seen in Figure 10A, the height of sample 1 exhibited a continuous decline following the commencement of the test, culminating in a reduction of approximately 1.77 mm. This outcome indicates that the sample represents a negative dilatancy soil. Due to the low initial water content, the reduction in soil volume did not result in a notable alteration in pore water pressure. The shear stress of sample 1 exhibited a continuous increase initially, reaching a peak strength of 95.39 kPa. Subsequently, the shear stress exhibited slight fluctuations before stabilising at approximately 90.24 kPa. This indicates that the shear strength caused by shearing shrinkage did not undergo significant changes, and that no notable alterations in pore water pressure under the conditions of low water content. 2) As seen in Figure 10B, the sample height exhibited a similar decline to that observed in sample 1, resulting from the negative dilatancy of the soil. This decline culminated in a reduction of approximately 2.05 mm. The shear stress of the sample exhibited a rapid increase, reaching 90.30 kPa at the outset of the test. Thereafter, a slight decrease was observed, followed by a stabilization at approximately 83.79 kPa. In comparison to sample 1, sample 2 owned a higher water content. Consequently, the pore water pressure of the sample exhibited a slight increase during the test, and the residual shear strength was also slightly lower than that of sample 1. 3) As seen in Figure 10C, the height of sample 3 exhibited a decline of approximately 2.35 mm. During the test, the sample shear stress decreased rapidly to approximately 69.59 kPa after reaching a peak value of 92.24 kPa. However, the shear stress also decreased gradually to approximately 36.58 kPa due to the continuous increase in pore water pressure caused by negative dilatancy. In comparison to samples 1 and 2, the pore water pressure of sample 3 exhibited a more pronounced change during the test, reaching a peak value of 41.76 kPa. The significant increase in pore water pressure resulted in a rapid decrease in shear stress, accompanied by a notable reduction in residual shear strength. 4) As seen in Figure 10D, the height of sample 4 eventually decreased by about 2.48 mm. During the test, the shear stress of sample 4 increased rapidly to 97.81 kPa at the beginning of shear and then decreased rapidly to about 60.19 kPa; as the pore water pressure of sample continued to increase to about 71.32 kPa, the shear stress finally decreased further to only about 8.01 kPa. The increase in pore water pressure and decrease in shear stress in sample 4 were much greater than those in the first three groups of samples.
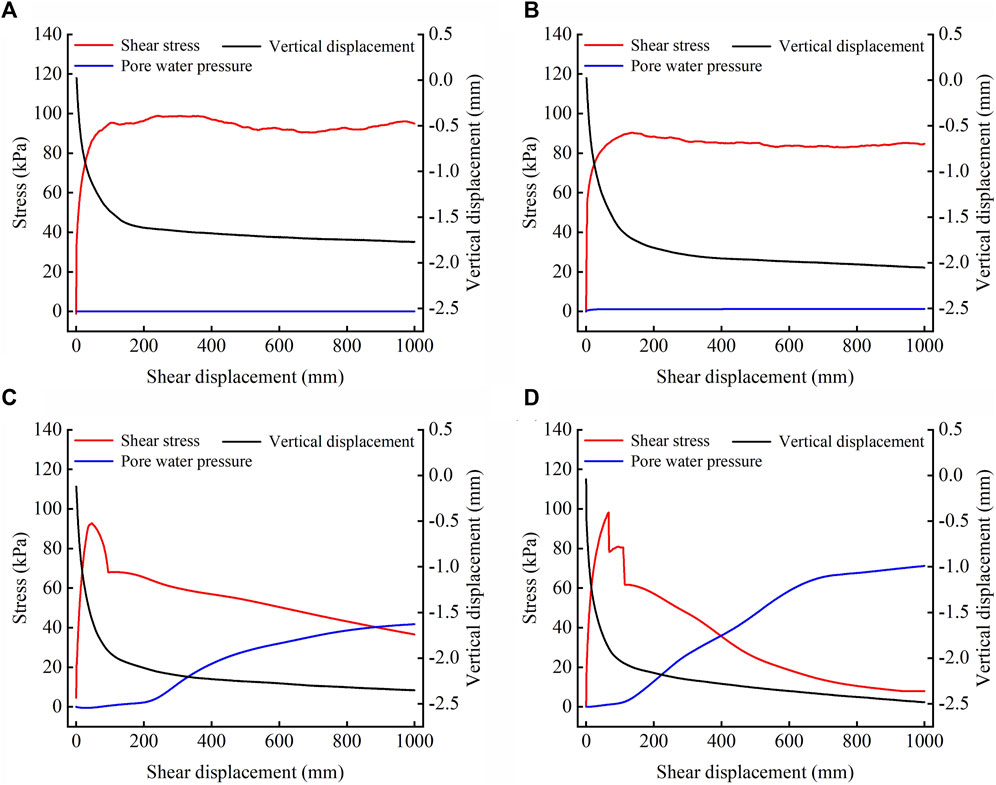
Figure 10. Variation curves of shear stress, pore water pressure and vertical displacement of samples with shear displacement. (A) Water content 22.58%; (B) Water content 29.63%; (C) Water content 36.69%; (D) Water content 43.74%.
The test is carried out under consolidation un-drained condition, and the water content and pore water pressure of the soil will increase continuously during the test due to negative dilatancy; when the soil reaches saturation, the pore water pressure of the sample still increases continuously, which indicates that with the continuous shearing shrinkage of the sample during the test, the excess pore water pressure is generated inside the soil and a certain degree of liquefaction has occurred. The critical initial water content for soil liquefaction is between 29.63% and 36.69%. It can be observed that the higher the initial water content of the soil, the more pronounced the liquefaction phenomenon.
A quantitative comparison of shear strength and shear stress was conducted for the soil depths of 1.9 m and 2.3 m as an example (Figure 11). The results demonstrated that the decrease in shear strength was considerably greater than the increase in shear stress. This indicates that the substantial decrease in shear strength is the main cause for inducing slope instability. The soil shear strength is primarily influenced by the pore water pressure. Rainfall infiltration results in a continuous increase in pore water pressure within the soil, which can lead to the formation of positive pore water pressure. This not only reduces the matrix suction in the soil but also reduces the soil effective stress, significantly impairing its anti-slip capacity. This indicated that positive pore water pressure was the primary factor responsible for the slope failures. The shear stress is calculated based on the soil weight and the plant self-weight. Although the plant self-weight increased the shear stress of the slope, the soil had moderate porosity, and the change in soil water content was small under the high initial saturation. Consequently, the shear stress had little effect on the slope stability.
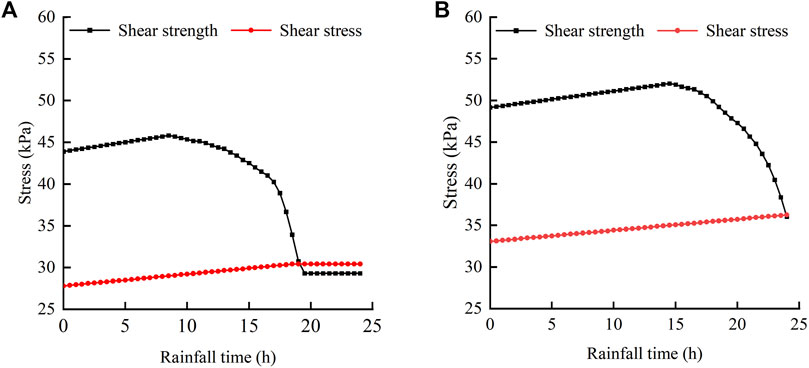
Figure 11. Shear strength and shear stress at potential sliding surface. (A) Soil depth of 1.9 m; (B) Soil depth of 2.3 m.
It is difficult to initiate mass landslides on slopes with soil depths between 1.7 and 2 m, given the typical conditions for landslide development in the Longchuan area. Hence, the mechanism of the landslide in this event deserves to be explored. In this extreme rainfall event, it becomes challenging for rainfall to penetrate deeper into a bare slope. The majority of the rainfall is lost as slope runoff, with the maximum depth of impact confined to a zone within 0.5–1 m of the slope surface (Figure 12A). The absence of landslides in this depth range in this disaster may be attributed to the shallow soil layer lacking sufficient sliding force. Macropores related to vegetation enhance the permeability of the soil, and rainfall can affect the deeper soil layers (Figure 12B). Concurrently, an increase in the quantity of rainfall infiltrating into the soil exerts a greater sliding force on the slope. Another significant contributor to the sliding force is the weight of the vegetation itself. A comparison of the change in the safety factor for different soil depths, with or without consideration of the vegetation self-weight, indicates that the safety factor for slopes considering the self-weight of vegetation is smaller. It can be demonstrated that the self-weight constitutes a non-negligible proportion of the sliding force. This effect diminishes with depth and is observed to primarily affect shallow landslides, which is consistent with the findings of previous studies (Reichenbach et al., 2018; Li et al., 2022). The depth range of the effect of vegetation self-weight is about 2.3 m in this paper (Figure 13). Consequently, the shallow landslide hazard is currently more pronounced in areas with a more luxuriantly vegetated slope, as evidenced by this event. Rainwater tends to accumulate at the bottom of the rhizosphere layer, forming a temporary water table (Figure 7A). This process results in the formation of positive pore water pressure at the soil interface (Figure 7B). The soil interface becomes a weak plane within the slope under water-soil interaction. The accumulated rainwater forms seeps that descend the interface (Figure 8), continuously dragging the slope and causing traction deformation. As rainfall continues, the saturated zone gradually diffuses downward and separates from the root mechanical reinforcement zone. At this point, the resisting force decreases significantly and the slope is susceptible to translational sliding along this weak plane under the sliding force.
Pore water pressure plays a pivotal role in the conversion of landslides into debris flows (Fen, et al., 2005; Yu, 2023). In instances where the pore water pressure is sufficiently elevated, it can dissipate positive stress and facilitate the liquefaction of landslide soil (Zhuang, et al., 2018). The results of the ring shear test showed that the soil in the slip zone exhibited negative dilatancy. Upon reaching the critical water content for liquefaction, the soil becomes susceptible to generating excess pore water pressure under shear. Furthermore, if the soil is saturated when the slope is damaged, the likelihood of the landslide transforming into a debris flow is significantly increased (Iverson, et al., 2010; Iverson, 2015). In this landslide event, the vegetation effect causes the critical slip surface to be saturated or nearly saturated with soil prior to failure. When the landslide initiates, the instantaneous excess pore water pressure generated by soil shrinkage deformation leads to small disturbances, which may cause local instability of the slope body and rapidly spread, leading to the overall instability of the slope. A rapidly moving landslide releases great kinetic energy (Figure 9B). Concomitantly, the soil undergoes rapid liquefaction, and the landslide immediately transforms into a debris flow. In fact, infiltrated rainwater is retained in the rhizosphere zone and the soil interface remains unsaturated during normal rainfall events. The occurrence of extreme rainfall was a significant contributing factor in the triggering of this mass landslides.
One question that merits further discussion is the extent to which the model presented in this paper can be applied to the analysis of landslides triggered by heavy rainfall in other vegetated areas. Landslide events in Fujian Province, China, and New Zealand, where the dominant vegetation type is pine, were selected for comparison with the model calculations in this paper. Landslides occurring in Fujian also tend to occur in areas of high vegetation cover. The sliding surfaces are mostly located at the base of the root system (Zhuang et al., 2023). The bedrock surface in this area may also be a critical slip surface for slopes, possibly due to the thin residual layer, where rainfall infiltration can reach the soil-rock interface to form a temporary water table (Sun et al., 2020). The two major hazard events reported in the New Zealand region were predominantly associated with landslides on grassland, with minimal evidence of landslides on woodland (Marden and Rowan, 1994; Petley, 2022). This seems to contradict the findings of this paper. The investigation revealed that the majority of the slopes were shallow damage, with approximately 55% of the sliding surfaces being less than 1 m deep. The landslides were predominantly composed of residual soil and a minor quantity of weathered rock, indicating that the location of the sliding surfaces was mainly proximate to the soil-rock interface (Reid and Page, 2002). The pine roots extend to the depth of 1.8 m and penetrate the soil layer, inserting itself into the bedrock interior in a manner that resembles an anti-slip pile (Waston et al., 1999; Kc et al., 2018). The vegetation serves as an effective means of slope stabilization for the area. The effect of vegetation on slopes depends on a multitude of specific factors such as topography, soil type, and vegetation type (Pawlik et al., 2016; Jiang et al., 2023). Consequently, the applicability of this model must be considered within the context of the relevant circumstances.
High vegetation cover is a distinctive feature of the mass landslides in Mibei Village. Based on field surveys, this paper explores the cause and mechanism of the well-vegetated soil landslides under extreme rainfall through numerical simulation and ring shear tests. The following main conclusions are drawn.
(1) The numerical simulation results indicate that the rainfall infiltration under extreme rainfall does not directly recharge groundwater. Instead, it forms a temporary saturation zone of a specific thickness in the shallow layer of the slope. The slope tends to slide at the near-saturated or saturated position of the residual layer with suddenness.
(2) The results of the ring shear test show that the slip zone soil exhibits shearing shrinkage and liquefaction occurs under shear. The critical initial water content for liquefaction is found to range from 29.63% to 36.69%.
(3) The rhizosphere soil exhibits superior infiltration properties. Under extreme rainfall, the rhizosphere zone is the first to become saturated. The saturated zone then then extends beyond the boundary of the rhizosphere layer. The positive pore water pressure deteriorates the soil, forming a weak plane that is almost parallel to the bottom surface of the rhizosphere zone. The sliding force causes slopes to translational slide along the weak plane. Concurrently, the saturated slip zone soil liquefies under the shear, facilitating the transformation of landslides into debris flows.
The original data presented in the study are included in the article; further inquiries can be directed to the corresponding author.
JC: Writing–original draft, Methodology, Investigation. QG: Writing–review and editing, Funding acquisition. JW: Writing–original draft, Validation, Funding acquisition. SY: Supervision, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research work was supported by the National Natural Science Foundation of China (42101084; 42271091); Natural Science Foundation of Guangdong Province (2024A1515030114; 2022A1515011898).
First, we would like to acknowledge Nonferrous Mine Geological Disaster Prevention Center of Guangdong Province and the Geographical Science Data Center of Guangdong (Guangzhou Institute of Geography) for providing the relevant data; besides, we thank the reviewers and the editors for their comments and suggestions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahmed, B. (2021). The root causes of landslide vulnerability in Bangladesh. Landslides 18, 1707–1720. doi:10.1007/s10346-020-01606-0
Bellprat, O., Guemas, V., Doblas-Reyes, F., and Donat, M. G. (2019). Towards reliable extreme weather and climate event attribution. Nat. Commun. 10 (1), 1732–1738. doi:10.1038/s41467-019-09729-2
Benegas, L., Ilstedt, U., Roupsard, O., Jones, J., and Malmer, A. (2014). Effects of trees on infiltrability and preferential flow in two contrasting agroecosystems in Central America. Agr. Ecosyst. Environ. 183, 185–196. doi:10.1016/j.agee.2013.10.027
Brunella, B., Alessandro, T., and Andrew, R. (2019). Preliminary analysis on the impacts of the rhizosphere on occurrence of rainfall-induced shallow landslides. Landslides 16, 1885–1901. doi:10.1007/s10346-019-01197-5
Chen, J. Y., Wang, J., Gong, Q. H., Yuan, S. X., Xu, A. Z., and Luo, Y. Z. (2023). Influence mechanism of vegetation infiltration effect on shallow landslides of granite residual soil. Hydrogeol. Eng. Geol. 50 (3), 115–124. doi:10.16030/j.cnki.issn.1000-3665.202205054
Crozier, M. J. (2005). Multiple-occurrence regional landslide events in New Zealand: hazard management issues. Landslides 2 (4), 247–256. doi:10.1007/s10346-005-0019-7
Cui, Z., Huang, Z., Liu, Y., López-Vicente, M., and Wu, G. L. (2022). Natural compensation mechanism of soil water infiltration through decayed roots in semi-arid vegetation species. Sci. Total Environ. 819, 151985. doi:10.1016/j.scitotenv.2021.151985
Fen, Z. L., Cui, P., and He, S. M. (2005). Mechanism of conversion of landsldes to debris flows. J. Nat. Dis. 3, 8–14. doi:10.13577/j.jnd.2005.0302
Garcia-Delgado, H., Petley, D. N., Bermúdez, M. A., and Sepúlveda, S. A. (2022). Fatal landslides in Colombia (from historical times to 2020) and their socio-economic impacts. Landslides 19, 1689–1716. doi:10.1007/s10346-022-01870-2
Gasmo, J. M., Rahardjo, H., and Leong, E. C. (2000). Infiltration effects on stability of a residual soil slope. Comput. Geotech. 26 (2), 145–165. doi:10.1016/s0266-352x(99)00035-x
GEO-SLOPE International Ltd (2008). Stability modelling with SLOPW/W 2007 version. Calgary, 73. GEO-SLOPE International Ltd.
GEO-SLOPE International Ltd (2018a). Seepage modeling with SEEP/W2018: an engineering methodology, user's guide. Calgary: GEO-SLOPEInternational Ltd.
GEO-SLOPE International Ltd (2018b). Stress-defommation modeling with SIGMA/W 2018: an engineering methodology. Calgary: GEO-SLOPEInternational Ltd.
Ghestem, M., Sidle, R. C., and Stokes, A. (2011). The influence of plant root systems on subsurface flow: implications for slope stability. Bioscience 61 (11), 869–879. doi:10.1525/bio.2011.61.11.6
Giadrossich, F., Cohen, D., Schwarz, M., Ganga, A., Marrosu, R., Pirastru, M., et al. (2019). Large roots dominate the contribution of trees to slope stability. Earth. Surf. Proc. Land. 44, 1602–1609. doi:10.1002/esp.4597
Gong, Q. H., Wang, J., Zhou, P., and Guo, M. (2021). A regional landslide stability analysis method under the combined impact of rainfall and vegetation roots in South China. Adv. Civ. Eng. 2021, 1–12. doi:10.1155/2021/5512281
Grima, N., Edwards, D., Edwards, F., Petley, D., and Fisher, B. (2020). Landslides in the Andes: forests can provide cost-effective landslide regulation services. Sci. Total. Environ. 141128, 141128. doi:10.1016/j.scitotenv.2020.141128
Guo, L., Liu, Y., Wu, G. L., Huang, Z., Cui, Z., Cheng, Z., et al. (2019b). Preferential water flow: influence of alfalfa (Medicago sativa L.) decayed root channels on soil water infiltration. J. Hydrol. 578, 124019. doi:10.1016/j.jhydrol.2019.124019
Guo, W. Z., Chen, Z. X., Wang, W. L., Gao, W. W., Guo, M. M., Kang, H. L., et al. (2019a). Telling a different story: the promote role of vegetation in the initiation of shallow landslides during rainfall on the Chinese Loess Plateau. Geomorphology 350, 106879. doi:10.1016/j.geomorph.2019.106879
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2008). The rainfall intensity-duration control of shallow landslides and debris flows: an update. Landslides 5, 3–17. doi:10.1007/s10346-007-0112-1
Han, T. C., and Huang, F. M. (2012). Rainfall infiltration process and stability analysis of two-layered slope. J. Zhejiang Univ. Eng. Sci. 46 (1), 39–45. doi:10.3785/j.issn.1008-973X.2012.01.07
Huang, S. P., Chen, Y. J., Xiao, H. L., and Tao, G. L. (2023). Test on rules of rainfall infiltration and runoff erosion on vegetated slopes with different gradients. Rock Soil Mech. 44 (12), 3435–3447. doi:10.16285/j.rsm.2022.1936
Iverson, R. M. (2015). Scaling and design of landslide and debris-flow experiments. Geomorphology 244, 9–20. doi:10.1016/j.geomorph.2015.02.033
Iverson, R. M., Reid, M. E., Logan, M., LaHusen, R. G., Godt, J. W., and Griswold, J. P. (2010). Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 4 (2), 116–121. doi:10.1038/ngeo1040
Ji, J. N., Kokutse, N., Genet, M., Fourcaud, T., and Zhang, Z. Q. (2012). Effect of spatial variation of tree root characteristics on slope stability. A case study on Black locust (Robinia pseudoacacia) and Arborvitae (Platycladus orientalis) stands on the Loess Plateau, China. Catena 92, 139–154. doi:10.1016/j.catena.2011.12.008
Jiang, H., Zou, Q., Zhou, B., Jiang, Y., Cui, J. F., Yao, H. K., et al. (2023). Estimation of shallow landslide susceptibility incorporating the impacts of vegetation on slope stability. Int. J. Disast. Risk. Sc. 14, 618–635. doi:10.1007/s13753-023-00507-9
Kc, B., Mohssen, M., Chau, H., Curtis, A., Cuenca, R., Bright, J., et al. (2018). Irrigation strategies for rotational grazing pasture in Canterbury, New Zealand, and impacts on irrigation efficiency. Irrig. Drain. 67 (5), 779–789. doi:10.1002/ird.2290
Keim, R. F., and Skaugset, A. E. (2003). Modelling effects of forest canopies on slope stability. Hydrol. Process. 17 (7), 1457–1467. doi:10.1002/hyp.5121
Kim, D., Im, S., Lee, C., and Woo, C. (2013). Modeling the contribution of trees to shallow landslide development in a steep, forested watershed. Ecol. Eng. 61, 658–668. doi:10.1016/j.ecoleng.2013.05.003
Leung, A. K., Garg, A., and Ng, C. W. W. (2015). Effects of plant roots on soil-water retention and induced suction in vegetated soil. Eng. Geol. 193, 183–197. doi:10.1016/j.enggeo.2015.04.017
Li, J. Y., Cui, P., and Yin, Y. Z. (2023a). Field observation and micro-mechanism of roots-induced preferential flow by infiltration experiment and phase-field method. J. Hydrol. 623, 129756. doi:10.1016/j.jhydrol.2023.129756
Li, M. Y., Ma, C., Du, C., Yang, W. T., Lyu, L. Q., and Wang, X. H. (2020). Landslide response to vegetation by example of July 25–26, 2013, extreme rainstorm, Tianshui, Gansu Province, China. B. Eng. Geol. Environ. 80, 751–764. doi:10.1007/s10064-020-02000-9
Li, T. L., Li, Y. Z., Zhao, D. Q., Hu, X. Y., and Li, P. (2022). Thoughts on modes of loess slope failure triggered by water infiltration and the principals for stability analysis. Chin. J. Geol. Haz. Contr. 33 (2), 25–32. doi:10.16031/j.cnki.issn.1003-8035.2022.02-04
Li, Y., Xue, K. X., Zhao, Y., Wang, C. L., Bi, J., Wang, T. Y., et al. (2023b). Study on the stability and disaster mechanism of layered soil slopes under heavy rain. Bull. Eng. Geol. Environ. 82, 272. doi:10.1007/s10064-023-03277-2
Liang, X., Segoni, S. S., Yin, K. L., Du, J., Chai, B., Tofani, V., et al. (2022). Characteristics of landslides and debris flows triggered by extreme rainfall in daoshi Town during the 2019 typhoon lekima, zhejiang province, China. Landslides 19, 1735–1749. doi:10.1007/s10346-022-01889-5
Liu, Q. J., Meng, S. W., Zhou, H., Zhou, G., and Li, Y. Y. (2017). Tree volume tables of China, 65. Beijing: China Forestry Press.
Löbmann, M. T., Geitner, C., Wellstein, C., and Zerbe, S. (2020). The influence of herbaceous vegetation on slope stability–a review. Earth-Sci. Rev. 209, 103328. doi:10.1016/j.earscirev.2020.103328
Marden, M., and Rowan, D. (1994). Protective value of vegetation on tertiary terrain before and during cyclone bola, east coast, north island, New Zealand. Nz. J. For. Sci. 23, 255–263.
Masi, E. B., Segoni, S., and Tofani, V. (2021). Root reinforcement in slope stability models: a review. Geosciences 11 (5), 212. doi:10.3390/geosciences11050212
McGuire, L. A., Rengers, F. K., Kean, J. W., Coe, J. A., Mirus, B. B., Baum, R. L., et al. (2016). Elucidating the role of vegetation in the initiation of rainfall-induced shallow landslides: insights from an extreme rainfall event in the Colorado Front Range. Geophys. Res. Lett. 43 (17), 9084–9092. doi:10.1002/2016GL070741
Nguyen, T. S., Likitlersuang, S., and Jotisankasa, A. (2018). Influence of the spatial variability of the root cohesion on a slope-scale stability model: a case study of residual soil slope in Thailand. B. Eng. Geol. Environ. 78, 3337–3351. doi:10.1007/s10064-018-1380-9
Nielsen, D. M., Cataldi, M., Belém, A. L., and Albuquerque, A. L. S. (2016). Local indices for the South American monsoon system and its impacts on Southeast Brazilian precipitation patterns. Nat. Hazards 83 (2), 909–928. doi:10.1007/s11069-016-2355-4
Pawlik, Ł., Phillips, J. D., and Šamonil, P. (2016). Roots, rock, and regolith: bio-mechanical and biochemical weathering by trees and its impact on hillslopes–a critical literature review. Earth Sci. Rev. 159, 142–159. doi:10.1016/j.earscirev.2016.06.002
Petley, D. (2022). Wairoa: hundreds of landslides triggered by heavy rainfall in New Zealand. Available at: https://blogs.agu.org/landslideblog/2022/04/21/wairoa-1-2/.
Picarelli, L., Olivares, L., Damiano, E., Darban, R., and Santo, A. (2020). The effects of extreme precipitations on landslide hazard in the pyroclastic deposits of Campania Region: a review. Landslides 17, 2343–2358. doi:10.1007/s10346-020-01423-5
Qin, M. Y., Cui, P., Jiang, Y., Guo, J., Zhang, G. T., and Ramzan, M. (2022). Occurrence of shallow landslides triggered by increased hydraulic conductivity due to tree roots. Landslides 19, 2593–2604. doi:10.1007/s10346-022-01921-8
Reichenbach, P., Rossi, M., Malamud, B. D., Mihir, M., and Guzzetti, F. (2018). A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 180, 60–91. doi:10.1016/j.earscirev.2018.03.001
Reid, L. M., and Page, M. J. (2002). Magnitude and frequency of landsliding in a large New Zealand catchment. Geomorphology 49 (1-2), 71–88. doi:10.1016/S0169-555X(02)00164-2
Senthilkumar, V., Chandrasekaran, S. S., and Maji, V. B. (2018). Rainfall-induced landslides: case study of the marappalam landslide, nilgiris District, Tamil nadu, India. Int. J. Geomech. 18 (9), 1–13. doi:10.1061/(asce)gm.1943-5622.0001218
Shao, W., Bogaard, T. A., Bakker, M., and Greco, R. (2015). Quantification of the influence of preferential flow on slope stability using a numerical modelling approach. Hydrol. Earth. Syst. Sc. 19, 2197–2212. doi:10.5194/hess-19-2197-2015
Song, X. H., and Tan, Y. (2024). Experimental study on the stability of vegetated earthen slopes under intense rainfall. Soil till. Res. 238, 106028. doi:10.1016/j.still.2024.106028
Sun, Z. H., Wang, S. H., Yang, T. J., and Liu, H. (2020). Infiltration mechanism and stability analysis of multilayer soil slope under rainfall conditions. J. Northeast. Univ. Nat. Sci. 41 (8), 1201–1208. doi:10.12068/j.issn.1005-3026.2020.08.022
Świtała, B. M., and Wu, W. (2018). Numerical modelling of rainfall-induced instability of vegetated slopes. Géotechnique 68 (6), 481–491. doi:10.1680/jgeot.16.P.176
Tang, G. P., Huang, J. S., Sheng, D. C., and Sloan, S. W. (2018). Stability analysis of unsaturated soil slopes under random rainfall patterns. Eng. Geol. 45 (1), 322–332. doi:10.1016/j.enggeo.2018.09.013
Tang, L. S., Yan, B., Li, Z. S., Yu, H. T., and Lin, G. W. (2008). The experimental research on the soil-water characteristic curve of the granite residual soil. Hydrogeol. Eng. Geol. 4, 62–65+79. doi:10.16030/j.cnki.issn.1000-3665.2008.04.018
Vergani, C., Chiaradia, E. A., Bassanelli, C., and Bischetti, G. B. (2013). Root strength and density decay after felling in a Silver Fir-Norway Spruce stand in the Italian Alps. Plant Soil 377 (1-2), 63–81. doi:10.1007/s11104-013-1860-4
Waston, A., Phillips, C., and Marden, M. (1999). Root strength, growth, and rates of decay: root reinforcement changes of two tree species and their contribution to slope stability. Plant Soil 217, 39–47. doi:10.1023/A:1004682509514
Wu, T. H. (2013). Root reinforcement of soil: review of analytical models, test results, and applications to design. Can. Geotech. J. 50 (3), 259–274. doi:10.1139/cgj-2012-0160
Xu, Y. G., Luo, L., Guo, W. Z., Jin, Z., Tian, P., and Wang, W. L. (2024). Revegetation changes main erosion type on the gully-slope on the Chinese Loess Plateau under extreme rainfall: reducing gully erosion and promoting shallow landslides. Water Resour. Res. 60, e2023WR036307. doi:10.1029/2023WR036307
Xu, Z. M., Huang, R. Q., Tang, Z. G., and Wang, S. Z. (2005). Limitations of biotechnical slope protection and contribution of vegetation to deep seated landslide preparation. Chin. J. Rock Mech. Eng. 24 (3), 438–450.
Yang, H. J., Yang, T. Q., Zhang, S. J., Zhao, F. H., Hu, K. H., and Jiang, Y. H. (2020). Rainfall-induced landslides and debris flows in Mengdong Town, yunnan province, China. Landslides 17, 931–941. doi:10.1007/s10346-019-01336-y
Yang, Z. Y., Zhou, B. Z., Ge, X. G., Cao, Y. H., Brunner, I., Shi, J. X., et al. (2021). Species-specific responses of root morphology of three co-existing tree species to nutrient patches reflect their root foraging strategies. Front. Plant Sci. 11, 618222. doi:10.3389/fpls.2020.618222
Yu, G. A. (2023). Re-discussion on the formation mechanism of two types of debris flows. J. Nat. Dis. 31 (1), 238–250. doi:10.13577/j.jnd.2022.0123
Zeng, L., Bian, H. B., Shi, Z. N., and He, Z. (2017). Forming condition of transient saturated zone and its distribution in residual slope under rainfall conditions. J. Cent. South Univ. 24, 1866–1880. doi:10.1007/s11771-017-3594-6
Zhan, L. T., Li, H., Chen, Y. M., and Fredlund, D. G. (2012). Parametric analyses of intensity-duration curve for predicting rainfall-induced landslides in residual soil slope in Southeastern coastal areas of China. Rock Soil Mech. 33 (3), 872–880+886. doi:10.16285/j.rsm.2012.03.016
Zhan, T. L. T., and Ng, C. W. W. (2004). Analytical analysis of rainfall infiltration mechanism in unsaturated soils. Int. J. Geomech. 4 (4), 273–284. doi:10.1061/(asce)1532-3641(2004)4:4(273)
Zhang, C. Y., Zhang, M., Zhang, T. L., Dai, Z. W., and Wang, L. Q. (2020). Influence of intrusive granite dyke on rainfall-induced soil slope failure. Bull. Eng. Geol. Environ. 79, 5259–5276. doi:10.1007/s10064-020-01895-8
Zhang, J. R., Tang, H. M., Li, C. D., Gong, W. P., Zhou, B. Y., and Zhang, Y. Q. (2024). Deformation stage division and early warning of landslides based on the statistical characteristics of landslide kinematic features. Landslides 21, 717–735. doi:10.1007/s10346-023-02192-7
Zhang, Y. B., Zhang, Y., Chen, G., and Yin, M. Y. (1997). The system of engineering category dividing of granite residual soil. Acta Geosci. Sin. 2, 89–93.
Zhu, J. Q., Wang, Y. Q., Wang, Y. J., and Ma, C. (2018). Analyses on root reinforcement mechanism based on plant growth process and parameters optimization of Wu model. Sci. Silvae Sin. 54 (4), 49–57. doi:10.11707/j.1001-7488.20180406
Zhuang, J. Q., Peng, J. B., Wang, G. H., Javed, I., Wang, Y., and Li, W. (2018). Distribution and characteristics of landslide in Loess Plateau: a case study in Shaanxi province. Eng. Geol. 236, 89–96. doi:10.1016/j.enggeo.2017.03.001
Zhuang, Y., Xing, A. G., Jiang, Y. H., Sun, Q., Yan, J. K., and Zhang, Y. B. (2022). Typhoon, rainfall and trees jointly cause landslides in coastal regions. Eng. Geol. 298, 106561. doi:10.1016/j.enggeo.2022.106561
Zhuang, Y., Xing, A. G., Petley, D., Jiang, Y. H., Sun, Q., Bilal, M., et al. (2023). Elucidating the impacts of trees on landslide initiation throughout a typhoon: preferential infiltration, wind load and root reinforcement. Earth. Surf. Proc. Land 48, 3128–3141. doi:10.1002/esp.5686
Keywords: mass landslides, vegetation effect, numerical simulation, ring shear test, damage cause and mechanism
Citation: Chen J, Gong Q, Wang J and Yuan S (2024) Damage cause and mechanism of well-vegetated soil slopes under extreme rainfall: a case study. Front. Earth Sci. 12:1402798. doi: 10.3389/feart.2024.1402798
Received: 18 March 2024; Accepted: 07 May 2024;
Published: 22 May 2024.
Edited by:
Wenbo Zheng, University of Northern British Columbia, CanadaReviewed by:
Adolfo Quesada-Román, University of Costa Rica, Costa RicaCopyright © 2024 Chen, Gong, Wang and Yuan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qinghua Gong, Z3FoMTAwNjA4QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.