The retarding effect of glacier degradation on the Earth’s rotation

Introduction: The massive loss of global glacier mass caused by climate problems has caused concern, while the Earth’s rotation as the most significant form of motion has also been subtly affected. However, the quantitative effects of massive glaciers losing mass on Earth’s rotation have not been revealed.

Methods: Herein, the knowledge of moment of inertia and suitable rotational inertia models in classical mechanics is initially utilized to assess the effect of quantitative glaciers losing mass on Earth's rotation.

Results: After specific calculations, the putative 200 billion tons of glaciers losing mass bring on an increase of 1.4099×10^-4s in Earth’s rotation time in 365 days.

Discussion: This work examines the connection between glaciers losing mass and Earth’s rotation from classical mechanics, thus providing the way for investigations of relationship between climate changes and Earth.

1 Introduction

The Earth’s self-rotation, which refers to the rotation around its polar axis, is a vital form of motion, along with its revolution and progression (Schuh et al., 2021) and plays a decisive role in the ecological balance of living organisms (Sinturel et al., 2020; Reddy et al., 2023; van Wyk and Prinsloo, 2019; Klatt et al., 2021), the physical phenomena of nature (Ukhorskiy et al., 2014; Williams et al., 2014), the Earth’s magnetic field (Richards et al., 1997; Roberts and King, 2013; Modiri et al., 2021), climate (Hunt, 1979; Kuhn et al., 1989), etc. The fact that the speed of the Earth’s rotation is not constant is, of course, well known (Carter et al., 1984; Hide and Dickey, 1991; Triana et al., 2022). For the past few decades, the BIMP (Bureau International des Poids et Mesures) has used “leap seconds” to measure changes in the time of the Earth’s rotation (Gibney, 2022; Leap Seconds Information Sheet, 2023). Moreover, there is no shortage of explanations for long-term changes in Earth’s rotation through known factors such as tidal dissipation (Riguzzi et al., 2010; Daher et al., 2021; Chao and Ray, 1996; Madzak et al., 2016) and earthquakes (Xu and Li, 2022; Chao and Gross, 1987; Maddox, 1988; Anderson, 1974). Chao and Gross determined that earthquakes slow the Earth’s rotation by approximately 0.1 microseconds per year. (Daher et al., 2021). Chao and Ray reviewed tidal research models and found that tidal effects affect the Earth’s rotation by about 1–2 microseconds per year (Chao and Gross, 1987). The above factors change the distribution of material to affect the rotation of the Earth, while the glacier losing mass is also listed among the reasons. In recent years, climate issues have caused a steady increase in glacier losing mass on Earth, especially in Greenland (Jani-Friend, 2022; Ramirez, 2022; Guy, 2023; Shepherd and Wingham, 2007; Rounce et al., 2023). Glacier mass loss not only causes natural disasters such as rising sea levels, freshwater shortages, and the intensification of the greenhouse effect but also has deeper effects on the Earth, such as its rotation. However, the trend of development and quantitative relationship (the exact amount of time changes in the Earth’s rotation) between glaciers losing mass and the Earth’s rotation has yet to be determined. Therefore, the specific impact of glaciers on the rotation of the Earth and the prediction of the development trend can be described by physical connections and quantitative calculations in the Newtonian mechanical system.

As early as the 1960s, Runcorn used knowledge of the moment of inertia (I) in classical mechanics to investigate variations in the Earth’s moment of inertia (Runcorn, 1964). Etkins and Epstein calculated that melting over 50,000 cubic kilometers of glacier between 1900 and 1940, which shifted mass from the polar regions to the thin shell covering all the oceans, should have increased Earth’s moment of inertia and correspondingly reduced its rotation by about 1.5 parts per 108 (Etkins and Epstein, 1982). In recent years, as various Earth data have been gradually refined, Ren et al. have studied the increasing trend of Earth’s moment of inertia through data measured by the widely used 15-year Gravity Recovery and Climate Experiment (GRACE) (Ren and Hu, 2021). However, to better measure the specific impact of glacier lost mass on Earth’s rotation, we choose the equations of moment of inertia (J), moment of momentum (L), angular velocity (ω), and linear velocity (v) in the classical mechanical system for calculation (Young et al., 2019; Kittel et al., 2016). The detailed classical mechanical formulas are displayed in the supporting methods. According to the relevant theoretical mechanical theorem, the moment of momentum is conserved during the Earth’s rotation, and when the Earth’s moment of inertia changes, the angular velocity and the period will also change. This research explores the physical and scientific links between glacier lost mass and the Earth’s rotation in the context of changes in the distribution of the Earth’s mass because of large-scale glaciers’ lost mass on Earth in recent years. After assuming a quantitative pre- and post-melting glacier lost mass distribution, the magnitude of the moment of inertia before and after glacier melting is quantified by selecting the exact moment of inertia model and performing comparative analytical calculations to verify the effect of glacier lost mass on the Earth’s rotation.

2 Earth’s land and ocean distribution

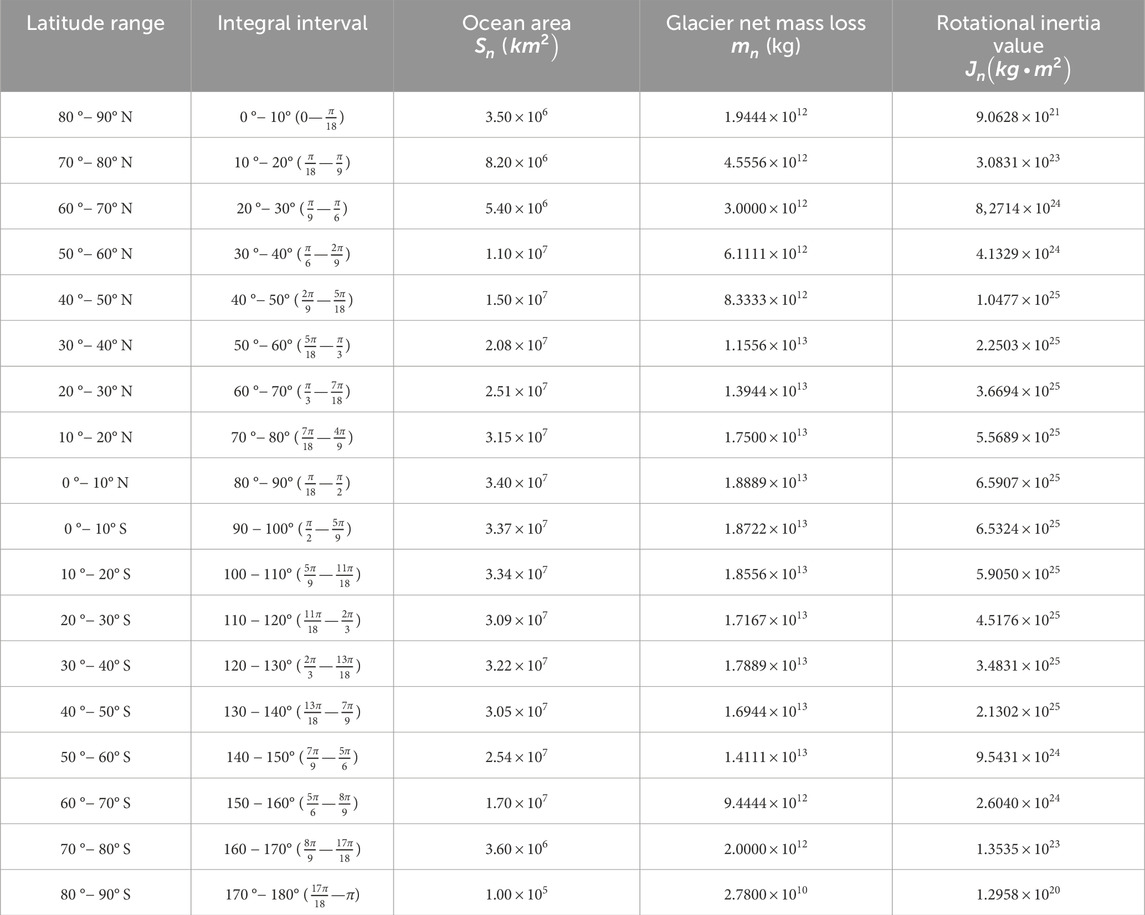
First, the Earth’s land and sea are unevenly distributed, with oceans covering a much larger area than land, and the area of the ocean is much higher than that of the land (Figure 1A). About 510 million square kilometers of the Earth’s surface area is covered by oceans, of which 360 million square kilometers (71%) and 150 million square kilometers (29%) are land area. To better apply the calculation of the moment of inertia model in classical mechanical systems, the Earth is divided into 18 intervals from the South Pole to the North Pole with 10° as an interval for subsequent computations, and each dimension interval has specific values for sea and land (Figure 1B) (Historical Geography of the National).

Figure 1

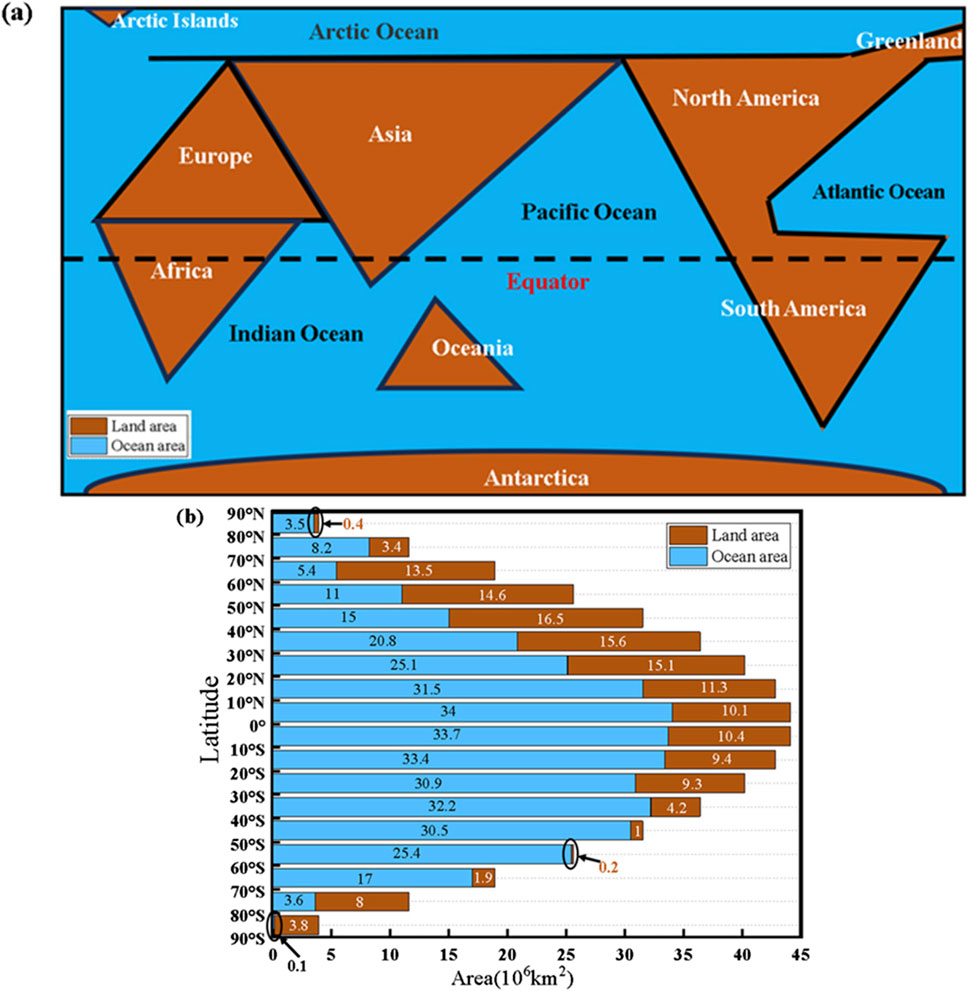
Figure 1. (A) Simplified diagram of Earth’s land and sea distribution; (B) The sizeof the ocean and land area in different latitude intervals.

3 Glaciers

3.1 Total mass of glacier

Currently, Earth’s three most glaciated regions are the Antarctic continent, Greenland, and the Arctic islands. Simultaneously, 95% of the Earth’s glacier area and 99% of the glacier volume are contained in the Antarctic and Greenland, so the North and South Polar regions should be the essential areas for calculating the glacier lost mass before melting. Relative to the glacier mass and volume content in the polar regions, the glaciers in the middle and low-altitude alpine areas are no longer considered in this article. In this calculation of moment of inertia, we define the glacier to encompass all types of glaciers found in the high-latitude polar regions, specifically referring to the mass loss occurring in the polar ice sheets and peripheral mountain glaciers.

Combined with the research of Hugonnet (Hugonnet et al., 2021), Vargo (Vargo et al., 2020) and Zemp (Zemp et al., 2019) on accelerating glacier mass loss in the 21st century and related news reports (Satellite Data Shows Antarctic Peninsula, 2023; Gaind and Stoye, 2019), an average of 267 billion tons of glaciers lost mass each year from 2000 to 2019. Given that glaciers in high latitudes lose mass at a slower rate compared to those in middle and low latitudes and considering the issue of climate change, the calculation value of 200 billion tons is chosen for the total net mass value of glacier melt. Moreover, this value is established to simplify further calculations of the moment of inertia.

3.2 Glaciers distribution

Before the calculation can begin, the specific distribution of 200 billion tons of glaciers before and after mass loss needs to be specified. First, the distribution of glaciers before mass loss is specified. Combined with the latitude of the polar regions and the distribution of glaciers, we assume that before the 200 billion tons of glaciers melted, 150 billion tons of glaciers and 50 billion tons of glaciers similar to the spherical shell uniformly distributed in the north-south latitude 80°–90° land region (Figure 2A). Second, the distribution of glaciers after mass loss is specified. Since the climate and seasonal changes in each latitude region have a significant influence on glacier melting and flow, for the convenience of model building and rotational inertia calculation, these effects are not considered in this article, while only the distribution mode of glaciers distributed in each dimensional interval after all mass loss is considered. Consequently, this research postulates that the 200 billion tons of glaciers will be uniformly distributed throughout the ocean area of the Earth’s surface at all latitudes after melting, resulting in the same height of worldwide sea level rise (Figure 2B).

Figure 2

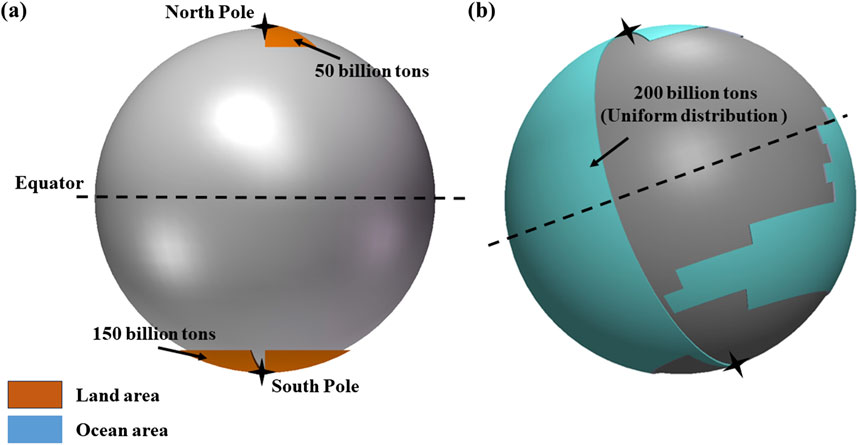
Figure 2. Glacier distribution model. (A) Before the glaciers mass loss; (B) After the glaciers mass loss.

4 Calculation and results

4.1 Earth’s own moment of inertia

Earth is known to be an irregular sphere with slightly flattened poles and a slight bulge at the equator. While we assume the Earth is a rigid sphere for calculation purposes, and this simplification allows us to apply the sphere model to classical mechanical models (Figure 3A). The parameters of the Earth rigid body model are derived from Earth’s parameters (Williams, 2021), and all data are retained to four decimal places. The utilization of the rigid body model necessitates the employment of the uniform distribution method for calculating the moment of inertia of the Earth, which entails a certain degree of error when compared to the more precise and technically sophisticated methods for determining the moment of inertia of the Earth. However, considering the calculation model of the moment of inertia in classical physics used in this paper, although there is a certain error with more accurate calculation methods, the uniform distribution of the earth’s moment of inertia is more reasonable.

Figure 3

Figure 3. Calculation models of the moment of inertia in classical mechanics system. (A) Earth rigid body model; (B) Calculation Model of Glacier Shell; (C) Comparison chart of latitude and integral interval.

After screening the moment of inertia models, the sphere model (Supplementary Figure S1, $J=\frac{2}{5}m{r}^2$) (Young et al., 2019) is chosen to calculate the Earth’s rotational inertia. All calculations in this article are retained to 4 decimal places. Here, we need to calculate the glacier and the Earth separately due to differences in the model for calculating the moment of inertia. Due to the Earth’s measured mass containing the glacier mass, the assumed glacier mass is excluded when performing the Earth’s own moment of inertia calculation. The detailed derivation of the spherical model formula and the calculation process of the moment of inertia can be found in supplementary model.

The Earth’s own moment of inertia is:

$J_E=\frac{\left(2M_E{r_D}^2\right)}{5}=\frac{\left({2\times 5.9724\times {10}^{2}4\times \left(6.3714\times {10}^6\right)}^2\right)}{5}=9.6980\times 1{0^3}^{7}kg\cdot m^2$

where ${\mathrm{M}}_{\mathrm{E}}$ is the mass of the Earth minus 200 billion tons of glaciers $\left(M_E=M_D-M_I=5.9724\times 1{0^2}^4-2\times 1{0^1}^1\approx 5.9724\times 1{0^2}^4\right)$, and ${\mathrm{r}}_{\mathrm{D}}$ is the radius of the Earth $\left(r_D=6.371393\times {10}^{6}m\approx 6.3714\times {10}^{6}m\right)$.

4.2 Glacier’s moment of inertia

Combined with the preset glacier distribution and the moment of inertia model, the spherical shell model (Supplementary Figure S2, $J=\frac{2m{r}^2}{3}$) (Young et al., 2019) is chosen to perform rotational inertia calculations before and after glacier mass loss, and the detailed derivation of the spherical shell model formula is shown in Supplementary model. To facilitate the spherical shell model for the calculation of the integration interval, assuming 0° at the North Pole and 180° at the South Pole, the North Pole to the South Pole is 0°–180° as the coordinates of the integration interval, and the calculation is carried out with 10° as an integration interval (Figure 3B).

First, the moment of inertia before the 200 billion tons of glaciers mass loss is calculated. The moment of inertia of 50 billion tons of glaciers at 80°–90° north latitude is $J_N=2.3304\times 1{0^2}^{3}kg\cdot m^2$ (the Arctic), and the moment of inertia of 150 billion tons of glaciers at 80°–90° south latitude is $J_S=6.9913\times 1{0^2}^{3}kg\cdot m^2$ (the Antarctic). So, the total moment of inertia of 200 billion tons of glaciers before mass loss is $J_Q=J_N+J_S=9.3217\times 1{0^2}^{3}kg\cdot m^2$ (the sum of the Arctic and Antarctic). The calculation process of rotational inertia before glaciers mass loss located at 80°–90° in the North and South Poles is shown in supplementary calculation process.

Subsequently, the moment of inertia after the 200 billion tons of glaciers mass loss is calculated. Since the glaciers are evenly distributed in all latitudes of the earth after mass loss, the mass distributed and corresponding moment of inertia in each interval after mass loss of the glaciers is obtained through the spherical shell formula according to the 18 integral intervals (Figure 3C, corresponding to the 18 latitude intervals), and the result is reserved for four decimal places (Table 1). The calculation process of rotational inertia uniformly distributed in the ocean area of the Earth’s surface at various latitudes after glaciers mass loss is shown in supplementary calculation process.

Table 1

Table 1. Calculation table of the moment of inertia for each latitude integral interval.

The magnitude of the moment inertia after the 200 billion tons of glaciers mass loss can be obtained by adding up the moment of inertia of each interval in Table 1 is; $J_H={\displaystyle \sum _{n=1}^{18}}{J}_{\mathrm{n}}=4.3451\times 1{0^2}^{6}kg\cdot m^2$.

4.3 Earth’s rotation change time

From the law of conservation of momentum and moment in the Supplementary Material, the formula for the relationship between velocity, angular velocity and period (S1-1) to (S1-4) can be obtained (Khobragade and Roy, 2021):

$L_D=\left(J_E+J_Q\right){\omega }_1=\left(J_E+J_H\right){\omega }_2$

${\nu }_1={\omega }_1{r}_D,{\nu }_2={\omega }_2{r}_D$

$\frac{T_2}{T_1}=\frac{v_1}{v_2}=\frac{{\omega }_1}{{\omega }_2}=\frac{\left(J_E+J_H\right)}{\left(J_E+J_Q\right)}$

where $L_D$- angular momentum of the Earth (constant value), $J_E$-rotational inertia of the Earth itself, $J_Q$-rotational inertia before glaciers mass loss, $J_H$-rotational inertia after glacier glaciers mass loss, ${\omega }_1$-rotational angular velocity of the Earth itself before glacier glaciers mass loss, ${\omega }_2$-rotational angular velocity of the Earth itself after glacier glaciers mass loss, r_D-the radius of the Earth, $T_1$-the standard period of the Earth’s rotation of 365 days before glaciers mass loss, $T_2$-the time required for the Earth’s rotation period after glaciers mass loss.

After bringing the above calculation data into the calculation, the rotation period of the Earth increased due to the mass loss of the assumed 200 billion tons of glaciers in this article is calculated by the following:

$T=\left(T_2-T_1\right)\times 24\times 3600=1.4099\times {10}^{-4}s$

where, T-the increase of the earth’s rotation period time, $T_1$-the standard period of the Earth’s rotation of 365 days before glaciers mass loss, $T_2$-the time required for the Earth’s rotation period after glaciers mass loss.

5 Discussion and conclusion

In conclusion, the effect of a hypothetical 200 billion tons glaciers mass loss on the Earth’s rotation is calculated in detail by selecting a suitable rotational inertia model. The process of selection and calculation of specific rotational inertia models before and after the mass loss of glaciers is given. After comparative analyses and calculations, the detailed and specific results confirm that the glaciers mass loss caused by global warming affect the Earth’s rotation. Using the moment of inertia model method in classical mechanics, this article calculates that the assumed 200 billion tons of glaciers mass loss slow the rotation of the Earth by 1.4099×10^-4s in a standard year (365 days).

This article mainly uses the knowledge between the moment of inertia and angular momentum in classical mechanics to explore the effect of glacier mass loss on the earth’s rotation. Here, by assuming that the angular momentum of the earth is constant, the influence of the hypothetical mass loss of 200 billion tons of glaciers on the rotation period of the Earth is quantitatively analyzed through the physical relations such as angular momentum, moment of inertia, angular velocity, and velocity. Combined with the actual situation of the earth itself, the study of this article has certain limitations. Due to the intensification of global warming, the annual mass loss of the Earth’s glaciers far exceeds the 200 billion tons set in this paper, indicating that the actual change in the Earth’s rotation period exceeds the calculated value in this article. However, this article proves that the use of classical mechanics and other physical knowledge can prove that the mass loss of glaciers affects the Earth’s rotation period and provides new ideas for researchers to further study the Earth’s changes.

In recent years, under the influence of the climate problem of global warming, the amount of glacier mass loss has increased with each passing year, and the global sea level is also rising. This phenomenon has a direct impact on the global ecological environment and aggravates Marine disasters. Furthermore, the Earth itself is subject to profound and subtle effects, such as the slowing of Earth’s rotation worked in this article. Therefore, worldwide countries should pay more attention to the accelerated mass loss of glaciers and jointly solve the problem of global climate change.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

CW: Investigation, Methodology, Project administration, Supervision, Validation, Writing–review and editing. ZJ: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. HW: Formal Analysis, Methodology, Writing–review and editing. SJ: Formal Analysis, Investigation, Writing–review and editing. HM: Data curation, Investigation, Writing–review and editing. SL: Data curation, Investigation, Writing–review and editing. TL: Formal Analysis, Investigation, Writing–review and editing. RS: Data curation, Formal Analysis, Writing–review and editing. HZ: Formal Analysis, Investigation, Methodology, Writing–review and editing. YL: Conceptualization, Formal Analysis, Methodology, Supervision, Writing–review and editing. YW: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Writing–review and editing. BL: Conceptualization, Funding acquisition, Project administration, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (nos. 22279118, 22279117, 22075254).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1390303/full#supplementary-material

References

Anderson, D. L. (1974). Earthquakes and the rotation of the earth. Science. 186 (4158), 49–50. doi:10.1126/science.186.4158.49

PubMed Abstract | CrossRef Full Text | Google Scholar

Carter, W. E., Robertson, D. S., Pettey, J. E., Tapley, B. D., Schutz, B. E., Eanes, R. J., et al. (1984). Variations in the rotation of the earth. Science. 224 (4652), 957–961. doi:10.1126/science.224.4652.957

PubMed Abstract | CrossRef Full Text | Google Scholar

Chao, B. F., and Gross, R. S. (1987). Changes in the earth's rotation and low-degree gravitational field induced by earthquakes. Geophys J. Int. 3 (91), 569–596. doi:10.1111/j.1365-246X.1987.tb01659.x

CrossRef Full Text | Google Scholar

Chao, B. F., and Ray, R. D. (1996). Oceanic tidal angular momentum and earth's rotation variations. Prog. Oceanogr. 40 (1-4), 399–421. doi:10.1016/S0079-6611(98)00010-X

CrossRef Full Text | Google Scholar

Daher, H., Arbic, B. K., Williams, J. G., Ansong, J. K., Boggs, D. H., Müller, M., et al. (2021). Long-term earth-moon evolution with high-level orbit and ocean tide models. J. Geophys. Res-planet. 12, e2021JE006875. doi:10.1029/2021je006875

CrossRef Full Text | Google Scholar

Etkins, R., and Epstein, E. S. (1982). The rise of global mean sea level as an indication of climate change. Science. 215 (4530), 287–289. doi:10.1126/science.215.4530.287

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaind, N., and Stoye, E. (2019). How climate change is melting, drying and flooding earth — in pictures. Nat. News. doi:10.1038/d41586-019-02793-0

CrossRef Full Text | Google Scholar

Gibney, E. (2022). The leap second’s time is up: world votes to stop pausing clocks. Nat. News 11 (18), 18. doi:10.1038/d41586-022-03783-5

CrossRef Full Text | Google Scholar

Guy, J. (2023). Greenland and Antarctic ice sheets are melting rapidly and driving sea level rise, new satellite data finds [EB/OL]. CNN. Available at: https://www.cnn.com/2023/04/20/world/greenland-antarctic-ice-sheets-melt-climate-intl.

Google Scholar

Hide, R., and Dickey, J. O. (1991). Earth's variable rotation. Science 253 (5020), 629–637. doi:10.1126/science.253.5020.629

PubMed Abstract | CrossRef Full Text | Google Scholar

Historical Geography of the national unified examination for adult higher education enrollment in 2014. CNKI. China, Shanxi Educ. Entr. Exam. 2015 Z3 Issue.

Google Scholar

Hugonnet, R., McNabb, R., Berthier, E., Menounos, B., Nuth, C., Girod, L., et al. (2021). Accelerated global glacier mass loss in the early twenty-first century. Nature 592 (7856), 726–731. doi:10.1038/s41586-021-03436-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunt, B. G. (1979). The effects of past variations of the Earth's rotation rate on climate. Nature 281 (5728), 188–191. doi:10.1038/281188a0

CrossRef Full Text | Google Scholar

Jani-Friend, I. (2022). Greenland’s ice is melting from the bottom up – and far faster than previously thought, study shows [EB/OL]. CNN. Atlanta, GA. Available at: https://www.cnn.com/2022/02/22/world/greenland-ice-melting-sea-level-rise-climate-intl-scli-scn.

Google Scholar

Khobragade, N., and Roy, H. (2021). Classical mechanics and differential geometry. Saarbrücken, Germany: Harbin Institute of Technology Press.

Google Scholar

Kittel, C., Knight, W. D., Ruderman, M. A., and Lindsay, R. B. (2016). Mechanics, berkeley physics course-volume 1(in SI units). Beijing, China: China Machine Press.

Google Scholar

Klatt, J. M., Chennu, A., Arbic, B. K., Biddanda, B. A., and Dick, G. J. (2021). Possible link between Earth’s rotation rate and oxygenation. Nat. Geosci. 14 (8), 564–570. doi:10.1038/s41561-021-00784-3

CrossRef Full Text | Google Scholar

Kuhn, W. R., Walker, J. C., and Marshall, H. G. (1989). The effect on Earth's surface temperature from variations in rotation rate, continent formation, solar luminosity, and carbon dioxide. J. Geophys. Res. 20 (D8), 11129–11136. doi:10.1029/jd094id08p11129

PubMed Abstract | CrossRef Full Text | Google Scholar

Leap Seconds Information Sheet (2023). Time frequency bulletin. ISSN 45 (32), 1001–1811.

Google Scholar

Maddox, J. (1988). Earthquakes and the Earth's rotation. Nature 332, 11. doi:10.1038/332011a0

CrossRef Full Text | Google Scholar

Madzak, M., Schindelegger, M., Böhm, J., Bosch, W., and Hagedoorn, J. (2016). High-frequency Earth rotation variations deduced from altimetry-based ocean tides. J. Geod. 90, 1237–1253. doi:10.1007/s00190-016-0919-4

CrossRef Full Text | Google Scholar

Modiri, S., Heinkelmann, R., Belda, S., Malkin, Z., Hoseini, M., Korte, M., et al. (2021). Towards understanding the interconnection between celestial Pole motion and earth's magnetic field using space geodetic techniques. Sensors 21 (22), 7555. doi:10.3390/s21227555

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramirez, R. (2022). Greenland ice losses set to raise global sea levels by nearly a foot, new research shows [EB/OL]. CNN. Atlanta, GA. Available at: https://www.cnn.com/2022/08/29/world/greenland-ice-loss-sea-level-rise-study.

Google Scholar

Reddy, S., Reddy, V., and Sharma, S. (2023). in Physiology, circadian rhythm. 2023 may 1 (Treasure Island (FL): StatPearls Publishing).

Google Scholar

Ren, D. D., and Hu, A. X. (2021). Using GRACE data to estimate climate change impacts on the earth’s moment of inertia. Front. EARTH SCI-PRC. 9, 640304. doi:10.3389/feart.2021.640304

CrossRef Full Text | Google Scholar

Richards, M., Ricard, Y., Lithgow-Bertelloni, C., Spada, G., and Sabadini, R. (1997). An explanation for earth's long-term rotational stability. Science 275 (5298), 372–375. doi:10.1126/science.275.5298.372

PubMed Abstract | CrossRef Full Text | Google Scholar

Riguzzi, F., Panza, G., Varga, P., and Doglioni, C. (2010). Can Earth's rotation and tidal despinning drive plate tectonics? Tectonophysics 484 (1-4), 60–73. doi:10.1016/j.tecto.2009.06.012

CrossRef Full Text | Google Scholar

Roberts, P. H., and King, E. M. (2013). On the genesis of the Earth's magnetism. Rep. Prog. Phys. 76 (9), 096801. doi:10.1088/0034-4885/76/9/096801

PubMed Abstract | CrossRef Full Text | Google Scholar

Rounce, D. R., Hock, R., Maussion, F., Hugonnet, R., Kochtitzky, W., Huss, M., et al. (2023). Global glacier change in the 21st century: every increase in temperature matters. Science. 379 (6627), 78–83. doi:10.1126/science.abo1324

PubMed Abstract | CrossRef Full Text | Google Scholar

Runcorn, S. (1964). Changes in the earth's moment of inertia. Nature 204, 823–825. doi:10.1038/204823a0

CrossRef Full Text | Google Scholar

Satellite data shows antarctic Peninsula glaciers flow faster in summer (2023). Nat. Geosci., 16, 196–197.doi:10.1038/s41561-023-01135-0

CrossRef Full Text | Google Scholar

Schuh, H., and Böhm, S. (2021). “Earth rotation,” in Encyclopedia of solid earth geophysics. Encyclopedia of earth Sciences series. Editor H. K. Gupta (Cham: Springer). doi:10.1007/978-3-030-58631-7_177

CrossRef Full Text | Google Scholar

Shepherd, A., and Wingham, D. (2007). Recent sea-level contributions of the Antarctic and Greenland ice sheets. Science 315 (5818), 1529–1532. doi:10.1126/science.1136776

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinturel, F., Petrenko, V., and Dibner, C. (2020). Circadian clocks make metabolism run. J. Mol. Biol. 432 (12), 3680–3699. doi:10.1016/j.jmb.2020.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Triana, S. A., Dumberry, M., Cébron, D., Vidal, J., Trinh, A., Gerick, F., et al. (2022). Core eigenmodes and their impact on the earth's rotation. Surv. Geophys 43 (1), 107–148. doi:10.1007/s10712-021-09668-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ukhorskiy, A. Y., Sitnov, M. I., Mitchell, D. G., Takahashi, K., Lanzerotti, L. J., and Mauk, B. H. (2014). Rotationally driven 'zebra stripes' in Earth's inner radiation belt. Nature 507 (7492), 338–340. doi:10.1038/nature13046

PubMed Abstract | CrossRef Full Text | Google Scholar

van Wyk, A. S., and Prinsloo, G. (2019). Challenging current interpretation of sunflower movements. J. Exp. Bot. 70 (21), 6049–6056. doi:10.1093/jxb/erz381

PubMed Abstract | CrossRef Full Text | Google Scholar

Vargo, L. J., Anderson, B. M., Dadić, R., Horgan, H. J., Mackintosh, A. N., King, A. D., et al. (2020). Anthropogenic warming forces extreme annual glacier mass loss. Nat. Clim. Chang. 10 (9), 856–861. doi:10.1038/s41558-020-0849-2

CrossRef Full Text | Google Scholar

Williams, D. R. (2021). Earth fact sheet. Washington, DC: NASA.

Google Scholar

Williams, J. G., Turyshev, S. G., and Boggs, D. H. (2014). The past and present Earth-Moon system: the speed of light stays steady as tides evolve. Planet Sci. 3 (1), 2–9. doi:10.1186/s13535-014-0002-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C. Y., and Li, J. (2022). Seismic contributions to secular changes in global geodynamic parameters. J.Geophys.Res.Solid Earth. 8, 127. doi:10.1029/2022JB024590

CrossRef Full Text | Google Scholar

Young, H. D., Freedman, R. A., Sandin, T. R., and Ford, A. L. (2019). Sears and zemanky’s university physics with modern physics. 13th Edition. Beijing, China: China Machine Press.

Google Scholar

Zemp, M., Huss, M., Thibert, E., Eckert, N., McNabb, R., Huber, J., et al. (2019). Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 568, 382–386. doi:10.1038/s41586-019-1071-0

PubMed Abstract | CrossRef Full Text | Google Scholar