An improved radial basis function neural network for displacement prediction of a reservoir slope

Landslide prediction necessitates viewing the past, present, and future states of a slope as a constantly changing dialectical unity, with prediction laws derived from known past and present information. Through in-depth analysis of the structure and training methods of radial basis function (RBF) neural networks, an optimization method of RBF network diffusion velocity function based on the particle swarm optimization (PSO) algorithm was introduced in this study, aiming at the problem of limited coverage of spread value range determined by the empirical value or trial calculation method, so as to realize the large-scale and efficient search of RBF network diffusion function. To address the problem that the prediction accuracy of the data-driven model based on displacement increment sequences built by RBF intelligent algorithm is difficult to be guaranteed when the displacement increment mutation point exists, the PSO-RBF intelligent coupling model based on gray system theory pre-processing is constructed to improve the prediction accuracy of the model from the perspective of improving the prediction accuracy of displacement increment mutation points. Taking the data from ZG88 monitoring point of Shuping landslide as a case study, the slope displacement prediction analysis is carried out. The results demonstrate that the optimization method for RBF network diffusion velocity parameters based on PSO can efficiently and accurately identify the global optimal value within the range of 0–1,000. The computation process takes approximately 13 min, significantly enhancing the calculation efficiency. The RBF mixed model, incorporating gray system theory, leverages the valuable information extracted from prior calculations of the GM(1,1) model group. This integration enhances prediction accuracy compared with that achieved by the singular PSO-RBF method. The developed algorithms and research results may be expected to be applied in practical engineering.

1 Introduction

Surface displacement monitoring data consist of the most intuitive and effective information for characterizing slope conditions (Dong et al., 2022; Liu et al., 2024). A large number of landslide monitoring data indicate that the evolution processes of various gradient landslides not only have unique characteristics but also have common laws (Zhao et al., 2021; Li et al., 2023); that is, the displacement–time curves of the monitored slopes typically exhibit a three-stage evolution pattern characterized by initial deformation, sustained deformation, and accelerated deformation (Benac et al., 2011; Niu et al., 2012; Pei et al., 2019). Currently, establishing a data-driven mathematical model based on time series data of slope displacements is the most crucial method for landslide prediction (Xie et al., 2019; Gheorghe et al., 2023).

Recently, there have been many state-of-the-art research studies about optimization algorithms and machine learning for slope stability. Mohammad et al. (2022)developed an effective intelligent system based on artificial neural networks and a new version of the sine cosine algorithm to evaluate and predict the factor of safety of homogenous slopes under static and dynamic loading. Hoang and Pham (2016)proposed a hybrid artificial intelligence method for slope stability assessment based on metaheuristic and machine learning, and a dataset that contains 168 real cases of slope evaluation was used to confirm the proposed hybrid approach. Khajehzadeh and Keawsawasvong (2023)established the global best artificial electric field algorithm for the fine-tuning of the support vector regression hyperparameters, and the prediction accuracy of the proposed models for forecasting the slope’s safety factor was examined. Koopialipoor et al. (2019)predicted the safety factor of many homogenous slopes in static and dynamic conditions by applying various hybrid intelligent systems, namely, imperialist competitive algorithm (ICA)-artificial neural network (ANN), genetic algorithm (GA)-ANN, particle swarm optimization (PSO)-ANN, and artificial bee colony (ABC)-ANN. Similarly, Gordan et al. (2016)built two intelligent systems, namely, ANN and PSO-ANN models, to predict the factor of safety of homogeneous slopes. It can be said that the slope stability has been well evaluated in the previous studies by the factor of safety using variousintelligent algorithms.

However, it is still very necessary to the further development of landslide prediction for the slopes of complex geological structures. Based on an in-depth analysis of the structure and training techniques of the radial basis function (RBF) neural network (Zhao and San, 2011; Wu X. J. et al., 2013), an RBF neural network was adopted in this study as the research method. It comprehensively integrates the data analysis method, swarm intelligence optimization algorithm, and gray system theory to explore the issue of slope displacement prediction. For the RBF neural network, the particle swarm optimization (PSO) algorithm is always applied for its optimization by research workers. Koupae et al. (2018)integrated the PSO algorithm with Kansa’s method based on meshless collocation methods in order to determine a good shape parameter of RBF for solving partial differential equations. Tsoulos and Charilogis (2023)presented an innovative two-phase method for parameter tuning in the RBF neural network, and they developed a technique based on PSO to locate a promising interval of values for the network parameters. PSO is generally considered a highly reliable method for global optimization problems, and in addition, it is one of the fastest and most flexible techniques of its class (Koupae et al., 2018). Therefore, the optimization method of RBF network diffusion velocity function based on the PSO algorithm was proposed (Jain et al., 2022). On the basis of previous studies, ZG88 monitoring data of Shuping landslide were taken as an example in this study, and the applicability of PSO-RBF neural network for landslide predictionis discussed.

In this study, aiming at the problem that the spread coverage ability determined by the trial method is limited and easy to fall into local optimum (Zhao et al., 2021), a RBF network diffusion velocity function optimization method based on the PSO algorithm is proposed to realize the large-scale and efficient search of RBF network diffusion function. On this basis, in view of the fact that it is difficult to guarantee the prediction accuracy of the data-driven model based on the displacement increment sequence constructed by a single RBF intelligent algorithm when the displacement increment mutation point exists (Li and Liu, 2005), the PSO-RBF intelligent coupling model based on the graying layer pre-processing is established to improve the prediction accuracy of the model from the perspective of improving the prediction accuracy of displacement incrementmutation point.

2 Improvement of RBF neural network

2.1 RBF neural network

In 1988, Broomhead and Lowe (Wang and Xu, 2010) introduced the multivariate difference RBF into neural networks according to the local response phenomenon observed in biological neurons. Different from the slow learning velocity and complex network parameters resulting from the influence of one or more adjustable parameters on the global output in global approximation networks, the RBF neural network is a local approximation network. It possesses numerous advantages, including fast convergence velocity, simple structure, and strong approximation ability. Numerous studies have demonstrated that RBF neural networks can approximate arbitrary nonlinear functions within a compact set and achieve any desired level of precision (Jiang et al., 2021; Wang, 2023).

The RBF neural network consists of three layers: the input layer, the hidden layer, and the output layer, which are arranged in a forward architecture. The hidden layer employs the radial basis function as the activation function, as illustrated in Figure 1.

Figure 1

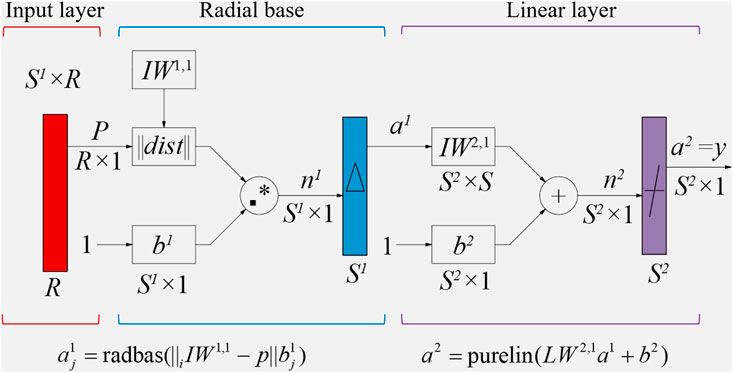
Figure 1. Structure of the RBF network (Koupae et al., 2018).

The output of the network is

$a^2=\text{purelin}\left(L{W}^2{a}^1+b^2\right),(1)$

where $a^1=\text{radbas}\left(n^1\right)$, ${n^1=‖IW-P‖.}^{*}{b}^1={\left(\text{diag}\left({\left(IW-ones{\left(S^1,1\right)}^{*}{P}^{\prime }\right)}^{\prime }\right)\right)}^{^}{0.5.}^{*}{b}^1$, $\text{diag}\left(x\right)$ represents a column vector composed of elements on the diagonal of a matrix vector, and“.^”and“.*”represent the scalar multiplication and scalar product (the multiplication and product of the corresponding elements in the matrix), respectively.

2.2 PSO neural network

The mathematical description of the PSO algorithm (Wang et al., 2018; Zeng et al., 2022) can be as follows. Consider that in a D-dimensional (D-D) space, population $X=\left(x_1,\dots x_i,\dots x_D\right)$ is composed of m randomly generated scattered particles, where the position of the ith particle is $V_i={\left(v_{i1},\dots v_{ii},\dots v_{iD}\right)}^{\mathrm{T}}$ and the velocity is $V_i={\left(v_{i1},\dots v_{ii},\dots v_{iD}\right)}^{\mathrm{T}}$. The fitness of each particle can be calculated based on the objective function. In each iteration calculation, the ith particle will calculate the displacement vector $PBES{T}_{ij}={\left(p_{i1},\dots p_{i2},\dots p_{iD}\right)}^{\mathrm{T}}$ of the particle according to the extreme value $PBES{T}_{ij}$ obtained in the past and the extreme value $GBES{T}_{ij}$ of the population. The particle vector and the displacement vector are utilized as the particle vector values of the next iteration. The individual extreme value is $PBES{T}_{ij}={\left(p_{i1},\dots p_{i2},\dots p_{iD}\right)}^{\mathrm{T}}$ and the global extreme value of the population is $GBES{T}_{ij}={\left(p_{i1},\dots p_{i2},\dots p_{iD}\right)}^{\mathrm{T}}$. Based on the principle of tracking the optimal particle, the particle $x_i$ adjusts its position and velocity according to the following formula:

$V_{ij}\left(t+1\right)=V_{ij}\left(t\right)+c_1{r}_1\left(t\right)\left(PBES{T}_{ij}\left(t\right)-x_{ij}\left(t\right)\right)+c_2{r}_2\left(t\right)\left(GBES{T}_{ij}\left(t\right)-x_{ij}\left(t\right)\right),(2)$

$x_{ij}\left(t+1\right)=x_{ij}\left(t\right)+v_{ij}\left(t+1\right).(3)$

2.3 Optimization of RBF network diffusion velocity parameters based on PSO

In the undetermined parameters of the RBF neural network prior to training, the value of network diffusion velocity spread directly influences the fitting and generalization abilities of the network. For function features exhibiting rapid changes, excessively large spread values will result in overly coarse approximation outcomes. In the existing research, the spread value range is typically determined through empirical values or trial calculation methods, and with the spread value being assigned a fixed step increment within this range. The mean square error (MSE) of the prediction results under various spread values is compared to achieve parameter optimization. However, under the influence of rainfall, geological structure, topography, and other factors, the deformation and stress release of natural slopes become highly complex processes (Liu et al., 2021). The cumulative displacement–time curves and single-period displacement–time curves of slopes vary across different stages of evolution. On the one hand, the spread value range determined by empirical values or trial calculation methods has limited coverage ability, potentially encompassing only one or several local optima and failing to include the global optimum value. On the other hand, the size of the incremental step impacts the accuracy of the spread value. If the step size is too large, the optimal solution may be missed. Conversely, if the step size is too small, the calculation time will significantly increase, making it impractical to efficiently search within a large range. To address the above issues encountered with the empirical value interval search method, this study employs the PSO algorithm to search for the optimal solution of the spread parameter.

2.4 PSO-RBF intelligent coupling model based on gray system theory

In 1982, the gray system theory was first proposed by Deng (1983). The theory focuses on studying uncertain systems characterized by “poor information” and “limited data,” where only “partial information is known and partial information is unknown.” By developing and generating “partial” known information, valuable information is extracted to accurately describe and effectively predict the behavior and evolution patterns of the system (Wu L. F. et al., 2013). In gray system theory, random variables are considered as gray quantities that vary within a certain range, whereas random processes are seen as gray processes that fluctuate within a defined range and time frame. The gray model (GM) is utilized to depict the progression of development and change within abstract systems. The gray model with n-order derivative h variables is typically described as necessitating variable h to encapsulate the comprehensive effect of the predicted object. In the prediction of slope displacement, the displacement monitoring time series represents a temporal sequence influenced by various factors combined. Order n of the differential equation is typically below the third order, as computational complexity escalates substantially with higher n, whereas the increase in prediction accuracy is not necessarily guaranteed. In this study, the value of n is set to 1, and the first-order dynamic gray model of singular sequence, known as the GM(1, 1) model,is constructed.

The whitened differential equation is

$\frac{\mathrm{d}{x}^{\left(1\right)}\left(t\right)}{\mathrm{d}t}+a{x}^{\left(1\right)}\left(t\right)=b,(4)$

where a and b are identified model parameters. According to the definition of white derivative,

$\frac{\mathrm{d}{x}^{\left(1\right)}\left(t\right)}{\mathrm{d}t}=\underset{\Delta x\to 0}{\lim }\frac{x^{\left(1\right)}\left(t+\Delta t\right)-x^{\left(1\right)}\left(t\right)}{\Delta t}.(5)$

Considering equidistant sampling, the discrete form of the above equation is expressed as

$\frac{\mathrm{d}{x}^{\left(1\right)}\left(t\right)}{\mathrm{d}t}=\frac{x^{\left(1\right)}\left(t+\Delta t\right)-x^{\left(1\right)}\left(t\right)}{\left(t+1\right)-t}=x^{\left(1\right)}\left(t+\Delta t\right)-x^{\left(1\right)}\left(t\right)={\alpha }^{\left(1\right)}\left[x^{\left(1\right)}\left(t+1\right)\right].(6)$

Substitute Eq. 6 into the differential equation to obtain the gray difference equation

${\alpha }^{\left(1\right)}\left[x^{\left(1\right)}\left(t+1\right)\right]+{\chi }^{\left(1\right)}=b,(7)$

where ${\chi }^{\left(1\right)}$ is the background value of derivative $\frac{\mathrm{d}{x}^{\left(1\right)}\left(t\right)}{\mathrm{d}t}$. As the gray derivative represents the difference between new and old information within a unit time, and any gray derivative is calculated based on a specific background value, this background value is applicable to both new and old information. Hence, the average of new and old information is adopted as the background value, and the equation is describedas follows:

${\chi }^{\left(1\right)}=z^{\left(1\right)}\left(t+1\right)=0.5\left[x^{\left(1\right)}\left(t+1\right)+x^{\left(1\right)}\left(t\right)\right].(8)$

Substituting Eq. 8 into the gray difference equation, considering ${\alpha }^{\left(1\right)}\left[x^{\left(1\right)}\left(t+1\right)\right]=x^{\left(0\right)}\left(t+1\right)$, we have

$\left[x^{\left(0\right)}\left(t+1\right)\right]+\alpha z^{\left(1\right)}\left(t+1\right)=bt=1,2,\cdots n-1.(9)$

Because of significant variations in the prerequisites for slope deformation disasters caused by geomorphological characteristics, stratigraphic lithology, geological structure, and hydrogeological environment, along with the impacts of inducing factorslike precipitation, reservoir water level fluctuation, earthquakes, and vegetation damage, the displacement increment sequences obtained from different landslide monitoring points exhibit distinct nonlinear characteristics. When employing a single RBF intelligent algorithm to build a data-driven model based on displacement increment sequences, ensuring prediction accuracy becomes challenging in the presence of displacement increment mutation points. Addressing the limitations of single prediction methods, Bates and Granger (1969)first proposed the idea of combined prediction in 1969. At present, this idea has been widely developed and applied. In this study, the PSO-RBF intelligent coupling model based on gray system theory is constructed, drawing upon the concept of combined prediction. Using the monitoring data from ZG88 of the Shuping landslide as a case study, the predictioneffect is assessed.

The PSO-RBF intelligent coupling model based on the GM(1, 1) model group is established. The fundamental process involves integrating the pre-processing steps of the GM(1, 1) model group before inputting into the PSO-RBF neural network. The GM(1, 1) model exhibits varying influential factors across different evolutionary stages. The validity of the GM(1, 1) model’s prediction results is closely related to the length of the data sequence used in modeling. The model established by different length sequences has different prediction accuracy. The corresponding GM(1, 1) model groups are established using data of varying dimensions, and the prediction results serve as input training samples for the PSO-RBF neural network. This facilitates high-precision training and prediction of the network. The algorithm implementation process is shown in Figure 2.

Figure 2

Figure 2. Implementation of PSO-RBF intelligent coupling model based on gray system theory.

3 Slope deformation displacement prediction

3.1 Research slope profile and data preparation

In this study, the Shuping landslide in the Three Gorges Reservoir area of the Yangtze River was selected as the research background. The longitudinal length of the sliding body is about 800 m from north to south and 700 m from east to west, with a thickness ranging between 40 and 70 m. The total volume is about 2,890×10⁴ m³. The Shuping landslide (Zhao, 2022; Jia et al., 2023) is an old landslide accumulation body, which is situated on the southern slope of the Yangtze River in Shuping Village, Shazhenxi Town, Zigui County, Hubei Province. It is approximately 47 km away from the Three Gorges Project dam site, with geographical coordinates at 110°37′0″longitudeand 30°59′37″latitude.

The research focuses on 73 months of monitoring data from monitoring point ZG88, situated in the eastern lower part of the Shuping landslide within the Three Gorges Reservoir area of the Yangtze River. These data were provided by the National Field Scientific Observation and Research Station of the Three Gorges Landslide in the Hubei Province. During these 73 months, the geological conditions have hardly changed, and their effects on the monitoring data can be ignored (Zhao, 2022). The original surface displacement monitoring data are filtered and processed, as shown in Figure 3.

Figure 3

Figure 3. Displacement of the monitoring point on Shuping landslide.

3.2 Optimization of the number of input nodes

The displacement increment data from the ZG88 monitoring points of the Shuping landslide are filtered and normalized to the range of [0.1, 0.9]. The optimal historical data point, n, is determined by calculating both the autocorrelation function and the partial correlation function. The calculation results of the autocorrelation coefficient (ACF) and partial autocorrelation coefficient (PACF) for the displacement increment sequence of ZG88 monitoring points are presented in Table 1, with the corresponding figures illustrated in Figure 4. The blue dotted line in the figure represents the upper and lower limits of the 95% confidence interval.

Table 1

Table 1. Calculated values of ACF and PACF of ZG88 monitoring point data of Shuping landslide.

Figure 4

Figure 4. ACF and PACF of displacement increment sequence of ZG88 monitoring points.

Based on the calculation results of the displacement increment data from monitoring point ZG88, when the optimal historical data point, n, is set to 2, the ACF of the displacement increment sequence is 0.483, which is notably higher than the subsequent values. Furthermore, the subsequent PACF value falls within the 95% confidence interval. Hence, the ZG88 monitoring point selects n = 2, indicating that the displacement increment data from the preceding 2 months can be chosen as the network input data.

3.3 Optimization of diffusion velocity parameters

To prevent parameter selection from falling into a local optimum, the selected spread search range should be as large as possible, and the incremental step size should be as small as possible. Both of them significantly increase the computation time. In this study, the search interval is set to [0.1, 10,000], with an incremental step size of 0.1. The computation time required to evaluate 100,000 candidate values for the ZG88 monitoring data is approximately 9 h, indicating a substantial time investment. Logarithmic coordinates (log10) are employed in both the horizontal and vertical axes, with selected calculation results depicted in Figure 5. Taking the [0.1, 100] search interval as an example, the ZG88 monitoring point data achieved a local optimal solution within the range of [90, 100]. Subsequently, within the subsequent [100, 1,000] range, the MSE further decreased. It is evident that the spread value range determined by empirical values or trial calculation methods has limited coverage ability. Such ranges may only encompass one or several local optima, thus failing to include the global optimum value. Setting the incremental step size to 0.1 may result in missing the optimal solution, whereas reducing it to 0.001 would increase the calculation time to 900 h, rendering efficient search impractical.

Figure 5

Figure 5. Fitness function curves of the empirical value interval search method.

To address the aforementioned challenges and enhance the fitting and generalization capabilities of the RBF neural network, this study employs the PSO algorithm to search for the optimal value of the objective function spread. In the algorithm parameters, the initial population number CPSO.N is 40, the inertia weight CPSO. ω is 0.7298, the individual acceleration coefficient CPSO. c₁ is 1.49445, and the group acceleration coefficient CPSO. c₂ is 1.49445. After trial calculation, the search interval is set to [0.001, 1,000] and the upper limit of evaluation times is set to 800. The calculation results for the optimal diffusion velocity spread of the RBF neural network using ZG88 monitoring point data are depicted in Figure 6. Each independent evaluation of the monitoring data takes approximately 13 min, with an upper limit of 800 evaluations. From the evaluation results, it can be seen that the monitoring data successfully identified the optimal solution for the SPREAD within the interval of [0.001, 1,000] within 100 steps of a single independent evaluation. This achievement contrasts with the approximately 900 h required to achieve a similar accuracy range using the empirical value interval search method. Based on these calculations, the spread of the ZG88 monitoring data is determined to be 985.262.

Figure 6

Figure 6. PSO fitness function curves of ZG88 data.

4 Analysis of prediction results of PSO-RBF

To verify the applicability of PSO-RBF neural network in landslide prediction after the parameters are optimized by the number of input nodes and the diffusion velocity parameters, the following experiments are carried out.

Based on the optimization results for the number of network input nodes, the network topology is configured with two input nodes. Furthermore, leveraging the optimization outcomes for diffusion velocity parameters, the diffusion function SPREAD is set to 985.262. The scalar GOAL is set to the default value of 0, and the number of output nodes is configured to be 1. Training samples consist of data from periods 1 to 63, whereas test samples encompass data from periods 64 to 73. The displacement increment monitoring data for each period are normalized to the interval [0.1, 0.9]. Figure 7 illustrates the displacement increment prediction curves, whereas Figure 8 depicts the displacement prediction curves. Additionally, Table 2 shows the displacement prediction results for the prediction period.

Figure 7

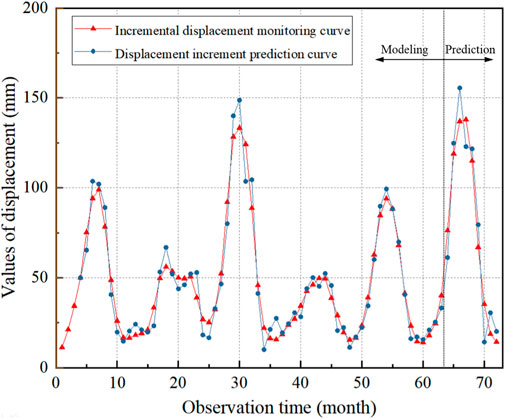
Figure 7. Prediction results of displacement increment at ZG88 monitoring point of Shuping landslide.

Figure 8

Figure 8. Prediction results of displacement of ZG88 monitoring point of Shuping landslide.

Table 2

Table 2. Prediction results of ZG88 monitoring point of Shuping landslide (unit: mm).

The prediction results indicate that the root mean square error, relative error, and average relative error of the experimental results in both the training and test periods are small, suggesting the absence of under-training or overfitting phenomena. The PSO-RBF neural network, optimized by the number of input nodes and diffusion velocity parameters as proposed in this paper, demonstrates robust applicability in landslide prediction. However, it is worth noting that the displacement increment sequence of the ZG88 monitoring point of the Shuping landslide exhibits a sudden change point during periods 67–70, coinciding with the presence of test samples within the same period range. The prediction curve exhibits a slight deviation from the monitoring curve, and there is a cumulative error in the displacement prediction results for the same period. Due to the limitations of the RBF neural network method, in the face of input samples with highly nonlinear characteristics, there is often a large degree of deviation from the predicted data.

To address the highly nonlinear characteristics of displacement increment sequences, this study introduces a PSO-RBF intelligent coupling model based on gray system theory. By incorporating principles from gray system theory, the displacement increment sequence is transformed into a monotonically increasing cumulative displacement sequence using the gray cumulative generation operator. Gray PSO-RBF and GM(1, 1)-PSO-RBF intelligent coupling models, based on gray system theory, are constructed to investigate the enhancement of prediction accuracy from the perspective of intelligentcoupling models.

5 Analysis of prediction effect of intelligent coupling model

The data from periods 1–63 were designated as the training set, whereas the data from periods 64–73 were assigned to the test set. Additionally, the information dimensions of the GM(1, 1) model were configured as 4D, 5D, 6D, 7D, and 8D. Accordingly, the number of input nodes in the PSO-RBF network is set to 5, aligning with the number of calculation results obtained from the GM(1, 1) model across various dimensional information settings. The number of output nodes remains at 1. The PSO algorithm was employed to search for the optimal value of the objective function spread within the range [0.001, 10,000], yielding a result of 6,321.25. The scalar GOAL is set to 0. The prediction results of the GM(1, 1) model for each dimension and the RBF mixed model based on the GM(1,1) model group are presented in Table 3. The cumulative displacement Nash–Sutcliffe efficiency (NSE) coefficient, mean absolute percentage error (MAPE), and RMSE of the RBF mixed model based on the GM(1,1) model group are 0.9996, 0.12%, and 4.984,respectively.

Table 3

Table 3. Prediction results of the RBF mixed model based on the GM(1, 1) model group.

Based on the above analysis, it can be seen that the RBF mixed models based on the GM(1, 1) model group exhibit no signs of inadequate training or overfitting phenomena, and they can effectively fulfill the data prediction requirements of this group. Compared with the RBF model, the slope displacement prediction model demonstrates improved accuracy under evaluation indexes such as the Nash coefficient, mean absolute error percentage, and root mean square error.

6 Conclusion

Slope displacement stands as a paramount parameter in landslide prediction, serving as the most crucial and readily obtainable information. It adeptly mirrors the failure characteristics and dynamic deformation of landslides. In this study, the intelligent algorithm is used as the research method, integrating data analysis techniques, swarm intelligence optimization algorithms, and gray system theory for comprehensive analysis of slope displacement prediction. The PSO-RBF slope displacement prediction model and the PSO-RBF intelligent coupling model, integrating gray system theory, have been constructed. These improved methods have been effectively validated and deployed for predicting displacement in the Shupinglandslide scenario.

In the undetermined parameters of the RBF neural network before training, the value of the diffusion velocity spread directly impacts the network’s fitting and generalization abilities. Aiming at the issue of limited coverage in determining the spread value range through empirical or trial calculation methods, the RBF network’s diffusion velocity parameter optimization method, based on PSO, accurately and efficiently identifies the global optimal value across a wide range. This approach significantly enhances the computational efficiency.

In the absence of landslide inducement monitoring data, it is difficult to ensure the prediction accuracy of displacement increment mutation point of a data-driven model based on cumulative displacement sequence by using a single RBF intelligent algorithm. The PSO-RBF intelligent coupling model developed in this study, based on gray system theory, maximizes the utility of the valuable information derived from the preceding calculations of the GM(1,1) model group. Consequently, the predictive performance of the model is significantly enhanced compared to that of the single PSO-RBF method. This approach can be recommended for adoption in engineering practices.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XZ: investigation, software, and writing–original draft. WL: conceptualization, formal analysis, writing–review and editing, and writing–original draft. GL: funding acquisition, methodology, and writing–review and editing. BY: data curation, formal analysis, supervision, and writing–review and editing. WB: data curation, software, and writing–review and editing. PZ: conceptualization, investigation, and writing–reviewand editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (42007241), the Joint Program (Fund) Project of Science and Technology Plan of Liaoning Province (2023-MSLH-259), and the Scientific Research Funding Project of Education Department of Liaoning Province (LQGD2020003).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bates, J. M., and Granger, C. W. J. (1969). The combination of forecasts. Oper. Res. Q. 20, 451–468. doi:10.2307/3008764

CrossRef Full Text | Google Scholar

Benac, C., Dugonjic, S., Vivoda, M., Ostric, M., and Arbanas, Z. (2011). A complex landslide in the Rječina Valley: results of monitoring 1998-2010. Geol. Croat. 64, 239–249. doi:10.4154/gc.2011.20

CrossRef Full Text | Google Scholar

Deng, J. L. (1983). Grey system review. J. World Sci. 7, 1–5.

Google Scholar

Dong, K., Yang, D. W., Chen, J. K., Zhou, J. R., Li, J. R., Lu, X., et al. (2022). Monitoring-data mechanism-driven dynamic evaluation method for slope safety. Comput. Geotech. 148, 104850. doi:10.1016/j.compgeo.2022.104850

CrossRef Full Text | Google Scholar

Gheorghe, S., Iancu, V. I., Ionescu, I. A., Pirvu, F., Paun, I. C., Pascu, L. F., et al. (2023). Adsorption of sunscreen compounds from wastewater using commercial activated carbon: detailed kinetic and thermodynamic analyses. Water 15, 4190. doi:10.3390/w15234190

CrossRef Full Text | Google Scholar

Gordan, B., Armaghani, D. J., Hajihassani, M., and Monjezi, M. (2016). Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 32, 85–97. doi:10.1007/s00366-015-0400-7

CrossRef Full Text | Google Scholar

Hoang, N. D., and Pham, A. D. (2016). Hybrid artificial intelligence approach based on metaheuristic and machine learning for slope stability assessment: a multinational data analysis. Expert. Syst. Appl. 46, 60–68. doi:10.1016/j.eswa.2015.10.020

CrossRef Full Text | Google Scholar

Jain, M., Saihjpal, V., Singh, N., and Singh, S. B. (2022). An overview of variants and advancements of PSO algorithm. Appl. Sci.-Basel 12, 8392. doi:10.3390/app12178392

CrossRef Full Text | Google Scholar

Jia, W. J., Wen, T., Li, D. C., Guo, W., Quan, Z., Wang, Y. H., et al. (2023). Landslide displacement prediction of Shuping landslide combining PSO and LSSVM model. Water 15, 612. doi:10.3390/w15040612

CrossRef Full Text | Google Scholar

Jiang, Q. H., Zhu, L. L., Shu, C., and Sekar, V. (2021). An efficient multilayer RBF neural network and its application to regression problems. Neural comput. Appl. 34, 4133–4150. doi:10.1007/s00521-021-06373-0

CrossRef Full Text | Google Scholar

Khajehzadeh, M., and Keawsawasvong, S. (2023). Predicting slope safety using an optimized machine learning model. Heiyon 9, e23012. doi:10.1016/j.heliyon.2023.e23012

PubMed Abstract | CrossRef Full Text | Google Scholar

Koopialipoor, M., Armaghani, D. J., Hedayat, A., Marto, A., and Gordan, B. (2019). Applying various hybrid intelligent systems to evaluate and predict slope stability under static and dynamic conditions. Soft Comput. 23, 5913–5929. doi:10.1007/s00500-018-3253-3

CrossRef Full Text | Google Scholar

Koupae, J. A., Firouznia, M., and Hosseini, S. M. M. (2018). Finding a good shape parameter of RBF to solve PDEs based on the particle swarm optimization algorithm. Alex. Eng. J. 57, 3641–3652. doi:10.1016/j.aej.2017.11.024

CrossRef Full Text | Google Scholar

Li, J., and Liu, J. H. (2005). On the prediction of chaotic time series using a new generalized radial basis function neural networks. Acta Phys. Sin. 54, 4569–4577. doi:10.7498/aps.54.4569

CrossRef Full Text | Google Scholar

Li, Y. Z., Shen, J. H., Zhang, W. X., Zhang, K. Q., Peng, Z. H., and Huang, M. (2023). Slope deformation partitioning and monitoring points optimization based on cluster analysis. J. Mt. Sci. 20 (8), 2405–2421. doi:10.1007/s11629-023-8015-8

CrossRef Full Text | Google Scholar

Liu, G. Y., Li, J. J., and Wang, Z. Z. (2021). Experimental verifications and applications of 3D-DDA in movement characteristics and disaster processes of rockfalls. Rock Mech. Rock Eng. 54, 2491–2512. doi:10.1007/s00603-021-02394-2

CrossRef Full Text | Google Scholar

Liu, G. Y., Zhong, Z. R., Ma, K., Bo, W., Zhao, P. H., Li, Y. X., et al. (2024). Field experimental verifications of 3D DDA and its applications to kinematic evolutions of rockfalls. Int. J. Rock Mech. Min. Sci. 175, 105687. doi:10.1016/j.ijrmms.2024.105687

CrossRef Full Text | Google Scholar

Mohammad, K., Mohd, R. T., Suraparb, K., Hamidreza, M., and Mohammadreza, J. (2022). An effective artificial intelligence approach for slope stability evaluation. IEEE Access 10, 5660–5671. doi:10.1109/access.2022.3141432

CrossRef Full Text | Google Scholar

Niu, J. T., Li, Z. C., and Su, H. Z. (2012). A monitoring model for high slope displacement considering the effects of dynamic structure mutation. Disaster Adv. 5, 1313–1320.

Google Scholar

Pei, H. F., Zhang, S. Q., Borana, L., Zhao, Y., and Yin, J. H. (2019). Slope stability analysis based on real-time displacement measurements. Measurement 131, 686–693. doi:10.1016/j.measurement.2018.09.019

CrossRef Full Text | Google Scholar

Tsoulos, I. G., and Charilogis, V. (2023). Locating the parameters of RBF networks using a hybrid particle swarm optimization method. Algorithms 16, 71. doi:10.3390/a16020071

CrossRef Full Text | Google Scholar

Wang, B. W. (2023). Research on nonlinear calibration of mine catalytic-combustion-based combustible-gas sensor based on RBF neural network. Heliyon 9, e14055. doi:10.1016/j.heliyon.2023.e14055

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D. S., Tan, D. P., and Liu, L. (2018). Particle swarm optimization algorithm: an overview. Soft Comput. 22, 387–408. doi:10.1007/s00500-016-2474-6

CrossRef Full Text | Google Scholar

Wang, J. J., and Xu, Z. B. (2010). New study on neural networks: the essential order of approximation. Neural Netw. 23, 618–624. doi:10.1016/j.neunet.2010.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L. F., Liu, S. F., Yao, L. G., Yan, S. L., and Liu, D. L. (2013b). Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. 18, 1775–1785. doi:10.1016/j.cnsns.2012.11.017

CrossRef Full Text | Google Scholar

Wu, X. J., Jiang, G. C., Wang, X. J., Fang, N., Zhao, L., Ma, Y. M., et al. (2013a). Prediction of reservoir sensitivity using RBF neural network with trainable radial basis function. Neural comput. Appl. 22, 947–953. doi:10.1007/s00521-011-0787-z

CrossRef Full Text | Google Scholar

Xie, J. R., Uchimura, T., Chen, P., Liu, J. P., Xie, C. R., and Shen, Q. (2019). A relationship between displacement and tilting angle of the slope surface in shallow landslides. Landslides 16, 1243–1251. doi:10.1007/s10346-019-01135-5

CrossRef Full Text | Google Scholar

Zeng, N. Y., Wang, Z. D., Liu, W. B., Zhang, H., Hone, K., and Liu, X. H. (2022). A dynamic neighborhood-based switching particle swarm optimization algorithm. Cybernetics 52, 9290–9301. doi:10.1109/tcyb.2020.3029748

CrossRef Full Text | Google Scholar

Zhao, P. H. (2022). Research on machine vision identification and monitoring of landslide in Southeast Tibet. PhD thesis. Dalian University of Technology.

Google Scholar

Zhao, P. H., Li, J. J., and Kang, F. (2021). Slope surface displacement monitoring based on a photogrammetric system. Optik 227, 166089. doi:10.1016/j.ijleo.2020.166089

CrossRef Full Text | Google Scholar

Zhao, W., and San, Y. (2011). RBF neural network based on q-Gaussian function in function approximation. Front. Comput. Sci. 5, 381–386. doi:10.1007/s11704-011-1041-7

CrossRef Full Text | Google Scholar