Yield estimation of North Korean underground nuclear tests using Lg-wave source spectra

In seismic nuclear monitoring, attenuation models are important prerequisites for reliably estimating the explosive yield in an uncalibrated region without the occurrence of standard events. The seismic moment obtained by fitting source spectra is related to the source energy. This approach is appropriate for estimating yield, as the attenuation effects on the propagation path can be accurately considered. In this study, we collected 2022 vertical component waveforms in and around the Korean Peninsula from May 2010 to May 2022 to construct a high-resolution broadband Lg-wave attenuation model and inverted the Lg-wave source excitation spectra of the nuclear explosion simultaneously with attenuation correction. We obtained the scalar seismic moments by fitting the theoretical source spectra based on the Brune (J. Geophys. Res., 1970, 75, 4997–5009) model. Under the given emplacement conditions and burial depths, the seismic moments can be used to estimate yields of the North Korean nuclear tests, which are 4.6, 8.5, 19.9, 20.9, 24.7, and 337.4 kt for six nuclear explosions that occurred between 2006 and 2017. Our results are consistent with those obtained from previous teleseismic observations.

Highlights

• A broadband Lg attenuation model is constructed for the Korean Peninsula and its surrounding areas.

• Both the seismic moment and corner frequency are obtained based on Lg-wave excitation spectra.

• The explosive yields of North Korean tests are increasing based on the seismic moments of Lg waves.

1 Introduction

When characterizing an explosive event, determining the yield is an important step (Pasyanos, 2022). With the rapid development of modern seismic networks, broadband digital seismograms on high-density stations have promoted the widespread application of regional monitoring techniques for yield estimation (Hong et al., 2008; Zhao et al., 2008; Pasyanos et al., 2012; Yao et al., 2018; Kim et al., 2019; Ma et al., 2020; Delbridge et al., 2023). The continental crustal-guided Lg-wave is the most prominent phase of a seismic event at a regional distance (e.g., Hong et al., 2008). The broad sampling of different ray paths from the source makes Lg particularly suitable for yield estimation (e.g., Zhao et al., 2008). However, Lg-derived yield estimations are critically dependent on regional attenuation and strongly dependent on the selected frequency band (e.g., Zhao et al. (2012)). For example, Zhao et al. (2008) used the third-peak amplitude and the root mean square (RMS) amplitude of Lg waves at approximately 1 Hz to measure body-wave magnitudes m_b (Lg) to obtain yield estimations. These results are different from those of magnitude-yield estimations based on teleseismic P waves (Zhang and Wen, 2013; Xie and Zhao, 2018; Yao et al., 2018; Voytan et al., 2019; Yang et al., 2021). The waveform energy difference may be a dominant factor within a selected frequency band (Aki and Richards, 2002).

Six underground nuclear explosion tests were conducted in North Korea on 9 October 2006, 25 May 2009, 12 February 2013, 6 January 2016, 9 September 2016, and 3 September 2017 (NKT1-6) (e.g., Voytan et al., 2019). Historical explosive yield estimations are obtained by converting seismic magnitudes from the amplitudes of teleseismic body waves to yields using empirical relationships (Bowers et al., 2001; Nuttli, 1973; Nuttli, 1986; Patton and Schlittenhardt, 2005; Patton and Taylor, 2011). Since the North Korean nuclear test site is uncalibrated, there are challenges in terms of absolute explosion magnitude and yield estimations (Delbridge et al., 2023). As a measurable and well-understood physical parameter of seismic sources, the seismic moment allows us to move away from purely empirical calibrations and directly calculate the yield of explosions theoretically (Pasyanos and Chiang, 2021). Unlike body wave magnitudes, which focus on the amplitude of narrowband high frequencies (>1 Hz), the seismic moment is obtained by fitting the long-period portion of observed seismic source spectra. Alvizuri and Tape (2018) and Chiang et al. (2018) calculated the seismic moment of NKT1-6 based on regional long-period surface waves between 0.02 and 0.05 Hz, all of which rely on the same 1D-layered Earth model, MDJ2 (Ford et al., 2009), with a constant attenuation assumption. Although the attenuation of low-frequency (<0.05 Hz) seismic waves may be relatively stable, the signal-to-noise ratio (SNR) for low-yield explosions is poor at relatively lower frequencies. Over a large frequency range, crustal seismic attenuation might introduce significant errors into seismic moment calculations (e.g., Delbridge et al., 2023). Delbridge et al. (2023) calculated coda wave spectral ratios to remove path and site effects to solve precise relative source moments. Therefore, if a high-resolution seismic attenuation model is used to calculate the seismic moment, the reliability of the explosive yield estimation can be effectively improved. The resolutions are lower for previous Lg-wave attenuation models due to sparse ray coverage (Zhao et al., 2010; Pasyanos et al., 2012; Ranasinghe et al., 2014). With the development of Lg attenuation tomography and the regional network around the Korean Peninsula, Lg-wave source excitation spectra can be extracted simultaneously by correcting path attenuation to further obtain seismic moments by fitting observed source spectra based on Brune’s source model (e.g., Brune (1970); Zhao et al. (2010); He et al. (2020)).

In this study, based on a large dataset from both the natural earthquake and nuclear explosion in the Korean Peninsula and surrounding regions, we extracted both single-station and two-station Lg-wave spectral data to develop a high-resolution broadband Lg attenuation tomography model and simultaneously inverted the Lg source excitation spectra. Thus, the source parameters, including the scalar seismic moment, corner frequency, and high-frequency falloff rate, were estimated for NKT1-6. Considering the burial depths and local rock conditions, such as P- and S-wave velocities, density, and gas porosity, we estimated the explosive yields of NKT1-6 based on the seismic moment–yield relationship (Yang et al., 2021; Pasyanos, 2022).

2 Data

2.1 Regional seismic datasets

We collected 2022 vertical-component digital seismograms from 155 seismic events recorded at 93 stations in and around the Korean Peninsula. The seismic events included 146 natural earthquakes between May 2010 and May 2022, six North Korean nuclear tests, and three chemical explosions that occurred in August 1998 (Zhang et al., 2002; Yang et al., 2021). These seismic events occurred within the crust at focal depths shallower than the Moho discontinuity from CRUST1.0 (Laske et al., 2012). Natural earthquakes with moderate magnitudes between m_b 3.5 and 5.3 were selected to ensure high SNRs and to avoid complex rupture effects. The epicentral distances are between 150 and 1700 km to observe the Lg-wave phase clearly (e.g., Zhao et al., 2010; 2013). We visually inspected individual traces to remove low-quality data that were saturated or noisy or had incorrect timing, possibly due to off-point records, low magnitudes, or the superposition of multiple events. Although the selection process reduces the amount of available data, a reasonable dataset is obtained following this process. The locations of the stations and events used in this study are shown in Figure 1, and their parameters are listed in Supplementary Tables S1, S2.

Figure 1

Figure 1. Map showing the surface topography of the Korean Peninsula and surrounding areas, which are overlapped by the locations of stations (blue triangles), natural earthquakes (red circles), North Korean nuclear tests (red stars), and chemical explosions for deep sounding (red diamonds).

2.2 Lg-wave amplitude spectrum

Following Zhao et al. (2013), we processed the seismic data to extract Lg-wave amplitude spectra. After removing the trends, means, and instrument responses from the raw vertical-component seismograms, we scanned the most energetic waveforms within a group velocity window of 0.6 km/s between 3.7 and 2.8 km/s for Lg amplitude measurements (Figure 2) (Zhao and Xie, 2016; Zhang et al., 2022). Subsequently, we captured the time series of pre-P noise and pre-Lg noise with a time length window equal to the Lg waveform and calculated the waveform energy. The fast Fourier transform was used to calculate the amplitude spectrum of the Lg waves and noises at 66 discrete frequencies log-evenly distributed between 0.05 and 20.0 Hz. Pre-P noise and pre-Lg phase noise were used for both data quality control and correction of the Lg-wave energy (e.g., Luo et al., 2021). Lg waves with an SNR to pre-P noise of less than 2.0 were removed to ensure Lg data quality. Furthermore, we also set a pre-Lg SNR threshold of 1.0 to remove data that were possibly dominated by Sn coda (Zhang et al., 2022). Then, the amplitude spectrum of the Lg wave can be obtained by using ${A_S}^2={A_O}^2-{A_N}^2$, where $A_S$, $A_O$, and $A_N$ are the amplitude spectra at different frequencies of the true signal, the observed data, and noise, respectively. After data screening and denoising, the Lg-wave spectral dataset can be obtained for Lg-wave attenuation tomography.

Figure 2

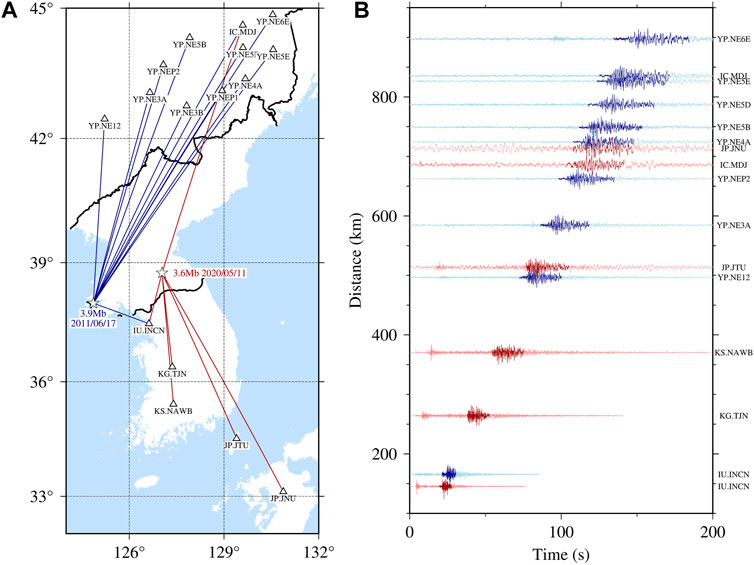
Figure 2. (A) Great circle paths from the epicenters (stars) of two earthquakes that occurred on 17 June 2011 and 11 May 2020 to selected stations (triangles), where the magnitudes and times of the earthquakes and the names of the network and stations are labeled. (B) The normalized vertical-component velocity records aligned according to epicentral distances, where the Lg phases are highlighted between 3.7 and 2.8 km/s.

3 Methods

3.1 Modeling of the Lg amplitudes

The Lg-wave amplitude spectrum recorded by station $i$ from event $k$ at frequency $f$ can be expressed as follows (Xie and Mitchell, 1990)

$A_{ki}\left(f,∆\right)=S_k\left(f\right)G_{ki}\left(∆\right){\mathrm{\Gamma }}_{ki}\left(∆,f\right)P_i\left(f\right)r_{ki}\left(f\right),(1)$

where $∆$ is the epicentral distance, $S_k\left(f\right)$ is the source term, $G_{ki}\left(∆\right)={\left({∆}_0{∆}_{ki}\right)}^{-1/2}$ is the geometrical spreading function with a reference distance of ${∆}_0=100km$ (Street et al., 1975), ${\mathrm{\Gamma }}_{ki}\left(∆,f\right)$ is the attenuation term, $P_i\left(f\right)$ is the site response and $r_{ki}\left(f\right)$ is the random effects of minor factors along the propagation path and computational errors.

The attenuation factor can be expressed as follows (Zhao et al., 2013)

${\mathrm{\Gamma }}_{ki}\left(\Delta ,f\right)=\exp \left(-\frac{\pi f}{v}{\displaystyle {\int }_k^i}\frac{ds}{Q\left(x,y,f\right)}\right),(2)$

where $v$ represents the Lg-wave group velocity, ${\int }_k^{i}ds$ is the integral along the great circle from event $k$ to station $i$, and $Q\left(x,y,f\right)$ is the Lg-wave quality factor related to the surface location coordinates $\left(x,y\right)$.

When two stations $i$ and $j$ record the same event $k$ and the locations of the stations and event are approximately aligned on a great circle, the two-station Lg-wave amplitude ratio from stations $i$ and $j$ can be calculated as follows (Zhao et al., 2013)

$A_{ij}=\frac{A_{kj}}{A_{ki}}\approx {\left(\frac{{∆}_{kj}}{{∆}_{ki}}\right)}^{-\frac{1}{2}}\bullet \exp \left(-\frac{\pi f}{v}{\int }_i^j\frac{ds}{Q\left(x,y,f\right)}\right)\bullet \frac{P_j}{P_i}\bullet \frac{r_{kj}}{r_{ki}},(3)$

where $A_{ki}$ and $A_{kj}$ are the observed amplitudes at stations $i$ and $j$ from a single event $k$, ${∆}_{ki}$ and ${∆}_{kj}$ are the epicentral distances from $k$ to $i$ and $j$, respectively, ${\int }_i^{j}ds$ is the integral along the great circle from $i$ to $j$, $P_i$ and $P_j$ are the site responses at $i$ and $j$, respectively, and $r_{ki}$ and $r_{kj}$ are random errors along the ray paths from $k$ to $i$ and $j$, respectively. Compared with the single-station data in Eq. 1, the two-station data shown in Eq. 3 effectively eliminate the compromise error between the attenuation and source.

3.2 Q_Lg tomography

To establish an inversion system for Lg-wave Q tomography, we apply the natural logarithm to Eqs 1, 2 based on perturbation theory (e.g., Zhao et al., 2010; 2013). By neglecting the random effects along the propagation path, we assume that $r\left(f\right)=1$; then, we have

$\mathit{ln}\left[A_{ki}\left(f,∆\right)\right]=\mathit{ln}\left[S_k\left(f\right)\right]+\mathit{ln}\left[S_i\left(∆\right)\right]-\frac{\pi f}{v}{\int }_k^i\frac{ds}{Q\left(x,y,f\right)}+\mathit{ln}\left[P_i\left(f\right)\right],(4)$

The terms $Q\left(x,y,f\right)$, $\mathit{ln}\left[S\left(f\right)\right]$ and $\mathit{ln}\left[P\left(f\right)\right]$ can be separated into a background value and a perturbation value (Zhao et al., 2013):

$\frac{1}{Q\left(x,y,f\right)}\approx \frac{1}{Q^0\left(x,y,f\right)}-\frac{\delta Q\left(x,y,f\right)}{{\left[Q^0\left(x,y,f\right)\right]}^2},(5)$

$\mathit{ln}\left[S_k\left(f\right)\right]=\mathit{ln}\left[S_k^0\left(f\right)\right]+\delta \mathit{ln}\left[S_k\left(f\right)\right],(6)$

$\mathit{ln}\left[P_i\left(f\right)\right]=\mathit{ln}\left[P_i^0\left(f\right)\right]+\delta \mathit{ln}\left[P_i\left(f\right)\right],(7)$

where $Q^0$, $S^0$ and $P^0$ are the background values of the Lg-wave quality factor, source spectrum and site response spectrum, respectively, for beginning the inversion. By substituting Eqs 5-7 into Eq. 4, we have

$\begin{array}{ll}\hfill \mathit{ln}\left[A_{ki}\left(f,∆\right)\right]& =\mathit{ln}\left[A_{ki}^0\left(f,∆\right)\right]+\delta \mathit{ln}\left[S_k\left(f\right)\right]\hfill \\ \hfill & +\frac{\pi f}{v}{\int }_k^i\frac{\delta Q\left(x,y,f\right)}{{\left[Q^0\left(x,y,f\right)\right]}^2}ds+\delta \mathit{ln}\left[P_i\left(f\right)\right],\hfill \end{array}(8)$

where

$\mathit{ln}\left[A_{ki}^0\left(f,∆\right)\right]=\mathit{ln}\left[S_k^0\left(f\right)\right]+\mathit{ln}\left[G_{ki}\left(∆\right)\right]-\frac{\pi f}{v}{\int }_k^i\frac{ds}{Q^0\left(x,y,f\right)}+\mathit{ln}\left[P_i^0\left(f\right)\right].(9)$

Then, we obtain the amplitude spectrum residual by taking Eq. 8 minus Eq. 9 as follows:

$\delta \mathit{ln}\left[A_{ki}\left(f,∆\right)\right]=\delta \mathit{ln}\left[S_k\left(f\right)\right]+\frac{\pi f}{v}{\int }_k^i\frac{\delta Q\left(x,y,f\right)}{{\left[Q^0\left(x,y,f\right)\right]}^2}ds+\delta \mathit{ln}\left[P_i\left(f\right)\right].(10)$

Therefore, the perturbations in the attenuation, source, and site response are related to the amplitude residual. The amplitude residual $\delta \mathit{ln}\left[A_{ki}\left(f,∆\right)\right]$ for event $k$ recorded by station $i$ at frequency $f$ is denoted as ${\stackrel{\sim }{h}}_{ki}\left(f\right)$. It can be distributed to the path based on the following mesh discretization:

${\stackrel{\sim }{h}}_{ki}\left(f\right)={\displaystyle \sum _{n=1}^N}\left[a_{in}·\delta Q_n\right]+e_k·\delta \mathit{ln}\left[S_k\left(f\right)\right]+u_i·\delta \mathit{ln}\left[P_i\left(f\right)\right],(11)$

where $n$ is the index of a grid point, $N$ is the total number of grids of a ray path, $a_{in}=-\frac{\pi f}{v}\frac{D_n}{{\left(Q^0\left(x_n,y_n,f\right)\right)}^2}$, $\left(x_n,y_n\right)$ and $D_n$ are the coordinates and the length of the ray path in grid $n$, and $e_k$ and $u_i$ are coefficients for event $k$ and station $i$, respectively, with $e_k=u_i=1$ for single-station data. Then, we have the linear matrix equation of the Lg-wave Q perturbation for single-station data

${\mathit{H}}_s={\mathit{A}}_s·\delta \mathit{Q}+{\mathit{E}}_s·\delta \mathit{S}+{\mathit{U}}_s·\delta \mathit{P},(12)$

where ${\mathit{H}}_s$ is a vector composed of Lg amplitude spectra residuals, $\delta \mathit{Q}$ is a vector composed of the perturbations of the Q models, matrix ${\mathit{A}}_s$ is composed of elements $a_{in}$ and sets up the relationship between Q perturbations and the observed Lg-wave spectra, $\delta \mathit{S}$ is a vector composed of the perturbations of source terms, matrix ${\mathit{E}}_s$ sets up the relationship between the source perturbation and the observed Lg-wave spectra (Zhao et al., 2010), $\delta \mathit{P}$ is a vector composed of the perturbations of site response terms, and matrix ${\mathit{U}}_s$ sets up the relationship between the site response perturbations and the observed Lg-wave spectra (Zhao and Mousavi, 2018).

For two-station data, since the source term is eliminated by taking the spectral ratios in Eq. 3, the similar linear matrix equation of the Lg-wave Q perturbation is

${\mathit{H}}_d={\mathit{A}}_d·\delta \mathit{Q}+{\mathit{U}}_{\mathit{d}}·\delta \mathit{P}.(13)$

In general, it is assumed that ${\sum }_{n=1}^N\delta \mathit{ln}\left[P_i\left(f\right)\right]=0$ when the stations are evenly distributed (Ottemöller et al., 2002; Zhao and Xie, 2016; Zhao and Mousavi, 2018); thus, the site response terms $\delta \mathit{P}$ are commonly ignored in the inversion of single- and two-station data. By combining Eqs 12, 13, we have

$\left[\begin{array}{c}{\mathit{H}}_s\\ {\mathit{H}}_d\end{array}\right]=\left[\begin{array}{c}{\mathit{A}}_s\\ {\mathit{A}}_d\end{array}\right]·\delta \mathit{Q}+\left[\begin{array}{c}{\mathit{E}}_s\\ \mathbf{0}\end{array}\right]·\delta \mathit{S}.(14)$

Eq. 14 forms a joint inversion problem for perturbation vectors $\delta \mathit{Q}$ and $\delta \mathit{S}$. The regional average Q obtained from the two-station data is used as the initial model. The inversion can be solved by the least-squares QR method, which includes regularization, damping and smoothing (Paige and Saunders, 1982). The current Lg-wave Q correction is used in the next iteration until satisfactory convergence is obtained, and there are 250 iterations at each frequency from 0.05 to 20 Hz. Following inversion, the amplitude residuals are closer to the Gaussian distribution, and the root mean square values of the total residuals at all 66 frequencies are significantly reduced (Figure 3).

Figure 3

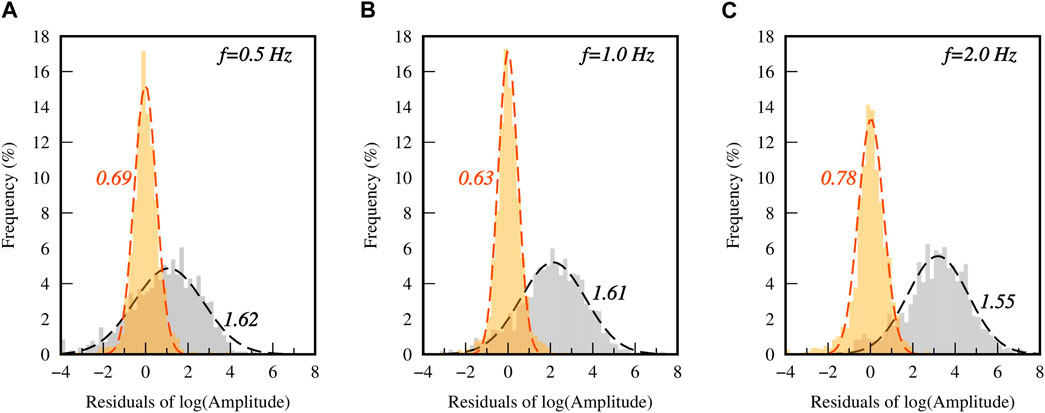
Figure 3. Histograms of the Lg spectral amplitude misfits before (gray) and after (orange) inversion at (A) 0.5, (B) 1.0, and (C) 2.0 Hz. The dashed lines represent the best-fitting normal curves, and the adjacent labels denote the RMS residuals.

3.3 Resolution test

The checkerboard method was used for the resolution analysis (Zelt, 1998; Morgan et al., 2002; Zhao et al., 2013). To create a checkerboard-shaped Q_Lg model, ±7% logarithmic perturbations are superimposed on a constant background Q_Lg (Zhao et al., 2013). We generated synthetic Lg spectral amplitudes according to actual ray paths (Figure 4A) and added 10% random noise to form a tomographic dataset (e.g., Zhang et al., 2022), where the source functions adopted inverted source spectra. Both single- and two-station synthetic data were jointly used to reconstruct the Q_Lg model (e.g., Zhang et al., 2022). Figure 4 shows the ray path coverage and reconstructed Q perturbation model at 1.0 Hz. Note that the resolution is significantly improved compared with that of previous studies (Zhao et al., 2010; 2013). The workflow for data collection, pre-processing, tomography, and verifications can be referred to Zhao et al. (2022).

Figure 4

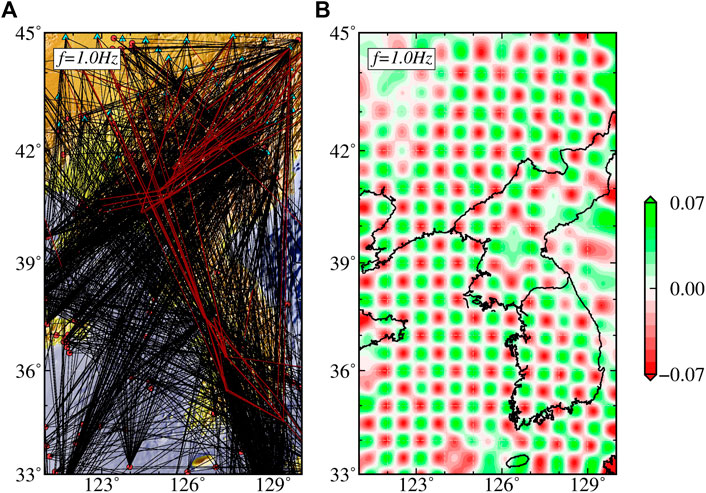
Figure 4. Ray path coverage for both a single-station (black) and two-station (red) ray paths (A) and the reconstructed 0.5°×0.5° checkerboard of Q perturbations (B) at 1 Hz.

4 Results

4.1 Broadband Q_Lg model in and around the Korean Peninsula

Based on the inversion procedure described in the previous section, we obtained the Q_Lg model at 66 individual frequencies between 0.05 and 20 Hz. Figure 5 shows the Q_Lg map coverages at 0.5, 1.0 and 2.0 Hz. The lateral Q_Lg variations are consistent with the regional tectonic conditions. In the Korean Peninsula region, the Q_Lg distribution is characterized by high values for the Nangrim Massif (NM) in the north and the Yeongnam Massif (YM) in the south and low values for the Gyeonggi Massif (GM) in the middle, especially at a frequency of 1.0 Hz (Figure 5B). Our results are consistent with those of previous studies but at relatively higher resolutions, and they cover the entire Korean Peninsula (Zhao et al., 2010; 2013; Pasyanos et al., 2012; Ranasinghe et al., 2014).

Figure 5

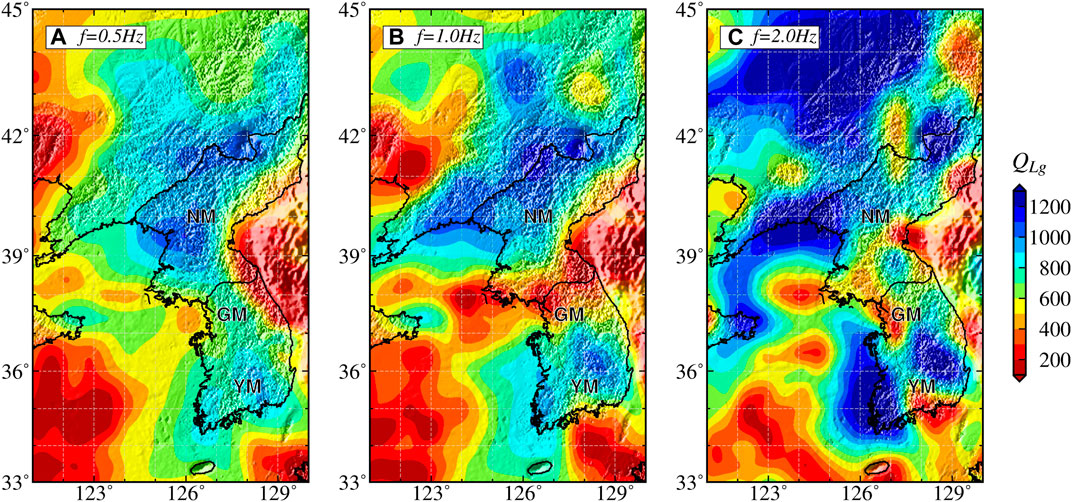
Figure 5. Q_Lg maps at 0.5 (A), 1.0 (B), and 2.0 Hz (C). Note that a similar scale was used for all the maps.

We investigated the regional variations and frequency dependence of Q_Lg in three massifs to characterize the Lg-wave attenuation for different geological formations on the Korean Peninsula. For example, the scattered distribution of observed Q_Lg values is shown for the Gyeonggi Massif (Figure 6A), whereas the average Q_Lg versus frequency is summarized for all three massifs in the Korean Peninsula (Figure 6B). The average Q_Lg values increase with increasing frequency for an individual massif below 0.3 Hz and above 3.0 Hz. However, the Q_Lg variation in the Gyeonggi Massif (GM) differs from that in the other two massifs between 0.3 and 3.0 Hz.

Figure 6

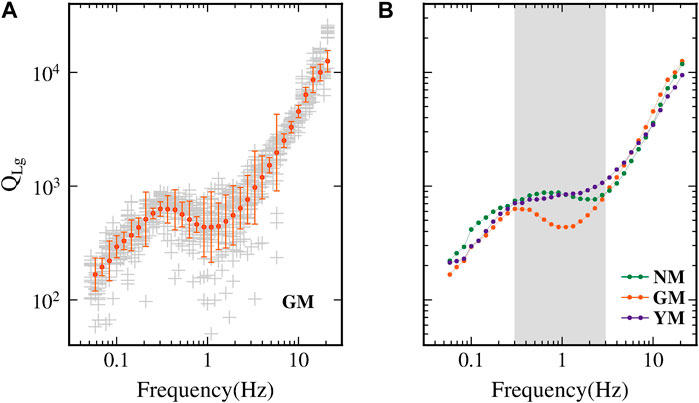
Figure 6. (A) Frequency dependence of the Q_Lg values for the Gyeonggi Massif (GM), where the average Q_Lg values (circles) and their standard deviations (error bars) are obtained based on the tomographic Q_Lg values (gray crosses) at reference frequencies. (B) Average Q_Lg versus frequency for the Nangrim Massif (NM), Gyeonggi Massif (GM), and Yeongnam Massif (YM).

Figure 7 shows a comparison of the resulting broadband Q_Lg with the surface topography, crustal thickness, and seismicity. The Lg attenuation variations indicate changes in the crustal waveguide and crustal physical properties across the three massifs. The boundary between the NM and GM corresponds to low Q_Lg values of approximately 1.0 Hz (Figures 7C, D). Q_Lg usually decreases with decreasing crustal thickness (Zhao et al., 2010; 2013). Numerical simulation studies have shown that the seismic Lg wave attenuates with crustal thinning along the waveguide (e.g., Hong et al., 2008). However, the abnormally low Q_Lg for the GM does not correspond to a significant Moho depth increase in the Korean Peninsula (Figure 7B). Therefore, the Lg attenuation is not strongly affected by a smooth anomaly in the Moho depth (Campillo, 1987). The thickness variation in the crustal waveguide is not the main factor affecting the Q_Lg on the Korean Peninsula. Strong seismicity can be observed in the uppermost mantle beneath the low-Q_Lg crust at approximately 38.5°N (Figure 7B). Therefore, the low-Q_Lg region, located at the boundary between the NM and the GM, can be attributed to complex tectonic sutrue between two ancient plates (the North China Craton and the South China Block), where the crustal structure has been strongly influenced by tectonic processes, including the extension of the Sulu collision Belt (Chough et al., 2000; Zhai et al., 2019).

Figure 7

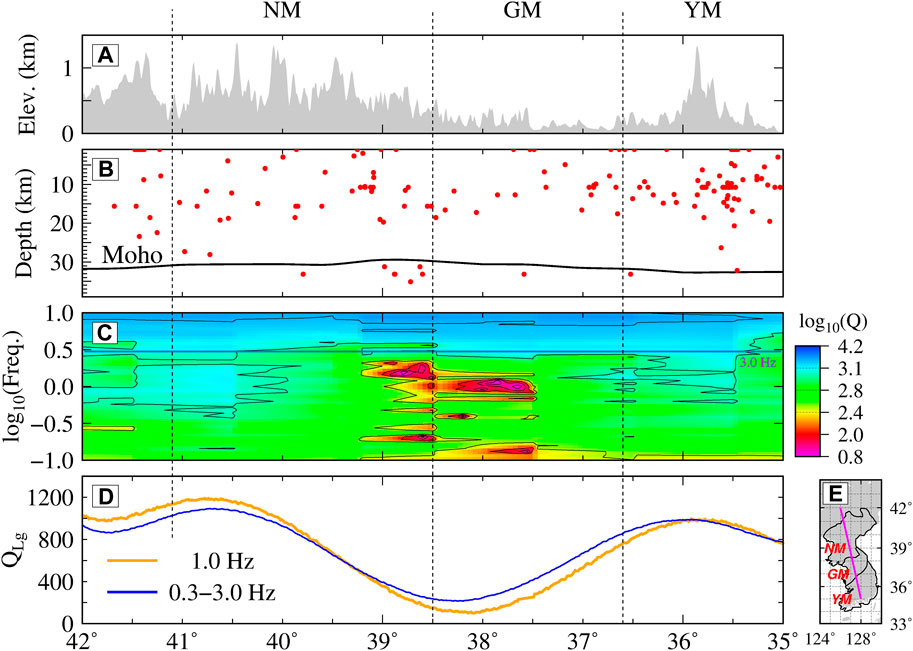
Figure 7. Cross-sections through three massifs, NM, GM, and YM, on the Korean Peninsula showing (A) surface topography, (B) Moho depth (black) and seismicity (red dot), (C) Q_Lg versus frequency, (D) variations in the average Q_Lg between 0.3 and 3.0 Hz and Q₀, and (D) the location of the cross-section between (126°E, 42°N) and (128°E, 35°N). The vertical black dashed lines represent the massif boundaries on the cross-section. The Moho depth was extracted from CRUST 1.0 (Laske et al., 2012). The seismicities of earthquakes with magnitudes higher than 1.0 are plotted for the period between 1968 and 2023.

4.2 Lg-wave source spectra

During the joint inversion, the Lg-wave source excitation spectral amplitudes at 66 discrete frequencies are calculated for all events. The source parameters are obtained by fitting the resulting Lg excitation spectra (Zhao et al., 2010; 2013; He et al., 2020). We calculated the scalar seismic moment $M_0$, the corner frequency $f_c$, and the high-frequency falloff rate $n$ by fitting the Lg-wave excitation spectrum with the ${\omega }^{-n}$ source model (Brune, 1970; Street et al., 1975; Sereno Jr et al., 1988). The source term in Eq 1 is expressed as follows:

$S\left(f\right)=\frac{M_0}{4\pi \rho {v_s}^3\left[1+{\left(\frac{f}{f_c}\right)}^n\right]},(15)$

where $\rho$ and $v_s$ are the average density and shear-wave velocity in the crust, respectively, with values of 2.7 g/cm³ and 3.5 km/s for Northeast China (Zhao et al., 2010). Figure 8 shows the best-fit source models with solid colored lines, and the shaded areas represent their standard deviations. Then, $M_0$, $f_c$, and $n$ can be determined by minimizing the L2 norm of the residuals between the theoretical source function and the network-determined source spectral data (Figure 8). The $M_0$ for NKT1-6 increased successively. According to the Mueller–Murphy model (Mueller and Murphy, 1971), the source corner frequency ($f_c$) is predicted to decrease with increasing yield and increase with increasing source depth. According to the source model parameters, the explosion yields increase for NKT1-6; however, the corner frequencies, represented by $f_c$, are not consistently reduced due to differences in burial depth. Figure 8 shows the source excitation spectra inverted from the observed Lg-wave spectra for NKT1-6. Figure 9 provides a comparison between the retrieved spectra and the synthetic spectra. Except for NKT3, the source spectra gradually increased from NKT1 to NKT6 at all frequencies. The NKT3 source spectra are larger than those of NKT5 at high frequencies (above 0.5 Hz); thus, NKT3 is larger according to the previously estimated m_b (Lg) based on an Lg-wave amplitude of approximately 1.0 Hz (Zhao et al., 2014), which is inconsistent with the order of m_b(P) from the USGS National Earthquake Information Center (NEIC) and the Comprehensive Test Ban Treaty Organization (CTBTO).

Figure 8

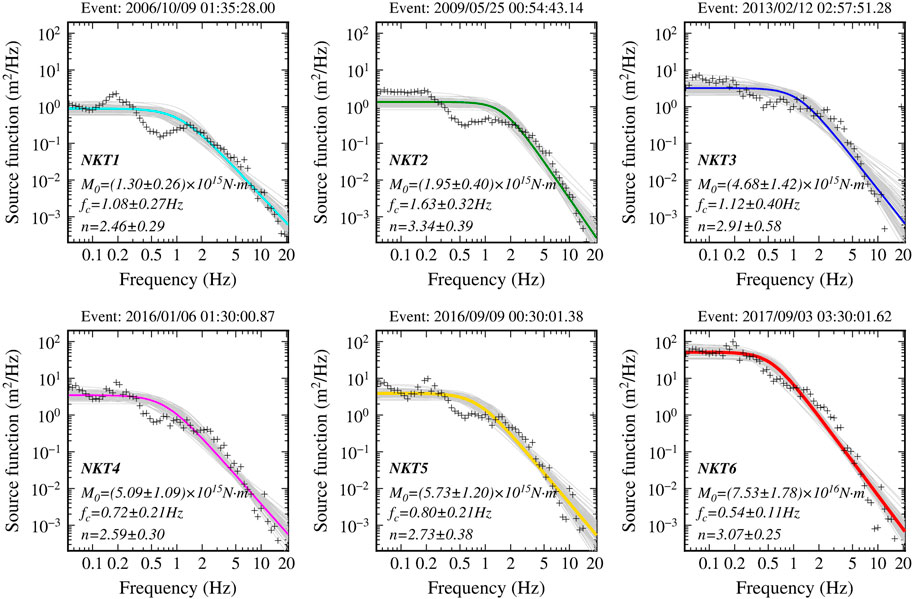
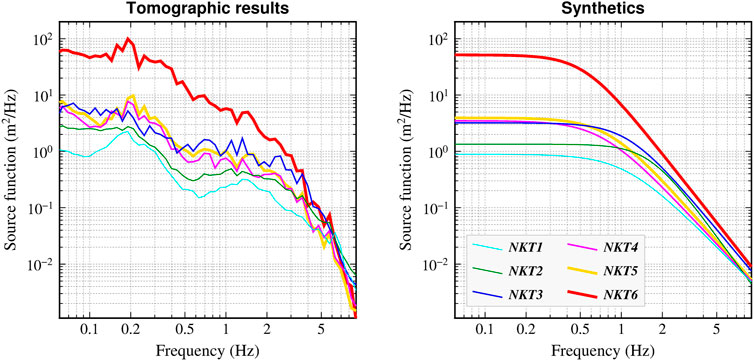
Figure 8. Retrieved Lg-source excitation spectra for NKT1-6. The black crosses are direct inversion results. The solid-colored lines are the best-fit source models, and the shaded areas are their standard deviations. The resulting $M_0$, $f_c$, and $n$ are labeled in each plot.

Figure 9

Figure 9. Comparisons between the retrieved (left) and best-fit (right) source models.

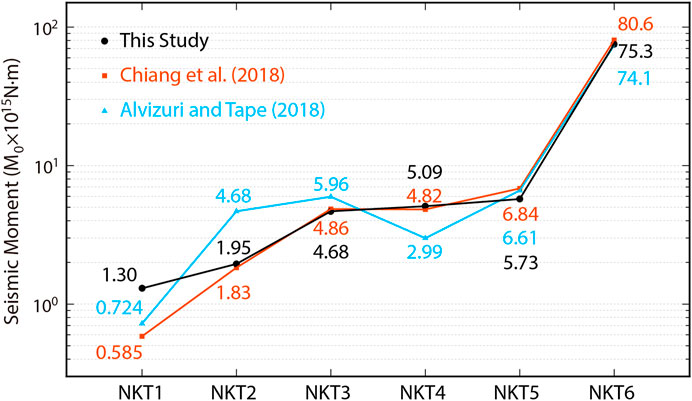
Figure 10 shows a comparison between the seismic moment $M_0$ for NKT1-6 and the results from other studies. Chiang et al. (2018) used a time-domain waveform inversion to calculate the full moment tensor from regional stations in China, South Korea, and Japan with the MDJ2 1D-layered Earth model (Ford et al., 2009) to calculate Green’s functions. Alvizuri and Tape (2018) applied a grid search and minimized the misfit function between observed and synthetic waveforms to determine the full moment tensor, and they used the MDJ2 1D-layered Earth model for calculations. The period band of analysis by Chiang et al. (2018) was typically 20–50 s, with shorter periods used for NKT1. The $M_0$ results in this study are consistent with those of Chiang et al. (2018) for NKT2-6, with a large deviation for NKT1. In the low-frequency (<0.05 Hz) band, crustal attenuation variations could be ignored. Therefore, the $M_0$ consistency in NKT2-6 verifies that the Lg source spectra accurately remove the path attenuation effect in this study, and inconsistency for NKT1 might be related to poor SNR at low frequency.

Figure 10

Figure 10. Scalar seismic moments compared with other results.

4.3 Yield estimation

Pasyanos (2022) estimated the yields of NKT1-6 by utilizing the seismic moment function of Denny and Johnson (1991), in which the moment is proportional to the yield. Replacing the units of yield from kilotons to joules, the moment-to-yield ratio ($M_0/W$) in units of N⸱m/J is obtained as follows:

$M_0/W=3.76\times {10}^{-3}{V_P}^2{V_S}^{-1.1544}{\rho }^{0.5615}{z}^{-0.4385}{10}^{-0.0344GP},(16)$

where the material properties ($V_P$, $V_S$, $\rho$, and $GP$) indicate the P-wave velocity, S-wave velocity, density, and gas porosity, respectively. The material properties ($V_P$, $V_S$, $\rho$ and $GP$) used in this study are 5500 m/s, 3175 m/s, 2550 kg/m³, and 0.02%, respectively, for granite at the NKT site (Stevens and Day, 1985). By using differential travel times from Pn and Pg waves, the burial depths (z) of NKT1-6 were determined to be 330, 540, 506, 468, 521, and 570 m (Yang et al., 2021). With the emplacement conditions and burial depths provided above, the yields can be estimated by dividing the seismic moment by the right side of Eq 16, and the values are 4.6, 8.5, 19.9, 20.9, 24.7, and 337.4 kt (Figure 11).

Figure 11

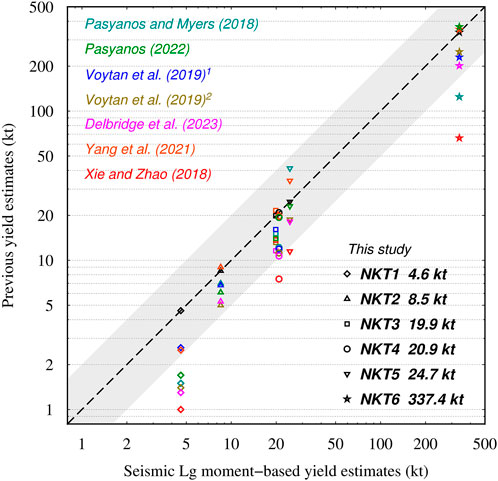
Figure 11. Comparison of the results of yield estimates from different studies. Different symbols indicate North Korean nuclear tests NKT1-6, whereas different colors indicate different methods, including regional waveform envelopes (Pasyanos and Myers, 2018), seismic moments (Chiang et al., 2018; Pasyanos, 2022), waveform equalization to teleseismic P and regional Pn seismograms and high-frequency (>4.0 Hz) P waves (Voytan et al., 2019), coda spectral ratios (Delbridge et al., 2023), NEIC m_b after burial depth correction (Yang et al., 2021), and m_b (Lg) (Xie and Zhao, 2018). The gray shading represents 0.5 to 2 times the deviation range of the yield estimations obtained in this study.

Figure 11 shows a comparison between the yield estimation results for NKT1-6 above and several other estimates based on (1) regional waveform envelopes (Pasyanos and Myers, 2018), (2) the seismic moment using the formula of Pasyanos (2022) with $M_0$ from Chiang et al. (2018), (3) the intercorrelation procedure, which applies waveform equalization to teleseismic P and regional Pn seismograms (Voytan et al., 2019), (4) high-frequency (>4 Hz) filtered P waves (Voytan et al., 2019), (5) source spectral ratios of narrow-band regional body-wave coda waveform envelopes (Delbridge et al., 2023), (6) NEIC teleseismic m_b using the empirical relationship of Bowers et al. (2001), followed by a depth correction using the equation of Patton and Taylor (2011) with the burial depths determined by Pn and Pg differential travel times (Yang et al., 2021), and (7) regional m_b (Lg) (Xie and Zhao, 2018). The yield estimations in this study are highly consistent with teleseismic m_b-derived yields. The body wave magnitude (m_b) based on teleseismic phases is rarely influenced by the crustal structure along the ray path. The purpose of using the Lg-wave to calculate the seismic moment in this study is to determine whether Q_Lg model can be used to eliminate the attenuation effect. The results show that after effectively removing the attenuation effect, the moment rather than the magnitude of the regional seismic Lg agreed with the teleseismic m_b yield estimation.

5 Discussion and conclusion

Based on 2022 vertical-component digital seismograms recorded at 93 stations from 155 seismic events over the past decade, we develop a new broadband Lg-wave attenuation (Q_Lg) model for the Korean Peninsula and its surrounding regions, which has a relatively dense ray path distribution (e.g., Zhao et al. (2010)). The Q_Lg lateral variations correlate with the geological units well. We directly removed the attenuation effect from the observed spectra to obtain the $M_0$, $f_c$ and high-frequency fall-off rates based on the theoretical source model (Brune, 1970). The $M_0$ values of NKT1-6 increase successively. However, there is no strict correlation between $M_0$ and $f_c$ in NKTs. This result may be because the corner frequency is predicted to decrease with increasing yield and increase with increasing source depth, whereas the burial depths for NKT1-6 are variable (Yang et al., 2021).

The corner frequency may directly cause bias between m_b(P) and m_b (Lg) values and hence lead to lower estimated yields. Pasyanos (2022) suggested that the m_b (Lg) value is not equivalent and is often significantly biased relative to teleseismic m_b. Several previous studies have shown that m_b (Lg)-derived yield estimations are smaller than the results of m_b(P) for NKT (Zhao et al., 2016; Zhao et al., 2017; Xie and Zhao, 2018; Yao et al., 2018) and the five historical nuclear tests at the Semipalatinsk nuclear test site in the Soviet Union (Ma et al., 2020). Following burial depth corrections, the absolute yields re-estimated (Xie and Zhao, 2018) by m_b (Lg) were close to the teleseismic observations (Yang et al., 2021) for NKT1-3; however, they were still significantly lower for NKT4-6. The Lg-wave corner frequencies of NKT1-3 are greater than 1.0 Hz; however, those of NKT4-6 are less than 1.0 Hz (Figure 8). The $f_c$ values based on P-wave source spectra for NKT1-6 are 7.6, 4.9, 4.0, 5.0, 3.5, and 2.1 Hz, which are larger than 1 Hz (Pasyanos and Myers, 2018). The m_b value is determined by the seismic wave amplitude at ∼1.0 Hz, below which $f_c$ generates the m_b calculation in the frequency domain where the amplitude spectrum has fallen off; thus, the yield estimation empirical relationships obtained by applying m_b(P) for NKT4-6 are greater than those obtained by applying m_b (Lg) (Yang et al., 2021). Voytan et al. (2019) estimated yields using P waves above 4.0 Hz, and the relative yield was lower than that of NEIC m_b(P), especially for high-yield NKTs, also confirming the effect of $f_c$ on yield estimation.

The amount of energy associated with larger explosions is more concentrated at low frequencies, and the source spectra of high-yield explosions fall faster with increasing frequency than do those of low-yield explosions. Thus, $M_0$ based on long-period fitting is beneficial for accurate yield estimations of low-$f_c$ explosions. Due to the simple nature of the 1-D-layered Earth model, ignoring the attenuation effect can result in uncertainties when calculating $M_0$ at high frequencies (>0.05 Hz); hence, Chiang et al. (2018) and Alvizuri and Tape (2018) performed moment tensor analyses using regional surface waves over long periods (20–50 s); however, the SNR of NKT1 was poor under such a frequency band. Therefore, the Aki, 1982 advantages Shen et al., 2023 of Wu and Aki, 1985 using Campillo, 1990 the Lg wave to obtain $M_0$ in this study are described as follows: (1) an acceptable SNR can be ensured for low-yield nuclear explosions, and (2) the attenuation effect can be removed by mature Q_Lg tomography technology. For relatively high-yield explosions, the teleseismic m_b(P), the long-period surface wave $M_0$, and the regional Lg $M_0$ might agree in terms of yield estimations, while the latter may be more reliable for low-yield explosions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Formal Analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing–original draft. L-FZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Methodology, Software, Supervision, Writing–review and editing. X-LP: Conceptualization, Funding acquisition, Investigation, Project administration, Supervision, Writing–review and editing. Z-XY: Methodology, Software, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The National Natural Science Foundation of China (U2139206, 41974054, and 41974061).

Acknowledgments

The comments from Editor K. H. Liu and two reviewers are valuable and greatly improved this manuscript. This research was supported by the National Natural Science Foundation of China (U2139206, 41974054, and 41974061). The broadband waveform data used in this study were collected from the Incorporated Research Institutions for Seismology Data Management Center (IRIS-DMC) and are available at https://ds.iris.edu/wilber3/find_event (last accessed October 2023). Certain figures were generated using the Generic Mapping Tools (GMT; https://www.generic-mapping-tools.org/).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1386932/full#supplementary-material

References

Aki, K. (1982). Scattering and attenuation. Bull. Seismol. Soc. Am. 72, S319–S330. doi:10.1785/BSSA07206B0319

CrossRef Full Text | Google Scholar

Aki, K., and Richards, P. G. (2002). Quantitative seismology. 2nd ed. Melville, NY, USA: University Science Books.

Google Scholar

Alvizuri, C., and Tape, C. (2018). Full moment tensor analysis of nuclear explosions in North Korea. Seismol. Res. Lett. 89, 2139–2151. doi:10.1785/0220180158

CrossRef Full Text | Google Scholar

Bowers, D., Marshall, P. D., and Douglas, A. (2001). The level of deterrence provided by data from the SPITS seismometer array to possible violations of the Comprehensive Test Ban in the Novaya Zemlya region. Geophys. J. Int. 146, 425–438. doi:10.1046/j.1365-246x.2001.01462.x

CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 75, 4997–5009. doi:10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Campillo, M. (1987). Lg wave propagation in a laterally varying crust and the distribution of the apparent quality factor in central France. J. Geophys. Res. 92, 12604–12614. doi:10.1029/JB092iB12p12604

CrossRef Full Text | Google Scholar

Campillo, M. (1990). Propagation and attenuation characteristics of the crustal phase Lg. Pure Appl. Geophys. 132, 1–19. doi:10.1007/BF00874355

CrossRef Full Text | Google Scholar

Chiang, A., Ichinose, G. A., Dreger, D. S., Ford, S. R., Matzel, E. M., Myers, S. C., et al. (2018). Moment tensor source-type analysis for the Democratic People’s Republic of Korea–declared nuclear explosions (2006–2017) and 3 september 2017 collapse event. Seismol. Res. Lett. 89, 2152–2165. doi:10.1785/0220180130

CrossRef Full Text | Google Scholar

Chough, S. K., Kwon, S. T., Ree, J. H., and Choi, D. K. (2000). Tectonic and sedimentary evolution of the Korean peninsula: a review and new view. Earth-Sci. Rev. 52, 175–235. doi:10.1016/S0012-8252(00)00029-5

CrossRef Full Text | Google Scholar

Delbridge, B. G., Carmichael, J. D., Phillips, W. S., Cleveland, K. M., Begnaud, M. L., and Gammans, C. (2023). Source characterization of the declared North Korean nuclear tests from regional distance coda wave spectral ratios. J. Geophys. Res. 128, e2022JB024728. doi:10.1029/2022JB024728

CrossRef Full Text | Google Scholar

Denny, M. D., and Johnson, L. R. (1991). The explosion seismic source function: models and scaling laws reviewed. Explos. Source Phenomenol. 65, 1–24. Am.Geophys.Monograph. doi:10.1029/GM065p0001

CrossRef Full Text | Google Scholar

Ford, S. R., Dreger, D. S., and Walter, W. R. (2009). Source analysis of the memorial day explosion, kimchaek, North Korea. Geophys. Res. Lett. 36. doi:10.1029/2009gl040003

CrossRef Full Text | Google Scholar

He, X., Zhao, L.-F., Xie, X.-B., Shen, L., Wang, W.-M., and Yao, Z.-X. (2020). Stress drop assessment of the August 8, 2017, Jiuzhaigou earthquake sequence and its tectonic implications. Earthq. Sci. 33, 161–176. doi:10.29382/eqs-2020-0161-01

CrossRef Full Text | Google Scholar

Hong, T.-K., Baag, C.-E., Choi, H., and Sheen, D.-H. (2008). Regional seismic observations of the 9 October 2006 underground nuclear explosion in North Korea and the influence of crustal structure on regional phases. J. Geophys. Res. 113. doi:10.1029/2007JB004950

CrossRef Full Text | Google Scholar

Kim, S. G., Gitterman, Y., and Lee, S.-k. (2019). Depth calculation for the January 06, 2016, the September 09, 2016 and the September 03, 2017 nuclear tests of North Korea from detailed depth phases using regional and teleseismic arrays. Pure Appl. Geophys. 176, 133–146. doi:10.1007/s00024-018-1958-y

CrossRef Full Text | Google Scholar

Laske, G., Masters, G., Ma, Z., and Pasyanos, M. (2012). Crust1.0: an updated global model of Earth's crust. Geophys. Res. Abs. 14, 3743.

Google Scholar

Luo, Y., Zhao, L., Ge, Z.-X., Xie, X.-B., and Yao, Z.-X. (2021). Crustal Lg-wave attenuation in Southeast Asia and its implications for regional tectonic evolution. Geophys. J. Int. 226, 1873–1884. doi:10.1093/gji/ggab122

CrossRef Full Text | Google Scholar

Ma, X., Zhao, L., Xie, X.-B., He, X., and Yao, Z.-X. (2020). Regional seismic characteristics of chemical explosions on the eastern margin of the Junggar basin, northwest China, and of historical Semipalatinsk nuclear tests. Bull. Seismol. Soc. Am. 111, 606–620. doi:10.1785/0120200151

CrossRef Full Text | Google Scholar

Morgan, J. V., Christeson, G. L., and Zelt, C. A. (2002). Testing the resolution of a 3D velocity tomogram across the Chicxulub crater. Tectonophysics 355, 215–226. doi:10.1016/S0040-1951(02)00143-9

CrossRef Full Text | Google Scholar

Mueller, R. A., and Murphy, J. R. (1971). Seismic characteristics of underground nuclear detonations: Part I. Seismic spectrum scaling. Bull. Seismol. Soc. Am. 61, 1675–1692. doi:10.1785/BSSA0610061675

CrossRef Full Text | Google Scholar

Ottemöller, L., Shapiro, N. M., Krishna Singh, S., and Pacheco, J. F. (2002). Lateral variation of Lg wave propagation in southern Mexico. J. Geophys. Res. 107, ESE 3–13. doi:10.1029/2001JB000206

CrossRef Full Text | Google Scholar

Paige, C. C., and Saunders, M. A. J. A. T. M. S. (1982). Lsqr: an algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 8, 43–71. doi:10.1145/355984.355989

CrossRef Full Text | Google Scholar

Pasyanos, M. E. (2022). Estimating explosion yields using moment tensor solutions and seismic moment. Seismol. Res. Lett. 93, 2230–2238. doi:10.1785/0220220032

CrossRef Full Text | Google Scholar

Pasyanos, M. E., and Chiang, A. (2021). Full moment tensor solutions of U.S. underground nuclear tests for event screening and yield estimation. Bull. Seismol. Soc. Am. 112, 538–552. doi:10.1785/0120210167

CrossRef Full Text | Google Scholar

Pasyanos, M. E., and Myers, S. C. (2018). The coupled location/depth/yield problem for North Korea’s declared nuclear tests. Seismol. Res. Lett. 89, 2059–2067. doi:10.1785/0220180109

CrossRef Full Text | Google Scholar

Pasyanos, M. E., Walter, W. R., and Mayeda, K. M. (2012). Exploiting regional amplitude envelopes: a case study for earthquakes and explosions in the Korean Peninsula. Bull. Seismol. Soc. Am. 102, 1938–1948. doi:10.1785/0120120012

CrossRef Full Text | Google Scholar

Patton, H. J., and Taylor, S. R. (2011). The apparent explosion moment: inferences of volumetric moment due to source medium damage by underground nuclear explosions. J. Geophys. Res. 116, B03310. doi:10.1029/2010JB007937

CrossRef Full Text | Google Scholar

Ranasinghe, N., Gallegos, A., Trujillo, A., Blanchette, A., Sandvol, E., Ni, J., et al. (2014). Lg attenuation in northeast China using NECESSArray data. Geophys. J. Int. 200, 67–76. doi:10.1093/gji/ggu375

CrossRef Full Text | Google Scholar

Sereno Jr, T. J., Bratt, S. R., and Bache, T. C. (1988). Simultaneous inversion of regional wave spectra for attenuation and seismic moment in Scandinavia. J. Geophys. Res. 93, 2019–2035. doi:10.1029/JB093iB03p02019

CrossRef Full Text | Google Scholar

Shen, L., Zhao, L.-F., Xie, X.-B., Yang, G., and Yao, Z.-X. (2023). Extremely weak Lg attenuation reveals ancient continental relicts in the South China block. Earth Planet Sci. Lett. 611, 118144. doi:10.1016/j.epsl.2023.118144

CrossRef Full Text | Google Scholar

Stevens, J. L., and Day, S. M. (1985). The physical basis of m_b: M_s and variable frequency magnitude methods for earthquake/explosion discrimination. J. Geophys. Res. 90, 3009–3020. doi:10.1029/JB090iB04p03009

CrossRef Full Text | Google Scholar

Street, R. L., Herrmann, R. B., and Nuttli, O. W. (1975). Spectral characteristics of the Lg wave generated by central United States earthquakes. Geophys. J. Int. 41, 51–63. doi:10.1111/j.1365-246X.1975.tb05484.x

CrossRef Full Text | Google Scholar

Voytan, D. P., Lay, T., Chaves, E. J., and Ohman, J. T. (2019). Yield estimates for the six North Korean nuclear tests from teleseismic P wave modeling and intercorrelation of P and Pn recordings. J. Geophys. Res. 124, 4916–4939. doi:10.1029/2019JB017418

CrossRef Full Text | Google Scholar

Wu, R. S., and Aki, K. (1985). Elastic wave scattering by a random medium and the small-scale inhomogeneities in the lithosphere. J. Geophys. Res. 90, 10261–10273. doi:10.1029/JB090iB12p10261

CrossRef Full Text | Google Scholar

Xie, J., and Mitchell, B. J. (1990). Attenuation of multiphase surface waves in the basin and range province, part I: Lg and Lg coda. Geophys. J. Int. 102, 121–137. doi:10.1111/j.1365-246X.1990.tb00535.x

CrossRef Full Text | Google Scholar

Xie, X.-B., and Zhao, L. (2018). The seismic characterization of North Korea underground nuclear tests. Chin. J. Geophys. 61, 889–904. doi:10.6038/cjg2018L0677

CrossRef Full Text | Google Scholar

Yang, G., Zhao, L. F., Xie, X. B., Zhang, L., and Yao, Z. X. (2021). High-precision relocation with the burial depths of the North Korean underground nuclear explosions by combining Pn and Pg differential traveltimes. J. Geophys. Res. 126. doi:10.1029/2020jb020745

CrossRef Full Text | Google Scholar

Yao, J., Tian, D., Sun, L., and Wen, L. (2018). Source characteristics of North Korea’s 3 September 2017 nuclear test. Seismol. Res. Lett. 89, 2078–2084. doi:10.1785/0220180134

CrossRef Full Text | Google Scholar

Zelt, C. A. (1998). Lateral velocity resolution from three-dimensional seismic refraction data. Geophys. J. Int. 135, 1101–1112. doi:10.1046/j.1365-246X.1998.00695.x

CrossRef Full Text | Google Scholar

Zhai, M., Zhang, X.-H., Zhang, Y.-B., Wu, F.-Y., Peng, P., Li, Q.-L., et al. (2019). The geology of North Korea: an overview. Earth-Sci. Rev. 194, 57–96. doi:10.1016/j.earscirev.2019.04.025

CrossRef Full Text | Google Scholar

Zhang, C. K., Zhang, X. K., Zhao, J. R., Liu, B. F., Zhang, J. S., Yang, Z. X., et al. (2002). Crust-mantle structure of the Changbaishan Tianchi volcanic region and its vicinity: an exploratory study and inferences. Chin. J. Geophys. 45. doi:10.1002/cjg2.301

CrossRef Full Text | Google Scholar

Zhang, L., Zhao, L., Xie, X.-B., Wu, Q.-J., and Yao, Z.-X. (2022). Lateral variations in crustal Lg attenuation in and around the Hangay Dome, Mongolia. Int. J. Earth. Sci. 111, 591–606. doi:10.1007/s00531-021-02131-8

CrossRef Full Text | Google Scholar

Zhang, M., and Wen, L. (2013). High-precision location and yield of North Korea's 2013 nuclear test. Geophys. Res. Lett. 40, 2941–2946. doi:10.1002/grl.50607

CrossRef Full Text | Google Scholar

Zhao, L., and Mousavi, S. M. (2018). Lateral variation of crustal Lg attenuation in eastern North America. Sci. Rep. 8, 7285. doi:10.1038/s41598-018-25649-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., Na, F., Zhao, X., and Yao, Z. X. (2017). The 9 September 2016 North Korean underground nuclear test. Bull. Seismol. Soc. Am. 107, 3044–3051. doi:10.1785/0120160355

CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., and Yao, Z.-X. (2008). Regional seismic characteristics of the 9 October 2006 North Korean nuclear test. Bull. Seismol. Soc. Am. 98, 2571–2589. doi:10.1785/0120080128

CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., and Yao, Z.-X. (2012). Yield estimation of the 25 May 2009 North Korean nuclear explosion. Bull. Seismol. Soc. Am. 102, 467–478. doi:10.1785/0120110163

CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., and Yao, Z.-X. (2014). The 12 February 2013 North Korean underground nuclear test. Seismol. Res. Lett. 85, 130–134. doi:10.1785/0220130103

CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., Zhang, J., and Yao, Z.-X. (2010). Seismic Lg-wave Q tomography in and around northeast China. J. Geophys. Res. 115. doi:10.1029/2009JB007157

CrossRef Full Text | Google Scholar

Zhao, L., Xie, X.-B., Wang, W., Zhang, J., and Yao, Z.-X. (2013). Crustal Lg attenuation within the North China Craton and its surrounding regions. Geophys. J. Int. 195, 513–531. doi:10.1093/gji/ggt235

CrossRef Full Text | Google Scholar

Zhao, L.-F., and Xie, X.-B. (2016). Strong Lg-wave attenuation in the Middle East continental collision orogenic belt. Tectonophysics 674, 135–146. doi:10.1016/j.tecto.2016.02.025

CrossRef Full Text | Google Scholar

Zhao, L.-F., Xie, X.-B., He, X., Shen, L., Zhang, L., and Yao, Z.-X. (2022). Seismic Lg-wave attenuation tomography: method, algorithm, data processing flow and application. Rev. Geophys. Planet. Phys. 53 (6), 721–744. (in Chinese). doi:10.19975/j.dqyxx.2022-024

CrossRef Full Text | Google Scholar

Zhao, L.-F., Xie, X.-B., Wang, W.-M., Hao, J.-L., and Yao, Z.-X. (2016). Seismological investigation of the 2016 January 6 North Korean underground nuclear test. Geophys. J. Int. 206, 1487–1491. doi:10.1093/gji/ggw239

CrossRef Full Text | Google Scholar