Analytical solution for mechanical behavior characterization of sandy dolomite tunneling

Tunneling in sandy dolomite strata often faces hazards such as collapse, water inrush, and water–sand inrush, seriously threatening the safety of tunnel construction. There are currently limited studies on the mechanical behaviors of sandy dolomite tunnels. In view of this, an analytical solution for tunneling in sandy dolomite strata is derived in this study, and then parametric analysis is performed to analyze the mechanical response of rock mass in sandy dolomite tunnels. The results demonstrate five tunnel sidewall stress scenarios according to the different lateral pressure coefficients (λ). Varying λ values impact stress distribution and tunnel stability, with extreme values posing risks of instability. Tunnel safety is greatly reduced when rock stress approaches the plastic limit. At different internal friction angles, cohesion, and initial rock stresses, radial stress decreases gradually as the radius increases. The stress values under different conditions tend to be similar, while the effects of internal friction angle, cohesion, and initial rock stress on stress in the elastic zone decrease with increasing distance from the center of the tunnel. Under different internal friction angles and cohesion, the plastic zone radius increases with increasing distance from the excavation surface, and a larger internal friction angle and cohesion lead to an increase in stress. The stress and cohesion of a rock mass significantly affect the plastic zone radius, and an increase in tunnel excavation radius also leads to an increase in the radius of plastic zone. These findings provide a reference and insight for similar geotechnical engineering practices in the future.

1 Introduction

The construction of the Central Yunnan Water Diversion Project was outlined in China’s 14th Five-Year Plan report. The construction of water conveyance tunnels in sandy dolomite strata faces a variety of challenging engineering geological issues, including significant soft rock deformation, fault zones, rock-bursts under high geo-stress, and water inrush at the tunnel face (Wang et al., 2022). Dolomite sandification is often the most prominent (Figure 1). Taking the Yuxi section of the Central Yunnan water diversion project as an example (Fu et al., 2020; Wu et al., 2021; Wang MQ. et al., 2023), the total length of the Yuxi section of the Central Yunnan Water Conveyance Project is 77.069 km. It has eight water conveyance tunnels with a total length of 72.775 km, accounting for 94.43% of the total project length. The total length of water conveyance tunnels located in the sandy dolomite strata is approximately 14.5 km (19.8% of the total project length). Dolomite sandification not only weakens the strength and quality of the rock mass but also affects the stability of slopes and underground caverns. This can result in challenges such as cavern construction difficulties, poor construction quality, collapse, and large deformation (Figure 2A–C). It can also lead to secondary geological hazards such as surging sand and debris flow in the water-rich tunnel section (Figure 2D–F), complicating the management of engineering hazards and raising safety concerns. This can cause delays and increase investment in the project, thus highlighting the necessity of focusing on rock mass stability in sandy dolomite tunnels.

Figure 1

Figure 1. Morphology of dolomite sandy outcrops.

Figure 2

Figure 2. Secondary hazards in sandy dolomite tunnels: (A–C) Severe sandification and large deformation of support structures, (D) Water and sand burst from the tunnel’s excavation surface, (E, F) Sand and debris flowing inside the cave.

Dolomite sandification is a unique geological phenomenon which is manifested in the microcrystalline-fine crystalline structure of dolomite gradually weathering into fine sand, gravel, or clasts (Figure 1) by the combined action of dissolution and weathering. This weathering process seriously reduces the quality and stability of the rock mass (Rabajczyk, 2012; Chanyshev, 2023). A series of hazards such as the large deformation of rock mass, underground karst damage, and water inrush and sand gushing are often encountered during the construction of conservancy projects in sandy dolomite strata (Zhang et al., 2023). Jiang et al. (2022) reported extrusion and deformation occurring at the tunnel face during tunneling in a water-rich sandy dolomite stratum, and they proposed a control strategy for preventing sand gushing. Zhou et al. (2022) discussed the challenges and risks of tunnel face instability in terms of mineral composition and its macroscopic and microscopic aspects. Dong et al. (2023) analyzed the main damage modes in a sandy dolomite tunnel and conducted a safety evaluation of it. Diez (2019) analyzed the rock mechanical properties of sandy dolomite after erosion and weathering in the quarry, revealed the mechanism of dissolving gravel in sandy dolomite, and evaluated the safety of rock construction. This literature indicates that dolomite sandification has a great impact on the project, and its safety and reliability must be assessed. If sandy dolomite leads to construction hazards in a water conveyance tunnel, it may force construction progress to slow down and, in serious cases, may also jeopardize the safety of tunnel construction workers and affect the social and economic benefits of the infrastructure.

Currently, there are limited studies on tunneling hazards in sandy dolomite strata. Zarei et al. (2011) analyzed the impact of geological features such as fault zones, open cracks, and dams in sandy dolomite on tunnel safety after the excavation of a water conveyance tunnel in Semnan, Iran. However, they did not assess the impact of mechanical coupling between the tunnel face and sandy dolomite on tunnel safety. Qin et al. (2019) discussed the factors affecting the stability of railway tunnels. They explained the safety problems caused by the desertification of the tunnel rock mass and used a theoretical model to make safety predictions. However, they also did not consider the impact of rock mass desertification. Wu et al. (2013) clarified the maximum horizontal stress generated by rock burst in tunnel engineering and evaluated tunnel safety based on this stress, but they did not address the changes in the mechanical properties of sandy rock mass. Taking a high-speed railway crossing the Taihang Mountain as an example, Di et al. (2020) characterized the rock resistivity distribution of a tunnel by using the controllable source audio magnetotelluric method. They analyzed the safety of the tunnel but did not record its stress condition. Liu et a. (2022) systematically analyzed the hazards and treatment methods of water inrush occurring in a large cross-section filling karst pipeline based on engineering practice, but they did not consider the impact of mechanical problems related to rock mass desertification on water inrush.

The construction of water conveyance tunnels in sandy dolomite strata poses significant challenges due to complex geological issues such as soft rock deformation, fault zones, rock bursts, and water inrush. A key innovation lies in the recognition of dolomite sandification as a primary concern; this weakens the strength and quality of rock mass, thus impacting tunnel stability. This unique geological phenomenon involves the gradual weathering of dolomite into fine sand, gravel, or clasts which reduces rock mass quality. Previous studies have highlighted hazards such as deformation, karst damage, and water inrush, emphasizing the need to assess safety and reliability. Additionally, researchers have identified challenges related to tunnel face instability and proposed control strategies to mitigate risks such as sand gushing. However, there is a lack of comprehensive studies that address the mechanical response of rock mass in sandy dolomite tunnels. Innovative research efforts have focused on developing an analytical solution for the mechanical behaviors of rock mass in sandy dolomite tunnels. The analytical approach adopted here aims to address the limited understanding of sandy dolomite tunnel mechanics and to provide insights into enhancing engineering practices. By investigating the impact of dolomite sandification on tunnel stability, this study aims to reduce and prevent instability issues in tunnel construction, ultimately improving project outcomes and safety. The findings not only contribute to the field of geotechnical engineering but also offer valuable guidance for future projects in carbonate rock regions.

2 Statement of the problem

2.1 Tunnel condition

Self-weight and associated geological tectonics are present in natural rock masses (Sperner et al., 2003; Dai et al., 2021; Lu et al., 2024). Generally, a tunnel is subjected to a gravitational (Dong et al., 2019; Wang Q. et al., 2023) and a tectonic stress field (Yale, 2003; Zhou et al., 2023).

$\sigma ={\sigma }_z+{\sigma }_{\tau }(1)$

Given the fact that the tectonic stress field is complex and is influenced by many factors, the current study only considers the effect of the gravitational stress field, which is expressed as:

${\sigma }_z=\gamma H(2)$

$\lambda =\frac{\mu }{1-\mu }(3)$

${\sigma }_x={\sigma }_y=\frac{\mu }{1-\mu }{\sigma }_z=\lambda {\sigma }_z(4)$

where σ_z is the self-weight stress with a unit of MPa, σ_τ is the tectonic stress with a unit of MPa, γ represents the weight of rock mass with a unit of kN/m³, H is the depth of rock mass with a unit of m, λ is the lateral pressure coefficient, σ_x, and σ_y are the rock mass stresses with a unit of MPa, and μ is Poisson’s ratio of rock mass.

2.2 Basic assumptions

Rock mass during tunnel excavation is mainly in two states. As indicated in Figure 3A, if the rock mass remains elastic after excavation, it is relatively stable and is in a secondary stress state (Aygar and Gokceoglu, 2020). If the excessive stress at the excavated profile exceeds the ultimate strength of rock mass, the rock mass will undergo plastic deformation, which may lead to deformation or a failure of the supporting structure through the relaxation and failure of the rock mass (Zheng and Wei, 2008). However, the rock mass further away from the excavated profile remains in an elastic state, resulting in a plastic zone in the rock mass (Leu and Chang, 2005). The following assumptions have been made to facilitate the elasto-plasticity analysis of rock mass (Wang et al., 2010; Zhang and Sun, 2011; van Bijsterveldt et al., 2021; Guo et al., 2023):

(1) The rock mass is homogeneous, isotropic, and incompressible, and exhibits ideal elastic–plastic mechanical behavior with a constitutive relationship (Figure 3B).

(2) The tunnel is deep-buried, satisfying the ideal plane hole problem, and it has a circular section and infinite length.

(3) Only the self-weight of the rock mass is considered for the initial stress field, with no tectonic stress.

Figure 3

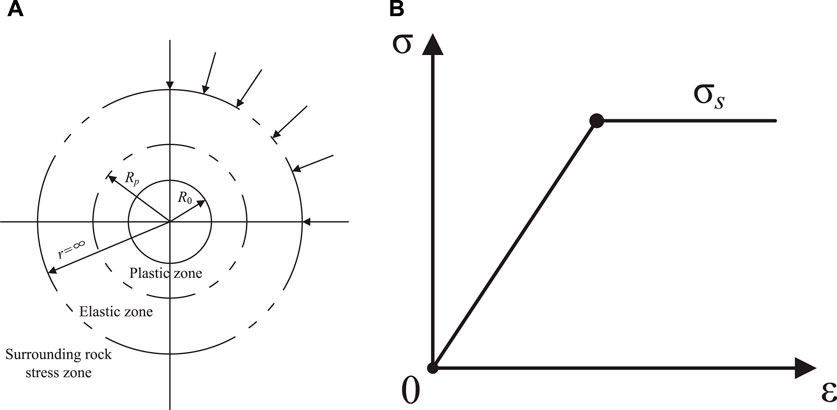
Figure 3. Two states of rock mass during tunnel excavation: (A) division of the elastic and plastic zones of rock mass; (B) constitutive relation diagram.

3 Elasto-plasticity solution for sandy dolomite tunnel

To analyze the mechanical behaviors of a tunnel constructed in sandy dolomite strata, it is simplified into an ideal circular tunnel model based on the principle of small hole stress (Toubal et al., 2005; Schajer, 2010). An elastic-plastic analytical solution of a circular tunnel is then derived to determine the deformation, stress, and radii of plastic zones of tunnel rock mass.

3.1 Solution for rock mass in the elastic zone

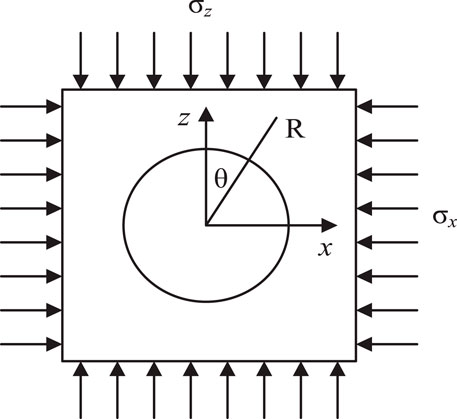
If the lateral pressure coefficient λ is not equal to 1, the rock mass stress can be divided into two parts according to the elastic mechanics and then be superimposed to determine the final stress state. Figure 4 illustrates a schematic diagram of the secondary stress in the tunnel rock mass.

Part I: the rock mass is subjected to an initial rock stress of p = p₀/2 (1+λ), the vertical stress is equal to the horizontal stress, and the distribution is axisymmetric.

Part II: the rock mass is subjected to an initial rock stress of p = p₀/2 (1-λ), the vertical stress is equal to the horizontal stress, and the distribution is antisymmetric.

Figure 4

Figure 4. Schematic diagram of tunnel model.

According to elastic mechanics, the radial σ_r, tangential σ_θ, and shear τ_rθ stresses can be obtained as:

${\sigma }_r=\frac{p_0}{2}\left[\left(1+\lambda \right)\left(1-\frac{R_0^2}{r^2}\right)-\left(1-\lambda \right)\left(1-4\frac{R_0^2}{r^2}+3\frac{R_0^4}{r^4}\right)\cos 2\theta \right](5)$

${\sigma }_{\theta }=\frac{p_0}{2}\left[\left(1+\lambda \right)\left(1+\frac{R_0^2}{r^2}\right)+\left(1-\lambda \right)\left(1+3\frac{R_0^2}{r^4}\right)\cos 2\theta \right](6)$

${\tau }_{r\theta }=-\frac{p_0}{2}\left[\left(1-\lambda \right)\left(1+2\frac{R_0^2}{r^2}-3\frac{R_0^4}{r^4}\right)\sin 2\theta \right](7)$

The radial displacement u_r and tangential displacement u_θ are expressed as:

$u_r=\frac{\left(1+v\right)p_0}{2E}\cdot \frac{R_0^2}{r}\left\{\left(1+\lambda \right)+\left(1-\lambda \right)\left[2\left(1-2v\right)+\frac{R_0^2}{r^2}\right]\cos 2\theta \right\}(8)$

$u_{\theta }=\frac{\left(1+v\right)p_0}{2E}\cdot \frac{R_0^2}{r}\left\{\left(1-\lambda \right)\left[2\left(1-2v\right)+\frac{R_0^2}{r^2}\right]\sin 2\theta \right\}(9)$

where p₀ is the initial rock stress with a unit of MPa, θ is the angle between the z-axis and the line connecting the computation point to the origin with a unit of °, R₀ is the excavation radius of the tunnel with a unit of m, r is the tunnel radius with a unit of m, v is the strain coefficient of the rock mass, and E is the elastic modulus of rock mass with a unit of MPa.

These equations characterize the detailed secondary stress of the rock mass. However, these equations are complicated as they involve not only tangential stress but also tangential displacement. To simplify this problem, the tunnel radius and the excavation radius are assumed to be equal at r = R₀.

Thereafter, the equation obtained can be simplified as:

${\sigma }_{\theta }=p_0\left[\left(1+\lambda \right)+2\left(1-\lambda \right)\cos 2\theta \right](10)$

${\sigma }_r={\tau }_{r\theta }=0(11)$

If 1 + 2cos2θ = K_z, 1 - 2cos2θ = K_x, then the above equation can be converted to:

${\sigma }_{\theta }=p_0\left(K_Z+\lambda K_x\right)={Kp}_0(12)$

where K is the total stress concentration factor of the tunnel rock mass, K_z is the vertical stress concentration factor, and K_x is the horizontal stress concentration factor. These parameters are dimensionless.

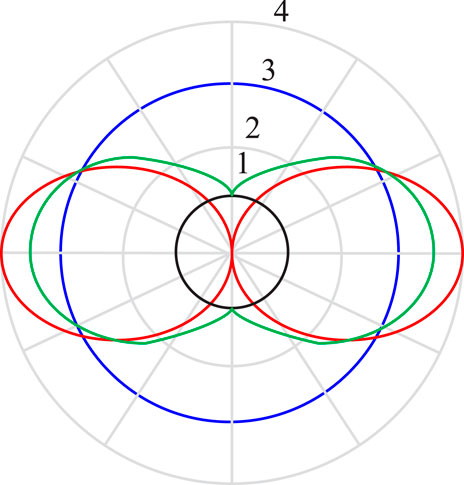
K varies with θ, p₀, and λ as independent variables (Figure 5). The origin position that is the intersection of the radial line with the tunnel sidewall changes dynamically. The stress value at the origin divided by the initial stress (σ_θ/p₀) is chosen as the scale.

Figure 5

Figure 5. Variation of total stress concentration factor of tunnels.

As indicated in Figure 5, when λ = 1, the stress values of the tunnel wall are all 2p₀—twice the initial stress. Since the tangential stress is independent of the angle, the stress of the tunnel wall is in the best state, and the tunnel is safer. When λ = 0, the stress on the tunnel wall is in the most unfavorable state. The left and right sides of the tunnel wall will be subjected to the maximum compressive stress 3p₀ (three times the initial rock stress), while the upper side of the tunnel wall will be subjected to the maximum tensile stress p₀ (equal to the initial rock stress). When λ = 1/3, the boundary point of tensile stress appears on the tunnel wall, while the tensile and compressive stresses on the upper side of the tunnel wall is 0. At this point, the tunnel is in stress equilibrium and is safest. When λ is less than ⅓, the tensile stress appears on the upper side of the tunnel wall. The safety of the tunnel is slightly improved, and the risk of tunnel wall damage and leakage is reduced. When λ is greater than ⅓, the compressive stress appears on the upper side of the tunnel wall, and a safety risk to the tunnel will be present.

3.2 Solution for rock mass in the plastic zone

The elastic zone can be expressed thus (Zareifard and Fahimifar, 2016):

$\begin{array}{l}{\sigma }_r\\ {\sigma }_{\theta }\end{array}=\mathrm{A}\pm \frac{\mathrm{B}}{r^2}(13)$

The equilibrium equation is (Wang M. et al., 2023):

$\frac{\mathrm{d}{\sigma }_r}{\mathrm{d}r}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0(14)$

The M–C criterion is adopted for the analysis, which is expressed as (Zheng et al., 2005):

${\sigma }_{\theta }=\frac{1+\sin \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}{\sigma }_r+\frac{2C\cos \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}(15)$

The stresses in the elastic and plastic zones can be obtained by combining Eqs 13-15.

Stress in elastic zone is expressed as (Oreste et al., 2019):

$\begin{array}{l}{\sigma }_{\theta }^e\\ {\sigma }_r^e\end{array}=p_0\pm \left(C\cos \mathrm{\Phi }+p_0\right){\left[\frac{\left(p_0+C\cot \mathrm{\Phi }\right)\left(1-\sin \mathrm{\Phi }\right)}{C\cot \mathrm{\Phi }}\right]}^{\frac{1-\sin \mathrm{\Phi }}{2\sin \mathrm{\Phi }}}{\left(\frac{R_0}{r}\right)}^2(16)$

${\sigma }_z^e=p_0(17)$

Stress in the plastic zone is expressed as (Wang C. et al., 2023):

${\sigma }_{\theta }^p=C\cot \mathrm{\Phi }\left[{\left(\frac{r}{R_0}\right)}^{\frac{2\sin \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}}-1\right](18)$

${\sigma }_r^p=C\cot \mathrm{\Phi }\left[\frac{1+\sin \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}{\left(\frac{r}{R_0}\right)}^{\frac{2\sin \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}}-1\right](19)$

${\sigma }_z^p=\frac{{\sigma }_{\theta }^p+{\sigma }_r^p}{2}=C\cot \mathrm{\Phi }\left[\frac{1}{1-\sin \mathrm{\Phi }}{\left(\frac{r}{R_0}\right)}^{\frac{2\sin \mathrm{\Phi }}{1-\sin \mathrm{\Phi }}}-1\right](20)$

The radius of the plastic zone can be obtained thus (Singh et al., 2016):

$R_p=R_0{\left[\frac{\left(p_0+C\cot \mathrm{\Phi }\right)\left(1-\sin \mathrm{\Phi }\right)}{C\cot \mathrm{\Phi }}\right]}^{\frac{1-\sin \mathrm{\Phi }}{2\sin \mathrm{\Phi }}}(21)$

where C is cohesion with a unit of MPa, Ф is the internal friction angle with a unit of °, and R_p is the radius of the plastic zone with a unit of m. Eqs 16–21 are derived from Eqs 1–15. The part 4 of the article mainly refers to Eqs 16–21.

4 Parametric analysis on the mechanical behaviors of rock mass

Parameter analysis is performed in this section by utilizing the mechanical parameters of sandy dolomite determined by laboratory tests (Dang et al., 2022; Tao et al., 2023b; Tao et al., 2023) which yields various mechanical response curves of rock mass.

4.1 Variation of stress in the elastic zone

4.1.1 Influence of the internal friction angle

Three internal friction angles—38°, 42°and 46°—are selected to explore the variations of stress σ^e_θ (tangential stress) and σ^e_r (radial stress) in the elastic zone. From Eq. 16, the results are presented in Figure 6.

Figure 6

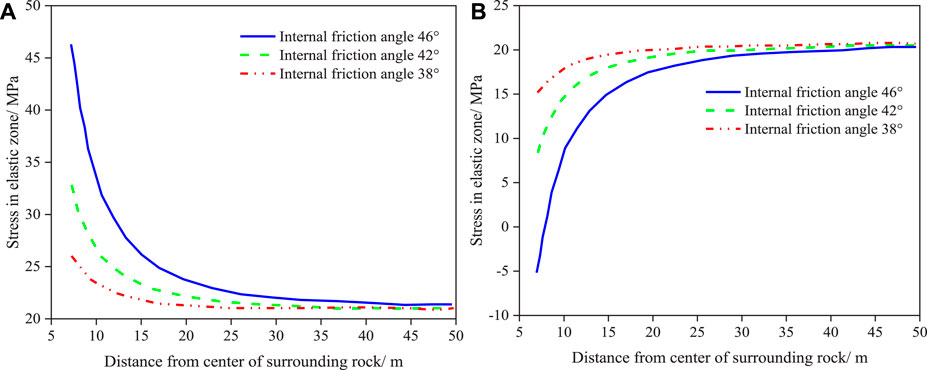
Figure 6. Variation of stress in elastic zone under different internal friction angles. (A) σ^e_r. (B) σ^e_θ.

It can be observed from Figure 6 that under different internal friction angles, with an increase in distance from the excavation center, σ^e_r displays a decreasing trend. A larger internal friction angle yields a larger initial σ^e_r value with a greater decline (Figure 6A). An increasing trend is experienced by σ^e_θ as the distance from the excavation surface increases, but the initial value is smaller and the growth rate is larger at a larger internal friction angle (Figure 6B).

4.1.2 Influence of cohesion

Cohesion values of 20, 30, and 40 MPa are selected to explore variations of stress in the elastic zone. From Eq. 16, the results are presented in Figure 7.

Figure 7

Figure 7. Variation of stress in elastic zone under different cohesions. (A) σ^e_r. (B) σ^e_θ.

Figure 7 confirms that the stress in the elastic zone varies with the distance from the excavation center under different cohesions. It is observed that σ^e_r decreases with an increase in the distance from the excavation center. However, higher cohesion leads to a higher initial σ^e_r and a greater decline (Figure 7A). With an increase in distance from the excavation surface, σ^e_θ experiences an increasing trend, but higher cohesion leads to a smaller initial σ^e_θ and a greater increase (Figure 7B).

4.1.3 Influence of initial rock stress

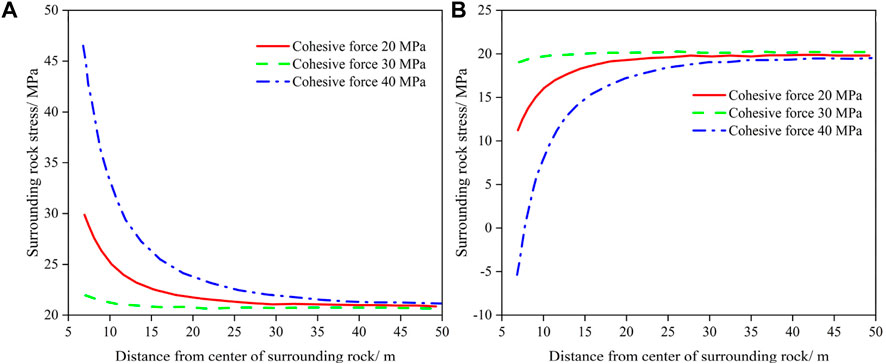
The initial rock stresses of 21, 25, and 29 MPa are selected to explore the variations of stress in the elastic zone. From Eq. 16, the results are presented in Figure 8.

Figure 8

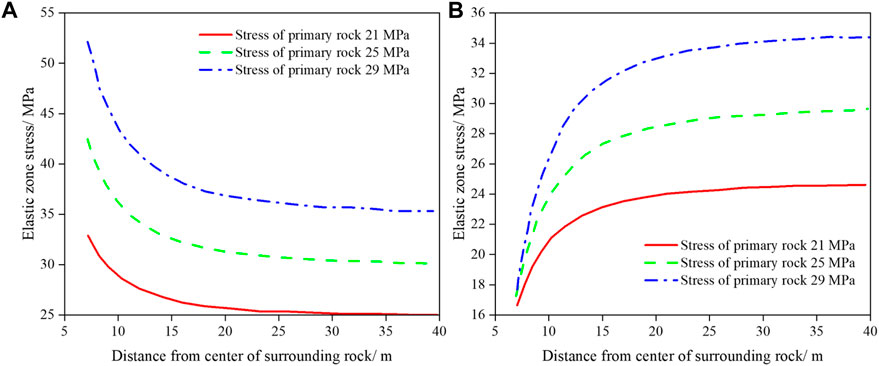
Figure 8. Variation of stress in elastic zone under different initial rock stresses. (A) σ^e_r. (B) σ^e_θ.

Figure 8 demonstrates that stress in the elastic zone varies with the distance from the excavation surface under different initial rock stresses. It can be observed that σ^e_r under three initial rock stresses decreases gradually with increased distance from the excavation surface. These three curves have similar shapes, are parallel to each other, and decrease by almost the same amount. Moreover, the initial values of σ^e_r and terminal values of σ^e_θ increase with increasing initial rock stresses. An increasing trend is shown by σ^e_θ under three initial rock stresses with increasing distance from the excavation surface, with very close initial values. However, the greater the initial rock stress, the greater the range of increase in σ^e_θ. When the distance from the excavation surface exceeds 25 m, both σ^e_r and σ^e_θ gently increase or decrease and the curves become almost horizontal.

4.2 Variation of stress in the plastic zone

4.2.1 Influence of the internal friction angle

Three internal friction angles of 38°, 42°, and 46° are selected to explore the variations of stress σ^p_θ (tangential stress) and σ^p_r (radial stress) in the plastic zone. From Eqs 18, 19, the results are shown in Figure 9.

Figure 9

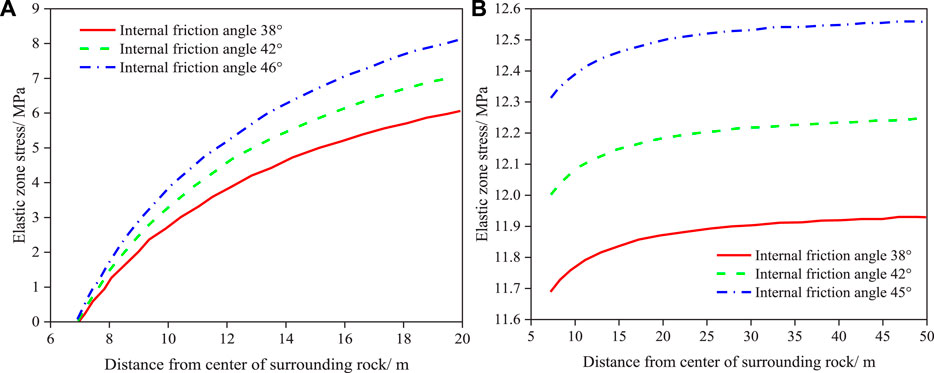
Figure 9. Variation of stress in plastic zone under different internal friction angles. (A) σ^p_r. (B) σ^p_θ.

As shown in Figure 9, stress in the plastic zone varies with the distance from the excavation surface under different internal friction angles. It can be observed that σ^p_r and σ^p_θ under the three internal friction angles increase with increased distance from the excavation surface. In addition, the larger the internal friction angle, the greater the increase in value of the two types of stresses. However, the radial stress growth curve consists of three curves with the same starting point; the larger the internal friction angle, the steeper the curve. This indicates that there is little difference in the radial stresses in the plastic zone at different internal friction angles. In contrast, the σ^p_θ curve is composed of three parallel and gentle curves, especially when the distance from the excavation surface is more than 25 m. Furthermore, the rising range of the σ^p_θ curve increases with an increase in the internal friction angle.

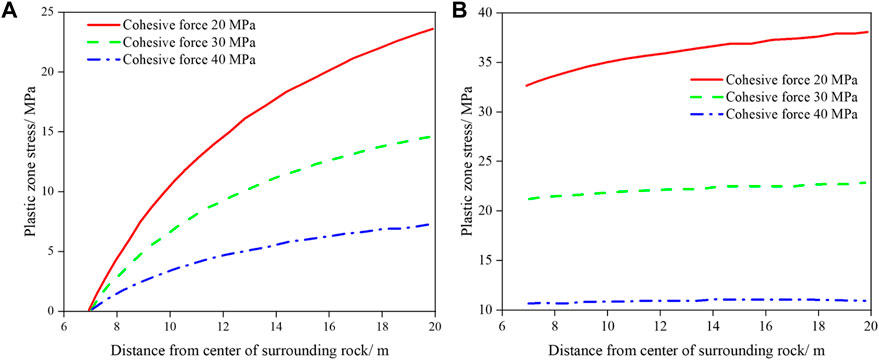
4.2.2 Influence of cohesion

Cohesion values of 20, 30, and 40 MPa are selected to explore variations of stress in the plastic zone. From Eqs 18,19, the results are shown in Figure 10.

Figure 10

Figure 10. Variation of stress in plastic zone under different cohesions. (A) σ^p_r. (B) σ^p_θ.

As shown in Figure 10, the stress in the plastic zone varies with the distance from the excavation surface under different cohesions. It is observed that σ^p_r and σ^p_θ under the three cohesion values increase with increased distance from the excavation surface. In addition, the greater the cohesion, the greater the increase in corresponding stress. However, the radial stress growth curve consists of three curves with the same starting point, and the smaller the cohesion, the steeper the curve. This indicates that there is little difference in σ^p_r in the plastic zone at different cohesions. In contrast, the σ^p_θ growth curve consists of three parallel and gentle curves. Furthermore, the rising range of the σ^p_θ growth curve with increasing cohesion is smaller, indicating that σ^p_θ hardly varies with the distance from excavation surface when cohesion and initial rock stress are constant.

5 Discussion

(1) Influence on stress in elastic zone

Based on the analysis above, it is evident that both the σ^e_r and σ^e_θ, curves at different internal friction angles and cohesions are close and almost overlap when the distance from the excavation surface exceeds 40 m. This indicates that within a certain range, the internal friction angle and cohesion have less influence on stress in the elastic zone as the distance from the excavation surface increases.

(2) Variation of the radius of the plastic zone

Cohesion values of 20, 30, and 40 MPa are selected to explore variations in the radius of the plastic zone under different initial rock stresses and tunnel excavation radii. From Eq. 21, the results are shown in Figure 11.

Figure 11

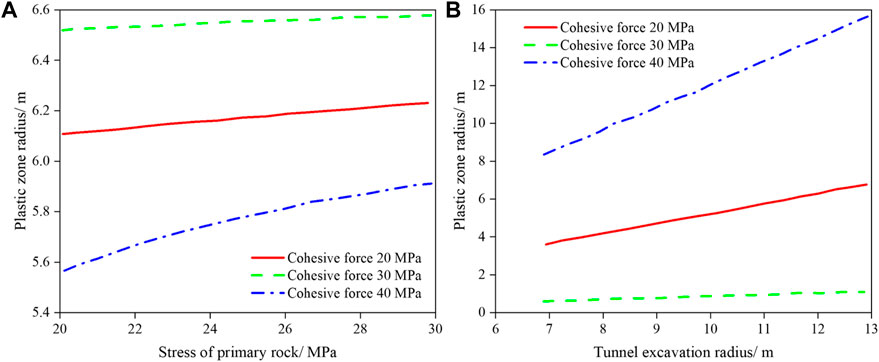
Figure 11. Variation of radius of plastic zone under different cohesions. (A) The initial rock stress. (B) Tunnel excavation radius.

Figure 11 indicates that the radius of the plastic zone varies with the initial rock stress and tunnel excavation radius at different cohesions. The radius of the plastic zone nonlinearly increases with the initial rock stress. Higher cohesion results in a decrease in the radius of plastic zone, and an increase in radius of the plastic zone is dependent on an increase in the initial rock stress at different cohesions. Furthermore, an increase in tunnel excavation radius also leads to an increase in the radius of the plastic zone, and an increase in radius of plastic zone is associated with an increase in excavation radius at different cohesion conditions.

Therefore, initial rock stress has a significant impact on the radius of the plastic zone. Higher initial rock stress results in a larger plastic zone radius which demonstrates a significant effect on the rock plasticity. Cohesion also plays a significant role in determining the radius of the plastic zone, with higher cohesion leading to a smaller radius. This suggests that increasing cohesion will greatly enhance the resistance of rock mass to plastic failure. Furthermore, an increase in tunnel excavation radius correlates with an increase in plastic zone radius, highlighting the significant impact of tunnel excavation on the plastic zone of rock mass. This should be fully considered in engineering design and practice. These research results serve as an important theoretical reference for rock mechanical properties and have significant guiding implications for geotechnical engineering practice.

6 Conclusion

This study develops an analytical solution for sandy dolomite tunneling, and then conduct parametric analysis to investigate the mechanical response of rock mass in sandy dolomite tunnels. It draws the following analytical conclusions.

(1) The stress of tunnel sidewalls under different λ values exhibits different characteristics. Varying λ values impacts stress distribution and tunnel stability, with extreme values posing instability risks. When the stress of a rock mass approaches the plastic limit, the deformation rate of rock mass increases. A smaller plastic zone radius leads to lower safety for a tunnel.

(2) In cases of varying internal friction angles, cohesion, and initial rock stress, radial stress exhibits a gradually decreasing trend with increasing distance from the excavation surface. Higher values lead to a greater decline of radial stress. Stress values increase with distance from the excavation surface but become similar within a certain range. The effects on stress in elastic zone decrease as distance from the excavation surface increases.

(3) The plastic zone size increases with a larger tunnel excavation radius, while the internal friction angle and cohesion determine the corresponding stress increase value. The initial rock stress significantly affects the plastic zone radius, with a higher initial rock stress resulting in a larger plastic zone radius while higher cohesion leading to a smaller plastic zone radius. Increased tunnel excavation radius also contributes to the expansion of the plastic zone, demonstrating the significant influence of tunnel excavation on rock mass. These findings provide important reference and guidance for geotechnical engineering practice.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

DS: Conceptualization, Investigation, Methodology, Writing–original draft. ZT: Conceptualization, Methodology, Validation, Writing–review and editing. HY: Funding acquisition, Resources, Supervision, Writing–original draft. HS: Data curation, Investigation, Visualization, Writing–original draft. XL: Formal Analysis, Investigation, Supervision, Writing–original draft. FW: Formal Analysis, Investigation, Supervision, Writing–original draft. SH: Formal Analysis, Investigation, Supervision, Writing–original draft. HS: Data curation, Investigation, Visualization, Writing–original draft. WX: Data curation, Investigation, Visualization, Writing–original draft. ZW: Data curation, Investigation, Visualization, Writing–original draft. MH: Conceptualization, Methodology, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research received the financial support provided by the Major Science and Technology Special Plan of Yunnan Province Science and Technology Department (Grant No. 202002AF080003), the Fundamental Research Funds for the Central Universities (Grant No. 2022YJSSB04).

Acknowledgments

Many thanks are due to China Institute of Water Resources and Hydropower Research, Yunnan Institute of Water & Hydropower Engineering Investigation, Design and Research, China Railway No.5 Engineering Group Co., Ltd, and China Railway Tunnel Group Co., Ltd. The authors gratefully acknowledge the financial support provided by the Major Science and Technology Special Plan of Yunnan Province Science and Technology Department (Grant Nos.202002AF080003) and the Fundamental Research Funds for the Central Universities (Grant Nos.2022YJSSB04).

Conflict of interest

Author HY was employed by China Railway 12^th Bureau Group Co. Ltd.

Author FW was employed by Shanxi Provincial Transportation Technology Research and Development Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aygar, E. B., and Gokceoglu, C. (2020). Problems encountered during a railway tunnel excavation in squeezing and swelling materials and possible engineering measures: a case study from Turkey. Sustainability-Basel 12 (3), 1166. doi:10.3390/su12031166

CrossRef Full Text | Google Scholar

Chanyshev, A. (2023). A way to determine the positive direction of the shear force on the elemental area. Geohazard Mech. 1 (2), 179–184. doi:10.1016/j.ghm.2023.04.004

CrossRef Full Text | Google Scholar

Dai, L. P., Pan, Y. S., Li, Z. H., Wang, A. W., Xiao, Y. H., Liu, F. Y., et al. (2021). Quantitative mechanism of roadway rockbursts in deep extra-thick coal seams: theory and case histories. Tunn. Undergr. Space Technol. 111, 103861. doi:10.1016/j.tust.2021.103861

CrossRef Full Text | Google Scholar

Dang, W., Tao, K., and Chen, X. (2022). Frictional behavior of planar and rough granite fractures subjected to normal load oscillations of different amplitudes. J. Rock Mech. Geotech. Eng. 14 (3), 746–756. doi:10.1016/j.jrmge.2021.09.011

CrossRef Full Text | Google Scholar

Di, Q. Y., Fu, C. M., An, Z. G., Wang, R., Wang, G., Wang, M., et al. (2020). An application of CSAMT for detecting weak geological structures near the deeply buried long tunnel of the Shijiazhuang-Taiyuan passenger railway line in the Taihang Mountains. Eng. Geol. 268, 105517. doi:10.1016/j.enggeo.2020.105517

CrossRef Full Text | Google Scholar

Diez, J. A. (2019). “Analysis of the alterability of quarry rock used in the Alcorlo rock fill dam (Guadalajara, Spain),” in 14th ISRM congress (Foz do Iguaçu, Brazil: ISRM). ISRM-14CONGRESS-2019-208.

Google Scholar

Dong, J. X., Shen, Z. L., Cao, L., Mi, J., Li, J., Zhao, Y., et al. (2023). Water-sand inrush risk assessment method of sandy dolomite tunnel and its application in the Chenaju tunnel, southwest of China. Geomatics Nat. Hazard. Risk 14 (1), 2196369. doi:10.1080/19475705.2023.2196369

CrossRef Full Text | Google Scholar

Dong, W., Song, S. Z., Zhang, B. S., and Yang, DJEFM (2019). SIF-based fracture criterion of rock-concrete interface and its application to the prediction of cracking paths in gravity dam. Eng. Fract. Mech. 221, 106686. doi:10.1016/j.engfracmech.2019.106686

CrossRef Full Text | Google Scholar

Fu, P., Yin, J. M., Ding, X. L., and Liu, Y. K. (2020). “Deformation-strain field characteristics and fault activities in central Yunnan water diversion project area,” in IOP Conference Series: Earth and Environmental Science, 570 October 23–26, 2020 (Beijing, China: IOP Publishing). doi:10.1088/1755-1315/570/6/062029

CrossRef Full Text | Google Scholar

Guo, W., Shui, H. C., Liu, Z., Wang, Y., and Tu, J. W. (2023). Reliability analysis of elastic graphite packer in heat injection well during oil shale in-situ conversion. Adv. Geo-Energy Res. 7 (1), 28–38. doi:10.46690/ager.2023.01.04

CrossRef Full Text | Google Scholar

Jiang, Y. F., Zhou, P., Zhou, F. C., Lin, J. Y., Li, J. Y., Lin, M., et al. (2022). Failure analysis and control measures for tunnel faces in water-rich sandy dolomite formations. Eng. Fail. Anal. 138, 106350. doi:10.1016/j.engfailanal.2022.106350

CrossRef Full Text | Google Scholar

Leu, S. S., and Chang, S. L. (2005). Digital image processing based approach for tunnel excavation faces. Autom. Constr. 14 (6), 750–765. doi:10.1016/j.autcon.2005.02.004

CrossRef Full Text | Google Scholar

Liu, N., Pei, J. H., Cao, C. Y., Liu, X. Y., Huang, Y. X., Mei, GXJT, et al. (2022). Geological investigation and treatment measures against water inrush hazard in karst tunnels: a case study in Guiyang, southwest China. Tunn. Undergr. Space Technol. 124, 104491. doi:10.1016/j.tust.2022.104491

CrossRef Full Text | Google Scholar

Lu, B., Sheil, B. B., Zhao, W., Jia, P. J., Bai, Q., and Wang, W. T. (2024). Laboratory testing of settlement propagation induced by pipe-roof pre-support deformation in sandy soils. Tunn. Undergr. Space Technol. 146, 105645. doi:10.1016/j.tust.2024.105645

CrossRef Full Text | Google Scholar

Oreste, P., Hedayat, A., and Spagnoli, G. (2019). Effect of gravity of the plastic zones on the behavior of supports in very deep tunnels excavated in rock masses. Int. J. Geomech. 19 (9), 04019107. doi:10.1061/(asce)gm.1943-5622.0001490

CrossRef Full Text | Google Scholar

Qin, S. W., Ma, Z. J., Jiang, C. D., Lin, J., Bai, M., Lin, T., et al. (2019). Application of magnetic resonance sounding to tunnels for advanced detection of water-related disasters: a case study in the Dadushan Tunnel, Guizhou, China. Tunn. Undergr. Space Technol. 84, 364–372. doi:10.1016/j.tust.2018.11.032

CrossRef Full Text | Google Scholar

Rabajczyk, A. (2012). The relationship between metal forms found in river bottom sediments and land development (review). Rijeka: Water Pollut. InTech, 189–202.

Google Scholar

Schajer, G. S. (2010). Advances in hole-drilling residual stress measurements. Exp. Mech. 50, 159–168. doi:10.1007/s11340-009-9228-7

CrossRef Full Text | Google Scholar

Singh, A., Rao, K. S., and Ayothiraman, R. (2016). “Effect of intermediate principal stress on cylindrical tunnel in an elasto-plastic rock mass,” in 11th International Symposium on Plasticity and Impact Mechanics (IMPLAST) (New Delhi, INDIA: Indian Inst Technol), 1056–1063.

Google Scholar

Sperner, B., Müller, B., Heidbach, O., Delvaux, D., Reinecker, J., and Fuchs, K. (2003). Tectonic stress in the Earth’s crust: advances in the World Stress Map project. Geol.Soc.London Spec. Publ. 212 (1), 101–116. doi:10.1144/gsl.sp.2003.212.01.07

CrossRef Full Text | Google Scholar

Tao, K., Dang, W., and Li, Y. (2023). Frictional sliding of infilled planar granite fracture under oscillating normal stress. Int. J. Min. Sci. Technol. 33 (6), 687–701. doi:10.1016/j.ijmst.2022.12.001

CrossRef Full Text | Google Scholar

Tao, K., Dang, W., Liao, X., and Li, X. (2023b). Experimental study on the slip evolution of planar fractures subjected to cyclic normal stress. Int. J. Coal Sci. Technol. 10 (1), 67. doi:10.1007/s40789-023-00654-w

CrossRef Full Text | Google Scholar

Toubal, L., Karama, M., and Lorrain, B. (2005). Stress concentration in a circular hole in composite plate. Compos. Struct. 68 (1), 31–36. doi:10.1016/j.compstruct.2004.02.016

CrossRef Full Text | Google Scholar

van Bijsterveldt, C. E., van Wesenbeeck, B. K., Ramadhani, S., Raven, O. V., van Gool, F. E., Pribadi, R., et al. (2021). Does plastic waste kill mangroves? A field experiment to assess the impact of macro plastics on mangrove growth, stress response and survival. Sci. Total Environ. 756, 143826. doi:10.1016/j.scitotenv.2020.143826

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Liu, X., Song, D., Wang, E., and Zhang, J. (2023d). Elasto-plastic analysis of the surrounding rock mass in circular tunnel using a new numerical model based on generalized nonlinear unified strength theory. Comput. Geotech. 154, 105163. doi:10.1016/j.compgeo.2022.105163

CrossRef Full Text | Google Scholar

Wang, M., Zhang, Z., Ren, L., Zhang, R., Zheng, L., Zhang, L., et al. (2023c). Analysis of rock mass parameters and plastic zone of a tunnel in southwest mountainous area. KSCE J. Civ. Eng. 27 (12), 5448–5459. doi:10.1007/s12205-023-0886-2

CrossRef Full Text | Google Scholar

Wang, M. Q., Xu, W., Mu, H. Y., Mi, J., Wu, Y. H., and Wang, Y. X. (2022). Study on construction and reinforcement Technology of dolomite sanding tunnel. Sustainability-Basel 14 (15), 9217. doi:10.3390/su14159217

CrossRef Full Text | Google Scholar

Wang, M. Q., Zhang, C. X., Song, B. H., Liu, H. M., and Xu, W. (2023a). Study on the mechanical properties of anisotropic red sandstone under point load strength test and uniaxial compression strength. J. Civ. Eng. Environ. Sci. 9 (1), 025–032. doi:10.17352/2455-488x.000064

CrossRef Full Text | Google Scholar

Wang, Q., Wang, Y. C., Jiang, B., Jiang, Z. H., and Xue, H. J. (2023b). Geomechanics model test research on large deformation control mechanism of roadway disturbed by strong dynamic pressure. Geohazard Mech. 1 (2), 140–152. doi:10.1016/j.ghm.2023.06.002

CrossRef Full Text | Google Scholar

Wang, S. L., Yin, X. T., Tang, H., and Ge, X. R. (2010). A new approach for analyzing circular tunnel in strain-softening rock masses. Int. J. Rock Mech. Min. Sci. 47 (1), 170–178. doi:10.1016/j.ijrmms.2009.02.011

CrossRef Full Text | Google Scholar

Wu, K., Chen, J. M., Su, J. G., Gao, R., and Gu, S. (2021). “Optimal allocation and integrated dispatch of regional water resources in Yunnan Province—problems and countermeasures,” in IOP Conference series: earth and environmental science 7th International Conference on Advances in Energy, Environment and Chemical Engineering. 831. Chengdu, China. July 9-11, 2011. (Beijing, China: IOP Publishing). doi:10.1088/1755-1315/831/1/012065

CrossRef Full Text | Google Scholar

Wu, L., Xu, C. M., Wu, S. L., and Shi, LJAM (2013). Materials, geostress measurement and rock burst prediction analysis for a deep-buried long and large high-speed railway tunnel. Appl. Mech. Mater. 256, 1359–1364. doi:10.4028/www.scientific.net/AMM.256-259.1359

CrossRef Full Text | Google Scholar

Yale, D. P. (2003). Fault and stress magnitude controls on variations in the orientation of in situ stress. Geol.Soc.London Spec. Publ. 209 (1), 55–64. doi:10.1144/gsl.sp.2003.209.01.06

CrossRef Full Text | Google Scholar

Zarei, H., Uromeihy, A., Sharifzadeh, M. J. T., and Technology, U. S. (2011). Evaluation of high local groundwater inflow to a rock tunnel by characterization of geological features. Tunn. Undergr. Space Technol. 26 (2), 364–373. doi:10.1016/j.tust.2010.11.007

CrossRef Full Text | Google Scholar

Zareifard, M. R., and Fahimifar, A. (2016). Analytical solutions for the stresses and deformations of deep tunnels in an elastic-brittle-plastic rock mass considering the damaged zone. Tunn. Undergr. Space Technol. 58, 186–196. doi:10.1016/j.tust.2016.05.007

CrossRef Full Text | Google Scholar

Zhang, B. Y., Liu, G., Li, Y. C., and Lin, Z. B. (2023). Experimental study on the seepage mutation of natural karst collapse pillar (KCP) fillings over mass outflow. Environ. Sci. Pollut. Res. 30 (51), 110995–111007. doi:10.1007/s11356-023-30230-3

CrossRef Full Text | Google Scholar

Zhang, Z. Z., and Sun, Y. Z. (2011). Analytical solution for a deep tunnel with arbitrary cross section in a transversely isotropic rock mass. Int. J. Rock Mech. Min. Sci. 48 (8), 1359–1363. doi:10.1016/j.ijrmms.2011.10.001

CrossRef Full Text | Google Scholar

Zheng, G., and Wei, S. W. (2008). Numerical analyses of influence of overlying pit excavation on existing tunnels. J. Cent. South Univ. Sci. Technol. 15, 69–75. doi:10.1007/s11771-008-0438-4

CrossRef Full Text | Google Scholar

Zheng, H., Lui, D. F., Lee, C. F., and Ge, X. R. (2005). Principle of analysis of brittle-plastic rock mass. Int. J. Solids Struct. 42 (1), 139–158. doi:10.1016/j.ijsolstr.2004.06.050

CrossRef Full Text | Google Scholar

Zhou, P., Jiang, Y. F., Zhou, F. C., Wu, F., Qi, Y., and Wang, ZJEFA (2022). Disaster mechanism of tunnel face with large section in sandy dolomite stratum. Eng. Fail. Anal. 131, 105905. doi:10.1016/j.engfailanal.2021.105905

CrossRef Full Text | Google Scholar

Zhou, X. P., Long, Y. D., and Ye, W. (2023). Experimental investigations on the cracking and mechanical responses of PMMA samples with two 3D embedded elliptic flaws under uniaxial compression. Geohazard Mech. 1 (1), 77–85. doi:10.1016/j.ghm.2022.11.004

CrossRef Full Text | Google Scholar