Variable gearing at the ankle during walking in adults and young children: implications for foot development and evolution

Introduction: The human foot has evolved over the past seven million years from a relatively mobile, grasping appendage to a highly derived structure with a heel pad and longitudinal arch that can absorb shock at heel strike and weight-bearing yet also function as a powerful lever at toe-off. It has been proposed that the modern human foot evolved to allow our species to use “variable gearing” during walking and running. In this model, the gears of the human foot are defined relative to the ankle center of rotation as R, the distance from the ground reaction resultant vector, and r, the distance from the calf muscle vector. The gear ratio defines the torque generated to propel the body or stretch the triceps surae muscles. We test the hypothesis that variable gearing is associated with modern human pedal anatomy and a heel-to-toe rollover that allows a shift from “low gear” to “high gear” during stance.

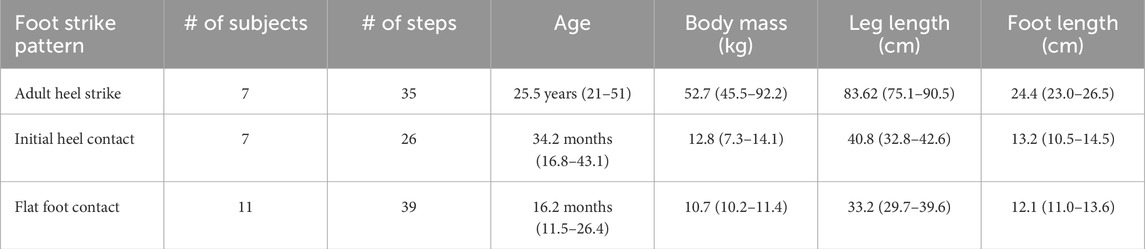
Methods: Using force plate and video analysis, we examined variable gearing in adults and children engaging in adult heel strike (AHS = 35), flat foot contact (FFC = 39), or initial heel contact (IHC = 26).

Results and Discussion: Our hypothesis was partly supported. Although variable gearing was observed in IHC steps and was greater than in FFC steps, it was not as developed as in AHS steps. This may be related to anatomical and motor control differences between juvenile and adult feet, suggesting that adult anatomy, including a high arch, and neural control are critical for full use of variable gearing and that this feature would have evolved in later hominins around two million years ago with the appearance of a fully modern foot.

Introduction

The functional evolution of the human foot—with its defining characteristic of making complete contact with the ground from heel to toe—continues to be essential for answering questions of how and why bipedalism evolved in our fossil ancestors. Still unresolved is how our feet developed over the last 7 million years from the relatively mobile climbing feet of hominoids to our modern condition of a stiff lever with a powerful forefoot push-off. There is a wide range of ways to approach these questions of form-function development in the foot, many of which are covered in this issue by other authors. One effective way to explore the functional role of changes in foot length and mobility on foot mechanics is to take an explicitly ontogenetic approach by examining foot mechanics in young children at the earliest stages of walking compared to older children and adults. Changes in foot anatomy, kinematics, and neural control with age during bipedal development may illuminate scenarios concerning pedal evolution and inferences about foot mechanics in early hominins.

Modern humans walk and sometimes run with a plantigrade foot posture in which the heel strikes the ground first, the entire plantar surface of the foot is in contact with the ground by midstance, and the step is completed with a powerful push-off at digits I and II. In this specialized pattern of foot contact, the entire foot is applied progressively to the ground, allowing weight support and the center of pressure (COP) to progress along its entire length (Elftman and Manter, 1935; Grundy et al., 1975).

There are many debated explanations for this pattern of foot contact, including increased stability, speed, effective limb length (Webber and Raichlen, 2016), increased hip translation (Zeininger et al., 2020), and reduction of collision losses at the step-to-step transition (Holowka and Lieberman, 2018). However, one of the most intriguing and least explored potential adaptive benefits is the proposed ability to exploit what has been called by David Carrier and others (1994) “variable gearing” (change in the ratio of the ground reaction force moment arm to the plantar flexor muscle moment arm) at the ankle to optimize triceps surae muscle force or stretch during different phases of stance. This pattern has been demonstrated explicitly for plantigrade running (Carrier et al., 1994; Braunstein et al., 2010) but only to a limited extent in walking in adults and has never been explored as a function of behavioral and anatomical changes during development. This area has further implications beyond that of pedal evolution and can apply to our understanding of developmental patterns, foot injury, and pathology.

Here, we test the hypothesis that modern adult foot strike pattern and relative foot stiffness allow for variable gearing mechanics at the ankle during walking. We use an ontogenetic approach and compare young adult heel strike walking steps to those of children who use an immature heel strike (initial heel contact but with some mechanical differences from adults; Hallemans et al., 2003; Zeininger et al., 2018) and children who lack a defined heel strike (flat foot contact).

Background

Torques on both sides of the joint must be balanced to maintain a stable ankle posture in which there is no angular change. Thus, in static or quasi-static settings, the product of the triceps surae muscle force (Fm) and triceps surae moment arm (r) to the ankle joint will equal the product of the magnitude of the ground reaction force resultant (GRFr) and the GRFr moment arm (R) from the point of force application to the ankle. Throughout the stance phase in running and walking, in which the ankle angle position changes, the relationships among these variables are constantly changing to accommodate ankle dorsiflexion during weight acceptance and plantarflexion during the propulsive phase of stance. While r is anatomically relatively constrained, allowing little change during stance, R has the potential to change significantly during a step (Carrier et al., 1994). Humans can actively change (a) the location of the COP (the anchor point of the GRFr) under the foot or (b) the orientation of the GRFr, both of which adjust the distance of R. Resultant changes in the ratio R/r can affect ankle angular velocity, triceps surae muscle stretch, and ankle torque. R is susceptible, however, to constraints induced by foot posture. For example, many cursorial mammals that run and walk with a forefoot strike and an elevated heel in a digitigrade foot posture experience a limited range of ankle R (Carrier et al., 1998) compared to animals with a plantigrade posture. Digitigrade postures align the ankle more closely with the COP and GRFr and reduce R. Digitigrady, therefore, provides relatively high ankle effective mechanical advantage (EMA, r/R) and minimizes the Fm required to maintain ankle posture (Smith and Savage, 1956; Biewener, 1989; Biewener, 1990; Biewener et al., 2004; Polk, 2004), but it also constrains the gear ratios possible for such animals.

High values of EMA may not always be advantageous when working to move heavy loads at low ankle velocity (Bojsen-Møller, 1978; Bojsen-Møller, 1979). In these situations, animals with posturally flexible feet and toes may choose to increase R throughout the stance phase by using a plantigrade foot posture and allowing the COP to translate away from the ankle and toward the distal toes. Adjusting R throughout stance varies the ratio of R to r from touchdown to toe-off (Smith and Savage, 1956; Bojsen-Møller, 1978; Bojsen-Møller, 1979; Carrier et al., 1994).

Carrier et al. (1994) were among the first to express this ratio in terms of a “gear ratio” and use that idea to suggest that the human foot, unlike the feet of other animals, could engage in variable gearing during stance. They used this concept to explain the length of the human foot and toes as an evolutionary mechanism to allow changing gears (Carrier et al., 1994). To date, no data on foot gearing in nonhuman primates, especially the large apes with their plantigrade feet, are available.

In this model, the length of the moment arms around the ankle is considered in terms of two gears working together (Smith and Savage, 1956). A low gear ratio in which the GRFr gear (R, gear 2) is small relative to the muscle gear (r, gear 1) provides low torque, low load movement (e.g., the fast spin of the pedal crank on a bike in low gear) and very little rotation of gear 2 (Figure 1). In this case, it is possible to move the joint quickly, as might be useful in rapid acceleration (Bojsen-Møller, 1978; 1979; Shorten et al., 1990; Carrier et al., 1994; Erdemer and Piazza, 2002). A high gear ratio in which gear 2 is large relative to gear 1 provides high torque, high load movement, and a lot of gear 2 rotation (e.g., a bike in high gear in which each rotation of the pedal crank provides a large rotation of the gears that move the chain and wheels) (Figure 1). Gear 2 can also operate on gear 1 and move the joint such that the opposing muscle is stretched, muscle fiber cross-bridges are placed in a relatively efficient position, and/or energy is stored in tendons, which is especially useful during the early stance phase (Carrier et al., 1994).

Figure 1

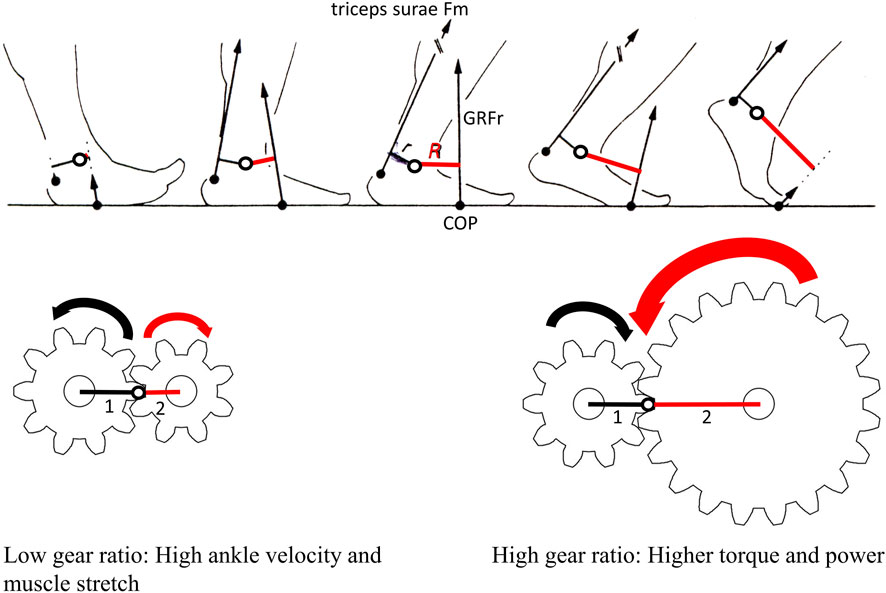
Figure 1. Gear ratios. Changes in the center of pressure (COP, black dot), ground reaction force resultant (GRFr) magnitude and orientation, and GRFr moment arm (R. red line), all relative to ankle position (white circle with black outline), as well as triceps surae muscle force (Fm) line of action and triceps surae moment arm (r, black line) throughout the stance phase in steady-state running (image modified from Carrier et al. [1994]). As the center of pressure moves distally beneath the foot, the triceps surae gear (gear 1) around the ankle stays relatively constant, but the GRFr gear (gear 2) increases. During early stance in human running, the gear ratio (R/r) is low, with high ankle velocity, low torque, and triceps surae muscle stretch, as gear 1 is driven by gear 2 (represented in the direction of black and red arrows). During the propulsive phase of stance, the gear ratio shifts to a high gear with lower velocity but higher torque as the small gear 1 drives the larger gear 2 (represented in the direction of black and red arrows).

Accelerating runners who land with a forefoot strike cannot take advantage of variable gearing at the ankle because of the limited possible range of change in R, while steady-state human runners who land with a plantigrade foot translate the COP along a larger proportion of their foot length and make use of variable gearing (Carrier et al., 1994). Steady-state runners have a relatively small R and low gear ratio during early stance, at which time the triceps surae muscles are stretched, and energy is stored in their calcaneal tendon (i.e., there is a negative muscle–tendon shortening velocity [MTV]) (Carrier et al., 1994). The gear ratio remains relatively low (i.e., EMA is relatively high) at midstance when the COP is under the midfoot. Translation of the COP to the toes allows for a large R, high gear ratio, increased Fm, positive MTV, and a toe-off at the end of the stance phase (Carrier et al., 1994). In modeling the absence of variable gearing (i.e., when the relatively low R/r at midstance was held constant throughout stance), Carrier et al. (1994) found that runners would have less triceps surae stretch and less calcaneal tendon energy storage during early stance and would require a higher MTV to power toe-off. Thus, plantigrady and translation of the COP from the heel to toe and the use of variable gearing appear to optimize triceps surae muscle mechanics during steady-state human running.

Similar to steady-state running, during walking, adult humans land with a dorsiflexed ankle and a plantigrade foot, initiating contact at the heel (heel-strike plantigrady). The COP translates along a large proportion of the adult human foot length, from heel to toes (Elftman and Manter, 1935; Grundy et al., 1975), as the foot transforms into a relatively rigid lever for a propulsive hallucial toe-off. As in plantigrade running, adult human walking makes use of variable gearing; R increases throughout the stance phase, and gear ratios vary from low during weight acceptance and midstance to high during the propulsive phase (Karamanidis and Arampatzis, 2007). Added stiffness (via stiff shoes and insoles) increases the gear ratio but reduces the plantarflexor shortening length, reduces the EMA, and therefore increases metabolic cost (Takahashi et al., 2016).

Older adults (60–69 years of age) with age-related degeneration in triceps surae muscle strength (Karamanidis and Arampatzis, 2007) may adjust their foot posture at contact to reduce triceps surae Fm required to maintain ankle posture. Compared to young adults (21–32 years of age), older adults have a less dorsiflexed ankle at foot contact (Boyer et al., 2017) and a more flat foot landing approach (Winter et al., 1990) that may position the COP near the ankle at foot contact, thereby reducing R and lowering R/r (i.e., increasing EMA) during weight acceptance and midstance (Karamanidis and Arampatzis, 2007).

The stepping characteristics of older adults (see Boyer et al., 2017 for a review) share similarities with young children, including a more flat-foot landing approach. Co-activation of the triceps surae and tibialis anterior during walking prohibits ankle dorsiflexion at foot contact (Myklebust, 1990), and as such, young children with around 4 months of walking experience (16 months of age on average) use a flat foot contact (FFC). In FFC steps, the COP is anterior to the heel or under the anterior portion of the heel during contact and weight acceptance (Zeininger et al., 2018). As reciprocal recruitment of the triceps surae and tibialis anterior develops with age, children transition from using a FFC to an initial heel contact (IHC; an average of around 22 months walking experience, 34 months of age on average) in which the COP is under the heel during contact and weight acceptance (Zeininger et al., 2018). FFC steps lack a heel-to-toe rollover of the COP (Hallemans et al., 2003). Although IHC steps have a heel-to-toe rollover, the COP does not translate under the entire foot length in these young children (Hallemans et al., 2006). Ankle plantarflexion is limited in young children (Hallemans et al., 2005) and passive until approximately 7 years of age (Sutherland et al., 1980), as the whole body center of mass moves anteriorly over the foot. Ankle power is also limited (Hallemans et al., 2005), a feature that may be associated with the lack of a longitudinal arch and, thus, a more mobile and less rigid midfoot than in adults (Bertsch et al., 2004). Rather than a powerful toe-off, forward progression into the swing phase is initiated by high degrees of flexion and power generation at the hip (Hallemans et al., 2005).

Ontogenetic differences in the location of the COP at foot contact and midfoot mobility offer the opportunity to test the effects of foot strike pattern and relative foot stiffness on translation of the COP and ankle gearing mechanics during walking in young children and adults. We predict that in FFC steps of young children, the anterior location of the COP at contact positions the GRFr close to the ankle joint and results (as in older adults) in a relatively short and positive (anterior to the ankle) R, low gear ratio (i.e., high EMA), and a negative MTV to store energy in the calcaneal tendon during weight acceptance (Figure 2). During contact and weight acceptance in both IHC and young adult heel-strike (AHS) steps, we predict that a more posterior COP (presumably posterior to the ankle joint) and a more posteriorly directed GRFr (Zeininger et al., 2018) will result in a negative (posterior to the ankle) R, potentially higher gear ratio, and higher (but still negative) MTV than in FFC steps (Figure 2). In other words, if the foot strike pattern influences ankle gearing, then during the weight acceptance phase, we expect to find differences in ankle gearing mechanics between FFC steps and IHC/AHS steps, but not between AHS and IHC steps. If a relatively stiff foot allows the COP to translate away from the ankle to the distal toes, then we predict that the COP will translate farther in AHS steps than in either FFC or IHC steps because younger children have a relatively mobile midfoot, but we predict no differences between FFC and IHC steps. Compared to FFC and IHC steps, we predict a longer R, higher gear ratio, larger Fm, and larger positive MTV during the propulsive phase in AHS steps, allowing for a propulsive hallucial toe-off (Figure 2). These hypotheses address the larger questions of the mechanics of human walking and the developmental timing and mechanical associations of features of human walking.

Figure 2

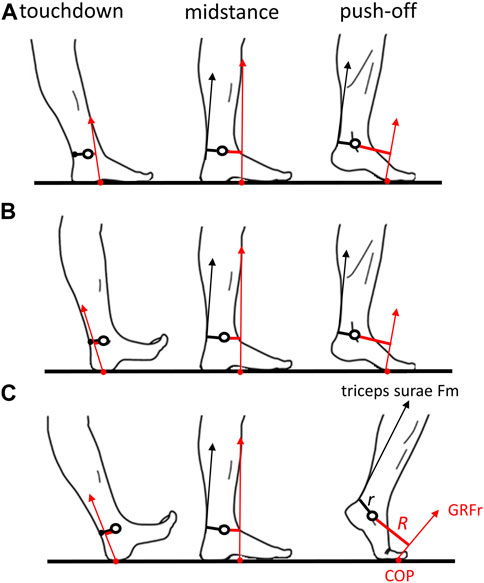
Figure 2. Predicted center of pressure (COP), triceps surae muscle force (Fm), and ground reaction force resultant (GRFr) moment arm (R) throughout stance. (A) Flat foot contact in the youngest children. At touchdown, R is predicted to be anterior to the ankle. The COP is predicted to translate anteriorly but not all the way to the distal hallux at push-off. (B) Initial heel contact in older children. At touchdown, R is predicted to be posterior to the ankle. The COP is predicted to translate anteriorly but not all the way to the distal hallux at push-off. (C) Adult heel strike. At touchdown, R is predicted to be posterior to the ankle. The COP is predicted to translate anteriorly all the way to the distal hallux at push-off. Image modified from Cunningham et al. (2010).

Materials and methods

Subject participation was approved by the Institutional Review Board of the University of Texas at Austin. Informed consent was obtained by participants or their legal guardian. Data were collected on seven adults and eighteen children (Table 1) at the Developmental Motor Control Laboratory in the Department of Kinesiology and Health Education at the University of Texas at Austin. For adults, kinematic data were collected at 60 Hz with a five-camera Vicon 250 motion analysis system (1272x1024 pixel resolution). Kinematic data on children were collected at 120 Hz via a 10-camera Vicon MX (Vicon, Centennial, CO) motion analysis system. Both Vicon systems were synchronized with two Bertec force plates (Bertec, Columbus, OH). Reflective markers were placed on the greater trochanter, lateral tibial condyle, lateral malleolus, fifth metatarsal head, and hallucial distal phalanx. For the lab, the coordinate system was: x = mediolateral, y = fore-aft, and z = vertical. For adults, foot length was measured on the subjects as the distance from the distal hallux to the posterior aspect of the heel. Using the coordinates of the hallucial distal phalanx marker, a virtual calcaneal marker was created where calcaneus x = hallucial distal phalanx x, calcaneus y = hallucial distal phalanx y − foot length, and calcaneus z = hallucial distal phalanx z. In children, an expanded foot marker set included a proximal calcaneus marker and a marker at the calcaneal tendon insertion (modified from Stebbins et al., 2006; see Zeininger et al., 2018). At the end of each session, body weight was measured with a standing spring balance.

Table 1

Table 1. Means and ranges of subject information.

Barefoot subjects walked, unassisted, at a self-selected speed over two adjacent force plates that recorded GRFs at 600 Hz in adults and 1,200 Hz in children. Only trials in which one foot was on the plate at a time were used for this analysis. Data were reconstructed in Vicon Workstation for adults and Vicon Nexus 1.8.2 (Vicon, Centennial, CO) for children. Raw kinematic and kinetic data were filtered using a fourth-order zero-lag phase Butterworth low-pass filter with a cut-off frequency of 12 Hz (kinematic) or 100 Hz (kinetic), as determined following methods of Winter (2005). Vertical, horizontal, and mediolateral ground reaction forces were used to calculate the GRFr magnitude.

The foot strike pattern was determined visually following methods by Zeininger et al. (2018). The relative position of the COP beneath the foot was determined as the distance from the heel to the COP as a proportion of the total foot length. Total foot length was measured from the posterior calcaneus (0% foot length) to the hallucial distal phalanx (100% foot length). To account for differences in hind limb length, speed was assessed as the Froude number (√[v2/gh]), where v is the velocity (hip displacement over stance duration), g is the acceleration of gravity (9.8 m/s²), and h is hind limb length (thigh length + leg length + foot length) (Hof, 1996; Raichlen, 2005).

The GRFr moment arm (R) was measured as the perpendicular distance from the lateral malleolus to the line of action of the GRFr. In children, the calcaneal tendon moment arm (r) was measured as the perpendicular distance from the lateral malleolus to the line of action of the calcaneal tendon, represented by the two calcaneal markers. Adults did not have calcaneal tendon markers; thus, we used data published for r (Sheehan, 2012; compiled from Leardini and O'Connor, 2002; Maganaris, 2003; Magnusson and Kjaer, 2003; Rugg et al., 1990) to create a regression equation for r and ankle angle. In our subjects, ankle angle was measured as the internal angle formed between the leg (lateral tibial condyle to lateral malleolus) and foot (lateral malleolus to 5th metatarsal head), and the value of r throughout the stance phase was calculated from the regression equation. The gear ratio was then calculated as R/r. Using R, r, and GRFr, we calculated the triceps surae muscle force (Fm) required to maintain ankle posture. To normalize Fm, we divided it by body weight for each subject. Triceps surae MTV was calculated as the product of r and the instantaneous ankle angular velocity (change in ankle angle [foot relative to shank] in radians divided by change in time). Following Carrier et al. (1994), we also modeled the MTV required in the absence of variable gearing by dividing the instantaneous ankle-to-toe velocity (instantaneous R times the instantaneous ankle angular velocity) by a low gear ratio, fixed at 50% of stance phase. In addition, we modeled MTV with a high gear ratio, fixed at 75% of the stance phase, to explore the possible advantages and disadvantages of maintaining a high gear ratio throughout the stance.

To normalize for different stance durations across trials, data for the COP position, R/r, Fm, and MTVs were analyzed in 5% intervals throughout stance phase. The COP position, R/r, and Fm at 5% (contact), 50% (midstance), and 95% (push-off) of stance and magnitude and timing of peak R/r, peak Fm, and minimum and maximum MTV were compared between AHS, IHC, and FFC using ANCOVA with Froude number as a covariate in JMP^®, Version Pro (SAS Institute Inc., Cary, NC, 1989–2019). Although some heel compression and triceps surae tendon stretch may occur in the first 5% of stance (Schmitt and Larson, 2005; Addison and Lieberman, 2015), we chose to not analyze force data before 5% of stance because of low GRF and the potential for error in the R calculation (Karamanidis and Arampatzis, 2007). Within each foot strike pattern, observed MTV was compared to models of MTV fixed at 50% of stance and MTV fixed at 75% of stance using an ANCOVA with Froude number as a covariate in JMP. When results were significant at p <0.05, Tukey HSD tests were run. The effect size for the comparisons was calculated using Cohen’s d for a three-sample comparison (Lakens, 2013).

Results

A total of 100 steps (AHS = 35; IHC = 26; FFC = 39) were analyzed (Table 1). At 5% of stance (contact), COP position differed significantly across foot strike patterns (p < 0.0001), with the COP significantly more distal in FFC steps than in IHC (p < 0.0001) or AHS steps (p = 0.0325), and more distal in AHS steps than in IHC steps (p = 0.0259) (Table 2; Figure 3). At 50% of stance (midstance), during weight acceptance, the COP also differed significantly across foot strike patterns (p < 0.0001), with a more distal COP in AHS steps than in IHC (p = 0.0122) and FFC steps (p < 0.0001). However, there were no significant differences between the IHC and FFC steps (p = 0.1433) at 50% of stance. That pattern of distal progress continued throughout stance with significant differences at 95% of stance (push-off) (p < 0.0001). The COPs for AHS steps were significantly more distal than those of IHC (p = 0.0023) and FFC (p < 0.0001) steps, with no significant differences between IHC and FFC steps (p = 0.3389) at 95% of stance. From 5% to 95% of stance, the COP translated an average of 70% of full foot length in AHS, 66% of foot length in IHC steps, and only 49% of foot length in FFC steps (Figure 3). For the COP position, all effect sizes were greater than 0.9 for all comparisons at 5% of stance. For COP position at 50% and 95% of stance, all effect sizes for AHS to IHC and AHS to FFC were greater than 0.9. However, at those same points, comparisons of COP position in IHC to FFC were nonsignificant and had small effect sizes (less than 0.2).

Table 2

Table 2. Means and standard deviations for each variable.

Figure 3

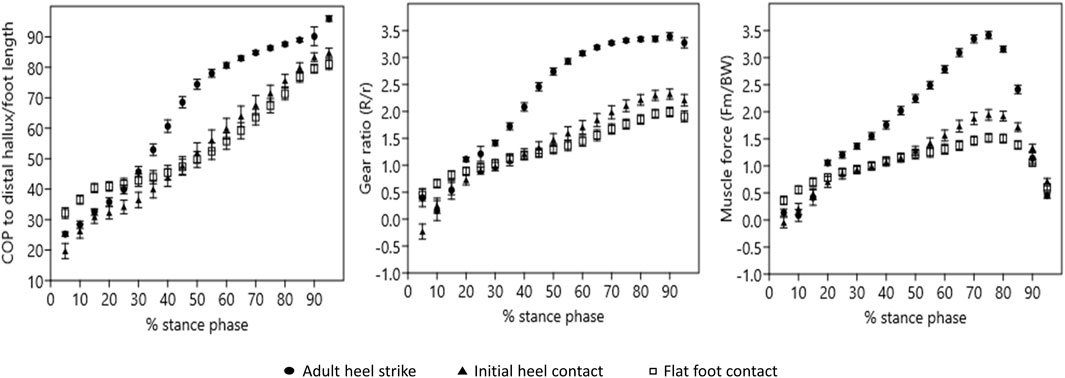
Figure 3. Position of the center of pressure (COP), gear ratios, and triceps surae muscle force throughout stance. For each graph, means and standard errors are plotted in 5% intervals throughout stance phase. For all variables, the pattern of change throughout stance phase in adult heel-strike steps differs from that of initial heel contact and flat foot contact steps.

The gear ratio (R/r) at 5% of stance differed significantly across foot strike patterns (p = 0.0021), with a significantly lower R/r in IHC steps than in AHS steps (p = 0.0064) or FFC steps (p = 0.0032) steps but no significant differences between AHS steps and FFC steps (p = 0.9993) (Table 2; Figure 3). This pattern reflects the fact that at the early, low gear ratio stage (all less than 0.5), the R/r for IHC steps was negative while the others were positive (Table 2). At 50% of stance, R/r differed significantly across foot strike patterns (p <0.0001). R/r was significantly higher in AHS steps than in IHC (p < 0.0001) and FFC (p < 0.0001) steps at 50%, but there were no significant differences between IHC and FFC steps (p = 0.1180). This same pattern of significant differences across foot strike patterns was also true for 95% of stance (p < 0.0001), with R/r significantly higher in AHS steps than in IHC (p < 0.0001) or FFC (p < 0.0001) steps but no significant differences between IHC and FFC steps (p = 0.2820). Average peak R/r occurred at 90% of stance in all foot strike patterns; however, peak R/r magnitude differed significantly across foot strike patterns (p < 0.0001). Peak R/r magnitude was significantly higher in AHS steps than in IHC (p < 0.001) and FFC (p < 0.0001) steps, but there were no significant differences between IHC and FFC steps (p = 0.0671). For R/r, effect sizes were small (less than 0.3) for all comparisons at 5% of stance. However, later in stance, comparisons of AHS to IHC and AHS to FFC were strong (greater than 0.6 at both 50% of stance and at peak and greater than 0.5 at 95% of stance), but the effect sizes for IHC to FFC were small (less than 0.3) at all those same points.

The triceps surae muscle force (Fm) at 5% of stance differed significantly across foot strike patterns (p = 0.0036), with a significantly lower Fm in IHC steps than in FFC steps (p = 0.0024). However, there were no significant differences between AHS and IHC (p = 0.1527) or AHS and FFC (p = 0.2749) steps (Table 2; Figure 2). At 50% of stance, Fm differed significantly across foot strike patterns (p < 0.0001). Fm was significantly higher in AHS steps than in IHC (p < 0.0001) and FFC (p < 0.0001) steps at 50%, but there were no significant differences between IHC and FFC (p = 0.8220) steps. Average peak Fm occurred at 75% of stance in all foot strike patterns; however, peak Fm magnitude differed significantly across foot strike patterns (p < 0.0001). Peak Fm magnitude was significantly higher in AHS steps than in IHC (p < 0.0001) or FFC (p < 0.0001) steps (p < 0.0001), and Fm was significantly higher in IHC steps than in FFC steps (p < 0.0100). By 95% of stance, Fm converged, and there were no significant differences across foot strike patterns (p = 0.0815). All effect sizes for comparisons of Fm were weak (less than 0.2) at 5%, including for IHC vs. FFC, despite statistical significance (p = 0.0024). However, all effect sizes for comparisons of Fm at 50% of stance and peak were small or medium (greater than 0.4 and 0.5, respectively) for comparisons of AHS to IHC and AHS to FFC, but small (less than 0.2) for IHC vs. FFC despite a p-value of 0.01 for that comparison at peak.

MTV was negative (i.e., the calcaneal tendon was stretched) during early stance in all foot strike patterns (Figure 4). Average minimum MTV (maximum stretch) differed in timing and magnitude (p = 0.0015) across foot strike patterns (Table 2). Minimum MTV occurred at 15% of stance in AHS steps, 10% of stance in IHC steps, and 5% of stance in FFC steps (Figure 4). At minimum MTV, FFC steps had significantly more muscle stretch than AHS steps (p = 0.0010), but there was no significant difference between FFC and IHC (p = 0.410) or between IHC and AHS (p = 0.1000) steps (Table 2). Maximum MTV occurred at 95% of stance in all groups, and there were no significant differences in magnitude across foot strike patterns (p = 0.9774) (Table 2). For MTV, effect sizes for comparisons of AHS to IHC and AHS to FFC were strong (greater than 0.9), while effect sizes for comparisons of IHC to FFC were small (0.4).

Figure 4

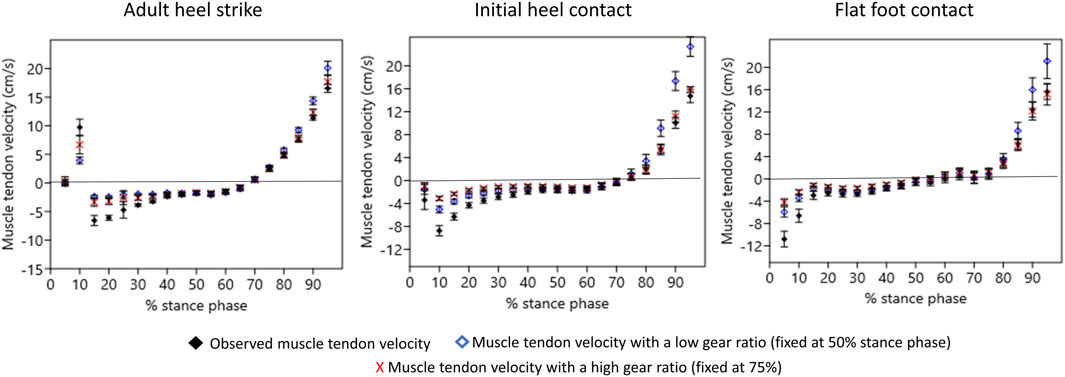
Figure 4. Muscle–tendon shortening velocity. For each foot strike pattern, means and standard errors are plotted in 5% intervals throughout the stance phase. Observed muscle–tendon velocity is compared to muscle-tendon velocity fixed at a low gear ratio (at 50% of stance) and fixed at a high gear ratio (at 75% of stance). Negative velocities indicate that the triceps surae muscle fibers or tendon are being stretched, and there is the potential for energy to be stored in the calcaneal tendon. Positive velocities indicate that the triceps surae muscle is actively shortening.

Within each foot strike pattern, the observed minimum MTV differed significantly from that of the minimum modeled MTV fixed at 50% or 75% (AHS p < 0.0001; IHC p < 0.0001; FFC p = 0.0002) (Table 2). For each foot strike pattern, the observed minimum MTV was significantly lower (i.e., the triceps surae was stretched more) than the minimum modeled MTV fixed at 50% (AHS p < 0.0010; IHC p < 0.0010; FFC p =0.0630) or 75% (AHS p 0.0062; IHC p < 0.0001; FFC p = 0.0020) (Figure 4; Table 2). However, within each foot strike pattern, the minimum modeled MTV fixed at 50% and fixed at 75% did not differ significantly (AHS p = 0.4128; IHC p = 0.1636; FFC p = 0.5832). In AHS and IHC steps, the maximum observed MTV differed significantly from that of the minimum modeled MTV fixed at 50% or 75% (AHS p < 0.0001; IHC p = 0.0004). In AHS steps, the maximum modeled MTV fixed at 50% was significantly higher than the observed maximum MTV (p = 0.0403) but was not significantly different from that modeled at 75% (p = 0.7077), and there were no significant differences between the maximum modeled MTVs fixed at 50% and 75% (p = 0.2204). In IHC steps, the maximum modeled MTV fixed at 50% was significantly higher than the observed maximum MTV (p = 0.0007) and the maximum modeled MTV fixed at 75% (p = 0.0040), but there were no significant differences between the observed maximum MTV and the maximum modeled MTV fixed at 75% (p = 0.8500). However, no significant differences were found between the maximum observed and modeled MTV at 50% or 75% in FFC steps (p = 0.1000).

In AHS, comparisons of minimum observed MTV against modeled MTV fixed at 50% and 75% effect sizes were medium or large (1.12 and 0.7, respectively). In AHS, when the maximum observed MTV was compared to the modeled MTV, the effect sizes were large (0.9) for 50% and small (0.2) for 75%. In IHC, for the minimum observed MTV against the modeled MTV fixed at 50% and 75%, effect sizes were large (1.0 and 1.3, respectively). In IHC, when the maximum observed MTV was compared to the modeled MTV, effect sizes were large (1.15) for 50% and small (0.23) for 75%. In FFC, for comparisons of the minimum observed MTV against the modeled MTV fixed at 50% and 75%, the effect sizes were medium or large (0.7 and 0.9, respectively). In FFC, when the maximum observed MTV was compared to the modeled MTV, the effect sizes were large (0.96) for 50% and medium (0.8) for 75%.

Discussion

This study addresses questions about locomotor development and pedal evolution by exploring the association of anatomical changes in the foot with the onset of adult-like foot mechanics, specifically, the specialized modern human trait of utilizing variable gearing (the ratio of ground reaction force moments [R] to calf muscle moments [r]). We found that there is a predictable change in foot gearing with changes in anatomy and behavior and that these differences may predict foot mechanics of living apes, early hominins, and modern humans.

In AHS walking steps, we found that, on average, the COP translated beneath 70% of the full foot length from heel strike to toe-off. The ankle gear ratio changed from relatively low (<1) during early stance to relatively high (>3) during late stance in AHS steps. These ankle gear ratios are consistent with those previously reported for young adult walking (Karamanidis and Arampatzis, 2007) and are within the range of gear ratios used during running (Carrier et al., 1994; Braunstein et al., 2010).

Our hypothesis that variable gearing at the ankle is enhanced by the use of a heel strike during walking regardless of age (AHS or IHC) was not fully supported. Instead, it appears that variable gearing is enhanced by heel strike in adults and is less well-demonstrated in early walkers using a heel contact pattern. Although gear ratio changed throughout stance in IHC steps, the degree of change in gear ratio, from <1 at 5% to just over 2 at its peak, was reduced in IHC steps compared to AHS steps but was similar to the degree of change we observed in FFC steps (Figure 3; Table 2). The distinction between AHS and IHC/FFC in gear ratio may be related to anatomical differences between juvenile and adult feet, including a less stiff midfoot in children. The relatively small number of steps with a negative gear ratio in adults may suggest that analyzing 5% of the stance phase underestimated the degree of change in gear ratio throughout stance in adults.

Our hypothesis that a heel strike and a stiff midfoot (AHS) with a powerful, hallucial toe-off would be linked with the use of variable gearing was strongly supported. As predicted, at 5% of stance in AHS steps, the COP was beneath the proximal foot, the ankle gear ratio was relatively low (although not as low as in IHC steps), and Fm was relatively low (i.e., EMA was high) (Figure 3). The COP translated distally relatively quickly, such that it was generally beneath the forefoot by 50% of stance and beneath the hallucial distal phalanx at 95% of stance in AHS steps (Figure 3). This rapid translation of the COP resulted in an equally rapid increase in R/r and Fm (Figure 3). A relatively high peak R/r, Fm, and a positive MTV allowed for a propulsive hallucial toe-off in AHS steps. Although the COP did not translate as far distally in IHC steps as it did in AHS steps, a significantly higher peak Fm in AHS and IHC than in FFC steps indicates that the ankle contributes more to a powerful toe-off when a heel strike is used. These results also suggest that a heel strike and powerful toe-off may be linked developmentally. Future studies that take into account the mediolateral position of the COP under the forefoot at toe-off are needed to confirm whether toe-off is, indeed, hallucial in IHC and FFC steps.

For all foot strike patterns, observed muscle–tendon shortening velocity followed the same pattern, and this walking pattern matched that of steady-state running (Carrier et al., 1994). During early stance, MTV was negative as the triceps surae muscle was stretched, and during late stance, MTV was positive, indicating that the muscle was contracting and helping to power toe-off. Contrary to predictions, AHS steps had the least triceps surae stretch, and FFC had the most stretch (largest negative MTV magnitude) in early stance. The overall increased stretching of triceps surae and presumed energy storage within the calcaneal tendon in FFC steps may be particularly energetically efficient for young children who generate relatively little triceps surae muscle force at toe-off (Figure 2). Similarities in the MTV curves across foot strike types in children and adults suggest that sarcomere performance is similar in children and adults and that the rapidly growing feet of young children may limit the useful work that can be done at the ankle joint. In that light, the similarity of the shortening velocity curves might further support the argument that the structure of the feet of young children, as well as possibly nonhuman apes and early hominins, limits performance compared to modern adult human foot structure.

In modeling a fixed low and a fixed high gear ratio throughout stance, the results for walking steps were similar to those for steady-state running steps (Carrier et al., 1994). In all foot strike patterns, we found that a fixed low or high gear ratio would allow for less muscle-tendon stretch and energy storage during early stance and that, in AHS and IHC steps, a fixed low gear ratio would require a higher MTV to power toe-off. Thus, for all foot strike patterns, the observed MTV provided the most triceps surae muscle stretch and calcaneal tendon energy storage during early stance and the sufficient (but not excessive) MTV to power toe-off. Our results confirm Carrier et al.’s (1994) conclusion that the use of variable gearing appears to optimize triceps surae muscle mechanics (during steady-state running and now during walking); this is an advantage that is not exploited by digitigrade animals such as dogs (Carrier et al., 1998). Our results also suggest that humans who use a midfoot or forefoot strike (toe-walkers) would also lose the advantages of variable gearing at the ankle.

Carrier et al. (1994) postulated that the existence of feet and toes in tetrapods, especially humans, is essential for enabling variable gearing at the ankle and maintaining plantarflexion moments at the appropriate, efficient working range. Early hominins, however, also had long feet and toes (Stern and Susman, 1983) but most likely walked rather than ran when on the ground. Thus, the question remains: what selective advantages are provided by long feet and long toes? While these features may have been retained from an arboreal ancestor (Stern and Susman, 1983), the question remains whether long feet and toes were advantageous or a mechanical challenge. Long toes are thought to prevent great apes from using pedal digitigrady because bending moments on the long digits are predicted to be too high (similar to why great apes are thought to use knuckle-walking instead of manual digitigrady). Holowka and Lieberman (2018) and Zeininger et al. (2020) have argued that a heel strike with a complete heel-to-toe progression increases effective hind limb length (by placing the fulcrum beneath the ground) and effective hip translation and may moderate collisional losses (McGeer, 1990; Ruina et al., 2005; Adamczyk et al., 2006) in plantigrade apes compared to digitigrade monkeys. Here, we explore another potential advantage: variable gearing. The current study has shown that the same advantage provided by long feet and toes in plantigrade postures during running (Carrier et al., 1994) is accrued in walking and, in addition, that the use of variable gearing is enhanced by a heel-to-toe progression of the COP with a mature heel strike and a relatively stiff midfoot. This provides a deeper understanding of foot function and pathology and adds to a list of advantages of heel-strike plantigrady (Adamczyk et al., 2006; Cunningham et al., 2010; Webber and Raichlen, 2016), illuminating the evolution of hominin walking and running over the last seven million years.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the University of Texas at Austin IRB. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants or their legal guardians.

Author contributions

AZ: writing–review and editing, writing–original draft, project administration, methodology, investigation, and funding acquisition, formal analysis, data curation, and conceptualization. DS: writing–review and editing, writing–original draft, methodology, conceptualization. JJ: writing–review and editing, writing–original draft, supervision, resources, project administration, methodology, and conceptualization. LS: writing–review and editing, writing–original draft, supervision, resources, project administration, methodology, and conceptualization.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Leakey Foundation (AZ) and an NSF Doctoral Dissertation Improvement Grant (BCS-1028958 to AZ).

Acknowledgments

We thank Amber N. Heard-Booth, Kelly Manrriquez, Graham Noblit, Perla Santillan, and Renate Van Zandwijk-Rowley for assistance during data collection with the children. We are grateful to two reviewers whose suggestions greatly improved this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adamczyk, P. G., Collins, S. H., and Kuo, A. D. (2006). The advantages of a rolling foot in human walking. J. Exp. Biol. 209, 3953–3963. doi:10.1242/jeb.02455

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertsch, C., Unger, H., Winkelmann, W., and Rosenbaum, D. (2004). Evaluation of early walking patterns from plantar pressure distribution measurements. First year results of 42 children. Gait Posture 19, 235–242. doi:10.1016/s0966-6362(03)00064-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Biewener, A. A. (1989). Scaling body support in mammals: limb posture and muscle mechanics. Science 245, 45–48. doi:10.1126/science.2740914

PubMed Abstract | CrossRef Full Text | Google Scholar

Biewener, A. A. (1990). Biomechanics of mammalian terrestrial locomotion. Science 250, 1097–1103. doi:10.1126/science.2251499

PubMed Abstract | CrossRef Full Text | Google Scholar

Biewener, A. A., Farley, C. T., Roberts, T. J., and Temaner, M. (2004). Muscle mechanical advantage of human walking and running: implications for energy cost. J. Appl. Physiology 97, 2266–2274. doi:10.1152/japplphysiol.00003.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bojsen-Møller, F. (1978). The human foot—a two speed construction. Baltimore: University Park Press, 261–266.

Google Scholar

Bojsen-Møller, F. (1979). Anatomy of the forefoot, normal and pathologic. Clin. Orthop. 142, 10–18. doi:10.1097/00003086-197907000-00003

CrossRef Full Text | Google Scholar

Boonpratatong, A., and Ren, L. (2010). The human ankle-foot complex as a multi-configurable mechanism during the stance phase of walking. J. Bionic Eng. 7, 211–218. doi:10.1016/s1672-6529(10)60243-0

CrossRef Full Text | Google Scholar

Boyer, K. A., Johnson, R. T., Banks, J. J., Jewell, C., and Hafer, J. F. (2017). Systematic review and meta-analysis of gait mechanics in young and older adults. Exp. Gerontol. 95, 63–70. doi:10.1016/j.exger.2017.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Braunstein, B., Arampatzis, A., Eysel, P., and Brüggemann, G. P. (2010). Footwear affects the gearing at the ankle and knee joints during running. J. Biomechanics 43, 2120–2125. doi:10.1016/j.jbiomech.2010.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrier, D. R., Gregersen, C. S., and Silverton, N. A. (1998). Dynamic gearing in running dogs. J. Exp. Biol. 201, 3185–3195. doi:10.1242/jeb.201.23.3185

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrier, D. R., Heglund, N. C., and Earls, K. D. (1994). Variable gearing during locomotion in the human musculoskeletal system. Science 265, 651–653. doi:10.1126/science.8036513

PubMed Abstract | CrossRef Full Text | Google Scholar

Cunningham, C. B., Schilling, N., Anders, C., and Carrier, D. R. (2010). The influence of foot posture on the cost of transport in humans. J. Exp. Biol. 213, 790–797. doi:10.1242/jeb.038984

PubMed Abstract | CrossRef Full Text | Google Scholar

Elftman, H., and Manter, J. (1935). Chimpanzee and human feet in bipedal walking. Am. J. Phys. Anthropol. 20, 69–79. doi:10.1002/ajpa.1330200109

CrossRef Full Text | Google Scholar

Erdemir, A., and Piazza, S. J. (2002). Rotational foot placement specifies the lever arm of the ground reaction force during the push-off phase of walking initiation. Gait Posture 15, 212–219. doi:10.1016/s0966-6362(01)00192-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Grundy, M., Tosh, P. A., McLeish, R. D., and Smidt, L. (1975). An investigation of the centres of pressure under the foot while walking. J. bone Jt. Surg. Br. 57 (1), 98–103. doi:10.1302/0301-620x.57b1.98

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallemans, A., D’Aout, K., De Clercq, D., and Aerts, P. (2003). Pressure distribution patterns under the feet of new walkers: the first two months of independent walking. Foot Ankle Int. 24, 444–453. doi:10.1177/107110070302400513

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, O., Harper, D. A. T., and Ryan, P. D. (2024). PAST: paleontological statistics software package for education and data analysis. Paleontol. Electron. 4 (1), 9.

Google Scholar

Hof, A. L. (1996). Scaling gait data to body size. Gait Posture 4, 222–223. doi:10.1016/0966-6362(95)01057-2

CrossRef Full Text | Google Scholar

Holowka, N. B., and Lieberman, D. E. (2018). Rethinking the evolution of the human foot: insights from experimental research. J. Exp. Biol. 221, jeb174425. doi:10.1242/jeb.174425

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchinson, J. R., Delmer, C., Miller, C. E., Hildebrandt, T., Pitsillides, A. A., and Boyde, A. (2011). From flat foot to fat foot: structure, ontogeny, function, and evolution of elephant “sixth toes”. Science 334, 1699–1703. doi:10.1126/science.1211437

PubMed Abstract | CrossRef Full Text | Google Scholar

Karamanidis, K., and Arampatzis, A. (2007). Aging and running experience affects the gearing in the musculoskeletal system of the lower extremities while walking. Gait posture 25, 590–596. doi:10.1016/j.gaitpost.2006.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerr, B. A., Beuchamp, L., Fisher, V., and Neil, R. (1983). “Footstrike patterns in distance running,” in Biomechanical aspects of short shoes and playing surfaces (Calgary, Canada: University Printing), 135–142.

Google Scholar

Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs. Front. Psychol. 4, 863. doi:10.3389/fpsyg.2013.00863

PubMed Abstract | CrossRef Full Text | Google Scholar

Leardini, A., and O'Connor, J. J. (2002). A model for lever-arm length calculation of the flexor and extensor muscles at the ankle. Gait Posture 15, 220–229. doi:10.1016/s0966-6362(01)00153-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Maganaris, C. N. (2004). Imaging-based estimates of moment arm length in intact human muscle-tendons. Eur. J. Appl. Physiology 91, 130–139. doi:10.1007/s00421-003-1033-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Magnusson, P. S., and Kjaer, M. (2003). Region-specific differences in Achilles tendon cross-sectional area in runners and non-runners. Eur. J. Appl. Physiology 90, 549–553. doi:10.1007/s00421-003-0865-8

PubMed Abstract | CrossRef Full Text | Google Scholar

McGeer, T. (1990). Passive dynamic walking. Int. J. Robotics Res. 9, 62–82. doi:10.1177/027836499000900206

CrossRef Full Text | Google Scholar

Patel, B. A. (2010). The interplay between speed, kinetics, and hand postures during primate terrestrial locomotion. Am. J. Phys. Anthropol. 141, 222–234. doi:10.1002/ajpa.21138

PubMed Abstract | CrossRef Full Text | Google Scholar

Raichlen, D. A. (2005). Effects of limb mass distribution on the ontogeny of quadrupedalism in infant baboons (Papio cynocephalus) and implications for the evolution of primate quadrupedalism. J. Hum. Evol. 49, 415–431. doi:10.1016/j.jhevol.2005.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, L., Howard, D., Ren, L. Q., Nester, C., and Tian, L. M. (2008). A phase-dependent hypothesis for locomotor functions of human foot complex. J. Bionic Eng. 5, 175–180. doi:10.1016/s1672-6529(08)60022-0

CrossRef Full Text | Google Scholar

Rugg, S. G., Gregor, R. J., Mandelbaum, L. C., and Chiu, L. (1990). In vivo moment arm calculations at the ankle using magnetic resonance imaging (MRI). J. Biomechanics 23, 495–501. doi:10.1016/0021-9290(90)90305-m

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruina, A., Bertram, J. E., and Srinivasan, M. (2005). A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walk-to-run transition. J. Theor. Biol. 237, 170–192. doi:10.1016/j.jtbi.2005.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmitt, D., and Larson, S. G. (1995). Heel contact as a function of substrate type and speed in primates. Am. J. Phys. Anthropol. 96, 39–50. doi:10.1002/ajpa.1330960105

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheehan, F. T. (2012). The 3D in vivo Achilles' tendon moment arm, quantified during active muscle control and compared across sexes. J. Biomechanics 45, 225–230. doi:10.1016/j.jbiomech.2011.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Shorten, M. R., Eden, K. B., and Himmelsbach, J. A. (1989). Plantar pressures during barefoot walking. J. Biomechanics 22, 1083. doi:10.1016/0021-9290(89)90461-2

CrossRef Full Text | Google Scholar

Smith, J. M., and Savage, R. J. G. (1956). Some locomotory adaptations in mammals. Zoological J. Linn. Soc. 42, 603–622. doi:10.1111/j.1096-3642.1956.tb02220.x

CrossRef Full Text | Google Scholar

Stebbins, J., Harrington, M., Thompson, N., Zavatsky, A., and Theologis, T. (2006). Repeatability of a model for measuring multi-segment foot kinematics in children. Gait Posture 23, 401–410. doi:10.1016/j.gaitpost.2005.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Stern Jr, J. T., and Susman, R. L. (1983). The locomotor anatomy of Australopithecus afarensis. Am. J. Phys. Anthropol. 60, 279–317. doi:10.1002/ajpa.1330600302

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, K. Z., Gross, M. T., Van Werkhoven, H., Piazza, S. J., and Sawicki, G. S. (2016). Adding stiffness to the foot modulates soleus force-velocity behaviour during human walking. Sci. Rep. 6, 29870. doi:10.1038/srep29870

PubMed Abstract | CrossRef Full Text | Google Scholar

Webber, J. T., and Raichlen, D. A. (2016). The role of plantigrady and heel-strike in the mechanics and energetics of human walking with implications for the evolution of the human foot. J. Exp. Biol. 219, 3729–3737. doi:10.1242/jeb.138610

PubMed Abstract | CrossRef Full Text | Google Scholar

Winter, D. (2005). Biomechanics and motor control of human movement. Hoboken: John Wiley and Sons, Inc.

Google Scholar

Zeininger, A., Schmitt, D., Jensen, L. J., and Shapiro, L. J. (2018). Ontogenetic changes in foot strike pattern and calcaneal loading during walking in young children. Gait Posture 59, 18–22. doi:10.1016/j.gaitpost.2017.09.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeininger, A., Schmitt, D., and Wunderlich, R. E. (2020). Mechanics of heel-strike plantigrady in African apes. J. Hum. Evol. 145, 102840. doi:10.1016/j.jhevol.2020.102840

PubMed Abstract | CrossRef Full Text | Google Scholar