Can machine learning models predict soil moisture evaporation rates? An investigation via novel feature selection techniques and model comparisons

Extreme weather events and global climate change have exacerbated the problem of evaporation rates. Thus, accurately predicting soil moisture evaporation rates affecting soil cracking becomes crucial. However, less is known about how novel feature engineering techniques and machine-learning predictions may account for estimating the soil moisture evaporation rate. This research focuses on predicting the evaporation rate of soil using machine learning (ML) models. The dataset comprised twenty-one ground-based parameters, including temperature, humidity, and soil-related features, used as features to predict evaporation potential. To tackle the high number of features and potential uncorrelated features, a novel guided backpropagation-based feature selection technique was developed to rank the most relevant features. The top-10 features, highly correlated with evaporation rate, were selected for ML model input, alongside the top-5 and all features. Several ML models, including multiple regression (MR), K-nearest neighbor (KNN), multilayer perceptron (MLP), sequential minimal optimization regression (SMOreg), random forest (RF), and a novel K-Nearest Oracles (KNORA) ensemble, were constructed for the purpose of forecasting the evaporation rate. The average error of these models was assessed using the root mean squared error (RMSE). Experimental results showed that the KNORA ensemble model performed the best, achieving a 7.54 mg/h RMSE in testing with the top-10 features. MLP was followed closely by a 25.1 mg/h RMSE in the same testing. An empirical model using all features showed a higher RMSE of 1319.1 mg/h, indicating the superiority of the ML models for accurate evaporation rate predictions. We highlight the implications of our results for climate-induced soil cracking in the real world.

1 Introduction

In recent years, the frequency of extreme weather events has increased, exacerbated by global climate change, further aggravating the problem of evaporation rates (Robinson and Vahedifard, 2016). The evaporation rate is a complex phenomenon resulting from the interplay between soil and environmental factors (Morris et al., 1992). Soils are prone to drying due to atmospheric conditions like sunlight, airflow, temperature, radiation, and humidity. Additionally, human activities such as underground conduit installation, buried electrical cables, land burning, and improper disposal of toxic waste near the surface can contribute to soil desiccation. When soil loses moisture, it undergoes shrinkage, particularly evident in fine-grained soils (Kodikara et al., 1999). Constrained shrinkage leads to the development of internal stress within the soil, and if these stresses exceed the soil’s tensile strength, it results in soil cracking (Tao et al., 2005). These cracks, whether isolated or coalesced, negatively impact the hydraulic and mechanical properties of near-surface soils, making them vital factors in assessing various geotechnical hazards (Morris et al., 1992). The cracking of fine-grained soils has significant implications for construction activities, including hydraulic barriers, dams, clay liners, excavations, highway embankments, earth slopes, landfill top covers, and bottom seals (Yesiller et al., 2000).

The complex phenomenon of cracking in fine-grained soils may primarily be influenced by physical, chemical, and mineralogical characteristics. These include clay content, soil mineralogy, wetting and drying rates, cation exchange capacity, starting water content, density, temperature, and humidity (Uday et al., 2015). Extensive experimental studies have been conducted in this area to explore the cracking process by regulating the environmental variables as well as monitoring and recording the major crack parameters (Uday and Singh, 2012). Evaporation characteristics of the soil are used to determine the cracking potential, i.e., another essential parameter to map the response of the behavior of the soil under differing moisture conditions (Uday and Singh, 2013). Such an analysis is pivotal for analyzing the unsaturated behavior of soil, soil-root micromechanical properties, and erosion of the soil at the surface (Uday and Singh, 2013). In this context, Uday and Singh (2013) demonstrated the effect of exposure circumstances (temperature and humidity) and soil-specific characteristics (soil type and specimen geometry) on evaporation rate, which in turn influences fine-grained soil cracking (Uday and Singh, 2013). Furthermore, an empirical relationship based on these parameters was proposed to facilitate the computation of the evaporation rate from the measured parameters. Various Machine Learning (ML) models also have been developed to predict and detect the formation of cracks in the soils (Andrushia et al., 2022; Xu et al., 2022). The results of these ML models can be compared to existing analytic methods that are grounded in geotechnical engineering. Fine-grained soil cracking can also be controlled by controlling evaporation rates using appropriate materials (Naresh and Uday, 2018; Wanare et al., 2022).

In the literature related to ML in the geotechnical field, several ML models have been developed to investigate the influence of geotechnical factors on soil cracks (Yilmaz and Kaynar, 2011; Chou et al., 2016; Wani et al., 2021; Kardani et al., 2022; More et al., 2022; Nguyen et al., 2022; Verma et al., 2023). For instance, researchers have employed Random Forest (RF) models to study this phenomenon, while others have utilized K-nearest neighbor (KNN) models (Kardani et al., 2022; Verma et al., 2023). Additionally, support vector machine (SVM) models have been developed by various researchers for this purpose (Chou et al., 2016; More et al., 2022). Furthermore, multilayer perceptron (MLP) models have been explored by different researchers, and multiple regression (MR) models have also been investigated in relevant studies (Yilmaz and Kaynar, 2011; Wani et al., 2021; Nguyen et al., 2022). These various ML approaches offer valuable insights into understanding and predicting soil crack behaviors in geotechnical engineering.

Although various ML models have been created in the literature to forecast soil motions or other soil features, the prediction of soil moisture evaporation rate has yet to be attempted. The primary goal of this study is to design a unique feature selection technique and compare several ML models in terms of their capacity to forecast soil moisture evaporation rates, which can lead to desiccation cracking. First, we discuss the underlying literature on the utilization of various soil qualities and their impact on evaporation rate. Next, we rank the features relevant to soil moisture evaporation rate prediction by developing a novel feature selection technique. Then, we detailed the working of the ML models like RF, MLP, MR, SVM, and KNN models and found out the least RMSE value to data. Finally, we provide our findings from several models and analyze the consequences of their application.

2 Background

In the literature related to ML in the geotechnical field, several ML models have been developed to investigate the influence of geotechnical factors on soil cracks (Yilmaz and Kaynar, 2011; Chou et al., 2016; Kumar et al., 2019; Wani et al., 2021; Kardani et al., 2022; More et al., 2022; Nguyen et al., 2022; Verma et al., 2023). For instance, researchers have employed RF models to study this phenomenon, while others have utilized KNN models (Kumar et al., 2019; Kardani et al., 2022; Verma et al., 2023). Additionally, SVM models have been developed by various researchers for this purpose (Chou et al., 2016; More et al., 2022). Furthermore, MLP models have been explored by different researchers, and MR models have also been investigated in relevant studies (Yilmaz and Kaynar, 2011; Wani et al., 2021; Nguyen et al., 2022). A range of ML models provides valuable insights for comprehending and forecasting soil crack behavior within the field of geotechnical engineering. The study by Kardani employed various ensemble machine learning methods, such as voting, stacking, and bagging ensembles, to consolidate diverse model results (Kardani et al., 2022). After rigorous testing, the bagging ensemble emerged as the most effective tool for evaluating subgrade soil strength. This research underscores the significance of ensemble methods in accurately predicting MR, contributing to safer and more sustainable pavement design practices. Several authors investigate the prediction of debris flow at the Tangni landslide in Uttarakhand state, a landslide-prone region (Kumar et al., 2019). In this study, the author utilized a combination of ensemble models (RF, Bagging, Stacking, and Voting) and non-ensemble models (Sequential Minimal Optimization regression-SMOreg, and Autoregression) to forecast weekly debris flow incidents spanning 2013 to 2014. The results showed that ensemble models, particularly Bagging, Stacking, and RF, outperformed the non-ensemble models. In other research efforts, computational algorithms were explored to predict California Bearing Ratio (CBR) values for saturated soil conditions (Verma et al., 2023). Various methods, including Kernel Ridge Regression, KNN, and Gaussian Process Regression (GPR), were investigated. A substantial dataset comprising 1011 in-situ soil samples from a highway construction site was collected for the study. The study identified key input parameters such as Sand content, Fine Content, Plastic Limit (PL), Plasticity Index, Maximum Dry Density, and Optimum Moisture Content as the most influential factors affecting the CBR of fine-grained plastic soils when saturated. The experimental results validated the efficacy of KNN and GPR models created using K-Fold and FCM data partitioning techniques. Additionally, it was observed that the geographical origin of the soils or materials used for model development influenced predictive accuracy.

Furthermore, to address the shortcomings of previous models in forecasting FRS shear strength, various researchers gathered a comprehensive database of triaxial and direct shear experiments on fiber-reinforced soil (FRS) (Chou et al., 2016). Using data mining techniques, including SVM, the study identifies influential factors and predicts the peak friction angle of FRS. The SVM model emerges as the optimal model, achieving a strong association with the measured values (correlation coefficient of 0.89). The model’s performance shows significant improvement compared to other reported models, contributing valuable insights for predicting FRS behavior in soil engineering. In a recent study, researchers investigated the application of 3 ML models, namely, Extreme Learning Machine (ELM), SVM, and Adaptive Neuro-Fuzzy Inference System (ANFIS), to construct Pedotransfer Functions (PTFs) for the estimation of saturated hydraulic conductivity (Kfs) based on fundamental soil parameters (More et al., 2022). Among these models, SVM demonstrated notable performance, yielding relatively high Nash-Sutcliffe Efficiency (NSE) values. The SVM model outperformed other models with remarkable NSE values. In particular, at the Murarji Peth and Punanaka locations, the SVM model demonstrated strong predictive performance, achieving NSE values of 0.90 and 0.83, respectively. Meanwhile, the ANFIS model yielded promising results at the Mulegoan site, with a correlation coefficient (R) of 0.80 and an NSE of 0.64.

This research also investigated the application of neural networks, notably MLP and Adaptive Neuro-Fuzzy Inference System (ANFIS), for forecasting soil swell percent (S%) (Yilmaz and Kaynar, 2011). The standard MR statistical model is also compared. The results demonstrate that the developed Radial Basis Function (RBF) outperformed MLP, ANFIS, and MR in predicting S%. The paper emphasizes the effectiveness of soft computing techniques, such as MLP, in reducing uncertainty in soil engineering projects and providing novel approaches to handle potential discrepancies in correlations. In a similar vein, this research focused on the prediction of swelling potential in fine-grained soils, a factor that can significantly influence the stability of geotechnical infrastructure (Nguyen et al., 2022). ML models, including MLP, Gaussian Process (GP), and Bagging-MLP neural networks, were trained using site-specific data from residual soils along Vietnam’s Mong Cai-Van Don highway. These models utilized basic soil index indicators such as particle size distribution and Atterberg limits to assess swelling potential. Among the various models evaluated, the Bagging-MLP model demonstrated the highest level of predictive accuracy, underscoring the potential of data-driven approaches in supporting geotechnical design.

Several researchers also helped to create the MR model for assessing crack intensity in biochar-amended soils (BAS) (Wani et al., 2021). They evaluated the influence of several parameters on crack propagation using MR analysis, including compaction state, PL, liquid limit (LL), biochar concentration (%), and soil-specific gravity. The study’s findings demonstrated that wood biochar (WB) was more resistant to crack propagation than pig manure biochar (PMB). The MRM also revealed that increasing biochar content reduced crack intensity, although specific gravity and PL impacted crack intensity, with WB having more apparent impacts than PMB. When basic soil parameters are known, the suggested MRM provides a valuable tool for predicting crack intensity in BAS samples, providing useful insights for geotechnical engineering and soil improvement activities.

Prior studies aimed to predict various geotechnical properties of soils, which are crucial for engineering applications like infrastructure projects and environmental management, using ML algorithms. These properties included saturated hydraulic conductivity, friction angle of FRS, CBR of fine-grained plastic soils, and subgrade soil properties. However, the influence of both geotechnical and environmental factors on soil moisture evaporation rate prediction has not been explored. This study focuses on predicting soil moisture evaporation rate, which is vital for slope stability and landslide mitigation while considering environmental factors such as temperature and humidity.

In conclusion, based on the rich literature survey conducted in the geotechnical field, we have selected the RF, KNN, SVM, MLP, and MR models for the prediction of evaporation rate in soils. These models have shown their prowess in predicting various geotechnical factors and phenomena, indicating their potential to address the soil moisture evaporation rate prediction, a topic yet to be fully explored. By applying these powerful ML tools to soil moisture evaporation prediction, we hope to contribute new insights to the field of geotechnical engineering, enabling more informed decision-making and sustainable soil management practices.

Several researchers in the literature have explored various feature selection techniques to identify important features in datasets. For instance, Priyanka et al. (2022) utilized correlation-based, filter approach, wrapper approach, instance-based, and classifier-based methods to rank geotechnical parameters. However, these traditional techniques have limitations. Correlation-based methods, as described by Hall (1999), rank features based on their correlation with the target variable. It utilizes the Pearson correlation coefficient to quantify the linear relationship between features and the target. However, Correlation-based methods only capture linear relationships and may overlook nonlinear dependencies between features and the target variable. Additionally, they may not consider interactions between features, leading to the potential exclusion of relevant features from the final subset. Similarly, Next, Kohavi and John (1997) developed the wrapper approach, which exhaustively searches all possible feature subsets and evaluates their performance using an induction algorithm. It iteratively adds or removes features to maximize the algorithm’s accuracy. However, Wrapper methods are computationally intensive, especially for datasets with a large number of features. They may also suffer from overfitting if the search space is not properly constrained. Additionally, wrapper methods may not guarantee the selection of the optimal feature subset due to the exhaustive search.

Furthermore, Kira and Rendell (1992) developed the instance-based feature selection, which is a statistical algorithm that assigns weights to features based on their relevance to the target variable. It iteratively updates feature weights by comparing instances from the same and opposite classes. However, this method focuses on instance-level feature relevance and may overlook global feature importance. It also requires careful tuning of parameters, such as the threshold value, and may be sensitive to noise in the data. Moreover, Hall (1999) developed a classifier-based feature selection, which assesses feature strength by measuring the classifier’s accuracy with and without each feature. This method employs a predefined classifier to predict the target class based on input features. However, classifier-based methods face challenges in capturing feature synergy Meinhardt et al. (2004). They rely on comparing the classifier’s performance with and without individual features, but they may overlook relationships where combinations of multiple features significantly impact the target variable.

To address these limitations, we propose a novel Guided Backpropagation Feature Selection Technique. This approach leverages the nonlinear capabilities of neural networks to capture complex relationships in the data, ensuring that selected features align closely with the target variable and enhance overall predictive performance. Unlike traditional methods, our technique is capable of capturing complex and nonlinear relationships that linear models or simplistic feature selection approaches may miss. Moreover, the proposed technique does not eliminate any features. It considers all features to find the relationship between features and combinations of features to the target variable to identify the feature synergy.

3 Data features

The experimental data considered in the current study for analysis has been taken from Uday and Singh (2013). They demonstrated the effect of exposure circumstances (temperature and humidity) as well as soil-specific characteristics (soil type and specimen geometry) on evaporation rate, which may have an impact on fine-grained soil cracking.

Twenty ground-based parameters included in this experiment to assess their effects on soil moisture evaporation are as follows:

• Soil Type (Mineralogy-Sand, Silt, Clay): Soil type influences the pore structure, permeability, and water retention characteristics of the soil. Sandy soils have larger particles and better drainage, leading to higher evaporation rates. Clay-rich soils have smaller particles and higher water-holding capacity, resulting in slower evaporation. Silt soils fall in between.

• Atterberg Limits: These include three moisture concentrations that define the consistency of a soil-water mixture: the LL, the PL, and the Shrinkage Limit (SL): The moisture content at which a soil transforms from a plastic to a liquid condition is indicated by the LL. Soils with high LL tend to retain more water, which can lead to longer drying periods. This increased moisture content can hinder the overall rate of evaporation. Soils with high PL and significant SL undergo substantial volume changes during drying. These changes can create cracks and openings in the soil, altering the pathways and rates of water movement, including evaporation. Highly plastic and shrinkable soils may trap moisture in the pores, limiting the exposed surface area available for evaporation and potentially slowing the overall rate.

• Specific Gravity (G) and Maximum Dry Unit Weight (γ_dmax): G regulates the soil particle density. Higher G leads to denser particles, hindering water movement and reducing surface area for evaporation. Soils with higher G typically have lower evaporation rates due to reduced water accessibility. γ_dmax is the peak weight of compacted soil per volume. Evaporation increases void spaces, potentially lowering compaction and γ_dmax. This impacts water retention and evaporation. Soils with lower γ_dmax may experience higher evaporation due to increased porosity.

• Soil Friction Angle (Phi): A higher Phi value indicates increased friction and shear strength between particles, making it more difficult for water molecules to move through the soil matrix. Therefore, soils with a higher Phi value may experience slower water vapor movement and reduced exposure of water molecules to the surface, ultimately leading to a potentially lower evaporation rate. Conversely, a lower Phi value signifies reduced friction and shear strength, allowing water molecules to move more freely within the soil. This can result in enhanced water vapor transport to the surface, potentially leading to a higher evaporation rate.

• Optimum Moisture Content (Womc): Womc represents the moisture content at which a soil attains its maximum compaction and, consequently, its highest dry density. Soils with moisture below Womc have higher porosity, leading to faster evaporation. Above Womc, compaction reduces pore space, lowering evaporation.

• Air Entry Value (AEV), Moisture Content (Wr): As soil evaporates, its moisture content decreases. A higher AEV indicates that water requires more negative pressure to move through the soil pores. This means that soils with a higher AEV can retain water more effectively against evaporation. Consequently, these soils may experience slower water loss through vapor movement, potentially leading to a lower evaporation rate. Furthermore, Wr is directly tied to the amount of water present in the soil. Evaporation causes this content to decrease over time. Soils with higher initial Wr have more water available for evaporation, which can lead to higher initial evaporation rates. However, evaporation may also decrease as Wr decreases due to reduced water availability.

• Mineral Composition Analysis: Minerals exhibit distinct hygroscopic characteristics and diverse water retention capacities. The research considered five distinct soil types: white clay (referred to as WC), bentonite (referred to as BT), and naturally occurring soils (S1, S2, and S3). As documented by Uday and Singh (2013), each soil type encompassed a blend of diverse minerals within its composition. In the first most abundant mineral (FMAM), the following minerals were found: Kaolinite, Calcite, Hallosite, Montmorillonite, and Quartz. Similarly, the second most abundant mineral (SMAM) category comprised the following minerals: Illite, Montmorillonite, and Quartz. Finally, the third most abundant mineral (TMAM) category comprised the following minerals: Berilonite and Feldspar. It is important to note that the specific mineral composition may significantly influence the rate of evaporation and the overall dynamics of water movement within the soil matrix.

• Temperature and Humidity: Higher temperatures generally result in faster evaporation due to increased energy for vaporization, while higher humidity levels impede evaporation by reducing the moisture gradient between the soil and the air. These two factors together dynamically govern the rate at which water is lost from the soil surface through evaporation.

• Thickness of the Specimen: The thickness of the soil specimen directly impacts the evaporation rate. Thicker specimens tend to hinder moisture movement from the interior to the surface, resulting in a longer distance for water molecules to reach the evaporative surface. This increased distance can lead to slower evaporation rates, as it takes more time for water to traverse the thicker soil layers and be released into the atmosphere.

Table 1 displays the mean, standard deviation (stdev), minimum, and maximum values of the geotechnical parameters, providing a summary of their statistical characteristics. In this experiment, we employ a feature selection technique to choose the top features exclusively. We then proceed to compare the outcomes obtained using these selected features with the empirical results obtained through Eq. 2.

Table 1

Table 1. Summary statistics of the geotechnical parameters.

4 Methodology

This section will explore novel feature selection techniques used for ranking features in the context of geotechnical engineering. These techniques aim to identify the most influential geotechnical factors on soil cracks and other relevant properties. Next, we will delve into the discussion of different ML models, namely, RF, KNN, SMO, MLP, and MR. We will examine their applications in predicting soil behavior and crack intensity, highlighting their unique parameters and advantages. By understanding these models and their parameter settings, we can gain valuable insights into their suitability and effectiveness for tackling geotechnical engineering challenges.

4.1 Guided backpropagation feature selection technique

A novel feature selection technique has been developed based on an MLP model, which is a type of feed-forward neural network (Rosenblatt et al., 1962). In this technique, the goal is to predict the evaporation rate using the MLP model by providing all input features in the forward pass.

To determine the influence of the input features (x_i) on the output neuron (o_l), the algorithm calculates the gradient $\frac{\partial o_l}{\partial x_i}$. This gradient represents the sensitivity of the output neuron to changes in the input features, indicating the influence of each input feature on the evaporation rate.

In this algorithm, guided backpropagation techniques are employed within a feed-forward neural network, where the Rectified Linear Unit (ReLU) activation function is utilized to produce these gradients (Springenberg et al., 2014). These gradients are propagated from the output layer to the input layer through the intermediary hidden layers, facilitated by the application of the chain rule.

During the training process, the MLP model’s parameters are adjusted to fit the evaporation rate. The algorithm explores different variations of the model’s parameters, as discussed in Table 3, to optimize the model’s performance.

Once the model is trained, the algorithm accumulates the gradients along the path from the output neuron to each input feature. This accumulation allows for the determination of the relative influence or importance of each input feature in predicting the evaporation rate. In Figure 1, the gradient flow between neurons in the MLP model for feature selection is illustrated. Starting from the output neuron (o_l), the gradient $\frac{\partial o_l}{\partial (h_1^2)}$ represents the sensitivity of the output with respect to the first neuron of the second hidden layer $(h_1^2)$. Moving backward, the gradient $\frac{\partial (h_1^2)}{\partial (h_1^1)}$ indicates the influence of the first neuron of the second hidden layer on the first neuron of the first hidden layer $(h_1^1)$. Subsequently, the gradient $\frac{\partial (h_1^1)}{\partial x_1}$ signifies the impact of the first neuron of the first hidden layer on the first input (x₁). To determine the accumulated gradient along the path from the input (x₁) to the output neuron (o_l), we consider the product of these individual gradients mentioned in Eq. 1:

$\frac{\partial o_l}{\partial x_i}={\displaystyle \sum _{j=1}^m}\left(\frac{\partial h_j^1}{\partial x_i}\left[{\displaystyle \sum _{k=1}^n}\left(\frac{\partial h_k^2}{\partial h_j^1}\frac{\partial o_l}{\partial h_k^2}\right)\right]\right)(1)$

where m represents the number of neurons in the first hidden layer, and n denotes the number of neurons in the second hidden layer.

Figure 1

Figure 1. Sechematic diagram of the novel feature selection technique based on an MLP model.

By analyzing the accumulated gradients, the algorithm ranks the input features based on their impact on the evaporation rate. Features with higher gradient magnitudes indicate a stronger influence on the evaporation rate prediction. Therefore, they are considered more important or influential in the feature selection process. This ranking provides valuable insights for feature selection, enabling the identification of the most influential features for predicting the evaporation rate.

4.2 ML models

4.2.1 Empirical model

The empirical model considered in the current study for analysis has been taken from Uday and Singh (2013) (Uday and Singh, 2013). Eq. 2 establishes the empirical relationship between the evaporation rate (E_r) in mg/h, temperature (θ), relative humidity (Rh), and the initial thickness of the specimen (t) (Uday and Singh, 2013).

$E_r=p\cdot t_i^q\cdot {\theta }^r\cdot {\text{Rh}}^s(2)$

where p, q, r, and s are the constants related to specific soil, as provided by Uday and Singh (2013).

4.2.2 RF

The RF model is a classification and regression ensemble learning method developed by Breiman (2001). RF can be used for regression and classification tasks. In the training process, RF generates multiple random Decision Trees (DTs). The RF model provides its output by considering the majority value, effectively representing the average prediction derived from each individual tree. Notably, RF addresses the problem of overfitting that decision trees may encounter by means of aggregation (Breiman, 2001). An important parameter to fine-tune in RF is the number of features (nF) to be evaluated at each split point. In our study, we conducted experiments by varying the nF value within the range of 0–5 to optimize the RF model (see Table 2).

Table 2

Table 2. Range of parameters in the ML models.

4.2.3 KNN

The KNN model assesses the distance between the query data point and the k closest data points, all without the necessity for prior training (Peterson, 2009). This distance calculation can be based on either the Manhattan distance or the Euclidean distance as the distance function. Consequently, this approach yields the average of the k-nearest data points. Therefore, KNN relies on two key parameters: the choice of distance function and the value of k. In our study, we explored both the Manhattan distance and the Euclidean distance as distance metrics, and the k value was varied across the range of 1–10. You can refer to Table 2 for a detailed overview of the parameter ranges considered for KNN.

4.2.4 SMOreg

SMOreg is a specialized version of SVM designed for handling large datasets efficiently (Platt, 1998). It uses an iterative approach to speed up the training process, providing Lagrange multipliers (alpha) in each iteration to identify critical support vectors that define the margin boundary. SMOreg relies on two key parameters: the margin complexity (C) and the exponent (E) for the kernel function. The C parameter allows for flexible margin selection by disregarding specific support vectors, while the E parameter determines the kernel function’s exponential power.

SMOreg employs various kernel functions, including radial basis function (RBF), Pearson VII kernel (PUK), and polynomial kernel (PK), to effectively model the data (Patle and Chouhan, 2013). Our study explored a range of SMOreg parameters, including C values ranging from 0 to three and the use of RBF, PUK, and PK kernels. The E parameter varied from 1 to 5. Refer to Table 2 for a comprehensive overview of the considered parameters for SMOreg.

4.2.5 MLP

MLP is a widely used neural network to approximate nonlinear functions (Rosenblatt et al., 1962). It is made up of three layers: input, concealed, and output. Multiple neurons with activation functions are present in each layer. Data is sent from the input layer to the hidden layer, where it is transformed to improve feature representation before being routed to the output layer for regression tasks. Backpropagation, which uses gradient descent, is employed to update the layer weights and minimize the MLP error. The error in each iteration is computed to modify the weights for better performance.

In the experiment, the input layer’s dimensionality matches the number of features used. The hidden layers comprise different quantities of neurons, ranging from 100 to 1500. The experiment involved various configurations, including one to three hidden layers, and the batch size was systematically adjusted, increasing in powers of 2 and ranging from 16 to 512. For more information on the experiment’s parameters and their ranges, please refer to Table 2.

4.2.6 MR

Multiple Regression (MR) is a statistical method for investigating the connection between a dependent variable (Y) and several independent factors (X₁, X₂, …, X_i). It uses a linear Eq. 3 to model the relationship between these variables:

$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_i{x}_i+\epsilon (3)$

where y is the dependent variable, (X₁, X₂, …, X_i) are the input features, (β₀, β₁, β₂, …, β_i) are regression coefficients (indicating the impact of each independent variable), and ɛ is the error term. The goal is to estimate the coefficients that best match the data and minimize the sum of squared errors (ɛ) between predicted and actual dependent variable values.

MR analysis was performed in this work using the M5 (Modeled Tree) or greedy strategy for feature selection. The ridge parameter, a regularization term that helps prevent overfitting, was varied in steps of 5 from 10 to 50. In addition, Table 2 shows the parameters considered for the MR model.

4.2.7 K-Nearest oracles (KNORA) ensemble

The KNORA ensemble method dynamically aggregates predictions from multiple base regression models, such as MLP, SMOreg, and RF regressor. Initially, a set of base models is trained on a training dataset, each model capturing distinct patterns from the data. Subsequently, predictions are generated for instances in the validation or test dataset using these trained base models.

In KNORA, the competence of each base model is assessed by evaluating its predictive performance through RMSE metrics between its prediction and the true target value for each instance. Based on these evaluations, KNORA identifies the k-nearest base models with the lowest error (or highest competence) for each instance. The parameter “k” denotes the number of nearest models and is adjustable. These selected models are deemed the most reliable for predicting that specific instance, thus constituting an ensemble of competent models to enhance overall performance.

By aggregating predictions from the chosen base models through averaging, the KNORA ensemble generates a refined prediction for each instance. This methodology effectively leverages the collective knowledge of the most competent base models while disregarding the contributions of less reliable ones. The parameter “k” in the KNORA ensemble denotes the number of nearest models and is adjustable. The range of “k” values typically varies between 2 and 5, as shown in Table 2.

4.3 Train-test splits

The train-test split was used to assess the performance of the ML models. The dataset was randomly shuffled and split into 70% train data and 30% test data.

4.4 Error measures

The root mean squared error (RMSE) was used to determine the error between the actual and predicted values. The following is the equation for RMSE:

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(y_i-\left({\widehat{y}}_i\right)\right)}^2}(4)$

where y_i represents the actual data point, $({\widehat{y}}_i)$ signifies the value predicted by the ML model, and “n” denotes the total count of data points.

5 Results

In this study, the guided backpropagation feature selection technique was employed, and the models were trained using 10-fold cross-validation. During the feature selection process, the nineteen features were evaluated, and their rankings were determined based on their frequency of being ranked as the top feature across the ten folds. Table 3 presents the ranks assigned to each feature, which were determined according to the highest accumulated gradient observed in the ten folds. This approach allowed for the identification of the most influential features that significantly contributed to the model’s performance and predictive accuracy. The optimized MLP model for feature selection consisted of two hidden layers with 100 and 500 neurons, respectively. The activation function used in all layers was ReLU.

Table 3

Table 3. Rank of the attributes given by feature selection technique.

The results of the several ML models using the train-test split techniques for top-5, top-10, and all features are displayed in Table 4. The top-5 features are Temp, Humidity, Silt, Thickness, and Soil Type. Table 4 illustrates that the KNORA ensemble model demonstrated the highest performance among the models considered, achieving a test RMSE of 7.54 mg/h with the top-10 features. Following closely, the MLP model, utilizing the top-10 features, emerged as the second best-performing model with a test RMSE of 25.1 mg/h. Furthermore, the KNORA ensemble model possessed the smallest RMSE among all models for top-5, top-10, and all features in the dataset. Table 5 shows the performance of the empirical model over train and test data, where 70% of the original data was taken for train, and the remaining 30% of the data was taken for testing. The calibrated values of various parameters used by the RF, MR, KNN, SMOreg, and MLP models are displayed in Table 6. For instance, for the top-5 features, the RF in Table 6 contains 300 bags and four numbers of iterations. The ridge value five and the M5 feature selection method were the best MR parameters. The Manhattan distance was chosen for the KNN model’s distance measurement after determining that 3 was the best number for the k parameter. Additionally, 14 and 1 were the optimal values for the C and E parameters in SMOreg. In the SMOreg model, the PUK function selects a kernel function. Furthermore, two hidden layers of the MLP model, each including 100 and 500 neurons, produced the best result. Next, in KNORA ensemble, the value of k was set to 2 for the top-5 and top-10 features, and 3 for all features.

Table 4

Table 4. The performance of various ML models in the train-test split.

Table 5

Table 5. The performance of the empirical model in the train test split.

Table 6

Table 6. Optimized parameters for RF, MR, SMOreg, MLP, and KNORA ensemble.

Figure 2 presents the detailed results analysis of 5 ML models, namely, MLP, SMOreg, RF, KNN, and MR, with varying feature selections. The analysis includes three scenarios: using the top-5 features, the top-10 features, and all features in the training and testing. The y-axis represents the RMSE values under different feature selections: using the top-5 features, the top-10 features, and all features. The x-axis denotes the different models and feature selections. The chart allows for a comprehensive comparison of each model’s RMSE performance under different feature selections, providing insights into the impact of feature importance on the predictive capabilities of the ML models.

Figure 2

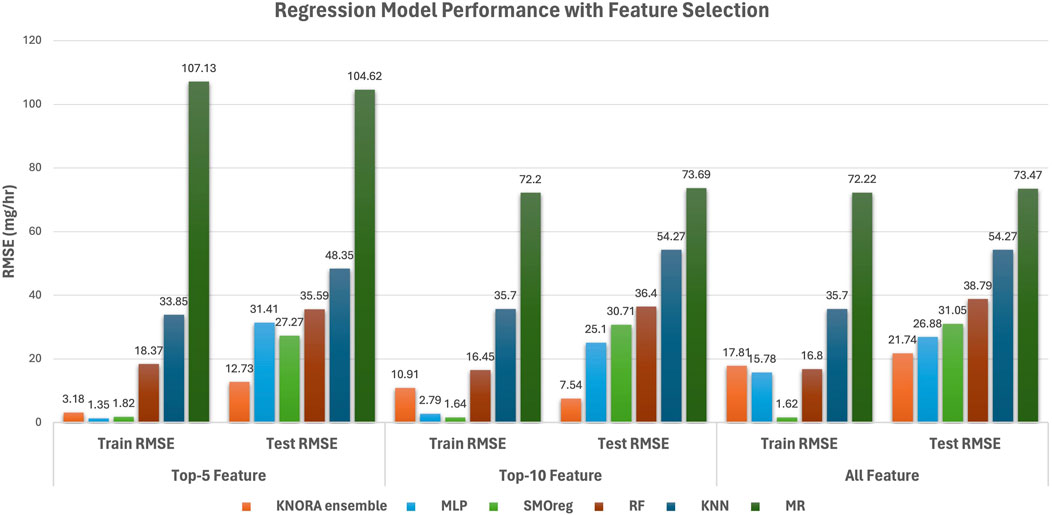
Figure 2. Results of the KNORA ensemble, MLP, SMOreg, RF, KNN, and MR Models with Top-5, Top −10, and all features in the training and testing.

6 Discussion

The increased occurrence of evaporation rates in soils, driven by global climate change and extreme weather events, may have significant implications for natural hazards such as soil movements and slope stability. As soils undergo swift dehydration, especially those rich in clay content, distinct geometric patterns of cracks emerge on the soil’s surface. These cracks can weaken the soil structure, leading to increased susceptibility to soil movements such as landslides and slope instability. Therefore, understanding and predicting soil moisture evaporation rates are crucial for assessing and mitigating the risks associated with these natural hazards.

Historically, soil moisture evaporation rates have been estimated using empirical methods (Uday et al., 2015), which often resulted in significant errors. To address this issue, this study focused on developing ML models to predict soil moisture evaporation rates more accurately, aiming to minimize estimation errors and improve predictive capabilities. By leveraging ML techniques, we aimed to enhance our understanding of soil moisture evaporation dynamics and provide more reliable predictions to support decision-making processes in mitigating natural hazards. The dataset utilized in this study encompassed twenty-one ground-based parameters, including variables such as temperature, humidity, thickness, and other pertinent soil attributes. These parameters were meticulously collected through field sampling and rigorous laboratory analyses, ensuring a comprehensive representation of soil characteristics.

To identify the most influential features from the complex dataset, we introduced an innovative guided backpropagation-based feature selection technique. This method not only prioritized the top ten parameters exhibiting the strongest correlation with evaporation rates but also emphasized the importance of these parameters based on their gradient values, reflecting their direct influence on model predictions. It involved spotlighting the top-5 features, the top-10 features, and the entire feature set, creating a comprehensive framework for comparative analysis. The evaluation of various ML models followed a train-test split approach, with 70% of the data allocated for training and the remaining 30% reserved for testing. The RMSE served as the primary metric for assessing predictive accuracy.

Comparing the array of ML models developed, particularly the top two models, KNORA ensemble and MLP, it was evident that both models exhibited superior predictive capabilities compared to the empirical (physical) model. Across all feature subsets and on both training and testing data, the KNORA ensemble consistently outperformed the MLP model regarding RMSE values. For instance, on the testing set, the KNORA ensemble achieved an RMSE of 7.54 mg/h, compared to MLP’s 25.1 mg/h, showcasing the KNORA ensemble’s capacity to effectively discern intricate patterns within the data, leading to reduced prediction errors. Furthermore, the KNORA ensemble and MLP exhibited substantial improvements over the empirical model’s performance, as highlighted by the notable contrast in RMSE values. The empirical model, with RMSE values of 1319.1 mg/h on the testing set, underscored its limitations in capturing the underlying relationships within the dataset. In contrast, the KNORA ensemble and MLP models achieved significantly lower RMSE values on the testing set while consistently displaying enhancements in training RMSE values. Overall, these results underscore the considerable enhancement in predictive accuracy achievable by adopting advanced ML techniques, highlighting their potential to surpass traditional empirical approaches.

The selection of key features, notably temperature, humidity, silt content, thickness, and soil type, stems from their substantial influence on the intricate dynamics of evaporation (Budhu, 2010). The most influential minerals within the soil matrix (the SMAM category) included Illite, Montmorillonite, and Quartz. These minerals greatly influenced the prediction of soil moisture evaporation rates. Following closely, the second most important minerals in soil composition, including Kaolinite, Calcite, Hallosite, Montmorillonite, and Quartz, influenced the prediction of soil moisture evaporation rates. Finally, the third tier of importance (TMAM category) consisted of Berilonite and Feldspar minerals influencing the prediction of soil moisture evaporation rates.

Beyond these mineral rankings, parameters such as γ_dmax and SL held the ninth and 10th positions, respectively. These parameters were prioritized due to their demonstrated significance in shaping the evaporation process. These features encompass pivotal facets of the soil’s physical composition, moisture-retaining capacity, mineralogical composition, and structural behavior. The selection of these features was based on their well-documented and strong correlations with evaporation rates, underscoring their capacity to offer valuable insights into the underlying mechanisms that govern the process of evaporation (Budhu, 2010). By integrating these crucial features, the resultant predictive models could tap into a comprehensive comprehension of the intricate relationship between these variables and evaporation, thereby enabling more accurate and informed predictions.

The complexity of soil behavior under real-world conditions, including variability in soil properties such as cohesion, infiltration rate, water table levels, and environmental factors, presents significant challenges in accurately modeling soil moisture evaporation rates. As highlighted by Morris et al. (1992), the dynamic nature of soil physical properties can greatly influence moisture dynamics, necessitating models that can adapt to this variability to predict evaporation rates accurately. Moreover, Tao et al. (2005) emphasizes the importance of considering soil volume changes and crack development, which are critical in understanding soil moisture evaporation under varying environmental conditions.

Environmental factors may likely play a pivotal role in the evaporation process. Uday et al. (2015) and Wanare et al. (2022) have documented the significant impact of temperature, humidity, and solar radiation on soil moisture dynamics. These studies underscore the necessity of incorporating a broad spectrum of environmental conditions into predictive models to enhance their applicability to real-world scenarios. This includes integrating temporal data on weather patterns and precipitation events, as these factors are crucial in shaping the soil’s moisture content over time.

Recognizing the limitations of studies conducted in controlled settings, our research echoes the call by Xu et al. (2022) and Andrushia et al. (2022) for the development of hybrid models that leverage both field and laboratory data. Such models would offer a more comprehensive framework for understanding the interplay between soil properties, environmental factors, and soil moisture evaporation. By incorporating a wider range of data reflecting the natural variability of these factors, predictive models can be significantly improved to reflect the complexities of real-world conditions.

The inclusion of dynamic soil properties and environmental factors in soil moisture evaporation models not only enhances their predictive accuracy but also their practical applicability in addressing geotechnical and agricultural challenges. For instance, the work of Yesiller et al. (2000) on the desiccation and cracking behavior of soils provides a foundation for understanding how these processes can impact soil stability and plant growth. Similarly, the exploration of ML techniques in geotechnical engineering by Kardani et al. (2022) and Nguyen et al. (2022) illustrates the potential of these models to adapt and learn from complex datasets, offering promising avenues for future research.

In light of these considerations, our study acknowledges the need for ongoing efforts to refine and enhance ML models for soil moisture evaporation prediction. Future research should aim to integrate a more diverse array of soil types, environmental conditions, and temporal variability to capture the full spectrum of factors influencing soil moisture dynamics. Through these advancements, we can move closer to developing robust models capable of assisting in the sustainable management of soil resources in the face of changing global climate conditions.

7 Conclusion

The study’s findings underscore the importance of accurately predicting soil moisture evaporation rates, particularly in the context of mitigating natural hazards such as soil movements and slope instability. By leveraging advanced ML models, we have demonstrated the potential to significantly improve the accuracy of soil moisture evaporation rate predictions compared to traditional empirical methods. We have developed a robust methodology for forecasting soil moisture evaporation rates through a meticulous analysis of twenty-one ground-based parameters, including temperature, humidity, thickness, and soil attributes.

Our innovative guided backpropagation-based feature selection technique has identified key parameters that exhibit strong correlations with evaporation rates, shedding light on the intricate dynamics of soil moisture evaporation. Through comparative analysis, we have shown that ML models, particularly the novel KNORA ensemble and MLP, outperform empirical models in predicting soil moisture evaporation rates with higher accuracy.

Moreover, our study has highlighted the significance of specific soil minerals and physical characteristics, such as clay content and soil type, in influencing soil moisture evaporation dynamics. By integrating these crucial features into predictive models, we can better understand the underlying mechanisms governing soil moisture evaporation and make more informed decisions regarding natural hazard mitigation.

Looking ahead, future research should focus on refining ML algorithms, incorporating additional variables, and conducting field validation studies to further enhance the accuracy and applicability of soil moisture evaporation rate predictions. By continuing to advance our understanding of soil moisture evaporation dynamics, we can better safeguard against natural hazards and ensure the resilience of ecosystems and infrastructure in the face of global climate change.

In our study, we employed a novel feature selection technique, guided backpropagation, to identify and rank the most relevant features correlated with soil moisture evaporation rates. While direct experimental studies to correlate each individual feature with moisture evaporation were not conducted due to the scope and resource limitations of our work, the selection of features was grounded in an extensive literature review and prior experimental findings from related studies (Yilmaz and Kaynar, 2011; Chou et al., 2016; Kumar et al., 2019; Wani et al., 2021; Kardani et al., 2022; More et al., 2022; Nguyen et al., 2022; Verma et al., 2023), including the foundational work of (Uday and Singh, 2013) that detailed the impact of various soil and environmental factors on evaporation rates. The guided backpropagation method allowed us to prioritize features scientifically known to influence evaporation, such as temperature, humidity, soil type, and specific gravity, among others. Our ML model’s performance, particularly the MLP and SMOreg models, further validated the significance of these selected features in accurately predicting soil moisture evaporation rates, demonstrating their empirical correlation through advanced computational techniques. The guided backpropagation method allowed us to prioritize features scientifically known to influence evaporation, such as temperature, humidity, soil type, and specific gravity, among others. Our ML model’s performance, particularly the KNORA ensemble, MLP, and SMOreg models, further validated the significance of these selected features in accurately predicting soil moisture evaporation rates, demonstrating their empirical correlation through advanced computational techniques.

This study has not only advanced our understanding of soil moisture evaporation rates through the application of ML models but also set a precedent for future research in this vital area of environmental science. Key takeaways from our investigation include the successful implementation of hybrid models, such as the stacking ensemble model incorporating the novel KNORA ensemble technique, which significantly improved prediction accuracy. Additionally, our work highlights the importance of considering real-world variability in soil properties and environmental conditions to enhance model robustness and applicability.

In conclusion, this study highlights the critical role of thoughtful feature selection and the application of ML models in enhancing the accuracy of evaporation rate predictions. The selected top features emphasize the intricate relationship between the soil’s inherent characteristics and the evaporation process. Our study contributes a critical piece to the puzzle of understanding soil water dynamics, offering a foundation upon which future researchers can build. It is our hope that the methodologies and insights presented herein will inspire continued exploration and innovation in the quest to develop sustainable solutions to the challenges posed by changing environmental conditions. Looking ahead, this research paves the way for further studies aimed at refining predictive models for soil moisture dynamics, incorporating a wider array of environmental variables, and employing advanced ML models. Specifically, future work could explore the integration of temporal and spatial data to better understand the effects of climate change on soil moisture and evaporation processes. Moreover, our findings have practical implications for soil management practices, offering insights that can inform water conservation strategies, agricultural planning, and the design of infrastructural projects to mitigate the impacts of soil moisture variability. Looking ahead, exploring hybrid approaches that combine methods like Principal Component Analysis (PCA) with neural network-based feature selection holds promise for further improving the accuracy of evaporation rate predictions, especially in complex datasets. In considering future research directions, it is crucial to acknowledge the importance of rainfall in the natural soil water cycle and suggest that future research could specifically address the complex dynamics between rainfall, soil moisture, and evaporation. Incorporating rainfall as a variable would indeed enhance the model’s applicability to real-world conditions, providing a more comprehensive framework for predicting soil moisture dynamics in various climatic scenarios.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: NA. Requests to access the datasets should be directed to uday@iitmandi.ac.in.

Author contributions

PP: Formal Analysis, Writing–original draft. PK: Formal Analysis, Methodology, Project administration, Supervision, Writing–review and editing. SP: Data curation, Formal Analysis, Writing–review and editing. KU: Funding acquisition, Supervision, Validation, Writing–review and editing. VD: Funding acquisition, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. IITM/DDMA-M/VD/358, IITM/DDMA-Kinn/VD/345, IITM/DDMA-Kan/KVU/357, and DST/TDT/DDP-11/2021.

Acknowledgments

The authors would like to thank the district disaster management authority of Mandi, Kangra, and Kinnaur of Himachal Pradesh for providing the fund for this research. They are also thankful to the IIT Mandi, for providing the space and computing facilities for this research work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andrushia, A. D., Neebha, T. M., Umadevi, S., Anand, N., and Cashell, K. A. (2022). Shrinkage crack detection in expansive soil using deep convolutional neural network and transfer learning. KSCE J. Civ. Eng. 26, 4202–4213. doi:10.1007/s12205-022-1354-0

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Budhu, M. (2010). Soil mechanics and foundations. John Wiley and Sons.

Google Scholar

Chou, J.-S., Yang, K.-H., and Lin, J.-Y. (2016). Peak shear strength of discrete fiber-reinforced soils computed by machine learning and metaensemble methods. J. Comput. Civ. Eng. 30, 04016036. doi:10.1061/(asce)cp.1943-5487.0000595

CrossRef Full Text | Google Scholar

Hall, M. A. (1999). Correlation-based feature selection for machine learning. The University of Waikato. Ph.D. thesis.

Google Scholar

Kardani, N., Aminpour, M., Raja, M. N. A., Kumar, G., Bardhan, A., and Nazem, M. (2022). Prediction of the resilient modulus of compacted subgrade soils using ensemble machine learning methods. Transp. Geotech. 36, 100827. doi:10.1016/j.trgeo.2022.100827

CrossRef Full Text | Google Scholar

Kira, K., and Rendell, L. A. (1992). “A practical approach to feature selection,” in Machine learning proceedings 1992 (Elsevier), 249–256.

CrossRef Full Text | Google Scholar

Kodikara, J., Barbour, S., Fredlund, D., et al. (1999). Changes in clay structure and behaviour due to wetting and drying. Proc. 8th Aust. N. Z. Conf. geomechanics Consol. Knowl. Aust. Geomechanics Soc. 179, 179–185.

Google Scholar

Kohavi, R., and John, G. H. (1997). Wrappers for feature subset selection. Artif. Intell. 97, 273–324. doi:10.1016/s0004-3702(97)00043-x

CrossRef Full Text | Google Scholar

Kumar, P., Sihag, P., Pathania, A., Agarwal, S., Mali, N., Chaturvedi, P., et al. (2019). “Landslide debris-flow prediction using ensemble and non-ensemble machine-learning methods: a case-study in chamoli, India,” in Contributions to statistics: proceedings of the 6th international conference on time series and forecasting (ITISE) (Granda, Spain: Springer), 614–625.

Google Scholar

Meinhardt, G., Schmidt, M., Persike, M., and Röers, B. (2004). Feature synergy depends on feature contrast and objecthood. Vis. Res. 44, 1843–1850. doi:10.1016/j.visres.2004.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

More, S. B., Deka, P. C., Patil, A. P., and Naganna, S. R. (2022). Machine learning-based modeling of saturated hydraulic conductivity in soils of tropical semi-arid zone of India. Sadhana 47, 26. doi:10.1007/s12046-022-01805-6

CrossRef Full Text | Google Scholar

Morris, P. H., Graham, J., and Williams, D. J. (1992). Cracking in drying soils. Can. Geotechnical J. 29, 263–277. doi:10.1139/t92-030

CrossRef Full Text | Google Scholar

Naresh, M., and Uday, K. (2018). “Cracking characteristics of cemented fiber reinforced fine-grained soils,” in PanAm unsaturated soils 2017 (ASCE), 323–331.

CrossRef Full Text | Google Scholar

Nguyen, D. D., Roussis, P. C., Pham, B. T., Ferentinou, M., Mamou, A., Vu, D. Q., et al. (2022). Bagging and multilayer perceptron hybrid intelligence models predicting the swelling potential of soil. Transp. Geotech. 36, 100797. doi:10.1016/j.trgeo.2022.100797

CrossRef Full Text | Google Scholar

Patle, A., and Chouhan, D. S. (2013). “Svm kernel functions for classification,” in 2013 International conference on advances in technology and engineering (ICATE) (IEEE), 1–9.

CrossRef Full Text | Google Scholar

Peterson, L. E. (2009). K-nearest neighbor. Scholarpedia 4, 1883. doi:10.4249/scholarpedia.1883

CrossRef Full Text | Google Scholar

Platt, J. (1998). Sequential minimal optimization: a fast algorithm for training support vector machines. Adv. Kernel Methods, 185–208. doi:10.7551/mitpress/1130.003.0016

CrossRef Full Text | Google Scholar

Priyanka, K., Chaturvedi, P., Uday, K., and Dutt, V. (2022). “Data-driven approach for predicting surface subsidence velocity from geotechnical parameters,” in International advanced computing conference (Springer), 64–81.

Google Scholar

Robinson, J. D., and Vahedifard, F. (2016). Weakening mechanisms imposed on California’s levees under multiyear extreme drought. Clim. change 137, 1–14. doi:10.1007/s10584-016-1649-6

CrossRef Full Text | Google Scholar

Rosenblatt, F., et al. (1962). Principles of neurodynamics: perceptrons and the theory of brain mechanisms, 55. Spartan books Washington, DC).

Google Scholar

Springenberg, J. T., Dosovitskiy, A., Brox, T., and Riedmiller, M. (2014). Striving for simplicity: the all convolutional net. arXiv preprint arXiv:1412.6806.

Google Scholar

Tao, T., Peng, X., and Lee, D. (2005). Thermal drying of wastewater sludge: change in drying area owing to volume shrinkage and crack development. Dry. Technol. 23, 669–682. doi:10.1081/drt-200054164

CrossRef Full Text | Google Scholar

Uday, K., Prathyusha, J., Singh, D., and Apte, P. (2015). Application of the taguchi method in establishing criticality of parameters that influence cracking characteristics of fine-grained soils. Dry. Technol. 33, 1138–1149. doi:10.1080/07373937.2015.1015032

CrossRef Full Text | Google Scholar

Uday, K., and Singh, D. (2012). Application of laser microscopy for studying crack characteristics of fine-grained soils. Geotechnical Test. J. 36, 20120004–20120154. doi:10.1520/gtj20120004

CrossRef Full Text | Google Scholar

Uday, K., and Singh, D. (2013). Investigation on cracking characteristics of fine-grained soils under varied environmental conditions. Dry. Technol. 31, 1255–1266. doi:10.1080/07373937.2013.785433

CrossRef Full Text | Google Scholar

Verma, G., Kumar, B., Kumar, C., Ray, A., and Khandelwal, M. (2023). Application of krr, k-nn and gpr algorithms for predicting the soaked cbr of fine-grained plastic soils. Arabian J. Sci. Eng. 48, 13901–13927. doi:10.1007/s13369-023-07962-y

CrossRef Full Text | Google Scholar

Wanare, R., Jayanthi, P., and Iyer, K. K. (2022). Experimental study on sustainable stabilization of marine soil with ultrafine slag and activator for controlling its cracking characteristics. Constr. Build. Mater. 345, 128310. doi:10.1016/j.conbuildmat.2022.128310

CrossRef Full Text | Google Scholar

Wani, I., Kumar, H., Rangappa, S. M., Peng, L., Siengchin, S., and Kushvaha, V. (2021). Multiple regression model for predicting cracks in soil amended with pig manure biochar and wood biochar. J. Hazard. Toxic, Radioact. Waste 25, 04020061. doi:10.1061/(asce)hz.2153-5515.0000561

CrossRef Full Text | Google Scholar

Xu, J.-J., Zhang, H., Tang, C.-S., Cheng, Q., Tian, B.-g., Liu, B., et al. (2022). Automatic soil crack recognition under uneven illumination condition with the application of artificial intelligence. Eng. Geol. 296, 106495. doi:10.1016/j.enggeo.2021.106495

CrossRef Full Text | Google Scholar

Yesiller, N., Miller, C., Inci, G., and Yaldo, K. (2000). Desiccation and cracking behavior of three compacted landfill liner soils. Eng. Geol. 57, 105–121. doi:10.1016/s0013-7952(00)00022-3

CrossRef Full Text | Google Scholar

Yilmaz, I., and Kaynar, O. (2011). Multiple regression, ann (rbf, mlp) and anfis models for prediction of swell potential of clayey soils. Expert Syst. Appl. 38, 5958–5966. doi:10.1016/j.eswa.2010.11.027

CrossRef Full Text | Google Scholar