Seismic landslide hazard assessment using improved seismic motion parameters of the 2017 Ms 7.0 Jiuzhaigou earthquake, Tibetan Plateau

Seismic landslide hazard assessment plays a very important guiding role during urgent earthquake relief. In August 2017, an Ms 7.0 earthquake in Jiuzhaigou County, Sichuan Province, China, triggered thousands of landslides. Based on the analysis of geological settings and coseismic landslide characteristics, the Newmark model is used to complete the seismic landslide hazard assessment. Three seismic motion parameters, namely, peak ground acceleration (PGA), traditional Arias intensity (Arias_P), and improved Arias intensity (Arias_C), are adopted. A publicly published coseismic landslide catalog is used as the validation samples. The results show that the coseismic landslides are mainly distributed in the deep gullies and steep mountainous slopes on the north and south sides of the epicenter. The seismic landslide hazard accuracy based on Arias_C is the best, followed by that based on PGA and Arias_P. The spatial distribution of seismic landslide hazards based on Arias_C shows an almost standard elliptical ring and is in good agreement with that of coseismic landslides. These results fully reflect the combined influence of the epicenter and seismogenic fault on landslide development. The middle seismic landslide hazard and over are mainly located at areas with seismic intensity of VII degree and above. The Arias intensity is very suitable for rapid seismic landslide hazard assessment in emergency situations. The study results can provide scientific and technological support for rapid earthquake relief and have reference significance for future seismic landslide hazard assessment.

Introduction

The seismic landslide is one of the important geo-hazard types, which seriously enhances the damaging effect of earthquake-induced disasters. The spatial distribution characteristics, formation mechanism, and causative factor sensitivity of a lot of seismic landslide cases have been analyzed in depth. Many valuable methods and models have been established and widely used in the seismic landslide hazard assessment at a regional scale, such as the multi-criteria evaluation method (Kamp et al., 2008), artificial neural network (Yilmaz, 2010; Nayek and Gade, 2022), support vector machine (Yao et al., 2008), Bayesian network (Song et al., 2012), logistic regression (Nefeslioglu et al., 2006), and transfer learning (Ai et al., 2022). Based on the limit equilibrium theory of infinite slope, the Newmark displacement model was developed to conduct seismic landslide hazard assessment (Wilson and Keefer, 1983; Miles and Ho, 1999). Based on many research results of the statistical laws of seismic landslides, the simplified regression-based Newmark displacement model (Jibson, 2007; Chousianitis et al., 2014; Pareek et al., 2014; Gade et al., 2021; Nayek and Gade, 2022; Cheng et al., 2023) and various statistical probability models (Rathje and Saygili, 2008; Du and Wang, 2014; Nowicki et al., 2014; Du and Wang, 2016) were established. The simplified regression-based Newmark displacement model is applicable and can quickly conduct the seismic landslide hazard assessment at a regional scale, and has been widely used all over the world (Liu et al., 2018; Ma and Xu, 2019; Nayek and Gade, 2021; Zeng et al., 2023).

On 8 August 2017, an Ms 7.0 earthquake occurred in Jiuzhaigou County, Sichuan Province, China, with the epicenter at E103.82° and N33.20° and a focal depth of 20 km. The maximum seismic intensity was IX degree. The area with seismic intensity of VII degree and above covers approximately 4,294.81 km², and the major axis of the isoseismal line generally shows an NW direction. As of 14 August 2017, a total of 3,704 aftershocks were recorded, which included three aftershocks with magnitudes 4.0–4.9 and 27 aftershocks with magnitudes 3.0–3.9. The largest aftershock with magnitude 4.8 occurred in Jiuzhaigou County on 9 August 2017 (National Earthquake Data Center, https://data.earthquake.cn/gxdt/info/2017/39880.html). The Jiuzhaigou earthquake had triggered thousands of collapses and landslides (Li et al., 2019; Ling et al., 2021; Cai et al., 2022), which resulted in heavy casualties and damage to transportation, power, communications, buildings, and other infrastructures. After the earthquake, studies on landslide investigation and assessment were carried out in time (Fan et al., 2018; Tian et al., 2019), which effectively guided the emergency relief and reduced earthquake disaster losses.

In the existing studies on deterministic seismic landslide hazard assessment using Newmark displacement, the adopted seismic motion parameters rarely consider the influence of seismogenic faults (Nayek and Gade, 2021; Zeng et al., 2023), and it only has fewer applications in probabilistic seismic landslide hazard assessment (Zhang et al., 2017; Liu et al., 2018). However, the seismogenic fault has a significant control effect on coseismic landslide development (Gorum and Carranza, 2015; Fan et al., 2018). So, taking the Jiuzhaigou earthquake as a typical example, the simplified regression-based Newmark displacement model and three kinds of seismic motion parameters are used to carry out the seismic landslide hazard assessment. The assessment results are validated by taking the coseismic landslide as test samples. The result accuracy based on three kinds of seismic motion parameters [peak ground acceleration (PGA), traditional Arias intensity (Arias_P), and improved Arias intensity (Arias_C)] is compared and analyzed to elaborate the significant effect of the seismogenic fault on seismic landslide development. The study ideas and results have significant reference for promoting rapid seismic landslide hazard assessment during emergency earthquake relief.

Study area

The eastern margin of the Qinghai–Tibet Plateau is characterized by strong tectonic and fault activities, extremely complex stress fields, and frequent strong earthquakes, such as the Ms 8.0 Wenchuan earthquake in 2008 (Dai et al., 2011), the Ms 7.0 Lushan earthquake in 2013 (Zhang et al., 2013), and the Ms 6.8 Luding earthquake in 2023 (Dai et al., 2023). These strong earthquakes have triggered many landslides and their chain hazards. The Jiuzhaigou earthquake occurred in the northeast margin of the Bayankela block and the middle of the famous North–South (NS) seismic tectonic belt, where the developed active faults mainly include the Minjiang fault, Tazang fault, and Huya fault (Figures 1, 2). The Minjiang fault is a Quaternary thrust and strike-slip fault with a total length of approximately 170 km, with a general NS trend and NW dip direction (Deng et al., 1994). It has been highly active since the late Pleistocene, with a strike-slip rate of approximately 1 mm/y. The Zhenjiangguan–Lianghekou section of the Minjiang fault is the most active since the late Quaternary and even the Holocene, where the most recent event was the Ms 7.5 Diexi earthquake in 1933. The Tazang fault is the east branch of the East Kunlun fault zone, with a total length of 170 km and a general NW trend, and is the northeast boundary of the Bayankela block. The late Quaternary activities of the Tazang fault are segmented and multiphase, with dominated horizontal shear movement in the west section and gradually decreasing strike-slip movement and an increasing vertical component in the east section (Ren et al., 2013). The Huya fault is a Quaternary thrust and left strike-slip fault, with a general NNW trend and a vertical slip rate of approximately 0.5 mm/y and left strike-slip rate of approximately 1.4 mm/y (Qi et al., 2018). There have been many strong historical earthquakes in the Huya fault zone, such as the Ms 6¾ Xiaohe earthquake in 1630 and the Ms 7.2 earthquake between Songpan County and Pingwu County in 1976.

Figure 1

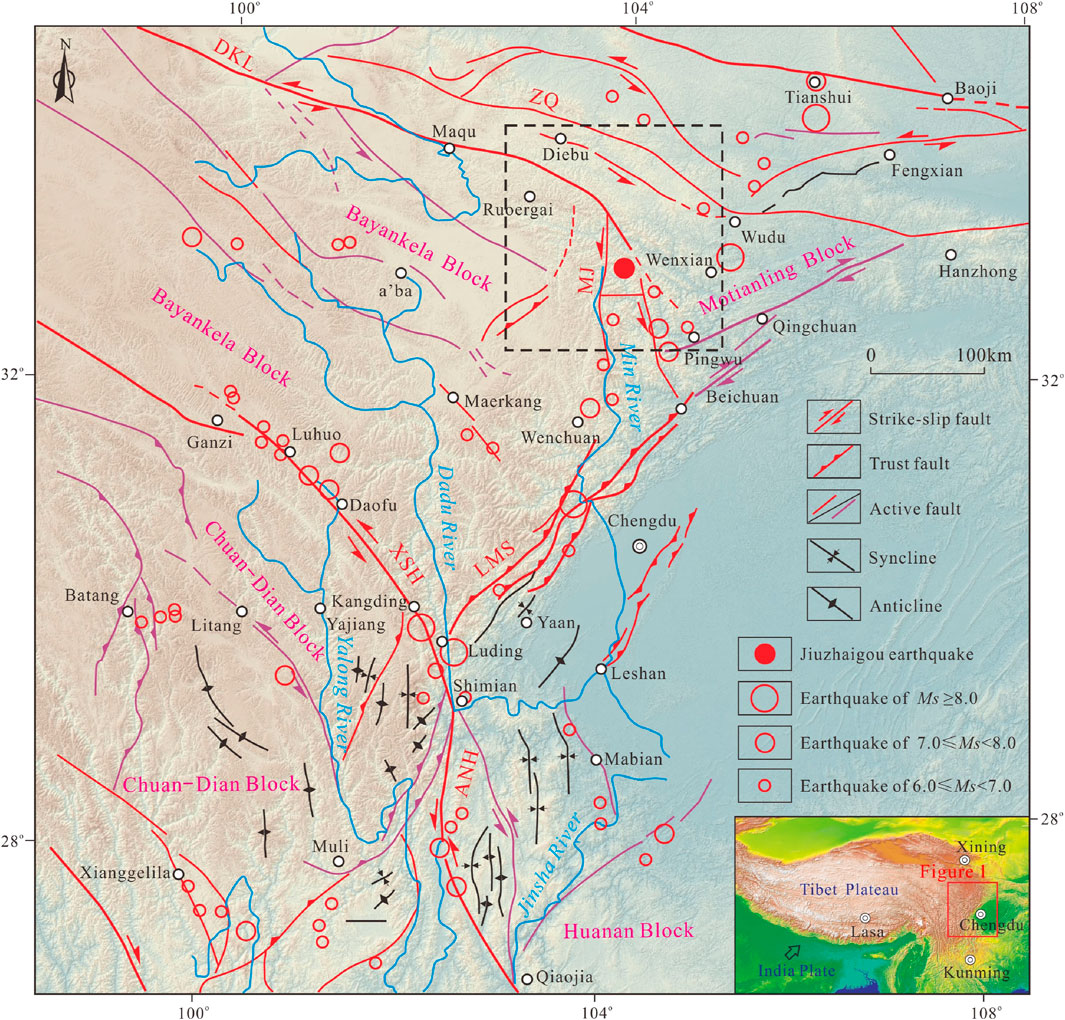
Figure 1. Schematic diagram of regional major active structures in the eastern Qinghai–Tibet Plateau. The black dashed rectangular box is the scope of Figure 2. DKL is the Dongkunlun fault zone, ZQ is the Zhouqu fault zone, MJ is the Minjiang fault zone, XSH is the Xianshuihe fault zone, LMS is the Longmenshan fault zone, and ANH is the Anninghe fault zone. The fault data are obtained from the 1:500,000 geological maps.

Figure 2

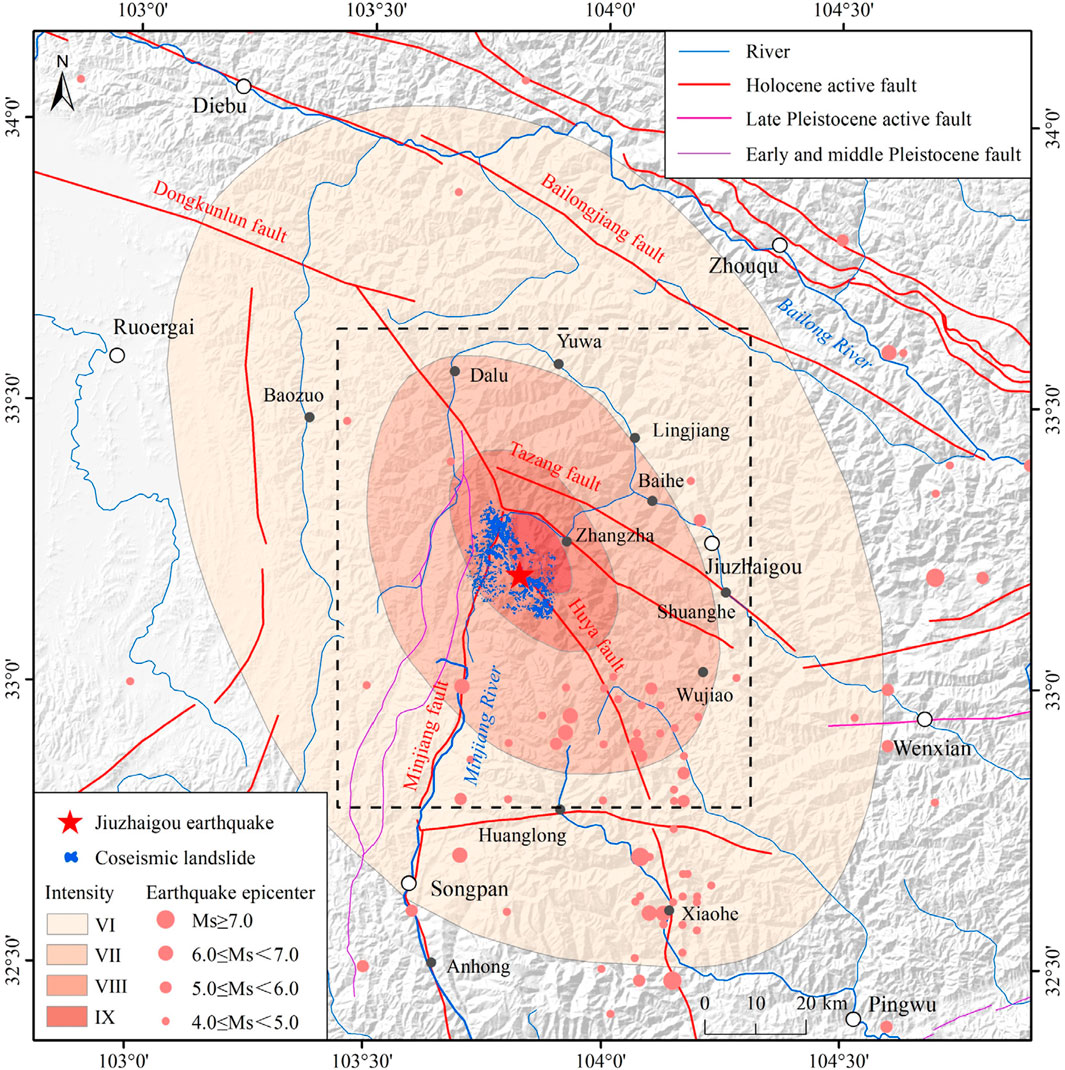
Figure 2. Seismic intensity, epicenter, and coseismic landslides of the Ms 7.0 Jiuzhaigou earthquake. The black dashed rectangular box indicates the main assessment area and is the scope of Figures 5–13. The fault data are obtained from the 1:200,000 geological maps.

The seismogenic fault of the Jiuzhaigou earthquake is the northern section of the Huya fault. The direction of the maximum principal stress around the Jiuzhaigou earthquake is NWW-SEE, which is consistent with the direction of the regional stress field, indicating that the Jiuzhaigou earthquake is mainly controlled by regional stress (Sun et al., 2018). The Jiuzhaigou earthquake is in the Pingwu potential seismic-prone area in western China, which has the seismic geological conditions for the occurrence of large earthquakes, with the upper limit of magnitude 7.5. The Jiuzhaigou earthquake is in the transition zone from the Sichuan Basin to west Sichuan Plateau, which belongs to the middle–high mountainous erosion landform. Its regional terrain is high in the northwest and low in the southeast, with an average altitude of more than 4,000 m.

Here, the Jiuzhaigou earthquake area mainly includes areas with seismic intensity of VI and above (Figure 2), which extends to the Diebu County in the north, Pingwu County in the south, Wenxian County in the east, and Ruoergai County in the west. The black dashed rectangular box shown in Figure 2 was selected as the main assessment area to conduct seismic landslide hazard assessment, which is the scope of Figures 5–13 and extends to the Yuwa town in the north, Huanglong town in the south, Shuanghe town in the east, and the Baozuo town in the west.

Data and methods

Basic data such as seismic motion parameters, geology, topography, and coseismic landslides and the simplified Newmark model are used to carry out the landslide hazard assessment for the Jiuzhaigou earthquake.

Data

The geographical, geological, and surveying data are used to realize the presented study work. The regional tectonic and active fault data are obtained from the geological cloud website of the China Geological Survey (https://geocloud.cgs.gov.cn/#/home). The regional historical earthquake data and Jiuzhaigou earthquake parameters (epicenter, seismic intensity, and aftershock) are obtained from the National Earthquake Data Center (https://data.earthquake.cn/index.html). The stratigraphic lithology data used to divide the engineering geological units are obtained from the 1:200,000 geological maps. The PGA data of the Jiuzhaigou earthquake are obtained from the Strong Motion Observation Data Subcenter of the National Earthquake Data Center and related references (Yue et al., 2018). The terrain elevation data [digital elevation model (DEM)] adopt the ASTER GDEM V3 with a spatial resolution of 30 m (https://search.asf.alaska.edu/#/), from which the terrain slope data can be calculated. The publicly published coseismic landslide data triggered by the Jiuzhaigou earthquake are obtained from Tian et al. (2019), whose acquisition methods are mainly remote sensing interpretation and field verification. The vector data (such as polygon data) are converted into raster data for use in the algebraic calculations of the spatial layer, and the resolution of the raster data is 30 m. All vector and raster data operations and calculations are implemented on the ArcGIS Platform.

Methods

The Newmark model can predict seismic landslide hazards by calculating the slope displacement under seismic loading (Newmark, 1965). Its theoretical basis is the limit equilibrium theory of infinite slope. The Newmark model regards the sliding body as a rigid body and mainly considers the critical acceleration and safety factor of the sliding body itself. When the external force is greater than the critical acceleration, the finite displacement of the sliding body occurs, which accumulates continuously to produce permanent displacement (Jibson, 1993; Roberto, 2000). Based on many statistical analysis results of seismic landslides, a simplified Newmark displacement model based on statistical laws was developed (Miles and Ho, 1999; Jibson et al., 2000) and has been widely used in seismic landslide hazard assessment at the regional scale (Maharjan et al., 2021). Referring to the existing study results, the general calculation steps of the simplified Newmark model are sorted out.

Firstly, the static safety factor is calculated. The static safety factor represents the safety situation of a slope body without internal and external dynamic effects, which can be calculated by the traditional slope stability factor formula (Eq. 1) based on the limit equilibrium theory (Miles and Ho, 1999; Jibson et al., 2000). In Eq. 1, F_s is the slope static safety factor, c′ is the effective cohesion of rock and soil mass (kPa), φ′ is the effective internal friction angle of rock and soil mass (°), γ is the unit weight of rock and soil mass (kN/m³), γ_w is the unit weight of groundwater (kN/m³), t is the thickness of the potential sliding body (m), α is the inclination angle of the potential sliding surface (°), and m is the proportion of the saturated part of the total potential sliding body.

$F_s=\frac{c^{\prime }}{\gamma t\sin \alpha }+\frac{\tan {\phi }^{\prime }}{\tan \alpha }-\frac{m{\gamma }_w\tan {\phi }^{\prime }}{\gamma \tan \alpha }=\frac{c^{\prime }}{\gamma t\sin \alpha }+\left(1-\frac{m{\gamma }_w}{\gamma }\right)\times \frac{\tan {\phi }^{\prime }}{\tan \alpha }.(1)$

Secondly, the critical acceleration is calculated. The slope critical acceleration refers to the seismic motion acceleration corresponding to the sliding force of the slider equal to the anti-sliding force. The calculation formula (Eq. 2) of the slope critical acceleration was derived from the limit equilibrium state equation of the potential slider (Wilson and Keefer, 1983). In Eq. 2, a_c is the critical acceleration (m/s²), g is the gravity acceleration (m/s²), and α is the inclination angle of the sliding surface (°).

$a_c=\left(F_s-1\right)g\sin \alpha .(2)$

Finally, the seismic slope displacement and seismic landslide hazard are calculated. The seismic slope displacement can be calculated by the slope critical acceleration and PGA (Eq. 3) proposed by Jibson (2007). Based on the statistical analysis of a large number of existing study results, the seismic slope displacement can also be expressed as a functional relationship between the slope critical acceleration and the Arias intensity (Eq. 4) (Jibson et al., 2000; Jibson, 2007). The seismic slope displacement is positively correlated with the PGA and Arias intensity and negatively correlated with the slope critical acceleration. There are no precise conditions for using either the PGA or Arias intensity. The seismic motion parameters can be selected based on their accessibility. In Eqs 3, 4, D_n is the slope displacement, a_max is the PGA, and I_a is the Arias intensity.

$\log D_n=0.215+\log \left[{\left(1-\frac{a_c}{a_{\max }}\right)}^{2.341}{\left(\frac{a_c}{a_{\max }}\right)}^{-1.438}\right]\pm 0.510,(3)$

$\lg D_n=2.401\lg I_a-3.481\lg a_c-3.230.(4)$

The slope displacement does not mean that there will be a significant landslide. Only when the slope displacement accumulates to a certain extent, do the slope masses lose their stability and slide along the sliding surface to cause a landslide. Therefore, the landslide occurrence is a probability problem. The seismic landslide probability can be calculated using the statistical relationship formula (Eq. 5) proposed by Jibson et al. (2000). In Eq. 5, P(f) is the seismic landslide probability.

$P\left(f\right)=0.335\left[1-\exp \left(-0.048D_n^{1.565}\right)\right].(5)$

Seismic landslide characteristics

Remote sensing interpretation and field investigation reveal that there are 4,834 coseismic landslides in the Jiuzhaigou earthquake area (Figures 2, 3). The total landslide area is 9.64 km², and the largest landslide area is 0.24 km² (Tian et al., 2019). The coseismic landslides are mainly distributed in areas with seismic intensity of VII degree and above. These landslides are mainly composed of small- and medium-sized shallow fractured landslides, collapses, rockfalls, and rock/debris slides (Figure 4). Many shallow coseismic landslides are mostly developed in the Quaternary deposits such as residual slope deposits. The instability of rock masses occurs at the slope shoulders, forming the landslide–debris flow disaster chain. The coseismic landslides mainly develop along roads and gullies. The landslide density is relatively high in the two NE-SW-oriented valleys close to the epicenter (Fan et al., 2018; Tian et al., 2019). The highest coseismic landslide density was found at special locations where the valley shape evolves from the U-shape to V-shape, with an inclination between 20° and 50° (Chang et al., 2021). The coseismic landslides are mainly distributed in a strip area with NW-SE trending. The spatial distribution pattern of coseismic landslides has revealed that a previously unknown blind fault segment (which is possibly the north-western extension of the Huya fault) is the plausible seismogenic fault (Fan et al., 2018). The inferred result of the seismogenic fault suggests that seismic energy is released concentratedly near the epicenter and along the fault.

Figure 3

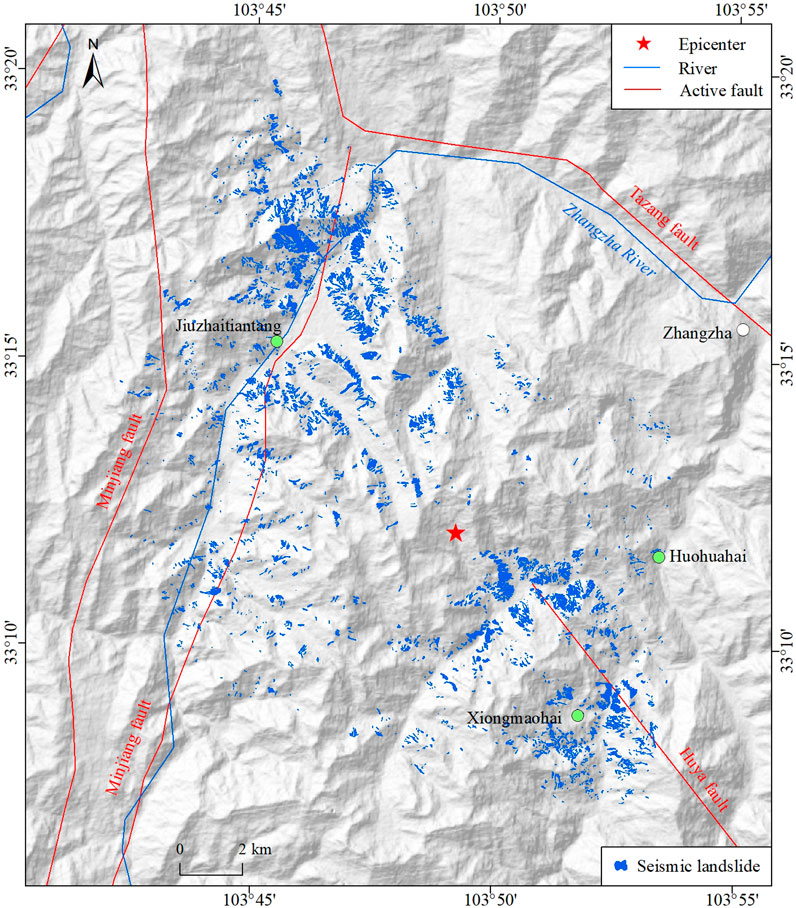
Figure 3. Spatial distribution of coseismic landslides triggered by the Ms 7.0 Jiuzhaigou earthquake. Landslide data are obtained from Tian et al. (2019).

Figure 4

Figure 4. Typical landslides triggered by the Ms 7.0 Jiuzhaigou earthquake. Landslide figures are obtained from the web and from Fan et al. (2018) and Ling et al. (2021).

Results and analysis

Based on the presented data, model, and seismic landslide characteristics, the seismic landslide hazard can be calculated, validated, and analyzed.

Result calculation

The seismic motion parameters such as the PGA and two types of Arias intensity are obtained to calculate seismic landslide hazard in the main assessment area.

Static safety factor

The physical and mechanical parameters of the rock and soil mass and terrain parameters are crucial for calculating the slop static safety factor. Comprehensively considering the geological structure, stratigraphic lithology, rock and soil type, and rock mass weathering degree, the engineering geological units in the main assessment area were divided into 11 types (Figure 5; Table 1). With reference to the existing literature (Jibson et al., 2000; Jibson, 2007; Hua et al., 2018; Yang et al., 2023), the physical and mechanical parameters for all engineering geological units were carefully initialized (Table 1). The terrain slope angle (α) was calculated from the DEM data. The thickness of the potential sliding body (t) was approximately set to 3 m for shallow landslides. The parameter γ_w was approximately 10 kN/m³. Considering the local climate and geological conditions, as well as the existing research results on seismic landslide hazards in the Xianshuihe fault zone (Zhang et al., 2017), the parameter m was approximately 0.3. The slope static safety factor was finally calculated using Eq. 1, as shown in Figure 6. The slope static safety factor in the western plateau region with a relatively flat terrain is larger, while it is smaller in the central and eastern mountainous regions with a relatively large topographic relief.

Figure 5

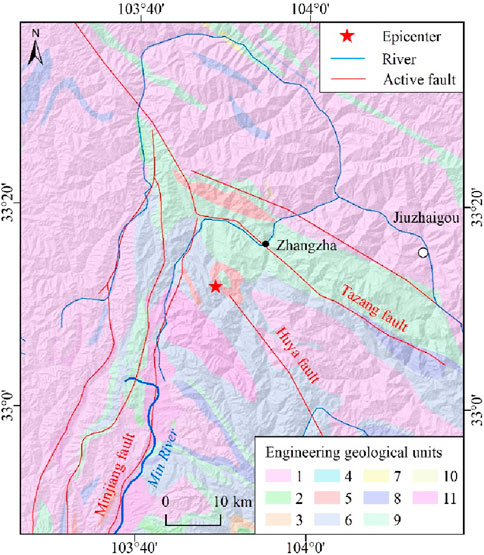
Figure 5. Engineering geological units in the main assessment area. The number of engineering geological units in the legend corresponds to ID in Table 1.

Table 1

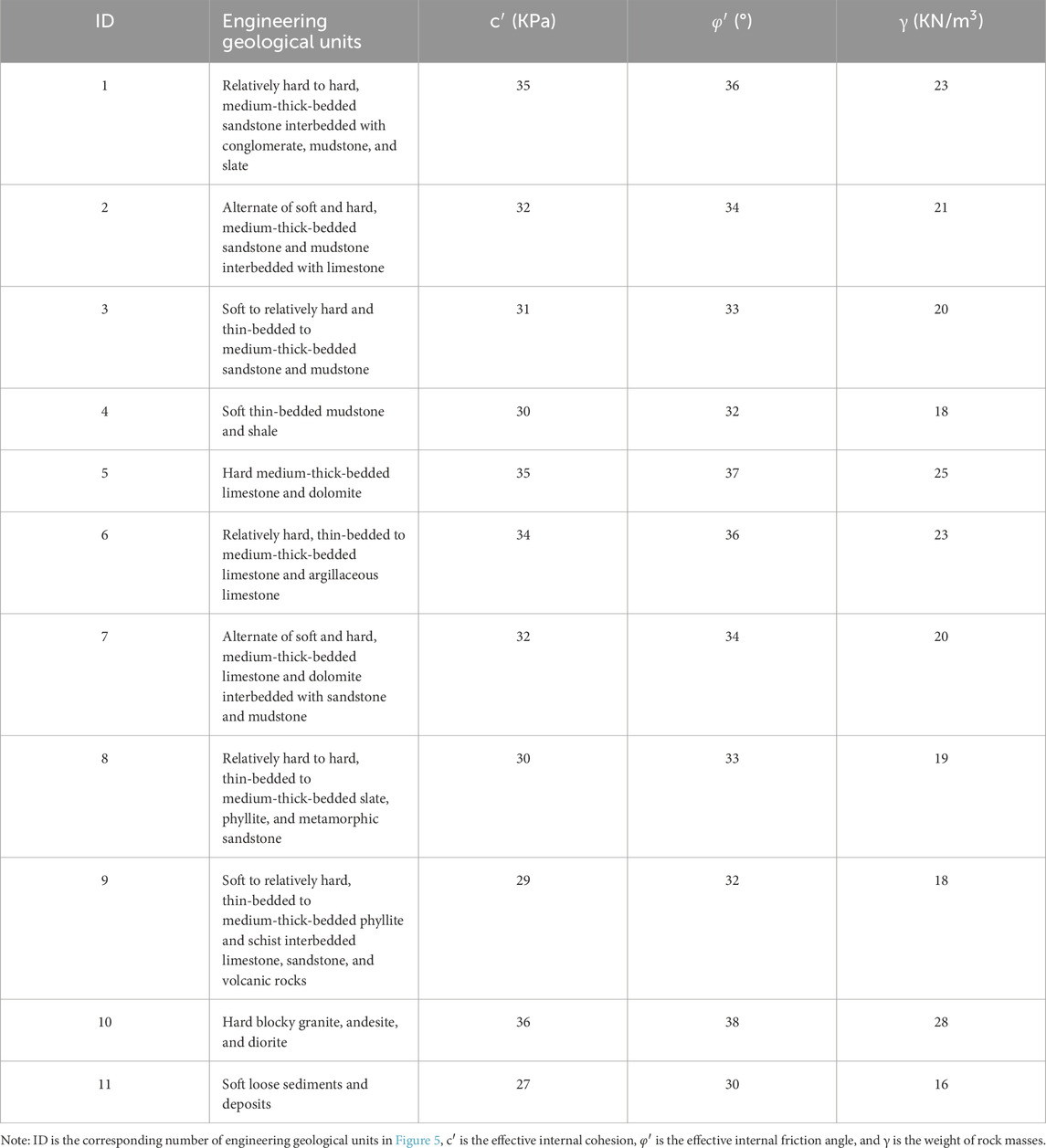
Table 1. Physical and mechanical parameters of engineering geological units in the main assessment area.

Figure 6

Figure 6. Slope static safety factor in the main assessment area.

Critical acceleration

The critical acceleration can represent the landslide sensitivity, and the smaller the static safety factor, the greater the landslide sensitivity. According to the slope static safety factor and terrain slope angle obtained above, the slope critical acceleration in the Jiuzhaigou earthquake area is calculated using Eq. 2, as shown in Figure 7. The smaller the slope static safety factor is, the smaller is the critical acceleration and the more unstable is the slope.

Figure 7

Figure 7. Slope critical acceleration in the main assessment area.

Seismic motion parameters

The Newmark model is compatible with a variety of seismic motion parameters (Jibson et al., 2000; Jibson, 2007; Zeng et al., 2023). The seismic motion parameters should be comprehensively selected according to seismic geological settings and seismogenic mechanisms. Here, the PGA and two types of Arias intensity parameters are adopted.

During the Jiuzhaigou earthquake, the China Earthquake Administration recorded the strong motion observation data. For example, the Baihe strong motion station in the Jiuzhaigou county is 30.5 km away from the epicenter, and its maximum PGA values in the east–west, north–south, and vertical directions are 129.5, 185.0, and 124.7 cm/s², respectively (National Earthquake Data Center, https://data.earthquake.cn/). Using these valuable strong motion observation data, the PGA contour of the Jiuzhaigou earthquake area is fitted (Figure 8) (Yue et al., 2018).

Figure 8

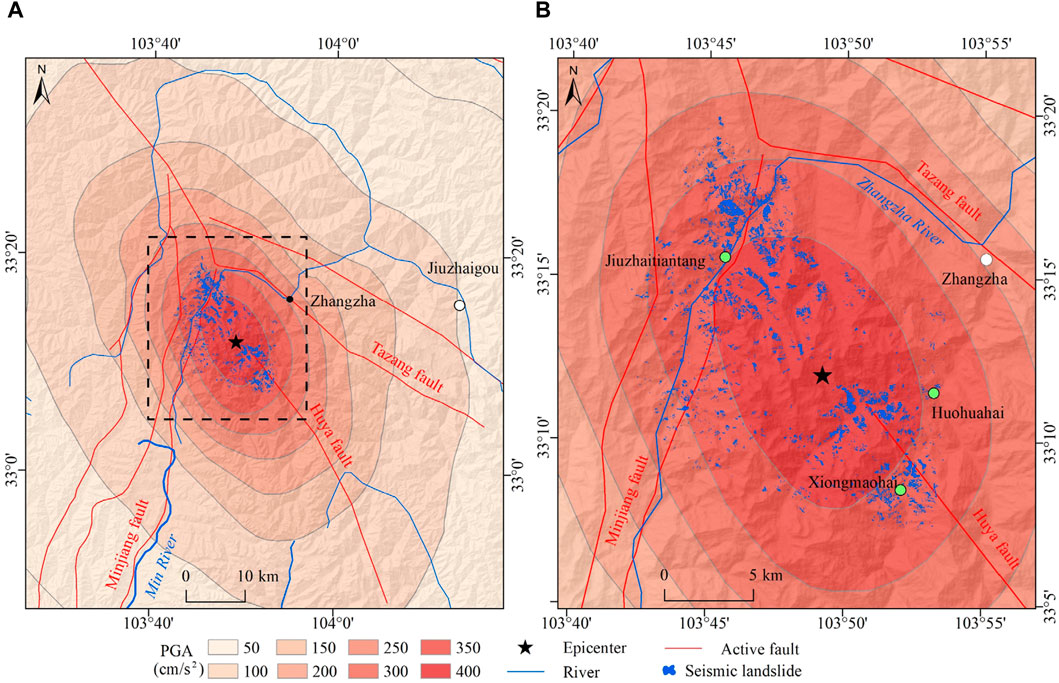
Figure 8. Peak ground acceleration in the main assessment area. The black dashed rectangular box in (A) is the scope of (B).

The Arias intensity (I_a) is a meaningful physical quantity to measure seismic intensity, which is determined by integrating the square of seismic acceleration within the duration of a strong earthquake and multiplying by a constant (Arias, 1970). At the regional scale, several complex empirical attenuation equations are developed to calculate the Arias intensity with the rupture distance parameter (Travasarou et al., 2003; Fulser-Piggott and Stafford, 2012). However, these equations require complex conditions and parameters, such as fictitious hypocentral depth, indicator variables for the soil types, indicator variables for the fault types, and average shear wave velocity. It is difficult to obtain these complex parameters in the process of urgent and rapid coseismic landslide hazard assessment. Here, the simplest empirical equation (Eq. 6) based on statistical laws is adopted, which only requires the seismic moment magnitude (M_w) and focal distance (R) (Wilson and Keefer, 1985). The focal distance is the closest distance from a particular site to the seismic source. The seismic moment magnitude can be obtained by converting the surface wave magnitude (Ms) (Eq. 7).

$\lg I_a=\left\{\begin{array}{l}{\mathrm{M}}_{\mathrm{w}}-2\lg R-4.1M_w\le 7.0\\ 0.75{\mathrm{M}}_{\mathrm{w}}-2\lg R-2.35M_w>7.0\end{array}\right.,(6)$

${\mathrm{M}}_{\mathrm{w}}=0.884{\mathrm{M}}_{\mathrm{s}}+0.951.(7)$

The epicenter of the Jiuzhaigou earthquake is used as the point focal source to calculate the focal distance using the buffer analysis method. The surface wave magnitude of the Jiuzhaigou earthquake is M_s 7.0, so the corresponding moment magnitude is M_w 6.9 using Eq. 7. The traditional Arias intensity with a point focal source (abbreviated as Arias_P) is calculated using Eq. 6, which is distributed in a circular shape in space (Figure 9). The seismic intensity, PGA, and landslides of the Jiuzhaigou earthquake all show a NW trending distribution. So, it can be inferred that the macroscopic seismic action is determined by both the epicenter and seismogenic fault. The existing study results suggest that the seismogenic fault of the Jiuzhaigou earthquake is the northern section of the Huya fault with left-lateral strike-slip characteristics. The rupture length of the seismogenic fault is approximately 33–35 km, and the rupture depth is approximately 23–26 km (Qi et al., 2018; Wang and Mao, 2022). The ground projection of the seismogenic fault is used as the linear focal source (Figure 10). The comprehensive focal distance, a kind of virtual focal distance that considers the combined influence of the point focal source (epicenter) and linear focal source (seismogenic fault), can be calculated by Eq. 8 (Zhang et al., 2017). In Eq. 8, R is the comprehensive focal distance, R_p is the point focal distance, and R_l is the linear focal distance. The Arias intensity with a comprehensive focal source (abbreviated as Arias_C) is calculated using the comprehensive focal distance (Figure 10), showing a NW trending elliptical distribution in space.

$R=\frac{R_l\left(R_p+1\right)R_{l\min }}{{\left(R_l\left(R_p+1\right)\right)}_{\max }}.(8)$

Figure 9

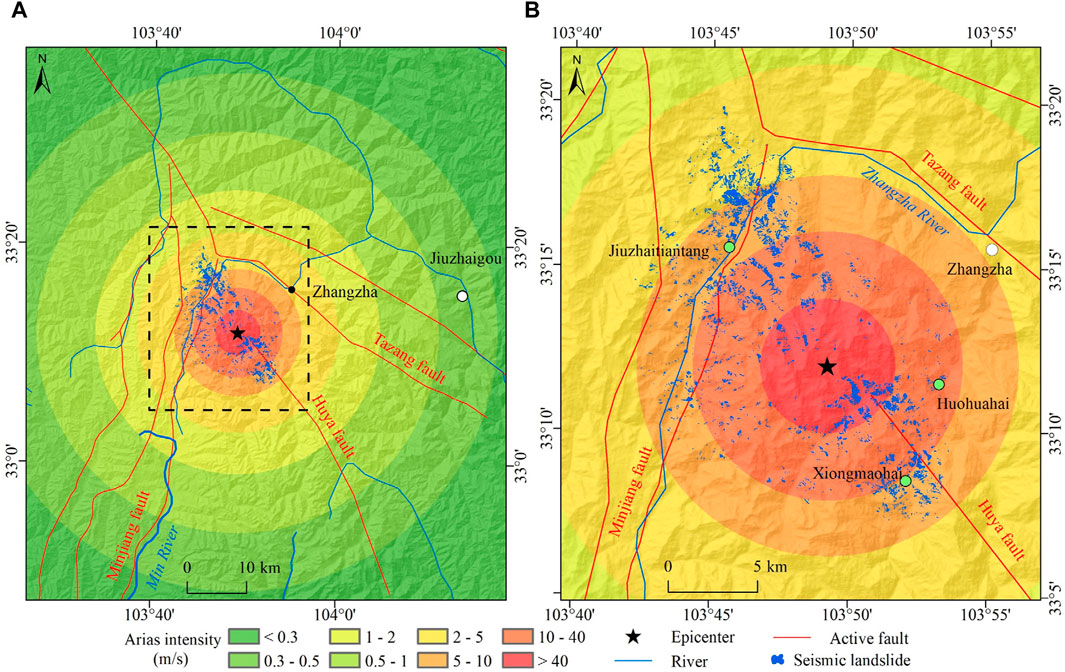
Figure 9. Arias intensity in the main assessment area (point focal source). The black dashed rectangular box in (A) is the scope of (B).

Figure 10

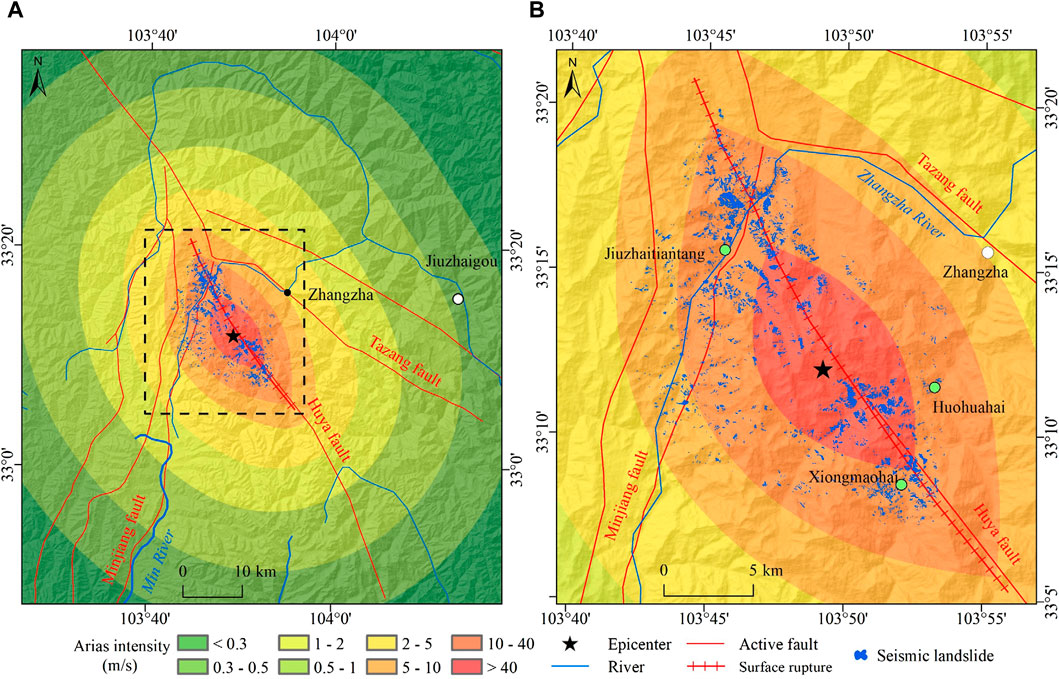
Figure 10. Arias intensity in the main assessment area (comprehensive focal source). The black dashed rectangular box in (A) is the scope of (B).

Seismic landslide hazard

The seismic landslide hazard can be represented by seismic landslide probability. The seismic slope displacement was calculated using the slope critical acceleration (Figure 7) and PGA (Figure 8) in the main assessment area. Similarly, the slope critical acceleration (Figure 7), Arias_P (Figure 9), and Arias_C (Figure 10) were used to calculate the seismic slope displacement in the main assessment area. Then, the seismic landslide probability was calculated according to the seismic slope displacement. The natural break method in the ArcGIS and field experiences are used to divide the seismic landslide hazard into 5 grades: very high (seismic landslide probability ≥25%), high (seismic landslide probability 15%–25%), middle (seismic landslide probability 5%–15%), low (seismic landslide probability 1%–5%), and very low (seismic landslide probability <1%) (Figures 11–13).

Figure 11

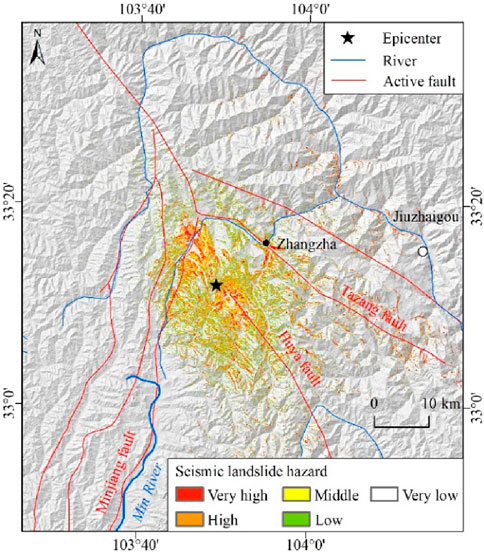
Figure 11. Seismic landslide hazard using peak ground acceleration (PGA) in the main assessment area.

Figure 12

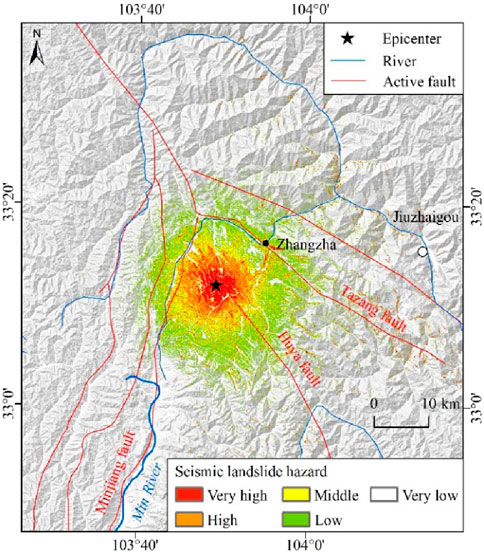
Figure 12. Seismic landslide hazard using the Arias intensity in the main assessment area (point focal source).

Figure 13

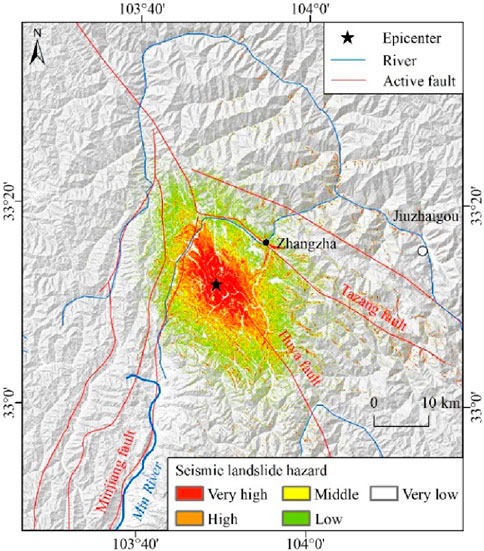
Figure 13. Seismic landslide hazard using the Arias intensity in the main assessment area (comprehensive focal source).

Result validation

The receiver operating characteristic (ROC) curve method and the coseismic landslide samples (Figure 3) are adopted to validate the results of seismic landslide hazards. The area under the curve (AUC) is used to characterize the accuracy of the mathematical model (Yilmaz, 2010; Guo et al., 2015). It is generally believed that the closer the AUC is to 1, the better the model accuracy is. When the AUC is 0.5–0.7, the model accuracy is poor; when the AUC is 0.7–0.9, the model accuracy is good; and when the AUC is above 0.9, the model accuracy is excellent.

Based on the spatial statistical correlation between seismic landslide hazards and coseismic landslide samples, the seismic landslide hazard indexes were arranged in the descending order and divided into 50 bins. The accumulative area percentage with respect to 50 bins (as the horizontal coordinate) and their corresponding accumulative area percentage of coseismic landslide samples (as the vertical coordinate) were calculated. These values of the accumulative area percentage were used to draw the desired ROC curve and calculate the AUC (Figure 14) (Chung and Fabbri, 1999). With the increase in the accumulative area percentage, the corresponding accumulative area percentage of coseismic landslides increased rapidly at a faster rate, then increased slowly, and finally reached 100%. The accuracies of seismic landslide hazard results based on the PGA, Arias_P, and Arias_C are 0.79, 0.73, and 0.82, respectively. The accuracy of seismic landslide hazard results based on Arias_C is the highest, followed by that based on PGA and Arias_P.

Figure 14

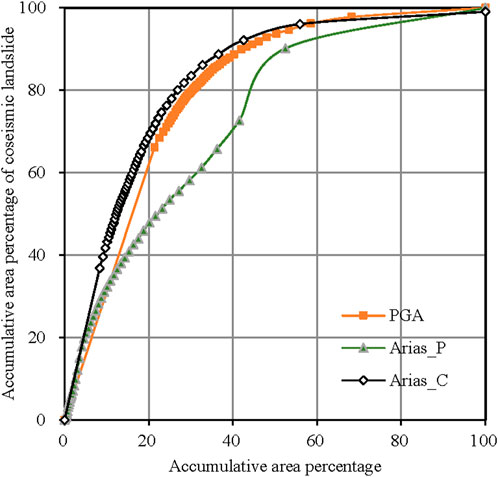
Figure 14. Receiver operating characteristic (ROC) curve of the seismic landslide hazard in the main assessment area (Arias_P indicates the Arias intensity with point focal source, and Arias_C indicates the Arias intensity with comprehensive focal source).

Result analysis

By analyzing the spatial distribution characteristics of seismic landslide hazards, it can be found that the seismic landslide hazard based on the PGA presents an approximate elliptical ring distribution. The seismic landslide hazard based on Arias_P presents a circular ring distribution. The seismic landslide hazard based on Arias_C presents an almost standard elliptical ring distribution with a major axis in the NW trend, which is more significantly affected by the seismogenic fault.

The coseismic landslides are mainly distributed in the area with seismic intensity of VII degree and above. The number of coseismic landslides with seismic intensity of VII, VIII, and IX is 47, 3,612, and 1,175, respectively. In this area, the spatial distribution characteristics of seismic landslide hazards are statistically analyzed (Table 2; Figure 15). Areas with very high and high seismic landslide hazards based on Arias_C, PGA, and Arias_P are 323 km², 317 km², and 586 km², accounting for 7.51%, 7.38%, and 13.64% of the total area, respectively. In these areas, the corresponding coseismic landslide proportion is 90.19%, 80.43%, and 64.07%, respectively. The results show that the seismic landslide hazard zone can be well identified based on the presented Arias_C parameter. The middle seismic landslide hazard and over are mainly located at areas with seismic intensity of VII degree and above, which is also the concentrated area of the coseismic landslides. The coseismic landslides are mainly distributed in the deep gullies and steep mountainous slopes on the north and south sides of the epicenter. The spatial distribution of seismic landslide hazards is in good agreement with that of the coseismic landslides.

Table 2

Table 2. Result analysis of seismic landslide hazard in the Jiuzhaigou earthquake area.

Figure 15

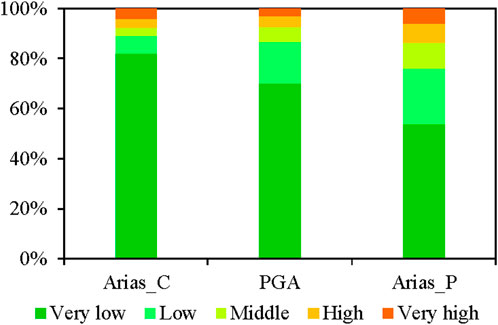
Figure 15. Statistical area proportion of the seismic landslide hazard zone in the main assessment area.

Discussion

The accuracy of seismic landslide hazard assessment is significantly affected by various factors such as seismic geological data, modeling methods, and landslide data set size and type (Comert, 2021). Many studies on seismic landslide hazard assessment have been carried out in the 2017 Jiuzhaigou earthquake area (Yue et al., 2018; Ai et al., 2022), the 2008 Wenchuan earthquake area (Li et al., 2013; Wang et al., 2016), and the 2005 Kashmir earthquake area (Kamp et al., 2008). In these studies, the Newmark model mostly used the PGA parameter and traditional point focal source, while the fault parameter (such as distance to the fault) has often been used in statistical models, such as in the transfer learning and logistic regression model (Li et al., 2013; Ai et al., 2022). Most of these results have an accuracy of above 0.80, indicating that the fault is an important parameter for seismic landslide hazard assessment (Li et al., 2013; Ai et al., 2022). It also shows the effectiveness of the proposed calculation method of the comprehensive focal distance.

The seismic energy is released concentratedly near the epicenter and along the plausible seismogenic fault, which has seriously affected the spatial distribution characteristics of coseismic landslides, that is, the elliptic distribution in the NW-SE direction. Where the fault passes through, valleys, gullies, and summit landforms are often formed, which are geographical environments prone to landslides. In particular, the coseismic landslide intensity is relatively high in the intersection area of the seismogenic fault and the Minjiang fault in the northwest of the epicenter. Among the three presented seismic motion parameters, the spatial distribution characteristics of Arias_C are more similar to those of coseismic landslides, followed by those of PGA and Arias_P. So, the newly proposed Arias intensity showed better results.

The Jiuzhaigou earthquake area presents mountainous and canyon landforms, and the number of seismic stations deployed is limited, which does not completely cover the seismic area, especially the zones along the seismogenic fault. Therefore, the simulated PGA results based on the seismic station data are biased. The PGA requires a certain number of seismic stations and simulation analyses, and so takes a long time after strong earthquakes. However, the Arias intensity can be calculated only by knowing the focal location and magnitude parameters so that the general seismic landslide hazard situation can be obtained more quickly, and it is very suitable for emergency seismic landslide hazard assessment.

The slope displacement does not necessarily mean landslide occurrence, and there is a probability problem between them. This work adopts the worldwide formula between slope displacement and landslide probability, which are obtained from the statistical analyses of many seismic landslide data (Jibson et al., 2000). However, for different seismic areas, there exit many differences in complicated geological environmental conditions such as landforms, stratigraphic lithology, and hydrogeology. So, it is necessary to further analyze coseismic landslide samples and propose a new formula between slope displacement and landslide probability, which is more suitable for the geological environmental settings in the Jiuzhaigou earthquake area.

The high and steep mountain has an obvious topographic amplification effect on seismic ground motion, and it is more significant at the mountain top. Here, the seismic landslide hazard assessment is carried out on a regional scale, and the topographic amplification effect of seismic ground motion is not considered. So, from this aspect, the current presented results are relatively conservative.

After strong earthquakes, the trend of increasing landslide development intensity lasts for several decades (Wasowski et al., 2011; Fan et al., 2019; Wu et al., 2019; Tanyas et al., 2021). This work only completes a preliminary study on the Jiuzhaigou coseismic landslide hazard. It is necessary to analyze the duration period of increasing landslide development intensity. Moreover, the long-term seismic influence should be carefully considered for the post-earthquake rainfall-triggered landslide hazard.

Conclusion

The 2017 Ms 7.0 Jiuzhaigou earthquake in the Tibetan Plateau is a valuable case because of its complex topography, landform, geological settings, and developed coseismic landslides. Based on the analysis of the geological settings and coseismic landslide development characteristics, the simplified Newmark model is used to complete the seismic landslide hazard assessment in the Jiuzhaigou earthquake area, which effectively enriches the valuable case study of seismic landslide hazard assessment.

Considering the combined effect of the point focal source (epicenter) and linear focal source (seismogenic fault), the improved calculation method is used to determine the Arias_C parameter under the constraint of seismogenic fault. A better seismic landslide hazard result has been obtained using the new Arias_C parameter. It embodies the advanced nature, precision, and practicability of the seismic landslide hazard assessment model. The Arias intensity is very suitable for rapid seismic landslide hazard assessment under emergency situations.

The seismic landslide hazard based on the Arias_C parameter shows a spatial distribution pattern with a clear elliptical ring, which indicates a significant impact of the seismogenic fault on seismic landslide development and can better identify seismic landslide hazard areas. The high and very high seismic landslide hazard is mainly distributed in the areas with seismic intensity of VIII degree. The spatial distribution pattern of seismic landslide hazards is highly consistent with that of coseismic landslides.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZY: Manuscript writing–original draft, review, and editing; methodology, investigation, and funding acquisition. GD: Manuscript writing–original draft, review, and editing; validation, software, and formal analysis. YZ: Manuscript writing–review and editing, methodology, and formal analysis. CX: Manuscript writing–review and editing, supervision, formal analysis, and data curation. PY: Manuscript writing–review and editing, investigation, and data curation. WS: Manuscript writing–review and editing, methodology, and investigation. XM: Manuscript writing–review and editing, validation, and investigation.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (42277180), State Key Laboratory of Resources and Environmental Information System, and the China Geological Survey Project (DD20221816).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai, X., Sun, B. T., and Chen, X. Z. (2022). Construction of small sample seismic landslide susceptibility evaluation model based on Transfer Learning: a case study of Jiuzhaigou earthquake. B. Eng. Geol. Environ. 81, 116. doi:10.1007/s10064-022-02601-6

CrossRef Full Text | Google Scholar

Arias, A. (1970). A measure of earthquake intensity. Seismic design for nuclear power plants. Cambridge, MA: Massachussetts Institute of Technology Press, 438–483.

Google Scholar

Cai, J. H., Zhang, L., Dong, J., Dong, X. J., Li, M. H., Xu, Q., et al. (2022). Detection and characterization of slow-moving landslides in the 2017 Jiuzhaigou earthquake area by combining satellite SAR observations and airborne lidar DSM. Eng. Geol. 305, 106730. doi:10.1016/j.enggeo.2022.106730

CrossRef Full Text | Google Scholar

Chang, M., Cui, P., Xu, L., and Zhou, Y. (2021). The spatial distribution characteristics of coseismic landslides triggered by the Ms7.0 lushan earthquake and Ms7.0 Jiuzhaigou earthquake in southwest China. Environ. Sci. Pollut. Res. 28, 20549–20569. doi:10.1007/s11356-020-11826-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Y., Wang, J., and He, Y. (2023). Prediction models of newmark sliding displacement of slopes using deep neural network and mixed-effect regression. Comput. Geotech. 156, 105264. doi:10.1016/j.compgeo.2023.105264

CrossRef Full Text | Google Scholar

Chousianitis, K., Del, G. V., and Kalogeras, I. (2014). Predictive model of Arias intensity and Newmark displacement for regional scale evaluation of earthquake-induced landslide hazard in Greece. Soil Dyn. Earthq. Eng. 65, 11–29. doi:10.1016/j.soildyn.2014.05.009

CrossRef Full Text | Google Scholar

Chung, C. J. F., and Fabbri, A. G. (1999). Probabilistic prediction models for landslide hazard mapping. Photogramm. Eng. Rem. S. 65 (12), 1389–1399. doi:10.1016/S0924-2716(99)00030-1

CrossRef Full Text | Google Scholar

Comert, R. (2021). Investigation of the effect of the dataset size and type in the earthquake-triggered landslides mapping: a case study for the 2018 hokkaido iburu landslides. Front. Earth Sci. 9, 633665. doi:10.3389/feart.2021.633665

CrossRef Full Text | Google Scholar

Dai, F. C., Xu, C., Yao, X., Xu, L., Tu, X. B., and Gong, Q. M. (2011). Spatial distribution of landslides triggered by the 2008 Ms8.0 wenchuan earthquake, China. J. Asian Earth Sci. 40 (4), 883–895. doi:10.1016/j.jseaes.2010.04.010

CrossRef Full Text | Google Scholar

Dai, L. X., Fan, X. M., Wang, X., Fang, C. Y., Zou, C. B., Tang, X. C., et al. (2023). Coseismic landslides triggered by the 2022 luding Ms6.8 earthquake, China. Landslides 20, 1277–1292. doi:10.1007/s10346-023-02061-3

CrossRef Full Text | Google Scholar

Deng, Q. D., Chen, S. F., and Zhao, X. L. (1994). Tectonics, scismisity and dynamics of longmenshan mountains and its adjacent regions. Seismol. Geol. 16 (4), 389–403. (in Chinese with English abstract).

Google Scholar

Du, W., and Wang, G. (2014). Fully probabilistic seismic displacement analysis of spatially distributed slopes using spatially correlated vector intensity measures. Earthq. Engng Struct. Dyn. 43, 661–679. doi:10.1002/eqe.2365

CrossRef Full Text | Google Scholar

Du, W., and Wang, G. (2016). A one-step Newmark displacement model for probabilistic seismic slope displacement hazard analysis. Eng. Geol. 205, 12–23. doi:10.1016/j.enggeo.2016.02.011

CrossRef Full Text | Google Scholar

Fan, X. M., Scaringi, G., Korup, O., West, A. J., Westen Cees, J. V., Tanyas, H., et al. (2019). Earthquake-induced chains of geologic hazards: patterns, mechanisms, and impacts. Rev. Geophys. 57 (2), 421–503. doi:10.1029/2018RG000626

CrossRef Full Text | Google Scholar

Fan, X. M., Scaringi, G., Xu, Q., Zhan, W. W., Dai, L. X., Li, Y. S., et al. (2018). Coseismic landslides triggered by the 8th August 2017 Ms 7.0 Jiuzhaigou earthquake (sichuan, China): factors controlling their spatial distribution and implications for the seismogenic blind fault identification. Landslides 15 (5), 967–983. doi:10.1007/s10346-018-0960-x

CrossRef Full Text | Google Scholar

Foulser-Piggott, R., and Stafford, P. J. (2012). A predictive model for Arias intensity at multiple sites and consideration of spatial correlations. Earthq. Engng. Struct. Dyn. 41 (3), 431–451. doi:10.1002/eqe.1137

CrossRef Full Text | Google Scholar

Gade, M., Nayek, P. S., and Dhanya, J. (2021). A new neural network–based prediction model for Newmark’s sliding displacements. B. Eng. Geol. Environ. 80, 385–397. doi:10.1007/s10064-020-01923-7

CrossRef Full Text | Google Scholar

Gorum, T., and Carranza, E. G. M. (2015). Control of style-of-faulting on spatial pattern of earthquake-triggered landslides. Int. J. Environ. Sci. Technol. 12, 3189–3212. doi:10.1007/s13762-015-0752-y

CrossRef Full Text | Google Scholar

Guo, C., Montgomery, D. R., Zhang, Y., Wang, K., and Yang, Z. H. (2015). Quantitative assessment of landslide susceptibility along the Xianshuihe fault zone, Tibetan plateau, China. Geomorphology 248, 93–110. doi:10.1016/j.geomorph.2015.07.012

CrossRef Full Text | Google Scholar

Hua, J. X., Zheng, J. G., and Wang, D. L. (2018). Engineering geology handbook (fifth edition) of China. Beijing: China architecture and building press. in Chinese.

Google Scholar

Jibson, R. W. (1993). Predicting earthquake-induced landslide displacements using newmark’s sliding block analysis. Transp. Res. Rec. 1411, 9–17.

Google Scholar

Jibson, R. W. (2007). Regression models for estimating coseismic landslide displacement. Eng. Geol. 91 (2-3), 209–218. doi:10.1016/j.enggeo.2007.01.013

CrossRef Full Text | Google Scholar

Jibson, R. W., Harp, E. L., and Michael, J. A. (2000). A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 58 (3–4), 271–289. doi:10.1016/S0013-7952(00)00039-9

CrossRef Full Text | Google Scholar

Kamp, U., Growley, B. J., Khattak, G. A., and Owen, L. A. (2008). GIS-based landslide susceptibility mapping for the 2005 Kashmir earthquake region. Geomorphology 101 (4), 631–642. doi:10.1016/j.geomorph.2008.03.003

CrossRef Full Text | Google Scholar

Li, W. L., Huang, R. Q., Tang, C., Xu, Q., and Westen, C. V. (2013). Co-Seismic landslide inventory and susceptibility mapping in the 2008 wenchuan earthquake disaster area, China. J. Mt. Sci. 10 (3), 339–354. doi:10.1007/s11629-013-2471-5

CrossRef Full Text | Google Scholar

Li, X. N., Ling, S. X., Sun, C. W., Xu, J. X., and Huang, T. (2019). Integrated rockfall hazard and risk assessment along highways: an example for Jiuzhaigou area after the 2017 Ms 7.0 Jiuzhaigou earthquake, China. J. Mt. Sci. 16 (6), 1318–1335. doi:10.1007/s11629-018-5355-x

CrossRef Full Text | Google Scholar

Ling, S. X., Sun, C. W., Li, X. N., Ren, Y., Xu, J. X., and Huang, T. (2021). Characterizing the distribution pattern and geologic and geomorphic controls on earthquake-triggered landslide occurrence during the 2017 Ms 7.0 Jiuzhaigou earthquake, sichuan, China. Landslides 18, 1275–1291. doi:10.1007/s10346-020-01549-6

CrossRef Full Text | Google Scholar

Liu, J., Shi, J., Wang, T., and Wu, S. (2018). Seismic landslide hazard assessment in the Tianshui area, China, based on scenario earthquakes. B. Eng. Geol. Environ. 77, 1263–1272. doi:10.1007/s10064-016-0998-8

CrossRef Full Text | Google Scholar

Ma, S., and Xu, C. (2019). Assessment of co-seismic landslide hazard using the Newmark model and statistical analyses: a case study of the 2013 Lushan, China, Mw6.6 earthquake. Nat. Hazards 96, 389–412. doi:10.1007/s11069-018-3548-9

CrossRef Full Text | Google Scholar

Maharjan, S., Gnyawali, K. R., Tannant, D. D., Xu, C., and Lacroix, P. (2021). Rapid terrain assessment for earthquake-triggered landslide susceptibility with high-resolution DEM and critical acceleration. Front. Earth Sci. 9, 689303. doi:10.3389/feart.2021.689303

CrossRef Full Text | Google Scholar

Miles, S. B., and Ho, C. L. (1999). Rigorous landslide hazard zonation using newmark’s method and stochastic ground motion simulation. Soil Dyn. Earthq. Eng. 18, 305–323. doi:10.1016/S0267-7261(98)00048-7

CrossRef Full Text | Google Scholar

Nayek, P. S., and Gade, M. (2021). Seismic landslide hazard assessment of central seismic gap region of Himalaya for a Mw 8.5 scenario event. Acta geophys. 69, 747–759. doi:10.1007/s11600-021-00572-y

CrossRef Full Text | Google Scholar

Nayek, P. S., and Gade, M. (2022). Artificial neural network-based fully data-driven models for prediction of newmark sliding displacement of slopes. Neural comput. Appl. 34 (11), 9191–9203. doi:10.1007/s00521-022-06945-8

CrossRef Full Text | Google Scholar

Nefeslioglu, H. A., Duman, T. Y., and Durmaz, S. (2006). Landslide susceptibility mapping for A part of tectonic kelkit valley (eastern black sea region of Turkey). Geomorphology 94 (3–4), 401–418. doi:10.1016/j.geomorph.2006.10.036

CrossRef Full Text | Google Scholar

Newmark, N. M. (1965). Effects of earthquakes on dams and embankments. Geotechnique 15 (2), 139–160. doi:10.1680/geot.1965.15.2.139

CrossRef Full Text | Google Scholar

Nowicki, M. A., Wald, D. J., Hamburger, M. W., Hearne, M., and Thompson, E. M. (2014). Development of A Globally applicable model for near real-time prediction of seismically induced landslides. Eng. Geol. 173, 54–65. doi:10.1016/j.enggeo.2014.02.002

CrossRef Full Text | Google Scholar

Pareek, N., Pal, S., Kaynia, A. M., and Sharma, M. L. (2014). Empirical-based seismically induced slope displacements in A geographic information System environment: a case study. Georisk Assess. Manage. Risk Eng. Syst. Geohazards. 8 (4), 258–268. doi:10.1080/17499518.2014.980273

CrossRef Full Text | Google Scholar

Qi, Y. P., Long, F., Xiao, B. F., Lu, Q., and Jiang, P. (2018). Focal mechanism solutions and tectonic stress field characteristics of the 2017 Ms7.0 Jiuzhaigou earthquake sequence. Acta. geo. Sin. 39 (5), 622–634. (in Chinese with English abstract). doi:10.3975/cagsb.2018.061901

CrossRef Full Text | Google Scholar

Rathje, E. M., and Saygili, G. (2008). Probabilistic seismic hazard analysis for the sliding displacement of slopes: scalar and vector approaches. J. Geotech. Geoenviron. Eng. 134 (6), 804–814. doi:10.1061/(ASCE)1090-0241(2008)134:6(804)

CrossRef Full Text | Google Scholar

Ren, J. J., Xu, X. W., Yeats, R. S., and Zhang, S. M. (2013). Millennial slip rates of the Tazang fault, the eastern termination of Kunlun fault: implications for strain partitioning in eastern tibet. Tectonophysics 608, 1180–1200. doi:10.1016/j.tecto.2013.06.026

CrossRef Full Text | Google Scholar

Roberto, R. (2000). Seismically induced landslide displacements: a predictive model. Eng. Geol. 58 (3–4), 337–351. doi:10.1016/S0013-7952(00)00042-9

CrossRef Full Text | Google Scholar

Song, Y. Q., Gong, J. H., Gao, S., Wang, D. C., Cui, T. J., Li, Y., et al. (2012). Susceptibility assessment of earthquake-induced landslides using bayesian network: a case study in beichuan, China. Comput. Geosci. 42, 189–199. doi:10.1016/j.cageo.2011.09.011

CrossRef Full Text | Google Scholar

Sun, J. B., Yue, H., Shen, Z. K., Fang, L. H., Zhan, Y., and Sun, X. Y. (2018). The 2017 Jiuzhaigou earthquake: a complicated event occurred in A young fault System. Geophys. Res. Lett. 45 (5), 2230–2240. doi:10.1002/2017GL076421

CrossRef Full Text | Google Scholar

Tanyas, H., Kirschbaum, D., Gorum, T., van Westen, C. J., and Lombardo, L. (2021). New insight into post-seismic landslide evolution processes in the tropics. Front. Earth Sci. 9, 700546. doi:10.3389/feart.2021.700546

CrossRef Full Text | Google Scholar

Tian, Y. Y., Xu, C., Ma, S. Y., Xu, X. W., Wang, S. Y., and Zhang, H. (2019). Inventory and spatial distribution of landslides triggered by the 8th August 2017 MW 6.5 Jiuzhaigou earthquake, China. J. Earth Sci. 30, 206–217. doi:10.1007/s12583-018-0869-2

CrossRef Full Text | Google Scholar

Travasarou, T., Bray, J. D., and Abrahamson, N. A. (2003). Empirical attenuation relationship for Arias intensity. Earthq. Engng. Struct. Dyn. 32 (7), 1133–1155. doi:10.1002/eqe.270

CrossRef Full Text | Google Scholar

Wang, X. M., and Mao, H. (2022). Spatio-temporal evolution of post-seismic landslides and debris flows: 2017 Ms 7.0 Jiuzhaigou earthquake. Environ. Sci. Pollut. Res. 29, 15681–15702. doi:10.1007/s11356-021-16789-9

CrossRef Full Text | Google Scholar

Wang, Y., Song, C. Z., Lin, Q. G., and Li, J. (2016). Occurrence probability assessment of earthquake-triggered landslides with Newmark displacement values and logistic regression: the Wenchuan earthquake, China. Geomorphology 258, 108–119. doi:10.1016/j.geomorph.2016.01.004

CrossRef Full Text | Google Scholar

Wasowski, J., Keefer, D. K., and Lee, C. (2011). Toward the next generation of research on earthquake-induced landslides: current issues and future challenges. Eng. Geol. 122 (1-2), 1–8. doi:10.1016/j.enggeo.2011.06.001

CrossRef Full Text | Google Scholar

Wilson, R. C., and Keefer, D. K. (1983). Dynamic analysis of A slope failure from the 6 August 1979 coyote lake, California, earthquake. B. Eng. Geol. Environ. 73 (3), 863–877. doi:10.1785/bssa0730030863

CrossRef Full Text | Google Scholar

Wilson, R. C., and Keefer, D. K. (1985). Predicting areal limits of earthquake induced landsliding. Geol. Surv. Prof. Pap. 1360, 317–345.

Google Scholar

Wu, Z. H., Barosh, P. J., Ha, G. H., Yao, X., Xu, Y. Q., and Liu, J. (2019). Damage induced by the 25 april 2015 Nepal earthquake in the Tibetan border region of China and increased post-seismic hazards. Nat. Hazard. Earth Syst. Sci. 19 (4), 873–888. doi:10.5194/nhess-19-873-2019

CrossRef Full Text | Google Scholar

Yang, Z. H., Guo, C. B., Wu, R. A., Shao, W. W., Yu, P. F., and Li, C. H. (2023). Potential seismic landslide hazard and engineering effect in the ya’an-linzhi section of the sichuan-tibet transportation corridor, China. China Geol. 6, 1–13. doi:10.31035/cg2023032

CrossRef Full Text | Google Scholar

Yao, X., Tham, L. G., and Dai, F. C. (2008). Landslide susceptibility mapping based on support vector machine: a case study on natural slopes of Hong Kong, China. Geomorphology 101, 572–582. doi:10.1016/j.geomorph.2008.02.011

CrossRef Full Text | Google Scholar

Yilmaz, I. (2010). Comparison of landslide susceptibility mapping methodologies for koyulhisar, Turkey: conditional probability, logistic regression, artificial neural networks, and support vector machine. Environ. Earth Sci. 61 (4), 821–836. doi:10.1007/s12665-009-0394-9

CrossRef Full Text | Google Scholar

Yue, X. L., Wu, S. H., Yin, Y. H., Gao, J. B., and Zheng, J. Y. (2018). Risk identification of seismic landslides by joint newmark and rockfall analyst models: a case study of roads affected by the Jiuzhaigou earthquake. Int. J. Disast. Risk Sci. 9, 392–406. doi:10.1007/s13753-018-0182-9

CrossRef Full Text | Google Scholar

Zeng, Y., Zhang, Y., Liu, J., Wang, Q., and Zhu, H. (2023). Rapid emergency response assessment of earthquake-induced landslides driven by fusion of InSAR deformation data and newmark physical models. Remote Sens. 15, 4605. doi:10.3390/rs15184605

CrossRef Full Text | Google Scholar

Zhang, Y. S., Dong, S. W., Hou, C. T., Guo, C. B., Yao, X., Li, B., et al. (2013). Geohazards induced by the lushan Ms7.0 earthquake in sichuan province, southwest China: typical examples, types and distributional characteristics. Acta. geo. Sin. 87 (3), 646–657. doi:10.1111/1755-6724.12076

CrossRef Full Text | Google Scholar

Zhang, Y. S., Yang, Z. H., Guo, C. B., Wang, T., Wang, D. H., and Du, G. L. (2017). Predicting landslide scenes under potential earthquake scenarios in the Xianshuihe fault zone, southwest China. J. Mt. Sci. 14 (7), 1262–1278. doi:10.1007/s11629-017-4363-6

CrossRef Full Text | Google Scholar