Application of the principal component analysis–cloud model in the assessment of the seismic stability of slopes

The seismic stability assessment of slopes is important for the evaluation of slope instability, so an accurate estimation of the seismic stability level of slopes is vital. However, many factors affect the seismic stability of slopes, and their instability has a certain fuzziness and randomness. The principal component analysis–cloud model is introduced at first to assess the seismic stability of slopes. Second, the index coefficients are calculated using the principal component analytical method. Then, the characteristic value of the normal cloud model is obtained based on the classification standards of different indexes, and the relevant evaluation model is established. The conclusions are drawn that the method is feasible for the accurate assessment of the seismic stability of slopes, and its accuracy is very high. So, the suggested model can be widely applied in many fields, and a new approach can be provided for the future seismic stability assessment of slopes.

1 Introduction

As the main type of landslide in the western mountain area of China, the earthquake landslide is a kind of main secondary disasters triggered by a strong earthquake that has the characteristics of wide distribution, strong burst, and large quantity; it often causes road disruption, river blockage, house collapse, lifeline project damage, etc. So, it seriously hinders the rescue work after the earthquake and aggravates the impact of earthquake disasters (Azarafza et al., 2021; Nanehkaran et al., 2021; Cemiloglu et al., 2023; Nanehkaran et al., 2023).

The losses caused by earthquake-induced landslides in many earthquake-prone countries are often more significant than those directly caused by earthquakes. For example, in the last century, landslides caused by earthquakes at home and abroad have killed tens of thousands of people and caused losses of one billion million yuan (Azarafza et al., 2021). In 1964, seismic landslides in Alaska caused a loss of $640 million, which accounts for 64% of the total loss. Furthermore, the total death toll reached 130. In total, 48 people died in landslides triggered by the earthquake (Nanehkaran et al., 2023). In addition, in China, there are also many examples of earthquake-induced landslides, one notable instance being the large-scale landslide caused by the MS8.5 earthquake in Haiyuan, Ningxia Province, on 16 December 1920 (Cemiloglu et al., 2023). The landslide covered an area of 31 km². A total of 503 landslides occurred, and more than 500,000 people were killed or injured; many of them were caused by landslides. The enormous disaster-causing capacity of earthquake-induced landslides has been widely considered by the government and scientific and technological circles (Nanehkaran et al., 2021). Hence, it is of great theoretical and practical significance to predict the seismic stability of slopes (Gu and Wu, 2019).

Many researchers (Zhou et al., 2018; Song et al., 2023) provided various methods to assess the seismic stability of slopes. The quasi-static or finite element methods for slope stability analysis are often adopted; for example, the critical problem of dynamic analysis of slope using FLAC3D was discussed in detail by Jing et al. (2022); the dynamic factor of safety method was proposed by Gu et al. (2019) to provide the variation in the slope factor of safety with the time history of the earthquake; and some scholars have put forward a more suitable two-polar method to predict the seismic collapse of slopes (Gu et al., 2021). The first-order prediction method is the primary criterion of earthquake collapse-slip (Liu et al., 2004; Zhou et al., 2015), and many methods are proposed for the secondary prediction (Wu and Li, 2004; Zhou et al., 2016; Jing et al., 2020). Wang Yuqing et al. (Gu and Wu, 2016; Chen et al., 2022; Gu et al., 2022) suggested four feasible calculation schemes for the comprehensive index method and provided two improved formulas for the comprehensive platform index method for predicting seismic collapse. Then, the catastrophe progression method (GuWu and Ma, 2022) was adopted by Jin et al. to predict the stability of seismic slopes; Gao et al. (Wang and Wu, 2001) provided a practical approach and a specific calculation process to judge the seismic stability of slopes using the gray correlation analysis based on the standard slope samples. In addition, Persichillo et al. (Bi et al., 2016) assessed the impact of land use changes on shallow landslide susceptibility in the northern Apennines region between 1954 and 2012 based on the long-term scale; Reichen-bach et al. (Zhou et al., 2014) found a strong relationship between forest cover and slope stability when they assessed the impact of land use change on landslide susceptibility in northeastern Sicily, Italy, since 1954.

The above-mentioned models have promoted the development of the seismic stability of the slope. However, its influential factors exhibit a considerable degree of randomness and uncertainty, and the rock and soil parameters have the characteristics of spatial uncertainty. The spatial variability determines that the rock and soil mechanics parameters do not have certain values, and their parameter mechanical values change within an uncertain range; furthermore, this range exhibits fuzzy uncertainty (Ye et al., 2019). However, the randomness and fuzziness of the occurrence of seismic landslides are not taken into consideration (Zhou and Yang, 2007) in the above methods. So, the principal component analysis–cloud model is introduced in the paper; for this method, not only the inner relationship between fuzziness and randomness is described but also the conversion between qualitative concepts and quantitative features is considered (Gao and Wang, 2005; Persichillo et al., 2017); the principal component method and cloud model are combined, and their respective advantages are sufficiently utilized. Therefore, the application of this method can improve the predictive accuracy and stability of seismic slopes. The suggested model has enormous application prospects in the future; it can provide a new method and perspective for the stability assessment of seismic slopes.

In Section 1, the engineering background in the study area is introduced. The remainder of this paper is organized as follows: in Section 2, a new predicting theory of seismic slope is correlated based on the principal component analysis–cloud model; in Section 3, the correlated model is established and the results are analyzed; and in Section 4, conclusions are drawn.

2 Methodology

2.1 Principal component analysis

The principal component analysis was introduced by Pirsson (Reichenbach et al., 2014) in 1901. The calculative procedure is as follows: assuming there are n samples and m variables in one sample, matrix $X$ is expressed as follows:

$X=\left[\begin{array}{ccc}{x}_{11}& \dots & x_{1m}\\ \dots & \dots & \dots \\ x_{1n}& \dots & x_{nm}\end{array}\right],(1)$

where $x_{nm}$ denotes the $m\text{th}$ variable in the $n\text{th}$ sample. Assuming that new variables $\begin{array}{ccc}{z}_1& z_2& z_3\end{array}$, $\begin{array}{cc}\dots ,& z_t\end{array}$ $\left(t\le m\right)$ are the synthetic index of dimensional reduction, they can be met with

$\left\{\begin{array}{c}\begin{array}{c}{z}_1=l_{11}{x}_{11}+l_{12}{x}_{12}+...+l_{1m}{x}_{1m}\\ z_2=l_{21}{x}_{21}+l_{22}{x}_{22}+...+l_{2m}{x}_{2m}\end{array}\\ \begin{array}{c}...\\ z_m=l_{m1}{x}_{m1}+l_{m2}{x}_{m2}+...+l_{mm}{x}_{mm}\end{array}\end{array}\right.,(2)$

where the means of coefficients l satisfy the following conditions: (1) the square sum of coefficients in the formula is equal to 1, (2) the principle components are independent, and (3) $z_1$ is the maximum variance of all the linear combinations for the variable $x_1,x_2,...,x_m$; $z_2$ is irrelevant of $z_1$.

According to the relevant matrix, the weight coefficients of different indicators can be expressed as follows (Zhou XP. et al., 2012):

1) The normalization of the sample matrix is as follows:

$X_{\text{ij}}=\frac{x_{ij}-\overline{x_j}}{s_i}\left(i=1,2,...,n;j=1,2,...,m\right),(3)$

$\overline{x_j}=\frac{{\displaystyle \sum _{i=1}^n}{x}_{ij}}{n},s_j^2=\frac{{\displaystyle \sum _{i=1}^n}\left(x_{ij}-\overline{x_j}\right)}{n-1},(4)$

where $x_{ij}$ denotes the normalized $j\text{th}$ index of the $i\text{th}$ sample and $\overline{x_j}$ and $s_j^2$, respectively, denote the mean and variance of the $j\text{th}$ index.

2) The relative coefficient matrix $R$ can be expressed as

$R={\left(r_{ij}\right)}_{m\times m}\left(i=1,2,...,m\right),(5)$

where $r_{ij}$ is the relative coefficient between the $i\text{th}$ and $j\text{th}$ index; $r_{ij}$ is expressed as

$r_{ij}=\frac{{\displaystyle \sum _{k=1}^m}\left(x_{ki}-\overline{x_i}\right)\left(x_{ki}-\overline{x_j}\right)}{\sqrt{{\displaystyle \sum _{k=1}^m}{\left(x_{ki}-\overline{x_i}\right)}^2{\left(x_{ki}-\overline{x_j}\right)}^2}}.(6)$

3) Calculating eigenvalues and eigenvectors of the relevant coefficient matrix $R$.

4) Calculating the number of principal components: The accumulative contribution rate is expressed as

${\nu }_{\mathrm{s}}=\raisebox{1ex}{${\lambda }_s$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{s=1}^m}{\lambda }_s$}\right.\left(s=1,2,...,m\right),(7)$

${\nu }_{\text{sumk}}=\raisebox{1ex}{${\displaystyle \sum _{s=1}^k}{\lambda }_s$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{s=1}^m}{\lambda }_s$}\right.\left(k=1,2,...,m\right),(8)$

where ${\nu }_{\mathrm{s}}$ is the contribution rate and ${\nu }_{sumk}$ is the contribution rate of accumulative variance.

5) The coefficient matrix can be expressed as

$U_k=\left(p_1,p_2,...,p_k\right).(9)$

6) Calculation of different index weights $\omega$:

$\omega =\raisebox{1ex}{$\left|U_k\times \raisebox{1ex}{${\nu }_k$}\!\left/ \!\raisebox{-1ex}{${\nu }_{sumk}$}\right.\right|$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{i=1}^k}\left|U_k\times \raisebox{1ex}{${\nu }_i$}\!\left/ \!\raisebox{-1ex}{${\nu }_{sumk}$}\right.\right|$}\right..(10)$

2.2 Normal cloud model

The cloud model, introduced by Li et al. (Zhou et al., 2008a) in the 1990s, is a cognitive model used for the two-way conversion between qualitative concepts and quantitative data. It can deal with vague and random events; the cloud model has found successfully applications in various fields (Zhou et al., 2008b).

The cloud model is defined as follows: $x,Y,C$ is assumed as a common quantitative set, where $Y$ is called the domain; in this context, $x\in Y$, $C$ is the qualitative conception in domain $Y$. If $x$ satisfies $x\sim N\left(Ex,E{n}^{,2}\right)$ and E_n satisfies $E{n}^{,}\sim N\left(En,H{e}^2\right)$, then $u\left(x\right)$ can be expressed as

$u\left(x\right)=\exp \left[-\frac{{\left(x-Ex\right)}^2}{2E{n}^{,2}}\right],(11)$

where the distribution definitive degree $u\left(x\right)$ in the domain $Y$ is named the normal cloud. For the seismic stability assessment of slopes, expectation $Ex$, entropy $En$, and hyperentropy $\frac{d{x}^{\left(1\right)}}{dt}+a{x}^{\left(1\right)}=u$ in the cloud model are depicted as

$Ex=\frac{c^{+}+c^{-}}{2},(12)$

$En=\frac{c^{+}-c^{-}}{6},(13)$

$H_{\mathrm{e}}=k_1,(14)$

where $c^{+}$ and $c^{-}$ are, respectively, the upper and lower bounds corresponding to the specific index; $k_1$ is set as 0.01 in the investigation.

3 Study area

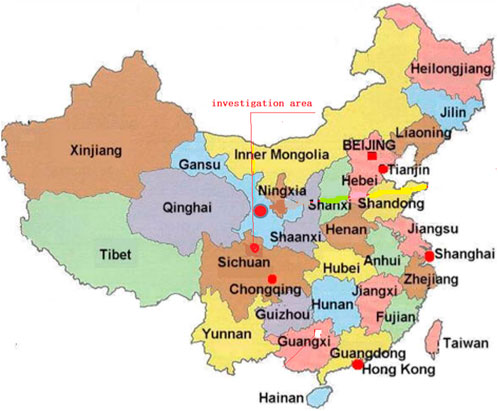
The investigation area is located in Qingchuan County, Sichuan Province, China (it is plotted in Figure 1). Its location is on the northern frontier of the Sichuan Basin, and its coordinates are east longitude 104°36′–105°38′ and north latitude 32°12′–32°56’. Its area is 3269 m², and its terrain is high in the west and low in the east. The mountains run through, and the valleys are steep. The cutting depth of the terrain is between 500 m and 1,500 m; it is divided into erosional alluvial valleys and erosional tectonic topography according to geomorphology. The area belongs to the subtropical moist monsoon type; the annual rainfall arrives at 1,021.7 mm.

FIGURE 1

FIGURE 1. Location of the survey area.

Except for the lack of Cretaceous strata in the study area, there are all other types of strata. The exposed area of the Devonian and Silurian strata is the largest. The different stratum systems are distributed along the structural line in a strip pattern. Magmatic, metamorphic, and clastic rocks are widely distributed in the stratum. Due to new and old tectonic movement, soft and hard lithologies often occur alternately. Fault structures developed in the study area: two significant faults are running through the territory.

4 Establishment of the assessment model

4.1 Construction of the index system

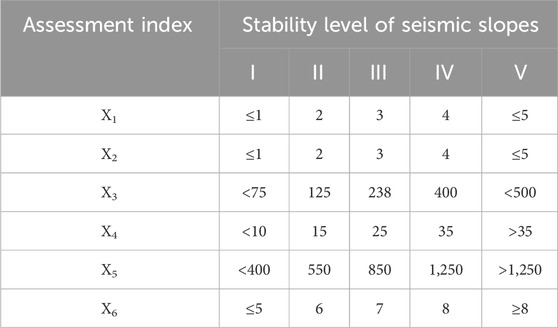
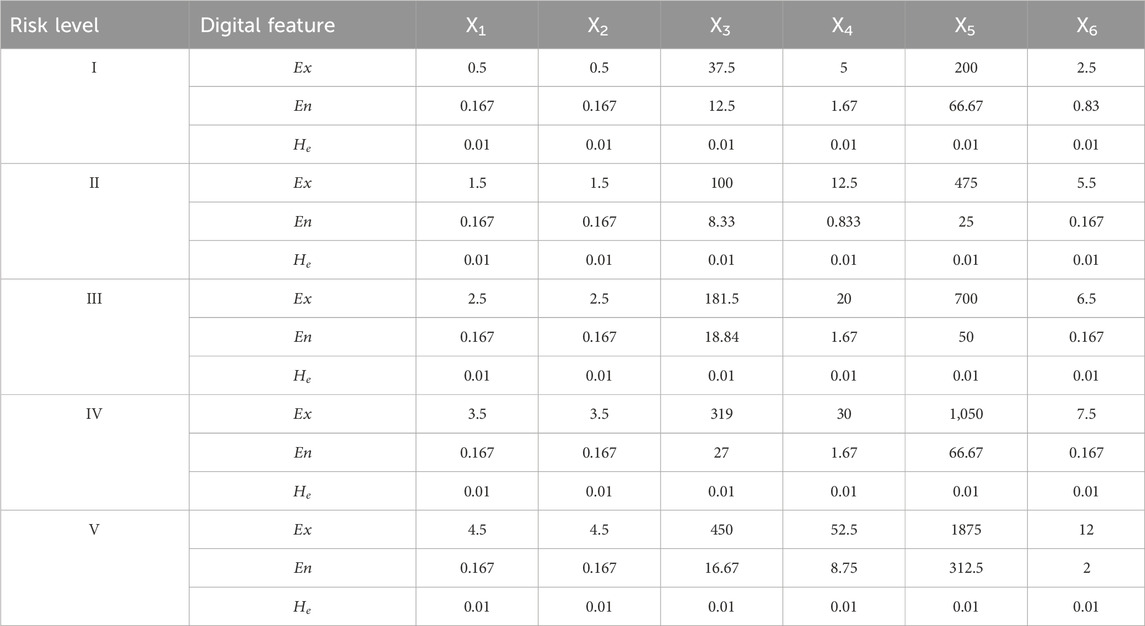
Many factors contribute to the stability of seismic slopes; according to Zhou Xiao-Ping et al. (2012); Song et al. (2021), the seismic stability of slopes is affected by six assessment indices: the value of the characteristics of rock and soil mass (X₁), value of the characteristics of neotectonic movement (X₂), slope height (X₃), slope angle (X₄), average annual rainfall (X₅), and earthquake intensity of the site (X₆). These indices are quantitative; the risk assessment is classified into five levels: extremely stable (I), stable (II), medium stable (III), unstable (IV), and extremely unstable (V), as shown in Table 1.

TABLE 1

TABLE 1. Classification standards of the assessment index.

4.2 Construction of the assessment frame

The slope’s seismic stability not only affects the normal operation of road traffic but also endangers people’s life security. Consequently, the risk evaluation of the seismic stability of the slope has great significance.

The flowchart of the assessment frame is shown in Figure 2. Its calculative process is listed as follows:

(1) The evaluation index and corresponding classification level of the assessment index are determined.

(2) The weighting coefficient of the assessment index is determined using the principal component analytical method using Eqs 3–10.

(3) The characteristic parameters $Ex$, $En$, and $\frac{d{x}^{\left(1\right)}}{dt}+a{x}^{\left(1\right)}=u$ in the cloud model are calculated using Eqs 12–14.

(4) The membership degree of each assessment index is determined when the characteristic parameters are instituted into Eq. 11.

(5) The synthetic membership degree $M$ of each level for different samples can be calculated using the following equation:

$M={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{u}_i{\omega }_i.(15)$

(6) The level corresponding to the maximum synthetic membership degree is regarded as the final risk grade of seismic slopes according to the maximum membership degree criterion.

FIGURE 2

FIGURE 2. Flowchart of the assessment frame.

4.3 Determination of index weight coefficients

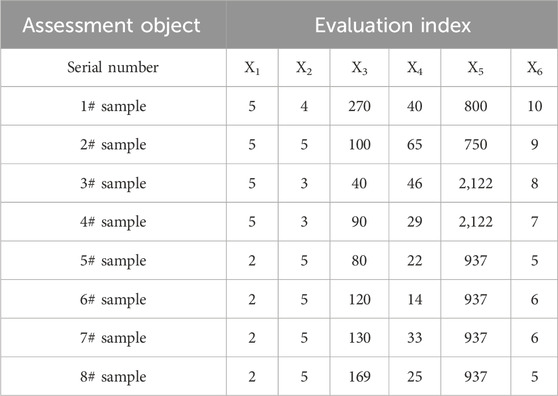
The abnormal cloud model is constructed because of the randomness and fuzziness of seismic landslides. To evaluate the weight coefficients of each assessment index, the original data of six assessment indexes are shown in Table 2.

TABLE 2

TABLE 2. Synthetic parameters of seismic slopes.

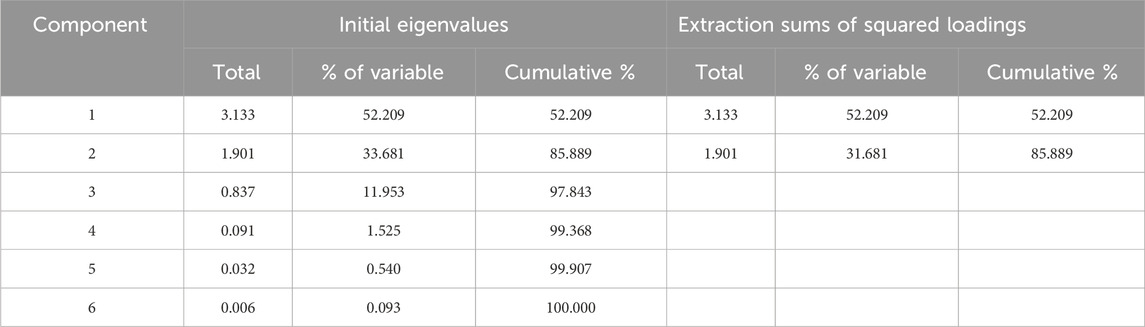
Based on Eqs 1–9, the accumulative contribution rate of the principle component is shown in Table 3.

TABLE 3

TABLE 3. Accumulative contribution rate.

It can be found in Table 3 that the accumulative contribution rate of the former two principle components arrives at 85.889%. Its magnitude is greater than 85%, so the former two principle components are selected to calculate the weight of the predicting index. According to Eqs 9, 10, the corresponding index weight is calculated as

$\omega =\left[0.254,0.112,0.285,0.239,0.007,0.102\right].(16)$

It can be found in Eq. 16 that indices X₁, X₃, and X₄ have a significant influence on the seismic stability of slopes, and the effects of the other three indices are relatively minor.

4.4 Determination of digital features in the normal cloud model

Based on Table 1, and in combination with Eqs 11–14, the classification standard of normal clouds about seismic slopes is depicted in Table 4.

TABLE 4

TABLE 4. Digital features of the cloud model.

According to Table 1, the characters of the cloud model corresponding to different indices are calculated using the forward cloud generator, which is plotted in Figure 3. Its horizontal coordinates present the magnitude of different variables; the vertical coordinates present the magnitude of the degree of certainty. A sub-figure in Figure 3 includes five grades: I, II, III, IV, and V. When a certain variable is fixed, the certainty degree of a certain point at the state grade can be obtained.

FIGURE 3

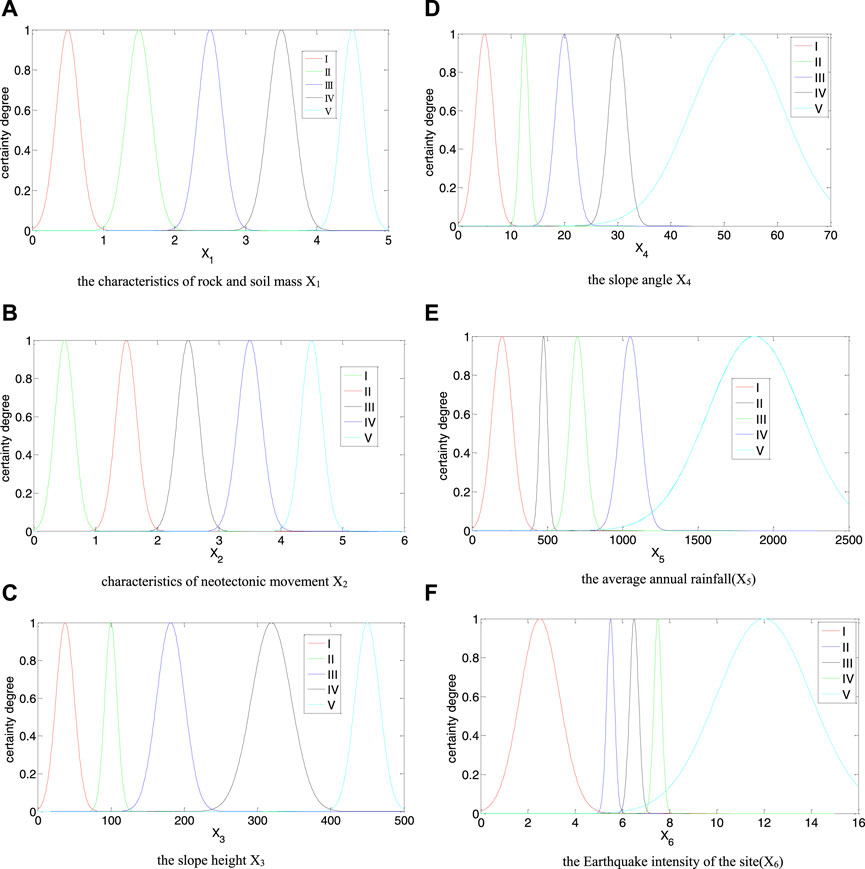
FIGURE 3. Cloud of each assessment index. (A) Characteristics of rock and soil mass X₁. (B) Characteristics of neotectonic movement X₂. (C) Slope height X₃. (D) Slope angle X₄. (E) Average annual rainfall (X₅). (F) Earthquake intensity of the site X₆.

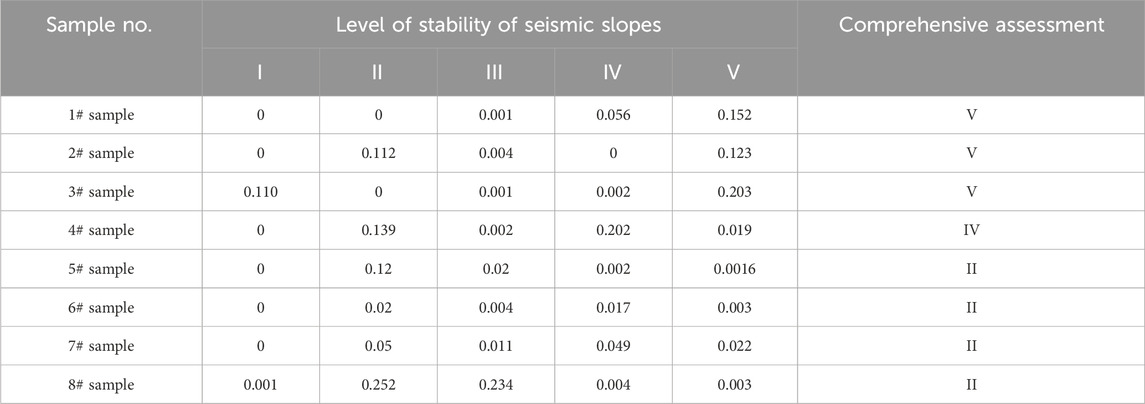
According to Tables 2, 4, and in combination with Eqs 15, 16, a comprehensive certainty degree is obtained and presented in Table 5. The results are then compared with those of the actual investigation and are plotted in Figure 4.

TABLE 5

TABLE 5. Comprehensive certainty degree of the suggested model.

FIGURE 4

FIGURE 4. Comparison results of the three methods.

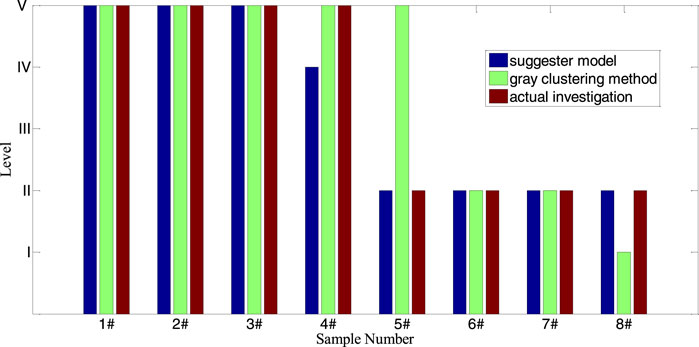
The principal component analysis–cloud model is applied to assess the seismic stability level of slopes. The whole set of outcomes is shown in Table 5. It can be seen in Figure 4 that the seismic stability levels of slopes from the 1# to 8# samples are different. The stability level from 1# to 4# samples is V, which means that these seismic slopes are extremely unstable, so the necessary consolidation measurement should be performed for these slopes; on the other hand, the stability level from 5# to 8# samples is II, which means that these seismic slopes are stable, so no measurement is required.

According to the comparative results of the different evaluation models in Figure 4, it can be concluded that the outcomes assessed using the principal component analysis–cloud method are consistent with the actual investigations for eight different samples; its accuracy arrives at 87.5%, which is higher than the results from the gray clustering method (75%) (Jing et al., 2020). The conclusion is drawn that using the text model makes it feasible to evaluate the seismic stability level of slopes.

The model not only achieves accurate results but also provides more details for the seismic stability level of slopes. For example, the stability level of the 3# sample more likely belongs to level V compared to 1# and 2# because the certainty degree of the 3# sample for level IV (0.203) is higher than that of 1# (0.152) and 2# (0.123).

In summary, the results based on the principal component analysis–cloud model can reflect the seismic stability level of slopes, providing a new method and thought for the stable evaluation of seismic slopes in the future.

5 Discussion

In comparison with the other traditional models, the fuzziness and randomness of the evaluating index are considered for the suggested model, and interval-oriented evaluation criteria are adopted. So, it improves the reliability of the assessment process and enhances the predictive accuracy of assessment results. Because the randomness and fuzziness of the evaluation index can be expressed correctly using the provided method, it can be applied to the assessment of many fields, such as the assessment of geological hazards and water quality assessment. The suggested model can be widely applied in civil engineering, hydraulic engineering, and environmental engineering in the future. Therefore, it has great application prospects.

However, some shortcomings still exist, for example, the great calculative load and the neglected correlation among the indexes; these insufficiencies limit the development of the suggested method. However, it still provides a new perspective for the stable evaluation of seismic slopes.

6 Conclusion

Taking into consideration the value of the characteristics of rock and soil mass (X₁), value of the characteristics of neotectonic movement (X₂), slope height (X₃), slope angle (X₄), average annual rainfall (X₅), and earthquake intensity of the site (X₆), a new multi-index evaluation method was introduced in this paper to evaluate the seismic stability level of slopes using the principal component analysis–cloud model. The different indexes’ weighting coefficients were calculated using the principal component analysis method. The seismic stability level of slopes is judged using the normal cloud model.

The present model is used for the seismic stability of slopes. The seismic stability levels of slopes from the 1# to 8# samples are different. The stability level from 1# to 4# samples is V, which means that these seismic slopes are extremely unstable, so the necessary consolidation measurement should be performed for these slopes; however, the stability level from 5# to 8# samples is II, which means that these seismic slopes are stable, so no measurement is needed. Finally, its outcomes are compared with the actual investigation, and the calculated results are obtained using the gray clustering method; its accuracy arrives at 87.5%, which is higher than the results from the gray clustering method (75%). Therefore, the conclusion is drawn that it is feasible to evaluate the seismic stability level of slopes using the text model, and the model not only achieves accurate results but also provides more details on the seismic stability level of slopes. In summary, the suggested method provides a new method and thought for the future seismic stable evaluation of slopes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

W-WL: investigation, methodology, and writing–original draft. E-WX: formal analysis, supervision, and writing–original draft. X-BG: conceptualization, funding acquisition, and writing–original draft. CY: software, validation, and writing–review and editing. CZ: data curation, formal analysis, visualization, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Opening Project of Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing (2022QYJ02 and 2022QYY02) and Key Scientific Research Projects of Colleges and Universities in Henan Province (23B560019).

Conflict of interest

Author E-WX was employed by China MCC Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azarafza, M., Azarafza, M., Akgün, H., Atkinson, P. M., and Derakhshani, R. (2021). Deep learning-based landslide susceptibility mapping. Sci. Rep. 11, 24112. doi:10.1038/s41598-021-03585-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, J., Zhou, X. P., and Qian, Q. H. (2016). The 3D numerical simulation for the propagation process of multiple pre-existing flaws in rock-like materials subjected to biaxial compressive loads. ROCK Mech. ROCK Eng. 49 (5), 1611–1627. doi:10.1007/s00603-015-0867-y

CrossRef Full Text | Google Scholar

Cemiloglu, A., Zhu, L., Mohammednour, A. B., Azarafza, M., and Nanehkaran, Y. A. (2023). Landslide susceptibility assessment for maragheh county, Iran, using the logistic regression algorithm. Land 12, 1397. doi:10.3390/land12071397。

CrossRef Full Text | Google Scholar

Chen, J., Shou, Y., and Zhou, X. (2022). Implementation of the novel perfectly matched layer element for elastodynamic problems in time-domain finite element method. Soil Dyn. Earthq. Eng. 152, 107054. doi:10.1016/j.soildyn.2021.107054

CrossRef Full Text | Google Scholar

Gao, Y., and Wang, X. (2005). Practical method of predicting the slope seismic stability with grey correlation method. Chin. J. Rock Mech. Rock Eng. 24 (s1), 4947–4950.(in Chinese)

Google Scholar

Gu, X.-B., Wang, Li, and Wu, Q.-H. (2022). The risk assessment of debris flow in the duba river watershed using intuitionistic fuzzy sets: TOPSIS model. Math. Problems Eng. 2022, 1–12. doi:10.1155/2022/2031907Article ID 2031907, 12 pages

CrossRef Full Text | Google Scholar

Gu, X. B., and Wu, Q. H. (2016). The application of nonordinary, state-based peridynamic theory on the damage process of the rock-like materials. Math. Problems Eng. 3 (8), 1–9. doi:10.1155/2016/9794605

CrossRef Full Text | Google Scholar

Gu, X. B., and Wu, Q. H. (2019). Seismic stability analysis of waterfront rock slopes using the modified pseudo-dynamic method. Geotechnical Geol. Eng. 37 (3), 1743–1753. doi:10.1007/s10706-018-0718-1

CrossRef Full Text | Google Scholar

Gu, X. B., Wu, Q. H., and Zhu, Y. H. (2019). The experimental investigation on the propagation process of crack for brittle rock similar material. Geotechnical Geol. Eng. 37 (6), 4731–4740. doi:10.1007/s10706-019-00934-w

CrossRef Full Text | Google Scholar

Gu, X. B., Wu, S. T., Ji, X. J., and Zhu, Y. H. (2021). The risk assessment of debris flow hazards in banshanmen gully based on the Entropy weight-normal cloud method. Adv. Civ. Eng. 8 (20), 1–11. doi:10.1155/2021/8841310

CrossRef Full Text | Google Scholar

GuWu, X.-B. Q.-H., and Ma, Y. (2022). Risk assessment of the rockburst intensity in a hydraulic tunnel using an intuitionistic fuzzy sets-TOPSIS model. Adv. Mater. Sci. Eng. 2022, 1–14. doi:10.1155/2022/4774978Article ID 4774978

CrossRef Full Text | Google Scholar

Jing, Bi, Liu, P., and Gan, F. (2020). Effects of the cooling treatment on the dynamic behavior of ordinary concrete exposed to high temperatures. Constr. Build. Mater. 248, 118688. doi:10.1016/j.conbuildmat.2020.118688

CrossRef Full Text | Google Scholar

Jing, Bi, Tang, J., Wang, C., Quan, D., and Teng, M. (2022). Crack coalescence behavior of rock-like specimens containing two circular embedded flaws. Lithosphere 2022 (Special 11), 9498148. doi:10.2113/2022/9498148

CrossRef Full Text | Google Scholar

Liu, C., Qi, S., Tong, L., and Zhang, Y. (2004). Stability analysis of slope under Earthquake in FLAC3D. Chin. J. Rock Mech. Eng. 23 (16), 2730–2733.(in chinese)

Google Scholar

Nanehkaran, Y. A., Chen, B., Cemiloglu, A., Chen, J., Anwar, S., Azarafza, M., et al. (2023). Riverside landslide susceptibility overview: leveraging artificial neural networks and machine learning in accordance with the united nations (UN) sustainable development goals. Water 15, 2707. doi:10.3390/w15152707

CrossRef Full Text | Google Scholar

Nanehkaran, Y. A., Mao, Y., Azarafza, M., Kockar, M. K., and Zhu, H.-H. (2021). Fuzzy-based multiple decision method for landslide susceptibility and hazard assessment: a case study of Tabriz, Iran. Geomechanics Eng. 24 (5), 407–418. doi:10.12989/gae.2021.24.5.407

CrossRef Full Text | Google Scholar

Persichillo, M. G., Bordeni, M., and Meisina, C. (2017). The role of land use changes in the distribution of shallow landslides. Sci. Total Environ. 574, 924–937. doi:10.1016/j.scitotenv.2016.09.125

PubMed Abstract | CrossRef Full Text | Google Scholar

Reichenbach, P., Busca, C., Mondini, A. C., and Rossi, M. (2014). The influence of land use change on landslide susceptibility zonation: the briga catchment test site (messina, Italy). Environ. Manag. 54 (6), 1372–1384. doi:10.1007/s00267-014-0357-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Z., Su, W., Tian, X., Zhang, Y., and Zhou, G. (2021). Risk analysis of tunnel construction scheme change based on field monitoring and numerical analysis. Adv. Civ. Eng. 2021, 1–15. doi:10.1155/2021/8888886Article ID 8888886, 15 pages

CrossRef Full Text | Google Scholar

Song, Z., Yang, Z., Huo, R., and Zhang, Y. (2023). Inversion analysis method for tunnel and underground space engineering: a short review. Appl. Sci. 13, 5454. doi:10.3390/app13095454

CrossRef Full Text | Google Scholar

Wang, Y., and Wu, S. (2001). Study on comprehensive index method for predicting earthquake induced landslide. Chin. J. Geotechnical Eng. 23 (3), 311–314.

Google Scholar

Wu, Z., and Li, Q. (2004). A method for evaluating dynamic safety factor rock slope seismic stability analysis. J. Disaster Prev. Mitig. Eng. 24 (3), 237–241.(in Chinese)

Google Scholar

Ye, S. H., Fang, G. W., and Ma, X. R. (2019). Reliability analysis of grillage flexible slope supporting structure with anchors considering fuzzy transitional interval and fuzzy randomness of soil parameters. Arabian J. Sci. Eng. 44, 8849–8857. doi:10.1007/s13369-019-03912-9

CrossRef Full Text | Google Scholar

Zhou, X. P., Bi, J., and Qian, Q. H. (2015). Numerical simulation of crack growth and coalescence in rock-like materials containing multiple pre-existing flaws. ROCK Mech. ROCK Eng. 48 (3), 1097–1114. doi:10.1007/s00603-014-0627-4

CrossRef Full Text | Google Scholar

Zhou, X. P., Cheng, H., and Feng, Y. F. (2014). An experimental study of crack coalescence behaviour in rock-like materials containing multiple flaws under uniaxial compression. ROCK Mech. ROCK Eng. 47 (6), 1961–1986. doi:10.1007/s00603-013-0511-7

CrossRef Full Text | Google Scholar

Zhou, X.-P., En-Ming, X., Yang, H.-Q., and Qi-Hu, Q. (2012b). Different crack sizes analyzed for surrounding rock mass around underground caverns in Jinping I hydropower station. Theor. Appl. Fract. Mech. 57 (1), 19–30. doi:10.1016/j.tafmec.2011.12.004

CrossRef Full Text | Google Scholar

Zhou, X. P., Gu, X. B., and Qian, Q. H. (2016). Seismic bearing capacity of shallow foundations resting on rock masses subjected to seismic loads. KSCE J. Civ. Eng. 20 (1), 216–228. doi:10.1007/s12205-015-0283-6

CrossRef Full Text | Google Scholar

Zhou, X. P., Xia, E. M., Yang, H. Q., and Qian, Q. H. (2012a). Different crack sizes analyzed for surrounding rock mass around underground caverns in Jinping I hydropower station. Theor. Appl. Fract. Mech. 57 (1), 19–30. doi:10.1016/j.tafmec.2011.12.004

CrossRef Full Text | Google Scholar

Zhou, X. P., and Yang, H. Q. (2007). Micromechanical modeling of dynamic compressive responses of mesoscopic heterogenous brittle rock. Theor. Appl. Fract. Mech. 48 (1), 1–20. doi:10.1016/j.tafmec.2007.04.008

CrossRef Full Text | Google Scholar

Zhou, X.-P., Zhang, J.-Z., and Wong Louis, N. Y. (2018). Experimental study on the growth, coalescence and wrapping behaviors of 3D cross-embedded flaws under uniaxial compression. ROCK Mech. ROCK Eng. 51 (5), 1379–1400. doi:10.1007/s00603-018-1406-4

CrossRef Full Text | Google Scholar

Zhou, X. P., Zhang, Y. X., Ha, Q. L., and Zhu, K. S. (2008a). Micromechanical modelling of the complete stress-strain relationship for crack weakened rock subjected to compressive loading. Rock Mech. Rock Eng. 41 (5), 747–769. doi:10.1007/s00603-007-0130-2

CrossRef Full Text | Google Scholar

Zhou, X. P., Zhang, Y. X., Ha, Q. L., and Zhu, K.-S. (2008b). Micromechanical modelling of the complete stress-strain relationship for crack weakened rock subjected to compressive loading. ROCK Mech. ROCK Eng. 41 (5), 747–769. doi:10.1007/s00603-007-0130-2

CrossRef Full Text | Google Scholar