A seismic prediction method of reservoir brittleness based on mineral composition and pore structure

The Lucaogou Formation, a typical fine-grained mixed formation in the Jimusaer Sag of the Junggar Basin, exhibits considerable potential for hydrocarbon exploration. Accurate brittle prediction is a crucial factor in determining hydraulic fracturing effectiveness. However, the area features complex lithological characteristics, including carbonate rocks, clastic rocks, volcanic rocks, and gypsum interbeds, along with thin layering and sporadic sweet spots. Traditional prediction methods offer limited resolution and there is an urgent need for a seismic brittle prediction method tailored to this complex geological environment. This paper presents a multi-mineral composition equivalent model for complex lithologies that enables the accurate calculation of Vp and Vs These ratios serve as the foundation for pre-stack elastic parameter predictions, which include Poisson’s ratio and Young’s modulus. By comparing the predicted parameters with well-logging measurements, the prediction accuracy is improved to 82%, with particularly high conformity in intervals characterized by high organic matter and clay content. Additionally, a three-dimensional brittle modeling approach reveals that the brittleness of the reservoir exceeds that of the surrounding rock, showing a gradual improvement in brittleness with increasing burial depth from southeast to northwest. The central area exhibits relatively good brittleness, with a stable, blocky distribution pattern.

1 Introduction

The Lucaogou Formation in the Jimusaer Sag of the Junggar Basin hosts significant potential for hydrocarbon exploration, with estimated recoverable resources of approximately 238 million tons (Cao et al., 2016; Liu et al., 2017; Zhi et al., 2018; Cai, 2020; Yin et al., 2021; Yin et al., 2022). This formation represents one of the oldest terrestrial mixed clastic rock sequences in China, deposited in a saline lake basin. It features complex characteristics, such as the intermixing of carbonate rocks, clastic rocks, volcanic rocks, gypsum interbeds, source-reservoir integration, thin layering, and sporadic sweet spots (Zhang et al., 2019; Duan et al., 2020; Li et al., 2020; Wang and Wang, 2021; Wei et al., 2022). Rock physics and brittleness modeling are crucial components of comprehensive oil and gas seismic-geological-engineering research in this area. The modeling results not only impact pre-drilling sweet spot predictions but also influence the optimization of reservoir hydrofracturing processes (Wang et al., 2013; Yu et al., 2016; Wu et al., 2017; Feng et al., 2020; Gui et al., 2020; Jahed et al., 2020; Shan et al., 2021).

Prediction methods for rock physics and brittleness can generally be categorized into three types: 1) brittleness prediction based on rock mineral composition, which calculates the brittleness index profile for the entire well section using the mineral composition, achieving a high level of accuracy (Mukerji et al., 1995; Zhi and Zan, 2015; Li et al., 2019; Ma et al., 2019; Ba et al., 2021; Meng et al., 2021); 2) brittleness evaluation based on rock mechanical elastic parameters, relying on vertical and horizontal well logging wave data and pre-stack inversion. It employs the Rickman formula to compute the correlation between Young’s modulus, Poisson’s ratio, and the brittleness index (Meng et al., 2015; Li et al., 2017; Gui et al., 2023); 3) utilization of uniaxial and triaxial stress-strain tests on core samples to obtain correlations between rock physical parameters, mineral composition, bedding characteristics, hydrocarbon content, and other parameters (Wang et al., 2017; Chen et al., 2019; Tao et al., 2020; Liu et al., 2021). However, as rock physics and brittleness parameters are fundamentally a result of the comprehensive response of rock material composition, structure, porosity, and fluid under specific temperature and pressure conditions, predictions based solely on mineral composition or rock mechanical parameters have inherent limitations (Li, 2022; Li, 2023).

Regarding research methods, rock physics models can be broadly classified into three categories: 1) effective medium models that use volume-averaged mineral properties, such as Voigt–Reuss–Hill models (Chung and Buessem, 1967), Hashin-Shtrikman models (Neumann and Bohlke, 2016), Wood equations, Wyllie equations (Saleh and Castagna, 2004), and Raymer equations (Raymer et al., 1980), etc.,; 2) adaptive and scattering theory models that study the influence of internal pore structure and fluids on rock properties, such as the Differential Effective Medium (DEM) model, Kuster-Toksöz model (Hu and Weng, 2000), self-consistent approximation (SCA) model (Ignatchenko and Polukhin, 2016), and Gassmann equation.; 3) contact theory models based on particle interactions, such as the Hertz contact model (Muthukumar &DesRoches, 2006). These models can reflect the brittleness characteristics of reservoirs to some extent. However, the complex interplay between mixed clastic rock’s intricate pore structure and mineral composition has made it challenging to establish a clear relationship between rock mechanical properties and geological parameters in the Lucaogou Formation of the Jimusaer Sag. Moreover, the reservoir in the study area consists of thin interbeds with multiple minerals, with each layer having a thickness of 1–4 m, making identification and prediction based solely on seismic data difficult.

In light of these challenges, this paper focuses on the Lucaogou Formation in the Jimusaer Sag, considering factors such as mineral composition and pore structure in combination to evaluate their impact on rock seismic elastic parameters. Appropriate rock physics equivalent theory models are chosen for the study area to obtain rock elastic parameters, and a brittleness index theoretical template is established to determine the spatial distribution model of reservoir brittleness. This research holds significant guidance for sweet spot predictions and fracturing process optimization.

2 Research data and methods

2.1 Research area

Jimusaer Sag is located in the southeast edge of the Junggar Basin, surrounded by Qitai uplift, Santai fault, Xidi fault and Jimusaer fault, which is in the form of a dustpan high in the east and low in the west. The Lucaogou Formation has developed throughout the entire depression, with an average thickness of about 200–350 m (Figure 1) (Yin et al., 2022; Yin et al., 2023a; Yin et al., 2023b). It belongs to the sedimentary system of saline lake basins, characterized by mixed carbonate clastic volcanic gypsum rocks, integrated source and reservoir, thin layer stacking, and dispersed desserts. The Lucaogou Formation has developed two “dessert bodies,” upper and lower. The upper dessert body is located in the second section of the Lucaogou Formation, and the lithology is mainly composed of lithic sandstone, sandy dolomite, and feldspar lithic sandstone, interbedded with mudstone and dolomite mudstone; The porosity ranges from 1.1% to 2.4%, with an average of 9.88%; Permeability at 0.01 × 10⁻³ μm²∼36.3 × 10⁻³ μm², with an average of 0.07 × 10⁻³ μm². The lower dessert body is located in the first section of the Lucaogou Formation, mainly composed of fine sandstone and cloudy sandstone, interbedded with muddy sandstone and mudstone. The porosity ranges from 2.1% to 26.5%, with an average of 8.75%; Permeability at 0.01 × 10⁻³ μm²–52.6 × 10⁻³ μm², with an average of 0.05 × 10⁻³ μm². This Formation is divided into two members, Lu1 and Lu2, and four sand groups, P₁l₁¹, P₁l₁², P₂l₂¹ and P₂l₂² from bottom to top. The major reservoirs are two sweet spot layers, the lower one (P₂l₁²)is mainly dolomitic siltstone; the upper one (P₂l₂²)is primarily composed of felsic siltstone, dolomitic siltstone and silty dolomite (Figure 1B).

FIGURE 1

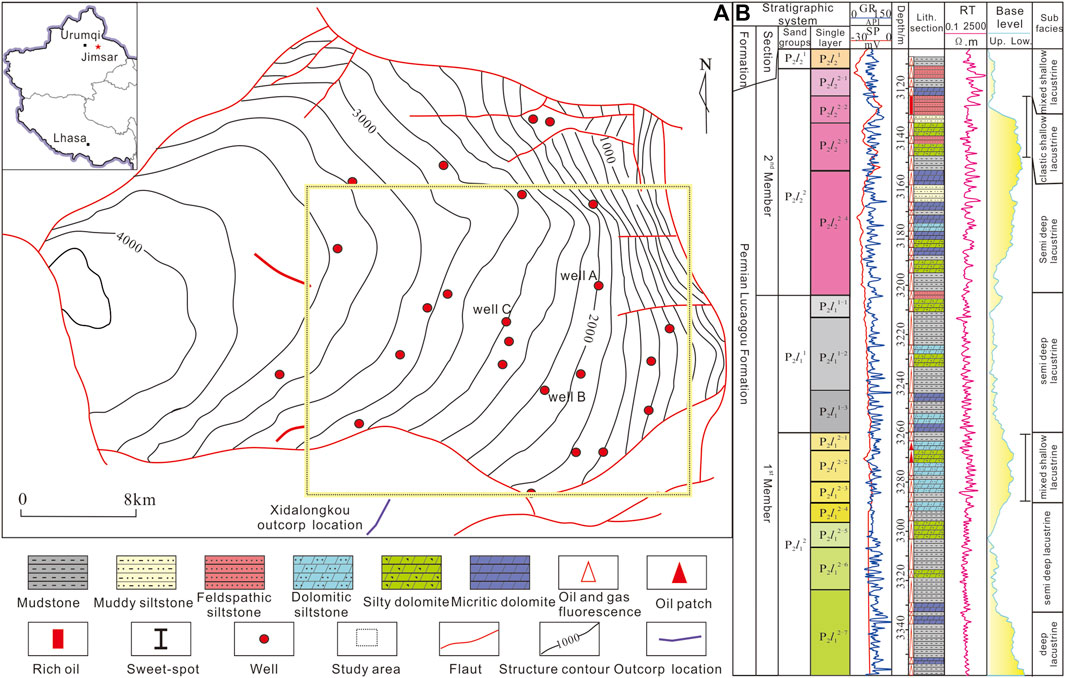
FIGURE 1. Location and composite stratigraphic column of the study area (A) Location and structures of the work area; (B) Composite stratigraphic column of the Lucaogou Formation.

2.2 Research data

For this research, over 100 thin-section photomicrographs were used to investigate the mineral composition and pore structure in the studied region. In terms of seismic data quality, a significant improvement was achieved by conducting a comprehensive and integrated interpretation based on the high-density 3D seismic data collected in the Ji25 area, which covered an area of 25 km² and included 484 coverage passes with a density of 774,400 traces. The seismic data has a dominant frequency of approximately 25 Hz, an effective bandwidth of 10–60 Hz, a signal-to-noise ratio greater than 15 dB, and a vertical resolution of approximately λ/8, as calculated by seismic inversion theory, allowing for the recognition of sand body thicknesses of around 20 m in areas with high signal-to-noise ratios. This quality largely satisfies the precision requirements for lithology and brittleness index prediction.

Utilizing data from core thin-section photomicrographs, scanning electron microscopy, and X-ray diffraction analysis, the research first identifies the microstructure and mineral composition of the rocks. Subsequently, considering the impact of factors such as mineral composition and pore structure on rock seismic elastic parameters, suitable rock physics equivalent theory models applicable to the study area are selected to obtain rock elastic parameters. A theoretical template for brittleness index is then established. Finally, integrating well-logging, seismic, and core data, a spatial distribution model for reservoir brittleness is developed.

2.3 Research methods

The research builds upon the Xu-White model (Keys and Xu, 2002) and refines the process of complex multi-mineral rock physics modeling to create a complex multi-mineral seismic rock physics model. The proposed model accounts for the layering and mineral composition characteristics of mixed clastic rocks, optimizing the process of mixing the matrix minerals. To address the complexity of pore structures in mixed clastic rocks, variable values are determined for layered and brittle mineral-related porosities, replacing previously used empirical constants to enhance pore description accuracy. The fluid mixture section is modified using the Beri model (Kőrösi et al., 2021) for fluid mixture equivalency, and the Boris model (Oran and Boris, 1981) is employed for fluid replacement. This results in the establishment of a saturated mixed clastic rock equivalent model. The specific workflow is depicted in Figure 2.

FIGURE 2

FIGURE 2. Complex multi-mineral mixed rock seismic rock physics model.

2.3.1 Equivalent model for brittle minerals

Among the four brittle minerals distributed in the studied area, quartz, feldspar, and calcite have similar abundancy, while dolomite content is relatively lower. Therefore, based on the characteristics of the content of these four brittle minerals, the following equivalent methods were employed.

1) Quartz, feldspar, and calcite were mixed using a self-consistent approximation (SCA) model that can simultaneously account for multiple mineral phases. Specifically, Berryman proposed a calculation of the equivalent volume and shear modulus for rock containing elliptical inclusions based on elastic wave scattering theory (Formula 1):

${\displaystyle {\sum }_{i=1}^N}{f}_i\left(K_i-K\right)P^i=0(1)$

In the equation, $f_i$ represents the volume modulus of the ith inclusion, $K$ is the equivalent volume/shear modulus for mineral grains, i is the mineral medium index, $P^i$ is a parameter related to the composition and pore shape.

2) Using the mixture obtained in the previous step as the background medium and dolomite, as the filler, both are mixed using the Differential Effective Medium (DEM) model to obtain the equivalent modulus for brittle minerals (Formulas 2, 3):

$\left(1-\phi \right)\frac{d}{d\phi }\left[K*\left(\phi \right)\right]=\left(K_2-K^{*}\right)P^i\left(\phi \right)(2)$

$K^{*}\left(0\right)=K_{gr}(3)$

In the equation, $K^{*}$ represents the elastic modulus of the rock matrix as inclusions are gradually added; $K_2$ represents the elastic modulus of the inclusions that are gradually added.

2.3.2 Layered minerals and equivalent models

Mixed clastic rocks often exhibit good clay layering, with a variety of clay mineral types. Additionally, different clay minerals have varying elastic properties. The heterogeneity of organic matter, such as kerogen, at different maturities also affects the heterogeneity of mixed clastic rocks. Considering the distribution and interactions of clay and organic matter in mixed clastic rocks, a self-consistent differential effective medium (SCA-DEM) model is used to mix layered minerals (organic matter and clay), resulting in an equivalent modulus with interconnected properties for organic matter-clay:

1) An equal amount of clay is taken in combination with kerogen, and both are mixed using a self-consistent model.

2) With the remaining clay as the background medium and the mixture obtained in step 1 as the filler, both are mixed using the differential effective medium (DEM) model (Cundall and Strack, 1979), resulting in an equivalent modulus with interconnected properties for kerogen-clay plastic minerals.

3) Using the plastic equivalent material composed of clay-kerogen as the background medium and brittle equivalent materials such as quartz and calcite as the filler, both are mixed using the DEM model to obtain the equivalent modulus of the rock framework.

2.3.3 Dry rock equivalent model

Using the rock framework as the background medium, pores are added to the background medium using the differential effective medium (DEM) model, resulting in the equivalent modulus for dry rock. A porosity anisotropy parameter is introduced in this context.

2.3.4 Saturated rock equivalent model

1) Fluid properties are calculated using the Batzle & Wang model (Han and Batzle, 2020) based on known temperature, pressure, oil density, formation water salinity, and gas-oil ratio. Fluid mixing is performed using Brie’s exponent method (Kőrösi et al., 2021).

2) Since mixed clastic rock layers under oil saturation conditions exhibit significant velocity dispersion, the full-band Boris fluid replacement model is used to introduce mixed fluids into dry rock, thereby establishing a mixed clastic rock equivalent model that closely resembles real conditions. Boris fluid replacement model is shown below (Formula 4):

$\frac{1}{K_{mf}\left(P,\omega \right)}=\frac{1}{K_h}+\frac{1}{\frac{1}{\frac{1}{K_{dry}\left(P\right)}-\frac{1}{K_h}}+\frac{3i\omega \eta }{8{\phi }_c\left(P\right)a^2}}(4)$

The mineral composition of the mixed clastic rocks in the target area is primarily quartz, feldspar, carbonate minerals, clay, etc. When modeling, the mechanical parameters of each mineral component are set based on Mavko et al.’s work (Mavko and Nur, 1979). For example, the volume modulus of quartz is set to 37 GPa, the shear modulus to 44 GPa, and the density to 2.65 g/cm³.

3 Mineral and pore structure characteristics

The study area in the Jimsar sag of the Junggar Basin hosts the Lucaogou Formation, which is a sedimentary sequence in a saline lake basin. The rock samples exhibit a wide variety of mineral components, including quartz, potassium feldspar, plagioclase feldspar, calcite, dolomite, ankerite, pyrite, pyrrhotite, siderite, natrolite, thomsonite, and various clay minerals. XRD mineral content analysis was conducted on 142 core samples from the target interval in the study area. The results revealed that there are as many as 12 different minerals in the overall composition. Among these, calcite and plagioclase feldspar are the predominant minerals, each accounting for over 20% of the composition. Quartz and siderite follow, with a content range of 10%–15%. There are at least six minerals with an absolute content greater than 4%, indicating a complex mixed composition of multiple mineral components forming the mixed clastic rock’s intricate rock framework. Specifically, in the upper sweet spots, the content of felsic minerals (feldspar and quartz) is relatively high, exceeding 40%, while in the lower sweet spots, mafic minerals are predominant, with a content exceeding 45%. The absolute content of clay minerals is generally low (less than 10%) and is primarily composed of illite and smectite, with small amounts of montmorillonite and kaolinite. The difference in clay mineral composition between the upper and lower sweet spots is not significant (Figure 3).

FIGURE 3

FIGURE 3. Mineral composition in the Jimusaer Lucaogou Formation.

The complex mineral composition and content combinations in this region differ significantly from fine-grained sedimentary rocks and shale oil reservoirs in other basins. This reflects a mixed sedimentary rock type transitioning from clastic sedimentation to chemical sedimentation, or from volcanic clastic rocks to normal sedimentary rocks. The relative mineral content varies considerably in different depth intervals, and there are frequent changes in the relative mineral content along the vertical profile. This complexity indicates that the rock types and their combinations are highly intricate.

Pore structure is a crucial factor that influences fluid presence and changes in rock physical properties. Based on core and thin-section analysis data, the primary pore types in the Lucaogou Formation include intergranular dissolution pores (Figure 3A), intragranular dissolution pores, intercrystalline pores, microfractures, and a small number of oomoldic intergranular dissolution pores and biogenic framework pores, among others. In general, the relative content of intergranular pores in terrigenous clastic rock reservoirs is higher compared to other types of rock reservoirs, while in carbonate rock reservoirs, intergranular dissolution pores have a relatively higher content than in other rock types. Various types of fractures, including structural fractures, dissolution fractures, bedding fractures, and pressure solution fractures, have developed. The degree of fracture development is closely related to lithology, with carbonate rock fractures typically more well-developed than sandstone fractures. Overall, carbonate rock exhibits a stronger brittleness compared to sandstone (Figure 4).

FIGURE 4

FIGURE 4. Microscopic Structure of Pore Types in the Jimusaer Lucaogou Formation (A) Primary intergranular pore (B) Intragranular and intergranular dissolution pores (C) intragranular dissolved pore (D) Residual intergranular pores (E) Intragranular and intergranular dissolution pores (F) Organic matter pore (G) Intergranular pore (H) Diagenetic contraction joint (I) Intragranular dissolved pores.

4 Analysis of brittleness prediction effect

4.1 Prediction of mineral content and pore aspect ratio

The Lucaogou Formation exhibits a diverse range of mineral components, making it challenging to provide detailed characterizations for each mineral’s content. However, by analyzing the petrophysical parameters of minerals and optimizing the consolidation of multiple mineral components, effective prediction of mineral content can be achieved. Initially, considering that minerals such as pyrite and siderite have minimal content, constituting less than 4% and having a negligible impact on the modeling results, they were excluded from the analysis. For both orthoclase and plagioclase feldspar, with densities of 2.59 and 2.61 g/cm³, and compressional wave velocities of 5,590 and 5,749 m/s, respectively, their petrophysical properties are similar. As a result, they were combined and simplified into a single category, referred to as “feldspar.” Using this approach, the complex mineral components were ultimately reduced to six categories: quartz, feldspar, calcite, dolomite, clay minerals, and kerogen. Through optimized well log interpretations, it became possible to predict the content of quartz, feldspar, calcite, dolomite, and clay minerals. However, the precise prediction of kerogen content (total organic carbon) is relatively complex (Formulas 5, 6). Therefore, this study applied the Passey formula to predict the kerogen content (Figure 5).

$\Delta \text{logR}=\log \left(\frac{\mathrm{R}}{R^{*}}\right)+\mathrm{K}\times \left(\Delta \mathrm{t}-{\Delta \mathrm{t}}^{*}\right)(5)$

$\text{TOC}={10}^{2.297-0.1688\times {\mathrm{R}}_{\mathrm{O}}}\times \Delta \text{logR}+\mathrm{B}(6)$

FIGURE 5

FIGURE 5. Comparison of results obtained by different methods for obtaining kerogen.

Where, TOC represents the kerogen content, %; R stands for resistivity, ohm·m; K is the corresponding calibration factor, which is set at 0.02 in this area; Δt represents the sonic transit time, ohm·m; Δt* denotes the baseline for the sonic transit time, ohm·m; and B represents the TOC value for non-source rock intervals. There are usually four methods for calculating the content of cheese roots, namely, the Passey formula method, multivariate fitting method, density method, and natural gamma spectroscopy method. The calculation of kerogen was carried out using the four calculation methods mentioned above, and comparative verification showed that the content of kerogen obtained by the Passey formula method was in good agreement with the measured values in the well (Figure 5).

The fixed constant of pore aspect ratio cannot accurately describe the complex porosity types of the Lucaogou formation. In this study, mineral content is introduced, and a weighted method is used to calculate the porosity aspect ratio curve. The specific formula is as follows (Formula 7):

$\mathrm{A}=\mathrm{\Sigma }\left(\left(\acute{\mathrm{V}}/\text{VT}\right)*\acute{\mathrm{A}}\right)(7)$

Where, A represents the porosity aspect ratio curve, Σ denotes the summation formula, V′ stands for the content of a specific mineral, VT is the total mineral content, and A′ represents the theoretical aspect ratio of a certain mineral. Table 1 contains the theoretical values of aspect ratios for different minerals. By applying the formula with the mineral content at various depth points and their respective theoretical aspect ratios, accurate determination of rock porosity aspect ratios can be achieved (Figure 6).

TABLE 1

TABLE 1. Theoretical pore aspect ratio values for different pore types.

FIGURE 6

FIGURE 6. Prediction curve of pore width to length ratio in well C.

4.2 Comparison of rock physical template and logging data

The above method was used to complete the rock physics modeling of 72 vertical wells in the area. Taking a C well with shear wave logging data as an example, the predicted results were compared with the measured results. The prediction accuracy was improved especially in the layers with higher organic matter and clay content, where the consistency was higher (Figure 7). An overall analysis was conducted on 11 wells in the entire region with measured shear wave data. After using the Xu-White and Mixed rock Physics methods, and the point-to-point parameters are compared with the predicted longitudinal wave velocity (Vp), density and shear wave velocity (Vs), the measured data from 3,152–3,208 m in well C. The correlation coefficient between predicted and measured values was as high as 0.82, indicating that this method is highly accurate and reliable (Figure 8).

FIGURE 7

FIGURE 7. Comparison between Xu-White model and joint equivalent model in Well C.

FIGURE 8

FIGURE 8. Correlation between rock physical prediction and actual measurement in well C.

4.3 Analysis of brittleness prediction effect

1) Establishment of Brittleness Index Based on Elastic Parameter Method

The method for assessing brittleness based on elastic parameters primarily considers that higher Young’s modulus (E) and lower Poisson’s ratio (ν) indicate better rock brittleness. Rickman, using statistical methods, studied the relationship between rock brittleness and Young’s modulus (E) and Poisson’s ratio (ν). While, Young’s modulus can be regarded as an index to measure the difficulty of rock elastic deformation. The greater the value, the greater the stress of the rock elastic deformation occurs to a certain extent, that is, the greater the rock stiffness, and the smaller the elastic deformation occurs under the action of a certain stress. Poisson’s ratio refers to the ratio of the absolute value of the lateral positive strain to the axial positive strain when the rock is pulled or pressed, which is the elastic constant reflecting the lateral deformation of the rock. Rock brittleness is an inherent property of rock when ruptured by force. The fragility index characterizes the speed or difficulty of transient changes before rock rupture, rMeflecting the complexity of cracks formation after reservoir fracturing. Usually, rocks with a higher brittle index are harder and more brittle.

Young proposed that the ability of rocks to fail under loading can be quantified by Poisson’s ratio, while Young’s modulus reflects the rock’s ability to maintain internal fractures after failure. He suggested that rock brittleness is positively correlated with Young’s modulus and negatively correlated with Poisson’s ratio. He established a brittleness index, which has been widely applied in oil fields in South America.

Obtain relevant elastic parameter data through the triaxial stress test of Jimusaer Lucaogou Formation, and conduct intersection analysis between elastic parameters and brittleness. It can be seen that the Young’s modulus and Poisson’s ratio are more sensitive to rock brittleness, and the Young’s modulus is positively correlated with brittleness. The better the brittleness, the greater the Young’s modulus; The Poisson’s ratio is negatively correlated with brittleness. The better the brittleness, the smaller the Poisson’s ratio, and a single Young’s modulus or Poisson’s ratio cannot better characterize the degree of brittleness of the rock. Based on the above understanding, the final optimal formula BI₁₀ is selected to evaluate the reservoir brittleness index.

$\mathrm{B}{\mathrm{I}}_{10}={\mathrm{E}}_{\text{BRIT}}/{\mathrm{\upsilon }}_{\text{BRIT}}(8)$

Where, ${\mathrm{E}}_{\text{BRIT}}$ is normalized Young’s modulus, GPa; ${\mathrm{\upsilon }}_{\text{BRIT}}$ is normalized Poisson’s ratio.

The above method considers not only the influence of mineralogy but also the impact of pore shape and pore fluids. It effectively characterizes the interaction of stress and strain in rocks and provides a reliable reflection of rock brittleness. It establishes a well-defined relationship between brittleness index and elastic parameters, serving as a valuable bridge for brittleness characterization based on seismic data. As a result, it finds wide application in unconventional reservoir brittleness assessment.

3) Brittleness Sensitivity Analysis

Through triaxial stress tests on the Lucaogou Formation in the Junggar Basin, relevant elastic parameter data were obtained, and a cross-plot analysis of elastic parameters and brittleness was conducted. The results show that Young’s modulus and Poisson’s ratio are sensitive indicators of rock brittleness. Young’s modulus is positively correlated with brittleness, meaning that higher brittleness corresponds to larger Young’s modulus. By contrast, Poisson’s ratio is negatively correlated with brittleness, meaning that better brittleness corresponds to a smaller Poisson’s ratio. It was observed that a single parameter, either Young’s modulus or Poisson’s ratio, cannot effectively represent the brittleness of the rock. The analysis confirms the validity of the previously mentioned formula (Figure 9).

3) Seismic Brittle Index Prediction

FIGURE 9

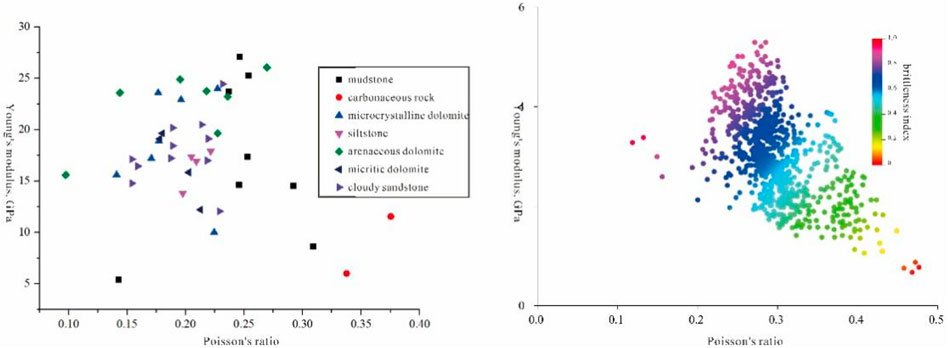
FIGURE 9. Intersection of Young’s modulus and Poisson’s ratio in the Permian Lucaogou Formation of Well C (A) Crossplot of data from different lithologies; (B) Crossplot of different brittle data.

Leveraging the complex lithology and multiple mineral components of the mixed sedimentary rocks, high-precision Vp/Vs ratios can be obtained as the basis for pre-stack elastic parameter prediction. This allows for the calculation of sensitive rock mechanics parameters such as Poisson’s ratio and Young’s modulus (Figure 10), enabling quantitative predictions of brittleness and geomechanical sweet spots.

FIGURE 10

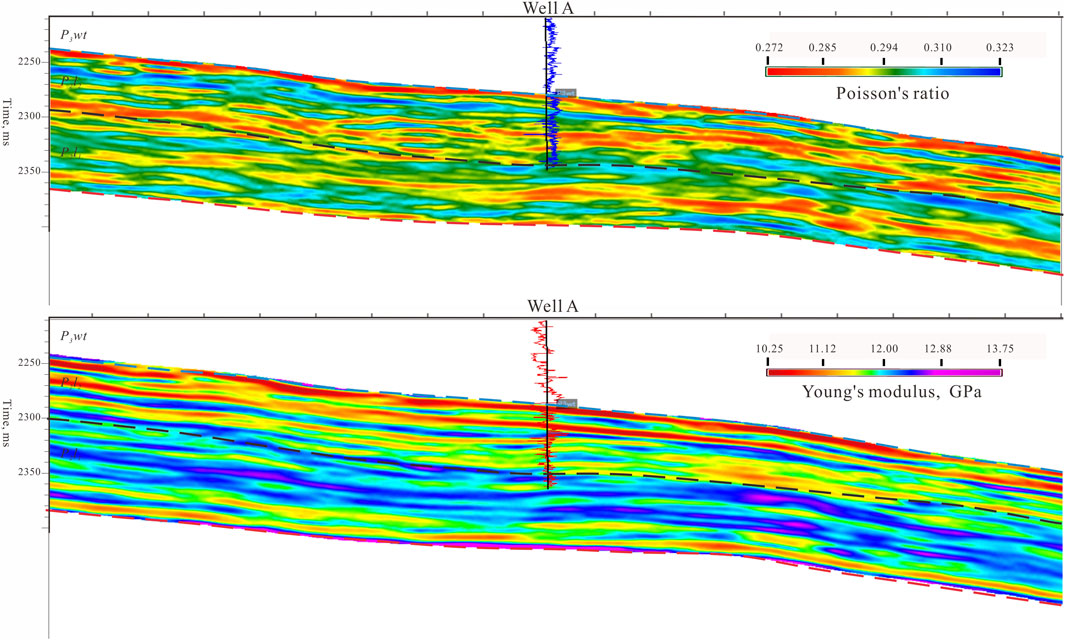
FIGURE 10. (A) Prediction Profile of Poisson’s Ratio through Well A; (B) Yang’s modulus prediction profile.

Building upon the pre-stack inversion, data on Young’s modulus and Poisson’s ratio are obtained, normalized, and entered into the brittleness index calculation formula to achieve quantitative brittleness characterization. From the prediction results, the upper and lower sweet spots exhibit better brittleness compared to the surrounding rocks, consistent with drilling observations. Additionally, to validate the reliability of the results, two wells (C and B) with similar sweet spot quality and hydraulic fracturing parameters were selected. The prediction results show that the sweet spot in well C has better brittleness, forming a complex fracture network with excellent reservoir space and high oil richness. By contrast, the sweet spot in well B exhibits lower brittleness and relatively lower oil richness. When considering the actual oil production results, well C averages 7.76 tons of daily oil production, while well B averages 0.71 tons of daily oil production. The prediction results align well with the actual situation, demonstrating the reliability of the prediction method. This also reflects that brittleness is one of the key controlling factors for high oil production in this mixed sedimentary rock region (Figure 11).

FIGURE 11

FIGURE 11. Brittle parameter profile of well B-C.

From the brittleness index contour map, it is observed that the brittleness in the study area gradually improves as the depth increases from southeast to northwest. Simultaneously, there is a clear east-west zonation feature. The central part of the area exhibits relatively good brittleness, showing stable block-like distribution. This central region is a favorable area for the subsequent deployment of horizontal wells (Figure 12).

FIGURE 12

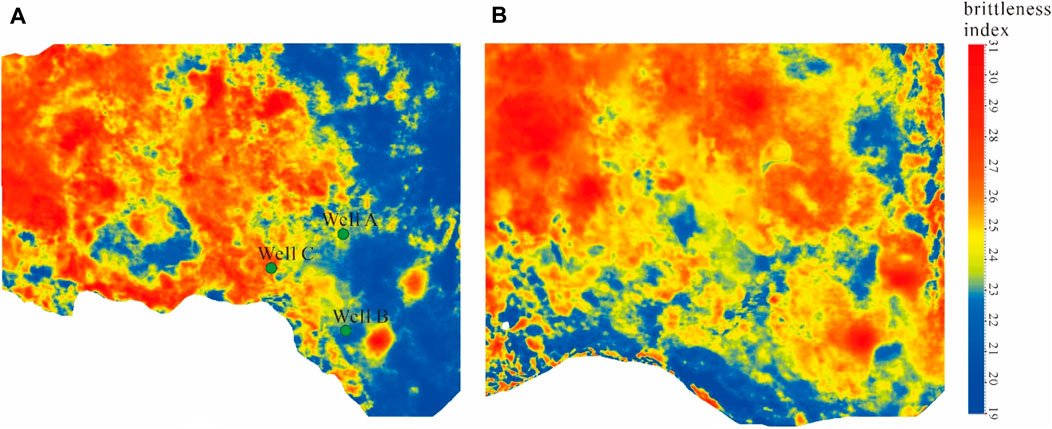
FIGURE 12. Brittleness Index Plan (?) of the Permian Lucaogou Formation in Well Block A (A) Top dessert body; (B) Lower dessert body.

5 Conclusion

1) In response to the complex lithology and pore structure of the Lucaogou Formation in the Jimusaer Sag, by utilizing a complex lithology multi-mineral component mixed rock equivalent model, high-precision brittleness index are obtained. These ratios serve as the basis for predicting elastic parameters in pre-stack analysis, including Poisson’s ratio and Young’s modulus, which are sensitive rock mechanics parameters. This enables the quantitative prediction of brittleness, stress conditions, and other engineering parameters.

2) The rock physics model developed in this study shows good alignment with well-logging interpretation results. The prediction accuracy has improved, especially in the intervals with high organic content and clay content, where the alignment is even better. This indicates that the method is highly accurate and reliable.

3) Examining the prediction results reveals that the brittleness of the upper and lower sweet spots is better than that of the surrounding rock, consistent with drilling observations. Analyzing the spatial distribution of brittleness indices, it can be observed that the brittleness in the study area gradually improves as depth increases from the southeast to the northwest. Furthermore, there is a distinct zonal pattern in the east-west direction, with the central area exhibiting relatively higher brittleness. This area demonstrates stable, block-like distribution and is considered a favorable region for future horizontal well deployment.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZF: Writing–original draft, Writing–review and editing. DY: Conceptualization, Data curation, Software, Writing–review and editing. ZD: Data curation, Methodology, Writing–review and editing. LY: Supervision, Writing–review and editing. HJ: Validation, Writing–review and editing. ZX: Project administration, Validation, Writing–review and editing. SY: Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors ZF, HJ, and SY were employed by PetroChina Xinjiang Oilfield Company. Authors DY, ZD, LY, and, ZX were employed by PetroChina Oriental Geophysical Company.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ba, J., Hu, P., Tan, W., Müller, T. M., and Fu, L. Y. (2021). Brittle mineral prediction based on rock-physics modelling for tight oil reservoir rocks. J. Geophys. Eng. 18 (6), 970–983. doi:10.1093/jge/gxab062

CrossRef Full Text | Google Scholar

Cai, M. F. (2020). Key theories and technologies for surrounding rock stability and ground control in deep mining. J. Min. Strata Control Eng. 2 (3), 033037. doi:10.13532/j.jmsce.cn10-1638/td.20200506.001

CrossRef Full Text | Google Scholar

Cao, Z., Liu, G., Kong, Y., Wang, C., Niu, Z., Zhang, J., et al. (2016). Lacustrine tight oil accumulation characteristics: permian lucaogou formation in Jimusaer sag, junggar basin. Int. J. Coal Geol. 153, 37–51. doi:10.1016/j.coal.2015.11.004

CrossRef Full Text | Google Scholar

Chen, G., Jiang, W., Sun, X., Zhao, C., and Qin, C. (2019). Quantitative evaluation of rock brittleness based on crack initiation stress and complete stress–strain curves. Bull. Eng. Geol. Environ. 78, 5919–5936. doi:10.1007/s10064-019-01486-2

CrossRef Full Text | Google Scholar

Chung, D. H., and Buessem, W. R. (1967). The voigt-reuss-hill approximation and elastic moduli of polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 38 (6), 2535–2540. doi:10.1063/1.1709944

CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). The development of constitutive laws for soil using the distinct element method. Numer. methods geomechanics 1, 289–317. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Duan, Y., Xie, J., Li, B., Wang, M., Zhang, T., and Zhou, Y. (2020). Lithology identification and reservoir characteristics of the mixed siliciclastic-carbonate rocks of the lower third member of the Shahejie Formation in the south of the Laizhouwan Sag, Bohai Bay Basin, China. Carbonates Evaporites 35, 55–19. doi:10.1007/s13146-020-00583-8

CrossRef Full Text | Google Scholar

Feng, R., Zhang, Y., Rezagholilou, A., Roshan, H., and Sarmadivaleh, M. (2020). Brittleness Index: from conventional to hydraulic fracturing energy model. Rock Mech. Rock Eng. 53, 739–753. doi:10.1007/s00603-019-01942-1

CrossRef Full Text | Google Scholar

Gui, J., Guo, J., Sang, Y., Chen, Y., Ma, T., and Ranjith, P. (2023). Evaluation on the anisotropic brittleness index of shale rock using geophysical logging. Petroleum 9 (4), 545–557. doi:10.1016/j.petlm.2022.06.001

CrossRef Full Text | Google Scholar

Gui, J. C., Mat, S., and Chen, P. (2020). Rock physics modeling of transversely isotropic shale: an example of the Longmaxi Formation in the Sichuan basin. Chin. J. Geophys. 63 (11), 4188–4204. doi:10.6038/cjg2020N0294

CrossRef Full Text | Google Scholar

Han, D., and Batzle, M. (2020). Velocity, density and modulus of hydrocarbon fluids--empirical modeling[C]//SEG international exposition and annual meeting. China: SEG, 2000–1867.

Google Scholar

Hu, G. K., and Weng, G. J. (2000). The connections between the double-inclusion model and the ponte castaneda–willis, mori–tanaka, and kuster–toksoz models. Mech. Mater. 32 (8), 495–503. doi:10.1016/s0167-6636(00)00015-6

CrossRef Full Text | Google Scholar

Ignatchenko, V. A., and Polukhin, D. S. (2016). Development of a self-consistent approximation. J. Phys. A Math. Theor. 49 (9), 095004. doi:10.1088/1751-8113/49/9/095004

CrossRef Full Text | Google Scholar

Jahed, A. D., Asteris, P. G., Askarian, B., Hasanipanah, M., Tarinejad, R., and Huynh, V. V. (2020). Examining hybrid and single SVM models with different kernels to predict rock brittleness. Sustainability 12 (6), 2229. doi:10.3390/su12062229

CrossRef Full Text | Google Scholar

Keys, R. G., and Xu, S. (2002). An approximation for the Xu-White velocity model. Geophysics 67 (5), 1406–1414. doi:10.1190/1.1512786

CrossRef Full Text | Google Scholar

Kőrösi, M., Béri, J., Arany, D., Varga, C., and Székely, E. (2021). Experimental investigation of chiral melting phase diagrams in high-pressure CO2 containing organic modifiers. J. Supercrit. Fluids 178, 105352. doi:10.1016/j.supflu.2021.105352

CrossRef Full Text | Google Scholar

Li, H. (2022). Research progress on evaluation methods and factors influencing shale brittleness: a review. Energy Rep. 8, 4344–4358. doi:10.1016/j.egyr.2022.03.120

CrossRef Full Text | Google Scholar

Li, H. (2023). Coordinated development of shale gas benefit exploitation and ecological environmental conservation in China: a mini review. Front. Ecol. 11, 1232395. doi:10.3389/fevo.2023.1232395

CrossRef Full Text | Google Scholar

Li, H., Tang, H. M., Qin, Q. R., Zhou, H., Qin, Z., Fan, C., et al. (2019). Characteristics, formation periods and genetic mechanisms of tectonic fractures in the tight gas sandstones reservoir: a case study of Xujiahe Formation in YB area, Sichuan Basin, China. J. Petroleum Sci. Eng. 178, 723–735. doi:10.1016/j.petrol.2019.04.007

CrossRef Full Text | Google Scholar

Li, T., Huang, Z., Feng, Y., Chen, X., Ma, Q., Liu, B., et al. (2020). Reservoir characteristics and evaluation of fluid mobility in organic-rich mixed siliciclastic-carbonate sediments: a case study of the lacustrine Qiketai Formation in Shengbei Sag, Turpan-Hami Basin, Northwest China. J. Petroleum Sci. Eng. 185, 106667. doi:10.1016/j.petrol.2019.106667

CrossRef Full Text | Google Scholar

Li, Y., Jia, D., Rui, Z., Peng, J., Fu, C., and Zhang, J. (2017). Evaluation method of rock brittleness based on statistical constitutive relations for rock damage. J. Petroleum Sci. Eng. 153, 123–132. doi:10.1016/j.petrol.2017.03.041

CrossRef Full Text | Google Scholar

Liu, B., Bechtel, A., Sachsenhofer, R. F., Gross, D., Gratzer, R., and Chen, X. (2017). Depositional environment of oil shale within the second member of permian lucaogou Formation in the santanghu basin, northwest China. Int. J. Coal Geol. 175, 10–25. doi:10.1016/j.coal.2017.03.011

CrossRef Full Text | Google Scholar

Liu, X., Zhang, Z., Ge, Z., Zhong, C., and Liu, L. (2021). Brittleness evaluation of saturated coal based on energy method from stress–strain curves of uniaxial compression. Rock Mech. Rock Eng. 54, 3193–3207. doi:10.1007/s00603-021-02462-7

CrossRef Full Text | Google Scholar

Ma, T., Peng, N., Chen, P., et al. (2019). Experimental investigation of anisotropic brittleness under confining pressure for gas shale rocks[C]//ARMA US Rock Mechanics/Geomechanics Symposium. USA: ARMA, 2019–0136.

Google Scholar

Mavko, G. M., and Nur, A. (1979). Wave attenuation in partially saturated rocks. Geophysics 44 (2), 161–178. doi:10.1190/1.1440958

CrossRef Full Text | Google Scholar

Meng, F., Wong, L. N., and Zhou, H. (2021). Rock brittleness indices and their applications to different fields of rock engineering: a review. J. rock Mech. geotechnical Eng. 13 (1), 221–247. doi:10.1016/j.jrmge.2020.06.008

CrossRef Full Text | Google Scholar

Meng, F., Zhou, H., Zhang, C., Xu, R., and Lu, J. (2015). Evaluation methodology of brittleness of rock based on post-peak stress–strain curves. Rock Mech. Rock Eng. 48, 1787–1805. doi:10.1007/s00603-014-0694-6

CrossRef Full Text | Google Scholar

Mukerji, T., Berryman, J., Mavko, G., and Berge, P. (1995). Differential effective medium modeling of rock elastic moduli with critical porosity constraints. Geophys. Res. Lett. 22 (5), 555–558. doi:10.1029/95gl00164

CrossRef Full Text | Google Scholar

Muthukumar, S., and DesRoches, R. (2006). A Hertz contact model with non-linear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 35 (7), 811–828. doi:10.1002/eqe.557

CrossRef Full Text | Google Scholar

Neumann, R., and Böhlke, T. (2016). Hashin–Shtrikman type mean field model for the two-scale simulation of the thermomechanical processing of steel. Int. J. Plasticity 77, 1–29. doi:10.1016/j.ijplas.2015.09.003

CrossRef Full Text | Google Scholar

Oran, E. S., and Boris, J. P. (1981). Detailed modelling of combustion systems. Prog. Energy Combust. Sci. 7 (1), 1–72. doi:10.1016/0360-1285(81)90014-9

CrossRef Full Text | Google Scholar

Raymer, L. L., Hunt, E. R., and Gardner, J. S. (1980). An improved sonic transit time-to-porosity transform[C]//SPWLA Annual Logging Symposium. London: SPWLA, 1980.

Google Scholar

Saleh, A. A., and Castagna, J. P. (2004). Revisiting the Wyllie time average equation in the case of near-spherical pores. Geophysics 69 (1), 45–55. doi:10.1190/1.1649374

CrossRef Full Text | Google Scholar

Shan, S. C., Wu, Y. Z., Fu, Y. K., and Zhou, P. H. (2021). Shear mechanical properties of anchored rock mass under impact load. J. Min. Strata Control Eng. 3 (4), 043034. doi:10.13532/j.jmsce.cn10-1638/td.20211014.001

CrossRef Full Text | Google Scholar

Tao, W., Tang, H., Wang, Y., and Ma, J. (2020). Evaluation of methods for determining rock brittleness under compression. J. Nat. Gas Sci. Eng. 78, 103321. doi:10.1016/j.jngse.2020.103321

CrossRef Full Text | Google Scholar

Wang, J., Deng, Q., Wang, Z., Qiu, Y. s., Duan, T. z., Jiang, X. s., et al. (2013). New evidences for sedimentary attributes and timing of the “Macaoyuan conglomerates” on the northern margin of the Yangtze block in southern China. Precambrian Res. 235, 58–70. doi:10.1016/j.precamres.2013.06.003

CrossRef Full Text | Google Scholar

Wang, J., and Wang, X. L. (2021). Seepage characteristic and fracture development of protected seam caused by mining protecting strata. J. Min. Strata Control Eng. 3 (3), 033511. doi:10.13532/j.jmsce.cn10-1638/td.20201215.001

CrossRef Full Text | Google Scholar

Wang, Y., Li, C. H., Hu, Y. Z., and Zhou, X. L. (2017). A new method to evaluate the brittleness for brittle rock using crack initiation stress level from uniaxial stress–strain curves. Environ. earth Sci. 76, 799–818. doi:10.1007/s12665-017-7117-4

CrossRef Full Text | Google Scholar

Wei, W., Azmy, K., and Zhu, X. (2022). Impact of diagenesis on reservoir quality of the lacustrine mixed carbonate-siliciclastic-volcaniclastic rocks in China. J. Asian Earth Sci. 233, 105265. doi:10.1016/j.jseaes.2022.105265

CrossRef Full Text | Google Scholar

Wu, C., Li, B., Liu, Y., and Liang, S. Y. (2017). Surface roughness modeling for grinding of silicon carbide ceramics considering co-existence of brittleness and ductility. Int. J. Mech. Sci. 133, 167–177. doi:10.1016/j.ijmecsci.2017.07.061

CrossRef Full Text | Google Scholar

Yin, S., Chen, G., Xu, C., and etal, (2022). Lithofacies architecture of lacustrine fine-grained mixed reservoirs and its controller sweet spot: a case study of Permian Lucaogou Formation shale oil reservoir in the Jimsar Sag, Juggar Basin. Oil Gas Geol. 43 (5), 1180–1193. doi:10.11743/ogg20220514

CrossRef Full Text | Google Scholar

Yin, S., Chen, X., Yang, Y., et al. (2023a). Origin and sweet spots of typical low-resistivity oil reservoirs of fine-grained sedimentary rocks. Oil Gas Geol. 44 (8), 946–961.

Google Scholar

Yin, S., Zhu, B., Guo, H., Xu, Z., Li, X., Wu, X., et al. (2023b). Architectural model of a dryland gravel braided river, based on 3D UAV oblique photogrammetric data: a case study of west dalongkou river in Eastern Xinjiang, China. Acta Geol. Sin. Engl. Ed. 97 (1), 269–285. doi:10.1111/1755-6724.14967

CrossRef Full Text | Google Scholar

Yin, S., Zhu, B., Wu, Y., and Xu, F. (2021). Lithofacies architecture and distribution patterns of lacustrine mixed fine-grained rocks —a case study of permian lucaogou Formation in jimsar sag, NW China. Front. Earth Sci. 9, 782208. doi:10.3389/feart.2021.782208

CrossRef Full Text | Google Scholar

Yu, W., Algeo, T. J., Du, Y., Zhang, Q., and Liang, Y. (2016). Mixed volcanogenic–lithogenic sources for Permian bauxite deposits in southwestern Youjiang Basin, South China, and their metallogenic significance. Sediment. Geol. 341, 276–288. doi:10.1016/j.sedgeo.2016.04.016

CrossRef Full Text | Google Scholar

Zhang, J., Liu, G., Cao, Z., Tao, S., Felix, M., Kong, Y., et al. (2019). Characteristics and formation mechanism of multi-source mixed sedimentary rocks in a saline lake, a case study of the Permian Lucaogou Formation in the Jimusaer Sag, northwest China. Mar. Petroleum Geol. 102, 704–724. doi:10.1016/j.marpetgeo.2019.01.016

CrossRef Full Text | Google Scholar

Zhi, S., and Zan, D. (2015). New brittleness indexes and their application in shale/clay gas reservoir prediction. Petroleum Explor. Dev. 42 (1), 129–137. doi:10.1016/s1876-3804(15)60016-7

CrossRef Full Text | Google Scholar

Zhi, Y., Lian, H., Lin, S., et al. (2018). Geologic characteristics and exploration potential of tight oil and shale oil in Lucaogou Formation in Jimsar sag. China Pet. Explor. 23 (4), 76.

Google Scholar