Computationally simulating the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit, Gejiu ore district, Yunnan, China: an example of pore-fluid convection controlled mineralization

The Laochang Pb-Zn deposit can be typically considered as a hydrothermal mineralizing deposit in the Gejiu ore district. Although extensive studies were conducted to understand the mineralizing system associated with the Laochang Pb-Zn deposit through using the traditional geoscience methods, the mineralizing process involved in this deposit has not been justified in a strictly scientific manner to date. In this article, the hydrothermal mineralizing mechanism of the Laochang Pb-Zn deposit is computationally simulated through using the dual length-scale approach associated with the finite element method (FEM). The related computationally simulating outcomes have revealed the following understanding: 1) the pore-fluid convection provides a continuous source of mineralizing fluid and material for the Laochang Pb-Zn deposit; 2) the convective flow of pore-fluid is the primary dynamic mechanism, which controls the temperature, chemical species and pore-fluid velocity distributions in the Laochang Pb-Zn deposit; 3) the localized structure plays a key role in controlling the localized pore-fluid flow pattern, which can further control the location and grade of the orebody in the Laochang Pb-Zn deposit; 4) the dual length-scale approach associated with the FEM is very useful for dealing with the computational simulation of the hydrothermal mineralizing mechanism involved in the Laochang Pb-Zn deposit.

1 Introduction

The location of Gejiu ore district can be found a few kilometers away from the southeast of Gejiu city, Yunnan, South China. This district approximately contains 5 million tonnes (Mt) Cu, 3 Mt Sn, and 28 Mt Pb-Zn (Cheng et al., 2013a; Wang and Yu, 2014). This means that the Gejiu ore district can be considered as not only the largest Pb-Zn deposit in China, but the largest Sn-Cu deposit in the world as well (Chang et al., 2019; Cheng et al., 2019). Although extensive studies were conducted on the Sn-Cu deposit, only a few studies have been done on the Pb-Zn deposit in the Gejiu ore district. However, the Laochang Pb-Zn deposit is one of the important deposits in the Gejiu ore district (Cheng et al., 2012a), with 50% of the metal reserves. The types of mineralization in the Laochang Pb-Zn deposit are relatively complex, with concentrated Sn-Cu mineralization and associated lead and zinc mineralization (Zhao, 2022; Zhao et al., 2022). This implies that not only does the study of the Laochang Pb-Zn deposit have great economic value, but it is also beneficial for enriching the theoretical understanding of the compound metallogenic system in the Gejiu ore district. Based on the previous studies of the Laochang polymetallic deposit (Liao et al., 2014; Guo et al., 2018; Cheng et al., 2019; Zhao et al., 2019; Zhao, 2022; Zhao et al., 2022; Li et al., 2023), a brief summary of the primary outcomes from the previous studies can be described as follows: 1) the structures and strata of the Gejiu ore district were investigated, so that the related information is available for designing the geological model of the Laochang Pb-Zn deposit; 2) the alteration and mineralization characteristics of the sphalerite and galena associated with the Laochang Pb-Zn deposit were determined; 3) the stable isotopes, fluid inclusions and trace elements in the Laochang Pb-Zn deposit were studied; 4) The Laochang Pb-Zn deposit involves multiple mineralization styles, which can be reflected by the obvious metal vertical zoning and extensive hydrothermal alteration; 5) the genesis involved in the Laochang Pb-Zn deposit is associated with the Yanshanian biotite monzogranitic intrusion, which took place at about 77.4 million years ago (Cheng and Mao, 2010; Li et al., 2012; Cheng et al., 2013a; Zhang et al., 2015); 6) the geologically-stable period may be very long, which may amount to over 77 million years after the intruded magma was completely solidified and cooled, because no magma activity occurred after the Yanshanian biotite monzogranitic intrusion (Cheng and Mao, 2010; Li et al., 2012; Cheng et al., 2013a; Zhang et al., 2015). This means that according to the main outcomes from the previous studies, the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit could reach a steady state or a quasi-steady state after the intruded magma was completely solidified and cooled. Therefore, the main purpose of this study is to investigate the mineralizing process of the Laochang Pb-Zn deposit during such a long geologically-stable period after the intruded magma was completely solidified and cooled. For this reason, the initial condition can be avoided in computationally simulating both the regional and deposit models of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Consequently, only the boundary conditions are needed, in this study, for computationally simulating both the regional and deposit models of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit.

However, due to the complicated mineralizing process involved in the Laochang Pb-Zn deposit, some key issues involved in this deposit still need to be resolved. For example, 1) where did the large amount of hydrothermal fluid, which is necessary for forming such a huge deposit, come from? 2) What were the spatiotemporal evolution characteristics of the temperature, velocity of pore-fluid and pressure of pore-fluid in the mineralizing system? 3) What was the effect of sulfate reduction on mineralization during mineralizing fluid mixing? 4) What was the effect of nonlinearly-coupled physical and chemical fields on mineralization? 5) What was the influence of the intrusion and tectonic faults on the orebody distribution in the mineralizing system? Obviously, it is very difficult to answer these five fundamental questions involved in the Laochang Pb-Zn deposit through using the traditional geological methods, because the controlling dynamic processes and mechanisms involved in the Laochang Pb-Zn deposit cannot be considered in a strictly scientific manner (Hobbs et al., 2000; Gow et al., 2002; Ord et al., 2002; Schaubs and Zhao, 2002; Sorjonen-Ward et al., 2002; Liu et al., 2015; Zhao et al., 2016a; Zou et al., 2017; Zhao et al., 2018; Fan et al., 2021; Hu et al., 2022).

As one of the most-encountered geological phenomena, mineralization within the Earth’s upper crust was extensively observed and investigated since ancient times. Although the traditional geoscience method is commonly used to describe the observed mineralization phenomena, it cannot be used to explain, in a strictly scientific manner, how and why the observed ore deposits formed where they are located, because the controlling dynamic processes involved in the mineralization and orebody formation are not considered in the traditional geoscience method (Hobbs et al., 2000; Zhao et al., 2008a; Zhao et al., 2009). In order to address this fundamental issue, the computational simulation method, which is closely associated with the emerging computational geosciences field, has been developed and used in recent years (Hobbs et al., 2000; Gow et al., 2002; Ord et al., 2002; Schaubs and Zhao, 2002; Sorjonen-Ward et al., 2002; Zhao et al., 2009; Gao et al., 2015; Liu et al., 2015; Zhao et al., 2016a; Zou et al., 2017; Zhao et al., 2018; Fan et al., 2021; Hu et al., 2022). Compared with the traditional geoscience method, the specific characteristics of the computational simulation method include the following four aspects. First, specific physical processes can be accurately taken into account in the computational simulation method. For instance, the pore-fluid flow can be described using Darcy’s law, while the mass flux associated with solute diffusion and the heat flux associated with heat conduction can be respectively described using Fick’s law and Fourier’s law. Second, three fundamental scientific principles in nature, such as mass conservation, energy conservation and momentum conservation, can be strictly satisfied in the considered mineralizing system. Third, mathematical governing equations (MGEs) can be derived and used for describing the controlling dynamic processes involved in the mineralization and orebody formation associated with the considered mineralizing system. Fourth, advanced computational algorithms can be developed and used for solving the MGEs associated with the considered mineralizing system. Due to the aforementioned characteristics, computational simulation methods have been broadly used for solving many different types of problems in the field of geosciences (Hobbs et al., 2000; Gow et al., 2002; Ord et al., 2002; Schaubs and Zhao, 2002; Sorjonen-Ward et al., 2002; Zhao et al., 2009; Gao et al., 2015; Liu et al., 2015; Zhao et al., 2016a; Zou et al., 2017; Zhao et al., 2018; Fan et al., 2021; Hu et al., 2022; Zhao and Liu 2023a). Therefore, the computational simulation method is naturally chosen as a research tool in this study.

It should be pointed out that from the mathematical point of view, analytical solutions for the MGEs associated with a mineralizing system are strongly dependent on the boundary conditions of the mineralizing system (Phillips, 1991; Nield and Bejan, 1992; Zhao et al., 2008b). However, it is very difficult, even if possible, to mathematically derive analytical solutions for the MGEs associated with a mineralizing system. Alternatively, it is commonly to solve the MGEs associated with a mineralizing system through using computational simulation methods (Hobbs et al., 2000; Gow et al., 2002; Ord et al., 2002; Schaubs and Zhao, 2002; Sorjonen-Ward et al., 2002; Zhao et al., 2009; 2016a; 2018; Gao et al., 2015; Liu et al., 2015; Zou et al., 2017; Fan et al., 2021; Hu et al., 2022; Zhao and Liu 2023b). This means that from the computational simulation point of view, computational simulation solutions should be also strongly dependent on the boundary conditions of a mineralizing system (Gao et al., 2015; Liu et al., 2015; Zou et al., 2017; Fan et al., 2021; Hu et al., 2022; Zhao and Liu 2023b). Therefore, the boundary conditions of a mineralizing system should be carefully and reasonably determined in the process of computationally simulating the mineralizing system. For this reason, the double length-scale approach was proposed in a recent publication (Zhao and Liu 2023a). The main advantage of using the double length-scale approach is that the boundary conditions of the deposit model associated with computationally simulating a mineralizing system can be determined in a scientifically consistent manner.

2 The geological setting of the Laochang Pb-Zn deposit

2.1 Geological background

As stated previously (Zhao et al., 2022), the Gejiu ore district is located close to the intersection of three blocks, namely, the Indochina and Cathaysia blocks as well as the Yangtze Craton (Yuan et al., 2019; Figure 1A). Tectonically, the Gejiu ore district is also located in the western part of the Youjiang basin (Guo et al., 2022; Figure 1B). The location of Laochang Pb-Zn deposit is “in the middle region of eastern Gejiu, which is bounded by the Beiyinshan fault to the north, the Laoxiongdong fault to the south, the Gejiu fault to the west and the Jiajieshan fault to the east (Zhao, 2022; Zhao et al., 2022).”

FIGURE 1

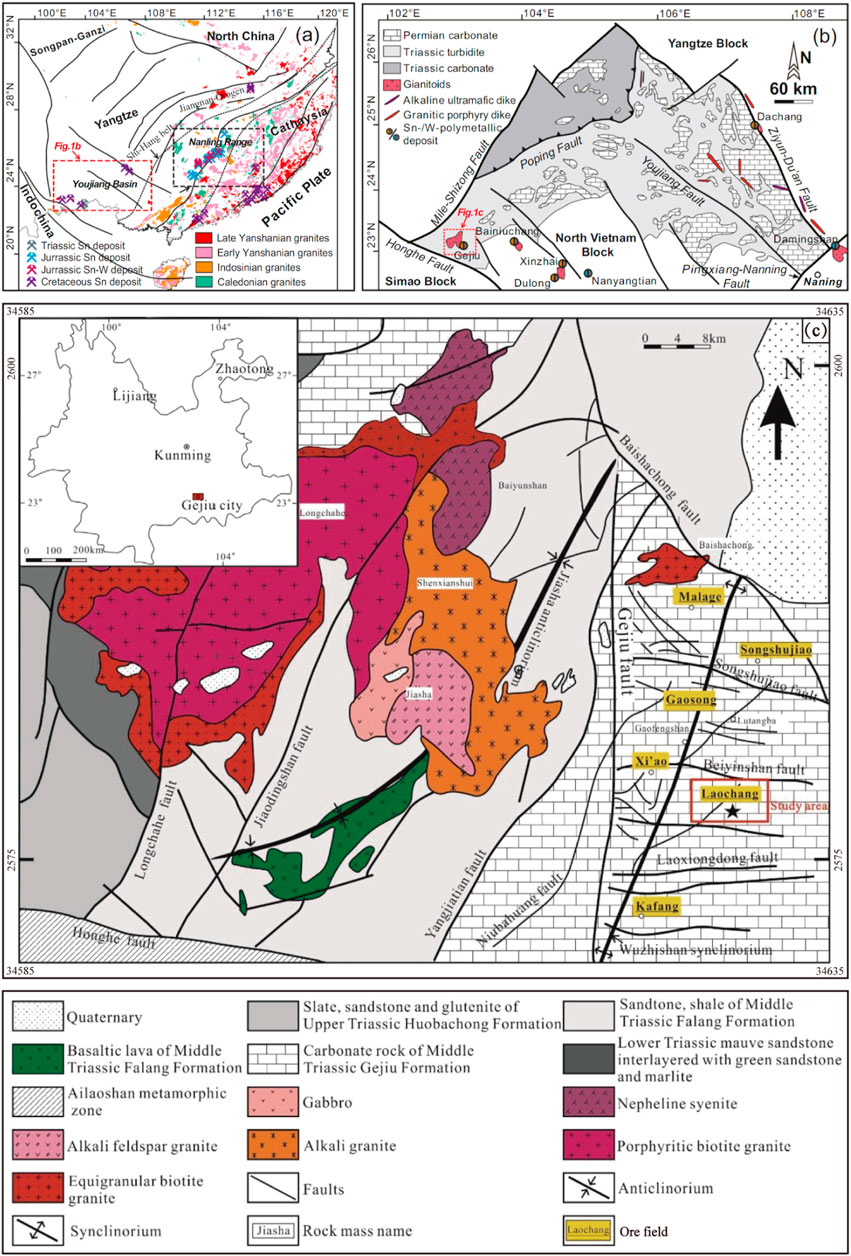
FIGURE 1. (A) Geologic map of the South China block showing the location of major Mesozoic deposits (modified from Yuan et al., 2019). (B) Schematic map showing distribution of Late Cretaceous granitoids and polymetallic deposits in the Youjiang Basin, South China (modified from Guo et al., 2022). (C) Geologic map of the Gejiu ore district (modified from Cheng et al., 2019).

Based on the previous study (Zhao et al., 2022), it is known that as the consequence of the related tectonic events, the predominant rocks are comprised of Precambrian to Quaternary sedimentary rocks, while Cretaceous rocks are absent in the Gejiu ore district (Guo et al., 2018; Zhao et al., 2019). It is observed that in the Gejiu area, the Falang Formation and the underlying Triassic Gejiu Formation are the primary outcrops, but the main ore-hosting strata can be regarded as the Triassic Gejiu Formation. In the Triassic Gejiu Formation, there is mainly the thick-bedded limestone, with some minor interbedded materials, such as mafic lavas, dolomite and dolomitic limestone. In the Falang Formation, there are mainly the carbonates and finegrained clastic sedimentary rocks. However, in the Middle Triassic Gejiu Formation, the primary ore-hosting rocks are considered to be carbonate rocks in the Laochang ore deposit. The thickness of the primary ore-hosting rocks is about 1,200–2,400 m. They are comprised of gray, dolomitic limestone, argillaceous limestone and medium-thick limestone (Zhao, 2022; Zhao et al., 2022).

In the Gejiu ore district, there are some primary structures (Zhao et al., 2022). For example, there are the Baishachong fault (which trends in the NW direction), the Jiaodingshan, Yangjiatian and Longchahe faults (which trend in the NNE direction), the Wuzhishan anticlinorium (which trends in the ENE direction), the Gejiu fault (which trends in the NS direction) and the Jiasha synclinorium (which also trends in the NS direction). It was observed that the location of the orebodies is controlled by these primary structures (Guo et al., 2022; Figure 1B). As indicated previously (Zhao et al., 2022), the Gejiu ore district can be divided into the following two main parts: an eastern part and a western part. This division was made by considering the Gejiu fault, which trends in the NS direction. In the eastern part, the metal reserves can count to 90% of their total amount (Zhuang et al., 1996). Similarly, in the Laochang ore deposit, it was also observed that the location and morphology of the orebodies are controlled by the well-developed structures (Zhao et al., 2022). These structures include the Zhulinxinshan anticline (which trends in the NE direction), the Heimajing and Huangmaoshan anticlines (which trend in the NW direction), and the Zhuyeshan and Wanzijie anticlines (which trend in the ENE direction). It is observed that the Zhulinxinshan, Heimajing and Huangmaoshan anticlines play an important role in controlling the flow pathways of the ore-forming fluids (Zhao, 2022).

It was observed that in the Gejiu ore district, the exposed intrusive complex comprises primarily porphyritic quartz monzonite, gabbro, alkali syenite, monzonite, feldspathoid syenite, porphyritic/equigranular biotite monzogranites and syenogranite (Cheng et al., 2019; Figure 1C). The time span of these emplaced granites varies from 77.4 to 85.8 Ma (Cheng and Mao, 2010; Li et al., 2012; Cheng et al., 2013a; Zhang et al., 2015). In the Laochang Pb-Zn deposit, the magmatic rocks primarily comprise the Indosinian basalt and Yanshanian granitoids. These magmatic rocks are slightly exposed. In the previous study (Cheng and Mao, 2010), it was indicated that the Yanshanian Laoka granite is formed at a late stage of 85 ± 0.85 Ma. The location of the Yanshanian Laoka granite is about 200–1,800 m under the surface. Compared with the normal granite, the contents of Pb, Zn, Sn, Cu and other metal elements are relatively higher in the Yanshanian Laoka granite. In the Laochang Pb-Zn deposit, the formation of the basalt took place during the Middle Triassic Anisian period (Li et al., 2008; Li et al., 2016). The distribution of the basalt is mainly located in the Wanzijie and Zhuyeshan ore blocks, which are located within the Qibeishan area.

2.2 Metallogenic characteristics

According to a series of previous studies (Cheng et al., 2013a; Cheng et al., 2013b; Cheng et al., 2019; Liao et al., 2014; Guo et al., 2018; Li et al., 2023; Wang and Ren, 2019; Zhao et al., 2019; Zhao et al., 2022; Zhao, 2022), it is known that in the Gejiu ore district, the distribution of ore bodies is primarily around the granite body. Based on the distance between the ore body and the granite, the ore bodies can be classified into the following nine kinds. 1) The first kind is the alluvial tin ore. 2) The second kind is the stratiform-like and interlayer vein oxide ore. This kind of ore is primarily comprised of Cu and Sn, and is located in the fracture zone, which is away from the granite within 500–1,500 m. 3) The third kind is the stratiform-like and interlayer vein sulfide ore. This kind of ore is primarily comprised of Zn, Pb, Sn and Ag, and is located in the carbonate rocks, which is away from the granite within 300–800 m. 4) The fourth kind is the vein-type sulfide ore. This kind of ore is primarily comprised of Zn, Pb, Sn and Ag. 5) The fifth kind is the skarn-type Sn-Cu ore. This kind of ore is primarily comprised of Cu and Sn, and is located in the contact zone between the marble and granite. 6) The sixth kind is the basalt-type copper ore. This kind of ore is primarily comprised of Cu, Sn, Mo and W, and is located within the basalt near the contact zone between the basalt and granite. 7) The seventh kind is the greisen-type ore. This kind of ore is primarily comprised of Cu, Sn, Bi and W, and is located in the contact zone between the marble and granite, which is away from the granite within 0–50 m. 8) The eighth kind is the altered rock-type Cu-Sn ore. This kind of ore is primarily comprised of Cu, Sn and W, and is located in the alteration zone of the deeper granite. 9) The ninth kind is the interlayer Pb-Zn mineralization (Figure 2).

FIGURE 2

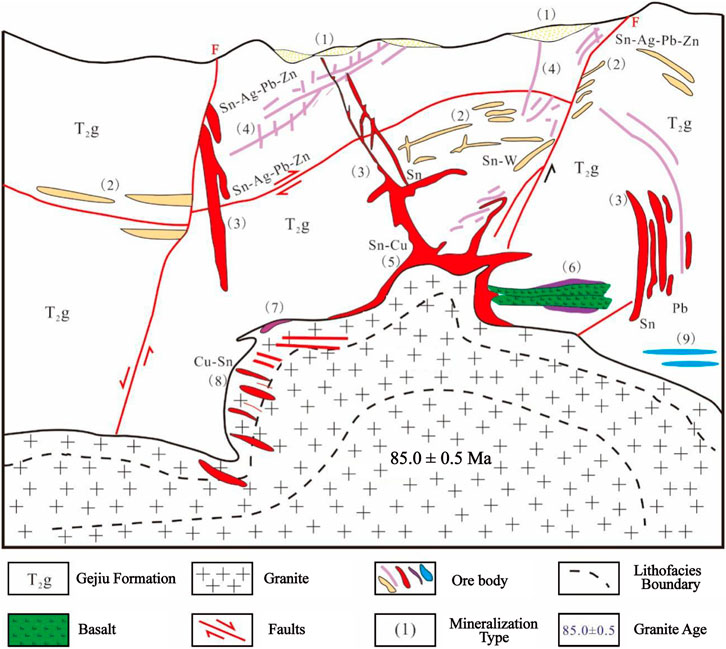
FIGURE 2. The schematic diagram showing different types of mineralization in the Laochang deposit (modified from Liao et al., 2014; Zhao, 2022).

According to the existing investigation (Zhao et al., 2022), it is noted that the locations of the Laochang Pb-Zn orebodies are clearly controlled by the strata. Consequently, the Laochang Pb-Zn orebodies can be found in the stratoid and stratiform shapes. For example, the dips and strikes of these orebodies are consistent with the attitudes of the wall rocks. Generally, the length of the Laochang Pb-Zn orebodies are tens to hundreds meters, while the width of the Laochang Pb-Zn orebodies are 100–200 m. It is observed that the sulfide Pb-Zn ores are primarily comprised of sphalerite and galena, although some other minerals, such as pyrrhotite, pyrite, chalcopyrite and secondary arsenopyrite, can be found in them (Zhao et al., 2022).

2.3 Basic questions associated with establishing computational models for simulating the Laochang Pb-Zn deposit

It is necessary to answer the following five basic questions before a computational simulation is utilized for studying the controlling mineralizing processes of a hydrothermal deposit (Hobbs et al., 2000; Gow et al., 2002; Ord et al., 2002; Schaubs and Zhao, 2002; Sorjonen-Ward et al., 2002; Zhao et al., 2012a): 1) What was the architecture and material distribution characteristics of the entire mineralizing system? 2) What was the geodynamic history that leads to the evolution of temperature, pore-fluid pressure and pore-fluid velocity distributions? 3) What were the chemical and physical characteristics of the pore-fluids involved in the mineralizing system? 4) What were the mechanisms to drive the pore-fluid flow? 5) What were the processes and mechanisms involved in the metal dissolution, metal transport and metal precipitation?

To answer these five questions, a large number of geophysical and geochemical studies related to the Laochang Pb-Zn deposit were conducted (Liao et al., 2014; Guo et al., 2018; Cheng et al., 2019; Zhao et al., 2019; Zhang et al., 2020; Xu et al., 2021; Xu et al., 2022a; Xu et al., 2022b; He et al., 2022; Li et al., 2022; Zhao, 2022; Zhao et al., 2022; Li et al., 2023). Based on the review of these geophysical and geochemical investigations, the above five questions can be answered as follows: 1) Through considering the data of geology, geophysics, geochemistry and remote sensing image interpretation, it is believed that there may be a Yanshanian granite body below the Laochang Pb-Zn deposit. The granite body and tectonic faults in the carbonate strata together control the distribution of the Laochang Pb-Zn deposit. 2) Through referring to the tectonic background, the different fault patterns are different in the eastern and western sectors of the Gejiu fault. This implies that the eastern sector of the Gejiu fault may have an extensional and/or transtensional setting environment, while the western sector of the Gejiu fault may have a compressional and/or transpressional setting environment. 3) From the stable isotope analysis, the mineralizing fluid in the Laochang Pb-Zn deposit was mainly the mixing product of the formation water and deep magmatic hydrothermal fluid. In the migration and evolution processes of the mineralizing fluid, the seawater sulfate may contribute part of sulfur through thermochemical reduction. 4) According to the analysis of metallogenic characteristics, a temperature-triggered density change was the main mechanism to drive the pore-fluid flow. 5) Through the geochemical analysis, the cooling of mineralizing fluid and the mixing of magmatic hydrothermal fluid with atmospheric precipitation were the main mechanisms to cause metal precipitation during mineralization in the Laochang Pb-Zn deposit.

3 Computationally simulating the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit

3.1 The mathematical model of the hydrothermal mineralizing system

Based on the related physical and chemical laws as well as the three fundamental scientific principles in nature, namely, mass conservation, energy conservation and momentum conservation, the mathematical governing equations of the hydrothermal mineralizing system under consideration can be expressed in Eqs 1-8 as follows (Zhao et al., 2002; Zhao et al., 2008b):

$\frac{\partial }{\partial x}\left[{\rho }_f\frac{k\left(\phi \right)}{\mu \left(T\right)}\frac{\partial p}{\partial x}\right]+\frac{\partial }{\partial y}\left[{\rho }_f\frac{k\left(\phi \right)}{\mu \left(T\right)}\left(\frac{\partial p}{\partial y}-{\rho }_{f}g\right)\right]=-Q_f(1)$

$u=-\frac{k\left(\phi \right)}{\mu \left(T\right)}\frac{\partial p}{\partial x}(2)$

$v=-\frac{k\left(\phi \right)}{\mu \left(T\right)}\left(\frac{\partial p}{\partial y}-{\rho }_{f}g\right)(3)$

${\rho }_f{c}_{pf}\left(v\frac{\partial T}{\partial y}+u\frac{\partial T}{\partial x}\right)=\left(\frac{\partial }{\partial y}\left({\lambda }^e\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial x}\left({\lambda }^e\frac{\partial T}{\partial x}\right)\right)+Q_T(4)$

${\lambda }^e=\phi {\lambda }_f+\left(1-\phi \right){\lambda }_s {\rho }_f={\rho }_{ref}\left[1-{\beta }_T\left(T-T_{ref}\right)\right](5)$

$\left(u\frac{\partial C_{H_{2}S}}{\partial x}+v\frac{\partial C_{H_{2}S}}{\partial y}\right)=\left(\phi D\frac{{\partial }^2{C}_{H_{2}S}}{\partial x^2}+\phi D\frac{{\partial }^2{C}_{H_{2}S}}{\partial y^2}\right)-\phi k_R{C}_{H_{2}S}{C}_{S{O}_4^{=}}(6)$

$\left(u\frac{\partial C_{S{O}_4^{=}}}{\partial x}+v\frac{\partial C_{S{O}_4^{=}}}{\partial y}\right)=\left(\phi D\frac{{\partial }^2{C}_{S{O}_4^{=}}}{\partial x^2}+\phi D\frac{{\partial }^2{C}_{S{O}_4^{=}}}{\partial y^2}\right)+\phi k_R{C}_{H_{2}S}{C}_{S{O}_4^{=}}(7)$

$\left(u\frac{\partial C_{H^{+}}}{\partial x}+v\frac{\partial C_{H^{+}}}{\partial y}\right)=\left(\phi D\frac{{\partial }^2{C}_{H^{+}}}{\partial x^2}+\phi D\frac{{\partial }^2{C}_{H^{+}}}{\partial y^2}\right)+2\phi k_R{C}_{H_{2}S}{C}_{S{O}_4^{=}}(8)$

where $u$ is the x-direction component of the pore-fluid velocity; $v$ is the y-direction component of the pore-fluid velocity in the fluid-saturated porous rock; $p$ is the pore-fluid pressure; $T$ is the porous rock temperature; ${\rho }_f$ is the pore-fluid density; $Q_f$ is the pore-fluid source term; $\phi$ is the porosity of the porous rock; $k\left(\phi \right)$ is the permeability of the porous rock; $\mu \left(T\right)$ is the temperature-dependent dynamic viscosity of the pore-fluid; ${\rho }_{ref}$ is the pore-fluid reference density; $T_{ref}$ is the porous rock reference temperature; ${\beta }_T$ is the pore-fluid thermal volume-expansion coefficient; $\mathrm{g}$ is the gravity acceleration in the vertical direction; ${\lambda }_f$ is the pore-fluid thermal conductivity coefficient; $c_{pf}$ is the pore-fluid specific heat; $Q_T$ is the heat source; ${\lambda }_s$ is the porous (dry) rock thermal conductivity coefficient; $C_{H_{2}S}$, $C_{S{O}_4^{2-}}$ and $C_{H^{+}}$ are the concentrations of $H_{2}S$, $S{O}_4^{2-}$ and $H^{+}$ in the pore-fluid respectively; $D$ is the diffusion coefficient of the solute in the pore-fluid of the fluid-saturated porous rock.

It is noted that in deriving the aforementioned mathematical governing equations, the following chemical reaction processes are also considered in Eqs 9-13 as Zhao et al., (2002); Zhao et al., (2008b):

$H_{2}S+2O_2\stackrel{k_R}{\iff }S{O}_4^{2-}+2H^{+}(9)$

$P{b}^{2+}+H_{2}S\iff PbS+2H^{+}(10)$

$R=k_R{C}_{H_{2}S}{C}_{S{O}_4^{2-}}(11)$

$C_{P{b}^{2+}}^e=\frac{C_{H^{+}}^2}{K_{Pb}{C}_{H_{2}S}}(12)$

$M{R}_{Pb}=u\frac{\partial C_{P{b}^{2+}}^e}{\partial x}+v\frac{\partial C_{P{b}^{2+}}^e}{\partial y}(13)$

where R is the experimental reaction rate of the mixing between the sulfide and sulfate fluids (Ohmoto and Lasage, 1982); $k_R$ is the overall reaction rate constant, which is strongly dependent on temperature; $C_{P{b}^{2+}}^e$ is the equilibrium concentration of Pb in the pore-fluid; $K_{Pb}$ is the chemical equilibrium reaction constant (Zhao et al., 2002; Zhao et al., 2008b); $M{R}_{Pb}$ is the mineralization rate of galena.

It needs to be pointed out that Darcy’s law is established under the condition that the pore-fluid flow within a fluid-saturated porous medium is in a steady state. It was based on Darcy’s original experiments, which revealed that the flow rate through a fluid-saturated porous medium is directly proportional to the applied pressure difference, which is applied to the fluid-saturated porous medium (Phillips, 1991; Nield and Bejan, 1992; Zhao et al., 2008b). Generally, Darcy’s law can play the following two roles in the study of pore-fluid flow within a fluid-saturated porous rock. The first role is that as an experimental law, just like Fick’s law and Fourier’s law, Darcy’s law states that the pore-fluid flow within a fluid-saturated porous rock is driven by the pore-fluid pressure gradient, which is applied to the fluid-saturated porous rock. The second role is that in terms of the momentum in a steady-state pore-fluid flow system within a fluid-saturated porous rock, Darcy’s law describes the momentum conservation of the steady-state pore-fluid flow system within the fluid-saturated porous rock. However, if the pore-fluid flow system within a fluid-saturated porous rock is in a transient state, then Darcy’s law cannot be directly used to describe the momentum conservation of the transient-state pore-fluid flow system within the fluid-saturated porous rock. In this case, Darcy’s law, which is expressed by Eqs 2 and 3, needs to be modified by considering the momentum change rate in the transient-state pore-fluid flow system within a fluid-saturated porous rock. According to the momentum conservation principle in nature, which states that the momentum change rate in a transient-state pore-fluid flow system should be equal to the summation of all the external forces acted on the transient-state pore-fluid flow system, the momentum conservation equations of a transient pore-fluid flow system can be written as follows:

$\frac{D}{Dt}\left({\rho }_f\frac{u}{\phi }\right)=-\frac{\mu \left(T\right)}{k\left(\phi \right)}u-\frac{\partial p}{\partial x}(14)$

$\frac{D}{Dt}\left({\rho }_f\frac{v}{\phi }\right)=-\frac{\mu \left(T\right)}{k\left(\phi \right)}v-\left(\frac{\partial p}{\partial y}-{\rho }_{f}g\right)(15)$

where $\frac{D}{Dt}\left({\rho }_f\frac{u}{\phi }\right)$ is the momentum change rate in the horizontal direction of the transient-state pore-fluid flow system; $\frac{D}{Dt}\left({\rho }_f\frac{v}{\phi }\right)$ is momentum change rate in the vertical direction of the transient-state pore-fluid flow system. Other quantities have exactly the same meanings as those defined in Eqs 2 and 3.

Since Eqs 14 and 15 are different from Eqs 2 and 3, which are the specific forms of Darcy’s law, Eqs 14 and 15 can be regarded as the specific forms of the extended Darcy’s law. Therefore, Darcy’s law can be used to describe the momentum conservation in a steady-state pore-fluid flow within a fluid-saturated porous rock, while the extended Darcy’s law can be used to describe the momentum conservation in a transient-state pore-fluid flow within a fluid-saturated porous rock. As mentioned previously, since the considered hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit is in a steady state, Darcy’s law, instead of the extended Darcy’s law, can be used to describe the momentum conservation in the considered hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. This is the main reason why the hydrothermal fluid flow conforms to Darcy’s law in this study.

Due to the versatility of the FEM, it has been used for solving scientific and engineering problems of many different kinds (Zienkiewicz, 1977; Lewis and Schrefler, 1998). This means that it is possible to use the FEM for solving hydrothermal mineralizing problems involved in the convective flow of pore-fluid within porous rocks (Zhao et al., 1997; Zhao et al., 2002; Zhao et al., 2008b). For this reason, a FEM-based computer code was developed and validated in the previous study (Zhao and Liu, 2023a). Regarding the details about how to use this code for implementing the numerical modeling of the hydrothermal mineralizing system associated with the pore-fluid convection controlled ore deposit, please refer to the open publication (Zhao and Liu, 2023a). For the sake of saving space, it is unnecessary to repeat them in this article.

3.2 The computational models of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit

In the dual length-scale approach (Zhao and Liu, 2023a), two computational models of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit need to be established. One computational model is called the regional model, while the other is called the deposit model. The main advantage of using the dual length-scale approach is that the overall convective pore-fluid flow pattern can be predicted through computationally simulating the regional model of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit, while the detailed Pb distribution pattern can be predicted through computationally simulating the deposit model of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. In particular, the deposit model boundary conditions can be accurately and consistently determined from the computational simulation results of the regional model.

3.2.1 The finite element meshes and geometric shapes of the computational models

According to the geophysical data and the metallogenetic model of the Laochang Pb-Zn deposit (Zhang, 2011; Cheng et al., 2012a; Cheng et al., 2012b; Zhao, 2022; Zhao et al., 2022), the two computational models can be established and shown in Figure 3. The length and height of the regional model are equal to 24 and 10 km, while the length and height of the deposit model are equal to 1.5 and 1.15 km respectively. Note that in the process of determining the top surface of the regional model, the eroded part from the past surface during mineralization is added on the present surface of the Laochang Pb-Zn deposit. The purpose of setting the lateral extent of the domain at a large value of 24 km is to avoid the boundary effects on the computationally simulating results of the regional model. In particular, the post-solidification influence of the intruded magma on the regional mineralization is primarily considered in the regional model, while the influence of the fault zone (including the vein type, stratiform-like type and interlayer type) on the orebody location is primarily considered in the deposit model. For these reasons, the solidified magma is artificially placed but not simulated in the middle of the regional model, while the fractured area of a high permeability is placed in the deposit model through considering the geophysical data at the corresponding location. The morphology of the intrusion is determined by the corresponding geophysical data and research results (Cheng et al., 2012a; Cheng et al., 2012b; Zhao, 2022; Zhao et al., 2022). For both the regional and deposit models, the whole computational domains are filled with the Triassic Gejiu Formation limestone rock.

FIGURE 3

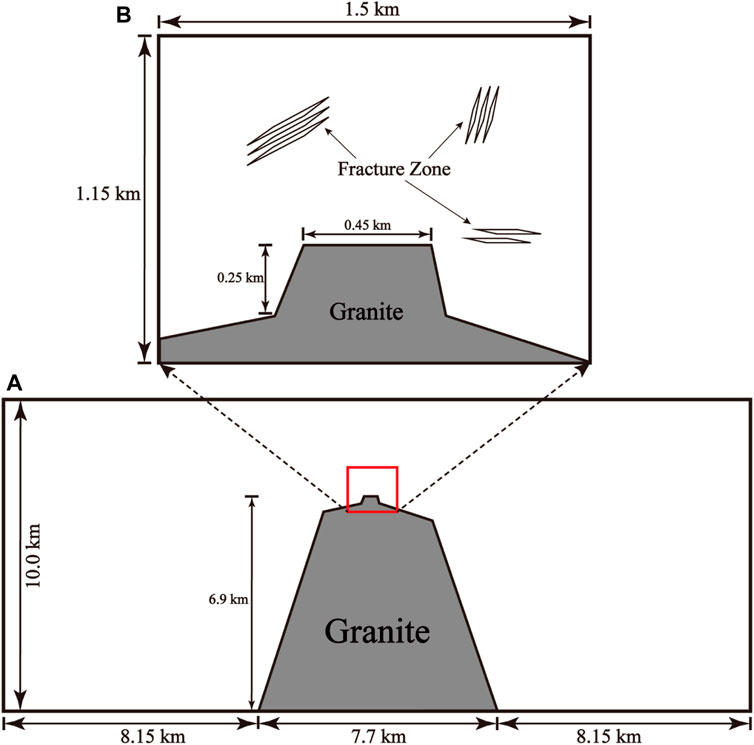
FIGURE 3. The geometry model of the Laochang Pb-Zn deposit: (A) The geometry of the regional model; (B) The geometry of the deposit model.

Figure 4 shows the finite element meshes of the regional and deposit models. In the regional model, which is also named as the large-length scale model, the computational domain is simulated using a coarse mesh, which is comprised of 8335 six-node triangular elements. On the other hand, in the deposit model, which is also named as the small-length scale model, the computational domain is simulated using a fine mesh, which is comprised of 23,751 six-node triangular elements. According to the previous studies (Zienkiewicz, 1977; Zhao et al., 2003), the mesh Peclet number requirement can be utilized for determining the maximum finite element size, which is used in both the regional and deposit models. Consequently, the maximum side length of the finite elements used in the regional model is equal to 300 m, while the maximum side length of the finite elements used in the deposit model is equal to 30 m. In addition, the minimum side length of the finite elements used in the regional model is equal to 150 m, while the minimum side length of the finite elements used in the deposit model is equal to 5 m.

FIGURE 4

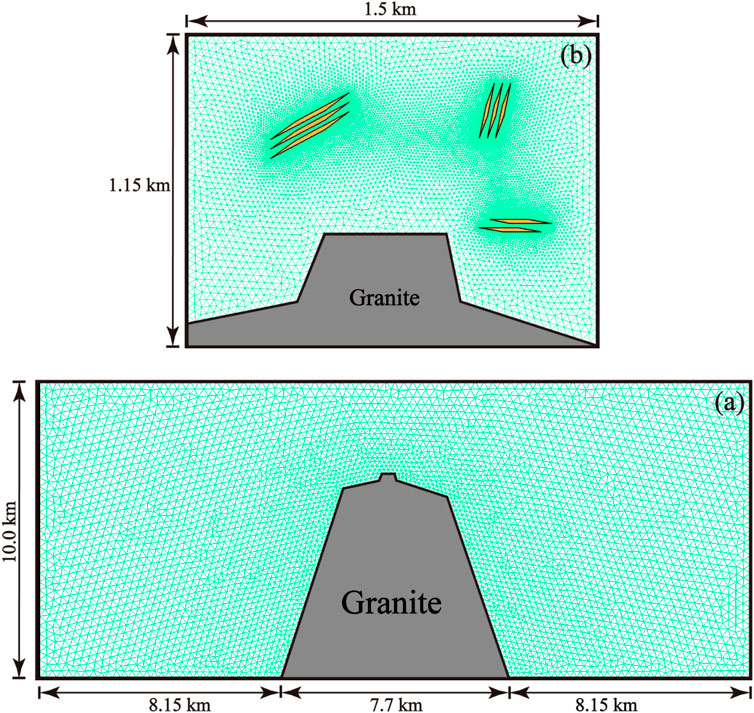
FIGURE 4. The finite element meshes of the two computational models: (A) The finite element meshes of the regional mode; (B) The finite element meshes of the deposit model.

3.2.2 The parameters of the computational models

In computationally simulating the hydrothermal mineralizing mechanism associated with the Laochang Pb-Zn deposit, the related parameters are listed in Table 1. In order to consider the pore-fluid dynamic viscosity of the temperature-dependent feature, the following expression is used in the computational simulation (Kestin et al., 1978; Rabinowicz et al., 1998; Eldursi et al., 2009):

$\mu \left(T\right)=2.414\times {10}^{-5}\times {10}^{\left(\frac{247.8}{T+133.15}\right)}(16)$

where the unit of temperature is Celsius degrees (i.e., $℃$).

TABLE 1

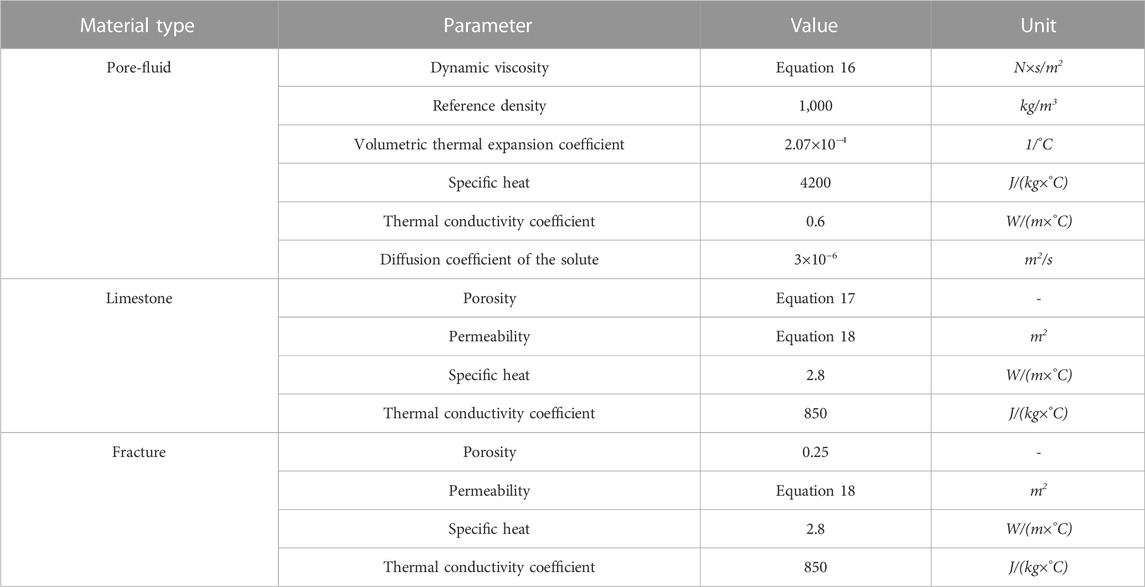
TABLE 1. The parameters used in this study (Nield and Bejan, 1992; Zhao et al., 2008b; Schon, 2011).

The porosity of the porous rock generally depends on the burial depth, especially at shallow depths where the pressure solution, mechanical compaction and diagenesis play an important role in modifying the initial porosity during burial (Bethke, 1985; Harrison and Summa, 1991; Shmonov et al., 2003; Ingebritsen and Appold, 2012; Kuang and Jiao, 2014). For this reason, the following expression, which states that the porosity decreases exponentially with the burial depth (Schon, 2011), is used for the limestone rock in this study:

$\phi \left(h\right)=A{e}^{\left(-Ch\right)}+B(17)$

where $\phi \left(h\right)$ is the limestone rock porosity, which is a dimensionless quantity; $h$ is the burial depth with a unit of kilometer; $A$ and $B$ are two dimensionless parameters, while $C$ is a parameter with a unit of unity per kilometer. For the limestone rock considered in this study, $A$ and $B$ are selected to be 0.1 and 0.05, while $C$ is selected to be 0.75. This means that at the surface of the upper crust, where the burial depth is equal to zero, the reference porosity of the limestone rock is equal to 0.15, while the reference permeability of the limestone rock is equal to $1.0\times {10}^{-15}{m}^2$ (Schon, 2011).

For the purpose of expressing a relationship between permeability and porosity, the Carman-Kozeny law (Carman, 1956) is utilized, so that the relationship used in the computational simulation can be written as:

$k\left(\phi \right)=\frac{k_{ref}{\left(1-{\phi }_{ref}\right)}^2{\phi }^3}{{\phi }_{ref}^3{\left(1-\phi \right)}^2}(18)$

where $k\left(\phi \right)$ is the porous rock permeability value; $k_{ref}$ and ${\phi }_{ref}$ are the reference permeability and porosity of the porous rock.

3.2.3 The boundary conditions of the computational models

The following boundary conditions for the regional model of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit are used. Based on the annually averaged temperature of about 20 $℃$ in the considered region, the temperature at the top boundary of the regional model is assumed to be equal to 20 $℃$. On the other hand, based on the regional geothermal gradient of about 30 $℃/km$ in the considered region, the temperature at the boundary of the solidified magma and the bottom boundary of the regional model is assumed to be equal to 320 $℃$, because the depth of the regional model considered in this study is equal to 10 km. For the regional model, both the two lateral boundaries are considered to be impermeable in the horizontal direction. Except for the portion of the solidified magma, the bottom boundary of the regional model is impermeable in the vertical direction. The solidified magma boundary is impermeable in the normal direction along the boundary. In addition, both the two lateral boundaries of the regional model are heat-isolative in the horizontal direction. All the porous rocks are initially saturated with water. The top boundary pore-fluid pressure of the regional model is equal to the atmospheric pressure. The $H_{2}S$ and $S{O}_4^{2-}$ concentrations are equal to zero and 0.01 $kmol/m^3$ at the top of the regional model, while the $H_{2}S$ and $S{O}_4^{2-}$ concentrations are assumed to be equal to 0.001 $kmol/m^3$ and zero at the boundary of the solidified magma in the regional model respectively. This means that the concentration boundary conditions, instead of the flux boundary conditions, are used in computationally simulating the regional model of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit.

According to the dual length-scale approach (Zhao and Liu, 2023a), the boundary conditions of the deposit model of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit should be accurately and consistently evaluated from the computationally simulating results of the regional model.

4 The computationally simulating results of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit

4.1 The computationally simulating results of the regional model

Figure 5 shows the distributions of the temperature, excess pore-fluid pressure and pore-fluid velocity in the regional model (i.e., the large length-scale model) of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Due to the supercritical state of the hydrothermal mineralizing system, the pore-fluid convection occurs in the regional model. It is noted that in Figure 5A, the simulated geothermal gradient in the regional model is approximately equal to 30 $℃/km$ at large, especially in the places that are close to both the left and right boundaries of the regional model. This fact indicates that the assumption of the temperature at the boundary of the solidified magma in the regional model being equal to 325 $℃$ can be roughly justified (Zhao et al., 2016b). As shown in Figure 5C, the convective flow of pore-fluid can be clearly observed from the distributions of the pore-fluid velocity. Because of the convective pore-fluid flow, the temperature distribution is highly localized in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit, as can be clearly observed from the computational results shown in Figure 5A. Since the temperature distribution affects the pore-fluid density distribution, as shown in Figure 5B, the abnormal distribution of excess pore-fluid pressure is capable of taking place in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Consequently, the pore-fluid convection is maintainable in the mineralizing system involved in the Laochang Pb-Zn deposit.

FIGURE 5

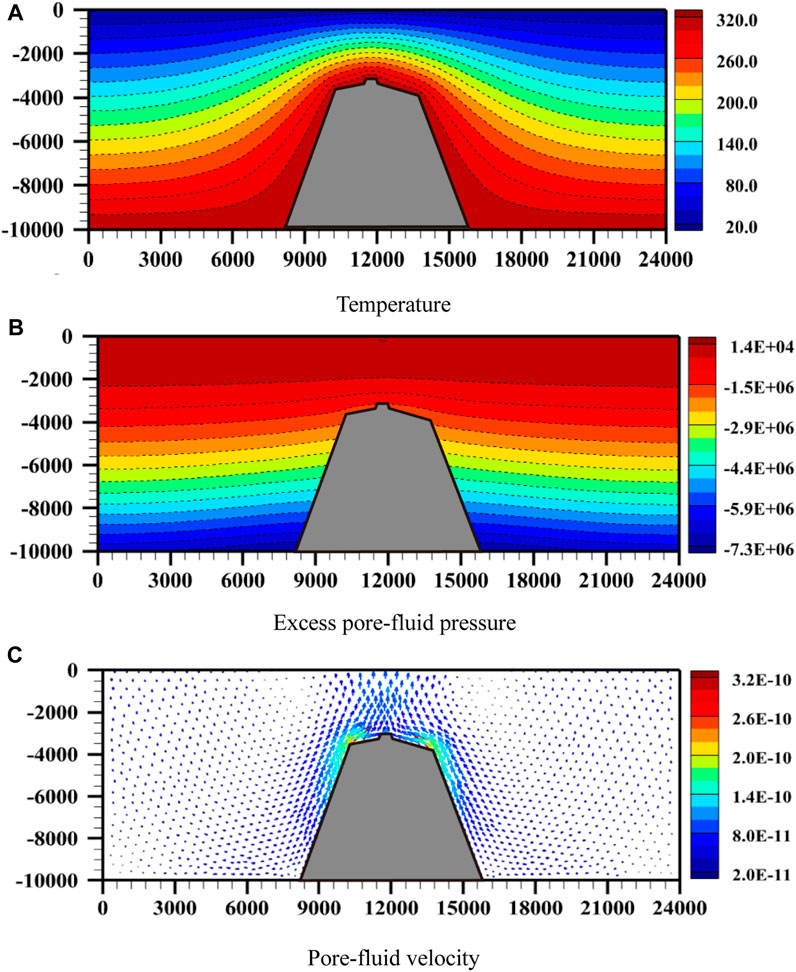
FIGURE 5. Computational simulation results of the regional model: (A) Temperature; (B) Excess pore-fluid pressure; (C) Pore-fluid velocity.

Figure 6 shows the $H_{2}S$, $S{O}_4^{2-}$ and $H^{+}$ concentration distributions in the regional model of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. The localized distributions of these chemical species can be clearly observed from the computational results shown in this figure. Except for $S{O}_4^{2-}$, which is widely distributed in the regional model (see Figure 6B), $H_{2}S$ and $H^{+}$ are mainly distributed around the intrusion (see Figures 6A, C). This means that the convective flow of pore-fluid may lead to the localized distributions of these chemical species within the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. In particular, the sulfate fluid comes from the rain water on the upper crust surface, while the sulfide fluid comes from the hot magma in the deep Earth. The convective pore-fluid brings $H_{2}S$ into the hydrothermal mineralizing system from the deep strata, while it brings $S{O}_4^{2-}$ into the hydrothermal mineralizing system from the shallow strata. Consequently, these two chemical species can be mixed to enable chemical reactions to occur at the appropriate place in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. More importantly, through the mixing and chemical reactions of the sulfide and sulfate fluids, the concentration gradient of $H^{+}$ can be formed within the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. This phenomenon is obviously observable through the computationally simulating results shown in Figure 6C.

FIGURE 6

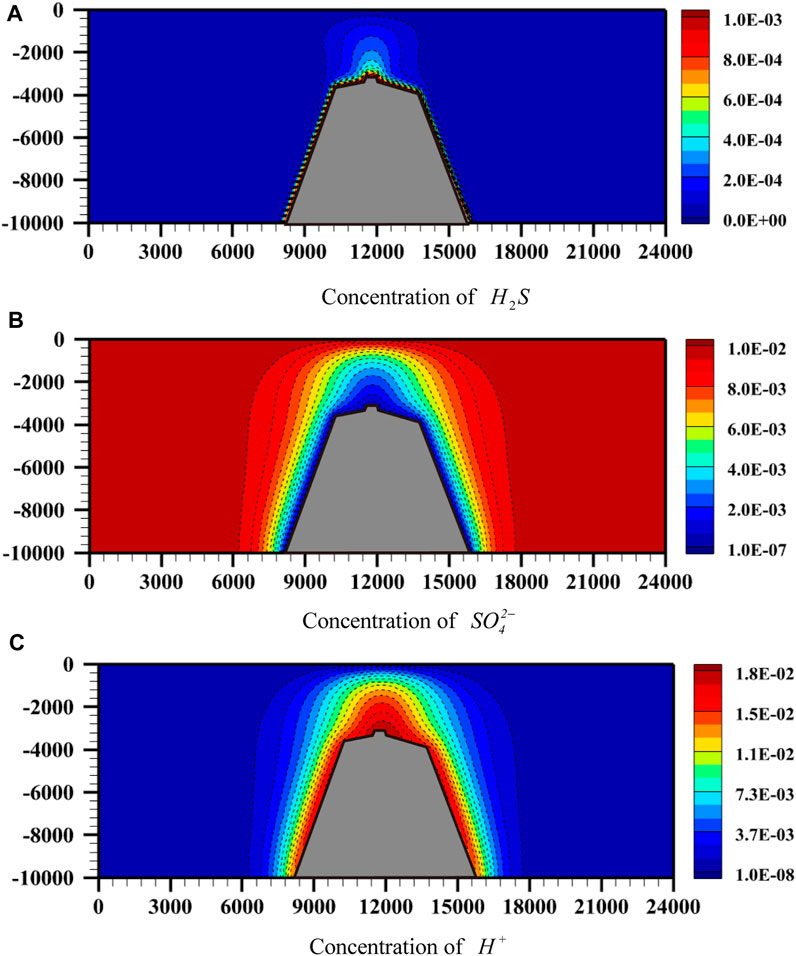
FIGURE 6. Computational simulation results of the regional model: (A) Concentration of $H_{2}S$; (B) Concentration of $S{O}_4^{2-}$; (C) Concentration of $H^{+}$.

4.2 Determining the deposit model boundary conditions using the computationally simulating results of the regional model

As mentioned previously, the deposit model boundary conditions are accurately and consistently determinable through using the computationally simulating results of the regional model. Figure 7 shows the boundary conditions applied to the deposit model of the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. In this figure, the boundary conditions applied to the deposit model up and down boundaries are marked with “Up” and “Down,” while the boundary conditions applied to the deposit model left and right boundaries are marked with “Left” and “Right.” Because five fundamental unknown variables, such as the temperature, excess pressure of pore-fluid, concentration of $S{O}_4^{2-}$, concentration of $H_{2}S$ and concentration of $H^{+}$, are taken into account in the hydrothermal mineralizing system, the boundary conditions for each of them should be applied in the deposit model of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit.

FIGURE 7

FIGURE 7. The boundary conditions applied to the deposit model: (A) Temperature; (B) Excess pore-fluid pressure; (C) Concentration of $H_{2}S$; (D) Concentration of $S{O}_4^{2-}$; (E) Concentration of $H^{+}$.

It should be pointed out that on the one hand, the abscissas in the left column of Figure 7 represent the x coordinates along the corresponding boundaries of the deposit model, while the abscissas in the right column of Figure 7 represent the y coordinates along the corresponding boundaries of the deposit model. On the other hand, the ordinates in Figure 7 represent the values of the five fundamental unknown variables, namely, the temperature, excess pore-fluid pressure, concentration of $H_{2}S$, concentration of $S{O}_4^{2-}$ and concentration of $H^{+}$ in the hydrothermal mineralizing system. For example, the ordinate in Figure 7A represents the temperature, while the ordinate in Figure 7B represents the excess pore-fluid pressure. Similarly, the ordinates in Figures 7C–E represent the concentration of $H_{2}S$, the concentration of $S{O}_4^{2-}$ and the concentration of $H^{+}$, respectively.

From the boundary conditions shown in Figure 7, it is clearly observed that except for the bottom boundary, the boundary values applied to the other three boundaries, namely, the top boundary, the left boundary and the right boundary, of the deposit model are no longer constants for each of the five fundamental unknown variables. However, for the bottom boundary, the applied boundary values of the temperature, $H_{2}S$ and $S{O}_4^{2-}$ concentrations are constants, because the bottom boundary of the deposit model is in coincident with the bottom boundary of the regional model.

Nevertheless, if the computationally simulating results, which are obtainable from computationally simulating the regional model, are not used, then it is impossible to correctly determine the reasonable deposit model boundary conditions for the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. This clearly indicates that the computationally simulating results, which are obtainable from computationally simulating the regional model, play a crucial role in correctly determining the deposit model boundary conditions for the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit.

4.3 The computationally simulating results of the deposit model

Figure 8 shows the distributions of the temperature, excess pressure of pore-fluid and velocity of pore-fluid in the deposit model (i.e., the small length-scale model) of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. It can be clearly observed that in the fracture zone of the deposit model, there are remarkably abnormal distributions of the temperature, excess pressure of pore-fluid and velocity of pore-fluid, especially for the excess pressure of pore-fluid and velocity of pore-fluid (see Figures 8B, C). It is also noted that the hydrothermal fluid focusing may occur in the deposit model fracture zone of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. This fact indicates that more hydrothermal fluids may flow through the fracture zone in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit.

FIGURE 8

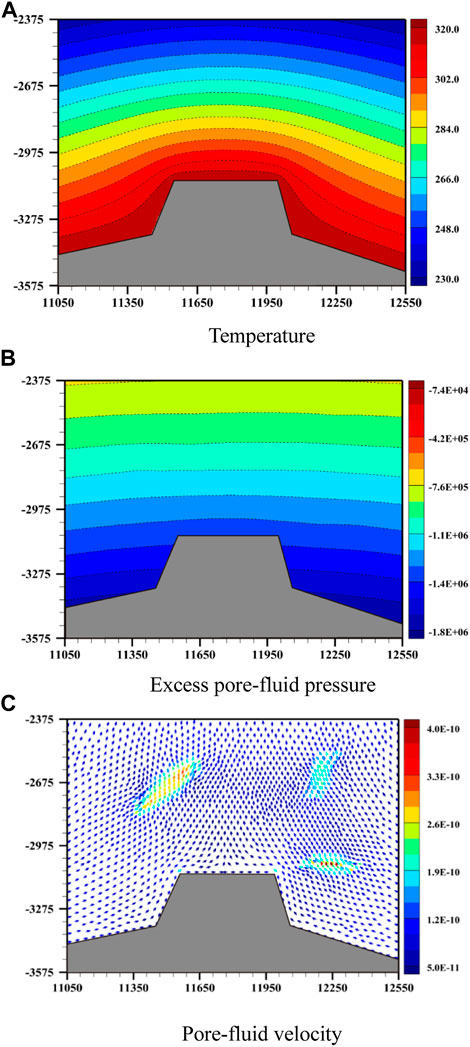
FIGURE 8. Computational simulation results of the deposit model: (A) Temperature; (B) Excess pore-fluid pressure; (C) Pore-fluid velocity.

Figure 9 shows the $H_{2}S$, $S{O}_4^{2-}$ and $H^{+}$ concentration distributions in the deposit model of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. It can be noted that in the deposit model fracture zone, there are remarkably abnormal $H_{2}S$, $S{O}_4^{2-}$ and $H^{+}$ concentration distributions, especially for the $H_{2}S$ and $H^{+}$ concentration distributions (see Figures 9A, C). This is mainly because the abnormal distributions of temperature and pore-fluid velocity within the fracture zone can alter the mixing and chemical reactions of these chemical species in the deposit model of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit.

FIGURE 9

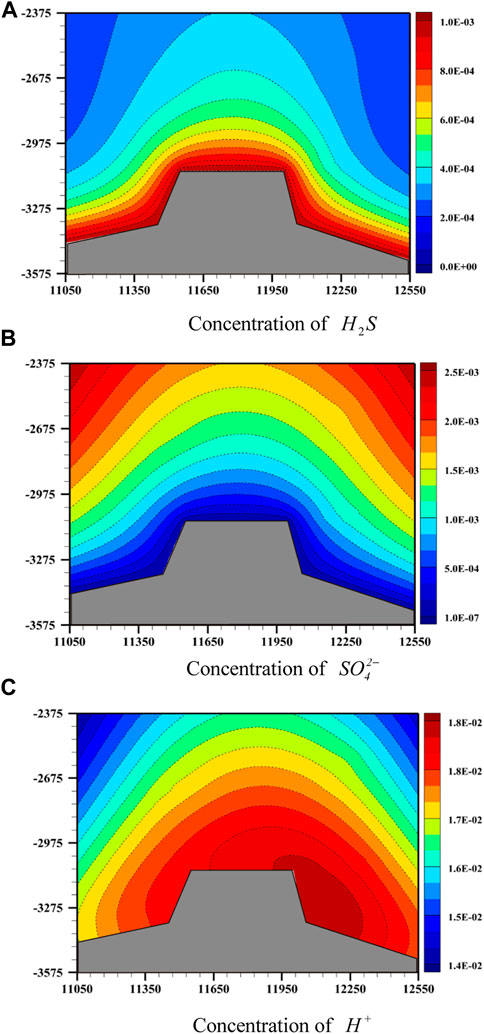
FIGURE 9. Computational simulation results of the deposit model: (A) Concentration of $H_{2}S$; (B) Concentration of $S{O}_4^{2-}$; (C) Concentration of $H^{+}$.

4.4 The simulating results of the mineralization rate

According to the modern mineralization theory (Zhao et al., 2002; Zhao et al., 2008b), the mineralization rate of a specific mineral can be used to identify the mineral precipitation and dissolution regions in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Theoretically, the negative value of the mineralization rate indicates the precipitation region of the specific mineral, while the positive value indicates the dissolution region of the specific mineral. Figure 10 shows the comparison of the computationally simulated Pb precipitation region with the observed Pb distribution (Zhao et al., 2022) in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. Since the computationally simulated Pb precipitation region is almost identical to the observed Pb distribution (Zhao et al., 2022), it may be concluded that the convective flow of pore-fluid is the primary dynamic mechanism for controlling the Pb mineralization in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. The above-mentioned conclusion can further demonstrate that the computational simulation method associated with the emerging field of computational geosciences is a useful tool for identifying the main dynamic mechanism, which controls the mineralization pattern in the hydrothermal mineralizing system within the Earth’s upper crust.

FIGURE 10

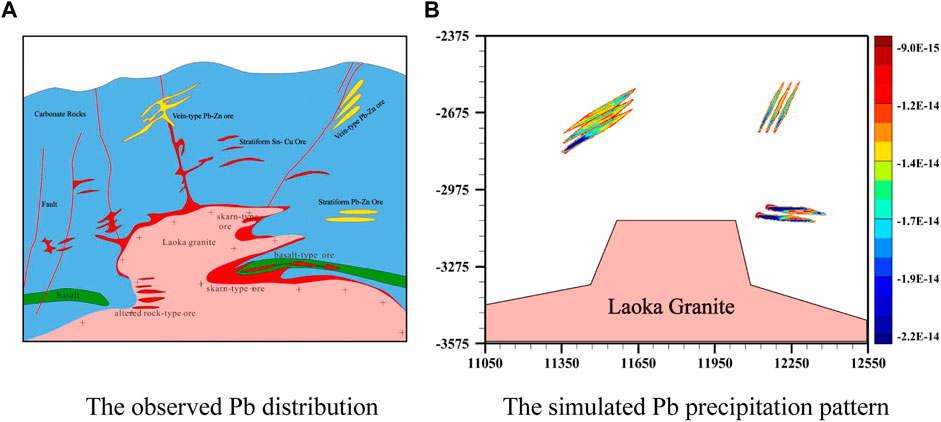
FIGURE 10. Comparison of the computationally simulated Pb distribution pattern with the observed Pb distribution: (A) The observed Pb distribution (Zhao et al., 2022); (B) The computationally simulated Pb precipitation pattern.

4.5 The effect of the lower boundary condition and the reliability of the obtained simulation results

4.5.1 The effect of the lower boundary condition

Since the concentration of $H_{2}S$ at the solidified magma portion of the lower boundary of the regional model depends on the liquidus magma solidification at the interface between the liquidus magma and the surrounding rock, it cannot be accurately determined unless the transient process of liquidus magma solidification is considered in the mathematical model (Zhao et al., 2005). However, all the currently-available computational programs cannot be used to deal with the transient process of liquidus magma solidification. Alternatively, it is desirable to investigate how the concentration of $H_{2}S$ at the solidified magma portion of the lower boundary of the regional model affects the computationally simulated Pb precipitation in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. For this purpose, five different values of the $H_{2}S$ concentration at the solidified magma portion of the lower boundary of the regional model are considered in five different simulations of the regional model involved in the Laochang Pb-Zn deposit.

Figures 11 and 12 show the effects of five different values of the $H_{2}S$ concentration, which are applied at the solidified magma portion of the lower boundary of the regional model, on the computationally simulated Pb precipitation patterns and maximum precipitation rates in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit. As can be seen from the computational simulation results shown in Figure 11, the computationally simulated Pb precipitation locations in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit are almost identical for using five different values of the $H_{2}S$ concentration, which are applied at the solidified magma portion of the lower boundary of the regional model. This further confirms that the orebody location in the mineralizing system associated with the Laochang Pb-Zn deposit is completely controlled by the pore-fluid convection, rather than by the $H_{2}S$ concentration, which are applied at the solidified magma portion of the lower boundary of the regional model. Therefore, in terms of determining the orebody location in the mineralizing system associated with the Laochang Pb-Zn deposit, the effect of the $H_{2}S$ concentration, which is applied at the solidified magma portion of the lower boundary of the regional model, can be neglected.

FIGURE 11

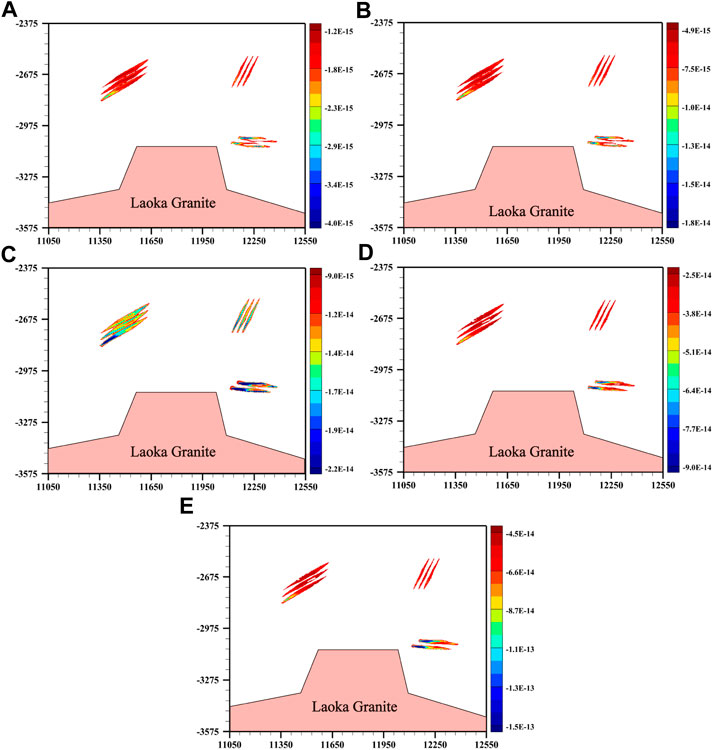
FIGURE 11. Effects of five different lower boundary values of the $H_{2}S$ concentration on the computationally simulated Pb precipitation patterns in the Laochang Pb-Zn deposit: (A) ${\mathrm{C}}_{H_{2}S}=0.0002kmol/m^3$; (B) ${\mathrm{C}}_{H_{2}S}=0.0006kmol/m^3$; (C) ${\mathrm{C}}_{H_{2}S}=0.0001kmol/m^3$; (D) ${\mathrm{C}}_{H_{2}S}=0.0014kmol/m^3$; (E) ${\mathrm{C}}_{H_{2}S}=0.0018kmol/m^3$.

FIGURE 12

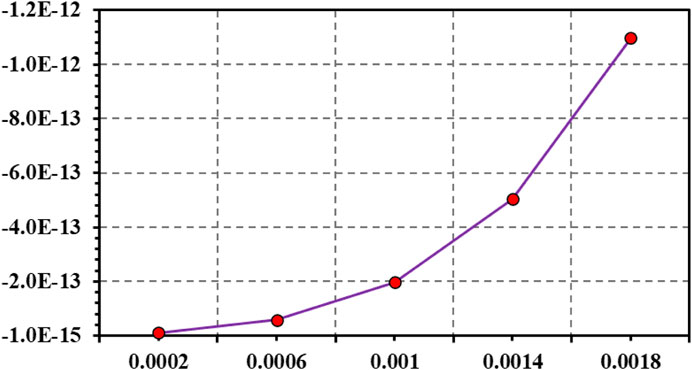
FIGURE 12. Effects of five different lower boundary values of the $H_{2}S$ concentration on the computationally simulated Pb maximum precipitation rates in the Laochang Pb-Zn deposit.

However, as can be seen from the computational simulation results shown in Figure 12, the computationally simulated Pb maximum precipitation rates in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit are remarkably different for using five different values of the $H_{2}S$ concentration, which are applied at the solidified magma portion of the lower boundary of the regional model. Therefore, it can be concluded that in terms of determining the orebody grade in the mineralizing system associated with the Laochang Pb-Zn deposit, the effect of the $H_{2}S$ concentration, which is applied at the solidified magma portion of the lower boundary of the regional model, should be considered. This may be regarded as the main limitation of this study. To remove this limitation, it is necessary to develop computational tools for simulating the transient process of liquidus magma solidification in the future research.

4.5.2 The reliability of the obtained simulation results

Since the computational simulation method, such as the FEM used in this study, belongs to the numerical method, it can only produce approximate solutions for a scientific problem or an engineering problem, from the mathematical point of view. In theory, if the finite element size, which is used in the computational simulation of either a scientific problem or an engineering problem, approaches zero, then the obtained numerical solution approaches the true solution of either the scientific problem or the engineering problem. In this limiting case, the numerical error between the obtained numerical solution and the true solution approaches zero, so that the obtained numerical solution is absolutely reliable. However, in practice, it is impossible to use the finite element of zero size in the computational simulation of either a scientific problem or an engineering problem. To get out of this dilemma, it is necessary to establish a criterion to determine the allowable maximum finite element size, so as to guarantee the reliability of the obtained numerical solution in the computational simulation of either a scientific problem or an engineering problem.

Through conducting a large number of mesh sensitivity analyses and parameter studies (Zienkiewicz, 1977; Daus et al., 1985; Zhao et al., 2001; Zhao et al., 2003; Zhao et al., 2012b), it was found that as long as the maximum size of the finite element is determined by satisfying the following mesh Peclet number requirement, the convergence and accuracy of the computational simulation results can be automatically guaranteed.

$P{e}_{mesh}=\frac{v_{\max }{l}_{mesh}}{2\alpha }\le 1.0(19)$

where $P{e}_{mesh}$ is the mesh Peclet number; $v_{\max }$ is the maximum Darcy velocity; $\alpha$ is the diffusivity of a considered physical process and $l_{mesh}$ is the side length of the finite element to be used in the computational simulation of the considered physical process (Zienkiewicz, 1977; Daus et al., 1985; Zhao et al., 2001; Zhao et al., 2003; Zhao et al., 2012b).

Since Eq. 19 can be used to automatically guarantee the convergence and accuracy of the computational simulation results, which are obtained from using the FEM, it is called the reliability criterion of the obtained numerical solution for either a scientific problem or an engineering problem in the computational simulation. However, since a hydrothermal mineralizing system involves multiple physical processes (Zhao et al., 2012a), namely, a pore-fluid flow process, a heat transfer process and a mass transport process, it is necessary to determine the controlling physical process among these three physical processes. According to the previous study (Zhao and Liu., 2023a), the mass transport process is the controlling physical process in the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit.

Figure 13 shows the distributions of the mesh Peclet number in both the regional model and the deposit model for computationally simulating the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. It can be observed that the maximum value of the mesh Peclet number is less than unity in both the regional model (see Figure 13A) and the deposit model (see Figure 13B). This means that the reliability criterion of the obtained numerical solution can be satisfied for every finite element used in the computational simulation of the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Consequently, it can be concluded that all the obtained numerical results in this study are reliable, at least from the computational simulation point of view.

FIGURE 13

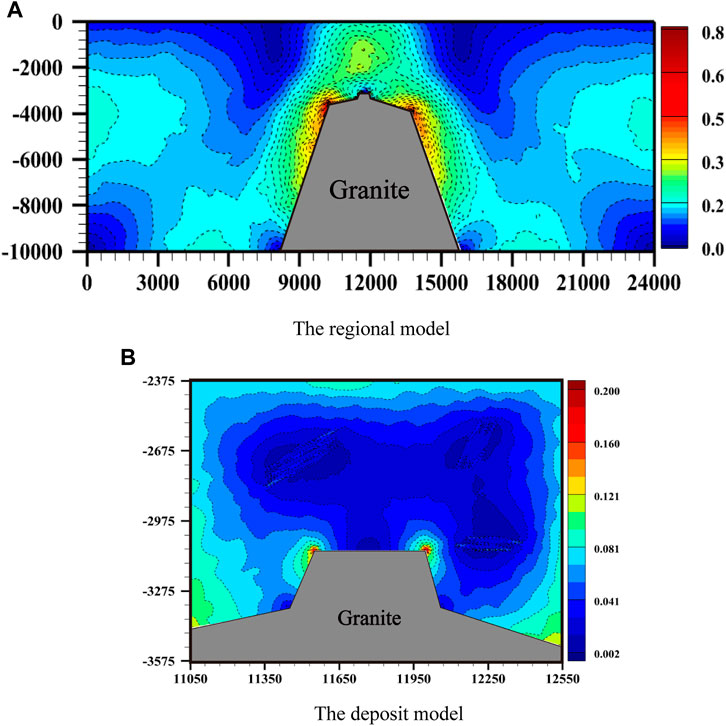
FIGURE 13. Distributions of the mesh Peclet number in both the regional and deposit models for computationally simulating the hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit: (A) The regional model; (B) The deposit model.

5 Conclusion

Through using both the FEM and the dual length-scale approach to simulate the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit, the following main conclusions can be made from this study: 1) the convective flow of pore-fluid can occur within the regional model (namely, the large length-scale model), but it cannot take place within the deposit model (namely, the small length-scale model); 2) the deposit model boundary conditions are accurately and consistently determinable from the computationally simulating results of the regional model in the strictly scientific manner; 3) the convective flow of pore-fluid is the primary dynamic mechanism for controlling the Pb mineralization in the hydrothermal mineralizing system involved in the Laochang Pb-Zn deposit; and 4) the computational simulation method associated with the emerging field of computational geosciences is a useful tool for identifying the main dynamic mechanism, which controls the mineralization pattern in the hydrothermal mineralizing system within the Earth’s upper crust.

It should be pointed out that the work presented in this study has a limited application scope, because it is only valid for the specific situation that is established on the bases of a steady-state or a quasi-steady-state hydrothermal mineralizing system associated with the Laochang Pb-Zn deposit. Nevertheless, the effects of the transient process associated with the liquidus magma solidification and cooling on the formation of the Laochang Pb-Zn deposit may need to be considered in the future research.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GL: Conceptualization, Data curation, Formal Analysis, Software, Validation, Visualization, Writing–original draft. CZ: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is financially supported by the National Natural Science Foundation of China (Grant Nos: 42030809 and 72088101).

Acknowledgments

The authors express sincere thanks to the anonymous referees for their valuable comments, which led to a significant improvement over an early version of the article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bethke, C. M. (1985). A numerical model of compaction-driven groundwater flow and heat transfer and its application to the paleohydrology of intracratonic sedimentary basins. J. Geophys. Res. 90, 6817–6828. doi:10.1029/jb090ib08p06817

CrossRef Full Text | Google Scholar

Carman, P. C. (1956). “Flow of gases through porous media”. New York: Academic Press.

Google Scholar

Chang, Z. S., Shu, Q. H., and Meinert, L. D. (2019). “Chapter 6, skarn deposits of China,” in Mineral deposits of China (Houston, TX: SEG Special Publications), 189–234.

CrossRef Full Text | Google Scholar

Cheng, Y., Mao, J., Chang, Z., and Pirajno, F. (2013b). The origin of the world class tin-polymetallic deposits in the Gejiu district, SW China: constraints from metal zoning characteristics and 40Ar–39Ar geochronology. Ore Geol. Rev. 53, 50–62. doi:10.1016/j.oregeorev.2012.12.008

CrossRef Full Text | Google Scholar

Cheng, Y. B., and Mao, J. W. (2010). Age and geochemistry of granites in Gejiu area, Yunnan province, SW China: constraints on their petrogenesis and tectonic setting. Lithos 120, 258–276. doi:10.1016/j.lithos.2010.08.013

CrossRef Full Text | Google Scholar

Cheng, Y. B., Mao, J. W., and Spandler, C. (2013a). Petrogenesis and geodynamic implications of the Gejiu igneous complex in the western Cathaysia block, South China. Lithos 175-176, 213–229. doi:10.1016/j.lithos.2013.04.002

CrossRef Full Text | Google Scholar

Cheng, Y. B., Mao, J. W., Xie, G. Q., Chen, M. H., and Yang, Z. X. (2012a). Zircon U-Pb dating of granites in Gejiu superlarge tin polymetallic ore field and its significance. Mineral. deposits 28 (3), 297–312.

Google Scholar

Cheng, Y. B., Spandler, C., Kemp, A., Mao, J. W., Rusk, B., Hu, Y., et al. (2019). Controls on cassiterite (SnO2) crystallization: evidence from cathodoluminescence, trace element chemistry, and geochronology at the Gejiu Tin District. Am. Mineral. 104, 118–129. doi:10.2138/am-2019-6466

CrossRef Full Text | Google Scholar

Cheng, Y. B., Spandler, C., Mao, J. W., and Rusk, B. G. (2012b). Granite, gabbro and mafic microgranular enclaves in the Gejiu area, Yunnan Province, China: a case of two-stage mixing of crust- and mantle-derived magmas. Contributions Mineralogy Petrology 164, 659–676. doi:10.1007/s00410-012-0766-0

CrossRef Full Text | Google Scholar

Daus, A. D., Frid, E. O., and Sudicky, E. A. (1985). Comparative error analysis in finite element formulations of the advection-dispersion equation. Adv. Water Resour. 8, 86–95. doi:10.1016/0309-1708(85)90005-3

CrossRef Full Text | Google Scholar

Eldursi, K., Branquet, Y., Guillou-Frottier, L., and Marcoux, E. (2009). Numerical investigation of transient hydrothermal processes around intrusions: heat-transfer and fluid-circulation controlled mineralization patterns. Earth Planet. Sci. Lett. 288, 70–83. doi:10.1016/j.epsl.2009.09.009

CrossRef Full Text | Google Scholar

Fan, X., Hu, Z. W., Xu, S. F., Chen, C., and Yi, N. (2021). Numerical simulation study on ore-forming factors of the Gejiu ore deposit, China. Ore Geol. Rev. 135, 104209. doi:10.1016/j.oregeorev.2021.104209

CrossRef Full Text | Google Scholar

Gao, X., Zhang, D., Absai, V., Feng, H., and Yi, J. (2015). Computational simulation of coupled geodynamics for forming the Makeng deposit in Fujian Province, China: constraints of mechanics, thermotics and hydrology. J. Geochem. Explor. 160, 31–43. doi:10.1016/j.gexplo.2015.10.010

CrossRef Full Text | Google Scholar

Gow, P., Upton, P., Zhao, C., and Hill, K. (2002). Copper-gold mineralisation in New Guinea: numerical modelling of collision, fluid flow and intrusion-related hydrothermal systems. Aust. J. Earth Sci. 49, 753–771. doi:10.1046/j.1440-0952.2002.00945.x

CrossRef Full Text | Google Scholar

Guo, J., Wu, K., Seltmann, R., Zhang, R. Q., Ling, M. X., Li, C. Y., et al. (2022). Unraveling the link between mantle upwelling and formation of Sn-bearing granitic rocks in the world-class Dachang tin district, South China. Geol. Soc. Am. Bull. 134, 1043–1064. doi:10.1130/b35492.1

CrossRef Full Text | Google Scholar

Guo, J., Zhang, R. Q., Li, C. Y., Sun, W. D., Hu, Y. B., Kang, D. M., et al. (2018). Genesis of the Gaosong Sn–Cu deposit, Gejiu district, SW China: constraints from in situ LA-ICP-MS cassiterite U–Pb dating and trace element fingerprinting. Ore Geol. Rev. 92, 627–642. doi:10.1016/j.oregeorev.2017.11.033

CrossRef Full Text | Google Scholar

Harrison, W. J., and Summa, L. L. (1991). Paleohydrology of the gulf of Mexico basin. Am. J. Sci. 291 (2), 109–176. doi:10.2475/ajs.291.2.109

CrossRef Full Text | Google Scholar

He, X., Zhao, J., Zhou, R., Feng, Y., Leonard, N., Li, F., et al. (2022). The distribution and substitution mechanism of trace elements in cassiterites: constraints from LA-ICP-MS U Pb dating, elemental mapping and in situ trace element analyses of the Gejiu tin polymetallic deposit, SW China. Chem. Geol. 609, 121063. doi:10.1016/j.chemgeo.2022.121063

CrossRef Full Text | Google Scholar

Hobbs, B. E., Zhang, Y. H., Ord, A., and Zhao, C. (2000). Application of coupled deformation, fluid flow, thermal and chemical modelling to predictive mineral exploration. J. Geochem. Explor. 69, 505–509. doi:10.1016/s0375-6742(00)00099-6

CrossRef Full Text | Google Scholar

Hu, X., Chen, Y., Liu, G., Yang, H., Luo, J., Ren, K., et al. (2022). Numerical modeling of formation of the Maoping Pb-Zn deposit within the Sichuan-Yunnan-Guizhou Metallogenic Province, Southwestern China: implications for the spatial distribution of concealed Pb mineralization and its controlling factors. Ore Geol. Rev. 140, 104573. doi:10.1016/j.oregeorev.2021.104573

CrossRef Full Text | Google Scholar

Ingebritsen, S. E., and Appold, M. S. (2012). The physical hydrogeology of ore deposits. Econ. Geol. 107 (4), 559–584. doi:10.2113/econgeo.107.4.559

CrossRef Full Text | Google Scholar

Kestin, J., Khalifa, H. E., Abe, Y., Grimes, C. E., Sookiazan, H., and Wakehan, W. A. (1978). Effect of pressure on the viscosity of aqueous sodium chloride solutions in the temperature range 20-150.degree.C. J. Chem. Eng. Data 23, 328–336. doi:10.1021/je60079a011

CrossRef Full Text | Google Scholar

Kuang, X., and Jiao, J. J. (2014). An integrated permeability-depth model for Earth’s crust. Geophys. Res. Lett. 41, 7539–7545. doi:10.1002/2014gl061999

CrossRef Full Text | Google Scholar

Lewis, R. W., and Schrefler, B. A. (1998). “The finite element method in the static and dynamic deformation and consolidation of porous media”. New York: John Wiley and Sons.

Google Scholar

Li, J., Chen, S. Y., and Zhao, Y. H. (2022). Trace elements in apatite from Gejiu Sn polymetallic district: implications for petrogenesis, metallogenesis and exploration. Ore Geol. Rev. 145, 104880. doi:10.1016/j.oregeorev.2022.104880

CrossRef Full Text | Google Scholar

Li, X., Zheng, Y., Shen, Y., Wu, C., Xu, P., Yang, Y., et al. (2023). Petrogenesis of Sn-related granitoids and implications for the formation of the world-class Gejiu Sn district, South China: insights from whole-rock and accessory mineral geochemistry. Lithos 448-449, 107166. doi:10.1016/j.lithos.2023.107166

CrossRef Full Text | Google Scholar

Li, X. L., Mao, J. W., Cheng, Y. B., and Zhang, J. (2012). Petrogenesis of the gaofengshan granite in Gejiu area, yunnan province: zircon U-Pb dating and geochemical constraints. Acta Petrol. Sin. 28, 183–198.

Google Scholar

Li, Y. S., Qin, D. X., Zou, T., Jia, F. J., and Wan, C. Y. (2008). Geochemical features and tectonic setting of the ladinian basalt in Gejiu, yunnan province. China: Journal of Jilin University, 624–630.

Google Scholar

Li, Z. K., Li, J. W., Cooke, D. R., Danyushevsky, L., Zhang, L., O’Brien, H., et al. (2016). Textures, trace elements, and Pb isotopes of sulfides from the Haopinggou vein deposit, southern North China Craton: implications for discrete Au and Ag-Pb-Zn mineralization. Contrib. Min. Petrol. 171, 99. doi:10.1007/s00410-016-1309-x

CrossRef Full Text | Google Scholar

Liao, S., Chen, S., Deng, X., Li, P., Zhao, J., and Liao, R. (2014). Fluid inclusion characteristics and geological significance of the Xi’ao copper–tin polymetallic deposit in Gejiu, Yunnan Province. J. Asian Earth Sci. 79, 455–467. doi:10.1016/j.jseaes.2013.10.023

CrossRef Full Text | Google Scholar

Liu, Y., Dai, T., Xia, S., and Tian, H. (2015). Computational simulation of iron ore-forming processes in the Caiyuanzi siderite ore district, Guizhou, China. J. Geochem. Explor. 158, 155–167. doi:10.1016/j.gexplo.2015.07.012

CrossRef Full Text | Google Scholar

Nield, D. A., and Bejan, A. (1992). “Convection in porous media”. New York: Springer-Verlag.

Google Scholar

Ohmoto, H., and Lasage, A. C. (1982). Kinetics of reactions between aqueous sulfates and sulfides in hydrothermal systems. Geochem. Cosmochimica Acta 46, 1725–1745.

CrossRef Full Text | Google Scholar

Ord, A., Hobbs, B. E., Zhang, Y., Broadbent, G. C., Brown, M., Willetts, G., et al. (2002). Geodynamic modelling of the century deposit, Mt isa province, queensland. Aust. J. Earth Sci. 49, 1011–1039. doi:10.1046/j.1440-0952.2002.00968.x

CrossRef Full Text | Google Scholar

Phillips, O. M. (1991). “Flow and reactions in permeable rocks”. Cambridge: Cambridge University Press.

Google Scholar

Rabinowicz, M., Boulegue, J., and Genthon, P. (1998). Two- and three-dimensional modeling of hydrothermal convection in the sedimented Middle Valley segment, Juan de Fuca Ridge. J. Geophys. Res. 103, 24045–24065. doi:10.1029/98jb01484

CrossRef Full Text | Google Scholar

Schaubs, P., and Zhao, C. (2002). Numerical models of gold-deposit formation in the bendigo-ballarat zone, victoria. Aust. J. Earth Sci. 49, 1077–1096. doi:10.1046/j.1440-0952.2002.00964.x

CrossRef Full Text | Google Scholar

Schon, J. H. (2011). “Physical properties of rocks: a workbook”. Amsterdam, Boston: Elsevier.

Google Scholar

Shmonov, V. M., Vitiovtova, V. M., Zharikov, A. V., and Grafchikov, A. A. (2003). Permeability of the continental crust: implications of experimental data. J. Geochem. Explor. 78-79, 697–699. doi:10.1016/s0375-6742(03)00129-8

CrossRef Full Text | Google Scholar

Sorjonen-Ward, P., Zhang, Y., and Zhao, C. (2002). Numerical modelling of orogenic processes and gold mineralisation in the southeastern part of the Yilgarn Craton, Western Australia. Aust. J. Earth Sci. 49, 935–964. doi:10.1046/j.1440-0952.2002.00969.x

CrossRef Full Text | Google Scholar

Wang, D. D., and Yu, X. G. (2014). 40Ar/39Ar and LA-ICP-MS zircon dating of the Gejiu Sn-cuploymetallic camp, yunnan, China. Acta Geol. Sin. 88, 1013–1014. doi:10.1111/1755-6724.12378_25

CrossRef Full Text | Google Scholar

Wang, X., and Ren, M. (2019). Assessment of the ore-forming process of the Gejiu tin district (South China). Ore Geol. Rev. 107, 707–734. doi:10.1016/j.oregeorev.2019.03.017

CrossRef Full Text | Google Scholar

Xu, R., Romer, R. L., and Glodny, J. (2021). External fluids cause alteration and metal redistribution in the granite-hosted Tangziwa Sn Cu deposit, Gejiu district, China. Lithos, 382–383. 105937.

CrossRef Full Text | Google Scholar

Xu, R., Romer, R. L., and Glodny, J. (2022b). Metal mobilization and precipitation in a Sn-W skarn system, Gejiu Sn district, China. Lithos 414-415, 106621. doi:10.1016/j.lithos.2022.106621

CrossRef Full Text | Google Scholar

Xu, R., Romer, R. L., Kroner, U., and Deng, J. (2022a). Tectonic control on the spatial distribution of Sn mineralization in the Gejiu Sn district, China. Ore Geol. Rev. 148, 105004. doi:10.1016/j.oregeorev.2022.105004

CrossRef Full Text | Google Scholar

Yuan, S. D., Williams-Jones, A. E., Romer, R. L., Zhao, P. L., and Mao, J. W. (2019). Protolith-related thermal controls on the decoupling of Sn and W in Sn-W metallogenic provinces: insights from the nanling region, China. China”. Econ. Geol. 114, 1005–1012. doi:10.5382/econgeo.4669

CrossRef Full Text | Google Scholar

Zhang, J., Dai, C., Huang, Z., Luo, T., Qian, Z., and Zhang, Y. (2015). Age and petrogenesis of Anisian magnesian alkali basalts and their genetic association with the Kafang stratiform Cu deposit in the Gejiu supergiant tin-polymetallic district, SW China. Ore Geol. Rev. 69, 403–416. doi:10.1016/j.oregeorev.2015.03.011

CrossRef Full Text | Google Scholar

Zhang, S. S. (2011). “Numerical simulation of magmatic hydrothermal system: a case study of Gejiu polymetallic mining district”. Master degree thesis. Wuhan: China University of Geosciences, 1–54.

Google Scholar

Zhang, Y. H., Zhou, J.-X., Tan, S.-C., Li, H.-M., Hao, S., Jiang, Y.-G., et al. (2020). Genesis of the oxidized Sn ores in the Gejiu district, yunnan province, SW China. Ore Geol. Rev. 121, 103474. doi:10.1016/j.oregeorev.2020.103474

CrossRef Full Text | Google Scholar

Zhao, C., Hobbs, B. E., and Ord, A. (2008a). “Convective and advective heat transfer in geological systems”. Berlin: Springer.

Google Scholar

Zhao, C., Hobbs, B. E., and Ord, A. (2009). “Fundamentals of computational geoscience: numerical methods and algorithms”. Berlin: Springer.

Google Scholar

Zhao, C., Hobbs, B. E., and Ord, A. (2012b). Effects of domain shapes on the morphological evolution of nonaqueous-phase-liquid dissolution fronts in fluid-saturated porous media. J. Contam. Hydrology 138-139, 123–140. doi:10.1016/j.jconhyd.2012.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, C., Hobbs, B. E., and Ord, A. (2018). Effects of different numerical algorithms on simulation of chemical dissolution-front instability in fluid-saturated porous rocks. J. Central South Univ. 25, 1966–1975. doi:10.1007/s11771-018-3887-4

CrossRef Full Text | Google Scholar

Zhao, C., Hobbs, B. E., Walshe, J. L., Muhlhaus, H. B., and Ord, A. (2001). Finite element modeling of fluid–rock interaction problems in pore-fluid saturated hydrothermal/sedimentary basins. Comput. Methods Appl. Mech. Eng. 190, 2277–2293. doi:10.1016/s0045-7825(00)00304-2

CrossRef Full Text | Google Scholar

Zhao, C., Lin, G., Hobbs, B. E., Ord, A., Wang, Y., and Muhlhaus, H. B. (2003). Effects of hot intrusions on pore-fluid flow and heat transfer in fluid-saturated rocks. Comput. Methods Appl. Mech. Eng. 192, 2007–2030. doi:10.1016/s0045-7825(03)00215-9

CrossRef Full Text | Google Scholar

Zhao, C., Lin, G., Hobbs, B. E., Wang, Y., Muhlhaus, H. B., and Ord, A. (2002). Finite element modelling of reactive fluids mixing and mineralization in pore-fluid saturated hydrothermal/sedimentary basins. Eng. Comput. 19, 364–387. doi:10.1108/02644400210423990

CrossRef Full Text | Google Scholar

Zhao, C., and Liu, G. (2023a). FEM-based dual length-scale simulation of hydrothermal ore-forming systems involving convective flow in fluid-saturated porous media. Int. J. Numer. Anal. Methods Geomechanics 47, 3090–3113. doi:10.1002/nag.3613

CrossRef Full Text | Google Scholar

Zhao, C., and Liu, Q. (2023b). Investigating effects of structural deformation regimes on mineralization distributions in fluid-saturated rocks: computational simulation approach through generic models. Minerals 13, 664. doi:10.3390/min13050664

CrossRef Full Text | Google Scholar

Zhao, C., Mühlhaus, H. B., and Hobbs, B. E. (1997). Finite element analysis of steady-state natural convection problems in fluid-saturated porous media heated from below. Int. J. Numer. Anal. Methods Geomechanics 21, 863–881. doi:10.1002/(sici)1096-9853(199712)21:12<863::aid-nag923>3.0.co;2-f

CrossRef Full Text | Google Scholar

Zhao, C., Reid, L. B., and Regenauer-Lieb, K. (2012a). Some fundamental issues in computational hydrodynamics of mineralization: a review. J. Geochem. Explor. 112, 21–34. doi:10.1016/j.gexplo.2011.10.005

CrossRef Full Text | Google Scholar

Zhao, C., Schaubs, P., and Hobbs, B. E. (2016a). Computational simulation of seepage instability problems in fluid-saturated porous rocks: potential dynamic mechanisms for controlling mineralisation patterns. Ore Geol. Rev. 79, 180–188. doi:10.1016/j.oregeorev.2016.05.002

CrossRef Full Text | Google Scholar

Zhao, C., Schaubs, P., and Hobbs, B. E. (2016b). Acquisition of temporal-spatial geochemical information in ore-forming and carbon-dioxide sequestration systems: computational simulation approach. J. Geochem. Explor. 164, 18–27. doi:10.1016/j.gexplo.2015.09.005

CrossRef Full Text | Google Scholar

Zhao, C. B., Hobbs, B. E., and Ord, A. (2008b). Investigating dynamic mechanisms of geological phenomena using methodology of computational geosciences: an example of equal-distant mineralization in a fault. Sci. China Earth Sci. 51, 947–954. doi:10.1007/s11430-008-0070-z

CrossRef Full Text | Google Scholar

Zhao, C. B., Hobbs, B. E., Ord, A., Peng, S., Muhlhaus, H. B., and Liu, L. (2005). Numerical modelling of chemical effects of magma solidification problems in porous rocks. Int. J. Numer. Methods Eng. 64, 709–728. doi:10.1002/nme.1372

CrossRef Full Text | Google Scholar

Zhao, Y. H. (2022). Geochemical characteristics and prospecting significance of Laochang Sn-Cu polymetallic deposit in Gejiu District,Yunnan province. Ph.D. Thesis. Wuhan: China University of Geosciences, 1–145.

Google Scholar

Zhao, Y. H., Chen, S. Y., Huang, Y. Q., Zhao, J. N., Tong, X., and Chen, X. S. (2019). U-Pb ages, O isotope compositions, Raman spectrum, and geochemistry of cassiterites from the Xi’ao copper-tin polymetallic deposit in Gejiu district, Yunnan province. Minerals 9, 212. doi:10.3390/min9040212

CrossRef Full Text | Google Scholar

Zhao, Y. H., Tian, H., Li, J., Chen, S., and Zhao, J. (2022). Constraints on the genesis of the Laochang Pb-Zn ore, Gejiu district, Yunnan: evidence from sulfide trace element and isotope geochemistry. Ore Geol. Rev. 150, 105162. doi:10.1016/j.oregeorev.2022.105162

CrossRef Full Text | Google Scholar

Zhuang, Y. Q., Wang, R. Z., Yang, S. P., and Yin, J. M. (1996). “Gejiu tin (Cu) polymetallic ore deposit in yunnan”. Beijing: Seismological Press House.

Google Scholar

Zienkiewicz, O. C. (1977). “The finite element method”. London: McGraw-Hill.

Google Scholar

Zou, Y., Liu, Y., Dai, T., Mao, X., Lei, Y., Lai, J., et al. (2017). Finite difference modeling of metallogenic processes in the Hutouya Pb-Zn deposit, Qinghai, China: implications for hydrothermal mineralization. Ore Geol. Rev. 91, 463–476. doi:10.1016/j.oregeorev.2017.09.008

CrossRef Full Text | Google Scholar