Numerical study of the fluid fracturing mechanism of granite at the mineral grain scale

Hydraulic fracturing is an essential technique for reservoir stimulation in the process of deep energy exploitation. Granite is composed of different rock-forming minerals and exhibits obvious heterogeneity at the mesoscale, which affects the strength and deformation characteristics of rocks and controls the damage and failure processes. Therefore, in this paper, based on the discrete element fluid-solid coupling algorithm and multiple parallel bond-grain based model (Multi Pb-GBM), a numerical model of a granite hydraulic fracturing test is established to study the evolution of hydraulic fractures in crystalline granite under different ground stress conditions. The main conclusions are as follows. The crack propagation of hydraulic fractures in granite is determined by the in situ stress state, crystal size, and mineral distribution, and the ground stress is the main controlling factor. The final fracture mode affects the maximum principal stress and shear stress, and the generation of cracks changes the distribution of the stress field. The hydraulic fracturing initiation pressure decreases with decreasing crystal size. The influence of the crystal size on the crack inclination angle is mainly reflected in local areas, and the general trend of the fissure dip angle distribution is along the direction of the maximum in situ stress. This study not only has important theoretical significance for clarifying the propagation mechanism of hydraulic fractures but also provides a theoretical basis for deep reservoir reconstruction and energy extraction.

1 Introduction

With the increasing depletion of traditional fossil energy, efficient utilization of the abundant, widespread, safe, reliable, clean, and renewable hot dry rock (HDR) geothermal resources is one of the fundamental trends in future energy development (Tester, et al., 2007; Wang et al., 2021; Zhu, et al., 2021). Granite-dominated, tight, waterless HDR reservoirs have extremely low permeability and need to be artificially stimulated to improve the effective fluid conductivity (Hooijkaas et al., 2006; Zhai et al., 2016; Yin, et al., 2021). Reservoir reconstruction is the key technology to determine the efficiency of thermal mining, and the main means is hydraulic fracturing (Zhao et al., 2013; Frash et al., 2015; Kamali-Asl et al., 2018). In enhanced geothermal systems, hydraulic fracturing shoulders the dual task of increasing the reservoir permeability and the heat exchange area, which requires the induction of complex dense fracture networks with high permeability in the reservoir (Frash et al., 2015; Wang et al., 2020).

The mesoscale mechanical properties of deep granite are the basis of reservoir development and utilization and guide the selection of important physical and mechanical parameters in the process of geological drilling, hydraulic fracturing, and thermal mining (Martin and Chandler, 1994; Eberhardt et al., 1999; Cowie and Walton, 2018). Existing studies have shown that the internal mineral crystal structure (e.g., the mineral composition, shape, spatial distribution, and particle size) of granite controls its overall strength and deformation characteristics and influences the initiation, propagation, and interaction of microcracks (Kranz, 1983; Lindqvist et al., 2007; Lan et al., 2010; Huang et al., 2021). However, there are some limitations: (1) The heterogeneity of the granite makes it difficult to control a single variable during tests. (2) Most rock mechanics tests are destructive tests, so repeated tests cannot be carried out on the same sample. (3) The evolution of the macroscopic fracture behavior of granite cannot be captured by the experimental process (Papanastasiou, 1997; Taron and Elsworth, 2009; Liu et al., 2016; Zhang et al., 2017).

At present, there are many numerical simulation methods of simulating rock mechanical behavior, e.g., the finite element method based on continuous damage mechanics and the discrete element method based on fracture mechanics criterion (Kolditz et al., 2012; Liu et al., 2018; Wang and Cai, 2018; Zhang and Wong, 2018; Zhang and Wong, 2018; Zhou et al., 2018; Nagel et al., 2016; Pirnia et al., 2019; Qi et al., 2020). Among these methods, the discrete particle flow code (PFC) proposed by Cundall has clear advantages in the efficient simulation of complex fracture networks and can truly depict rock failure processes such as micro-crack initiation, propagation, and polymerization (Lambert and Coll, 2014; Zhou et al., 2016; Feng et al., 2017; Han et al., 2018). In view of the mechanical properties and the brittle failure behavior of rock, a series of practical models have been developed using the PFC program, and a great deal of excellent results have been obtained (Cho et al., 2007; Potyondy, 2010; Wu and Xu, 2016; Bahrani and Kaiser, 2017; Peng et al., 2017; Li et al., 2018; Xu et al., 2018). However, granite is often simplified into a simple homogeneous model, and the effect of its mineral crystal structure is ignored. Moreover, in the study of a mineral crystal model, the linear parallel contact model is used to characterize the contact between particles inside the crystal, and the smooth joint model is used to simulate the crystal boundary. The smooth joint model has discernible defects, i.e., it ignores the initial boundary cohesion and the rolling between particles, so the actual performance of the boundary node is low.

Therefore, in this paper, considering the crystal structure of granite, based on the discrete element fluid-solid coupling algorithm and multiple parallel bond-grain based model (Multi Pb-GBM), a numerical model of a granite hydraulic fracturing test is established to study the hydraulic fracture evolution in crystalline granite under different in situ stress conditions. The results of this study are of great significance for the safety and sustainable development of deep reservoir reconstruction and resource exploitation.

2 Methodology

2.1 Fluid-solid coupling algorithm

Based on the PFC fluid algorithm model, it is assumed that the object studied is a solid medium with a low porosity, and there is no real fluid substance in the model. The fluid domain space and fluid pipeline are constructed to simulate the seepage process (Figure 1). The closed areas formed by the connections between the center points of adjacent particles (black line segments) are called fluid domains, which are equivalent to reservoirs. The pore water pressure is stored in the center of the domain space (green dots), and the contacts between adjacent particles are regarded as potential fluid pipelines for seepage (red line segments) (Liu and Cai, 2020).

FIGURE 1

FIGURE 1. Model of pipes and domains for fluid-solid coupling.

Laminar flow occurs in the parallel plate channel and the volume velocity follows the cubic law:

$\mathrm{q}=\mathrm{k}{\mathrm{a}}^3\cdot \frac{p_2-p_1}{\mathrm{L}}(1)$

where k is the conductivity coefficient; a is the average pipe aperture; P₂–P₁ is the fluid pressure difference between two adjacent domains; and L is the length of the seepage channel.

In a time step Δt, the fluid pressure increment Δp is as follows (Han et al., 2018):

$\Delta \mathrm{p}=\frac{{\mathrm{k}}_{\mathrm{f}}}{{\mathrm{V}}_{\mathrm{d}}}\left(\sum \mathrm{q}\Delta \mathrm{t}-\Delta {\mathrm{V}}_{\mathrm{d}}\right)(2)$

where Δt is the unit time step; k_f is the volume modulus of the fluid; V_d is the apparent volume of the fluid domain; and ΔV_d is the change in the apparent volume of the fluid domain caused by external forces.

In the original algorithm, the length of the seepage channel after the fracture is generated is calculated as the sum of the radii of two adjacent particles or the harmonic average of the radii of two adjacent particles, but neither of them is connected with the initial opening of the pipeline. Based on the existing discrete element fluid-solid coupling algorithm, the Fish function is used to improve the original method and to update the fluid channel length and the interaction mode between the water pressure and particle element (Liu et al., 2020).

The method for determining the length and location of the penetration channels is shown in Figure 2A. Point O is located at the center of the distance between two adjacent particles (red line segment), and the length satisfies the following formula:

$\mathrm{L}=2\times \left(\frac{{\mathrm{R}}_{\mathrm{b}1}+1/2\text{dis}}{{\mathrm{R}}_{\mathrm{b}1}+{\mathrm{R}}_{\mathrm{b}2}+\text{dis}}\times \left({\mathrm{R}}_{\mathrm{b}2}-{\mathrm{R}}_{\mathrm{b}1}\right)+{\mathrm{R}}_{\mathrm{b}1}\right)(3)$

where R_b1 is the radius of particle 1; R_b2 is the radius of particle 2; and dis is the distance between the two particles (red line in Figure 2).

FIGURE 2

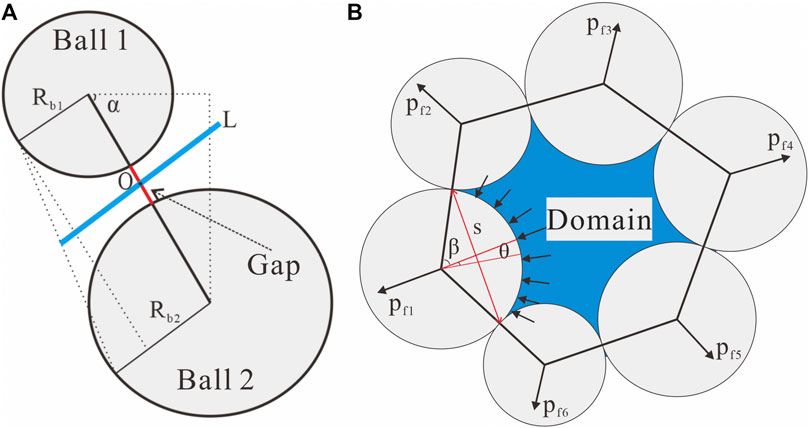
FIGURE 2. Fluid pipe and fluid-particle interaction mechanism. (A) length and position of fluid pipe; and (B) fluid-particle interaction mechanism.

As shown in Figure 2B, after completing a time step, a new fluid pressure F_p acts on the particle surface:

${\mathrm{F}}_p=2{\int }_0^{\beta }\mathrm{p}\cos \theta \mathrm{R}\mathrm{d}\theta =\mathrm{p}\cdot \mathrm{s}(4)$

where β is half the boundary angle of the fluid domain; and s is the acting width of the fluid pressure.

2.2 Multi Pb-GBM

There are differences between different mineral boundaries and the internal crystal boundaries of the same mineral, and the bond strength of the crystal boundaries is affected by the types of crystals on both sides. However, this property difference is not taken into account in the parallel bond (Pb) model. The GBM model has a strong ability to simulate fracture behavior in crystalline rocks and is suitable for granite simulations. Each crystal consists of several bonded particles, and the crystal is allowed to deform and break. The GBM model in PFC2D can not only simulate the initiation of microcracks and the interaction with the crystal boundary but can also capture the crack behavior inside the crystal’s structure (Liu et al., 2018; Zhang and Wong, 2019).

The traditional GBM method uses polygons to simulate the crystals in granite samples, which are bonded by the parallel bond model, and the smooth joint (SJ) model is used to simulate the grain boundaries. However, the SJ model has obvious shortcomings. (1) The crystal boundaries are treated as cracks with a bond strength and do not produce local geometric expansion effects, resulting in a loss of the ability to force the particles to roll against each other. (2) The contact ignores the initial cohesion around the boundary, and the rotational resistance of the particles is not considered. (3) Under a large strain, the SJ model only works when the surface clearance is negative (Potyondy and Cundall, 2004; Li et al., 2022).

To overcome the shortcomings of the SJ model, a Multi-Pb-GBM model is proposed. The parallel contact model is used to describe the crystal boundary instead of the traditional SJ model. Taking granite as an example, considering that the granite contains four basic minerals, after the construction of the internal filling particles of the polygon, the filling particles are grouped into crystals using the geom.set.name geometric polygon pointer function. The parallel contacts in the model can be divided into three types: intra-crystal contacts, intra-crystal boundary contacts between the same mineral, and boundary contacts between different mineral species (Figure 3) (Li et al., 2022).

FIGURE 3

FIGURE 3. Multistage PBM import GBM. (A) Grain-based model; (B) a parallel bonded model; and (C) classification of the three levels of the PBM.

In light of the above, the uniaxial compression test and Brazil splitting test were used to correct the microscopic parameters of the model. Several numerical experiments were carried out to study the dynamic damage to and fracture evolution process in brittle granite samples under the influence of the crystal size distribution coefficient, proving the accuracy and feasibility of the method. Each type of contact can be endowed with different strength parameter values using the contact property command, which can describe the boundary mechanical properties of crystalline rocks more precisely. The model provides a new means to understand the fracture damage to crystalline rocks at the mesoscale. The detailed modeling principles and optimization process have been described by Li et al. (2022).

2.3 Numerical model and experimental scheme

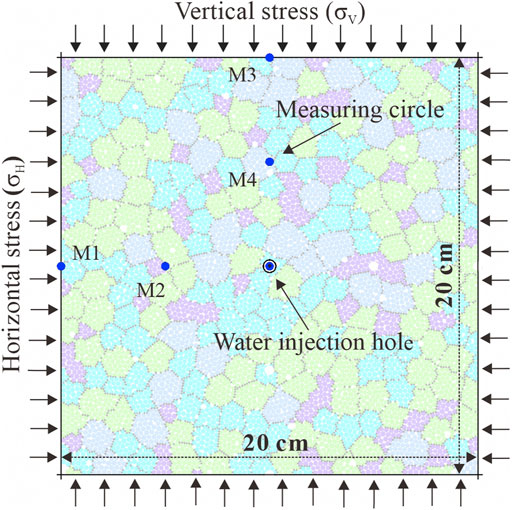
Figure 4 shows the model and boundary conditions of the numerical experiment. The model is composed of 11,706 particles with lengths and widths of 20 cm. The particle radius ranges from 0.09 to 0.13 cm, and the water injection hole in the center of the rock mass model is 0.6 cm in diameter. To make the circular hole wall as smooth as possible, the particles around the hole were dense, and the radius was reduced to 0.07–0.10 cm. In addition, the fluid pressure boundary was set as a circle to avoid stress concentration. Four walls were controlled by the servo system to simulate the ground stress, and four measuring circles were set around the central water injection hole.

FIGURE 4

FIGURE 4. The numerical model.

Based on laboratory tests, the granite used in this study was composed of K-feldspar, plagioclase, quartz, and biotite, with volume contents of 40, 20, 30, and 10%, respectively. These four minerals were randomly distributed to generate three models with the same grain sizes of each mineral. The average grain size distribution coefficient was defined to reflect the change in the crystal size:

$I={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{N}_{\mathrm{i}}\cdot R_{\mathrm{i}}/N_{\mathrm{i}}(5)$

where R_i is the particle size; N_i is the number of the particles with size R_i; and I is the average crystal size distribution coefficient.

Considering the research purpose and computational efficiency, two sets of experiments were designed (Table 1). Group A studied the influence of the different mineral distribution forms on the hydraulic fracturing failure modes under the same crystal size, and three randomly arranged mineral combinations were developed through the Set random command in PFC, which were recorded as Cry-Dis-1, Cry-Dis-2, and Cry-Dis-3. Group B studied the evolution of the hydraulic fractures in the granite under different mineral crystal sizes, and the mineral distribution mode Cry-Dis-3 was adopted. Based on defining I, three series of models were generated, which were recorded as Size-dis-1 (I₁ = 1.41), Size-dis-2 (I₂ = 1.88), and Size-dis-3 (I₃ = 2.44).

TABLE 1

TABLE 1. Experimental schemes.

3 Results

3.1 Hydraulic fracture mode

3.1.1 Effects of mineral distributions

The granite hydraulic fracturing test results for Group A considering the mineral distribution are shown in Figure 5. Among them, the vertical stress is the principal ground stress in Figure 5A. Due to the different mineral distributions, the propagation modes of the hydraulic fractures were different. A principal fracture was produced in the model, extending along the vertical direction, which was the direction of the maximum principal stress. The fracture was caused primarily by crystal boundary failure, and a small number of secondary cracks were generated on both sides of the main crack.

FIGURE 5

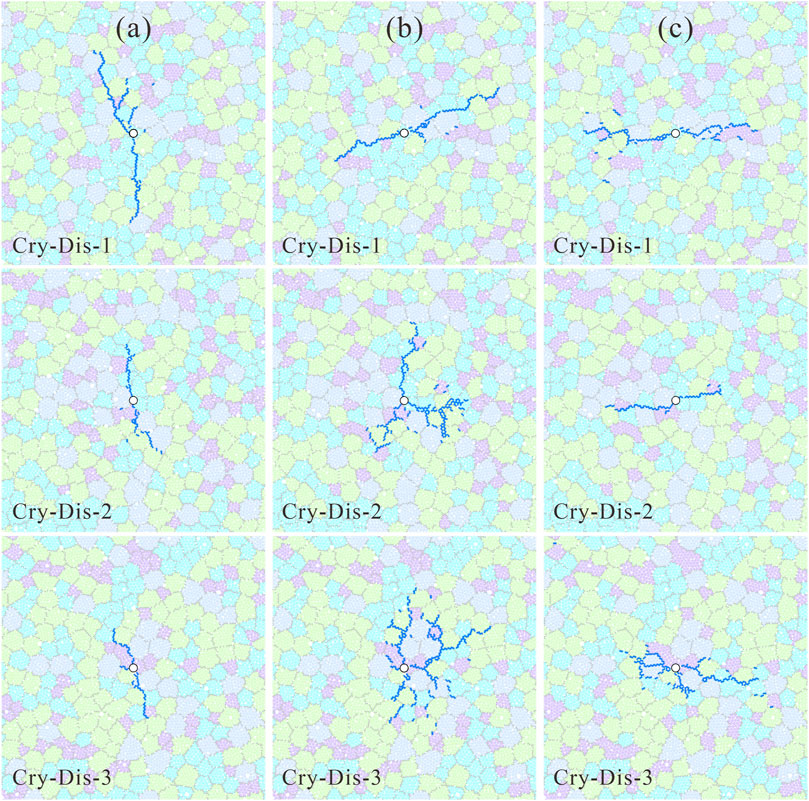
FIGURE 5. Hydraulic fracture mode of Group A. (A) σ_H:σ_V = 5:11; (B) σ_H:σ_V = 5:5; and (C) σ_H:σV = 11:5.

Figure 5B shows the situations under uniform ground stress, which was visibly different from the differential stress condition. When the mineral distribution was Cry-Dis-1, the angle between the hydraulic crack and the horizontal direction was about 30° because there was no directional effect of the maximum ground stress. In the water injection experiment with a constant flow rate, it was concluded that the crack propagation was completely controlled by the mechanical properties of the contacts. When the mineral distributions were Cry-Dis-2 and Cry-Dis-3, the hydraulic fractures were radially distributed, and the end of the main fracture was bifurcated into secondary fractures. The morphology of the entire fracture exhibited a mesh distribution, and the main fractures had no obvious direction.

Figure 5C shows the result of the hydraulic fracturing when the horizontal stress was greater than the vertical stress. When the mineral distributions were Cry-Dis-1 and Cry-Dis-3, the secondary fractures were still scattered far from the main fracture because these fractures were located at the boundaries of the minerals. When the main crack met quartz or other minerals in its expansion path, its propagation was blocked. According to the calculation, the fluid gathered around the crack tip and increased the osmotic pressure, causing the adjacent intergranular contact to reach its tensile strength first and leading to failure.

3.1.2 Effects of grain scale

The granite hydraulic fracturing test results for Group B are shown in Figure 6. Overall, the grain scale of the mineral had a significant effect on the crack propagation during the hydraulic splitting test. When the average grain size distribution coefficient decreased from 2.44 to 1.41, the crystal size decreased, the number increased, and the expansion direction of the hydraulic fracture also changed. The larger the coefficient was, the fewer crystal particles were generated. Transgranular failure easily occurred in the process of hydraulic crack propagation, and the main cracks were tensile. With decreasing crystal size, the transgranular failure was reduced, the crystal boundary became smoother, and the hydraulic cracks were more inclined to extend along the crystal boundary. Due to the different microscopic parameters assigned by the Pb model at the second- and third-stage crystal boundaries, the hydraulic cracks generated in the process did not expand in a straight line, and they tended to expand towards the weaker boundary (potassium feldspar-plagioclase). However, the crack propagation was also affected by the in situ stress. When the maximum principal stress was horizontal, the principal crack was horizontal. At the macroscopic level, the effect of the ground stress on the crack growth was greater than that of the mineral grain size.

FIGURE 6

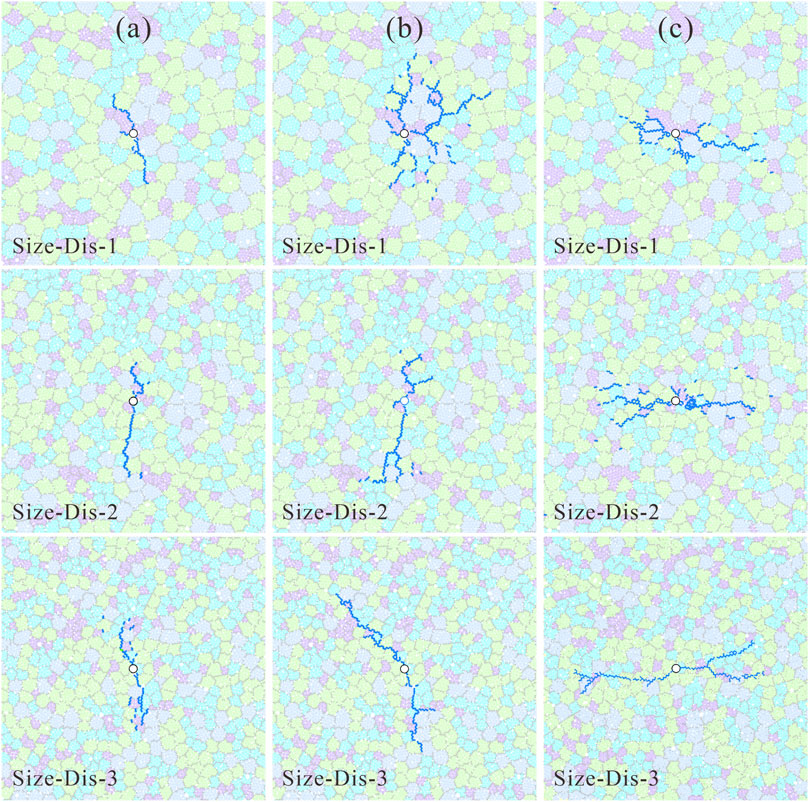
FIGURE 6. Hydraulic fracture mode of Group B. (A) σ_H:σ_V = 5:11; (B) σ_H:σ_V = 5:5; and (C) σ_H σ_V = 11:5.

3.2 Stress distribution characteristics

The stresses were monitored at typical points during the experiment through measurement circles, and the maximum principal stress and shear stress were calculated. The previous part, which did not cause a significant change in the principal stress at the monitoring point, was omitted, and the change in the maximum stress during the process of crack initiation and expansion was emphasized.

3.2.1 Maximum principal stress

Figure 7 shows the monitoring results for the measurement circles. Under the vertical maximum principal stress, M1 and M3 did not change significantly because they were far away from the water injection holes and hydraulic fractures, while M2 increased and M4 decreased (Figure 7A). This can be explained by the fact that the hydraulic fracture expanded upward and the water pressure accumulated at the crack tip, resulting in the release of the strain energy in the vertical direction of the new crack. The generation of the crack caused displacement in the horizontal direction, then the confining pressure increased, and the maximum principal stress in the horizontal direction increased accordingly.

FIGURE 7

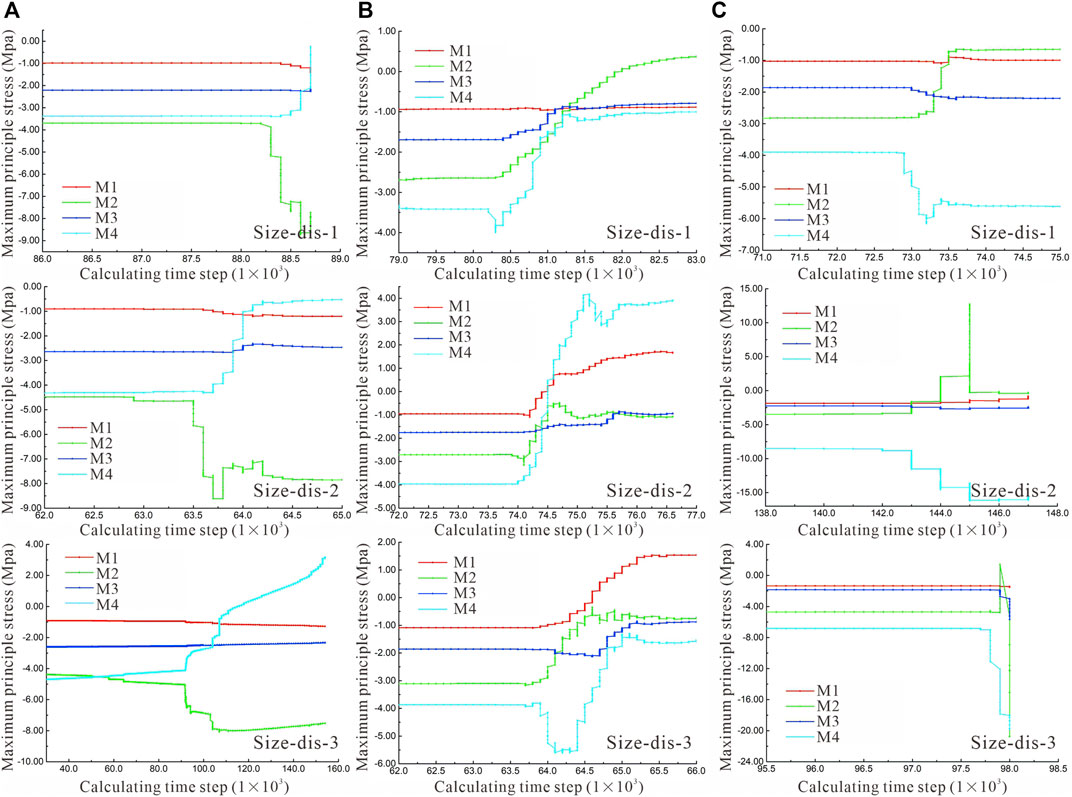
FIGURE 7. Maximum principal stress curve for the four measurement points: (A) σ_H:σ_V = 5:11; (B) σ_H:σ_V = 5:5; and (C) σ_H:σ_V = 11:5.

The stress at the monitoring point mainly depended on the propagation mode of the hydraulic crack if the horizontal stress was equal to the vertical stress (Figure 7B). When the average grain size distribution coefficient I was 1.41, the maximum principal stress of M1 was relatively stable, and the compression-tension transition occurred at M2. When the average grain size distribution coefficient I was 1.88, M1, M2, and M4 underwent compression-tension transition and the change in the maximum principal stress was the most severe at M4. In addition, the changes at M3 were most active between 74000 time steps and 75000 time steps, which was a rapid fracture development period.

Under the horizontal maximum principal stress, the cracks mainly spread along the horizontal direction. As shown in Figure 7C, the monitoring values at M1 and M3 were basically unchanged. When I was 1.41 and 1.88, the maximum principal stress at M2 decreased; while when I was 2.44, the crystal size decreased and the principal compressive stress increased. This was because when the particle size was large, the longitudinal distribution range of the crack was thick, but the single main crack extended laterally for a long distance (I = 2.44). In the three tests with different particle sizes, the stress distribution characteristics at M4 were consistent, and the maximum principal stress increased.

3.2.2 Maximum shear stress

Figure 8A shows the monitoring results of the maximum shear stress of the measured circles under different crystal particle sizes and a stress ratio of 5:11. In the three groups of experiments, M1 and M3 were far away from the water injection hole and the hydraulic fracture, so the maximum shear stress changed little. M4 experienced the process of approaching, trapping, and crossing the fracture, and the maximum shear stress increased generally. The stress at M2 initially decreased and then increased.

FIGURE 8

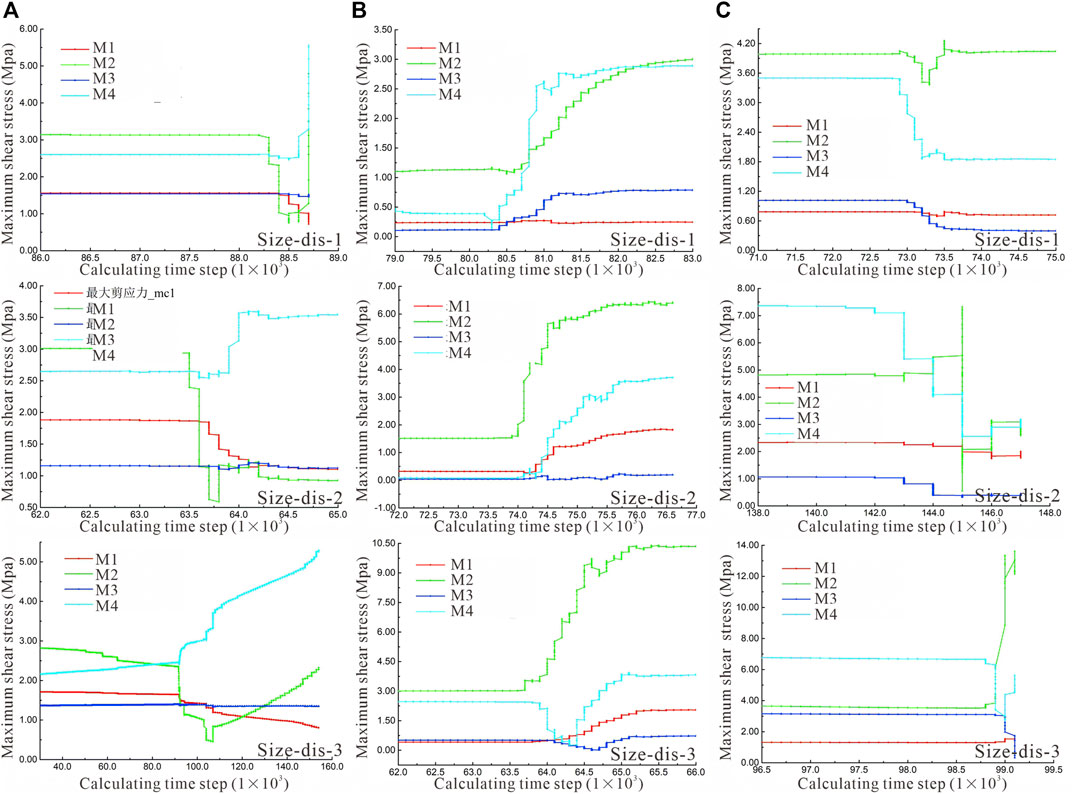
FIGURE 8. Maximum shear stress curve for the four measurement points. (A) σ_H:σ_V = 5:11; (B) σ_H:σ_V = 5:5; and (C) σ_H:σ_V = 11:5.

The stress at the monitoring point mainly depended on the propagation mode of the hydraulic crack if the horizontal stress was equal to the vertical stress (Figure 8B). When the average grain size distribution coefficient I was 1.41, the maximum shear stress at M1 was relatively stable, the stress at M2, M3, and M4 increased to different degrees, and the stress at M4 (near the water hole) increased the most. When the average grain size distribution coefficient I was 1.88, the maximum shear stress at M3 was basically not affected. The cracks developed rapidly from 74,000 time steps to 75,000 time steps, and the stress changes were the most active. The shear stress values at M1, M2, and M4 increased to 1.50, 6.45, and 3.51 MPa, respectively. As the crystal size decreased further, the maximum shear stress at M1 increased slightly, and that at M2 (near the water hole) increased greatly, reaching 10.20 MPa.

Figure 8C shows the experimental results for the tests in which the direction of the principal stress was horizontal. The shear stress at M1, located in the direction of the main crack growth, exhibited no obvious response; while at M3, located in the vertical direction of the crack growth, the maximum shear stress decreased slightly. When I = 1.41, the maximum shear stress at M2 fluctuated greatly between 72.75 thousand time steps and 73.5 thousand time steps, and that at M4 decreased from 3.50 MPa to 1.85 MPa. When I = 1.88, the maximum shear stress at M2 fluctuated during crack propagation, and that at M4 decreased. When I = 1.88, the maximum shear stress at M2 increased rapidly to 3.72 MPa at 98.85 thousand time steps, and that at M4 initially decreased and then increased.

4 Discussion

4.1 Hydraulic fracturing initiation pressure

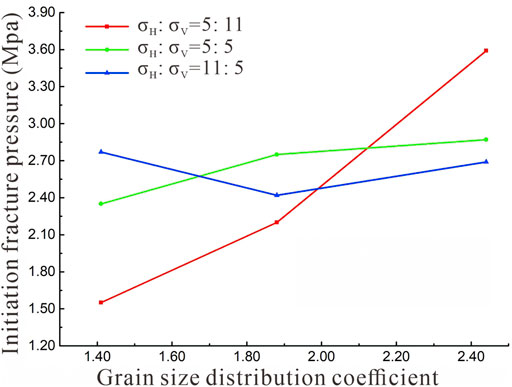
As shown in Figure 9, when I = 1.41, the crack initiation pressures corresponding to the three stress ratios were 3.59, 2.87, and 2.77 MPa. As the ground stress ratio increased, the pressure decreased gradually. When I = 1.88, the values of the initiation pressure corresponding to the three stress ratios were 2.20, 2.75, and 2.42 MPa, and the pressure initially increased and then gradually decreased. When the crystal size decreased further, the cracking pressures corresponding to the three stress ratios were 1.55, 2.35, and 2.69 MPa, and the pressure gradually increased as the original rock stress ratio increased. The fracture initiation values in the hydraulic fracturing tests under three different particle sizes did not exhibit obvious regular changes with the in situ stress ratio because the theoretical formula only considers the influence of the ground stress, and the materials in the theoretical model are uniform and impermeable (Fairhurst, 2003). However, the seepage problem, the crystal size, and the heterogeneity were all considered in the numerical simulation. Through a comprehensive comparison of the experimental results, it was found that under the same ground stress condition, the crack initiation pressure decreased with decreasing crystal size. This was because when the crystal size of the mineral was very small, the number of crystals arranged around the water injection hole was greater, and the proportion of the contact between the secondary and tertiary crystals was greater. The water injection pressure more easily reached the local tensile strength of the sample, and then, the initiation of a hydraulic crack was triggered.

FIGURE 9

FIGURE 9. Relationship between the hydraulic fracturing initiation pressure and the grain size.

4.2 Statistics and analysis of the fractures

According to the statistical analysis of the above test results, most of the hydraulic fractures were tensile fractures, and only a few shear fractures occurred between the particles. During the Group B tests, the generation process of the hydraulic fractures was recorded, the number of and morphology information about the cracks in the final fracture state was output t, and rose maps of the crack inclination were drawn (Figure 10). When the horizontal and vertical stress ratio was 5:11, the change in the crack dip angle distribution as the crystal particle size distribution coefficient decreased was not obvious. The dip angles were concentrated within 55°–75° and 110°–130°, and the hydraulic fractures basically developed along the direction of the maximum principal stress. When the horizontal stress and vertical stress were equal, the expansion of the hydraulic fracture was not affected by the directivity of the in situ stress. The hydraulic fracture radially expanded from the water injection hole and the distribution range of the hydraulic fracture was wide. When the maximum principal stress was horizontal, the fracture dip angles were concentrated in the ranges of 10°–30° and 150°–170°, and the hydraulic fractures were basically arranged along the horizontal direction. Compared with Size-Dis-3 and Size-Dis-1, it was found that the directional distribution of the fracture was relatively more uniform when the crystal size was smaller. Through comprehensive comparison, it was found that the influence of the principal stress direction on the crack distribution during hydraulic fracturing was greater than that of the crystal size distribution coefficient. The influence of the crystal size on the crack inclination angle was mainly reflected in local areas. As the crystal size decreased, the proportion of secondary and tertiary contacts increased, and more hydraulic cracks appeared around the crystal. The cracks tended to extend to the contact boundary of the different mineral crystals, but the general trend was still along the direction of the maximum in situ stress.

FIGURE 10

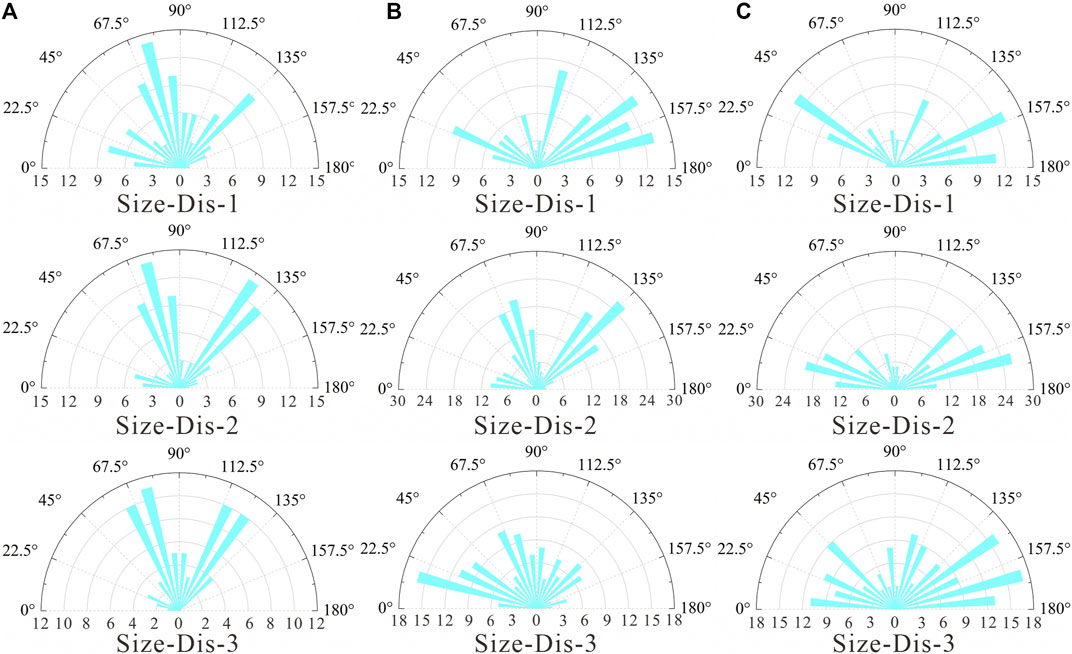
FIGURE 10. Rose diagrams of the fracture inclination. (A) σ_H:σ_V = 5:11; (B) σ_H:σ_V = 5:5; and (C) σ_H:σ_V = 11:5.

5 Conclusion

In this study, the following findings were revealed.

1. The introduction of the Multi Pb-GBM model increased the heterogeneity of the rock, which made it possible to describe hydraulic fracture propagation at the crystal scale. In the hydraulic fracturing tests on granite, the crack propagation in granite during hydraulic fracturing was determined by the in situ stress state, crystal size, and mineral distribution; ground stress was the main controlling factor. The changes in the maximum principal stress and maximum shear stress were not only affected by the ground stress and water injection pressure but also by the final fracture mode of the sample.

2. The hydraulic fracturing initiation pressure did not change regularly with the ground stress ratio. Under the same ground stress condition, the crack initiation pressure decreased with the decreasing crystal size. This was because when the crystal size of the mineral was very small, the number of crystals arranged around the water injection hole was greater, and the proportion of the contacts between the secondary and tertiary crystals was greater. The water injection pressure more easily reached the local tensile strength of the sample, and then, the initiation of a hydraulic crack was triggered.

3. The influence of the principal stress direction on the crack distribution during hydraulic fracturing was greater than that of the crystal size distribution coefficient. The influence of the crystal size on the crack inclination angle was reflected primarily in local areas. As the crystal size decreased, the proportion of secondary and tertiary contacts increased, and more hydraulic cracks appeared around the crystal. The cracks tended to extend to the contact boundary of the different mineral crystals, but the general trend was still along the direction of the maximum in situ stress.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

SL: Data curation, Software, Writing–original draft. YZ: Data curation, Formal analysis, Funding acquisition. HZ: Methodology, Project administration, Resources. JZ: Supervision, Visualization. MQ: Conceptualization, Software. GL: Conceptualization, Writing–original draft, Writing–review and editing. FM: Funding acquisition, Supervision, Writing–review and editing. JG: Funding acquisition, Investigation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research received support from the National Natural Science Foundation of China (Grant Nos. 41831293, U22A20597, and 42072305).

Conflict of interest

Authors SL, YZ, HZ, MQ, and JZ were employed by China National Petroleum Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bahrani, N., and Kaiser, P. K. (2017). Estimation of confined peak strength of crack-damaged rocks. Rock Mech. rock Eng. 50 (2), 309–326. doi:10.1007/s00603-016-1110-1

CrossRef Full Text | Google Scholar

Cho, N., Martin, C. D., and Sego, D. C. (2007). A clumped particle model for rock. Int. J. rock Mech. Min. Sci. 44 (7), 997–1010. doi:10.1016/j.ijrmms.2007.02.002

CrossRef Full Text | Google Scholar

Cowie, S., and Walton, G. (2018). The effect of mineralogical parameters on the mechanical properties of granitic rocks. Eng. Geol. 240, 204–225. doi:10.1016/j.enggeo.2018.04.021

CrossRef Full Text | Google Scholar

Eberhardt, E., Stimpson, B., and Stead, D. (1999). Effects of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock Mech. rock Eng. 32 (2), 81–99. doi:10.1007/s006030050026

CrossRef Full Text | Google Scholar

Fairhurst, C. (2003). Stress estimation in rock: a brief history and review. Int. J. Rock Mech. Min. Sci. 40 (7-8), 957–973. doi:10.1016/j.ijrmms.2003.07.002

CrossRef Full Text | Google Scholar

Feng, Z., Lo, C. M., and Lin, Q. F. (2017). The characteristics of the seismic signals induced by landslides using a coupling of discrete element and finite difference methods. Landslides 14 (2), 661–674. doi:10.1007/s10346-016-0714-6

CrossRef Full Text | Google Scholar

Frash, L. P., Gutierrez, M., Hampton, J., and Hood, J. (2015). Laboratory simulation of binary and triple well EGS in large granite blocks using AE events for drilling guidance. Geothermics 55, 1–15. doi:10.1016/j.geothermics.2015.01.002

CrossRef Full Text | Google Scholar

Han, Z., Zhou, J., and Zhang, L. (2018). Influence of grain size heterogeneity and in-situ stress on the hydraulic fracturing process by PFC2D modeling. Energies 11 (6), 1413. doi:10.3390/en11061413

CrossRef Full Text | Google Scholar

Hooijkaas, G. R., Genter, A., and Dezayes, C. (2006). Deep-seated geology of the granite intrusions at the Soultz EGS site based on data from 5 km-deep boreholes. Geothermics 35 (5-6), 484–506. doi:10.1016/j.geothermics.2006.03.003

CrossRef Full Text | Google Scholar

Huang, X., Qi, S., Zheng, B., Liang, N., and Xue, L. (2021). An advanced grain-based model to characterize mechanical behaviors of crystalline rocks with different weathering degrees. Eng. Geol. 280, 105951. doi:10.1016/j.enggeo.2020.105951

CrossRef Full Text | Google Scholar

Kamali-Asl, A., Ghazanfari, E., Perdrial, N., and Bredice, N. (2018). Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics 72, 205–224. doi:10.1016/j.geothermics.2017.11.014

CrossRef Full Text | Google Scholar

Kolditz, O., Bauer, S., Bilke, L., Böttcher, N., Delfs, J. O., Fischer, T., et al. (2012). Open Geo Sys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 67 (2), 589–599. doi:10.1007/s12665-012-1546-x

CrossRef Full Text | Google Scholar

Kranz, R. L. (1983). Microcracks in rocks: a review. Tectonophysics 100 (1-3), 449–480. doi:10.1016/0040-1951(83)90198-1

CrossRef Full Text | Google Scholar

Lambert, C., and Coll, C. (2014). Discrete modeling of rock joints with a smooth-joint contact model. J. Rock Mech. Geotechnical Eng. 6 (1), 1–12. doi:10.1016/j.jrmge.2013.12.003

CrossRef Full Text | Google Scholar

Lan, H., Martin, C. D., and Hu, B. (2010). Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading. J. Geophys. Res. Solid Earth 115 (B1). doi:10.1029/2009jb006496

CrossRef Full Text | Google Scholar

Li, G., Liu, S. Q., Ma, F. S., and Guo, J. (2022). A multilevel parallel bonded grain based model (Multi Pb GBM) accounting for microstructure failures of typical crystalline rocks. Bull. Eng. Geol. Environ. 81, 475. doi:10.1007/s10064-022-02976-6

CrossRef Full Text | Google Scholar

Li, X. F., Zhang, Q. B., Li, H. B., and Zhao, J. (2018). Grain-based discrete element method (GB-DEM) modelling of multi-scale fracturing in rocks under dynamic loading. Rock Mech. Rock Eng. 51 (12), 3785–3817. doi:10.1007/s00603-018-1566-2

CrossRef Full Text | Google Scholar

Lindqvist, J. E., Åkesson, U., and Malaga, K. (2007). Microstructure and functional properties of rock materials. Mater. Charact. 58 (11-12), 1183–1188. doi:10.1016/j.matchar.2007.04.012

CrossRef Full Text | Google Scholar

Liu, G., and Cai, M. (2020). Modeling time-dependent deformation behavior of brittle rock using grain-based stress corrosion method. Comput. Geotechnics 118, 103323. doi:10.1016/j.compgeo.2019.103323

CrossRef Full Text | Google Scholar

Liu, G., Cai, M., and Huang, M. (2018). Mechanical properties of brittle rock governed by micro-geometric heterogeneity. Comput. Geotechnics 104 (12), 358–372. doi:10.1016/j.compgeo.2017.11.013

CrossRef Full Text | Google Scholar

Liu, S. Q., Ma, F. S., Zhao, H. J., Guo, J., Lu, R., and Feng, X. (2020). Numerical analysis on the mechanism of hydraulic fracture behavior in heterogeneous reservoir under the stress perturbation. J. Nat. Gas Sci. Eng. 78, 103277. doi:10.1016/j.jngse.2020.103277

CrossRef Full Text | Google Scholar

Liu, W., Chen, Z., and Zhang, M. (2016). Numerical simulation and Site measurement of development height of fracture zone in overburden strata. Min. Saf. Environ. Prot. 43 (1), 57–60. doi:10.1016/j.compgeo.2017.11.013

CrossRef Full Text | Google Scholar

Martin, C. D., and Chandler, N. A. (1994). The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomechanics 31 (6), 643–659. doi:10.1016/0148-9062(94)90005-1

CrossRef Full Text | Google Scholar

Nagel, T., Beckert, S., Lehmann, C., Gläser, R., and Kolditz, O. (2016). Multi-physical continuum models of thermochemical heat storage and transformation in porous media and powder beds—A review. Appl. Energy 178, 323–345.

CrossRef Full Text | Google Scholar

Papanastasiou, P. C. (1997). A coupled elastoplastic hydraulic fracturing model. Int. J. rock Mech. Min. Sci. 34 (3-4), 240.e1–240.e15. doi:10.1016/s1365-1609(97)00132-9

CrossRef Full Text | Google Scholar

Peng, J., Wong, L. N. Y., and Teh, C. I. (2017). Influence of grain size heterogeneity on strength and microcracking behavior of crystalline rocks. J. Geophys. Res. Solid Earth 122 (2), 1054–1073. doi:10.1002/2016jb013469

CrossRef Full Text | Google Scholar

Pirnia, P., Duhaime, F., Ethier, Y., and Dubé, J. S. (2019). ICY: an interface between COMSOL multiphysics and discrete element code YADE for the modelling of porous media. Comput. Geosciences 123, 38–46. doi:10.1016/j.cageo.2018.11.002

CrossRef Full Text | Google Scholar

Potyondy, D. O. (2010). A grain-based model for rock: approaching the true microstructure. Proc. rock Mech. Nordic Ctries., 9–12.

Google Scholar

Potyondy, O., and Cundall, P. A. (2004). A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 41 (8), 1329–1364. doi:10.1016/j.ijrmms.2004.09.011

CrossRef Full Text | Google Scholar

Qi, S., Lan, H., Martin, D., and Huang, X. (2020). Factors controlling the difference in Brazilian and direct tensile strengths of the Lac du Bonnet Granite. Rock Mech. Rock Eng. 53 (3), 1005–1019. doi:10.1007/s00603-019-01946-x

CrossRef Full Text | Google Scholar

Taron, J., and Elsworth, D. (2009). Thermal-hydrologic-mechanical-chemical processes in the evolution of engineered geothermal reservoirs. Int. J. rock Mech. Min. Sci. 46 (5), 855–864. doi:10.1016/j.ijrmms.2009.01.007

CrossRef Full Text | Google Scholar

Tester, J. W., Anderson, B. J., Batchelor, A. S., Blackwell, D. D., DiPippo, R., Drake, E. M., et al. (2007). Impact of enhanced geothermal systems on US energy supply in the twenty-first century. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 365 (1853), 1057–1094. doi:10.1098/rsta.2006.1964

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Zhou, J., Zhang, L., and Han, Z. (2020). Numerical investigation of injection-induced fracture propagation in brittle rocks with two injection wells by a modified fluid mechanical coupling model. Energies 13 (18), 4718. doi:10.3390/en13184718

CrossRef Full Text | Google Scholar

Wang, S., Zhou, J., Zhang, L., Han, Z., and Zhang, F. (2021). Parameter studies on the mineral boundary strength influencing the fracturing of the crystalline rock based on a novel Grain Based Model. Eng. Fract. Mech. 241, 107388. doi:10.1016/j.engfracmech.2020.107388

CrossRef Full Text | Google Scholar

Wang, X., and Cai, M. (2018). Modeling of brittle rock failure considering inter-and intra-grain contact failures. Comput. Geotechnics 101, 224–244. doi:10.1016/j.compgeo.2018.04.016

CrossRef Full Text | Google Scholar

Wu, S., and Xu, X. (2016). A study of three intrinsic problems of the classic discrete element method using flat joint model. Rock Mech. Rock Eng. 49 (5), 1813–1830. doi:10.1007/s00603-015-0890-z

CrossRef Full Text | Google Scholar

Xu, Z., Li, T., Chen, G., Ma, C., and Qiu, S. (2018). The grain-based model numerical simulation of unconfined compressive strength experiment under thermal-mechanical coupling effect. KSCE J. Civ. Eng. 22 (8), 2764–2775. doi:10.1007/s12205-017-1228-z

CrossRef Full Text | Google Scholar

Yin, Q., Wu, J. Y., Zhu, C., He, M. C., Meng, Q. X., and Jing, H. W. (2021). Shear mechanical responses of sandstone exposed to high temperature under constant normal stiffness boundary conditions. Geomechanics Geophys. Geo-Energy Geo-Resources 7, 35. doi:10.1007/s40948-021-00234-9

CrossRef Full Text | Google Scholar

Zhai, M., Zhang, Q., Chen, G., and Wang, R. (2016). Adventure on the research of continental evolution and related granite geochemistry. Chin. Sci. Bull. 61 (13), 1414–1420. doi:10.1360/n972015-01272

CrossRef Full Text | Google Scholar

Zhang, W., Li, B., Zhang, G., and Li, Z. (2017). Investigation of water-flow fracture zone height in fully mechanized cave mining beneath thick alluvium. Geotechnical Geol. Eng. 35, 1745–1753. doi:10.1007/s10706-017-0205-0

CrossRef Full Text | Google Scholar

Zhang, Y., and Wong, L. N. Y. (2018). A review of numerical techniques approaching microstructures of crystalline rocks. Comput. geosciences 115, 167–187. doi:10.1016/j.cageo.2018.03.012

CrossRef Full Text | Google Scholar

Zhang, Y. H., Wong, L. N. Y., and Chan, K. K. (2019). An extended grain-based model accounting for microstructures in rock deformation. J. Geophys. Res. Solid Earth 124 (1), 125–148. doi:10.1029/2018jb016165

CrossRef Full Text | Google Scholar

Zhao, X. G., Cai, M., and Wang, J. (2013). Damage stress and acoustic emission characteristics of the Beishan granite. Int. J. Rock Mech. Min. Sci. 64, 258–269. doi:10.1016/j.ijrmms.2013.09.003

CrossRef Full Text | Google Scholar

Zhou, J., Zhang, L., and Pan, Z. (2016). Numerical investigation of fluid-driven near-borehole fracture propagation in laminated reservoir rock using PFC2D. J. Nat. Gas Sci. Eng. 36, 719–733. doi:10.1016/j.jngse.2016.11.010

CrossRef Full Text | Google Scholar

Zhou, S., Zhuang, X., Zhu, H., and Rabczuk, T. (2018). Phase field modelling of crack propagation, branching and coalescence in rocks. Theor. Appl. Fract. Mech. 96, 174–192. doi:10.1016/j.tafmec.2018.04.011

CrossRef Full Text | Google Scholar

Zhu, C., He, M. C., Jiang, B., Qin, X. Z., Yin, Q., and Zhou, Y. (2021). Numerical investigation on the fatigue failure characteristics of water-bearing sandstone under cyclic loading. J. Mt. Sci. 18 (12), 3348–3365. doi:10.1007/s11629-021-6914-0

CrossRef Full Text | Google Scholar