Compressed sensing with log-sum heuristic recover for seismic denoising

The compressed sensing (CS) method, commonly utilized for restructuring sparse signals, has been extensively used to attenuate the random noise in seismic data. An important basis of CS-based methods is the sparsity of sparse coefficients. In this method, the sparse coefficient vector is acquired by minimizing the ${\mathbf{l}}_{\mathbf{1}}$ norm as a substitute for the ${\mathbf{l}}_{\mathbf{0}}$ norm. Many efforts have been made to minimize the ${\mathbf{l}}_{\mathbf{p}}$ norm (0 < p < 1) to obtain a more desirable sparse coefficient representation. Despite the improved performance that is achieved by minimizing the ${\mathbf{l}}_{\mathbf{p}}$ norm with 0 < p < 1, the related sparse coefficient vector is still suboptimal since the parameter p is greater than 0 rather than infinitely approaching 0 $\left(\mathbf{p}\to {\mathbf{0}}^{+}\right)$. Therefore, the CS method with the limit $\mathbf{p}\to {\mathbf{0}}^{+}$ is proposed to enhance the sparse performance and thus generate better denoised results in this paper. Our proposed method is referred to as the CS-LHR method because the solving process for minimizing $\mathbf{p}\to {\mathbf{0}}^{+}$ is the log-sum heuristic recovery (LHR). Furthermore, to improve the computational efficiency, we incorporate the majorization-minimization (MM) algorithm in this CS-LHR method. Experimental results of synthetic and real seismic records demonstrate the remarkable performance of CS-LHR in random noise suppression.

1 Introduction

Random noise is frequently present in raw seismic data, which disrupts the continuity of seismic events and reduces the signal-to-noise ratio (SNR) of seismic data. Low SNR and discontinuous seismic events can blur the stratigraphic information in seismic profiles, reduce the interpretability of seismic data, and lead to incorrect identification of subsurface targets. Hence, it is essential to perform seismic noise separation and attenuation during both prestack and poststack seismic data processing (Wu et al., 2019; Dong et al., 2022a; 2022b; Liu et al., 2022a; Liu et al., 2022b; Wu B Y et al., 2022; Zhong et al., 2022; Zhong et al., 2023).

In recent years, numerous signal processing methods have emerged for the separation and suppression of seismic noise (Yuan et al., 2012; Li et al., 2014; 2022; Zhang et al., 2021; Ni et al., 2022; Sun et al., 2022; Wu H et al., 2022). These methods include singular spectrum analysis (Oropeza and Sacchi, 2011), empirical mode decomposition-based techniques (Bekara and Baan, 2009), wavelet transform (Yang et al., 2018), and curvelet transform (Qu et al., 2016). Most of these methods are typically developed based on the distinguishing characteristics of seismic signals and specific types of noise in transform domains. Notably, sparse representation-based techniques have gained significant popularity (Candès et al., 2006; Chen et al., 2017; Wu B Y et al., 2022). While seismic data is not inherently sparse, it can be effectively transformed into a sparse signal by sparse transformation (Siahsar et al., 2016). Random noise cannot be transformed into a sparse signal due to lacking sparsity. Then, during sparse transformation, the noisy seismic signal is separated into a sparse signal and random noise. Subsequently, the denoised seismic signal is reconstructed using the sparse signal, thereby the separation of the seismic signal and random noise is achieved by sparse transformation and sparse signal reconstruction. In practical applications, the denoising effectiveness of sparse transformation is linked to the sparsity of the resulting sparse signal. Greater sparsity leads to improved denoising performance. Thus, enhancing the sparsity of sparse transformation is crucial for its denoising applications (Wu H et al., 2022).

Compressed sensing (CS) is a well-established method that combines sparse transformation and signal reconstruction (Donoho, 2006). In contrast to the conventional Nyquist–Shannon sampling theory, the CS method can reconstruct signals without higher sampling rates and has received significant attention and been widely applied in separating random noise. Regrettably, obtaining sparse signals through the $l_0$ norm minimization in the CS method is an NP-hard problem (Candès and Wakin, 2008; Yang et al., 2022). As such, the minimization of $l_1$ norm and $l_p$ norm (0<p<1) are often adopted as replacements for the minimization of $l_0$ norm in some improved CS methods (Yang et al., 2009; Liu et al., 2023a). And the $l_p$ norm (0<p<1) minimization has been demonstrated as having superior sparsity capabilities compared to $l_1$ norm minimization (Wu B Y et al., 2022; Liu et al., 2023b). Although the aforementioned methods for tackling NP-hard problems can enhance the convergence and effectiveness of the solution process, they also diminish the sparsity of the sparse signal; their sparse performance can still be further enhanced by incorporating the limiting form $\mathrm{p}\to 0^{+}$.

Thus, a novel algorithm leveraging norm minimization with $\mathrm{p}\to 0^{+}$ in the CS method is proposed in this paper; it can enhance the sparsity of sparse signals, achieve proficient signal reconstruction, and effectively suppress seismic noise. The minimization utilizing the limiting form $\mathrm{p}\to 0^{+}$ is referred to as log-sum heuristic recovery (LHR) because the expansion of the limiting form norm is a logarithmic sum (Zou and Hastie, 2015). Therefore, we also call the proposed algorithm the CS-LHR method. In our approach, the minimization with $\mathrm{p}\to 0^{+}$ poses a non-convex problem, making its solution process more intricate than that of convex problems. Encouragingly, significant progress has been achieved in addressing non-convex problems, and the majorization-minimization (MM) iterative optimization algorithm is one effective method for solving such problems. The MM algorithm substitutes a complex optimization problem with a series of simpler ones, thus approximating the objective function that encompasses non-differentiable and non-convex traits with a differentiable and convex surrogate function to facilitate optimal solution retrieval (Fazel et al., 2003; Foo et al., 2009). To ensure good convergence rates, our workflow incorporates the majorization-minimization (MM) algorithm.

In the subsequent sections of this article, we provide a detailed description of the proposed workflow. Subsequently, a synthetic dataset and a field dataset containing noise are utilized to demonstrate the effectiveness of the approach. The results show that our method can suppress noise from seismic reflections effectively and results in a seismic profile with good continuity of seismic events and high resolution.

2 Compressed sensing with the limit form $\mathrm{p}\to {\mathrm{0}}^{+}$ (CS-LHR)

Compressed sensing (CS), which challenges the traditional Nyquist–Shannon sampling theory, has emerged as a hot topic in the field of signal processing (Donoho, 2006.). Although many studies on the applications of CS have been conducted, there is still value in exploring how to enhance its performance (Candès and Wakin, 2008; Yang et al., 2009). In this paper, we will explore how to enhance the sparsity of sparse signals in the CS method and apply the related research to seismic signal denoising.

If a signal $\mathrm{X}\in R^N$ can be sparsely represented, it can be written as

$X=\mathbf{\Psi }\theta (1)$

where the matrix $\mathbf{\Psi }$ consists of a set of sparse basis vectors, and the vector $\theta$ represents a sparse signal within the space defined by these basis vectors in matrix $\mathbf{\Psi }$. In the CS method, the sparse signal $\theta$ can be obtained by minimizing the norm as ${}_{\theta }{}^{\mathit{min}}{‖\theta ‖}_0$ and should satisfy the constraint as

$Y=\mathbf{\Phi }\mathbf{\Psi }\theta (2)$

In Eq. 2 $\mathrm{\Phi }$ is referred to as the sensing matrix, and $Y$ is the sampled data of $X$ obtained by the sensing matrix $\mathrm{\Phi }$.

Then, the CS theory can be described by

$\begin{array}{c}{}_{\theta }{}^{\mathit{min}}{‖\theta ‖}_0\\ s.t.Y=\mathbf{\Phi }\mathbf{\Psi }\theta \end{array}(3)$

In practice, the matrix $\mathrm{\Psi }$ and the sensing matrix $\mathrm{\Phi }$ are pre-determined. As the description by Eq. 1 and Eq. 3, the sparse signal $\theta$, when acquired, allows for the reconstruction of X utilizing $X=\mathrm{\Psi }\theta$.

Eq. 3 presented above is an NP-hard problem that is challenging to solve. To overcome this NP-hard problem, the optimization of $l_0$ norm in Eq. 3 can be replaced with a convex optimization of $l_1$ norm which is the convex approximation of the $l_0$ norm, and easier to solve. Then, the related CS method with the $l_1$ norm is (Candès and Wakin, 2008)

$\begin{array}{c}{}_{\theta }{}^{\mathit{min}}{‖\theta ‖}_1^1\\ s.t.Y=\mathbf{\Phi }\mathbf{\Psi }\theta \end{array}(4)$

where ${‖\bullet ‖}_1^1$ represents the $l_1$ norm.

Although the convex relaxation in Eq. 4 reduces the complexity of the original NP-hard problem, it unfortunately yields a solution $\theta$ with suboptimal sparsity due to the $l_1$ norm deviating significantly from the $l_0$ norm. To address this issue, the $l_p$ norm is introduced (Candès et al., 2006). Subsequently, the optimization problem described by Eq. 4 with the $l_p$ norm can be written as

$\begin{array}{c}{}_{\theta }{}^{\mathit{min}}{f}_p\left(\theta \right)\\ s.t.Y=\mathbf{\Phi }\mathbf{\Psi }\theta \end{array}(5)$

In which $f_p\left(\theta \right)={‖\theta ‖}_p^p$ and p $\in$ (0,1]. For $\forall \mathrm{p}>0$, $\underset{\mathrm{\theta }}{\min }{f}_p\left(\theta \right)$ is equivalent to

$\underset{\theta }{\min }\frac{1}{p}\left[f_p\left(\theta \right)-N\right]=\underset{\theta }{\min }{\displaystyle {\sum }_{i=1}^N}\frac{\left|{\vartheta }_i\right|-1}{p}(6)$

in Eq. 6 N is the length of the sparse signal $\theta$ and ${\vartheta }_i$ denotes the element of $\theta$ (Caiafa and Cichocki, 2013).

Presented above corresponds to a non-convex optimization and exhibits superior sparsity performance compared to the $l_1$ norm minimization. Although the advantages of CS method with the $l_p$ p $\in$ (0,1] norm shown as Eq. 5 have been demonstrated, the CS method with limit $\mathrm{p}\to 0^{+}$ has not been studied. It is important that the $l_p$ norm minimization based on $\mathrm{p}\to 0^{+}$ differs from other p values in p $\in$ (0,1]; it possesses greater sparse capability (Deng et al., 2012). Additionally, the $l_p$ norm minimization based on $\mathrm{p}\to 0^{+}$ also differs from $l_p$ (p=0) that yields an NP-hard problem; it is solvable. Thus, in order to acquire a sparse signal $\theta$ with high sparsity, we propose a novel approach that combines the optimization of the limit norm with the CS method to enhance the sparsity of $\theta$, described as

$\begin{array}{c}\underset{\theta }{\min }\underset{\mathrm{p}\to 0^{+}}{\lim }{f}_{\mathrm{p}}\left(\theta \right)\\ s.t.Y=\mathbf{\Phi }\mathbf{\Psi }\theta \end{array}(7)$

According to L’Hôspital’s rule (Caiafa and Cichocki, 2013), $\underset{\mathrm{p}\to 0^{+}}{\lim }{f}_{\mathrm{p}}\left(\theta \right)$ in Eq. 7 can be expressed as

$\underset{\mathrm{p}\to 0^{+}}{\lim }{f}_{\mathrm{p}}\left(\theta \right)=\underset{\mathrm{p}\to 0^{+}}{\lim }{\displaystyle {\sum }_{i=1}^N}\frac{\left|{\vartheta }_i\right|-1}{p}={\displaystyle {\sum }_{i=1}^N}\mathit{log}\left(\left|{\vartheta }_i\right|+\delta \right)(8)$

where $\mathrm{\delta }>0$ is a small positive number to guarantee the stability of the algorithm. In practice, $\mathrm{\delta }$ should be set to a value slightly smaller than the expected non-zero element ${\vartheta }_i$. Typically, the solve process of Eq. 8 is robust enough to tolerate different choices of $\mathrm{\delta }$. Therefore, combined with Eq. 8, 7 can be rewritten as

$\left\{\begin{array}{c}\left\{\begin{array}{c}\underset{\theta }{\mathit{min}}{\displaystyle {\sum }_{i=1}^N}\mathit{log}\left(\left|{\vartheta }_i\right|+\delta \right)\\ s.t.Y=\mathit{\Phi }\mathit{\Psi }\theta \end{array}\right.\\ {\displaystyle {\sum }_{i=1}^N}\mathit{log}\left(\left|{\vartheta }_i\right|+\delta \right)=f_L\left(\theta \right)\end{array}\right.(9)$

in which the logarithmic sum ${\displaystyle {\sum }_{i=1}^N}\mathit{log}\left(\left|{\vartheta }_i\right|+\delta \right)$ is denoted as $f_L\left(\theta \right)$, and $\underset{\theta }{\min }{\displaystyle {\sum }_{i=1}^N}\mathit{log}\left(\left|{\vartheta }_i\right|+\delta \right)$ is the log-sum heuristic recovery (LHR) model. Therefore, the improved method described by Eq. 9 is named as the CS-LHR method by us because it is the composition of the CS and the LHR. In contrast to the traditional CS methods, the CS-LHR method can attain a best sparse signal $\theta$ that exhibits the optimal sparsity.

Note that Eq. 9 is non-convex due to the non-convexity of its log-sum. According to recent progress in non-convex optimization, the non-convex problem can be solved efficiently. In this paper, we incorporate the alternating direction method of the majorization-minimization (MM) algorithm into our workflow to ensure faster convergence (Fazel et al., 2003; Foo et al., 2009). The MM algorithm transforms the original non-differentiable, non-convex function into a differentiable and convex surrogate function, facilitating the retrieval of optimal solutions. Then, Eq. 9 can be equivalently expressed as Eq. 10 based on the MM algorithm as

$\begin{array}{c}{}_{\theta }{}^{\mathit{min}}{‖W\odot \theta ‖}_{l_1}\\ s.t.Y=\mathbf{A}\theta \end{array}(10)$

where $\mathbf{A}=\mathbf{\Phi }\mathbf{\Psi },$ $W$ represents the vector of weighted parameters with each element $w_i={\left(\left|{\vartheta }_i+\delta \right|\right)}^{-1}$. Eq. 10 demonstrates that the log-sum penalty function performs the re-weighted $l_1$ minimization, which promotes sparsity more effectively compared to the $l_p$ norm (0<p<1) minimization. Moreover, each iteration of the MM algorithm for solving Eq. 10 corresponds to a convex optimization that can be easily solved.

Eq. 10 can also be rewritten as

$\underset{\theta }{\min }{‖Y-\mathit{A}\theta ‖}_{l_2}+\lambda {‖W\odot \theta ‖}_{l_1}(11)$

in Eq. 11 $\lambda$ is the positive weighting parameter. Once the solution ${\theta }^{*}$ of Eq. 10 is obtained, the signal ${\mathrm{X}}^{*}=\mathrm{\Psi }{\theta }^{*}$ can be recovered.

3 Seismic denoising by the CS-LHR

Section 2 suggests that the CS-LHR can achieve the optimal sparse signal through the limit norm minimization. The resulting optimal sparse signal complies with the constraints and is well-suited for signal reconstruction. This paper focuses on the application of the CS-LHR method to seismic signal denoising. A general form of an observed seismic signal $Y\left(\mathrm{n}\right)$ that is contaminated by noise can be expressed as

$\left\{\begin{array}{c}Y\left(\mathrm{n}\right)=\mathit{A}\theta \left(\mathrm{n}\right)+E\left(\mathrm{n}\right)\\ \mathbf{A}=\mathbf{\Phi }\mathbf{\Psi }\\ X\left(n\right)=\mathrm{\Psi }\theta \left(\mathrm{n}\right)\end{array}\right.(12)$

in Eq. 12 $\theta \left(\mathrm{n}\right)$ is a sparse signal, $E\left(\mathrm{n}\right)$ represents the noise term that can either be stochastic or deterministic, and $\mathrm{n}\in \left[1,\mathrm{N}\right]$ represents the index of time sampling point. Assuming that $\mathrm{\Phi }$ and $\mathrm{\Psi }$ represent the sensing and sparse basis matrices, and are independent as the CS theory, it becomes feasible to separate the noise $E\left(\mathrm{n}\right)$ from the observed seismic signal $Y\left(\mathrm{n}\right)$. Subsequently, the denoised result $X\left(n\right)$ can be reconstructed by $\theta \left(\mathrm{n}\right)$. Moreover, the effectiveness of denoising is associated with the sparsity of $\theta \left(\mathrm{n}\right)$. Greater sparsity leads to improved noise separation. Based on the foregoing analysis, the CS-LHR, utilizing limit norm optimization, yields an optimally sparse signal $\theta \left(\mathrm{n}\right)$.

According to the CS theory, the sparse basis matrix $\mathrm{\Psi }$ and the sensing matrix $\mathrm{\Phi }$ should be irrelevant (Donoho, 2006). However, achieving complete independence between $\mathrm{\Psi }$ and $\mathrm{\Phi }$ in practical applications is challenging. Then, some special matrices are chosen as $\mathrm{\Phi }$ to ensure a certain degree of independence with the sparse basis matrix $\mathrm{\Psi }$. In this study, a Gaussian random matrix is chosen as sensing matrix $\mathrm{\Phi }$ due to its excellent characteristic of having minimal correlation with other matrices. Additionally, since a seismic signal is non-stationary, the sparse basis matrix $\mathrm{\Psi }$ should be provided by an algorithm which facilitates the analysis of non-stationary signals. To obtain a sparse basis matrix $\mathrm{\Psi }$ for non-stationary signals, the sparse S-transform is introduced (Wang et al., 2016). Furthermore, as the log-sum penalty term in Eq. 8 is non-convex, a suitable starting point for iterative computation is necessary. Consequently, we initialize $\theta$ with the solution of Eq. 3 with the $l_1\text{\hspace{0.17em}norm\hspace{0.17em}minimization}$. The proposed workflow is summarized in Algorithm 1 (Table 1):

TABLE 1

TABLE 1. The workflow of seismic denoising by CS-LHR.

4 Synthetic and real data examples

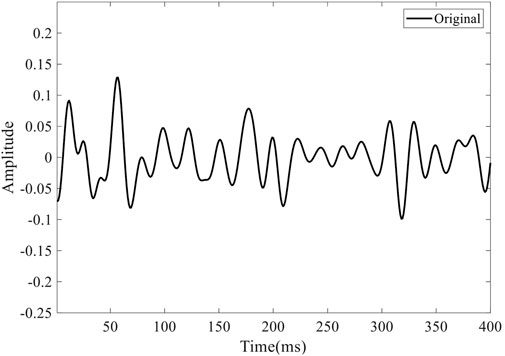
In order to illustrate the effectiveness of the proposed CS-LHR method, we initially apply it to synthetic seismic data with different levels of signal noise ratios (SNRs). Then, the proposed method is utilized for field data denoising. Figure 1 displays a 2-D synthetic seismic trace without noise. Figure 2 shows the 2-D synthetic trace with different SNRs (5dB, 5dB, -3dB, and 3 dB). Figure 3 exhibits a 3-D noisy field data acquired over the Scotian shelf, offshore Canada, and termed Penobscot. For comparison, the traditional CS method based on $l_p$ norm (0<p<1) is utilized as an alternative method.

FIGURE 1

FIGURE 1. A 2-D synthetic seismic trace without noise.

FIGURE 2

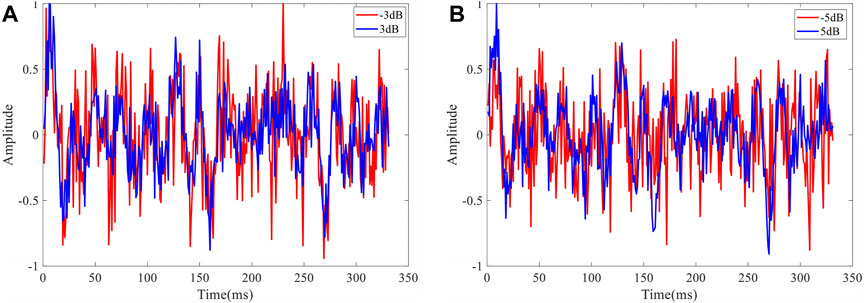
FIGURE 2. (A) The 2-D synthetic seismic trace with SNRs −3dB, 3dB. (B) The 2-D synthetic seismic trace with SNRs −5dB, 5dB.

FIGURE 3

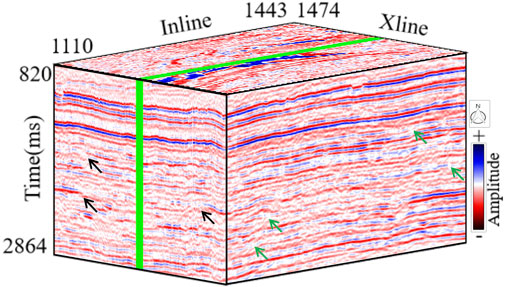
FIGURE 3. A 3-D noise-contaminated field data acquired over the Scotian shelf, offshore Canada, comprised 401 inlines and 401 crosslines, with a time sampling interval of 4 ms. Discontinuous seismic events are indicated by black arrows, seismic artifacts caused by random noises are represented by green arrows. The green lines correspond to the location of X-line 1273.

4.1 Seismic signal enhancement with different SNRs

The denoising results for noisy 2-D synthetic data using the traditional CS method are depicted in Figures 4A,B, while those obtained from the CS-LHR method are presented in Figures 5A,B. It is clear that the traditional CS method can effectively attenuate noise in smooth areas of noisy synthetic data; however, it introduces artifacts and exhibits a poor denoising effect in the oscillatory areas marked by black ellipses. Although the traditional CS method based on $l_p$ norm (0<p<1) exhibits greater effect on noise attenuation compared to that based on $l_1$ norm, its sparse signal $\theta \left(\mathrm{n}\right)$ exhibits varying reconstruction capabilities across different regions of the signals. During noise separation using sparse transformation in the traditional CS method, the suboptimal sparsity of the sparse signal leads to the inclusion of some noise characteristics in the sparse signal, which become apparent in the reconstructed original signal. While the sparse signal $\theta \left(\mathrm{n}\right)$ effectively captures the primary information within smooth areas of the signal, it also incorporates some noise features in oscillatory regions. To enhance the denoising performance across all areas of the noisy signal, it is crucial that the sparsity of the sparse signal is increased to enhance the reconstruction effectiveness of the original signal. Consequently, this paper introduces the CS-LHR method which can achieve the best sparse reconstruction ability due to the norm minimization based on $\mathrm{p}\to 0^{+}$. The denoising results shown in Figure 5 illustrate the random noises are successfully removed while the seismic events are preserved well. Notably, the proposed method demonstrates exceptional noise filtering capabilities, even under low signal-to-noise ratio (SNR) conditions.

FIGURE 4

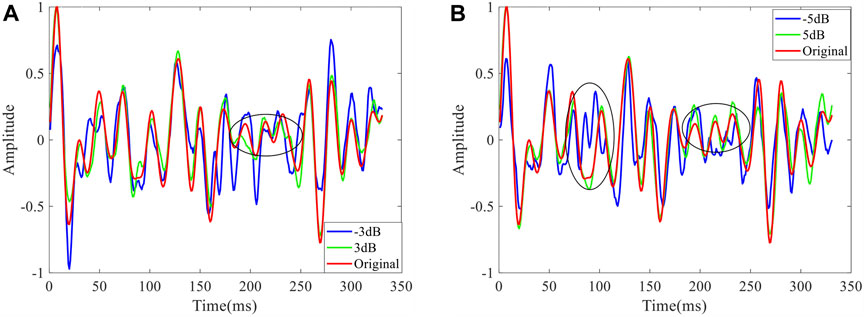
FIGURE 4. The denoising results of 2-D synthetic seismic traces by the traditional CS model with 0<p<1. (A) The denoising results for SNRs −3dB and 3dB. (B) The denoising results for SNRs −5dB and 5dB. From these results, we can see that the traditional CS model with 0<p<1 effectively attenuates noise in smooth areas of noisy synthetic data; however, it introduces artifacts and exhibits a poor denoising effect in oscillatory areas marked by black ellipses.

FIGURE 5

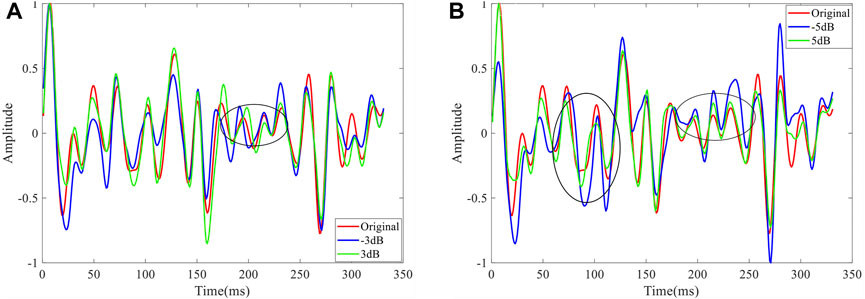
FIGURE 5. The denoising results of 2-D synthetic seismic trace by the CS-LHR method. (A) The denoising results for SNRs −3dB and 3dB. (B) The denoising results for SNRs −5dB and 5dB. Compared to Figure 4, Figure 5 illustrates the random noises are successfully removed while the seismic events are preserved well.

4.2 Field data applications

To verify the effectiveness of the proposed method, 3-D noise-contaminated field data obtained from the Scotian shelf, offshore Canada, referred to as Penobscot, are shown in Figure 3. The 3-D field data comprise 401 inlines and 401 crosslines, with a time sampling interval of 4 ms.

In Figure 3, black arrows indicate discontinuous seismic events, while green arrows represent seismic artifacts caused by random noise. The green lines correspond to the location of X-line 1273, as depicted in Figure 6A. Obviously, this seismic volume contains significant random noises which hinder subsequent seismic data processing and interpretation. Our method’s denoising result is shown in Figure 6B, where the improved resolution and well-preserved reflection events are evident. Regions marked by the black ellipses demonstrate efficient attenuation of random noise, enhanced continuity, and resolution of seismic events. Additionally, the seismic fault structures indicated by black arrows are preserved well. Further, Figure 6C shows no useful information in the difference profile.

FIGURE 6

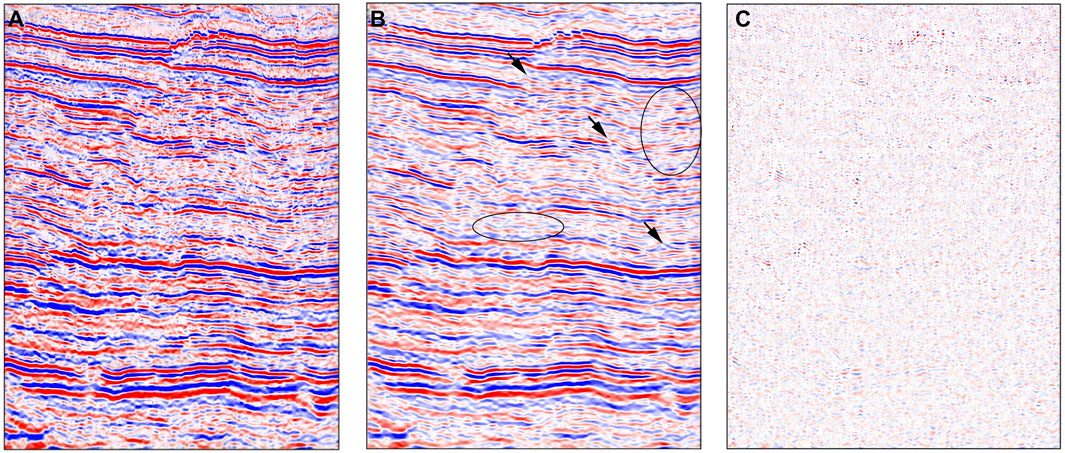
FIGURE 6. (A) The noise-contaminated field section, which is marked by green lines in 3-D field data, contains significant random noises. (B) From the denoising result by CS-LHR, we can see that the improved resolution and well-preserved reflection events are evident. (C) The difference profile between Figures 6A, B; there is no useful information in this difference profile.

To further demonstrate the effectiveness of our method, we compare it with the traditional CS method with 0<p<1 on the same field data. The corresponding results are presented in Figure 7. Figure 7A shows the denoising result, and Figure 7B represents the related difference profile. We can observe that valid seismic events are generally preserved in Figure 7A. However, compared to the CS-LHR result, the fault structures and seismic events, indicated by black arrows and black ellipses in Figure 7A, respectively, are less subtle. Additionally, some valuable information that can improve the resolution of the denoising result is contained in the difference profile Figure 7B.

FIGURE 7

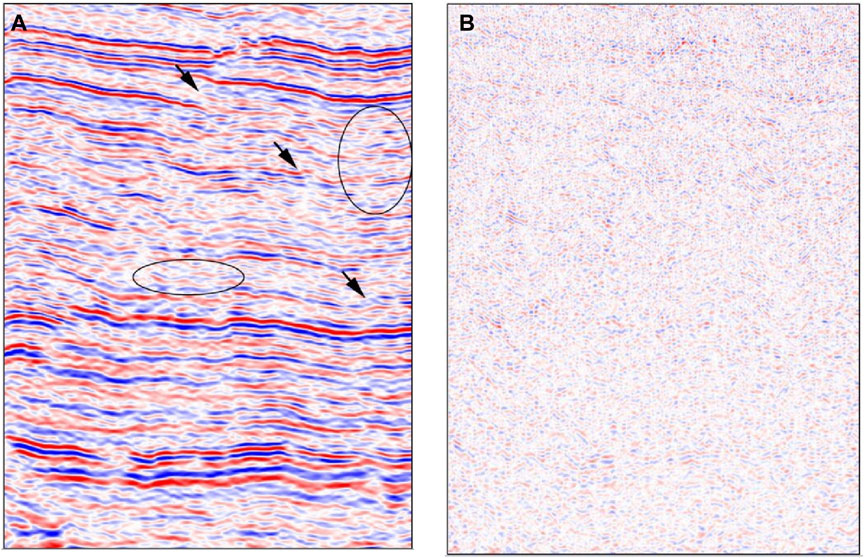
FIGURE 7. (A) Denoising result of Figure 6A by CS with $l_p$ norm (0<p<1); the fault structures and seismic events, indicated by black arrows and black ellipses, respectively, are less subtle. (B) The difference profile between Figure 6A; Figure 7A; it contains some valuable information.

5 Conclusion

This paper proposes the CS-LHR method, a novel method for seismic noise attenuation. Compared to the traditional CS methods with 0<p $\le$ 1, the CS-LHR method with the limit $\mathrm{p}\to 0^{+}$ provides enhanced sparse representation ability and denoising performance. Testing results on field data demonstrate that our workflow efficiently recovers noise-free signals. Additionally, we implement the MM algorithm to improve calculation efficiency.

The CS method can be used for denoising, but its primary contribution to the scientific domain lies in accomplishing the compression and reconstruction of original signals via sparse signal representation. This process facilitates the reduction of data acquisition and transmission costs while preserving data quality, essential for diverse applications including medical imaging, remote diagnosis, earth observation, and wireless transmission. The CS-LHR method introduced in this paper can achieve the optimal sparsity of the sparse signal, leading to additional reductions in storage and transmission costs. This holds particular significance for industrial applications driven by cost considerations.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FS: Conceptualization, Methodology, Writing–original draft. QZ: Formal Analysis, Writing–review and editing. ZW: Validation, Writing–review and editing. WH: Validation, Improving the quality, Writing–review and editing, Formal Analysis.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Natural Science Foundation of Guangxi (2021GXNSFBA196071 and 2021JJA170177), Guangxi Key Laboratory of Precision Navigation Technology and Application, and Key Laboratory of Microwave and Optical Wave Application Technology, Guilin University of Electronic Technology.

Acknowledgments

The authors would like to thank the dGB Earth Sciences, Nova Scotia Department of Energy, Canada-Nova Scotia Offshore Petroleum Board, for providing the 3-D field data used in this study.

Conflict of interest

Author ZW was employed by The china state shipbuilding corporation limited.

Author WH was employed by Xi’an Engineering Investigation and Design Research Institute of China National Nonferrous Metals Industry Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bekara, M., and Baan, M. V. D. (2009). Random and coherent noise attenuation by empirical mode decomposition. Geophysics 74 (5), 89–98. doi:10.1190/1.3157244

CrossRef Full Text | Google Scholar

Caiafa, C. F., and Cichocki, A. (2013). Multidimensional compressed sensing and their applications. Wires Data Min. Knowl. Discov. 3, 355–380. doi:10.1002/widm.1108

CrossRef Full Text | Google Scholar

Candès, E. J., Romberg, J., and Tao, T. (2006). Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52, 489–509. doi:10.1109/TIT.2005.862083

CrossRef Full Text | Google Scholar

Candès, E. J., and Wakin, M. B. (2008). An introduction to compressive sampling. IEEE Signal Process. Mag. 25, 21–30. doi:10.1109/MSP.2007.914731

CrossRef Full Text | Google Scholar

Chen, Y. K., Zhou, Y. T., Chen, W., Zu, S., Huang, W., and Zhang, D. (2017). Empirical low-rank approximation for seismic noise attenuation. IEEE Trans. Geoscience Remote Sens. 55 (8), 4696–4711. doi:10.1109/TGRS.2017.2698342

CrossRef Full Text | Google Scholar

Deng, Y., Liu, Y. B., Dai, Q. H., Zhang, Z., and Wang, Y. (2012). Noisy depth maps fusion for multiview stereo via matrix completion. IEEE J. Sel. Top. Signal Process. 6, 566–582. doi:10.1109/JSTSP.2012.2195472

CrossRef Full Text | Google Scholar

Dong, X. T., Lin, J., Lu, S. P., Huang, X., Wang, H., and Li, Y. (2022a). Seismic shot gather denoising by using a supervised-deep-learning method with weak dependence on real noise data: a solution to the lack of real noise data. Surv. Geophys. 43 (5), 1363–1394. doi:10.1007/s10712-022-09702-7

CrossRef Full Text | Google Scholar

Dong, X. T., Lin, J., Lu, S. P., Wang, H., and Li, Y. (2022b). Multiscale spatial attention network for seismic data denoising. IEEE Trans. Geoscience Remote Sens. 60, 1–17. doi:10.1109/TGRS.2022.3178212

CrossRef Full Text | Google Scholar

Donoho, D. L. (2006). Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306. doi:10.1109/TIT.2006.871582

CrossRef Full Text | Google Scholar

Fazel, M., Hindi, H., and Boyd, S. P. (2003). “Log-det heuristic for matrix rank minimization with applications to Hankel and Euclidean distance matrices,” in The 2003 American Control Conference, Denver, CO, USA, 04-06 June 2003, 2156–2172.

Google Scholar

Foo, C. S., Do, C. B., and Ng, A. Y. (2009). “A majorization-minimization algorithm for (multiple) hyper-parameter learning,” in The 26th annual international conference on machine learning (Montreal, Quebec, CA: Association for Computing Machinery), 321–328. doi:10.1145/1553374.1553415

CrossRef Full Text | Google Scholar

Li, F. Y., Sun, F. Y., Liu, N. H., and Xie, R. (2022). Denoising seismic signal via resampling local applicability functions. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2020.3048110

CrossRef Full Text | Google Scholar

Li, F. Y., Zhang, B., Marfurt, K. J., and Hall, I. (2014). “Random noise suppression using normalized convolution filter,” in The SEG technical program expanded abstracts 2014 (Denver, USA: SEG). doi:10.1190/segam2014-1478.1

CrossRef Full Text | Google Scholar

Liu, N. H., Lei, Y. B., Liu, R. C., Yang, Y., Wei, T., and Gao, J. (2023a). Sparse time-frequency analysis of seismic data: sparse representation to unrolled optimization. IEEE Trans. Geoscience Remote Sens. 61, 1–10. doi:10.1109/TGRS.2023.3300578

CrossRef Full Text | Google Scholar

Liu, N. H., Lei, Y. B., Yang, Y., Wang, Z., Liu, R., Gao, J., et al. (2023b). Sparse time-frequency analysis of seismic data via convolutional neural network. Interpretation 12 (1), T47–T62. doi:10.1190/int-2023-0020.1

CrossRef Full Text | Google Scholar

Liu, N. H., Wang, J. L., Gao, J. H., Chang, S., and Lou, Y. (2022a). Similarity-informed self-learning and its application on seismic image denoising. IEEE Trans. Geoscience Remote Sens. 60, 1–13. doi:10.1109/tgrs.2022.3210217

CrossRef Full Text | Google Scholar

Liu, N. H., Wang, J. L., Gao, J. H., Yu, K., Lou, Y., Pu, Y., et al. (2022b). NS2NS: self-learning for seismic image denoising. IEEE Trans. Geoscience Remote Sens. 60, 1–11. doi:10.1109/TGRS.2022.3217289

CrossRef Full Text | Google Scholar

Ni, W. D., Lou, Y. H., Xu, X. L., Xue, A., and Wang, W. (2022). “Seismic random noise attenuation via noise assisted-multivariate EMD based MSSA,” in The 2022 International Conference on Automation, Robotics and Computer Engineering (ICARCE), Wuhan, China, 16-17 December 2022. doi:10.1109/ICARCE55724.2022.10046637

CrossRef Full Text | Google Scholar

Oropeza, V., and Sacchi, M. (2011). Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics 76 (3), 25–32. doi:10.1190/1.3552706

CrossRef Full Text | Google Scholar

Qu, S., Zhou, H., Liu, R. W., Chen, Y., Zu, S., Yu, S., et al. (2016). Deblending of Simultaneous-source seismic data using fast iterative shrinkage-thresholding algorithm with firm-thresholding. Acta Geophys. 64 (4), 1064–1092. doi:10.1515/acgeo-2016-0043

CrossRef Full Text | Google Scholar

Siahsar, M. A. N., Gholtashi, S., Kahoo, A. R., Marvi, H., and Ahmadifard, A. (2016). Sparse time-frequency representation for seismic noise reduction using low-rank and sparse decomposition. Geophysics 81 (2), 117–124. doi:10.1190/geo2015-0341.1

CrossRef Full Text | Google Scholar

Sun, F. Y., Liao, G. S., Lou, Y. H., and Jiang, X. (2022). Seismic data denoising with correlation feature optimization via S-mean. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2021.3117965

CrossRef Full Text | Google Scholar

Wang, Y. Q., Peng, Z. M., and He, Y. M. (2016). “Time-frequency representation for seismic data using sparse S transform,” in The2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14-17 October 2016. doi:10.1109/CompComm.2016.7925036

CrossRef Full Text | Google Scholar

Wu, B. Y., Yu, J. Y., Ren, H. R., Lou, Y. H., and Liu, N. H. (2022). Seismic traffic noise attenuation using $l_{p}$ -norm robust PCA. IEEE Geoscience Remote Sens. Lett. 17, 1998–2001. doi:10.1109/lgrs.2019.2955737

CrossRef Full Text | Google Scholar

Wu, H., Zhang, B., Lin, T. F., Li, F., and Liu, N. (2019). White noise attenuation of seismic trace by integrating variational mode decomposition with convolutional neural network. Geophysics 84 (5), 307–317. doi:10.1190/geo2018-0635.1

CrossRef Full Text | Google Scholar

Wu H, H., Zhang, B., and Liu, N. H. (2022). Self-adaptive denoising net: self-supervised learning for seismic migration artifacts and random noise attenuation. J. Petroleum Sci. Eng. 214, 110431. doi:10.1016/j.petrol.2022.110431

CrossRef Full Text | Google Scholar

Yang, J. Y., Peng, Y. G., Xu, W. L., and Dai, Q. H. (2009). Ways to sparse representation: an overview. Sci. China (Series F:Information Sci. 52, 695–703. doi:10.1007/s11432-009-0045-5

CrossRef Full Text | Google Scholar

Yang, Y., Lei, Y. B., Liu, N. H., Wang, Z., Gao, J., and Ding, J. (2022). Sparse TFNet: a physically informed auto encoder for sparse time–frequency analysis of seismic data. IEEE Trans. Geoscience Remote Sens. 60, 1–12. doi:10.1109/TGRS.2022.3213851

CrossRef Full Text | Google Scholar

Yang, Y., Li, D. Q., Tong, T. G., Zhang, D., Zhou, Y., and Chen, Y. (2018). Denoising controlled-source electromagnetic data using least-squares inversion. Geophysics 83 (4), 229–244. doi:10.1190/geo2016-0659.1

CrossRef Full Text | Google Scholar

Yuan, S. Y., Wang, S. X., and Li, G. F. (2012). Random noise reduction using Bayesian inversion. J. Geophys. Eng. 9, 60–68. doi:10.1088/1742-2132/9/1/007

CrossRef Full Text | Google Scholar

Zhang, Y. J., Zhang, H. R., and Yang, Y. (2021). Seismic random noise separation and attenuation in based on MVMD and MSSA. IEEE Trans. Geoscience Remote Sens. 60, 5908916. doi:10.1109/TGRS.2021.3131655

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., and Dong, X. T. (2023). RMCHN: a residual modular cascaded heterogeneous network for noise suppression in DAS-VSP records. IEEE Geoscience Remote Sens. Lett. 20, 7500205. doi:10.1109/LGRS.2022.3229556

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X. T., Li, Y., and Wu, N. (2022). Seismic random noise suppression by using deep residual U-Net. J. Petroleum Sci. Eng. 209, 109901. doi:10.1016/j.petrol.2021.109901

CrossRef Full Text | Google Scholar

Zou, H., and Hastie, T. (2015). Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 67, 301–320. doi:10.1111/j.1467-9868.2005.00503.x

CrossRef Full Text | Google Scholar