Employing convolution-enhanced attention mechanisms for earthquake detection and phase picking models

In response to the challenge of improving the performance of deep learning models for earthquake detection in low signal-to-noise ratio environments, this article introduces a new earthquake detection model called ECPickNet. Drawing inspiration from the EQTransformer, this model leverages Convolution-Enhanced Transformer technology, Conformer architecture, and incorporates the Residual Stacking Block Unit with Channel-Skipping (RSBU-CS) module. The manuscript provides a detailed overview of the model’s network architecture, parameter settings used during the training process, and compares it with several similar methods through a series of experiments. The experimental results highlight ECPickNet’s well performance on both the STEAD and Gansu datasets, particularly performing exceptionally well in the processing of low signal-to-noise ratio data. Interested readers can access and download the proposed method from the following website address: https://github.com/20041170036/EcPick.

1 Introduction

With the ever-increasing density of seismograph networks, there is a growing need for automation in earthquake phase detection to reduce the reliance on human labor and enhance the overall efficiency of seismic monitoring systems. In recent years, deep learning methods have emerged as the state-of-the-art approaches for various tasks, including automatic analysis of seismic signals, due to their ability to learn complex features and patterns from large-scale data (Perol et al., 2018; Mousavi et al., 2019). Consequently, the development of highly effective deep learning models for earthquake detection bears significant implications for both seismic research and hazard mitigation efforts.

Automatic earthquake phase detection using deep learning techniques can alleviate the burden on seismologists, enabling faster and more accurate event identification and location, which are essential for real-time seismic hazard assessment and early warning systems (Ross et al., 2018; Zhu and Beroza, 2019). Furthermore, these models can adapt to different seismological settings and types of seismic data, ensuring their wide applicability across various regions and seismograph networks.

However, the performance of deep learning models for earthquake detection depends on the quality and quantity of available labeled data. Obtaining high-quality labeled data can be challenging, especially in regions with complex tectonic environments or limited historical seismic records. To address this issue, recent studies have explored the use of synthetic data, data augmentation techniques, and transfer learning to improve the training and generalization capabilities of deep learning models for earthquake detection (Ross et al., 2018; Li et al., 2020).

In this study, we present a advanced approach deep learning-based model for earthquake phase detection, specifically designed for the Gansu region in China, a region characterized by high seismicity and complex tectonic settings. Our model demonstrates outstanding performance, capitalizing on the latest advancements in both seismology and deep learning to provide an efficient and reliable tool for earthquake early warning and hazard assessment. The main contributions of this study are as follows:

1) Earthquake detection, traditionally reliant on labor-intensive manual analysis, is crucial for timely hazard mitigation. Our advanced deep learning-based model presents a promising opportunity to replace human labor, significantly reducing the required manpower while maintaining high detection accuracy, thus enhancing seismic monitoring and assessment efficiency.

2) This paper smartly incorporates a convolutional layer into the original Transformer structure, thus forming an augmented Conformer capable of robust local feature extraction. This improvement enables ECPickNet to adeptly capture the spatiotemporal correlations within earthquake signals, consequently enhancing detection accuracy. By introducing this cleverly designed structure, the advantages of the Transformer architecture in natural language processing are extended to earthquake signal detection tasks.

3) This article also uses a key module called RSBU-CS. This module introduces a channel attention mechanism that adaptively adjusts the weights of disparate channels, reinforcing earthquake-related features while suppressing noise. This innovation holds paramount significance for low signal-to-noise ratio earthquake event detection, as noise substantially influences detection outcomes in such scenarios.

4) The ECPickNet model amalgamates the enhanced convolutional Transformer structure and the Residual Shrinkage Building Unit with Channel-Shared thresholds (RSBU-CS) module, endowing the model with remarkable robustness in low signal-to-noise ratio situations. This enables the efficient identification and extraction of earthquake signal features, averting mis-detections or omissions induced by noise interference. Furthermore, ECPickNet’s end-to-end training strategy empowers the entire model to concurrently learn earthquake signal representation and classification, ultimately elevating detection accuracy. This approach provides a worth thinking avenue for deep learning models in the realm of earthquake detection.

2 Related work

Earthquake detection and arrival time picking are the most critical steps in the process, as their accuracy greatly impacts the validity of the earthquake catalog (Liao et al., 2021; Su et al., 2021; Zhao et al., 2021; Yin et al., 2022). Traditional phase detection methods (such as Short Time Average over Long Time Average--STA/LTA, an information criterion--AIC, improved Coppens method, higher-order statistics) each have their advantages and drawbacks. Despite the availability of numerous algorithms, accurately selecting arrival times remains a challenge, primarily due to the singularity of calculation methods (Allen, 1978; Takanami and Kitagawa, 1991; Sabbione and Velis, 2010; Yung and Ikelle, 1997; Akram and Eaton, 2016). The advent of machine learning, a representative computer technology, offers novel approaches to earthquake event detection and classification (Yin et al., 2022). By applying rapidly developing audio recognition and computer vision technologies, such as object detection, to seismology, we can improve earthquake event detection techniques. Unlike traditional methods, which require setting a threshold for seismic waveform energy or amplitude variations, most machine learning algorithms do not necessitate human intervention and are better suited for big data processing, enabling rapid processing of massive seismic data. Mousavi et al. (2020) proposed the attention mechanism-based earthquake detection and arrival time picking model EQTransformer (hereafter referred to as EqT), which demonstrated outstanding performance on the Stanford earthquake dataset STEAD (Mousavi et al., 2019). EqT is a commonly used automatic detection model in seismology, and several deep learning frameworks for processing seismic signals, such as Siamese EqT (Xiao et al., 2021) and ESPRH (Wu et al., 2022), have been developed based on it, offering unique advantages in phase identification accuracy and false detection rates (Jiang et al., 2021). Saad et al. (2023) proposed the EQCCT model, which introduces a deep learning approach centered on the Convolutional Compact Transformer for seismic waveform analysis. It significantly improves feature extraction from large training datasets, yielding lower error rates, higher precision, recall, and F1 scores compared to traditional methods. EQCCT’s successful application across diverse test datasets, including Japan, Texas, and Instance, as well as in microseismic monitoring, underscores its significance as a valuable tool in seismology. However, seismic signals exhibit regional characteristics, with significant waveform differences due to varying geological conditions and instrumentation in different regions (Chai et al., 2020). To evaluate those methods above applicability in Gansu Province, we compiled a dataset of earthquake events in the region. In comparison to STEAD, this dataset is smaller, with fewer than 140,000 manually recorded earthquake events between 2009 and 2021, many of which lack P-wave or S-wave arrival times. To maintain consistency, we only selected data with complete P and S wave phases. After using those methods for initial detection, we found a high rate of missed detections, indicating poor generalization performance in Gansu Province. Because there are few seismic monitoring networks in Gansu, China, there are few monitoring options available. Robust models that can function well in low signal-to-noise ratio (SNR) situations are urgently needed to overcome this problem, improving the network’s seismic monitoring capabilities. It is important to note that the models currently in use have mostly shown excellent performance in datasets with greater SNR values (Jiang et al., 2021). To address this issue, we developed a new model, ECPickNet, based on Conformer technology (Gulati et al., 2020), which outperforms EqT in low signal-to-noise ratio (SNR) data and achieves higher performance on the Gansu dataset. Conformer is a self-attention mechanism-based sequence modeling neural network architecture employed in natural language processing, speech recognition, and computer vision. Similar to Transformers, Conformer models utilize self-attention mechanisms to encode input sequences. The key difference lies in Conformer’s adoption of a novel multi-layer convolutional neural network structure called Depthwise Separable Convolution (Chollet, 2017) in place of the fully connected layers in Transformers, thereby reducing computational complexity. Conformer also incorporates a novel module called the Convolutional Block Attention Module (CBAM), which further enhances the model’s representational capabilities (Gulati et al., 2020). The Conformer model has achieved excellent results in multiple natural language processing tasks, including language modeling, text classification, machine translation, and speech recognition, becoming one of the research hotspots in the field of natural language processing (Guo et al., 2021). In this study, we applied the Conformer Block to a deep neural network for earthquake detection and phase picking tasks. We applied the new model to two different seismic datasets and compared other detection models to evaluate the detection ability of our proposed new method for seismic signals.

3 Datasets introduction

Two earthquake datasets were used for model training and validation: the Stanford University earthquake dataset (STEAD) and the custom Gansu Province dataset (hereafter referred to as the Gansu dataset). A brief introduction to these datasets is provided below.

3.1 STEAD

With the rapid development of machine learning technology, its application in seismology has become a popular research direction. However, a large amount of high-quality labeled data is crucial for building effective supervised learning models. In seismology, the lack of high-quality, standardized labels and uncertainty in label reliability have severely hindered the research progress in combining seismology and machine learning. To address this issue, Mousavi et al. (2019) proposed a high-quality, large-scale, and global earthquake dataset. The dataset contains two types of waveform samples: seismic waveforms and noise waveforms without earthquake signals. The dataset comprises approximately 1.2 million time series, equivalent to over 19,000 h of recorded earthquake signals. These records cover seismic waveforms within a 350 km range. The earthquake events in the dataset encompass various scenarios, including urban, rural, underground, and mountainous terrains. Each earthquake event contains a wealth of seismic waveform data, including P-wave and S-wave types, with a duration of approximately 60 s. The release of the STEAD dataset provides a valuable data resource for researchers in seismology and earthquake engineering. The introduction of this dataset contributes to promoting the application of machine learning and artificial intelligence technologies in the field of seismology. By using the STEAD dataset, researchers can develop more accurate, faster, and more reliable seismic waveform recognition algorithms, offering enormous potential and value for the research and practice in the field of seismology.

3.2 Gansu dataset

We have collected waveform data from 47 seismograph stations in Gansu Province between 2009 and 2021, extracting earthquake signals with manual annotations at a sampling rate of 100 Hz. The distribution of the stations is shown in Figure 1. Each signal contains data from three components: east-west (E-W), north-south (N-S), and vertical (Z) directions.

FIGURE 1

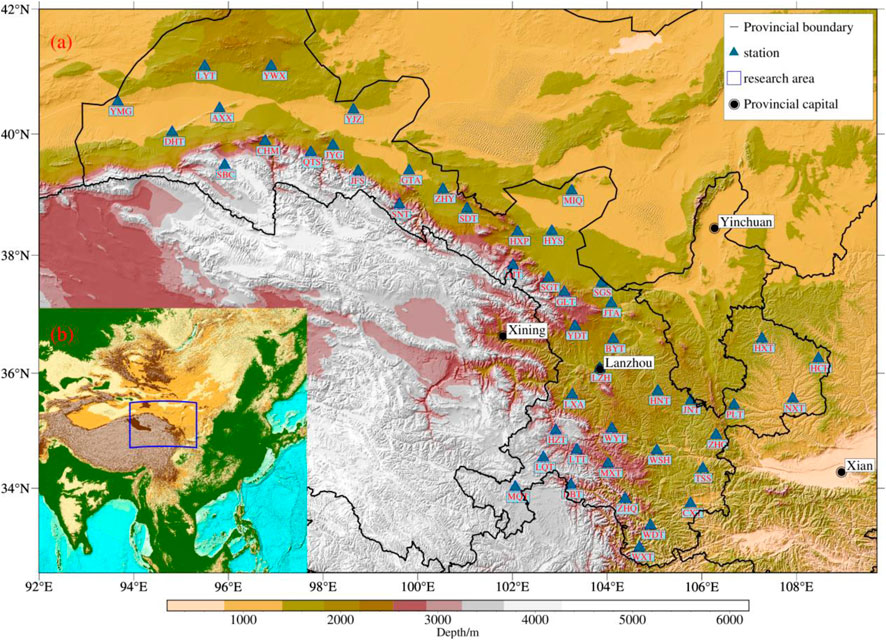
FIGURE 1. The geographical distribution map of the seismograph stations utilized in this study for the Gansu region delineates the specific locations of these earthquake monitoring stations. All stations are equipped with broadband seismometers, which are capable of capturing seismic oscillations across diverse frequency ranges, thereby facilitating effective monitoring and recording of seismic activity. The longitudinal span of the seismograph stations in the Gansu region is approximately 15°, while the latitudinal span is around 10°. The southeastern portion of the region exhibits a higher concentration of the region exhibits a higher concentration of stations due to demographic and economic factors. Subfigure (A) shows the spatial distribution of the stations, while Subfigure (B) shows the location of the large area where the research area is located.

The original format of the data was in mseed files. Based on the seismic phase reports produced by the Gansu seismograph station network, we selected records with both P-wave and S-wave arrivals, extracted from mseed files with a starting point of 10 s before the arrival of P-wave and 50 s after, totaling 60 s or 6,000 sampling points. Combining the data from the three components, the final data size is 1×3×6,000. However, not all data are as shown in Figure 2; some stations may be subject to various interferences, resulting in low signal-to-noise ratios and strong background noise. This kind of data can cause low detection rates in deep learning models, so it is necessary to filter out high-frequency and low-frequency noise interference. In this paper, we use detrending and bandpass filtering. Detrending centralizes the input data for all three components to zero, making it easier to fit and reducing the likelihood of gradient vanishing. We use a bandpass filter to filter the seismic waves, with a low-frequency cutoff of 1.0 Hz and a high-frequency cutoff of 45 Hz (Mousavi et al., 2020). In the end, we obtained a total of 283,467 records from 47 stations in Gansu Province between 2009 and 2021.

FIGURE 2

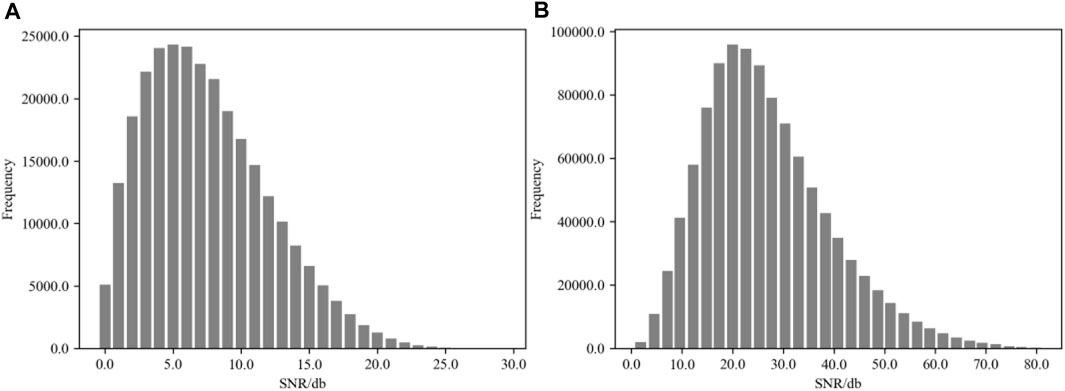
FIGURE 2. The signal-to-noise ratio distribution for the datasets employed in this study (on the left subfigure a is the statistical chart for the Gansu dataset, while on the right subfigure (A,B) lies the chart for the STEAD dataset. As can be discerned from the graphical representation, the STEAD dataset boasts an average signal-to-noise ratio of approximately 20, whereas the Gansu dataset exhibits a mean signal-to-noise ratio of around 5 dB).

3.3 Dataset comparison

We calculated the signal-to-noise ratios of the two datasets using a unified method, observing the distribution of signal-to-noise ratios in different datasets and finding that the average signal-to-noise ratio of the STEAD dataset is approximately four times that of the Gansu dataset, as shown in Figure 2.

4 Methodology

4.1 Introduction to EQTransformer

EQTransformer, proposed by Mousavi et al. (2020), is a multi-task neural network composed of a very deep encoder and three independent decoders. The network is implemented through structures such as 1D convolution, bidirectional and unidirectional long short-term memory (LSTM) networks, networks in networks (NiN), residual connections, feedforward layers, Transformers, and self-attention layers. The encoder processes the earthquake signals in the time domain, generating high-level representations and contextual information of their temporal dependencies. The decoders then use this information to map the high-level features to three probability sequences related to the presence of earthquake signals, P-wave seismic phases, and S-wave seismic phases at each time point.

In the self-attention model, the amount of memory increases with the length of the sequence. Therefore, they added a downsampling section consisting of convolution and max-pooling layers at the front end of the encoder. These downsampled features are transformed into high-level representations through a series of residual convolutions and LSTM blocks. The global attention section at the end of the encoder aims to guide the network to focus on parts related to the earthquake signals. These high-level features are then directly mapped to a probability vector representing the probability of earthquake signal presence (detection) using a decoder branch. The other two decoder branches are related to the P-wave seismic phases and S-wave seismic phases, with an LSTM/local attention unit placed at the beginning. This local attention will further guide the network to focus on the local features within the seismic phases related to each individual earthquake waveform. Residual connections within each block and techniques such as networks in networks help expand the depth of the network while maintaining error rates and training speeds under control.

The advantages of the network structure are mainly reflected in the following aspects: multi-task learning improves the generalization ability of the model; deep network structure (56 layers) helps capture complex temporal information; global and local attention mechanisms guide the network to focus on key parts; using residual connections, NiN, and other techniques to increase network depth without significantly increasing the number of parameters; the network has only about 372K trainable parameters, reducing the risk of overfitting.

4.2 Introduction to ECPickNet

Inspired by EQTransformer, the deep learning model network architecture in this paper adopts the Encoder-Decoder pattern and introduces the convolution-enhanced attention mechanism module (Conformer Block) and the residual shrinkage module RSBU-CS. The Conformer can better capture local relationships and long-distance dependencies in time series signals, thus better adapting to the characteristics of seismic wave signals. The deep residual shrinkage network was initially proposed for image denoising and image super-resolution tasks but was later applied to one-dimensional sequence data, such as speech signal denoising and electrocardiogram signal classification tasks (Guo et al., 2021).

The architecture of the model we designed (ECPickNet, abbreviated as EcP) is shown in Figure 3. Drawing inspiration from EQTransformer, we replace the stacked residual modules with three RSBU-CSs following the one-dimensional convolution. The output is then fed into two layers of bidirectional Long Short-Term Memory (LSTM) networks and subsequently into the Conformer block to obtain high-level information from the data. At this point, the encoding phase of the data is completed. The decoder section employs three decoding branches, similar to EQTransformer. For the task branch that requires arrival time picking, we add an additional LSTM (Hochreiter and Schmidhuber, 1997) and a Self Attention mechanism specific to arrival time picking (Vaswani et al., 2017), thus directing the network’s attention to specific tasks (e.g., P-wave and S-wave arrival time picking). The topmost branch in the three-branch design decodes high-level information about seismic events, outputting the probability of whether a seismic signal exists within a waveform segment. The middle and bottom branches are similar, with the decoder beginning with an LSTM and Self Attention mechanism to focus the network’s attention on local features related to the arrival time of seismic body waves, ultimately outputting the probability of each time point in the waveform being a P-wave or S-wave arrival time. This three-branch design not only enhances the decoder’s performance but also enables targeted secondary training for poorly performing branches.

FIGURE 3

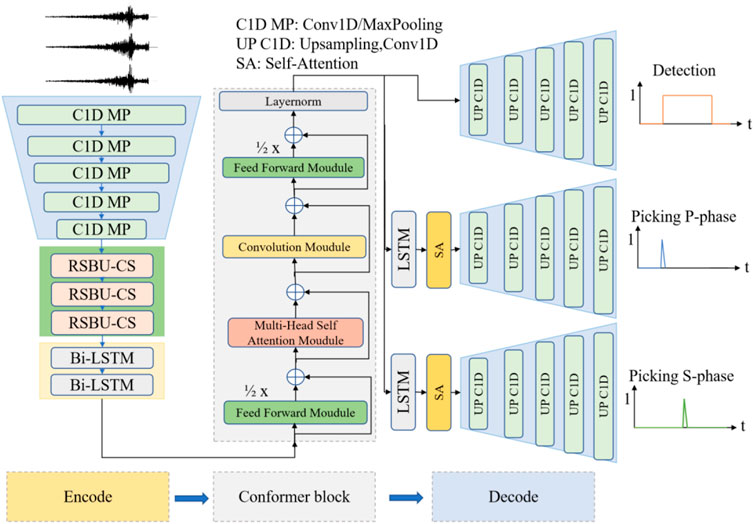
FIGURE 3. The architecture of the proposed ECPickNet model, wherein 60-s triaxial waveform data is directly inputted and subsequently subjected to encoding and decoding processes, ultimately yielding the classification of seismic events, along with the probabilistic arrival times of P-wave and S-wave phases.

5 Model training

5.1 Data augmentation

To improve the performance and generalization capabilities of the deep learning model, we use data augmentation methods to expand the dataset and increase the sample size. Within a 60-s time window, we increase the amount of data by randomly shifting valid seismic signals. We also randomly add Gaussian noise to the seismic signals at different ratios to increase the diversity of positive samples (Figure 4). The formula for adding Gaussian noise to seismic signals is as follows:

$S\left(\mathrm{y}\right)=s\left(y\right)+\mathrm{\alpha }*gauss\left(\mu ,{\sigma }^2\right)(1)$

FIGURE 4

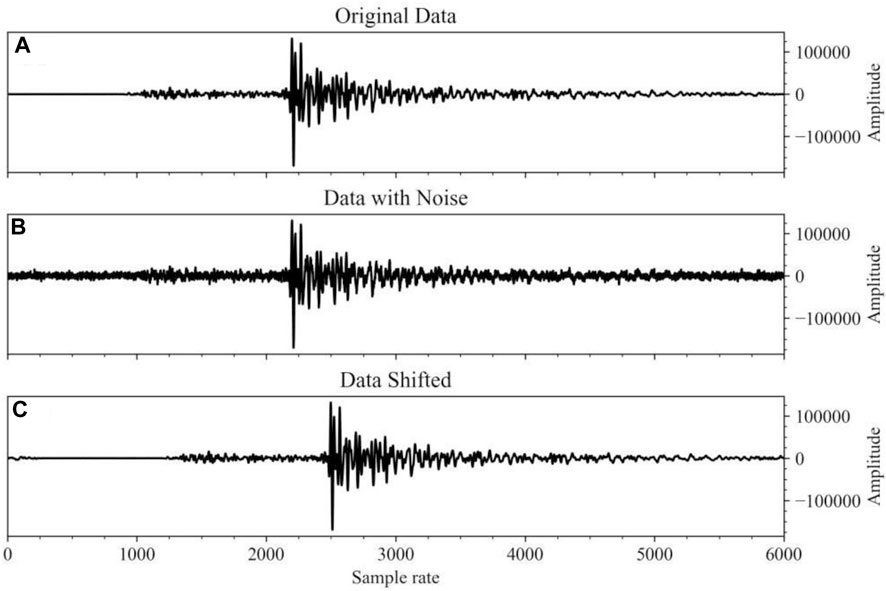
FIGURE 4. The original time series data and the results obtained through various data augmentation techniques are exhibited. Subfigure (A) portrays the original time series data, highlighting its intrinsic fluctuation patterns. Subfigure (B) demonstrates the enhanced data acquired by incorporating Gaussian noise into the original data. By calculating the noise amplitude based on the original data’s maximum value and generating a Gaussian noise set of commensurate amplitude and length, we were able to simulate real-world environmental factors that may impact the signal, thereby bolstering the model’s robustness to such influences. Subfigure (C) reveals the augmented data produced by performing time shifts on the original data. By displacing data points along the temporal axis, we emulated signal time offsets, enabling the model to discern analogous patterns at varying time instances. This method can assist the model in adapting to temporal variations of signals within practical scenarios.

In the equation, $s\left(y\right)$ represents the base seismic signal, $\mathrm{\alpha }$ is the ratio of added Gaussian noise, $\mu$ is the mean of the Gaussian distribution, and $\sigma$ is the standard deviation of the Gaussian distribution.

5.2 Loss function

For the output of each branch, we use the Binary Cross-Entropy $\text{Loss}$ function:

$\text{Loss}=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{y}_i*\log \left(p\left(y_i\right)\right)+\left(1-y_i\right)*\log \left(1-p\left(y_i\right)\right)(2)$

In this formula, $p\left(y_i\right)$ represents the probability that the signal is a seismic event at the current sampling point, and $N$ is the number of data samples. Similarly, as different branches have varying task complexities, we add weights to the cross-entropy loss for each branch. Thus, our final loss function ${\text{Loss}}_{\text{dps}}$ is:

${\text{Loss}}_{\text{dps}}=\mathrm{\alpha }*{loss}_d+\mathrm{\beta }*{loss}_p+\mathrm{\gamma }*{loss}_s(3)$

${\text{loss}}_{\mathrm{d}}$ represents the loss rate for event detection, ${\text{loss}}_{\mathrm{p}}$ for P-wave detection, and ${\text{loss}}_{\mathrm{s}}$ for S-wave detection. The fine-tuning selection of the weights remains fixed. Since the current network employs randomly initialized weights for training, our values $\mathrm{\alpha }、\mathrm{\beta }、\mathrm{\gamma }$ are 0.1, 0.4, and 0.5, respectively.

5.3 Optimizer

In this study, we use the Adam Optimizer to refine the model parameters. Adam (Adaptive Moment Estimation) is an adaptive learning rate optimization algorithm commonly utilized for training neural networks. This approach combines the advantages of Momentum optimization (Sutskever et al., 2013) and RMSProp optimization (Hinton et al., 2012), exhibiting the following characteristics:

Adaptive learning rate: The Adam algorithm employs an adaptive learning rate, enabling the automatic adjustment of learning rates according to each parameter’s gradient. This accelerates convergence and mitigates overfitting.

Momentum optimization: The Adam algorithm utilizes momentum to expedite the training process. Momentum aids the algorithm in striking a balance between stable regions and steep areas, reducing oscillations in gradient updates.

Adaptive regularization: The Adam algorithm estimates the second-order moment (i.e., variance) of the parameters by calculating the exponential moving average of the gradient squares, adapting the regularization term accordingly. This facilitates the handling of gradients at different scales, enhancing the model’s generalization capabilities.

In this study, we set the exponential moving average hyperparameter β1 for adjusting the first-order moment (i.e., gradient) to 0.9, and the exponential moving average hyperparameter β2 for adjusting the second-order moment (i.e., gradient square) to 0.99. To prevent division by zero in anti-shock calculations, ε is set to 10⁻⁸, and the initial learning rate is set to 0.001. The learning rate is dynamically adjusted when the model’s performance on the validation set plateaus or declines (Kingma and Ba, 2014).

5.4 Other parameter settings

The other parameter settings in this study are shown in Table 1. Based on the memory size of the device, we set the Batch Size to 128, resulting in an input data size of 128 × 3 × 6000 for the model. For the training data, in addition to standard filtering and mean removal operations, we perform standard normalization (with the Signal normalization mode set to ‘std’). For each channel’s data, we divide by the standard deviation of the corresponding channel’s data. Alternatively, one could use min-max normalization. However, this method may yield inadequate training assistance for the model when large amplitude seismic waves are contrasted with low amplitude background noise, causing arrival time values to approach 1 and the remaining sample data to approach 0. Consequently, we ultimately use standard normalization. For the P-wave and S-wave arrival time labels (Label type), we construct a Gaussian distribution near the arrival time point.

TABLE 1

TABLE 1. Parameter settings for the experiment (The parameter configurations were established following numerous experimental iterations).

5.5 Experimental configuration

In this study, we utilize Python 3.8 as the programming environment and conduct our research on a high-performance cluster server to ensure ample and reliable computing resources. This cluster server boasts formidable computing power, equipped with 64 processor cores and two NVIDIA A100 GPUs, allowing it to concurrently execute a vast number of computing tasks. The primary model development framework used for training is PyTorch-gpu 1.8.0, while seismic data processing is performed using the open-source Python library ObsPy (Beyreuther et al., 2010) and the convenient data processing library NumPy.

5.6 Comparison model selection

In order to verify the performance of our designed model, we have collected several other models and algorithms for earthquake event prediction and arrival time picking, and compared them on the STEAD dataset and Gansu dataset. These methods include: EQTransformer, PhaseNet (Zhu and Beroza, 2019), PickNet (Wang et al., 2019), Filter Picker (Baer and Kradolfer, 1987), GPD (Ross et al., 2018), and STA/LTA.

6 Experimental result

This study compares the performance of various models on different datasets, recording their $Precision$ (pr), $Recall$ (re), and $Error$ on different datasets.

Precision refers to the proportion of actual positive cases among all cases predicted as positive by the model, that is:

$Precision=\frac{TP}{TP+FP}(4)$

Where $TP$ represents true positive, $FP$ represents false positive, and $FN$ represents false negative. Recall is an indicator of classifier performance, typically used to evaluate the coverage capability of the classifier. It refers to the ratio of the number of samples correctly identified as positive by the classifier to the total number of actual positive samples. Recall is also known as true positive rate or sensitivity. The calculation method for recall is as follows:

$Recall=\frac{TP}{TP+FN}(5)$

The calculation formula for the custom evaluation metric, Error, is as follows:

$Error=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{X}_{pred}\left(i\right)-X_{true}\left(i\right)(6)$

In the formula, $X$ represents the signal vector, and $N$ represents the number of data points. The Error is calculated as the predicted arrival time minus the actual label arrival time, in units of one sampling point.

6.1 Comparison of experimental results on the STEAD dataset

According to Table 2, the performance of EqT and EcP on the STEAD dataset is close, both better than other network models. We compared the experimental results of this study with the original experimental results of EqT, and although there are slight differences in various data, considering that our training set and test set are randomly divided and we use a custom evaluation function, there may be some errors.

TABLE 2

TABLE 2. Performance of various model approaches on the STEAD test dataset (A negative value of Error indicates that the predicted seismic phase arrival time is later than the actual arrival time).

From the experimental results, it can be concluded that EqT and EcP both show good performance on the STEAD dataset, higher than other methods. However, according to the traditional STA/LTA detection results, the earthquake signal characteristics of the STEAD dataset are relatively obvious, with a high signal-to-noise ratio, so most deep learning models have achieved good results on this dataset. The EcP model proposed in this paper is basically consistent with EqT in terms of precision and recall, but has a lower Error value compared to EqT. Since the STEAD dataset can only reflect part of the model’s capabilities, in order to verify the applicability of the EcP model on other datasets, we also conducted the same test experiment on the Gansu dataset.

6.2 Gansu dataset experimental result comparison

In Table 3, the accuracy of traditional STA/LTA method for detecting earthquake events significantly decreases compared to the STEAD dataset, indicating the complexity and difficulty in discerning the Gansu dataset. As can be seen from Table 3, EcP applied to the Gansu dataset outperforms other models in terms of earthquake detection and arrival time picking capabilities. In earthquake detection, the precision of EcP is on par with EqT, but it is 3% higher in identifying earthquake events. In picking P-wave arrival times, the accuracy of EcP is comparable to other methods, with a recall rate 1% higher than EQCCT and PhaseNet, and the lowest prediction Error of -9.11 sample points. In picking S-wave arrival times, EcP has a recall rate 3% higher than EQCCT, 14% higher than EqT and 4% higher than PhaseNet, with the lowest average Error of 18.7 for EQCCT and -29.6 for EcP, just behind EqT with has an error of 23.4. It is worth noting that PhaseNet has great potential in picking P-wave and S-wave arrival times. Its pre-trained model can still perform well when directly detecting the Gansu dataset test set, which may be related to the network model structure and the dataset used for training. Since this paper mainly discusses the performance comparison between EqT and EcP, we will not discuss the gap between PhaseNet and EcP models in detail here.

TABLE 3

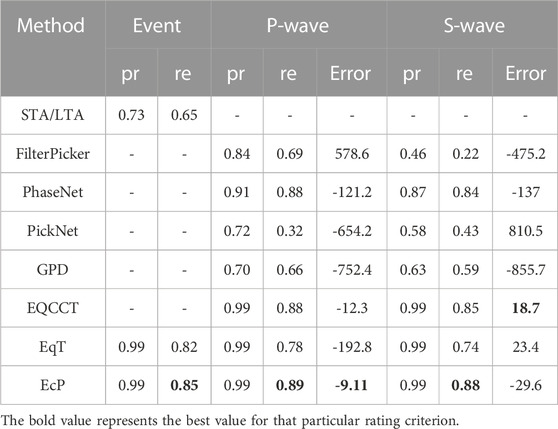
TABLE 3. Performance of various earthquake detection model approaches on the Gansu region test dataset (A negative value of Error indicates that the predicted seismic phase arrival time is later than the actual arrival time).

6.3 Signal SNR stress test

Our results have shed light on the performance of our model under various circumstances, allowing us to further investigate the application of our model. To do this, we classified data sets according to SNR in increments of 5, ranging from 0 to 5 SNR to 5–10 SNR. Using the average precision of P-phase and S-phase predictions, we evaluate and contrast. Our model’s accuracy in the first 0–5 SNR range was 0.75, showing that there is still potential for improvement in handling circumstances with extremely low signal clarity. Then, with an accuracy of 0.92, we noticed a substantial improvement in the 5–10 SNR range. Despite these improvements, there is still room for improvement in how well our model performs when the SNR is below 10.

The performance of our model in comparison to other models, especially the EQCCT model, provided insightful information. While our model demonstrated a similar performance with an accuracy of 0.75 in the 0–5 SNR range, the EQCCT model displayed a similar performance with an accuracy of 0.71. However, our model beat the EQCCT model with an accuracy of 0.92 compared to 0.88 in the 5–10 SNR range. These findings highlight the need for additional model improvement, especially in tackling the difficult situations brought on by SNR levels below 10. To increase the model’s robustness in low SNR settings, methods like improved feature extraction, sophisticated noise reduction techniques, or model parameter modification may be investigated. As a result, this analysis highlights the model’s potential for development in managing lower SNR situations as well as its competitive performance when compared to other models, opening the door for more successful earthquake detection in difficult environments.

7 Discussion

The processing and identification of seismic data and phases are focal points in the field of seismological research. Generally, the seismic data processing workflow consists of earthquake detection, arrival time picking, phase correlation, earthquake localization, and magnitude calculation, ultimately generating an earthquake catalog.

In this study, we compared the detection results of the earthquake signal detection model EcP on different datasets with other models. Overall, our proposed model has certain advantages, especially in low signal-to-noise ratio events similar to those in Gansu region, where our model achieved superior results. We believe this is mainly due to the Conformer and RSBU-CS modules used in the network. The Transformer structure itself has achieved remarkable results in the field of natural language processing, and its self-attention mechanism can capture long-distance dependencies in sequences. The convolution-enhanced Conformer, on the other hand, adds a convolutional layer to the original Transformer. Convolutional layers exhibit superior performance in local feature extraction (Gulati et al., 2020), enabling ECPickNet to fully capture the spatiotemporal correlation in earthquake signals, thereby improving detection accuracy. The RSBU-CS module is an important component of ECPickNet. By introducing channel attention mechanism, this module can adaptively adjust the weights of different channels, thereby strengthening earthquake-related features and suppressing noise. This is of great significance for low signal-to-noise ratio earthquake event detection, as noise has a particularly significant impact on detection results in such cases. The ECPickNet model combines the convolution-enhanced Transformer structure and RSBU-CS module, giving the model good robustness. Even in low signal-to-noise ratio situations, the model can still effectively identify and extract earthquake signal features, avoiding misdetection or omission caused by noise interference. ECPickNet adopts an end-to-end training strategy, allowing the entire model to learn earthquake signal representation and classification in one go. This enables the model to better capture the relationship between earthquake signals and phases, thus improving detection accuracy.

In order to gain a more intuitive understanding of the model’s detection performance, we visualize typical cases in the detection results and then conduct detailed analysis and discussion on these results. The visualization results are shown in Figure 5, where each subplot shows the three-channel earthquake signals in the first three waveform charts, and the probability curves for earthquake detection (Event) and phase picking (P-wave and S-wave) in the fourth chart. As shown in Figure 5, in Figures A and B, the model identifies the earthquake events but fails to pick the arrival times of P and S waves well (i.e., not exceeding our set threshold of 0.5), representing types of earthquake signals with partially poor recognition performance. In Figures C and D, the model misses the two earthquake events, representing types of earthquake signals with partial omissions; Figure C is a relatively obvious earthquake event, but the interval between P and S waves is very small, which may be due to the lack of similar signals in the STEAD dataset, causing the model to miss the event due to insufficient learned knowledge; Figure D represents a low signal-to-noise ratio earthquake signal, with an inconspicuous P-wave arrival time almost indistinguishable from background noise, and a heavily noise-disturbed S-wave arrival time. In Figures E and F, the model correctly identifies the two earthquake signals, representing types of earthquake signals with partially correct identification; Figure F is a near-earthquake event, while Figure E is a slightly more distant earthquake, as the arrival times of P and S waves differ more in the waveform due to their different speeds, indicating a greater distance between the source and the station. From the negative detection results, there is still much room for improvement in the model, which we believe is mainly due to the insufficient sample size of the training data; earthquake signals are high-dimensional non-linear data, and the sample size of the STEAD dataset has not reached the level required to train a model that approaches or even surpasses manual analysis.

FIGURE 5

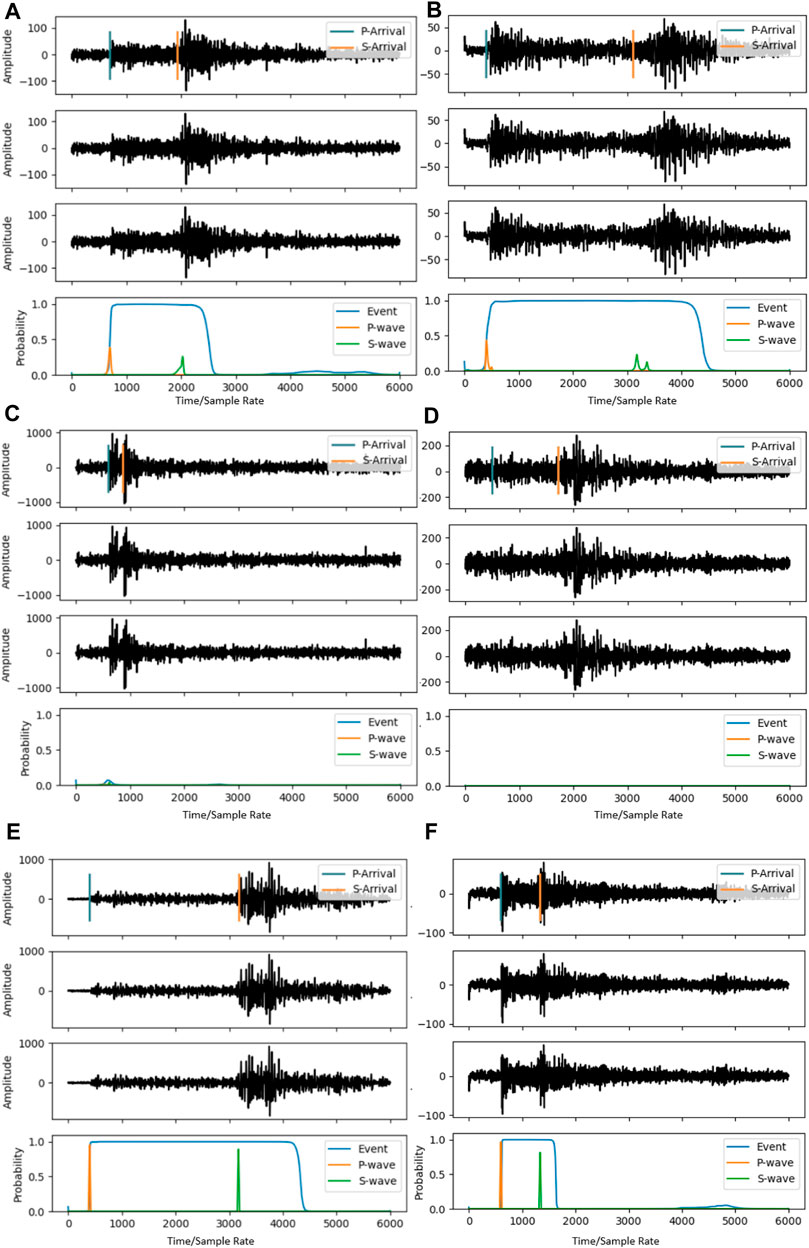
FIGURE 5. Detection and picking results of EcP on a subset of Gansu data (The vertical lines denoting the arrival times of P-waves and S-waves represent the manually annotated results. Subfigures (A) and (B) depict scenarios in which the seismic event identification is accurate, but the P-wave and S-wave phase recognition is not. Subfigures (C) and (D), on the other hand, represent cases where both the seismic event identification and the P-wave and S-wave phase recognition are inaccurate. Lastly, subfigures (E) and (F) exemplify instances in which the identification of the seismic event and the recognition of P-wave and S-wave phases are all precisely discerned).

In the future, several research directions can be pursued to address the limitations and further improve the performance of deep learning models for earthquake detection. Firstly, developing advanced data augmentation techniques and generating synthetic seismic data will help increase the quantity and diversity of training data, thereby enhancing the robustness and generalization capabilities of deep learning models. Secondly, investigating the use of transfer learning and domain adaptation techniques can help build models that are more adaptable to different regional seismic characteristics and variations in waveform features caused by instrumental factors. Additionally, incorporating data standardization methods will ensure that deep learning models are trained on consistent, comparable data, reducing the impact of variability in seismic data and improving model performance. Finally, developing explainable Artificial Intelligence (AI) methodologies and incorporating uncertainty quantification techniques can help improve the interpretability and reliability of deep learning models for earthquake detection, making them more acceptable to the seismology community. By pursuing these research directions, we can continue to advance the capabilities of deep learning models in the field of earthquake detection and hazard assessment.

8 Conclusion

In this paper, we propose a new deep learning method, ECPickNet, based on convolution-enhanced Conformer, to enhance earthquake detection and phase picking performance. Additionally, we introduce various parameter configurations for model training and conduct comparative experiments with several similar methods, yielding the following key findings:

We refer to the EQTransformer model in the model architecture and improve upon it by incorporating the convolution-enhanced Transformer and introducing the RSBU-CS module. And through extensive experimental validation and screening, we were able to get optimum parameter combinations, ensuring the precision of model training. In order to fully assess the performance of our model, we compare it to a number of sophisticated models, displaying its potential. Additionally, the EcP suggested in this research outperforms other deep learning model approaches in terms of performance on the STEAD dataset, performing on par with EqT.The EcP model exhibits significant benefits on the Gansu dataset with a lower signal-to-noise ratio, demonstrating its greater applicability in low signal-to-noise ratio data. Through experiments conducted on two datasets, it has been unequivocally demonstrated that our approach outperforms others in terms of comprehensive performance in earthquake detection and onset picking, and it has been verified that our method ECPickNet possesses a higher capability to handle low signal-to-noise ratio data compared to existing methods. Albeit the proposed EcP model exhibits a certain advantage in regions with low signal-to-noise ratios, there remains a considerable gap between it and manual earthquake signal detection, rendering it difficult to supplant human labor at this stage. As computer hardware advances and the volume of seismic data burgeons, the capacity of deep learning models will continue to augment, paving the way for future exploration of more precise deep learning detection models.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

SW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Methodology, Writing–original draft. FL: Conceptualization, Data curation, Methodology, Project administration, Supervision, Writing–original draft, Writing–review and editing. X-xY: Conceptualization, Data curation, Methodology, Project administration, Writing–review and editing. KC: Data curation, Formal Analysis, Software, Writing–original draft. RC: Data curation, Formal Analysis, Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the science and technology development fund of Gansu Seismological Bureau (2021Y04), the science and technology plan of Gansu Province (21JR7RA795, 21JR7RA790, and 23YFFA0015) are jointly funded and also supported by the Fundamental Research Funds for the Central Universities.

Conflict of interest

Author RC was employed by Chengdu Surveying Geotechnical Research Institute Co, Ltd of MCC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, R. (1978). Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 68, 1521–1532. doi:10.1785/bssa0680051521

CrossRef Full Text | Google Scholar

Baer, M., and Kradolfer, U. (1987). An automatic phase picker for local and teleseismic events. Bull. Seismol. Soc. Am. 77 (4), 1437–1445. doi:10.1785/bssa0770041437

CrossRef Full Text | Google Scholar

Beyreuther, M., Barsch, R., Krischer, L., Megies, T., Behr, Y., and Wassermann, J. (2010). ObsPy: a Python toolbox for seismology. Seismol. Res. Lett. 81 (3), 530–533. doi:10.1785/gssrl.81.3.530

CrossRef Full Text | Google Scholar

Chai, C., Maceira, M., Santos Villalobos, H. J., Venkatakrishnan, S. V., Schoenball, M., Zhu, W., et al. EGS Collab Team (2020). Using a deep neural network and transfer learning to bridge scales for seismic phase picking. Geophys. Res. Lett. 47 (16), e2020GL088651. doi:10.1029/2020gl088651

CrossRef Full Text | Google Scholar

Chollet, F. (2017). “Xception: deep learning with depthwise separable convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1251–1258.

CrossRef Full Text | Google Scholar

Gulati, A., Qin, J., Chiu, C. C., Parmar, N., Zhang, Y., Yu, J., et al. (2020). Conformer: convolution-augmented transformer for speech recognition. arXiv preprint arXiv:2005.08100.

Google Scholar

Guo, P., Boyer, F., Chang, X., Hayashi, T., Higuchi, Y., Inaguma, H., et al. (2021). “Recent developments on espnet toolkit boosted by conformer,” in ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), 5874–5878.

CrossRef Full Text | Google Scholar

Hinton, G., Srivastava, N., and Swersky, K. (2012). Neural networks for machine learning lecture 6a overview of mini-batch gradient descent, 2. Cited on, 14.8

Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, C., Fang, L., Fan, L., and Li, B. (2021). Comparison of the earthquake detection abilities of PhaseNet and EQTransformer with the Yangbi and Maduo earthquakes. Earthq. Sci. 34 (5), 425–435. doi:10.29382/eqs-2021-0038

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: a method for stochastic optimization. arXiv preprint arXiv:14126980, 2014.

Google Scholar

Liao, S. R., Zhang, H. C., Fan, L. P., Li, B. R., Huang, L. Z., Fang, L. H., et al. (2021). Development of a real-time intelligent seismic processing system and its application in the 2021 Yunnan Yangbi MS6.4 earthquake. Chin. J. Geophys. (in Chinese) 64 (10), 3632–3645. doi:10.6038/cjg2021O0532

CrossRef Full Text | Google Scholar

Mousavi, S. M., Ellsworth, W. L., Zhu, W., Chuang, L. Y., and Beroza, G. C. (2020). Earthquake transformer—an attentive deep-learning model for simultaneous earthquake detection and phase picking. Nature communications 11 (1), 3952. doi:10.1038/s41467-020-17591-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Mousavi, S. M., Sheng, Y., Zhu, W., and Beroza, G. C. (2019). STanford EArthquake dataset (STEAD): a global data set of seismic signals for AI. IEEE Access 7, 179464–179476. doi:10.1109/ACCESS.2019.2947848

CrossRef Full Text | Google Scholar

Ross, Z. E., Meier, M. A., Hauksson, E., and Heaton, T. H. (2018). Generalized seismic phase detection with deep learning. Bulletin of the Seismological Society of America 108 (5A), 2894–2901. doi:10.1785/0120180080

CrossRef Full Text | Google Scholar

Saad, O. M., Chen, Y., Siervo, D., Zhang, F., Savvaidis, A., Huang, G. C. D., et al. (2023). EQCCT: a production-ready EarthQuake detection and phase picking method using the Compact Convolutional Transformer. IEEE Transactions on Geoscience and Remote Sensing 61, 1–15. doi:10.1109/tgrs.2023.3319440

CrossRef Full Text | Google Scholar

Sabbione, J. I., and Velis, D. (2010). Automatic first-breaks picking: new strategies and algorithms. Geophysics 75 (4), V67–V76. doi:10.1190/1.3463703

CrossRef Full Text | Google Scholar

Su, J. B., Liu, M., Zhang, Y. P., Wang, W. T., Li, H. Y., Yang, J., et al. (2021). High resolution earthquake catalog building for the 21 May 2021 Yangbi, Yunnan, MS6.4 earthquake sequence using deep-learning phase picker. Chinese Journal of Geophysics (in Chinese) 64 (8), 2647–2656. doi:10.6038/cjg2021O0530

CrossRef Full Text | Google Scholar

Sutskever, I., Martens, J., Dahl, G., and Hinton, G. (2013). “On the importance of initialization and momentum in deep learning,” in International conference on machine learning (PMLR), 1139–1147.

Google Scholar

Takanami, T., and Kitagawa, G. (1991). Estimation of the arrival times of seismic waves by multivariate time series model. Annals of the Institute of Statistical mathematics 43 (3), 407–433. doi:10.1007/bf00053364

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Advances in neural information processing systems 30.

Google Scholar

Wang, J., Xiao, Z., Liu, C., Zhao, D., and Yao, Z. (2019). Deep learning for picking seismic arrival times. Journal of Geophysical Research Solid Earth 124 (7), 6612–6624. doi:10.1029/2019jb017536

CrossRef Full Text | Google Scholar

Wu, X., Huang, S., Xiao, Z., and Wang, Y. (2022). Building precise local submarine earthquake catalogs via a deep-learning-empowered workflow and its application to the challenger deep. Frontiers in Earth Science 10, 34. doi:10.3389/feart.2022.817551

CrossRef Full Text | Google Scholar

Xiao, Z., Wang, J., Liu, C., Li, J., Zhao, L., and Yao, Z. (2021). Siamese earthquake transformer: a pair-input deep-learning model for earthquake detection and phase picking on a seismic array. J. Geophys. Res. Solid Earth 126, 1–15. doi:10.1029/2020JB021444

CrossRef Full Text | Google Scholar

Yin, X., Liu, F., Cai, R., Yang, X., Zhang, X., Ning, M., et al. (2022). Research on seismic signal analysis based on machine learning. Applied Sciences 12 (16), 8389. doi:10.3390/app12168389

CrossRef Full Text | Google Scholar

Yin, X., Yang, X., Cai, R., Wang, Z., Ju, P., Wang, W., et al. (2022). Accuracy analysis of automatic seismic signal processing method based on PhaseNet. Journal of Geodesy and Geodynamics(in Chinese) 42 (8), 870–873. doi:10.14075/j.jgg.2022.08.018

CrossRef Full Text | Google Scholar

Yung, S. K., and Ikelle, L. T. (1997). An example of seismic time picking by third-order bicoherence. Geophysics 62 (6), 1947–1952. doi:10.1190/1.1444295

CrossRef Full Text | Google Scholar

Zhao, M., Tang, L., Shi, C., Su, J. R., and Zhang, M. (2021). Machine learning based automatic foreshock catalog building for the 2019 M_S6.0 Changning, Sichuan earthquake. Chinese Journal of Geophysics (in Chinese) 64 (1), 54–66. doi:10.6038/cjg2021O0271

CrossRef Full Text | Google Scholar

Zhao, M., Xiao, Z., Chen, S., and Fang, L. (2022). Diting: a large-scale Chinese seismic benchmark dataset for artificial intelligence in seismology. Earthquake Science 35, 1–11. doi:10.1016/j.eqs.2022.01.022

CrossRef Full Text | Google Scholar

Zhu, W., and Beroza, G. C. (2019). PhaseNet: a deep-neural-network-based seismic arrival-time picking method. Geophysical Journal International 216 (1), 261–273. doi:10.1093/gji/ggy423

CrossRef Full Text | Google Scholar