Occurrence conditions of the reverse rotation of rockfall and its influence on the restitution coefficient

When rockfall occurs along dense rock slopes, the rotation direction of rockfall is not always downhill. Specifically, the rockfall may obtain a reverse rotation speed (RRS) after impact under certain conditions, the effect of which on the restitution coefficient (RC) cannot be ignored. According to the statistical results of the reverse rotation (RR) phenomena of blocks obtained from previous experiments, the occurrence of RR is correlated to the block shape, incident angle, and contact attitude. In this study, considering a typically shaped cubic block, the critical condition for the RR is preliminarily deduced. Based on the results, the influence of the RRS on the RC for four typically shaped blocks is examined using a customized device. Results show that the tangential RC (R_t) values of each block are not sensitive to the change in the RRS, the distribution is relatively concentrated and the values are high. Moreover, the normal RC (R_n) values are not sensitive to the RRS, and the distribution is relatively discrete. The RRS influences R_n; however, it is difficult to directly establish the relationship between them. To this end, considering the contact attitude and shape of the block, an integral variable, the impact coefficient (I_c), is proposed to determine the influence of RRS on R_n. Moreover, the impact-bounce behaviours of the block are categorized and analysed. For the block rebound following a single impact, I_c and R_n are positively and negatively correlated when the mass centre of the block (MC) is in front and behind the contact point (CP), respectively. For the block rebound following two successive impacts, with the increase in I_c, the R_n increases. These conclusions help clarify the mechanism of the influence of the RRS on RC and provide vital information and ideas for the development and optimization of a program to accurately predict rockfall trajectories.

1 Introduction

Rockfall is a geological hazard that frequently occurs in mountainous and canyon regions. It is characterized by its suddenness, strong randomness, and high energy, posing a serious threat to surrounding infrastructure, personnel, and vehicle safety (Guccione et al., 2021; Chen et al., 2023; Noël et al., 2023; Wang et al., 2023). Particularly in areas with developed structural planes on slopes, incidents such as planar sliding, rotational failure, toppling failure, and wedge failure often occur, forming hazardous rock masses (Azarafza et al., 2020; Azarafza et al., 2021; Nanehkaran et al., 2022). These masses are prone to instability due to factors such as rain erosion, vehicle vibrations, blasting, earthquakes, animal activity, and root splitting, eventually leading to downhill rolling (Hu et al., 2018).

During the downhill movement of rockfalls along a slope, they not only possess a certain translational velocity but often come with a certain initial rotational speed. (Ritchie, 1963; Ujihira et al., 1993; Azzoni and Freitas, 1995; Basson, 2012; Giacomini et al., 2012; Asteriou, 2019; Dattola et al., 2021). When the rockfalls impact the slope, a significant transformation occurs between translation and rotational energies, which directly affecting the restitution coefficient (RC) and the rockfall trajectory (Chau et al., 2002; Basson, 2012; Buzzi et al., 2012; Spadari et al., 2012; Vijayakumar et al., 2012; Nishimura et al., 2014; Preh et al., 2015; Ji et al., 2019; Lu et al., 2021; Tang et al., 2021). Hence, exploring the effect of rotational speed on the RC of rockfall holds great significance.

The influence of the rotational speed (RS) on RC has been examined through indoor and on-site tests, and many important conclusions have been obtained. Through a series of on-site rockfall tests, Spadari et al. (2012) estimated the RS of a block by evaluating the rotation of the block about an axis and noted that the normal restitution coefficient (Rn) and tangential restitution coefficient (Rt) were insensitive to the changes in the RS. Dong and Moys (2006) conducted indoor impact tests between a steel ball without or with a pre-impact spin and a steel flat surface. The results demonstrated a modest influence of the initial rotation on R_n. Moreover, the R_n values approached 0.90 ± 0.035 in various situations. Giacomini et al. (2010) used irregular basalt blocks with a volume from 0.01 to 0.06 m³ to impact the natural slope covered with low grass. Results showed that the rotation of the test block influenced R_n, and R_n increased with the increase in the ratio of the rotational energy to the translational energy. Buzzi et al. (2012) designed an apparatus to spin blocks of different shapes and release them to impact a landing surface. The authors noted that R_n tended to increase with the rotational speed for pentagonal and square blocks; however, no clear influence of the rotational speed on R_n for round blocks was observed. Furthermore, the rotational speed influenced R_t for the three types of blocks, and a higher rotational speed corresponded to a higher R_t. Asteriou (2019) applied different angular velocities to sandstone blocks with diameters of 2.9, 4.0 and 4.3 cm and then released them to impact the flat surface of the same material. The results indicated that R_n and R_t were not sensitive to the change in the angular velocity, and their values were similar. Ji et al. (2019) used a hand-held adjustable speed motor to apply various RSs to a marble ball and released the ball to impact a slope of the same material. The authors noted that the RS considerably influenced R_t, and R_t increased linearly with increasing RS. In contrast, the effect of the RS on R_n was not significant.

In the existing studies on the influence of the RS on the RC, only the case in which the rotation of the block is in the downhill direction (i.e., forward rotation) is considered (Figure 1A), while the reverse rotation (RR) (uphill direction, Figure 1B) of the block is often ignored (Spadari et al., 2012; Dattola et al., 2021; Tang et al., 2021; Chen et al., 2023). It seems that this situation does not exist in general cognition; however, in our recent experimental studies on the RC, we have observed the frequent occurrence of this phenomenon (Ji et al., 2019; Ji et al., 2021). In particular, for specially shaped blocks with initial rotational speeds (such as cuboids, cubes, and cylinders), the probability of the blocks obtaining the reverse rotation speeds after impacting a dense rock slope is approximately 25% based on the team’s comprehensive analysis and statistics regarding the process images of more than 1000 groups of impact tests of non-spherical blocks (including tests with and without an initial rotational speed) (Table 1 presents some experimental data). These speeds correspond to the initial motion conditions of the blocks at the subsequent impact and directly affect the RC and rockfall trajectory. In this scenario, the accurate prediction and prevention of rockfall disasters become challenging. Furthermore, in actual rockfall events, non-spherical rockfalls are also commonly observed, and they often exhibit significant rotational speeds during their downhill motion along slopes (Dattola et al., 2021). With the extensive construction of transportation infrastructure in mountainous areas in recent years, numerous exposed rock slopes have been formed, providing favorable conditions for the occurrence of rockfall RR after impact. However, due to the suddenness and stealthiness of rockfall events, it is often challenging to obtain effective records of this phenomenon. Currently, there is a lack of attention given to this issue, which greatly hinders the complete understanding of rockfall dynamics. Therefore, it has an indescribable significance to systematically investigate the conditions for the occurrence of rockfall RR and the effect of the RRS on the RC in order to improve the deficiencies in predicting impact motion behavior and enhance the accuracy of predicting the dynamic processes of rockfall on slopes.

FIGURE 1

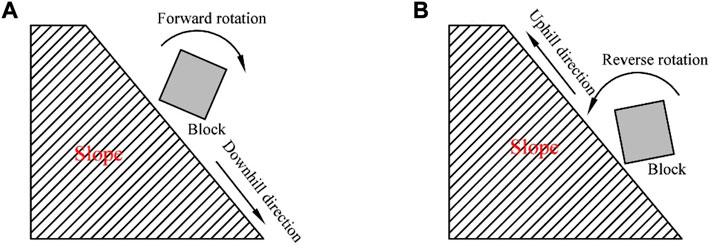
FIGURE 1. Two types of rotations that occur during the movement of a block along a slope [(A): forward rotation; (B) reverse rotation].

TABLE 1

TABLE 1. Summary of the initial conditions for the RR of the blocks after impacts.

In this study, first, considering the statistical results of the RR phenomena obtained in previous indoor tests, the conditions for the RR of blocks were preliminarily analysed and deduced. Next, four typically shaped blocks were machined, and impact tests between each block and the slope under different RRSs were conducted by using a customized device. Finally, the influence mechanism of the RRS on the RC was discussed based on the impact dynamics theory, and the relationships between them were established. The objective of this research is to clarify the criteria for the occurrence of rockfall RR and the control mechanism of RRS on the RC, addressing the deficiencies in understanding the characteristics of rockfall impact motion, thereby providing a scientific reference for accurately predicting slope rockfall trajectories and developing effective disaster mitigation measures.

2 Conditions for the occurrence of RR of blocks

2.1 RR of blocks observed in previous experiments

Before this research, tests were conducted to examine the influence of the multifactor interaction on R_n and the influence of the forward rotation speed (FRS) on the RC. Results indicated that the blocks often rotate in reverse after impacts, which is the motivation for this research. The statistics of the initial conditions for the RR of the blocks in the previous tests are shown in Table 1.

According to Table 1, the possibility of a block rotating in reverse after impact is closely related to the block shape, incident angle (θ), and contact attitudes (the mass centre is in front or behind the contact point (F or B) at the first impact, and the degree of contact angle (α)), while it is relatively insensitive to the changes in the block size, initial rotational speed (ω), incident velocity (V) and hardness of the block and slope (SHV1/2). Although blocks with many shapes are used in the tests, RR phenomena mainly occur in the non-normal impact tests of cubic, cuboidal, cylindrical and disc-shaped blocks with slopes. Compared with blocks of other shapes, blocks with the abovementioned shapes have a common feature, i.e., the impact moments when the blocks contact the slope are often large. Moreover, RR phenomena are likely to occur under impact conditions involving a large incident angle. In terms of the contact attitudes of the block, frame-by-frame analysis of the images of each impact test indicates that the RR of the block mainly occurs in the condition in which the mass centre of the block is behind the contact point (B) at the moment of impact (Table 1), and the occurrence possibility is lower when the mass centre is in front of the contact point (F). The professional image analysis tool Tracker V2.0 (developed by Hefei Jun Da High-tech Information Technology Co., Ltd.) is used to measure the contact angles (α) between the blocks and slope under various working conditions, as indicated in Table 1. Under condition B, α of the cubic and cube-like blocks varies in the range 45.05°–75°. Moreover, α for the cuboidal blocks and disc-shaped blocks varies in the ranges 47°–76° and 34°–66.9°, respectively. Under condition F, α of the cylindrical, disc-shaped, rectangular parallelepiped, and cube-like blocks is 34°–66.8°, 34°–56°, 32°, and 52.22°, respectively. Compared with that in the former condition, α varies in a narrower range in the latter condition.

2.2 Preliminary analysis of the occurrence conditions for the RR of the block

The occurrence conditions of the RR of the blocks have been derived based on limited tests, which cannot completely cover all the scenarios involving the RR of the blocks. Consequently, the obtained conclusions also have relative limitations. Moreover, it is impossible to perform tests covering all cases owing to implementation challenges. Considering these aspects, this study considers the example of a typically shaped cubic block (Figure 2) and uses the theoretical derivation method to preliminarily analyse and discuss the occurrence conditions of RR.

FIGURE 2

FIGURE 2. Impact diagram of cube-shaped block under condition B.

The kinetic energy of the block before and after impact can be expressed as:

$\frac{1}{2}m\left({V_{x0}}^2+{V_{y0}}^2\right)+\frac{1}{2}J{{\omega }_0}^2=\frac{1}{2}m\left({V_{x1}}^2+{V_{y1}}^2\right)+\frac{1}{2}J{{\omega }_1}^2+\mathit{\Delta }E(1)$

where m is the mass of the block; V_x0 and V_x1 are the tangential velocity components before and after impact, respectively; V_y0 and V_y1 are the normal velocity components before and after impact, respectively; J is the moment of inertia of the block around the mass centre; ω₀ and ω₁ are the angular velocities of the block before and after impact, respectively; and $\Delta E$ is the energy dissipated.

In the relevant tests, the R_t values of angular blocks with RS are stable in a relatively small range, and approach one (refer to the results obtained in the experiment of Spadari et al. (2012) and the following test results). Therefore, it can be assumed that the tangential velocity does not change before and after impact. If $V_{x0}=V_{x1}$, Eq. 1 can be simplified as follows:

$\frac{1}{2}m{V_{y0}}^2+\frac{1}{2}J{{\omega }_0}^2=\frac{1}{2}m{V_{y1}}^2+\frac{1}{2}J{{\omega }_1}^2+\mathit{\Delta }E(2)$

The normal momentum is conserved, and if the direction of $V_{y1}$ remains downwards,

$m\left(V_{y0}-V_{y1}\right)=I_n(3)$

where I_n is the normal impulse.

The impulse moment equation is

$J\left({\omega }_0+{\omega }_1\right)=I_n\cdot d(4)$

where d is the arm of force.

It is considered that the block has been rotated in the reverse direction, and the following analysis only needs to prove that ω₁ is a positive value. The result of simultaneous Eqs 3, 4 is as follows:

${\omega }_1=\frac{m}{J}\left(V_{y0}-V_{y1}\right)\cdot d-{\omega }_0(5)$

To satisfy ${\omega }_1\ge 0$,

$\frac{m}{J}\left(V_{y0}-V_{y1}\right)\cdot d-{\omega }_0\ge 0(6)$

According to Figure 2, we calculate $d=\frac{\sqrt{2}}{2}a\cos \alpha$, $J=\frac{1}{6}m{a}^2$ in Eqs 4–6 (a is the side length of the cube) and substitute the values of d and J into Eq. 6 to obtain

$\cos \alpha \ge \frac{{\omega }_0\cdot a}{3\sqrt{2}\left(V_{y0}-V_{y1}\right)}(7)$

Equation 7 is discussed considering three cases: case (1): If V_y1=0, $\cos \alpha \ge \frac{{\omega }_0\cdot a}{3\sqrt{2}{V}_{y0}}=kk$, that is, the reverse rotation occurs when $\alpha \le \arccos \left(kk\right)=\theta$ (kk and θ are the critical cosine and critical angle in this case, respectively); case (2): If the direction of V_y1 is still downwards and its value is positive, $\frac{{\omega }_0\cdot a}{3\sqrt{2}\left(V_{y0}-V_{y1}\right)}>kk$, that is, the reverse rotation occurs when $\alpha \le \arccos \left(\frac{{\omega }_0\cdot a}{3\sqrt{2}\left(V_{y0}-V_{y1}\right)}\right)=\beta <\theta$ (β is the critical angle in this case); and case (3): If the direction of V_y1 is upwards and negative, $\frac{{\omega }_0\cdot a}{3\sqrt{2}\left(V_{y0}-V_{y1}\right)}<kk$, that is, the reverse rotation occurs when $\alpha \le \arccos \left(\frac{{\omega }_0\cdot a}{3\sqrt{2}\left(V_{y0}-V_{y1}\right)}\right)=\varphi \ge \theta$ (φ is the critical angle in this case).

However, the direction of V_y1 (upwards or downwards) must be further analysed. In the critical case, (i.e., the reverse angular velocity ω₁ approaches zero), Eq. 2 can be transformed as

$\frac{1}{2}m{V_{y0}}^2+\frac{1}{2}J{{\omega }_0}^2=\frac{1}{2}m{V_{y1}}^2+\mathit{\Delta }E(8)$

If $\Delta E$ is ignored, $m{V_{y0}}^2+J{{\omega }_0}^2=m{V_{y1}}^2$, and V_y1>V_y0. However, it is almost impossible for the direction of V_y1 to be downwards and its value to increase [i.e., case (2) does not exist]. The case in which the direction of V_y1 is upward and its value increases is possible, but its possibility is small.

Based on the above analysis, if the test block rotates in a reverse manner, the direction of V_y1 can only be upwards, and the critical situation (ω₁ is approximately zero; V_y1>V_y0) is less likely to occur. After impact, the test block either does not rotate in the reverse direction or the angular velocity of the reverse rotation is large (not approaching 0). Therefore, it is reasonable to consider $\alpha =\arccos \left(\frac{{\omega }_0\cdot a}{3\sqrt{2}{V}_{y0}}\right)=\theta$ obtained by approximating V_y1 to zero as the critical condition for the occurrence of RR. According to the initial parameters of the impact test of the cube-shaped block listed in Table 1, the θ values at different initial speeds (50/150/250/350/450 RPM) are calculated to be 88.6°, 86.5°, 84°, 81.7° and 79.5° respectively, and the statistical α values in Table 1 meet the conditions.

3 Effect of the RRS on RC

When the shapes and initial motion parameters of the blocks meet the conditions specified in Section 2.1, the blocks after impact exhibit not only translation speeds but also RRSs. When these blocks impact the slope again, the RRSs of the blocks affect the RC. To clarify the influence mechanism between them, based on the aforementioned analysis results of the occurrence conditions for the RR of the blocks, impact tests of four typical shaped blocks with various RRSs are conducted.

3.1 Testing method

3.1.1 Testing equipment

The equipment (Figure 3) required for impact tests in this study includes a block ejection system and a slope angle control system. The former system is developed to include a flipping barrel, electric tension meter, limiting rope, slideway, slider, pulling rope, electromagnetic lock, base, and hydraulic support. The block is installed in the groove at the top of the steel barrel through a hexagonal axis. The incident velocity of the block can be controlled by applying different tensile forces to the slider, and the rotational speed of the block is applied using an adjustable speed motor through the hexagonal axis. The slider is released using an infrared remote control when the applied tension and rotational speed meet the preset values, and the block is released when the restraining rope connecting the front end of the barrel bottom and rear end of the slideway is tightened. A simple slope angle control system is assembled using a rock plate, two steel plates, a restraining rope and a hinge. The slope angle is controlled by adjusting the length of the restraining rope.

FIGURE 3

FIGURE 3. Block impact test equipment (A) schematic diagram, and (B) photographs.

3.1.2 Materials

According to the statistical results presented in Table 1 and classified statistical results of rockfall shapes in alpine gorge areas (Fityus et al., 2013), cubes, cuboids, cylinders and discs were selected as the shapes of the blocks used in this experiment (Figure 4). The blocks had the same volume and were made of natural limestone. The material of the slope was the same as that of the blocks. The slope was prepared through infrared fine cutting, and the surface was extremely flat (the friction coefficient was 0.45). Detailed parameters of the samples are given in Table 2. The physical and mechanical properties of the material, presented in Table 2, were determined according to ISRM recommended methods (ISRM, 2007).

FIGURE 4

FIGURE 4. Blocks used in the experiment and corresponding rockfall in the field (hexagonal axes were introduced in each block along the X and Y axes, and the bearings were nested at both ends of hexagonal axes to facilitate block rotation).

TABLE 2

TABLE 2. Characteristic parameters of blocks and slope used in this experiment.

3.1.3 Experimental programme

In the experiment, the four blocks with different shapes rotated reversely around the X and Y axes (based on the occurrence conditions of RR, the impact test between the cuboid-shaped block rotating around the Y-axis and slope surface was also performed) at 100–500 revolutions per minute (RPM). The incident speed was set as 3.5 m/s, the impact angle was set as 45°, and every test was repeated fivefold. Details of the experiment are presented in Table 3.

TABLE 3

TABLE 3. Experimental programme.

3.1.4 Image analysis and calculations

A high-speed camera (Model Phantom 710, 1280 × 800 pixels, 7,400 frames per second complete resolution) with a 1,000 fps operating speed was used to capture the impacts and bounces of the blocks. The velocities before and after impact were determined using the image-tracking program Tracker V2.0 and the abovementioned series of images. During the tests, the block was initially sprayed with a colour that was significantly different from the background, and thus, its pixel value in the image was distinguished from other background colours. After the tracking object (test block) was circled in the batch images, the software (Tracker V2.0) automatically tracked it according to the pixel value of the block colour and calculated the velocity of the block before and after the impact through the displacement of the centre point of the test block (automatically locked by the program) in two or several adjacent images and the elapsed time. The rebound angle of the block after the impact was determined using the software’s own measurement tool based on its post-impact trajectory. Eqs 9, 10 were used to calculate the RC values, which correspond to the definitions most commonly employed in the literature (Giani et al., 2004; Wyllie, 2014; Asteriou and Tsiambaos, 2016) as

$R_n=\frac{V_n^{\prime }}{V_n}(9)$

and

$R_t=\frac{V_t^{\prime }}{V_t}(10)$

where $V_n^{\prime }$ and $V_n$ are the normal components, and $V_t^{\prime }$ and $V_t$ are the tangential components of the block velocity after and before the impact, respectively.

3.2 Results

3.2.1 Influence of the RRS on R_n and R_t

(1) Influence of the RRS on R_n

As shown in Figure 5, the R_n values of the four blocks with different shapes did not exhibit a certain trend with the increase in the RRS, and the R_n values were not sensitive to the changes in the RRS. This phenomenon is consistent with the conclusions derived by Spadari et al. (2012), although their study was aimed at testing the influence of different forward rotation speeds on the R_n of the block. In different RRS conditions, the R_n value distributions of the blocks were relatively discrete, and the differences in the values were large. The narrowest value ranges of R_n for disc, cylinder, cuboid, cuboid (Y) and cube-shaped blocks were 0.036–0.275, 0.111–0.172, 0.039–0.132, 0.21–0.47 and 0.095–0.3, respectively, and the maximum value ranges were 0.085–0.56, 0.065–0.41, 0.024–0.29, 0.049–0.41 and 0.03–0.51, respectively. Buzzi et al. (2012) used the average value of five test results to analyse the effect of the forward rotation speed on the RC to alleviate the influence of the random error. However, this setting is inappropriate because it can lead to the loss of important information and is not conducive to the accurate prediction of the rockfall motion path. Therefore, the results of each test must be treated with caution.

FIGURE 5

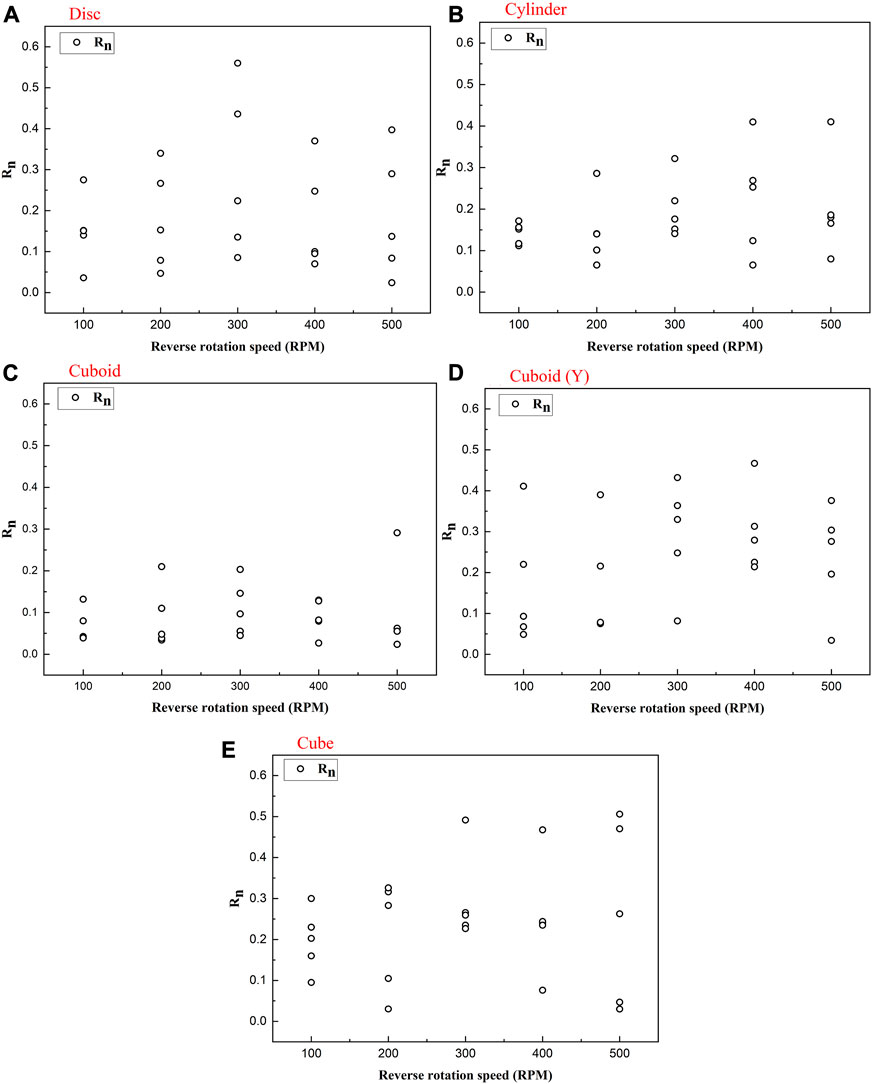
FIGURE 5. R_n of blocks with different shapes versus the RRS (A, B, C, E): Test results of impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Test results of impacts between a cuboid-shaped block rotating around the Y-axis and slope surface).

Although R_n does not vary with the RRS in Figure 5, the RRS may still influence R_n. In theory, the change in the RRS influences the contact velocity of the block, which is directly related to the normal impact force, and thus, the RRS influences R_n. The preceding results just demonstrate that the RRS is not the only factor affecting R_n, and the RRS does not play a dominant role in R_n. In other words, to establish an effective relationship between the RRS and R_n, other factors must be comprehensively considered.

According to the comparison of the R_n values of four blocks with different shapes, the R_n values of cube- and cuboid (Y)-shaped blocks are higher, while the R_n values of the disc-, cylinder- and cuboid-shaped blocks are lower. This phenomenon occurs because the α ranges of cube and cuboid (Y)-shaped blocks are naturally smaller than those of the disc, cylinder, and cuboid-shaped blocks, which leads to a higher probability of normal or nearly normal impact between the cube and cuboid (Y)-shaped blocks and the slope in multiple tests. This finding highlights the influence of the block shape on R_n, and thus, this factor cannot be ignored when examining the influence of RRS on R_n. In addition, the contact attitudes of the same block are different even under the same RRS, and the influence mechanisms of the impact force on R_n are also considerably different under various contact attitudes. Therefore, it may be inappropriate to summarize the mechanisms with a simple and general rule, and classification and refinement may help solve this problem.

(2) Influence of the RRS on R_t

The relationships between R_t and RRS of four differently shaped blocks are shown in Figure 6. R_t is independent of RRS. The R_t value distributions of blocks of different shapes under various RRSs are relatively concentrated, exhibiting similar distribution ranges. The R_t value ranges of the disc, cylinder, cuboid, cuboid (Y) and cube-shaped blocks are 0.79–1.00, 0.80–1.06, 0.77–1.00, 0.78–1.00 and 0.86–0.99, respectively. This finding is more consistent with the conclusions derived by Asteriou (2019) and Spadari et al. (2012) in tests pertaining to the effect of the forward rotation speed on the R_t value of blocks having different shapes. Compared with the normal impulse, the tangential impulse is extremely small, while the RRS directly affects the normal impact force, which leads to an extremely small change in the tangential impulse in an extremely small impact time Consequently, the effect of the RRS on R_t is not significant. Moreover, under this test condition, the contact point of the block has a forward movement speed relative to the slope surface, and the direction of the frictional force is backwards, which decreases the tangential velocity such that the overall R_t values are less than 1. However, in the test, the block may rotate forward after the first impact and later contact the slope surface. At this time, the direction of the frictional force may be consistent with that of the tangential velocity, and the friction force may increase the tangential velocity such that a few R_t values of the blocks are greater than 1.

FIGURE 6

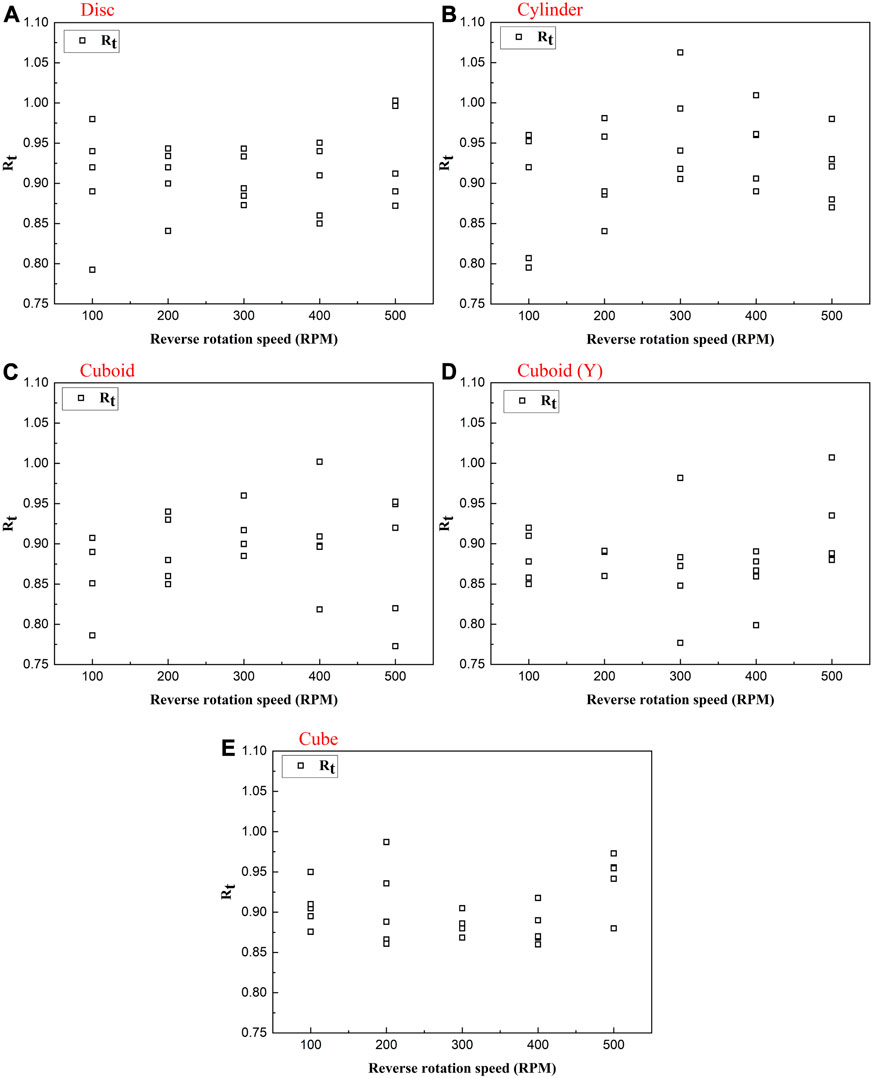
FIGURE 6. R_t of differently shaped blocks versus the RRS (A, B, C, E): Test results of impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Test results of impacts between a cuboid-shaped block rotating around the Y-axis and slope surface).

The effect of the RRS on R_t has been essentially identified based on the analysis of the test results. However, the effect of the RRS on R_n is unclear due to the diversity of contact attitudes of the blocks and sophisticated mechanical mechanism. Notably, this problem is not impossible to solve. The findings of the preceding study provide certain information and tools that may aid in the resolution of this problem, such as categorization and discussion based on various mechanical mechanisms and joint examination of the effects of block shape and contact attitudes. These aspects are thoroughly considered and adopted, as described in the following sections.

3.2.2 Influence of impact coefficient on R_n

The impact-bounce behaviours of the blocks may be divided into two categories based on the observations of the impact-bounce processes of the blocks in each test: rebound following a single impact [I(1)] and rebound following two consecutive impacts [I(2)]. Buzzi et al. (2012) also observed these two circumstances and categorized them. In addition, according to the preliminary theoretical analysis, the rebound behaviours of the block with the initial RRS are closely related to the impulse moment equation. The position of the normal impact force relative to the mass centre (C) is different, and the effect of the impulse moment of the normal impulse of the contact point to the mass centre on the motion of the block after impact is different. Considering this aspect, I(1) can be subdivided into two subtypes, depending on whether the MC is in front of [F(1)] (Figure 7A) or behind the CP [B(1)] (Figure 7B). Similarly, I(2) may be subdivided into two subtypes, depending on whether the MC is in front of or behind the CP at the initial impact [F(2)/B(2)] (Figures 7C, D).

FIGURE 7

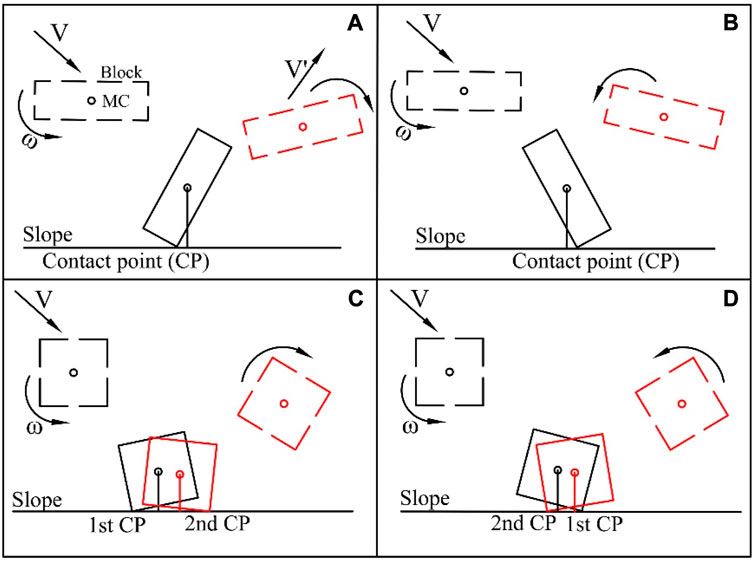
FIGURE 7. Categorizations of impact-bounce behaviours of the block (block rebounds following a single impact [I(1)]: the MC is in (A) front and (B) behind the CP; block rebounds following two impacts [I(2)], wherein the MC is in (C) front and (D) behind the CP during the first impact.).

Although the impact-bounce behaviours of the block are categorized, the impact dynamic equation cannot be directly used to analyse the effect of the RRS on R_n based on this aspect. According to the findings in Section 3.2.1, the influencing variable must be re-determined. Considering the shape features of the block, RRS and contact posture, a new integrated variable, namely, the impact coefficient (I_c) is proposed to evaluate the effect of the RRS on R_n, expressed as.

$I_c=\omega \cdot d(11)$

where ɷ represents the angular velocity of the block (Figure 8) (rad/s), and d is the distance from the CP to the projection of the MC, reflecting the characteristics of the block shape and contact posture (m). The unit of I_c is m/s, which is essentially the change in the normal velocity of the CP relative to the slope caused by the rotation of the block. Changing the normal impact velocity of the CP leads to a change in the normal impact force, thereby influencing R_n.

FIGURE 8

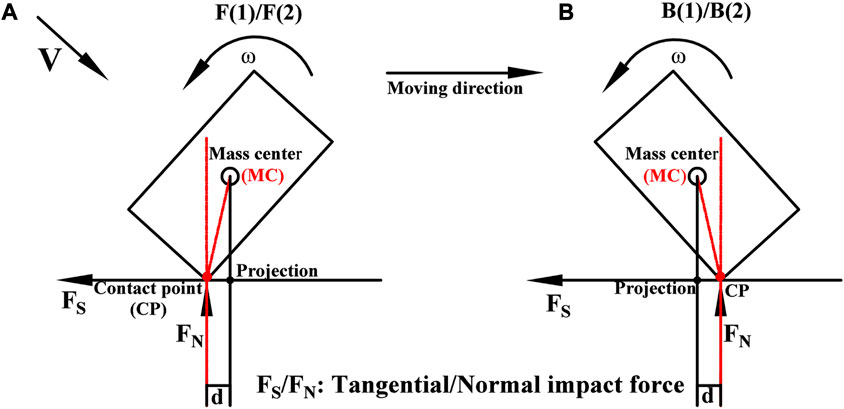
FIGURE 8. Schematic of the influence of I_c on R_n where the MC is in (A) front of the CP and (B) behind the CP at the first impact.

Using the measurement module in the software tracker V2.0, the ω and d values of each test are measured, and the I_c values are calculated using Eq. 11. The relationships between the R_n values and I_c of the blocks with different impact-bounce behaviours are shown in Figures 9, 10.

(1) Influence of I_c on the Rn of blocks with I(1)-type impact-bounce behaviours

FIGURE 9

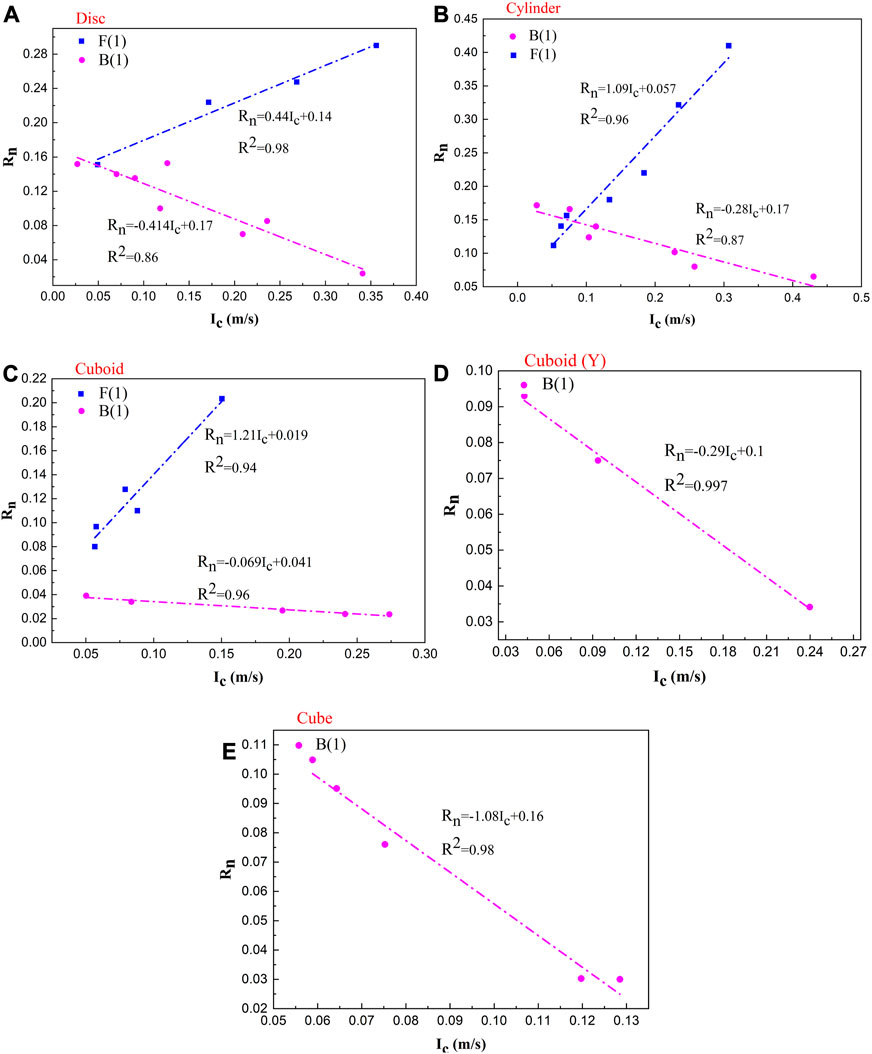
FIGURE 9. Relationships between I_c (at the first impact) and R_n of blocks with I(1)-type impact-bounce behaviours (A, B, C, E): Test results of impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Test results of impacts between a cuboid-shaped block rotating around the Y-axis and slope surface).

FIGURE 10

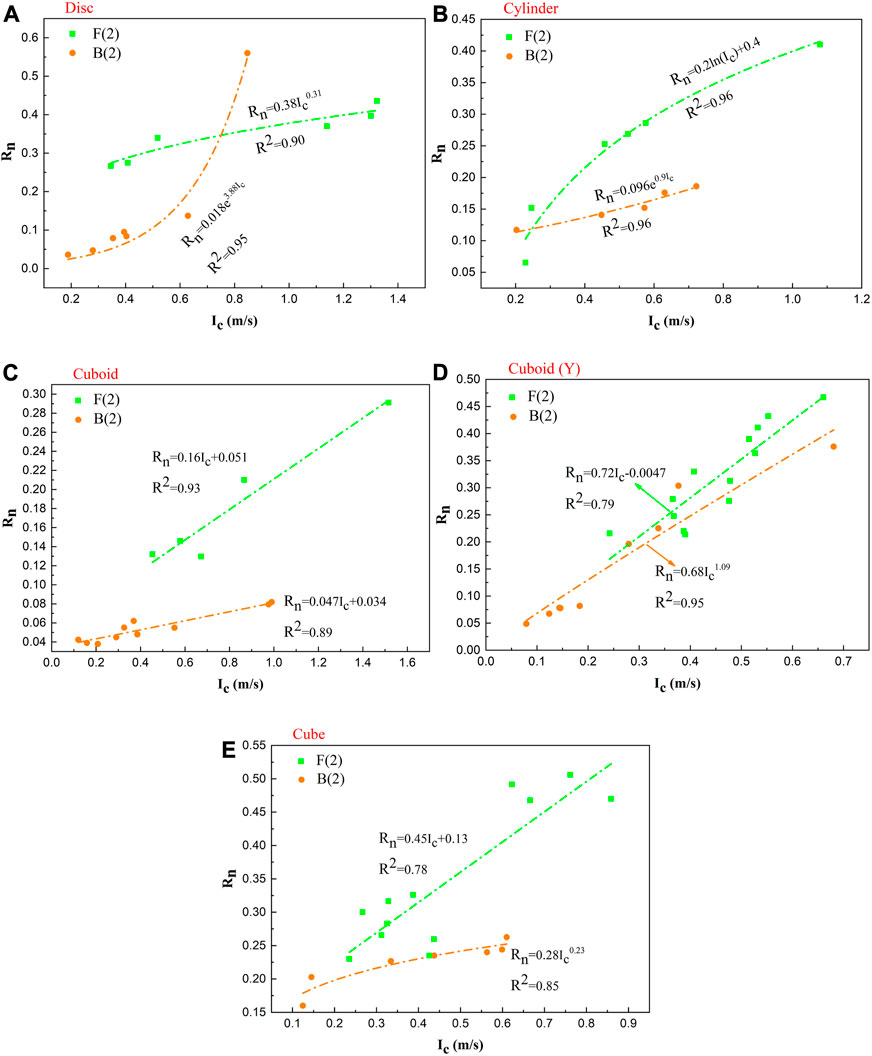
FIGURE 10. Relationship between I_c (at first impact) and R_n of blocks with I(2)-type impact-bounce behaviours (A, B, C, E): Test results of impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Test results of impacts between a cuboid-shaped block rotating around the Y-axis and slope surface).

The relationships between I_c and R_n of blocks with I(1)-type impact-bounce behaviours are shown in Figure 9. Regardless of the F(1) or B(1) conditions, the R_n values of the four blocks with different shapes are more sensitive to changes in the I_c values. By fitting the data, under condition F(1), the R_n values of the disc, cylinder and cuboid-shaped blocks exhibit strong linear positive correlations with the I_c values (the data of cuboid (Y) and cube-shaped blocks are not collected under this condition), and the R² values are 0.98, 0.96 and 0.94, respectively. Under this scenario, I_c contributes to an increase in the normal impact velocity (V_n). As shown in Figure 8A, as I_c increases, the normal impact velocity of the CP relative to the slope surface and normal impact force increase, resulting in an increasing R_n. Under condition B(1), the R_n values of the disc, cylinder, cuboid and cube-shaped blocks exhibit strong linear negative correlations with the I_c values, and the R² values are 0.86, 0.87, 0.96, 0.997 and 0.98, respectively. Under this scenario, I_c tends to decrease the normal impact velocity (Figure 8B). As I_c increases, the normal impact velocity of the CP relative to the slope surface decreases, thereby decreasing the normal impact force and R_n.

The linear correlation between I_c and R_n, as shown in Figure 9, established by straightforward data fitting, can be supported by the corresponding mechanical theory. According to the relevant theory of impact dynamics (Meyers, 1994), during impact, the normal impact force is approximately proportional to the normal impact velocity when the same material deforms in the linear elastic range. In this experiment, the mass centre of the blocks has the same initial velocity in each test, and a linear relationship must exist between the change in the initial normal impact velocity (I_c) and change in the normal impact force. Because the value of R_n is directly determined by the normal impact force, the correlation between I_c and R_n is expected to be linear.

(2) Influence of I_c on the R_n of blocks with I(2)-type impact-bounce behaviours

When the included angle (α) between line L and the slope surface is smaller than a certain critical value at the moment of impact (Figure 11), the block may rebound after two consecutive impacts on the slope, which is essentially the result of the combined action of an impact in which the MC is in front of the CP and that in which the MC is behind the CP. As shown in Figure 10, for blocks that exhibit I(2)-type impact-bounce behaviours, the R_n values of four differently shaped blocks under conditions F(2) and B(2) increase with increasing I_c. By fitting the data, under the F(2) condition, the R_n values of the disc, cylinder, cuboid, cuboid (Y) and cube-shaped blocks exhibit power, logarithmic and linear functional relationships with I_c, respectively, and the R² values are 0.90, 0.96, 0.93, 0.79 and 0.78, respectively, corresponding to a strong correlation. Under condition B(2), the R_n values of the disc, cylinder, cuboid, cuboid (Y) and cube-shaped blocks exhibit exponential, linear and power functional relationship with I_c, and the R² values are 0.95, 0.96, 0.89, 0.95 and 0.85, respectively.

FIGURE 11

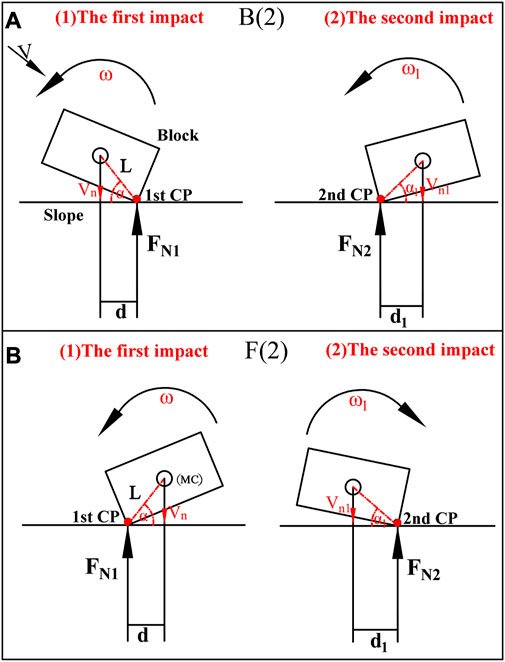
FIGURE 11. Impact diagram of the block with I(2)-type impact-bounce behaviours [(A, B) respectively represent the MC behind and in front of the CP during the first impact; F_N1 and F_N2 are the normal impact forces during the first and second impacts, respectively].

For the blocks under condition B(2) (Figure 11A), the restitution coefficients (R_n1, which is equal to V_n1/V_n, with V_n1 being the normal velocity of the MC after the first impact or before the second impact) after the first impact with the slope decrease with the increase in I_c (the influencing mechanism is similar to that under B(1)). However, according to the observation of the impact processes of the blocks under this condition, the intensity of the first impact is significantly less than that of the second impact (Figure 12), and the restitution coefficients (R_n2, which is equal to V_n′/V_n1) after the second impact dominantly influence the magnitude of R_n. After the first impact of the blocks on the slope, the RRSs of the blocks increase [as shown in Figure 11A (1), the normal impact force increases the RRS of the block], that is, ω₁>ω (ω₁ is the angular velocity of the block following the first impact or before the second impact). Moreover, the α₁ values at the second impact are slightly smaller than the α values at the first impact (Figure 12), that is, d₁>d [d₁ is the distance from the CP to the projection of the MC during the second impact, as shown in Figure 11A (2)]. In this context, as I_c increases, ω₁ and d₁ during the second impact increase, and R_n2 increases [the influencing mechanism is similar to that under F(1)], owing to which, R_n increases.

FIGURE 12

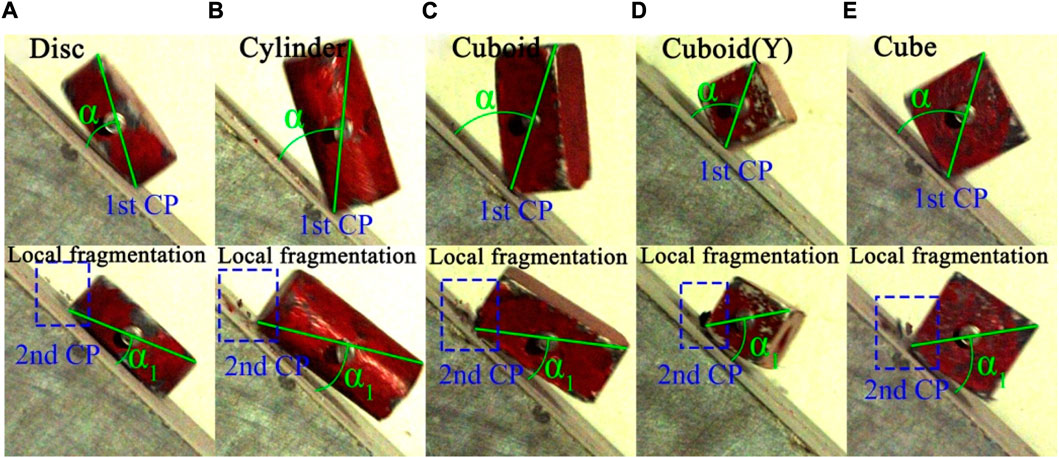
FIGURE 12. Comparison of the intensity and contact angles for the first and second impacts of the blocks under condition B(2) [(A, B, C, E): Impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Impact between a cuboid-shaped block rotating around the Y-axis and slope surface].

For the blocks under condition F(2), after the first impact with the slope surface, the R_n1 values increase with increasing I_c [as shown in Figure 11B (1), and the influencing mechanism is similar to that under F(1)]. However, the relationship between I_c and R_n cannot be determined based on only this aspect. R_n eventually increasing or decreasing with the I_c also needs to consider the relationship between the R_n2 and I_c after the second impact. As the tangential velocities of the blocks change slightly before and after impact, the tangential velocities can be considered to be nearly unchanged. The energy conservation equation and momentum equation before and after the first impact can be defined as follows:

$\frac{1}{2}m{V_n}^2+\frac{1}{2}J{\omega }^2=\frac{1}{2}m{V_{n1}}^2+\frac{1}{2}J{{\omega }_1}^2+\mathit{\Delta }E(12)$

$F_{N1}\cdot d\cdot t=J\left({\omega }_1+\omega \right)(13)$

$F_{N1}\cdot t=m\left(V_n-V_{n1}\right)(14)$

where m is the mass of the block; J is the moment of inertia of the block around the centre of mass; ΔE is the energy loss; t is the impact time; the rotation speed is positive in the clockwise direction; the directions of V_n1 and V_n are the same (both positive and downwards), consistent with the phenomenon observed in the experiment. As shown in Figure 13, the α value of each block is less than α₁.②

FIGURE 13

FIGURE 13. Comparison of the contact angles during the first and second impacts of the blocks under condition F(2) [(A, B, C, E): Impacts between disc, cylinder, cuboid and cube-shaped blocks rotating around the X-axis and the slope surface, respectively; (D) Impact between a cuboid-shaped block rotating around the Y-axis and slope surface].

The results of simultaneous Eqs 12–14 are

$\begin{array}{l}\frac{V_n+V_{n1}}{d}=\frac{J\left({\omega }_1-\omega \right)\left({\omega }_1+\omega \right)+\mathit{\Delta }E}{J\left({\omega }_1+\omega \right)}\\ =\frac{\begin{array}{c}①\\ \overbrace{\mathit{\Delta }E}\end{array}}{J\left({\omega }_1+\omega \right)}+\begin{array}{c}②\\ \overbrace{\left({\omega }_1-\omega \right)}\end{array}\end{array}(15)$

The value of $\frac{V_n+V_{n1}}{d}$ in Eq. 15 is positive, and the energy loss (ΔE) of the block in the impact process is extremely small relative to the total energy. Therefore, term ① can be ignored in the simplified analysis, and from this, it can be deduced that ω₁ and ω are equivalent or ω₁ is greater than ω. In this context, ω₁ increases with the increase in ω, and d is less than d₁ under this working condition (Figure 13). Therefore, R_n2 increases with the increase in ωd (the influencing mechanism is similar to that of F(1)). Taking into account the relationship between I_c and R_n1 determined in the aforementioned analysis, it can be considered that R_n = R_n1 · R_n2 is also positively correlated with I_c.

In addition, Figure 10 shows that the R_n values of the blocks under condition F(2) are generally greater than those of the blocks under condition B(2). This phenomenon occurs because I_c increases the normal velocity of the contact point in the two impacts of the block under condition F(2). In contrast, under condition B(2), although I_c affects the normal velocity of the contact point during the second impact of the block, I_c decreases the normal velocity of the contact point in the first impact. Consequently, the increase in R_n under this condition is smaller than that under condition F(2).

In this manner, the influence mechanism of RRS on R_n can be clarified according to the analysis of the influence mechanism of I_c on R_n. For blocks with I(1)-type impact-bounce behaviours, when the block shape and contact attitude are fixed, the RRS and R_n are linearly positively correlated and negatively correlated under working conditions F(1) and B(1), respectively. For blocks with I(2)-type impact-bounce behaviours, under working conditions B(2) or F(2), when the block shape and contact attitudes are fixed, R_n is positively correlated with the RRS. Nevertheless, maintaining the contact attitudes of the block consistent in every laboratory or outdoor test is challenging, and the varied contact attitudes of the irregular rockfall are an essential characteristic of the rockfall event. Therefore, investigating the influence of only the RRS on R_n is nearly impossible and meaningless, and it is more feasible to clarify the influence of the RRS on R_n in terms of I_c.

4 Discussion

In actual rockfall events, moving rockfalls are often accompanied by certain rotational speeds, which generally undergo noticeable changes after impact, including increasing, decreasing, or reversing (Buzzi et al., 2012; Dattola et al., 2021; Ji et al., 2021). For rockfalls that have undergone RR after impact, they experience more two impacts when they make contact with the slope again. Due to the difficulty in accurately determining the pre-impact motion state of the rockfall before the second impact, accurately determining the value of the R_n becomes even more challenging. However, existing rockfall trajectory prediction programs, whether based on lumped-mass approach or rigid body theory, have not addressed the occurrence of non-spherical rockfall RR and the its influence on the RC (Volkwein et al., 2011; Li and Lan, 2015). As a result, the obtained post-impact motion characteristics and the subsequently predicted trajectories of the rockfalls may have limited reference value for the construction of protective measures against actual rockfall hazards. Therefore, there is an urgent and essential need to systematically investigate the criteria for the occurrence of rockfall RR and the influence of RRS on the RC.

According to the summary of the RR phenomena observed in the previous impact tests, this study analyses the initial conditions in which the block is prone to RR. Moreover, combined with the impact dynamics theory, the judgement criterion of whether the typically shaped block-cube obtains the RRS after impact is preliminarily analysed and deduced. In the process of predicting the trajectory of rockfall, when calculating the motion parameters after the current impact, it is necessary to first calculate the pre-impact posture parameters (impact angle, contact angle, d, angular velocity, normal and tangential velocities relative to the slope) based on the motion parameters after the previous impact combined with the spatial dimensions of the slope. At this time, according to the criteria for determining RR occurrence, it can be determined whether the rockfall reverses after the current impact, and thus the appropriate control relationship can be chosen to obtain the motion parameters after the current impact. The findings provide valuable information for the development and optimization of simulation programs to accurately predict the rockfall trajectories and enhance the understanding of the rockfall impact process. However, many parameters (such as the energy loss and motion parameters after the first impact) are difficult to obtain under the existing technical conditions, and the proposed judgment criterion is still relatively rough. If it is to be effectively applied in the prediction of rockfall disasters, further detailed testing and analysis must be performed. In addition, in the process of analyzing the occurrence conditions of RR, since some of the aforementioned parameters cannot be obtained theoretically and precisely, we have given certain assumptions based on the experimental phenomena for the time being only for the shape of the block (regular hexahedron) with the highest probability of RR for derivation, and expect to obtain some meaningful conclusions during the initial analytical study. The conditions for the occurrence of RR of other typical shapes of rockfalls will be investigated after the detailed parameters are clarified.

To examine the effect of the RRS on R_n, this study introduces a comprehensive variable (I_c) for quantification, and the influence laws between I_c and R_n under different working conditions are obtained through classifications and discussions. If the initial I_c of a counter-rotating rockfall is known in a certain slope environment, the normal velocity of the rockfall after impact may be estimated using the derived rules, and the subsequent rockfall trajectory and I_c value of the next impact can be precisely predicted in combination with the tangential velocity and rotational speed after impact (to be further studied in detail). These research results offer significant theoretical support and technical accumulation for the refinement of rockfall impact motion control mechanisms and the improvement of rockfall disaster prediction programs. Nevertheless, this does not mean the end of this research work, several aspects remain to be examined. The experiment highlighted that the shape factor considerably affects the influence of I_c on R_n. Although several typical shaped blocks are used in this study, the shapes of rockfall vary. Future work can be aimed at conducting tests involving blocks with other shapes to identify the quantitative relationship between the block shape and relevant laws of I_c and R_n.

Furthermore, it is worth noting that the conclusions regarding the occurrence conditions of RR and the influence of the RRS on the RC derived in this study are based on a hard rock slope. In actual rockfall events, the slope surface is often covered with various materials that can be categorized as loose media (such as sand, talus or soil) and dense hard rock. The interaction mechanism between rockfall and slopes involving loose media during impact is completely different from that of hard rock slopes (e.g., contact time, magnitude of impact force, slope surface deformation, and tangential resistance). Further detailed research is needed to investigate whether rockfall RR can occur under these conditions. Meanwhile, it’s important to highlight that the findings of this study are based on impact tests for small test blocks with low energy, which differ considerably from the actual rockfall in terms of the size and impact energy (mainly manifested in terms of the differences in the impact time, local damage degree, etc.). Consequently, the applicability of the conclusions may be somewhat limited. In follow-up research, impact tests for massive rockfall can be performed to correlate the rockfall size and related laws of I_c and R_n, thereby extending the research findings to broader engineering applications.

5 Conclusion

In the process of rockfall moving along a dense rock slope, the rockfall may also rotate in the reverse direction in certain cases, the probability of occurrence of which is significant. According to the statistical analysis of the RR phenomena after the impacts of the blocks in previous tests, RR mainly occurs after the non-normal impacts of cuboid, cube, cylinder and disc-shaped blocks with the slope surface, the incident angle is often large, and the mass centre of most test blocks is located behind the contact point at the moment of impact. Moreover, the degree of the contact angle between the block and slope is key to the occurrence of the RR of the blocks, and the ranges of the contact angles of differently shaped blocks are different. For example, for a cubic block, the critical condition for RR is preliminarily deduced as $\alpha =\arccos \left(\frac{{\omega }_0\cdot a}{3\sqrt{2}{V}_{y0}}\right)$.

R_t values are independent of the RRS and do not change with the RRS. The distributions of the R_t values of blocks having different shapes under various RRSs are relatively concentrated, and the values are similar. The R_n values do not exhibit a clear trend with increasing RRS, and the distributions under different RRSs are relatively discrete. However, this aspect does not imply that the RRS does not affect R_n; instead, it is difficult to directly establish an effective relationship between the two. Considering the RRS, block shape and contact attitudes, a comprehensive variable-impact coefficient is proposed to analyse the effect of the RRS on R_n. The impact-bounce behaviours of the block are categorized and analysed considering the variation among the influence mechanisms of the impact force on R_n under various contact attitudes. For the blocks with I(1)-type impact-bounce behaviours, I_c and R_n are linearly positively correlated and negatively correlated under conditions F(1) and B(1), respectively. For the blocks with I(2)-type impact-bounce behaviours, I_c and R_n exhibit a strong positive relationship under conditions F(2) and B(2). The overall R_n values of the blocks under conditions F(1) and F(2) are higher than those under conditions B(1) and B(2). These findings clarify the mechanism of influence of the RRS on R_n and provide valuable reference for the prediction of the impact process of irregular rockfall with reverse rotation.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Z-MJ: Conceptualization, Data curation, Investigation, Writing–original draf. T-HW: Data curation, Formal Analysis, Investigation, Writing–review and editing. F-QW: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing. D-PW: Data curation, Formal Analysis, Investigation, Methodology, Writing–review and editing. Z-HL: Data curation, Investigation, Validation, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was financially supported by the National Natural Science Foundation of China (No. U2244228; No. 42307250; No. 41831290), Opening fund of State Key Laboratory of Geohazard Prevention and Geoenvironment Protection (Chengdu University of Technology) (Grant No. SKLGP2023K007), China Postdoctoral Science Foundation (No. 2022M721033) and Natural Science Foundation of Henan (No. 222300420366).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asteriou, P. (2019). Effect of impact angle and rotational motion of spherical blocks on the coefficients of restitution for rockfalls. Geotechnical Geol. Eng. 37, 2523–2533. doi:10.1007/s10706-018-00774-0

CrossRef Full Text | Google Scholar

Asteriou, P., and Tsiambaos, G. (2016). Empirical model for predicting rockfall trajectory direction. Rock Mech. Rock Eng. 49, 927–941. doi:10.1007/s00603-015-0798-7

CrossRef Full Text | Google Scholar

Azarafza, M., Akgün, H., Ghazifard, A., and Asghari-Kaljahi, E. (2020). Key-block based analytical stability method for discontinuous rock slope subjected to toppling failure. Comput. Geotechnics 124, 103620. doi:10.1016/j.compgeo.2020.103620

CrossRef Full Text | Google Scholar

Azarafza, M., Akgün, H., Ghazifard, A., Asghari-Kaljahi, E., Rahnamarad, J., and Derakhshani, R. (2021). Discontinuous rock slope stability analysis by limit equilibrium approaches–a review. Int. J. Digital Earth 14 (12), 1918–1941. doi:10.1080/17538947.2021.1988163

CrossRef Full Text | Google Scholar

Azzoni, A., and De Freitas, M. (1995). Experimentally gained parameters, decisive for rock fall analysis. Rock Mech. Rock Eng. 28, 111–124. doi:10.1007/BF01020064

CrossRef Full Text | Google Scholar

Basson, F. R. P. (2012). Rigid body dynamics for rock fall trajectory simulation. Chicago, Illinois, United States: U.S. Rock Mechanics/Geomechanics Symposium.

Google Scholar

Buzzi, O., Giacomini, A., and Spadari, M. (2012). Laboratory investigation on high values of restitution coefficients. Rock Mech. Rock Eng. 45, 35–43. doi:10.1007/s00603-011-0183-0

CrossRef Full Text | Google Scholar

Chau, K. T., Wong, R. H. C., and Wu, J. J. (2002). Coefficient of restitution and rotational motions of rockfall impacts. Int. J. Rock Mech. Min. Sci. 39, 69–77. doi:10.1016/S1365-1609(02)00016-3

CrossRef Full Text | Google Scholar

Chen, T. J., Zhang, G. C., and Xiang, X. (2023). Research on rockfall impact process based on viscoelastic contact theory. Int. J. Impact Eng. 173, 104431. doi:10.1016/j.ijimpeng.2022.104431

CrossRef Full Text | Google Scholar

Dattola, G., Crosta, G. B., and di Prisco, C. (2021). Investigating the influence of block rotation and shape on the impact process. Int. J. Rock Mech. Min. Sci. 147, 104867. doi:10.1016/j.ijrmms.2021.104867

CrossRef Full Text | Google Scholar

Dong, H., and Moys, M. H. (2006). Experimental study of oblique impacts with initial spin. Powder Technol. 161, 22–31. doi:10.1016/j.powtec.2005.05.046

CrossRef Full Text | Google Scholar

Fityus, S. G., Giacomini, A., and Buzzi, O. (2013). The significance of geology for the morphol-ogy of potentially unstable rocks. Eng. Geol. 162, 43–52. doi:10.1016/j.enggeo.2013.05.007

CrossRef Full Text | Google Scholar

Giacomini, A., Spadari, M., Buzzi, O., Fityus, S. G., and Giani, G. P. (2010). Rockfall motion characteristics on natural slopes of eastern Australia. Lausanne, Switzerland: ISRM International Symposium - EUROCK 2010.

Google Scholar

Giacomini, A., Thoeni, K., Lambert, C., Booth, S., and Sloan, S. W. (2012). Experimental study on rockfall drapery systems for open pit highwalls. Int. J. Rock Mech. Min. Sci. 56, 171–181. doi:10.1016/j.ijrmms.2012.07.030

CrossRef Full Text | Google Scholar

Giani, G. P., Giacomini, A., Migliazza, M., and Segalini, A. (2004). Experimental and theoretical studies to improve rock fall analysis and protection work design. Rock Mech. Rock Eng. 37 (5), 369–389. doi:10.1007/s00603-004-0027-2

CrossRef Full Text | Google Scholar

Guccione, D. E., Thoeni, K., Fityus, S., Nader, F., Giacomini, A., and Buzzi, O. (2021). An experimental setup to study the fragmentation of rocks upon impact. Rock Mech. Rock Eng. 54 (8), 4201–4223. doi:10.1007/s00603-021-02501-3

CrossRef Full Text | Google Scholar

Hu, J., Li, S. C., Li, L. P., Shi, S. S., Zhou, Z. Q., Liu, H. L., et al. (2018). Field, experimental, and numerical investigation of a rockfall above a tunnel portal in southwestern China. Bull. Eng. Geol. Environ. 77 (4), 1365–1382.

CrossRef Full Text | Google Scholar

ISRM (2007), The complete ISRM suggested methods for rock characterization testing and monitoring: 1974–2006 Editors R. Ulusay, and J. A. Hudson (Lisbon, Portugal: International Society for Rock Mechanics).

Google Scholar

Ji, Z. M., Chen, Z. J., Niu, Q. H., Wang, T. J., Wang, T. H., and Chen, T. L. (2021). A calculation model of the normal coefficient of restitution based on multi-factor interaction experiments. Landslides 18 (4), 1531–1553. doi:10.1007/s10346-020-01556-7

CrossRef Full Text | Google Scholar

Ji, Z. M., Chen, Z. J., Niu, Q. H., Wang, T. J., Song, H., and Wang, T. H. (2019). Laboratory study on the influencing factors and their control for the coefficient of restitution during rockfall impacts. Landslides 16 (10), 1939–1963. doi:10.1007/s10346-019-01183-x

CrossRef Full Text | Google Scholar

Li, L. P., and Lan, H. X. (2015). Probabilistic modeling of rockfall trajectories: A review. Bull. Eng. Geol. Environ. 74, 1163–1176. doi:10.1007/s10064-015-0718-9

CrossRef Full Text | Google Scholar

Lu, G., Ringenbach, A., Caviezel, A., Sanchez, M., Christen, M., and Bartelt, P. (2021). Mitigation effects of trees on rockfall hazards: does rock shape matter? Landslides 18, 59–77. doi:10.1007/s10346-020-01418-2

CrossRef Full Text | Google Scholar

Meyers, M. A. (1994). Dynamic behavior of materials. New York, NY, USA: John Wiley & Sons.

Google Scholar

Nanehkaran, Y. A., Licai, Z., Chen, J., Azarafza, M., and Yimin, M. (2022). Application of artificial neural networks and geographic information system to provide hazard susceptibility maps for rockfall failures. Environ. Earth Sci. 81 (19), 475. doi:10.1007/s12665-022-10603-6

CrossRef Full Text | Google Scholar

Nishimura, T., Kohno, M., Kitasako, K., and Ikezoe, Y. (2014). A laboratory test on rockfall impacts coefficient of restitution and rotational motions. Minneapolis, MN, USA: US Rock Mechanics/Geomechanics Symposium.

Google Scholar

Noël, F., Nordang, S. F., Jaboyedoff, M., Travelletti, J., Matasci, B., Digout, M., et al. (2023). Highly energetic rockfalls: back analysis of the 2015 event from the mel de la Niva, Switzerland. Landslides 20, 1561–1582. doi:10.1007/s10346-023-02054-2

CrossRef Full Text | Google Scholar

Preh, A., Mitche, A., Hungr, O., and Kolenpratc, B. (2015). Stochastic analysis of rock fall dynamics on quarry slopes. Int. J. Rock Mech. Min. Sci. 80, 57–66. doi:10.1016/j.ijrmms.2015.09.010

CrossRef Full Text | Google Scholar

Ritchie, A. M. (1963). The evaluation of rockfall and its control. Highw. Res. Rec. 17, 13–28.

Google Scholar

Spadari, M., Giacomini, A., Buzzi, O., Fityus, S., and Giani, G. P. (2012). In situ rockfall testing in new south wales, Australia. Int. J. Rock Mech. Min. Sci. 49, 84–93. doi:10.1016/j.ijrmms.2011.11.013

CrossRef Full Text | Google Scholar

Tang, J., Zhou, X., Liang, K., Lai, Y., Zhou, G., and Tan, J. (2021). Experimental study on the coefficient of restitution for the rotational sphere rockfall. Environ. Earth Sci. 80 (11), 419. doi:10.1007/s12665-021-09684-6

CrossRef Full Text | Google Scholar

Ujihira, M., Takagai, N., and Iwasa, T. (1993). An experimental study on the characteristics of the impact load of falling rock. Int. J. Surf. Min. Reclam. Environ. 2 (7), 81–89. doi:10.1080/09208119308964692

CrossRef Full Text | Google Scholar

Vijayakumar, S., Yacoub, T., Ranjram, M., and Curran, J. H. (2012). Effect of rockfall shape on normal coefficient of restitution. Chicago, Illinois, United States: U.S. Rock Mechanics/Geomechanics Symposium. .

Google Scholar

Volkwein, A., Schellenberg, K., Labiouse, V., Agliardi, F., Berger, F., Bourrier, F., et al. (2011). Rockfall characterisation and structural protection–a review. Nat. Hazards Earth Syst. Sci. 11 (9), 2617–2651. doi:10.5194/nhess-11-2617-2011

CrossRef Full Text | Google Scholar

Wang, L. Q., Xiao, T., Liu, S. L., Zhang, W. G., Yang, B. B., and Chen, L. C. (2023). Quantification of model uncertainty and variability for landslide displacement prediction based on Monte Carlo simulation. Gondwana Res. doi:10.1016/j.gr.2023.03.006

CrossRef Full Text | Google Scholar

Wyllie, D. C. (2014). Calibration of rockfall modeling parameters. Int. J. Rock Mech. Min. Sci. 67, 170–180. doi:10.1016/j.ijrmms.2013.10.002

CrossRef Full Text | Google Scholar