
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 01 September 2023
Sec. Quaternary Science, Geomorphology and Paleoenvironment
Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1223785
This article is part of the Research TopicWater-Related Natural Disasters in Mountainous Area, volume IIView all 16 articles
 Zheng-rong Li1,2
Zheng-rong Li1,2 Ming-gui Jiang1
Ming-gui Jiang1 Xing-long Feng2
Xing-long Feng2 Shao-yong Wang3
Shao-yong Wang3 Qing-tian Zeng2
Qing-tian Zeng2 Chong Chen3
Chong Chen3 Wen-lian Liu4
Wen-lian Liu4 Wei Sun1*
Wei Sun1*Glacial movement causes massive accumulation of fine-grained moraine, which often induces slope instability, moraine debris flow, and other geological hazards due to the effects of rain and the ice-snow melting. This study used a modified phosphoric acid-water glass slurry for grouting and curing moraine, and analyzed the influencing law of water glass Baume degree and curing age on energy consumption characteristics as well as the fracture properties of the grout-cured body of moraine using the uniaxial compression test. The results showed that the gel time of phosphoric acid-water glass slurry increased with the increasing addition of phosphoric acid and that it had a mutation phenomenon. The gel time increased linearly with the increasing addition of phosphoric acid before the mutation. Moreover, the compressive strength, pre-peak total energy, pre-peak elastic energy, pre-peak dissipative energy, elastic energy density, dissipative energy density, and pre-peak fracture toughness of the moraine curing body at same curing age increased linearly with the increase of water glass Baume degree by 46%–218%. The compressive strength, pre-peak elastic energy, and pre-peak elastic energy density of the moraine curing body increased with the curing age but grew slowly from 3 days to 7 days and rapidly from 7 days to 14 days. Through regression analysis of the test results, the fracture toughness calculation formula was derived from an energy perspective. These research results have significant implications for the reinforcement of moraine strata grouting and glacial debris flow disaster prevention and control.
The Pulang copper deposit has relatively complete Quaternary glacial relics, meaning that the overlying strata have many glacial deposits. These glacial deposits are comprised of sediment and stones that have been deposited during glacial movement, mainly composed of clay, silt, gravel, pebbles, and boulders. The grain size distribution is vast, the structure is different, and there is no stratification (Hart, 1998; Evans et al., 2021). The transport force of glaciers gradually decreases as they melt, resulting in the accumulation of large amounts of fine-grained moraines, which provide a rich source of material for forming glacial debris flows (Meng et al., 2023). With the increase of mining depth and the expansion of the surface collapse area, once the flood season arrives, the rainfall in the mining area, upstream surface runoff, and snow melt water in high mountains drive the surface moraine cover layer (tens of meters and weathered, broken rock debris) into the collapse area, which can easily cause underground mudflow accidents (Zaginaev et al., 2019; Gao et al., 2022). To date, research by both domestic and foreign scholars on glacial debris flow has mostly focused on the formation mechanisms, evolutionary process, risk evaluation and monitoring, and early warning (Marr et al., 2002; Li et al., 2016; Medeu et al., 2022), but research on the specific prevention and control measures for moraine debris flow disasters is needed. In response to the above problems, grouting reinforcement is used to change the moraine from powder to block, improve the integrity and stability of the loose accumulation, and improve the mechanical properties of the moraine as well as to preserve the surface vegetation to the maximum extent (Zhang et al., 2021; Fan et al., 2023). It is therefore important to study the mechanical properties and bearing mechanism of the moraine slurry curing body for both the prevention and control of downhole mudflow and the evaluation of the slurry effect. Coulter et al. (Coulter and Martin, 2006) and others have performed jet grouting in the boring tunnel process of moraine and analyzed the surface settlement of the grouting by numerical simulation in reverse, and the results showed that the narrow settlement trough was formed because of the local shear zone caused by high pressure during jet grouting. Luo et al. (Luo et al., 2019) and others have investigated the effects of different temperatures and envelope pressures on the strength of moraine permafrost by triaxial compression tests, and the results showed that the strength envelope is nonlinear when the average stress is less than the consolidation yield pressure defined as the strength envelope boundary stress, while it is approximately linear when the average stress is greater than the consolidation yield pressure. Li et al. (Li et al., 2022) investigated the effect of different ice forms, such as crushed ice and block ice, on the mechanical properties of moraine soils by triaxial constant strain rate (CSR) with coupled thermomechanical (CTM) tests. The test results show that moraine soils containing block ice have higher peak strength and moraine soils containing crushed ice are more sensitive to temperature changes. Begam et al. (Begam et al., 2018) showed that the height of the moraine dam and the volume of the lake upstream of the dam are the most sensitive parameters affecting the GLOF peak using coupled numerical simulations and indoor similar experimental simulations to verify the moraine dam overflow and erosion damage. Peng et al. (Peng et al., 2022) derived the flow discharge, erosion, entrainment, and deposition processes of glacial debris flows through field investigations and numerical simulations, revealing the origin mechanism and dynamic evolution process of the debris-ice landslide-debris flow hazard chain. Because there are few studies on moraine grouting and curing at home and abroad, the study was conducted with reference to the test and evaluation methods of the strength of fractured rock after grouting. Weng et al. (Weng et al., 2022) showed that the infiltration grouting tests on fractured sandstone samples analyzed the flow and diffusion mechanism of the slurry, and the results showed that the final injection volume of grouting decreased with the increase of temperature and surrounding pressure, and the effective grouting time was inversely proportional to the slurry flow rate, while it was positively correlated with temperature. Zhang et al. (Zhang et al., 2022) investigated the mechanical properties of compressed pre-cracked sandstone before and after grouting by triaxial compression tests with different surrounding pressures, and the results showed that the strength of grouted specimens mainly depended on the micromechanical properties of the contact surface between sandstone and cement paste, and the elastic modulus of grouted specimens was lower than that of uncracked sandstone. Liu et al. (Liu et al., 2022) proposed an NMM-HM grouting model based on the numerical flow form method (NMM) to study the flow of slurry, and the results showed that the fracture grouting pressure could increase the fracture aperture, which is beneficial to grouting efficiency. Salimian et al. (Salimian et al., 2017) performed direct shear tests on grout cracks by preparing specimens with three different surface roughnesses using dental silica gel, and the test results showed that the compressive grout strength increased with decreasing water-cement ratio, but not necessarily with increasing shear strength. Sui et al. (Sui et al., 2015) showed that the two largest factors affecting the sealing efficiency were the initial water flow velocity and the width of the hole diameter, with the former having a greater effect than the latter. Kumar et al. (Kumar et al., 2022) studied the mechanical properties of intact specimens, ungrouted joints, cement joint grout, and epoxy joint grout specimens under dynamic and static loads, and the test results showed that the strength of the epoxy grout joint samples was all greater than that of the cement grout samples.
In summary, research on grouting reinforcement for moraine strata is still in the exploration and development stage. The overlying moraines of the Purang copper mine are mostly composed of fine clay wrapped with stones that are randomly distributed, and the permeability of the soil body is extremely poor under the double extrusion of glacial accumulation and geological movement. Figure 1A shows that the traditional cement slurry cannot be injected permeably. The cement particles and the moraine soil have a noticeable percolation effect. Many cement particles are retained on the moraine’s surface to obstruct the continuous injection of the slurry. Because of the above engineering problems, the modified phosphoric acid-water glass slurry with better injectability is chosen to grout and cure the moraine, and its grouting effect is shown in Figure 1B; under the same grouting conditions, the slurry can be fully diffused in the moraine, and the slurry is distributed along both sides of the splitting channel and forms a large volume of slurry-soil complex at the end of the splitting track. After the grouting is completed, the grouting effect of the reinforced soil needs to be evaluated to determine the feasibility and sustainability of the grouting project. Therefore, this paper investigates the influence law of water glass Baume degree and curing age on moraine slurry curing body through a uniaxial compression test and discusses and analyzes the mechanical properties and energy consumption characteristics of moraine slurry curing, further revealing the damage mechanism of moraine slurry curing body and slurry consolidation mechanism. Based on the regression fitting analysis method, our study establishes a fracture toughness relationship model based on energy analysis and proposes an evaluation method for establishing slurry and the parameters and fracture toughness of the moraine slurry curing body. The results have great significance to engineering theories of moraine slurry reinforcement and the prevention and control of moraine debris flow disasters.

FIGURE 1. Dispersion distribution of different slurry injections: (A) cement slurry; (B) phosphoric acid-water glass slurry.
In this experiment, a modified phosphoric acid-water glass solution was chosen as the grouting material, and the water glass has a Baume degree of 35oB e' and a modulus of 3.05. The test water was ordinary tap water, and the moraine selected for the test was taken from the Pulang copper mine in Yunnan. According to the genesis of the formation, geotechnical type, and physical and mechanical properties, the soil within the 10 m exploration depth of the test site was divided into three layers, and the exploratory pit was excavated to take in-situ soil samples for each layer and carry out the test of physical and chemical indexes of the soil. According to the genesis of the stratum, geotechnical type, and physical and mechanical properties, the soil within the 10 m exploration depth of the test site was divided into three layers, pits were excavated, and in-situ soil samples were taken for each layer. The soil physicochemical index test was carried out, the grain-level composition and XRD patterns are shown in Figure 2 and Figure 3, respectively, and the chemical composition and basic properties of the original moraine formation are shown in Table 1 and Table 2, respectively. From Figure 2, the moraine inhomogeneity coefficient is 113.43, and the curvature coefficient is 2.77, which indicates that the moraine is well-graded and dense. As can be seen from Table 1 and Figure 3, the main constituents of moraines are SiO2, Na2O-Al2O3-6SiO2, and KAl2(AlSi3O) (OH)2, etc., of which quartz and nannofeldspar account for about 53.6% of the total weight, feldspar and quartz are all stable minerals in nature and are widely found in nature, chlorite does not show special properties when exposed to water. It does not contain montmorillonite, illite, Kaolinite, and other water-sensitive minerals (Zhao et al., 2018; Yi et al., 2022). As can be seen from Table 2, the wet density of the moraine stratum is 2.29 g/cm3, the dry density is 2.21 g/cm3, the plastic limit of the soil is 16%, the liquid limit is 22% its low liquid limit powdery clay, the permeability coefficient of the soil is 8.95×10-5 cm/s for the weak permeability level.
The slurry gelation time in actual engineering grouting should be controlled from 30 to 60 min to ensure slurry penetration or diffusion in the grouted reinforced area (Cui et al., 2022). If the gel time is less than 30min, the slurry condenses prematurely, which blocks the grouting line, and if it is more than 60min, the slurry spreads too far in the formation and causes slurry loss. In this experiment, modified phosphoric acid-water glass chemical slurry was used as grouting material, and the suitable gel time of phosphoric acid-water glass slurry with different Baume degrees was explored. This test uses a water glass Baume degree of 35 and modulus of 3.05; phosphoric acid is selected as a medical phosphoric acid solution, with a concentration of 95%. The project examined two-liquid groutings and used diluted phosphoric acid and water glass solution with a volume ratio of 1:1 to carry out the test. First of all, according to the experimental design of water glass, the phosphoric acid solution is diluted with water to get the concentration of water glass solution and the phosphoric acid solution required for the test, and then the diluted, filtered water glass solution and the phosphoric acid solution is poured into the beaker according to the volume ratio of 1:1, and constantly stirred with a glass rod to make it fully react, using the inverted cup method to determine its gel time, the PH of the mixed slurry was measured to record the test data, to avoid test errors for each group tests were performed three times. The average value of gel time was taken after each test was undertaken three times.
In situ moraines have a wide range of particle gradation distribution, with fine to micron-level clay particles as coarse as tens of meters of boulders. Due to the consideration of size effect (Zhu et al., 2020; Zheng et al., 2023) in this experiment, the moraine retrieved from the field was milled, dried, and screened through a 10 mm screen for backup. Tests were undertaken before the drying moraine should be rehydrated to restore the field moisture content after 24 h maintenance. The prepared phosphoric acid-water glass slurry was poured into the mixing bucket and mixed with moraine material, and the slurry was poured into a standard mold measuring 70.7×70.7×70.7 mm. After resting for 24 h for demolding, the specimens were placed in a constant temperature and humidity curing box with a temperature of 20°C and humidity of 90% for 3 days, 7 days and 14 days, respectively. The uniaxial compression test was carried out on the specimens that reached the curing age. This test uses microcomputer-controlled EM3.305 servo single-axis compression equipment, the maximum axial force is 300kN, the displacement control is used to load at a rate of 2 mm/min, and the average value is taken after three parallel tests for each group. The test flow is shown in Figure 4.
The essence of moraine solidification body deformation damage is the combined result of various dissipation and energy releases. Energy dissipation was used to induce internal damage to produce microcracks, leading to the deterioration of material properties and loss of strength. Energy release triggers sudden damage to the solidified body of the moraine (Huang et al., 2021; Li et al., 2021). Assuming that there is no heat energy dissipation during the deformation and damage of the specimen under load, it is known from the principle of energy conservation:
In the formula:
Dissipative energy density and elastic energy density are introduced to analyze the energy consumption characteristics of the specimen, which are calculated as shown in (4) to (5):
The irreversible energy consumed by the pores and microcracks inside the specimen during the bearing process is compacted, or the microcracks expand and connect to form a new fracture surface, which leads to the dissipation of energy. That is, the fracture energy consumed during the deformation and damage of the specimen can be characterized as shown in Equation 6. The relation (7) holds in the linear elastic fracture mechanics when the crack is the stable quasi-static extension, i.e., when the dynamic effect is zero (Dong et al., 2018). At this point, the fracture toughness was introduced to characterize the ability of the specimen to prevent crack expansion, i.e., to reflect the ability of the material to resist brittle fracture (Guo et al., 2005). The expansion law of fracture toughness of moraine solidified specimens is shown in Equation 9:
In the formula:
According to the mechanics of materials and current research (Kivi et al., 2018; Lin et al., 2022; Jiao et al., 2023a; Zou et al., 2023), the area enclosed by the force-displacement curve and the horizontal axis represents the total work done on the material. The area enclosed by the stress-strain curve and the horizontal axis indicates the ability of the material to absorb energy, also known as the strain energy density. The force-displacement curve and stress-strain curve of moraine-cured specimens with a curing age of 14 days and a Baume degree of 20oB e' are used to illustrate the total energy consumption and elastic energy density characterization method. As shown in Figures 5A is the peak load point, the area S1 is enclosed by its pre-peak deformation phase OA, the x-axis is the total pre-peak energy consumption, and the area S2 is enclosed by the post-peak deformation phase AB, and the x-axis is the total post-peak energy consumption. As shown in Figure 5B, Point A is the peak stress point, and the area S1 enclosed by OA and x-axis in its pre-peak deformation phase is the pre-peak elastic energy density, and the area S2 enclosed by AB and x-axis in the post-peak deformation phase is the post-peak elastic energy density. Since the curves of all post-peak deformation stages cannot be recorded during the actual test, to ensure the comparability of the test data, only the pre-peak change stages of the force-displacement curve and the stress-strain curve are studied in this paper.
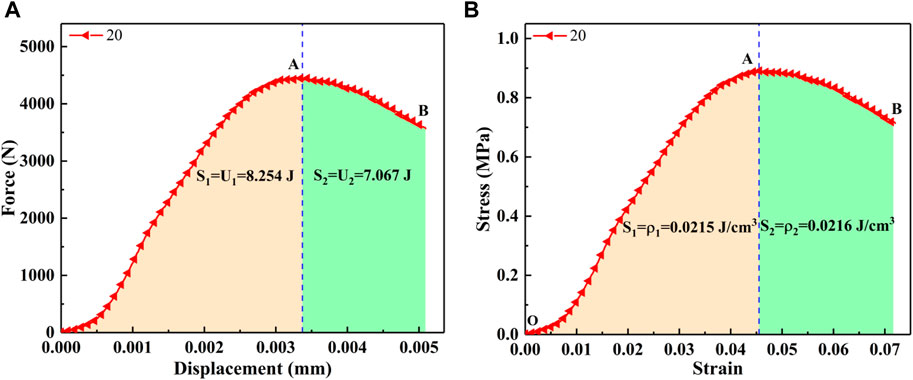
FIGURE 5. Schematic diagram of energy consumption and energy density characterization: (A) Schematic representation of energy consumption; (B) Schematic representation of elastic energy density.
Acidic water glass can gel in a neutral or acidic environment, and the gel is not alkaline, so there is no toxicity because there is no alkali leaching, meaning it does not cause pollution to the environment. It is durable and cheaper than alkaline water glass, so it is widely used. The main anions in the water-glass solution are H2SiO42−and H3SiO4−, and the phosphoric acid solution contains cations H+. The phosphoric acid solution will be added to the water glass solution in the anion and cation reaction. The chemical reaction equation is as follows:
In an acidic water-glass solution, the coordination number of the silicic acid molecule is 6. The silicic acid molecule and positive monovalent silicic acid ion carry out a hydroxyl association reaction to form bisilicicic acid, and the specific chemical reaction equation is as follows:
Bisilicicic acid will polymerize again to trisilicicic acid by hydroxyl linkage reaction, and then continue to polymerize to form polysilicicic acid until the formation of silica sol. As the reaction time continues, the SiO2 particles in the silica sol continue to increase. When the content of SiO2 particles in the sol exceeds a certain value, these particles condense with each other to form an open and continuous gel network structure. The particles in the gel can intermittently condense to form Si-O-Si bonds, eventually forming a silicon gel with a certain degree of stiffness (Koohestani et al., 2021).
As shown in Table 3, the gelation time of phosphoric acid-water glass slurry is non-linearly related to the phosphoric acid addition, and there are mutation points. For example, when the water glass Baume degree is 22oB e', phosphoric acid addition from 10% to 14%, its gel time increased from 2min to 9min relative to each 1% phosphoric acid addition, and its average gel time increased by 1.75min. The gel time increased from 9min to 54min when the acid addition was increased from 14% to 14.5%, and the average gel time increased by 900min for every 1% phosphoric acid addition. The sensitivity of its water glass to the phosphoric acid gel reaction system increases sharply when the phosphoric acid addition exceeds a certain range. As shown in Figure 6, the gel time mutation points of the phosphoric acid-water glass slurry systems with different wavelengths are different. When the phosphoric acid addition amount is less than the phosphoric acid addition amount required for the gel time mutation point, its gel time increases linearly with the increase of the phosphoric acid addition amount. For example, when the water glass Baume degree is 24oB e' its gel time mutation point required phosphoric acid addition is 16.8%. When the phosphoric acid addition is from 10% to 14%, its gel time with phosphoric acid addition follows a linear function y=0.56x-5.07 increasing. This is because the cationic H+ content in phosphoric acid at this stage is not enough to combine with all the anions H2SiO42- and H3SiO4− ions in the water glass solution, and the H+ in phosphoric acid at this stage is quickly consumed to form a chain hydroxyl linkage reaction, so the gel time is very short. As phosphoric acid increases, the H+ ions required to reach the gel time mutation point are sufficient, and the ability of the anions H2SiO42- and H3SiO4− ions in the water glass solution to consume H+ is limited, resulting in a small pH of the solution, so the gel time increases sharply.
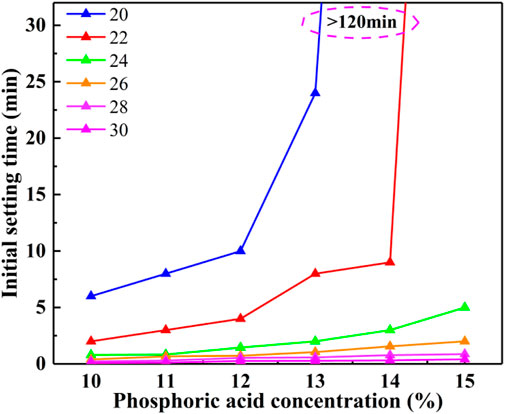
FIGURE 6. Relationship between phosphoric acid concentration and slurry initial setting time at different wavelengths.
To investigate the effect of phosphoric acid-water glass slurry with different wavelengths on the curing effect of moraines, stress-strain curves with a maintenance age of 3 days were selected for analysis. As shown in Figure 7, the stress-strain curves of moraine curing bodies with different wavelengths have the same variation pattern. The stresses all increase slowly with the increase of axial strain and then increase approximately linearly to reach the peak stress point and decay rapidly after reaching the peak stress point. It is suggested that the load-bearing deformation damage of moraine curing bodies with different wavelengths under uniaxial loading are the same type of damage process. In addition, it can be seen from the changing pattern of the curve that the deformation and damage of the solidified body of moraine can all be divided into four stages: initial pressure density, linear elastic deformation, elastic-plastic deformation, and post-peak rupture destabilization. As shown in Figure 8, OA is the initial pressure-density stage. The stress-strain curve of the moraine curing body at the early loading stage is concave, mainly because the moraine curing body is a multi-phase composite damage material. The internal inevitably contains many micro-pores, micro-cracks and bubbles, and other structures. In the uniaxial compression of the moraine curing body, internal micro-pores, micro-cracks, and other structures experience gradual pressure-density closure. The pore volume inside the moraine curing body at this stage gradually decreases with the increase of stress, and the stress growth and radial expansion are smaller. AB is the linear elastic deformation stage. This stage of stress with the increase in strain is a linear growth law. It is mainly because a large number of microcracks and microporous structures previously existing inside the moraine curing body have closed, and the damage deformation of the moraine curing body has entered the elastic deformation stage. Its internal microcracks are in a stable development stage, and the damage is also growing, but it has not yet reached the inflection point of the crack damage stress. BC is the elastoplastic deformation stage. This stage curve shows that with the increase of strain, the stress has a small convexity, reaching the bearing limit C point of the specimen. At this time, the moraine solidification internal body undergoes new crack sprouting, crack interlocking, and crack expansion simultaneously. The internal crack grows rapidly during the non-stationary development stage and the evolution of the damage follows a non-stationary growth trend. The internal specimen has not yet generated a macroscopic crack. At the CD for the peak after rupture destabilization stage, the interconnection between the microcracks will form the moraine curing body in the macroscopic formation of a dominant crack after reaching the peak stress. Its direction is nearly parallel to the main stress direction. Damage takes place during the development of the dominant crack and its rupture (Jiao et al., 2023b). At this stage of the moraine curing body, the bearing capacity decreases sharply whilst retaining a certain strength, meaning the curve shows a gradual decrease in stress with the increase in strain law, and damage deformation shows accelerated evolution until the specimen damaged.
Figure 9 shows the relationship between the compressive strength of the cured body of moraine under early curing age and different water-glass boehmites. The relevant data were fitted, and the results of the fitting showed that the compressive strength of the moraine curing body under the same curing age condition increased linearly with the increase of the water glass Baume degree, which followed the growth law of the unitary linear regression equation
Through the above energy dissipation principle, the energy of the moraine solidified body in different stages of the uniaxial loading process can be calculated, and the total energy before the peak, elastic energy before the peak, dissipation energy before the peak corresponding to the peak stress point of moraine solidified body under different Baume degree and curing age. The relevant data were fitted, as shown in Figure 9. As can be seen from Figure 10, under the same maintenance age conditions, the total energy before the peak, the elastic energy before the peak, and the dissipation energy before the peak linearly increases with the increase of the water glass Baume degree, which follows the one-dimensional linear regression equation
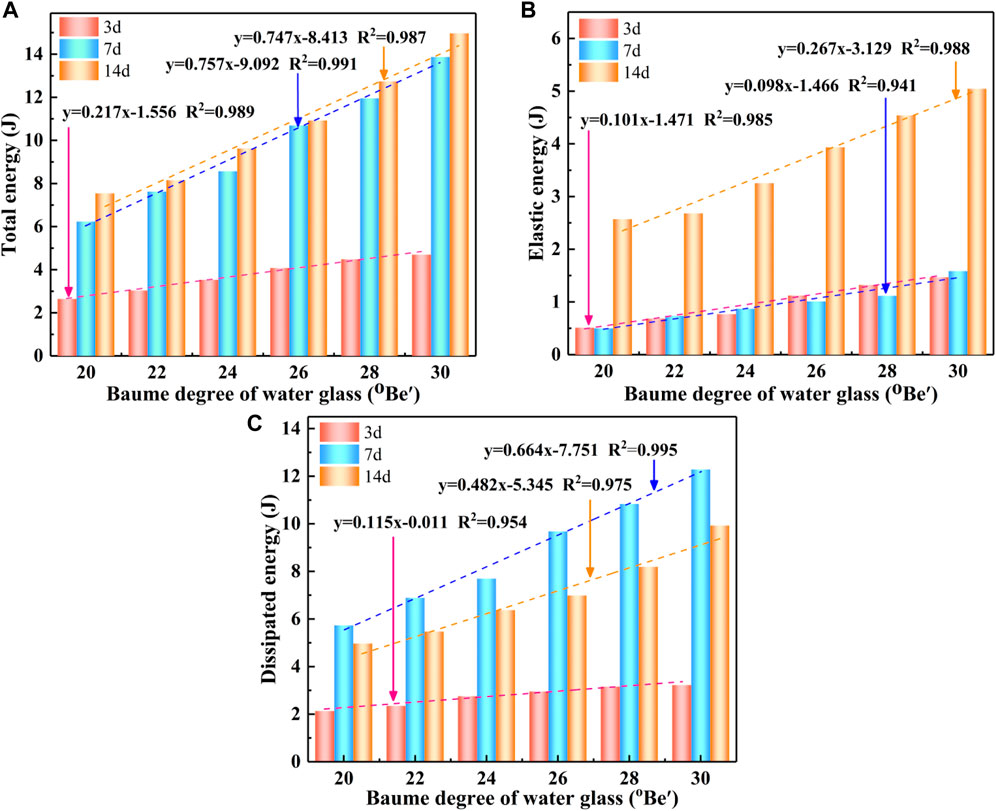
FIGURE 10. Relationship between total energy, elastic energy, dissipative energy, and Baume degree: (A) Total energy; (B) Elastic energy; (C) Dissipation energy.
The essence of the deformation damage of the solidified body of the moraine is the result of the interaction of the energy of the components so that it can be described from the energy point of view: When the curing age is 3 days, the moraine curing body has viscoelastic characteristics, specimen internal hydration reaction is not entirely in the early stage, and at this stage the moraine curing body bearing limit and energy storage capacity are small, resulting in the absorption of smaller energy is sufficient to deformation damage, and at this stage, energy is mainly dissipated in the form of dissipation energy. Although the moraine curing body damage form is mainly manifested in the axial central crack expansion and penetration, the degree of the broken ring depends primarily on the internal microporosity and microfracture structure. Compared to the curing age of 3 days, when the curing age was 7 days, the moraine solidified body specimen’s internal hydration reaction into the middle stage generated more C-S-H gel filled parts in the pore structure to improve the energy storage capacity of the specimen. The total energy before the peak of the moraine solidified body increased at this stage, but the number of hydration products inside the specimen was not enough to link the formation of the skeletal structure. This was because the adhesion between the particles was weak, meaning the bearing limit and energy absorption capacity of the moraine solidified body did not grow significantly, increasing the dissipation energy of the specimen. When the curing age was 14 days, the hydration reaction inside the specimen completely entered the final stage, the number of microcracks and microporosity inside the moraine curing body was obviously reduced, the denseness between the particles was better, and the hydration products are cross-linked to each other as the skeleton, meaning the moraine curing body in the later stage of curing has stronger bearing capacity.
Figure 11 shows the relationship between the moraine curing body and energy consumption density for different Baume degrees. As can be seen from Figure 11, the elastic energy density and dissipative energy density of the moraine curing body increase with the increase of water glass Baume degree under the same maintenance age condition, which follows the law of increasing unity linear function
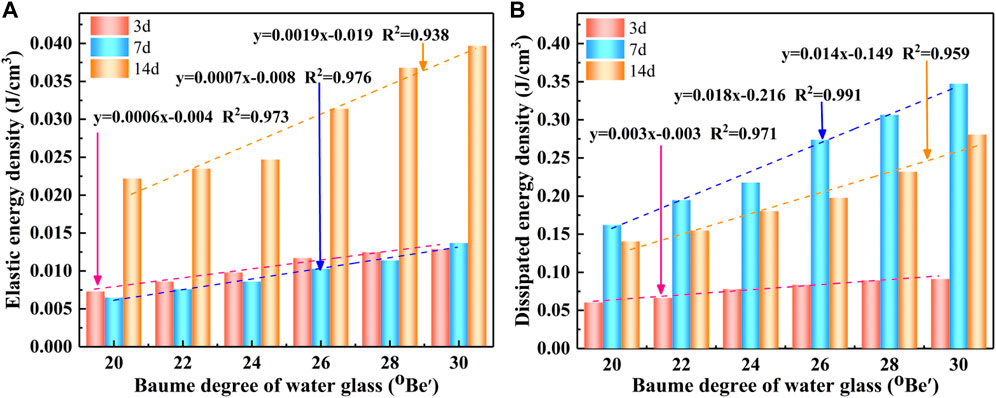
FIGURE 11. Relationship between elastic energy density, dissipative energy density, and Baume degree: (A) Elastic energy density; (B) Dissipation energy density.
Figure 12 shows the peak front fracture toughness versus water glass Baume for moraine-cured bodies with different Baume degrees. To qualitatively analyze the variation law of fracture toughness and water glass Baume degree before the peak of the moraine curing body, the relevant data are linearly fitted to show that the pre-peak fracture toughness of the moraine curing body increases linearly with the increase of the water glass Baume degree under the same curing age condition, which follows a linear unity function
The moraine produced by melting glaciers includes accumulated sediment that is transported into the surrounding landscpae. Surface moraine and side moraine are mostly a mixture of fine particles including soil and stones. When combined with rainfall and ice and snow melt water, moraine soil water content very easily reaches saturation, resulting in the original soil stability structure being destroyed, which quickly collapses to form a debris flow. Moraine debris flow has the characteristics of long movement distance, fast movement speed, and grand scale washout. To effectively prevent and control the debris flow disaster of the moraine in the Pulang copper mine, grouting reinforcement is used to solidify the moraine stratum, solidify the moraine from independent powder fine particles into a whole, and reduce the hazard of debris flow by decreasing the material source of debris flow initiation. It is therefore of great engineering significance to carry out grouting and curing research on moraine soils rich in fine particles to prevent and control moraine debris flow hazards. In this experiment, modified phosphoric acid-water glass slurry was selected as the material used to grout and cure the moraine soil to evaluate the grouting effect by using uniaxial compression equipment. The study analyzed the influence law of water glass Baume degree and the curing age on the energy consumption characteristics and fracture toughness of the grouted fixed body. The calculation formula of the fracture toughness of the moraine was derived and constructed based on the energy consumption principle, the gelling mechanism of phosphoric acid-water glass slurry is revealed, and the suitable slurry ratio is preferred, which is of great significance for the theory of grouting and strengthening of moraine and the mitigation and prevention of glacial debris flow.
Scholars at home and abroad have yet to study the grouting and curing of moraine strata. Yang et al. (Yang et al., 2021) used cement slurry for grouting on moraine slopes with more overhead structures. The effective reinforcement radius was 20–55 cm, and the radius of the hard shell body was only 8–10 cm. In this test, cement slurry and modified phosphoric acid-water glass slurry were used for grouting with a high content of fine particles and poor permeability, and dense moraine formation, respectively, as shown in Figure 13. At the same grouting pressure, the cement slurry spreads in the moraine formation only by splitting, and the effective reinforcement radius is 12–30 cm. While the modified phosphoric acid-water glass grout spreads in the moraine formation by penetration and splitting together, the effective reinforcement radius of the slurry was 50–100cm, and the penetration distance was 20–45 cm. The curing volume was much larger than that of the cement slurry, which indicates that the grouting material has a better grouting effect on the moraine formation with abundant fine particles. This study was mainly based on the principle of energy consumption and evaluates the grouting effect of slurry. Results indicated that the slurry in the moraine stratum diffusion distribution law needs to be further improved, while the test found that the strength of the modified phosphoric acid-water glass slurry, which was used to cure the moraine, was less than 3 MPa. For moraine with a rich content of fine particles, further in-depth study of the poor permeability of the stratum should be undertaken, with the aim of developing a strong injectability and high curing strength of the material.

FIGURE 13. Morphology of the cured body of different slurry injections: (A) cement slurry; (B) phosphoric acid-water glass slurry.
In order to study the curing effect of modified phosphoric acid-water glass slurry on moraine after grouting, the present study investigated initial setting times for phosphoric acid-water glass slurry for grouting and the gelation mechanism of the slurry through the slurry gelation test. The influence law of water glass Baume degree and maintenance age on the mechanical properties, energy consumption characteristics and fracture characteristics of the moraine curing body were analyzed with the help of uniaxial compression test. The research conclusions are as follows.
1) In the phosphoric acid-water glass slurry system, the gel time increases with the addition of phosphoric acid but has a mutation point. The gel time increases linearly with increasing phosphoric acid addition when the required phosphoric acid addition is not reached at the mutation site. After reaching the required phosphoric acid addition at the mutation point, the sensitivity of the water glass to phosphoric acid in the gelation reaction increases sharply, leading to a sharp increase in gelation time. The amount of phosphoric acid addition required for the abrupt gel time change point increases with increasing water glass Baume.
2) The axial stress of the moraine curing body under uniaxial compression is nonlinear with the increase of axial strain. Peak stress increases with increasing water glass Baume degree. The stress-strain curves of different wavelength moraine curing bodies have the same change pattern. Stress is related to the increase of axial strain, which, at first, slowly increases and then shows a near linear increase to reach the peak stress point. The peak stress point is reached after the rapid decay. Its damage evolution process can be divided into four stages the initial pressure density, linear elastic deformation, and elastoplastic deformation after the peak rupture instability.
3) The compressive strength, total pre-peak energy, pre-peak elastic energy, pre-peak dissipation energy, elastic energy density, dissipation energy density, and pre-peak fracture toughness of the moraine curing body under the same curing age conditions show a linear increasing law with the increase of water glass Baume degree. The compressive strength, pre-peak elastic energy, and pre-peak elastic energy density of the moraine curing body increased with the increase of the curing age under different curing age conditions. Despite this, the increase was not the same, and the curing age increased slowly from 3 days to 7 days and increased rapidly from 7 days to 14 days.
4) Moraine solidification body in the curing age of 7 days and 14 days occurs when the total energy before the peak is similar and 1.5 times the total energy before the height of the curing age of 3 days. The curing age from 3days to 7 days and the total energy before the peak increases sharply and in 7 days to 14 days as soon as the growth is slow. The pre-peak dissipation energy, dissipation energy density, and pre-peak fracture toughness of the moraine curing body were at their maximum at a curing age of 7 days and minimum at a curing age of 3 days.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Investigation, Z-rL and S-yW; methodology, Z-rL; conceptualization, M-gJ and S-yW; writing—original draft preparation, Z-rL; funding acquisition, S-yW; writing—review and editing, Z-rL and M-gJ; supervision, Q-tZ and WS; visualization, X-lF; validation, CC; data curation, W-lL. All authors contributed to the article and approved the submitted version.
This research was financially supported by the National Natural Science Foundation of China (Grant No. 51964023), the Yunnan Major Scientific and Technological Projects (Grant No. 202202AG050014), and by Yunnan Fundamental Research Projects (Grant No. 202101BE070001-038; 202201AT070146).
Z-rL, X-lF, Q-tZ were employed by Yunnan Diqing Non-Ferrous Metal Co, Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Begam, S., Sen, D., and Dey, S. (2018). Moraine dam breach and glacial lake outburst flood generation by physical and numerical models. J. Hydrol. 563, 694–710. doi:10.1016/j.jhydrol.2018.06.038
Bi, J., Liu, P., and Gan, F. (2020). Effects of the cooling treatment on the dynamic behavior of ordinary concrete exposed to high temperatures. Constr. Build. Mat. 248, 118688. doi:10.1016/j.conbuildmat.2020.118688
Bi, J., Ning, L., Zhao, Y., Wu, Z., and Wang, C. (2023). Analysis of the microscopic evolution of rock damage based on real-time nuclear magnetic resonance. Rock Mech. Rock Eng. 56, 3399–3411. doi:10.1007/s00603-023-03238-x
Bi, J., Tang, J., Wang, C., Quan, D., and Teng, M. (2022). Crack coalescence behavior of rock-like specimens containing two circular embedded flaws. Lithosphere 11, 9498148. doi:10.2113/2022/9498148
Coulter, S., and Martin, C. (2006). Effect of jet-grouting on surface settlements above the Aeschertunnel, Switzerland. Tunn. Undergr. Sp. Tech. 21, 542–553. doi:10.1016/j.tust.2005.07.005
Cui, Y., Tan, Z., and An, C. (2022). Research and application of multi-functional acrylic resin grouting material. Constr. Build. MATER 359, 129381. doi:10.1016/j.conbuildmat.2022.129381
Dong, L., Jin, L., Xui, D., and Liu, J. (2018). A theoretical method to predict the mechanical properties of concrete considering of the size effect in material. J. Hydraul. Eng. 49, 464–473. doi:10.13243/j.cnki.slxb.20171162
Evans, D., Smith, I., Gosse, J., and Galloway, J. (2021). Glacial landforms and sediments (landsystem) of the smoking hills area, northwest territories, Canada: implications for regional pliocene – pleistocene laurentide ice sheet dynamics. Quat. Sci. Rev. 262, 106958. doi:10.1016/j.quascirev.2021.106958
Fan, H., Xu, Q., Lai, J., Liu, T., Zhu, Z., Zhu, Y., et al. (2023). Stability of the loess tunnel foundation reinforced by jet grouting piles and the influence of reinforcement parameters. Transp. Geotech. 40, 100965. doi:10.1016/j.trgeo.2023.100965
Feng, H., Liang, J., Pang, Y., Zhao, X., Wang, Y., and Sheikh, S. (2022). Effects of the fly ash and water glass on the mechanical properties and water stability of the high ductile magnesium phosphate cement-based composite. Constr. Build. MATER 333, 127395. doi:10.1016/j.conbuildmat.2022.127395
Gao, T., Sun, W., Liu, Z., and Cheng, H. (2022). Investigation on fracture characteristics and failure pattern of inclined layered cemented tailings backfill. Constr. Build. Mater 343, 128110. doi:10.1016/j.conbuildmat.2022.128110
Guo, X., Fang, K., and Leng, F. (2005). Analysis of the theory of fracture energy of concrete. J. Harbin Inst. Technol. 37, 1219–1222. doi:10.3321/j.issn:0367-6234.2005.09.017
Hart, J. (1998). The deforming bed/debris-rich basal ice continuum and its implications for the formation of glacial landforms (flutes) and sediments (melt-out till). Quat. Sci. Rev. 17, 737–754. doi:10.1016/S0277-3791(98)00065-6
Huang, Z., Yilmaz, E., and Cao, S. (2021). Analysis of strength and microstructural characteristics of mine backfills containing fly ash and desulfurized gypsum. Minerals 11, 409. doi:10.3390/min11040409
Jiao, H., Yang, W., Ruan, Z., Yu, J., Liu, J., and Yang, Y. (2023a). The micro-scale mechanism of tailings thickening processing from metal mines. Int. J. Min. Metall. Mater 2023, 2587. doi:10.1007/s12613-022-2587-0
Jiao, H., Zhang, W., Yang, Y., Chen, X., Yang, L., Shen, H., et al. (2023b). Static mechanical characteristics and meso-damage evolution characteristics of layered backfill under the condition of inclined interface. Constr. Build. Mater 366, 130113. doi:10.1016/j.conbuildmat.2022.130113
Kivi, I., Ameri, M., and Molladavoodi, H. (2018). Shale brittleness evaluation based on energy balance analysis of stress-strain curves. J. Pet. Sci. Eng. 167, 1–19. doi:10.1016/j.petrol.2018.03.061
Koohestani, B., Mokhtari, P., Yilmaz, E., Mahdipour, F., and Darban, A. (2021). Geopolymerization mechanism of binder-free mine tailings by sodium silicate. Constr. Build. Mater 268, 121217. doi:10.1016/j.conbuildmat.2020.121217
Kumar, S., Tiwari, G., Parameswaran, V., and Das, A. (2022). Rate-dependent mechanical behavior of jointed rock with an impersistent joint under different infill conditions. J. Rock Mech. Geotech. Eng. 14, 1380–1393. doi:10.1016/j.jrmge.2022.05.002
Li, C., Wang, R., Gu, D., Wang, J., Chen, X., Zhou, J., et al. (2022). Temperature and ice form effects on mechanical behaviors of ice-richmoraine soil of Tianmo valley nearby the Sichuan-Tibet Railway. Eng. Geol. 305, 106713. doi:10.1016/j.enggeo.2022.106713
Li, J., Yilmaz, E., and Cao, S. (2021). Influence of industrial solid waste as filling material on mechanical and microstructural characteristics of cementitious backfills. Constr. Build. Mater 299, 124288. doi:10.1016/j.conbuildmat.2021.124288
Li, L., Tu, W., Shi, S., Chen, J., and Zhang, Y. (2016). Mechanism of water inrush in tunnel construction in karst area. Geomat. Nat. HAZ RISK 7, 35–46. doi:10.1080/19475705.2016.1181342
Lin, H., Liu, J., Yang, J., Ran, L., Ding, G., Wu, Z., et al. (2022). Analysis of damage characteristics and energy evolution of salt rock under triaxial cyclic loading and unloading. J. Energy Storage 56, 106145. doi:10.1016/j.est.2022.106145
Liu, X., Chen, H., Liu, Q., Liu, B., and He, J. (2022). Modelling slurry flowing and analyzing grouting efficiency under hydro-mechanical coupling using numerical manifold method. Eng. Anal. BOUND Elem. 134, 66–78. doi:10.1016/j.enganabound.2021.09.030
Luo, F., Liu, E., and Zhu, Z. (2019). A strength criterion for frozen moraine soils. COLD Reg. Sci. Technol. 164, 102786. doi:10.1016/j.coldregions.2019.102786
Marr, J. G., Anders, E., Harbitz, C., Imran, J., and Harff, P. (2002). Numerical simulation of mud-rich subaqueous debris flows on the glacially active margins of the Svalbard–Barents Sea. Mar. Geol. 188, 351–364. doi:10.1016/S0025-3227(02)00310-9
Medeu, A., Popov, N., Blagovechshenskiy, V., Askarova, M., Medeu, A., Ranova, S., et al. (2022). Moraine-dammed glacial lakes and threat of glacial debris flows in South-East Kazakhstan. Earth-Sci. Rev. 229, 103999. doi:10.1016/j.earscirev.2022.103999
Meng, Z., Lyu, L., Xu, M., Yu, G., Ma, C., Wang, Z., et al. (2023). Effects of frequent debris flows on barrier lake formation, sedimentation and vegetation disturbance, Palongzangbo River, Tibetan Plateau. CATENA 220, 106697. doi:10.1016/j.catena.2022.106697
Noritake, F., Sato, T., Yamamoto, A., Wakabayashi, D., Urakawa, S., and Funamori, N. (2022). Structure of sodium silicate water glass—X-Ray scattering experiments and force-field molecular dynamics simulations. J. NON-CRYST SOLIDS 579, 121370. doi:10.1016/j.jnoncrysol.2021.121370
Peng, D., Zhang, L., Jiang, R., Zhang, S., Shen, P., Lu, W., et al. (2022). Initiation mechanisms and dynamics of a debris flow originated from debris-ice mixture slope failure in southeast Tibet, China. Eng. Geol. 307, 106783. doi:10.1016/j.enggeo.2022.106783
Salimian, M., Baghbanan, A., Hashemolhosseini, H., Dehghanipoodeh, M., and Norouzi, S. (2017). Effect of grouting on shear behavior of rock joint. Int. J. ROCK Mech. Min. 98, 159–166. doi:10.1016/j.ijrmms.2017.07.002
Sui, W., Liu, J., Hu, W., Qi, J., and Zhan, K. (2015). Experimental investigation on sealing efficiency of chemical grouting in rock fracture with flowing water. Tunn. Undergr. Sp. Tech. 50, 239–249. doi:10.1016/j.tust.2015.07.012
Weng, L., Wu, Z., Zhang, S., Liu, Q., and Chu, Z. (2022). Real-time characterization of the grouting diffusion process in fractured sandstone based on the low-field nuclear magnetic resonance technique. Int. J. ROCK Mech. Min. 152, 105060. doi:10.1016/j.ijrmms.2022.105060
Yang, D., Wang, J., Shi, S., and Yang, D. (2021). Reinforcement of the moraine slope with steel screen pipe grouting. Drill. Eng. 48, 89–95. doi:10.12143/j.ztgc.2021.08.014
Yi, Q., Pu, H., Preuße, A., Bian, Z., and Wu, J. (2022). Effect of dry-wet cycles on dynamic mechanic and microstructure of cemented broken mudstone. Constr. Build. MATER 357, 129347. doi:10.1016/j.conbuildmat.2022.129347
Zaginaev, V., Petrakov, D., Erokhin, S., Meleshko, A., Stoffel, M., and Ballesteros-Cánovas, J. (2019). Geomorphic control on regional glacier lake outburst flood and debris flow activity over northern Tien Shan. Glob. Planet. Change 176, 50–59. doi:10.1016/j.gloplacha.2019.03.003
Zhang, C., Yang, J., Fu, J., Wang, S., Yin, J., Xie, Y., et al. (2021). Cement based eco-grouting composite for pre-reinforcement of shallow underground excavation in vegetation protection area. Tunn. Undergr. Sp. Tech. 118, 104188. doi:10.1016/j.tust.2021.104188
Zhang, G., Xiao, M., Zhang, Y., Liu, H., Zhuo, L., Xie, H., et al. (2022). Experimental and numerical study on the mechanical properties of compressively precracked sandstone repaired by grouting. Constr. Build. MATER 350, 12881. doi:10.1016/j.conbuildmat.2022.128816
Zhao, J., Lu, C., Deng, L., and Liu, G. (2018). Impacts of simulated acid solution on the disintegration and cation release of purple rock (mudstone) in Southwest China. GEOMORPHOLOGY 316, 35–43. doi:10.1016/j.geomorph.2018.05.009
Zheng, Y., Zhang, Y., Zhuo, J., Zhang, P., and Hu, S. (2023). Mesoscale synergistic effect mechanism of aggregate grading and specimen size on compressive strength of concrete with large aggregate size. Constr. Build. MATER 367, 130346. doi:10.1016/j.conbuildmat.2023.130346
Zhu, H., Alam, S., and Loukili, A. (2020). An experimental investigation on the correlation between the aggregate size effect and the structural size effect. Eng. Fract. Mech. 234, 107101. doi:10.1016/j.engfracmech.2020.107101
Keywords: moraine, phosphoric acid-water glass, grouting reinforcement, energy dissipation, fracture toughness
Citation: Li Z-r, Jiang M-g, Feng X-l, Wang S-y, Zeng Q-t, Chen C, Liu W-l and Sun W (2023) Analysis of energy consumption characteristics and fracture characteristics of moraine grouting solidified body under uniaxial compression. Front. Earth Sci. 11:1223785. doi: 10.3389/feart.2023.1223785
Received: 16 May 2023; Accepted: 14 August 2023;
Published: 01 September 2023.
Edited by:
Jia-wen Zhou, Sichuan University, ChinaReviewed by:
Chong Xu, Ministry of Emergency Management, ChinaCopyright © 2023 Li, Jiang, Feng, Wang, Zeng, Chen, Liu and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Sun, a211c3Rzd0BrdXN0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.