Failure characteristics and the law of the energy evolution of granite with different pre-crack inclination angles under uniaxial compression loading

Cracks affect the strength of rock masses and eventually threaten their stability in engineering. In order to study the fracture characteristics and mechanical properties of cracked rocks, uniaxial compression tests of pre-cracked granite samples with a central circular through hole were carried out by using MTS816 rock mechanics testing system. The inclination angles of different pre-cracks are 0°, 15°, 30°, 45°, 60°, 75°, and 90° respectively, and the influence of the crack stop hole near the crack tip on the failure behavior of pre-cracked samples is also considered. The results indicate that, compared with the intact sample, the peak strength of pre-cracked samples decreases significantly and is related to the pre-crack inclination angle. The failure mode of the sample varies with the pre-crack inclination angle, and the crack stop hole near the crack tip also has a certain influence on the crack growth to a certain extent. However, in terms of failure mode and its transformation law, the influence of central circular through hole and crack stop hole can be ignored. Generally speaking, the larger the inclination angle of the pre-crack, the more the total energy required for failure of the sample, and the more the stored elastic strain energy. Before the peak strength, the elastic strain energy of the sample is greater than the dissipated energy, after the peak strength, the dissipated energy gradually exceeds the elastic strain energy due to energy conversion. It is found that the pre-crack reduces the energy storage capacity of the sample, and the total energy is ultimately dominated by sample integrity. The dissipated energy rate increases first, then decreases, and finally increases again, the inflection points are the end of micro-crack closure and the peak strength, respectively. The crack stop hole changes the law of energy evolution to a certain extent, which can improve the ability of rocks to accumulate energy when designed at an appropriate position, so as to improve its load-bearing capacity in a certain range. The results display the mechanical properties of pre-cracked granite samples under uniaxial compression and are conducive to its application in engineering.

1 Introduction

It is well known that the stability of rock masses is often determined by different factors (Wang et al., 2023), in nature, the internal defects in rock masses, such as micro-cracks, joints, intergranular pores, are significant factors affecting their mechanical properties and stability (Zhu et al., 2018; Ban et al., 2021; Chen et al., 2022; Sonmez et al., 2022; Zhao et al., 2022; Ban et al., 2023). For example, in underground roadways, tunnels and stopes, unfavorable joint surfaces may lead to rock bursts, and even threaten the safety of underground mining operations. Therefore, the study of the influence of cracks on the mechanical properties of rocks is of great significance in mining and engineering construction.

The mechanical properties of cracked rocks have been a hot topic in the field of rock mechanics for at least half a century. Advances in the mechanics of fracture development have been paralleled by related yet largely independent work on the statistical physics of fracture systems (Griffith, 1924; Schultz, 2000). In order to better study the fracture behavior of rocks, the International Society of Rock Mechanics (ISRM) has recommended some standard test methods (Xie et al., 2023), such as the cracked chevron notched Brazilian disc (CCNBD) test (Fowell, 1995), the short rod (SR) and chevron bend (CB) test (Ouchterlony, 1988), the notch semi-circular bend (NSCB) test (Kuruppu et al., 2014), etc. In recent years, many achievements have also been continuously reported. For example, Aliha and Ayatollahi (2014) observed that the average mode II fracture toughness was considerably larger than that of mode I fracture toughness. Mahdavi et al. (2020) provided comprehensive data for determining the normalized critical crack length of semi-circular bend specimen with chevron notch and under pure mode I loading. In order to characterize the stress field near the crack tip under external stress, many studies on stress intensity factors have been carried out. Ayatollahi et al. (2016) calculated the minimum dimensionless stress intensity factors of semi-circular bend specimen (SCB) with straight-through and chevron notches. Combined with the finite element analysis of three kinds of Brazilian disc samples with prefabricated widths less than 2 mm, it is found that the dimensionless stress intensity factor increases with crack width increasing (Li C. et al., 2019).

Currently, some researchers have focused on the failure characteristics of different fractured rocks. Zhong et al. (2020) observed that fractures were initiated at the tips of pre-existing cracks and rapidly propagated to upper mortar-granite bonded surfaces. Xiong et al. (2022) found two main fracture evolution processes of sandstone containing intersecting fissures under uniaxial compression. Based on the experimental results, Liu and Lv (2019) proposed a new model to calculate the growth path of wing cracks under compressive shear stress. Li S. et al. (2019) stated that the flaw inclination angle had little effect on the optimum index, but had a certain effect on sample fracture modes. Nara et al. (2017) stated that the crack velocity increased with increasing temperature and/or relative humidity. The crack propagation in rock sample with inclined crack under uniaxial compression had been investigated by Eftekhari et al. (2016). The progressive failure and mechanical properties of pre-cracked marble with planar or non-planar cracks were studied by using the lattice-spring-based synthetic rock mass (LS-SRM) modeling method (Bastola and Cai, 2019).

Moreover, digital image correlation (DIC) and acoustic emission (AE) technology were used to study the influence of bolt on fracture behavior of infilled jointed rock under uniaxial loading (Li et al., 2023). The freeze-thaw failure characteristics and strength loss of non-penetrating fractured rock mass with different fracture densities were studied by means of theoretical derivation and laboratory tests (Chen et al., 2023a). Wang et al. (2021) declared that the peak strength and elastic modulus first decrease and then increase as the crack inclination angle increases. Zhao et al. (2017) investigated the mechanical and permeability properties of fractured limestone during full-range stress-strain processes. With the development of computer technology, advanced numerical simulation technology has been widely applied in geotechnical engineering (Lei et al., 2022), taking the study of fractured rocks as an example, a grain-based distinct element model (GBM) was used to investigate the influence of grain size on the fracturing response of pre-cracked granite (Saadat and Taheri, 2019). Chen et al. (2023b) discussed the internal relations among compression-shear angle, fracture distribution and crack propagation, and the changes in mechanical properties of cracked rock samples were explored combining with the discrete element method. Haeri et al. (2015) carried out a coupled numerical-experimental analysis on crack propagation, crack coalescence and failure process of jointed rock slopes.

The deformation and failure of rocks are caused by the continuous input of external energy (Tang et al., 2021), therefore, the study of the failure process of rocks from the perspective of energy is conducive to exploring the mechanical mechanism of its failure. Yu et al. (2022) discussed the relationship among the strain energy, volume fraction, confining pressure and failure mode of the backfill-encased-rock through triaxial compression test, acoustic emission, and microscopic tomography. Lin H. et al. (2022) concluded that the dissipated energy difference increases with the increase of confining pressure when the strain increases to a certain value. Gong et al. (2022a) and Gong et al. (2022b) put forward and verified the damage constitutive model of brittle rock based on linear energy dissipation law. Xu et al. (2021) found that the total input energy density, elastic strain energy density, and dissipated energy density of the red sandstone with five different fracture dip angles show obvious quadratic growth in response to the actual unloading stress. There is a good consistency between the experimentally obtained fracture loads and the theoretical predictions based on the constancy of the mean strain energy density over the material volume (Razavi et al., 2018). Bertram and Kalthoff (2003) found that the energy dissipated by a crack propagating at a high velocity was almost two orders of magnitude larger than the energy to initiate a crack. The relationship between energy dissipation and fracture mechanism in graphite fracture zone was evaluated by a tri-linear softening model (Tang et al., 2021).

The above discussion indicates that the mechanical properties of cracked rocks have been one of the hot topics concerned by scholars all over the world, and their achievements also provide an important reference for this study. In this experiment, the pre-cracked granite samples with seven different inclination angles were prepared, different from the traditional oblique straight pre-crack, a central circular through hole with a diameter of 5 mm was drilled at the center of the sample. In addition, for samples with pre-crack inclination angle of 45°, the influence of the crack stop hole near the crack tip is considered. In brief, we discussed the failure behavior of pre-cracked samples under uniaxial compression, and analyzed the laws of their energy evolution. The results verify the mechanical properties of this type of granite, which is conducive to its application in engineering.

2 Preparation and methods

2.1 Test sample and equipment

Experiment is an important research method in the field of geotechnical engineering (Kang et al., 2022; Lin S. Q. et al., 2022; Wang et al., 2022; Zhao et al., 2023). In this study, the common granite was selected as the research object. The granite samples obtained after processing have no obvious joints and cracks, and have a very good compositional homogeneity. Its shape is a thin cuboid with length, width and thickness equal to 160, 80, and 10 mm respectively. In addition, there is a circular through hole with a diameter of 5 mm in the center of the sample, an oblique straight pre-crack passes through the hole, and their centers coincide with each other. The length and width of the pre-crack are 10 and 1 mm respectively. The pre-crack inclination angles α are 0°, 15°, 30°, 45°, 60°, 75°, and 90° respectively. The left side of Figure 1 shows a typical sample, its pre-crack inclination angle α is equal to 45°.

FIGURE 1

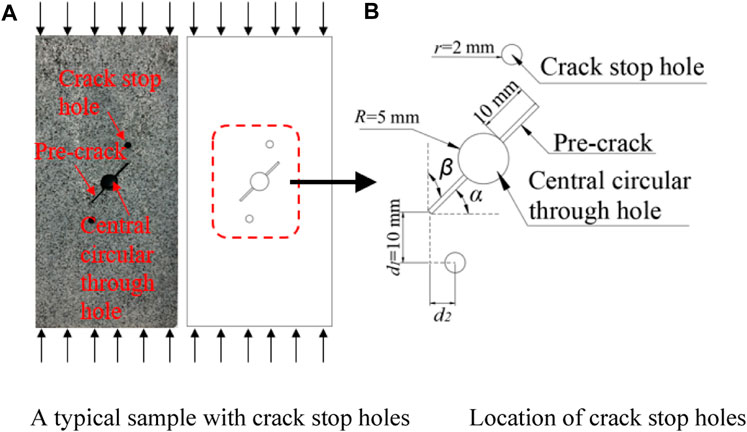
FIGURE 1. A typical sample with pre-crack inclination angle equal to 45° and the location of crack stop holes. (A) A typical sample with crack stop holes. (B) Location of crack stop holes.

In order to study the influence of crack stop holes on the failure behavior of granite samples, for some samples with pre-crack inclination angle equal to 45°, a crack stop hole was drilled near each end of the pre-crack for comparative analysis. The function of the crack stop hole is to prevent further propagation of cracks in areas where stress is easily concentrated (Deng et al., 2022). Nevertheless, the role of crack stop hole in this study is to change the crack growth path, therefore, it is arranged near the route of wing crack propagation, as shown in Figure 1. The vertical distance d₁ from the center of the crack stop hole to the tip of the pre-crack is 10 mm, while the corresponding horizontal distance d₂ from their center to the corresponding pre-crack tip is 0, 5, and 10 mm respectively, and the radius of the crack stop hole is 2 mm. Figure 1 shows two typical crack stop holes with a horizontal distance of 5 mm and a vertical distance of 10 mm.

Uniaxial compression test was carried out by MTS816 rock mechanics testing system, as shown in Figure 2. During the test, the axial stress was applied to samples by displacement control, and the loading rate was 0.002 mm/s. The system can automatically acquire parameters such as time, axial load and displacement, etc., and the collection interval was set to 0.1 s.

FIGURE 2

FIGURE 2. MTS816 rock mechanics testing system and its main components.

2.2 Principle of energy calculation

Energy evolution plays an important role in the analysis of mechanical characteristics, there are mainly four types of energy changes in the process of rock failure under external load, namely, energy input, energy accumulation, energy dissipation and energy release. According to the laws of thermodynamics, based on the assumption that there is no heat exchange with the external environment during loading, and ignoring the energy released through thermal radiation, heat exchange and other forms, the total energy input from the outside is completely converted into elastic strain energy and dissipated energy inside the sample (Peng et al., 2020). Therefore, the energy of the pre-cracked granite sample under uniaxial compression is calculated as follows (Liu et al., 2020; Qiao et al., 2022).

$U=U_e+U_d(1)$

where U is the total energy input from the outside, MJ·mm⁻³; U_e is the elastic strain energy, MJ·mm⁻³; U_d is the dissipated energy, MJ·mm⁻³.

In the principal stress space, the total energy and elastic strain energy absorbed by sample element can be calculated by the following formula (Liu et al., 2020):

$U={\int }_0^{{\epsilon }_1}{\sigma }_{1}d{\epsilon }_1+{\int }_0^{{\epsilon }_2}{\sigma }_{2}d{\epsilon }_2+{\int }_0^{{\epsilon }_3}{\sigma }_{3}d{\epsilon }_3(2)$

$U_e=\frac{1}{2}{\sigma }_1{\epsilon }_1^e+\frac{1}{2}{\sigma }_2{\epsilon }_2^e+\frac{1}{2}{\sigma }_3{\epsilon }_3^e(3)$

${\epsilon }_i^e=\frac{1}{E_i}\left[{\sigma }_i-{\mu }_i\left({\sigma }_j+{\sigma }_k\right)\right](4)$

where ${\sigma }_i$, ${\sigma }_j$, ${\sigma }_k$ ($i$, $j$, $k$ =1, 2, 3) are the principal stresses in each direction; ${\epsilon }_i$, ${\epsilon }_i^e$ are the total strain and elastic strain in each principal stress direction; ${\mu }_i$, $E_i$ are Poisson’s ratio and elastic modulus during the unloading stage, which can be replaced by ${\mu }_0$, $E_0$ at elastic stage (Xie et al., 2008).

In this study, it should be noted here that the elastic modulus of pre-cracked granite samples should be called apparent stiffness. Under uniaxial compression, the circumferential stress is 0 MPa, and only the axial stress does work. Therefore, according to Eqs 2–4, the energy can be calculated as follows (Liu et al., 2020; Qiao et al., 2022):

$U={\int }_0^{{\epsilon }_i}{\sigma }_{1}d{\epsilon }_1={\sum }_{i=1}^n\frac{1}{2}\left[{\sigma }_{1\left(i\right)}+{\sigma }_{1\left(i-1\right)}\right]\left[{\epsilon }_{1\left(i\right)}+{\epsilon }_{1\left(i-1\right)}\right](5)$

$U_e=\frac{1}{2}{\sigma }_1{\epsilon }_1^e=U_e=\frac{1}{2}{\sigma }_1\frac{{\sigma }_1}{E_0}=\frac{{\sigma }_1^2}{2E_0}(6)$

where ${\sigma }_{1\left(i\right)}$, ${\epsilon }_{1\left(i\right)}$ are the stress and strain values corresponding to each point on the stress-strain curve.

According to Eqs 1, 5, 6, the dissipated energy of the sample is the difference between the total energy and the elastic strain energy (Peng et al., 2020).

$U_d=U-U_e={\sum }_{i=1}^n\frac{1}{2}\left[{\sigma }_{1\left(i\right)}+{\sigma }_{1\left(i-1\right)}\right]\left[{\epsilon }_{1\left(i\right)}+{\epsilon }_{1\left(i-1\right)}\right]-\frac{{\sigma }_1^2}{2E_0}(7)$

3 Results

3.1 Variation of mechanical parameters

It can be seen from Figure 3A that the trend of stress-strain curves of samples with different pre-crack inclination angles is basically consistent with that of samples without cracks, and they all go through four stages, namely, micro-crack compaction stage, elastic deformation stage, unstable fracture development stage and post failure stage. In addition, the peak strength of the pre-cracked samples is always lower than that of the sample without pre-cracks, indicating that pre-crack reduces the peak strength of the granite sample, and make it more vulnerable to damage.

FIGURE 3

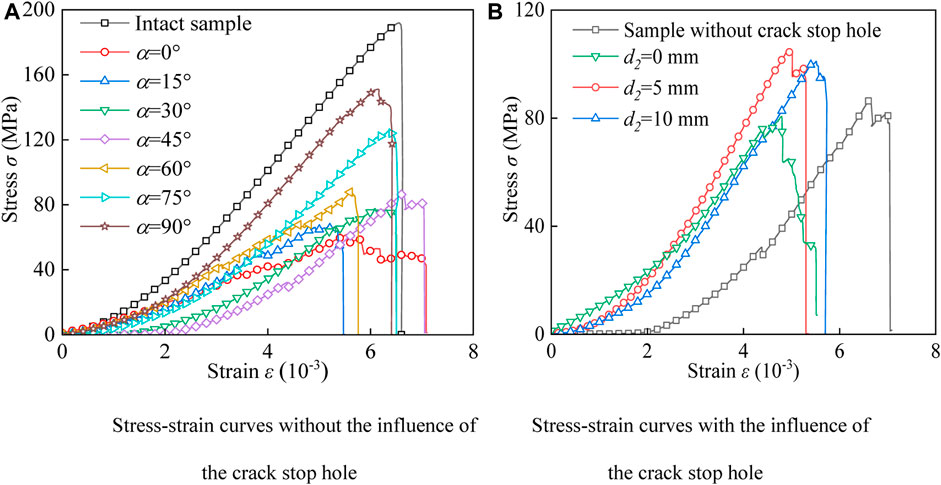
FIGURE 3. Stress-strain curves of different granite samples. (A) Stress-strain curves without the influence of the crack stop hole. (B) Stress-strain curves with the influence of the crack stop hole.

As shown in Figure 3B, for granite samples with pre-crack inclination angle of 45°, crack stop hole has a certain influence on the stress-strain curve. When the horizontal distance d₂ between the center of the crack stop hole and the tip of the pre-crack is equal to 0 mm, the peak strength of the sample is slightly lower than that of the one without crack stop hole. However, when the horizontal distance d₂ is equal to 5 and 10 mm, the peak strength is increased slightly. Moreover, the overall strain decreases under the influence of crack stop hole, indicating that the crack stop hole reduces the ductility of the sample before failure. Although there are differences in the position of crack stop holes, the distance between curves is closer than that of the sample without crack stop holes, and the slope of the stress-strain curve is larger than that of the sample without crack stop holes, indicating that crack stop holes increase the apparent stiffness of granite samples. Finally, in Figures 3A, B, the stress-strain curve drops rapidly after the peak strength, reflecting the brittle fracture characteristics of granite.

Figure 4 shows the peak strength of different pre-cracked granite samples, it can be seen that the peak strength increases with the increase of the inclination angle, as shown in Figure 4A. When the inclination angle of the pre-crack is 0°, the peak strength of the sample reaches the lowest value equal to 49.22 MPa, and when the inclination angle rises to 90°, the peak strength increases to 151.14 MPa. According to fracture mechanics theory and Figure 5, the stress field near the crack tip in polar coordinate system can be obtained (Zhang et al., 2020), as shown in Eq. 8.

$\left\{\begin{array}{l}{\sigma }_r=\frac{1}{2\sqrt{2\pi r}}\left[K_{Ⅰ}\left(3-\cos \theta \right)\cos \frac{\theta }{2}+K_{Ⅱ}\left(3\cos \theta -1\right)\sin \frac{\theta }{2}\right]\\ {\sigma }_{\theta }=\frac{1}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[K_{Ⅰ}\left(1+\cos \theta \right)-3K_{Ⅱ}\sin \theta \right]\\ {\tau }_{r\theta }=\frac{1}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[K_{Ⅰ}\sin \theta +K_{Ⅱ}\left(3\cos \theta -1\right)\right]\end{array}\right.(8)$

where σ_r is the radial stress; σ_θ is the circumferential stress; τ_rθ is the shear stress; θ is the angle in polar coordinate system; r is the distance from the crack tip; K_I and K_II are the stress intensity factors of type I and II cracks, respectively.

FIGURE 4

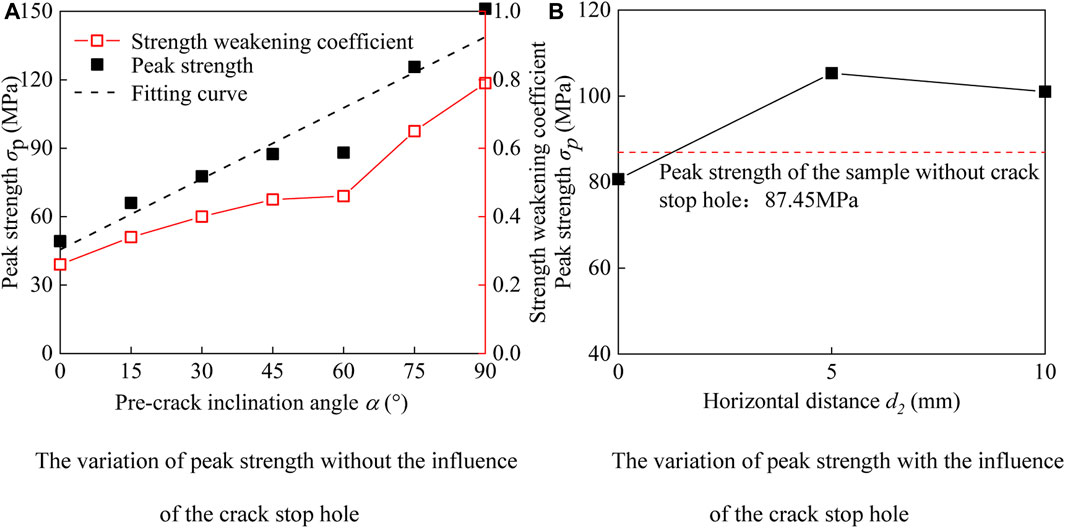
FIGURE 4. The variation of peak strength of pre-cracked granite samples. (A) The variation of peak strength without the influence of the crack stop hole. (B) The variation of peak strength with the influence of the crack stop hole.

FIGURE 5

FIGURE 5. Stress components at the crack tip in polar coordinate system.

Under uniaxial compression, the pre-cracked granite sample is only subjected to axial stress. Therefore, for an open crack, K_I and K_II are determined by Eq. 9.

$\left\{\begin{array}{l}{K}_{Ⅰ}={\sigma }_1\sqrt{\pi a}\sin 2\beta \\ K_{Ⅱ}={\sigma }_1\sqrt{\pi a}\sin \beta \cos \beta \end{array}\right.(9)$

where a is half the length of the long axis of the crack and equal to the distance from the crack tip to the crack center; β is the angle between crack strike and the direction of axial stress, as shown in Figure 1B.

According to Eq. 9, when β is equal to 90°, that is, the pre-crack inclination angle α (see Figure 1) is 0°, in this case, K_I obtains the maximum value and K_II = 0, therefore, it only shows the characteristics of type I crack. Considering that the tensile strength of rocks is far lower than the shear strength and compressive strength, the granite sample with pre-crack inclination angle of 0° does have the lowest peak strength. As pre-crack inclination angle increases, K_I gradually decreases, K_II is no longer zero, and the sample shows the characteristics of both type I and II cracks. Moreover, the width of the pre-crack in this study is 1 mm, according to the results obtained by Zhang et al. (2020), when the crack width is greater than 0.8 mm, the peak strength decreases with the increase of β, and the minimum value is obtained when β = 90°. When β = 0°, the pre-crack inclination angle α is 90°, both K_I and K_II are equal to zero, indicating that there is no stress concentration at the crack tip, in this case, the pre-cracked granite sample obtains the highest value of peak strength. Combined with the experimental results in this paper, it can be seen that the theoretical results mentioned above have been verified again.

For pre-cracked samples with crack stop holes, the peak strength changes with the horizontal distance d₂ between the crack stop hole and the crack tip from 0 to 10 mm, as shown in Figures 3B, 4B. In detail, the peak strength is 80.68 MPa when the horizontal distance d₂ is 0 mm, which is smaller than the peak strength of the sample without crack stop holes (87.45 MPa). The peak strength increases to 105.33 MPa when the horizontal distance d₂ is equal to 5 mm, and decreases to 101.02 MPa when d₂ is equal to 10 mm. It is estimated that the crack stop hole changes the law of crack propagation, resulting in changes in stress distribution. Therefore, there is a reasonable location of the crack stop hole to obtain the extreme value of the peak strength of the pre-cracked granite sample. In summary, the arrangement of the crack stop hole plays an important role in improving the stability of the structure of cracked rocks.

The peak strength of pre-cracked granite samples under uniaxial compression is positively and linearly correlated with the inclination angle of the pre-crack, and the fitting equation is as follows:

${\sigma }_p=1.04\alpha +45.54\left(R^2=0.92\right)(10)$

where ${\sigma }_p$ represents the peak strength of the pre-cracked granite samples, MPa; α is the pre-crack inclination angle, °, as shown in Figure 1B.

The ratio of the peak strength of the pre-cracked sample to the peak strength of the intact sample is defined as strength weakening coefficient to characterize the weakening degree of the peak strength of granite caused by pre-crack inclination angle, as shown in Figure 4A. When the pre-crack inclination angle is 0°, the peak strength of the sample is only 26% of that of the intact sample. When the pre-crack inclination angle increases from 0° to 60°, the strength weakening coefficient increases from 0.26 to 0.46, indicating that the peak strength of the pre-cracked granite sample increases relatively slowly. However, when the pre-crack inclination angle increases from 60° to 90°, the peak strength increases relatively quickly, for example, the peak strength is 78.73% of that of intact sample when the inclination angle is 90°.

The slope of the straight line segment of the stress-strain curve is defined as the elastic modulus of the rock. However, considering that the elastic modulus is only related to the performance of the rock, such as lithology, composition, particle size, water content and pore size, therefore, the so-called elastic modulus here should actually be regarded as apparent stiffness. According to the stress-strain curve in Figure 3, the apparent stiffness of different pre-cracked samples can be obtained, as shown in Figure 6. It can be seen that the apparent stiffness increases linearly with the increase of the pre-crack inclination angle. The linear fitting equation is as follows:

$E_t=0.21\alpha +17.29\left(R^2=0.98\right)(11)$

where $E_t$ is the apparent stiffness of different pre-cracked granite samples, MPa.

FIGURE 6

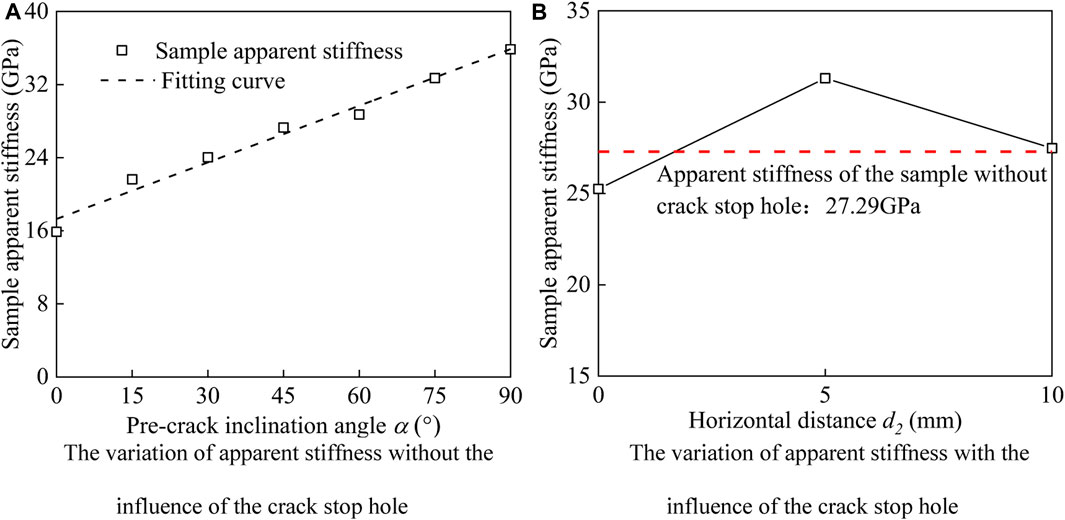
FIGURE 6. The variation of apparent stiffness of pre-cracked granite samples. (A) The variation of apparent stiffness without the influence of the crack stop hole. (B) The variation of apparent stiffness with the influence of the crack stop hole.

3.2 Failure mode

The failure mode of the sample is a key feature reflecting its failure mechanism (Li et al., 2022). Generally speaking, the failure of the sample starts from the initial cracking, and then the crack propagates until it penetrates the sample. In this study, as the pre-crack inclination angle increases, the characteristics of tensile failure gradually weaken, while the characteristics of shear failure strengthen, and shear failure plays a dominant role during this process, as shown in Figure 7A, this characteristic can be clearly seen as the inclination angle increases from 0° to 90°. For example, when α = 0°, a tensile crack initially forms and propagates on the upper edges of the central circular through hole, however, as the pre-crack gradually closed during the loading process, the wing crack appears at the pre-crack tip, whose growth rate is gradually faster than that of the initial tensile crack, and finally the tensile failure mode is dominant, and the tensile crack still penetrates the upper part of the sample. Moreover, the number of cracks caused by shear increases with the increase of the pre-crack inclination angle, including wing cracks and secondary cracks, especially when α = 90°, the shear failure characteristics are more significant.

FIGURE 7

FIGURE 7. Different failure modes of pre-cracked granite samples. (A) Failure modes of pre-cracked granite examples without crack stop holes. (B) Failure modes of pre-cracked granite examples with crack stop holes.

It can be seen from Figure 7B that, the crack propagation of samples is significantly affected by crack stop holes. The number of cracks after sample failure is relatively minimum when the horizontal distance d₂ is equal to 0 mm, is maximum when d₂ = 5 mm, and ranks second when d₂ = 10 mm. This is closely related to the variation of peak strength of granite samples, in general, the more crack propagation, the higher the peak strength.

3.3 Energy evolution

According to Eqs 1–3, the total energy, elastic strain energy and dissipation energy of different granite samples during uniaxial compression can be calculated respectively, the results are depicted in Figures 8, 9. It can be seen from Figure 8A that the change of total energy of different samples is roughly similar, that is, the total energy absorbed by each sample increases non-linearly. Except when α = 0°, the total energy increases with the increase of the pre-crack inclination angle, indicating that the larger the pre-crack inclination angle, the more energy the sample consumes during the failure process, which reflects the compression resistance of the sample macroscopically. In Figure 8B, the change of elastic strain energy is similar to the change of stress-strain curve, showing a non-linear increase at first and then a rapid decline, that is, the elastic strain energy is released rapidly after the peak strength, resulting in rapid failure of rock samples, especially when the pre-crack inclination angle is relatively large. In addition, similar to the total energy, the elastic strain energy increases with the increase of the pre-crack inclination angle, except when α = 0°, indicating that the energy storage capacity of the sample increases.

FIGURE 8

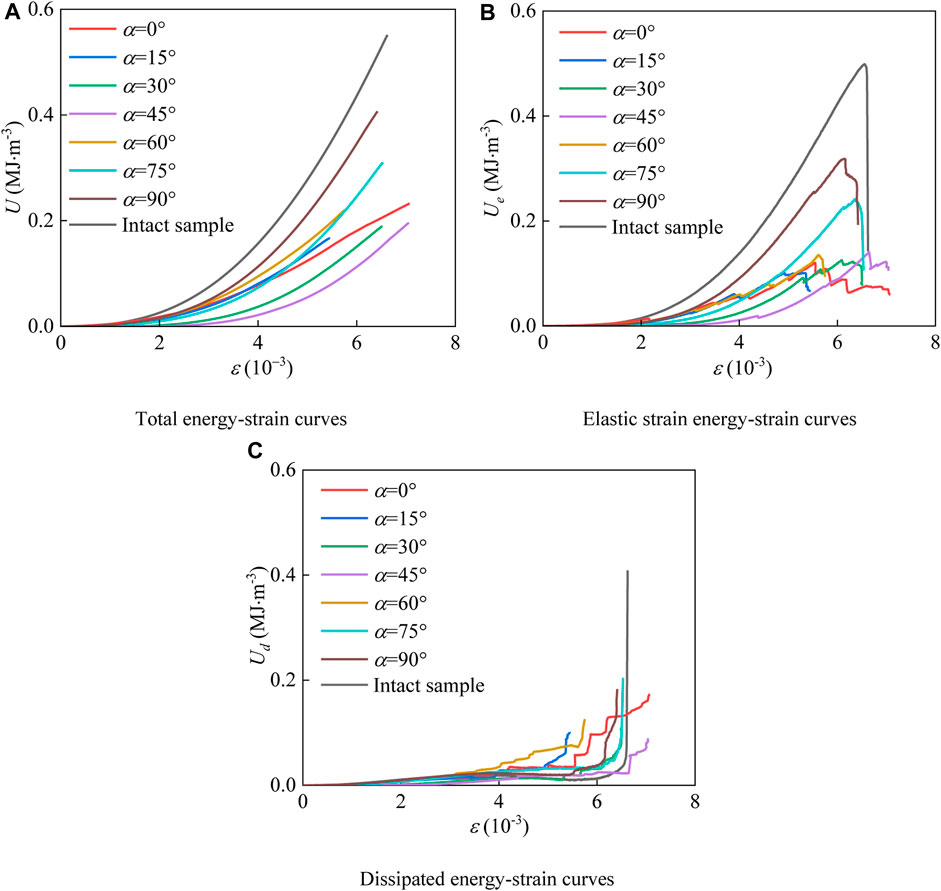
FIGURE 8. The variation of different energy-strain curves of granite samples without crack stop holes. (A) Total energy-strain curves. (B) Elastic strain energy-strain curves. (C) Dissipated energy-strain curves.

FIGURE 9

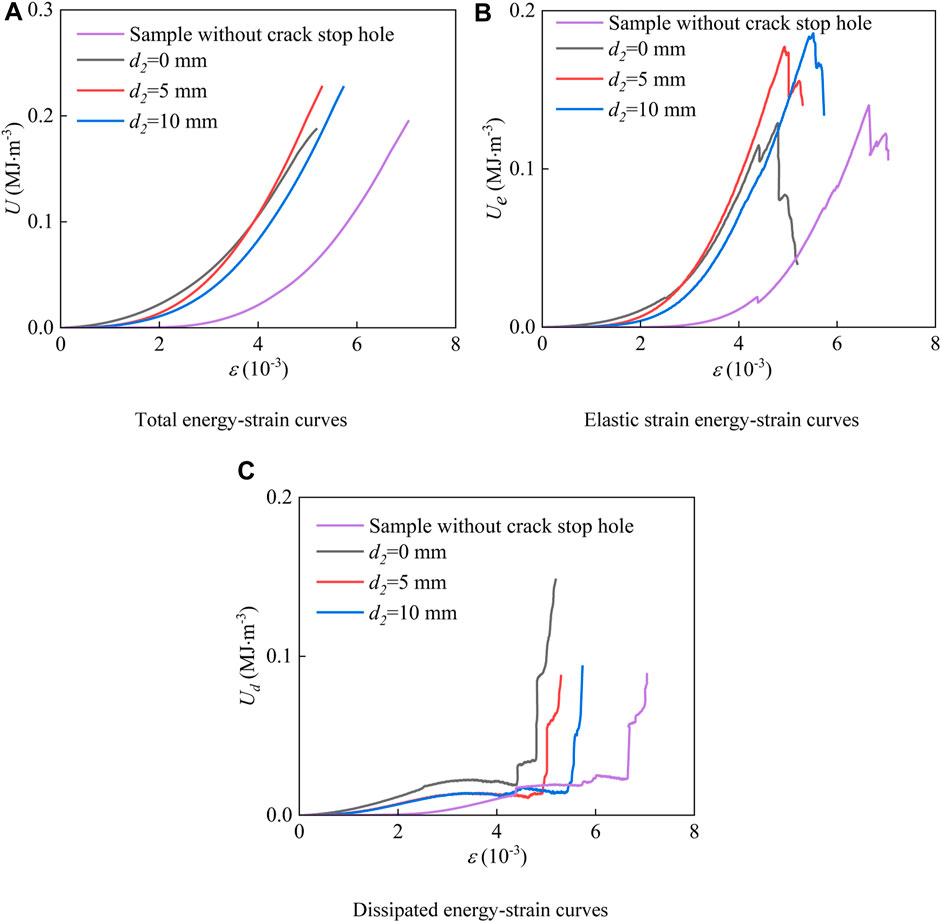
FIGURE 9. Energy variation of pre-cracked granite samples with crack stop holes. (A) Total energy-strain curves. (B) Elastic strain energy-strain curves. (C) Dissipated energy-strain curves.

In Figure 8C, dissipated energy increases slowly and linearly at first, and then rapidly and non-linearly after reaching the peak strength. The reason why the dissipated energy increases slowly before the peak strength is that most of the energy is stored as elastic strain energy. After the peak strength, the elastic strain energy is released rapidly, leading to a rapid increase in dissipated energy. It should be noted that the data of elastic strain energy and dissipated energy in the residual stage cannot be collected due to the rapid failure of the sample after the peak strength.

It can be seen from Figures 9A, B that, under the influence of the crack stop hole, the total energy and elastic strain energy stored in the sample increase under the same strain. In addition, compared with the sample without crack stop hole, the total energy-strain curve and elastic strain energy-strain curve of the sample are closer to each other respectively, and the crack stop hole reduces the total strain. When d₂ = 0 mm, the total energy and elastic strain energy are smaller than those without crack stop holes. When d₂ = 5 mm and 10 mm, both types of energy are greater than those without crack stop holes. The results show that if the horizontal distance d₂ is relatively small, the elastic strain energy of the sample will be reduced, therefore, the reasonable arrangement of crack stop holes can improve the energy storage capacity of the sample.

When the peak strength is reached, the elastic strain energy reaches the maximum value. If the loading continues, the elastic strain energy is released in the form of dissipated energy, resulting in a rapid growth of dissipated energy after the peak strength, as shown in Figure 9C.

The various energies of different samples at peak strength are shown in Table 1. It can be seen that the elastic strain energy of intact sample at peak strength accounts for 92.43%, while the dissipated energy accounts for 7.57%. For samples with pre-crack inclination angles of 0°, 15°, 30°, 45°, 60°, 75°, 90°, elastic strain energy accounts for 64.87%, 75.71%, 70.03%, 85.64%, 64.81%, 83.47%, 86.42% respectively, and dissipated energy accounts for 35.13%, 24.29%, 29.97%, 14.36%, 35.19%, 16.53%, 13.58% respectively. For the sample with crack stop holes, the elastic strain energy accounts for 78.69%, 92.39%, 89.51% respectively, and the dissipated energy accounts for 21.31%, 7.61%, 10.49% respectively. It shows that the elastic strain energy at peak strength is far more than the dissipated energy, in addition, the storage capacity of elastic strain energy of the intact sample is stronger than that of the pre-cracked samples.

TABLE 1

TABLE 1. Energy values and their proportions of typical samples at peak strength.

The pre-crack significantly reduces the total energy absorbed by the sample, which may be due to the reduction of peak strength caused by the pre-crack, thus reducing its energy storage capacity. The total energy, elastic strain energy and their proportion can be increased within a limited range by crack stop holes, and both kinds of energy are ultimately dominated by the integrity of the sample. According to Table 1, the elastic strain energy and dissipated energy of each sample at peak strength are shown in Figure 10. Generally speaking, the elastic strain energy increases non-linearly with the increase of pre-crack inclination angle, and can be expressed by Eq. 12. The dissipated energy fluctuates between 0.032 and 0.073, and its distribution can be expressed mainly by Eq. 13. It should be noted that Eq. 13 does not consider the values of points where the pre-crack inclination angle is 30° and 60° in Figure 10, otherwise the correlation coefficient will fall to a relatively low value. The reason may be that the dissipation energy is very small at peak strength, and its slight fluctuation can easily lead to a larger change in the correlation coefficient. In addition, the dispersion of granite samples increases the difference of dissipated energy.

$U_e=-0.00164\alpha +4.26{\alpha }^2*{10}^{-5}+0.116\left(R^2=0.93\right)(12)$

$U_d=-0.00134\alpha +1.501{\alpha }^2*{10}^{-5}+0.0547\left(R^2=0.79\right)(13)$

FIGURE 10

FIGURE 10. The variation of elastic strain energy and dissipated energy at peak strength.

3.4 Change in dissipated energy rate

The mechanical behavior of rock sample under uniaxial compression can be reflected by energy dissipation (Lin H. et al., 2022). The ratio of dissipated energy to total energy is defined as the dissipated energy rate η_e, as shown in Eq. 14, which reflects the relationship between the dissipated energy and the total energy during loading.

${\eta }_e=\frac{U_e}{U}(14)$

The variation of dissipated energy rate of each sample with axial strain is shown in Figure 11. The dissipated energy rate increases first and then decreases during the microcracks compaction stage. The reason may be that the internal microcracks of the sample are compacted at the initial stage, and the energy is released as dissipated energy. After that, if the loading continues, strain hardening gradually takes a leading position, and the energy is mainly stored in the form of elastic strain energy. When approaching the peak strength, the decline of dissipated energy rate slows down, and then the dissipated energy rate gradually increases, which may be caused by the accelerated growth of microcracks. After the peak strength, the elastic strain energy is released rapidly due to the macroscopic failure of the sample, resulting in a sharp rise in the dissipated energy rate.

FIGURE 11

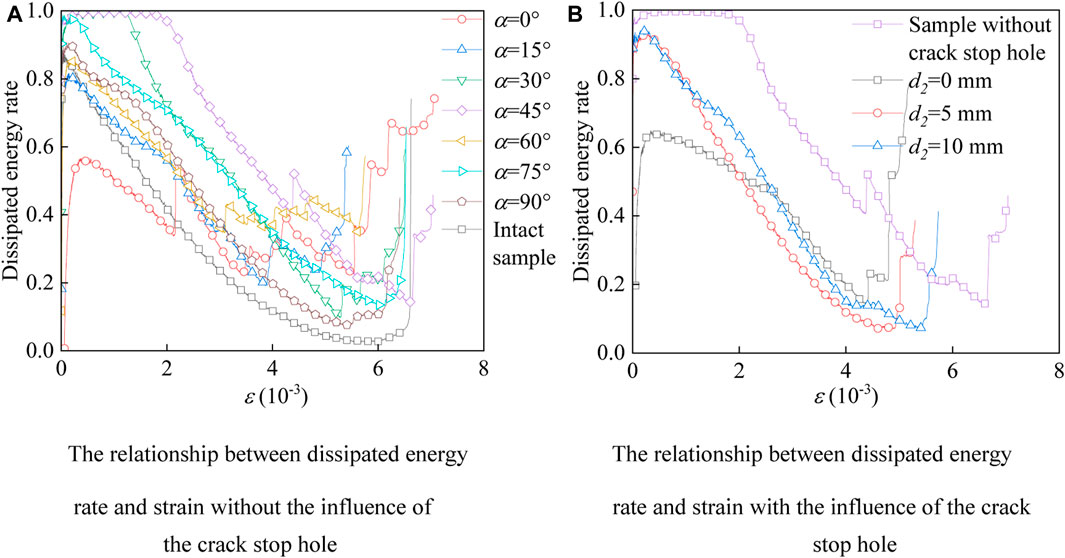
FIGURE 11. Evolution of dissipated energy rate of different granite samples. (A) The relationship between dissipated energy rate and strain without the influence of the crack stop hole. (B) The relationship between dissipated energy rate and strain with the influence of the crack stop hole.

As shown in Figure 11B, all curves show rising characteristics at the initial stage, however, the dissipated energy rate of the sample without crack stop hole (α = 45°) keeps stable before ε = 0.002, and begins to decline after ε is greater than 0.002, indicating that the internal microcracks of the sample without crack stop hole are relatively more developed, so its dissipated energy rate remains at a higher value. On the other hand, the crack stop hole inhibits the crack growth from the initial stage of loading, thus reducing the dissipated energy rate of samples. In addition, the difference in the location of the crack stop hole leads to the difference of the dissipated energy rate.

4 Discussion

Regardless of the well-known achievements, the new findings will be further discussed in this section. First of all, different from the traditional oblique straight pre-crack, a central circular through hole with a diameter of 5 mm was drilled at the center of the sample. Although the central circular through hole may affect the strength of pre-cracked granite samples, the law of variation of mechanical parameters has not been changed correspondingly. For example, pre-crack inclination angle has a significant influence on the peak strength, which increases with the increase of the inclination angle (Liu et al., 2017; Saadat and Taheri, 2019; Wu et al., 2021; Ma et al., 2022), furthermore, Ma et al. (2022) pointed out that the elastic modulus (apparent stiffness) increases linearly with the increase of the pre-crack inclination angle, their results are the same as those in Figures 4A, 6A. Despite the fact that the central circular through hole does not change the law of variation of mechanical parameters, its influence on the value of mechanical parameters of pre-cracked samples is still worthy of further study.

The failure modes of pre-cracked rock samples with different inclination angle are inevitably different from each other. Wu et al. (2021) stated that, with the increase of friction angle (inclination angle), the change of crack type occurred, and more transition from tensile cracks to shear cracks can be observed. Compared with Section 3, it can be seen that the addition of the central circular through hole does not change the law of transformation of the failure mode of pre-cracked granite samples. In addition, according to Figure 7, the crack stop hole also fails to change the failure mode of the granite sample with pre-crack inclination angle of 45°, namely, the failure of the sample is dominated by both tensile and shear modes during the loading process, and the crack stop hole mainly affects the crack growth path.

Crack stop holes are always used to prevent crack propagation in areas where stress is easily concentrated, especially in the field of metal materials. For example, the experiment carried out by Fu et al. (2017) indicated that the stress at the crack tip was reduced by a crack stop hole. Since stop-holes are regarded as an emergency measure to delay crack propagation, Okura and Ishikawa (2002) presented the conditions under which stop-holes prevent the re-initiation of fatigue cracks. A model was modified based on the short crack effect and the residual stress effect to estimate the fatigue crack growth with the stop-hole retardation (Lu et al., 2020). The excellent performance of the crack stop hole has also attracted the attention of rock mechanics researchers. Rao et al. (2009) and Rao et al. (2022) stated that the adoption of optimal double holes symmetrical to the original crack plane is an effective method to prevent shear crack in brittle rocks, and pointed out that the design of stop holes is of great significance to improve the stability of mining activities by calculating the stress intensity factor of anisotropic elastic solids with multiple oval-holes and cracks.

At present, the application of crack stop holes in rock mechanics is relatively few compared with the field of metal materials, and the research on crack stop holes mainly focuses on stress concentration and crack initiation (Okura and Ishikawa, 2002; Rao et al., 2009; Fu et al., 2017; Liu et al., 2017; Saadat and Taheri, 2019; Lu et al., 2020; Wu et al., 2021; Ma et al., 2022; Rao et al., 2022). In this paper, we introduce the crack stop hole into the study of granite materials, nevertheless, the focus of attention is different from the existing researches, that is, we care about the effect of the crack stop hole on apparent stiffness, peak strength, energy evolution, stress-strain curve, failure mode and shape. Therefore, the layout of the crack stop hole in this paper is inevitably different from that of previous studies, we are concerned about the location of the crack stop hole where the rock sample has the optimal mechanical properties. However, in this study, we only considered the influence of crack stop hole on granite samples with pre-crack inclination angle of 45°, in the future, the research scope can be expanded, for example, the effect of the crack stop hole on rock samples under different factors, such as different crack inclination angle, sample shape and lithology, can also be considered. Finally, numerical simulation can also be carried out in the future to further reveal the mechanical properties of rocks under the influence of central circular through hole and crack stop hole.

5 Conclusion

The study in this paper is beneficial to verify the mechanical properties of fractured granite rocks with different inclination angles, in which there is a circular through hole in the center of the sample, and the effect of the crack stop hole on its mechanical behavior. The main conclusions are as follows:

(1) The central circular through hole does not change the law of variation of mechanical parameters of pre-cracked granite samples. With the increase of the pre-crack inclination angle, the growth of tension cracks gradually becomes less obvious, indicating that the central circular through hole does not change the law of transformation of the failure mode of pre-cracked samples. The crack stop hole also failed to change the failure mode of the pre-cracked granite sample with inclination angle of 45°, but affected the crack propagation path and its peak strength to a certain extent.

(2) In general, the larger the inclination angle of the pre-crack, the more total energy required for failure of the sample and the more stored elastic strain energy, and reflecting the compressive resistance of the sample. The crack stop hole can change the law of evolution of energy to a certain extent. The pre-crack reduces the energy storage capacity of the sample, and the total energy is ultimately dominated by its integrity.

(3) The law of dissipated energy rate during loading is analyzed, which implies the energy evolution mechanism of deformation and failure of granite samples. In addition, it is also found that the ability of the sample to accumulate elastic strain energy can be improved within a certain range by using crack stop holes at appropriate locations. In a word, the mechanical properties of pre-cracked granite samples are further verified in this study, thus contributing to its application in engineering.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, writing—original draft preparation, EZ, CZ, and QR; Writing—review and editing, EZ and JL; Methodology, investigation, XZ; Resources, visualization, YW; Supervision, TT; Project administration, CZ. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the Project (Grant No. 52174088) supported by the National Natural Science Foundation of China; Project (Grant No. Z020015) supported by the Open Research Fund of State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences; Project (Grant Nos. 42277154, 42077249, and 51774107) supported by the National Natural Science Foundation of China; The authors declare that this study received funding from Hefei Rail Transit Group Co., Ltd (2021BFFBZ02689). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors EZ and XZ were employed by Lanzhou Engineering and Research Institute of Non-ferrous Metallurgy Co., Ltd. Author JL was employed by Cscec Aecom Consultants Co., Ltd. Author CZ was employed by Sinosteel Maanshan General Institute of Mining Research Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aliha, M. R. M., and Ayatollahi, M. R. (2014). Rock fracture toughness study using cracked chevron notched Brazilian disc specimen under pure modes I and II loading–A statistical approach. Theor. Appl. Fract. Mec. 69, 17–25. doi:10.1016/j.tafmec.2013.11.008

CrossRef Full Text | Google Scholar

Ayatollahi, M. R., Mahdavi, E., Alborzi, M. J., and Obara, Y. (2016). Stress intensity factors of semi-circular bend specimens with straight-through and chevron notches. Rock Mech. Rock Eng. 49, 1161–1172. doi:10.1007/s00603-015-0830-y

CrossRef Full Text | Google Scholar

Ban, L., Du, W., Jin, T., Qi, C., and Li, X. (2021). A roughness parameter considering joint material properties and peak shear strength model for rock joints. Int. J. Min. Sci. Technol. 31 (3), 413–420. doi:10.1016/j.ijmst.2021.03.007

CrossRef Full Text | Google Scholar

Ban, L., Tao, Z., Du, W., and Hou, Y. (2023). A consecutive joint shear strength model considering the 3D roughness of real contact joint surface. Int. J. Min. Sci. Technol. 33, 617–624. doi:10.1016/j.ijmst.2022.12.009

CrossRef Full Text | Google Scholar

Bastola, S., and Cai, M. (2019). Investigation of mechanical properties and crack propagation in pre-cracked marbles using lattice-spring-based synthetic rock mass (LS-SRM) modeling approach. Comput. Geotech. 110, 28–43. doi:10.1016/j.compgeo.2019.02.009

CrossRef Full Text | Google Scholar

Bertram, A., and Kalthoff, J. F. (2003). Crack propagation toughness of rock for the range of low to very high crack speeds. Adv. Fract. Damage Mech. 251-2, 423–430. doi:10.4028/www.scientific.net/kem.251-252.423

CrossRef Full Text | Google Scholar

Chen, B., Shen, B. T., Zhang, S. C., Li, Y. Y., and Jiang, H. Y. (2022). 3D morphology and formation mechanism of fractures developed by true triaxial stress. Int. J. Min. Sci. Technol. 32 (6), 1273–1284. doi:10.1016/j.ijmst.2022.09.002

CrossRef Full Text | Google Scholar

Chen, Y., Lin, H., and Liang, L. (2023a). Freeze-thaw failure characteristics and strength loss of non-penetrating fractured rock mass with different fracture densities. Theor. Appl. Fract. Mec. 124, 103792. doi:10.1016/j.tafmec.2023.103792

CrossRef Full Text | Google Scholar

Chen, Y., Sheng, B., Xie, S., Cao, R., Wang, Y., Zhao, Y., et al. (2023b). Crack propagation and scale effect of random fractured rock under compression-shear loading. J. Mater. Res. Technol. 23, 5164–5180. doi:10.1016/j.jmrt.2023.02.104

CrossRef Full Text | Google Scholar

Deng, Q. M., Yin, X. C., Wang, D. G., and Wahab, M. A. (2022). Numerical analysis of crack propagation in fretting fatigue specimen repaired by stop hole method. Int. J. Fatigue. 156, 106640. doi:10.1016/j.ijfatigue.2021.106640

CrossRef Full Text | Google Scholar

Eftekhari, M., Baghbanan, A., and Hashemolhosseini, H. (2016). Crack propagation in rock specimen under compressive loading using extended finite element method. Arab. J. Geosci. 9 (2), 145. doi:10.1007/s12517-015-2196-6

CrossRef Full Text | Google Scholar

Fowell, R. J. (1995). Suggested method for determining mode I fracture toughness using Cracked Chevron Notched Brazilian Disc (CCNBD) specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 32 (1), 57–64. doi:10.1016/0148-9062(94)00015-u

CrossRef Full Text | Google Scholar

Fu, Z. Q., Ji, B. H., Xie, S. H., and Liu, T. J. (2017). Crack stop holes in steel bridge decks: Drilling method and effects. J. Cent. South Univ. 24 (10), 2372–2381. doi:10.1007/s11771-017-3649-8

CrossRef Full Text | Google Scholar

Gong, F. Q., Zhang, P. L., and Du, K. (2022a). A novel staged cyclic damage constitutive model for brittle rock based on linear energy dissi pation law: Modelling and validation. Rock Mech. Rock Eng. 55 (10), 6249–6262. doi:10.1007/s00603-022-02930-8

CrossRef Full Text | Google Scholar

Gong, F. Q., Zhang, P. L., and Xu, L. (2022b). Damage constitutive model of brittle rock under uniaxial compression based on linear energy dissipation law. Int. J. Rock Mech. Min. Sci. 160, 105273. doi:10.1016/j.ijrmms.2022.105273

CrossRef Full Text | Google Scholar

Griffith, A. A. (1924). “The theory of rupture,” in Proceedings of the first international congress on applied mechanics. Editors C. B. Biezeno, and J. M. Burgers, 55±63.

Google Scholar

Haeri, H., Khaloo, A., and Marji, M. F. (2015). A coupled experimental and numerical simulation of rock slope joints behavior. Arab. J. Geosci. 8 (9), 7297–7308. doi:10.1007/s12517-014-1741-z

CrossRef Full Text | Google Scholar

Kang, F. Q., Wang, G. J., Liu, W. L., Zhao, K., Wang, M. L., Li, X. S., et al. (2022). Experimental study on the evolution of dynamic pore pressure and unidirectional and bidirectional vibrations of phosphogypsum. Front. Earth Sci. 10, 929777. doi:10.3389/feart.2022.929777

CrossRef Full Text | Google Scholar

Kuruppu, M. D., Obara, Y., Ayatollahi, M. R., Chong, K. P., and Funatsu, T. (2014). ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock Mech. Rock Eng. 47 (1), 267–274. doi:10.1007/s00603-013-0422-7

CrossRef Full Text | Google Scholar

Lei, Z. D., Wu, B. S., Wu, S. S., Nie, Y. X., Cheng, S. Y., and Zhang, C. Y. (2022). A material point-finite element (MPM-FEM) model for simulating three-dimensional soil-structure interactions with the hybrid contact method. Comput. Geotech. 152, 105009. doi:10.1016/j.compgeo.2022.105009

CrossRef Full Text | Google Scholar

Li, C., Gao, M. Z., Lu, Y. Q., Liu, Q., He, Z. Q., and Peng, G. Y. (2019). “Effect of prefabricated crack width on stress intensity factors of Brazilian disc sample with center crack,” in Deep rock mechanics: From research to engineering, 335–342. doi:10.1201/9781351042666-33

CrossRef Full Text | Google Scholar

Li, X. S., Peng, J., Xie, Y. L., Li, Q. H., Zhou, T., Wang, J. W., et al. (2022). Influence of high-temperature treatment on strength and failure behaviors of a quartz-rich sandstone under true triaxial condition. Lithosphere 2022, 3086647. doi:10.2113/2022/3086647

CrossRef Full Text | Google Scholar

Li, S., Lin, H., Hu, S., Cao, R., and Luo, X. (2023). Mechanical behavior of anchored rock with an infilled joint under uniaxial loading revealed by AE and DIC monitoring. Theor. Appl. Fract. Mec. 123, 103709. doi:10.1016/j.tafmec.2022.103709

CrossRef Full Text | Google Scholar

Li, S., Zhang, D., Bai, X., Zhang, X. M., Chu, Y. P., and Guo, K. Y. (2019). Experimental study on mechanical properties, acoustic emission energies and failure modes of pre-cracked rock materials under uniaxial compression. Pure Appl. Geophys. 176, 4519–4532. doi:10.1007/s00024-019-02201-8

CrossRef Full Text | Google Scholar

Lin, H., Liu, J. F., Yang, J. X., Ran, L. N., Ding, G. S., Wu, Z. D., et al. (2022). Analysis of damage characteristics and energy evolution of salt rock under triaxial cyclic loading and unloading. J. Energy Storage 56, 106145. doi:10.1016/j.est.2022.106145

CrossRef Full Text | Google Scholar

Lin, S. Q., Wang, G. J., Liu, W. L., Zhao, B., Shen, Y. M., Wang, M. L., et al. (2022). Regional distribution and causes of global mine tailings dam failures. Metals 6 (12), 905. doi:10.3390/met12060905

CrossRef Full Text | Google Scholar

Liu, H. Y., and Lv, S. R. (2019). A model for the wing crack initiation and propagation of the inclined crack under uniaxial compression. Int. J. Rock Mech. Min. Sci. 123, 104121. doi:10.1016/j.ijrmms.2019.104121

CrossRef Full Text | Google Scholar

Liu, T., Lin, B. Q., and Yang, W. (2017). Mechanical behavior and failure mechanism of pre-cracked specimen under uniaxial compression. Tectonophysics 712-713, 330–343. doi:10.1016/j.tecto.2017.06.004

CrossRef Full Text | Google Scholar

Liu, W. L., Yan, E. C., Dai, H., Du, Y., Xiao, W. B., and Zhao, S. (2020). Study on characteristic strength and energy evolution law of Badong formation mudstone under water effect. Chin. J. Rock Mech. Eng. 39 (2), 311–326. (in Chinese).

Google Scholar

Lu, Y. C., Yang, F. P., Chen, T., and Gong, H. (2020). The retardation effect of combined application of stop-hole and overload on sheet steel. Int. J. Fatigue. 132, 105414. doi:10.1016/j.ijfatigue.2019.105414

CrossRef Full Text | Google Scholar

Ma, S. Z., Liu, K. W., Guo, T. F., Yang, J. C., Li, X. D., and Yan, Z. X. (2022). Experimental and numerical investigation on the mechanical characteristics and failure mechanism of cracked coal & rock-like combined sample under uniaxial compression. Theor. Appl. Fract. Mech. 122, 103583. doi:10.1016/j.tafmec.2022.103583

CrossRef Full Text | Google Scholar

Mahdavi, E., Aliha, M. R. M., Bahrami, B., and Ayatollahi, M. R. (2020). Comprehensive data for stress intensity factor and critical crack length in chevron notched semi-circular bend specimen subjected to tensile type fracture mode. Theor. Appl. Fract. Mec. 106, 102466. doi:10.1016/j.tafmec.2019.102466

CrossRef Full Text | Google Scholar

Nara, Y., Kashiwaya, K., Nishida, Y., and Ii, T. (2017). Influence of surrounding environment on subcritical crack growth in marble. Tectonophysics 706, 116–128. doi:10.1016/j.tecto.2017.04.008

CrossRef Full Text | Google Scholar

Okura, I., and Ishikawa, T. (2002). Stop-hole conditions to prevent re-initiation of fatigue cracks. Steel Compos. Struct. 2 (6), 475–488. doi:10.12989/scs.2002.2.6.475

CrossRef Full Text | Google Scholar

Ouchterlony, F. (1988). ISRM commission on testing methods. Suggested methods for determining fracture toughness of rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 25, 71–96.

Google Scholar

Peng, K., Liu, Z. P., Zou, Q. L., Wu, Q. H., and Zhou, J. Q. (2020). Mechanical property of granite from different buried depths under uniaxial compression and dynamic impact: An energy-based investigation. Powder Technol. 362, 729–744. doi:10.1016/j.powtec.2019.11.101

CrossRef Full Text | Google Scholar

Qiao, L., Hao, J. W., Liu, Z. Y., Li, Q. W., and Deng, N. F. (2022). Influence of temperature on the transformation and self-control of energy during sandstone damage: Experimental and theoretical research. Int. J. Min. Sci. Technol. 32 (4), 761–777. doi:10.1016/j.ijmst.2022.02.008

CrossRef Full Text | Google Scholar

Rao, Q. H., Xie, H. F., Xie, Q., and Wang, Z. (2009). “Effect of crack-stopping hole on shear fracture of rock,” in 7th International Symposium on Rockburst and Seismicity in Mines, 1581–1586.1 and 2.

Google Scholar

Rao, Q. H., Zhao, C. C., Yi, W., Sun, D. L., and Liu, Z. L. (2022). Stress intensity factor calculation of the cracks interacted by the oval-holes in anisotropic elastic solids under remote and non-uniform surface stresses. Theor. Appl. Fract. Mech. 121, 103475. doi:10.1016/j.tafmec.2022.103475

CrossRef Full Text | Google Scholar

Razavi, S. M. J., Aliha, M. R. M., and Berto, F. (2018). Application of an average strain energy density criterion to obtain the mixed mode fracture load of granite rock tested with the cracked asymmetric four-point bend specimens. Theor. Appl. Fract. Mech. 97, 419–425. doi:10.1016/j.tafmec.2017.07.004

CrossRef Full Text | Google Scholar

Saadat, M., and Taheri, A. (2019). A numerical approach to investigate the effects of rock texture on the damage and crack propagation of a pre-cracked granite. Comput. Geotech. 111, 89–111. doi:10.1016/j.compgeo.2019.03.009

CrossRef Full Text | Google Scholar

Schultz, R. A. (2000). Growth of geologic fractures into large-strain populations: Review of nomenclature, subcritical crack growth, and some implications for rock engineering. Int. J. Rock Mech. Min. Sci. 37 (1-2), 403–411. doi:10.1016/s1365-1609(99)00115-x

CrossRef Full Text | Google Scholar

Sonmez, H., Ercanoglu, M., and Dagdelenler, G. (2022). A novel approach to structural anisotropy classification for jointed rock masses using theoretical rock quality designation formulation adjusted to joint spacing. J. Rock Mech. Geotech. Eng. 14 (2), 329–345. doi:10.1016/j.jrmge.2021.08.009

CrossRef Full Text | Google Scholar

Tang, Y. X., Su, R. K. L., and Chen, H. N. (2021). Energy dissipation during fracturing process of nuclear graphite based on cohesive crack model. Eng. Fract. Mech. 242, 107426. doi:10.1016/j.engfracmech.2020.107426

CrossRef Full Text | Google Scholar

Wang, Y. Y., Deng, H. C., Deng, Y., Chen, K. P., and He, J. H. (2021). Study on crack dynamic evolution and damage-fracture mechanism of rock with pre-existing cracks based on acoustic emission location. J. Pet. Sci. Eng. 201, 108420. doi:10.1016/j.petrol.2021.108420

CrossRef Full Text | Google Scholar

Wang, G. J., Zhao, B., Lan, R., Liu, D. W., Wu, B. S., Li, Y. J., et al. (2022). Experimental study on failure model of tailing dam overtopping under heavy rainfall. Lithosphere 2022. doi:10.2113/2022/5922501

CrossRef Full Text | Google Scholar

Wang, G. J., Zhao, B., Wu, B. S., Zhang, C., and Liu, W. L. (2023). Intelligent prediction of slope stability based on visual exploratory data analysis of 77 in situ cases. Int. J. Min. Sci. Technol. 33 (1), 47–59. doi:10.1016/j.ijmst.2022.07.002

CrossRef Full Text | Google Scholar

Wu, D., Li, H. B., Shao, Z. S., Chen, S. H., Zhou, C. B., and Liu, L. W. (2021). Effects of infilling materials on mechanical behaviors and cracking process of pre-cracked rock: Insights from a hybrid continuum-discontinuum method. Eng. Fract. Mech. 253, 107843. doi:10.1016/j.engfracmech.2021.107843

CrossRef Full Text | Google Scholar

Xie, H. P., Ju, Y., Li, L. Y., and Peng, R. D. (2008). Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 27 (9), 1729–1740. (in Chinese).

Google Scholar

Xie, Q., Liu, X. L., Fan, L., Peng, S. Q., and Zeng, Y. (2023). Evaluation of equivalent crack propagation length and fracture energy of two commonly used rock fracture toughness test configurations based on Bazant’s size effect law. Eng. Fract. Mech. 281, 109067. doi:10.1016/j.engfracmech.2023.109067

CrossRef Full Text | Google Scholar

Xiong, F., Liu, X. R., Zhou, X. H., Lin, G. Y., Liu, D. S., Han, Y. F., et al. (2022). Mechanical behaviours of sandstone containing intersecting fissures under uniaxial compression. J. Rock Mech. Geotech. Eng. 14 (2), 460–476. doi:10.1016/j.jrmge.2021.09.008

CrossRef Full Text | Google Scholar

Xu, L., Gong, F. Q., and Luo, S. (2021). Effects of pre-existing single crack angle on mechanical behaviors and energy storage characteristics of red sandstone under uniaxial compression. Theor. Appl. Fract. Mech. 113, 102933. doi:10.1016/j.tafmec.2021.102933

CrossRef Full Text | Google Scholar

Yu, X., Song, W. D., Tan, Y. Y., Kemeny, J., and Wang, J. (2022). Energy dissipation and 3d fracturing of Backfill-encased-rock under triaxial compression. Constr. Build. Mater. 341, 127877. doi:10.1016/j.conbuildmat.2022.127877

CrossRef Full Text | Google Scholar

Zhang, C. Y., Wang, Y. X., and Jiang, T. T. (2020). The propagation mechanism of an oblique straight crack in a rock sample and the effect of osmotic pressure under in-plane biaxial compression. Arab. J. Geosci. 13 (15), 736. doi:10.1007/s12517-020-05682-3

CrossRef Full Text | Google Scholar

Zhao, Y. L., Tang, J. Z., Chen, Y., Zhang, L. Y., Wang, W. J., Wan, W., et al. (2017). Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress–strain process. Environ. Earth Sci. 76 (1), 24. doi:10.1007/s12665-016-6322-x

CrossRef Full Text | Google Scholar

Zhao, D. C., Xia, Y. J., Zhang, C. Q., Tang, C. A., Zhou, H., Liu, N., et al. (2022). Failure modes and excavation stability of large-scale columnar jointed rock masses containing interlayer shear weakness zones. Int. J. Rock Mech. Min. Sci. 159, 105222. doi:10.1016/j.ijrmms.2022.105222

CrossRef Full Text | Google Scholar

Zhao, B., Wang, G. J., Wu, B. S., and Kong, X. Y. (2023). A study on mechanical properties and permeability of steam-cured mortar with iron-copper tailings. Constr. Build. Mater. 383, 131372. doi:10.1016/j.conbuildmat.2023.131372

CrossRef Full Text | Google Scholar

Zhong, Z. B., Deng, R. G., Zhang, J., and Hu, X. Z. (2020). Fracture properties of jointed rock infilled with mortar under uniaxial compression. Eng. Fract. Mech. 228, 106822. doi:10.1016/j.engfracmech.2019.106822

CrossRef Full Text | Google Scholar

Zhu, J. B., Zhou, T., Liao, Z. Y., Sun, L., Li, X. B., and Chen, R. (2018). Replication of internal defects and investigation of mechanical and fracture behaviour of rock using 3D printing and 3D numerical methods in combination with X-ray computerized tomography. Int. J. Rock Mech. Min. Sci. 106, 198–212. doi:10.1016/j.ijrmms.2018.04.022

CrossRef Full Text | Google Scholar