
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 02 August 2023
Sec. Geohazards and Georisks
Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1214536
This article is part of the Research TopicSeismic Microzonation and Risk ReductionView all 5 articles
At certain depths, the elastic properties of the ground are not affected by seismic waves. However, as they reach the surface, the soil density decreases and so does its elastic limit. This means that the expected ground motion acting at the foundation of a structure cannot be adequately described without considering the inelastic response of the soil near the surface. Therefore, one of the key elements in characterizing the seismic response of civil structures is the site effect. These depend mainly on the parameters of the soil beneath the structure and the features of the ground motion acting at the depth, where non-linear effects are negligible. Therefore, the main objective of this paper is to find an intensity measure that incorporates the information provided by the soil profile under the structure and the ground motion acting at the bedrock level. Due to the random nature of both elements, a probabilistic framework using Monte Carlo simulation has been developed to analyze this problem. For this purpose, random soil profiles have been generated to obtain a representative sample of likely scenarios of the study area. A large database of Colombian ground motion records has been used to model the seismic hazard. Finally, power functions capable of relating the input variables to the dynamic response of a large set of reinforced concrete structures have been derived by considering multi-regression analysis. It has been observed that, in several cases, intensity measures extracted from the displacement spectrum appear in the mathematical arrangements. These functions could be used to improve the efficiency of seismic risk prediction at the urban level.
Soil–structure interaction is becoming fundamental in the estimation of seismic risk (Cruz and Miranda, 2021). It is because the soil beneath the structure acts as an ultimate filter that may amplify or de-amplify harmonics at specific frequencies depending on its dynamic properties. Thus, it is expected that structures having significant mass participation at specific periods may enter in resonance with the soil. One of the most remarkable examples of this effect was observed during the earthquake that affected Mexico City in 1985 (Beck and Hall, 1986). A large amplification has been observed of long-period waves produced by a highly attenuated ground motion since the earthquake occurred far away from the site. This event shifted several conceptual paradigms on aspects related to the estimation of seismic risk. More recently, the use of advanced non-linear models considering the soil–structure interaction has provided information to better understand this complex phenomenon (Pitilakis and Petridis, 2022).
In sites of high seismic risk, and depending on the complexity (or importance) of a civil infrastructure, it is recommended to analyze its dynamic interaction with the ground by using advanced non-linear models. There are several ways to model this interaction depending on the type of foundation (Lou et al., 2011). Yet, in most cases, it is necessary to obtain a set of signals acting at the base of a soil–structure model, below which the elastic rebound theory is expected to apply (Ohnaka, 1976). These signals should be recorded on a hard rock site for the latter assumption to hold.
Therefore, a key aspect of the study of seismic risk is the characterization of the dynamic response of the soil profile (Pagliaroli et al., 2014). In this respect, it is common practice to use simplified 1D soil models to advanced 3D finite-element-method-based representations (Kaklamanos et al., 2015; Fiorentino et al., 2019). However, the higher the complexity of the model, the higher the computational time involved in solving dynamic problems. In order to tackle this computational effort, more simplified soil models are widely used. One of the most employed is the 1D model, in which the soil layers are considered Kelvin–Voigt solids (Hardin and Scott, 1967). This model is represented by a purely viscous damper and an elastic spring connected in parallel. In several cases, it allows a good approximation of the dynamic response of a soil profile. Moreover, this model has been extended to consider non-linearities associated to the loss of stiffness of the soil, and the consequent increase in damping due to shear strains (Yoshida et al., 2002).
In line with the aforementioned concept, the frequency content of the surface ground motions generated by earthquakes depends on several complex phenomena such as the type of rupture, the proximity to the epicenter and the depth, and the mechanical properties of the media through which the seismic waves pass. The variability associated with seismological parameters (i.e., rupture type, proximity to the epicenter, and depth) can be taken into account by not conditioning the selection of ground motion records to specific values. Regarding the mechanical properties of the media, depending on the depth, seismic waves may degrade the stiffness at very low shear strains (Okur and Ansal, 2007); the deeper, the lesser the stiffness degradation. Therefore, in each location, there is a depth limit in which stiffness degradation and the consequent increase in damping do not occur. Notwithstanding, close to the surface, and depending on the seismic intensity and soil type, a significant degradation of the soil properties is expected (Kostinakis et al., 2018).
Scaling ground motion records is another challenging problem in estimating seismic risk. In this respect, there are several methodologies to scale ground motions from a database. Typically, the goal is to find a significant set of records leading the structure to multiple performance levels. However, as indicated by the well-known Richter’s law (Wesnousky, 1994), the number of high-magnitude earthquakes is much smaller than the number of low-magnitude earthquakes; therefore, finding high-intensity ground motion records is less probable.
Consequently, it is sometimes necessary to scale low-intensity records by significantly high factors. Therefore, scaling a single record to increased intensity values may not take into account the likely inelastic response of soils. It becomes important since some soil types modify their dynamic properties at very low shear strains. Not to mention that scaling natural ground motions to too high or too low scale factors can lead to modified records that are far from the physical properties of real ground motions (Bommer and Acevedo, 2004).
This article has been oriented to develop a computational framework for seismic risk assessment, capable of simultaneously considering in a probabilistic manner i) the main characteristics of the ground motion acting at the bedrock level; ii) the dynamic soil properties and their evolution due to the degradation caused by the seismic waves; and iii) the main features influencing the dynamic behavior of reinforced concrete frame structures. Therefore, an iterative algorithm has been designed to simulate random profiles that meet the statistical distributions of the soil properties, given a specific area. This algorithm randomizes the geometrical features used in characterizing soil profiles. It takes into account the dependency of layer thickness with depth, the correlation exhibited between closer layers, and the total length of the soil profiles.
A probabilistic set of reinforced concrete frame structures has been simulated to analyze its seismic response. Ground motion records resulting at the surface, after seismic waves had propagated through the soil model, have been used as input. The main reason for considering this structural typology is its widespread use. For instance, buildings with reinforced concrete elements are common in many earthquake-prone countries and regions (Park and Paulay, 1991). In relation to this study, buildings of this type are very common in the Andean and Caribbean regions of Colombia. In fact, this type of building is mainly found in densely populated urban areas, where there is a need to provide many housing units in a relatively small area.
It has been assumed that the simulated structures rest on a specific soil profile, which propagates seismic waves from the bedrock to the surface, by considering the equivalent linear method (Yoshida et al., 2002). The resulting seismic waves at the surface are used to perform several non-linear dynamic analyses of the structure. To do so, the city of Bogotá has been chosen as a case study. Specifically, the information regarding geotechnical studies performed over more than 20 locations within this urban area has been analyzed (FOPAE, 2011). Then, a subset of 10 locations providing information on lacustrine soil deposits was employed. In addition, a Colombian database was used to characterize the seismicity, which was provided by the “Servicio Geologico Colombiano (SGC)” (SGC, 2020).
Finally, results stemming from the following three situations were compared: i) analyzing the causal relationship between both intensity measures (IMs) extracted from the resulting ground motion that acts at the base of the building models and engineering demand parameters (EDPs) able to quantify expected damage; ii) using the ground motion records employed as input at the bedrock level to estimate IMs; iii) developing a mathematical arrangement that allows combining information provided by the soil profile and the IMs calculated from the ground motion acting at the bedrock level. The results indicate that a power combination of information variables (IVs), such as those related to IMs and the soil dynamic properties, becomes an efficient intensity measure identified herein as IMGD; the subscript GD stands for ground-dependent.
A probabilistic soil model is generally used in geotechnical applications to consider the spatial (Vanmarcke, 1977) and temporal (Carrière et al., 2018) variability of soil properties and their effects on civil structures. These models rely on statistics and probability theory to simulate soil features such as strength and stiffness, which can vary with location and time. These models estimate the uncertainties and risks associated to both the behavior of soil and the structures built on it. This helps engineers design safer and efficient structures.
Figure 1 is a sketch of the computational framework developed in this research. Input ground motions act at bedrock level. It is worth recalling that in each of the locations, there is a depth limit in which stiffness degradation and the consequent increase in damping do not occur. Below this limit, the elastic rebound theory is assumed (Ohnaka, 1976). Consequently, close to the surface, and depending on the seismic intensity (Tothong and Luco, 2007), significant degradation of soil properties is expected.
The variables represented within the soil profile scheme (shear modulus, density, damping, and layer thickness,
All the aforementioned elements have been integrated into a probabilistic framework by following these steps:
i. Introduce a ground motion record at bedrock level.
ii. Estimate the stiffness degradation and increase in damping of each soil layer.
iii. Calculate the resulting ground motion at the surface after propagation through the soil profile, taking into account the degradation of soil properties.
iv. The resulting ground motion estimated in the previous step acts at the base of one of the probabilistic building models.
These steps have been applied after generating samples of soil profiles and structures affected by ground motion records randomly selected from a seismic database. It is preferable that these records should have been acquired at seismic stations where the rock reaches the surface.
Since 1993, the Mayor Office of Bogotá has decided to carry out seismic microzonation studies to improve design requirements for civil infrastructure (FOPAE, 2011). The objective has been two-fold: first, to better parameterize the dynamic response of the soil in front of earthquake-induced ground motions; second, to identify areas with similar seismic behavior to develop improved classification maps according to the soil type.
In accordance with the aforementioned case, a seismic response zonation map of the city was developed. The latter shows that there are six different zones, which in turn are subdivided into 16 subsets that depend on the depth of the bedrock level. This classification has considered the geotechnical description of each site, the thickness of the soil deposit, the fundamental period of the ground, and possible site effects.
In this study, calculations are performed for the lacustrine soil type, which is the most important deposit in the city. It is composed of soft clays with high compressibility, interspersed with lenses of loose sand, volcanic ash, and peat that can reach a thickness of up to 1 m. This soil type is characterized by sediment thicknesses ranging from 50 m to 500 m. In terms of dynamic properties, for lacustrine soil profiles with depths up to 200 m, the fundamental period of vibration fluctuates between 1.1 s and 2.6 s, with shear wave velocities between 140 and 280 m/s. For profiles with depths between 200 m and 300 m, the fundamental period varies from 3.5 to 3.8 s, whose wave velocities are in the range 260–290 m/s. Finally, for soil profiles that reach more than 300 m, the expected fundamental periods vary from 4.9 up to 5.8 s, with a shear wave velocity in the range 280–340 m/s. It should be noted that within the analyzed area, the lacustrine soils exhibit amplifications at high periods (between 2 s and 2.5 s) due to the effect of the soft soils and the shape of the basin in which they are located (FOPAE, 2011).
As previously stated, of the total set of analyzed locations (more than 20), 10 correspond to lacustrine deposits. Table 1 shows the number and identification (Station ID) of the stations located in lacustrine soils, as well as the main characteristics corresponding to each station, such as latitude, longitude, length of the soil deposit, number of layers into which the deposit is divided, the first three periods of the soil vibration (Ti), maximum amplitude (Max Amp.), and average shear wave velocity (Vsavg). In addition, the median values (
In the following section, the random generation process to simulate statistically compatible soil profiles, with data provided in Table 1, is explained.
Toro et al. (Silva et al., 1996) proposed a probabilistic model for the variation of shear-wave velocity in soil and rock sites. In brief, this probabilistic model consists of three main elements: i) a model describing the random stratigraphy at the site; ii) the median wave velocity profile; and iii) a model describing the deviations of the velocity in each layer from the median, together with its correlation with respect to the layer above. In sites where there is not enough information to properly characterize uncertainties, this model appears to be an effective solution. The main elements of Toro’s model, applied to the lacustrine data for Bogotá city, are described as follows.
For soil parameterization, the 10 lacustrine profiles specified in the aforementioned report (FOPAE, 2011) are used. The random stratigraphy is characterized by using the “Layering Model” (Silva et al., 1996). This allows considering that as the layer gets deeper, it becomes thicker. In general, this model improves the prediction of ground motion intensity at the surface by providing a better picture of stratigraphic conditions at sites with different soil types.
Hence, this model assumes that the thickness of each layer follows a depth-dependent probability distribution, where the thickness of layer i is independent of the thickness of layer i-1. The model also recognizes that soil layers tend to be thinner near the surface and thicker at greater depths (Silva et al., 1996). Accordingly, the following power law is adopted to characterize the depth-dependent rate of layer boundaries:
where λ is the layer boundary rate (1/m) and h is the depth in m. The estimation of the values C1, C2, and C3 is carried out by using the capabilities of the Monte Carlo method to minimize multi-dimensional functions (Kucherenko et al., 2015).
Therefore, to estimate the probable evolution of λ, the entire number of layers composing the 10-initial set of soil profiles (193 layers) has been used; Figure 2A shows the relationship between the entire set of λ versus the median depth associated to each layer. Then, a second approach proposed in Toro (2022) has also been analyzed. It consists of running averages of λ values over a 10-m window; Figure 2B shows this relationship. After several simulations of the soil profiles, the regression obtained from the first approach was used (Figure 2A) because the resulting number of layers is more consistent with the observed information.
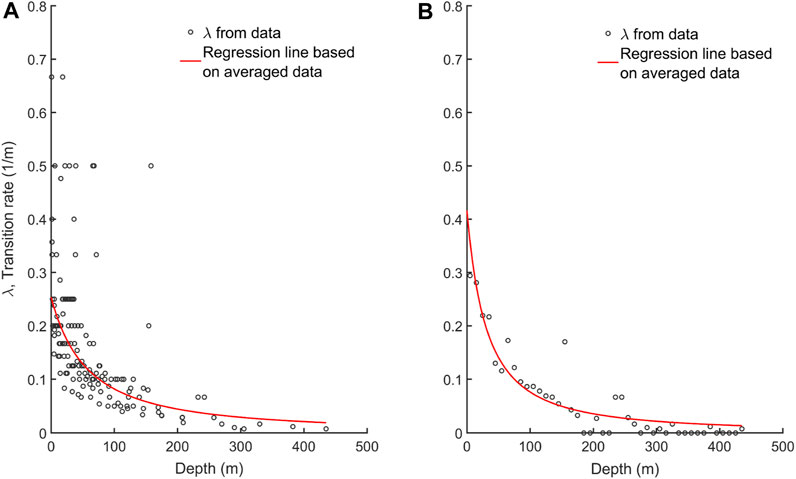
FIGURE 2. Transition rates by considering direct values (A) and those obtained as a running average over a 10-m window (B).
Due to the cumulative process associated to the formation of sedimentary deposits, it has been observed that a log-normal distribution adequately parametrizes the aleatory characteristic of shear wave velocities (Toro, 2022). This parametric distribution has been adopted in the sampling process of the shear wave velocity. It should be noted that, according to Toro’s model, the velocity is estimated at the layer midpoints.
Figure 3 shows wave velocity soil profiles at low shear strains (<10–3%) for the selected locations (thinner gray lines) and their corresponding median values. Two main conclusions can be drawn from these profiles: i) the deeper, the higher the shear wave velocity; ii) the deeper, the thicker the layer, which confirms the conclusions reached in Silva et al. (1996). Both features should be considered when generating random samples of the profiles.
Another important aspect observed in soil profiles is related to the spatial correlation of properties between closer layers. The closer the layers, the higher the correlation (Angelini and Heuvelink, 2018). This implies that widely separated layers tend to be less correlated.
In order to consider the likely correlation exhibited by the shear wave velocity between closer layers, it is necessary to employ a correlation hypothesis (Vargas–Alzate et al., 2018). It has been assumed that the correlation between adjacent soil layers (ψi,j) decreases with distance by means of the following model
where w is a number related to the position of a layer belonging to the same profile; r is a coefficient associated with the rate of correlation between adjacent layers. In this research, r has been fixed to 100/3.
The Monte Carlo simulation can be applied to solve a large variety of numerical problems (Kroese and Rubinstein, 2012). It is mostly used as a tool to assess the uncertainty in complex models and systems. It can be seen as a numerical technique to generate random datasets for assessing uncertainty in a system. Accordingly, for each variable, random datasets are generated by assuming parametric statistical distributions that fit the conditions of the study. This simulation technique also makes it possible to develop a mathematical arrangement that includes variables that influence the model. Based on the description of the probabilistic features that must meet the soil profiles, their statistical realizations have been obtained via Monte Carlo simulations. Figures 4A, B show the random set of 1,000 shear wave velocity soil profiles that have been employed in the development of the probabilistic framework proposed in this research. It is worth mentioning that these soil profiles correspond to low shear strains.
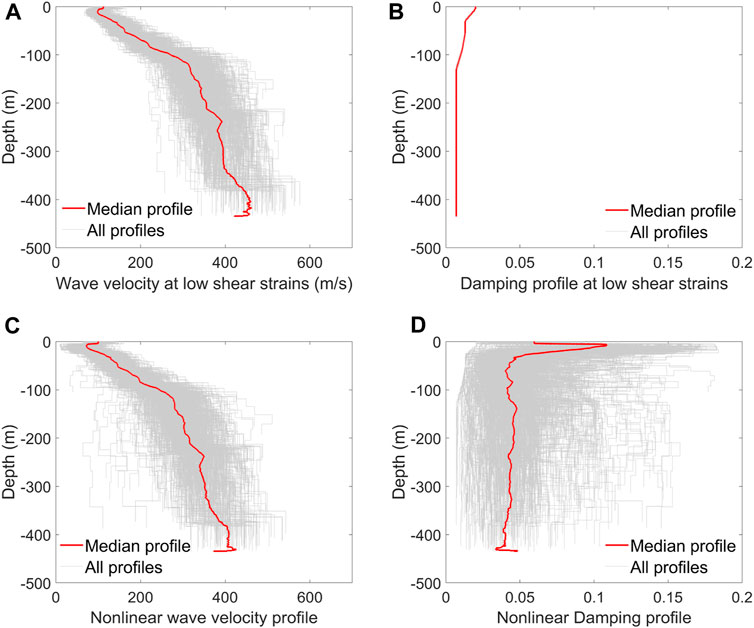
FIGURE 4. Probabilistic soil profiles for shear wave velocity and damping. (A,B) Soil profiles at low shear strains. (C,D) Degraded soil profiles.
The damping properties at low shear strains have been obtained by using degrading curves for the soil type analyzed. This is discussed further in Section 4 of this article. Another important variable influencing the dynamic properties of the simulated soil profiles is density. This has been indirectly considered a random variable by using the following relationship proposed in Nakamura (1989):
where H stands for depth in m,
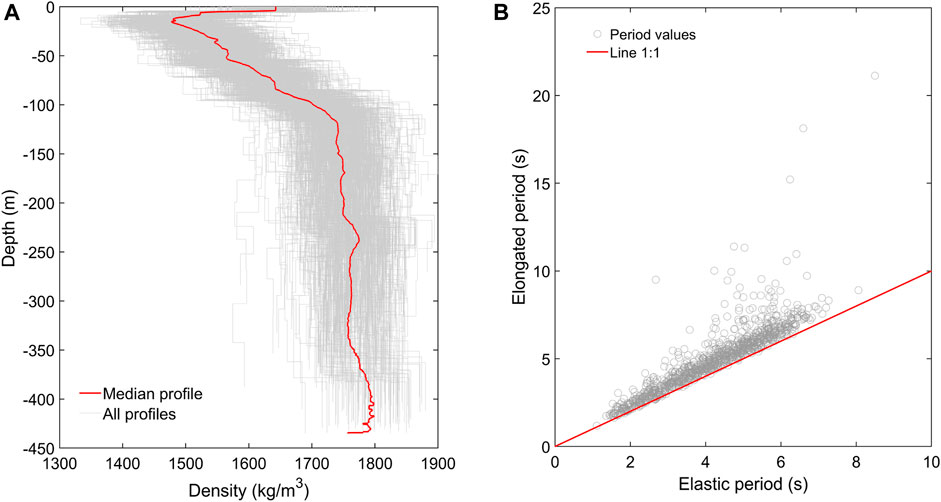
FIGURE 5. (A) Probabilistic soil profiles for density. (B) Relationship between elastic vs elongated periods.
A seismic hazard is defined as the potential for future earthquakes at a given site (Shedlock, 2002). This hazard is usually expressed in terms of acceleration and the probability that a certain level of ground motion is exceeded within a given period of time. Seismic hazards can be estimated using several methods, including probabilistic seismic hazard analysis (PSHA) and deterministic seismic hazard analysis (DSHA) (Krinitzsky, 2003). Accurate seismic hazard characterization is essential for several reasons, including risk assessment, effective planning, and informed decision-making, to prevent potential earthquake-related risks. In addition, accurate seismic hazard characterization can lead to the development of a resilient civil infrastructure that can better withstand seismic events.
Colombia is located on the Pacific Ring of Fire, an area with the highest concentration of earthquakes in the world (Comartin et al., 2000). The country lies at the intersection of three tectonic plates: the Caribbean, the South American, and the Nazca plates. This geological feature significantly increases the seismic risk in Colombia when compared to other regions. The main source of seismicity is related to the subduction zone of the Colombian Pacific plate and to the geological faults caused by the convergence of the three plates. Studies show that almost 83% of the population lives in moderate-to-high seismic risk areas.
In terms of geographical configuration, Colombia has been divided into five regions. The city of Bogotá is located in the central region, which is the most densely populated and economically active in the country. It includes the central, eastern, and western mountain ranges, running from southwest to northeast, and covers approximately 2,825,540 km2, or 30% of Colombia’s territory, with a population density of 121.82 inhabitants/km2.
Ground motions recorded in Colombia between 1993 and 2017 have been compiled, with a magnitude greater than 4.0 Mw. Accordingly, a total of 1992 records have been extracted from the SGC (2020). They have been divided into two groups based on the ground conditions in which they were recorded. The first category includes signals recorded on rock, with a total of 1,236 records. The second group includes signals recorded on less rigid ground, with a total of 756 records. In both cases, environmental noise and other factors that could affect the accuracy of the signal have been corrected. It is worth recalling that the elastic rebound theory applies below the bedrock level (see Figure 1). This implies that linear scaling of ground motions below this limit can be accepted without excessive error. Therefore, it seems logical to use the outcrop datasets as input at the base of the soil model (see Figure 1).
In order to obtain a more precise representation of the seismogenic environment of Bogotá, an algorithm has been developed to identify the seismic records acquired at the stations closest to a study point within the Colombian territory. It starts by taking the entire set of 1992 ground motions and collecting the relevant information, such as date of the seismic event, magnitude, station name, and epicentral and hypocentral distance. Then, based on the coordinates of the studied area and the maximum radius around this point, the nearest stations are identified and the signals recorded are extracted and addressed to two folders depending on whether the station is located on soil or on rock. In parallel, a map that allows identifying the analyzed point, and the stations delimited within the radius, is created. Moreover, the program provides the acceleration, velocity, and displacement spectra.
For this study, Bogotá city (latitude 4.6097 and longitude −74.0817) has been used as a reference point by considering a radius of 400 km. Thus, using the aforementioned algorithm, a set of 1,023 ground motions recorded on rock have been identified.
Figure 6 shows both the study point and the nearest stations. Table 2 shows the distances and IDs of the nearest stations found within a radius of 400 km around Bogotá.
There are several methods for selecting ground motions from a database (Haselton et al., 2012). Typically, the aim is to have enough records leading the structure to different performance levels. However, in current databases, there are often no strong ground motion records with high intensity values. This can cause excessive scaling, which may introduce bias in the structural response (Haselton et al., 2012). To address this issue when using cloud analysis (Jalayer et al., 2015), the method proposed by Vargas–Alzate et al. (2022b) to select and scale ground motion records has been used.
i. Identify the database.
ii. Identify the IM for selecting and scaling records.
iii. Calculate the IM for each ground motion in the dataset.
iv. Sort the ground motion records in descending order based on the calculated IM values.
v. Define both the intensity intervals for scaling and the number of records per interval.
vi. Scale the first ranked ground motion record so that the IM value falls into the highest interval. Calculate the scale factor so that the IM values are uniformly distributed within the interval. If the IM fulfills the interval condition, no scaling factor is considered. Repeat the process until there are Nrec records in the highest interval.
vii. Repeat the previous steps to have the desired number of ground motion records in each interval.
The choice of an optimal IM for this article mainly depends on its efficiency. In this regard, Sa (T1), the spectral acceleration at the fundamental period, is one of the most frequent IMs. However, its ability to explain the non-linear dynamic response of systems has been questioned (Grigoriu, 2016; Luco and Cornell, 2019). Instead, an IM based on the geometric mean of spectral acceleration values estimated at periods covering both higher and elongated modes of response, Saavg, is more efficient than Sa (T1) (Eads et al., 2015; Kazantzi and Vamvatsikos, 2015). Analogously, an IM identified as AvSa is used here to select and scale the datasets. It should be noted that AvSa differs from Saavg, in that it is calculated using the arithmetic mean rather than the geometric one.
The period range for averaging the spectral ordinates of AvSa should be determined from the dynamic properties of the entire building population (Kohrangi et al., 2017). This range has been set at (0.1–1.8) sec, which contains the fundamental periods of the generated models, as can be seen in Vargas–Alzate et al. (2022b). The intensity levels defining the upper and lower limits of each band (step v) range from 0.04 to 0.4 g at 0.04 g intervals (i.e., 10 bands have been defined). Therefore, the horizontal components of 1,000 ground motion records (100 per band) have been obtained from the seismic database. It should be noted that the scaling is applied to the ground motion records acting at the bedrock level.
Figure 7A shows the spectra of the selected and scaled ground motion records, and it can be seen that the spectral acceleration values at low periods are by far unexpected. In this regard, it is worth mentioning that these structures have been developed so that they meet the performance levels of a high-seismic hazard region (Vargas–Alzate et al., 2022b).
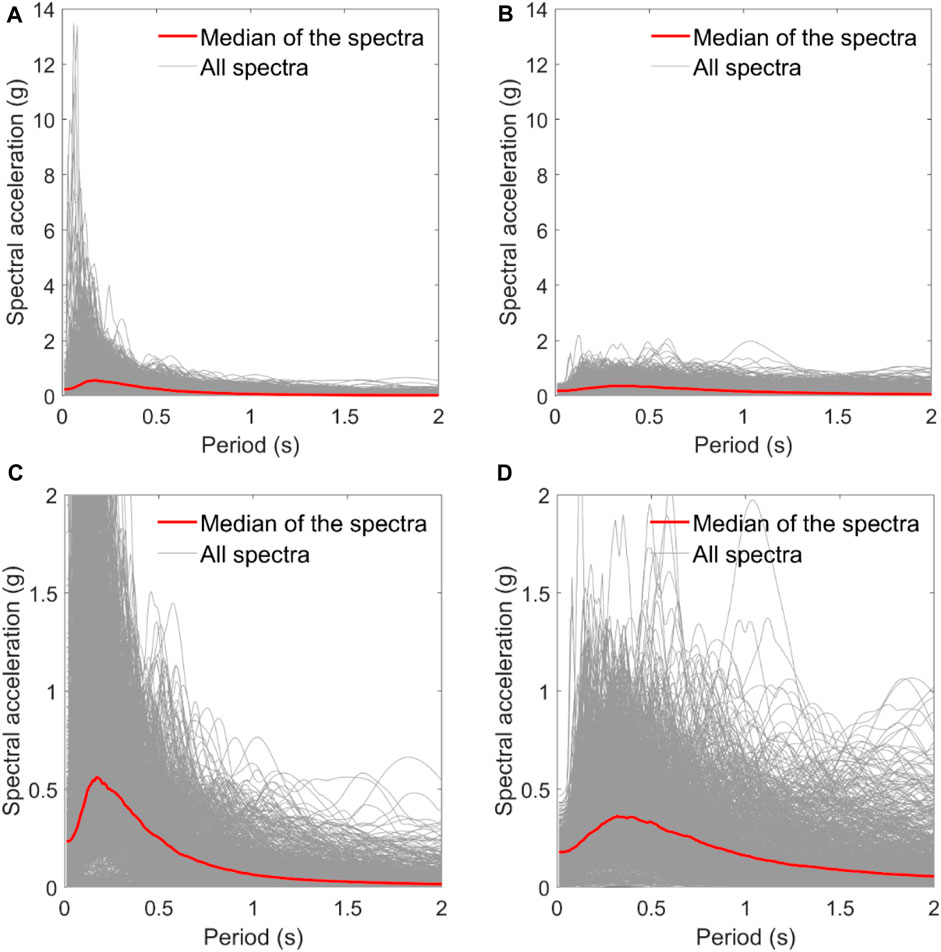
FIGURE 7. (A) Spectra of ground motion records acting at bedrock level. (B) Spectra of the resulting ground motions at the surface after the propagation process. (C,D) Close-up of the spectral acceleration below 2 g.
In order to fully explore the inelastic response of the analyzed set of structures, the intensity of some ground motion records should be increased by using high scale factors. For instance, it is necessary to scale some ground motion records until the PGA values are in the order of 4 g, which can be seen as improbable according to observed seismicity. Yet, by only considering these high intensity values, it is possible to properly derive fragility functions.
In line with the aforementioned concept, it should be noted that the window of periods in which the intensity measure is calculated includes high abscissa (i.e., higher than 1 s). This causes the resulting average intensity values (AvSa) to be much lower than the peak ordinate in the corresponding spectrum. This effect is more notorious when considering records acquired in stiff soil, as in the current study, which exhibit large amplifications at low period values. Consequently, very small displacements in the structures are expected. Moreover, these high spectral ordinates are observed within the ground motions acting at the bedrock level, as can be seen in Figure 7A. Since a soil profile acts as a filter, and in the current study it attenuates low period values due to the stiffness of the lacustrine soil, it should be noted that the resulting spectral ordinates at the surface (see Figure 7B) agree with realistic values.
One-dimensional site response analysis is associated with vertically propagating shear waves through horizontally layered media. To account for material damping, the soil layer is modeled as a Kelvin–Voigt solid. This is a material whose resistance to shearing deformation is the summation of the elastic and viscous parts (Kumar and Mondal, 2017). Numerically, site response analysis based on 1D models can be performed using linear, equivalent linear, and non-linear methodologies. Among them, the equivalent linear method is widely followed because of its simplicity and reasonable accuracy with respect to non-linear-based results (Yoshida et al., 2002). This methodology has been used here to assess the stiffness degradation and the consequent increase in damping within the soil profile.
At present, there are numerous software programs and codes that can perform site response analysis following 1D models. In this article, the WaveProp code (Pitilakis, 2023) has been used as a solver to develop the iterative procedure related to the equivalent linear method. In addition, due to the low computational time that this method consumes, it becomes an ideal candidate to consider the uncertainties in the mechanical properties of the materials. Hence, this method has been used with a twofold objective: i) account for uncertainties in the mechanical properties of soils; ii) provide an estimate of the modified properties of soil layers affected by seismic waves.
As described previously, the propagation of the seismic waves produces the degradation of soil stiffness and, consequently, the increase of material damping in each layer. These changes depend on the maximum shear strain reached during a seismic event. There are several methods to consider this effect. One of the most commonly used is the equivalent linear method (Kumar and Mondal, 2017). This method consists of estimating, from iterative linear approximations, the physical properties of an analogous soil profile whose dynamic response is similar to that obtained by an exhaustive but computationally expensive method, such as non-linear dynamic analysis. These calculations are performed in the frequency domain, which substantially reduces the computational effort.
In the equivalent linear method, the degradation of the stiffness and the consequent increase in the damping of the material in each layer are considered using the normalized shear modulus (G0/Gmax) and hysteretic damping curves, both as a function of the maximum shear strain reached during the dynamic process. For the case study, the reference curves have been selected from the geotechnical report described previously (FOPAE, 2011). Figure 8 shows the stiffness degradation (A) and damping curves (B) used in this study.
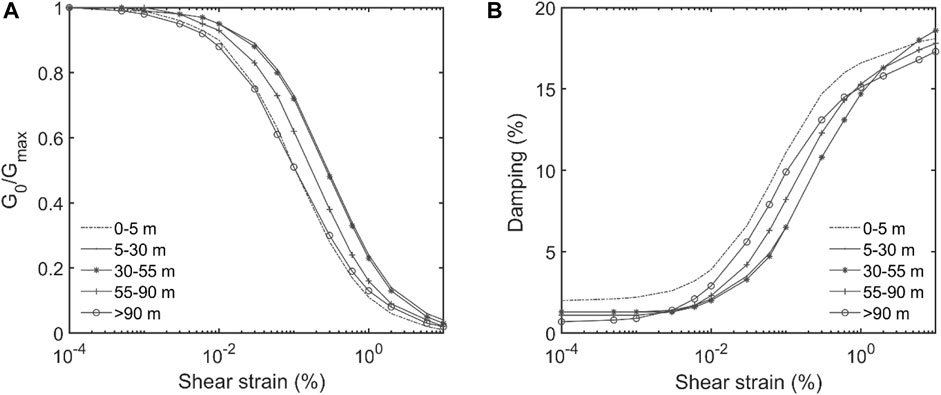
FIGURE 8. Degrading curves for lacustrine soil type. (A) G0/Gmax. (B) Damping (FOPAE, 2011).
The iterative process associated to the equivalent linear approximation is described step by step as follows.
i. Initially, each soil layer is modeled considering initial stiffness (
ii. From the properties described in the previous step, the time-history of shear strains in each soil layer is calculated,
iii. From the maximum strain reached during the propagation,
iv. For each layer, a new pair of Gi and
v. Steps ii to iv are repeated until the difference between two consecutive values of G and
vi. From the final values of G and
This iterative procedure has been used to estimate the non-linear response of the probabilistic soil profiles shown in Figures 4A, B. It should be noted that the density values (see Figure 5A) are used to estimate Vs from the resulting G values. Thus, Figures 4C, D show the resulting soil profiles after performing the equivalent linear approximation. Finally, Figure 5B compares the elastic versus the elongated periods. In all cases, a stiffness degradation of the soil profile has occurred. It should be noted that there are several outliers, which indicate that the equivalent linear method has not been able to achieve convergence. This is probably because the maximum shear strain reached the ultimate value shown in Figure 8. It has been estimated that the number of profiles meeting this condition is 122.
The development of accurate building models depends on the amount of information about the mechanical and geometric properties of structural components (Vargas–Alzate et al., 2022b). In urban contexts, knowledge of the spatial distribution of several physical properties is also of importance. Basic information should include the number of structures belonging to specific typologies, the distribution of building height and length, number of stories, and spans. Hence, the number of stories,
Data on the variability of the mechanical and geometric properties of the structural elements and those of the applied loads are also useful. Accordingly, random variables such as the concrete compressive strength, fc; the elastic modulus of the concrete, Ec; the steel yielding, fy; the elastic modulus of the steel, Es; live loads, LL; and permanent loads, DL, are assumed as continuous Gaussian distributions. It is worth noting that live loads are assigned as a fraction (33%) of the design value (Eurocode 8). Table 3 shows the statistical moments of these variables.
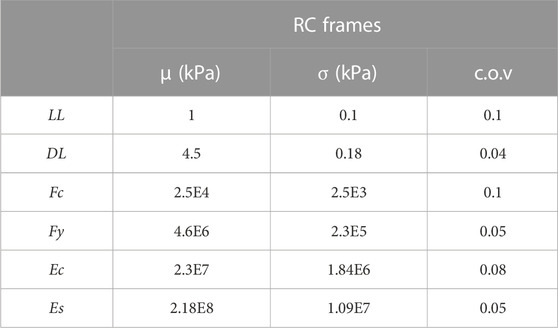
TABLE 3. Mean values, µ; standard deviations, σ; and coefficient of variation, c.o.v., of the assumed random variables.
In order to assign the cross-section dimensions of the first story columns, the following equation has been used.
where ci are coefficients that may be adjusted depending on the data distribution of the analyzed area. For this study,
The width of beams,
where bi are coefficients that depend on the characteristics of the study zone. For the hypothetical case study,
where
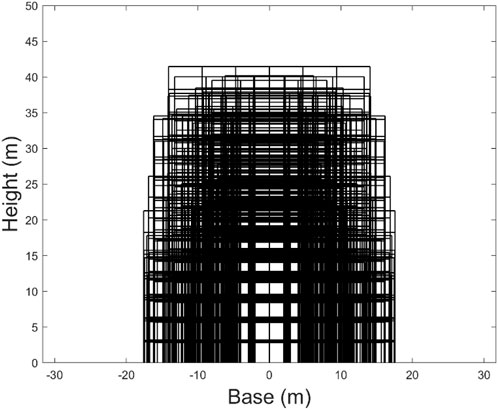
FIGURE 9. One hundred building samples generated according to the approach developed in Vargas–Alzate et al. (2022b).
For a dataset of ground motion records, a basic mathematical background along with proper numerical tools allow extracting some variables representing the seismicity of an area. In the context of earthquake engineering, such variables are known as instrumental IMs. Ideally, an IM should contain enough information about the earthquake, so according to it, the structural response can be predicted with confidence (Pejovic and Jankovic, 2015). Notice that an IM can depend either on the ground motion record or on both the ground motion and structural features (Eads et al., 2015). In this article, information related to the soil properties arises to increase the efficiency of the IMs.
Three types of IMs have been considered in this research. The first type corresponds to IMs derived from the dynamic equilibrium equation for single-degree of freedom (SDoF) systems.
where
EDPs are used to design or assess the expected behavior of buildings. Their most valuable feature is that they provide the best possible quantification of the level of performance of structures that are subjected to the ground motions induced by earthquakes. One of the most used EDPs for estimating this level is the maximum inter-story drift ratio, MIDR (Mayes, 1995). This EDP is highly used in both designing and assessing the vulnerability of buildings.
For a story i, the evolution of the inter-story drift is given by
where
In order to estimate the damage level of the most affected story, the maximum inter-story drift ratio observed in the building, MIDR, is given by
Based on Equation 10, this EDP has been employed in this research to estimate the expected performance of the simulated structures.
There are many numerical methods to simulate the non-linear dynamic response of buildings. They range from adapted linear-static-based methods to more advanced ones, considering the non-linear static (pushover-based methods) or dynamic response of a structure (non-linear dynamic analysis, NLDA). The latter has been employed in this research since it is the most reliable numerical tool to simulate the non-linear dynamic response of buildings.
Once defined and characterized hazard (see Section 3) and exposure (see Section 5), 1,000 NLDAs are performed. The Ruaumoko software has been used to perform structural analyses (Carr, 2007). After performing these analyses, it has been found that there are several simulations in which the capacity of the structure to withstand gravity loads is exceeded; in other words, the model is indicating structural collapse. These results must be excluded from the statistical analysis as they are excessively governed by chaos. Collapses have been identified as simulations providing a Park–Ang damage index higher than 1 (Park et al., 1987). This criterion is very efficient in detecting structural collapses in the current research. In addition, profiles whose elongated periods indicated lack of convergence in the equivalent linear method have also been excluded. Accordingly, 670 out of the 1,000 generated samples have been used to perform the statistical analysis. The resulting cloud of IM-EDP points is then employed to analyze some statistical properties related to data variability.
In this study, IM-EDP relationships are characterized by performing a non-linear regression analysis in the log–log space. In this sense, the following general linear least-square model allows several types of non-linear regressions:
where
This equation allows multi-linear (n = 1) and -quadratic (n = 2) regression models in the log–log space. In this way, several sources of information can be considered simultaneously to better predict a specific EDP.
Cloud analysis requires calculating the best-fit curve between a set of IM–EDP realizations in the log–log space. The resultant curve is used to estimate the median of a parametric statistical distribution, given an IM value. The variability of this parametric distribution is estimated as the logarithmic standard deviation of the regression (
In this case, IMs have been calculated by using the resulting ground motions at the surface once the seismic waves pass and degrade the soil profile properties. In this way, Figure 10 shows the bivariate distribution between IMs and MIDR. From this figure, it can be seen that several IMs, especially those related to velocity and displacement quantities, exhibit high efficiency. This result is consistent with that of the previous research, which has highlighted the capabilities of velocity as an enhanced physical magnitude to predict the deformation field of a structure (Vargas–Alzate et al., 2022b).
Using ground motion records at the surface implies that the effect of seismic wave propagation through the soil is not explicitly considered in the estimation of seismic risk. In this section, the resulting clouds of IM–EDP pairs have been analyzed using the ground motion records acting at the bedrock level. Figure 11 shows the bivariate distribution for IMs and MIDR under the aforementioned condition. As expected, a significant decrease in
It can be attributed to the influence of the filtering induced by the soil profile. Notwithstanding, Sd (T1) and AvSd remain at a significant level of efficiency. This efficiency is not as high as the one observed in the previous approach, where AvSv reached an
As previously stated, Eq. 12 allows identifying enhancing arrangements that consider statistical information from several IVs. To do so, it is necessary to replace
A large set of soil information variables has been included in the identification of the enhanced arrangements. In Table 5, a description of these variables is presented.
For the case of
If
In this article, the efficiency prediction of the non-linear dynamic response of reinforced concrete frame structures has been analyzed. The aim has been to develop advanced IMs that consider the dynamic interaction between the building and the underlying soil. The non-linear behavior of the latter has been considered by employing the equivalent linear method (Yoshida et al., 2002). A set of probabilistic soil profiles, structural models, and ground motion records has been used in this research. They have been integrated into a probabilistic framework based on the Monte Carlo method, which allowed the identification of mathematical arrangements highly correlated to the EDP of interest. A 1D model to represent the soil profile has been employed to predict the intensity of ground motions at the surface, once the seismic waves generated by an earthquake reach the base of the building. In doing so, a large group of statistically compatible random soil profiles is generated starting from the main features of a basic set of soil profiles. A database that collects almost 2,000 ground motion records acquired in Colombia has been used to characterize the seismic hazard.
The relationship between IMs and EDPs has been characterized using non-linear regression analysis in the log–log space. In this respect, the linear least squares model allows for different types of regression, and it can be used to extract statistical information from IM–EDP pairs. In general, a polynomial regression model has been used to quantify the efficiency of these pairs, where the higher the coefficient of determination, R2, the lower the variability in seismic risk estimates. It allowed identifying the most efficient IMs, given specific approaches.
First, the causal relationship between IMs acting at the base of the structural models and the MIDR has been analyzed. From these results, it has been observed that AvSv is the most efficient IM to predict this EDP. This is consistent with previous observations performed in Vargas–Alzate et al., 2022b. The second approach has been applied to identify the most efficient IM to predict the same EDP, but, in this case, IMs have been extracted from the ground motions acting at the bedrock level. As a consequence, two main conclusions have been drawn: i) the efficiency to predict the EDP significantly decreased, and ii) the most efficient IM has been AvSd. In fact, it has been observed that the IMs extracted from the displacement spectra [Sd (T1) and AvSd] are least likely to lose efficiency when the soil–structure interaction model is employed. The third approach has been to develop a mathematical arrangement with increased efficiency, called IMGD, that extracts information not only from the acting ground motion at the bedrock level but also from the dynamic properties of the soil. In this approach, two cases have been explored. First, the most efficient pair of IVs providing the best fit has been found. This significantly increased the efficiency, although it was not as close to the maximum correlation provided by the first approach, where AvSv exhibited an
Future research should be oriented toward extending the computational framework to 3D soil models. Moreover, multi-regression models can also be used to develop vector-valued (Baker, 2007) IMs, which generally increase the efficiency of predicting EDPs (Vargas-Alzate et al., 2022a). It is also important to analyze how efficiency behaves when analyzing results classified according to the number of storeys. Preliminary results indicate that these sub-classifications tend to increase efficiency. It is worth mentioning that the results presented in this research are tied to the soil type studied. Therefore, a correct parametrization of the degradation curves (see Figure 8) is a key aspect of the presented framework. In general, the analysis of new soil configurations, EDPs, IMs, and structural typologies will also provide valuable information to enhance the capabilities of the proposed model.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Conceptualization, AZ-F and YV-A. Methodology, AZ-F, YV-A, and LP. Software, AZ-F and YV-A. Writing—original draft preparation, AZ-F and YV-A. Writing—review and editing, AZ-F, YV-A, LP, and RG-D. Visualization, AZ-F, YV-A, LP, and RG-D. All authors contributed to the article and approved the submitted version.
This research has been funded by the Spanish Research Agency (AEI) of the Spanish Ministry of Science and Innovation (MICIN) through the projects with references: PID 2020-117374RB-I00/AEI/10.13039/501100011033 and TED 2021-132559B-I00—J-02970.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Angelini, M. E., and Heuvelink, G. B. M. (2018). Including spatial correlation in structural equation modelling of soil properties. Spat. Stat. 25, 35–51. doi:10.1016/j.spasta.2018.04.003
Arias, A. (1970). “Measure of earthquake intensity,” in Seismic design for nuclear power plants. Editors Hansen, and J. Robert (Cambridge: Massachusetts Inst. of Tech. Press), 438–483.
Baker, J. W. (2007). Probabilistic structural response assessment using vector-valued intensity measures. Earthq. Eng. Struct. Dyn. 36, 1861–1883. doi:10.1002/eqe.700
Beck, J. L., and Hall, J. F. (1986). Factors contributing to the catastrophe in Mexico City during the earthquake of September 19, 1985. Geophys Res. Lett. 13, 593–596. doi:10.1029/GL013i006p00593
Benavent-Climent, A., Akiyama, H., López-Almansa, F., and Pujades, L. G. (2004). Prediction of ultimate earthquake resistance of gravity-load designed RC buildings. Eng. Struct. 26, 1103–1113. doi:10.1016/j.engstruct.2004.03.011
Bommer, J. J., and Acevedo, A. B. (2004). The use of real earthquake accelerograms as input to dynamic analysis. J. Earthq. Eng. 8, 43–91. doi:10.1080/13632460409350521
Carrière, S. R., Jongmans, D., Chambon, G., Bièvre, G., Lanson, B., Bertello, L., et al. (2018). Rheological properties of clayey soils originating from flow-like landslides. Landslides 15, 1615–1630. doi:10.1007/s10346-018-0972-6
Chapra, S. C. (2018). Applied numerical methods with MATLAB® for engineers and scientists. New York, NY: McGraw-Hill Education.
Cheng, Y., Lucchini, A., and Mollaioli, F. (2015). Correlation of elastic input energy equivalent velocity spectral values. Earthquakes Struct. 8, 957–976. doi:10.12989/eas.2015.8.5.957
Comartin, C. D., Niewiarowski, R. W., Freeman, S. A., and Turner, F. M. (2000). Seismic evaluation and retrofit of concrete buildings: A practical overview of the atc 40 document. Earthq. Spectra 16, 241–261. doi:10.1193/1.1586093
Cruz, C., and Miranda, E. (2021). Insights into damping ratios in buildings. Earthq. Eng. Struct. Dyn. 50, 916–934. doi:10.1002/eqe.3356
Eads, L., Miranda, E., and Lignos, D. G. (2015). Average spectral acceleration as an intensity measure for collapse risk assessment. Earthq. Eng. Struct. Dyn. 44, 2057–2073. doi:10.1002/eqe.2575
Fajfar, P., Vidic, T., and Fischinger, M. (1990). A measure of earthquake motion capacity to damage medium-period structures. Soil Dyn. Earthq. Eng. 9, 236–242. doi:10.1016/S0267-7261(05)80002-8
Fiorentino, G., Quaranta, G., Mylonakis, G., Lavorato, D., Pagliaroli, A., Carlucci, G., et al. (2019). Seismic reassessment of the leaning tower of pisa: Dynamic monitoring, site response, and SSI. Earthq. Spectra 35, 703–736. doi:10.1193/021518EQS037M
FOPAE (2011). Procesamiento e interpretación de señales de la red de acelerógrafos de Bogotá 2009 - 2011. IDIGER. Bogotá.
Grigoriu, M. (2016). Do seismic intensity measures (IMs) measure up. undefined 46, 80–93. doi:10.1016/J.PROBENGMECH.2016.09.002
Güllü, A., Yüksel, E., Yalçın, C., Anıl Dindar, A., Özkaynak, H., and Büyüköztürk, O. (2019). An improved input energy spectrum verified by the shake table tests. Earthq. Eng. Struct. Dyn. 48, 27–45. doi:10.1002/eqe.3121
Hardin, B. O., and Scott, G. D. (1967). Generalized Kelvin-Voigt used in soil dynamics study. J. Eng. Mech. Division 93, 79–79. doi:10.1061/JMCEA3.0000830
Haselton, C. B., Atkinson, S., Jonathan, H. A., and Grant, N. (2012). “Selecting and scaling earthquake ground motions for performing response-history analyses,” in 15th world conference on earthquake engineering (Lisboa, Portugal: NIST GCR).
Housner, G. W. (1975). “Measures of severity of earthquake ground shaking,” in Proc. US natl. Conf. Earthq. Eng. Earthquake Engineering Research Institute (Ann Arbor Michigan).
Jalayer, F., De Risi, R., and Manfredi, G. (2015). Bayesian Cloud Analysis: Efficient structural fragility assessment using linear regression. Bull. Earthq. Eng. 13, 1183–1203. doi:10.1007/S10518-014-9692-Z
Kaklamanos, J., Baise, L. G., Thompson, E. M., and Dorfmann, L. (2015). Comparison of 1D linear, equivalent-linear, and nonlinear site response models at six KiK-net validation sites. Soil Dyn. Earthq. Eng. 69, 207–219. doi:10.1016/j.soildyn.2014.10.016
Kazantzi, A. K., and Vamvatsikos, D. (2015). Intensity measure selection for vulnerability studies of building classes. Earthq. Eng. Struct. Dyn. 44, 2677–2694. doi:10.1002/EQE.2603
Kohrangi, M., Bazzurro, P., Vamvatsikos, D., and Spillatura, A. (2017). Conditional spectrum-based ground motion record selection using average spectral acceleration. Earthq. Eng. Struct. Dyn. 46, 1667–1685. doi:10.1002/EQE.2876
Kostinakis, K., Fontara, I. K., and Athanatopoulou, A. M. (2018). Scalar structure-specific ground motion intensity measures for assessing the seismic performance of structures: A review. J. Earthq. Eng. 22, 630–665. doi:10.1080/13632469.2016.1264323
Krinitzsky, E. L. (2003). How to combine deterministic and probabilistic methods for assessing earthquake hazards. Eng. Geol. 70, 157–163. doi:10.1016/S0013-7952(02)00269-7
Kroese, D. P., and Rubinstein, R. Y. (2012). Monte Carlo methods. Wiley Interdiscip. Rev. Comput. Stat. 4, 48–58. doi:10.1002/wics.194
Kucherenko, S., Albrecht, D., and Saltelli, A. (2015). Exploring multi-dimensional spaces: A comparison of Latin hypercube and quasi Monte Carlo sampling techniques. arXiv.
Kumar, A., and Mondal, J. K. (2017). Newly developed MATLAB based code for equivalent linear site response analysis. Geotechnical Geol. Eng. 35, 2303–2325. doi:10.1007/s10706-017-0246-4
Lou, M., Wang, H., Chen, X., and Zhai, Y. (2011). Structure–soil–structure interaction: Literature review. Soil Dyn. Earthq. Eng. 31, 1724–1731. doi:10.1016/j.soildyn.2011.07.008
Luco, N., and Cornell, C. A. (2019). Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Sage Journals 23, 357–392. doi:10.1193/1.2723158
Mayes, R. L. (1995). Interstory drift design and damage control issues. Struct. Des. Tall Build. 4, 15–25. doi:10.1002/tal.4320040104
Nakamura, Y. (1989). A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railw. Tech. Res. Institute/Tetsudo Gijutsu Kenkyujo 30, 25–33.
Ohnaka, M. (1976). A physical basis for earthquakes based on the elastic rebound model. Bull. Seismol. Soc. Am. 66, 433–451. doi:10.1785/BSSA0660020433
Okur, D. V., and Ansal, A. (2007). Stiffness degradation of natural fine grained soils during cyclic loading. Soil Dyn. Earthq. Eng. 27, 843–854. doi:10.1016/j.soildyn.2007.01.005
Pagliaroli, A., Lanzo, G., Tommasi, P., and Di Fiore, V. (2014). Dynamic characterization of soils and soft rocks of the central archeological area of rome. Bull. Earthq. Eng. 12, 1365–1381. doi:10.1007/s10518-013-9452-5
Park, R., and Paulay, T. (1991). Reinforced concrete structures. New York, NY: John Wiley and Sons. Available at: https://books.google.es/books?id=QPDvchXv5zUC.
Park, Y. J., Ang, A. H. S., and Wen, Y. K. (1987). Damage-limiting aseismic design of buildings. Earthq. Spectra 3, 1–26. doi:10.1193/1.1585416
Pejovic, J., and Jankovic, S. (2015). Selection of ground motion intensity measure for reinforced concrete structure. Procedia Eng. 117, 588–595. doi:10.1016/j.proeng.2015.08.219
Pinzón, L. A., Vargas-Alzate, Y. F., Pujades, L. G., and Diaz, S. A. (2020). A drift-correlated ground motion intensity measure: Application to steel frame buildings. Soil Dyn. Earthq. Eng. 132, 106096. doi:10.1016/j.soildyn.2020.106096
Pitilakis, D., and Petridis, C. (2022). Fragility curves for existing reinforced concrete buildings, including soil–structure interaction and site amplification effects. Eng. Struct. 269, 114733. doi:10.1016/j.engstruct.2022.114733
Pitilakis, D. (2023). Waveprop. Available at: https://www.mathworks.com/matlabcentral/fileexchange/60589-waveprop.
Reed, J. W., and Kassawara, R. P. (1990). A criterion for determining exceedance of the operating basis earthquake. Nucl. Eng. Des. 123, 387–396. doi:10.1016/0029-5493(90)90259-Z
Sarma, S. K. (1971). Energy flux of strong earthquakes. Tectonophysics 11, 159–173. doi:10.1016/0040-1951(71)90028-X
Sarma, S. K., and Yang, K. S. (1987). An evaluation of strong motion records and a new parameterA95. Earthq. Eng. Struct. Dyn. 15, 119–132. doi:10.1002/eqe.4290150109
SGC (2020). Sistema de Consulta de la Amenaza Sísmica de Colombia. Available at: https://amenazasismica.sgc.gov.co/.
Shedlock, K. M. (2002). “Global seismic hazards,” in Encyclopedia of physical science and technology (Elsevier), 825–832. U.S. Geological Survey, Denver, Colorado, USA. doi:10.1016/B0-12-227410-5/00295-7
Silva, W. J., Abrahamson, N., Toro, G., and Constantino, C. (1996). Description and validation of the stochastic ground motion model. California: Pacific Engineering and Analysis.
Toro, G. R. (2022). Uncertainty in shear-wave velocity profiles. J. Seismol. 26, 713–730. doi:10.1007/s10950-022-10084-x
Tothong, P., and Luco, N. (2007). Probabilistic seismic demand analysis using advanced ground motion intensity measures. Earthq. Eng. Struct. Dyn. 36, 1837–1860. doi:10.1002/eqe.696
Vanmarcke, E. H. (1977). Probabilistic modeling of soil profiles. J. Geotechnical Eng. Div. 103, 1227–1246. doi:10.1061/AJGEB6.0000517
Vargas Alzate, Y. F., Pujades Beneit, L. G., Barbat, A. H., Hurtado Gomez, J. E., Diaz Alvarado, S. A., and Hidalgo Leiva, D. A. (2018). Probabilistic seismic damage assessment of reinforced concrete buildings considering directionality effects. Struct. Infrastructure Eng. 14, 817–829. doi:10.1080/15732479.2017.1385089
Vargas-Alzate, Y. F., Gonzalez-Drigo, R., and Avila-Haro, J. A. (2022a). Multi-regression analysis to enhance the predictability of the seismic response of buildings. Infrastructures (Basel) 7, 51. doi:10.3390/infrastructures7040051
Vargas-Alzate, Y. F., Hurtado, J. E., and Pujades, L. G. (2022b). New insights into the relationship between seismic intensity measures and nonlinear structural response. Bull. Earthq. Eng. 20, 2329–2365. doi:10.1007/s10518-021-01283-x
Wesnousky, S. G. (1994). The Gutenberg-Richter or characteristic earthquake distribution, which is it? Bull. Seismol. Soc. Am. 84, 1940–1959. doi:10.1785/BSSA0840061940
Yazgan, U. (2012). Proposal of energy spectra for earthquake resistant design based on Turkish registers. Available at: https://dialnet.unirioja.es/servlet/tesis?codigo=95317.
Keywords: soil profiles, inelastic response of soils, seismic wave propagation, Monte Carlo simulation, multi-regression analysis
Citation: Zapata-Franco AM, Vargas-Alzate YF, Pujades LG and Gonzalez-Drigo R (2023) Improved intensity measures considering soil inelastic properties via multi-regression analysis. Front. Earth Sci. 11:1214536. doi: 10.3389/feart.2023.1214536
Received: 29 April 2023; Accepted: 13 July 2023;
Published: 02 August 2023.
Edited by:
Sergio Molina-Palacios, University of Alicante, SpainReviewed by:
Gabriele Fiorentino, University of Bristol, United KingdomCopyright © 2023 Zapata-Franco, Vargas-Alzate, Pujades and Gonzalez-Drigo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. M. Zapata-Franco, YW5hLm1hcmlhLnphcGF0YUB1cGMuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.