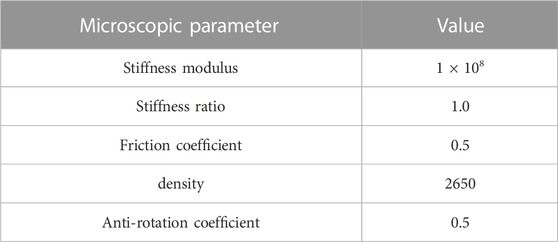
- 1Faculty of Land Resources Engineering, Kunming University of Science and Technology, Kunming, China
- 2Yunnan International Technology Transfer Center for Mineral Resources Development and Solid Waste Resource Utilization, Kunming, China
- 3Yunnan Phosphate Group Co., Ltd., Kunming, China
Under the Castor earthquake, there is a risk of liquefaction instability of saturated tailings, and the evolution of dynamic pore pressure can indirectly reflect its instability process. Before applying dynamic loads, the static stress state of soil is one of the main factors affecting the development of soil dynamic strength and dynamic pore pressure, and there are significant differences in soil dynamic strength under different consolidation ratios. This paper conducted dynamic triaxial tests on saturated tailings silt with different consolidation ratios, and analyzed the dynamic strength variation and liquefaction mechanism of the samples using the discrete element method (PFC3D). The results showed that 1) as the Kc′ gradually increased, and there was a critical consolidation ratio Kc′ during the development of the dynamic strength of the sample. The specific value of Kc′ was related to the properties and stress state of saturated sand. The Kc′ in this research was about 1.9. When Kc < 1.9, dynamic strength was increased with the increase in Kc; when Kc > 1.9, dynamic strength was decreased with the Kc. 2) Under the impact of cyclic load, when samples were normally consolidated (Kc =1), the pore water pressure would tend to be equal to the confining pressure to cause soil liquefaction. In the case of eccentric consolidation (Kc > 1), the pore water pressure would be less than the confining pressure, thus, the soil liquefaction would not be induced, and the pore pressure value would decrease with the increase of consolidation ratio. This paper provides engineering guidance value for the study of dynamic strength and liquefaction mechanism of tailings sand and silt in Castor earthquake prone areas under different consolidation ratios.
1 Introduction
As is well known, The pre-earthquake action of the on-site soil unit has vertical effective force force
As shown in Figure 1, The Karst landform area in southwestern China is prone to earthquakes. The dynamic instability of the tailings dam during the earthquake has gradually been paid attention to (Yan-Qiang et al., 2016); besides, most of the tailings dams are in the state of anisotropic consolidation, so it is important to study the dynamic characteristics of sand with different consolidation ratios (wang and Zhou, 2001).
At present, scholars have studied dynamic strength and the evolution law of dynamic pore water pressure of soil different consolidation ratios
However, during studying ynamic characteristics of soil, the dynamic pore pressure evolution of tailings under different consolidation conditions has not been paid enough attention. In practical projects, the dynamic failure process and dynamic pore pressure evolution law of tailings under different consolidation conditions also have certain differences (ZHANG et al., 2018). Therefore, in this paper, the influence of different consolidation ratios
2 Experiment scheme
2.1 Experiment apparatus and material
As shown in Figure 2, KTL-DYN10 dynamic triaxial equipment was selected for this experiment, and its hardware system consists of axial loading equipment, a controlling chamber of dynamic confining pressure, a back pressure controller, 8-channel high-speed control and acquisition equipment; The software system is a DSP high-speed digital control system with a maximum operating frequency of 10 Hz and a maximum dynamic stress amplitude of ±10 kN.
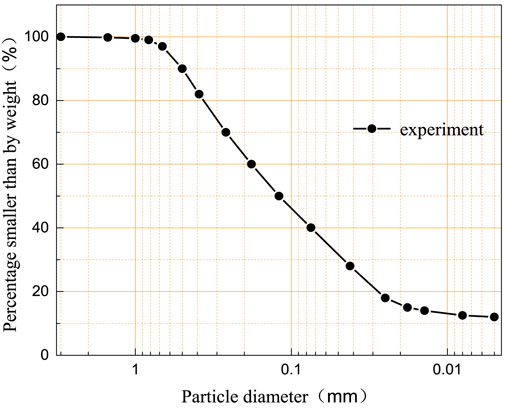
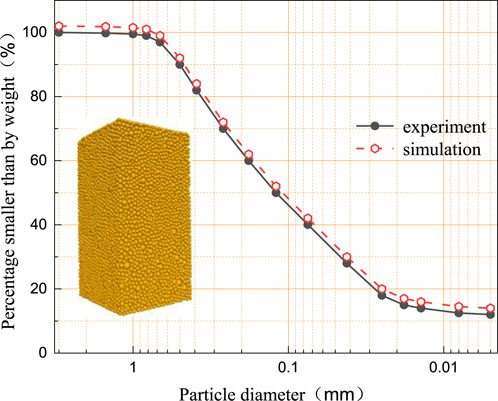
In this research, the tailings silty sand was taken from an iron tailings pond in Sichuan, and it is the main damming material of the tailings dam. Figure 3 shows the grading analysis of the tailings samples, the sample used in this test is Void ratio
2.2 Sample preparation
In the process of sample preparation, according to the 《Code for Geotechnical Test: GBT 50123-2019》 (General Institute of Water Resources and Hydropower Planning and Design, 2019), the drying temperature was determined to be 110°C. In this test, a cylindrical sample with a diameter of 50 mm and a height of 105 mm was processed, which was compacted in four layers; at the same time, the sample density was controlled according to the dry density, and the dry density of samples was determined to be 1.63 g/cm3 according to the deposition law of the tailings pond. Then, prepared samples were installed as shown in Figure 4.
2.3 Test procedure and scheme
After the sample preparation, the first action was to use the back-pressure controller to test its air impermeability, and then the CO2 saturation, water head saturation, and back-pressure saturation were subsequently performed to improve the sample saturation. After the sample saturation reached 98% (B>0.98), it was consolidated under the corresponding conditions; After that, the cyclic load with fixed frequency was applied for the test under the undrained condition.
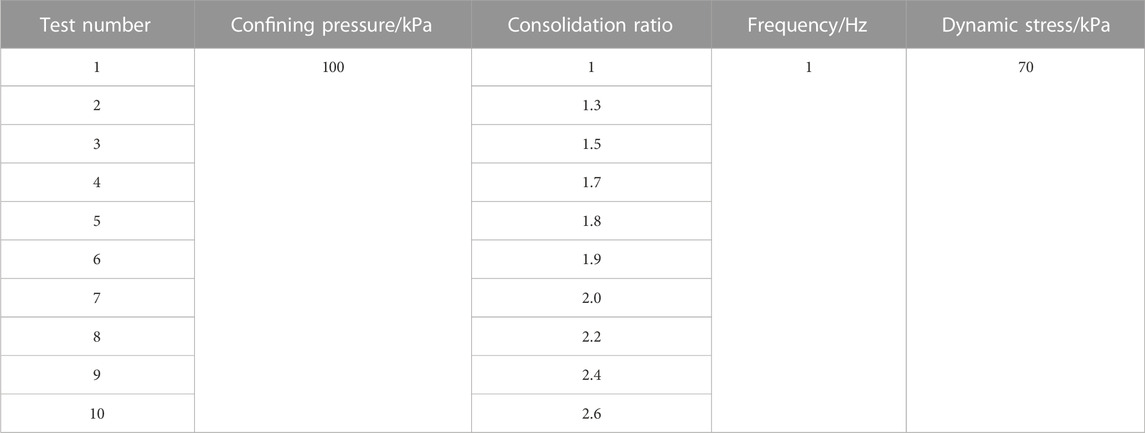
In this test, the load frequency was set as 1 Hz, the dynamic stress was set as 70 kPa, the consolidation confining pressure was kept to be 100 kPa, and the cyclic load was subjected using the method of equal stress amplitude. For the isotropic consolidation (
3 Analysis of test results
3.1 The influence of
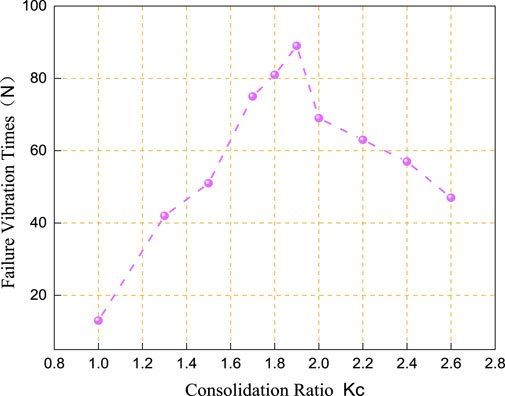
As shown in Figure 5, When
3.2 The influence of
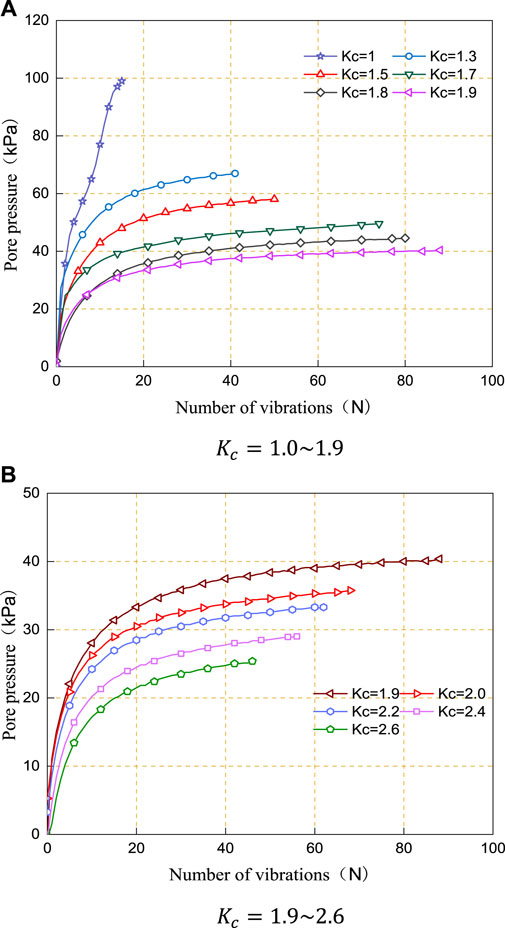
Figure 7 shows development curves of dynamic pore water pressure of the sample under different consolidation ratios
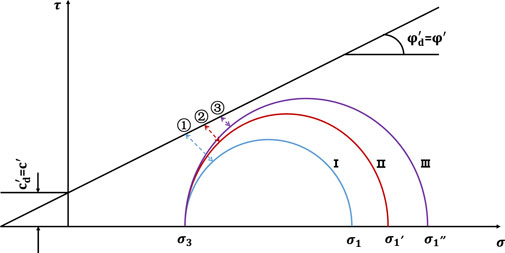
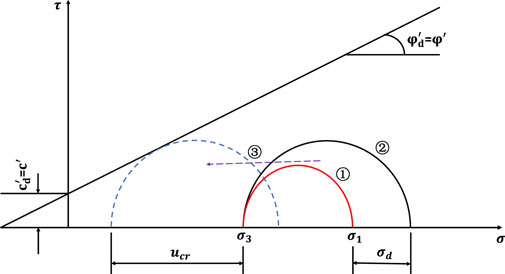
In order to analyze the influence of different consolidation ratios on the evolution of dynamic pore pressure of tailing silty sand, this paper used the limit equilibrium criterion to analyze the pore water pressure of materials under the limit equilibrium state, namely, the critical pore water pressure
According to the geometric conditions shown in Figure 8, the pore water pressure at the limit equilibrium state can be deduced as follows.
Where:
Setting
making
then
For common tailings, when
When
Because
Therefore, for a given dynamic stress amplitude, the pore water pressure will approach the confining pressure during isobaric consolidation, and during anisotropic consolidation, the critical pore pressure will be e less than the confining pressure, and the larger the consolidation ratio, the smaller the critical pore pressure.
4 Microscopic analysis
4.1 The introduction of simulation
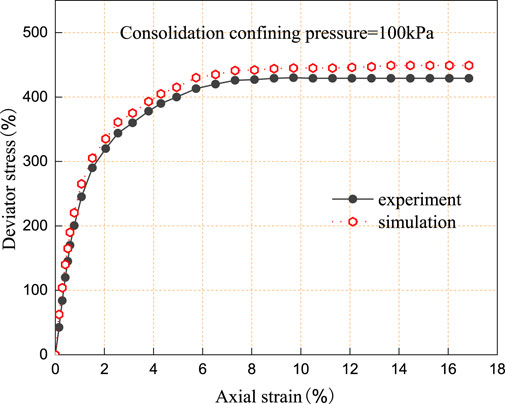
In this paper, PFC 3D was used to simulate the standard indoor undrained dynamic triaxial test of saturated tailing silty sand, and the simulated effective confining pressure was controlled to be 100 kPa; the test was carried out using the loading method of equal stress amplitude. The upper and lower walls are loaded uniformly by the control program, and when the bias stress reaches the set stress amplitude qcyc, the upper and lower walls reverse and continue to move until they reach the set stress amplitude qcyc in the opposite direction and then reverse again.
During the loading process, the lateral strain
4.2 Analysis of mechanical coordination number
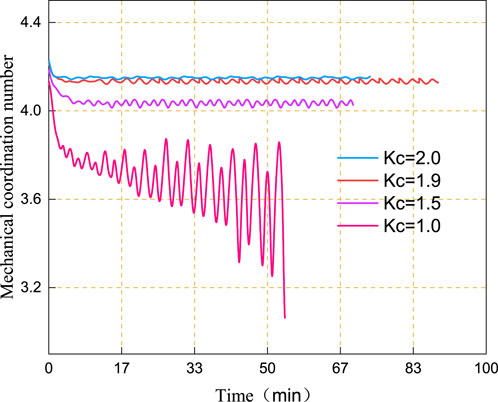
The mechanical coordination number refers to the average number of contacts per particle in the sample (MAHMOOD et al., 2020; AHMAD et al., 2021), excluding suspended particles with contact numbers less than or equal to 1. For granular materials, their mechanical properties are mainly affected by the density, which is affected by the indirect contact density of particles at the microscopic level (Thornton, 2000; Li et al., 2021b), which can be expressed by the mechanical coordination number of particles.
It can be seen from Figure 11 that with the increase of the consolidation ratio, the initial value of the mechanical coordination number became larger, as well as the number of particle contacts and the compactness of the sample, at the initial stage of cyclic loading, the mechanical coordination number of the sample continued to decrease. Figure 12 shows the changing curve of the instantaneous dynamic pore water pressure and corresponding mechanical coordination number curve while meeting the failure criteria under different consolidation ratios
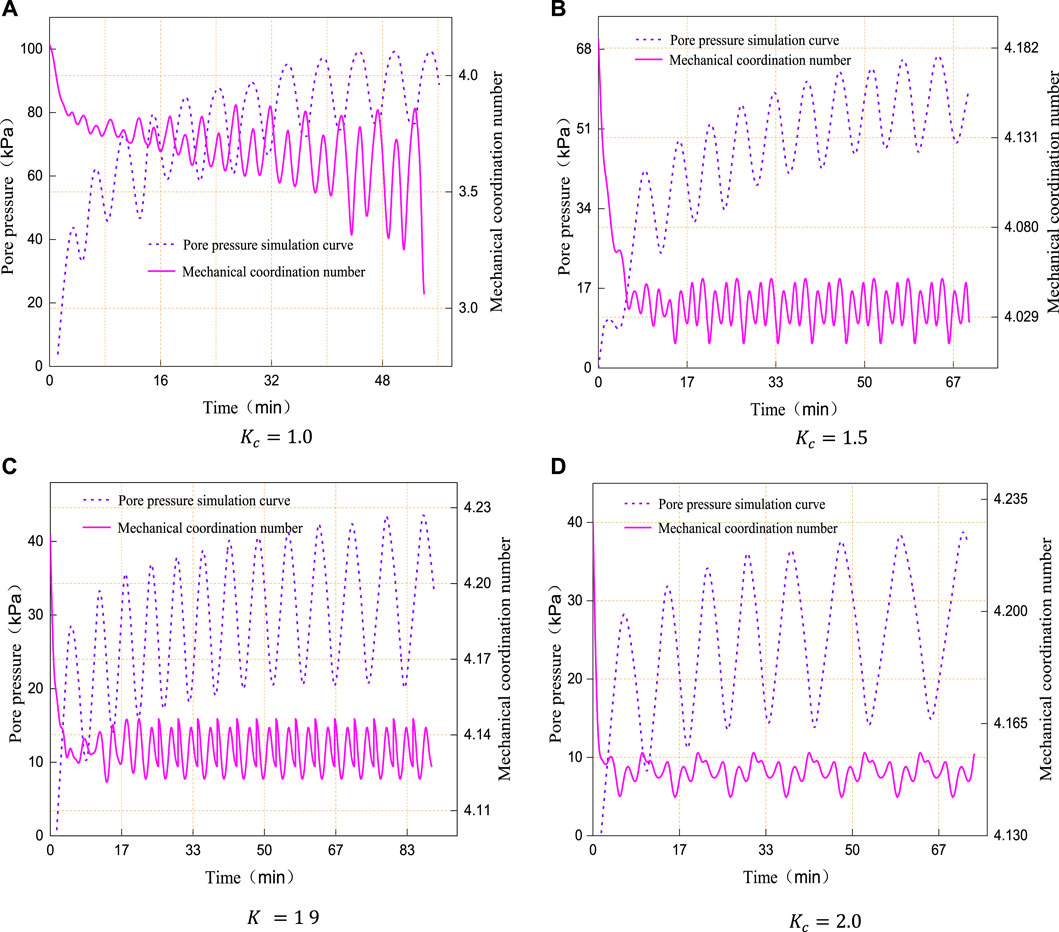
FIGURE 12. Pore pressure simulation and mechanical coordination curves under different consolidation conditions (A–D).
4.3 Energy analysis
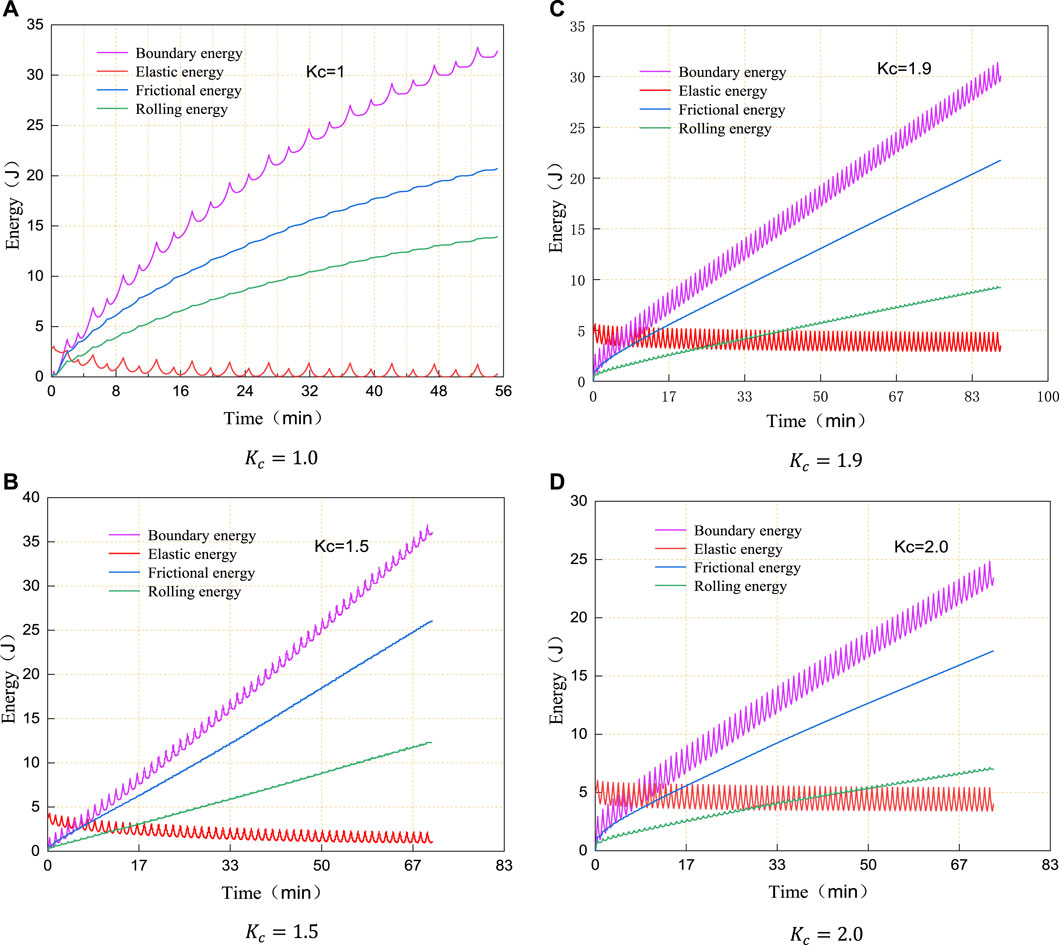
The energy storage and dissipation of particles during the loading process can represent their macroscopic mechanical response to a certain extent, and their failure actually experienced the evolution process of energy dissipation and instability (AHMAD et al., 2019b; AHMAD et al., 2020). The following will focus on the evolution law of The evolution law of elastic energy of particles (refers to the energy stored in the contact area of particles to deform the particles), particle friction (Bolton et al., 2008; Li et al., 2023), rolling energy dissipation (refers to the energy dissipated by sliding friction and anti-rolling between particles respectively) and boundary energy (refers to the energy generated by wall driving) (AHMAD et al., 2019c; Gao et al., 2023).
Figure 13 shows the energy evolution curves of the saturated tailing silty sand samples. it can be seen when the wall was subjected to cyclic loading and unloading, the wall would generate a certain amount of energy named boundary energy. At the same time, there was a certain amount of elastic energy stored at the contact of particles, and it increased and decreased successively with the loading and unloading process, but the decreasing amplitude was greater than the increasing amplitude so that the elastic energy was gradually released. In addition, under the effect of cyclic load, relative sliding (friction energy consumption) occurred between particles, which was followed by different degrees of rolling between particles (rolling energy consumption).
At the initial state, the elastic energy of particles increased with the increase of the consolidation ratio. As shown in Figure 13A, when
5 Conclusion
In this paper, in order to study the dynamic strength and liquefaction mechanism of tailings sand in karst seismic prone areas under different static stress states, a series of dynamic triaxial tests were conducted on saturated tailings fines in an iron tailings pond in Sichuan, and combined with discrete element simulations to further explore the dynamic properties of the fines under different consolidation ratios. The main conclusions are as follows.
(1) The critical consolidation ratio
(2) The variation of dynamic strength showed different trends before and after reaching the
(3) The limit equilibrium theory and particle flow simulation were used to explain the phenomenon that for the isobaric consolidation
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.
Author contributions
JC: Writing—review and editing WG: Conceptualization LS: Methodology KF: Software CB: Validation ZL: Formal analysis. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors LS, CB, and ZL were employed by Yunnan Phosphate Group Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmad, M., Tang, X. W., Qiu, J. N., Gu, W-J., and Ahmad, F. (2020). A step forward towards a comprehensive framework for assessing liquefaction land damage vulnerability: Exploration from historical data. Front. Struct. Civ. Eng. 14 (6), 1476–1491. doi:10.1007/s11709-020-0670-z
Ahmad, M., Tang, X. W., Qiu, J. N., Gu, W-J., and Ahmad, F. (2021). Application of machine learning algorithms for the evaluation of seismic soil liquefaction potential. Front. Struct. Civ. Eng. 15 (2), 490–505. doi:10.1007/s11709-020-0669-5
Ahmad, M., Tang, X-W., Qiu, J-N., and Ahmad, F. (2019a). Evaluating seismic soil liquefaction potential using bayesian belief network and C4.5 decision tree approaches. Appl. Sci. 9 (20), 4226. doi:10.3390/app9204226
Ahmad, M., Tang, X-W., Qiu, J-N., and Ahmad, F. (2019b). Interpretive structural modeling and MICMAC analysis for identifying and benchmarking significant factors of seismic soil liquefaction. Appl. Sci. 9 (2), 233. doi:10.3390/app9020233
Ahmad, M., Xiaowei, T., and Jiangnan, Q. (2019c). Response and tolerability of sofosbuvir plus daclatasvir in elderly patients with chronic hepatitis-C. IEEE 14th Int. Conf. Intelligent Syst. Knowl. Eng. (ISKE) Proc. 31, 527–529.
Bolton, M. D., Nakata, Y., and Cheng, Y. P. (2008). Micro- and macro-mechanical behaviour of DEM crushable materials. Geotechnique 58 (6), 471–480. doi:10.1680/geot.2008.58.6.471
Chang-Rong, H. E. (1998). Compression and extrusion elongation characteristics of the dynamic triaxial test[J]. Sichuan United Univ. Sci. Ed. 2(04), 49–54. doi:10.15961/j.jsuese.1998.04.009
Chen-Yang, B. A. O., Xiang-Juan, Y., and Gao, Z. B. (2006). Experimental study on the dynamic properties of Yunnan chalk soil[J]. J. Disaster Prev. Mitig. Eng. 26 (03), 321–325. doi:10.13409/j.cnki.jdpme.2006.03.015
Chien, L. K., Oh, Y. N., and Chang, C. H. (2000). “In the effects of anisotropy consolidation on liquefaction strength and deformation for reclaimed soil,” in 10th international offshore and polar engineering conference (ISOPE-2000). Seattle,Wa; International Society Offshore& Polar Engineers. 594–599. Seattle, Wa May 28-Jun 02.
Dai, B. B., Yang, J., and Zhou, C. Y. (2013). Numerical simulation of unstable behavior of loose sand[J]. Chin. J. Geotechnical Eng. 35 (09), 1737–1745.
Ding-Yi, X. I. E., Zhi-Hui, W. U., and Yao-Tang, G. U. O. (1981). Application of limit equilibrium theory in the analysis of dynamic instability process of saturated sand[J]. China Civ. Eng. J. 14 (04), 17–28. doi:10.15951/j.tmgcxb.1981.04.003
Gao, Y., Yu, Z., Chen, W., Yin, Q., Wu, J., and Wang, W. (2023). Recognition of rock materials after high-temperature deterioration based on SEM images via deep learning. J. Mater. Res. Technol. 25, 273–284. doi:10.1016/j.jmrt.2023.05.271
General Institute of Water Resources and Hydropower Planning and Design (2019). “Ministry of water Resources, nanjing Institute of water Resources science,” in Geotechnical test procedures: Gbt 50123 -2019[S] (China Plan Press.
Hong-Jian, L., Mao-Hong, Y., and Qi-Ming, W. A. I. (1998). Study of dynamic shear strength of loess-like soils and volcanic ash clayey soils[J]. J. Xi'an Jiaot. Univ. 32 (10), 73–77.
Hu, Y. F. (1996). Engineering properties and stability analysis of fly ash dam construction. Sichuan United University.
Jiang, M. J., Sun, R. H., and Tao, L. I. (2020). CFD-DEM simulation of undrained cyclic triaxial shear of microbial treated sand[J]. Chin. J. Geotechnical Eng. 42 (01), 20–28. doi:10.11779/CJGE202001002
Jiang, Y. X. (2019). Study on the vibration liquefaction characteristics of gravelly sandy soil and rubbery sandy soil[D]. China University of Mining and Technology.
Ke-Xu, Z. (1984). Liquefaction stress condition of saturated sand[J]. Earthq. Eng. Eng. Vib. 4 (1), 99–109. doi:10.13197/j.eeev.1984.01.009
Kong, L., Liang-Liang, J. I., and Cao, J. F. (2013). Meso-mechanism of the effect of stress path and particle size on sand deformation[J]. Chin. J. Rock Mech. Eng. 32 (11), 2334–2341.
Konstadinou, M., and Georgiannou, V. N. (2013). Cyclic behaviour of loose anisotropically consolidated Ottawa sand under undrained torsional loading. Geotechnique 63 (13), 1144–1158. doi:10.1680/geot.12.p.145
Li, X. L., Chen, S. J., Liu, S. M., and Li, Z. H. (2021a). AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Central South Univ. 28 (6), 1843–1856. doi:10.1007/s11771-021-4734-6
Li, X. L., Chen, S. J., Wang, S., Zhao, M., and Liu, H. (2021b). Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example. Adv. Mater. Sci. Eng. 9 (4), 5594181–5594211. doi:10.1155/2021/5594181
Li, X. L., Zhang, X. Y., and Shen, W. L. (2023). Abutment pressure distribution law and support analysis of super large mining height face. Int. J. Environ. Res. Public Health 20 (2), 227. doi:10.3390/ijerph20010227
Lian-Hong, Y. U., and Wang, Bo (1999). Experimental study of vibratory pore water pressure in saturated powder soils[J]. J. Dalian Univ. | J Dalian Univ 20 (4), 59–64.
Liao, H. J., Song, L., and Zheng, Y. A. N. G. (2001). Experimental study on the strength of cohesive soils under reciprocal loading and the criteria for taking values[J]. Rock Soil Mech. 2001 (01), 1620. doi:10.16285/j.rsm.2001.01.004
Liu, H. Y., Zhang, B. Y., Li, X. L., Liu, C., Cheng, W., Feng, W., et al. (2022). Research on roof damage mechanism and control technology of gob-side entry retaining under close distance gob. Eng. Fail. Anal. 138 (5), 106331. doi:10.1016/j.engfailanal.2022.106331
Liu, S. M., Li, X. L., Wang, D. K., and Zhang, D. (2020). Investigations on the mechanism of the microstructural evolution of different coal ranks under liquid nitrogen cold soaking. Energy Sources, Part A Recovery, Util. Environ. Eff., 1–17. doi:10.1080/15567036.2020.1841856
Mahmood, A., Tang, X-W., Qiu, J-N., Gu, W-J., and Ahmad, F. (2020). A hybrid approach for evaluating CPT-based seismic soil liquefaction potential using Bayesian belief networks. J. Central South Univ. 27 (2), 500–516. doi:10.1007/s11771-020-4312-3
Mei-Ying, M. A. (1988). Effect of initial consolidation shear stress on the dynamic strength of saturated sandy soils[J]. Water Resour. Water Transp. Sci. Res. 2 (1), 63–68. doi:10.16198/j.cnki.1009-640x.1988.01.007
Mei-Ying, M. A. (1980). Several problems of standard sand liquefaction test[J]. Chin. J. Geotechnical Eng. 2 (4), 46–54.
Shen, Y., Tao, M. A., and Guo-Jian, X. U. (2015). PFC numerical experimental study on dynamic collapse characteristics of silt under stress control mode[J]. Chin. J. Geotechnical Eng. 37 (12), 2280–2285.
Shou-Zhi, N. E. I. (1980). Liquefaction and strength of saturated sand under dynamic load[J]. Chin. J. Geotechnical Eng. (03), 64–73.
Thornton, C. (2000). Numerical simulations of deviatoric shear deformation of granular media. Geotechnique 50 (1), 43–53. doi:10.1680/geot.2000.50.1.43
Wang, X. H., and Zhou, H. L. (2001). Influence of consolidation ratio on liquefaction of saturated sand[J]. China Railw. Sci. 22 (6), 121–126.
Wang, Y. Z., Pan-Bo, Y. A. N. G., and Sun, Xi-Ping (2015). Study on strength weakening of soft clay under cyclic load and its dynamic calculation application[J]. Chin. J. Geotechnical Eng. 37 (05), 821–828. doi:10.11779/CJGE201505007
Yan-Qiang, D. U., Chun-He, Y. A. N. G., and Shang-Wei, W. U. (2016). Pore water pressure characteristics of tailings silt undercyclic loading[J]. J. Northeast. Univ. Sci. 37 (04), 583–588. doi:10.3969/j.issn.1005-3026.2016.04.027
Yang, L. I. U., Zhou, J., and Wu, S. C. (2007). Fine view numerical simulation of sandy soil deformation under cyclic loading I:Loose sand test results[J]. Chin. J. Geotechnical Eng. 29 (7), 1035–1041.
Yao-Hui, G. U. O., Peng, Z., and Tian, Y. K. (2021). Numerical simulation of particle flow in triaxial compressionof tailings from a metal mine[J]. Min. Res. Dev. 41 (05), 118–123. doi:10.13827/j.cnki.kyyk.2021.05.021
Zhang, J. H., and Chang-Rong, H. E. (1994). Liquefaction strength and pore pressure law of unsaturated sandy soils under reciprocal loading[J]. J. Chengdu Univ. Sci. Technol. (01), 1–8.
Zhang, Ru, Chang-Rong, H. E., Wen-Ping, F. E. I., and Mingzhong, G. A. O. (2006). Effect of consolidation stress ratio on the development pattern of dynamic strength and dynamic pore pressure of soil samples[J]. Chin. J. Geotechnical Eng. (01), 101–105.
Zhang, X. Z., Shang-Wei, W. U., and Zhang, Chao (2018). Evolution of dynamic pore pressure in tailings under different consolidation conditions[J]. Rock Soil Mech. 39 (03), 815–822. doi:10.16285/j.rsm.2016.0921
Zhou, J., Yang, Y. X., and yang, L. I. U. (2009). Numerical simulation of granular flow with sandy soil liquefaction characteristics under cyclic loading[J]. Rock Soil Mech. 30 (04), 1083–1088. doi:10.16285/j.rsm.2009.04.053
Keywords: Castor earthquake area, saturated tailings sand soil, consolidation ratio, dynamic triaxial test, particle flow simulation
Citation: Chunlin J, Guangjin W, Shujian L, Fuqi K, Binting C and Lei Z (2023) Study on dynamic strength and liquefaction mechanism of silt soil in Castor earthquake prone areas under different consolidation ratios. Front. Earth Sci. 11:1206252. doi: 10.3389/feart.2023.1206252
Received: 15 April 2023; Accepted: 03 July 2023;
Published: 17 July 2023.
Edited by:
Xuelong Li, Shandong University of Science and Technology, ChinaReviewed by:
Yiming Liu, Hubei University of Technology, ChinaJunxin Liu, Southwest University of Science and Technology, China
Feezan Ahmad, Dalian University of Technology, China
Copyright © 2023 Chunlin, Guangjin, Shujian, Fuqi, Binting and Lei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wang Guangjin, d2FuZ2d1YW5namluMjAwNUAxNjMuY29t
 Jiang Chunlin
Jiang Chunlin Wang Guangjin
Wang Guangjin Li Shujian3
Li Shujian3