A three-dimensional microseismic downhole noise suppression based on polarization filtering method in Shearlet transform

Microseismic noise suppression is widely used in the exploration of unconventional oil and gas resources. The effective microseismic downhole signals have extremely weak energy and are contaminated by strong interference, making data processing and interpretation difficult. The need for high-frequency effective signal reservation presents a basic problem in the design of noise suppression methods. The effective signals represent as the continuous reflection event and have more concentrated features in the transform domain, which can be used to tell the signal from the irregular microseismic noise. However, the high-frequency signal and extremely complex noise bring difficulty in accurately separating them by a single threshold. In this study, we propose a novel denoising method called Shearlet-polarization filtering to effectively suppress the microseismic noise. In general, Shearlet-polarization filtering is the combination of polarization filtering and conventional Shearlet transform. Specifically, the Shearlet transform can decompose the microseismic data into multi-directional and multi-scale information, providing a solid foundation for the separation of effective signals and background noise. From this basis, polarization filtering achieves signal reservation and noise attenuation by making full use of the three-dimensional information. To evaluate the performance, we also compare the proposed method with conventional Shearlet threshold filtering and polarization filtering. Experimental results both in synthetic and field data processing indicate that the Shearlet-polarization filtering is superior to the competing methods because it can significantly improve the continuity and smoothness of the microseismic events, even in low SNR conditions.

1 Introduction

Microseismic is a technique used in the oil and gas industry to monitor the propagation of fractures in subsurface rock formations. It involves recording very small seismic events caused by the fracturing of the rock during hydraulic fracturing or other activities. The recorded data can provide valuable insights into the extent and direction of the fractures, which can be used to explore unconventional oil and gas resources (Lu et al., 2018), (Liu et al., 2022), (Negi et al., 2021). In general, the effective signals in the microseismic records are often represented as the high-frequency reflection events with weak energy and short duration (Maxwell and Urbanic, 2001), (Shemeta and Anderson, 2010). Meanwhile, the recorded data is always contaminated by the intense background noise, bringing difficulty in extracting meaningful information (Yu et al., 2015), (Yu et al., 2016). Therefore, telling the desired signals from the unwanted noise has great significance in the microseismic data processing.

Over the past few decades, microseismic noise suppression has been extensively discussed, and numerous denoising methods have been proposed. Non-stationary signal processing techniques, such as wavelet and time-frequency analysis, have established a solid theoretical foundation for microseismic denoising (Wang and Gao, 2014), (Mousavi et al., 2016). Nonetheless, they also showed limited effects when confronted with complex microseismic data. Matched filtering recovers the desired signal with the need for the given reflection events as a reference, so the low SNR condition restricts its filtering effect (Han and Van Der Baan, 2015), (Kakhki et al., 2020). F-K filtering makes use of the apparent velocity distinction between the microseismic signal and complex noise. This distinction in the time-space domain is quite apparent, while it suffers from effectual signal distortion and still needs further improvement (Li et al., 2016). Interference suppression in the τ-p domain is proposed in the microseismic signal processing, and the propagation direction is used to extract the desired signal. However, weak energy and high frequency may cause the overlapped phenomenon between the signal and noise in the τ-p domain (Wail and Abdullatif, 2012). Sparse representation filtering and hyperbolic Radon domain filtering share similar problems in separating the desired signals (Rodriguez et al., 2012), (Sabbione et al., 2013). As a result, threshold filtering in the transform domain needs further improvement.

Compared with the above methods, multi-scale wavelet transform (such as Curvelet transform and Contourlet transform) meets the microseismic signal processing requirements and shows more potential (Castro de Matos et al., 2007). Shearlet transform is a new type of multi-directional and multi-scale geometric analysis that combines the advantages of Curvelet and Contourlet transforms (Guo and Labate, 2007). It offers a directional multiscale framework with the ability to precisely analyze the optimal representations in terms of their directional information (Lim, 2010). Specifically, Shearlet transform can capture additional information about the geometry of the singularity set, which can be precisely described with a variation of the scale parameters (Houska, 2012). Consequently, it presents a more significant difference between the signal and noise relative to the time domain, frequency domain, and some other time-space domains. In contrast, noise and signal often share the high-frequency bands, and the amplitudes of effective signals may be attenuated when using pure threshold filtering (part of the high-frequency signals are also filtered out with the noise) (Zhao et al., 2016). A lot of effort is being spent on improving these weaknesses, and an efficient and effective method is still needed simultaneously.

In this paper, we concentrate on the background noise attenuation in downhole microseismic data through a novel Shearlet-polarization filtering, combing the Shearlet transform with polarization filtering. The Shearlet transformation has good locality, directionality and sparsity, the method can generally convert the three-dimensional microshock data into different scales and direction information, but the selection of the threshold is difficult to use the corresponding characteristics of effective signal, leading to a mixed superposition of the desired signal and unwanted noise (Wang et al., 2021).

As we know, polarization filtering is a spatial filtering technology that weakens the noise interference according to the polarization feature difference between signal and noise (Du et al., 2000). It can offer a satisfying filtering result with a single direction in the transform domain (Benhama et al., 1988). But the expected direction of the filter factor of the polarization filter method is fixed. For the more complex wave field, the waveform of the effective signal will distort because the wave vector deviates from the fixed component, making the in-phase axis discontinuous. Therefore, polarization filtering combining Shearlet transform could effectively retain the effective high-frequency signal, suppress the intense background noise, and avoid the false axis at the maximum limit, overcoming the limitation of the simplex direction in polarization filtering method, as well the simplex threshold criterion in Shearlet threshold filtering method. The performance of this proposed approach is explained and discussed thoroughly in the synthetic model and real field data. The results show that Shearlet-polarization filtering can significantly suppress the complex noise and effectively preserves the desired microseismic signal. The rest of this paper is organized as follows: Section 2, for one thing, describes the definition and optimal sparse approximation properties of shearlets, and for another, illustrates the principle of polarization filtering based on the shearlet transform in detail. The validity of the proposed method is tested on the synthetic records and field data in sections Ⅲ. Finally, Section 4 concludes the paper.

2 Model building

2.1 Shearlet transfom

Shearlet transform is a novel approach for capturing the geometric information associated with the singularity sets of bivariate functions and distributions (Han and Van Der Baan, 2015). This multiscale method provides a precise and straightforward metric characterization for signal analysis, such as rotation, translation, and scale. In addition, Shearlet transform not only has the same optimal approximation order as the Curvelet transform but also shows better performance in frequency separation (Lim, 2010). In this section, the basic principle is briefly introduced.

A continuous affine system (Zhao et al., 2016) with composite dilation $L^2\left({\mathbf{R}}^2\right)$ is a functions collection:

$\left\{T_t{D}_M\mathrm{\psi }:t\in {\mathbf{R}}^2,M\in G\right\},(1)$

where $\mathrm{\psi }\in L^2\left({\mathbf{R}}^2\right)$ and $T_t$ is a translation, described as follows:

$T_{t}f\left(x\right)=f\left(x-t\right),t\in {\mathbf{R}}^2.(2)$

Moreover, the dilation matrix $D_M$ (for any $M\in G$) is defined by:

$D_{M}f\left(x\right)={\left|\det M\right|}^{-1/2}f\left(M^{-1}x\right).(3)$

Additionally, the matrix $M_{as}$ is the composition of the shear matrix $S_s=\left(\begin{array}{cc}1& -s\\ 0& 1\end{array}\right)$ and the anisotropic dilation matrix $A_a=\left(\begin{array}{cc}a& 0\\ 0& \sqrt{a}\end{array}\right)$. Accordingly, G is defined as the 2-parameter dilation group:

$G=\left\{M_{as}=\left(\begin{array}{cc}a& -\sqrt{as}\\ 0& \sqrt{a}\end{array}\right):\left(a,s\right)\in {\mathbf{R}}^{+}\times \mathbf{R}\right\}.(4)$

As a result, the continuous shearlet transform is defined as the function

$S{H}_{\mathrm{\psi }}\left(f\right)=〈f,{\mathrm{\psi }}_{ast}〉,(5)$

where $S{H}_{\mathrm{\psi }}\left(\cdot \right)$ represents Shearlet transform, and $〈\cdot 〉$ defines the inner product. Moreover, $\mathrm{\psi }\in L^2\left({\mathbf{R}}^2\right)$ is defined as:

$\left\{{\mathrm{\psi }}_{ast}\left(x\right)=T_t{D}_{S_s{A}_a}\mathrm{\psi }=a^{-3/4}\mathrm{\psi }\left(A_a^{-1}{S}_s^{-1}\left(x-t\right)\right):a\in {\mathbf{R}}^{+},s\in \mathbf{R},t\in {\mathbf{R}}^2\right\}.(6)$

Shearlet transform is onto the functions ${\mathrm{\psi }}_{ast}$ at location t, orientation s and scales a (Zhao et al., 2016). The above equations show that these calculations involve mathematical operations in the Fourier domain and space domain at the same time.

And the inverse Shearlet transform $S{H}^{-1}\left(\cdot \right)$ is shown as follows:

$f=S{H}_{\mathrm{\psi }}^{-1}\left({\mathrm{S}\mathrm{H}}_{\mathrm{\psi }}\left(f_{ast}\right)\right)={\int }_{{\mathbf{R}}^2}{\int }_{-\infty }^{\infty }{\int }_0^{\infty }〈f,{\mathrm{\psi }}_{ast}〉{\mathrm{\psi }}_{ast}\frac{da}{a^3}dsdt,a\in {\mathbf{R}}^{+},s\in \mathbf{R},t\in {\mathbf{R}}^2.(7)$

Afterward, the discrete Shearlet transform is introduced by Kutyniok and Labate as:

$\left\{{\mathrm{\psi }}_{jkm}\left(x\right)={\left|{\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{A}}_4\right|}^{-j/2}\mathrm{\psi }\left(S_1^{-k}{A}_4^{-j}x-m\right):j,k\in \mathbf{Z},m\in {\mathbf{Z}}^2\right\}.(8)$

Compared with the continuous Shearlet transform in Eq. 6, the discrete one samples the parameters a, s and t into a discrete set. Respectively, these parameters are substituted for the sequence: the scales parameter $a_j=4^j$, the orientation parameter $s_{jk}=k{2}^j$, and the location parameter $t_{jkm}=S_{k{2}^j}{A}_{4^j}m$ (where $a>0$, $s\in \mathbf{R}$, $t\in {\mathbf{R}}^2$, and $j,k\in \mathbf{Z}$, $m\in {\mathbf{Z}}^2$). So the relationship between the continuous and discrete transform can be described as:

$\left\{\left(a_j,s_{jk},t_{jkm}\right)=\left(4^j,k{2}^j,S_{k{2}^j}{A}_{4^j}m\right):j,k\in \mathbf{Z},m\in {\mathbf{Z}}^2\right\},(9)$

${\mathrm{\psi }}_{a_j{s}_{jk}{t}_{jkm}}\left(x\right)=D_{A_{4^j}{S}_k}{T}_m\mathrm{\psi }\left(x\right).(10)$

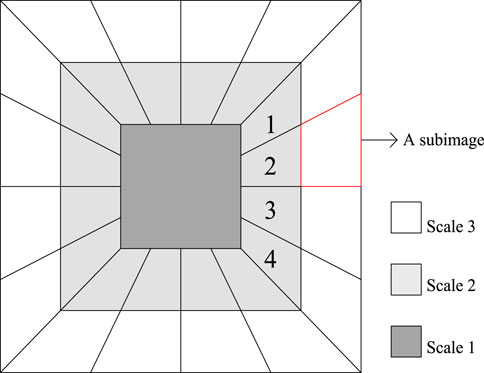
In Figure 1, a sub-image within the red borders is set as an example for the Shearlet domain. In the figure, we can observe the energy distribution of different records based on the direction and energy. Specifically, $A_a$ controls the scale by a dilation factor along the two axes, while $S_s$ dominates the orientation. It is essential to emphasize that the transform has strong potential in image denoising, edge extraction and fine-structure approximation (Houska, 2012).

FIGURE 1

FIGURE 1. A shearlet sketch map with the subimage distribution depended on the parameters a and s.

2.2 Shearlet-polarization filtering method

A three-dimensional noisy downhole microseismic record can be described as follows:

$G\left(t,d,i\right)=F\left(t,d,i\right)+N\left(t,d,i\right),(11)$

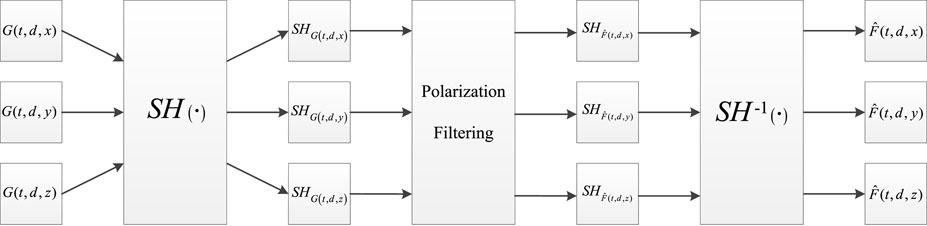
where G represents the noisy record, while F and N denote the pure desired signal and complex microseismic noise, respectively. At the same time, t and d indicate the time samples and trace number. Moreover, i is the dimensional index (described as x, y, and z). The specific procedures of Shearlet-polarization filtering could be concluded as:

First, the three-dimensional microseismic record is transformed into a Shearlet domain with each direction. In addition, Shearlet transform is a linear transform; as a result, the Shearlet coefficients of the noisy form can be expressed as:

$S{H}_{G\left(t,d,i\right)}=S{H}_{F\left(t,d,i\right)}+S{H}_{N\left(t,d,i\right)},(12)$

the coefficients of the noisy record comply with the sparse representation theory, where the desired signal and noise components respectively correspond to the significant and small coefficients, especially in the high-frequency bands. The distinction is obvious in separating the desired signal from the noise in the Shearlet domain. However, threshold filtering has a simplex criterion and suffers from the confusion between the signal and noise. In other words, the desired downhole microseismic data is relatively concentrated in the high-frequency scales, while the noise may distribute in the similar bands, bringing difficulty for the denoising task. Additionally, the weak signal and strong noise worsen the situation. Compared with the disordered noise, the desired signals often share similar propagation characteristics and show relevant polarization properties. Therefore, Shearlet-polarization filtering is proposed by leveraging the differences between the signals and background noise in polarization properties, aiming to accurately suppress the background noise with the consideration of signal reservation.

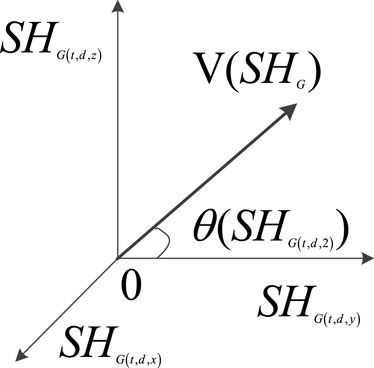
Secondly, Shearlet-polarization filtering makes use of the polarization property of the downhole microseismic data, and the polarization filter with spatial orientation features is applied. The modulating function is described as follows:

$f\left(S{H}_{G\left(t,d,i\right)}\right)=T^p\left(S{H}_{G\left(t,d,i\right)}\right){\cos }^q\theta \left(S{H}_{G\left(t,d,i\right)}\right),(13)$

where $T\left(S{H}_{G\left(t,d,i\right)}\right)$ denotes the polarization coefficient, $\theta (S{H}_{G\left(t,d,i\right)}$ is the included angle between the three-dimensional coordinate axis and the direction of the principal eigenvector $\mathrm{V}\left(S{H}_G\right)$. The sketch map of the filter and each parameter is shown in Figure 2. And, $p$ and $q$ stand for the degree and weighted value of the polarization direction, respectively. Generally, the value range of $p$ is set to $\left[\mathrm{0,2}\right.)$, and the signal under the shearlet domain becomes linearly polarized, thus having little effect on the filtering. Meanwhile, the scope of q can be expressed as $q\in [\mathrm{0,4})$. Moreover, the larger the value always indicates the smaller the passband and the stronger the effect of suppressing performance. The filtering result in the Shearlet domain $S{H}_{\widehat{F}\left(t,d,i\right)}$ is generated with the aforementioned processing strategy.

FIGURE 2

FIGURE 2. The sketch map of the Shearlet-polarization filtering and corresponding parameters.

Notably, the polarization coefficient $T\left(S{H}_{G\left(t,d,i\right)}\right)$ and the main eigenvector $\mathrm{V}\left(S{H}_G\right)$ are calculated from the noisy microseismic records. With a given window length $N$, the covariance matrix $M_c$ is generated as follows:

$M_c=\frac{1}{N}\left[\begin{array}{ccc}\sum S{H}_{\mathrm{x}}^2& \sum S{H}_{x}S{H}_y& \sum S{H}_{x}S{H}_z\\ \sum S{H}_{y}S{H}_x& \sum S{H}_y^2& \sum S{H}_{y}S{H}_z\\ \sum S{H}_{z}S{H}_x& \sum S{H}_{z}S{H}_y& \sum S{H}_z^2\end{array}\right],(14)$

where $S{H}_i=S{H}_{G\left(t,d,i\right)}-\frac{1}{N}\sum S{H}_{G\left(t,d,i\right)}$ denotes the removing mean value. The main eigenvector $\mathrm{V}\left(S{H}_G\right)$ is $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$, where ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ $\left({\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\right)$ are the eigenvalues of a matrix $M_c$. Then, the polarization coefficient $T\left(S{H}_{G\left(t,d,i\right)}\right)$ is calculated as follows:

$T\left(S{H}_{G\left(t,d,i\right)}\right)=\frac{{\left(1-e_{21}^2\right)}^2+{\left(1-e_{31}^2\right)}^2+{\left(e_{21}^2-e_{31}^2\right)}^2}{2{\left(1+e_{21}^2{+}_{31}^2\right)}^2},(15)$

where $e_{21}=\sqrt{{\lambda }_2/{\lambda }_1}$ and $e_{31}=\sqrt{{\lambda }_3/{\lambda }_1}$.

Finally, the filtering result $\widehat{F}\left(t,d,i\right)$ is acquired by the inverse transformation (shown in Eq. 7) of $S{H}_{\widehat{F}\left(t,d,i\right)}$. Figure 3 shows the schematic diagram of the Shearlet-polarization filtering for a clearer understanding.

FIGURE 3

FIGURE 3. The schematic diagram of the Shearlet-polarization filtering algorithm.

3 Application to the seismic records

3.1 Synthetic seismic records

To verify the feasibility and effectiveness of the proposed filtering method, we have selected a synthetic downhole microseismic record with 36 traces (namely, x-, y-, z-components, each component having 12 traces). In addition, the stratum depth and corresponding apparent velocities are 100 m (1500 m/s), 350 m (2000 m/s), 100 m (3000 m/s), and 100 m (4,500 m/s), respectively. The focal depth is 205 m. Meanwhile, the horizontal distance between the focus and detectors is 150 m, and the first downhole detector depth is 283 m with a vertical length of 8 m (12 sensors in total). The dominant frequency f is 200 Hz, and the sampling frequency is 1,000 Hz. The expression of the Ricker wavelet x(t) is expressed as follows:

$x\left(t\right)=\left(1-2{\pi }^2{f}^2{t}^2\right)e^{-{\pi }^2{f}^2{t}^2},(16)$

to quantitatively evaluate the denoising performance, the signal-to-noise ratio (SNR) is selected as the indicator, as shown in the following equation:

$SNR=10\lg \left({\displaystyle \sum _{i=1}^N}\frac{F{\left(t,d\right)}^2}{{\left(\widehat{F}\left(t,d\right)-F\left(t,d\right)\right)}^2}\right),(17)$

where N denotes the data length, while $F\left(t,d\right)$ and $\widehat{F}\left(t,d\right)$ are the clean signals and predicted results, respectively.

The clean synthetic record is shown in Figure 4A. Here, we use white Gaussian noise to simulate the microseismic background noise, and a noisy record with a signal-to-noise ratio (SNR) of -3 dB (Figure 4B) is used as the processing data. Notably, the desired signals are corrupted in the intense noise, and the reflection events are weak and intersect with each other, making it difficult to extract them, especially for the small amplitude ones in some directions. From the basis, we use the Shearlet threshold filtering method, the polarization filtering and the proposed Shearlet-polarization filtering to attenuate the background noise in the noisy synthetic record. The detailed comparison results and filtered noise for different filtering methods are shown in Figures 4C–H. We also select two areas of interest for detailed comparisons, as the red and green blocks indicated. After being filtered by the three methods, the filtering results are all differently improved relative to the noise-containing recording, and the same-phase axis is clearer. However, the polarization filtering shows a weakness in high-frequency and multi-directional signal recovery, and the effective signal of some seismic channels is easy to be removed as noise, leading to excessive removal of the effective signal, as shown in Figure 4C. It is almost impossible to keep the weakest signal among the three directions. This is because high-frequency signals have a small length in the time domain, and the effective signal duration is short, meanwhile, the waveform changes too drastically, making it hard to distinguish between multiple directions. Similarly, the Shearlet threshold filtering (Figures 4E, F) is limited by the simplex criterion and confuses the weak signal with the intense noise, falling short of expectation in intense noise suppression, such as the signals in the deep strata (marked by the green blocks). This is because the selection of threshold can only show a certain scale, more concentrated energy signal, signals in microseismic wells in low SNR environments, too small a threshold will retain more random noise, too large a threshold will suppress more effective signals. Due to the large amplitude gap in the same-phase axis, effective recordings and partial random noise with larger amplitude are retained, while valid records with smaller amplitude are annihilated. In contrast, the Shearlet-polarization filtering method in Figure 4G has a better denoising effect than the competing methods. For a certain scale and direction, the Shearlet coefficients meet the limitation of the polarization property and increase accuracy by using three-dimensional information. The noise removal in Figure 4H is more thorough, such as the contents shown in the blue blocks. Meanwhile, the event recovery is more prominent (no conspicuous signal leakage in the filtered noise), and the intersecting portions have less distortion.

FIGURE 4

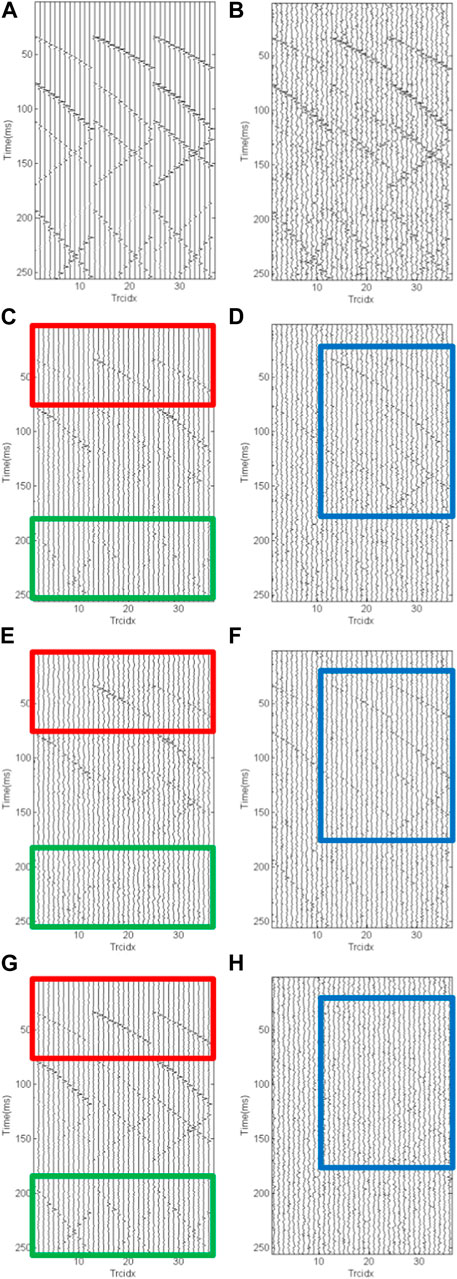
FIGURE 4. Results of a synthetic microseismic record. (A) Pure record. (B) Noisy record. (C) Result of polarization filtering in time domain. (D) Differences between noisy and recovered data by polarization filtering in time domain. (E) Result of Shearlet threshold filtering. (F) Differences between noisy and recovered data by Shearlet threshold filtering. (G) Result of Shearlet-polarization filtering. (H) Differences between noisy and recovered data by Shearlet-polarization filtering.

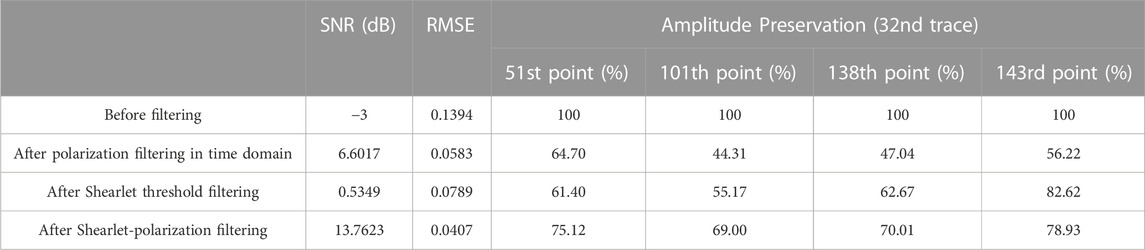
To perform intensive analysis, we choose the 32nd trace record for a detailed comparison, whereas the corresponding results are shown in Figure 5. By observing the results, from the two dimensions of amplitude retention degree and noise suppression, we can find that Shearlet threshold filtering reserves more wave crests than polarization filtering, and polarization filtering performs better in noise suppression. Both methods have their corresponding benefits and drawbacks. In contrast, the Shearlet-polarization filtering method shows advantages in both aspects, compared with the competing methods. In specific, the denoising result is closer to the noise-free signal on the wave crest component, and the noise component is almost completely attenuated. From the basis, the quantitative analysis in SNR, root mean square error (RMSE) and amplitude preservation is conducted, and the results are listed in Table 1. The algorithm mentioned in this paper substantially maintains the amplitude by more than 70%, and only the peak amplitude at the 101 ms position recovers 69%, and the gap is not very large, meanwhile the recovery results for the other two methods are less than 56%, so the results obtained by the Shearlet-polarization filtering methodthis method are relatively good. The other two algorithms are deficient in amplitude retention because they do not take full advantage of the corresponding properties of valid signals when processing high-frequency recordings with low signal-to-noise ratios. It is shown that the proposed method achieves the most significant improved SNR of 16.76 dB, which is over 7 dB increment over the competing methods. And it has minimal RMSE, reflecting the advantages of this method in terms of signal preservation ability. In addition, Shearlet-polarization filtering method also represents the most excellent performance in signal-amplitude preservation. Thus, theoretical analysis and synthetic microseismic model processing results show that the Shearlet-polarization filtering method can effectively remove the background noise and improve the SNR without severe amplitude loss.

FIGURE 5

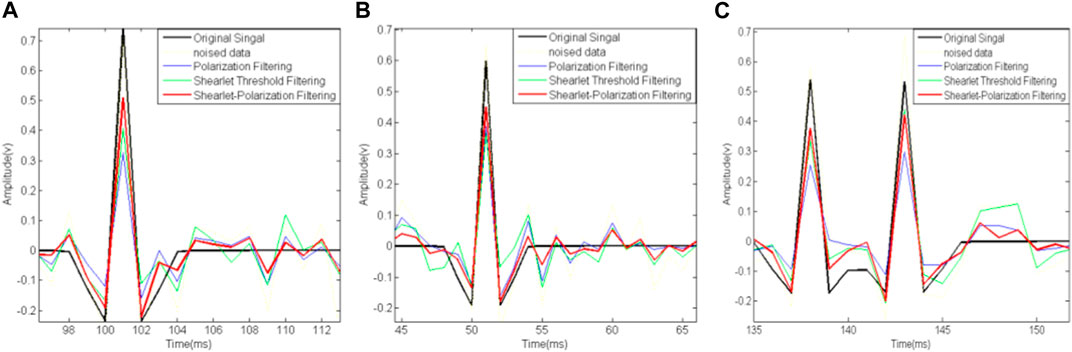
FIGURE 5. Waveform Preservation of the three methods in the 32nd trace. (A) The 1st wavelet with the dominant frequency of 200 Hz. (B) The 2nd wavelet with the dominant frequency of 200 Hz. (C) The 3rd and 4th wavelets with the dominant frequency of 200 Hz.

TABLE 1

TABLE 1. SNR, RMSE and Amplitude preservation of differrent methods.

3.2 Field data processing

To verify the practical application of the proposed Shearlet-polarization filtering method, a field downhole microseismic record with 15 traces acquired in certain areas of China has been processed. The aforementioned methods are used to process the field microseismic data, and the results are shown in Figure 6. Figure 6A displays the three-dimensional field microseismic record that contains 15 traces in total (x-, y-, and z-component have 5 traces each), and the dominant frequency of the desired signals ranges from 100 to 300 Hz. It can be seen that in the actual seismic recording, the effective signal is drowned in random noise, and it can be found that it is difficult to identify the effective signals of the X component and the Y component, and it is necessary to rely on the Z component with strong energy for auxiliary analysis. The waveform of the desired signal is similar to the noise and changes intensely. As a result, the polarization filtering retains all three component effective signals, but the waveform has certain distortion in the filter results, and the recovered filter results are not smooth enough, mainly because the extraction process of time domain signal is greatly affected by noise, as shown in Figure 6B. The Shearlet transform recovers the effective signal of the Z component well, and the effective signal recovery degree for the X component and the Y component is at a low degree, especially the X component recording with a small signal amplitude, due to the low signal-to-noise ratio of this part, the effective signal in the filtering result is almost completely suppressed, as shown in Figure 6D. On the other hand, the result obtained by the Shearlet-polarization filtering method (shown in Figure 6F) is better in background noise attenuation and signal preservation. Meanwhile, the recovered events are in great continuity and smoothness with a clean background (especially the parts labeled by the rectangle boxes). The corresponding results demonstrate that the proposed method outperforms the competing algorithms in weak signal recovery and intense noise suppression. Thus, we can get the point safely that Shearlet-polarization filtering is competent in denoising the complex microseismic data and represents great ability in amplitude preservation, even for the desired signals buried in the intense background noise.

FIGURE 6

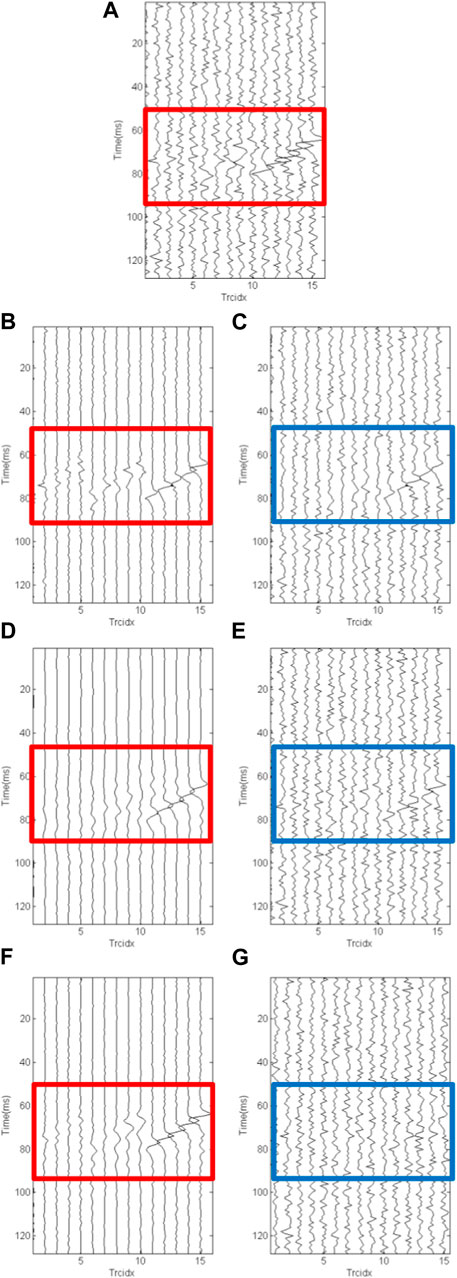
FIGURE 6. Results of a set of field data by the three methods. (A) Real downhole microseismic record. (B) Denoising results of polarization filtering in time domain method. (C) Differences between noisy and recovered data by polarization filtering in time domain method. (D) Result of Shearlet threshold filtering method. (E) Result of Shearlet threshold filtering method. (F) Denoising results of Shearlet-polarization filtering method. (G) Differences between noisy and recovered data by the Shearlet-polarization filtering method.

4 Conclusion

As for the denoising of downhole microseismic data, the Shearlet-polarization filtering method, viewed as the modification of the polarization filtering and Shearlet threshold method is proposed in this study. The polarization filtering proved to be limited in application because it demands single directivity and an appropriate window. Meanwhile, the Shearlet threshold method suffers from a restraint in the simplex criterion for the complex microseismic environment. On this basis, the Shearlet transform provides a multiscale and multi-directional condition for polarization filtering, which fully uses the microseismic signal’s three-dimensional polarization feature for filtering. It shows that in the process of the filtering method, the corresponding characteristics of the effective signal and the analysis of the properties of the effective signal can be analyzed and processed in a targeted manner. The SNR comparison results indicate that Shearlet-polarization filtering can accurately recover the weak signals with an SNR increment over 17 dB, reflecting its effectiveness in complex microseismic data processing. Meanwhile, the experimental results on synthetic and microseismic field data also demonstrate that the Shearlet-polarization filtering method can achieve better performance in high-frequency signal preservation and noise attenuation when compared to the competing methods. Therefore, the Shearlet-polarization filtering method has application prospects, which is of certain significance for accurately judging and identifying the geological information contained in seismic data. Although the proposed method have achieved impressive performance, the denoising accuracy may degrade when confronted with microseismic data having a low SNR. All the same, the proposed method still can provide a reference for the designing of denoising methods.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LH was responsible for data curation, methodology and writing initial draft preparation. DY contributed to the conceptualization and supervision. PY carried out the methodology and reviewing and editing of the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of interest

PY was employed by FAW-VOLKSWAGEN.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Benhama, A., Cliet, C., and Dubesset, M. (1988). Study and applications of spatial directional filtering in three-component recordings. Geophys. Prospect. 36 (6), 591–613. doi:10.1111/j.1365-2478.1988.tb02182.x

CrossRef Full Text | Google Scholar

Castro de Matos, M., Osorio, P. L., and Johann, P. R. (2007). Unsupervised seismic facies analysis using wavelet transform and self-organizing maps. Geophysics 72 (1), 9–21. doi:10.1190/1.2392789

CrossRef Full Text | Google Scholar

Du, Z. J., Foulger, G. R., and Mao, W. J. (2000). Noise reduction for broad-band, three-component seismograms using data-adaptive polarization filters. Geophys. J. Int. 141 (3), 820–828. doi:10.1046/j.1365-246x.2000.00156.x

CrossRef Full Text | Google Scholar

Guo, K. H., and Labate, D. (2007). Optimally sparse multidimensional representation using shearlets. Siam J. Math. Analysis 39 (1), 298–318. doi:10.1137/060649781

CrossRef Full Text | Google Scholar

Han, J. J., and Van Der Baan, M. (2015). Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding. Geophysics 80 (6), 69–80. doi:10.1190/geo2014-0423.1

CrossRef Full Text | Google Scholar

Houska, R. (2012). The nonexistence of Shearlet scaling functions. Appl. Comput. Harmon. analysis 32 (1), 28–44. doi:10.1016/j.acha.2011.03.001

CrossRef Full Text | Google Scholar

Kakhki, M. K., Mansur, W. J., and Peters, F. C. (2020). Rayleigh wave separation using high-resolution time-frequency polarization filter. Geophys. Prospect. 68 (7), 2014–2118.

Google Scholar

Li, H. J., Wang, R. Q., Cao, S. L., Chen, Y., Tian, N., and Chen, X. (2016). Weak signal detection using multiscale morphology in microseismic monitoring. J. Appl. Geophys. 133, 39–49. doi:10.1016/j.jappgeo.2016.07.015

CrossRef Full Text | Google Scholar

Lim, W. Q. (2010). The discrete shearlet transform: A new directional transform and compactly supported shearlet frames. IEEE Trans. Image Process. 19 (5), 1166–1180. doi:10.1109/TIP.2010.2041410

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, P., Li, R., Yue, Y. H., Liao, S. J., and Qian, F. (2022). Robust prestack seismic facies analysis using shearlet transform-based deep learning. J. Geophys. Eng. 19 (3), 521–533. doi:10.1093/jge/gxac015

CrossRef Full Text | Google Scholar

Lu, J., Wang, Y., and Chen, J. Y. (2018). Noise attenuation based on wave vector characteristics. Appl. Sci. 8 (5), 672. doi:10.3390/app8050672

CrossRef Full Text | Google Scholar

Maxwell, S. C., and Urbanic, T. I. (2001). The role of passive micro seismic monitoring in the instrumented oil field. Lead. Edge 20 (6), 636–639. doi:10.1190/1.1439012

CrossRef Full Text | Google Scholar

Mousavi, S. M., Langston, C. A., and Horton, S. P. (2016). Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform. Geophysics 81 (4), 341–355. doi:10.1190/geo2015-0598.1

CrossRef Full Text | Google Scholar

Negi, S. S., Kumar, A., Ningthoujam, L. S., and Pandey, D. K. (2021). An efficient approach of data adaptive polarization filter to extract teleseismic phases from the ocean-bottom seismograms. Seismol. Res. Lett. 92 (1), 528–542. doi:10.1785/0220200034

CrossRef Full Text | Google Scholar

Rodriguez, I. V., Bonar, D., and Sacchi, M. (2012). Microseismic data denoising using a 3C group sparsity constrained time-frequency transform. Geophysics 77 (2), V21–V29. doi:10.1190/geo2011-0260.1

CrossRef Full Text | Google Scholar

Sabbione, J. I., Velis, D. R., and Sacchi, M. D. (2013). “Microseismic data denoising via an apex-shifted hyperbolic Radon transform,” in SEG technical program expanded abstracts. 2155–2161. doi:10.1190/segam2013-1414.1

CrossRef Full Text | Google Scholar

Shemeta, J., and Anderson, P. (2010). It's a matter of size: Magnitude and moment estimates for microseismic data. Lead. Edge 9 (3), 296–302. doi:10.1190/1.3353726

CrossRef Full Text | Google Scholar

Wail, A. M., and Abdullatif, A. A. (2012). Enhancement of first arrivals using the τ-p transform on energy-ratio seismic shot records. Geophysics 77 (3), 101–111. doi:10.1190/geo2010-0331.1

CrossRef Full Text | Google Scholar

Wang, D. H., and Gao, J. H. (2014). A new method for random noise attenuation in seismic data based on anisotropic fractional-gradient operators. J. Appl. Geophys. 1 (110), 135–143. doi:10.1016/j.jappgeo.2014.09.011

CrossRef Full Text | Google Scholar

Wang, X. N., Zhang, J., and Cheng, H. (2021). A joint framework for seismic signal denoising using total generalized variation and shearlet transform. IEEE Access 9, 6661–6673. doi:10.1109/ACCESS.2021.3049644

CrossRef Full Text | Google Scholar

Yu, P. J., Li, Y., Cheng, Y. L., and Lin, H. B. (2015). The L-DVV method for the seismic signal extraction. J. Appl. Geophys. 117, 60–66. doi:10.1016/j.jappgeo.2015.03.016

CrossRef Full Text | Google Scholar

Yu, P. J., Li, Y., Lin, H. B., and Wu, N. (2016). Removal of random noise in seismic data by time-varying window-length time-frequency peak filtering. Acta Geophys. 64 (5), 1703–1714. doi:10.1515/acgeo-2016-0059

CrossRef Full Text | Google Scholar

Zhao, H. T., Li, Y., and Zhang, C. (2016). SNR enhancement for downhole microseismic data using CSST. IEEE Geoscience Remote Sens. Lett. 13 (8), 1139–1143. doi:10.1109/LGRS.2016.2572721

CrossRef Full Text | Google Scholar