GIS-based landslide susceptibility modeling using data mining techniques

Introduction: Landslide is one of the most widespread geohazards around the world. Therefore, it is necessary and meaningful to map regional landslide susceptibility for landslide mitigation. In this research, landslide susceptibility maps were produced by four models, namely, certainty factors (CF), naive Bayes (NB), J48 decision tree (J48), and multilayer perceptron (MLP) models.

Methods: In the first step, 328 landslides were identified via historical data, interpretation of remote sensing images, and field investigation, and they were divided into two subsets that were assigned different uses: 70% subset for training and 30% subset for validating. Then, twelve conditioning factors were employed, namely, altitude, slope angle, slope aspect, plan curvature, profile curvature, TWI, NDVI, distance to rivers, distance to roads, land use, soil, and lithology. Later, the importance of each conditioning factor was analyzed by average merit (AM) values, and the relationship between landslide occurrence and various factors was evaluated using the certainty factor (CF) approach. In the next step, the landslide susceptibility maps were produced based on four models, and the effect of the four models were quantitatively compared by receiver operating characteristic (ROC) curves, area under curve (AUC) values, and non-parametric tests.

Results: The results demonstrated that all the four models can reasonably assess landslide susceptibility. Of these four models, the CF model has the best predictive performance for the training (AUC=0.901) and validating data (AUC=0.892).

Discussion: The proposed approach is an innovative method that may also help other scientists to develop landslide susceptibility maps in other areas and that could be used for geo-environmental problems besides natural hazard assessments.

1 Introduction

Landslide is one of the most common geohazards around mountainous regions (Moayedi et al., 2019; Sharma and Mahajan, 2019; Xiong et al., 2019). Generally, the disaster-causing capacity of landslide hazards is particularly significant, causing enormous losses to houses, infrastructure, land resources, and human life (Corominas et al., 2014; Pourghasemi and Rahmati, 2018). China stands as one of the nations with a relatively high frequency of geological hazards. In the year 2021, a total of 4,772 geological disasters occurred in China, resulting in the unfortunate loss of 80 lives, with 11 individuals reported missing, and inflicting direct economic losses of 3.2 billion dollars. Landslides, as a perilous geological hazard, prevail as the primary disaster type across China, predominantly afflicting the northwest and southwest regions of the country. Hence, the study and implementation of measures for geological hazard prevention and mitigation hold tremendous significance. Furthermore, the matter of geological hazard prediction demands urgent attention and resolutions.

In view of the severe consequences, the tasks of landslide control and prevention have attracted the attention of government organizations and scholars (An et al., 2016; Pham et al., 2016a; Wu et al., 2017). In this respect, landslide susceptibility assessment (LSA) is the research focus, and the results can guide landslide prevention engineering (Polykretis et al., 2015). Essentially, LSA is the work that is performed to find out whether landslide occurrence is intrinsically associated with conditioning factors, which can be used to predict the future spatial development of landslide hazards (Magliulo et al., 2008; Jaafari et al., 2014).

Currently, statistical models and machine learning (ML) models are the most popular approaches to build landslide susceptibility models (Huang and Zhao, 2018; Pourghasemi et al., 2018; Arabameri et al., 2019a). For the former, the probability and frequency of landslide occurrence are analyzed by conventional statistical approaches, such as the landslide susceptibility index model (Jamal and Mandal, 2016), frequency ratio model (Aditian et al., 2018), and weight of evidence model (Xu et al., 2012). However, when using conventional statistical methods, we have to first subjectively determine the statistical model, and it is hard to measure the relative importance among various conditioning factors (Elith et al., 2008). For the latter, a vast variety of landslide susceptibility models have been constructed by widely using ML approaches in recent years, and sequences of novel ML and ensemble learning algorithms have been proposed, for instance, random forest (Sun et al., 2021), alternating decision tree (Wu et al., 2020), kernel logistic regression (Chen and Chen, 2021), random subspace (Pham et al., 2018a), rotation forest, and decision tree (Hong et al., 2018; Pham et al., 2018b). It is considered that machine learning approaches are more suitable for large databases and can reveal the non-linear and complex linkage between landslide occurrence and each conditioning factor (Zare et al., 2013). Moreover, to acquire results with higher accuracy and a model with better generalization ability, numerous comparative studies of machine learning algorithms have been conducted (Akgun, 2012; Zhu et al., 2018; Juliev et al., 2019; Lei et al., 2020a; Li et al., 2021).

As known, landslides are a very complex natural phenomenon that cause severe loss of human lives and properties worldwide. An accurate assessment of the occurrence of these extreme events is needed in order to understand their spatial correlations with the landslides. An effective method is to map the areas that are susceptible to landslide occurrence. In recent years, various machine learning techniques have been applied for landslide susceptibility mapping. However, we cannot conclude which model is the best universally. Moreover, even a small increment of the prediction accuracy may control the resulting landslide susceptibility zones. Therefore, many more case studies must be performed to reach a reasonable conclusion.

In this paper, we employed the naive Bayes, J48 decision tree, and multilayer perceptron models to predict landslide occurrence in Xiaojin County, Sichuan Province, China. The contents of this paper are as follows: 1) The contribution of conditioning factors to three used ML models are investigated; 2) the CF bivariate model is integrated with ML methods for the spatial prediction of landslides; 3) CF illuminates a superior reliable model that is far ahead of the state-of-the-art ML in landslide susceptibility assessment; 4) the model performance is considered based on their discrimination capacity and reliability. The primary difference here between this study and the literature mentioned is that the approaches in this paper are seldom used and compared in landslide susceptibility assessment. Another point is that four models were first applied in Xiaojin County, and statistical models and machine learning models possess superior interpretability compared to deep learning models, and they can be trained using smaller datasets, which aim to improve the accuracy of the results in the study area. The performance of the models was quantitatively evaluated and comprehensively compared, and the proposed approach is an innovative method that may also help other scientists to develop landslide susceptibility maps in other areas and that could be used for geo-environmental problems other than natural hazard assessments.

2 The study area

Xiaojin County is located in Sichuan Province, China (Figure 1). The study area is between longitude 102°01′E and 102°59′E and latitude 30°35′N and 31°43′N. The area is dominated by a subtropical monsoon climate. However, the climate vertical differentiation is extremely distinct due to the dramatic changes of altitudes. Generally, the annual average temperature is 12.2°C, and the average annual rainfall is 613.9 mm (http://www.xiaojin.gov.cn/). Hydrologically, the Fubian River and Xiaojin River are the main rivers in this area. The length of these two rivers are 83 km and 150 km, respectively (Xie et al., 2021).

FIGURE 1

FIGURE 1. Study area.

Xiaojin County presents a distinctive topography, with higher elevations in the northwest and lower ones in the southeast, characterized by a modest mountainous terrain. Historical landslides in Xiaojin County encompass both rockslides and soil slides, with rockslides constituting the majority and soil slides being relatively scarce. In terms of magnitude, the study area primarily exhibits small to medium-sized landslides, with a lesser occurrence of large-scale landslides. Due to its location within a high mountainous and hilly terrain, situated along the Circum-Pacific Mediterranean Fault Zone, Xiaojin County experiences frequent and intense tectonic movements. It represents a typical high-risk zone for geological hazards in southwestern China, particularly noteworthy for its proximity of a mere 100 km to Wenchuan City in Sichuan Province. On 12 May 2008, Wenchuan City was struck by a severe earthquake measuring over a magnitude of 8, which severely impacted Xiaojin County as well. This event triggered numerous slope instability incidents. Compounded by the concentrated population and the predominant construction of buildings and public facilities in mountainous areas, the potential landslide risks pose a significant threat to the social security of Xiaojin County. Furthermore, up until now, there has been a dearth of research on landslide susceptibility specific to Xiaojin County, which serves as the rationale for selecting it as the study area.

3 Data preparation

Through collection of historical data, satellite image interpretation, and field investigation, 328 landslides in total were extracted from this area. The average dimension of a landslide is about 6.9×10³ m², and the average volume is 4.3×10⁴ m³, respectively. Due to the relatively diminutive size of landslide areas within the study area, the centroid method was employed to generate landslide points. Additionally, an equivalent number of non-landslide points was randomly generated within regions where the slope angle is non-zero. For establishing a landslide susceptibility model, these landslides and non-landslides were randomly divided into two datasets, the training dataset (accounting for 70%) and validating dataset (accounting for 30%) (Figure 1).

Afterwards, slope angle, slope aspect, altitude, plan curvature, profile curvature, topographic wetness index (TWI), distance to rivers, distance to roads, normalized difference vegetation index (NDVI), land use, soil, and lithology were selected as conditioning factors for landslide susceptibility mapping according to the existing literature (Althuwaynee et al., 2012; Felicísimo et al., 2013; Conforti et al., 2014; Ada and San, 2018), and the corresponding thematic maps were acquired (Figure 2). In the process of producing thematic maps, the DEM image, obtained from the website http://www.gscloud.cn/, was adopted to extract regional values of the slope angle, slope aspect, altitude, plan curvature, profile curvature, and TWI. The buffer zones of rivers and roads can be generated by regional water system and traffic maps. The NDVI was obtained by Landsat 8 OLI images (http://www.gscloud.cn/). Land use, soil, and lithology were extracted from land use, soil, and geological maps with scales of 1:100000, 1:1000000, and 1:500000, respectively. All the thematic maps were rasterized with a resolution of 20 m × 20 m. The data source is shown in Table 1.

FIGURE 2

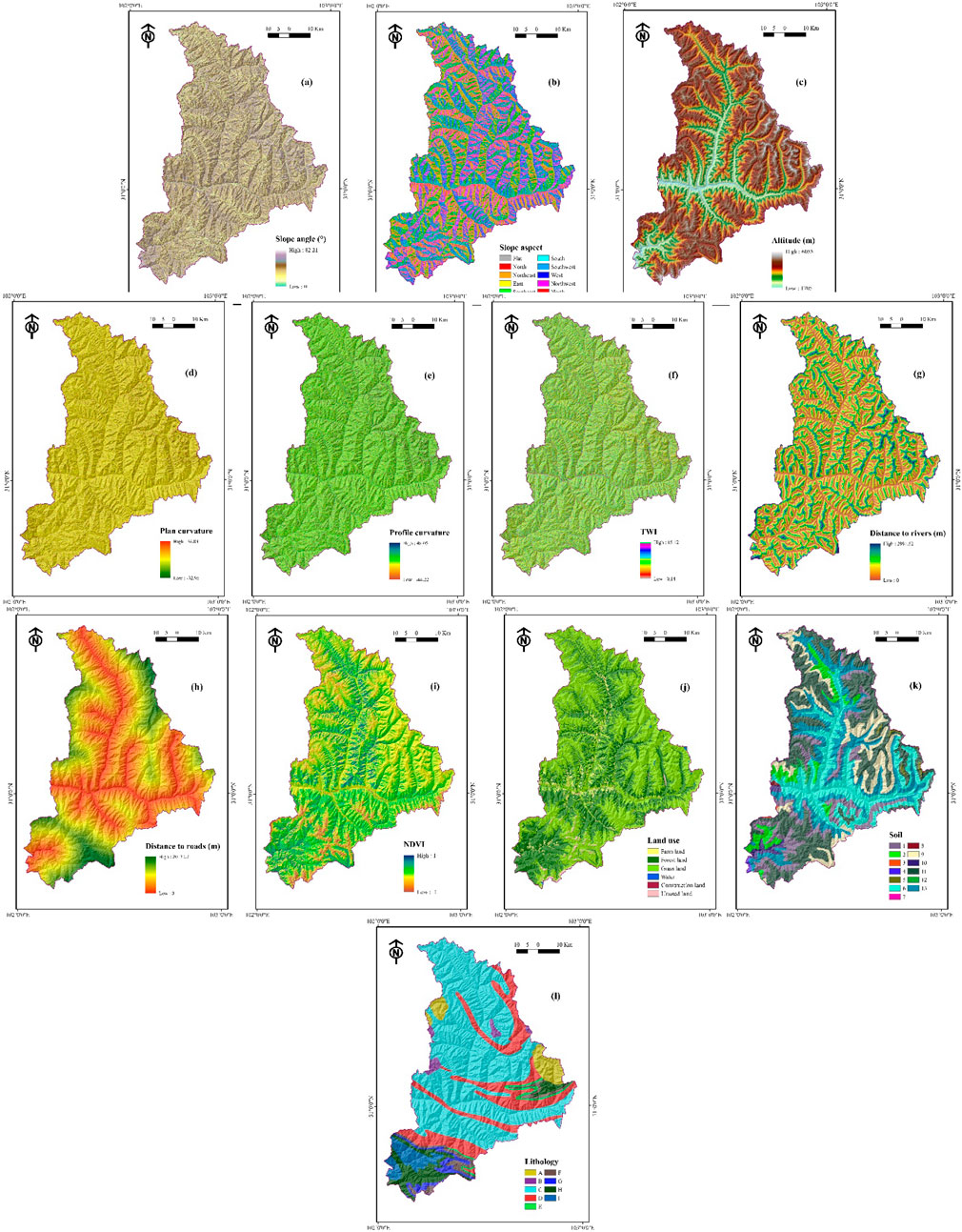
FIGURE 2. Thematic maps. (A) slope angle; (B) slope aspect; (C) altitude; (D) plan curvature; (E) profile curvature; (F) TWI; (G) distance to rivers; (H) distance to roads; (I) NDVI; (J) land use; (K) soil; (L) lithology.

TABLE 1

TABLE 1. Data source.

The slope angle is a necessary conditioning factor in this task (Eiras et al., 2021). The slope stability and failure modes usually vary with slope angle values (Dai et al., 2001). Here, the slope angle values were reclassified into nine categories with an interval of 10°, <10°, 10°–20°, 20°–30°, 30°–40°, 40°–50°, 50°–60°, 60°–70°, 70°–80°, and >80°.

The slope aspect has a prominent influence on temperature and humidity around slopes (Ercanoglu and Gokceoglu, 2002). Therefore, the slope aspect is related to the slope stability. In this paper, the slope aspects were divided into nine directions, namely, flat, north, northeast, east, southeast, south, southwest, west, and northwest.

It is clear that the degree of vegetation coverage, freezing, thawing, and moisture changes dramatically with the variety of altitude (Ding et al., 2017). With an interval of 500 m, nine groups were generated, namely, <2000 m, 2000–2500 m, 2500–3000 m, 3000–3500 m, 3500–4000 m, 4000–4500 m, 4500–5000 m, 5000–5500 m, and >5500 m.

Plan curvature and profile curvature are two indexes that are employed to measure slope shapes, which always affect the stress distribution of slopes (Aghdam et al., 2016). Moreover, the curvature values have impacts on surface runoff (Chen et al., 2017). In this study, curvature values were derived from DEM using the ArcGIS toolbox (ESRI, 2014). The plan curvature values were reclassified as (−32.95)-(−1.70) (−1.70)-(-0.65) (−0.65)-0.14, 0.14-1.19, and1.19-34.02, while the profile curvature values were (−44.22)-(-2.24) (−2.24)-(-0.80), (−0.80)-0.28, 0.28-1.73, and 1.73-48.04.

The topographic wetness index (TWI) is employed to quantitatively evaluate the control function of topography on hydrological characteristics (Moore et al., 1991). In this way, five categories of TWI values were formed by the natural break method: 0.14-1.55, 1.55-2.26, 2.26-3.20, 3.20-4.78, and 4.78-15.12.

Rivers can affect the hydrogeology characteristics of slopes and usually corrode the toe of a slope, which may decrease the anti-slide force (Nsengiyumva et al., 2018). By analyzing buffer zones, eight buffer zones of rivers were produced, namely, <200 m, 200–400 m, 400–600 m, 600–800 m, and >800 m.

In mountainous areas, it is common that numerous landslide hazards are triggered by road construction (Vuillez et al., 2018). Hence, the distance to roads was regarded as a conditioning factor in this study and reclassified into five buffer zones: <300 m, 300–600 m, 600–900 m, 900–1200 m, and >1200 m.

The normalized difference vegetation index (NDVI) is used to reflect the degree of vegetation coverage on a slope surface (Han et al., 2019). Thus, the NDVI values of the study area were arranged into five classes (−1.00)-(−0.16) (−0.16)-(-0.01), (−0.01)-0.01, 0.01-0.16, and 0.16-1.00.

It has been proved that landslide occurrence is indeed connected with land-use type (Leventhal and Kotze, 2008). In the study area, a total of six land-use types were identified, namely, farmland, forestland, grassland, water, construction land, and unused land.

Soil type and lithology, which affect the physical and mechanical texture of soil and rock mass, determine slope stability (Yalcin et al., 2011). Based on the soil map of the study area, thirteen soil types were classified. The outcrops in the study area formed in several geological ages, which include the Sinian period, Ordovician period, Silurian period, Devonian period, Carboniferous period, Permian period, Triassic period, and Quaternary period. The main lithologies are marble, quartzite, phyllite, limestone, sandstone, and soil. Correspondingly, nine lithology groups were reclassified.

4 Modeling approach

4.1 Selection of landslide conditioning factors

It is usually considered that the selection of conditioning factors has significant effects on the certainty and outcome of landslide predictive models (Lei et al., 2020a). These important instructions point to the need to take the optimal combination of conditioning factors into consideration as part of the criteria of raising the accuracy of landslide susceptibility models. In this case, we compared the relative importance of various conditioning factors by a chi-square test based on the Weka workbench (Frank et al., 2016).

4.2 Certainty factors

The certainty factors method, which was proposed by Buchanan and Shortliffe in 1984 (Buchanan and Shortliffe, 1984), has been extensively represented in tasks of LSA (Kanungo et al., 2011; Devkota et al., 2013). In this process, each conditioning factors can generate a corresponding data layer. Then, the weights of all the pixels in different data layers can be figured out by Eq. 1:

$CF=\left\{\begin{array}{l}\frac{H{H}_a-H{H}_s}{H{H}_a\left(\mathit{1}-H{H}_s\right)},H{H}_a\ge H{H}_s\\ \frac{H{H}_a-H{H}_s}{H{H}_s\left(\mathit{1}-H{H}_a\right)},H{H}_s<H{H}_a\end{array}\right.(1)$

where HH_a is the conditional probability of landslide occurrence in a class, and HH_s is the prior probability of landslide events in the whole study area (Devkota et al., 2013).

4.3 Naive bayes

The naive Bayes classifier is based on the Bayes theorem and independence assumption, and it has been popular in various domains in recent decades (Lee, 2018; Sun et al., 2018; Berrar et al., 2019; He et al., 2019). In terms of the naive Bayes algorithm, the training data are used to calculate the prior probability of various classifications. Then, the classification results can be determined by the posteriori probability and conditional probability density function. Assuming that X is the vector of new observation data, and x_i denotes the ith observation value, for a certain class c_j, the conditional probability p (X|c_j) can then be figured out through the following equation:

$p\left(X|c_j\right)=\prod _{i=\mathit{1}}p\left(\frac{x_i}{c_j}\right)(2)$

In the tasks of landslide susceptibility, assuming that y_j (i = landslide, non-landslide) represents the classification results, the final prediction results can be identified through the following equation:

$y_j=argmaxp\left(y_j\right)\prod _{i=\mathit{1}}p\left(\frac{x_i}{y_j}\right)(3)$

4.4 J48 decision tree

The J48 decision tree (C4.5) is a type of decision tree algorithm, and it presents an improvement on the ID3 decision tree (Hong et al., 2018). In terms of the J48 decision tree, the information gain ratio is introduced to select splitting attributions, and the information gain ratio can be calculated by Eq. 4:

$InformationGainRatio=\frac{InformationGain}{-{\displaystyle \sum _{i=\mathit{1}}^m}\frac{n_i}{N}\square \mathit{log}\left(\frac{n_i}{N}\right)}(4)$

where the information gain is calculated by entropy or the Gini value, m is the number of sub-nodes, and N represents the data quantity of a parent node when n_i denotes that of the ith sub-node.

When constructing a decision tree, overfitting may occur under the effects of noisy data (Sathyadevan et al., 2015). Therefore, tree pruning techniques are employed to avoid overfitting occurrence and simplify the construction of a decision tree. Generally, there are two pruning approaches, namely, prepruning and postpruning. The postpruning approaches can be further divided into reduced error pruning, pessimistic error pruning, cost-complexity pruning, and error-based pruning (Sathyadevan et al., 2015).

4.5 Multilayer perceptron

Multilayer perceptron (MLP) is a typical perceptron learning algorithm. Compared with traditional neural networks, MLP consists of one input layer, one output layer, and multiple hidden layers. The training data are input into MLP through the input layer, and the mapping between the input data and output data is established by hidden layers. Because there is no restriction on the hidden function types and number of neurons of the output layer, MLP is more suitable for non-linear data multi-classification problems (Manaswi and Manaswi, 2018). In the process of MLP training, according to the back-propagation regulation, the weights of various hidden layers are optimized by the following loss function:

$E=\frac{\mathit{1}}{\mathit{2}}{{\displaystyle \sum }_{j\mathit{?}{L}_k}\left(t^{\left(j\right)}-y_k^{\left(j\right)}\right)}^{\mathit{2}}(5)$

where E is the loss, L_k represents all the neurons of the output layer, y(j) k means the output of the jth node of L_k, and t^(j) is the corresponding label of the input data.

4.6 Receiver operating characteristic (ROC) curve

The receiver operating characteristic (ROC) curve has been understood as the standard method for measuring classifier performance (Amiri et al., 2019; Arabameri et al., 2019b; Lei et al., 2020b). Taking the “1-specificity” as the transverse axis and the “sensitivity” as the longitudinal axis, the ROC curve can be obtained by connecting the coordinate points, which are drawn under various classification threshold values (Chen W. et al., 2021; Chen et al., 2021b). Based on the ROC curve, the optimal classification threshold value can be easily found, and the model performance is obviously reflected by the shape of curve. Furthermore, to quantitatively assess model performance with the ROC curve, a higher value of area under the ROC curve (AUC) embodies a better classification performance (Chen et al., 2021c).

5 Results and analysis

This section reports the results from an interpretative framework of both predictors’ effects and model performance in terms of different perspectives.

5.1 Selection of landslide conditioning factors

The average merit (AM) values of the twelve conditioning factors were figured out and are shown in Figure 3. Among these factors, altitude has the highest AM value (NB and J48 of 0.329; MLP of 0.322). The second highest AM value (NB of 0.307; J48 and MLP of 0.305) is for soil type, which is followed by distance to roads (NB, J48, MLP AM = 0.272, 0.275, 0.265) and distance to rivers (NB, J48, MLP AM = 0.233, 0.232, 0.231). For the NB model, the AM values are lithology = 0.098, slope angle = 0.091, TWI = 0.087, profile curvature = 0.07, land use = 0.066, plan curvature = 0.061, NDVI = 0.044, and slope aspect = 0.043. For the J48 model, the AM values are lithology = 0.095, TWI = 0.084, slope angle = 0.083, land use = 0.064, plan curvature = 0.05, profile curvature = 0.048, NDVI = 0.036, and slope aspect = 0.031. For the MLP model, the AM values are lithology = 0.088, slope angle = 0.082, TWI = 0.081, profile curvature = 0.063, land use = 0.055, plan curvature = 0.045, slope aspect = 0.035, and NDVI = 0.032. Moreover, it is observed that the NB model has the greatest contribution. Therefore, the NB model should be considered as better than the other models.

FIGURE 3

FIGURE 3. Importance of conditioning factors.

Moreover, there may exist a multicollinearity problem among the conditioning factors, and severe multicollinearity can have an impact on the model by increasing the variance of regression coefficients and rendering them unstable. To assess the potential multicollinearity problem among the conditioning factors, we verified it by calculating the variance inflation factor (VIF) and tolerance (TOL) of the conditioning factors. From Table 2, it can be observed that the VIF values of all the conditioning factors are less than 10, and the TOL values are greater than 0.1, indicating the absence of multicollinearity among the conditioning factors. Hence, all the conditioning factors were retained in the subsequent modeling process.

TABLE 2

TABLE 2. Verification result of potential multicollinearity problem among the conditioning factors.

5.2 Correlation analysis using CF model

In this study, the different response relationship between the fitting models and each conditioning factor was analyzed by the CF model (Figure 4). In terms of the slope angle, the highest CF value (0.717) belongs to the class of <10°, which indicates that most landslides occur in regions with lower slope angles. For altitude, the regions in which altitudes are less than 3500 m have promoting effects on landslide occurrence, and the CF value is the highest (0.961) when altitudes are 2000 m–2500 m. For plan curvature, there are only two positive CF values of .117 and 0.187, which belong to the classes of (−0.65)-0.14 and 0.14-1.19, respectively. For profile curvature, the class of 0.28–1.73 has the highest CF value of 0.190, followed by the class of (−0.80)-0.28 (0.125). It can be observed that the CF values significantly rise with the increase of the TWI values, and the CF value is the highest for the class of 4.78–15.12 (0.859). For the distance to rivers, the highest CF value is the only positive value, which is observed for <200 m. As obvious from the results of distance to roads, landslide occurrence density decreases with the lengthening of the distance to roads. Thus, there is no doubt that rivers and road construction generally trigger landslide hazards. For NDVI, the CF value is the highest (0.350) for the class of (−0.16)-(−0.01), followed by the class of (−0.01)-0.01 (0.263). The results show that vegetation on a slope surface can prevent landslide occurrence. For the influence situation of land use, construction land, farmland, and unused land have higher CF values of 0.984, 0.810, and 0.027, respectively, indicating that human activities play a critical role in landslide distribution. In terms of soil type, the highest CF value of 0.866 is found in group 8, followed by group 10 (0.861). Moreover, for lithology, group C and group I have the positive CF values of 0.232 and 0.416, respectively.

FIGURE 4

FIGURE 4. Correlation between landslides and factors by CF.

5.3 Application of models

After determining the most effective conditioning factors, based on the CF analysis result of correlation, LSI analyses were performed following the formula below (Eq. 5). The factors first had to be reclassified to calculate the landslide distribution for each class shown in pixel amount. The final LSM was determined by the superposition of the results of the twelve factor maps using the Raster Calculator Module. The output values were reclassified into five categories, namely, very low, low, moderate, high, and very high, according to geometrical interval method (Pham et al., 2016b) (Figure 5A).

$\begin{array}{l}LS{I}_{CF}=\mathrm{A}ltitud{e}_{CF}+\mathrm{S}lope\hspace{1em}angl{e}_{CF}+\mathrm{S}lope\hspace{1em}aspec{t}_{CF}+\mathrm{P}lan\hspace{1em}curvatur{e}_{CF}\\ +\mathrm{P}rofile\hspace{1em}curvatur{e}_{CF}+TW{I}_{CF}+NDV{I}_{CF}+\mathrm{D}istance\hspace{1em}to\hspace{1em}river{s}_{CF}\\ +\mathrm{D}istance\hspace{1em}to\hspace{1em}road{s}_{CF}+\mathrm{L}andus{e}_{CF}+\mathrm{S}oi{l}_{CF}+\mathrm{L}itholog{y}_{CF}\end{array}(6)$

FIGURE 5

FIGURE 5. Landslide susceptibility map: (A) CF model, (B) NB model, (C) J48 model, (D) MLP model.

It is evident that a large drawback of bivariate models, such as the CF mode, is that they only consider a single factor, that is, sub-factors weights. A CF and ML model coupling pattern that can augment the result of the ML models can thus be envisaged. We denoted landslide (328) and non-landslide (328) pixels by value 1 or value 0 in this study using 656 input variables. Input variables must be split into two parts: 70% training and 30% validation. After the CF model was successfully established, these data were pretreated with the CF value as the input of the NB model. The NB model was implemented in the Weka software to output the LSI value of each pixel in the full study area. The range of output values was from 0 to 1, which reflects the probability of landslide occurrence of this pixel position. Along these lines, all the LSI values were converted to ArcGIS, and the spatial mapping process was performed. Similarly to the CF classification, the NB classification model was established, in which each category area indicates the different intensity of the landslide. Then, the validating data were input into the trained model to test the accuracy of the trained network. The final LSM was presented by the machine learning NB model (Figure 5B).

In the present study, Weka software was employed to form landslide susceptibility with the J48 model. When running the J48 program, we chose the confidence factor as 0.25, which is the threshold to determine whether there shall be pruning or not. The minimum number of objects of each leave is 2, and the number of folds is 3. The pruning scheme is a reduced error pruning approach. Finally, the landslide susceptibility index (LSI) values were calculated, and the corresponding landslide susceptibility map (Figure 5C) was generated using ArcGIS software. Similarly, the LSI values were arranged into five classes.

For the MLP algorithm, the BP learning approach and auto hidden layer were adopted to model highly non-linear functions. Every layer consists of a number of neurons, which independently process information, and these neurons connect with the other layers of neurons by the weight. Then, the output values were imported into ArcGIS software to produce a landslide susceptibility map (Figure 5D). Through reclassification based on the geometrical interval method, five different susceptibility classes were obtained.

As suggested from the four visual inspections of Figures 5A–D, there is a similar pattern of susceptibility distribution, which exhibit an obvious rule. All the very high categories are distributed along national road G350 and provincial road S210 and the river and valley. In addition, very high categories are also located in the calcareous cinnamon soil-type area, which is the cause of highly weathered soil damage slope stability. Different susceptibility maps have the same total number of pixels, but the pixels for each category of susceptibility are different. The comparison of area pixels for each category of the four maps is shown in Figure 6, and the accuracy of these maps shown in Figures 7, 8. Although the four models yield high accuracy, the four LSMs highlight significant differences. CF and NB depict reasonable patterns, whereas the very high area only has a few pixels, and the categories of “low and very low” have the majority of pixels. By contrast, J48 and MLP encounter an unreasonable problem. As the very high category occupies more pixels, some of them appear in flat areas.

FIGURE 6

FIGURE 6. Percentages of landslide susceptibility classes.

FIGURE 7

FIGURE 7. ROC curves of the models using training dataset.

FIGURE 8

FIGURE 8. ROC curves of the models using validation dataset.

5.4 Validation and comparison of models

In this section, the performance study of various models with training data and validating data would make great progress by the evaluation and comparison of the ROC curves, AUC values, and non-parametric testing approaches.

In this study, the general performance of a bivariate model and three ML models has been assessed by the ROC curves and AUC values. For the training data (Table 3), the CF bivariate model has the best fit quality, and the AUC value is as high as 0.901 with a correspondingly perfect confidence interval of 0.872–0.931. In the three ML models, NB is the highest reached (0.893), and the 95% confidence interval is from 0.863 to 0.923. The AUC value of the MLP model is 0.835 with a confidence interval of 0.797–0.872. The performance of the J48 model is inferior to the other models, and the AUC value of the MLP model is 0.798 with a confidence interval of 0.754–0.843.

TABLE 3

TABLE 3. Parameters of ROC curves using training dataset.

In the more important case of validating data (Table 4), the CF model remains stable at first place in model performance in terms of AUC with a value of 0.892, and NB model remains stable at first place in the three ML models, thus presenting the best AUC with a value of 0.887. The MLP and J48 models also exhibit good predictive ability with AUC values of 0.831 and 0.804. In addition, the CF and NB models possess the lowest standard errors and confidence intervals, with standard error values of 0.023 and 0.024 and 95% confidence intervals of 0.847–0.937 and 0.84 to 0.935, respectively. The predictive performance of the J48 and MLP models seems poor compared that of the other models.

TABLE 4

TABLE 4. Parameters of ROC curves using validation dataset.

Determining the effective identify among the models, whether or not there exist significant differences, has been a critical step in the LSA tasks. In the session, the chi-square was adopted, and the results are listed in Table 5. It can be seen that the p values (0.481 and 0.367) exceed the significant level (0.05). Hence, it can be inferred that the performance of CF is similar to NB statistically, and J48 is similar to the MLP model statistically. Furthermore, in terms of the quantitative difference of the models, it is clear seen from the calculated chi-square values that there is no significant difference between the CF and NB models and the MLP and J48 models as the value does not exceed 3.841. The two sets of models have no significant difference compared to other model sets, because both of these values are below the threshold, and the other model sets only have a low significance level because these values are slightly higher than the threshold.

TABLE 5

TABLE 5. Pairwise comparison for the four models using the validation dataset based on chi-square.

6 Discussion

Based on the field survey information, the CF, J48, MLP, and NB models were implemented to produce landslide susceptibility maps of the study area. The AUC values and a series of statistical indexes were used to measure the accuracy of four maps. The results obviously demonstrate that four models have excellent performance in landslide susceptibility mapping, and a similar outcome appears both for the training and validation subsets. Among them, the CF and NB models have a superior effect, while the performance of the other two models has no significant difference. In terms of the present study, the initial data best accord with the pre-assumptions of the CF models, and this model naturally has a solid mathematical foundation. Thus, the landslide susceptibility map generated by the CF and NB models exhibits better accuracy and rationality. It seems preferable to select CF and NB as the susceptibility model over the study area. It is striking that the actual validation subset of J48 received better performance than the training set, especially for decision trees. It is very rare that it produces an overfit for within-sample models and loses much predictive power when predicting an out-of-sample situation (Schaffer, 1993), as is well known. This uncommon result may be explained due to the randomness of the sampling. This relationship shows that the original landslide data exhibit low internal variability, regardless of the sampling scheme. In turn, this allows us to consider the resulting susceptibility maps as a reliable tool to predict landslides in Xiaojin County. In addition, the parameters of the classifiers and the correlation among the conditioning factors determine the classification results to some degree. It can be believed that the comprehensive performance of the MLP and J48 models may be further improved by parameter optimization and conditioning factor selection. Therefore, due to the uncertainties in landslide susceptibility modeling, there is more than one approach to generate satisfying results, and the optimized approach is hard to determine.

For the twelve conditioning factors mentioned above, the importance of altitude is the highest, followed by soil type, distance to roads, and distance to rivers. Generally, lower altitude areas have a higher probability of landslide occurrence (Polykretis et al., 2015; Hong et al., 2019). Landslide susceptibility delineation depends on the selected conditioning factors and the weight of each variable. If the modeling’s objective is to improve the process performance measures rather than just surveillance and prediction, the thorough understanding of the causes leading to this result is of great value. Being able to show the relative importance of the variables using different models may pique the interest of the model utility. In the present analysis, the J48, NB, MLP, and three ML models were used to calculate the relative contribution of each variable to the three models themselves. A total of 12 selected conditioning factors were tested (Figure 3), and according to results, we can confirm that the top four conditioning factors are the most significant in all the models. This result is consistent with the visual inspection of the LSM analyzed in Section 5.3. The LSM and the four most significant factor maps obey a similar spatial pattern. Even if all four factor maps have this feature, as can be intuitively seen, the contribution percentage to models (in descending order) was: altitude, soil, distance to roads, and distance to river. For the remaining eight non-significant conditioning factors, the contribution of slope aspect occupies the lowest percentages for the NB and J48 models, while for the MLP model, NDVI reveals the lowest percentages; moreover, the profile curvature factor importance value is lower than that of land use and plan curvature for the J48 model but not for NB and MLP. All in all, different factors have different importance values due to different evaluation models (Tien Bui et al., 2016). Finally, we provide a hypothesis that there may be factor overestimation and underestimation presence.

In this study area, most landslides spread in areas in which altitudes are less than 3000 m. The main reason is that human activities are always more severe in lower altitude areas, which is one of the most critical landslide-triggering factors in Xiaojin County. Normally, areas covered by loose deposits are prone to cause landslides (Cui et al., 2019; Huang et al., 2019; Zhang et al., 2019), which has been proved by this study as well. Moreover, the results showed that the density of landslide points basically decreases as the distance to rivers and roads increases. This is because the incidence of river erosion and road construction disturbance is usually finite (Dang et al., 2019). In the case of the slope angle, areas with low slope angles have a higher possibility of landslide occurrence, which does not conform to conventional cognition. The basic reason is that areas with gentle terrain are generally suitable for land development activities such as farming, irrigation, and construction. The land use–landslide susceptibility relationship also indicates that farmland and construction land have positive effects on landslide occurrence. Therefore, it can be inferred that landslide occurrence in Xiaojin County has firm connections with human activities. Meanwhile, the slope aspect is regarded as a useless conditioning factor, indicating that the influence of this factor can be neglected to raise the computing efficiency of classifiers. For the other conditioning factors, the correlation between them and landslide occurrence is relatively reasonable according to the relevant literature (Hong et al., 2017a; Hong et al., 2017b). Considering the model construction and overall performance, the conclusion obtained in this paper is that the CF bivariate model proved best because it performed excellently and with stable classification ability in predicting landslides in Xiaojin County. This is a unique conclusion of the predictive studies: traditional statistical computing models are far ahead of intelligent ML models. Moreover, CF could greatly improve time efficiency as it eliminates the lengthy modeling process of ML. Therefore, future studies should not only pursue state-of-the-art algorithms. The final recommendation is centered on combining data analysis with GIS applications as framework templates so that this could become more widely used.

7 Conclusion

In this study, the CF, NB, J48, and MLP models were applied to evaluate landslide susceptibility in Xiaojin County, China. The information of regional geology and landslide points was obtained by a field survey and aerial photographs interpretation. To establish the set of conditioning factors regarding landslide occurrence, a total of twelve initial conditioning factors were determined. Furthermore, the importance of various conditioning factors was assessed using AM values, and slope aspect was removed from the landslide susceptibility modeling process. Moreover, the interaction between landslide occurrence and each conditioning factor was analyzed by the CF method. As a result, it was found that the negative synergy that forms high landslide susceptibility consists of 0°–10° slopes, 2000–2500 m altitude, 0.14–1.19 interval in plan curvature, 0.28–1.73 interval in profile curvature, 4.78 < TWI <15.12, distance <200 m from rivers, distance <300 m from roads, −0.16 < NDVI < −0.01, construction land in land use, group 8 of soil types, and group I of lithology types. Additionally, the comprehensive performance of the four models in landslide susceptibility mapping was compared by statistic indexes, ROC curves, and AUC values. It can be concluded that the CF bivariate model has the best predictive capacity with an AUC value of 0.892 AUC, and the NB model also has a better predictive capacity with an AUC value of 0.887, followed by the MLP model (AUC=0.831) and J48 model (AUC=0.804). Based on the results of the Wilcoxon signed-rank test (two-tailed), it is clear that the performance of NB model is significantly similar to the CF model and likewise for the J48 and MLP models. Finally, four landslide susceptibility maps were reclassified into five categories, and all the produced landslide susceptibility maps were found to have profound applicability and practical significance on landslide prevention in Xiaojin County. The obtained landslide susceptibility map can inform local authorities in their endeavors to undertake disaster prevention and mitigation measures, effectively reducing the scope of landslide investigations. In the event of a landslide occurrence, it enables the judicious selection of appropriate refuge sites.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, LX; methodology, LX and JS; software, JS; validation, JS, GD, and TZ; formal analysis, GD; investigation, LX; resources, TZ; data curation, GD; writing—original draft preparation, LX; writing—review and editing, LX, GD, and TW; visualization, JS; supervision, TW; project administration, LX; funding acquisition, TW. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the Shaanxi Province Natural Science Basic Research Program (2022JQ-457), Shaanxi Land Construction-Xi’an Jiaotong University Land Engineering and Human Settlement Environment Technology Innovation Center Open Fund Project (2021WHZ0089). The authors declare that this study received funding from the Inner Scientific Research Project of Shaanxi Land Engineering Construction Group (DJNY-ZD-2023-1, DJNY-YB-2023-18, DJNY-YB-2023-28, DJNY2022-16, DJNY2022-36). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors GD and TW were employed by the company Shaanxi Provincial Land Engineering Construction Group.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ada, M., and San, B. T. (2018). Comparison of machine-learning techniques for landslide susceptibility mapping using two-level random sampling (2lrs) in alakir catchment area, antalya, Turkey. Nat. Hazards 90, 237–263. doi:10.1007/s11069-017-3043-8

CrossRef Full Text | Google Scholar

Aditian, A., Kubota, T., and Shinohara, Y. (2018). Comparison of gis-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of ambon, Indonesia. Geomo 318, 101–111. doi:10.1016/j.geomorph.2018.06.006

CrossRef Full Text | Google Scholar

Aghdam, I. N., Varzandeh, M. H. M., and Pradhan, B. (2016). Landslide susceptibility mapping using an ensemble statistical index (wi) and adaptive neuro-fuzzy inference system (anfis) model at alborz mountains (Iran). Environ. Earth Sci. 75, 553. doi:10.1007/s12665-015-5233-6

CrossRef Full Text | Google Scholar

Akgun, A. (2012). A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at i̇zmir, TTurkey Landslides 9, 93–106. doi:10.1007/s10346-011-0283-7

CrossRef Full Text | Google Scholar

Althuwaynee, O. F., Pradhan, B., and Lee, S. (2012). Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 44, 120–135. doi:10.1016/j.cageo.2012.03.003

CrossRef Full Text | Google Scholar

Amiri, M., Pourghasemi, H. R., Ghanbarian, G. A., and Afzali, S. F. (2019). Assessment of the importance of gully erosion effective factors using boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 340, 55–69. doi:10.1016/j.geoderma.2018.12.042

CrossRef Full Text | Google Scholar

An, H., Viet, T. T., Lee, G., Kim, Y., Kim, M., Noh, S., et al. (2016). Development of time-variant landslide-prediction software considering three-dimensional subsurface unsaturated flow. Environ. Model. Softw. 85, 172–183. doi:10.1016/j.envsoft.2016.08.009

CrossRef Full Text | Google Scholar

Arabameri, A., Pradhan, B., Rezaei, K., and Lee, C.-W. (2019a). Assessment of landslide susceptibility using statistical- and artificial intelligence-based fr–rf integrated model and multiresolution dems. Remote Sens. 11, 999. doi:10.3390/rs11090999

CrossRef Full Text | Google Scholar

Arabameri, A., Rezaei, K., Cerdà, A., Conoscenti, C., and Kalantari, Z. (2019b). A comparison of statistical methods and multi-criteria decision making to map flood hazard susceptibility in northern Iran. ScTEn 660, 443–458. doi:10.1016/j.scitotenv.2019.01.021

CrossRef Full Text | Google Scholar

Berrar, D. (2019). “Bayes’ theorem and naive bayes classifier,” in Encyclopedia of bioinformatics and computational biology. Editors S. Ranganathan, M. Gribskov, K. Nakai, and C. Schönbach (Oxford: Academic Press), 403–412.

CrossRef Full Text | Google Scholar

Buchanan, B., and Shortliffe, E. (1984). Rule-based expert systems, 571–588.

Google Scholar

Chen, X., and Chen, W. (2021). Gis-based landslide susceptibility assessment using optimized hybrid machine learning methods. CATENA 196, 104833. doi:10.1016/j.catena.2020.104833

CrossRef Full Text | Google Scholar

Chen, W., Pourghasemi, H. R., Panahi, M., Kornejady, A., Wang, J., Xie, X., et al. (2017). Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 297, 69–85. doi:10.1016/j.geomorph.2017.09.007

CrossRef Full Text | Google Scholar

Chen, W., Lei, X., Chakrabortty, R., Chandra Pal, S., Sahana, M., and Janizadeh, S. (2021a). Evaluation of different boosting ensemble machine learning models and novel deep learning and boosting framework for head-cut gully erosion susceptibility. J. Environ. Manage. 284, 112015. doi:10.1016/j.jenvman.2021.112015

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Chen, W., Chandra Pal, S., Saha, A., Chowdhuri, I., Adeli, B., et al. (2021b). Evaluation efficiency of hybrid deep learning algorithms with neural network, decision tree and boosting methods for predicting groundwater potential. Geo. Inter. 37, 5564–5584. doi:10.1080/10106049.2021.1920635

CrossRef Full Text | Google Scholar

Chen, Y., Chen, W., Janizadeh, S., Bhunia, G. S., Bera, A., Pham, Q. B., et al. (2021c). Deep learning and boosting framework for piping erosion susceptibility modeling: Spatial evaluation of agricultural areas in the semi-arid region. Geo. Inter. 37, 4628–4654. doi:10.1080/10106049.2021.1892212

CrossRef Full Text | Google Scholar

Conforti, M., Pascale, S., Robustelli, G., and Sdao, F. (2014). Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the turbolo river catchment (northern calabria, Italy). Catena 113, 236–250. doi:10.1016/j.catena.2013.08.006

CrossRef Full Text | Google Scholar

Corominas, J., van Westen, C., Frattini, P., Cascini, L., Malet, J. P., Fotopoulou, S., et al. (2014). Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 73, 209–263.

CrossRef Full Text | Google Scholar

Cui, Y., Jiang, Y., and Guo, C. (2019). Investigation of the initiation of shallow failure in widely graded loose soil slopes considering interstitial flow and surface runoff. Landslides 16, 815–828. doi:10.1007/s10346-018-01129-9

CrossRef Full Text | Google Scholar

Dai, F. C., Lee, C. F., Li, J., and Xu, Z. W. (2001). Assessment of landslide susceptibility on the natural terrain of lantau island, Hong Kong. Environ. Geol. 40, 381–391. doi:10.1007/s002540000163

CrossRef Full Text | Google Scholar

Dang, V.-H., Dieu, T. B., Tran, X.-L., and Hoang, N.-D. (2019). Enhancing the accuracy of rainfall-induced landslide prediction along mountain roads with a gis-based random forest classifier. Bull. Eng. Geol. Environ. 78, 2835–2849. doi:10.1007/s10064-018-1273-y

CrossRef Full Text | Google Scholar

Devkota, K. C., Regmi, A. D., Pourghasemi, H. R., Yoshida, K., Pradhan, B., Ryu, I. C., et al. (2013). Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in Nepal himalaya. Nat. Hazards 65, 135–165. doi:10.1007/s11069-012-0347-6

CrossRef Full Text | Google Scholar

Ding, Q., Chen, W., and Hong, H. (2017). Application of frequency ratio, weights of evidence and evidential belief function models in landslide susceptibility mapping. Geocarto Int. 32, 1–21. doi:10.1080/10106049.2016.1165294

CrossRef Full Text | Google Scholar

Eiras, C., Souza, J., Freitas, R., Barella, C. F., and Pereira, T. M. (2021). Discriminant analysis as an efficient method for landslide susceptibility assessment in cities with the scarcity of predisposition data. Nat. Hazards 107, 1427–1442. doi:10.1007/s11069-021-04638-4

CrossRef Full Text | Google Scholar

Elith, J., Leathwick, J. R., and Hastie, T. (2008). A working guide to boosted regression trees. J. Animal Ecol. 77, 802–813. doi:10.1111/j.1365-2656.2008.01390.x

CrossRef Full Text | Google Scholar

Ercanoglu, M., and Gokceoglu, C. (2002). Assessment of landslide susceptibility for a landslide-prone area (north of yenice, nw Turkey) by fuzzy approach. Environ. Geol. 41, 720–730. doi:10.1007/s00254-001-0454-2

CrossRef Full Text | Google Scholar

ESRI (2014). Arcgis desktop: Release 10.2 redlands, ca. Environmental systems research institute.

Google Scholar

Felicísimo, Á. M., Cuartero, A., Remondo, J., and Quirós, E. (2013). Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 10, 175–189. doi:10.1007/s10346-012-0320-1

CrossRef Full Text | Google Scholar

Frank, E., Hall, A., M., and Witten, H., I. (2016). “The weka workbench,” in Online appendix for "data mining: Practical machine learning tools and techniques". fourth edition (morgan kaufmann).

Google Scholar

Han, J.-C., Huang, Y., Zhang, H., and Wu, X. (2019). Characterization of elevation and land cover dependent trends of ndvi variations in the hexi region, northwest China. J. Environ. Manag. 232, 1037–1048. doi:10.1016/j.jenvman.2018.11.069

CrossRef Full Text | Google Scholar

He, Q., Shahabi, H., Shirzadi, A., Li, S., Chen, W., Wang, N., et al. (2019). Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. ScTEn 663, 1–15. doi:10.1016/j.scitotenv.2019.01.329

CrossRef Full Text | Google Scholar

Hong, H., Tsangaratos, P., Ilia, I., Chen, W., Xu, C., and Mikos, M. (2017a). “Comparing the performance of a logistic regression and a random forest model in landslide susceptibility assessments. The case of wuyaun area, China,” in Advancing culture of living with landslides. Editors B. Tiwari, Y. Yin, and K. Sassa (Cham: Springer International Publishing), 1043–1050.

CrossRef Full Text | Google Scholar

Hong, H., Ilia, I., Tsangaratos, P., Chen, W., and Xu, C. (2017b). A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the wuyuan area, China. Geomorphology 290, 1–16. doi:10.1016/j.geomorph.2017.04.002

CrossRef Full Text | Google Scholar

Hong, H., Liu, J., Bui, D. T., Pradhan, B., Acharya, T. D., Pham, B. T., et al. (2018). Landslide susceptibility mapping using j48 decision tree with adaboost, bagging and rotation forest ensembles in the guangchang area (China). CATENA 163, 399–413. doi:10.1016/j.catena.2018.01.005

CrossRef Full Text | Google Scholar

Hong, H., Shahabi, H., Shirzadi, A., Chen, W., Chapi, K., Ahmad, B. B., et al. (2019). Landslide susceptibility assessment at the wuning area, China: A comparison between multi-criteria decision making, bivariate statistical and machine learning methods. Nat. Hazards 96, 173–212. doi:10.1007/s11069-018-3536-0

CrossRef Full Text | Google Scholar

Huang, Y., and Zhao, L. (2018). Review on landslide susceptibility mapping using support vector machines. Catena 165, 520–529. doi:10.1016/j.catena.2018.03.003

CrossRef Full Text | Google Scholar

Huang, H., Song, K., Yi, W., Long, J., Liu, Q., and Zhang, G. (2019). Use of multi-source remote sensing images to describe the sudden shanshucao landslide in the three gorges reservoir, China. Bull. Eng. Geol. Environ. 78, 2591–2610. doi:10.1007/s10064-018-1261-2

CrossRef Full Text | Google Scholar

Jaafari, A., Najafi, A., Pourghasemi, H. R., Rezaeian, J., and Sattarian, A. (2014). Gis-based frequency ratio and index of entropy models for landslide susceptibility assessment in the caspian forest, northern Iran. Int. J. Environ. Sci. Technol. 11, 909–926. doi:10.1007/s13762-013-0464-0

CrossRef Full Text | Google Scholar

Jamal, M., and Mandal, S. (2016). Monitoring forest dynamics and landslide susceptibility in mechi–balason interfluves of darjiling himalaya, West Bengal using forest canopy density model (fcdm) and landslide susceptibility index model (lsim). Model. Earth Syst. Environ. 2, 1–17. doi:10.1007/s40808-016-0243-2

CrossRef Full Text | Google Scholar

Juliev, M., Mergili, M., Mondal, I., Nurtaev, B., Pulatov, A., and Hübl, J. (2019). Comparative analysis of statistical methods for landslide susceptibility mapping in the bostanlik district, Uzbekistan. Sci. Total Environ. 653, 801–814. doi:10.1016/j.scitotenv.2018.10.431

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanungo, D. P., Sarkar, S., and Sharma, S. (2011). Combining neural network with fuzzy, certainty factor and likelihood ratio concepts for spatial prediction of landslides. Nat. Hazards 59, 1491–1512. doi:10.1007/s11069-011-9847-z

CrossRef Full Text | Google Scholar

Lee, C.-H. (2018). An information-theoretic filter approach for value weighted classification learning in naive bayes. Data and Knowl. Eng. 113, 116–128. doi:10.1016/j.datak.2017.11.002

CrossRef Full Text | Google Scholar

Lei, X., Chen, W., and Pham, B. T. (2020a). Performance evaluation of gis-based artificial intelligence approaches for landslide susceptibility modeling and spatial patterns analysis. ISPRS Int. J. Geo-Information 9, 443. doi:10.3390/ijgi9070443

CrossRef Full Text | Google Scholar

Lei, X., Chen, W., Avand, M., Janizadeh, S., Kariminejad, N., Shahabi, H., et al. (2020b). Gis-based machine learning algorithms for gully erosion susceptibility mapping in a semi-arid region of Iran. Remote Sens. 12, 2478. doi:10.3390/rs12152478

CrossRef Full Text | Google Scholar

Leventhal, A. R., and Kotze, G. P. (2008). Landslide susceptibility and hazard mapping in Australia for land-use planning — With reference to challenges in metropolitan suburbia. Eng. Geol. 102, 238–250. doi:10.1016/j.enggeo.2008.03.021

CrossRef Full Text | Google Scholar

Li, Y., Chen, W., Rezaie, F., Rahmati, O., Davoudi Moghaddam, D., Tiefenbacher, J., et al. (2021). Debris flows modeling using geo-environmental factors: Developing hybridized deep-learning algorithms. GeoIn 37, 5150–5173. doi:10.1080/10106049.2021.1912194

CrossRef Full Text | Google Scholar

Magliulo, P., Di Lisio, A., Russo, F., and Zelano, A. (2008). Geomorphology and landslide susceptibility assessment using gis and bivariate statistics: A case study in southern Italy. Nat. Hazards 47, 411–435. doi:10.1007/s11069-008-9230-x

CrossRef Full Text | Google Scholar

Manaswi, N. K. (2018). “Multilayer perceptron,” in Deep learning with applications using python: Chatbots and face, object, and speech recognition with tensorflow and keras. Editor N. K. Manaswi (Berkeley, CA: Apress), 45–56.

CrossRef Full Text | Google Scholar

Moayedi, H., Mehrabi, M., Mosallanezhad, M., Rashid, A. S. A., and Pradhan, B. (2019). Modification of landslide susceptibility mapping using optimized pso-ann technique. Eng. Comput. 35, 967–984. doi:10.1007/s00366-018-0644-0

CrossRef Full Text | Google Scholar

Moore, I. D., Grayson, R. B., and Ladson, A. R. (1991). Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. HyPr 5, 3–30. doi:10.1002/hyp.3360050103

CrossRef Full Text | Google Scholar

Nsengiyumva, J. B., Luo, G., Nahayo, L., Huang, X., and Cai, P. (2018). Landslide susceptibility assessment using spatial multi-criteria evaluation model in Rwanda. Int. J. Environ. Res. Public Health 15, 243–255. doi:10.3390/ijerph15020243

PubMed Abstract | CrossRef Full Text | Google Scholar

Pham, B. T., Pradhan, B., Tien Bui, D., Prakash, I., and Dholakia, M. B. (2016a). A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of uttarakhand area (India). Environ. Model. Softw. 84, 240–250. doi:10.1016/j.envsoft.2016.07.005

CrossRef Full Text | Google Scholar

Pham, B. T., Bui, D. T., Prakash, I., and Dholakia, M. B. (2016b). Evaluation of predictive ability of support vector machines and naive bayes trees methods for spatial prediction of landslides in uttarakhand state (India) using gis. J. Geomatics 10, 71–79.

Google Scholar

Pham, B. T., Prakash, I., and Tien Bui, D. (2018a). Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 303, 256–270. doi:10.1016/j.geomorph.2017.12.008

CrossRef Full Text | Google Scholar

Pham, B. T., Shirzadi, A., Tien Bui, D., Prakash, I., and Dholakia, M. B. (2018b). A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: A case study in the himalayan area, India. Int. J. Sediment Res. 33, 157–170. doi:10.1016/j.ijsrc.2017.09.008

CrossRef Full Text | Google Scholar

Polykretis, C., Ferentinou, M., and Chalkias, C. (2015). A comparative study of landslide susceptibility mapping using landslide susceptibility index and artificial neural networks in the krios river and krathis river catchments (northern peloponnesus, Greece). Bull. Eng. Geol. Environ. 74, 27–45. doi:10.1007/s10064-014-0607-7

CrossRef Full Text | Google Scholar

Pourghasemi, H. R., and Rahmati, O. (2018). Prediction of the landslide susceptibility: Which algorithm, which precision? CATENA 162, 177–192. doi:10.1016/j.catena.2017.11.022

CrossRef Full Text | Google Scholar

Pourghasemi, H. R., Teimoori Yansari, Z., Panagos, P., and Pradhan, B. (2018). Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arabian J. Geosciences 11, 193. doi:10.1007/s12517-018-3531-5

CrossRef Full Text | Google Scholar

Sathyadevan, S., Nair, R. R., Jain, L. C., and Behera, H. S. (2015). “Comparative analysis of decision tree algorithms: Id3, c4.5 and random forest,” in Computational intelligence in data mining. Editors J. K. Mandal, and D. P. Mohapatra (New Delhi: Springer India), 1, 549–562.

CrossRef Full Text | Google Scholar

Schaffer, C. (1993). Overfitting avoidance as bias. Mach. Learn. 10, 153–178. doi:10.1007/bf00993504

CrossRef Full Text | Google Scholar

Sharma, S., and Mahajan, A. K. (2019). A comparative assessment of information value, frequency ratio and analytical hierarchy process models for landslide susceptibility mapping of a himalayan watershed, India. Bull. Eng. Geol. Environ. 78, 2431–2448. doi:10.1007/s10064-018-1259-9

CrossRef Full Text | Google Scholar

Sun, N., Sun, B., Lin, J., and Wu, M. Y.-C. (2018). Lossless pruned naive bayes for big data classifications. Big Data Res. 14, 27–36. doi:10.1016/j.bdr.2018.05.007

CrossRef Full Text | Google Scholar

Sun, D., Shi, S., Wen, H., Xu, J., and Wu, J. (2021). A hybrid optimization method of factor screening predicated on geodetector and random forest for landslide susceptibility mapping. Geomorphology 379, 107623. doi:10.1016/j.geomorph.2021.107623

CrossRef Full Text | Google Scholar

Tien Bui, D., Tuan, T. A., Klempe, H., Pradhan, B., and Revhaug, I. (2016). Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 13, 361–378. doi:10.1007/s10346-015-0557-6

CrossRef Full Text | Google Scholar

Vuillez, C., Tonini, M., Sudmeier-Rieux, K., Devkota, S., Derron, M.-H., and Jaboyedoff, M. (2018). Land use changes, landslides and roads in the phewa watershed, Western Nepal from 1979 to 2016. Appl. Geogr. 94, 30–40. doi:10.1016/j.apgeog.2018.03.003

CrossRef Full Text | Google Scholar

Wu, Z., Wu, Y., Yang, Y., Chen, F., Zhang, N., Ke, Y., et al. (2017). A comparative study on the landslide susceptibility mapping using logistic regression and statistical index models. Arabian J. Geosciences 10, 187. doi:10.1007/s12517-017-2961-9

CrossRef Full Text | Google Scholar

Wu, Y., Ke, Y., Chen, Z., Liang, S., and Hong, H. (2020). Application of alternating decision tree with adaboost and bagging ensembles for landslide susceptibility mapping. CATENA 187, 104396. doi:10.1016/j.catena.2019.104396

CrossRef Full Text | Google Scholar

Xie, W., Li, X., Jian, W., Yang, Y., Liu, H., Robledo, L. F., et al. (2021). A novel hybrid method for landslide susceptibility mapping-based geodetector and machine learning cluster: A case of xiaojin county, China. ISPRS Int. J. Geo-Inf. 10, 93. doi:10.3390/ijgi10020093

CrossRef Full Text | Google Scholar

Xiong, S., Yao, W., and Li, C. (2019). Stability evaluation of multilayer slopes considering runoff in the saturated zone under rainfall. Eur. J. Environ. Civ. Eng. 25, 1718–1732. doi:10.1080/19648189.2019.1600038

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., Lee, Y. H., Tan, X., Yu, G., and Dai, F. (2012). The 2010 yushu earthquake triggered landslide hazard mapping using gis and weight of evidence modeling. Environ. Earth Sci. 66, 1603–1616. doi:10.1007/s12665-012-1624-0

CrossRef Full Text | Google Scholar

Yalcin, A., Reis, S., Aydinoglu, A. C., and Yomralioglu, T. (2011). A gis-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in trabzon, ne Turkey. CATENA 85, 274–287. doi:10.1016/j.catena.2011.01.014

CrossRef Full Text | Google Scholar

Zare, M., Pourghasemi, H. R., Vafakhah, M., and Pradhan, B. (2013). Landslide susceptibility mapping at vaz watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (mlp) and radial basic function (rbf) algorithms. Arabian J. Geosci. 6, 2873–2888. doi:10.1007/s12517-012-0610-x

CrossRef Full Text | Google Scholar

Zhang, M., Wu, L., Zhang, J., and Li, L. (2019). The 2009 jiweishan rock avalanche, wulong, China: Deposit characteristics and implications for its fragmentation. Landslides 16, 893–906. doi:10.1007/s10346-019-01142-6

CrossRef Full Text | Google Scholar

Zhu, A. X., Miao, Y., Yang, L., Bai, S., Liu, J., and Hong, H. (2018). Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping. CATENA 171, 222–233. doi:10.1016/j.catena.2018.07.012

CrossRef Full Text | Google Scholar