
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 15 February 2023
Sec. Environmental Informatics and Remote Sensing
Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1143003
This article is part of the Research Topic Advances in Development and Utilization of Underground Space, volume II View all 13 articles
The accurate understanding of the influence of confining pressure on the mechanical characteristics of soft rock and how to comprehensively consider this influence in the elastoplastic analysis of tunnels are the fundamental premises for the effective evaluation of the deformation control and stability of soft rock tunnels. Therefore, this paper firstly investigates the effect of confining pressure on the deformation and strength characteristics of phyllite and slate, using triaxial experiment results and proposed variable models for the mechanical parameters (E, v, c, φ) of soft rock with confining pressure variation. Secondly, according to the second stress state around tunnels and these variable models for the mechanical parameters of soft rock, a new elastoplastic solution for tunnels is devised, which simultaneously considers the effect of confining pressure on the deformation and strength characteristics of the surrounding rock. Finally, with the proposed elastoplastic solution, the effect of multiple factors (initial pressure, supporting force, and tunnel radius) on the stress and displacement of tunnel surrounding rock is analyzed.
In recent years, increasing numbers of tunnels have been constructed in soft rock stratum. However, major deformation of tunnels occurs frequently when tunnels pass through soft rock with high geo-stress, which often leads to the destruction of the tunnel support structure and brings about significant potential safety hazards for constructors (Chen et al., 2020; Li et al., 2020). Essentially, the fundamental reason why the problem of tunnel deformation occurs frequently is that the influence of confining pressure on the mechanical characteristics of soft rock has not yet been completely ascertained, resulting in the existing elastoplastic solution not being accurately analyzed and evaluated for stress and displacement around tunnels (Li F et al., 2021; Luo et al., 2021). Therefore, the influence of confining pressure on the mechanical characteristics of soft rock and more accurate elastoplastic solutions for tunnels are current research hotspots (Wu et al., 2022).
Regarding the influence of confining pressure on the mechanical characteristics of soft rock, the achievements of numerous scholars in the past decades can be divided into three categories. Firstly, the influence of confining pressure on the stress-strain curves of soft rock was discovered by (Alam et al., 2008; Debecker and Vervoort, 2009; Chen et al., 2016; Fu et al., 2018) through triaxial experiments. The results of these experiments show that the lithology of soft rock is usually slate and phyllite, and the range of confining pressure is 0MPa–40 MPa (Gholami and Rasouli, 2013; Hu et al., 2016; Hao et al., 2019). Secondly, based on the above-mentioned experiment results, the evolution of mechanical characteristics with the influence of confining pressure was analyzed, for example, the effect of confining pressure on failure patterns, peak strength, etc. (Xu et al., 2018). Thirdly, a series of new strength criteria and a constitutive model, which considers the influence of confining pressure, was proposed, for example, the GZZ strength criterion, the uniform strength criterion, and the elastoplastic damage constitutive model, etc. (Saeidi et al., 2013; Singh et al., 2015). In addition, several scholars devoted to the influence of confining pressure on the creep mechanical behavior and gas tightness characteristics of soft rock, such as Lyu and Liu, have investigated the creep gas tightness characteristics through experiments and proposed a corresponding creep-damage constitutive model (Lyu et al., 2021; Lyu et al., 2022). However, the majority of existing studies only focus on the influence of confining pressure on the strength parameters of soft rock but neglect the influence of confining pressure on the deformation parameters of soft rock. Therefore, a new, universal variable model for the mechanical parameters (including strength and deformation parameters) of soft rock considering the influence of confining pressure is urgently needed, which is one of the main purposes of this paper.
In terms of elastoplastic solutions for soft rock tunnels, the influence of confining pressure on the strength of soft rock and the strain-softening behavior of soft rock are the current research focuses. For instance, Kang et al. (Yi et al., 2020) and Chen et al. (Chen et al., 2022) devised a series of new solutions, which consider the influence of confining pressure on the strength of soft rock. In developing these solutions, they considered that it introduces many new strength criteria, such as GZZ, improved M-C, and D-P strength criteria to elastoplastic solutions. Many other scholars (Cui et al., 2015) have devised a series of new solutions for the strain-softening behavior of soft rock. In developing these solutions, they defined the plastic softening parameters (η) and assumed that η linearly controls the strength parameter variation in the post-failure stage. However, the effect of confining pressure is not considered in these solutions. Most existing solutions only consider the effect of confining pressure or the strain-softening behavior of soft rock on strength characteristics but ignore the influence of confining pressure on deformation characteristics, which leads to these solutions not calculating and evaluating stress and displacement around soft rock tunnels. Therefore, it is necessary to propose a new elastoplastic solution for soft rock tunnels, which simultaneously considers the effect of confining pressure on the deformation and strength of soft rock, which is another of the main purposes of this paper.
Therefore, this paper firstly investigates the effect of confining pressure on the mechanical characteristics of soft rock using triaxial experiment results and proposes variable models for the mechanical parameters (E, v, c, φ) of soft rock considering the influence of confining pressure. Secondly, a new elastoplastic solution for tunnels was devised, which simultaneously considers the mechanical characteristic variation of the surrounding rock due to the influence of confining pressure. Finally, the effect of multiple factors (initial pressure, supporting force, and tunnel radius) on the stress and displacement of tunnel surrounding rock is analyzed.
Based on the triaxial experiment results of 69 samples (35 samples of slate and 34 samples of phyllite from eight regions), the variation of the elasticity modulus under the influence of confining pressure for slate and phyllite, respectively, is revealed in Figure 1. Experimental result sources can be found in Supplementary Appendix SA.
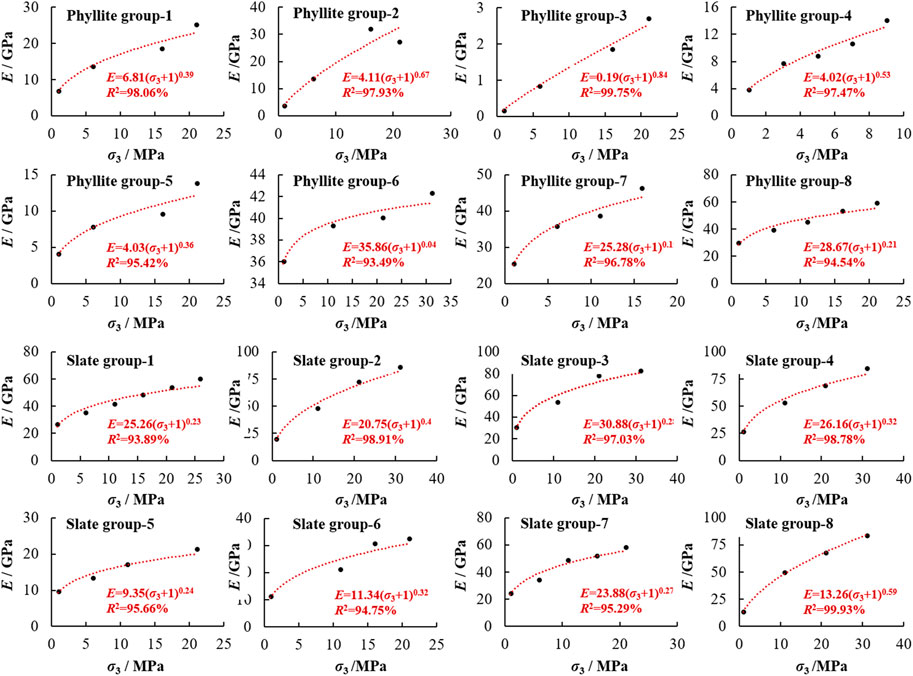
FIGURE 1. Variation of elasticity modulus with the influence of confining pressure of slate and phyllite.
As shown in Figure 1, the elasticity modulus of phyllite and slate gradually increases with increasing confining pressure, not constant. Further, using the universal global optimization method, it has been found that the power function can represent this variation with the influence of confining pressure, and the correlation coefficient of fitting results of all sample groups are more than 90%. Therefore, the variable model for the elasticity modulus of soft rock with the influence of confining pressure is proposed in Figure 5, and the undetermined parameters of variable models can be obtained by means of triaxial compression experiments.
Based on the triaxial experiment results of 67 samples (35 samples of slate and 32 samples of phyllite from nine regions), the variation of the Poisson ratio with the influence of confining pressure for slate and phyllite, respectively, is revealed in Figure 2. Experimental result sources can be found in Supplementary Appendix SA.
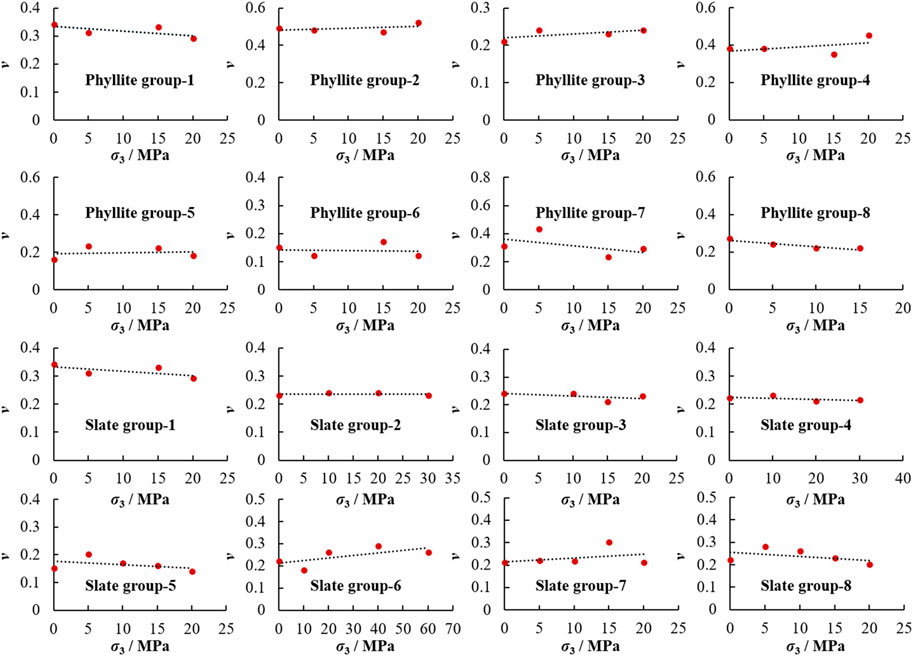
FIGURE 2. Variation of Poisson ratio with the influence of confining pressure influence for slate and phyllite.
As shown in Figure 2, the variation trend for the Poisson ratio of soft rock with variable confining pressure is almost linear, and the value of the Poisson ratio under different confining pressure conditions is practically equal to that under the 0 MPa confining pressure condition, which means the confining pressure does not have a significant influence on the Poisson ratio of soft rock. Therefore, the variable model for the Poisson ratio of soft rock with the influence of confining pressure is proposed in Figure 5.
Based on the triaxial experiment results of 57 samples (31 samples of slate and 26 samples of phyllite from six regions), the variation of the friction angle with the influence of confining pressure for slate and phyllite, respectively, is revealed in Figure 3. Experimental result sources can be found in Supplementary Appendix SA.
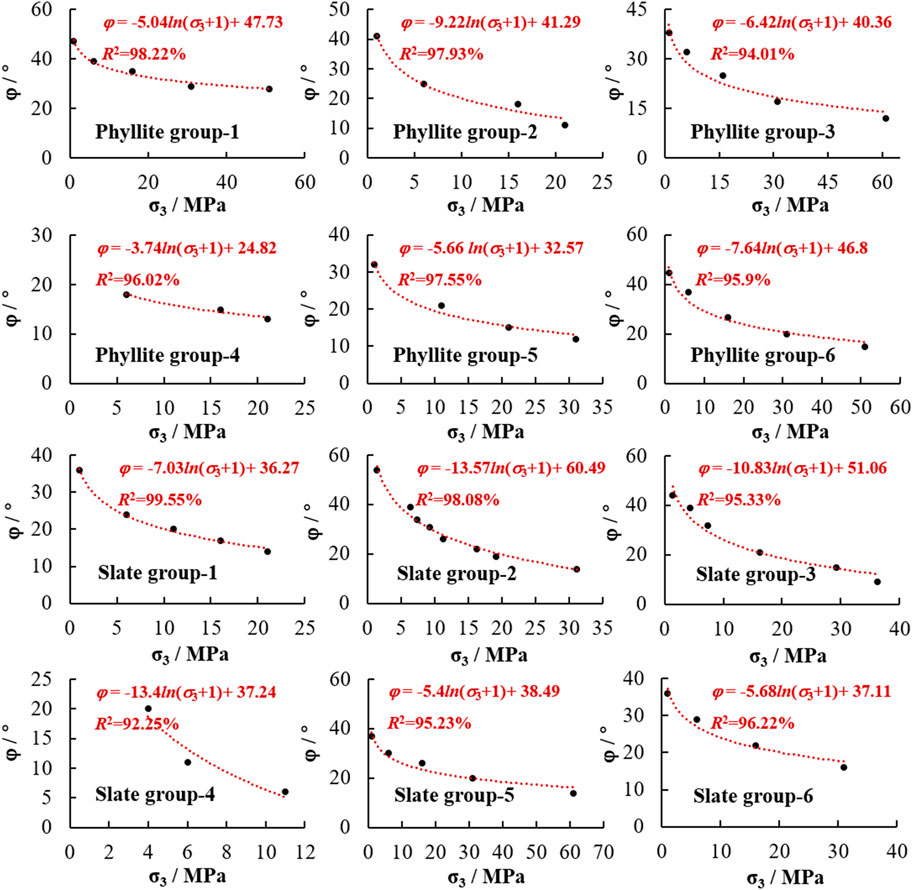
FIGURE 3. Variation of friction angle with the influence of confining pressure influence for slate and phyllite.
As shown in Figure 4, the friction angle of soft rock gradually decreases with increasing confining pressure. Further, using the universal global optimization method, it is found that the logarithmic function can represent this variation with the influence of confining pressure, and the correlation coefficient of fitting results of all sample groups are more than 90%. Therefore, the variable model for the friction angle of soft rock with the influence of confining pressure is proposed in Figure 5, and the undetermined parameters of the variable model can be obtained by means of triaxial compression experiments.
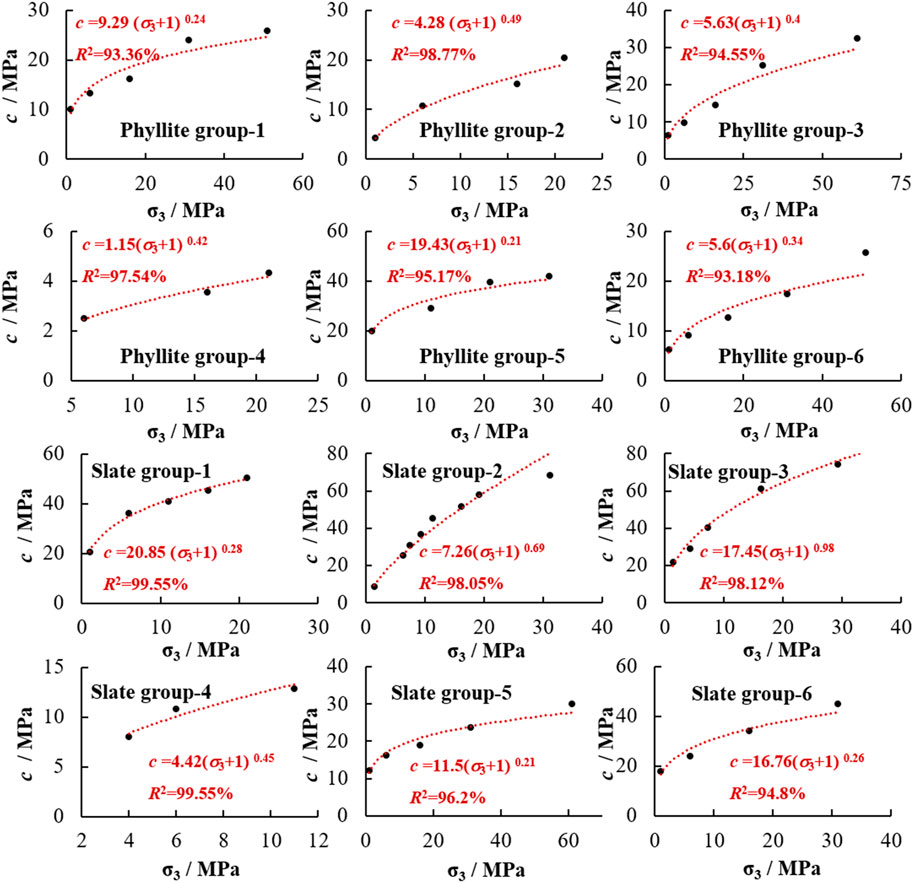
FIGURE 4. Variation of cohesion with the influence of confining pressure influence for slate and phyllite.
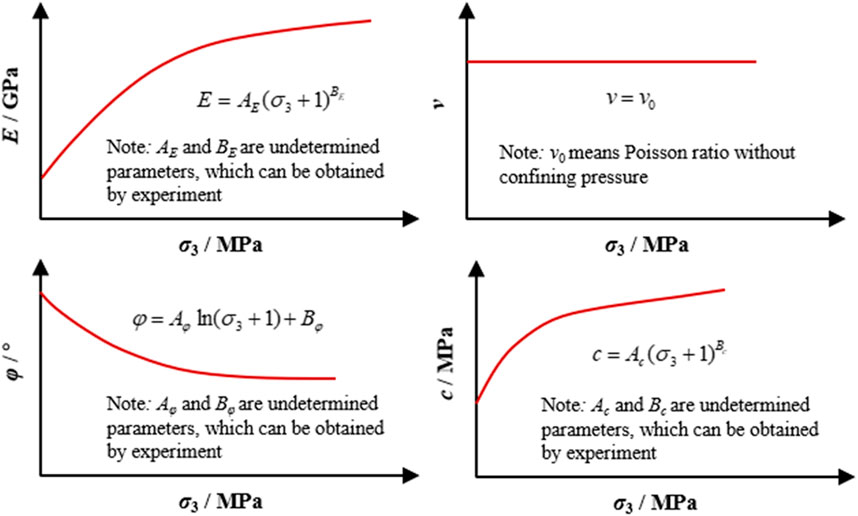
FIGURE 5. Variable models for mechanical parameters of soft rock with the influence of confining pressure.
Based on the triaxial experiment results of 57 samples (31 samples of slate and 26 samples of phyllite from six regions), the variation of cohesion with the influence of confining pressure for slate and phyllite is revealed in Figure 4. Experimental result sources can be found in Supplementary Appendix SA.
As shown in Figure 4, the cohesion of soft rock gradually decreases with increasing confining pressure. Further, using the universal global optimization method, it has been found that the power function can represent this variation with the influence of confining pressure, and the correlation coefficient of fitting results of all sample groups are more than 90%. Therefore, the variable model for the cohesion of soft rock with the influence of confining pressure is proposed in Figure 5, and the undetermined parameters of variable models can be obtained by means of triaxial compression experiments. In variable models for the mechanical parameters of soft rock, the units of confining pressure and cohesion are both MPa, the unit of the elasticity modulus is GPa, and the unit of the friction angle is degree.
After the circular tunnel excavation, the secondary stress state of the surrounding rock is shown in Figure 6 (Fang et al., 2021). Radial stress increases with increasing radial distance, which means confining pressure on the surrounding rock increases with increasing radial distance, not constant. Meanwhile, by combining the variable model for the mechanical parameters of soft rock with the influence of confining pressure, it can be concluded that the mechanical parameters of surrounding rock vary with radial stress variation, not constant.
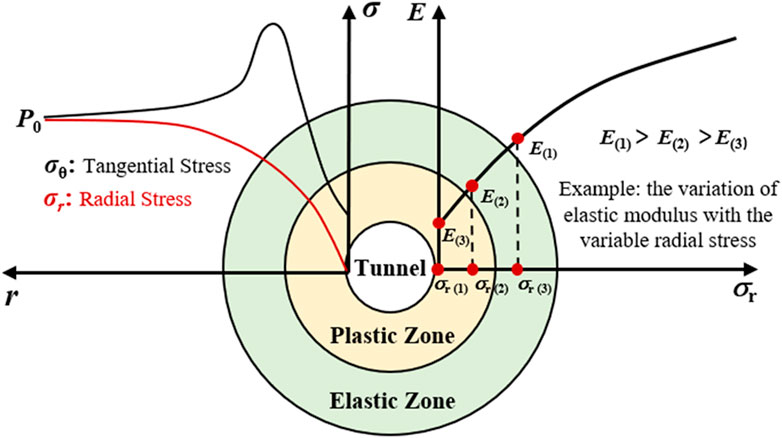
FIGURE 6. Secondary stress state of surrounding rock and variation of mechanical parameters of surrounding rock.
Therefore, in order to derive an elastoplastic solution for tunnels considering the influence of confining pressure, the stress field of the rock surrounding the tunnel is divided and the stress partition of the surrounding rock is: surrounding rock are divided into numerous concentric circle rings, the center of which is the center of the tunnel in polar coordinates, as shown in Figure 7. The mechanical parameters of each concentric circle ring are controlled by radial stress, which can be calculated using a variable model for the mechanical parameters of soft rock, and the mechanical parameters at different angles are the same in each ring.
The derivation process of elastoplastic solutions for tunnels considering the influence of confining pressure is subject to the following basic assumptions: (1) Surrounding rock is homogeneously isotropic. (2) The tunnel excavation disturbance process is considered a plane strain problem. (3) Surrounding rock is in a hydrostatic stress field without considering the influence of gravity before tunnel excavation, and the hydrostatic stress is
The yielding function controls the yielding process of the surrounding rock:
In Eq. 1,
Based on the non-associative plastic flow rule (Chen et al., 2022), the plastic potential function is:
and, if
When the tunnel radius is equal to that of the plastic zone,
Then, the expression of
So,
As shown in Figure 8, the plastic zone is divided into n concentric annuli and the boundary of i th is in Eq. 7:
The outer stress boundary condition (
Eq. 9 can be solved using MATLAB software, then
Then, the strain in the first ring is:
Meanwhile,
Eq. 12 could be transformed as:
Where:
Then,
And stress increment is:
Total strains can be separated into two parts:
So that Eq. 18 can be reformulated as:
Combined with Eqs 16, 17, the elastic strain increments are:
Combined with Eqs 19–21, the compatibility equation (Eq. 12) can be approximated as:
Approximating Eq. 22 with regard to ρ and rearranging
Total strain is:
For a sufficiently large n, mechanical parameters of the (i+1) ring can be replaced by those of the i ring and the stop condition of finite difference iterative process is:
After tunnel excavation, the elastic zone can be regarded as a thick-walled cylinder. The stress conditions at inner and outer boundaries are:
Lame solution (Yi et al., 2020) can calculate radial and tangential stresses at any radius. So, the stress expressions at any radius in the elastic zone are listed below:
Further, combined with the mechanical parameter expression of the surrounding rock, the strain expressions at any radius in the elastic zone are as follows, and the subscript “elastic” is applied in the expression to represent the elastic zone of the surrounding rock.
The above-mentioned expressions were compiled by MATLAB software for automatic solution operation. The finite difference calculation process is shown in Figure 9.
If the undetermined coefficient of the confining pressure term is equal to zero in every variable model for the mechanical parameters of surrounding rock, the finite difference process can be reduced to the classic elastoplastic solution.
Therefore, in order to validate this new solution, the results of two methods (new solution and classic solution) are compared with each other. Parameters of verification examples are listed in Table 1. Expressions of classic solutions are obtained from (Fang et al., 2021).
As shown in Figure 10, the plastic zone radius and radial stress distribution results of the proposed solution agree with those of the classic solutions, and displacement around the tunnel resulting from the proposed method is slightly greater than that of the classic solution, but the deviation does not affect the accuracy of the proposed method. The reason for the deviation in the displacement of tunnel surrounding rock is that the classic solution ignores the small quantity of higher order in the derivation process, so the calculated result is smaller than that obtained by the proposed solution. However, the deviation cannot affect the accuracy of the proposed method; therefore, the above result validates the proposed solution as accurate and correct.
The influence of initial pressure, supporting force of the tunnel, and radius of the tunnel on stress and displacement around the tunnel is analyzed by the proposed solution. Taking the Muzhailin tunnel as an example, variable models for the mechanical parameters of surrounding rock are based on experimental results from the Muzhailin tunnel in Table 2 (Li Z et al., 2021). The Muzhailing tunnel is a typical soft rock tunnel under high geo-stress conditions and belongs to the Lanzhou-Chongqing Railway in China. The longitudinal length of the Muzhailing tunnel is 19020m, and the height and width of the tunnel section are 11.98 m and 10.48m, respectively. The maximum geo-stress of the Muzhailing tunnel is 27.5 MPa and the surrounding rock of the Muzhailing tunnel is carbonaceous slate.
In the influence analysis of the initial pressure (
As shown in Figure 11, the stress level of tunnel surrounding rock significantly increases with increasing initial pressure. Moreover, the distance from the tunnel center to the appearance location of peak tangential stress of the surrounding rock increases gradually. When the initial pressure is 5 MPa, the peak tangential stress is 7.84 MPa, and its location is 2.16 times the tunnel radius. However, the peak tangential stress is 29.66 MPa, and its location is 5.2 times the tunnel radius when the initial pressure increases to 20 MPa. Displacement around the tunnel and the plastic zone radius of the surrounding rock increase with the increasing initial pressure. When initial pressure is 5 MPa, the plastic zone radius and displacement around the tunnel are 10.63 m and 3.81cm, but they increase to 25.9m and 55.22 cm (increasing by 143% and 1,349%) when initial stress is 20 MPa.
In the influence analysis of the supporting force (
As shown in Figure 12, the stress state of tunnel surrounding rock gradually changes to a three-dimensional state from a two-dimensional plane state with increasing supporting force. When supporting force increases, the stress level of tunnel surrounding rock increases, but the distance from the tunnel center to the appearance location of peak tangential stress of the surrounding rock gradually decreases. When the supporting force is 200kPa, the distance is 4.42 times the tunnel radius; however, the distance decreases to 2.99 times the tunnel radius (decreasing by 32.35%) when the supporting force increases to 1000 kPa. The peak stresses (including radial and tangential stress) of tunnel surrounding rock are determined only by the strength parameters of the surrounding rock; therefore, the supporting force only affects the appearance location of the peak stresses, not their values. Displacement around the tunnel and the plastic zone radius of the surrounding rock both decrease with increasing supporting force. The plastic zone radius of the surrounding rock and displacement around the tunnel are 22.12 m and 40cm, respectively, when the supporting force is 200 kPa. However, the radius and the displacement decrease to 14.97 m (decreasing by 32.32%) and 17.9 cm (decreasing by 61.96%), respectively, when the supporting force increases to 1000 kPa.
In the influence analysis of the tunnel radius (
As shown in Figure 13, the stress level of tunnel surrounding rock gradually decreases, but the stress disturbance range of the surrounding rock increases as the tunnel radius increases. The distance from the tunnel center to the appearance location of peak tangential stress of the surrounding rock gradually increases as the tunnel radius increases. When the radius of the tunnel is 3 m, the distance is 15.54m; however, the distance increases to 25.9 m (increasing by 66.67%) when the tunnel radius increases to 5 m. The tunnel radius only affects the appearance location of peak tangential stress of the surrounding rock, not its values. With the increasing tunnel radius, displacement around the tunnel and the plastic zone radius of the surrounding rock both increase. The plastic zone radius of the surrounding rock and displacement around the tunnel are 15.54 m and 33.13 cm, respectively, when the tunnel radius is 3 m. However, the radius and the displacement respectively increase to 25.9 m (increasing by 66.67%) and 55.22 cm (increasing by 66.68%) when the tunnel radius increases to 5 m.
This paper firstly investigates the effect of confining pressure on the deformation and strength characteristics of soft rock (slate and phyllite) using triaxial experiment results and proposed variable models for the mechanical parameters (E, v, c, φ) of soft rock with confining pressure variation. Secondly, according to the second stress state around tunnels and these variable models for the mechanical parameters of soft rock, a new elastoplastic solution for tunnels was devised, which simultaneously considers the effect of confining pressure on the deformation and strength characteristics of the surrounding rock. Moreover, this new solution is validated by classical solutions. Finally, the effect of multiple factors (initial pressure, supporting force, and tunnel radius) on the stress and displacement of tunnel surrounding rock are analyzed. Several main conclusions can be summarized as follows.
1. Regarding the influence of confining pressure on the deformation parameters (E, v) of soft rock, confining pressure has a significant influence on the elasticity modulus but does not significantly affect the Poisson ratio of soft rock. With increasing confining pressure, the elasticity modulus significantly increases, but the Poisson ratio is practically constant. Variable parameter models for the elasticity modulus (its form being power function) and the Poisson ratio (its form being constant function) were established, respectively, with the influence of confining pressure.
2. Regarding the influence of confining pressure on the strength parameters (c, φ) of soft rock, confining pressure has a significant influence on the friction angle and cohesion of soft rock. With increasing confining pressure, the friction angle decreases and cohesion increases gradually. Variable parameter models for the friction angle (its form being logarithmic function) and cohesion (its form being power function) were established, respectively, with the influence of confining pressure.
3. After soft rock tunnel excavation, with the variable radial stress of the surrounding rock, the mechanical parameters (E, v, c, φ) of the surrounding rock vary and are controlled by radial stress, not constant. Based on the secondary stress state of surrounding rock and variable models for the mechanical parameters of soft rock, a new elastoplastic solution was devised, which simultaneously considers the effect of confining pressure on the deformation and strength characteristics of the surrounding rock. Meanwhile, this new solution can be reduced to the classical solution, and its correctness and accuracy are validated by the classical solution.
4. The influence of multiple factors (initial pressure, supporting force, and tunnel radius) on the stress and displacement of tunnel surrounding rock are analyzed. With increasing initial pressure, the displacement around the tunnel and the plastic zone radius of the surrounding rock both gradually increase. With the increasing supporting force of the tunnel, the distance from the tunnel center to the appearance location of peak tangential stress of the surrounding rock decreases. With increasing supporting force, the plastic zone radius of the surrounding rock and displacement around the tunnel both decrease gradually. With increasing tunnel radius, the distance increases from the tunnel center to the appearance location of peak tangential stress of the surrounding rock. With increasing tunnel radius, the plastic zone radius of the surrounding rock and displacement around the tunnel both increase gradually.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
This study’s goals and ideas are offered by YZ and YD derived the formula and wrote the first manuscript, HZ analyzed the original data, and MW and LY revised and polished the manuscript. All the listed authors contributed substantially to the research and approved the paper’s publication.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Major Science and Technology project (2019-A05) of China Railway Construction Co. LTD, Hebei Technology Innovation Center for Intelligent Development and Control of Underground Built Environment, opening research project (KF2021-09) and research project (QN202203) supported this paper.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer XZ declared a shared affiliation with the authors MW, YL to the handling editor at time of review.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1143003/full#supplementary-material
Alam, M. R., Swamidas, A. S. J., Gale, J., and Munaswamy, K. (2008). Mechanical and physical properties of slate from britannia cove, newfoundland. Can. J. Civ. Eng. 35 (7), 751–755. doi:10.1139/l08-042
Chen, J., Liu, W., Chen, L., Luo, Y., Li, Y., Gao, H., et al. (2020). Failure mechanisms and modes of tunnels in monoclinic and soft-hard interbedded rocks: A case study. KSCE J. Civ. Eng. 24 (4), 1357–1373. doi:10.1007/s12205-020-1324-3
Chen, W., Zhang, D., Fang, Q., Chen, X., and Xu, T. (2022). A new numerical finite strain procedure for a circular tunnel excavated in strain-softening rock masses and its engineering application. Appl. Sci. 12 (5), 2706. doi:10.3390/app12052706
Chen, Y.-F., Wei, K., Liu, W., Hu, S.-H., Hu, R., and Zhou, C.-B. (2016). Experimental characterization and micromechanical modelling of anisotropic slates. Rock Mech. Rock Eng. 49 (9), 3541–3557. doi:10.1007/s00603-016-1009-x
Cui, L., Zheng, J.-J., Zhang, R.-J., and Dong, Y.-K. (2015). Elasto-plastic analysis of a circular opening in rock mass with confining stress-dependent strain-softening behaviour. Tunn. Undergr. Space Technol. 50, 94–108. doi:10.1016/j.tust.2015.07.001
Debecker, B., and Vervoort, A. (2009). Experimental observation of fracture patterns in layered slate. Int. J. Fract. 159 (1), 51–62. doi:10.1007/s10704-009-9382-z
Fang, H., Zhang, D., Fang, Q., and Wen, M. (2021). A generalized complex variable method for multiple tunnels at great depth considering the interaction between linings and surrounding rock. Comput. Geotechnics 129, 103891. doi:10.1016/j.compgeo.2020.103891
Fu, H., Zhang, J., Huang, Z., Shi, Y., and Chen, W. (2018). A statistical model for predicting the triaxial compressive strength of transversely isotropic rocks subjected to freeze–thaw cycling. Cold Regions Sci. Technol. 145, 237–248. doi:10.1016/j.coldregions.2017.11.003
Gholami, R., and Rasouli, V. (2013). Mechanical and elastic properties of transversely isotropic slate. Rock Mech. Rock Eng. 47 (5), 1763–1773. doi:10.1007/s00603-013-0488-2
Hao, X., Xu, Q., Yang, D., Wang, S., and Wei, Y. (2019). Effect of bedding angle and confining pressure on the brittleness of geomaterials: A case study on slate. Adv. Mater. Sci. Eng. 2019, 1–17. doi:10.1155/2019/1650170
Hu, K., Feng, Q., and Wang, X. (2016). Experimental research on mechanical property of phyllite tunnel surrounding rock under different moisture state. Geotechnical Geol. Eng. 35 (1), 303–311. doi:10.1007/s10706-016-0107-6
Li, F., Jiang, A., and Zheng, S. (2021). Anchoring parameters optimization of tunnel surrounding rock based on particle swarm optimization. Geotechnical Geol. Eng. 39 (6), 4533–4543. doi:10.1007/s10706-021-01782-3
Li, Y., Yang, S., Tang, X., Ding, Y., and Zhang, Q. (2020). Experimental investigation of the deformation and failure behavior of a tunnel excavated in mixed strata using transparent soft rock. KSCE J. Civ. Eng. 24 (3), 962–974. doi:10.1007/s12205-020-0072-8
Li, Z., Li, Z., Huang, W., Xu, Z., Zhang, W., and Chen, K. (2021). Tunnel bottom cavity laws of heavy-haul Railway tunnel under train load and groundwater in weak surrounding rock condition. KSCE J. Civ. Eng. 26 (3), 1451–1464. doi:10.1007/s12205-021-5953-y
Luo, Y., Wu, Y., Chen, J., Dong, F., Liu, W., Chen, L., et al. (2021). Back-calculation method of rock mass pressure in a shallow-buried super large-span tunnel using upper-bench CD method. KSCE J. Civ. Eng. 26 (1), 433–447. doi:10.1007/s12205-021-0312-6
Lyu, C., Liu, J., Ren, Y., Liang, C., and Liao, Y. (2021). Study on very long-term creep tests and nonlinear creep-damage constitutive model of salt rock. Int. J. Rock Mech. Min. Sci. 146, 104873. doi:10.1016/j.ijrmms.2021.104873
Lyu, C., Liu, J., Ren, Y., Liang, C., and Zeng, Y. (2022). Mechanical characteristics and permeability evolution of salt rock under thermal-hydro-mechanical (THM) coupling condition. Eng. Geol. 302, 106633. doi:10.1016/j.enggeo.2022.106633
Saeidi, O., Vaneghi, R. G., Rasouli, V., and Gholami, R. (2013). A modified empirical criterion for strength of transversely anisotropic rocks with metamorphic origin. Bull. Eng. Geol. Environ. 72 (2), 257–269. doi:10.1007/s10064-013-0472-9
Singh, M., Samadhiya, N. K., Kumar, A., Kumar, V., and Singh, B. (2015). A nonlinear criterion for triaxial strength of inherently anisotropic rocks. Rock Mech. Rock Eng. 48 (4), 1387–1405. doi:10.1007/s00603-015-0708-z
Wu, F., He, C., Kou, H., Wang, B., Meng, W., Meng, H., et al. (2022). Discussion on reasonable clear spacing of twin-tunnels in weak surrounding rock: Analytical solution and numerical analysis. KSCE J. Civ. Eng. 26 (5), 2428–2442. doi:10.1007/s12205-022-0898-3
Xu, G., He, C., Su, A., and Chen, Z. (2018). Experimental investigation of the anisotropic mechanical behavior of phyllite under triaxial compression. Int. J. Rock Mech. Min. Sci. 104, 100–112. doi:10.1016/j.ijrmms.2018.02.017
Keywords: soft rock, circular tunnel, mechanical parameter, variable model, elastoplastic solution
Citation: Dong Y, Zhang H, Wang M, Yu L and Zhu Y (2023) Variable model for mechanical parameters of soft rock and elastoplastic solutions for tunnels considering the influence of confining pressure. Front. Earth Sci. 11:1143003. doi: 10.3389/feart.2023.1143003
Received: 12 January 2023; Accepted: 31 January 2023;
Published: 15 February 2023.
Edited by:
Zhanping Song, Xi’an University of Architecture and Technology, ChinaReviewed by:
Cheng Lyu, Sichuan University, ChinaCopyright © 2023 Dong, Zhang, Wang, Yu and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yongquan Zhu, eW9uZ3F1YW5femh1MjAyMkAxNjMuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.