Time transfer and significance of vertical land motion in relativistic geodesy applications: a review paper

Determination of the Earth’s gravity field and geopotential value is one of the fundamental topics in physical geodesy. Traditional terrestrial gravity and precise leveling measurements can be used to determine the geopotential values at a local or regional scale. However, recent developments in optical atomic clocks have not only rapidly improved fundamental science but also contributed to applied research. The latest generation of optical clocks is approaching the accuracy level of 10⁻¹⁸ when facilitating atomic clock networks. These systems allow examining fundamental theories and many research applications, such as atomic clocks applications in relativistic geodesy, to precisely determine the Earth’s gravity field parameters (e.g., geopotential values). According to the theory of relativistic geodesy, the frequency difference measured by an optical clock network is related to the gravity potential anomaly, provided that the effects of disturbing signals (i.e., tidal and non-tidal contributions) are filtered out. The relativistic geodesy principle could be used for a practical realization of global geodetic infrastructure, most importantly, a vertical datum unification or realization of height systems. This paper aims to review the background of relativistic (clock-based) geodesy and study the variations of optical atomic clock measurements (e.g., due to hydrology loading and land motion).

Highlights

• A review of relativistic geodesy and performance and recent developments of optical atomic clocks are presented in this article

• The variations of optical atomic clock measurements due to tidal and non-tidal contributions are discussed.

• A practical approach is suggested to validate the performance of atomic clocks in relativistic geodesy applications.

1 Introduction

Determination of the Earth’s gravity field and the geopotential values is an important task in geodesy. For global and regional applications, the satellite gravimetry techniques such as the Gravity Recovery and Climate Experiment (GRACE), the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) and the CHAllenging Minisatellite Payload (CHAMP) missions (cf. Pail, 2014) have been employed for this purpose. Terrestrial gravity and precise geometric leveling measurements have mainly been used to determine the geopotential values on local or regional scales. All of these methods have been used extensively for different geodetic purposes, particularly for geoid determination and the establishment of geodetic reference frames. Recently, because of the rapid development of optical atomic clocks, it has become possible to determine the geopotential values with high accuracy using optical clock network data (Bondarescu et al., 2012; Riehle, 2017). This method was proposed for the first time by Bjerhammar, (1975). Later, he introduced the idea of relativistic geodesy (see Bjerhammar, 1985). Vermeer, (1983), who introduced chronometric leveling, also studied relativistic geodesy (see also Delva and Lodewyck, 2013). This novel approach helps determine the potential differences directly using clock measurements as it adds valuable and independent information about the Earth’s gravitational potential.

The relativistic (or clock-based) geodesy is based on the relativistic gravitational time dilation as the local gravitational potential changes the frequency of an atomic clock. In physics, this is called gravitational redshift. A determination of the geopotential values using relativistic geodesy has some advantages. This method could significantly reduce the cost of geodetic levelling and remeasurement of benchmarks due to vertical land motions in future. It also can be used as an independent technique for calibration or assessment of the existing gravimetric geoid models (i.e., in combination with GNSS leveling) and leveling networks. Potential applications are also related to vertical datum unification, filling gravity data gaps in uncharted areas, or determining height systems.

We have been witnessing significant development in high-precision optical atomic clocks over the last decades regarding clocks’ stability and accuracy. Mehlstäubler et al. (2018) provided a comprehensive review of existing concepts of optical atomic clocks. They summarized a recent development of atomic clocks in terms of their stability, accuracy and reliability for geodetic applications. As stated by Takamoto et al. (2005), clocks are used to realize the unit of time and frequency not only in fundamental science but are also essential tools in geoscience applications. It is well-known that the Sr-lattice (Strontium) clock is one of the most stable optical atomic clocks which approaches the accuracy level of 10⁻¹⁸ (in terms of accuracy). This factor increases interest of using atomic clocks in geodetic applications (Riehle, 2017). It is worth mentioning that, in the context of optical frequencies and clocks, it is customary to talk about a fractional frequency resolution, uncertainty, etc., as being related to dimensionless redshift quantity. The redshift is related to the gravitational potential difference where a fractional frequency shift of 10⁻¹⁸ corresponds to a height difference of 1 cm at or near the Earth’s surface (Mehlstäubler et al., 2018). This level of accuracy obviously could not be achieved without taking into account systematic corrections for optical clocks (Takamoto et al., 2005) and filtering tidal and non-tidal effects (Voigt et al., 2016). Bloom et al. (2014) demonstrated an atomic clock with a many-atom system that reaches an accuracy of 6×10⁻¹⁸ and could improve the accuracy of optical lattice clocks by a factor of 22. They used two generations of Sr-lattice clocks to demonstrate the improved performance of lattice clocks and analyzed both uncertainty and instability of clocks by investigating the Allan deviation parameter (cf. Riehle, 2017).

An optimal clock network is practically established by connecting single optical clocks, using, e.g., optical fiber links or other frequency transfer techniques. Currently, there are some optical clock network projects, such as Paris and Braunschweig’s network based on using 1,415 km of telecom fiber (Lisdat et al., 2016) of which the accuracy is studied by Lisdat et al. (2016). They reached the accuracy of 3×10⁻¹⁷ using two Sr-lattice clocks with an uncertainty of 5×10⁻¹⁷ between Paris and Braunschweig stations. There are also fiber links in Europe (Riehle, 2017), a 120 km long fiber link in Japan (Hong et al., 2009) and a 251 km long fiber optic link in the US (Williams et al., 2008). The above-mentioned studies are very promising, indicating that optical clocks are suitable tools for different applications in geodesy. However, it is necessary to emphasize that optical atomic clocks applications in geodesy depend on the size (i.e., transportability), price, and link technology which are very important for future developments, as discussed in the review paper by Mehlstäubler et al. (2018). Recently, the atomic clocks have been used for geodetic proposes after the above-mentioned optical clocks developments (see Denker et al., 2018; Müller et al., 2018). Müller et al. (2018) reviewed quantum clocks and their applications for space-borne (e.g., GRACE-type low-low satellite-to-satellite tracking) and terrestrial applications. Denker et al. (2018) reviewed the application of relativistic redshift and presented some practical results. They validated the results obtained from atomic clock sites using two geodetic approaches, i.e., geometric leveling and the Global Navigation Satellite Systems (GNSS) leveling and, for large distances, the GNSS/geoid approach, to determine the geopotential values. They showed that the GNSS/geoid approach provides better results than geometric levelling. In other studies Takano et al. (2016) and Kawasaki, (2021) employed the relativistic geodesy technique to determine the gravitational redshift. Takano et al. (2016) used three Sr optical lattice clocks to determine the height difference between two benchmarks with a 15 km distance and could reach an uncertainty of 5 cm. The distant clocks connected by a telecom fibre to synchronously operate. Kawasaki, (2021) studied the stability optical lattice clocks to obtain the height difference below 1 cm.

In this study, we have reviewed the performance and recent developments of optical atomic clocks. For completeness, we summarized the most fundamental theoretical definitions in relativistic geodesy. In addition, we have reviewed different methods for high-performance clock networks, i.e., different methods for transferring frequency using optical atomic clocks. We also studied the variations of optical atomic clock measurements due to tidal and non-tidal contributions. In addition, we studied the vertical land motions due to hydrology loading, other geophysical phenomena and their impact on the optical atomic clock measurements. Finally, a practical approach is suggested (using precise leveling) to validate the performance of relativistic geodesy. At the end, it is worth mentioning that one of the aims of this paper is to provide a comprehensive overview of relativistic geodesy for those who are not familiar with this field. The paper will help readers get a broader perspective on the current state of knowledge, the existing gaps, synthesizing information from multiple sources and future directions of the relativistic geodesy. We also present the quality and reliability of existing methods of frequencies transfer for relativistic geodesy applications. In other words, this study can help researchers identify existing research limitations and to open new research horizon.

2 Precise time scale for relativistic geodesy

2.1 Time scale and optical atomic clocks evolution

It is well-known that uncertainties of sidereal or solar time systems are too high (because of irregularities in the Earth’s rotation and in orbit) to allow their use in modern geodetic applications. Atomic clock-derived time system is used instead because of its uniform time scale. According to the International System of Units (SI), the formal definition of the precise time is “the duration of 9 192 631 770 periods of the radiation corresponding to the transition between two hyperfine levels of the ground state of the cesium 133 atom”. There are more than 400 atomic clocks around the world to determine the International Atomic Time (TAI). In other words, the weighted average, obtained from different atomic clocks, is used to determine the international time scale, i.e., Coordinated universal Time (UTC). The synchronization of different time scales is thus performed using atomic times. Nowadays, employing a precise time scale is very important for different applications, e.g., GPS time and its application in precise positioning using GNSS. UTC is introduced because TAI differs from UT1 (universal Time scale corrected by the Earth’s rotation and polar motion) by about 37 s due to irregularities in the Earth’s rotation. The International Earth Rotation and Reference Systems Service (IERS) monitors the difference between UTC and UT1 and adjusts the UTC if the difference is greater than 0.9 (Teunissen and Montenbruck, 2017, Chapter 2):

$\left|\mathrm{U}\mathrm{T}1–\mathrm{U}\mathrm{T}\mathrm{C}\right|\le 0.9\mathrm{s}(1)$

It is assumed that TAI ≈ UTC on 1 January 1958. It is worth mentioning that TAI is currently ahead of UTC by 37 s (i.e., UTC = TAI −37s) (https://www.nist.gov/pml/time-and-frequency-division/time-realization/leap-seconds).

The concept of optical atomic clocks can be found in numerous scientific publications, e.g., Takamoto et al. (2005), Riehle, (2017), Lombardi, (2012) and McGrew et al. (2018). The first generation of atomic clocks have a special microwave range frequency (generated, e.g., by the transformation of quartz oscillation) and an atomic feedback loop to correct the oscillator when it deviates from its predefined frequency (see, e.g., Lombardi (2012); Figure 2).

The atomic clock performance principle is based on unique energy, which is required to change the electrons’ orbits in each atom. As an atomic physics principle, this energy level is constant for all atoms of an element (/substance) all over the Universe. As a result, only a very precise wave frequency can transmit the electrons of a given matter/substance to the next atomic level. Therefore, the number of electrons in the higher energy level drops significantly in the feedback loop when the clock (i.e., the microwave oscillator) deviates from the predefined frequency (which is exactly set to the atomic level transition frequency). Accordingly, the off frequency is recognizable and it will be aligned back to the exact frequency again (cf. Lombardi, 2012; Petrov et al., 2018). This kind of atomic feedback loop improved the clock stability by several orders of magnitude. While a quartz clock may be off by a full millisecond after about 6 weeks, an atomic clock, e.g., NASA’s Deep Space Atomic Clock, will deviate by a millisecond after about 10,000 years [https://www.nasa.gov/feature/jpl/what-is-an-atomic-clock].

However, the new optical atomic clocks developed in the last decade have achieved much better performance by using ytterbium and strontium atom lattices in the feedback loop, which allowed them to increase the oscillator frequency to the visible region with at least five orders of magnitude higher frequencies. Today, atoms such as ytterbium and strontium (in the visible part of the electromagnetic spectrum) are used in the optical atomic clocks. Using ytterbium and strontium atoms has attained a new record uncertainty because they oscillate faster than microwave frequencies (about 100,000 times higher) (cf. Mehlstäubler et al. (2018); Figure 6). In optical clocks, the laser is pre-stabilized, and then it locks the frequency of the laser to a narrow-bandwidth to generate a stable and absolute optical frequency reference. The system needs a third component, which records the total number of oscillations of the clock oscillator laser using an optical frequency counter Hollberg, (2005), Le Targat et al. (2013). Since the 1980s, the uncertainty and stability of optical atomic clocks have gradually improved, with the current level of accuracy to about 10⁻¹⁸. Therefore, optical atomic clocks are better than microwave clocks because of their high performance, as they provide high accuracy and ultrahigh stability. Figure 1 shows a graphical summary of standard frequency uncertainties published by the Bureau International des Poids et Mesures (BIPM).

FIGURE 1

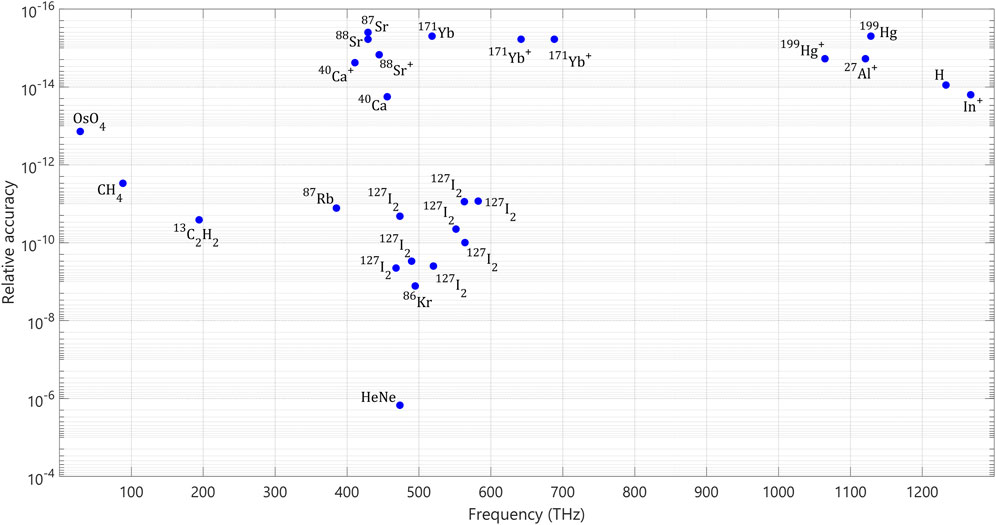
FIGURE 1. Comparison of the frequency standards uncertainty that can be used in optical atomic clocks (Source: Bureau International des Poids et Mesures (BIPM)).

2.2 Clocks’ accuracy, instability and reproducibility or repeatability

Clocks deviate from the ideal time scale (or ideal clock) because of deterministic biases (drift) and random deviations (due to frequency fluctuations) (Blair, 1974). There are three important parameters and quantities in the atomic clocks, namely, the uncertainty (or accuracy), instability (statistical uncertainty) and reproducibility, that are important for clock-based geodesy applications (McGrew et al., 2018). The accuracy of clocks is about the deviation of the atomic clock frequency from a reference frequency, assuming that the clock is at rest and all possible corrections were considered. The instability of a clock is defined by Allan deviation, which is a measure of clock frequency variations with respect to a stable oscillator or more accurate reference clock (cf. Takamoto et al., 2005; Riehle, 2017). On the other hand, instability indicates how much the atomic clock frequency changes over a certain time interval (cf. McGrew et al., 2018). To improve the clocks’ stability, integration times in a certain time interval (e.g., from seconds of days to weeks) are required to obtain a fractional frequency resolution (e.g., 10^–18). Allan Deviation (ADEV) is a measure that is used to describe the noise of frequency standard. In other words, the ADEV determines the theoretical prediction of the frequency instability (Mehlstäubler et al., 2018). The Allan variance is one-half of the time average of the squares of the differences between successive readings, i.e., ${\left({\overline{y}}_{n+1}-{\overline{y}}_n\right)}^2$, over the sampling period τ (or observation time):

${\sigma }_y^2\left(\tau \right)=\frac{1}{2}〈{\left({\overline{y}}_{n+1}-{\overline{y}}_n\right)}^2〉=\frac{1}{2{\tau }^2}〈{\left(x_{n+2}-2x_{n+1}+x_n\right)}^2〉(\mathrm{2a})$

where

${\overline{y}}_n=\frac{x\left(nT+\tau \right)-x\left(nT\right)}{\tau }(\mathrm{2b})$

where $x\left(t\right)$ is the clock reading (in seconds) measured at time t, T is the time between each frequency sample and $〈.〉$ denotes averaging operator over frequency fluctuations [see also Allan and Barnes (1981)]. For improving the clock’s stability, integration times in a certain time interval (e.g., from seconds of days to weeks) are required to obtain a fractional frequency resolution (e.g., 10^–18). It is worth mentioning that the ADEV cannot distinguish the white phase noise from flicker phase noise, and hence one should use the modified Allan variance (Griggs et al., 2015).

According to McGrew et al. (2018), the reproducibility of the atomic clocks denotes the agreement between similar (same design) but distinct clocks (i.e., being synchronous of the clocks). Mehlstäubler et al. (2018) have reviewed the reproducibility and involved parameters in the clock’s systematic shifts. Generally, the observed frequencies are influenced by environmental factors, such as temperature changes, supply voltages, magnetic field, barometric pressure, humidity, hydrology loading, stress, vibration, acceleration, etc. Hence, for example, the temperature-compensated oscillator and oscillators for voltage and severe environments are important components to correct unwanted side effects in the atomic clocks. It is important to mention that sometimes the reproducibility and accuracy are used incorrectly. The accuracy of an optical clock can never be better than its reproducibility (Blair, 1974).

The optical atomic clocks can be calibrated by a side-by-side calibration with a reference clock before starting measurements at a remote site. However, one can evaluate the clock’s reproducibility instead of its accuracy. The uncertainty in terms of reproducibility means that the shifts (from unperturbed transition frequency) are assumed to be constant between measurements, but without knowing their exact value (cf. Ludlow et al., 2015).

Existing studies of optical clocks’ and link accuracies (optical clock network stability) and instabilities are summarized in Table 1.

TABLE 1

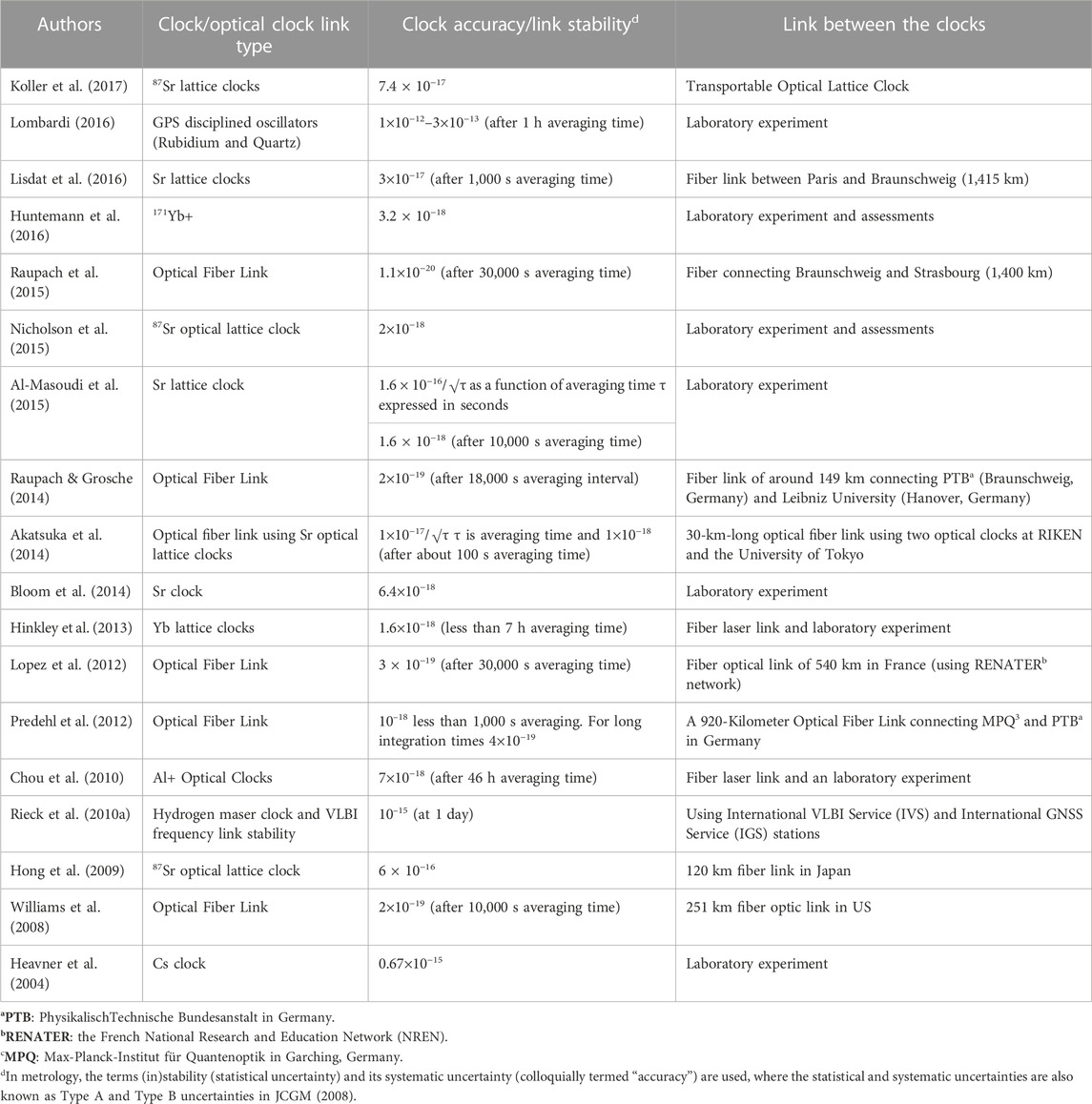
TABLE 1. A non-comprehensive summary of optical clocks accuracy and optical link assessments (clock network stability).

2.3 Different types of clock networks

A future progress in improved timescales will critically depend on how the atomic clocks are linked in a network, i.e., how the frequencies of remote atomic clocks are compared. Different methods can be used to transfer and compare the frequencies of atomic clocks, namely, microwave link, GNSS common-view, Very Long Baseline Interferometry (VLBI), laser link, and optical fiber (cf. Riehle, 2017). However, the performance of the intracontinental and intercontinental clock networks is different, as the uncertainty of the distant atomic clocks is further restricted in the intercontinental networks by the satellite transfer technique performance (Pizzocaro et al., 2020). The idea of using satellites with microwave signals is based on time and frequency transfer, which can effectively establish systems for frequency comparison between distant atomic clocks. Accordingly, two different techniques can be utilized. The first method relies on the received microwave signals with time information from GNSS on a Medium Earth’s Orbit (MEO). Consequently, the time signals from the satellites can be received simultaneously in distant laboratories located at different locations. After applying different corrections like the path delay, these signals are compared with the corresponding local clocks. Consequently, the difference between the two distant clocks can be obtained by comparing the measured time differences. Using an integration time of 1 day, an uncertainty of 10⁻¹⁵ can result from evaluating the satellite signal’s carrier phase. In the second satellite-based technique, different stations with distant clocks use the same signal path to exchange their signals simultaneously through a geostationary satellite. Based on this method, over intracontinental distances, the statistical relative frequency instability of a frequency comparison has been reported to be about 10⁻¹⁵. A two-way carrier-phase-based data processing approach provided long-term stability of 10⁻¹⁶, which provides more accurate results than the first method mentioned here.

Very Long Baseline Interferometry (VLBI) is one of the space methods for determining the time delays between VLBI stations (https://ivscc.gsfc.nasa.gov/about/org/components/ns-list.html) using the extragalactic sources (quasars: quasi-stellar radio sources). The outcomes of VLBI measurements are 1) the high accuracy of the stations’ position and 2) accurate clock differences between the stations using hydrogen atomic clocks as frequency standard. The role of the hydrogen atomic clock is to provide an adequate signal-to-noise ratio and frequency stability.

The measurement principle in the VLBI is similar to the other space positioning systems. The received signals from the extragalactic sources are recorded and marked using the hydrogen atomic clocks in the VLBI stations. The time delay will be determined using the recorded data in the VLBI stations. The time delay is affected by the offset of the reference clocks in each observatory, the cable instrumental delay, and the tropospheric and ionospheric atmosphere propagation delays (cf. Ma et al., 1986; Wang et al., 2019). For example, the delay due to the ionospheric effect can be reduced using different frequencies similar to the GNSS precise positioning methods. The determined time delay will be used to determine the clock differences with high precision in the VLBI stations, provided that the station position with mm accuracy, the tropospheric and ionospheric atmosphere propagation delays are known (as a priori data). Hence, the VLBI technique can be used for time transfer and relativistic geodesy applications (cf. Wang et al., 2019; Haas, 2020).

Time and frequency within the VLBI method have been presented in detail by Rieck et al. (2010b). Using the VLBI approach, the stability of time transfer can be assessed by other methods (see Figure 2) such as GPS common view (GPS CV) method (cf. Allan and Weiss, 1980). The stability of the VLBI frequency link between the station clocks has been studied in different projects, e.g., by Rieck et al. (2010a) in Onsala Space Observatory in Sweden, Wang et al. (2019) in Kunming-Urumqi baseline in China, and Pizzocaro et al. (2020) in Italy and Japan (see also Bouman, 2012). The later study proposes using dedicated transportable VLBI stations and taking advantage of node-hub style observations. In other words, transportable stations (nodes) are compared with a large antenna VLBI (hub) to calculate the delay observable. Pizzocaro et al. (2020) showed that it is possible to reach 10⁻¹⁷ uncertainty level. The above-mentioned experimental results show that the VLBI time transfer stability is equivalent to the result of GPS CV method after several hours of averaging. It is important to mention that the VLBI method is not the best in a short average period due to its low sampling rate (see Takiguchi et al. (2007); Rieck et al. (2010a); Hobiger et al. (2015). However, its stability can be better than the other methods (e.g., GPS CV) if the averaging time increases. Different observing campaigns conducted by the International VLBI Service (IVS) and the most recent campaign is CONT17, which is a campaign of continuous VLBI sessions (https://ivscc.gsfc.nasa.gov/program/cont17/).

FIGURE 2

FIGURE 2. VLBI vs. GNSS common-view technique.

Time and frequency can also be transferred by laser link that, in comparison with the microwave links, provides better relative frequency instability. In this technique of time transferring, which is based on recording the Time of Flight of laser pulses, asynchronous pulsed laser beams from Earth’s stations (Earth’s terminals or ground stations) are retro-reflected from Low Earth’s Orbit (LEO) satellites. Each pulse is tagged with an onboard clock based on the arrival time. Accordingly, links between distant clocks can be established with the time instabilities of a few picoseconds.

Time and frequency can also be transferred via optical fiber links. Fiber links with bi-directional amplifiers (BDA) represent point-to-point connections and are a mature technology for transferring time and frequency within an optical clock network. However, to achieve higher accuracy in comparing and linking the optical atomic clocks, the existing fiber networks have to be actively stabilized. This can be done by sending the frequency back on a mutual path between the clock stations. Therefore, any occurring frequency shift can be measured and corrected. Over short distances, if the signal attenuation in the fiber is low enough for a given signal-to-noise level, the phase of the received signal can be determined unambiguously. However, over longer distances, a phase-coherent two-way amplification has to be done for the transferred frequency to compensate the signal attenuation, which requires considerable technical manipulation of the existing fiber infrastructure; for more details we refer readers to the study by Riehle, (2017). The fiber links can achieve stability better than 10⁻¹⁹ over about 1,400 km (Raupach et al., 2015).

Moreover, portable atomic clocks can be utilized for comparing remote optical atomic clocks. A transportable ⁸⁷Sr optical lattice clock has been developed, operating in a transportable container with the same stable environmental conditions at each operation site (Koller et al., 2017). Its complete characterization against a stationary lattice clock resulted in a systematic uncertainty of 7.4×10⁻¹⁷ and the frequency instability was reported to be 1.3×10⁻¹⁵/τ^1/2, with an averaging time τ in seconds.

3 Determination of geodetic height differences using relativistic geodesy technique

According to Bjerhammar, (1975) and Bjerhammar, (1985), the gravitational potential difference at points P and Q can be calculated using the general theory of relativity and frequency measurements obtained from atomic clocks, with the following formula [Sjöberg and Bagherbandi (2017), Chapter 7]:

$W_P-W_Q\approx \frac{\overline{f}\Delta f}{f_Q^2}{c}^2\approx \frac{\Delta f}{\overline{f}}{c}^2(3)$

where $\Delta f=f_P-f_Q$ , $\overline{f}=\left(f_P+f_Q\right)/2$ and c is the speed of the light in vacuum. In addition, Eq. 3 can be rewritten into the form used to calculate a height difference between two points after dividing by the mean gravity values ($g=\left(g_P+g_Q\right)/2$):

$H_P-H_Q\approx \frac{\Delta f}{g\overline{f}}{c}^2(4)$

which can be used to directly determine the geopotential difference between two points at the Earth’s surface or in space (see more about the derivation of formulas in Supplementary Materials). If we assume that the atomic clock accuracy can reach the level of 10⁻¹⁸ (i.e., $u\left(\Delta f/\overline{f}\right)\sim {10}^{-18}$), which is a realistic assumption and will be an achievable technique in the near future, then:

$\Delta W=W_P-W_Q\approx {10}^{-18}{c}^2=0.089\hspace{0.17em}\hspace{0.17em}{m}^2/s^2(\mathrm{5a})$

By considering two clocks at an altitude of $R$ (mean sea level or geoid) and $R+\Delta H$, the gravitational potential difference between two clocks can be written as:

$\Delta W_{PQ}=\frac{GM}{R}-\frac{GM}{R+\Delta H_{PQ}}(\mathrm{5b})$

where GM is the geocentric gravitational constant (398600460.55 ± 0.03) × 10⁶ m³s^-2 according to Amin et al. (2019) and R is the Earth’s mean radius. Finally, assuming the above-mentioned constants, $\Delta H_{PQ}$ is obtained with the accuracy of about 1 cm. It means that if we use a clock with an accuracy of 10⁻¹⁸, heights can be determined in the order of 1 cm.

4 Variations in optical atomic clock measurements

Different effects have to be considered while using atomic clock measurements. The consideration of the gravity potential as constant in time is not sufficient because it is affected by deformations and mass redistributions. Generally, all factors contributing to the Earth’s gravity field changes are sensed by the optical atomic clocks. Time-variable effects in the Earth’s gravity field can be categorized into two groups, namely, tides and non-tidal mass redistributions. The solid Earth tides, ocean tides, solid Earth pole tides, LOD (Length Of the Day) tides, ocean pole tides, and atmospheric tides are different tidal contributors to the Earth’s gravity field changes. On the other hand, non-tidal contributors can be classified as due to atmosphere, oceans, continental water storage, land hydrology, sea level changes, and tectonic and the Glacial Isostatic Adjustment (GIA) induced processes (e.g. see Voigt et al., 2016).

It should be noted that different contributors have different amplitude ranges for continental and inter-continental distances. For instance, the maximum amplitude range for the ocean tides is 0.3 m²/s² for continental and 1.1 m²/s² for inter-continental distances. The land water storage, on the other hand, has a maximum amplitude range 0.1 and 0.2 m²/s² for continental and inter-continental distances, respectively. Moreover, the sea level changes contribute to the Earth’s gravity field changes with a maximum amplitude of 0.01 m²/s²/yr and a secular dominant time scale between laboratory sites over continental scales (Voigt et al., 2016). Figure 3 shows the gravitational potential effect due to GIA using ICE-6G (VM5a) land uplift model (Peltier et al., 2015). The results illustrate that the GIA effect varies between 0.009 and −0.001 m²/s²/yr with a mean value of 0.0003 m²/s²/yr and a standard deviation of 0.001 m²/s²/yr. Moreover, dominant time scales differ from one contributor to another. For instance, it is diurnal and semidiurnal for ocean tides, while the dominant time scale for the land water storage contribution is seasonal (see Voigt et al. (2016) for more detailed information).

FIGURE 3

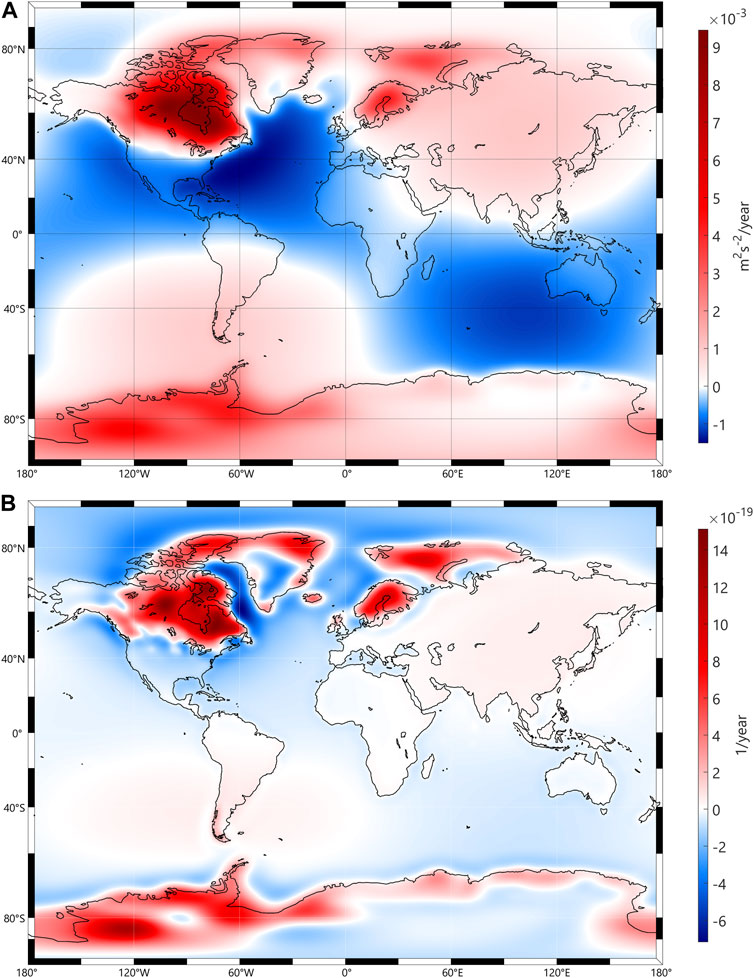
FIGURE 3. (A) Gravitational potential effect due to GIA using ICE-6G (VM5a) land uplift model Peltier et al. (2015) and (B) corresponding effect of the GIA on the relativistic redshift value, i.e., $\Delta f/\overline{f}$ obtained by Eq. 3.

Therefore, additional corrections, due to the tidal and non-tidal variations discussed above, should be considered. Hence, Eq. 4 can be rewritten as:

$H_P-H_Q\approx \frac{\Delta f}{g\overline{f}}{c}^2+e(\mathrm{6a})$

where

$e=e_{tidal}+e_{non-tidal}(\mathrm{6b})$

$e_{tidal}$ contains the tidal effects such as solid Earth tides, ocean tides, solid Earth pole tides, LOD (Length Of the Day) tides, ocean pole tides, and atmospheric tides (in meter). $e_{non-tidal}$ shows non-tidal contributors due to atmosphere, oceans, continental water storage, land hydrology, sea level changes, and tectonic and the GIA induced processes (in meter). For example, the gravitational redshift change due to hydrology loading (seasonal effect) can be written:

$\delta \left(\frac{\Delta f}{\overline{f}}\right)=\frac{\delta H_{hydro}\times g}{c^2}(\mathrm{7a})$

where $\delta H_{hydro}$ is the hydrology loading in meter. Similarly, one can study the effect of GIA on the gravitational redshift by:

$\dot{\left(\frac{\Delta f}{\overline{f}}\right)}=\frac{\dot{H}\times g}{c^2}(\mathrm{7b})$

where $\dot{H}$ is vertical land motion (in meter/year) due to the GIA.

4.1 An example for studying variations in optical atomic clock measurements due to hydrology loading

In this section, we quantify the impact of hydrology loading on the vertical land motions and, consequently, its effect on the atomic clock measurements using existing models. The contribution of hydrological loading in relativistic geodesy applications is studied in three space observatory stations in Fennoscandia, i.e., Onsala (in Sweden), Kiruna (in Sweden), and Metz (in Finland). Figure 4 shows the location of the selected stations.

FIGURE 4

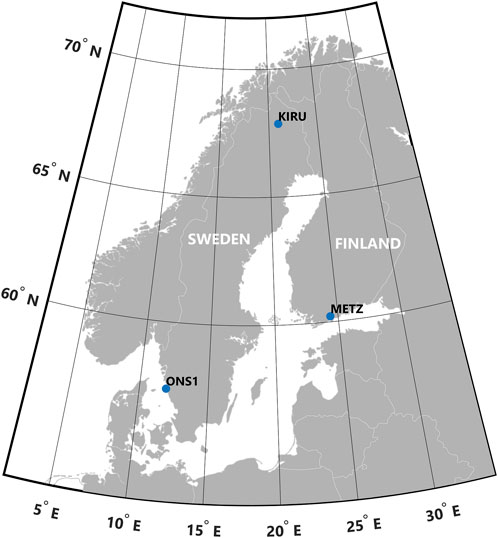
FIGURE 4. Location of selected sites for studying hydrology loading in Fennsocandia. Onsala station ID: ONS1_10402M007 (φ =57.395306° λ=11.9255°); Kiruna station ID: KIRU_10403M002 (φ =67.857306° λ=20.968389°); Metz station ID: METZ_10503M005 (φ =60.217472° λ=24.395333°).

Table 2 shows three different hydrological models and their characteristics that were used in this study. The European Centre for Medium-Range Weather Forecasts (ECMWF) released its most advanced reanalysis product, i.e., the ERA5 dataset since 1979 (cf. Hersbach and Dee, 2016). The ERA5 data are available on the Copernicus Climate Change Service (C3S) Climate Data Store. It contains a better spatial resolution (about a 30 km grid) and is archived at the hourly time step. To compile the ERA5 data, a more advanced assimilation system and more sources of data were used. The second model used in this study is the Global Land Data Assimilation System (GLDAS) model, Noah v2.0. The spatial resolution of GLDAS/Noah v2.0 is about a 27 km grid and is also archived at 3 hours time intervals (Rodell et al., 2004). The GLDAS/Noah v2.0 has provided hydrology data since 2000. In addition, the Modern-Era Retrospective analysis for Research and Applications (MERRA-2), Version 2, was used in this study to assess the impact of hydrology loading on time transfer applications. MERRA-2 has provided hydrology data since 1980. This model is the successor of the MERRA dataset and uses advanced assimilation techniques by employing modern hyperspectral radiance and microwave observations and GPS-Radio Occultation datasets. The spatial resolution remains about the same (about 50 km in the latitudinal direction) as in MERRA. The spatial resolution of MERRA-2 is about a 55 km grid and is also archived at the hourly time step (Gelaro et al., 2017).

TABLE 2

TABLE 2. List of hydrological models used in this study.

The vertical land motions due to the hydrology loading (provided in the Center of Figure (CF)) can be obtained from the loading service hosted by the School and Observatory of Earth Sciences (EOST) at the University of Strasbourg, France (http://loading.u-strasbg.fr/), for the selected stations, i.e., Onsala, Kiruna, and Metz stations. Figure 5 shows the vertical land motions due to hydrology loading obtained from the ERA5 model at the selected stations from 2000 to 2022. Similar plots can be seen in Supplementary Figures S1, S2 using GLDAS/Noah v2.0 and MERRA-2 models. Different models show different fluctuations and displacement amplitudes.

FIGURE 5

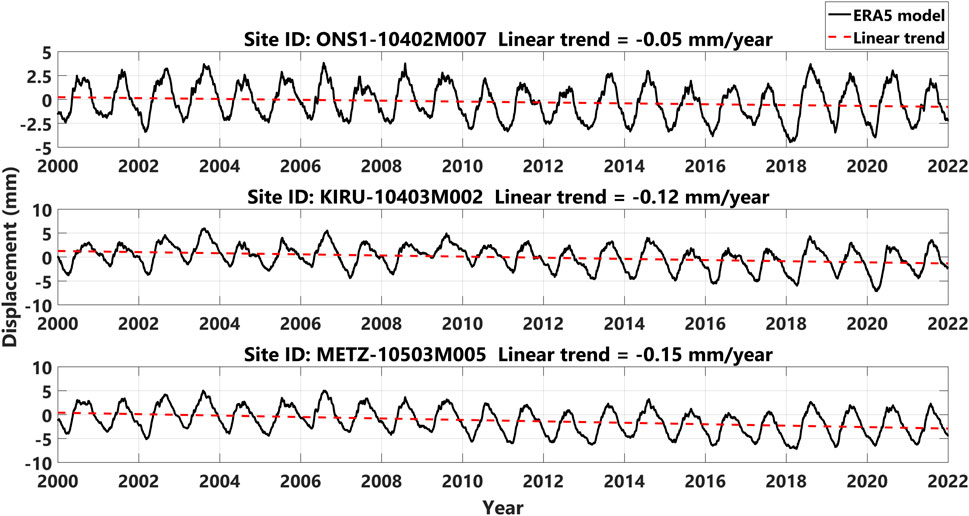
FIGURE 5. Vertical land displacement due to hydrology loading obtained from the ERA5 model in Onsala, Kiruna, and Metz stations.

We focused on the displacements for 2018 to scrutinize the impact of land motions on time transfer with more detail. The reason for selecting the year 2018 is that in the summer of 2018, a large number of wildfires occurred throughout much of Sweden due to extremely high temperatures. This can result in a larger amplitude, compared to other years (in terms of vertical land motion), which can be seen in Figures 5. Figures 6 shows the vertical land displacement due to hydrology loading using the ERA5 model (for 2018). Also, similar plots using MERRA-2 and GLDAS/Noah v2.0 models are presented in Supplementary Figures S3, S4. The ERA5 model shows that, in 2018, Onsala, Kiruna and Metz space observatory stations were experiencing vertical land motion of about 6.9, 8.6 and 8.7 mm/year, respectively.

FIGURE 6

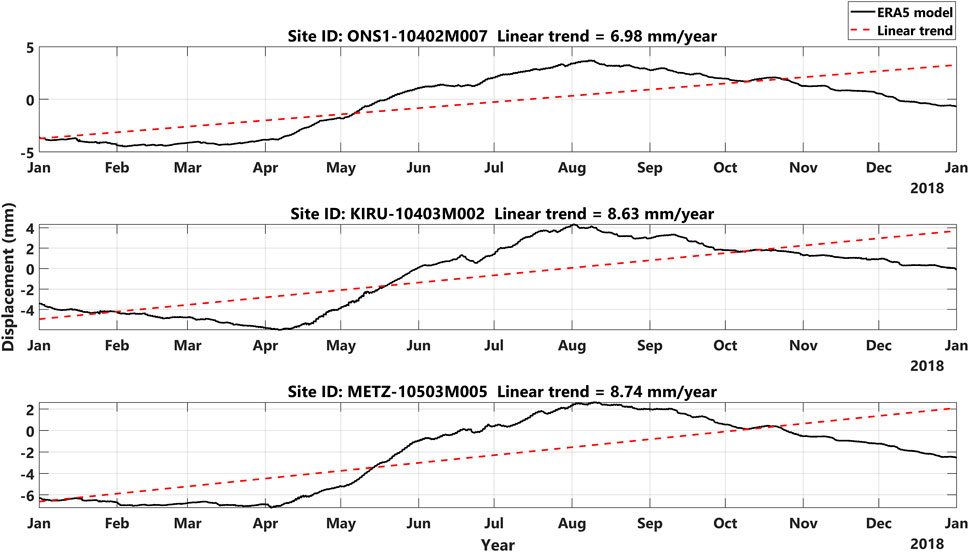
FIGURE 6. Vertical land displacement due to hydrology loading: ERA5 model (for 2018) in Onsala, Kiruna, and Metz stations.

Table 3 presents the maximum and minimum vertical land displacement due to hydrology loading by employing different hydrological models. Generally, the used hydrological models show a similar pattern in the plots. However, peak values are observed at different times. For example, ERA5 and MERRA-2 models that contain the same hydrology data (i.e., soil moisture and snow, see Table 3) show the maximum vertical land displacements on 4 February 2018 at 06:00:00 o’clock and 14 March 2018 at 07:00:00 o’clock, respectively. The numbers in parentheses indicate the effect of hydrology loading on the gravitational redshift obtained by Eq.7a. The results (peak values) show that the hydrology loading (using the ERA5 model) influences the gravitational redshift about −4.4 to −7.8 $\times {10}^{-19}$ in winter and 2.9 to 4.7 $\times {10}^{-19}$ in summer. However, these peak values are different by employing other hydrological models. For example, the impact of hydrology loading (using the GLDAS2 and MERRA2 models) can reach to 9 $\times {10}^{-19}$ in Metz station, which is close to the uncertainty that we are seeking in relativistic geodesy applications (i.e., ${10}^{-18}$). Therefore, the effect of hydrological loading should be considered if the atomic clocks are used at different periods.

TABLE 3

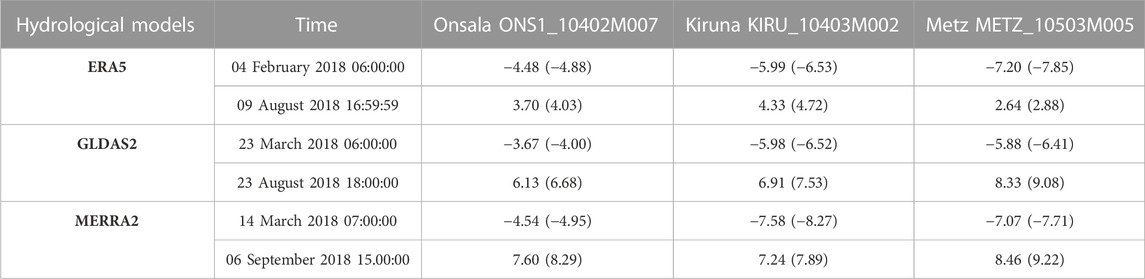
TABLE 3. Maximum and minimum vertical land displacement (in mm) due to hydrology loading using different hydrological models in selected stations (the values in parentheses show the effect of loading on the gravitational redshift $\times {10}^{-19}$).

However, typical vertical land motions are caused not only by the hydrology loading but also by landslides, land subsidence and uplift, volcanic and tectonic deformations. The interferometric synthetic aperture radar (InSAR) technique is a remote sensing technique that can monitor ground motions. It uses two or more synthetic aperture radar (SAR) images to generate maps of ground motions. The uncertainty of obtained vertical land motions, using InSAR technique, can be improved by using corner reflectors in the desired stations. For example, Figures 7, 8 show the vertical land motions obtained from InSAR in Onsala and Kiruna stations using the Swedish ground motion service (https://insar.rymdstyrelsen.se/) or the European Ground Motion Service (https://egms.land.copernicus.eu/). The data gaps between November to March are due to the snow cover.

FIGURE 7

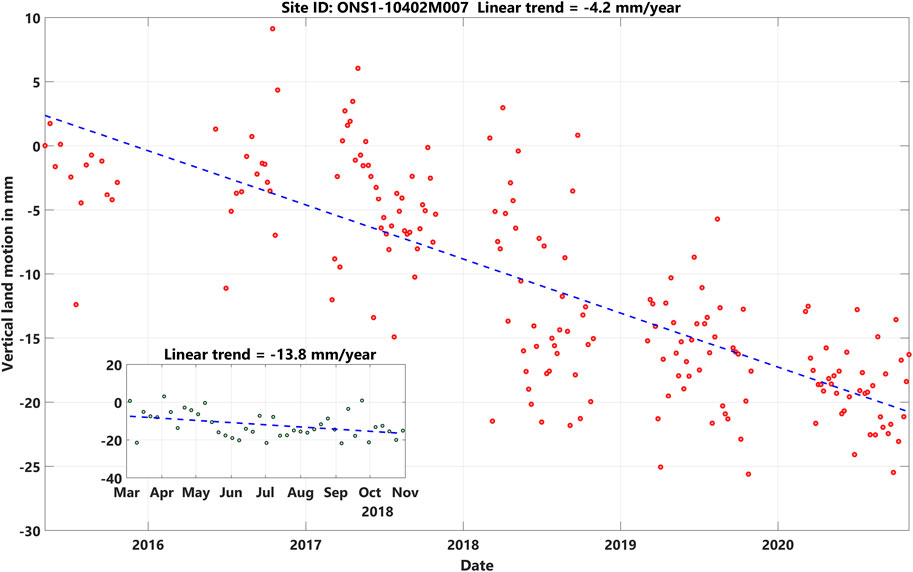
FIGURE 7. Vertical land displacement obtained from InSAR technique in Onsala station between 09th of June 2015 and 28th of October 2020 (the subplot shows the vertical displacements in 2018).

FIGURE 8

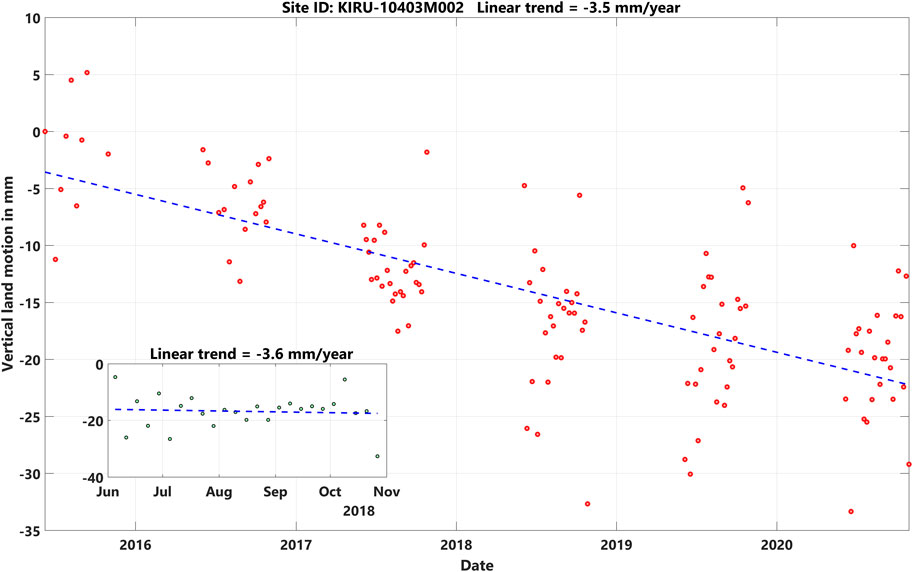
FIGURE 8. Vertical land displacement obtained from InSAR technique in Kiruna station between 09th of June 2015 and 28th of October 2020 (the subplot shows the vertical displacements in 2018).

4.2 Validating the performance of optical clocks: A standard geodetic approach

Optical clocks are expected to determine precise height differences of points according to Eqs 4–7b. Millimeter/submillimeter level of accuracy (order of 10⁻¹⁹ and 10⁻²⁰) is claimed in Raupach and Grosche, (2014); Raupach et al. (2015) for the stability of the optical frequency time transfer. However, one should validate these claims through practical tests which compare accurately determined height differences (with submillimetre accuracy level) with the height differences resulting from the optical clock networks. Denker et al. (2018) proposed a method to utilize precise levelling benchmarks in France and Germany to validate the performance of the optical fiber link between points in the two countries. This method, due to the error sources mentioned in Denker et al. (2018) such as uncertainties because of utilizing GNSS measurements, sprite leveling, geoid models, etc., is not accurate to millimeter/submillimeter level.

Our suggestion is the use of a baseline with a length of tens of meters and a height difference of a few meters, of which the height difference is measured by precise levelling at better than 1 mm accuracy. Then measure the redshift due to the height difference by utilizing two coherent atomic clocks A and B, for example, as proposed in Figure 1 of McGrew et al. (2018) (see also Figure 9 below). The two coherent clocks A and B are the clocks driven from clock O and show exactly the same time when they are at a strictly horizontal plane.

FIGURE 9

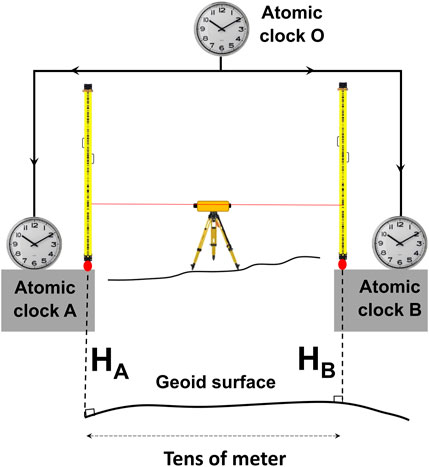
FIGURE 9. An example of a baseline for validating the performance of optical clocks (Not drawn to scale).

In such a network, the height difference between two atomic clocks at the two ends of the base-line vector could be measured with the accuracy of better than 1 mm by special spirit (precise) leveling. This height difference is a suitable tool to verify if the claimed accuracy of the optical clock network is valid. Eq. 8 reveals the functional model of the above suggestion:

$‖\Delta H_{AB}^{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}}-\Delta H_{AB}^{\mathrm{A}\mathrm{t}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}‖\le 1\mathrm{m}\mathrm{m}(8)$

where $\Delta H$ is the height difference. One can validate the clocks and the network performance in the same time by taking the points A and B so that they form the misclosure vector of a loop of the clocks’ network.

5 Conclusion

This study aimed to explore applications of relativistic (clock-based) geodesy and to delineate boundaries and challenges for realization of global geodetic infrastructure, which can be applied for vertical datum unification or realization of height systems in geodesy. At first, an initial review of relativistic geodesy and optical atomic clocks was given to document the state-of-the-art development. After that, the theoretical background of relativistic geodesy was briefly explained. In addition, we reviewed different types of clock networks and time transfer techniques. According to the gravity frequency shift equation, the accuracy of time-frequency transfer directly affects the accuracy of the determined gravitational potential difference and elevation difference. Moreover, we suggested a method for validating the performance of optical clocks by employing the precise leveling technique. In addition, we quantified and reviewed variations in optical atomic clock measurements. In other words, the tidal and non-tidal effects on atomic clocks were discussed. We also studied the effects of vertical land motions and hydrology loading in more detail in this paper. The variations in optical atomic clock measurements due to hydrology loading were studied in three space observatory stations in Fennoscandia, i.e., Onsala and Kiruna (in Sweden), and Metz (in Finland), using three hydrological models (i.e., ERA5, GLDAS2 and MERRA2 models). The results showed that the influence of the hydrological loading is close to the uncertainty we are seeking in relativistic geodesy applications (i.e., ${10}^{-18}$). Therefore, the effect of hydrological loading should be considered if the relativistic geodesy technique is used/repeated at different times. InSAR technique and using (passive or active) corner reflectors can play an essential role in determining the vertical land motions for this purpose.

Author contributions

MB: Conceptualization, Methodology, Investigation, Visualization, Writing–original draft, Writing–review and editing, Supervision. MS: Methodology, Investigation, Writing–review and editing. HA: Investigation, Visualization, Writing–review and editing. MH: Investigation, Writing–review and editing. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1139211/full#supplementary-material

References

Akatsuka, T., Ono, H., Hayashida, K., Araki, K., Takamoto, M., Takano, T., et al. (2014). 30-km-long optical fiber link at 1397 nm for frequency comparison between distant strontium optical lattice clocks. Jpn. J. Appl. Phys. 53 (3), 032801. doi:10.7567/jjap.53.032801

CrossRef Full Text | Google Scholar

Al-Masoudi, A., Dörscher, S., Häfner, S., Sterr, U., and Lisdat, C. (2015). Noise and instability of an optical lattice clock. Phys. Rev. A 92 (6), 063814. doi:10.1103/physreva.92.063814

CrossRef Full Text | Google Scholar

Allan, D. W., and Barmes, J. A. (1981). A modified allan variance with increased oscillator characterization abitity. Proc. 35th Annual Frequency Control Symposium.

Google Scholar

Allan, D. W., and Weiss, M. A. (1980). “Accurate time and frequency transfer during common-view of a GPS satellite,” in 34th Annual Symposium on Frequency Control, Philadelphia, PA, USA, 28-30 May 1980, 334–346.

CrossRef Full Text | Google Scholar

Amin, H., Sjöberg, L. E., and Bagherbandi, M. (2019). A global vertical datum defined by the conventional geoid potential and the Earth ellipsoid parameters. J. Geodesy 93 (10), 1943–1961. doi:10.1007/s00190-019-01293-3

CrossRef Full Text | Google Scholar

Bjerhammar, A. (1975). Discrete solutions of the boundary value problem in physical geodesy. Tellus 27 (2), 97–106. doi:10.3402/tellusa.v27i2.9892

CrossRef Full Text | Google Scholar

Bjerhammar, A. (1985). On a relativistic geodesy. Bull. Géodésique 59 (3), 207–220. doi:10.1007/bf02520327

CrossRef Full Text | Google Scholar

Blair, B. E. (1974). Time and frequency: Theory and fundamentals. NBS Monogr. 140, 459.

Google Scholar

Bloom, B. J., Nicholson, T. L., Williams, J. R., Campbell, S. L., Bishof, M., Zhang, X., et al. (2014). An optical lattice clock with accuracy and stability at the 10− 18 level. Nature 506 (7486), 71–75. doi:10.1038/nature12941

PubMed Abstract | CrossRef Full Text | Google Scholar

Bondarescu, R., Bondarescu, M., Hetényi, G., Boschi, L., Jetzer, P., and Balakrishna, J. (2012). Geophysical applicability of atomic clocks: Direct continental geoid mapping. Geophys. J. Int. 191 (1), 78–82. doi:10.1111/j.1365-246x.2012.05636.x

CrossRef Full Text | Google Scholar

Bouman, J. (2012). Relation between geoidal undulation, deflection of the vertical and vertical gravity gradient revisited. J. Geodesy 86 (4), 287–304. doi:10.1007/s00190-011-0520-9

CrossRef Full Text | Google Scholar

Brumberg, V. A., and Kopejkin, S. M. (1989b). Relativistic reference systems and motion of test bodies in the vicinity of the Earth. Nuovo Cim. B Ser. 11, 63–98. doi:10.1007/bf02888894

CrossRef Full Text | Google Scholar

Brumberg, V. A., and Kopejkin, S. M. (1989a). Relativistic theory of celestial reference frames. Ref. Fram. Astron. Geophys. 154, 115–141.

CrossRef Full Text | Google Scholar

Brumberg, V. A., and Kopejkin, S. M. (1990). Relativistic time scales in the solar system. Celest. Mech. Dyn. Astron. 48, 23–44. doi:10.1007/bf00050674

CrossRef Full Text | Google Scholar

Chou, C., Hume, D. B., Koelemeij, J. C. J., Wineland, D. J., and Rosenband, T. (2010). Frequency comparison of two high-accuracy Al+ optical clocks. Phys. Rev. Lett. 104 (7), 070802. doi:10.1103/physrevlett.104.070802

PubMed Abstract | CrossRef Full Text | Google Scholar

Delva, P., and Lodewyck, J. (2013). “Atomic clocks: New prospects in metrology and geodesy,” in Proceedings of the Workshop "Relativistic Positioning Systems and their Scientific Applications" held in Brdo near Kranj, Slovenia, 19-21 September 2012. ArXiv Preprint ArXiv:1308.6766.

Google Scholar

Denker, H., Timmen, L., Voigt, C., Weyers, S., Peik, E., Margolis, H. S., et al. (2018). Geodetic methods to determine the relativistic redshift at the level of 10^-18 in the context of international timescales: A review and practical results. J. Geodesy 92 (5), 487–516. doi:10.1007/s00190-017-1075-1

CrossRef Full Text | Google Scholar

Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., et al. (2017). The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 30 (14), 5419–5454. doi:10.1175/jcli-d-16-0758.1

CrossRef Full Text | Google Scholar

Griggs, E., Kursinski, E. R., and Akos, D. (2015). Short-term GNSS satellite clock stability. Radio Sci. 50 (8), 813–826. doi:10.1002/2015RS005667

CrossRef Full Text | Google Scholar

Haas, R. (2020). Clock comparison using black holes. Nat. Phys. 17 (2), 164–165. doi:10.1038/s41567-020-01071-5

CrossRef Full Text | Google Scholar

Heavner, T. P., Jefferts, S. R., Donley, E. A., Shirley, J. H., and Parker, T. E. (2004). “Recent improvements in NIST-fl and resulting accuracies of δf/f< 7x10^-16,” in 2004 Conference on Precision Electromagnetic Measurements, London, UK, 27 June 2004 - 02 July 2004, 498–499. doi:10.1109/CPEM.2004.305330

CrossRef Full Text | Google Scholar

Hersbach, H., and Dee, D. (2016). “ERA5 reanalysis is in production,” in ECMWF newsletter, 147 (Reading, UK: ECMWF).

Google Scholar

Hinkley, N., Sherman, J. A., Phillips, N. B., Schioppo, M., Lemke, N. D., Beloy, K., et al. (2013). An atomic clock with 10–18 instability. Science 341 (6151), 1215–1218. doi:10.1126/science.1240420

PubMed Abstract | CrossRef Full Text | Google Scholar

Hobiger, T., Rieck, C., Haas, R., and Koyama, Y. (2015). Combining GPS and VLBI for inter-continental frequency transfer. Metrologia 52 (2), 251–261. doi:10.1088/0026-1394/52/2/251

CrossRef Full Text | Google Scholar

Hollberg, L. (2005). “Optical atomic clocks: A revolution in performance,” in Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22-27 May 2005.

CrossRef Full Text | Google Scholar

Hong, F.-L., Musha, M., Takamoto, M., Inaba, H., Yanagimachi, S., Takamizawa, A., et al. (2009). Measuring the frequency of a Sr optical lattice clock using a 120 km coherent optical transfer. Opt. Lett. 34 (5), 692–694. doi:10.1364/ol.34.000692

PubMed Abstract | CrossRef Full Text | Google Scholar

Huntemann, N., Sanner, C., Lipphardt, B., Tamm, C., and Peik, E. (2016). Single-ion atomic clock with 3× 10− 18 systematic uncertainty. Phys. Rev. Lett. 116 (6), 063001. doi:10.1103/physrevlett.116.063001

PubMed Abstract | CrossRef Full Text | Google Scholar

JCGM (2008). Evaluation of measurement data—guide to the expression of uncertainty in measurement. Geneva, Switzerland: international organization for standardization.

Google Scholar

Kawasaki, A. (2021). Gravitational dephasing in optical lattice clocks. ArXiv Preprint ArXiv:2107.02405. Available at: https://arxiv.org/abs/2107.02405v1.

Google Scholar

Koller, S. B., Grotti, J., Al-Masoudi, A., Dörscher, S., Häfner, S., Sterr, U., et al. (2017). Transportable optical lattice clock with 7× 10− 17 uncertainty. Phys. Rev. Lett. 118 (7), 73601.

CrossRef Full Text | Google Scholar

Le Targat, R., Lorini, L., Le Coq, Y., Zawada, M., Guéna, J., Abgrall, M., et al. (2013). Experimental realization of an optical second with strontium lattice clocks. Nat. Commun. 4 (1), 2109–9. doi:10.1038/ncomms3109

PubMed Abstract | CrossRef Full Text | Google Scholar

Lisdat, C., Grosche, G., Quintin, N., Shi, C., Raupach, S. M. F., Grebing, C., et al. (2016). A clock network for geodesy and fundamental science. Nat. Commun. 7 (1), 12443–12447. doi:10.1038/ncomms12443

PubMed Abstract | CrossRef Full Text | Google Scholar

Lombardi, M. A. (2016). Evaluating the frequency and time uncertainty of GPS disciplined oscillators and clocks. NCSLI Meas. 11 (3–4), 30–44. doi:10.1080/19315775.2017.1316696

CrossRef Full Text | Google Scholar

Lombardi, M. A. (2012). The evolution of time measurement, Part 4: The atomic second [Recalibration]. IEEE Instrum. Meas. Mag. 15 (1), 47–51. doi:10.1109/MIM.2012.6145262

CrossRef Full Text | Google Scholar

Lopez, O., Haboucha, A., Chanteau, B., Chardonnet, C., Amy-Klein, A., and Santarelli, G. (2012). Ultra-stable long distance optical frequency distribution using the Internet fiber network. Opt. Express 20 (21), 23518–23526. doi:10.1364/oe.20.023518

PubMed Abstract | CrossRef Full Text | Google Scholar

Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E., and Schmidt, P. O. (2015). Optical atomic clocks. Rev. Mod. Phys. 87 (2), 637–701. doi:10.1103/revmodphys.87.637

CrossRef Full Text | Google Scholar

Ma, C., Clark, T. A., Ryan, J. W., Herring, T. A., Shapiro, I. I., Corey, B. E., et al. (1986). Radio-source positions from VLBI. Astronomical J. 92, 1020–1029. doi:10.1086/114232

CrossRef Full Text | Google Scholar

McGrew, W. F., Zhang, X., Fasano, R. J., Schäffer, S. A., Beloy, K., Nicolodi, D., et al. (2018). Atomic clock performance enabling geodesy below the centimetre level. Nature 564 (7734), 87–90. doi:10.1038/s41586-018-0738-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehlstäubler, T. E., Grosche, G., Lisdat, C., Schmidt, P. O., and Denker, H. (2018). Atomic clocks for geodesy. Rep. Prog. Phys. 81 (6), 064401. doi:10.1088/1361-6633/aab409

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, J., Dirkx, D., Kopeikin, S. M., Lion, G., Panet, I., Petit, G., et al. (2018). High performance clocks and gravity field determination. Space Sci. Rev. 214 (1), 5. doi:10.1007/s11214-017-0431-z

CrossRef Full Text | Google Scholar

Nicholson, T. L., Campbell, S. L., Hutson, R. B., Marti, G. E., Bloom, B. J., McNally, w, R. L., et al. (2015). Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Lond. 6, 6896. doi:10.1038/ncomms7896

PubMed Abstract | CrossRef Full Text | Google Scholar

Pail, R. (2014). in CHAMP-, GRACE-, GOCE-satellite projects BT - encyclopedia of geodesy. Editor E. Grafarend (Cham: Springer International Publishing), 1–11. doi:10.1007/978-3-319-02370-0_29-1

CrossRef Full Text | Google Scholar

Peltier, W. R., Argus, D. F., and Drummond, R. (2015). Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 120 (1), 450–487. doi:10.1002/2014jb011176

CrossRef Full Text | Google Scholar

Petrov, A. A., Davydov, V. v., Zalyotov, D. v., Shabanov, V. E., and Shapovalov, D. v. (2018). Features of direct digital synthesis applications for microwave excitation signal formation in quantum frequency standard on the atoms of cesium. J. Phys. Conf. Ser. 1124, 041004. IOP Publishing Ltd. doi:10.1088/1742-6596/1124/4/041004

CrossRef Full Text | Google Scholar

Pizzocaro, M., Sekido, M., Takefuji, K., Ujihara, H., Hachisu, H., Nemitz, N., et al. (2020). Intercontinental comparison of optical atomic clocks through very long baseline interferometry. Nat. Phys. 17, 223–227. doi:10.1038/s41567-020-01038-6

CrossRef Full Text | Google Scholar

Predehl, K., Grosche, G., Raupach, S. M. F., Droste, S., Terra, O., Alnis, J., et al. (2012). A 920-kilometer optical fiber link for frequency metrology at the 19th decimal place. Science 336 (6080), 441–444. doi:10.1126/science.1218442

PubMed Abstract | CrossRef Full Text | Google Scholar

Raupach, S. M. F., and Grosche, G. (2014). Chirped frequency transfer: A tool for synchronization and time transfer. IEEE Trans. Ultrasonics, Ferroelectr. Freq. Control 61 (6), 920–929. doi:10.1109/tuffc.2014.2988

PubMed Abstract | CrossRef Full Text | Google Scholar

Raupach, S. M. F., Koczwara, A., and Grosche, G. (2015). Brillouin amplification supports 1× 10− 20 uncertainty in optical frequency transfer over 1400 km of underground fiber. Phys. Rev. A 92 (2), 021801. doi:10.1103/physreva.92.021801

CrossRef Full Text | Google Scholar

Rieck, C., Haas, R., Jaldehag, K., and Johansson, J. (2010b). VLBI time-transfer using CONT08 data. EFTF 2010 - 24th Eur. Freq. Time Forum 46 (2), 6533654. doi:10.1109/EFTF.2010.6533654

CrossRef Full Text | Google Scholar

Rieck, C., Haas, R., Jaldehag, R. T., and Johansson, J. M. (2010a). “VLBI and GPS-based time-transfer using CONT08 data,” in Proceedings of the 6th IVS General Meeting, 365–369.

Google Scholar

Riehle, F. (2017). Optical clock networks. Nat. Photonics 11 (1), 25–31. doi:10.1038/nphoton.2016.235

CrossRef Full Text | Google Scholar

Rodell, M., Houser, P., Peters-Lidard, C., Kato, H., Kumar, S., Gottschalck, J., et al. (2004). “NASA/NOAA’s global land data assimilation system (GLDAS): Recent results and future plans,” in Proc. ECMWF/ELDAS workshop on land surface assimilation (United Kingdom: ECMWF), 61–68.

Google Scholar

Sánchez, L., Čunderlík, R., Dayoub, N., Mikula, K., Minarechová, Z., Šíma, Z., et al. (2016). A conventional value for the geoid reference potential $$W_{0}$$ W 0. J. Geodesy 90 (9), 815–835. doi:10.1007/s00190-016-0913-x

CrossRef Full Text | Google Scholar

Sjöberg, L. E., and Bagherbandi, M. (2017). Gravity inversion and integration. New York: Springer.

Google Scholar

Soffel, M., Klioner, S. A., Petit, G., Wolf, P., Kopeikin, S. M., Bretagnon, P., et al. (2003). The IAU 2000 resolutions for astrometry, celestial mechanics, and metrology in the relativistic framework: Explanatory supplement. Astronomical J. 126 (6), 2687–2706. doi:10.1086/378162

CrossRef Full Text | Google Scholar

Takamoto, M., Hong, F.-L., Higashi, R., and Katori, H. (2005). An optical lattice clock. Nature 435 (7040), 321–324. doi:10.1038/nature03541

PubMed Abstract | CrossRef Full Text | Google Scholar

Takano, T., Takamoto, M., Ushijima, I., Ohmae, N., Akatsuka, T., Yamaguchi, A., et al. (2016). Geopotential measurements with synchronously linked optical lattice clocks. Nat. Photonics 10 (10), 662–666. doi:10.1038/nphoton.2016.159

CrossRef Full Text | Google Scholar

Takiguchi, H., Hobiger, T., Ishii, A., Ichikawa, R., and Koyama, Y. (2007). Comparison with GPS time transfer and VLBI time transfer. IVS NICT-TDC News 28, 10–15.

Google Scholar

Teunissen, P., and Montenbruck, O. (2017). Springer handbook of global navigation satellite systems. Cham, Switzerland: Springer International Publishing.

Google Scholar

Vermeer, M. (1983). Chronometric levelling. Geodetiska Institutet: Geodeettinen Laitos.

Google Scholar

Voigt, C., Denker, H., and Timmen, L. (2016). Time-variable gravity potential components for optical clock comparisons and the definition of international time scales. Metrologia 53 (6), 1365–1383. doi:10.1088/0026-1394/53/6/1365

CrossRef Full Text | Google Scholar

Wang, P., Wang, G., Gao, Y., Cai, H., and Liu, N. (2019). Comparison of VLBI and GNSS common view for time transfer. Int. J. Metrology Qual. Eng. 10, 15. doi:10.1051/ijmqe/2019014

CrossRef Full Text | Google Scholar

Williams, P. A., Swann, W. C., and Newbury, N. R. (2008). High-stability transfer of an optical frequency over long fiber-optic links. JOSA B 25 (8), 1284–1293. doi:10.1364/josab.25.001284

CrossRef Full Text | Google Scholar