Study on the time-varying fatigue reliability of the invert structure of subway tunnel under the action of train loads

Introduction: The present study examines the fatigue reliability of subway tunnel invert structures subjected to train-induced loads, a critical factor in ensuring the safety and longevity of these vital infrastructures.

Methods: By integrating higher-order moment theory, fatigue equations, and cumulative damage theory, this research analyzes the impact of train loads on invert structures, taking into account factors such as tension stress, compression stress, train axle weight, speed, and lining thickness.

Results: The findings indicate that the reinforcement of the invert structure is required under tension stress, while it is not necessary for compression stress. Notably, the train’s axle weight and speed exert a significant influence on the fatigue reliability index, with speed displaying a marginally greater effect than axle weight. Conversely, the lining thickness demonstrates a negligible impact on the reliability index. As time progresses, the fatigue reliability index diminishes, resulting in an elevated probability of failure.

Discussion: In light of these findings, it is imperative to conduct regular inspections and maintain the tensile state of the invert structure, which warrants the most attention. To safeguard the safety and longevity of subway tunnel invert structures, it is essential to concentrate on the aspects related to tensile stress and closely monitor train loads, specifically axle weight and speed.

1 Introduction

The tunnel is an integral component of highway and railroad engineering construction projects (Zhou et al., 2020). Scholars have made significant progress in tunnel engineering theory over the past few decades. This research topic has shifted from deterministic research (Shi et al., 2021; Wang et al., 2022; Zhou et al., 2023) to randomness and uncertainty (Chen et al., 2014), which better reflect the realistic issues of underground engineering. As a result, most tunnel engineering research has become closely associated with reliability theory, which has become a significant subject of research, spanning the construction and operation periods. During the operation period, the tunnel is primarily subjected to dynamic cyclic train loads over an extended period, leading to deterioration of the structure beneath the rails.

In the field of engineering, various factors such as soil parameters, train loads, lining structure, and surrounding rock pressure can impact the fatigue of structures, and these effects are often unpredictable and unknown. In order to ensure the safety and reliability of subway tunnel components during operation, it is crucial to consider the randomness and uncertainty of these factors and conduct a reliability study based on the establishment of fatigue performance functions. Reliability methods are founded on the principles of probability theory. These methods involve randomly selecting parameters in a model and using these parameters to calculate the established reliability model, thus determining the reliability index and the likelihood of failure. When dealing with practical engineering problems, it is necessary to consider multiple random factors and utilize appropriate reliability methods, such as the first-order reliability method (FORM), the second-order reliability method (SORM) (Fattahi and Jiryaee, 2022), the Monte Carlo method (Xie et al., 2022), and the response surface method (Li and Yang, 2019), to calculate the reliability indices for different research objects. Examples have shown that the reliability technique is more aligned with real-world conditions as it takes into account the force situation in a complex geological environment.

The application of reliability theory to engineering problems dates back to early times, but its use in tunnel engineering was first proposed by Rosenblueth and Esteva (1972). They used reliability methods based on performance functions and determined the probability of failure in tunnel structures by assuming the type of distribution of random variables. In 1985, Ellingwood and Hwang conducted research on the reliability method and applied it in the safety analysis of geotechnical engineering (Ellingwood and Hwang, 1985). Laso et al. (1995) used the method to perform a reliability analysis of the tunnel support system and evaluated its safety based on the obtained failure probability. Lü and Low (2011) utilized the reliability method in the stability analysis of tunnel structural systems and established a stochastic polynomial model for the safety analysis of tunnel structures. Mollon et al. (2009) and Mollon et al. (2011) improved the traditional reliability method by using a quadratic polynomial model to calculate the failure probability of tunnel structures (Mollon et al., 2009; Mollon et al., 2011). Chen et al. (2014) improved the response surface method and the first-second-order moment method to calculate the safety of tunnels during construction. They confirmed the superiority of the improved method over traditional methods.

The reliability analysis methods mentioned above mainly focus on the stability of the surrounding rock, support systems, and settlement changes during the construction period of tunnels. However, during the tunnel operation period, the degradation of the structural components under train loads must also be considered. This idea is known as time-varying reliability. There are few studies that address this aspect. For example, Mori and Ellingwood (1993) examined the time-varying characteristics of external loads and simplified them to a stochastic process. The results of their predictions provided a theoretical foundation for the life prediction of similar bridge structures in service. Qing Li (2004) reviewed the current time-varying reliability methods and proposed several improved methods for the reliability index of time-varying degradation of bridge junction performance under chloride salt attack in coastal areas. Frangopol et al. (1997) conducted a study on the time-varying reliability of concrete girder bridges in service in the United States, proposing a time-varying resistance decay model. This model was integrated into the flexural and shear load capacity model of reinforced concrete bridges, resulting in accurate predictions. Val and Melchers (1996) used a similar reliability method to determine the time-varying laws of reinforced concrete slab bridges under the influence of specific parameters.

The reliability of tunnels has been studied by several researchers using various approaches. However, each method has its own strengths and limitations when applied to engineering problems. It is crucial to consider the actual engineering background while selecting the reliability method. The primary stress pattern during the tunnel’s operational phase is the cyclic train loads over a long period of time. Hence, the analysis of the tunnel structure’s reliability should consider not only the structural time-variability but also the randomness and uncertainty of the factors that influence it. Despite numerous studies on bridge structures, there are relatively fewer studies on tunnel structures. This highlights the need for research on subway tunnels. The present study aims to investigate the time-dependent reliability analysis of the structure under subway train loads. The goal is to determine the limit state function of fatigue failure of the invert structure, which is subjected to the combined action of train loads and surrounding rock pressure. The study also proposes a new time-varying reliability calculation method based on high-order moment theory.

2 Performance function of structures

The commonly used reliability methods for structural analysis include the First-Order Reliability Method (FORM), the Second-Order Reliability Method (SORM), the Monte Carlo Method, the Response Surface Method, and the higher-order Moment Theory. A review of existing literature shows that the higher-order Moment Theory is characterized by its high computational efficiency, accuracy, and wide application in engineering structural reliability analysis. In this paper, we adopt the Moment Method to analyze the time-varying reliability of the invert structure of subway tunnels under long-term dynamic fatigue loads. The study obtains the time-varying fatigue reliability index and failure probability of the invert structure under compression and tension and identifies the relationship between the fatigue reliability index and the service deterioration index of the invert structure. This research provides a new idea for the reliability calculation of the invert structure of subway tunnels and provides theoretical support for the evaluation of the service state of subway tunnel structures.

It is relatively convenient to obtain parameters for reliability analysis of the structure using the first-order second-moment theory. However, the method requires repeated iterative verification, which has minor computational efficiency and accuracy. Theoretically, the higher order, the higher the calculation accuracy. Structure engineering problems are much more complex, and various factors should be considered. Hence, establishing the performance functions is more complicated, and the computational difficulty and computation time will sharply increase. Currently, some scholars have proposed a higher-order moment theory that can better solve more complex issues with high computational efficiency and accuracy (Rosenblueth, 1975; Zhao and Ono, 2000; Zhao and Ono, 2001; Zhao et al., 2006). Therefore, this paper will use a higher-order moment method to analyze the time-varying fatigue reliability of the invert structure of subway tunnels.

The typical fatigue life curve (S-N curve) is shown in Figure 1. It can be separated into three fatigue areas with various tendencies of variation, i.e., low-cycle fatigue, high-cycle fatigue, and sub-fatigue. Different parts of the S-N curve can be fitted using various fitting functions, which include the exponential function equation, power function equation, three-parameter equation, four-parameter equations, etc. The subway tunnel is an important transportation facility with a high frequency of use, and the stress state of its invert structure is much lower than the strength limit of the concrete material. Hence, it is in line with the high-cycle fatigue, which will be the focus of this paper.

FIGURE 1

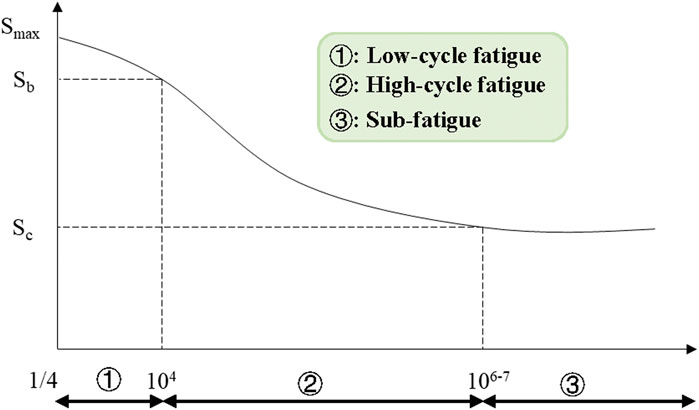
FIGURE 1. Typical fatigue life curve (S-N curve) (Shiozawa et al., 2001).

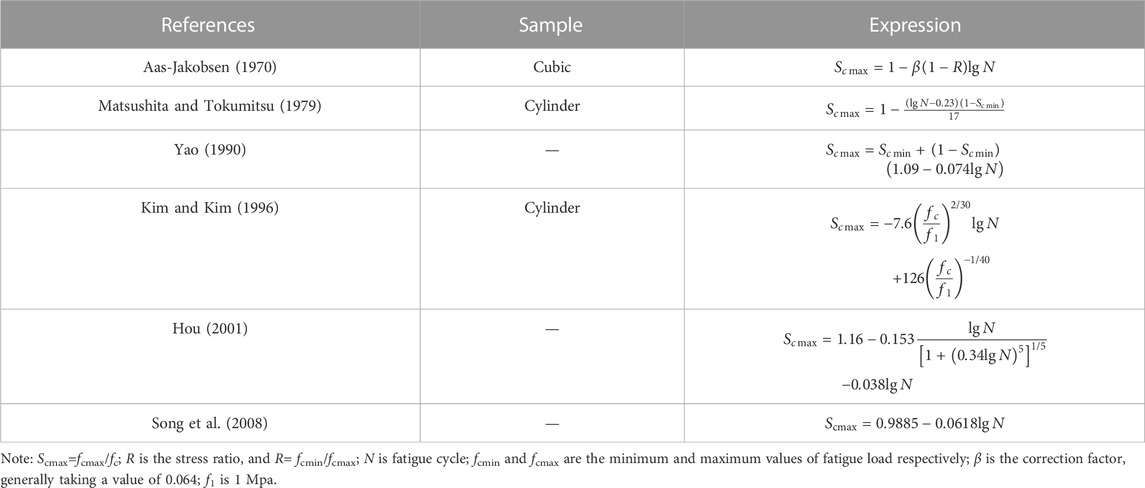
Figure 2 compares the results of the fatigue equation for concrete under different compression and tension conditions (as listed in Tables 1, 2) where the stress level is dimensionless. As shown in Figure 2A, with the increase in fatigue cycles, the stress level calculated by the concrete fatigue equation for each stress condition slowly and linearly decreases. However, the stress level calculated by Kim and Kim (1996) is greater than 1, while the other equations result in stress levels less than 1, indicating that concrete stress levels generally decrease with fatigue cycles. Considering the fatigue characteristics of subway tunnel structures, the results obtained from Song et al. (2008) are more consistent with the research object, have a clearer formula, and are more convenient for engineering applications. The predicted results are also conservative and in line with the fatigue stress state of subway tunnel structures, ensuring service safety. Although the stress level obtained by Hou (2001) fatigue equation is lower, it underestimates the fatigue stress level of subway tunnel structures. The formula proposed by Song et al. (2008) can be used to study the time-varying fatigue reliability of the subway tunnel under-track structure.

FIGURE 2

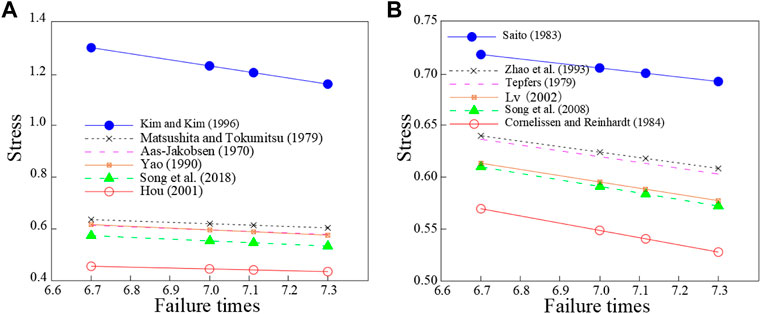
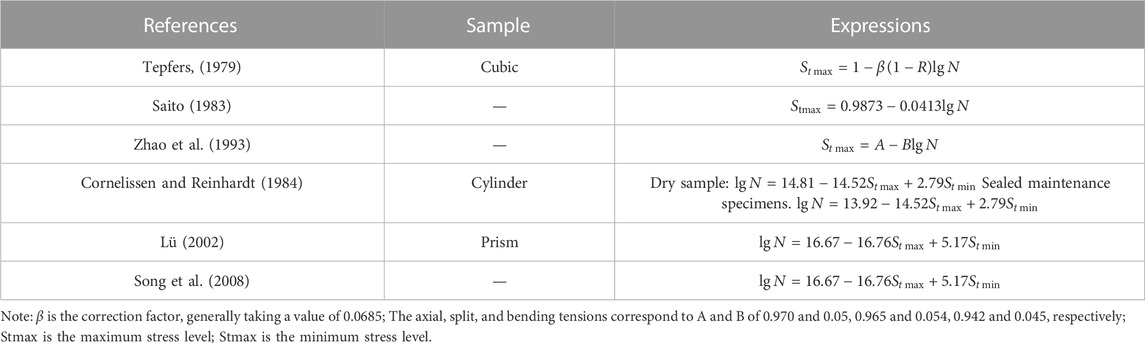
FIGURE 2. Comparative analysis of fatigue equation results for concrete under (A) compression conditions (Aas-Jakobsen, 1970; Matsushita and Tokumitsu, 1979; Yao, 1990; Kim and Kim, 1996; Hou, 2001; Song et al., 2008); and (B) tension conditions (Song et al., 2008; Tepfers, 1979; Saito, 1983; (Zhao et al., 1993) (Cornelissen and Reinhardt, 1984) (Lü, 2002).

TABLE 1

TABLE 1. Arrangement of fatigue equations of concrete under compression condition.

TABLE 2

TABLE 2. Arrangement of fatigue equation of concrete under tensile condition.

By analyzing the above results, the fatigue equation for concrete under pressure state proposed by Song et al. (2008) is used for the establishment of the fatigue function of the structure under the rail of the subway tunnel, and the expression of the equation is as follows:

$S_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}=0.9885-0.0618\lg N(1)$

Where S_cmax is the maximum compressive stress of concrete; N is the number of fatigue cycles.

In Figure 2B, the stress level calculated by the concrete fatigue equation in each tensile state decreases linearly as the number of fatigue cycles increases. Similar to the results obtained in the compressed state, the stress level in the tensile state is generally less than 1, consistent with the actual engineering situation. It is found that the stress level obtained from the concrete fatigue equation calculation by Cornelissen is too conservative, which may cause misjudgment of the fatigue calculation results of subway tunnel structures. The fatigue equation proposed by Song et al. (2008), as expressed in Eq. 2, is more consistent with the research object and has relatively conservative prediction results that are safe for actual engineering use and in line with the concept of safe operation of the subway tunnel.

$\lg N=16.67-16.76S_{t\max }+5.17S_{t\min }(2)$

Where S_tmax is the maximum tensile stress of concrete, S_tmin is the minimum tensile stress of concrete; N is the number of fatigue cycles.

3 Performance function of the invert structure of the subway tunnel

Long-term exposure of the subway tunnel structure to the cyclic stress imparted by the upper train loads will produce fatigue damage to the tunnel structure, particularly the tunnel invert structure. From the standpoint of fatigue stress damage to concrete, there is frequently both compressive and tensile damage. Thus, fatigue analysis will also be conducted from these two perspectives. Miner fatigue cumulative damage theory (Miner, 1945) is widely used in analyzing the fatigue failure probability of the invert concrete structure of the tunnel:

$P_f=P\left[D\left(t\right)>1\right](3)$

Where D (t) is the loss factor.

The total damage to the tunnel invert structure in the tension or compression state within 1 year is:

$D\left(1\right)={\displaystyle \sum _{i=1}^{\infty }}\frac{n_i}{N_i}(4)$

Assume that the concrete material is repeated n_i times under the action of the stress value of σ_i, which can be expressed by:

$C=N_i{\left({\sigma }_i-{\sigma }_{\min }\right)}^m(5)$

Where m is the concrete material constant, σ_min is the minimum stress level.

Hence, Eq. 4 can be expressed by:

$D\left(1\right)={\displaystyle \sum _{i=1}^{\infty }}\frac{n_i{\left({\sigma }_i-{\sigma }_{\min }\right)}^m}{C}(6)$

Therefore, the fatigue strength of the invert structure of the subway tunnel under N_e times equal amplitude repetitive stress after t years is obtained as σ_r(N₀), which can be obtained from the S-N curve of the concrete material, then the cumulative loss value after t years is:

$D\left(t\right)={\displaystyle \sum _{i=1}^{\infty }}\frac{n_i{\left({\sigma }_i-{\sigma }_{\min }\right)}^m}{N_{e}t{\left[{\sigma }_r\left(N_0-{\sigma }_{\min }\right)\right]}^m}(7)$

Here, set $\Delta {\sigma }_i={\sigma }_i-{\sigma }_{\min }$, assuming the probability density function of repeated random stress variation is $f_{\Delta {\sigma }_i}\left(\Delta {\sigma }_i\right)$. For high circumferential cyclic fatigue structures, when the total number of cycles is large enough (>10⁵), $N_0={\displaystyle \sum _{i=0}^{\infty }}{n}_i$, Then the number of cycles $n_i=N{f}_{\Delta {\sigma }_i}\left(\Delta {\sigma }_i\right)=N_{e}t{f}_{\Delta {\sigma }_i}\left(\Delta {\sigma }_i\right)$ and the cumulative loss value is:

$D\left(t\right)={\displaystyle \sum _{i=0}^{\infty }}\frac{f_{\Delta {\sigma }_i}\left(\Delta {\sigma }_i\right){\left(\Delta {\sigma }_i\right)}^m}{{\left[{\sigma }_r{N}_0-{\sigma }_{\min }\right]}^m}=\frac{E{\left(\Delta {\sigma }_i\right)}^m}{{\left[{\sigma }_r{N}_0-{\sigma }_{\min }\right]}^m}(8)$

Where $E{\left(\Delta {\sigma }_i\right)}^m$ is the m-order origin moment of $\Delta {\sigma }_i$; σ_r (N₀) is the concrete tensile or compressive fatigue strength under equal amplitude repetitive stress; m is the concrete material constant, and the value of m is determined according to the relevant literature and is taken as 19.38 in bending and tension and 16.90 in compression (Ou, 2016), hence:

$P_f=P\left\{\frac{E{\left(\Delta {\sigma }_i\right)}^m}{{\left[{\sigma }_r{N}_0-{\sigma }_{\min }\right]}^m}>1\right\}(9)$

Accounting for computational model uncertainty variables γ in the equation:

$P_f=P\left\{{\sigma }_r\left(N_0\right)<{\sigma }_{\min }+\gamma {\left[E{\left(\Delta {\sigma }_i\right)}^m\right]}^{\frac{1}{\mathit{m}}}\right\}=P\left\{{\sigma }_r\left(N_0\right)<{\sigma }_e\right\}(10)$

The limiting state equation is obtained as follows:

$g\left(X,Y,t\right)={\sigma }_r\left(N_0\right)-{\sigma }_e(11)$

Substituting Eqs 1, 2 into Eq. 11, respectively, we obtain the limit state equation for the compressive fatigue of concrete in the invert structure of the subway tunnel as

$g\left(X,Y,t\right)=0.9885f_{cu}-0.0618f_{cu}\lg \left(N_{e}t\right)-{\sigma }_{ec}(12)$

Where σ_ec is the equal amplitude equivalent repetitive compressive stress of the invert structure of the subway tunnel.

The tensile fatigue limit state equation is:

$g\left(X,Y,t\right)=0.994f_{tu}+0.3084{\sigma }_{t\min }-0.0602f_{tu}\lg \left(N_{e}t\right)-{\sigma }_{et}(13)$

Where σ_et is the equal amplitude equivalent repetitive tensile stress of the invert structure of the subway tunnel.

According to the Chinese code for the design of concrete structures GB 50010-2015 (Zhou et al., 2021), under fatigue loading, the tensile and compressive stress amplitudes of concrete can be calculated according to the following formula respectively:

${\sigma }_{t\max }=\frac{M_{\max }\left(h-x_0\right)}{I_0}(14)$

${\sigma }_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{M_{\max }{x}_0}{I_0}(15)$

Where M_max is the maximum moment caused by the combined effect of train loads and rock surrounding pressure; h is the height of the cross-section; x₀ is the center of gravity position; I₀ is the cross-sectional moment of inertia.

Therefore, the standard stress spectrums of concrete at the fatigue analysis location are:

$∆{\mathrm{\sigma }}_{et}={\mathrm{\sigma }}_{et}-{\mathrm{\sigma }}_{t\min }=\gamma {\left[\frac{1}{N_0}{\displaystyle \sum _{i=0}^{\infty }}{n}_i{\left(∆{\mathrm{\sigma }}_{ti}\right)}^{19.38}\right]}^{1/19.38}=\gamma {\left[{E\left(∆{\mathrm{\sigma }}_{ti}\right)}^{19.38}\right]}^{1/19.38}(16)$

$∆{\mathrm{\sigma }}_{ec}={\mathrm{\sigma }}_{ec}-{\mathrm{\sigma }}_{\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{n}}=\gamma {\left[\frac{1}{N_0}{\displaystyle \sum _{i=0}^{\infty }}{n}_i{\left(∆{\mathrm{\sigma }}_{ci}\right)}^{16.9}\right]}^{1/16.9}=\gamma {\left[{E\left(∆{\mathrm{\sigma }}_{ci}\right)}^{16.9}\right]}^{1/16.9}(17)$

The subway tunnel structure experiences the continuous cyclic impact of dynamic train load when in service. As a result, the invert structure may experience fatigue damage over time, which could affect train operation safety and passenger safety. When the subway tunnel operates for a long time in a complex underground environment, the material properties of both the tunnel structure and the surrounding rock structure may deteriorate. Hence, the reliability of the tunnel structure must be calculated, taking into account not only fatigue damage but also the time-varying decay of resistance (Stewart and Val, 1999).

$R_1\left(t\right)=R_{0}y\left(t\right)(18)$

Where R₀ is the original resistance without considering the effect of time, y(t) is a reasonable resistance decay function.

This paper uses a polynomial decay function to better express the correlation between parameters and the design life of the subway tunnel, considering the environment it will be used in. The expression for the polynomial decay function is as follows:

$\mathrm{y}\left(t\right)=1-k_{1}t+k_1{t}^2(19)$

Where k₁ and k₂ are the attenuation coefficient related to the type of structure, generally divided into high, medium, and low three different attenuation rates, combined with the subway tunnel structure used in this paper to study the environment, determine the parameters k₁ and k₂ in the function to take the value of 0.005 and 0, respectively (Vu and Stewart, 2000).

The invert structure of the subway tunnel may experience two different stress states depending on the action form of the train and the bottom surrounding rock pressure state. These stress states can be categorized into two types: compressive strength state and tensile strength state. The exact stress state experienced by the invert structure will depend on the specific environmental conditions.

When the invert structure of the subway tunnel is in the compressive state, the limit state equation is obtained as follows:

$g_1\left(t\right)=K_p\mathit{\beta abh}\min f_{c0}\left(1-0.005t\right)-{\sigma }_1(20)$

K_p is the uncertainty factor, β is the Longitudinal bending coefficient of the component, and β = 1 for tunnel linings, a is the eccentricity influence factor, b is Lining section width, h is Lining section height, f_c0 is the ultimate compressive strength of concrete, t is time, σ₁ is axial structural force.

When the invert structure of the subway tunnel is in the tensile state, the limit state equation is obtained as follows:

$g_1\left(t\right)=K_p\mathit{\beta }\frac{1.75bh}{\frac{6e_0}{h}-1}\min f_{t0}\left(1-0.005t\right)-{\sigma }_1(21)$

f_t0 is the ultimate tensile strength of concrete; e₀ is the axial force eccentricity distance.

To summarize, the subway tunnel operates under dynamic train loads and complex environmental conditions. The analysis conducted reveals that the final limit state equation for the tensile fatigue of the concrete structure of the invert structure of the subway tunnel can be expressed as follows:

$G\left(X,Y,t\right)=\left(0.994f_{tu}-0.0602f_{tu}\lg \left(N_{e}t\right)\right)\left(1-0.005t\right)+0.3084{\sigma }_{t\min }-{\sigma }_{et}(22)$

Similarly, the final limit state equation for the compressive fatigue of the invert structure of the subway tunnel can be obtained as follows:

$G\left(X,Y,t\right)=\left(0.9885f_{cu}-0.0618f_{cu}\lg \left(N_{e}t\right)\right)\left(1-0.005t\right)-{\sigma }_{ec}(23)$

4 Time-varying fatigue reliability analysis of invert structure of subway tunnel

In this section, a subway tunnel (liner thickness is 300 mm) with a daily operating time of 15 h is investigated. The subway train has a load vibration frequency of 1.0 Hz, a standard operating speed of 80 km/h, a total length of 80 m, and an axle weight of 14t. The cyclic train loads acting on the invert structure are considered as an equal amplitude fatigue load, and the number of repetitions is 4.

Combined with the research background of the subway tunnel provided in this paper, the time-varying fatigue limit state function of the invert structure of the subway tunnel under longitudinal compression can be obtained by using the equation as follows:

$G\left(X,Y,t\right)=\left(0.9885f_{cu}-0.0618f_{cu}\lg \left(1.7345\times {10}^{6}t\right)\right)\left(1-0.005t\right)-{\sigma }_{ec}(24)$

$f_{cu}$ is a variable that varies with time, and other variables neglect the effect of time. In this paper, six influencing factors that do not vary with time are considered, and their random variables are described in detail, as shown in Table 3.

TABLE 3

TABLE 3. General description of random variables.

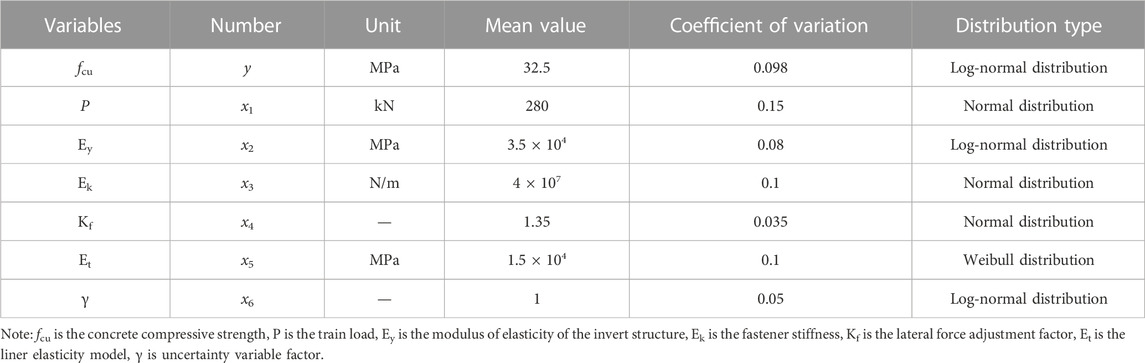
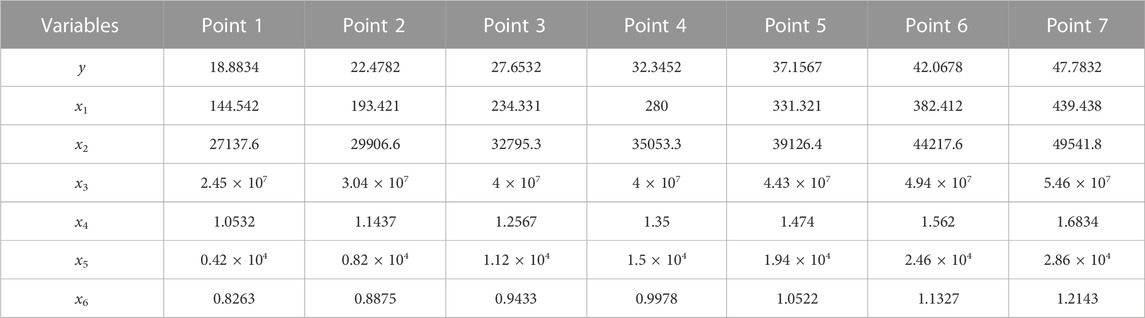
The general description of the random variables given in Table 3 is in the original spatial state, while the failure probability of the fatigue state of the tunnel invert is solved by the higher-order moment method. After Rosenblatt’s inverse normal transformation, the seven-point estimates corresponding to each random variable are determined, and the values obtained are shown in Table 4.

TABLE 4

TABLE 4. Random variable seven-point inverse normal transition value.

The above calculation steps have been conducted to obtain the origin moment of concrete under longitudinal compression. The calculation results are then substituted into Eq. 24, resulting in the following expression:

$G\left(X,Y,t\right)=\left(0.9885y-0.0618y\lg \left(1.7345\times {10}^{6}t\right)\right)\left(1-0.005t\right)-\left({\sigma }_{c\min }+5.124x_6\right)(25)$

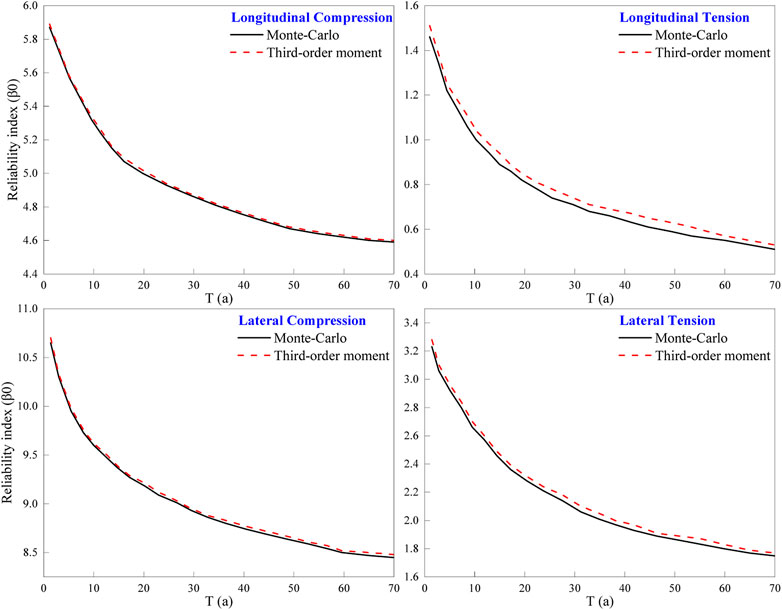
In order to study the effect of time on reliability and failure probability, it is essential to consider the continuity of time T. A time period of 70 years was selected, with a time interval of 1 year. When the selected time is 1 year, the expression with only two variables can be obtained. Then, the first third-order moments of this expression are estimated using the seven-point estimation method. Similarly, the first third-order moments of this expression can be obtained for each time period. Finally, the reliability indexes and corresponding failure probabilities of the concrete structure of the invert structure of the subway tunnel under fatigue stress in each time period are calculated using the third-order moment method. Additionally, the Monte Carlo method (4 million times) was used for comparative analysis to verify the feasibility and rapidity of the third-order moment method. The trend of the reliability indexes with time was obtained by collating and analyzing the calculation results shown in Figure 3.

FIGURE 3

FIGURE 3. Variation of time-varying fatigue reliability of invert structures of subway tunnels.

The fatigue reliability of the concrete structure of the invert structure of the subway tunnel was calculated, and the results indicate that there is no significant fatigue problem for this part of the structure under the action of dynamic train load. The calculated fatigue reliability indexes are above 4.5 in both lateral and longitudinal compression cases, with a corresponding failure probability of less than 0.86 × 10⁻⁷. The lateral fatigue results are even better, with all indexes above 8.0, and it can be considered that the failure probability under this force condition is close to zero. However, in the lateral bending-tension edge of the invert structure, the fatigue reliability indexes of concrete bending-tension fatigue cracking range from 1.774 to 3.235, with corresponding failure probabilities between 2.436 × 10⁻⁶ and 3.356 × 10⁻⁴. On the other hand, the fatigue reliability indexes of bending and tensile fatigue cracking of concrete in the longitudinal tension edge are only between 0.473 and 1.421, with corresponding failure probabilities between 0.104 and 0.293. These results indicate that bending and tensile fatigue cracking is more likely to occur in the longitudinal tension edge of the invert structure under train load and complex environmental conditions, especially in long-term service conditions. Moreover, the probability of failure increases significantly over time.

The results obtained from the two methods (the third-order moment method and the Monte Carlo method) overlap, indicating that the third-order moment method is both accurate and efficient in evaluating the fatigue reliability of concrete structures in subway tunnel invert structures. The Monte Carlo method, while commonly used for reliability verification, requires a high number of calculation runs, making it less efficient. Thus, the third-order moment method is a suitable choice for the analysis of fatigue reliability in invert structure of subway tunnels.

5 Parametric analysis

In the previous section, we examined the time-varying fatigue reliability of the invert structure of the subway tunnel under train load stress. However, during actual subway operation, there are variations in operating speed, train type, and lining thickness in different sections. These variations can impact the fatigue life of the subway tunnel structure, necessitating detailed research and comparative analysis. In this section, we will further discuss the influences of subway train speed, axle weight, and tunnel lining thickness.

5.1 Effects of the train speed

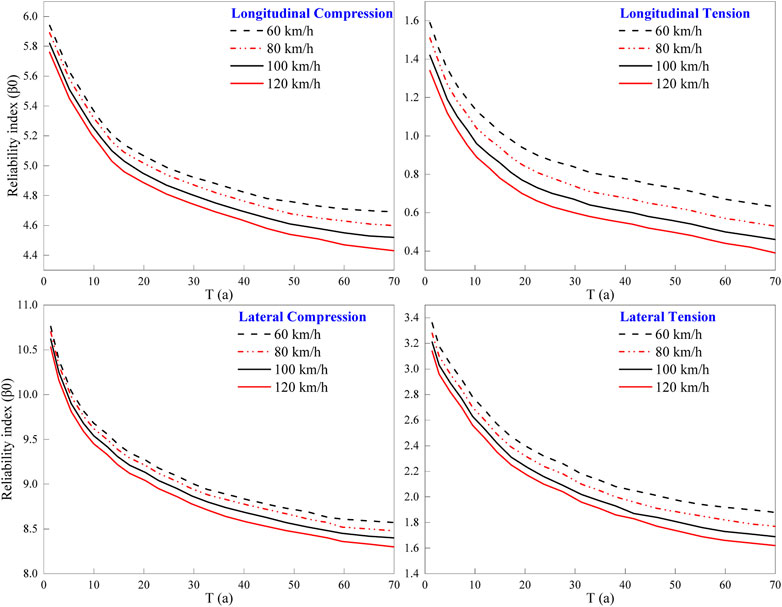
The train speeds are set to 60, 80, 100, and 120 km/h, and the fatigue reliability indices of the invert structure of the subway tunnel under different operating speeds are calculated using the third-order moment method. The calculated results are depicted in Figure 4.

FIGURE 4

FIGURE 4. Effects of different train speeds on the fatigue reliability of the invert structure.

Figure 4 illustrates how the time-varying fatigue reliability of the invert structure of the subway tunnel changes at four different speeds for longitudinal and lateral compression and tension. All four cases show a decrease in the fatigue reliability index and an increase in failure probability as the number of fatigue cycles increases. When the train speed increases, the fatigue reliability index decreases, and the failure probability increase, but the rate of change slows down. The worst damage occurs in the longitudinal tension position, followed by the lateral tension position. This suggests that the invert structure will experience significant concrete tension damage due to cyclic train loads, which are also affected by factors such as surrounding rock pressure, groundwater conditions, and structural form. Train speed has a significant impact on the fatigue reliability index of the invert structure, so a comprehensive analysis is necessary to determine the fatigue life in different regions and interval sections.

5.2 Effects of axle weight

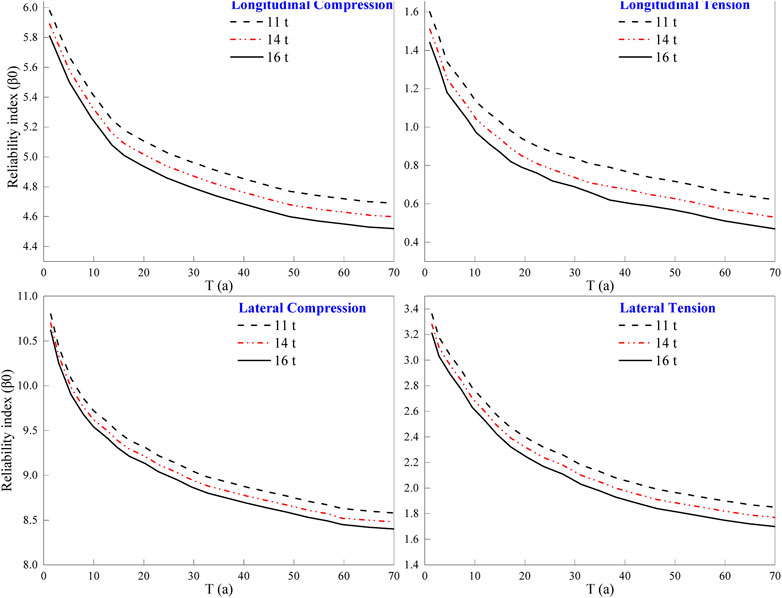
This study will evaluate the effects of axle weight on the fatigue reliability of the invert structure of the subway tunnel. The train axle weights are set to 11, 14, and 16 t based on the actual service conditions of the subway tunnel.

Figure 5 shows the fatigue time variation reliability indexes of the invert structure of a subway tunnel under three different train axle weights in both longitudinal and lateral compression and tension. As fatigue cycles increase, the reliability index decreases, and the probability of failure increases, indicating degradation of the concrete material during service. Increasing train axle weights results in a continuous decrease in the fatigue reliability index and an increase in the probability of failure, with the most severe damage occurring at the location of longitudinal tension and then transverse tension. This effect is consistent with the influence of train speed and reduces the service life of the invert structure of the subway tunnel. The effect of different train axle weights on the fatigue life is slightly greater than that of train speed and should be evaluated for tunnel sections with high pedestrian flow. While heavier trains may be needed for transporting large numbers of people, such sections require special attention to avoid unpredictable dangers. Therefore, it is important to evaluate the impact of different axle weights on the fatigue life of the invert structure in high-pedestrian-flow interval sections. While it may be necessary to use trains with heavier axle weights in these sections to meet capacity demands and prevent overcrowding, the increased weight will also accelerate the degradation of the concrete structure, potentially posing a safety risk.

FIGURE 5

FIGURE 5. Effect of different axle weights on the fatigue reliability of the invert structure.

5.3 Effects of lining thickness of the subway tunnel

The lining thicknesses of the subway tunnel are set to 300, 350, 400, and 450 mm. The fatigue reliability indices are calculated using the third-order moment method; the obtained fatigue reliability index calculation results are shown in Figure 6.

FIGURE 6

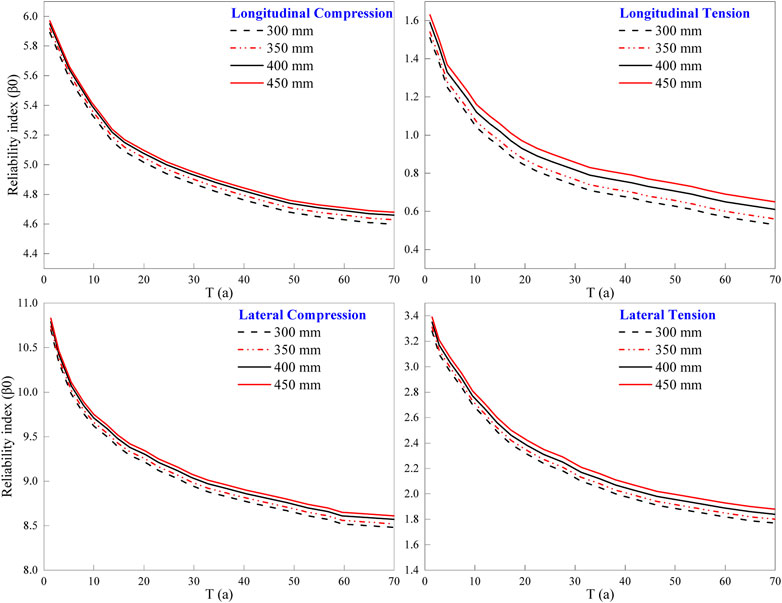
FIGURE 6. Effect of different lining thicknesses on the fatigue reliability of the invert structure.

Figure 6 shows the fatigue time variation reliability index of the concrete structure of the invert structure at four different lining thicknesses in longitudinal compression, tension, and lateral compression and tension, and they all exhibit similar trends. As the fatigue time increases, the fatigue reliability index decreases, and the failure probability increases. When the lining thickness increases under longitudinal tension, the fatigue reliability index decreases slowly, and the failure probability increases slowly. However, under longitudinal compression, lateral compression, and lateral tension, the fatigue reliability index does not change significantly. The most severe fatigue failure occurs under transverse tension, regardless of the lining thickness, and the most severe fatigue failure occurs under longitudinal tension. These findings suggest that the concrete structure of the invert structure of subway tunnel will experience severe concrete strain degradation from long-term cyclic train loads. This is also influenced by the surrounding rock pressure and tunnel structure type within the subway tunnel. Although the lining thickness has a certain influence on the fatigue reliability index of the concrete structure of the invert structure at the local position, this influence is less than that of the previous two influencing parameters. Therefore, when designing the tunnel lining thickness, it is necessary to meet only the minimum requirements of the design and save construction costs to realize the concept of green environment protection.

According to the analysis above, different factors such as train speeds, axle weights, and lining thicknesses have impacts on the fatigue reliability index and failure risk of the concrete construction of the subway tunnel. The influence pattern of these factors on the fatigue reliability index of the invert structure is similar, showing a gradual decrease of the fatigue reliability index and a corresponding increase in failure probability with increasing fatigue time, but none of these factors change the location of the most severe damage, which occurs mainly along the longitudinal axis. This is related to the uniform distribution of the surrounding rock pressure and the continuous force produced by the train’s dynamic load combined with the direction of the tunnel. The results of the fatigue reliability analysis of the concrete structure of the invert structure indicate that on-site inspections of the subway tunnel should focus on the areas most susceptible to damage. The time-varying fatigue reliability analysis of the invert structure of the subway tunnel is more consistent with the actual service period, and the computed results provide a scientific and theoretical basis and technical indicators for the subsequent evaluation of the subway tunnel’s health status.

6 Conclusion

A study was conducted to assess the reliability of the concrete structure of the invert structure in subway tunnels over time, considering the repeated loads from trains. Higher-order moment theory, fatigue equation, and cumulative damage theory were used for this purpose. The results of this study will provide insight into the health and reliability of subway tunnels and facilitate their condition monitoring. Key findings include the following:

(1) The extent of fatigue damage in the invert structure of subway tunnels is largely determined by the stress it is under. Stress levels were measured and used to predict the concrete’s stress tolerance, which was then used to determine the stress limit for the invert structure before fatigue damage occurs.

(2) The results of the time-varying fatigue performance function of the invert structure of the subway tunnel are essentially consistent with those obtained from the Monte Carlo method, indicating the method’s suitability for fatigue reliability analysis of the invert structure. The probability of failure in the case of compression is low, while the concrete is more susceptible to bending and tension fatigue cracking in the case of tension, necessitating reinforcement of the invert structure for longitudinal and lateral tension concrete detection and maintenance.

(3) Train axle weight and speed have a relatively large impact on the fatigue reliability index, with speed having a slightly greater effect than axle weight, and lining thickness having a negligible effect. As the number of fatigue cycles increases over time, the fatigue reliability index decreases continuously, and the corresponding probability of failure increases continuously. The area requiring the most inspection and maintenance is determined to be the tensile state of the invert structure.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aas-Jakobsen, K. T. (1970). Fatigue of concrete beam and s. Pichanur, Pichanur, Tamil Nadu; NTH Institute of Betongkonstruksjoner.

Google Scholar

Chen, L. H., Chai, X. B., and Fan, H. Z. (2014). “Tunnel reliability analysis based on the combination of modified FOSM and numerical calculation program,” in Applied mechanics and materials Switzerland; (Zürich, Switzerland: Trans Tech Publ), 1174–1181.

CrossRef Full Text | Google Scholar

Cornelissen, H. A. W., and Reinhardt, H. W. (1984). Uniaxial tensile fatigue failure of concrete under constant-amplitude and programme loading. Mag. Concr. Res. 36, 216–226. doi:10.1680/macr.1984.36.129.216

CrossRef Full Text | Google Scholar

Ellingwood, B., and Hwang, H. (1985). Probabilistic descriptions of resistance of safety-related structures in nuclear plants. Nucl. Eng. Des. 88, 169–178. doi:10.1016/0029-5493(85)90059-7

CrossRef Full Text | Google Scholar

Fattahi, H., and Jiryaee, F. (2022). Reliability analysis of surface settlement caused by mechanized tunneling-a case study. J. Min. Environ. 13, 201–216. doi:10.22044/jme.2022.11570.2143

CrossRef Full Text | Google Scholar

Frangopol, D. M., Lin, K.-Y., and Estes, A. C. (1997). Reliability of reinforced concrete girders under corrosion attack. J. Struct. Eng. 123, 286–297. doi:10.1061/(asce)0733-9445(1997)123:3(286)

CrossRef Full Text | Google Scholar

Hou, J. P. (2001). Study of fatigue damage criterion for concrete materials (PhD Thesis). Dalian, China, Dalian University of Technology.

Kim, J.-K., and Kim, Y.-Y. (1996). Experimental study of the fatigue behavior of high strength concrete. Cem. Concr. Res. 26, 1513–1523. doi:10.1016/0008-8846(96)00151-2

CrossRef Full Text | Google Scholar

Laso, E., Lera, M. S. G., and Alarcón, E. (1995). A level II reliability approach to tunnel support design. Appl. Math. Model. 19, 371–382. doi:10.1016/0307-904x(95)00019-g

CrossRef Full Text | Google Scholar

Li, T. Z., and Yang, X. L. (2019). An efficient uniform design for Kriging-based response surface method and its application. Comput. Geotech. 109, 12–22. doi:10.1016/j.compgeo.2019.01.009

CrossRef Full Text | Google Scholar

Lü, P. Y. (2002). Uniaxial and biaxial dynamic strength and deformation test study of concrete. PhD Thesis Dalian, China; (Dalian University of Technology).

Lü, Q., and Low, B. K. (2011). Probabilistic analysis of underground rock excavations using response surface method and SORM. Comput. Geotech. 38, 1008–1021. doi:10.1016/j.compgeo.2011.07.003

CrossRef Full Text | Google Scholar

Matsushita, H., and Tokumitsu, Y. (1979). “A study on compressive fatigue strength of concrete considered survival probability,” in Proceedings of the Japan society of civil engineers Tokyo, Japan; (Japan Society of Civil Engineers), 127–138.

CrossRef Full Text | Google Scholar

Miner, M. A. (1945). Cumulative damage in fatigue. J. Appl. Mech. 12 (3). doi:10.1115/1.4009458

CrossRef Full Text | Google Scholar

Mollon, G., Daniel, D., and Abdul-Hamid, S. (2009). Probabilistic analysis and design of circular tunnels against face stability. Int. J. Geomech. 9, 237–249. doi:10.1061/(asce)1532-3641(2009)9:6(237)

CrossRef Full Text | Google Scholar

Mollon, G., Dias, D., and Soubra, A.-H. (2011). Probabilistic analysis of pressurized tunnels against face stability using collocation-based stochastic response surface method. J. Geotech. Geoenvironmental Eng. 137, 385–397. doi:10.1061/(asce)gt.1943-5606.0000443

CrossRef Full Text | Google Scholar

Mori, Y., and Ellingwood, B. R. (1993). Reliability-based service-life assessment of aging concrete structures. J. Struct. Eng. 119, 1600–1621. doi:10.1061/(asce)0733-9445(1993)119:5(1600)

CrossRef Full Text | Google Scholar

Ou, Z. M. (2016). Fatigue reliability analysis methods and application for slab track structure. Nanjing, China: Southeast Univ.

Google Scholar

Qing Li, C. (2004). Reliability based service life prediction of corrosion affected concrete structures. J. Struct. Eng. 130, 1570–1577. doi:10.1061/(asce)0733-9445(2004)130:10(1570)

CrossRef Full Text | Google Scholar

Rosenblueth, E., and Esteva, L. (1972). Reliability basis for some Mexican codes. Spec. Publ. 31, 1–42. doi:10.14359/17921

CrossRef Full Text | Google Scholar

Rosenblueth, E. (1975). Point estimates for probability moments. Proc. Natl. Acad. Sci. 72, 3812–3814. doi:10.1073/pnas.72.10.3812

PubMed Abstract | CrossRef Full Text | Google Scholar

Saito, M. (1983). Direct tensile fatigue of concrete by the use of friction grips. J. Proc, 80, 431–438.doi:10.14359/10867

CrossRef Full Text | Google Scholar

Shi, Q., Pan, J., Wang, S., Liu, S., Mishra, B., and Seitz, S. (2021). Field monitoring of delayed coal burst in an advancing entry of a deep coal mine. Min. Metall. Explor 38, 2417–2431. doi:10.1007/s42461-021-00508-6

CrossRef Full Text | Google Scholar

Shiozawa, K., Lu, L., and Ishihara, S. (2001). S–N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel. Fatigue Fract. Eng. Mat. Struct. 24, 781–790. doi:10.1046/j.1460-2695.2001.00459.x

CrossRef Full Text | Google Scholar

Song, Y. P., Wang, H. L., and Jia, J. Q. (2008). Behavior of concrete under multi-axial fatigue loading. J. Build. Struct. 29, 260–265.

Google Scholar

Stewart, M. G., and Val, D. V. (1999). Role of load history in reliability-based decision analysis of aging bridges. J. Struct. Eng. 125, 776–783. doi:10.1061/(asce)0733-9445(1999)125:7(776)

CrossRef Full Text | Google Scholar

Tepfers, R. (1979). Tensile fatigue strength of plain concrete. J. Proc, 76, 919–934. doi:10.14359/6969

CrossRef Full Text | Google Scholar

Val, D. V., and Melchers, R. E. (1996). “Reliability assessment of existing concrete bridges,” in Structural reliability in bridge engineering: Design, inspection, assessment, rehabilitation and management. Proceedings of the WorkshopNational science foundation. Lakewood, Colorado; (Federal Highway Administration,Colorado Department of Transportation). 356,

Google Scholar

Vu, K. A. T., and Stewart, M. G. (2000). Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 22, 313–333. doi:10.1016/s0167-4730(00)00018-7

CrossRef Full Text | Google Scholar

Wang, X., Li, J., Zhao, X., and Liang, Y. (2022). Propagation characteristics and prediction of blast-induced vibration on closely spaced rock tunnels. Tunn. Undergr. Space Technol. 123, 104416. doi:10.1016/j.tust.2022.104416

CrossRef Full Text | Google Scholar

Xie, P., Zhang, R., Zheng, J., and Li, Z. (2022). Probabilistic analysis of subway station excavation based on BIM-RF integrated technology. Autom. Constr. 135, 104114. doi:10.1016/j.autcon.2021.104114

CrossRef Full Text | Google Scholar

Yao, M. C. (1990). Study of fatigue properties of concrete under equal and variable amplitude repetitive stresses. Beijing, China: Research report of the Ministry of Railways Scientific Research Institute.

Google Scholar

Zhao, G. Y., Wu, P. G., and Zhan, W. W. (1993). Tensile fatigue performance of high-strength concrete. J. Civ. Eng. 26, 13–19.

Google Scholar

Zhao, Y.-G., Lu, Z.-H., and Ono, T. (2006). A simple third-moment method for structural reliability. J. Asian Archit. Build. Eng. 5, 129–136. doi:10.3130/jaabe.5.129

CrossRef Full Text | Google Scholar

Zhao, Y.-G., and Ono, T. (2001). Moment methods for structural reliability. Struct. Saf. 23, 47–75. doi:10.1016/s0167-4730(00)00027-8

CrossRef Full Text | Google Scholar

Zhao, Y.-G., and Ono, T. (2000). New point estimates for probability moments. J. Eng. Mech. 126, 433–436. doi:10.1061/(asce)0733-9399(2000)126:4(433)

CrossRef Full Text | Google Scholar

Zhou, H., He, C., Wang, S., Peng, F., Zhu, S., and Yuan, D. (2020). Dynamic stress concentration factors and damage mode of horseshoe tunnels crossing fault fracture zone. Geotech. Geol. Eng. 38, 5127–5141. doi:10.1007/s10706-020-01352-z

CrossRef Full Text | Google Scholar

Zhou, H., He, C., Wang, X., Chen, Y., and Li, J. (2023). Assessment of the seismic response of shallow buried elliptical tunnels. J. Earthq. Eng. 27, 465–487. doi:10.1080/13632469.2021.2009057

CrossRef Full Text | Google Scholar

Zhou, Y., Zheng, S., Chen, L., Long, L., and Wang, B. (2021). Experimental investigation into the seismic behavior of squat reinforced concrete walls subjected to acid rain erosion. J. Build. Eng. 44, 102899. doi:10.1016/j.jobe.2021.102899

CrossRef Full Text | Google Scholar