- 1CCCC First Highway Consultants Co., Ltd, Xi’an, China
- 2Beijing Aidi Geological Engineering Technology Co., Ltd, Beijing, China
Mine geological disaster is a complex non-linear system. The traditional prediction model has the disadvantages of low prediction accuracy and poor reliability. In order to solve this problem, the open-pit mine slope displacement is taken as the research object. Based on a new algorithm extreme learning machine (ELM), the new intelligent algorithm sparrow search algorithm (SSA) are introduced to determine the weights and thresholds of the input layer and hidden layer of ELM. The open-pit mine slope displacement prediction model of improved ELM is constructed and applied to an engineering example. The results show that the root mean square error of SSA-ELM model is only a quarter of that of BP model, which is 50% higher than that of GM (1,1) and ELM models. The correlation coefficient of the prediction results of the SSA-ELM model is 0.983, and the accuracy is better than that of the traditional model. The single ELM model and the PSO-ELM model show that the SSA algorithm has better improvement effect. The SSA model has good comprehensive performance and high prediction accuracy. It is feasible to apply it to the prediction of slope displacement in open-pit mines.
Introduction
As the open-pit mine enters the deep mining stage, the mining environment becomes worse, and the frequency of geological disasters in the mine increases year by year. The mine landslide not only affects the normal mining operation, but also poses a threat to the ecological environment and the safety of the surrounding people’s lives and property. According to the statistical data in 2017, the total number of accidents and deaths of non-coal mine slope landslides in China accounted for 13.5% and 9.3% of mine safety accidents respectively, ranking third (Yang, et al., 2020; Zhang, et al., 2010). At the same time, research shows that every increase of 1° in the mining slope angle of a large open-pit mine will save tens of millions or even hundreds of millions of yuan in stripping costs, but it will also bring about corresponding disaster risks (Yang, et al., 2011). Macro creep deformation is the result of gradual damage and deterioration of materials inside the slope during the evolution of slope instability (Liu et al., 2020; Li et al., 2021a). Therefore, it is of great significance to grasp the slope failure law and predict and warn the landslide according to the mining slope displacement to ensure the safety production of open-pit mines and improve economic benefits.
The prediction of open-pit slope displacement is a vital method to landslide hazard prevention. The empirical model, statistical model and artificial intelligence model are three approaches to predict displacement of slope and describe the behaviors of slope by analyzing the on-site measured data of slope. The empirical model based on site monitor data is most widely used, however, it is not suitable the prediction the periodic and stepped landslides. To avoid above problems, other researchers have applied statistical analysis models to predict displacement considering the time and the slope surface characteristics, which included that there are grey system model (Liu, et al., 2016; Tasci, et al., 2018), Pearl Growth model (Xu, et al., 1998).However, these models only performs well when the data meets the modeling requirements or applicable to only one type slope, and its universality is not high.
In recent years, conventional models have been enhanced with some various artificial intelligence techniques.such as BPNN prediction model (Feng, et al., 2018; Jiang, et al., 2018; Yang, et al., 2013), improved genetic neural network model (Guan, et al., 2015; Han, et al., 2022), support vector machine model (Yusof, et al., 2017; Zhou, et al., 2017), etc. Although the BPNN prediction model can predict under any data, it calculates the weights and thresholds of the output layer and the hidden layer through the gradient descent method. The accuracy is not high, and it needs repeated trials. The SVM model has advantages in small sample and poor data, however, its parameter selection has always restricted the application of the model. The above models are also beneficial exploration for slope displacement prediction of open pit mine (Mahmoodzaden, et al., 2022), but they also have problems in generalization ability, robustness and prediction accuracy. Therefore, it is necessary to establish a displacement prediction model with high prediction accuracy and strong generalization ability to ensure the safety production of the open pit slope (Liu et al., 2022; Li et al., 2023). The extreme learning machine (ELM) is a new method of single-layer feed forward neural network that has emerged in recent years. ELM has been verified in many engineering practices, such as concrete dam deformation prediction (Zhou, et al., 2017), landslide displacement prediction (Guan, et al., 2018), short-term power load prediction (Cheng, et al., 2018), etc., but it is rarely used in the field of safety monitoring in open pit mines. Some previous studies revealed that ELM is better than ANN and SVM in overcoming low learning rates and local minimum problems of regression analysis (Kang, et al., 2017). Therefore, the ELM is used to predict displacement of open-pit slope. However, the ELM also need to be optimized enhance the predict ability of displacement of open-pit slope (Li et al., 2021b; Zhou et al., 2022). The metaheuristic algorithms inspired by the natural behavior of animals have good performance to optimize the singe neural network.
Therefore, in order to improve the shortcomings of poor prediction accuracy performance, poor robustness and weak generalization ability of traditional models, this paper establishes the SSA-ELM model for open-pit mine displacement prediction, determines the hidden layer node and activation function according to the gradual trial method, and introduces the sparrow search algorithm to optimize the connection weight and threshold value of ELM, which is applied to an example of open-pit mine slope displacement prediction.
Extreme learning machine
ELM was first proposed by Huang (Ding, et al., 2015) as a single hidden layer feed forward neural network. Different from the gradient descent method used by BP, it randomly generates the weights and thresholds of the input layer and the output layer, which will not be adjusted during the training process. As long as the number of hidden layers is determined, the unique solution can be obtained. Therefore, for N arbitrarily different samples (
Where
According to the theorem proposed by Huang, when the activation function is infinitely differentiable, the
According to equation (2), there are
Equation (3) can be expressed in matrix form
Where
Introduction to optimization algorithm
Particle swarm optimization algorithm
Particle swarm optimization algorithm (Yumin, et al., 2014) is a swarm intelligence global search algorithm, which performs well in the optimization and improvement of neural networks. The basic feature of this algorithm is that in the
In the equations,
In the equation (5), it can be seen that the speed of a particle is affected by its own speed
Sparrow search algorithm
The sparrow search algorithm (Yan, et al., 2022) is a new intelligent algorithm that imitates sparrow foraging and predation. In the SSA algorithm, the discoverer, joiner and scout cooperate to carry out local search and global search. Usually the finder has a higher fitness value and can provide the foraging area and direction for the joiner. The mathematical equation is expressed as:
Where t is the current number of iterations,
Joiners will always follow the discoverer to harvest better food, and at the same time monitor the discoverer and compete for food, so as to ensure their predation rate; its mathematical formula is expressed as:
Where
When the scout finds a predator, it immediately sends out an alarm signal, and all the sparrows make anti-predation behaviors. The mathematical formula is expressed as:
Where
Prediction model and evaluation index based on SSA-ELM and PSO-ELM
Improved ELM model for deformation prediction of open-pit mine slope
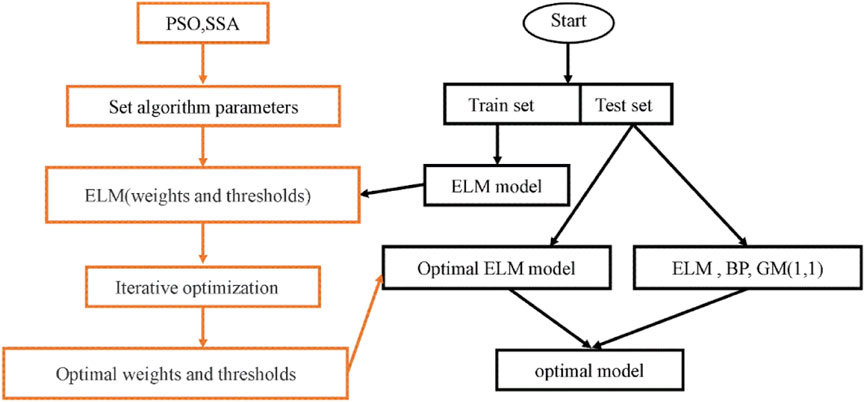
In order to be able to precisely forecast open-pit mine slope displacement, the extreme learning machine is used for modeling. Although the single extreme learning machine model has a simple structure and fast solution speed, it also needs to determine the number of hidden layers. The number of hidden layers can be determined according to the trial algorithm and the two-dimensional search method are determined, and the trial algorithm is used in this paper. The weights and thresholds of the ELM input and output layers are randomly generated and have nothing to do with the training data. The randomly generated values will make the algorithm good and bad, and it cannot guarantee that the solution sought must meet the requirements. Therefore, the new intelligent algorithm SSA are used to improve the ELM(Anupam, et al., 2020), and a combined open-pit mine slope displacement prediction combined model is established. The threshold of the hidden layer and the output layer, so as to obtain the expected vector that meets the requirements. Figure 1 depicts a process for optimizing ELM using the SSA and the PSO. The specific steps of the model are as follows.
Step 1. Divide the collected open-pit mine slope displacement data into two parts, the training set and the test set. At the same time, preprocess the data, eliminate the influence of dimensions and compress the data into the solution space of the activation function.
Step 2. , initialization, setting the particle swarm and sparrow dimensions, that is, the weights and thresholds of the input and output layers of the ELM, the parameters of the particle swarm algorithm and the sparrow search algorithm.
Step 3. Calculate the fitness function value. In this paper, the mean square error mse of the slope displacement prediction value of the open-pit mine is used as the objective function to calculate each fitness value.
Step 4. , iterative optimization, to obtain the optimal fitness value, at the same time, the optimization results are the optimal solutions obtained by the two algorithms, and the connection weights and thresholds of the ELM hidden layer and input layer are obtained.
Step 5. Based on the optimization results, establish an optimized extreme learning machine slope deformation prediction model for open pit mines, input the test set into the established model, and obtain the optimal model after evaluation.
Evaluation index
It is very necessary to evaluate the accuracy of the prediction results of the slope displacement prediction model in open-pit mines. The corresponding evaluation of the results of the deformation monitoring model can judge the accuracy and applicability of the proposed monitoring model, which can be compared with different models, and Can be used to define warning values. Indicators include root mean square error (
Where
Engineering example
Engineering background
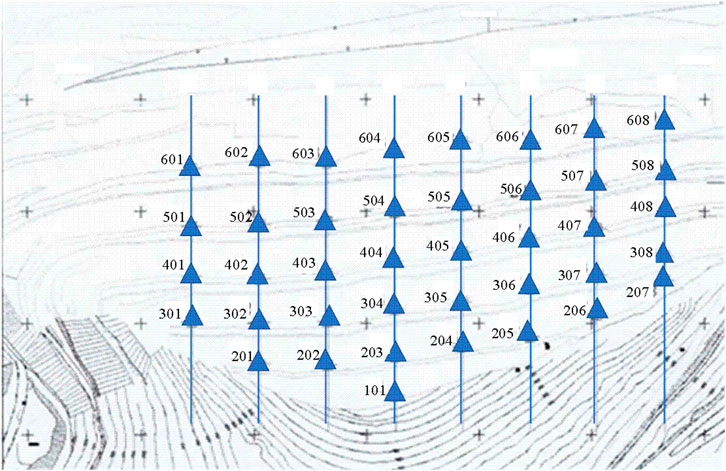
Jianshan mine is located in the middle of Jianshan mining area. The northern slope of Jianshan is the exposure part of rock stratum of meter field floor. The slope of Jianshanle mine is a continental dip bedding rock slope, and the mining area is located in Xiangtiaocun anticline of east-west tectonic belt。The stable state of the slope makes the slope deformed, and even leads to the overall instability or local instability of the slope. During the mining period, there were continuous sheet collapses and collapses under the slope platform. If the landslide disaster occurs on the slope, it will seriously affect the personal and equipment safety of the normal mining and stripping operation of the mine, and also affect the safety of the villages, farmland, railways, highways and so on around the slope. The stability state and hazard of the slope together determine the safety monitoring of the slope. From the monitoring technology and monitoring cost analysis, considering the economic benefit and monitoring effect and other factors combined with the actual situation of the slope, the automatic monitoring system is finally adopted to carry out real-time safety monitoring of the slope. The detailed layout of monitoring points is shown in Figure 2. There are 8 profile monitoring lines and 40 deformation monitoring points.
Deformation prediction and result analysis
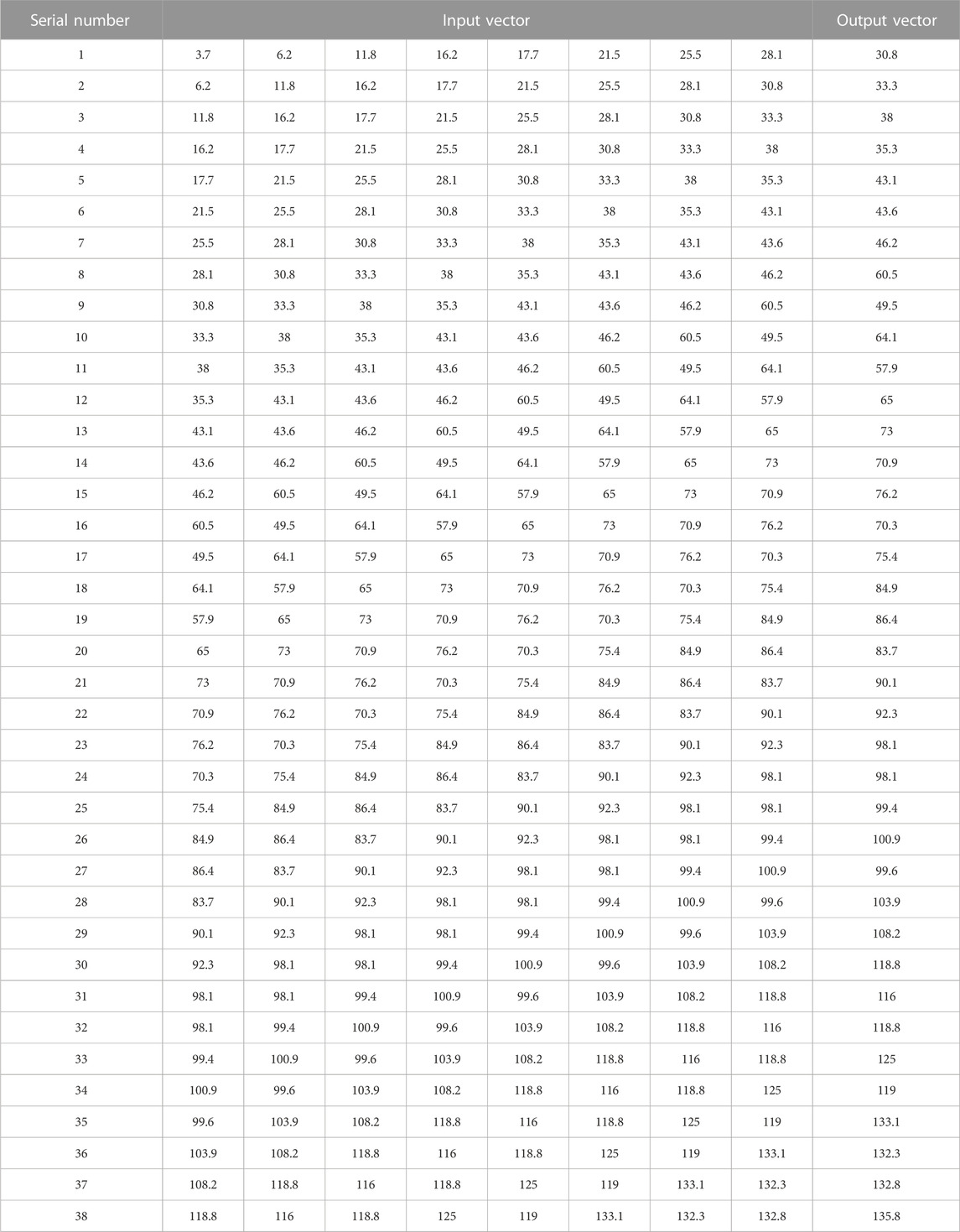
Taking the slope displacement data of an open-pit mine as an example, a total of 46 periods of monitoring data at No.601 monitoring point were selected (Sun, 2014), and only a single factor of displacement was considered. The Table 1 display the monitor data. The data of the first 8 days were used to predict the displacement of the next day, and a total of 38 sets of data were formed. The first 24 periods were used as The training set and the last 14 periods were used as the test set, ELM model, GM (1,1) and BP model were used to compare and analyze the prediction results.
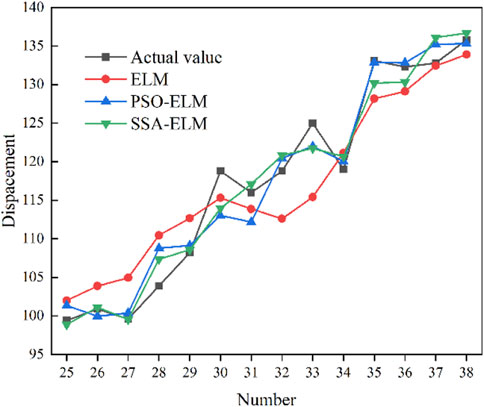
The number of hidden layers of the ELM model is 6 and the transfer function is sig type through the trial algorithm, and the prediction result of ELM is obtained, and compared with the BP(Sun, 2014; Xie, et al., 2014) and GM (1,1)(Sun, 2014; Sun et al., 2016; Wu, et al., 2015) models, as shown in Figure 2. Analysis of Figure 2 shows that the prediction results of the BP model can predict the trend of displacement, but almost every predicted value deviates from the real value, and the prediction result is the worst; the prediction effect of the GM (1,1) model is better than that of the BP model, but the model predicts Unstable, the predictive effect is also poor. The prediction results of the single ELM model are significantly better than the BP model, and the prediction effect is better than that of the GM (1,1) model in the early and late stages, while the prediction value of the GM (1,1) model in the middle part is closer to the real value, indicating that the ELM model is better than the BP model. The prediction accuracy of the model is high, but because of the randomly generated weights and thresholds, the prediction results will also be unstable.
To overcome the instability of the ELM prediction results, the new intelligent algorithm SSA is used to improve the ELM model, and the weight and threshold between the ELM input layer and the hidden layer are optimized through the optimization algorithm to improve the prediction ability of the ELM model.
The parameters of the PSO-ELM model are set as follows. The population size of the particle swarm optimization algorithm is 30, the maximum number of iterations is 400, and the sums are 2.4 and 1.5 respectively, and the inertia weight is linearly decreased from 0.9 to 0.4. The population size of the SSA algorithm is 30, and the maximum number of iterations is also 400, the warning value is 0.6, the proportion of discoverers is 0.7, and the proportion of sparrows aware of danger is 0.2.
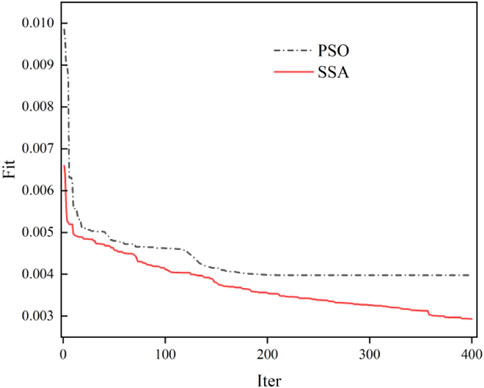
Figure 3 is the fitness graph of ELM optimized by PSO and SSA algorithms. As shown in Figure 4, although the particle swarm optimization algorithm converges at iteration 150, it falls into a local optimum, while SSA has been better than the PSO algorithm after 10 iterations, and has been looking for the optimal value, although it is close to convergence at about 380, but did not fall into the local optimum, and achieved better results, indicating that the optimization effect of the SSA algorithm is better than that of the PSO algorithm.
The prediction results of ELM optimized by SSA and PSO algorithms are shown in Figure 5. Compared with the ELM model, the prediction values of SSA-ELM and PSO-ELM are closer to the real value, and the prediction value of the optimized ELM model can better reflect the development trend of slope deformation. Each stage can approach the actual value very well, and the prediction stability is high. There is no situation where the prediction effect of GM (1,1) and a single ELM model is unstable, and the robustness is high, and the prediction effect is the best. It shows that SSA and PSO can improve the prediction performance of a single ELM model and find the optimal weight and threshold. The predicted value of SSA-ELM is closer to the on-site monitor values than the predicted value of PSO-ELM, indicating that the improvement effect of the SSA algorithm is better.
Model accuracy evaluation
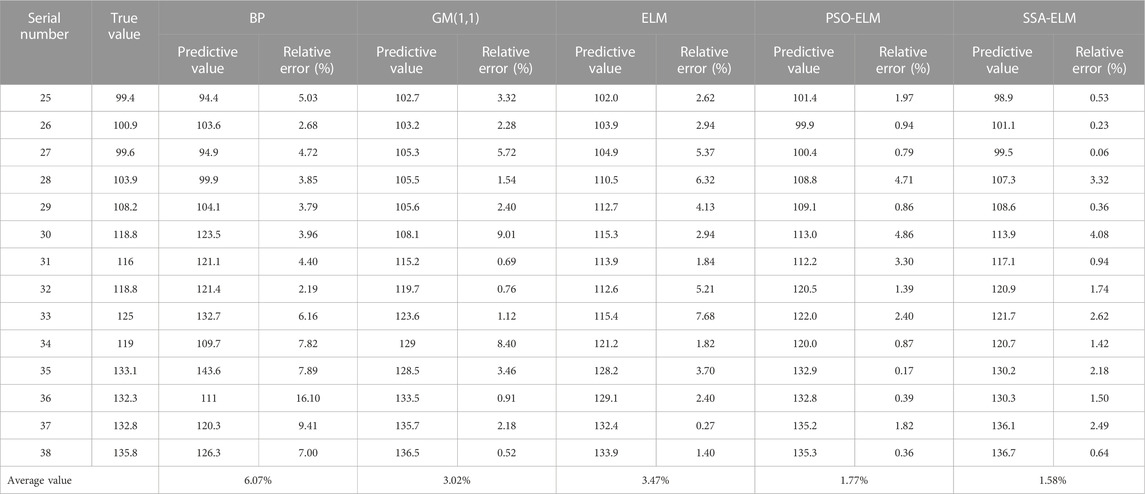
In order to further evaluate and obtain the optimal model, the prediction errors of the five models are shown in Table 2. The average relative errors of the BP model, the GM (1,1) model, the single ELM model, the PSO-ELM model and the SSA-ELM (Hu et al., 2022) model are respectively 6.02%, 3.02%, 3.47%, 1.77% and 1.58%. The relative errors of ELM model and GM(1,1) model are close to each other, obviously better than BP model, but their relative errors fluctuate greatly, and the prediction stability is slightly insufficient. Except for the 28th, 31st, 32nd and 33rd groups of PSO-ELM model, the prediction values of the 31st, 32nd and 33rd groups are slightly worse than the GM(1,1) model, the other 11 groups of prediction results are better than the GM(1,1) model, and the model is the largest The relative error and the minimum relative error are 4.86% and 0.17%, respectively, which are better than the single ELM model and the GM (1,1) model. The maximum, minimum and average relative errors of the SSA-ELM model are 4.08%, 0.06% and 1.58%, which is the smallest among the five models, indicating that the PSO and SSA algorithms have improved the prediction ability of the ELM model, and the SSA has a stronger optimization ability than the PSO. The improved ELM model is feasible for open-pit slope displacement prediction, and the SSA -ELM model and higher prediction accuracy.
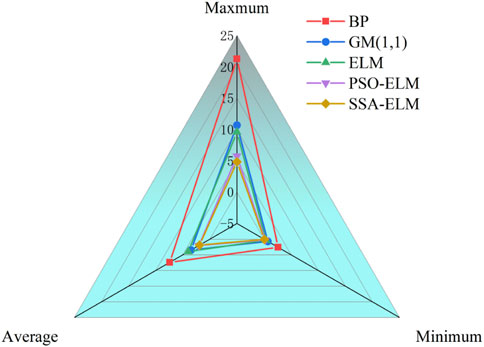
Figure 6 is the absolute error radar chart of five open-pit mine slope deformation prediction models. As shown in Figure 5, the maximum, minimum and average values of the absolute error of the BP model are the largest among the five models, and the absolute error of the single ELM model is The maximum and minimum values of the error are smaller than the GM(1,1) model, but the average absolute error of the GM(1,1) model is smaller, indicating that the ELM model needs to be further improved, and the absolute error of the PSO-ELM and SSA-ELM models The maximum, minimum and average values are smaller than those of the other three models, indicating that the SSA and PSO algorithms can improve the predictive ability of the ELM model. The ELM model does not show that the improvement effect of SSA is better.
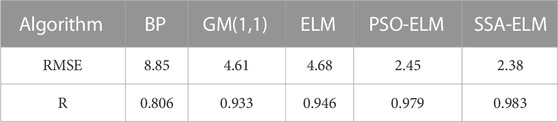
The root mean square error RMSE and correlation coefficient R are introduced as the five evaluation indexes of model accuracy. It can be seen from Table 3 that the root mean square errors of the PSO-ELM model and the SSA-ELM model are 2.45 and 2.38mm, respectively, which are only a quarter of the BP model, and the relative prediction accuracy of the GM(1,1) and ELM models The correlation coefficient of ELM among the five models is 0.946, which is higher than that of BP and GM (1,1) models, indicating that ELM is superior to traditional models in slope displacement prediction of open-pit mines, and has a certain degree of advancement. The correlation coefficients of the PSO-ELM model and the SSA-ELM model are 0.979 and 0.983, respectively, indicating that the improved ELM model overcomes the shortcomings of the single ELM algorithm that randomly generates weights and thresholds, and improves the model prediction accuracy. Because the PSO algorithm is stronger, it further proves that SSA-ELM is feasible and effective for slope displacement prediction in open-pit mines.
Conclusion
The slope displacement change of the open-pit mine is affected by many non-linear factors, and the traditional model performs poorly. Therefore, the new algorithm ELM is used to predict the displacement of this type of slope, which overcomes the shortcomings of the poor prediction accuracy performance of the traditional model, but the stability is slightly insufficient. .
Introduce SSA and PSO algorithms to determine the weights and thresholds of the ELM input layer and hidden layer, and improve the single ELM model. Compared with the two traditional models BP and GM (1,1) and the single ELM model, the prediction results of the improved ELM model, The correlation coefficient is higher, and the correlation coefficient of the SSA-ELM model is the highest among the four models. The root mean square error of SSA-ELM is 2.38mm, which is smaller than the other four models. This model has superior performance and high reliability, and is used in open air The prediction of mine slope deformation is feasible. The main limitation of this paper is that only one dataset was utilized to evaluate the results of developed models. Meanwhile, this study did not consider that the proposed algorithms have some limitations, such as local minima trapping issues and the inability to exploit local space. The developed model in this study will be applied to other datasets to demonstrate its generalization ability and robustness. Present strategies to avoid the problem of local minima trapping issues and the inability of metaheuristic algorithms to exploit local space and illustrate their impact on the current model.
Data availability statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, data curation, formal analysis, Software,methodology,validation,writing—review & editing: JQ; writing—review & editing, supervision, BL. All authors have read and agreed to the published version of the manuscript.
Conflict of interest
BL was employed by CCCC First Highway Consultants Co., Ltd. JQ was employed by Beijing Aidi Geological Engineering Technology Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anupam, S., and Pani, P. (2020). Flood forecasting using a hybrid extreme learning machine-particle swarm optimization algorithm (ELM-PSO) model. Model. Earth Syst. Environ. 6 (1), 341–347. doi:10.1007/s40808-019-00682-z
Cheng, Y. F., Jin, L. J., and Hou, K., (2018) Ieee,"Short-Term power load forecasting based on improved online ELM-K," Proceedings of the 7th International Conference on Control Automation and Information Sciences (ICCAIS), pp. 128–132, Hangzhou Dianzi Univ, Hangzhou, PEOPLES R CHINA,
Ding, S. F., Zhao, H., Zhang, Y. N., Xu, X. Z., and Nie, R. (2015). Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 44 (1), 103–115. doi:10.1007/s10462-013-9405-z
Feng, X. W., Guo, Y., and Li, J. Y. (2018). “A research on the methods for prediction of the slope stability of open-pit mine,” in Proceedings of the 9th China-Russia Symposium on Coal in the 21st Century - Mining, Intelligent Equipment and Environment Protection, Qingdao, PEOPLES R CHINA, October 2018, 73–77.
Guan, S. W., Zhu, Y., Zhou, L., Deng, H. G., and Luo, X. N. (2018). “Prediction of landslide displacement using EMD-PSO-ELM with multiple factors,” in Proceedings of the 7th International Conference on Digital Home (ICDH), Guilin, PEOPLES R CHINA (Guilin Univ Elect Technol), 230–235.
Guan, S., Wang, Z., and Zhang, L. (2015). Application of improved genetic neural network on anticipation of displacements of slope in open pit. J. Liaoning Tech. University:Natural Sci. 34 (05), 618–622.
Han, G., Li, W. L., Sun, X. Y., Jin, S. Y., Zheng, H. Q., and Wang, X. X. (2022). Intelligent optimization of a bolt support scheme for a single-stage slope. Eng. Optim. 10, 1–17. doi:10.1080/0305215x.2022.2086238
Hu, Y. F., Li, K. Q., Zhang, B., and Han, B.,"2022, Strength investigation of the cemented paste backfill in alpine regions using lab experiments and machine learning," Constr. Build. Mater., vol.323, Article ID126583, 126583, doi:10.1016/j.conbuildmat.2022.126583
Jiang, T., Shen, Z. Z., Yang, M., Xu, L. Q., Gan, L., and Cui, X. B. (2018). A new model approach to predict the unloading rock slope displacement behavior based on monitoring data. Struct. Eng. Mech. 67 (2), 105–113.
Kang, F., Liu, J., Li, J., and Li, S. (2017). Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control. Health Monit. 24–e1997. doi:10.1002/stc.1997
Li, X. L., Chen, S. J., Liu, S. M., and Li, Z. H. (2021a). AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Cent. South Univ. 28 (6), 1843–1856. doi:10.1007/s11771-021-4734-6
Li, X. L., Chen, S. J., and Wang, S. (2021b). Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example. Adv. Mater. Sci. Eng. 9 (4), 5594181. doi:10.1155/2021/5594181
Li, X. L., Zhang, X. Y., and Shen, W. L. (2023). Research on the mechanism and control technology of coal wall sloughing in the ultra-large mining height working face. Int. J. Environ. Res. Public Health 20 (2), 868. doi:10.3390/ijerph20010227
Liu, H. Y., Zhang, B. Y., and Li, X. L. (2022). Research on roof damage mechanism and control technology of gob-side entry retaining under close distance gob. Eng. Fail. Anal. 138 (5), 106331. doi:10.1016/j.engfailanal.2022.106331
Liu, S. F., Tao, L. Y., Xie, N. M., and Yang, Y. J. (2016). On the new model system and framework of grey system theory. J. Grey Syst. 28 (1), 1–15.
Liu, S. M., Li, X. L., Wang, D. K., and Zhang, D. (2020). Investigations on the mechanism of the microstructural evolution of different coal ranks under liquid nitrogen cold soaking. Energy Sources A: Recovery Util. Environ. Eff., 1–17. doi:10.1080/15567036.2020.1841856
Mahmoodzaden, A., Nejati, H. R., Mohammadi, M., Ibrahim, H. H., Rashidi, S., and Mohammed, A. H. (2022). Meta-heuristic optimization algorithms for prediction of fly-rock in the blasting operation of open-pit mines. Geomechanics Eng. 30 (6), 489–502.
Sun, H. F. (2014). Study on slope monitoring and prediction of jianshan phosphate mine [D]. China: Kunming University of Science and Technology.
Sun, S. G., Wang, C., Zhao, J., and Destech Publicat, I.,"The application of improved GM (1,1) model in deformation prediction of slope," Proceedings of the 2nd International Conference on Sustainable Energy and Environmental Engineering (SEEE), pp. Xiamen, PEOPLES R CHINA, 2016
Tasci, L., and Tuncez, M. (2018). Monitoring of deformations in open-pit mines and prediction of deformations with the grey prediction model. J. Grey Syst. 30 (4), 152–163.
Wu, H., Dong, Y. F., Shi, W. Z., Clarke, K. C., Miao, Z. L., Zhang, J. H., et al. (2015). An improved fractal prediction model for forecasting mine slope deformation using GM (1,1). Struct. Health Monitoring-an Int. J. 14 (5), 502–512. doi:10.1177/1475921715599050
Xie, Z. H., Liang, S. S., and Luan, T. T. (2014). “Instability warning model of open-pit mine slope based on BP neural network,” in Proceedings of the 3rd International Conference on Civil Engineering and Urban Planning (CEUP), Wuhan, PEOPLES R CHINA, 225–228.
Xu, J. L., and Ma, H. (1998). Discussion on prediction methods of landslide imminent sliding. Chin. J. Geol. Hazard Control 9, 364–369.
Yan, S. Q., Liu, W. D., Li, X. Q., Yang, P., Wu, F. X., and Yan, Z. (2022). Comparative study and improvement analysis of sparrow search algorithm. Wirel. Commun. Mob. Comput. 2022, 1–488252115. doi:10.1155/2022/4882521
Yang, F-Y., Xu, M-L., and Guo, Z-P. (2013). Wavelet denoising and BPANN forecast for monitoring slope deformation in open pit. Min. METALLURGICAL Eng. 33 (6), 1–5.
Yang, T., Wang, H., Dong, X., Liu, F., Zhang, P., and Deng, W. (2020). Current situation,problems and countermeasures of intelligent evaluation of slope stability in open pit. J. China Coal Soc. 45 (6), 19.
Yang, T-H., Zhang, F-C., Yu, Q-L., Cai, M., and Li, H. (2011). Research situation of open-pit mining high and steep slope stability and its developing trend. Rock Soil Mech. 32 (5), 1437–1451.
Yumin, D., and Li, Z.,"Quantum behaved particle swarm optimization algorithm based on artificial fish swarm," Math. Problems Eng., vol.2014, 1, 10, doi:10.1155/2014/5926822014, Article ID 592682, 2014
Yusof, K. W., Babangida, N. M., Mustafa, M. R., and Isa, M. H. (2017). Linear kernel support vector machines for modeling pore-water pressure responses. J. Eng. Sci. Technol. 12 (8), 2202–2212.
Zhang, D. M., Yin, G. Z., Chen, J. A., and Dai, G. F. (2010). Stability analysis of multi-step anti-tilt slope at open-pit mine. Disaster Adv. 3 (4), 30–34.
Zhou, X. M., Wang, S., and Li, X. L. (2022). Research on theory and technology of floor heave control in semicoal rock roadway: Taking longhu coal mine in Qitaihe mining area as an Example. Lithosphere 2022 (11), 3810988. doi:10.2113/2022/3810988
Keywords: extreme learning machine, particle swarm algorithm, open-pit slope, deformation prediction, PSO-ELM, sparrow search algorithm, SSA-ELM
Citation: Li B and Qiu J (2023) Displacement prediction of open-pit mine slope based on SSA-ELM. Front. Earth Sci. 11:1126394. doi: 10.3389/feart.2023.1126394
Received: 17 December 2022; Accepted: 18 January 2023;
Published: 03 February 2023.
Edited by:
Xuelong Li, Shandong University of Science and Technology, ChinaReviewed by:
Yu Xuguang, Tangshan Vocational and Technical College, ChinaLei Shi, China University of Mining and Technology, Beijing, China
Copyright © 2023 Li and Qiu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junbo Qiu, bGtkcWl1anVuYm9AMTI2LmNvbQ==
 Bo Li
Bo Li Junbo Qiu
Junbo Qiu