A dynamic learning method based on the Gaussian process for tunnel boring machine intelligent driving

Introduction: The application of intelligent learning methods to the mining of characteristics and rules of time-series data has gained increasing attention with the rapid development of deep learning. One critical application of such methods is the intelligent assistant driving of tunnel boring machines (TBMs), for which the optimization of driving parameters is essential to improve construction efficiency. However, existing prediction models for TBM parameters are “static” and cannot dynamically capture parameter evolution during real-time driving cycles.

Methods: In this study, we propose a novel dynamic learning model for TBM parameters by introducing the Gaussian process to address this problem. The model can learn decision-making experiences from historical driving cycles, dynamically update the model based on small sample data from current driving cycles, and simultaneously achieve driving parameter prediction. We focused on real-time prediction of TBM parameters in a tunnel project in western China.

Results: The results show that the average relative errors of predicted total thrust and torque values were 1.9% and 2.7%, respectively, and the prediction accuracy was higher than that of conventional models such as random forest and long short-term memory. The model fully exploited updating of small samples of parameters, reducing the average time cost of the model to 29.7 s, which satisfies the requirements of efficient application.

Discussion: The dynamic learning strategy of time-series data adopted in this study provides a reference for other similar engineering applications. The proposed model can improve the prediction accuracy of TBM parameters, thus facilitating the optimization of driving parameters and enhancing the construction efficiency of tunnels.

Conclusion: In summary, this study establishes a dynamic learning model of TBM parameters that can dynamically capture parameter evolution and achieve accurate real-time driving parameter prediction. The proposed model can contribute to the development of intelligent assistant driving of TBMs and similar engineering applications.

1 Introduction

Compared with the conventional drill and blast methods, the shield tunnelling method exhibits obvious advantages in construction safety, efficiency, and intelligence. Therefore, tunnel boring machines (TBMs) are increasingly being used in the western mountainous area of China. Because of the large size of TBM equipment and inflexible construction, TBM is sensitive to geological problems such as squeezing large deformation and water inrush typical in western mountainous areas. Furthermore, TBM performance depends considerably on the experience of the operators and the geological conditions ahead of the tunnel (Jing et al., 2021). An experienced operator can determine the working condition of the TBM based on tunnelling parameters that contain rock mass information and manually select tunnelling parameters. However, inexperienced operators can result in severe disk wear, low construction efficiency, and other engineering problems. Furthermore, TBM produces massive machine data during tunnelling, which contains non-linear coupled mapping relationships, rendering manual decisions increasingly difficult (Zhang et al., 2020; Chen et al., 2021). Therefore, helping the driver to select appropriate tunnelling parameters in accordance with the various geological conditions of the tunnel is necessary for improving boring efficiency and ensuring construction safety.

Methods for effective TBM design can be classified into two categories (Liu et al., 2020; Keshtegar et al., 2021; Liu et al., 2021): methods based on geological parameters and tunnelling parameters (Liu et al., 2019; Zhou et al., 2021a; Feng et al., 2021; Zeng et al., 2021). In the geological parameter-based method, the mapping relationship between geological parameters and tunnelling parameters and regression or artificial intelligence are used to establish the prediction model of tunnelling parameters (Gao et al., 2021). Minh et al. (2017) proposed a fuzzy logic prediction model to predict TBM tunnelling performance based on uniaxial compressive strength and brittleness index of rock mass. Koopialipoor et al. (2020) proposed a hybrid artificial neural network based on five rock properties and introduced the firefly algorithm. Yang et al. (2020) introduced a support vector machine method to predict tunnelling parameters and confirmed that the uniaxial compressive strength and rock quality indexes considerably affect model performance. Salimi et al. (2016) and Salimi et al. (2018) proposed a classification regression tree model to predict TBM performance. Ghasemi et al. (2014) developed a model to predict the TBM tunnelling rate based on fuzzy logic by using rock mass characteristics. Gholami et al. (2012) and Mohammadi et al. (2015) speculated that the artificial neural network could outperform the regression model on TBM performance in terms of prediction results and described complex non-linear integral effects. Although these methods based on geological parameters have achieved excellent results in predicting TBM tunnelling parameters, severe limitations exist in acquiring geological data in unexcavated sections and extending tunnel analogy under various geological conditions (Yang et al., 2019; Yao et al., 2019).

In the method based on tunnelling parameters, typically, the historical TBM tunnelling parameters are excavated and analyzed to infer future tunnelling parameters (Liu et al., 2020). Zhao et al. (2007) constructed a four-parameter ensemble neural network based on site data, and predicted the performance of TBM by considering the uncertainties embedded in the site data and using the re-sampling technique. The ENN-based prediction model outperformed the non-linear regression model. Sun et al. (2018) predicted dynamic loads by adopting the random forest method based on tunnelling parameters. Hajihassani et al. (2019) proposed a gene expression programming (GEP) model for predicting tunnel convergence, which is an important parameter for TBM performance. The model was developed based on data from a real tunneling project and showed good accuracy in predicting convergence values. Xu et al. (2019) developed a supervised machine learning model for predicting TBM penetration rate using a dataset of 75 tunneling projects. The model was trained using three different algorithms: artificial neural networks (ANN), support vector machines (SVM), and decision trees (DT). The results showed that the ANN model outperformed the other two models, with a mean absolute percentage error of 8.49%. Zhang et al. (2019) examined the responses of TBM parameters and predicted the rock mass grade using the clustering method. Zhu et al. (2020) categorized the driving cycle into three stages and predicted the parameters of subsequent stages in real time by mining the data of the first 30 s of the ascending stage. Guo et al. (2020) determined the appropriate tunnelling parameters of TBM by introducing the long short-term memory (LSTM) model. Jin et al. (2020) used the residual blocks of the LSTM network to extract the beneficial features of driving parameters and achieved an accurate prediction of the cutterhead torque. Harandizadeh et al. (2021) proposed a hybrid model that combined adaptive neuro-fuzzy inference system (ANFIS) and probabilistic neural network (PNN) for TBM performance prediction. The model was optimized using imperialist competitive algorithm (ICA) and evaluated using data from three tunneling projects. The results showed that the hybrid model outperformed the individual ANFIS and PNN models, with a mean absolute error of 0.0163. Yu et al. (2021) proposed a novel semi-supervised method to establish a rock mass type prediction model by utilizing a large amount of unlabeled data and limited labeled data. Zimu et al. (2021) developed a hybrid GEP and whale optimization algorithm (WOA) model for estimating the optimal TBM penetration rate in granitic rock mass. The model was trained using data from two tunneling projects and showed good accuracy in predicting the optimal penetration rate. Zhou et al. (2021b) introduced metaheuristics to optimize and improve the support vector machine method and used tunnelling data to predict the TBM propulsion speed. Yang et al. (2023) combined a Bayesian boosting probabilistic model with convolutional neural network (CNN) and random forest (RF) to predict unstable rock masses susceptible to tunnel collapse. These studies revealed that parameter prediction can be achieved by learning considerable tunnelling data. However, complex construction conditions require a large amount of data to be processed in a short period. Existing models are typically based on “static” learning strategies, which cannot perform dynamic learning and prediction of real-time tunnelling data.

The existing parameter prediction methods require, firstly, a large amount of data for training, which is costly in terms of time; secondly, new data obtained from excavations cannot be used in a timely manner, which is not very responsive to tunnels with sudden changes in conditions; finally, the training data cannot be generalized leading to results that do not fully fit the ongoing construction activities, so research is needed to address the above issues. A novel dynamic learning and prediction model of TBM tunnelling parameters was established for solving the problems. The model can be used in each construction cycle to obtain parameter evolution through dynamic learning and subsequently perform prediction. This paper is organized as follows. Chapter 2 introduces the double-shield TBM construction process and the data characteristics of each tunnelling parameter. Chapter 3 establishes a dynamic learning model of tunnelling parameters based on the Gaussian process model and a novel training strategy. Chapter 4 verifies the accuracy and time cost of the model and discussed the feasibility of the model in engineering practice. This model is fast even under small samples and can be applied in real-time tunnelling to ensure efficient and safe construction.

2 TBM principles and data characteristics

This study focused on the prediction of tunnelling parameters under double-shield TBM. The shield forms and tunelling parameters of double-shield, single-shield, and open TBM differ considerably. However, the primary tunnelling parameters, such as torque and total thrust, are similar.

The double-shield TBM structure is displayed in Figure 1A. During excavation, the cutter drive of the front shield rotates to cut through the rock. The telescopic shield connects the front and rear shields, with the main push cylinder inside providing power for the cutter to advance. The support shoe inside the shield compresses the rock wall during excavation and provides lateral support to the cutter to advance. The auxiliary push cylinder ensures that excavation and pipe sheet support are performed simultaneously. The tail shield protects the installation of the pipe sheet, which ensures that the personnel are not exposed to the surrounding rock.

FIGURE 1

FIGURE 1. (A) Double-shield TBM, (B) Structure of each TBM shield and corresponding tunnelling parameters.

Each part of the shield body of double-shield TBM generates corresponding parameters during tunnelling (Figure 1B). For example, the front shield generates torque and cutter head speed during excavation, the support shield generates support shoe pressure and shoe pitch angle, and the telescopic shield generates total thrust and propulsion speed. Among all TBM parameters, torque and total thrust are the two most crucial tunnelling parameters controlled by the driver and are considerably influenced

The everyday driving of the machine. Torque refers to the total torque (M) required for the machine to rotate when the cutter head rotates to break the rock. Total thrust is the sum of the thrust and friction of each cutter during driving and provides power for the cutter head to break the stone.

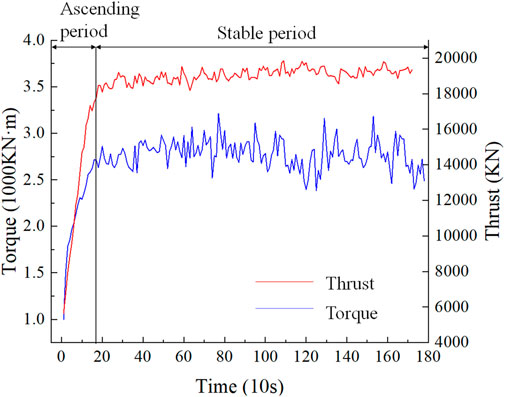
In a complete driving cycle generated by the TBM, the driver adjusts the values of torque and thrust to increase from 0 until they remain stable after the machine is tunnelling normally. Therefore, a complete driving cycle consists of an ascending period and a stable period when the parameters fluctuate within a certain range as displayed in Figure 2. The ascending period is the critical time to observe the tunnelling state of double-shield TBM and considerably affects the selection of tunnelling parameters during the stable period. To assist the driver in making an intelligent decision, in this study, the two core parameters of torque and total thrust in each driving cycle were analysed, and dynamic learning was performed on the parameters of ascending stage to predict the value of its stable stage.

FIGURE 2

FIGURE 2. Torque and total thrust in a driving cycle.

3 GP-based dynamic learning model

Existing prediction models for time-series analysis are based on a “static” learning strategy, which is applied in a new scenario after learning and fitting considerable essential data. However, constructing TBM requires the dynamic learning of tunnelling parameters to predict its subsequent evolution in a scenario (driving cycle).

The Gaussian process can effectively handle the different data distributions and data noise collected during the construction process, update the model in a timely manner, and avoid overfitting with its robustness. For the prediction results of excavation parameters, it can provide confidence intervals and uncertainty measures, and the prediction results are more suitable for assisting operators in decision making. Finally, Gaussian process has simple parameter setting and calculation method, which is easy to understand and implement.

Therefore, a novel dynamic learning model was developed for predicting tunnelling parameters based on the Gaussian process (GP), which is a collection of random variables that can be fitted to generate the probability prediction of function values of random variables (Liu et al., 2019). The principle of the GP satisfies our requirements. Therefore, this chapter focuses on using the GP to learn tunnelling parameters and realizing dynamic prediction.

3.1 GP principle

This section briefly introduces the basic principles of the GP. Consider a sample of tunnelling parameters $D=\left\{\left(x_i,y_i\right)\mid i=\mathrm{1,2}\dots n_1\right\}$, where $x_i$ denotes the time variable, and $y_i$ denotes the tunnelling parameter. Furthermore, $X={\left\{x_i\right\}}_{i=1}^{n_1}$ denotes the $n_1\times 1$ dimensional input matrix, and $Y={\left\{y_i\right\}}_{i=1}^{n_1}$ denotes the corresponding output matrix. The distribution of the GP is jointly defined by the mean function $m\left(x\right)$ and the covariance function $k\left(x,x^{\prime }\right)$ (Williams and Rasmussen, 2006; Schulz et al., 2018), and the GP is expressed as follows:

$f\left(x\right)\sim GP\left(m\left(x\right),k\left(x,x^{\prime }\right)\right)(1)$

where

$m\left(x\right)=E\left[f\left(x\right)\right](2)$

$k\left(x,x^{\prime }\right)=E\left[\left(f\left(x\right)-m\left(x\right)\right)\left(f\left(x^{\prime }\right)-m\left(x^{\prime }\right)\right)\right](3)$

Mean function $m\left(x\right)$ represents the expectation value of function $f\left(x\right)$ at input point x. Covariance function $k\left(x,x^{\prime }\right)$ represents the correlation between two independent variables. The mean function is generally set to zero to simplify the calculation. In practice, the mean and covariance functions should be developed in accordance with the data characteristics to obtain a specific GP.

A specific GP regression model is established for tunnelling parameters. The GP is defined by a kernel function (covariance function), and a posterior distribution is updated given some observed data. This posterior distribution can be used to predict the expectation value and probability of output variable $Y_{*}$ given the input variable $X_{*}$ (Deng et al., 2020; Zeng et al., 2020).

Next, $n_2$ new samples $\left(X_{*},Y_{*}\right)$ are predicted based on the prior distribution of the GP and $n_1$ previously given tunnelling parameter data $\left(X,Y\right)$, where $Y$ and $Y_{*}$ obey the joint Gaussian distribution. The expression is as follows:

$\mathrm{p}\left(\left[\mathrm{Y},{\mathrm{Y}^}^{\ast }\right]\mid \mathrm{X},{\mathrm{X}^}^{\ast },\mathrm{\theta }\right)=\mathrm{N}\left(0,\mathrm{\Sigma }\right)(4)$

In this expression, $\left[\mathrm{Y},{\mathrm{Y}^}^{*}\right]$ is a vector that contains all the observed and predicted data, Xand X^* are their corresponding input variables, θ is the hyperparameter of the Gaussian process, and Σ is the covariance matrix.

The posterior prediction for $Y_{*}$ can be derived as follows:

$Y_{*}\mid X,Y,X_{*}\sim N\left({\overline{Y}}_{*},\mathrm{c}\mathrm{o}\mathrm{v}\left(Y_{*}\right)\right)(5)$

where

${\overline{Y}}_{*}=E\left[Y_{*}\mid X,Y,Y_{*}\right]=m\left(X_{*}\right)+k\left(X_{*},X\right){\left[k\left(X,X\right)+{\sigma }_n^{2}I\right]}^{-1}\left(Y-m\left(X\right)\right)(6)$

$\mathrm{c}\mathrm{o}\mathrm{v}\left(Y_{*}\right)=k\left(X_{*},X_{*}\right)-k\left(X_{*},X\right){\left[k\left(X,X\right)+{\sigma }_n^{2}I\right]}^{-1}k\left(X,X_{*}\right)(7)$

New tunnelling data $Y_{*}$ can be predicted using the posterior distribution of the GP model. The GP provides the predicted value of the model and its confidence interval. For example, a 95% confidence interval (CI) can be calculated from $\left[{\overline{Y}}_{*}-2\times \sqrt{\mathrm{c}\mathrm{o}\mathrm{v}\left(Y_{*}\right)},{\overline{Y}}_{*}+2\times \sqrt{\mathrm{c}\mathrm{o}\mathrm{v}\left(Y_{*}\right)}\right]$.

The dynamic advantage of Gaussian processes lies in the fact that they are Bayesian methods that can perform Bayesian inference based on prior distributions and data, enabling online updates and iterations. This feature enables Gaussian processes to adapt to real-time changing environments and data, and dynamically adjust the model to improve its predictive accuracy. In addition to providing prediction results, Gaussian processes can also provide uncertainty estimates related to the prediction results. This feature makes Gaussian processes highly advantageous in decision-making and risk assessment.

3.2 GP-based dynamic learning model

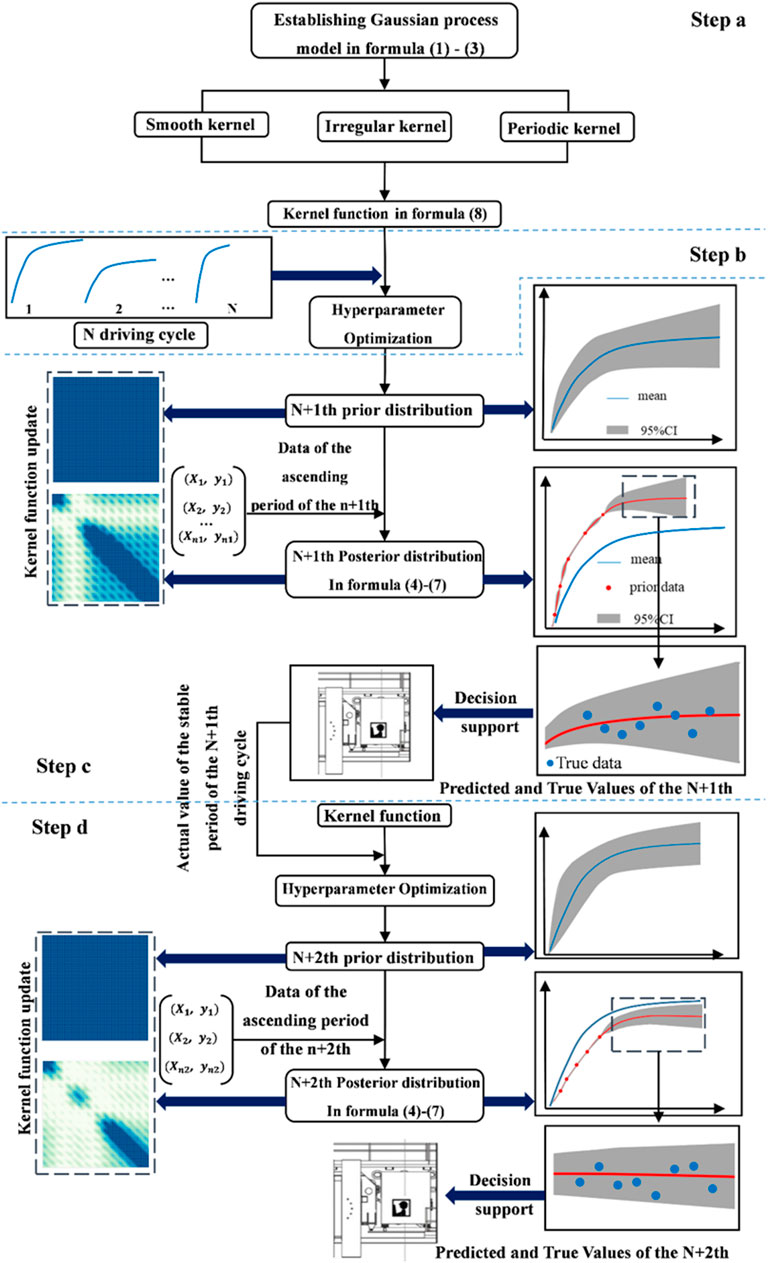
According to the Gaussian process principle and the requirement for the dynamic learning and prediction of TBM tunnelling parameters, the GP-based dynamic learning model (GDLM) was established as follows:

Step a. The most critical task in the GP is to establish a Gaussian kernel function (covariance function) according to data characteristics. Because actual data typically have multiple features, we can learn various data features by building a composite kernel function. Figure 2 displays that the time-series evolution of tunnelling parameters in each TBM driving cycle can be categorized into two distinct stages, namely, the ascending and stable stages. A periodic kernel was selected to learn the periodic evolution law of the tunnelling parameters. Furthermore, the overall trend of the driving cycle reveals a smooth change. Therefore, a smooth kernel (exponential quadratic kernel) can be used to learn the smooth evolution characteristics of the tunnelling parameters. Moreover, the evolution characteristics of the driving cycle in the stable period exhibit upward and downward fluctuations around the mean value so that we can select an irregular kernel (rational quadratic) to learn the characteristics of the parameters. Finally, the three kernel functions are added to form a composite kernel function that learns these three features:

$kernel=smooth\_kernel+irregular\_kernel+periodic\_kernel(8)$

Combining kernel functions can capture different features in the data by combining different kernel functions to improve the prediction ability of machine learning models.

Step b. Before using the kernel function for prediction, the hyperparameters in the Gaussian kernel function should be optimized. Appropriate hyperparameters can fit the characteristics of the data and generate an accurate prior distribution. The first N driving cycles are considered to be the training data, and the hyperparameters of the kernel function are tuned based on the training data. The process can be achieved by maximizing the marginal likelihood of GP distribution.

Step c. After tuning the hyperparameters based on the training data, the optimized model learns the data features of the first N driving cycles so that a priori prediction that conforms to the data features can be generated. The model is used to predict the N+1st driving cycle and generates a priori prediction of the N+1st driving cycle. The prior distribution curve has the evolution law of ascending and stable periods. As indicated in the Introduction section, the evolution of the ascending period in the driving cycle typically determines the selection of the stable period parameters. With ascending period data as the prior data, the kernel function is updated (i.e., Dynamic learning) based on the ascending period data to generate the posterior prediction of the stable period (the update and prediction process is performed simultaneously during the ascending period of the N+1st driving cycle). In the schematic of the kernel function update, the opacity of the gradient reveals the influence of a function value on its neighbors. The prediction result is the real-time expectation value and 95% CI of the parameter, in which the expectation value represents the most likely value of the parameter. The driver selects driving parameters according to the prediction results.

Step d. The parameters of N+1st driving cycle parameters are obtained after the drivers make decisions based on prediction results. Consider that the decision experience of the previous driving cycle affects the parameters of the current driving cycle. When predicting the N + 2 driving cycle, the kernel function is first used to fit the actual parameter of the N+1 driving cycle. After a priori prediction of the previous driving cycle, the kernel function is updated based on the data of the ascending period of the N + 2nd driving cycle, and a posterior prediction of the stable period is generated. After a priori prediction of the previous driving cycle, the kernel function is updated based on the data of the ascending period of the N+2nd driving cycle, and posterior prediction of the stable period is generated. Similarly, the prediction result is the expectation value and 95% CI at each moment of the stable period.

When predicting the N+3 driving cycle, the updating process of the model is similar to that of the N+2 driving cycle. This dynamic learning model is repeated to complete the parameter prediction of the entire tunnelling section. Figure 3 displays the flow of the GDLM for tunnelling parameter prediction.

FIGURE 3

FIGURE 3. Schematic of the GP-based dynamic learning model.

4 Application and discussion

4.1 Engineering background

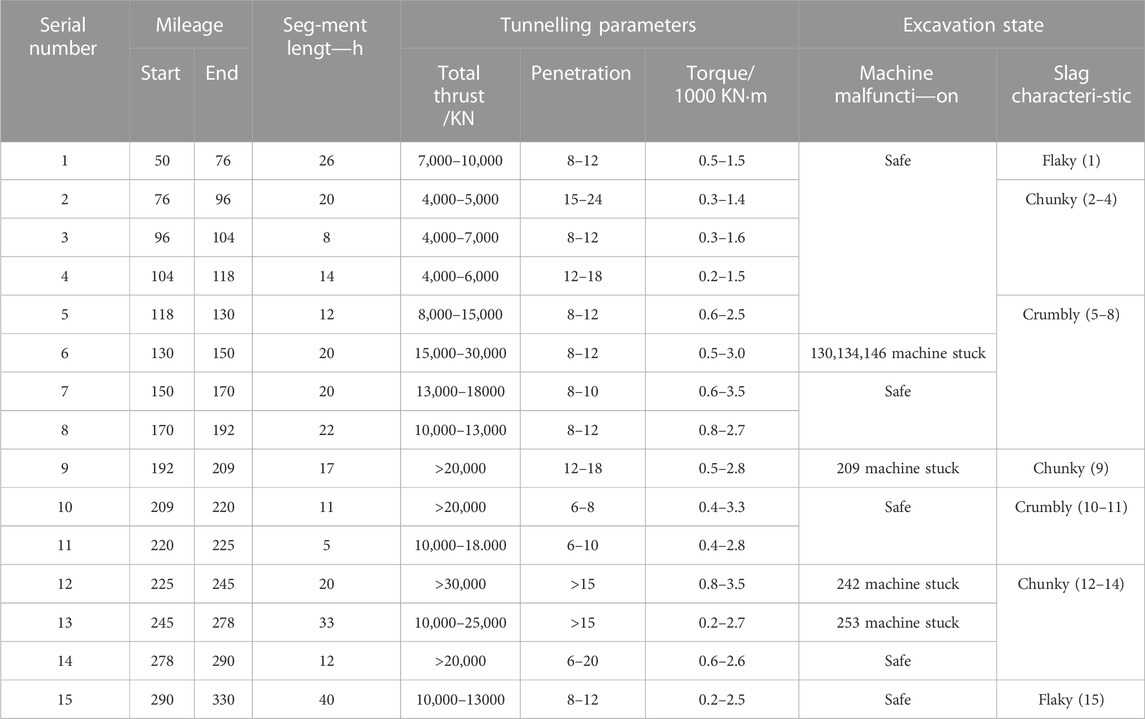
The GDLM was applied to a tunnel in western China, and its performance and the feasibility of engineering application were evaluated. A double-shield TBM was used to excavate the tunnel. The entrance and exit elevation of the tunnel were 3,500 m above the sea level, and the maximum buried depth was 820 m. The lithology of surrounding rock was primarily gneiss with mosaic or the sub-block structure. The surrounding rock is typically grade III, including sub-grades of III plus and III minus. IV-Grade surrounding rocks are presented in local deep-buried sections. Different driving parameters should be adopted when tunnelling in various grades of the surrounding rock. Figure 4A displays the cross-sectional view of the tunnel. The rock slag produced during excavation is in the form of flakes and blocks, and the shape of the rock slag is displayed in Figure 4B. In double-shield construction, the exposed space of surrounding rock is limited (Figure 4C), and the acquisition of conventional geological parameters is limited. Table 1 presents the tunnelling parameters and corresponding tunnelling conditions of tunnel section K10 + 050–K10 + 330, which indicates that the selection of tunnelling parameters plays a decisive role in normal tunnelling.

FIGURE 4

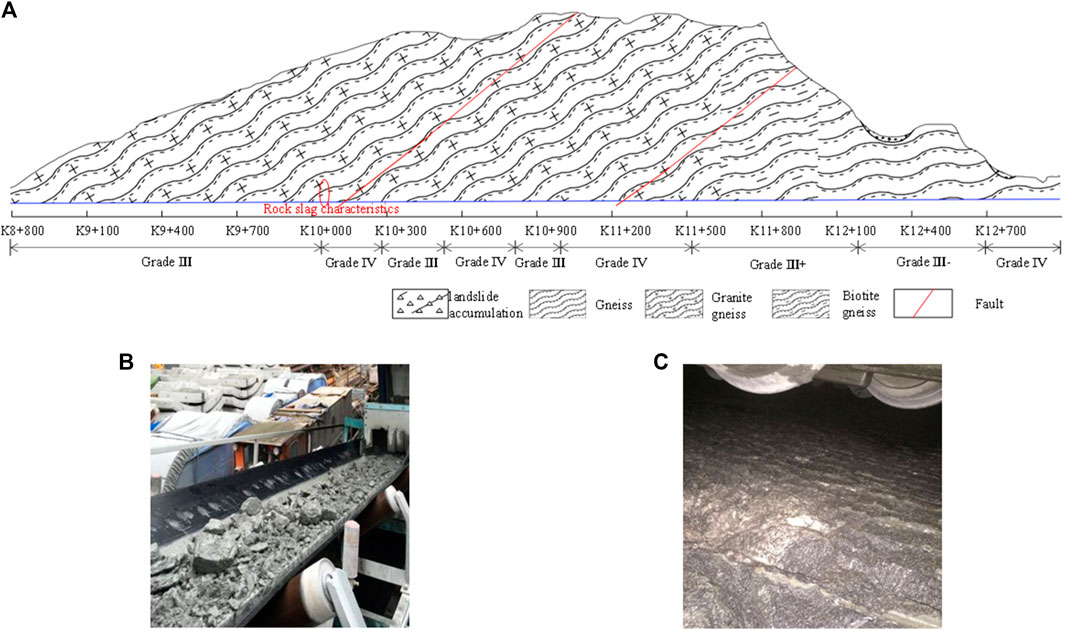
FIGURE 4. (A) Geological cross section along the tunnel, (B) Rock slag characteristics of section K10 + 080, (C) Tunnel condition of section K13+391.

TABLE 1

TABLE 1. Tunnelling parameters and condition of the K10 + 050–330 tunnel section.

4.2 Data processing

A total of 1,614 TBM driving cycles are recorded for the tunnel project, and the machine records the tunnelling parameters every 10 s during boring. The machine cannot excavate normally because of the incorrect parameter selection or improper driving, which results in machine jams and other accidents. Therefore, the recorded driving cycles do not comprehensively reflect the actual situation of the rock mass in Table 1. The existing driving conditions were screened, and the driving conditions of abnormal accident sections were eliminated. A total of 1,120 driving cycles corresponding to the normal working state of the machine were obtained. The outliers caused by equipment problems or human errors in the 1,120 driving cycles were eliminated in accordance with $P\left(\left|x-\mu \right|>3\delta \right)⩽0.003$.

The use of the GDLM to learn and predict complete driving cycle data requires a high time cost and cannot achieve real-time prediction. Therefore, the same duration of ascending and stable periods for each driving cycle were selected. The data of the first 50 s of the ascending period of each driving cycle were selected to obtain higher prediction accuracy at a lower time cost (Zhou et al., 2020). In the stable period, tunnelling parameters fluctuate slightly within a specific range, and the driver can usually make decisions according to the first 200 s of the tunnelling data. Therefore, the data for the first 50 s of the ascending period and the first 200 s of the stable period of each driving cycle were selected to construct the database. The data selection of ascending and stable period can be adjusted according to specific engineering scenarios.

Tunnelling parameters and conditions of the K10 + 050–330 tunnel section.

Table 2 presents the composition of the database and details the number of driving cycles at various rock grades and the value range of tunnelling parameters in the stable period. Data training is performed in a hardware environment equipped with an i5-7300HQ CPU, NVDIA GeForce GTX1050 GPU, and 8G of RAM and using Python-3.9.4 and TensorFlow-2.5.0 to construct a dynamic Gaussian process prediction model.

TABLE 2

TABLE 2. Number of driving cycles, range values of torque, and total thrust corresponding to each grade of surrounding rock.

Number of driving cycles, range values of torque, and total thrust corresponding to each grade of surrounding rock.

4.3 Model evaluation metrics

The average absolute error (MAE) and root mean square error (RMSE) were introduced to evaluate the validity of the model. The average time cost for model prediction was recorded to assess the feasibility of the real-time prediction of the model in engineering applications. The calculation formulas for each evaluation indicator are as follows:

$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{l}{\displaystyle \sum _{i=1}^l}\left|f\left(x_i\right)-y_i\right|(9)$

$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{l}{\displaystyle \sum _{i=1}^l}{\left(f\left(x_i\right)-y_i\right)}^2}(10)$

where $y_i$ is the true value of the data, $f\left(x_i\right)$ is the posterior prediction value, and $l$ is the number of predicted data. The more petite MAE and RMSE are, the closer the model prediction is to the actual value of the sample (i.e., the better the model predicts).

4.4 Model applications

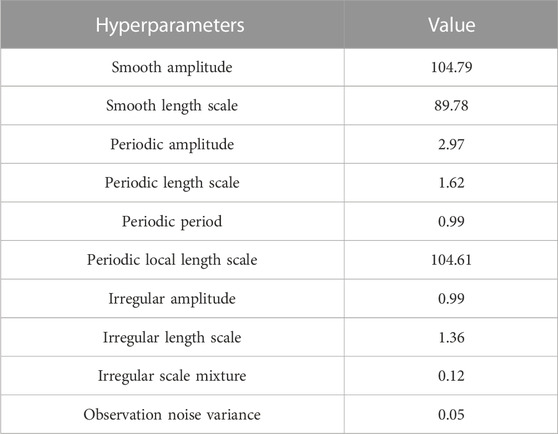
We build the prediction model based on the following compiled environment with the specific hyperparameters taken as shown in Table 3 and the python environment as shown in Table 4.

TABLE 3

TABLE 3. Values of parameter.

TABLE 4

TABLE 4. Python package versions.

According to the data processing in Section 4.2, the data of the first 50 s of the ascending period and the data of the first 200 s of the stable period were analysed for all the driving cycles, and 1,120 processed driving cycles were categorized into training and prediction data at a ratio of 5:1. Considering the torque prediction of grade III surrounding rock as an example, 508 driving cycles were selected as training data, and the remaining 102 driving cycles were dynamically learned and predicted.

First, the GDLM was trained based on 508 driving cycles to obtain the optimal kernel hyperparameters. The blue curve represents the expected value of the prior distribution (Figure 5A), which represents a trained prediction model. Next, the model was used to predict the tunnelling parameters of the 509th driving cycle and updated based on the first 50 s of actual ascending data to generate the posterior distribution. The red curve in Figure 5A displays the prediction value of torque in the stale period. The evolution trend of tunnelling parameters changed considerably after learning the ascending period parameter of the latest driving cycle dynamically. Figure 5B presents a comparison of the prior distribution, posterior distribution, and actual observed data of the 509th driving cycle. The results revealed that the posterior prediction of the model is accurate, and the driver can make decisions on the driving parameters of the stable period according to posterior prediction.

FIGURE 5

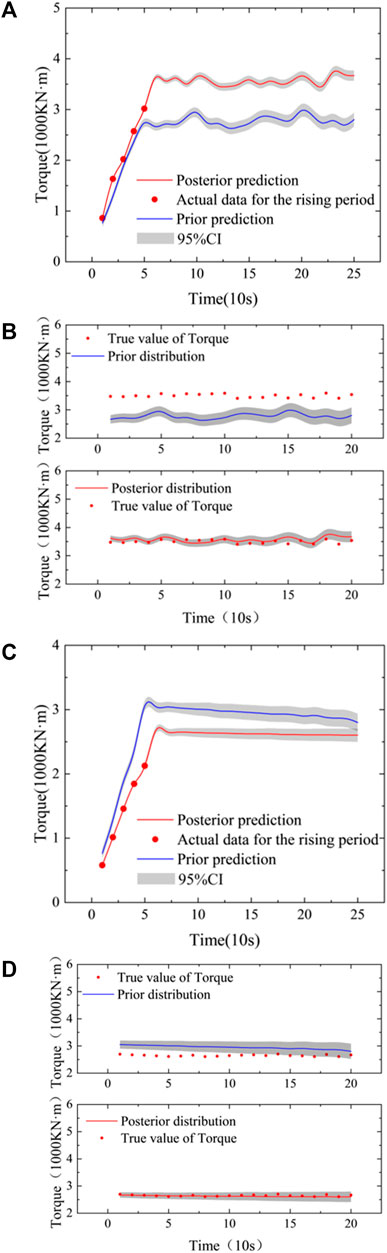
FIGURE 5. (A) Prior and posterior distributions for the 509th driving cycle, (B) Comparison of predicted and actual values for the 509th driving cycle, (C) Prior and posterior distributions for the 510th driving cycle, (D) Comparison of predicted and actual values for the 510th driving cycle.

To implement the model, the model was used to fit the actual parameters of the first 200 s of the 509th driving cycle, update the hyperparameter values, and generate the prior distribution of the 510th driving cycle in Figure 5C. The final model is updated based on the data of the first 50 s of the ascending period of the 510th driving cycle to generate a posterior distribution. Figure 5D displays a comparison between the prior and posterior distributions of the 510th driving cycle and the actual observed values. The figure also reveals that the posterior predicted value after dynamic learning and updating is closer to the actual value, which is beneficial to driver decision-making.

Figures 6A, B reveal the predicted results of the GDLM for torque and total thrust in the test. The predicted and actual values are the averages of the data. The predicted values are close to the actual values with minor absolute errors and relative errors of 2.7% and 1.9%, respectively. The prediction performance and average time cost of the model are presented in Table 5. Figure 6C displays the measured and predicted values of thrust and torque in a driving cycle of the test set in the chronological order. The predicted values of the total thrust force and cutter torque are consistent with the trend of the original curve, which indicates an excellent prediction capability.

FIGURE 6

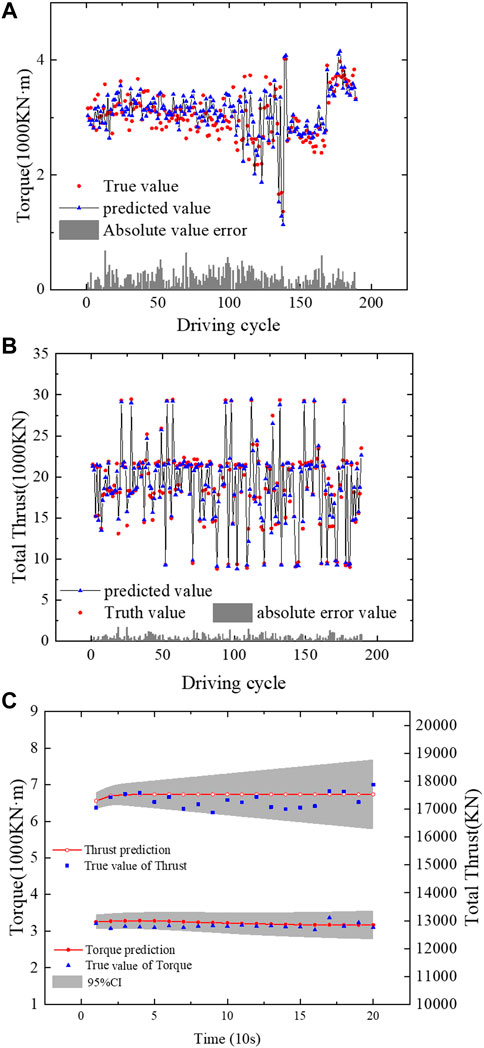
FIGURE 6. (A) Predicted results for torque, (B) Predicted results for the total thrust, (C) Predicted values of torque and total thrust for the first 200 s of a driving cycle.

TABLE 5

TABLE 5. Comparison of the three models.

4.5 Discussion

The performance of the GDLM is compared with those of random forest (RF) and LSTM models to discuss the feasibility of the GDLM in engineering applications. LSTM and RF models were established, and the torque prediction results were compared.

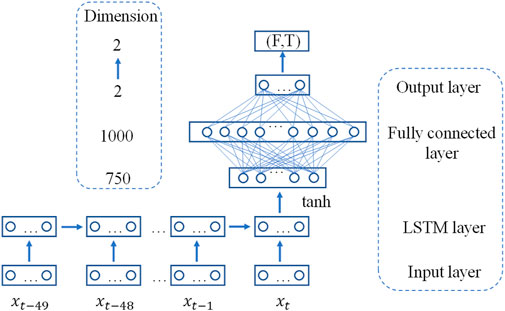
The LSTM model is displayed in Figure 7 (Li et al., 2020). Several tunnelling parameters were eliminated to avoid the influence of redundant features on the prediction accuracy of the model. The remaining parameters include total thrust, torque, excavation speed, cutter head rotation speed and penetration, cutter head power, propelling pump pressure, and support shoe pressure. LSTM is used to capture the relationship between the tunnelling parameters in the first 50 s of the ascending period. The tanh function is used as the activation function. The function is connected to the fully connected layer, which consists of two layers. The output dimension of the first layer is 1,000, and the output dimension of the final layer is 2, which corresponds to the predicted value of the total thrust and torque in the stable period. The average training and prediction time of the model is 53.3 s. Figure 8A reveals the prediction results of torque by using the LSTM model.

FIGURE 7

FIGURE 7. Long short-term memory (LSTM) model.

FIGURE 8

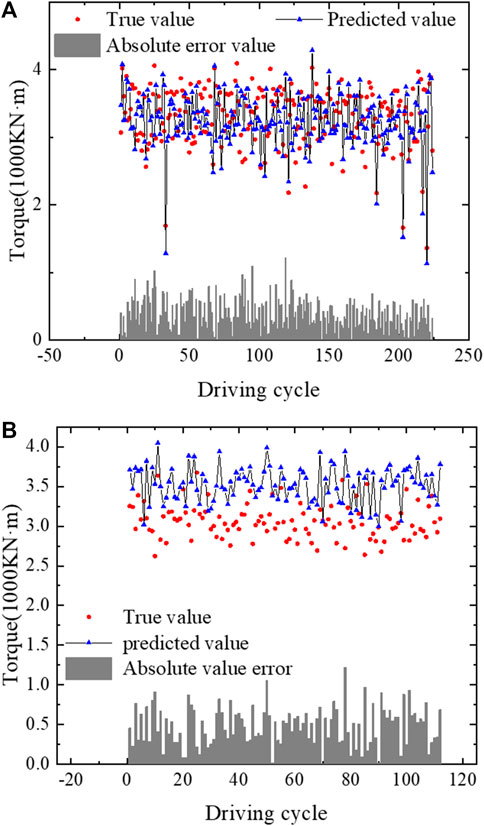
FIGURE 8. (A) Prediction results of torque by using the LSTM model, (B) Prediction results of torque by using the RF model.

The average values of the total thrust, cutter head speed, propelling pump pressure, propelling speed, and support shoe pressure in the ascending period were used for predicting the cutter head torque in the stable period during TBM tunnelling by using the feature importance calculation method based on the RF algorithm (Hou et al., 2022). The data of the first 50 s of the ascending period were used to predict the torque value of stable driving period, and the average training and prediction time of the model was 42.1 s. The parameters of the RF model are set as follows: Number of CARTs k = 50, characteristic variable m = 2 and max_depth = 4. Figure 8B displays the prediction results of the RF model.

In terms of prediction results, the GDLM can obtain the real-time prediction (expectation value and 95% CI) in a stable driving period. The prediction accuracy and model evaluation index value of GDLM were superior to those of the two other models, and the GDLM is more reliable when applied to engineering. IN the GDLM, the time cost of model prediction is reduced by updating a small amount of data in the ascending period and fitting a large amount of data in the stable period. The average time cost of prediction in the stable period is 29.7 s. The two other models are trained on multidimensional data, and their average time is longer than that of the GDLM.

5 Conclusion

To ensure efficient and safe construction of TBM tunnel engineering, an advanced dynamic learning model of tunnelling parameters based on the GP principle was proposed. Based on learning the decision-making experience of the historical driving cycles, the model can dynamically update by learning the evolution characteristics of the ascending period’s data of the current driving cycle and obtain the prediction interval of the subsequent stable period.

The model and the existing RF and LSTM models were applied to a tunnel project in western China. The results revealed that of the GDLM exhibited the highest prediction accuracy, and the relative errors of total thrust and torque were 1.9% and 2.7%, respectively. The fitting and update processes of GDLM were performed in the stable and ascending periods, and the time cost of model prediction was reduced. The posterior prediction of the stable period can be generated in an average of only 29.7 s. The prediction result is the real-time prediction means and 95%CI. Compared with the existing model, which can only provide a single average value in one driving cycle, the prediction result of the GDLM is consistent with the operating habits of the driver.

Compared with other traditional models, this model can not only deal with problems such as sudden changes in geological environment but also provide real-time prediction values to guide inexperienced field personnel in selecting appropriate excavation parameters. At the same time, in the face of the problem of insufficient on-site data, the model can update with less data and generate posterior predictions during the prediction process, making it very suitable for construction sites with high data costs.

The GDLM can dynamically update model features based on small sample data in an application scenario and obtain the predicted results of time-series parameters. This phenomenon is incomparable to the conventional learning strategy model, which can only be applied in a new scenario based on historical learning experiences. Furthermore, the dynamic learning strategy of the GDLM model can provide a reference for time-series data processing in similar engineering scenarios. For example, the model has considerable potential in decomposing signals of non-stationary time series, failure prediction through time-series analysis and dynamic fitting of non-linear multi-factor data.

Data availability statement

The datasets presented in this article are not readily available because the data that support the findings of this study are available from POWERCHINA SINOHYDRO BUREAU 10 CO., LTD. but restrictions apply to the availability of these data, which were used under license for the current study and are not publicly available. However, data are available from the authors upon reasonable request and with permission of POWERCHINA SINOHYDRO BUREAU 10 CO., LTD. Requests to access the datasets should be directed to http://www.chidi.com.cn/.

Author contributions

HL: Writing—original draft, Formal analysis. XL: Writing—original draft, Writing—Review & Editing. CM: Investigation, Funding acquisition. TL: Investigation, Methodolog. WY: Visualization. HZ: Data Curation. KD: Investigation. All authors contributed to the article and approved the submitted version.

Funding

This study was financially supported by the National Natural Science Foundation of China (Grant No. 42177173), State Key Laboratory of Geohazard Prevention and Geoenvironment Protection Independent Research Project (Grant No. SKLGP 2020Z010).

Acknowledgments

We thank the owner and construction personnel of the tunnel for providing us with rich data and kind support.

Conflict of interest

Author HL was employed by the company Power China Chengdu Engineering Corporation Limited. and Author HZ was employed by the company Chongqing City Construction Investment (Group) Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, Z. Y., Zhang, Y. P., Li, J. B., Li, X., and Jing, L. J. (2021). Diagnosing tunnel collapse sections based on TBM tunneling big data and deep learning: A case study on the yinsong project, China. Tunn. Undergr. Space Technol. 108, 103700. doi:10.1016/j.tust.2020.103700

CrossRef Full Text | Google Scholar

Deng, Z. W., Hu, X. S., Lin, X. K., Che, Y. H., Xu, L., and Guo, W. C. (2020). Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 205, 118000. doi:10.1016/j.energy.2020.118000

CrossRef Full Text | Google Scholar

Feng, S. X., Chen, Z. Y., Luo, H., Wang, S. Y., Zhao, Y. F., Liu, L. P., et al. (2021). Tunnel boring machines (TBM) performance prediction: A case study using big data and deep learning. Tunn. Undergr. Space Technol. 110, 103636. doi:10.1016/j.tust.2020.103636

CrossRef Full Text | Google Scholar

Gao, B. Y., Wang, R. R., Lin, C. J., Guo, X., Liu, B., and Zhang, W. G. (2021). TBM penetration rate prediction based on the long short-term memory neural network. Undergr. Space 6 (6), 718–731. doi:10.1016/j.undsp.2020.01.003

CrossRef Full Text | Google Scholar

Ghasemi, E., Yagiz, S., and Ataei, M. (2014). Predicting penetration rate of hard rock tunnel boring machine using fuzzy logic. Bull. Eng. Geol. Environ. 73 (1), 23–35. doi:10.1007/s10064-013-0497-0

CrossRef Full Text | Google Scholar

Gholami, M., Shahriar, K., Sharifzadeh, M., and Khademi, H. J. (2012). “A comparison of artificial neural network and multiple regression analysis in TBM performance prediction,” in ISRM regional symposium-7th asian rock Mechanics symposium (Seoul, Korea: ISRM).

Google Scholar

Guo, D., Li, J. H., Jiang, S. H., Li, X., and Chen, Z. Y. (2020). Intelligent assistant driving method for tunnel boring machine based on big data. Acta Geotech. 17 (4), 1019–1030. doi:10.1007/s11440-021-01327-1

CrossRef Full Text | Google Scholar

Hajihassani, M., Abdullah, S. S., Asteris, P. G., and Armaghani, D. J. (2019). A gene expression programming model for predicting tunnel convergence. Appl. Sci. 9, 4650. doi:10.3390/app9214650

CrossRef Full Text | Google Scholar

Harandizadeh, H., Armaghani, D. J., Asteris, P. G., and Gandomi, A. H. (2021). TBM performance prediction developing a hybrid ANFIS-PNN predictive model optimized by imperialism competitive algorithm. Neural Comput. Appl. 33 (23), 16149–16179. doi:10.1007/s00521-021-06217-x

CrossRef Full Text | Google Scholar

Hou, S. K., Liu, Y. R., Zhuang, W. Y., Zhang, K., Zhang, R. J., and Yang, Q. (2022). Prediction of shield jamming risk for double-shield TBM tunnels based on numerical samples and random forest classifier. Acta Geotech. 2022, 495–517. doi:10.1007/s11440-022-01567-9

CrossRef Full Text | Google Scholar

Jin, Y. R., Qin, C. J., Tao, J. F., and Liu, C. L. (2020). An accurate and adaptative cutterhead torque prediction method for shield tunneling machines via adaptative residual long-short term memory network. Mech. Syst. Signal Process. 165, 108312. doi:10.1016/j.ymssp.2021.108312

CrossRef Full Text | Google Scholar

Jing, L. J., Li, J. B., Zhang, N., Chen, S., Yang, C., and Cao, H. B. (2021). A TBM advance rate prediction method considering the effects of operating factors. Tunn. Undergr. Space Technol. 107, 103620. doi:10.1016/j.tust.2020.103620

CrossRef Full Text | Google Scholar

Keshtegar, B., Hasanipanah, M., Nguyen-Thoi, T., Yagiz, S., and Amnieh, H. B. (2021). Potential efficacy and application of a new statistical meta based-model to predict TBM performance. Int. J. Min. Reclam. Environ. 35 (7), 471–487. doi:10.1080/17480930.2021.1878087

CrossRef Full Text | Google Scholar

Koopialipoor, M., Fahimifar, A., Ghaleini, E. N., Momenzadeh, M., and Armaghani, D. J. (2020). Development of a new hybrid ANN for solving a geotechnical problem related to tunnel boring machine performance. Eng. Comput. 36 (1), 345–357. doi:10.1007/s00366-019-00701-8

CrossRef Full Text | Google Scholar

Li, G., Li, X., and Yang, W. (2020). Prediction of TBM tunnelling parameters based on deep learning. Mod. Tunn. Technol. 57, 154–159+176.

Google Scholar

Liu, B., Wang, R. R., Guan, Z. D., Li, J. B., Xu, Z. H., Guo, X., et al. (2019a). Improved support vector regression models for predicting rock mass parameters using tunnel boring machine driving data. Tunn. Undergr. Space Technol. 91, 102958. doi:10.1016/j.tust.2019.04.014

CrossRef Full Text | Google Scholar

Liu, K. L., Hu, X. S., Wei, Z. B., Li, Y., and Jiang, Y. (2019b). Modified Gaussian process regression models for cyclic capacity prediction of lithium-ion batteries. IEEE Trans. Transp. Electrification 5 (4), 1225–1236. doi:10.1109/TTE.2019.2944802

CrossRef Full Text | Google Scholar

Liu, Q. S., Wang, X. Y., Huang, X., and Yin, X. (2020). Prediction model of rock mass class using classification and regression tree integrated AdaBoost algorithm based on TBM driving data. Tunn. Undergr. Space Technol. 106, 103595. doi:10.1016/j.tust.2020.103595

CrossRef Full Text | Google Scholar

Liu, Z. B., Li, L., Fang, X. L., Qi, W. B., Shen, J. M., Zhou, H. Y., et al. (2021). Hard-rock tunnel lithology prediction with TBM construction big data using a global-attention-mechanism-based LSTM network. Automation Constr. 125, 103647. doi:10.1016/j.autcon.2021.103647

CrossRef Full Text | Google Scholar

Minh, V. T., Katushin, D., Antonov, M., and Veinthal, R. (2017). Regression models and fuzzy logic prediction of TBM penetration rate. Open Eng. 7, 60–68. doi:10.1515/eng-2017-0012

CrossRef Full Text | Google Scholar

Mohammadi, S. D., Torabi-Kaveh, M., and Bayati, M. (2015). Prediction of TBM penetration rate using intact and mass rock properties (case study: Zagros long tunnel, Iran). Arabian J. Geosciences 8 (6), 3893–3904. doi:10.1007/s12517-014-1465-0

CrossRef Full Text | Google Scholar

Salimi, A., Faradonbeh, R. S., Monjezi, M., and Moormann, C. (2018). TBM performance estimation using a classification and regression tree (CART) technique. Bull. Eng. Geol. Environ. 77 (1), 429–440. doi:10.1007/s10064-016-0969-0

CrossRef Full Text | Google Scholar

Salimi, A., Rostami, J., Moormann, C., and Delisio, A. (2016). Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 58, 236–246. doi:10.1016/j.tust.2016.05.009

CrossRef Full Text | Google Scholar

Schulz, E., Speekenbrink, M., and Krause, A. (2018). A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 85, 1–16. doi:10.1016/j.jmp.2018.03.001

CrossRef Full Text | Google Scholar

Sun, W., Shi, M. L., Zhang, C., Zhao, J. H., and Song, X. G. (2018). Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Automation Constr. 92, 23–34. doi:10.1016/j.autcon.2018.03.030

CrossRef Full Text | Google Scholar

Williams, C. K., and Rasmussen, C. E. (2006). Gaussian processes for machine learning. United States: MIT press Cambridge MA, 4.

Google Scholar

Xu, H., Zhou, J., Asteris, P. G., Armaghani, D. J., and Tahir, M. Md. (2019). Supervised machine learning techniques to the prediction of tunnel boring machine penetration rate. Appl. Sci. 9 (18), 3715. doi:10.3390/app9183715

CrossRef Full Text | Google Scholar

Yang, H. Q., Wang, Z. H., and Song, K. L. (2020). A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Eng. Comput. 38 (3), 2469–2485. doi:10.1007/s00366-020-01217-2

CrossRef Full Text | Google Scholar

Yang, J. H., Yan, C. B., Miao, D., and Wang, Yao. (2019). Comprehensive advanced geological prediction methods for tunnel construction with double sheild TBM. J. Eng. Geol. 27 (2), 250–259. doi:10.13544/j.cnki.jeg.2018-044

CrossRef Full Text | Google Scholar

Yang, W., Zhao, J., Li, J., Chen, Z., and Chen, S. (2023). A propensity score matching analysis of neutrophil to lymphocyte ratio forecasts the survival of individuals undergoing the transjugular intrahepatic portosystemic shunt. Acta Geotech. 2023, 1–15. doi:10.1080/02648725.2023.2196824

CrossRef Full Text | Google Scholar

Yao, L., Zhang, S., Cui, Z., and Peng, S. (2019). Study on comprehensive advanced geological prediction technology of double shield TBM construction. J. Undergr. Space Eng. 5, 1549–1556.

Google Scholar

Yu, H., Tao, J., Qin, C., Xiao, D., Sun, H., and Liu, C. (2021). Rock mass type prediction for tunnel boring machine using a novel semi-supervised method. Measurement 179, 109545. doi:10.1016/j.measurement.2021.109545

CrossRef Full Text | Google Scholar

Zeng, A. R., Ho, H. D., and Yu, Y. (2020). Prediction of building electricity usage using Gaussian Process Regression. J. Build. Eng. 28, 101054. doi:10.1016/j.jobe.2019.101054

CrossRef Full Text | Google Scholar

Zeng, J., Roy, B., Kumar, D., Mohammed, A. S., Armaghani, D. J., Zhou, J., et al. (2021). Proposing several hybrid PSO-extreme learning machine techniques to predict TBM performance. Eng. Comput. 38, 3811–3827. doi:10.1007/s00366-020-01225-2

CrossRef Full Text | Google Scholar

Zhang, Q. L., Hu, W. F., Liu, Z. Y., and Tan, J. R. (2020). TBM performance prediction with Bayesian optimization and automated machine learning. Tunn. Undergr. Space Technol. 103, 103493. doi:10.1016/j.tust.2020.103493

CrossRef Full Text | Google Scholar

Zhang, Q. L., Liu, Z. Y., and Tan, J. R. (2019). Prediction of geological conditions for a tunnel boring machine using big operational data. Automation Constr. 100, 73–83. doi:10.1016/j.autcon.2018.12.022

CrossRef Full Text | Google Scholar

Zhao, Z., Gong, Q., Zhang, Y., and Zhao, J. (2007). Prediction model of tunnel boring machine performance by ensemble neural networks. Geomechanics Geoengin. Int. J. 2 (2), 123–128. doi:10.1080/17486020701377140

CrossRef Full Text | Google Scholar

Zhou, J., Qiu, Y. G., Zhu, S. L., Armaghani, D. J., Khandelwal, M., and Mohamad, E. T. (2021b). Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 6 (5), 506–515. doi:10.1016/j.undsp.2020.05.008

CrossRef Full Text | Google Scholar

Zhou, J., Qiu, Y. G., Zhu, S. L., Armaghani, D. J., Li, C. Q., Nguyen, H., et al. (2021a). Optimization of support vector machine through the use of metaheuristic algorithms in forecasting TBM advance rate. Eng. Appl. Artif. Intell. 97, 104015. doi:10.1016/j.engappai.2020.104015

CrossRef Full Text | Google Scholar

Zhou, X., Gong, Q., and Yin, L. (2020). Predicting boring parameters of TBM stable stage based on BLSTM networks combined with attention mechanism. Chin. J. Rock Mech. Eng. 39, 3505–3515.

Google Scholar

Zhu, M. Q., Zhu, H. H., Wang, X., and Cheng, P. P. (2020). Study on CART-based ensemble learning algorithms for predicting TBM tunnelling parameters and classing surrounding rockmasses. Chin. J. Rock Mech. Eng. 39 (9), 1860–1871. doi:10.13722/j.cnki.jrme.2019.0924

CrossRef Full Text | Google Scholar

Zimu, L., Bejarbaneh, B. Y., Asteris, P. G., Koopialipoor, M., Armaghani, D. J., and Tahir, M. M. (2021). A hybrid GEP and WOA approach to estimate the optimal penetration rate of TBM in granitic rock mass. Soft Comput. 25 (17), 11877–11895. doi:10.1007/s00500-021-06005-8

CrossRef Full Text | Google Scholar