- 1Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD)/Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET)/Key Laboratory for Aerosol Cloud-Precipitation of China Meteorological Administration, Nanjing University of Information Science and Technology, Nanjing, China
- 2Qingdao Ecological and Agricultural Meteorological Center, Qingdao, China
- 3Fujian Meteorological Disaster Defense Technology Center, Fuzhou, China
Due to the propagation effect, the arrival time of the ground wave peak is delayed when sferics propagate at long distances. In this work, we propose a new method combined with a numerical algorithm to correct the effect of the ground wave peak time delay and calculate the ionosphere height using the difference between the arrival time of the ground wave and the skywave. The results showed that, with each increase of the propagation distance by 100 km, the delay in arrival time of the ground wave peak increased by an average of 0.9 μs. For the first and second reflectance heights, the maximum heights observed at night were 86 km and 89 km, and the minimum heights during the day were 66 km and 69 km, respectively. Using the difference in arrival time between the ground wave and skywave and the ionosphere equivalent reflection height, a single site was used to estimate the distance of lightning occurring within 900 km. This method had an average relative error of 14.6%, an average absolute error of 128.8 km, and a median distance error of 52.6 km. Finally, the percentage of data with an estimated deviation within 10% increased from 52% to 65%.
1 Introduction
The ionosphere D region is usually considered to be the atmospheric plasma layer at an altitude of 50–90 km above the ground, which is ionized by solar radiation and contains free electrons (Cummer et al., 1998). Due to the presence of electrons and ions, the ionosphere can reflect extremely-low-frequency (ELF; 3–3000 Hz) and very-low-frequency (VLF; 3–30 kHz) electromagnetic waves, which are commonly known as sferics (a shortened form of atmospherics). Sferics travel thousands of kilometers in the Earth–ionosphere waveguide (EIWG) with little attenuation (∼2–3 dB/1,000 km) (Ammar and Ghalila, 2020). Therefore, sferics have been widely used to examine ionosphere reflection characteristics (Inan et al., 2010). Since the development of detection technology in recent years, studying the ionosphere D region using sferics has also become a vital detection technology.
Smith et al. (2004) used VLF/LF electric-field-change signals recorded by the Los Alamos Sferic Array (LASA) to calculate the height of the ionosphere. On this basis, Jacobson et al. (2008) analyzed the effects of solar zenith angle, electromagnetic wave propagation distance, and propagation orientation on the ionosphere height. Lay and Shao (2011a), Lay and Shao (2011b), and Shao et al. (2013) used multi-station lightning location results to invert the temporal and spatial variations of ionosphere heights in the region near a large thunderstorm. The results showed that the height of the inverse ionosphere reflection exhibited temporal and spatial fluctuations even in the absence of thunderstorms beneath these regions. The phase propagation velocity of these fluctuations ranged from 45 to 85 m/s. It lasted for several hours, suggesting that it may be due to the perturbation of the ionosphere by the gravity waves of the thunderstorm. Tran et al. (2017) computed the vertical electric field and azimuthal magnetic field at distances of 50 to 500 km from the lightning channel using the 2-D FDTD method and estimated the apparent ionosphere reflection heights. The model predicted that within 300 km in the nighttime and 200 km in the daytime, the apparent reflection heights are within approximately 10% of the reference height h0 for both the first and the second skywaves. Azadifar et al. (2017) calculated the ionosphere reflection height using the waveform of the electric field generated by the upward lightning flash at a distance of 380 km. The difference between the arrival times of the ground wave and skywave was used to estimate ionosphere reflection height during day and night times, based on the so-called peak-to-peak and zero-to-zero methods. Zhou et al. (2021) assumed a parameter
The time difference between the ground wave and the skywaves can be used to calculate the reflection height of the ionosphere D region and estimate the distance of lightning. However, due to the curvature of the Earth and the finite conductivity of the ground, when the electromagnetic waves generated by lightning propagate along the ground, the ground wave will be attenuated. As propagation distance increases, the arrival time of the ground wave significantly lags the arrival time of the speed of light; thus, the actual time difference between the ground wave and the skywaves should be larger than that in the waveform data. Therefore, this work proposes a new method combined with a numerical algorithm to correct the ground wave time delay due to long-distance propagation to calculate a more reliable reflection height of the ionosphere D region. Moreover, the ionosphere reflection height combined with the arrival time difference between the ground wave and the skywaves can estimate the distance of the lightning source from a single site.
2 Data analysis method
2.1 Description of the experimental instrument and data
Based on a long-range lightning location network with a very-low-frequency band that we have established in China (Li et al., 2022), the original magnetic field waveform data are recorded and sent to the server as long as it exceeds the minimum threshold with a sampling rate of 1 MS/s. The modified empirical wavelet transform (MEWT) method based on the empirical wavelet transform (EWT) is used for the azimuthal magnetic fields field signal de-noising. A GPS receiver at the station provided a one-pulse-per-second (1 PPS) output as a reference source for tagging data sample times, with an accuracy of ±50 ns. Our previous work compared our lightning location results with the advanced direction-time lightning detection (ADTD) system. Compared with ADTD, the average location error was 4.32 km, with a standard deviation of 2.46 km (Zhang et al., 2022).
Since various time zones affect the sunlit point, the electron concentration in the ionosphere will vary depending on the location, which could result in variations in the ionosphere's equivalent reflection height. To obtain the complete curve of the ionosphere reflection height with time, we chose data within a region, as shown in Figure 1A, in which 6612 lightning strikes were recorded 430 km–1,240 km from the Nanjing station. The characteristics of the first and second skywaves in the sferics can be more clearly distinguished within this range, and we distinguished the time stamps of lightning by colors. Additionally, as shown in Figures 1B–D, we chose data from three distinct times and contrasted them with cloud top temperature (CTT) data obtained by the Advanced Geosynchronous Radiation Imager (AGRI) carried by Feng Yun IV. The black cross in the figure represents our multi-station lightning location results, while the red cross represents ADTD’s lightning location results. The dark blue area in the figure indicates a lower CTT value of the area and NJ is the single site we built. The lightning events were all observed in the cloud regions with CTT at about 210–220 K, suggesting a reasonable location accuracy. The good overlay of data from different periods with CTT and ADTD lightning location results further illustrates the reliability of the data.
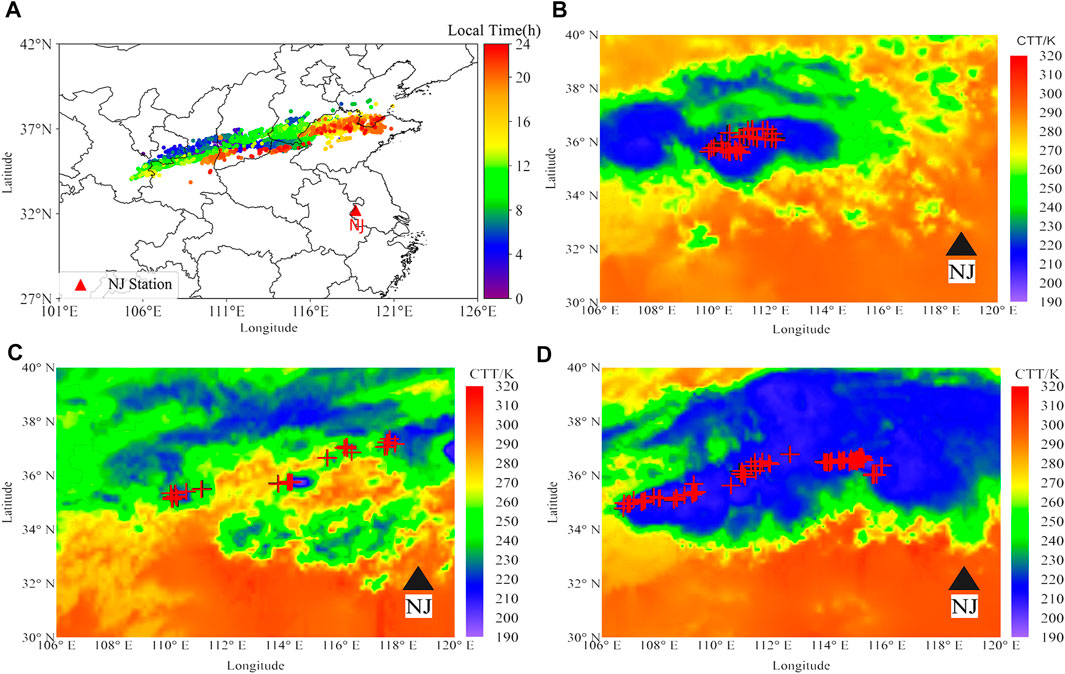
FIGURE 1. istribution of lightning events in selected regions on 3 October 2021(local time: UT+8) (A) from 00:00 to 23:59; (B) from 02:00 to 02:15; (C) from 09:00 to 09:15; and (D) from 20:00 to 20:15.
2.2 Ground wave peak delay versus distance
The arrival time and waveform of the electromagnetic waves are different from those under ideal ground conditions when the low-frequency (LF)/VLF electromagnetic waves radiated by the lightning discharge travel along the Earth’s surface because the electromagnetic waves propagated over long distances are affected by the irregular ground conductivity distribution on the propagation path, complex terrain, and other factors. Numerous observations and simulations support this phenomenon (Shao and Jacobson, 2009; Hou et al., 2020). The error in calculating the ionosphere reflection height and estimating the lightning distance by a single site using the time differential between the ground wave and the skywave will rise as the propagation distance increases. The ground wave arrival time delay caused by an increase in propagation distance is referred to in this study as
The background noise that interferes with the sferics during propagation comes from a variety of sources, including the power supply, the thermal noise of the device, the interference noise between the lines, the external noise brought by the signal transmitter around the station, the high-voltage power supply line, and equipment that does not consider electromagnetic compatibility, which makes it more difficult to identify the peak of the ground wave and the skywaves. A two-dimensional finite difference time domain (FDTD) model was used to simulate the propagation of sferics in EIWG to precisely determine the peak sites of the ground wave and the skywaves of the actual sferics waves. This simulation was conducted under typical daytime and nighttime ionosphere conditions at propagation paths of 100 km–3,000 km. The size of the FDTD simulation domain was 3,200 km × 100 km, the space step was set to ∆r = ∆z = 500 m, the time step ∆t was 1 µs to ensure the same time resolution as the observed data, and the length of the lightning channel was 10 km. The reference height of the ionosphere was set to 70 km for the daytime condition and 85 km for the nighttime condition. The density of positive ions was set to the same value as the electrons but with a minimum value of 200 cm−3 for the daytime condition and 100 cm−3 for the nighttime condition. The parameter settings of the simulations matched those of Li et al. (2022), Hou et al. (2018), and Hou et al. (2020). We used this model to simulate the propagation of VLF lightning electromagnetic waves in EIWG and establish a waveform bank containing simulated lightning waveforms with different propagation distances (from 100 km to 3,000 km, with a distance interval of 100 km).
It is simple to identify the peak points of the ground wave and skywaves on the simulated waveforms because they were created under perfect conditions. Following that, using the method suggested by Carvalho et al. (2017), the peak points of the ground wave and skywaves in the simulated waveform bank were determined by identifying the fast and slow breakpoints in the waveform. The waveform in the simulated waveform bank with the highest correlation coefficient to the real sferics waveform was found using the cross-correlation technique. The peak points of the simulated waveform were determined to accurately identify the peak points of the ground wave and skywaves of the actual waveform; we set the length of the sliding time window to 10 µs, centering on the peak points of the simulated waveform and searched for the peak points of the actual sferics waveform within the time window. This method was also used by Li et al. (2022), in which the peak point of the ground wave was obtained by matching. The matching approach can still precisely identify the peak spots of the ground wave and skywaves even though the sferics is impacted by noise, and there are some differences between the actual and matched waveforms in the waveform bank. The peak points of some actual waveforms, however, might appear not within the time window due to noise interference; this part of the data was not used in the following work in the present study.
2.3 Time delay revision
We used a model simulation based on the theories of ground wave propagation along the spherical Earth surface with finite conductivity proposed by Hill and Wait to account for the propagation (Hill and Wait, 1980).
When both finite ground conductivity and the curved surface of the Earth are considered, the attenuation factor in the frequency domain is calculated as (Wait, 1974)
In Eqs 1–5:
where
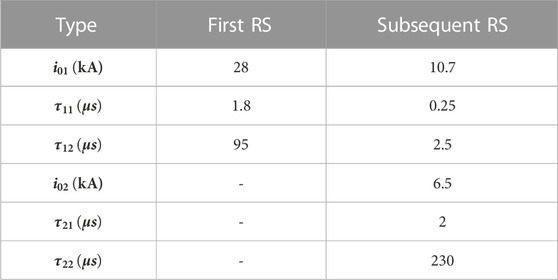
This study considered three current waveforms, corresponding to typical first return stroke (RS), subsequent RS, and dipole source waveforms. We calculated the spatial-temporal distribution of the lightning current along the channel by using the modified transmission line model with exponential current decay with height (MTLE) mode (Nucci et al., 1988). The current source waveforms for the first and subsequent RS were in the form of a double Heidler function (Heidler et al., 1999), assuming that the amplitude decreased exponentially with increasing height as the lightning current travels up the lightning channel, while the return stroke current waveform of dipole source was assumed to be uniform along the lightning discharge channel (Hu and Cummer, 2006). The lightning channel length
Table 1 shows the typical lightning-based current waveforms of the first and subsequent RS commonly used in engineering calculations (Rachidi et al., 2001).
The RS current waveform of the dipole source was assumed to be uniform along the lightning discharge channel as follows:
where
Figure 2A shows the current waveforms of the typical first and subsequent RS. Compared with the first RS, the rising edge of the subsequent RS is steeper and contains more high-frequency components. Figure 2B shows the current waveforms of the dipole source.
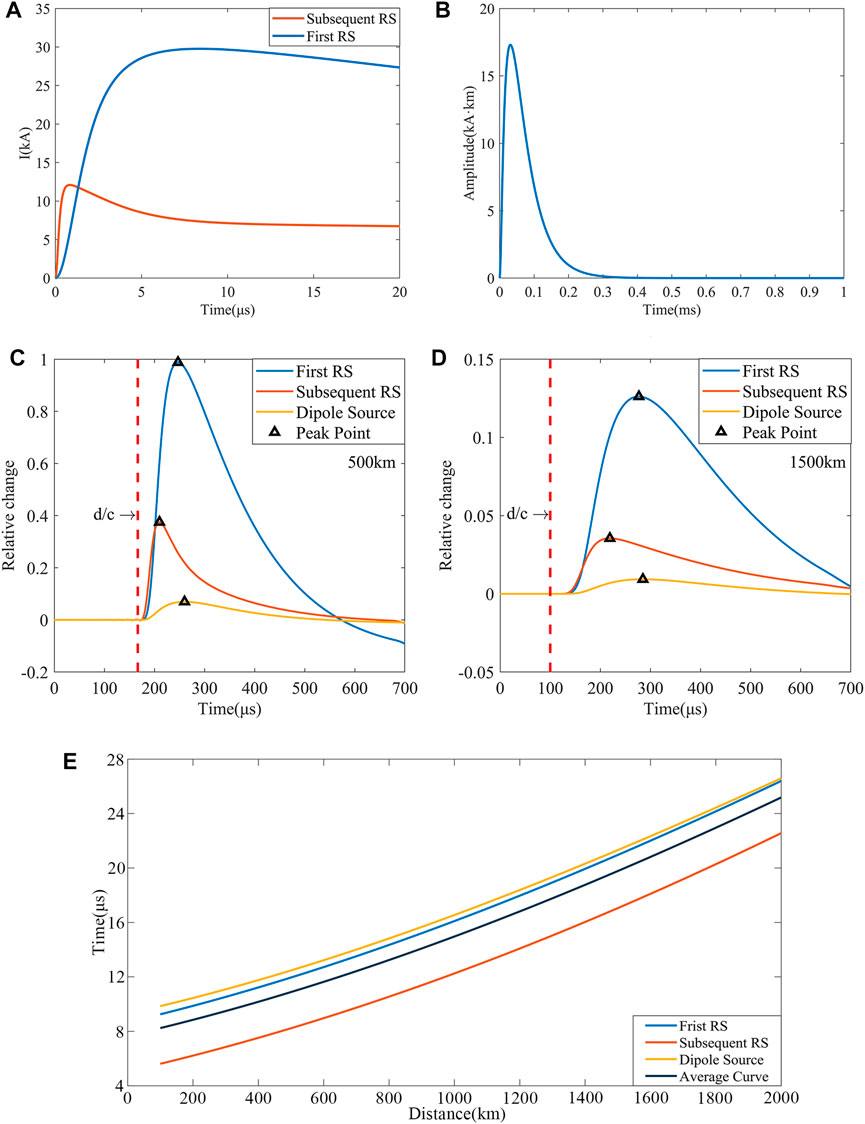
FIGURE 2. ightning current waveforms and time delay versus distance curves. (A) Current waveforms of the typical first RS and subsequent RS. (B) The current waveform of the dipole source. (C) Simulated waveforms of different current sources at 500 km. (D) Simulated waveforms of different current sources at 1500 km. (E) Delay in ground wave peak arrival time compared to
Figures 2C–E show simulated waveforms at different distances and the time difference between the peak time of the ground wave and
2.4 Inverse ionosphere reflection height
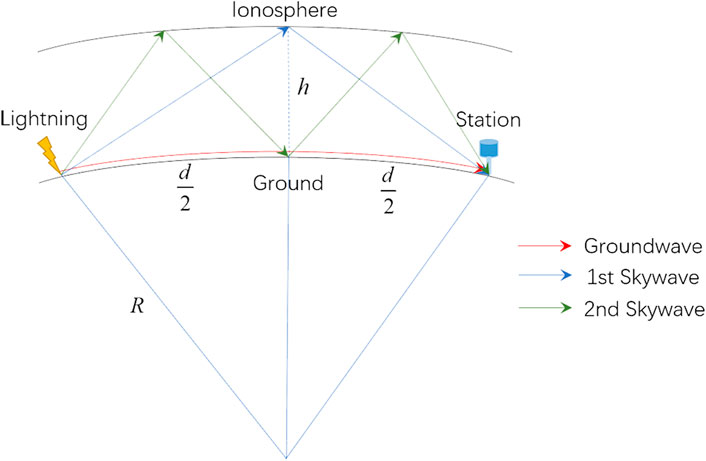
The geometric model of sferics propagation in the EIWG is given in Figure 3. The sferics propagate in the EIWG through multiple specular reflections from the Earth’s surface and the ionosphere D layer. The sferics propagating along the ground is the ground wave, while the sferics reflected by the ionosphere is the skywave. The model assumes that the ground is a good conductor and that electromagnetic waves propagate at the speed of light. The ionosphere equivalent reflection height can be determined (Wait, 1974) by considering the geometric relationship between the ground wave and skywave and the difference in their arrival times.
The reflection height of the first skywave (
Similarly, the expression of the second skywave reflection height (
In Eqs 9, 10,
However, when the lightning propagates long distances, using the aforementioned equation, a certain error is present due to the ground wave peak time delay. Previous research demonstrated that propagation over the land for a distance of about 130 km with a conductivity of 3 mS/m resulted in an average peak of RS pulse delay of 1.8 µs (Honma et al., 1998). According to the simulation results of Shao and Jacobson (2009), the leading edge and the peak were delayed by 5 μs and 13 µs, respectively, at a distance of 1,000 km. In general, electromagnetic wave propagation over terrain with lower ground conductivity results in a larger arrival time delay. The present study considered a ground wave arrival time delay caused by the propagation effect, with the theoretical time difference between the arrival time of the skywave and the ground wave assumed to be
where
We substituted the distance (
To determine the continuous 24-h variation of the ionosphere equivalent reflection height and calculate the distance between the lightning strike point and single site, we substituted the distance (
We applied the results discussed previously to the lightning events that occurred between 00:00 and 23:59 on 13 October 2021, to invert the day-by-day variation of the ionosphere equivalent reflection height. The distances of the lightning data used in this paper from Nanjing station ranged from 430 km to 1240 km. The altitudes of the source and receiving stations were neglected in the computation. The precision of the computation results was unaffected by treating the height as 0 km.
Figures 4, 5 show the ionosphere equivalent reflection height (
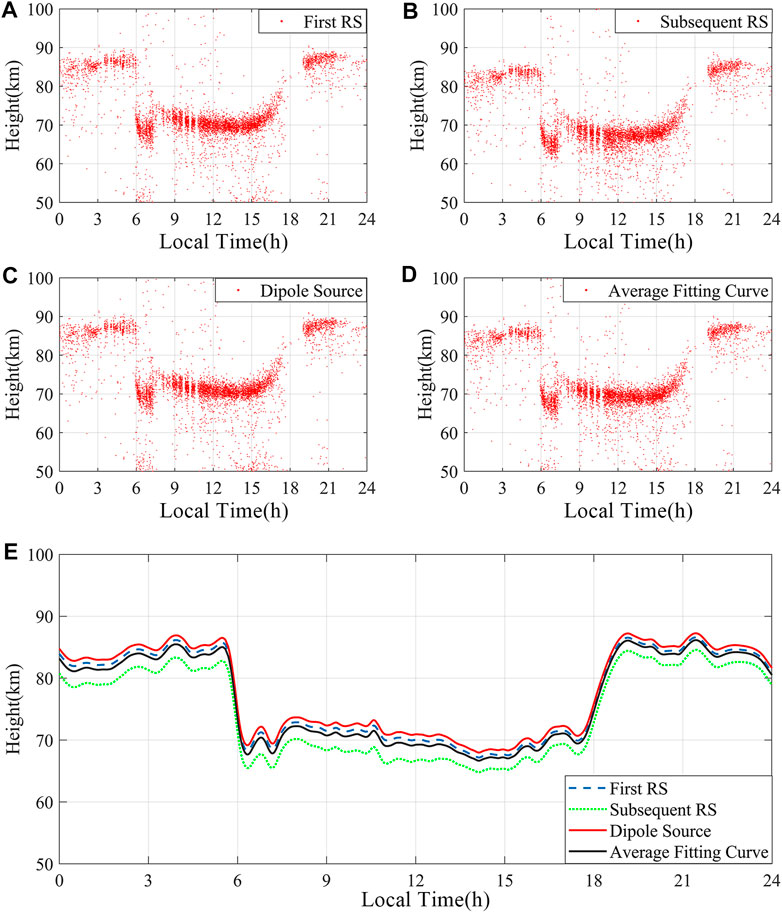
FIGURE 4. Scatter plot and a line graph of
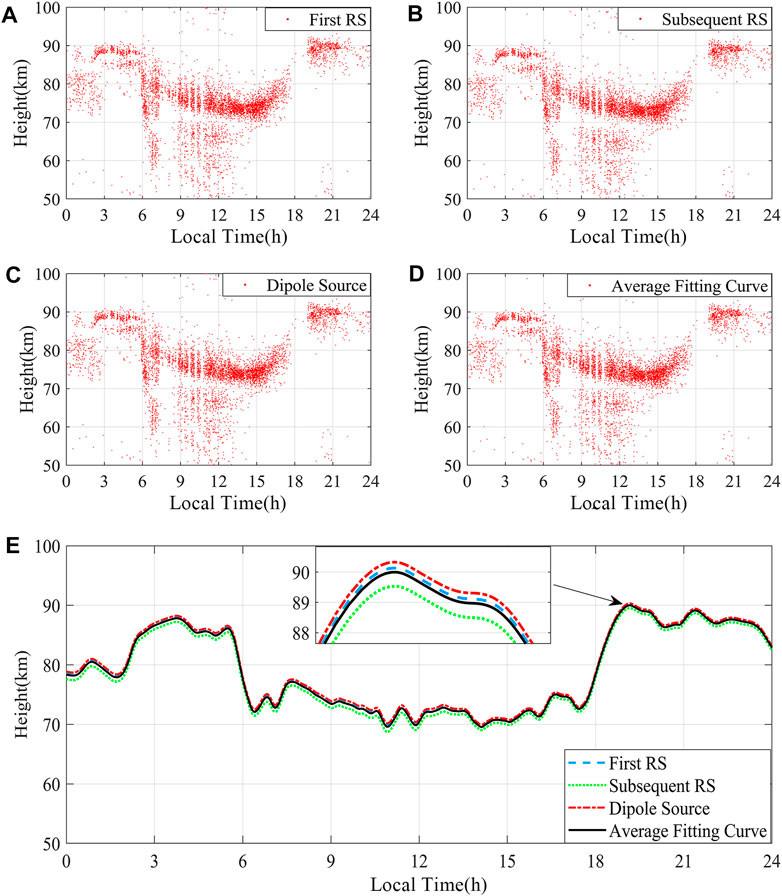
FIGURE 5. Scatter plot and a line graph of
Figures 5A–C are scatter plots of
Figure 2 shows that the
In both the time delay versus distance curves (Figure 2) and the ionosphere equivalent reflection heights (Figures 4, 5), the average fitted curves can be considered close to the results for the three different current sources. Thus, we used the average fitting curve to revise the ground wave arrival time delay and applied the revised ground wave arrival time in the following work.
3 Results and analysis
3.1 Temporal variations of continuous 24 h
Figures 6A, B show the scatter and line graphs of the ionosphere equivalent reflection height with time delay. From 00:00 to 05:30 LT (local time: UT + 8),

FIGURE 6. The scatter and line graphs of the ionosphere reflection heights in the ionosphere D region (Local Time: UT+8). (A) Scatter graph and without considering time delay; (B) Line graph and without considering time delay. (C) Scatter graph and considering time delay; (D) Line graph and considering time delay.
Figures 6C, D show the scatter and line graphs of the ionosphere equivalent reflection height without considering the time delay. The trend of the height changes over time in the figure is close to the result in Figures 6A, B; however, the calculated height is slightly lower than that obtained by considering the time delay. From 00:00 to 05:30 LT,
Figure 6 demonstrates that when a time delay is considered, the height difference between
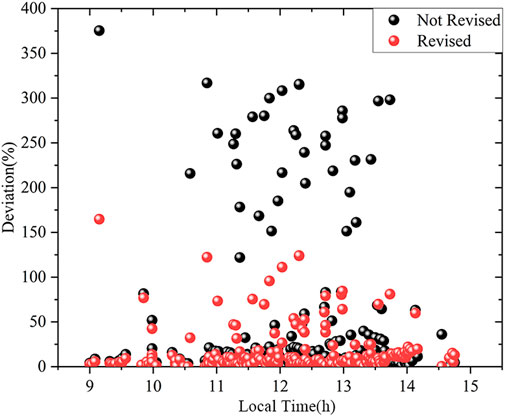
To further illustrate the reliability of the revised method in this study, the curve of the ionosphere equivalent reflection height variation with time was plotted using the method proposed by Zhou et al. (Azadifar et al., 2017). It should be noted that the “revised” and “not revised” in this study refer to the revision of the ground wave arrival time. It is significant to note that the approach described by Zhou presupposed that
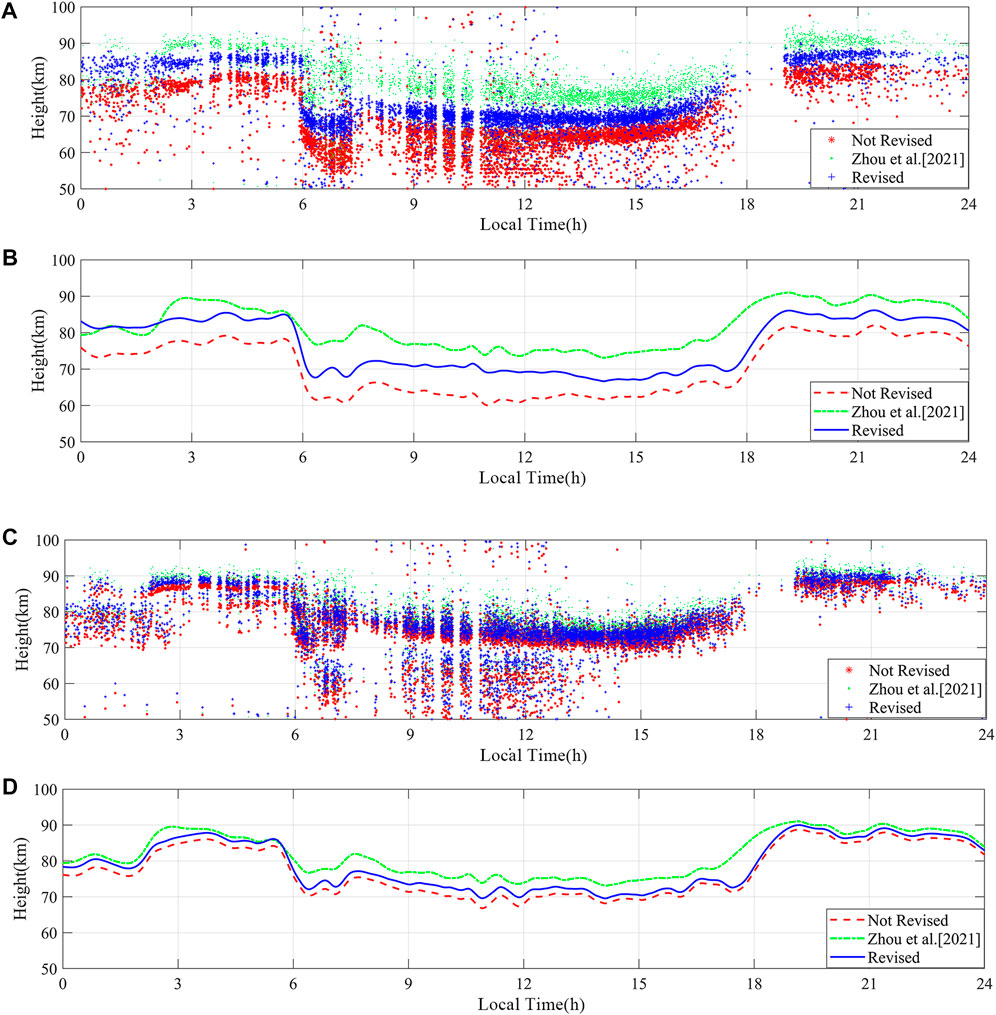
FIGURE 7.
The Consultative Committee on International Radio (CCIR) recommends an ionosphere equivalent reflection height at night and noon of about 87 km and 70 km, respectively (Azadifar et al., 2017), which is consistent with the results obtained in this study. These comparisons show that when lightning occurs over a long distance, the calculated height will be slightly lower due to the effect of delayed ground wave time. The method proposed in this study can better revise this error and increase the reliability of the height measurement value, which also supports the subsequent distance estimation using the ionosphere reflection height.
The
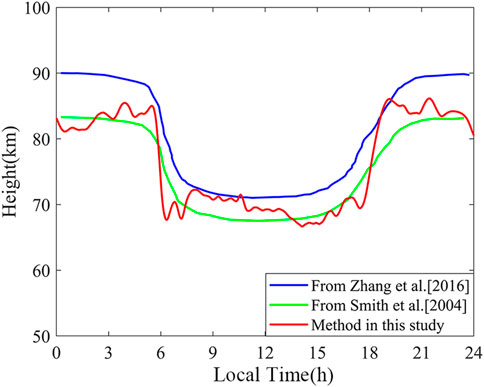
FIGURE 8. Diurnal variation in the reflection height of the ionosphere D region compared with those reported by Zhang et al. (Thomson et al., 2007) and Smith et al. (2004) (local time: UT+8).
3.2 Distance estimation using the revised time delay
The distance between the lightning source and the single site can be obtained by using the time difference between the arrival times of the ground wave and skywaves. The arrival time difference (
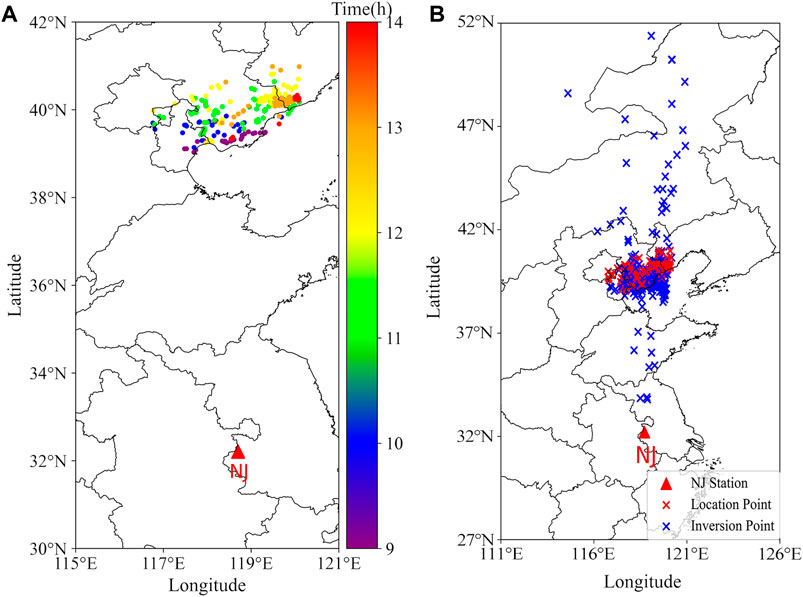
FIGURE 9. Estimated lightning distance by a single site. (A) Distributions of lightning events in selected regions on 3 October 2021, from 09:00 to 15:00 (local time: UT+8). (B) Single-site distance estimation results versus multi-station.
Figures 10, 11 show the relative and absolute deviations of the single-site distance estimation, respectively, using the multiple-station lightning location results as a reference. Figure 10A compares the difference between revising and not revising the ground wave time delay only for the distance estimation. Since the ground wave time delay was considered in calculating the ionosphere equivalent reflection height, not considering the delay in distance estimation will result in deviation from the true value. Figure 10B compares the results of the revised method proposed in this study with the method that does not consider the ground wave time delay. The distance estimation accuracy was also significantly improved. The percentage of data with errors within 10% increased from 52% to 65% and the percentage of data with errors >100% decreased from 18% to 8%.
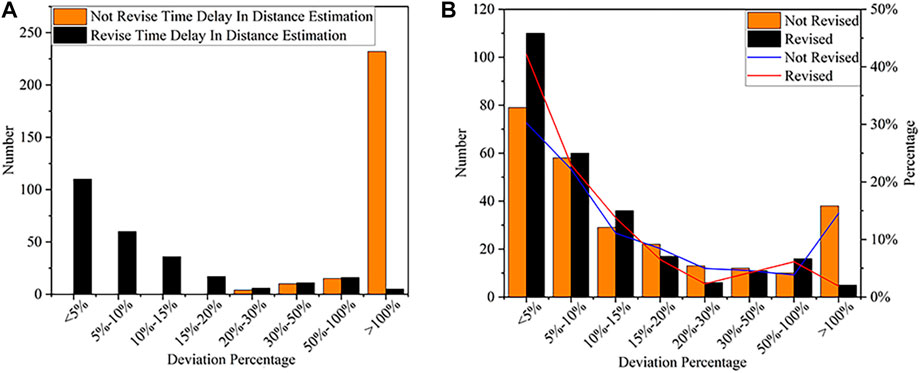
FIGURE 10. Relative deviation in single-station distance estimation. (A) Considering a ground wave peak time delay in distance estimation. (B) Comparing the revised method with the non-revised method.
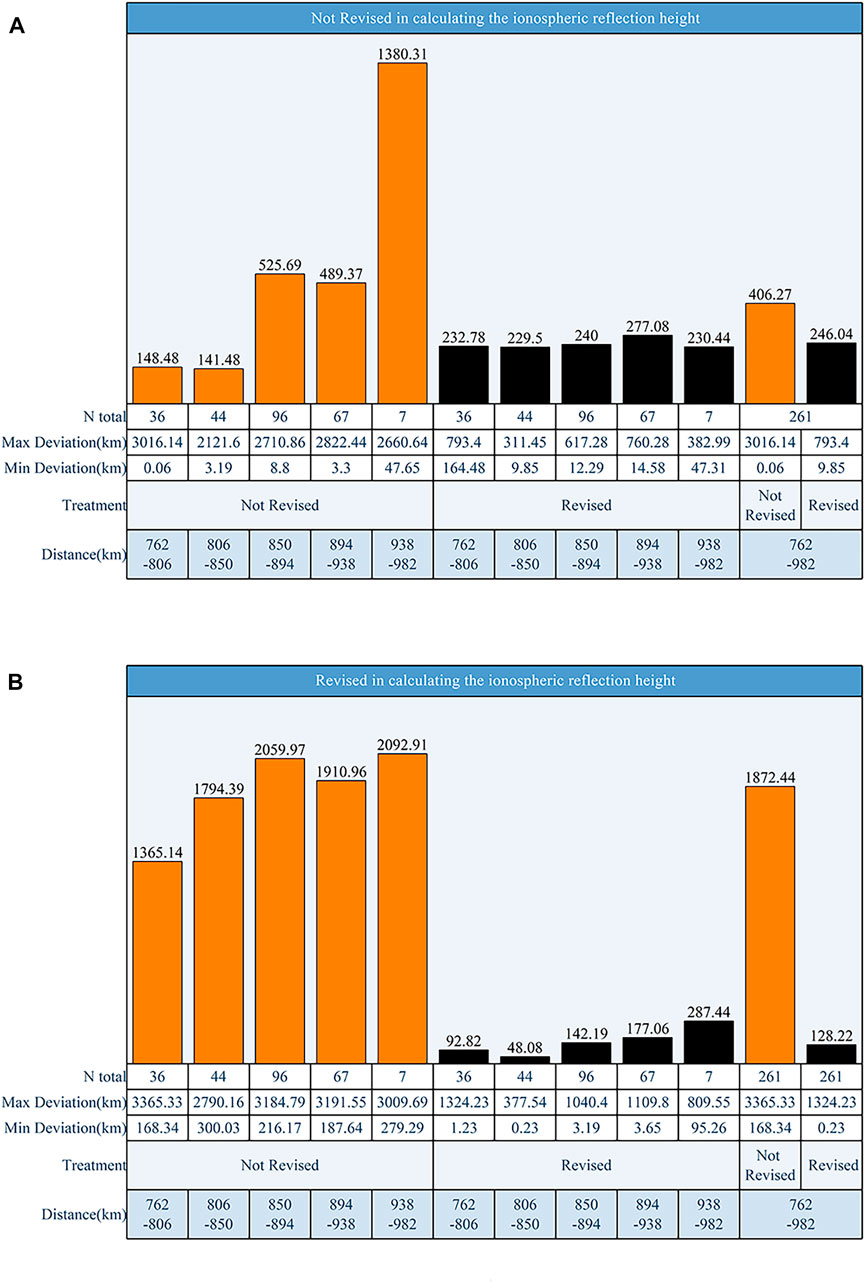
FIGURE 11. Histogram of single-station distance estimation error. Distance estimation using ionosphere heights obtained by unrevised (A) and (B) revised ground wave arrival time delays.
The absolute deviation of the single-site distance estimate is given in Figure 11. The treatment in the figure refers to whether the ground wave arrival time was revised in the distance estimation, N total indicates the number of data in each data group, and the bar chart represents the average absolute deviation. For the overall results of the distance estimates for the 261 lightning events in Figure 9, when the ground wave time delay was revised in calculating the ionosphere equivalent height and estimating the lightning occurrence distance, the absolute average error was 128.22 km; however, when the ground wave time delay was revised only in estimating the lightning occurrence distance and the ionosphere equivalent reflection height was calculated without considering the ground wave time delay, the absolute average error was 246.04 km. Thus, the ground wave time delay considerably impacted the precision of the distance estimate for the single-site lightning location. The average deviation of the entire data set in Figure 11A shows that revising the ground wave time delay could effectively reduce the inaccuracy of distance estimation.
To understand whether the proposed method will have the problem of decreasing accuracy with increasing distance, the statistical results of five distance bands are given in Figure 11. The average error increased with increasing distance. However, the deviation in the distance estimation in the range of 806 km–850 km was only 48.07 km, significantly better than the results for closer distances. Therefore, the method proposed in this study still applies to lightning that occurs at long distances. Moreover, for each distance band in the optimal group, the distance deviation of our proposed revised method was generally smaller than that of the original method, except for the 938 km–982 km distance interval. However, only seven data samples occurred in this interval.
The results of the distance estimates showed some data with errors >100%. Comparison of the revised and non-revised methods revealed a certain set of data with large deviations using both methods, ruling out the possibility that the method influenced these results. Considering that these reflected data with a longer time scale, this situation may occur due to variation in the ionosphere equivalent reflection height at different times. To verify this conjecture, Figure 12 represents a scatter plot of the error distribution with time, showing that the data with errors >100% are distributed over various periods and unrelated to the ionosphere equivalent reflection height variation. Figure 12 shows more intuitively that the method proposed in this paper significantly improved the estimation accuracy.
Since the variables used to solve the distance in Eq. 13 were the arrival time difference between the skywave and the ground wave, further inspection of the data revealed that for these data with errors >100%, the arrival time difference was much smaller than the other data. This may occur due to noise interference during the propagation process, resulting in a shift in the peak points of the ground wave or the first skywave, which, in turn, affects the accuracy of the estimation results.
4 Discussion
Based on the phenomenon that the ground wave arrival time will lag during long-distance propagation, we analyzed the effect of the curvature of the Earth and ground finite conductivity on the sferics waveform using the numerical method and statistically analyzed the delay in the arrival time of the far-field waveform. The delay time was also used to calculate the ionosphere equivalent reflection height and estimate the lightning distance using a single site.
The results of the estimated distances for a single site in Section 3 show an average error of 128.8 km. The comparison between the method used in this study and other methods is shown in Table 2. The data selected in the compared methods were mainly lightning data at close distances (∼200 km), while lightning data used in this study occurred between 700 km and 900 km. Some places, such as islands, forests, military bases, and ocean-going vessels, lack good network transmission capability or have many limitations in transmitting to external networks. Because the transmission with external networks is limited, it is impossible to establish a multi-station lightning location system and obtain the lightning location results given by other lightning location networks or the acquisition cost is relatively higher. The single-site lightning location system does not need to rely on high-precision time modules and the Internet to provide real-time lightning location results, and the operating cost is low. Due to the propagation effect, the arrival time difference between the first skywave and the ground wave in the actual waveform is much smaller than the ideal condition as the propagation distance of LEMP increases, which leads to an increasing deviation of the distance estimation results as the propagation distance increases. Therefore, the method proposed in this work may be an excellent solution to this problem. In this study, the relationship between the ground wave arrival time delay and the propagation distance obtained by the numerical algorithm could well correct the ground wave arrival time delay. The average error in Figure 11 shows that the average absolute deviation of distance estimation was reduced by 117.85 km when the ground wave arrival time delay was revised, thus demonstrating that the reliability of long-range lightning detected by the single site can be improved using the method proposed in this study. Moreover, the single-site lightning detection system proposed in this study can reach a detection range of 900 km. More reliable location results for long-range lightning can allow lightning risk warnings, prediction of lightning activity trends, and other functions, which have engineering applications.
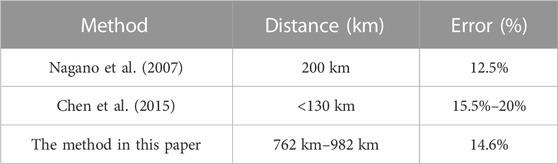
TABLE 2. Comparison between existing methods and the current method on the single-site lightning location.
Analysis of the waveform data showed that the data with large deviation values were mainly because of effects on the sferics by noise during propagation, resulting in different degrees of distortion in the received waveform. Thus, when matching with the waveform bank, the actual waveform is matched to the simulation waveform at a longer distance, resulting in deviations in the actual sferics peak points obtained according to the matching. The time difference between the skywave and ground wave peak points decreases, while the deviation of the estimated distance result increases.
The error in the distance estimation in this study mainly came from two aspects:
(1) The waveform bank used for waveform matching was simulated by two-dimensional FDTD without fully considering the influence of the geomagnetic field, which differs from the actual lightning waveform, especially in the skywave.
(2) In the calculation of the ground wave time delay, we assumed that the ground conductivity was 0.01 S/m and the ground was smooth. However, in the actual propagation process, we also need to consider the influence of the terrain on the lightning waveform.
5 Conclusion
In this study, the time delay versus distance curve was obtained by a numerical algorithm, which considered the ground wave time delay in the long-distance propagation process caused by the curvature of the Earth and the finite conductivity of the ground. This error was corrected by calculating the ionosphere equivalent reflection height to improve the reliability of the results. The accuracy of single-site estimation was evaluated using multi-station data. The main conclusions of this paper are as follows:
(1) In this work, we fit the time arrival delay versus the distance curve for the ground wave peak using a numerical algorithm. The ground wave time arrival delay versus distance showed a roughly linear relationship, with an average arrival time delay of 0.9 μs (compared with the arrival time at the speed of light) for every 100 km increase in propagation distance.
(2) The time difference between the actual sferics ground wave and the skywave peaks was identified by waveform bank matching and peak identification. The time delay was revised to calculate the ionosphere equivalent reflection height. For
(3) For a total of 261 lightning events occurring at the distance of 700 km–900 km from the single site, the distance estimation results obtained by the single-site system were compared with those of the multi-station lightning location and showed an average error of 128.8 km (14.6%) and a median distance error of 52.6 km. The average error of the results without considering the time delay was 246.04 km (45.9%). The percentage of distance estimation results with relative errors within 10% increased from 52% to 65%.
It should be noted that the proposed method is also applicable to lightning events at longer distances if sufficient data are available. In future research, we will combine the magnetic direction finder (MDF) to implement lightning location estimation and verify the accuracy of the method for estimating lightning at longer distances. We will also collect more data to build a bank of real waveforms by machine learning to improve the accuracy of waveform peak matching and further investigate the effects of different propagation directions and different terrain on the ionosphere equivalent reflection height.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, JiZ and QZ; Data curation, JiZ, JuZ, BD, YW, JZe and LS; Formal analysis, JiZ, JL, JY and JG; Funding acquisition, QZ; investigation, JiZ and QZ; methodology, JiZ and JuZ; software, JiZ; JuZ and JL; supervision, QZ; visualization, JiZ; writing—original draft, JiZ; writing—review and editing, QZ. All authors contributed to the article and approved the submitted version.
Funding
This research was funded by the National Natural Science Foundation of China (grant 41775006).
Acknowledgments
The authors thank the National Satellite Meteorological Center (NSMC) of the China Meteorological Administration for providing the FY4A-AGRI dataset. The author would like to thank the people and departments involved in the construction of the network. The authors would also like to thank the reviewers for their helpful feedback, which significantly improved the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ammar, A., and Ghalila, H. (2020). Estimation of nighttime ionospheric D-region parameters using tweek atmospherics observed for the first time in the North African region. Adv. Space Res. 66 (11), 2528–2536. doi:10.1016/j.asr.2020.08.025
Azadifar, M., Li, D., Rachidi, F., Rubinstein, M., Diendorfer, G., Schulz, W., et al. (2017). Analysis of lightning-ionosphere interaction using simultaneous records of source current and 380 Km distant electric field. J. Atmos. Solar-Terrestrial Phys. 159, 48–56. doi:10.1016/j.jastp.2017.05.010
Carvalho, F. L., Uman, M. A., Jordan, D. M., Hill, J. D., Cummer, S. A., Kotovsky, D. A., et al. (2017). Triggered lightning sky waves, return stroke modeling, and ionosphere effective height: Triggered lightning sky waves. J. Geophys. Res. Atmos. 122 (6), 3507–3527. doi:10.1002/2016JD026202
Chen, M., Lu, T., and Du, Y. (2015). An improved wave impedance approach for locating close lightning stroke from single station observation and its validation. J. Atmos. Solar-Terrestrial Phys. 122, 1–8. doi:10.1016/j.jastp.2014.11.001
Cummer, S. A., Inan, U. S., and Bell, T. F. (1998). IonosphericDregion remote sensing using VLF radio atmospherics. Radio Sci. 33 (6), 1781–1792. doi:10.1029/98RS02381
Dennis, A. S., and Pierce, E. T. (1964). The return stroke of the lightning flash to Earth as a source of VLF atmospherics. Radio Sci. 68D, 777. doi:10.6028/jres.068d.075
Han, F., and Cummer, S. A. (2010). Midlatitude nighttime D region ionosphere variability on hourly to monthly time scales: D region measurement. J. Geophys. Res. 115 (A9), n/a–n. doi:10.1029/2010ja015437
Heidler, F., Cvetic, J. M., and Stanic, B. V. (1999). Calculation of lightning current parameters. IEEE Trans. Power Deliv. 14 (2), 399–404. doi:10.1109/61.754080
Hill, D. A., and Wait, J. R. (1980). Ground wave attenuation function for a spherical earth with arbitrary surface impedance. Radio Sci. 15, 637–643. doi:10.1029/RS015i003p00637
Honma, N., Suzuki, F., Miyake, Y., Ishii, M., and Hidayat, S. (1998). Propagation effect on field waveforms in relation to time-of-arrival technique in lightning location. J. Geophys. Res. 103 (D12), 14141–14145. doi:10.1029/97JD02625
Hou, W., Azadifar, M., Rubinstein, M., Rachidi, F., and Zhang, Q. (2020). The polarity reversal of lightning-generated sky wave. J. Geophys. Res. Atmos. 125, e2020JD032448. doi:10.1029/2020jd032448
Hou, W., Zhang, Q., Zhang, J., Wang, L., and Shen, Y. (2018). A new approximate method for lightning-radiated ELF/VLF ground wave propagation over intermediate ranges. Int. J. Antennas Propag. 2018, 1–10. doi:10.1155/2018/9353294
Hu, W., and Cummer, S. A. (2006). An FDTD model for low and high altitude lightning-generated EM fields. IEEE Trans. Antennas Propagat. 54 (5), 1513–1522. doi:10.1109/TAP.2006.874336
Inan, U. S., Cummer, S. A., and Marshall, R. A. (2010). A survey of ELF and VLF research on lightning-ionosphere interactions and causative discharges: Elf and VLF signatures of lightning. J. Geophys. Res. 115 (6), n/a. doi:10.1029/2009ja014775
Jacobson, A. R., Holzworth, R., and Shao, X.-M. (2008). Low-frequency ionospheric sounding with narrow bipolar event lightning radio emissions: Energy-reflectivity spectrum. Ann. Geophys. 26 (7), 1793–1803. doi:10.5194/angeo-26-1793-2008
Koochak, Z., and Fraser-Smith, A. (2020). Single-station lightning location using azimuth and time of arrival of sferics. Radio Sci. 55 (2). doi:10.1029/2018RS006627
Lay, E. H., and Shao, X.-M. (2011). High temporal and spatial-resolution detection of D-layer fluctuations by using time-domain lightning waveforms: Detection of d-layer fluctuations. J. Geophys. Res. 116 (A1), n/a. doi:10.1029/2010ja016018
Lay, E. H., and Shao, X.-M. (2011). Multi-station probing of thunderstorm-generated D-layer fluctuations by using time-domain lightning waveforms: MULTI-STATION VLF measurement of d-layer. Geophys. Res. Lett. 38 (23), n/a. doi:10.1029/2011GL049790
Li, J., Dai, B., Zhou, J., Zhang, J., Zhang, Q., Yang, J., et al. (2022). Preliminary application of long-range lightning location network with equivalent propagation velocity in China. Remote Sens. 14 (3), 560. doi:10.3390/rs14030560
Mostajabi, A., Karami, H., Azadifar, M., Ghasemi, A., Rubinstein, M., and Rachidi, F. (2019). Single-sensor source localization using electromagnetic time reversal and deep transfer learning: Application to lightning. Sci. Rep. 9 (1), 17372. doi:10.1038/s41598-019-53934-4
Nagano, I., Yagitani, S., Ozaki, M., Nakamura, Y., and Miyamura, K. (2007). Estimation of lightning location from single station observations of sferics. Electron. Comm. Jpn. pt. I 90 (1), 25–34. doi:10.1002/ecja.20329
Nucci, C. A., Mazzetti, C., Rachidi, F., and Ianoz, M. (1988). On lightning return stroke models for LEMP calculations, paper presented at 19th International Conference on Lightning Protection. Graz, Austria: Assoc.
Ogawa, T., and Komatsu, M. (2007). Analysis of Q Burst waveforms: Analysis of Q burst waveforms. Radio Sci. 42 (2), n/a. doi:10.1029/2006rs003493
Rachidi, F., Janischewskyj, W., Hussein, A. M., Nucci, C., Guerrieri, S., Kordi, B., et al. (2001). Current and electromagnetic field associated with lightning-return strokes to tall towers. IEEE Trans. Electromagn. Compat. 43 (3), 356–367. doi:10.1109/15.942607
Ramachandran, V., Prakash, J. N., Deo, A., and Kumar, S. (2007). Lightning stroke distance estimation from single station observation and validation with WWLLN data. Ann. Geophys. 25 (7), 1509–1517. doi:10.5194/angeo-25-1509-2007
Shao, X.-M., and Jacobson, A. R. (2009). Model simulation of very low-frequency and low-frequency lightning signal propagation over intermediate ranges. IEEE Trans. Electromagn. Compat. 51 (3), 519–525. doi:10.1109/TEMC.2009.2022171
Shao, X.-M., Lay, E. H., and Jacobson, A. R. (2013). Reduction of electron density in the night-time lower ionosphere in response to a thunderstorm. Nat. Geosci. 6 (1), 29–33. doi:10.1038/ngeo1668
Smith, D. A., Heavner, M. J., Jacobson, A. R., Shao, X. M., Massey, R. S., Sheldon, R. J., et al. (2004). A method for determining intracloud lightning and ionosphere heights from VLF/LF electric field records: VLF/LF IC lightning and ionosphere height. Radio Sci. 39 (1), n/a. doi:10.1029/2002rs002790
Somu, V. B., Rakov, V. A., Haddad, M. A., and Cummer, S. A. (2015). A study of changes in apparent ionospheric reflection height within individual lightning flashes. J. Atmos. Solar-Terrestrial Phys. 136, 66–79. doi:10.1016/j.jastp.2015.09.007
Thomson, N. R., Clilverd, M. A., and McRae, W. M. (2007). Nighttime ionosphere D region parameters from VLF phase and amplitude: Night ionosphere D region parameters. J. Geophys. Res. 112 (7), n/a. doi:10.1029/2007ja012271
Tran, T. H., Baba, Y., Somu, V. B., and Rakov, V. A. (2017). FDTD modeling of LEMP propagation in the Earth-ionosphere waveguide with emphasis on realistic representation of lightning source. J. Geophys. Res. Atmos. 122 (12), 937. doi:10.1002/2017sJD027305
Wait, J. R. (1974). Recent analytical investigations of electromagnetic ground wave propagation over inhomogeneous earth models. Proc. IEEE 62, 1061–1072. doi:10.1109/PROC.1974.9570
Wang, J., Xiao, F., Yuan, S., Song, J., Ma, Q., and Zhou, X. (2022). A novel method for ground-based VLF/LF single-site lightning location. Measurement 196, 111208. doi:10.1016/j.measurement.2022.111208
Zhang, H., Lu, G., Qie, X., Jiang, R., Fan, Y., Tian, Y., et al. (2016). Locating narrow bipolar events with single-station measurement of low-frequency magnetic fields. J. Atmos. Solar-Terrestrial Phys. 143–144, 88–101. doi:10.1016/j.jastp.2016.03.009
Zhang, J., Zhou, J., Li, J., Gu, J., Zhang, Q., Dai, B., et al. (2022). Location accuracy improvement of long-range lightning detection network in China by compensating ground wave propagation delay. Remote Sens. 14, 3397. doi:10.3390/rs14143397
Keywords: ground wave peak time delay, ionospheric reflection height, single-site, lightning distance estimation, lightning location
Citation: Zhou J, Zhang Q, Song L, Zhang J, Dai B, Li J, Yang J, Wang Y, Gu J and Zeng J (2023) On the improvement of the single-site lightning distance estimation by using the time-delay correction. Front. Earth Sci. 11:1093020. doi: 10.3389/feart.2023.1093020
Received: 08 November 2022; Accepted: 04 May 2023;
Published: 30 May 2023.
Edited by:
Babalola Ogunsua, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Abhay Srivastava, North Eastern Space Application Centre, IndiaOladipo Abe, Federal University Oye-Ekiti, Nigeria
Louis Osei-Poku, Hong Kong Polytechnic University Kowloon, China in collaboration with reviewer OA
Copyright © 2023 Zhou, Zhang, Song, Zhang, Dai, Li, Yang, Wang, Gu and Zeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qilin Zhang, cWx6aGFuZ0BudWlzdC5lZHUuY24=; Jinquan Zeng, NTg4MDM1NzJAcXEuY29t
 Jiahao Zhou
Jiahao Zhou Qilin Zhang1*
Qilin Zhang1*