- 1State Key Laboratory of Green and Low-Carbon Development of Tar-Rich Coal in Western China, Xi’an University of Science and Technology, Xi’an, China
- 2College of Safety Science and Engineering, Xi’an University of Science and Technology, Xi’an, China
- 3College of Energy Engineering, Xi’an University of Science and Technology, Xi’an, China
The migration process of rockfall has certain complexity and randomness in steeply dipping coal seams (SDCS). The three-dimensional random migration of rockfall with random parameters cannot be accurately simulated. Taking the transport process of arbitrarily shaped rockfall formed by roof leakage in steep seam working face as the research object, a method for generating rockfall with the random shape of irregular polyhedrons based on the ellipsoid equation is provided. And based on the geographic information system data, such as the contour line of the bottom floor of the working face, the 3D grid model of the bottom floor is established. The random transport process of rockfall in three-dimensional mining space was simulated using Monte Carlo random simulation technology combined with the energy tracking method (ETM) to compile the program, considering the randomness of collision recovery coefficient and friction coefficient between rockfall and working face floor. The influence of randomness of parameters on the migration velocity, angular velocity and energy of rockfall is analyzed. With the increase of the coefficient of variation of parameters, the influence of the randomness of the parameters on the transport characteristics of rockfall becomes greater. The impact of the collision recovery coefficient on the migration process of rockfall is much more significant than that of the friction coefficient. The offset ratio of rockfall increases with the increase of the variation coefficient. The method presented in this paper can be used to simulate the motion of rockfall more accurately, and a theoretical basis is provided for predicting and protecting rockfall hazards.
1 Introduction
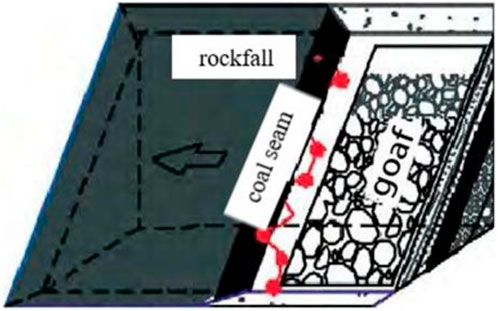
In recent years, SDCS mining has been made in theoretical research, technical application and equipment development, which has solved the safety problem of SDCS mining. However, the coal-forming surroundings of SDCS are complicated, and it is tough to mine safely and efficiently. The rockfalls formed by the coal wall spalling, coal cutting splash or roof falling have become the unique dynamic disasters in longwall face mining of SDCS. Rockfalls in the long walls of an SDCS also have a colloquial name, “flying gangue,” hazards. In addition, with the increasing mining efforts of deep coal seams, the output has increased. In the mining process of longwall face in SDCS, accidents of breaking equipment and hurting people by the large gangue or coal block frequently occur, which seriously restricts the safe and efficient production of mine (Wu et al., 2014; Lai et al., 2016; Liu et al., 2016; Wang and Jiao, 2016; Yun et al., 2017; Wu et al., 2019; Wu et al., 2020). The migration of rockfall is shown in Figure 1.
Although some scholars have made some research achievements in the disaster of rockfalls (Tu et al., 2015; Chu and Chen, 2017; Wu et al., 2018a; Liu et al., 2019; Liu et al., 2020a; Liu et al., 2020b; Hu et al., 2021), it is still necessary to strengthen the research on the random migration characteristics of rockfalls in three-dimensional mining space. Yongping Wu analyzes the impact energy characteristics of rockfalls under different working conditions by using the disaster monitoring experimental system of longwall mining in SDCS, combined with the principles of statistics and Kalman filter, preliminarily establish the rockfall damage risk discrimination model, and classified the rockfall damage grades according to this model. Taking the rockfall blocking net as the control element, the impact damage mechanism and control element parameters of rockfall are comprehensively studied by various means, and a control method of impact damage of rockfall is put forward (Wu et al., 2017a; Wu et al., 2017b; Wu et al., 2018b). In addition, Yongping Wu puts forward the risk index to characterize the cumulative damage effect of rockfalls, analyze the sensitivity of the risk index under different block diameters, coal seam dip angles and floor hardness of longwall working face, and establish the risk assessment model of rockfall disaster. According to the distribution of risk indicators, the risk of rockfall is divided into five grades, and the risk assessment method of rockfall in the longwall face of SDCS is put forward (Wu et al., 2021). Lingling Jing establishes the dynamic characteristic analysis model of spherical rockfall with uncertain parameters by using the non-probability interval analysis method and studying the influence of randomness of two-dimensional rockfall migration parameters on the rockfall migration process (Jing et al., 2019). Based on the dynamic Bayesian network method, the threat level of rockfall in the migration process is evaluated, and the fuzzy comprehensive evaluation method is used to assess the safety of rockfall disaster in SDCS by Ming Liu (Liu et al., 2020c; Liu et al., 2020d). In addition, the normal shock motion of spherical rockfall in the working face of SDCS is taken as the research background. Considering the influences of the randomness of the shock motion parameters of rockfall, based on Hertz’s classical elastic collision theory, Ming Liu establishes the typical shock motion model of rockfall by using the random factor method. And the mean and the variance of the maximum impact and collision restitution coefficient of rockfall in normal are derived (Liu and Chen, 2021a; Liu et al., 2021a; Liu et al., 2021b). Taking a large inclination thick coal seam in the Shanxi coal mine as the research background, according to the sphericity design, a numerical simulation test covering all ellipsoidal rockfall shapes is carried out on the migration process of rockfall in the 3D working face by using ETM, the trajectories of rockfall can be obtained, and at any time of the curves of velocity, angular velocity and energy, and the influence of shape on the migration process of rockfall is analyzed by Ming Liu (Liu and Chen, 2021b). Most models of the rockfall and working face floor in these studies are considered idealized models, often modelling the rockfall as a sphere or ellipsoid and the working face floor as a plane. However, the actual rockfall shape and working face floor are primarily irregular, leading to a multi-point collision between the rockfall and the working face floor. The migration process will be more complicated. In addition, the migration process of rockfalls has a great degree of randomness in reality. To accurately describe the random migration law of rockfalls, we must consider the influence of the randomness of parameters on the migration process of rockfalls. According to the research experience of rockfall movement, the fundamental parameters affecting rockfall movement are collision recovery coefficient and friction coefficient. Therefore, the author takes the three-dimensional migration of rockfall with a random shape formed by roof leakage in coal face with SDCS as an example and establishes the random shape models of rockfall with the improved ellipsoid equation. The working face floor grid model is based on geographic information system data such as floor contour lines in the steep seam. Considering the randomness of the collision recovery coefficient and friction coefficient between the rockfall and working face floor, the Monte Carlo method and ETM are used to systematically study the influence of randomness of parameters on the migration of rockfall, which can provide a reliable theoretical basis for the protection of rockfall disaster in SDCS mining.
2 Basic principles
2.1 ETM
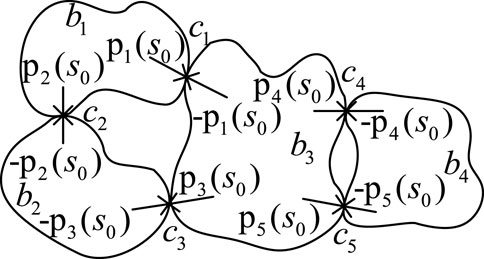
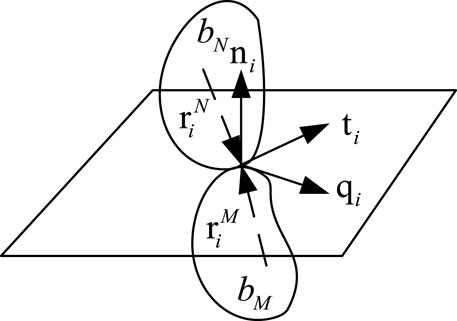
The principle of ETM is energy iteration. According to the elastic energy absorbed by the collision point of rockfall at the moment of collision, a pair of impulses is applied to the collision point to release energy until the migration stops continuously. As a result, the collision between the irregular rockfall and the working face floor, as well as the collision between the rockfall, is mainly a multi-point collision, as shown in Figure 2 (Tang et al., 2014).
Figure 2 shows the multi-point collision of multiple blocks
In each iteration step, multi-point collisions can be regarded as simultaneous collisions, and the calculated impulses can be applied to the contact points. The interaction of multi-point collisions is simulated by cyclic operation until all relative average velocities are non-negative.
ETM adopts the Stronge assumption to represent the energy dissipation in the normal direction. The work
where
According to the normal and tangential components of collision, the local coordinates system
The following expression can be obtained:
Where
The work
In the ETM method, the change of relative velocity along the normal direction is calculated first, and then the friction is considered. The change of relative normal velocity is:
The impulse
The condition of static friction is:
Where
The impulse should be calculated as follows
where
2.2 Improved MCETM
The Monte Carlo method is based on the probability model. According to the model’s process, The results of simulation experiments are regarded as the approximate solution of the problem, which relax the requirement of the idealization of the theoretical model. Therefore, it can generate a more realistic simulation model, and this method is often used as a relatively exact solution to verify or validate approximate analytical solutions.
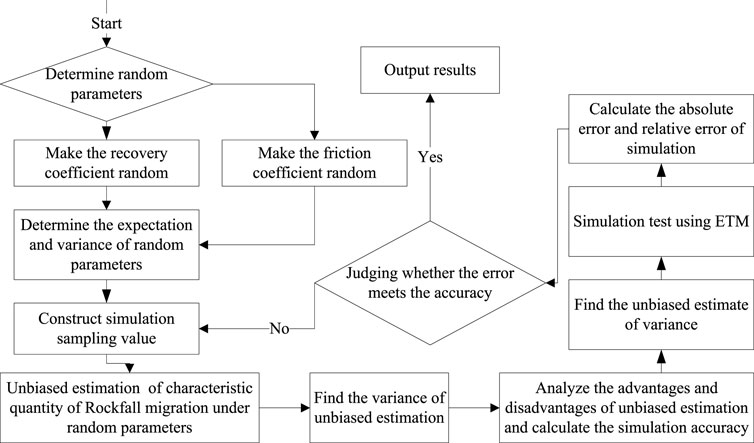
Therefore, in this paper, Monte Carlo random sampling technique combined with ETM (MCETM) can be used to simulate rockfall’s three-dimensional random migration process with the arbitrary shape when the parameters are random. Firstly, the random numbers of collision recovery coefficient and friction coefficient, which obey normal distribution, are generated. Then the standard normal distribution function and quantile are calculated, which are computed by continued fraction advancing an iterative method based on second-order expansion.
The random number of the normal distribution
For a given number of Monte Carlo simulations N, the sample values
where
The absolute error of estimator
The relative error of estimator
where
3 Establishment of the numerical model
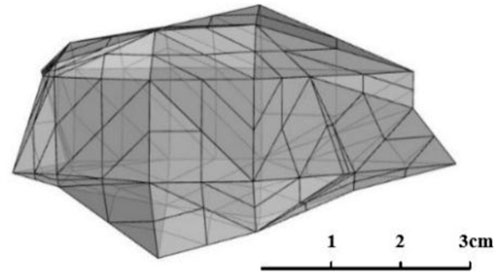
3.1 Modelling of irregular random shape rockfalls
The migration process and the shape of coal/rock blocks that have stopped migration show that the shape of rockfall is generally ellipsoidal. Therefore, the transformation of the ellipsoid equation to the rockfall model to generate irregular random shapes is more in line with the actual working face. The specific modelling process is as follows: the coordinates of any point are represented by r,
The first is to determine the
where
The
Plus
where
3.2 Geographic information system modeling
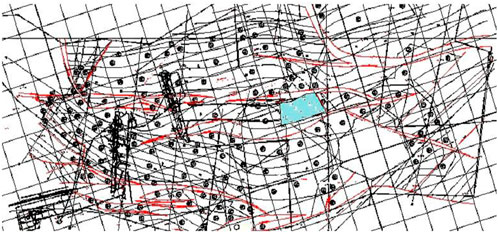
This paper takes a steeply dipping coal seam as an example in Gansu Province. Contour lines and drilling information of the working face floor can be shown in Figure 6. The buried depth of the working face is 270 m, the north side of the working face is 201 working face for mining, the west side is the mine field boundary (30 m), the east side is the main transportation lane, and the south side is the north return air lane. The average coal seam dip angle is 35°, and the dip angle is relatively stable. The coal seam thickness is between 1.8 and 2.8 m, with an average of 2.3 m.
The contour lines and drilling information are extracted, and the drilling information is regarded as elevation points, and a working face floor mesh model is established by using cass software. As shown in Figure 7.
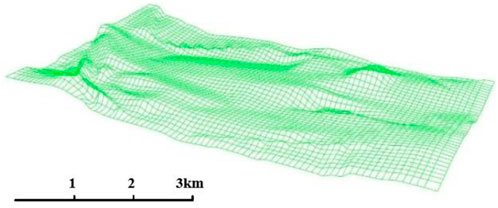
The model is a 3D mesh model of 4,500 m × 2,500 m × 500 m. It covers the geographic information of the entire working face floor. And the inclination of the coal seam is about 25°–35°, The upper limit of the inclination belongs to the SDCS. Rockyfor3D software is used to analyze the inclination of working face, and the results are shown in Figure 8.
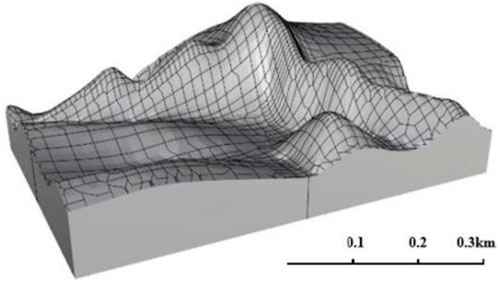
It can be seen from Figure 8 that the purple area appears in the lower left corner of the figure, which is the area most prone to rockfall hazards. The inclination of this area is about 35°, which belongs to the SDCS. It is consistent with the result of contour measurement and calculation in Figure 6. Capture the region to establish a 3D model of the working face floor, as shown in Figure 9.
3.3 Validation model
In this paper, hexahedral rockfall is used for modeling, and the model of working face floor is shown in Figure 9. The collision recovery coefficient of the working face floor is 0.84, the friction coefficient is 0.4, the density of the rockfall is 2,500 kg/m3, and the model size is 0.1 m × 0.2 m × 0.2 m. Rockfall is formed when coal or rock blocks leak from the roof of coal seam. The monitoring point is above the rockfall’s first falling point, the elastic modulus is 2.6 GPa, the Poisson’s ratio is 0.21, and the rockfall model is shown in Figure 10.
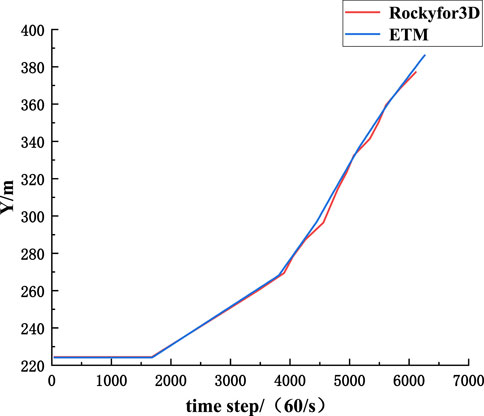
The rockfall moves freely from the face end of the working face at a height of 20 m, and collides with the working face floor, and then bounces and slides along the working face floor. The trajectories simulated by the ETM method and the Rockyfor3D software are compared. Figures 11, 12 show the inclination trajectories and lateral offset trajectories of rockfall along the working face floor, respectively. In Figure 12, X represents the motion track, Y represents the lateral offset track, and Z represents the height. It can be seen that the inclination trajectory and lateral migration trajectory of rockfall simulated by the ETM method are consistent with the trajectory of the Rockyfor3D simulation.
4 Analysis of random characteristics of rockfall migration
4.1 Random characteristic analysis of kinematic characteristic quantity of rockfall
In this paper, the model of the working face floor is shown in Figure 9, and the rockfall model is modelled by the modelling method of rockfall with irregular shapes. The lithology of rockfall is sandstone, and its shape is shown in Figure 5. The collision recovery coefficient and friction coefficient were separately regarded as random variables to analyze the influence of parameters on the randomness of rockfall movement. Let the random parameters conform to the normal distribution. Their mean values are
MCETM is used for numerical simulation, and the variation curves of rockfall speed, angular velocity and energy interval width with the coefficient of variation are shown in Figure 13. In the pictures, γ represents the coefficient of variation, e represents the coefficient of collision recovery, and f represents the coefficient of friction. It can be seen from Figure 13 that with the increase of the variable coefficient of parameters, the interval width of kinematic characteristic quantities such as velocity and angular velocity shows an upward trend. This is because the impact of the randomness of the collision recovery coefficient on the interval width of kinematic characteristics such as velocity and angular velocity is far more significant than that of the randomness of the friction coefficient, and the randomness of friction coefficient has relatively little impact on the transport speed of rockfall.
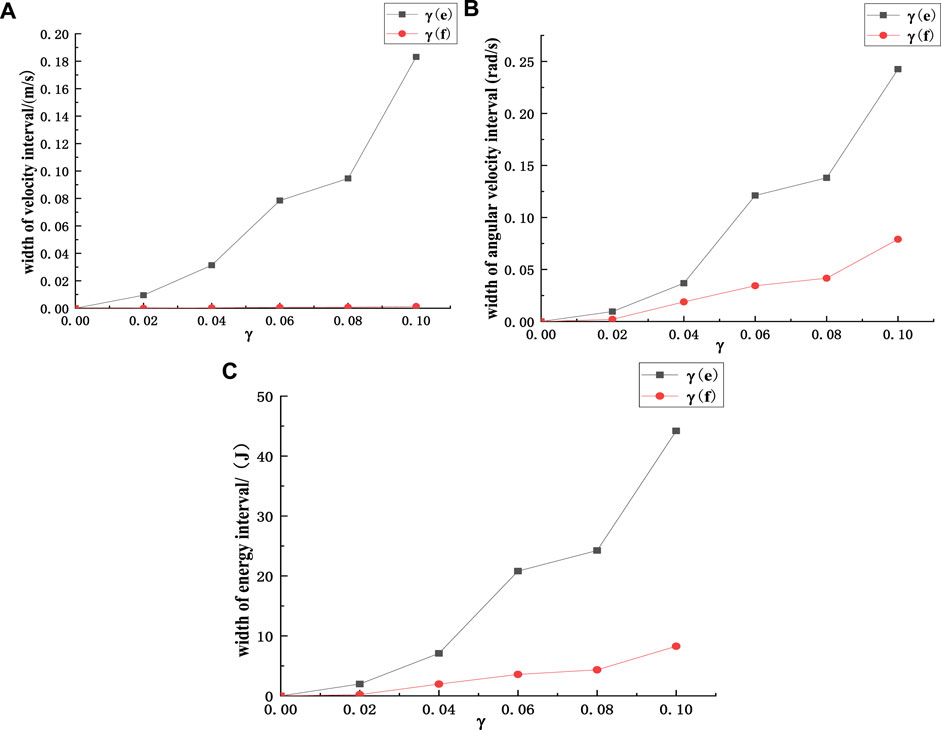
FIGURE 13. Kinematics characteristic quantity of rockfall, (A) Variation curve of velocity interval width of rockfall, (B) Variation curve of angular velocity interval width of rockfall, (C) Variation curve of energy interval width of rockfall.
Figure 14 shows the variation curves of rockfall velocity, angular velocity and energy variance with the coefficient of variation. It can be seen from Figure 14 that the dispersion of the characteristic quantity of rockfall migration is greatly influenced by the randomness of the collision recovery coefficient. In the picture, σ2 represents the variance curve. The randomness of the friction coefficient has a significant influence on the angular velocity of rockfall. The reason is that when rockfall slides along the floor of the working face, the work done by friction is converted into the rotational kinetic energy of rockfall, which increases its angular velocity. The randomness of the friction coefficient affects the angular velocity by affecting the friction force. The influence of the randomness of friction coefficient on the dispersion of kinematic characteristics of rockfall is still less than that of the randomness of collision recovery coefficient. The randomness of the collision recovery coefficient always occupies a dominant position in the process of rockfall migration.
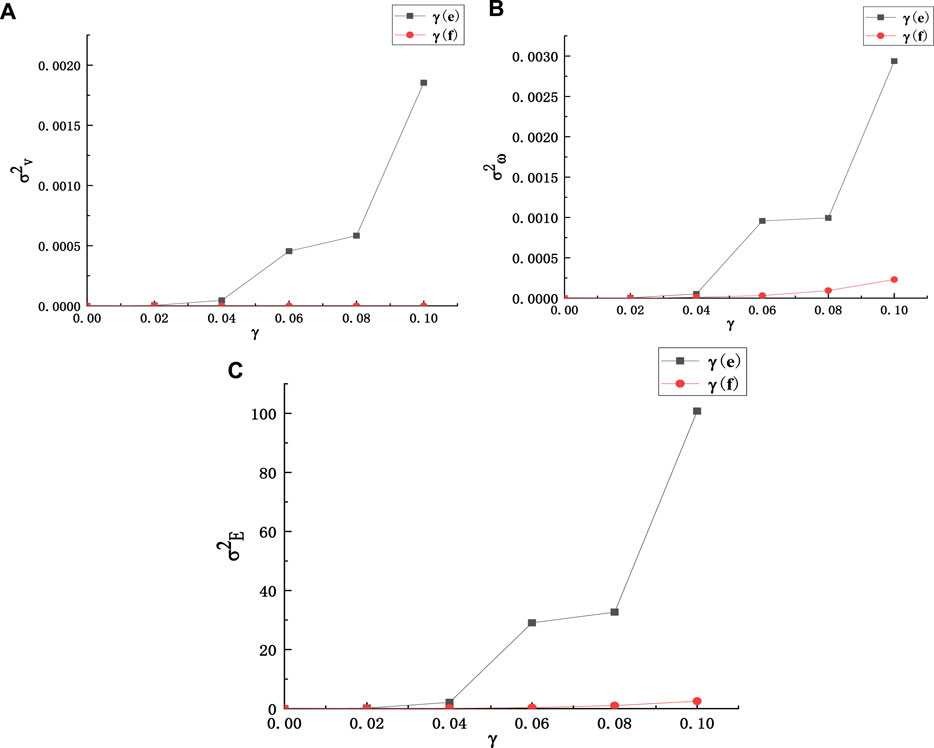
FIGURE 14. Variance of kinematics characteristics of rockfall, (A) Variation curve of velocity variance of rockfall, (B) Variation curve of angular velocity variance of rockfall, (C) Variance curve of rockfall energy.
4.2 Analysis of random characteristics of rockfall migration
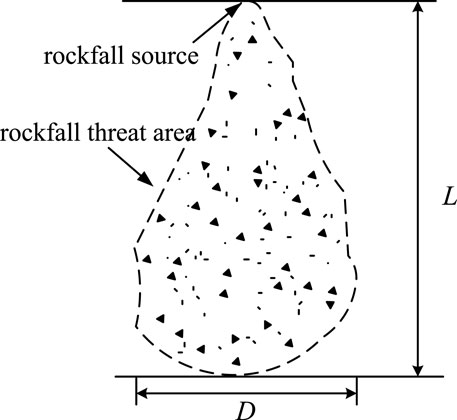
The influence of randomness of parameters on the migration trajectory of rockfall is reflected in the trend direction of the working face and the lateral migration along the strike direction of the working face. The lateral migration of rockfall can be described according to the migration index proposed by Azzoni et al., as shown in Figure 15.
Combined with the working face of SDCS, the offset ratio is defined as:
where D is the offset of the falling point of rockfall; L is the working face length.
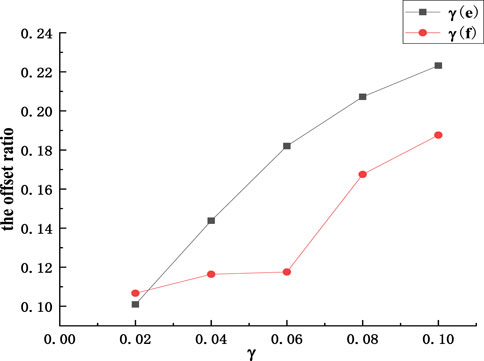
The offset ratio of rockfall is shown in Figure 16. In Figures 16–22, γ(e) represents the variable coefficient of collision recovery coefficient, and γ(f) represents the variable coefficient of friction coefficient. It can be seen from Figure 16 that the migration offset ratio of rockfall increases with the increase of the variation coefficient. Furthermore, the impact curve of the randomness of the collision recovery coefficient on migration ratio is smoother, the overall curve is higher than that of the friction coefficient, and the randomness of the collision recovery coefficient has a more significant impact on migration and migration ratio of rockfall. Therefore, when the coefficient of variation is small, the randomness of the collision recovery coefficient and friction coefficient has less influence on the offset ratio, which indicates that the smaller the randomness of the parameters, the less the offset ratio is affected by it.
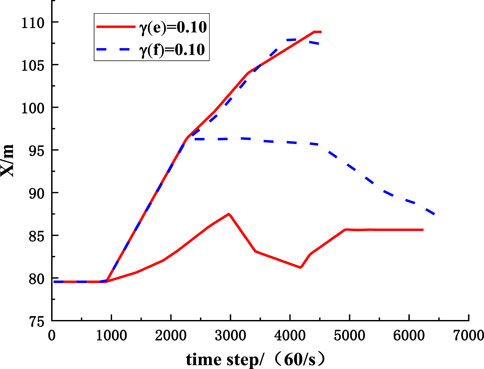
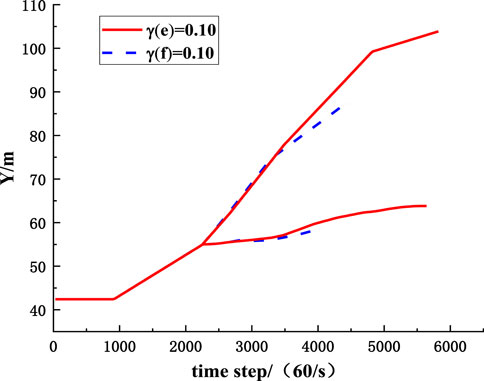
To compare the influence of parameters randomness on the migration of rockfall, the MCETM is used to simulate the variation curves of the upper and lower boundaries of the position coordinates of rockfall with time when the coefficient of variation of collision recovery and friction coefficient take different values, as shown in Figures 17–20. It can be seen from Figures 17–20 that the randomness of the collision recovery coefficient and friction coefficient has different effects on the tendency migration and lateral migration of rockfall, and with the increase of parameter variation coefficient, the randomness of parameters has a more significant influence on the migration of rockfall.
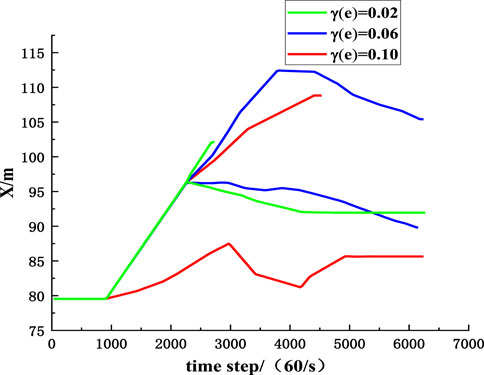
FIGURE 17. The influence of randomness of collision recovery coefficient on inclined position coordinates of rockfall.
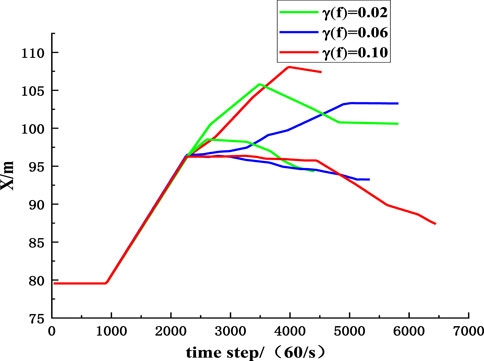
FIGURE 18. The influence of randomness of friction coefficient on inclined position coordinates of rockfall.
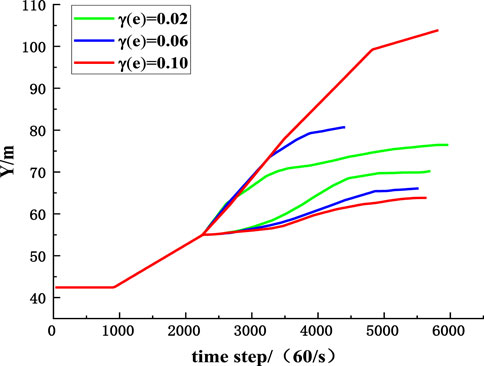
FIGURE 19. The influence of randomness of collision recovery coefficient on lateral position coordinates of rockfall.
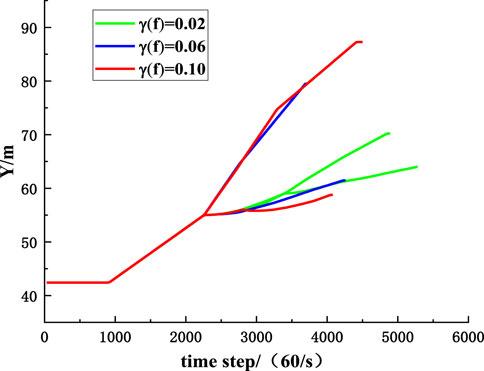
FIGURE 20. The influence of randomness of friction coefficient on lateral position coordinates of rockfall.
Figures 21, 22 are comparative diagrams of changes in inclined position coordinates and strike position coordinates of rockfall when the coefficient of variation of collision recovery and the friction coefficient is the same. It can be seen from Figures 21, 22 that the randomness of the collision recovery coefficient has a more significant influence on the migration of rockfall than the friction coefficient, and the randomness of the collision recovery coefficient still dominates the migration of rockfall.
5 Conclusion
(1) The generation method of erose rockfall proposed in this paper can generate its random model based on the ellipsoid. A 3D grid model of the working face floor is established according to its contour lines and drilling information in the steep seam, which ultimately opens the interface between the GIS data model and the ETM self-programming, and realizes the perfect combination of the visual modelling of the natural working face in SDCS and the ETM self-programming. The proposed method greatly improves the matching degree between numerical simulation and engineering practice.
(2) The Monte Carlo random simulation method and ETM can accurately simulate the three-dimensional random migration process of the erose rockfall, which solves the problem that previous studies were limited to the two-dimensional spontaneous migration of the erose rockfall but could not simulate its randomness of lateral migration. The larger the sample data, the more accurate the simulation results will be.
(3) As the variable coefficient of parameters increases, the interval width of kinematic characteristic quantities such as velocity and angular velocity shows a growing trend. This is because the impact of the randomness of the collision recovery coefficient on the interval width of kinematic characteristics such as velocity and angular velocity is far heavier than that of the randomness of the friction coefficient, and the randomness of the friction coefficient has relatively little impact on the transport speed of rockfall.
(4) The randomness of the collision recovery coefficient and friction coefficient has different effects on the inclined migration and lateral rockfall migration: as the parameter variation coefficient increases, the randomness of parameters influences the rockfall migration better; the randomness of collision recovery coefficient influences the rockfall migration better than that of friction coefficient. Nevertheless, the randomness of the collision recovery coefficient always dominates the rockfall migration.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
ML and YX developed the idea and edited the paper; JC designed and analyzed the mechanical model. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by Open Fund of State Key Laboratory of Green and Low-Carbon Development of Tar-Rich Coal in Western China, Xi’an University of Science and Technology (Program No. SKLCRKF21-03), Key Research and Development Program of Shaanxi (Program No. 2023-YBGY-318), Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-YB-439), the FuShun Revitalization Talents Program (Program No. FSYC202107004), and the National Natural Science Foundation of China (Program Nos. 51604213, 51974226 and 52174127).
Acknowledgments
The authors would like to extend their sincere appreciation to the X. H. Tang of Wuhan University for program debugging.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bi, R., Tang, X., and Liu, B. J. (2016). An implused-based energy tracking method for the analysis of slope stability of falling rocks. Chin. J. Geol. Hazard Control 27, 14–19. doi:10.16031/j.cnki.issn.1003-8035.2016.02.02
Chu, K. H., and Chen, Z. X. (2017). Research and application of coal flying gangue protection technology and device in steeply inclined fully mechanized face. Coal Mine Mach. 38, 79–81. doi:10.13436/j.mkjx.201706031
Hu, B. S., Wu, Y. P., Wang, H. W., Tang, Y. P., and Wang, C. R. (2021). Risk mitigation for rockfall hazards in steeply dipping coal seam: A case study in xinjiang, northwestern China. Geomatics Nat. Hazards Risk 12, 988–1014. doi:10.1080/19475705.2021.1909147
Jing, L. L., Qu, J. L., Liu, M., and Qiao, B. M. (2019). Non-probabilistic interval analysis method for estimation of flying gangue movement in steeply dipping seam. Coal Technol. 38, 105–108. doi:10.13301/j.cnki.ct.2019.05.035
Lai, X. P., Shan, P. F., Cao, J. T., Cui, F., and Sun, H. (2016). Simulation of asymmetric destabilization of mine-void rock masses using a large 3D physical model. Rock Mech. Rock Eng. 49, 487–502. doi:10.1007/s00603-015-0740-z
Liu, M., and Chen, J. (2021a). Influence of shape on flying gangue migration in steeply dipping coal seam. J. China Coal Soc. 46, 548–2556. doi:10.13225/j.cnki.jccs.2020.0598
Liu, M., and Chen, J. (2021b). Movement and protection for random shape rockfalls in steeply dipping coal seams. Adv. Civ. Eng. 2021, 1–14. doi:10.1155/2021/9965415
Liu, M., Geng, S., Wu, Y. P., and Lv, W. Y. (2020a). Design of flying gangue protection device driven by hydraulic system. Coal Mine Mach. 41, 102–103. doi:10.13436/j.mkjx.202001035
Liu, M., Li, K., Duo, Y. L., and Wu, Y. P. (2020b). Motion track analysis and protective device of flying gangue in roof leakage of steeply dip-ping working face. Coal Sci. Technol. 48, 139–144. doi:10.13199/j.cnki.cst.2020.08.017
Liu, M., Li, K., Wu, Y. P., Geng, S., and Zhang, G. D. (2019). Design of flying gangue protection device for steeply dipping seam by grating recognition. Coal Mine Mach. 40, 29–30. doi:10.13436/j.mkjx.201908010
Liu, M., Li, K., Wu, Y. P., and Lv, W. Y. (2020c). Safety evaluation and application for flying gangue of steeply dipping coal seam based on fuzzy comprehensive evaluation method. Saf. Coal Mines 51, 244–247. doi:10.13347/j.cnki.mkaq.2020.02.053
Liu, M., Wu, Y. P., Geng, S., Duo, Y. L., and Lv, W. Y. (2020d). Threat level assessment of flying gangue in steep seam mining. J. China Coal Soc. 45, 3688–3695. doi:10.13225/j.cnki.jccs.2019.1092
Liu, M., Wu, Y. P., and Xu, G. (2016). Research on rule of flying gangue in steeply dipping seam mining. Coal Technol. 35, 17–18. doi:10.13301/j.cnki.ct.2016.07.008
Liu, M., Zhou, Y. T., Lv, W. Y., and Duo, Y. L. (2021b). Threat evaluation of flying gangues in steeply dipping seam based on dynamic bayesian network. Coal Sci. Technol. 49, 99–104. doi:10.13199/j.cnki.cst.2021.11.013
Liu, M., Zhou, Y. T., and Lv, W. Y. (2021a). Normal characteristic quantity theory of flying gangue motion in steeply dipping seam with stochastic parameters. J. China Coal Soc. 46, 2237–2244. doi:10.13225/j.cnki.jccs.2020.0222
Tang, X. H., Paluszny, A., and Zimmerman, R. W. (2014). An impulse-based energy tracking method for collision resolution. Comput. Methods Appl. Mech. Eng. 278, 160–185. doi:10.1016/j.cma.2014.05.004
Tu, H. S., Tu, S. H., Yuan, Y., Wang, F., and Bai, Q. (2015). Present situation of fully mechanized mining technology for steeply inclined coal seams in China. Arabian J. Geosciences 8, 4485–4494. doi:10.1007/s12517-014-1546-0
Wang, J. A., and Jiao, J. L. (2016). Criteria of support stability in mining of steeply inclined thick coal seam. Int. J. Rock Mech. Min. Sci. 82, 22–35. doi:10.1016/j.ijrmms.2015.11.008
Wu, Y. P., Hu, B. S., Lang, D., and Tang, Y. P. (2021). Risk assessment approach for rockfall hazards in steeply dipping coal seams. Int. J. Rock Mech. Min. Sci. 138, 104626. doi:10.1016/J.IJRMMS.2021.104626
Wu, Y. P., Hu, B. S., Wang, H. W., and Liu, K. Z. (2018a). Simulation and experiment research on the evolution characteristics of flying gangue energy in steeply dipping coal seam. J. Xi’an Univ. Sci. Technol. 38, 37–42. doi:10.13800/j.cnki.xakjdxxb.2018.0106
Wu, Y. P., Hu, B. S., Wang, H. W., Xie, P. S., Liu, M., and Liu, M. Y. (2017a). Mechanism of flying gangue-causing disasters in longwall mining of steeply dipping seam. J. China Coal Soc. 42, 2226–2234. doi:10.13225/j.cnki.jccs.2017.0017
Wu, Y. P., Hu, B. S., and Xie, P. S. (2019). A new experimental system for quantifying the multidimensional loads on an on-site hydraulic support in steeply dipping seam mining. Exp. Tech. 43, 571–585. doi:10.1007/s40799-019-00304-4
Wu, Y. P., Hu, B. S., Xie, P. S., Li, S. H., and Huangfu, J. Y. (2018b). Impact damage of flying gangue in steeply dipping seams and its control. J. China Coal Soc. 43, 2694–2702. doi:10.13225/j.cnki.jccs.2017.1282
Wu, Y. P., Hu, B. S., Xie, P. S., and Zeng, Y. F. (2017b). Flying gangue regional control technology in longwall mining face of steeply dipping seam. Coal Sci. Technol. 45, 1–5. doi:10.13199/j.cnki.cst.2017.02.001
Wu, Y. P., Liu, K. Z., Yun, D. F., Xie, P. S., and Wang, H. W. (2014). Research progress on the safe and efficient mining technology of steeply dipping seam. J. China Coal Soc. 39, 1611–1618. doi:10.13225/j.cnki.jccs.2014.9039
Wu, Y. P., Yun, D. F., Xie, P. S., Wang, H. W., Lang, D., and Hu, B. S. (2020). Progress, practice and scientific issues in steeply dipping coal seams fully-mechanized mining. J. China Coal Soc. 45, 24–34. doi:10.13225/j.cnki.jccs.YG19.0494
Keywords: steeply dipping coal seam, rockfall, the energy tracking method, migration, random parameters
Citation: Liu M, Chen J, Xiao Y and Lv W (2023) Migration law for random parameters rockfall in steeply dipping coal seams. Front. Earth Sci. 11:1088188. doi: 10.3389/feart.2023.1088188
Received: 03 November 2022; Accepted: 08 February 2023;
Published: 27 February 2023.
Edited by:
Fangtian Wang, China University of Mining and Technology, ChinaReviewed by:
Gang Liu, Heilongjiang University of Science and Technology, ChinaAnxiu Liu, Taiyuan University of Technology, China
Copyright © 2023 Liu, Chen, Xiao and Lv. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Chen, Y2hlbmppZTIwMjA2QDE2My5jb20=
 Ming Liu
Ming Liu Jie Chen
Jie Chen Yang Xiao
Yang Xiao Wenyu Lv
Wenyu Lv