Eastward expansion of the Tibetan plateau: Insights from stress drops of the 2021 Ms 6.4 Yangbi, Yunnan and Ms 7.4 Maduo, Qinghai earthquake sequences in China

The eastward expansion of the Tibetan Plateau has resulted in extensive seismic activities in the eastern Tibetan Plateau, along with various types of faulting processes across this region. However, the crustal stress status related to these phenomena remains unclear. On 21 May 2021, the Ms 6.4 Yangbi and Ms 7.4 Maduo earthquakes with diverse focal mechanisms occurred consecutively in the Chuandian and Bayan Har blocks in the southern and northern parts of the eastern Tibetan Plateau, providing a distinct opportunity to directly compare the stresses in both flanks of the laterally expanding plateau. In this study, we estimate the stress drops of the Yangbi and Maduo earthquake sequences for all $M\ge 3.0$ events from the Lg-wave spectra. Both the path attenuation and site effect are properly removed based on an established broadband Lg-wave attenuation model. Then, the distribution of the stress drops is refined through high-precision earthquake relocation. Quick decays in stress drops were observed after both mainshocks. The Yangbi sequence has a relatively high median stress drop value, with significantly high stress drops for some foreshocks that possibly indicate a cascade triggering mechanism for the nucleation of the mainshock. In comparison, the Maduo sequence is characterized by a higher stress drop for the mainshock and sustained large fluctuation in stress drops for aftershocks. The Maduo aftershocks extend both the eastern and western directions from the mainshock, with relatively low stress drops in the east, suggesting a large amount of energy has been spent to drive the supershear rupture during the mainshock. We also find that the stress drops are associated with fault junctions for the Yangbi sequence, and are associated with variations in strength along the fault for the Maduo sequence, which are very likely linked with patterns of crustal motion and deformation in the eastern Tibetan Plateau.

1 Introduction

The geological evolution of the Tibetan Plateau during the Cenozoic is accompanied by well-developed fault systems and seismic activities (Figure 1); therefore, explorations into present-day seismicity and source parameters can shed light on structures and properties of the seismogenic layers, advancing our understanding of the growing process of the plateau (Molnar and Lyoncaen, 1989). In the southern and northern Tibetan Plateau, significant thrusting indicates the uplift of the Tibetan Plateau in response to the continued north-south convergence between the Indian and Eurasian plates (Yin and Harrison, 2000). Since the middle Miocene, north–south-trending normal faulting began to develop in the central Tibetan Plateau, signifying the east-west expansion of the high-rising plateau crust (e.g., Yin and Harrison, 2000; Blisniuk et al., 2001). The resulting eastward movements of crustal blocks, including the Bayan Har and Chuandian, led to reverse faulting on the Longmanshan faults that mark the eastern boundary of the Tibetan Plateau (e.g., Zheng et al., 2017) and devastating earthquakes, including the Wenchuan earthquake in 2008 and the Lushan earthquake in 2013 (Wang et al., 2015). In addition, significant strike-slip motions were also produced on the boundaries of the extruding blocks. In particular, on 21 May 2021, within ∼4.3 h, the Yangbi Ms 6.4 earthquake occurred in the Chuandian block, and the Maduo Ms 7.4 earthquake occurred in the Bayan Har block, both with primarily strike-slip faulting. However, the faulting behaviors vary across the southern boundaries of the Chuandian block and the northern boundaries of the Bayan Har block. Right-lateral strike-slip plus normal faulting and left-lateral strike-slip plus reverse faulting were obtained for the mechanism solutions of the Yangbi and Maduo earthquakes, respectively (Long et al., 2021; Zhang J. Y. et al., 2022). The various focal mechanisms may reflect intricate fault morphology and probably a complicated regional stress setting, yet the stress distributions within the fault system and related tectonic attributions remain unclear. Exploring the stress release of these earthquakes can shed light on the localized stress variability within seismogenic faults and improve our understanding of the nature of plateau expansion (Holt et al., 1991; Zhang et al., 2010; Sun et al., 2018).

FIGURE 1

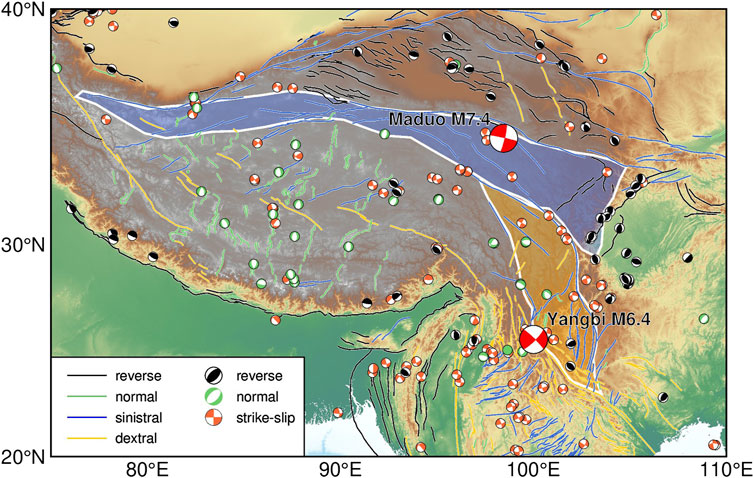
FIGURE 1. Map showing active faults (lines) and moderate to large earthquakes (beach balls) on the Tibetan Plateau, with their kinematic types coded by colors. Geological blocks filled with blue and yellow are the Bayan Har and Chuandian blocks, respectively. Locations and focal mechanisms of the 2021 May Yangbi and Maduo earthquakes are indicated by red beach balls.

The stress drop is defined as the difference between the average stresses on a fault before and after an earthquake (e.g., Shearer et al., 2006). It is one of the fundamental source-scaling parameters, providing information on the rupture processes and underlying tectonics controlling them (e.g., Allmann and Shearer, 2009; Abercrombie, 2014). The stress drop of earthquakes can be an indicator of the localized stress variability of the seismogenic fault (e.g., Allmann and Shearer, 2007; Yamada et al., 2010), whereas it is not equivalent to the overall stress levels of faults. Rupture simulations demonstrated that keeping the same stress drop at different stress levels can produce identical synthetic waveforms, even in near field (Weng and Yang, 2018; Yao and Yang, 2020). Since both Yangbi and Maduo earthquake sequences were primarily strike-slip faulting, it is not necessary to attribute the difference in stress drop to focal mechanisms and we can explore the localized stress variability in the eastern Tibetan Plateau by straightforward comparison of the stress drops between the two earthquake sequences. However, the stress drop is calculated based on reliable restoration of the earthquake source spectrum, which can be easily distorted by seismic attenuation and shallow structures beneath stations. Several methods have been developed to solve this, including the empirical Green’s function method (Shearer et al., 2006) and the generalized joint inversion method to solve for both the source and path attenuation (Oth et al., 2011). However, the rapid development in attenuation tomography over recent years has inspired us with a novel approach to directly remove the attenuation and site effects from the observed spectra based on the established attenuation model (He et al., 2020). Zhao et al. (2010) developed a broadband Lg-wave attenuation tomography scheme that utilized both source-station amplitudes and interstation amplitude ratios to obtain the high-resolution broadband Lg-wave Q model. This method was then improved to incorporate the interevent amplitude ratios thus the site response for each station could also be inverted (Zhao and Xie, 2016). By using the this method, a high-resolution broadband Lg-wave Q model was obtained for China, which is consistent with geological features (Zhao et al., 2010; 2013b; Zhao et al., 2013a; He X. et al., 2021). The site responses were also obtained for relevant stations. Taking advantage of attenuation and site response dataset, the accurate of the stress drop estimates for the 21 May 2021 Yangbi and Maduo earthquake sequences can be achieved.

In this study, we retrieve Lg-wave source spectra for earthquakes with magnitudes $\ge 3.0$ for both Yangbi and Maduo earthquake sequences. The effects of attenuation along the propagation path and site response are removed using the established broadband regional Lg-wave attenuation model and regional site response data. Based on the reliable source spectra and assuming a generalized source model (Boatwright, 1980), the seismic moment, corner frequency and high-frequency falloff rate are estimated for each event. The stress drop is then calculated for both the Yangbi and Maduo earthquake sequences. To investigate the temporal and spatial evolutions of these stress drops, we relocated earthquakes to refine their source locations. Finally, we discuss the tectonic implications of these stress drops and their relations with the eastward expansion of the Tibetan Plateau.

2 Data and method

2.1 Regional dataset

In this study, 105 earthquakes were selected from the catalog of the China Earthquake Network Center (CENC), including the 21 May 2021 Yangbi mainshock, with 11 foreshocks after 13 May and 39 aftershocks before 1 June, and the Maduo mainshock, with 53 aftershocks before 1 June. These earthquakes were selected according to magnitudes $\ge 3.0$ to improve the quality of Lg recordings, and their locations and origin times were obtained from the catalog. We collected more than 42 thousand vertical-component seismograms recorded by 376 permanent seismic stations to investigate the source properties of the 2021 Yangbi and Maduo earthquake sequences. These stations have good azimuthal coverage and were within epicentral distances between 200–3,000 km to ensure well developed Lg waves (Figure 2).

FIGURE 2

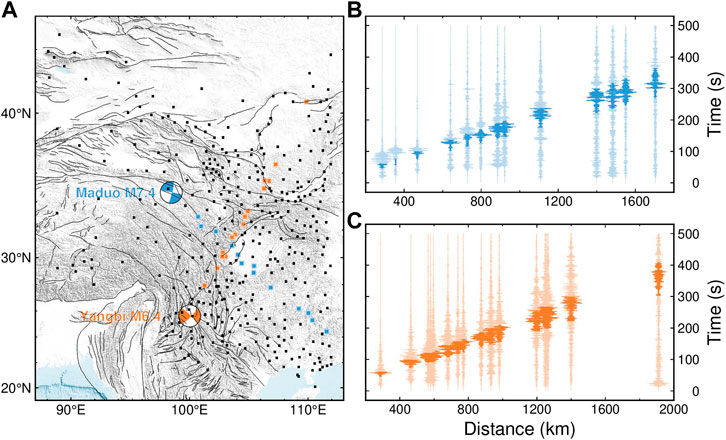
FIGURE 2. Map of the distribution of stations used in this study (A) and illustrations of seismograms (B,C). (A) Stations are represented by filled squares. Locations and focal mechanisms of the 2021 May Yangbi and Maduo earthquakes are indicated by orange and blue beach balls, respectively. Orange and blue squares represent stations selected to show their recordings for the Yangbi and Maduo mainshocks, respectively. (B,C) Waveforms are filtered between 0.5 and 1.0 Hz to improve the Lg demonstrations and are aligned with a reduced velocity of 8.4 km/s. Typical group velocities of the Lg phase, 3.6–3.0 km/s, are highlighted. The Lg-wave group velocity window can be slightly adjusted for each trace to capture the maximum energy arrival.

2.2 Lg-wave preprocessing

The seismic Lg-wave, developed from a reverberated S-wave in the continental crust, is one of the prominent seismic phases in regional seismograms and often used in amplitude analysis (Furumura and Kennett, 1997; Fisk, 2006; Pasyanos et al., 2009). To analyze the arrival times and frequency contents of different regional phases, illustrated in Figure 3A is a regional waveform, and in Figure 3B is the corresponding spectrogram. The spectrogram was obtained using the short-time Fourier transform, where the window was determined to be consistent with the regular Lg-extraction length, according to the velocity window with a length of 0.6 km/s. Due to the changing length of the window, we regularized the spectrogram at 58 frequencies within 0.05–10.0 Hz, and then normalized the spectrogram at each frequency. The first arrival in the spectrogram was Pn at ∼2–5 Hz, followed by Pg over ∼0.3–4 Hz. The Sn was very weak compared with other regional phases. Lg could be recognized as a prominent patch with a longer duration and dominating energy within ∼0.2–2.0 Hz. Based on the spectrogram, the velocity window is 3.6–3.0 km/s. We followed the procedure of Zhao et al. (2010) to process the Lg amplitudes. First, instrument responses were removed, and Lg waveforms were cut using the velocity window of 3.6–3.0 km/s (Figure 3B). The window can be slightly adjusted to capture the maximum Lg energy. The waveforms immediately before the first p arrivals were defined as noise (Figure 3B). Then, the spectra of Lg and corresponding noise were calculated by applying a cosine taper and fast Fourier transformation and were sampled at 58 frequency points between 0.05 and 10.0 Hz to obtain the spectral amplitudes $A_{obs}$ and $A_{noise}$ of Lg and noise, respectively (Figure 3C). Next, the signal-to-noise ratio (SNR) was calculated by $A_{obs}\left(f\right)/A_{noise}\left(f\right)$ at each frequency point $f$. We set the SNR threshold of 2.0, in consideration of the trade-off between the quality and amount of available data, to select the data to be used (Figure 3D). The quality control resulted in, for example, 18,039, 18,070 and 10,179 valid Lg spectral measurements at 0.5, 1.0 and 2.0 Hz, respectively. Finally, by assuming that the noise is not correlated with the Lg wave, the true Lg spectral amplitudes were obtained by $\sqrt{A_{obs}^2\left(f\right)-A_{noise}^2\left(f\right)}$.

FIGURE 3

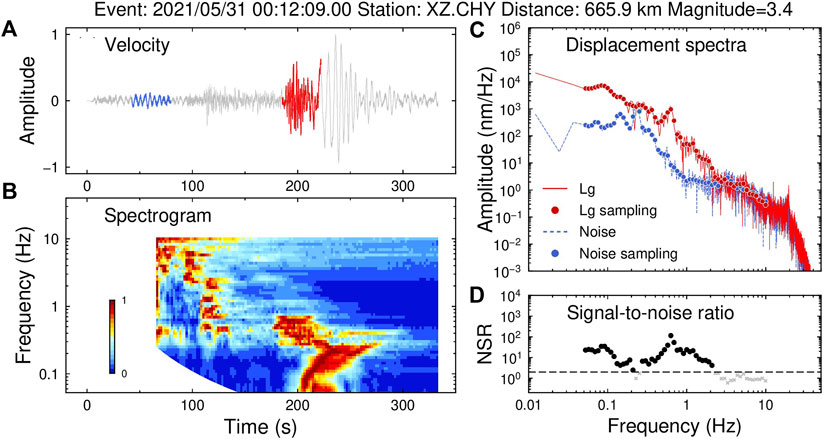
FIGURE 3. (A) Sample seismogram of the Yangbi aftershock recorded at station XZ. CHY. The Lg waveform and pre-event noise are highlighted in red and blue, respectively. (B) Time-frequency spectrogram of the sample seismograms. (C) Spectra of Lg and pre-event noise. (D) Signal-to-noise ratio. The SNR threshold of 2.0 is adopted and illustrated by a dashed line. Data points with SNRs lower than 2.0 are discarded and represented by gray crosses.

2.3 Lg spectra modeling and source spectra retrieval

According to Aki (1967), we modeled the Lg spectral amplitude $A\left(f,∆\right)$ as

$A\left(f,∆\right)=S\left(f\right)G\left(∆\right)\Gamma \left(f,∆\right)P\left(f\right)R\left(f\right)(1)$

where $\Delta$ is the epicentral distance, $S$ is the source spectrum, $G$ is the geometrical spreading term, $\Gamma$ is the attenuation term, $P$ is the site response and $R$ is the term containing modeling errors. The geometrical spreading term can be written as ${\left({\Delta }_0∆\right)}^{-\frac{1}{2}}$, where ${\Delta }_0$ is the reference distance to be fixed at 100 km (Street et al., 1975). The attenuation term has the form

$\Gamma \left(f,∆\right)=\exp \left[\frac{-\pi f}{v}\int \frac{ds}{Q\left(x,y,f\right)}\right](2)$

where the symbol ∫ denotes the integral along the source-station ray path and Q can be obtained from the established high-resolution broadband Lg-wave Q models (Zhao et al., 2013a; Zhao et al., 2013b; He X. et al., 2021). To compute the attenuation term, we mapped the ray path onto the Q model and split it into $N$ segments with a length of $ds$; then, Eq. 2 can be discretized and rewritten as summation

$\Gamma \left(f,∆\right)=\exp \left[\frac{-\pi f}{v}{\displaystyle \sum }_{n=1}^N\frac{ds}{Q_n}\right](3)$

where $n$ denotes the $n$ th segment of the ray, and $Q_n$ is the average Q within this segment. It is frequency-dependent and can be obtained from the broadband Lg-wave attenuation model. In previous studies, the relative site response has been determined in conjunction with attenuation (He X. et al., 2021) and is available for 375 stations in this study. For the only station without an available site term, we assigned it with a unit amplification. The Q model and site response dataset used are illustrated in Supplementary Figures S1, S2.

With known geometrical spreading, attenuation, and site response, we linearized Eq. 1 to relate source perturbations with the residuals between the observed and predicted Lg spectra (Zhao et al. (2010). The least squares QR (LSQR) factorization algorithm (Paige and Saunders, 1982) was used to obtain the source perturbations by minimizing the L2 norm of the residual. The source terms, starting with the unit source function, were iteratively updated until convergence. Based on the attenuation, site response and restored source terms, the synthetic Lg spectral amplitudes fit well to the observations. For example, the mean absolute error between synthetic and observed Lg amplitudes at 1 Hz decreased from 1.78 to 0.81 and the deviation from 1.27 to 0.84 (red and blue histograms in Figure 4). We also tested a constant Q to restore the source terms (yellow and green histograms in Figure 4), and found that Lg spectra can also be fitted to a certain degree, but not as good as that based on both laterally-varying Q model and site response.

FIGURE 4

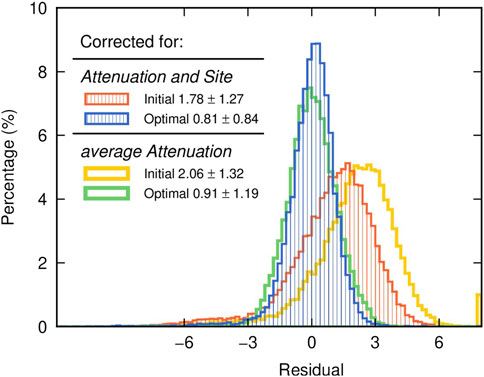
FIGURE 4. Histogram comparing the amplitude residuals. Red and blue histograms represent the distributions of residuals between the observed and predicted Lg spectra before and after inversion based on both attenuation and site corrections. Yellow and green histograms represent the distributions of residuals between the observed and predicted Lg spectra before and after inversion based on constant attenuation. The initial and final rms residual and deviation are labeled for both inversion schemes.

2.4 Source parameter estimation

After retrieving the source spectra $S\left(f\right)$ for each earthquake at 58 individual frequencies, we estimate the scalar seismic moment $M_0$ and the corner frequency $f_c$ based on the source model

$S\left(f\right)=\frac{M_0}{4\pi \rho {\nu }^3{\left[1+{\left(\frac{f}{f_c}\right)}^{\gamma n}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.}}(4)$

where $n$ is the high-frequency falloff rate, $\gamma$ controls the sharpness of the spectral corner, and $\rho$ and $\nu$ are the density and shear wave velocity in the source region, respectively. Typical values of $\rho =2.7kg/m^3$ and $\nu =3.5km/s$ were used. Generally, $\gamma$ can be set to 1, although a larger value of $\gamma =2$ was also used for some studies (Boatwright, 1980). Letting $\gamma =1$ and $n=2$ yields the commonly used Brune (1970) model. However, in this study, the high-frequency spectra often fall faster than 2. Therefore, we treated $n$ as a variable to be estimated as well. By fitting the theoretical source model to the retrieved source spectrum using the annealing simulation algorithm (Kirkpatrick et al., 1983), $M_0$, $f_c$ and $n$ can be determined for each earthquake. The above results were also compared to those using other source models, including the Brune model ($\gamma =1$; $n=2$), the ${\omega }^{-3}$ model ($\gamma =1$; $n=3$) and the Boatwright model ($\gamma =2$; $n$ as variable) (refer to Supplementary Figure S3)

The ideal scenario is that the source spectrum has a flat low-frequency asymptote and a high-frequency descending portion, permitting to accurately estimate $M_0$ and $f_c$. In practice, our analysis showed that for small earthquakes, the Lg source spectra at frequencies lower than ∼0.2 Hz were sometimes raised, possibly by ambient noise or surface waves generated by preceding earthquakes. Although not apparent for larger earthquakes because their source spectra were significantly higher than the noise level, the contaminated step-like spectrum would possibly result in an underestimated corner frequency and overestimated seismic moment for small earthquakes, introducing large errors into the following analysis. To suppress these effects and improve the reliability of parameter estimation, we set the fitting band truncations for small earthquakes and then screened problematic estimations based on comparisons of magnitude measurements. First, for $M\le 3.5$ earthquakes, we fitted the retrieved source spectra within only 0.3–10.0 Hz because the observed noise level is high at approximately 0.2 Hz and the corner frequencies for earthquakes with magnitudes between 3.0 and 3.5 are generally higher than 0.3 Hz (e.g., Madariaga, 1976). The fitting band of 0.3–10.0 Hz could generally exclude the noise spectrum and retain the high-frequency portion of source spectra as much as possible to estimate the corner frequencies. Such a magnitude-dependent fitting band strategy was also used in previous source analysis studies (Abercrombie, 1995; Allmann and Shearer, 2007; Allmann and Shearer, 2009). Although effective in finding $M_0$ and $f_c$ for small earthquakes, such rough truncation would sometimes omit all of the flat portion, leading to a problematic estimation. Therefore, next, we screened these problematic results based on the obtained seismic moment $M_0$. The moment magnitude $M_W$ can be calculated from $M_0$ using the China Earthquake Administration scaling relationship $M_W=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\left(\log M_0-9.1\right)$ ($M_0$ is in the unit of N m). Magnitude scaling analysis based on earthquakes in Switzerland demonstrated that the difference between $M_W$ and the local magnitude $M_L$, $M_W-M_L$ generally ranged from −1.0 to 0.5 (Goertz-Allmann et al., 2011). Considering the geological settings and algorithm used to calculate $M_0$, we set a broader threshold and discard earthquakes with $\left|M_L-M_W\right|>1.0$ (Figure 5). In total, 17 earthquakes were discarded due to abnormally high $M_0$ values. The remaining earthquakes yielded a linear relationship $M_L=1.31\left(\pm 0.02\right)M_W-1.64\left(\pm 0.12\right)$. The slope was in agreement with previous studies (e.g., Bethmann et al., 2011), whereas slight differences could result from geological settings, algorithms to calculate the $M_W$ or the uncertainty in the catalog magnitude.

FIGURE 5

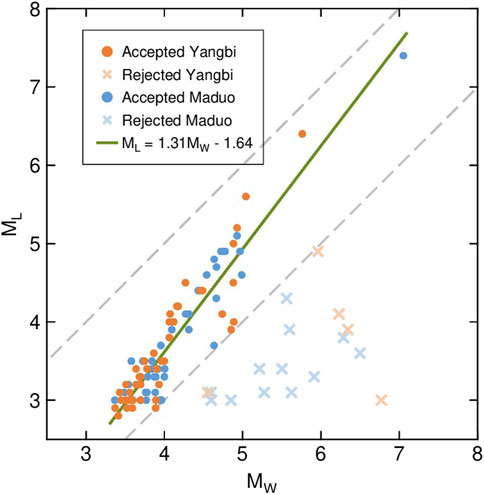
FIGURE 5. Comparison between the retrieved moment magnitude and catalog magnitude. Two gray dashed lines represent $M_L-M_W=\pm 1.0$, which are used to screen the retrieved source spectra with unusually large uncertainties (Goertz-Allmann et al., 2011).

Based on a circular fault model (Eshelby, 1957), the stress drop can be calculated using

$\mathit{\Delta }\sigma =\frac{7M_0}{16}{\left(\frac{f_c}{kv}\right)}^3(5)$

where the constant $k$ is 0.21 by assuming a rupture velocity of 0.9 shear wave velocity (Madariaga, 1976). The constant k was also suggested to be 0.29 and 0.37, depending on specific source model used (Brune, 1970; Sato and Hirasawa, 1973). We also tested the effects of using different k values, and found that the absolute stress drop values may vary with k, but their relative relationships are kept unchanged among events (Supplementary Figure S4). For simplicity, stress drops for all events were calculated based on same assumptions, including using the circular fault model, although it may be improper for large earthquakes with excessive long ruptures. Therefore, the mainshock stress drops will not be compared with aftershock stress drops.

2.5 Earthquake relocation

To refine the spatial distribution of the stress drop, we relocated the 2021 Yangbi and Maduo earthquake sequences for all earthquakes with local magnitudes greater than 3.0 using the HypoDD program, which allows for simultaneous accurate relocation of clusters of earthquakes based on double-difference travel times (Waldhauser and Ellsworth, 2000). Earthquake relocation and stress drop calculation based on consistent catalog avoid possible errors of assigning the calculated stress drops to incorrect events. We first visually inspected first P-wave arrivals automatically picked by the deep-learning-based PickNet program (Left panels in Figure 6) (Wang et al., 2019). This program can offer better picks at regional distances and was previously trained by the travel-time dataset from earthquakes in the Myanmar region (Wang et al., 2019). Then, we further processed the picked arrival times to calculate the double-difference first-P travel times of earthquake pairs at their common stations and only those pairs observed by more than eight stations were used. For the Yangbi earthquake sequence, a total of 1,493 first arrival P-wave travel times with epicentral distances less than 5° generated 20,124 P-phase pairs. The earthquake pairs had a separation of less than 10 km. For the Maduo earthquake sequence, a total of 2,594 first arrival P-wave travel times at 214 stations were used to generate 3,872 P-phase pairs. When processing the Maduo earthquake sequence, the performance of PickNet significantly reduced the amount of available data, and therefore, we allowed larger observation distances of 10°. Due to its ∼150-km-long aftershock zone, we also allowed a larger spatial separation of 20 km within each earthquake pair so to include as many earthquakes as possible into the relocation clusters. The station distributions have relatively good azimuthal coverage for both earthquake sequences (Supplementary Figure S5). Proper parameters were chosen through several trials to control the initial conditions, clustering of earthquakes and data weighting in the HypoDD program. During relocation, local 1D crustal structures for the source regions of Yangbi and Maduo sequences were extracted from the USTClitho1.0 model (Right panels in Figure 6) (Xin et al., 2018). The relocation results were obtained using the LSQR factorization algorithm (LSQR, Paige and Saunders, 1982) with eight iterations. For convergence purpose, in each iteration, the data outside of 3 times the standard deviation of the RMS residual were treated as outliers and dropped. The iterations updated epicenter locations. Meanwhile, the rms travel time residuals were reduced from 0.49 s to 0.28 s and from 0.67 s to 0.25 s for Yangbi and Maduo sequences, respectively (Supplementary Figure S6). To assess relocation errors, we relocated the events for 100 times, in each time, with only 80% randomly-selected double-different travel times being used. For the Yangbi sequence, the mean errors were 245, 200 and 558 m in the east-west, north-south and vertical directions, respectively (Supplementary Figure S7). For the Maduo sequence, the mean errors were 812, 667 and 1,053 m in the east-west, north-south and vertical directions, respectively (Supplementary Figure S8). The errors were comparable to those of previous studies (Long et al., 2021; Xu et al., 2021; Zhang J. Y. et al., 2022; Zhu et al., 2022). The accuracy and reliability of earthquake relocation could be further improved by incorporating the cross-correlation double-different travel times, which is, however, out of the scope of this study.

FIGURE 6

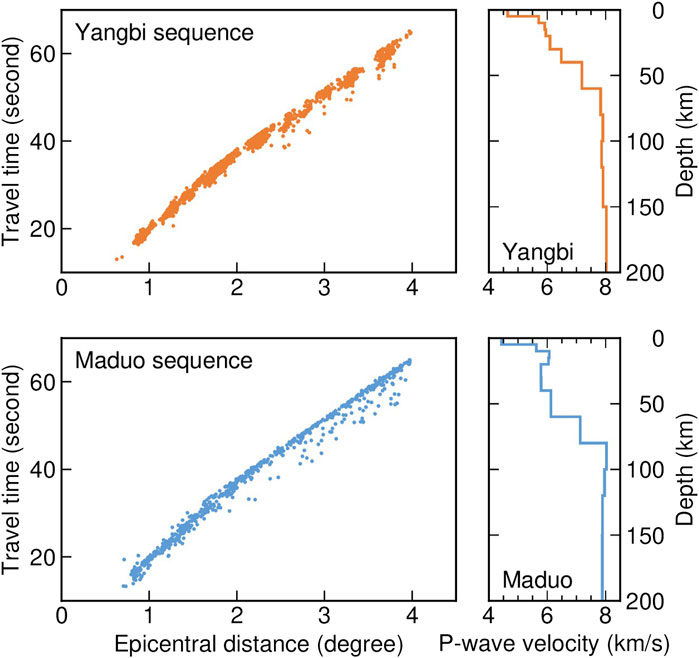
FIGURE 6. Left, travel times picked using the PickNet, and right, the USTClitho1.0 1D velocity models used in relocation calculations. The upper and lower panels are for Yangbi and Maduo sequences, respectively.

3 Results

In this study, we retrieved the source spectra for earthquakes with local magnitudes greater than 3.0 for both the Yangbi and Maduo earthquake sequences and estimated the seismic moment, corner frequency and high-frequency falloff rate for the 81 earthquakes with reliable Lg-wave source spectra (Figure 7; Supplementary Table S1). The obtained seismic moment ranged from $1.42\times {10}^{14}$ to $4.76\times {10}^{19}$ $\mathrm{N}\cdot \mathrm{m}$, corresponding to the moment magnitude $M_W$ between 3.4 and 7.1. The corner frequency ranged from 0.08 to 1.61 Hz, within the band limitation of 0.05–10.0 Hz in this study. The corner frequencies obtained in this study from Lg waves are generally consistent with previous studies using body waves, although there appears slight systematic difference (Supplementary Figure S9). The high-frequency falloff rate was between 2.1 and 3.6, with a mean value of 2.8, which was a value higher than 2.0 for the ${\omega }^{-2}$ model (Brune, 1970), demonstrating the necessity of setting this parameter as a variable. The stress drop was calculated for each earthquake through the seismic moment and corner frequency. Large variability in the stress drop is observed, with the value ranging from 0.08 to 22.59 MPa and a logarithmic standard deviation of 0.48 for Yangbi sequence, and with the value ranging from 0.05 to 28.31 MPa and a logarithmic standard deviation of 0.54 for Maduo sequence. The logarithmic standard deviation was used to quantify the variability of the stress drop, and recent studies found values generally between ∼0.35 and 0.45 (e.g., Trugman, 2020). The notably higher values obtained in this study indicate large variations in stress that may happen over short distances and thus could be related to the very complicated tectonics in both areas. To estimate the reliability of the result, the bootstrap method was used to assess the obtained Lg source spectra parameters (Efron, 1983). We repeat the Lg source calculation for 50 times, with each time involving randomly-sampled 80% of the observed displacement spectra (Figure 7). The seismic moment, corner frequency, high-frequency falloff rate and stress drop are calculated for each time, and we estimate errors in these parameters based on their standard deviations. The stress drop calculation is sensitive to the methods and source models (e.g., Shearer et al., 2006), and therefore, we mainly focus on relative variations within the May 2021 Yangbi and Maduo earthquake sequences. The logarithmic scale was used for the time axes to better demonstrate the temporal variations in stress drops for the early aftershocks. We also plotted trendlines to show the general temporal variations in stress drops (Figure 8). The trendlines were obtained by first resampling the time series of the stress drop with nearest point interpolation and an increment of 0.1 log(T) and then filtering using a low-pass Gaussian filter with a width of 0.5 log(T), where T denotes the time in days before or after the mainshock. The spatial distributions of the stress drop were investigated for both the Yangbi and Maduo earthquake sequences based on the epicenters relocated using the HypoDD program (Figures 9, 10). We also investigated the relationship between the stress drop and focal depth, and found no significant correlation, with correlation coefficients of 0.08 and 0.33 for Yangbi and Maduo sequences, respectively (Supplementary Figure S10).

FIGURE 7

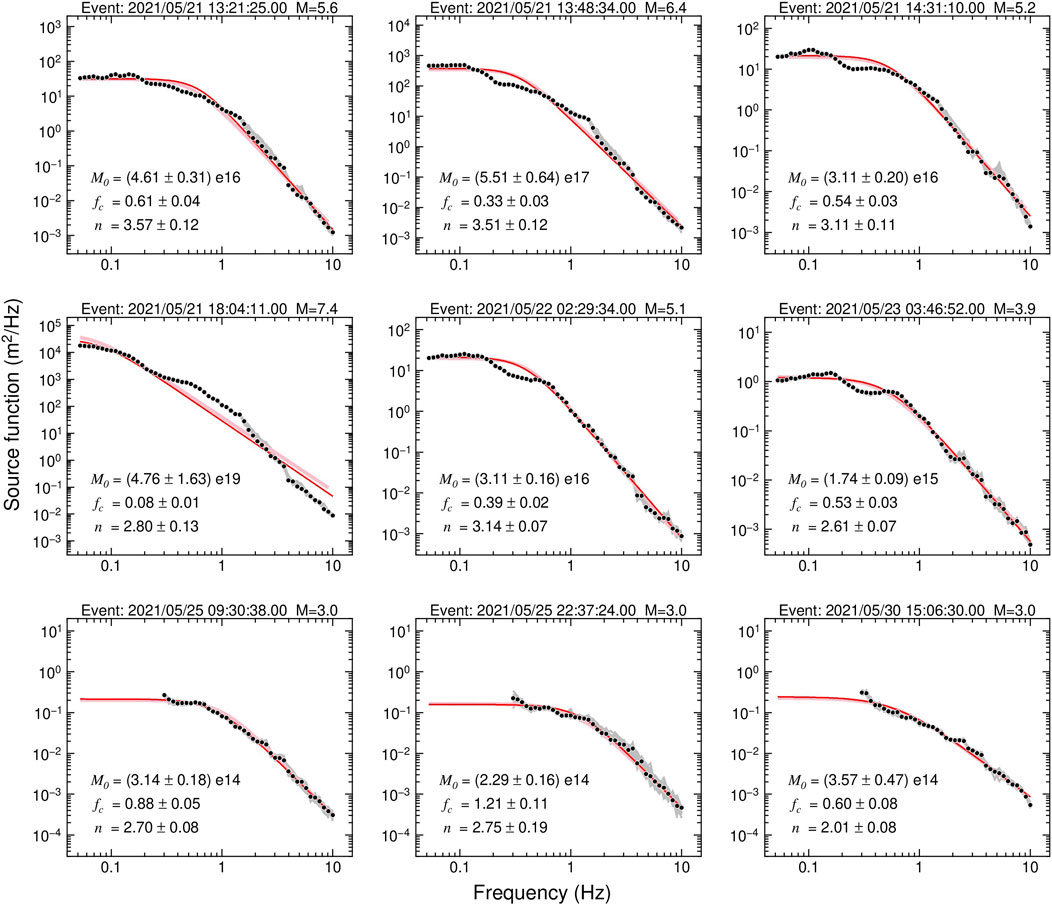
FIGURE 7. Illustrations of retrieved source spectra (black circles) and estimated source models (red lines). For earthquakes with magnitudes less than 3.5, the source models fit only the spectra above 0.3 Hz. Gray and pink lines represent the source spectra obtained using 80% randomly sampled data and corresponding source models, respectively. In each panel, the earthquake information, scalar seismic moment, corner frequency, and high-frequency falloff rate are labeled.

FIGURE 8

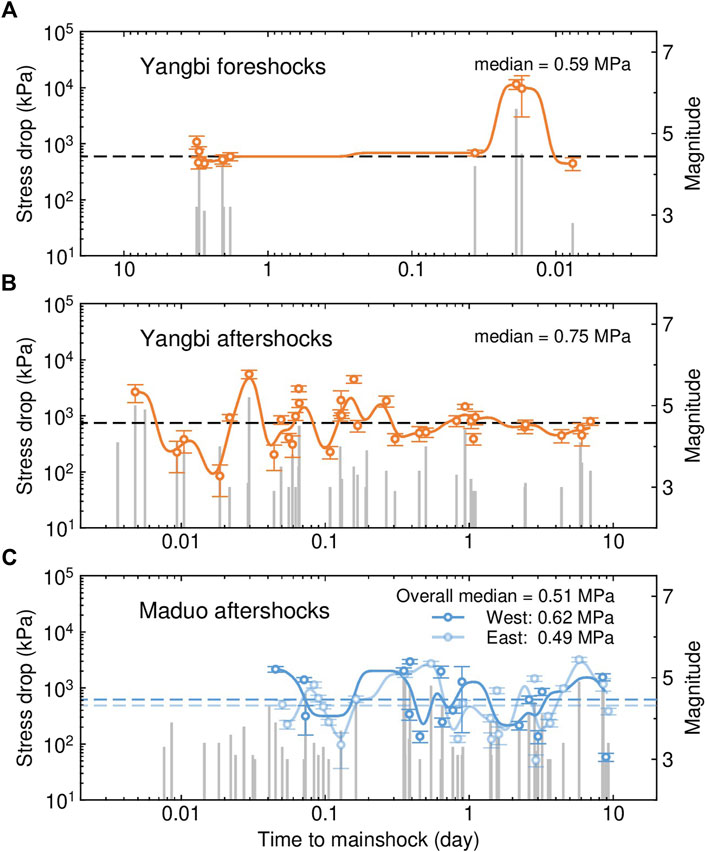
FIGURE 8. Temporal variations in the stress drop for the (A) Yangbi foreshock sequence, (B) Yangbi aftershock sequence and (C) Maduo aftershock sequence. The stress drop estimates are represented by open circles. Solid trendlines are obtained by applying a low-pass Gaussian filter. The seismicity of earthquakes with magnitudes greater than 3.0 is shown by vertical gray lines, with their heights corresponding to magnitudes. Error bars indicate the standard deviations of stress drops measurements, with their stress drop values indicated by dashed lines. Aftershocks in Maduo sequence are grouped according to their locations east (light blue) or west (blue) to the mainshock.

FIGURE 9

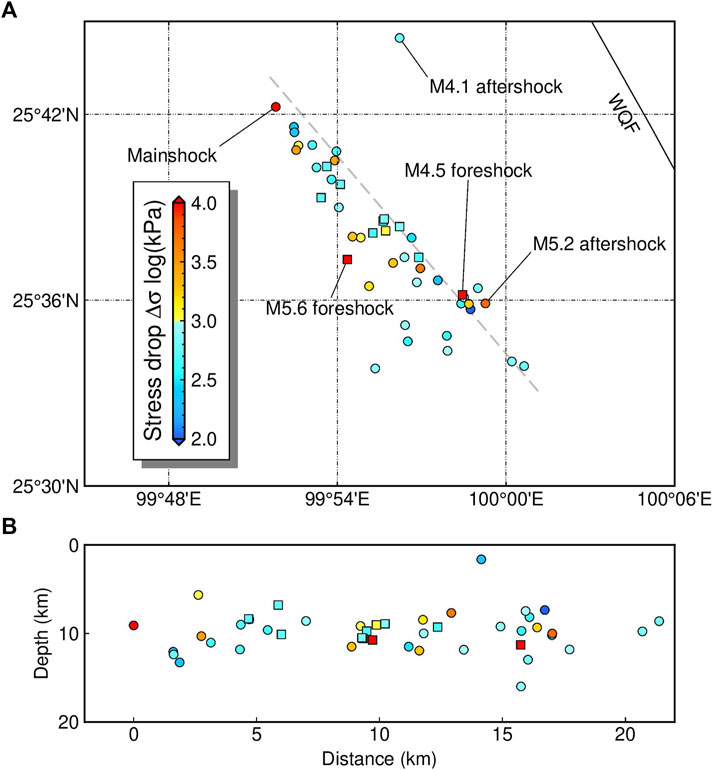
FIGURE 9. (A) Map view and (B) depth cross-section of stress drops for the 21 May 2021 Yangbi earthquake sequence. The filled symbols illustrate the relocated sources, with their stress drops coded by colors. The squares represent the foreshocks, and the circles represent the mainshock and aftershocks. The Weixi–Qiaohou fault (WQF) is represented by a black lines. The mainshock is located at distance=0 in the depth cross-section. Gray dashed line shows the location of the cross-section.

FIGURE 10

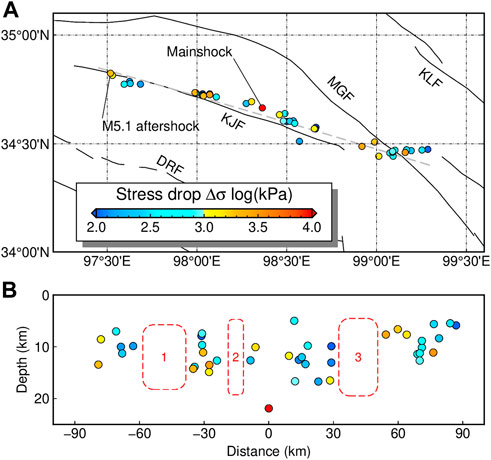
FIGURE 10. (A) Map view and (B) depth cross-section of the stress drops for the 21 May 2021 Maduo earthquake sequence. The filled circles illustrate the relocated epicenters, with their stress drops coded by colors. The active faults are indicated by black lines, with their names labeled in abbreviations: DRF, Dari fault; KJF, Kunlunshankou–Jiangcuo fault; MGF, Maduo–Gande fault; and KLF, Eastern Kunlun fault. The mainshock is located at distance=0 in the depth cross-section. Gray dashed line shows the location of the cross-section. Three aftershock gaps are marked in the depth profile with red dashed rectangles.

3.1 Stress drops for the Yangbi and Maduo earthquake sequences

The stress drop of the Yangbi mainshock is 22.59 ± 4.85 MPa. For the foreshocks, the stress drops range from 0.44 to 11.56 MPa, with a median value of 0.59 MPa, and for aftershocks ranged from 0.08 to 5.55 MPa, with a median value of 0.75 MPa (Figures 8A,B). The foreshocks emerged on 18 May, with their stress drops exhibiting a general decrease from the initial value, until foreshocks became active again on 19 May. After that, a gradual increase in stress drop was visible, followed by two earthquakes, including the largest Ms 5.6 one, characterized by a significantly higher stress drops of ∼10 MPa occurring ∼25–27 min before the mainshock. In the aftershock sequence, the stress drops were relatively fluctuated and decreased gradually along with the decrease of seismicity. The minimum stress drop appeared ∼26 min after the mainshock, indicating of a great amount of stress was released by the mainshock. The stress drop was again increased along with several strong aftershocks, including the largest Ms 5.2 aftershock occurring ∼43 min after the mainshock, with the highest stress drop among all aftershocks. After strong fluctuation lasting for approximately 1 day, the stress drop values remained around the median value, which could indicate the stress adjustment following the mainshock.

For the Maduo earthquake sequence, the stress drop of the mainshock is 28.31 ± 3.92 MPa, and the stress drops of aftershocks range from 0.05 to 3.21 MPa, with a median value of 0.51 MPa (Figure 8C). The values of the stress drop for the Maduo aftershock sequence are generally lower than those for the Yangbi sequence in terms of their maximum, minimum and median values, suggesting a possibly lower stress level on the Maduo seismogenic fault after the mainshock. The Maduo aftershock sequence is characterized by more scattered stress drop values undulated for ∼9 days after the mainshock. For example, several large aftershocks occurred ∼8 h and ∼8 days after the mainshock, with their stress drops greater than 1.5 MPa. Compared with the Yangbi sequence, the prolonged undulation in the stress drop and late occurrence of the minimum value nearly 3 days after the mainshock probably indicate a relatively long stress repartition process, which could be related to the longer seismogenic fault involved in the Maduo sequence.

3.2 Relocations of the Yangbi and Maduo earthquake sequences with stress drop estimated

Based on the first P arrivals picked by the PickNet program, we used the double-difference earthquake relocation program HypoDD to refine the locations of the calculated stress drop. The results were generally consistent to previous studies (e.g., Long et al., 2021; Xu et al., 2021; Zhang et al., 2021; Zhang J. Y. et al., 2022). For the May 2021 Yangbi earthquake sequence, we relocated 51 epicenters (Figure 9; Supplementary Table S1). The Yangbi earthquake sequence was generally distributed along a northwest‒southeast trend and extended for approximately 21 km. Although roughly parallel to regional tectonics, e.g., the northwest‒southeast-trending Red River fault and Jinshajiang fault, the distribution of the Yangbi earthquake sequence appeared not directly linked to any known faults, including the Weishan–Qiaohou fault ∼10 km to the northeast. The foreshock activities migrated back and forth within the epicentral area, including the largest M5.6 foreshock near the center and the M4.5 foreshock near the southeastern end occurring ∼2 min later. The Yangbi mainshock was located at $99.8635°\mathrm{E}$ and $25.7039°\mathrm{N}$, with a depth of 9.090 km at the northwestern end of the epicentral area, suggesting a unilateral rupture toward the southeast. For the aftershocks, their epicenters extended further southeast and gradually scattered to a wider area, possibly indicating secondary structures with variable orientations. An M4.1 event was located notably off the primary aftershock trend to the northeast, which may indicate a cluster of earthquakes on an activated secondary fault (Zhang et al., 2021). The sources of the Yangbi earthquake sequence were mostly located in the upper crust at approximately 10 km depths.

By relocation, we obtained the fine distribution of the stress drop. The highest stress drop in the foreshock sequence was observed for a M5.6 event located near the center of the foreshock zone, where foreshock activities had been initiated since 18 May. Another significantly high stress drop was linked to the M4.5 foreshock, occurred at the southeast end of the foreshock area. The mainshock and the largest aftershock were located at the northwestern and southeastern ends of the epicentral zone, respectively, both with notably high stress drops.

We relocated 54 earthquakes in the Maduo sequence (Figure 10; Supplementary Table S1). The results demonstrate that the mainshock was located at $98.3641°\mathrm{E}$ and $34.6656°\mathrm{N}$, with a depth of 21.909 km. The epicenter of the mainshock was ∼5 km northeast to the mapped trace of the Kunlunshankou–Jiangcuo fault (KJF). The aftershocks were nearly linearly distributed on both sides of the mainshock, extending approximately 170 km along a northwest–west trends and generally consisting with the KJF. Gaps with absent or sparse aftershocks are visible, for example, at sections ∼40–60 km (gap 1), ∼15–20 km northwest (gap 2), and ∼30–50 km southeast (gap 3) of the mainshock (Figure 10B). The aftershock zone intersected with the Maduo–Gande fault (MGF) near its southeast end, with the strike turning from northwest–west to west–east. The relocated focal depths in the Maduo sequence mainly ranged between ∼5–15 km, which were generally deeper than those in the Yangbi sequence and appeared more scattered. Except for the mainshock, which has the highest stress drop, other events with significantly high stress drops (e.g., >10^3.5 kPa) in the Maduo sequence can be generally associated with the aftershock gaps, especially the cluster ∼30 km northwest of the mainshock (gap 1). The cluster of high stress drops ∼60 km southeast of the mainshock may also be related to the intersection with the MGF.

4 Discussion

4.1 Earthquake stress drop and stress distributions on faults

The earthquake stress drop can be related to the localized stress variability on a seismogenic fault. Larger stress drop variations could result from fault plane heterogeneities (Kirkpatrick et al., 2020), e.g., a rougher fault plane may cause higher stress drops due to its additional resistance to slip (Fang and Dunham, 2013). Allmann and Shearer (2009) observed higher overall stress drops for strike-slip earthquakes at a global scale, which is consistent with previous findings of increased apparent stress for strike-slip events. However, at local scales, the dependence on the focal mechanism is less significant, and stress drops appear more dominated by the local tectonics (Shearer et al., 2006; Goebel et al., 2015; Boyd et al., 2017). Therefore, investigating stress drops in the Yangbi and Maduo earthquake sequences may reveal stress variations in the related seismogenic zones.

In the Yangbi sequence, the stress drops of foreshocks may suggest the accumulation of stress and hint the stress variation that led to the nucleation of the mainshock. The pre-slip mechanism is one of the popular explanations for how an earthquake initiates, in which concentrated and repeated seismicity is expected (Zhu et al., 2022). However, the relocated foreshock sequence revealed a back-and-forth migration pattern. In addition, high-stress-drop foreshocks, including the first and the largest ones, have their stress drops significantly higher than the median value of the entire sequence, implying the potential to trigger earthquake. By modeling the cumulative static stress change from large foreshocks, Zhu et al. (2022) found that the local shear stress at the Yangbi mainshock epicenter was increased by major foreshocks. Therefore, our results of foreshock relocation and stress drops were consistent with the cascade triggering process during the nucleation of the Yangbi mainshock (Long et al., 2021; Zhang et al., 2021; Zhu et al., 2022). For the aftershock sequence, fluctuations of stress drops including many significantly high and low stress drop events may be related to the stress adjustment and continually release of the local stress field disturbed by the mainshock. Similar stress development pattern were also suggested by the observed b-values, which demonstrated long-term low values before 20 May 2021, showed abrupt reductions before the Ms 5.6 foreshock and the Ms 6.4 mainshock, then demonstrated large fluctuations around their mean value after the mainshock (Duan et al., 2021; Jiang et al., 2021). The b-value measures the distribution of earthquakes with different sizes in the recurrence relation of Gutenberg and Richter (1941) and is found to be reversely related to the differential stress within the crust (Schorlemmer et al., 2005). A low b-value and high stress were also observed preceding the M6.4 and M7.1 Ridgecrest, California earthquakes in 2019 (Nanjo, 2020).

In the Maduo sequence, the aftershocks were distributed on both the northwest and southeast sides of the mainshock along the Kunlunshankou–Jiangcuo fault. For aftershocks to the east and west of the mainshock, our results showed their median stress drops were 0.49 MPa and 0.62 MPa, respectively. The difference probably suggested differentiated rupture processes between the east- and west-sections. Previous studies have suggested that the eastward rupture of the Maduo mainshock propagated at a speed exceeding 3.5 km/s S-wave velocity, i.e., supershear rupture (Zhang X. et al., 2022; Li et al., 2022; Lyu et al., 2022; Yue et al., 2022). The back-projection imaging technique is commonly used to obtain large earthquake rupture kinematics. With this method, the Maduo mainshock was found ruptured toward the east and west, with velocities of 3–5 km/s and 2–3 km/s, respectively (Zhang X. et al., 2022; Li et al., 2022; Yue et al., 2022). Zhang X. et al. (2022) further confirmed the eastward supershear rupture by recognizing far-field Love Mach waves. Joint analysis using Global Positioning System, Interferometric Synthetic Aperture Radar, and teleseismic data determined the westward and eastward rupture velocities to be 2.0 and 4.6 km/s, respectively (Yue et al., 2022). Near-field Global Navigation Satellite Systems recordings demonstrated significant sensitivity to determine rupture velocities and confirmed sub- and supershear ruptures on the west and east sections of the mainshock fracture, respectively (Lyu et al., 2022). We suggest that the lower aftershock stress drops on the east section can be related to the larger stress release due to the supershear rupture. Yue et al. (2022) pointed out that the coseismic slip east of the mainshock was concentrated in seismogenic layers, in which rate-weakening friction law might support instability failure to facilitate the supershear rupture. Since a large amount of energy was consumed to feed the supershear rupture, the remaining stress was low, resulting in low stress drops for the aftershocks to the east of the mainshock. The relatively high aftershock stress drops observed on the west section of the mainshock fracture suggest there were more strain stored within this part of the crust. This energy can be further released by later aftershocks or interseismic creeping.

4.2 Earthquake stress drop and fault complexity

In this study, stress drops from the relocated earthquake sequences demonstrated that high stress drops were often related to fault junctions or earthquake gaps, suggesting stress concentrations at these locations.

The relocated sources of the Yangbi sequence suggested a complicated fault system with a northwest‒southeast-trending major fault, which may split into multiple branches in the southeast section. This is consistent with previous earthquake relocations; however, a detailed fault structure can be suggested by relocation for a larger number of small earthquakes. Long et al. (2021) relocated more than 1,000 Yangbi events with local magnitudes greater than 1.0 based on the seismic phase bulletin, suggesting a northwest‒southeast-trending primary fault, with northeast‒southwest-trending conjugate faults in its northwestern segment, and multiple secondary faults along the primary fault and gradual turning toward the south in the southeast. The multiscale en echelon structures were further revealed by high-resolution catalogs built using a deep-learning phase picker (Su et al., 2021; Liu et al., 2022). Combining the fault structures with our relocation results, high-stress-drop events in the Yangbi sequence were generally related to fault junctions and tips. For example, the M4.5 and M5.6 foreshocks with significantly high stress drops were located around the middle of the epicentral zone, where the south-trending en echelon faults intersect with the primary fault; several aftershocks with high stress drops could be found near fault junctions and tips, including the M5.2 and M4.1 aftershocks. Simulations suggested significantly increased stress localized at the junctions of branching faults (e.g., Ando et al., 2018). Therefore, the high stress drops in the Yangbi sequence may result from the stress concentrations near the fault junctions and tips and may in turn indicate the precise locations of sophisticated fault branches.

In the Maduo sequence, the stress drops demonstrated a more fluctuating pattern than in the Yangbi sequence. The prolonged stress drop variations could be related to the fault properties. The cross-section view reveals that the clusters of earthquakes with significantly high-stress-drop values were generally associated with the earthquake gaps along the fault. These gaps should be robust features despite a magnitude threshold 3.0 was used for earthquake relocation in this study. In previous studies that relocated more than 1,300 earthquakes with magnitudes greater than 0, reduced seismicity was still pronounced at these locations, and in particular, few aftershocks occurred ∼50 km northwest and ∼30 km southeast of the mainshock (Wang W. L. et al., 2021; Xu et al., 2021) (corresponding to the gaps 1 and 3 in Figure 10B). The correspondence between high stress drops and aftershock gaps probably indicated redistributed stress following the mainshock. Geodetic observations revealed coseismic slip on the seismogenic fault following the mainshock. They varied significantly along the fault strike and concentrated at several localized segments with maximum slips of ∼3–4 m (He K. et al., 2021). These high-slip patches may represent the asperities where stresses were released by significant rupture during the mainshock, resulting in localized reduced or lack of aftershock activities. Since the asperities are generally related to variations in strength or friction properties due to the changes of fault geometry, and result in stress concentration (Mildon et al., 2019), we propose that the stress remaining on the fault was redistributed and concentrated near the edges of fault asperities, thus leading to the occurrence of larger aftershocks with high stress drops. A similar complementary correspondence between the stress drop and mainshock slip was also suggested for the 1992 Landers earthquake in southern California (Shearer et al., 2006).

4.3 Implications for the eastward expansion of the Tibetan plateau

The stress drops of the Yangbi, Yunnan and Maduo, Qinghai earthquake sequences in May 2021 demonstrated different temporal and spatial patterns, which reflected varying localized crustal stress variability and deformations across the eastern Tibetan Plateau. A deformation field recently constructed from GPS data revealed predominantly continuous strains inside the eastern Tibetan Plateau, with significant shear associated with large strike-slip faults to accommodate the eastward extrusion of geological blocks (Wang and Shen, 2020). On the southern flank of the extrusion, the Chuandian block represents the majority of the escaping crustal material from the interior plateau. Wang and Shen (2020) found that the translation of the Chuandian block was accompanied by notable clockwise rotation at a rate of ∼2.9°/Myr around the Eastern Himalayan syntax and widespread dilatation at 10–20 nanostrain/yr. The dilatation should be responsible for the normal component obtained in the focal mechanism solutions of the Yangbi earthquake sequence. The complicated combination of southeastward translation, clockwise rotation and interior deformations requires a large number of active faults to accommodate, possibly resulting in the multiscale en echelon faults and conjugate faults that inherited motions of the associated large strike-slip faults. Therefore, these small faults could also generate large earthquakes, including the 2021 Yangbi Ms 6.4 earthquake, with the repartitioned stress concentration subject to the geometric complexity of the fault systems, for example, the fault junctions and tips, giving rise to several high stress drops in the Yangbi earthquake sequence. The local stress field inverted from focal mechanisms suggested a change in the orientation of the horizontal maximum principal stress from near north–south to nearly east‒west in the southernmost epicentral zone, coincident with the regional stress and possibly reflecting the tectonic rotation of the Chuandian block (Wang Y. et al., 2021).

In contrast, the focal mechanism of the Maduo earthquake sequence demonstrated a consistent northwest‒southeast orientation of maximum principal stress, corresponding to the movement of the Bayan Har block (Xu et al., 2021). The Bayan Har block is bounded in the north by the Kunlun fault, with significant left-lateral strike-slip, to accommodate the northeastward expansion of the eastern Tibetan Plateau. The slip rate on the Kunlun fault shows a west–east decrease from ∼12.5 mm/yr to less than 3 mm/yr, which was suggested to be decomposed to slips on several secondary faults subparallel to and south of the Kunlun fault (Kirby et al., 2007), including the Kunlunshankou–Jiangcuo fault, which was the seismogenic fault of the 2021 Maduo earthquake sequence. The slip around the middle segment of the Kunlun fault, which is faster than that near the northern segment of the Red River fault, is more likely to result in a concentration of shear strain (Zheng et al., 2017; Wang and Shen, 2020). Localized variations in crustal strength could occur due to shear heating and increased crustal temperature (Leloup et al., 1999; Bao et al., 2012). As a consequence, large earthquakes would rupture the high-strength asperities, and the perturbed stresses were likely to be repartitioned around the asperities and lead to larger variability in the stress drops of aftershocks. Therefore, the stress drops of the Yangbi and Maduo earthquake sequences were controlled by the eastward expansion of the Tibetan Plateau, and the differences in their patterns showed varying impacts on the seismogenic environment.

Conclusion

In this study, the temporal and spatial variations in stress drop were investigated for Yangbi and Maduo earthquake sequences in May 2021, including all foreshocks, mainshocks and aftershocks with magnitudes greater than 3.0. The results reveal that the stress drop for Yangbi mainshock was relatively low than Maduo mainshock. Comparing with the Yangbi sequence, the Maduo sequence was characterized by stress drops of relatively low median value and rather scattered values for individual events. For stress drops in both sequences, no apparent depth dependency was found. The temporal-spatial pattern in stress drop for Yangbi sequence can be related to geometric complexity of the fault systems, which were resulted from the tectonic movement of the Chuandian block incorporating translation, rotation, and interior deformation. The Bayan Har block is regarded as another component in the eastward expansion of the Tibetan Plateau. Fast slip and high shear strain rate around its northern boundary may cause localized variations in fault strength, which controls the temporal-spatial pattern in the stress drop of Maduo sequence.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://data.earthquake.cn/yhsj/info/2016/5596.html.

Author contributions

XH: Conceptualization, formal analysis, writing—original draft, writing—review and editing, funding acquisition. L-FZ: Conceptualization, methodology, formal analysis, writing—review and editing, funding acquisition. LZ: Formal analysis. X-BX: Writing—review and editing. Z-XY: Funding acquisition, supervision.

Funding

This research was supported by the National Natural Science Foundation of China (U2139206, 42104055, 41974054, and 41974061) and the Special Fund of China Seismic Experimental Site (2019CSES0103).

Acknowledgments

The waveforms used in this study were collected from the National Earthquake Data Center (NEDC) at https://data.earthquake.cn/yhsj/info/2016/5596.html (in Chinese, last accessed August 2022) and the Incorporated Research Institutions for Seismology Data Management Center (IRIS-DMC) at https://ds.iris.edu/wilber3/find_event (last accessed August 2022). Researchers can register for an account to apply for the NEDC data. Some figures were generated using Generic Mapping Tools (GMT; https://www.generic-mapping-tools.org/).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1081605/full#supplementary-material

References

Abercrombie, R. E. (1995). Earthquake source scaling relationships from −1 to 5M_Lusing seismograms recorded at 2.5-km depth. J. Geophys Res. 100 (B12), 24015–24036. doi:10.1029/95JB02397

CrossRef Full Text | Google Scholar

Abercrombie, R. E. (2014). Stress drops of repeating earthquakes on the san andreas fault at parkfield. Geophys Res. Lett. 41, 8784–8791. doi:10.1002/2014GL062079

CrossRef Full Text | Google Scholar

Aki, K. (1967). Scaling law of seismic spectrum. J. Geophys Res. 72 (4), 1217–1231. doi:10.1029/JZ072i004p01217

CrossRef Full Text | Google Scholar

Allmann, B. P., and Shearer, P. M. (2009). Global variations of stress drop for moderate to large earthquakes. J. Geophys Res. 114 (B1). doi:10.1029/2008jb005821

CrossRef Full Text | Google Scholar

Allmann, B. P., and Shearer, P. M. (2007). Spatial and temporal stress drop variations in small earthquakes near Parkfield, California. J. Geophys Res. 112 (B4). doi:10.1029/2006JB004395

CrossRef Full Text | Google Scholar

Bao, X. Y., Sandvol, E., Chen, Y. S. J., Ni, J., Hearn, T., and Shen, Y. (2012). Azimuthal anisotropy of Lg attenuation in eastern Tibetan Plateau. J. Geophys Res. 117 (B10). doi:10.1029/2012jb009255

CrossRef Full Text | Google Scholar

Bethmann, F., Deichmann, N., and Mai, P. M. (2011). Scaling relations of local magnitude versus moment magnitude for sequences of similar earthquakes in Switzerland. Bull. Seismol. Soc. Am. 101 (2), 515–534. doi:10.1785/0120100179

CrossRef Full Text | Google Scholar

Blisniuk, P. M., Hacker, B. R., Glodny, J., Ratschbacher, L., Bi, S. W., Wu, Z. H., et al. (2001). Normal faulting in central Tibet since at least 13.5 Myr ago. Nature 412 (6847), 628–632. doi:10.1038/35088045

PubMed Abstract | CrossRef Full Text | Google Scholar

Boatwright, J. (1980). A spectral theory for circular seismic sources; simple estimates of source dimension, dynamic stress drop, and radiated seismic energy. Bull. Seismol. Soc. Am. 70 (1), 1.

Google Scholar

Boyd, O. S., McNamara, D. E., Hartzell, S., and Choy, G. (2017). Influence of lithostatic stress on earthquake stress drops in North America. Bull. Seismol. Soc. Am. 107 (2), 856–868. doi:10.1785/0120160219

CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys Res. 75 (26), 4997–5009. doi:10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Duan, M., Zhao, C., Zhou, L., Zhao, C., and Zuo, K. (2021). Seismogenic structure of the 21 May 2021 M(s)6. 4 Yunnan Yangbi earthquake sequence. Chin. J. Geophys (in Chin. 64 (9), 3101–3115. doi:10.6038/cjg2021P0423

CrossRef Full Text | Google Scholar

Efron, B. (1983). Estimating the error rate of a prediction rule: Improvement on cross-validation. J. Am. Stat. Assoc. 78 (382), 316–331. doi:10.1080/01621459.1983.10477973

CrossRef Full Text | Google Scholar

Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lon Ser-A 241 (1226), 376–396. doi:10.1098/rspa.1957.0133

CrossRef Full Text | Google Scholar

Fang, Z., and Dunham, E. M. (2013). Additional shear resistance from fault roughness and stress levels on geometrically complex faults. J. Geophys Res. 118, 3642–3654. doi:10.1002/jgrb.50262

CrossRef Full Text | Google Scholar

Fisk, M. D. (2006). Source spectral modeling of regional P/S discriminants at nuclear test sites in China and the former Soviet Union. Bull. Seismol. Soc. Am. 96 (6), 2348–2367. doi:10.1785/0120060023

CrossRef Full Text | Google Scholar

Furumura, T., and Kennett, B. L. N. (1997). On the nature of regional seismic phases-II. On the influence of structural barriers. Geophys J. Int. 129 (2), 221–234. doi:10.1111/j.1365-246X.1997.tb01577.x

CrossRef Full Text | Google Scholar

Goebel, T. H. W., Hauksson, E., Shearer, P. M., and Ampuero, J. P. (2015). Stress-drop heterogeneity within tectonically complex regions: A case study of san gorgonio pass, southern California. Geophys J. Int. 202 (1), 514–528. doi:10.1093/gji/ggv160

CrossRef Full Text | Google Scholar

Goertz-Allmann, B. P., Edwards, B., Bethmann, F., Deichmann, N., Clinton, J., Fäh, D., et al. (2011). A new empirical magnitude scaling relation for Switzerland. Bull. Seismol. Soc. Am. 101 (6), 3088–3095. doi:10.1785/0120100291

CrossRef Full Text | Google Scholar

Gutenberg, B., and Richter, C. F. (1941). Seismicity of the Earth seismicity of the Earth. Geol. Soc. Am. 34

Google Scholar

He, K., Wen, Y., Xu, C., and Zhao, Y. (2021a). fault geometry and slip distribution of the 2021 Mw 7.4 Maduo, China, earthquake inferred from InSAR measurements and relocated aftershocks. Seismol. Res. Lett. 93, 8–20. doi:10.1785/0220210204

CrossRef Full Text | Google Scholar

He, X., Zhao, L.-F., Xie, X.-B., Shen, L., Wang, W.-M., and Yao, Z.-X. (2020). Stress drop assessment of the August 8, 2017, Jiuzhaigou earthquake sequence and its tectonic implications. Earthq. Sci. 33 (4), 161–176. doi:10.29382/eqs-2020-0161-01

CrossRef Full Text | Google Scholar

He, X., Zhao, L.-F., Xie, X.-B., Tian, X., and Yao, Z.-X. (2021b). Weak crust in southeast Tibetan Plateau revealed by Lg-wave attenuation tomography: Implications for crustal material escape. J. Geophys Res. 126, e2020JB020748. doi:10.1029/2020JB020748

CrossRef Full Text | Google Scholar

Holt, W. E., Ni, J. F., Wallace, T. C., and Haines, A. J. (1991). The active tectonics of the eastern Himalayan syntaxis and surrounding regions. J. Geophys Res. 96 (B9), 14595–14632. doi:10.1029/91JB01021

CrossRef Full Text | Google Scholar

Jiang, C., Jiang, C. S., Yin, F. L., Zhang, Y. B., Bi, J. M., Long, F., et al. (2021). A new method for calculating b-value of time sequence based on data-driven (TbDD): A case study of the 2021 Yangbi M(s)6. 4 earthquake sequence in yunnan. Chin. J. Geophys (in Chin. 64 (9), 3116–3124. doi:10.6038/cjg2021P0385

CrossRef Full Text | Google Scholar

Kirby, E., Harkins, N., Wang, E., Shi, X., Fan, C., and Burbank, D. (2007). Slip rate gradients along the eastern Kunlun fault. Tectonics 26. No.2). doi:10.1029/2006tc002033

CrossRef Full Text | Google Scholar

Kirkpatrick, J. D., Edwards, J. H., Verdecchia, A., Kluesner, J. W., Harrington, R. M., and Silver, E. A. (2020). Subduction megathrust heterogeneity characterized from 3D seismic data. Nat. Geosci. 13 (5), 369–374. doi:10.1038/s41561-020-0562-9

CrossRef Full Text | Google Scholar

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220 (4598), 671–680. doi:10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

Leloup, P. H., Ricard, Y., Battaglia, J., and Lacassin, R. (1999). Shear heating in continental strike-slip shear zones: Model and field examples. Geophys J. Int., 136(1), 19–40. doi:10.1046/j.1365-246X.1999.00683.x

CrossRef Full Text | Google Scholar

Li, Q., Wan, Y., Li, C., Tang, H., Tan, K., and Wang, D. (2022). Source process featuring asymmetric rupture velocities of the 2021 Mw 7.4 Maduo, China, earthquake from teleseismic and geodetic data. Seismol. Res. Lett. 93 (3), 1429–1439. doi:10.1785/0220210300

CrossRef Full Text | Google Scholar

Liu, M., Li, H., Li, L., Zhang, M., and Wang, W. (2022). Multistage nucleation of the 2021 Yangbi MS 6.4 earthquake, Yunnan, China and its foreshocks. J. Geophys Res. 127 (5), e2022JB024091. doi:10.1029/2022JB024091

CrossRef Full Text | Google Scholar

Long, F., Qi, Y., Yi, G., Wu, W., Wang, G., Zhao, X., et al. (2021). Relocation of the MS6.4 Yangbi earthquake sequence on May 21,2021 in Yunnan Province and its seismogenic structure analysis. Chin. J. Geophys. 64 (8), 2631–2646.

Google Scholar

Lyu, M., Chen, K., Xue, C., Zang, N., Zhang, W., and Wei, G. (2022). Overall subshear but locally supershear rupture of the 2021 Mw 7.4 Maduo earthquake from high-rate GNSS waveforms and three-dimensional InSAR deformation. Tectonophysics 839, 229542. doi:10.1016/j.tecto.2022.229542

CrossRef Full Text | Google Scholar

Madariaga, R. (1976). Dynamics of an expanding circular fault. Bull. Seismol. Soc. Am. 66 (3), 639–666. doi:10.1785/bssa0660030639

CrossRef Full Text | Google Scholar

Mildon, Z. K., Roberts, G. P., Walker, J. P. F., and Toda, S. (2019). Coulomb pre-stress and fault bends are ignored yet vital factors for earthquake triggering and hazard. Nat. Commun. 10, 2744. doi:10.1038/s41467-019-10520-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Molnar, P., and Lyoncaen, H. (1989). Fault plane solutions of earthquakes and active tectonics of the Tibetan Plateau and its margins. Geophys J. Int. 99 (1), 123–154. doi:10.1111/j.1365-246X.1989.tb02020.x

CrossRef Full Text | Google Scholar

Nanjo, K. Z. (2020). Were changes in stress state responsible for the 2019 Ridgecrest, California, earthquakes? Nat. Commun. 11 (1), 3082. doi:10.1038/s41467-020-16867-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Oth, A., Bindi, D., Parolai, S., and Di Giacomo, D. (2011). Spectral analysis of K-NET and KiK-net data in Japan, Part II: On attenuation characteristics, source spectra, and site response of borehole and surface stations. Bull. Seismol. Soc. Am. 101, 667–687. doi:10.1785/0120100135

CrossRef Full Text | Google Scholar

Paige, C. C., and Saunders, M. A. (1982). Lsqr: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. 8 (1), 43–71. doi:10.1145/355984.355989

CrossRef Full Text | Google Scholar

Pasyanos, M. E., Matzel, E. M., Walter, W. R., and Rodgers, A. J. (2009). Broad-band Lg attenuation modelling in the Middle East. Geophys J. Int. 177 (3), 1166–1176. doi:10.1111/j.1365-246X.2009.04128.x

CrossRef Full Text | Google Scholar

Sato, T., and Hirasawa, T. (1973). Body wave spectra from propagating shear cracks. J. Phys. Earth 21 (4), 415–431. doi:10.4294/jpe1952.21.415

CrossRef Full Text | Google Scholar

Schorlemmer, D., Wiemer, S., and Wyss, M. (2005). Variations in earthquake-size distribution across different stress regimes. Nature 437 (7058), 539–542. doi:10.1038/nature04094

PubMed Abstract | CrossRef Full Text | Google Scholar

Shearer, P. M., Prieto, G. A., and Hauksson, E. (2006). Comprehensive analysis of earthquake source spectra in southern California. J. Geophys Res. 111 (B6). doi:10.1029/2005jb003979

CrossRef Full Text | Google Scholar

Street, R. L., Herrmann, R. B., and Nuttli, O. W. (1975). Spectral characteristics of the Lg wave generated by central United States earthquakes. Geophys J. Int. 41 (1), 51–63. doi:10.1111/j.1365-246X.1975.tb05484.x

CrossRef Full Text | Google Scholar

Su, J. B., Liu, M., Zhang, Y. P., Wang, W. T., Li, H. Y., Yang, J., et al. (2021). High resolution earthquake catalog building for the 21 May 2021 Yangbi, Yunnan, M-S 6. 4 earthquake sequence using deep-learning phase picker. Chin. J. Geophys (in Chin. 64 (8), 2647–2656. doi:10.6038/cjg2021O0530

CrossRef Full Text | Google Scholar

Sun, J., Yue, H., Shen, Z.-K., Fang, L., Zhan, Y., and Sun, X. (2018). The 2017 jiuzhaigou earthquake: A complicated event occurred in a young fault system. Geophys Res. Lett. 45, 2230–2240. doi:10.1002/2017gl076421

CrossRef Full Text | Google Scholar

Trugman, D. T. (2020). Stress drop and source scaling of the 2019 Ridgecrest, California, earthquake sequence. Bull. Seismol. Soc. Am. 110 (4), 1859–1871. doi:10.1785/0120200009

CrossRef Full Text | Google Scholar

Waldhauser, F., and Ellsworth, W. L. (2000). A double-difference earthquake location algorithm: Method and application to the northern Hayward fault, California. Bull. Seismol. Soc. Am., 90(6), 1353–1368. doi:10.1785/0120000006

CrossRef Full Text | Google Scholar

Wang, J., Xiao, Z., Liu, C., Zhao, D., and Yao, Z. (2019). Deep learning for picking seismic arrival times. J. Geophys Res. 124 (7), 6612–6624. doi:10.1029/2019JB017536

CrossRef Full Text | Google Scholar

Wang, M., and Shen, Z.-K. (2020). Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys Res. 125 (2), e2019JB018774. doi:10.1029/2019JB018774

CrossRef Full Text | Google Scholar

Wang, W. L., Fang, L. H., Wu, J. P., Tu, H. W., Chen, L. Y., Lai, G. J., et al. (2021a). Aftershock sequence relocation of the 2021 M(S)7.4 Maduo earthquake, Qinghai, China. Sci. China-Earth Sci. 64 (8), 1371–1380. doi:10.1007/s11430-021-9803-3

CrossRef Full Text | Google Scholar

Wang, Y., Hu, S., He, X., Guo, K., Xie, M., Deng, S., et al. (2021b). Relocation and focal mechanism solutions of the 21 May 2021 MS6.4 Yunnan Yangbi earthquake sequence. Chin. J. Geophys. Chin. 64 (12), 4501–4525. doi:10.6038/cjg2021P0401

CrossRef Full Text | Google Scholar

Wang, Z., Su, J., Liu, C., and Cai, X. (2015). New insights into the generation of the 2013 lushan earthquake (M_s7.0), China. J. Geophys Res. 120 (5), 3507–3526. doi:10.1002/2014jb011692

CrossRef Full Text | Google Scholar

Weng, H., and Yang, H. (2018). Constraining frictional properties on fault by dynamic rupture simulations and near-field observations. J. Geophys Res. 123 (8), 6658–6670. doi:10.1029/2017JB015414

CrossRef Full Text | Google Scholar

Xin, H., Zhang, H., Kang, M., He, R., Gao, L., and Gao, J. (2018). High-resolution lithospheric velocity structure of continental China by double-difference seismic travel-time tomography. Seismol. Res. Lett. 90 (1), 229–241. doi:10.1785/0220180209

CrossRef Full Text | Google Scholar

Xu, Z., Liang, S., Zhang, G., Liang, J., Zou, L., Li, X., et al. (2021). Analysis of seismogenic structure of Madoi, Qinghai M(s)7. 4 earthquake on May 22, 2021. Chin. J. Geophys (in Chin. 64 (8), 2657–2670. doi:10.6038/cjg2021P0390

CrossRef Full Text | Google Scholar

Yamada, T., Okubo, P. G., and Wolfe, C. J. (2010). Kiholo Bay, Hawai'i, earthquake sequence of 2006: Relationship of the main shock slip with locations and source parameters of aftershocks. J. Geophys Res. 115, B08304. doi:10.1029/2009jb006657

CrossRef Full Text | Google Scholar

Yao, S., and Yang, H. (2020). Rupture dynamics of the 2012 nicoya M_w 7.6 earthquake: Evidence for low strength on the megathrust. Geophys Res. Lett. 47 (13), e2020GL087508. doi:10.1029/2020GL087508

CrossRef Full Text | Google Scholar

Yin, A., and Harrison, T. M. (2000). Geologic evolution of the Himalayan-Tibetan orogen. Annu. Rev. Earth Planet Sci. 28, 211–280. doi:10.1146/annurev.earth.28.1.211

CrossRef Full Text | Google Scholar

Yue, H., Shen, Z.-K., Zhao, Z., Wang, T., Cao, B., Li, Z., et al. (2022). Rupture process of the 2021 M7.4 Maduo earthquake and implication for deformation mode of the Songpan-Ganzi terrane in Tibetan Plateau. Proc. Natl. Acad. Sci., 119(23), e2116445119. doi:10.1073/pnas.2116445119

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J. Y., Wang, X., Chen, L., and Liu, J. (2022a). Seismotectonics and fault geometries of the Qinghai Madoi M(s)7. 4 earthquake sequence: Insight from aftershock relocations and focal mechanism solutions. Chin. J. Geophys (in Chin. 65 (2), 552–562. doi:10.6038/cjg2022P0516

CrossRef Full Text | Google Scholar

Zhang, P. Z., Wen, X. Z., Shen, Z. K., and Chen, J. H. (2010). “Oblique, high-angle, listric-reverse faulting and associated development of strain: The Wenchnan earthquake of May 12, 2008, Sichuan, China,” in Annu. Rev. Earth Planet. Sci. Editors R. Jeanloz, and K. H. Freeman (Palo Alto: Annual Reviews), 3838, 353.

CrossRef Full Text | Google Scholar

Zhang, X., Feng, W., Du, H., Samsonov, S., and Yi, L. (2022b). Supershear rupture during the 2021 MW 7.4 Maduo, China, earthquake. Geophys Res. Lett. 49 (6), e2022GL097984. doi:10.1029/2022GL097984

CrossRef Full Text | Google Scholar

Zhang, Y., An, Y., Long, F., Zhu, G., Qin, M., Zhong, Y., et al. (2021). Short-term foreshock and aftershock patterns of the 2021 Ms 6.4 Yangbi earthquake sequence. Seismol. Res. Lett. 93, 21–32. doi:10.1785/0220210154

CrossRef Full Text | Google Scholar

Zhao, L. F., Xie, X. B., He, J. K., Tian, X. B., and Yao, Z. X. (2013a). Crustal flow pattern beneath the Tibetan Plateau constrained by regional Lg-wave Q tomography. Earth Planet Sci. Lett. 383, 113–122. doi:10.1016/j.epsl.2013.09.038

CrossRef Full Text | Google Scholar

Zhao, L. F., and Xie, X. B. (2016). Strong Lg-wave attenuation in the Middle East continental collision orogenic belt. Tectonophysics 674, 135–146. doi:10.1016/j.tecto.2016.02.025

CrossRef Full Text | Google Scholar

Zhao, L. F., Xie, X. B., Wang, W. M., Zhang, J. H., and Yao, Z. X. (2013b). Crustal Lg attenuation within the north China craton and its surrounding regions. Geophys J. Int. 195 (1), 513–531. doi:10.1093/gji/ggt235

CrossRef Full Text | Google Scholar

Zhao, L. F., Xie, X. B., Wang, W. M., Zhang, J. H., and Yao, Z. X. (2010). Seismic lg-wave Q tomography in and around northeast China. J. Geophys Res. 115 (B08), B08307. doi:10.1029/2009jb007157

CrossRef Full Text | Google Scholar

Zheng, G., Wang, H., Wright, T. J., Lou, Y., Zhang, R., Zhang, W., et al. (2017). Crustal deformation in the India-Eurasia collision zone from 25 years of GPS measurements. J. Geophys Res. 122 (11), 9290–9312. doi:10.1002/2017jb014465

CrossRef Full Text | Google Scholar

Zhu, G., Yang, H., Tan, Y. J., Jin, M., Li, X., and Yang, W. (2022). The cascading foreshock sequence of the Ms 6.4 Yangbi earthquake in Yunnan, China. Earth Planet Sci. Lett. 591, 117594. doi:10.1016/j.epsl.2022.117594

CrossRef Full Text | Google Scholar